Теория по геометрии 7 класс
Теория по геометрии 7 класс
Основные понятия
Теорема — утверждение, которое доказывается путем рассуждений. Доказательство — сами рассуждения.
Определение — предложение, в котором разъясняется смысл того или иного выражения или названия.
Аксиома или постулат — исходное положение, принимаемое без доказательств и лежащее в основе доказательств истинности других положений (предложение, не требующее доказательств; самоочевидный факт).
Аксиомы геометрии можно разбить на пять групп.
1. Аксиомы принадлежности
1.1 Какова бы ни была прямая, существуют точки, принадлежащие ей и не принадлежащие ей.
1.2 Через любые две точки можно провести прямую и притом только одну.
1.3 Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости и точки, не принадлежащие ей.
2. Аксиомы расположения
2.1 Из трех точек на прямой одна и только одна лежит между двумя другими.
2.2 Прямая разбивает плоскость на две полуплоскости.
2.3 Если две различные прямые имеют общую точку, то через них можно провести плоскость и притом только одну.
2.4 Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
3. Аксиомы измерения
3.1 Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
3.2 Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен . Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
4. Аксиомы откладывания.
4.1 На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины и притом только один.
4.2 От любой полупрямой в заданную полуплоскость можно отложить угол, с заданной градусной мерой, меньшей и притом только один.
4.3 Каков бы ни был треугольник, существует треугольник, равный ему, в заданном расположении относительно данной полупрямой.
5. Аксиома параллельности.
5.1 Через точку, не лежащую на данной прямой можно провести не более одной прямой, параллельной данной. (аксиома параллельных прямых).
Начальные геометрические сведения
Смежные углы — это углы, у которых одна сторона — общая, а другие стороны лежат на одной прямой. Сумма смежных углов равна 180º.
Вертикальные углы — это пары углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого. Вертикальные углы равны.
Перпендикулярные прямые — это прямые, при пересечении которых образуются четыре прямых угла.
Две прямые, перпендикулярные к третьей прямой, не пересекаются.
Треугольники
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Точки — вершины, отрезки — стороны. Элементы треугольника: углы и стороны.
Периметр треугольника— сумма длин всех сторон.
Если два треугольника равны, то соответственные элементы таких треугольников тоже равны.
Против соответственно равных сторон лежат соответственно равные углы и наоборот, против равных углов лежат соответственно равные стороны.
Признаки равенства треугольников
Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и прилежащим к ней углам другого треугольника то такие треугольники равны.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Перпендикуляр к прямой — отрезок, проведенный из точки к прямой под углом 90 градусов.
Из точки, не лежащей на данной прямой, можно провести перпендикуляр к этой прямой, и при том только один.
Медиана треугольника — отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса треугольника — это отрезок биссектрисы угла треугольника, проведенной из данной вершины, соединяющий эту вершину с точкой на противолежащей стороне.
Высота треугольника — перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противолежащую сторону.
В любом треугольнике:
-
медианты пересекаются в одной точке;
-
биссектрисы пересекаются в одной точке;
-
высоты пересекаются в одной точке.
Равнобедренный треугольник — треугольник, у которого две стороны равны.Равные стороны — боковые стороны, третья сторона — основание.
Свойства:
1.В равнобедренном треугольнике углы при основании равны.
2.В равнобедренном треугольнике высота, проведенная к основанию является биссектрисой и медианой (медиана является высотой и биссектрисой; биссектриса является высотой и медианой).
Признак равнобедренного треугольника: если в треугольнике два угла равны, то такой треугольник равнобедренный.
Равносторонний треугольник — треугольник, у которого все стороны равны.
Свойства:
1. В равностороннем треугольнике все углы равны по 60 градусов.
2. В равностороннем треугольнике все медианы — высоты и биссектрисы.
Признак: если в треугольнике все углы равны, то он равносторонний.
В треугольнике: 1) против большей стороны лежит больший угол; 2) против большего угла лежит большая сторона, и наоборот.
Неравенство треугольника: каждая сторона треугольника меньше суммы двух других сторон.
Сумма углов треугольника равна .
Внешний угол треугольника — угол, смежный с каким-нибудь внутренним углом треугольника.
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Виды треугольников :
Остроугольный — треугольник, у которого все углы острые.
Тупоугольный — треугольник, у которого один угол тупой.
Прямоугольный — треугольник, у которого один угол прямой (сторона, лежащая напротив угла в 90 градусов, называется гипотенузой; стороны, образующие угол в 90 градусов, называются катетами). В прямоугольном треугольнике гипотенуза больше катета.
Свойства:
1. Катет, лежащий напротив угла в равен половине гипотенузы.
2. Сумма острых углов прямоугольного треугольника равна 90°.
3. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий напротив этого катета, равен .
Окружность
Окружность — геометрическая фигура, состоящая их всех точек плоскости, равноудаленных от заданной точки, называемой центром окружности.
Радиус — отрезок, соединяющий центр окружности и точку на окружности.
Хорда — отрезок, соединяющий две точки на окружности.
Диаметр — хорда, проходящая через центр окружности.
Дуга окружности — часть окружности, ограниченная двумя точками.
Круг — часть плоскости, ограниченная окружностью.
Сектор — это часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги. Сектор, образованный радиусами, расположенными под углом в 90° называется квадрантом.
Параллельные прямые
Параллельные прямые — две прямые на плоскости, которые не пересекаются (не имеют общих точек).
Углы:
Образованы пересечением двух прямых и секущей
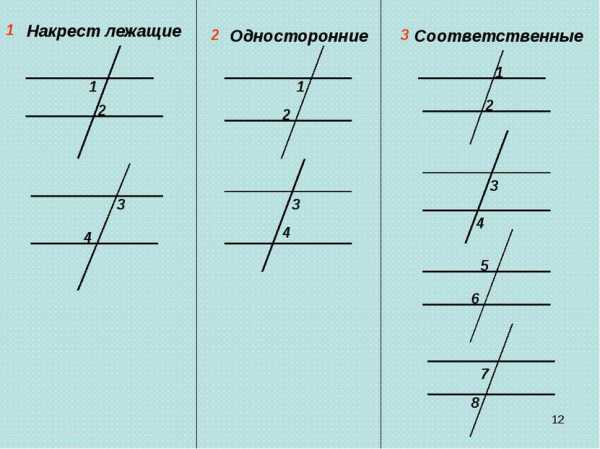
Накрест лежащие
При пересечении двух параллельных прямых секущей накрест лежащие углы равны.
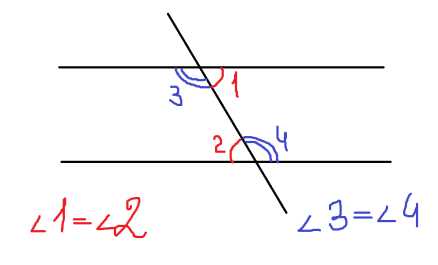
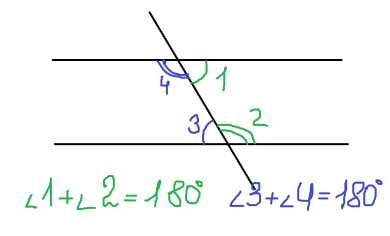
Односторонние
При пересечении двух параллельных прямых секущей сумма односторонних углов равна 180.
Соответственные
При пересечении двух параллельных прямых секущей соответственные углы равны.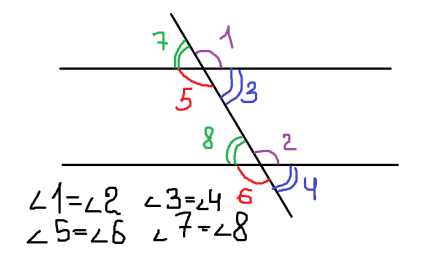
Признаки параллельности двух прямых:
1. Если при пересечении двух прямых третьей накрест лежащие(внутренние или внешние) углы равны, то такие прямые параллельны.
2. Если при пересечении двух прямых третьей соответственные углы равны, то прямые параллельны.
3. Если при пересечении двух прямых третьей сумма односторонних (внутренних или внешних) углов равна , то прямые параллельны.
Аксиома параллельных прямых: Через точку, не лежащую на данной прямой можно провести не более одной прямой, параллельной данной.
Следствия из аксиомы параллельных прямых:
1. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
2.Если две прямые параллельны третьей прямой, то они параллельны.
Теоремы об углах, образованных двумя параллельными прямыми и секущей
-
Если две параллельные прямые пересечены секущей, накрест лежащие углы равны.
-
Если две параллельные прямые пересечены секущей, то соответственные углы равны.
-
Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.
Следствие: Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.
Расстояние от точки до прямой — это перпендикуляр, проведенный из данной точки к данной прямой. Любая другая прямая, отличная от перпендикуляра, называется наклонной. Любая наклонная больше перпендикуляра. Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
infourok.ru
Теория по геометрии 7 класс. Вопросы и ответы
Геометрия.
Аксиома.
3 аксиомы планиметрии о взаимном расположении точек и прямых.
IV аксиома планиметрии о трех точках прямой.
V аксиома планиметрии о точке прямой.
VI аксиома планиметрии о прямой на плоскости.
Отрезок.
Луч.
Угол.
Развернутый угол.
Равные фигуры.
Середина отрезка.
Биссектриса угла.
Измерение отрезков.
Свойства измерения отрезков.
Измерение углов.
Свойства измерения углов.
Прямой угол.
Острый угол.
Тупой угол.
Смежные углы.
Свойство смежных углов.
Вертикальные углы.
Свойство вертикальных углов.
Перпендикулярные прямые.
Свойство перпендикулярных прямых.
Треугольник.
Периметр треугольника.
Равные треугольники.
Теорема, доказательство теоремы.
Первый признак равенства треугольников.
Второй признак равенства треугольников.
Третий признак равенства треугольников.
Теорема о единственности опущенного перпендикуляра.
Медиана треугольника.
Биссектриса треугольника.
Высота треугольника.
Свойство о пересечении медиан, биссектрис и высот треугольников.
Равнобедренный треугольник.
Равносторонний треугольник.
Свойства равнобедренного треугольника.
Определение.
Определение окружности.
Хорда окружности.
Диаметр окружности.
Дуга окружности.
Круг.
Определение параллельных прямых.
Параллельные отрезки.
Секущая.
Углы при параллельных прямых и секущей.
3 признака параллельности двух прямых.
Аксиома параллельных прямых.
2 следствия из аксиомы параллельных прямых.
Обратная теорема.
Свойства параллельных прямых.
Свойство прямой, перпендикулярной к одной из двух параллельных прямых.
Сумма углов треугольника.
Внешний угол треугольника.
Свойства внешнего угла треугольника.
Виды треугольников.
Элементы прямоугольного треугольника.
Теорема о соотношениях между сторонами и углами треугольника.
2 следствия из теоремы о соотношениях между сторонами и углами треугольника.
Неравенства треугольника.
Свойства прямоугольных треугольников.
Признаки равенства прямоугольных треугольников.
Свойство двух параллельных прямых о равноудаленности точек.
Расстояние между параллельными прямыми.
Замечательные точки треугольника.
А2: Имеются по крайней мере 3 точки, не лежащие на одной прямой.
А3: Через любые 2 точки проходит прямая, и притом только одна.
А4: Из трех точек прямой одна и только одна лежит между двумя другими.
А5: Каждая точка О прямой разделяет её на 2 части (два луча) так, что любые две точки одного и того же луча лежат по одну сторону от точки О, а любые две точки разных лучей лежат по разные стороны от точки О.
А6: Каждая прямая а разделяет плоскость на две части (две полуплоскости) так, что любые две точки одной и той же полуплоскости лежат по одну сторону от прямой а, а любые две точки разных полуплоскостей лежат по разные стороны от прямой а.
Отрезок – это часть прямой, ограниченная двумя точками. Точки, ограничивающие отрезок, называются его концами. Отрезок обозначается двумя заглавными латинскими буквами. Например, АВ или ВА.
Луч – это часть прямой, ограниченная одной точкой. Эта точка называется началом луча. Луч обозначается двумя заглавными латинскими буквами или одной строчной латинской буквой. Например, луч АВ или луч m.
Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а их общее начало – вершиной угла. Угол обозначается тремя заглавными латинскими буквами или одной заглавной латинской буквой или двумя строчными латинскими буквами. Например, 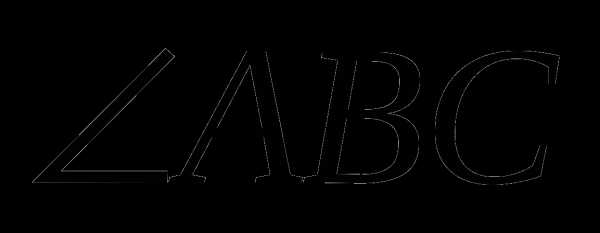 или
или или
или  .
.
Угол называется развернутым, если обе его стороны лежат на одной прямой.
Две геометрические фигуры называются равными, если их можно совместить наложением.
Середина отрезка – это точка отрезка, делящая его пополам, т.е. на два равных отрезка.
Биссектриса угла – это луч, исходящий из вершины угла и делящий его на два равных угла.
Измерение отрезков. Выбрав единицу измерения, можно измерить любой отрезок, т.е. выразить его длину некоторым положительным числом.
Свойства измерения отрезков. 1) Равные отрезки имеют равные длины. 3) Меньший отрезок имеет меньшую длину. 3) Когда точка делит отрезок на два отрезка, длина всего отрезка равна сумме длин этих двух отрезков.
Измерение углов. Градусной мерой угла называется положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле.
Свойства измерения углов. 1) Равные углы имеют равные градусные меры.2) Меньший угол имеет меньшую градусную меру. 3) Развернутый угол равен 180 градусам. 4Неразвернутый угол меньше 180 градусов. 5) Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.
Прямой угол – угол, градусная мера которого равна 90 градусов.
Острый угол – угол, градусная мера которого меньше 90 градусов.
Тупой угол – угол, градусная мера которого больше 90 градусов, но меньше 180 градусов.
Смежные углы – два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой.
Свойство смежных углов. Сумма смежных углов равна 180 градусов.
Вертикальные углы. Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
Свойство вертикальных углов. Вертикальные углы равны.
Перпендикулярные прямые. Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.
Свойство перпендикулярных прямых. Две прямые, перпендикулярные к третьей, не пересекаются.
Треугольник – геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, соединенных отрезками. Три точки называются вершинами, а отрезки – сторонами треугольника.
Периметр треугольника – это сумма длин трех сторон треугольника.
Равные треугольники – треугольники, которые при наложении совмещаются. Если два треугольника равны, то элементы одного треугольника соответственно равны элементам другого треугольника.
Теорема, доказательство теоремы. Утверждение, справедливость которого устанавливается путем рассуждения, называется теоремой, а сами рассуждения называются доказательством теоремы.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.
Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
В любом треугольнике медианы пересекаются в одной точке, биссектрисы пересекаются в одной точке, высоты или их продолжения также пересекаются в одной точке.
Треугольник называется равнобедренным, если его две стороны равны. Эти стороны называются боковыми, а третья – основанием.
Треугольник, все стороны которого равны, называется равносторонним.
В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Предложение, в котором разъясняется смысл того или иного выражения или названия, называется определением.
Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки. Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, - радиусом окружности.
Отрезок, соединяющий две точки окружности, называется её хордой.
Хорда, проходящая через центр окружности, называется диаметром.
Часть окружности, ограниченная двумя точками, называется дугой окружности.
Часть плоскости, ограниченная окружностью, называется кругом.
Две прямые на плоскости называются параллельными, если они не пересекаются.
Два отрезка называются параллельными, если они лежат на параллельных прямых.
Прямая с называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.
Углы при параллельных прямых и секущей:
2)Если две прямые параллельны третьей прямой, то они параллельны.
2) обратно, против большего угла лежит большая сторона.
multiurok.ru
Определения и теоремы геометрия 7 класс
Геометрия 7 класс
Определения
Отрезок-часть прямой, ограниченная двумя точками.
Концы отрезка-точки, ограничивающие прямую.
Луч-прямая, имеющая начало в точке, но не имеющая конца.
Угол-геометрическая фигура, состоящая из точки и двух лучей, исходящих из этой точки.
Стороны угла-лучи, составляющие угол.
Вершина угла-точка, из которой берут начало стороны угла.
Развернутый угол, если обе его стороны лежат на одной прямой.
Середина отрезка-точка, делящая отрезок пополам.
Прямой угол=900. Острый угол<900. 1800>Тупой угол>900.
Смежные-два угла, у которых одна сторона общая, а две другие-это продолжения друг друга.
Вертикальные-два угла, если стороны одного угла-это продолжение сторон другого.
Перпендикулярные-две пересекающиеся прямые, образующие четыре прямых угла.
Периметр-сумма длин всех сторон фигуры.
Перпендикуляр АН-отрезок, соединяющий точку А с точкой Н, лежащей на прямой. Этот отрезок с прямой образует прямой угол.
Биссектриса-луч, исходящий из вершины угла и делящий его на два равных угла.
Медиана-отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
Высота-перпендикуляр, проведенный из вершины угла к прямой, содержащей противолежащую сторону.
Равнобедренный треугольник, если две его стороны равны.
Окружность-геометрическая фигура, состоящая из множества точек, которые находятся на одинаковом расстоянии от одной единственной точки-центр окружности.
Радиус r — отрезок, соединяющий центр окружности с любой точкой, лежащей на этой окружности.
Хорда-отрезок, соединяющий две точки, лежащие на окружности.
Диаметр-хорда, проходящая через центр окружности.
Дуга-часть окружности, полученная делением этой окружности двумя точками.
Параллельные прямые-две не пересекающиеся на плоскости прямые.
Параллельные отрезки, если они лежат на параллельных прямых.
Секущая к двум прямым-прямая, пересекающая данные прямые в двух точках.
Гипотенуза-сторона прямоугольного треугольника, лежащая напротив прямого угла. Две другие стороны прямоугольного треугольника-катеты.
Неравенства треугольника: АВ<АС+СВ, АС<АВ+ВС, ВС<ВА+АС.
Расстояние от точки до прямой-длина перпендикуляра, проведенного из точки к прямой.
Расстояние между прямыми-расстояние от любой точки одной из параллельных прямых до другой прямой.
Правила и теоремы
-
Через любые две точки можно провести только одну прямую.
-
Две прямые имеют либо одну общую точку, либо ни одной.
-
Две геометрические фигуры называются равными, если их можно совместить наложением.
-
Равные отрезки имеют равные длины.
-
Сумма смежных углов равна 1800.
-
Вертикальные углы равны.
-
Развернутый угол равен 1800. Неразвернутый меньше 1800.
-
Две прямые, перпендикулярные к третьей, не пересекаются.
-
Признаки равенства треугольников:
Теорема 1 (по двум сторонам и углу). Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.
Теорема 2 (по стороне и двум углам). Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то эти треугольники равны.
Теорема 3 (по трём сторонам). Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то эти треугольники равны.
2.2.Теорема (о перпендикуляре к прямой). Из точки, не лежащей на прямой, можно провести только один перпендикуляр к этой прямой.
2.3. Медиана делит сторону на два равных отрезка.
2.4. Свойства равнобедренного треугольника:
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Теорема 2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
3.1. Признаки параллельности двух прямых (обратные теоремы тоже справедливы):
Теорема 1. Если при пересечении двух прямых секущей накрест лежащие углы равны, то данные прямые параллельны.
Теорема 2. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Теорема 3. Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то прямые параллельны.
3.2. Аксиома параллельных прямых. Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Следствия из аксиомы:
10. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
20. Если две прямые параллельны третьей, то все три прямые параллельны.
4.1. Теорема (о сумме углов треугольника). Сумма углов треугольника равно 1800.
4.2. В любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.
4.5. Теорема (о соотношении между сторонами и углами треугольника). В треугольнике против большей стороны лежит больший угол и против большего угла лежит большая сторона.
Следствия из теоремы:
10. В прямоугольном треугольнике гипотенуза больше катета.
20. Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).
4.6. Каждая сторона треугольника меньше суммы двух других сторон.
4.7. Свойства прямоугольного треугольника:
10. Сумма двух острых углов прямоугольного треугольника равна 900.
20. Катет прямоугольного треугольника, лежащий напротив угла в 300, равен половине гипотенузы.
30. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий напротив этого катета, равен 300.
4.8. Признаки равенства прямоугольных треугольников:
1. Если катеты одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то эти треугольники равны.
2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему углу другого треугольника, то эти треугольники равны.
Теорема 1. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузы и острому углу другого прямоугольного треугольника, то эти треугольники равны.
Теорема 2. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
4.9. Угол падения равен углу отражения.
4.10. Теорема. Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
infourok.ru
Теория по геометрии за 7 класс по учебнику Л.С. Атанасяна
Теория по геометрии за 7 класс по учебнику Л.С. Атанасяна
Доступные файлы (1):
n1.docx
Геометрия, теория 7 класс. Составила Аверкова Т.Е.
7 класс1
Аксиома: через любые две точки можно провести прямую, и притом только одну.
Поэтому: две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Угол — это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а их общее начало — вершиной угла.
Любой угол разделяет плоскость на две части. Если угол неразвернутый, то одна из частей называется внутренней, а другая — внешней областью этого угла.
Если угол развернутый, то любую из двух частей, на которые он разделяет плоскость, можно считать внутренней областью угла. Фигуру, состоящую из угла и его внутренней области, также называют углом.
Две геометрические фигуры называются равными, если их можно совместить наложением.
Точка отрезка, делящая его пополам, т. е. на два равных отрезка, называется серединой отрезка.
Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла.
Измерение отрезков основано на сравнении их с некоторым отрезком, принятым за единицу измерения (его называют также масштабным отрезком).
За единицу измерения можно принимать не только сантиметр, но и любой другой отрезок. Выбрав единицу измерения, можно измерить любой отрезок, т. е. выразить его длину некоторым положительным числом. Это число показывает, сколько раз единица измерения и ее части укладываются в измеряемом отрезке.
Если два отрезка равны, то единица измерения и ее части укладываются в этих отрезках одинаковое число раз, т. е. равные отрезки имеют равные длины. Если же один отрезок меньше другого, то единица измерения (или ее часть) укладывается в этом отрезке меньшее число раз, чем в другом, т. е. меньший отрезок имеет меньшую длину.
Когда точка делит отрезок на два отрезка, длина всего отрезка равна сумме длин этих двух отрезков.
Обычно за единицу измерения углов принимают градус — угол, равный -1/180 части развернутого угла.
Равные углы имеют равные градусные меры.
Меньший угол имеет меньшую градусную меру.
Развернутый угол равен 180°.
Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.
Угол называется прямым, если он равен 90°, острым, если он меньше 90°, т. е. меньше прямого угла, тупым, если он больше 90°, но меньше 180°, т. е. больше прямого, но меньше развернутого угла
Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными.
Сумма смежных углов равна 180°.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
Вертикальные углы равны.
Две пересекающиеся прямые называются перпендикулярными (или взаимно перпендикулярными), если они образуют четыре прямых угла.
Две прямые, перпендикулярные к третьей, не пересекаются.
Сумма длин трех сторон треугольника называется его периметром.
Признаки равенства треугольников:
- Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
- Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
- Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки. Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, — радиусом окружности.
Отрезок, соединяющий две точки окружности, называется ее хордой. Хорда, проходящая через центр окружности, называется диаметром. Часть плоскости, ограниченная окружностью, называется кругом.
Рассмотрим прямую а и точку А, не лежащую на этой прямой. Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.
Теорема: Из точки, не лежащей на прямой, можно провести перпендикуляр и только один.
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.
Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
В любом треугольнике медианы, высоты и биссектрисы пересекаются в одной точке.
Треугольник называется равнобедренным, если две его стороны равны.
Равные стороны называются боковыми сторонами, а третья сторона — основанием равнобедренного треугольника.
Треугольник, все стороны которого равны, называется равносторонним.
Теорема: В равнобедренном треугольнике углы при основании равны.
Теорема: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Две прямые на плоскости называются параллельными, если они не пересекаются.
Признаки параллельности:
- Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
- Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
- Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
Аксиомы:
- через любые две точки проходит прямая, и притом только одна.
- на любом луче от его начала можно отложить отрезок, равный данному, и притом только один.
- от любого луча в заданную сторону можно отложить угол, равный данному неразвернутому углу, и притом только один.
- Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Следствия из аксиом:
- Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
- Если две прямые параллельны третьей прямой, то они параллельны.
Обратные теоремы:
- Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
- Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.
- Если две параллельные прямые пересечены секущей, то соответственные углы равны.
- Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.
Сумма углов треугольника равна 180°.
Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
В любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.
Если все три угла треугольника острые, то треугольник называется остроугольным.
Если один из углов треугольника тупой, то треугольник называется тупоугольным.
Если один из углов треугольника прямой, то треугольник называется прямоугольным. Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две другие стороны — катетами.
Теорема: В треугольнике: 1) против большей стороны лежит больший угол; 2) обратно, против большего угла лежит большая сторона.
Следствие 1: В прямоугольном треугольнике гипотенуза больше катета.
Следствие 2: Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).
Теорема о неравенстве треугольника: Каждая сторона треугольника меньше суммы двух других сторон.
Следствие: Для любых трех точек А, В и С, не лежащих на одной прямой, справедливы неравенства: АВ
Некоторые свойства прямоугольных треугольников:
- Сумма двух острых углов прямоугольного треугольника равна 90°.
- Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
- Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.
Признаки равенства прямоугольных треугольников:
- Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
- Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
- Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
- Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
Перпендикуляр, проведенный из точки к прямой, меньше любой наклонной, проведенной из той же точки к этой прямой.
Длина перпендикуляра, проведенного из точки к прямой, называется расстоянием от этой точки до прямой.
Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
Расстояние от произвольной точки одной из параллельных прямых до другой прямой называется расстоянием между этими прямыми.
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.
perviydoc.ru
Геометрия 7-9 классы
Геометрия 7-9 классы
5. Измерение углов
7. Первый признак равенства треугольников
8. Медианы, биссектрисы и высоты треугольника
9. Второй и третий признаки равенства треугольников
10. Задачи на построение
11. Признаки параллельности двух прямых
12. Аксиома параллельных прямых
13. Сумма углов треугольника
14. Соотношение между сторонами и углами треугольника
15. Прямоугольные треугольники
16. Построение треугольника по трем элементам
17. Многоугольники
18. Параллелограмм и трапеция
19. Прямоугольник, ромб, квадрат
34. Многоугольники
35. Параллелограмм и трапеция
36. Прямоугольник, ромб, квадрат
20. Площадь многоугольника
21. Площади параллелограмма, треугольника и трапеции
22. Теорема Пифагора
37. Площадь многоугольника
38. Площадь Параллелограмм, треугольника, трапеции
39. Теорема Пифагора
23. Определение подобных треугольников
24. Признаки подобия треугольников
25. Применение подобия к доказательству теорем и решению задач
26. Соотношения между сторонами и углами прямоугольного треугольника
40. Определение подобных треугольников
41. Признаки подобия треугольников
42. Применение подобия к доказательству теорем и решению задач
27. Касательная к окружности
28. Центральные и вписанные углы
29. Четыре замечательные точки треугольника
30. Вписанная и описанная окружности
44. Касательная к окружности
45. Центральные и вписанные углы
46. Четыре замечательные точки треугольника
47. Вписанная и описанная окружность
31. Понятие вектора
32. Сложение и вычитание векторов
33. Умножение вектора на число. Применение векторов к решению задач
48. Понятие вектора
49. Сложение и вычитание векторов
50. Умножение вектора на число. Применение векторов к решению задач
51. Координаты вектор
52. Простейшие задачи в координата
53. Уравнения окружности и прямой
54. Синус, косинус и тангенс угла
55. Соотношения между сторонами и углами треугольника
56. Скалярное произведение векторов
58 Длина окружности и площадь круга
59. Понятие движения
60. Параллельный перенос и поворот
61. Многогранники
62. Тела и поверхности вращения
specclass.ru
Презентация к уроку по геометрии (7 класс) по теме: Теоретические тетради по геометрии
Слайд 1
Геометрия. Теоретическая тетрадь. 7 класс
Слайд 2
Начальные Геометрические сведения
Слайд 3
Геометрия Геометрия изучает: форму размер взаимное расположение объектов. Геометрическая фигура – это мысленный образ объектов, лишённый всех свойств, кроме формы и размеров.
Слайд 4
Введение нового объекта Изобразить Определить Обозначить Написать
Слайд 5
Простейшие фигуры планиметрии а А Прямая а (.) А
Слайд 6
Взаимное расположение прямой и точки а с В А В а А с
Слайд 7
Взаимное расположение двух прямых а m n с В О: пересекающимися О: параллельными прямыми прямыми называются две прямые, называются две прямые, лежащие имеющие общую точку. в одной плоскости и не имеющие общих точек а с =В m n
Слайд 8
Аксиомы планиметрии Каждой прямой принадлежат по крайней мере две точки Имеются по крайней мере три точки, не лежащие на одной прямой Через любые две точки проходит прямая, и притом только одна.
Слайд 9
Отрезок F T Отрезок FT О: Отрезком называется часть прямой, ограниченная двумя точками.
Слайд 10
луч F T Луч FT О: Лучом называется часть прямой, ограниченная одной точкой.
Слайд 11
Угол А стороны В вершина
Слайд 12
Развёрнутый угол A B C
Слайд 13
Сравнение фигур О: равными фигурами называются фигуры, которые можно совместить наложением.
Слайд 14
Середина отрезка F О T О — середина FT О: Серединой отрезка называется точка, которая делит отрезок на два равных отрезка.
Слайд 15
Биссектриса угла К А М С АМ- биссектриса
Слайд 16
Длина отрезка Свойства длин отрезков 1. Равные отрезки имеют равные длины. Если отрезки имеют равные длины, то они равны. 2. Меньший отрезок имеет меньшую длину. Если отрезок имеет меньшую длину, то он меньше. 3. Если точка делит отрезок на две части, то его длина равна сумме длин его частей.
Слайд 17
Градусная мера угла Градус – это угол, равный части развёрнутого угла Свойства градусных мер углов 1. Равные углы имеют равные град. меры. Если углы имеют равные град. меры, то они равны. 2. Меньший угол имеет меньшую град. меру. Если угол имеет меньшую град. меру, то он меньше. 3. Если луч делит угол на две части, то его град. мера равна сумме град. мер его частей.
Слайд 18
Классификация углов Неразвернутые углы Развёрнутые углы Острые углы Тупые углы О: Острым углом называется О: Тупым углом называется угол, град. мера которого угол, град. мера которого меньше 90˚. больше 90˚, но меньше 180˚. Прямые углы О: Прямым углом называется угол, град. мера которого равна 90˚.
Слайд 19
Смежные углы О: Смежными углами называются два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой.
Слайд 20
Теорема — это утверждение с доказательством. Состоит: Формулировка Рисунок Дано Доказать Доказательство
Слайд 21
Свойство смежных углов Т: Сумма градусных мер смежных углов равна 180˚. Дано:
Слайд 22
Вертикальные углы О: Вертикальными углами называются два угла, если стороны одного являются продолжениями сторон другого.
Слайд 23
Свойство вертикальных углов Т: Вертикальные углы равны. Дано:
Слайд 24
Перпендикулярные прямые О: Перпендикулярными прямыми называются две пересекающиеся прямые, если они образуют четыре прямых угла. а ┴ в а в
Слайд 25
Треугольники
Слайд 26
Треугольник А В С О: Треугольником называется геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой и отрезков их соединяющих. ∆ СВА Вершины: А, В, С Стороны: АВ,ВС, СА Углы:
Слайд 27
Равные треугольники О: см. определение равных фигур. Свойство равных треугольников: В равных треугольниках против соответственно равных сторон лежат равные углы и против равных углов лежат равные стороны А М О С Р В ∆ АОС=∆ РВМ АО=МР
Слайд 28
Первый признак равенства треугольников Т: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. А М О С Р В Дано: ∆ АОС и ∆ РВМ, АО=МР, ОС=РВ
Слайд 29
Перпендикуляр к прямой О: конструктивное. Рассмотрим прямую а и точку А, не лежащую на ней. Проведём через точку А прямую, перпендикулярную прямой а. Обозначим точку пересечения этой прямой с прямой а — Н. Отрезок АН называется перпендикуляром, проведённым из точки А к прямой а. А а Н Теорема существования и единственности перпендикуляра к прямой: Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один. Основание перпендикуляра
Слайд 30
Отрезки в треугольнике медиана треугольника А В С М О: Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны. АМ – медиана ∆ АВС
Слайд 31
Отрезки в треугольнике Биссектриса треугольника А В С М О: Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. АМ – биссектриса ∆ АВС
Слайд 32
Отрезки в треугольнике Высота треугольника А В М С О: Высотой треугольника называется перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону . АМ – высота ∆АВС А М В С
Слайд 33
Равнобедренный треугольник А В С О: Равнобедренным треугольником называется треугольник, у которого две стороны равны. ∆ СВА — равнобедренный АВ=АС – боковые стороны ВС — основание
Слайд 34
Свойства равнобедренного треугольника А 1 2 В М С Т: в равнобедренном треугольнике углы при основании равны. Дано: ∆ АВС- равнобедренный ВС – основание Доказать:
Слайд 35
Свойства равнобедренного треугольника А 1 2 3 4 В М С Т: в равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой. Дано: ∆ АВС- равнобедренный ВС – основание, АМ- биссектриса Доказать: АМ- медиана и высота. Доказательство: Рассмотрим ∆АВМ и ∆АМС АМ- общая АВ=ВС(по опр.р.т.)
Слайд 36
Свойства равнобедренного треугольника Т: высота равнобедренного треугольника, проведённая к основанию, является медианой и биссектрисой Т: Медиана равнобедренного треугольника, проведённая к основанию, является высотой и биссектрисой
Слайд 37
Второй признак равенства треугольников Т: если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. А М О С Р В ОС=РВ
Слайд 38
Третий признак равенства треугольников Т: если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны. А М О С Р В ОС=РВ АО=МР АС=МВ ∆ АОС=∆ РВМ
Слайд 39
Окружность О: окружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки. А В О С К Н О- центр окружности Окружность О( R) О:Радиусом окружности называется отрезок, соединяющий центр окружности с точкой на окружности. Длина этого отрезка – длина радиуса. АО- радиус О:Хордой называется отрезок, соединяющий любые две точки окружности. КН – хорда О: Диаметром окружности называется хорда, проходящая через центр. ВС – диаметр О: Дугой окружности называется часть окружности, ограниченная двумя точками. АВ
Слайд 40
Параллельные прямые
Слайд 41
Параллельные прямые О: Две прямые называются параллельными, если они не имеют общих точек. а в а в О: Два отрезка называются параллельными, если они лежат на параллельных прямых.
Слайд 42
Углы при пересечении двух прямых секущей. с а 1 2 3 в 8 4 5 6 7 О: прямая с называется секущей по отношению к прямым а и в , если она пересекает их в двух точках. Накрест лежащие углы: 3 и 5; 4 и 8 Односторонние углы:3 и 4; 5 и 8. Соответственные углы: 1 и 4 ;2 и 5 ;7 и 8; 3 и 6.
Слайд 43
Признаки параллельных прямых 1 признак: Т: если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. 2 признак: Т: если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. 3 признак: Т: если при пересечении двух прямых секущей сумма односторонних углов равна 180˚, то прямые параллельны.
Слайд 44
Аксиома параллельных прямых Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной. Свойства параллельных прямых 1.Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую. 2. Если две прямые параллельны третьей прямой, то они параллельны.
Слайд 45
Свойства параллельных прямых Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны. Если две параллельные прямые пересечены секущей, то соответственные углы равны. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180˚.
Слайд 46
Соотношения между сторонами и углами треугольника
Слайд 47
Теорема о сумме треугольника Т. Сумма углов треугольника равна 180˚. А
Слайд 48
Внешний угол треугольника О: Угол, смежный с каким – нибудь углом треугольника, называется внешним углом этого треугольника. А
Слайд 49
Классификация треугольников Остроугольный треугольник Тупоугольный треугольник Прямоугольный треугольник О: Треугольник называется остроугольным, если все его углы острые. О: Треугольник называется тупоугольным, если один его угол тупой О: Треугольник называется прямоугольным, если один его угол А прямой. АС – гипотенуза АВ и ВС — катеты В С
Слайд 50
Теорема о соотношениях между сторонами и углами треугольника Т. В треугольнике против большей стороны лежит больший угол, а против большего угла лежит большая сторона. А АС > АВ В С
Слайд 51
Неравенство треугольника Т. Каждая сторона треугольника меньше суммы двух других сторон. А АВ
Слайд 52
Свойства прямоугольного треугольника Сумма двух острых углов прямоугольного треугольника равна 90˚ А
Слайд 53
Свойства прямоугольного треугольника 2. Катет прямоугольного треугольника, лежащий против угла в 30˚, равен половине гипотенузы. А
Слайд 54
Свойства прямоугольного треугольника 3. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета равен 30˚. А АС= АВ С В
Слайд 55
Расстояния между геометрическими фигурами. А а Н Расстояние между двумя точками. О:Расстоянием между двумя точками А и В называется длина отрезка АВ. 2. Расстояние между прямой и точкой. О: Расстоянием от точки до прямой называется длина перпендикуляра, проведённого из точки к прямой. АН – расстояние от точки А до прямой а а А 3. Расстояние между параллельными прямыми. О: Расстоянием между параллельными прямыми называется расстояние от любой точки одной прямой до другой прямой. в В АВ – расстояние между прямыми а и в
Слайд 56
Расстояния между геометрическими фигурами. Расстояние между двумя точками. О:Расстоянием между двумя точками А и В называется длина отрезка АВ. 2. Расстояние между прямой и точкой. О: Расстоянием от точки до прямой наз
nsportal.ru
Зачёт по теории по геометрии 7-9 классы
Самарина Марина Николаевна
Муниципальное бюджетное образовательное учреждение
Средняя общеобразовательная школа №5
г. Лысково Нижегородской области
Зачет по теории геометрии за курс 7-9 класс
1.Определение вертикальных о смежных углов.
2.Теорема о смежных углах.
3.Теорема о вертикальных углах.
4.Признаки равенства треугольников.
5.Определение медиан, биссектрис, высот треугольника.
6.Определение равнобедренного треугольника и его свойства.
7.Признаки параллельности двух прямых.
8.Свойства параллельных прямых.
9. Теорема о сумме углов треугольника
10.Определение остроугольного, прямоугольного, тупоугольного треугольника.
11.Теорема о соотношениях между сторонами и углами треугольника.
12.Неравенство треугольника.
13.Свойство прямоугольного треугольника.
14.Признаки равенства прямоугольных треугольников.
15.Сумма углов выпуклого многоугольника.
16.Параллелограмм и его свойства.
17.Признаки параллелограмма.
18.Трапеция и ее виды.
19.Свойства равнобедренной трапеции.
20.Теорема Фалеса.
21.Прямоугольник и его свойства.
22.Признак прямоугольника.
23.Ромб и его свойства.
24.Квадрат и его свойства.
25.Формулы площадей квадрата, прямоугольника, треугольника, параллелограмма, ромба, трапеции.
26.Свойства площадей треугольников с равными высотами, и имеющими по равному углу.
27.Теорема Пифагора и обратная ей.
28.Определение подобных треугольников.
29.Свойство периметров и площадей подобных треугольников
30.Теорема о биссектрисе угла.
31.Признаки подобных треугольников.
32.Средняя линия треугольника и ее свойства.
33.Теорема о медианах треугольника.
34.Пропорциональные отрезки в прямоугольном треугольнике.
35.Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника.
36.Основное тригонометрическое тождество.
37.Касательная, ее свойство и признак.
38. Определение центрального и вписанного угла.
39.Теорема о центральном и вписанном углах.
40.Теорема о хордах.
41.Свойство о биссектрисе угла.
42.Свойство серединного перпендикуляра к отрезку.
43.Вписанная и описанная окружности.
44.Уравнение прямой и окружности.
45.Теорема синусов.
46.Теорема косинусов.
47.Скалярное произведение векторов.
48.Правильный многоугольник.
48.Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности.
49.Длина окружности и площадь круга.
50.Формулы медианы и биссектрисы.
51.Теорема Минелая.
infourok.ru