Самостоятельная по геометрии 7 класс атанасян: Самостоятельные работы по геометрии 7 класс по учебнику Л.С. Атанасян

Проверочные работы по геометрии 7 класс

Показывать

Геометрия

Проверочные работы

7 класс

Проверочные работы по геометрии 7 класс и другие
полезные материалы для учителя геометрии, которые вы можете выбрать и скачать бесплатно в этом разделе.

Самостоятельная работа по геометрии «Начальные геометрические сведения»

Проверочные работы

Самостоятельная работа по геометрии «Начальные геометрические сведения»

Самостоятельная работа «Признаки и свойства параллельных прямых»

Проверочные работы

Самостоятельная работа содержит 16 вариантов заданий на свойства параллельных прямых

Олимпиады: Биология 6 — 11 классы

Контрольная работа по геометрии № 1

Проверочные работы

Контрольная работа по геометрии № 1 по теме » Основные свойства простейших геометрических фигур «. Учебник Погорелова А. В. » ГЕОМЕТРИЯ

Домашнее задание по геометрии ( 7кл.)

Проверочные работы

Данная работа предлагается ученикам с целью качественной подготовки к контрольной работе № 1 по теме «Основные свойства простейших геометрических

Самостоятельная работа «Прямоугольные треугольники»- 1 вариант

Проверочные работы

Проверочная работа по теме Прямоугольные треугольники 7 класс. Применение к решению задач свойтв прямоугольного треугольника.Учебник Атанасян.

Суммативное оценивание за раздел «Взаимное расположение прямых»

Проверочные работы

Разработка охватывает темы: Параллельные прямые, их признаки и свойства Сумма углов треугольника. Внешний угол треугольника Признаки равенства прямоуг

Контрольная работа по теме «Соотношения между сторонами и углами треугольника»

Проверочные работы

Контрольная работа к УМК Атанасяна содержит 2 варианта.

Контрольная работа по теме «Параллельные прямые»

Проверочные работы

Контрольная работа к УМК Атанасяна содержит 2 варианта.

Математический диктант по теме: «Окружность»

Проверочные работы

Г-7 «Окружность» Математический диктант. Дополни предложение…

Признаки параллельных прямых

Проверочные работы

Самостоятельная работа по теме признаки параллельных прямых, содержит 2 варианта, работа расчитана на 15 минут

В начало

1
2

Получите свидетельство о публикации сразу после загрузки работы

Получите бесплатно свидетельство о публикации сразу после добавления разработки

Контрольная работа по геометрии за 1 четверть 7 класс

Контрольная работа по геометрии за 1 четверть 7 класс

по теме «Начальные геометрические сведения»

Вариант 1

Обязательная часть

1. Закончите предложения

1. Сумма смежных углов равна …… б) Вертикальные углы …….

1. Чему равен угол, если вертикальный с ним равен 46⁰?

2. Даны два угла АВС и КВС. Будут ли они смежными, если их величины равны:

а) 46⁰ и 144⁰; б) 90⁰ и 90⁰; в) 45⁰ и 135⁰?

1. Начертите тупой угол МРК, постройте ему смежный КРС.

2. Луч BD является биссектрисой угла АВС. Найдите

3. Найдите углы, полученные при пересечении двух прямых, если один из углов равен 74⁰. Оформите решение на чертеже.

Дополнительная часть.

Запишите обоснованное решение задач 7-10

1. Найдите на рисунке 2, если 76⁰.

2. Найдите длины отрезков BP и DP на рисунке из задачи 7, если BD=18 см, а отрезок DP на 4 см больше отрезка BP.

3. Из точки B проведены три луча: BM, BN, и BK. Найдите угол NBK, если .

   K

4. Найдите на рисунке 1.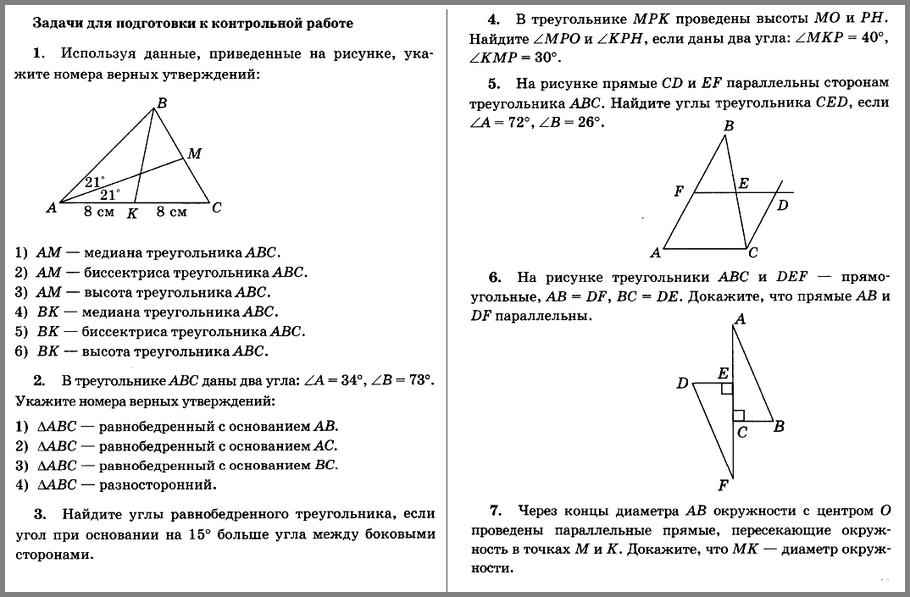

D

P

Рисунок 1

Рисунок 2

C

B

Вариант 2

Обязательная часть

1. Закончите предложения

а) Развернутый угол равен …… б) Вертикальные углы …….

1. Чему равен угол, если вертикальный с ним равен 25⁰?

2. Даны два угла АВС и КВС. Будут ли они смежными, если их величины равны:

а) 66⁰ и 124⁰; б) 91⁰ и 89⁰; в) 35⁰ и 145⁰?

1. Начертите острый угол МРК, постройте ему смежный МРС.

2. Угол DCB равен 148⁰, луч СК — биссектриса этого угла. Найдите

3. Один из четырех углов, полученных при пересечении двух прямых, равен 57⁰. Найдите остальные три угла. Оформите решение на чертеже.

Дополнительная часть.

Запишите обоснованное решение задач 7-10

1. Найдите на рисунке 2, если ⁰.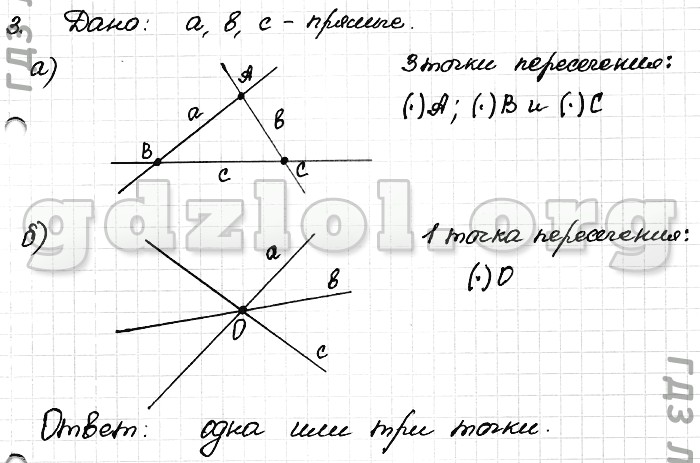

2. Найдите длины отрезков BD и DC на рисунке из задачи 7, если BC=24 см, а отрезок BD на 8 см больше отрезка DC.

3. Из точки M проведены три луча: MO, MN, и MK. Чему равен угол NМK, если .

4. Найдите на рисунке 1, если

B

E

D

C

Рисунок 2

Рисунок 1

A

Критерии оценивания

«3» 4-6 заданий обязательной части; «4» — 7-8 заданий; «5» — 9-10 заданий

Математика, 7 класс, выборки и вероятности, независимые и зависимые составные события#GoOpenNC

Обзор

Учащиеся продолжают расширять свое понимание составных событий, сравнивая независимые и зависимые события. Это включает в себя рисование образца пространства, чтобы понять, как первое событие влияет или не влияет на второе событие. Учащиеся будут решать задачи с зависимыми составными событиями.

Учащиеся узнают о различиях между зависимыми и независимыми событиями.

• События независимы, если исход одного события не влияет на исход других.
• События являются зависимыми, если исход одного события влияет на исход других.

Разницу можно увидеть, нарисовав диаграмму, представляющую пространство выборки. Для зависимых событий пространство выборки меньше.

• Поймите разницу между независимыми и зависимыми составными событиями.
• Рисование диаграмм для зависимых составных событий.
• Решение задач на составные события.

Предложите учащимся несколько минут поговорить с соседом о вступительных вопросах. Они должны работать индивидуально, чтобы ответить на них. Студентам не нужно заполнять их до начала обсуждения в классе.

• Выяснить у учащихся, что в примере с бросанием кубиков результат первого события не влияет на результат второго события. Для каждого числового куба по-прежнему есть 6 исходов, в результате чего всего 36 исходов. Вероятность того, что выпадет двойная шестерка, равна 136=0,027¯=2,7¯%. Это видно на уже знакомой табличной диаграмме:
• При вытягивании шариков, как только вытащен первый шарик, изменяется вероятность выпадения второго шарика. Сначала было 7 исходов, а теперь их 6. Каждый из 7 исходов первого события объединяется с оставшимися 6 исходами, в результате чего получается 42 исхода. Вероятность того, что вы вытащите 2 красных шарика, равна 2042=1021=0,4762=47,62%.
  Это уменьшение пространства выборки можно увидеть на табличной диаграмме:
• Учащиеся сравнивают независимые события с зависимыми событиями. Независимые события не влияют друг на друга, тогда как зависимые события затрагиваются.

Открытие

Посмотрите на эти три задачи и рассмотрите следующее:

• Вы бросаете 2 числовых кубика. Какова вероятность того, что выпадет двойная шестерка?

• Вы достаете 2 шарика из этого мешка. Какова вероятность того, что вы вытащите два красных шарика?

• Чем отличаются эти два многоэтапных эксперимента и сложные события?

Для задачи о мраморе эти события называются зависимые события потому что результат одного события влияет на другое. До сих пор мы рассматривали только независимые события.

Важно обсудить, что если туз вытянут и не заменен, то вероятность того, что выпадет еще один туз, будет равна 351. новые слова в более медленном темпе и запишите их. Попросите некоторых учащихся повторить за вами и/или поработать над произношением в малых группах. Убедитесь, что ELL чувствуют себя комфортно с произношением. Кроме того, разрешите ELL использовать словарь.

Открытие

Обсудите следующее со своими одноклассниками.

• Два события называются независимыми , если исход одного события не влияет на исход другого события.
• Два события называются зависимыми , если исход одного события влияет на исход второго события.
• Примером зависимого события является ситуация, когда вы вытягиваете туз из колоды карт и не заменяете его. После вытягивания туза в колоде на одного туза меньше, чем раньше. Таким образом, вероятность вытягивания туза со второй попытки зависит от исхода первого события.

Обсудить математическую миссию. Учащиеся рисуют диаграмму, чтобы определить вероятность зависимых составных событий.

Открытие

Нарисуйте диаграмму, чтобы определить вероятность зависимых составных событий.

Учащиеся должны работать с партнером в рабочее время.

Предложите учащимся нарисовать диаграммы, чтобы понять, влияет ли одно событие на выборочное пространство другого события. Ищите различные диаграммы, как правильные, так и неправильные, чтобы поделиться ими во время «Способов мышления», чтобы продемонстрировать как зависимые, так и независимые события.

Учащийся не имеет четкого представления о независимых и зависимых событиях.

• Влияет ли на второй исход то, что происходит с первым исходом?
• Можете ли вы начертить диаграмму, изображающую пространство выборки? Что вам говорит диаграмма?

Объяснения могут различаться. Ответы и возможные объяснения:

• Зависимый. При рисовании первого фрукта пространство образца составляет 16 штук. При рисовании второй детали пространство выборки уменьшается на 1,9.0010
• Независимый. Подбрасывание монеты и бросок числового кубика не влияют друг на друга. Подбрасывание монеты всегда будет иметь два исхода, а бросок числового куба всегда будет иметь шесть.
• Зависимый. Образцовое пространство для второго розыгрыша на единицу меньше из-за первого розыгрыша.
• Независимый. Демонстрационное пространство для обоих спинов имеет 20 исходов.
• Независимый. Пробное пространство для обоих спинов имеет 4 исхода.

Рабочее время

Какие из следующих событий являются независимыми, а какие зависимыми? Поясните свой ответ.

• В миске 4 апельсина и 12 яблок. Вы протягиваете руку и случайным образом берете фрукт, чтобы съесть его. Затем вы случайным образом получаете еще один фрукт.
• Вы подбрасываете монету и выбрасываете числовой куб.
• Вы лезете в ящик и достаете один носок. Ты снова протягиваешь руку и достаешь носок того же цвета.
• Вы вращаете спиннер A дважды. Вы хотите вращать четное число, а затем нечетное число.
• Вы вращаете спиннер B дважды. Вы хотите получить один и тот же цвет оба раза.

Учащиеся должны работать с партнером в рабочее время.

Предложите учащимся нарисовать диаграммы, чтобы понять, влияет ли одно событие на выборочное пространство другого события. Ищите различные диаграммы, как правильные, так и неправильные, чтобы поделиться ими во время «Способов мышления», чтобы продемонстрировать зависимость и независимость.

Найдите различные стратегии, которые учащиеся используют для решения задач с четырьмя счетчиками. Некоторые могут использовать древовидную диаграмму или таблицу, а другим это может не понадобиться.

Ученик дает неверное решение.

• Сколько исходов у каждого события?
• Сопоставили ли вы каждый из первых исходов с каждым из вторых исходов?
• Сколько исходов благоприятны?

• В пространстве выборки есть четыре исхода.
• P (5) = 14
  Вероятность выпадения 5 равна 14 = 0,25 = 25%.
• В пространстве выборки останется три исхода, если вы не замените 5.
• P (6) = 13
  Вероятность вытянуть 6, когда 5 не заменена, равна 13 = 0,3¯ = 33,3¯%.
• Tree diagram: List:
  • 5, 6
  • 5, 7
  • 5, 8
  • 6, 5
  • 6, 7
  • 6, 8
  • 7, 5
  • 7, 6
  • 7 , 8
  • 8, 5
  • 8, 6
  • 8, 7

Таблица:

P (5, затем 6) = 14 ⋅ 13 = 112

• Вероятность первого рисунка. 5, за которым следует рисование 6, если вы не замените 5, это 1 из 12.

Рабочее время

У вас есть коробка с четырьмя жетонами, пронумерованными 5, 6, 7 и 8. Вы случайным образом выбираете один жетон.

• Сколько результатов есть в выборке?
• Какова вероятность того, что вы выберете 5?
• Если вы выберете 5 и не замените его, сколько результатов будет в новом пространстве выборки?
• Какова вероятность выбора 6 на основе этого нового выборочного пространства?
• Проиллюстрируйте свое мышление древовидной диаграммой, списком и/или таблицей.
• Какова вероятность того, что вы сначала выберете 5, а затем 6, если вы не замените первый счетчик?

Студенты должны работать с партнером.

Предложите учащимся нарисовать диаграммы, чтобы понять, влияет ли одно событие на выборочное пространство другого события. Ищите различные диаграммы, как правильные, так и неправильные, чтобы поделиться ими во время «Способов мышления», чтобы продемонстрировать зависимость и независимость.

Найдите различные стратегии, которые учащиеся используют для решения задач с пятью шариками. Некоторые могут использовать древовидную диаграмму или таблицу, а другим это может не понадобиться.

Ученик дает неверное решение.

• Сколько исходов у каждого события?
• Сопоставили ли вы каждый из первых исходов с каждым из вторых исходов?
• Сколько исходов благоприятны?

• Ответы будут разными. Tree diagram: List:
  • B1, B2
  • B1, R1
  • B1, R2
  • B1, R3
  • B2, B1
  • B2, R1
  • B2, R2
  • B2, R3
  • R1, B1
  • R1, B2
  • R1, R2
  • R1, R3
  • R2, B1
  • R2, B2
  • R2, R1
  • R2, R3
  • R3, B1
  • R3, B2
  • R3, R1
  • R3, R2

Таблица:

• P (красный, затем синий) = 620 = 310 = 0,3 = 30%

Ответы

• Объяснения будут разными. Ответ с возможным объяснением: Вы можете составить число 63, вытащив 3, а затем 6, или вытащив 6, а затем 3. Это означает, что есть два благоприятных исхода. Один из способов рассчитать площадь выборки — нарисовать таблицу: есть 90 исходов, значит: Р (образуется 63) = Р (рисунок 6, затем 3) + Р (рисунок 3, затем 6) = 290 = 145 = 0,02¯ = 2,2¯%

Рабочее время

У вас есть сумка с 3 красными и 2 синими шариками. Вы берете 1 шарик, не заменяя его, а затем берете второй шарик.

• Покажите пример пространства, используя древовидную диаграмму, список и/или таблицу.
• Какова вероятность того, что вы вытащите сначала красный, а затем синий шарик?

У вас есть 10 карт с номерами от 0 до 9, лежащих лицевой стороной вниз. Если вы берете 2 карты, чтобы составить двузначное число, и не заменяете первую карту, какова вероятность того, что вы составите число 63?

• Объясните свой метод решения этой проблемы.

Во время обсуждения в классе выбранные учащиеся представляют свои схемы и стратегии для каждой из задач.

SWD: Пока учащиеся представляют свои решения, устанавливайте связи между различными решениями одной и той же задачи. Это позволяет учащимся увидеть несколько способов решения/анализа проблемы. Запишите важные связи и попросите учащихся скопировать информацию в свою тетрадь.

Обсудите первую задачу, определяющую зависимость и независимость:

• Какие события независимы? Почему?
• Какие события являются зависимыми? Почему?

Обсудите задачу о счетчиках и задачу о шариках:

• Чем пространство выборки для зависимого события отличается от независимого события?
• Какова вероятность того, что сначала вытащат синий шарик, а затем еще один синий шарик? Как изменится вероятность, если события независимы (т. е. вернуть первый шарик в мешок)?
• Какова вероятность того, что выпадет 5, а затем 6, если положить 5 обратно? Как изменится вероятность, если события зависимы?

Если какие-либо учащиеся решили задачу-вызов, попросите их представить свои методы и предложить остальным ученикам задать вопросы.

Математическая практика 6: Следите за точностью.

• Учащиеся должны использовать соответствующий математический язык, чтобы различать два типа составных событий.

Performance Task

Делайте заметки о диаграммах и решениях ваших одноклассников.

В присутствии одноклассников задайте такие вопросы, как:

• Как вы определили, какие события являются независимыми, а какие зависимыми?
• Чем ваше представление выборочного пространства для зависимых событий отличается от вашего представления независимых событий?
• Как изменилась бы вероятность, если бы два выбора были независимыми или зависимыми?

Составные события могут быть независимыми или зависимыми. На зависимые события влияют другие события. Порядок событий будет влиять на вероятность зависимого события, но не независимого события. Примером независимого события является взятие карты из колоды, возврат карты, затем взятие второй карты. Примером зависимого события является вытягивание карты из колоды, а затем вытягивание второй карты без замены первой. Выборочное пространство для зависимых событий меньше, чем для независимых событий, поэтому вероятности различаются.

SWD: убедитесь, что все учащиеся имеют эту информацию в своих заметках. Возможно, будет полезно предоставить некоторым учащимся определенные вещи, которые они могут прослушать во время этой части обучения. Некоторым учащимся могут понадобиться копии конспектов из этой части урока.

Формирующее оценивание

Напишите резюме о независимых и зависимых составных событиях.

Проверьте свое резюме:

• Вы определяете независимых событий и приводите пример?
• Вы определяете зависимых событий и приводите пример?
• Объясните, чем нахождение вероятности независимых событий отличается от нахождения вероятности зависимых событий?

Предложите учащимся написать краткое размышление перед окончанием урока.