7 класс. Геометрия. Атанасян. Учебник. Ответы к стр. 24
Начальные геометрические сведения
Перпендикулярные прямые
Смежные и вертикальные углы. Перпендикулярные прямые. Построение прямых углов на местности
Ответы к стр. 24
Практические задания
54. Начертите острый угол АОВ и на продолжении луча ОВ отметьте точку D. Сравните углы АОВ и AOD.
Углы АОВ и АОD — смежные, ∠АОВ — острый, ∠АОD — тупой ⇒ ∠АОВ < ∠АОD.
55. Начертите три угла: острый, прямой и тупой. Для каждого из них начертите смежный угол.
∠АОВ — острый, смежный угол ВОС (тупой).
∠DOE — прямой, смежный угол EOF (прямой).
∠KОL — тупой, смежный угол LOM (острый).
56. Начертите неразвернутый угол hk. Постройте угол h1k1 так, чтобы углы hk и h1k1 были вертикальными.
Углы hk и h1k1 — вертикальные (∠hk = ∠h1k1).
57. Начертите неразвернутый угол MON и отметьте точку Р внутри угла и точку Q — вне его. С помощью чертежного угольника и линейки через точки Р и Q проведите прямые, перпендикулярные к прямым ОМ и ON.
α ⊥ ОN, b ⊥ OM, c ⊥ ON, d ⊥ OM.
Задачи
58. Найдите угол, смежный с углом ABC, если: a) ∠ABC = 111°; б) ∠ABC = 90°; в) ∠ABC = 15°.
Р е ш е н и е
Сумма смежных углов равна 180°.
а) 180° — 111° = 69°;
б) 180° — 90° = 90°;
в) 180° — 15° = 165°.
О т в е т. а) 69°, б) 90°, в) 165°.
59. Один из смежных углов прямой. Каким (острым, прямым, тупым) является другой угол?
Р е ш е н и е
Сумма смежных углов равна 180°.
180° — 90° = 90° — прямой смежный угол.
О т в е т. Прямой.
60. Верно ли утверждение: если смежные углы равны, то они прямые?
Р е ш е н и е
Сумма смежных углов равна 180°.
180° : 2 = 90° — два смежных угла по 90° каждый.
О т в е т. Верно.
61. Найдите смежные углы hk и kl, если:
a) ∠hk меньше ∠kl на 40°;
б) ∠hk больше ∠kl на 120°;
в) ∠hk больше ∠kl на 47°18′;
г) ∠hk = 3∠kl;
д) ∠hk : ∠kl = 5 : 4.
Р е ш е н и е
Сумма смежных углов равна 180°.
а) ∠hk + ∠kl = 180°, ∠hk = ∠kl — 40°, тогда:
(∠kl — 40°) + ∠kl = 180°,
2∠kl = 180° + 40°,
∠kl = 220° : 2,
∠kl = 110°
∠hk = ∠kl — 40° = 110° — 40° = 70°
б) ∠hk + ∠kl = 180°, ∠hk = ∠kl + 120°, тогда:
(∠kl + 120°) + ∠kl = 180°,
2∠kl = 180° — 120°,
∠kl = 60° : 2,
∠kl = 30°
∠hk = ∠kl + 120° = 30° + 120° = 150°
в) ∠hk + ∠kl = 180°, ∠hk = ∠kl + 47°18′, тогда:
(∠kl + 47°18′) + ∠kl = 180°,
2∠kl = 180° — 47°18′,
∠kl = 132°42′ : 2,
∠kl = 66°21′
∠hk = ∠kl + 47°18′ = 66°21′ + 47°18′ = 113°39′
г) ∠hk + ∠kl = 180°, ∠hk = 3∠kl, тогда:
3∠kl + ∠kl = 180°,
4∠kl = 180°,
∠kl = 180° : 4,
∠kl = 45°
∠hk = 3∠kl = 3 • 45° = 135°
д) ∠hk + ∠kl = 180°, ∠hk : ∠kl = 5 : 4 или ∠hk : ∠kl = 5/4 ⇒ ∠hk = 5/4 • ∠kl, тогда:
5/4 ∠kl + ∠kl = 180°,
9/4 ∠kl = 180°,
∠kl = 180° : 9/4,
∠kl = 180° • 4/9,
∠kl = 80°
∠hk = 5/4 ∠kl = 5/4 • 80° = 100°
О т в е т. а) ∠kl = 110°, ∠hk = 70°;
а) ∠kl = 110°, ∠hk = 70°;
б) ∠kl = 30°, ∠hk = 150°;
в) ∠kl = 66°21′, ∠hk = 113°39′;
г) ∠kl = 45°, ∠hk = 135°;
д) ∠kl = 80°, ∠hk = 100°.
62. На рисунке 46 углы BOD и COD равны. Найдите угол AOD, если ∠COB = 148°.
Р е ш е н и е
∠AOD = ∠AOC + ∠COD
Углы AOC и COB — смежные, тогда:
∠AOC + ∠COB = 180° ⇒ ∠АОС = 180° — ∠СОВ = 180° — 148° = 32°.
∠СОВ = ∠СОD + ∠DOB = 148°, ∠СОD = ∠DOB ⇒ ∠СОD = 148° : 2 = 74°.
∠AOD = 32° + 74° = 106°.
О т в е т. ∠AOD = 106°.
63. Даны два равных угла. Равны ли смежные с ними углы?
Р е ш е н и е
∠1 = ∠2
∠1 + ∠3 = 180° ⇒ ∠3 = 180° — ∠1
∠2 + ∠4 = 180° ⇒ ∠4 = 180° — ∠2
Так как ∠1 = ∠2, то ∠3 = 180° — ∠1 = 180° — ∠2 = ∠4 или
∠4 = 180° — ∠2 = 180° — ∠1 = ∠3
О т в е т. Равны.
Равны.
64. Найдите изображенные на рисунке 41 углы:
а) 1, 3, 4, если ∠2 = 117°;
б) 1, 2, 4, если ∠3 = 43°27′.
Р е ш е н и е
а) Углы 2 и 4 — вертикальные, тогда ∠2 = ∠4 = 117°
Углы 1 и 2 — смежные, тогда ∠1 + ∠2 = 180° ⇒ ∠1 = 180° — ∠2 = 180° — 117° = 63°
Углы 1 и 3 — вертикальные, тогда ∠1 = ∠3 = 63°
б) Углы 1 и 3 — вертикальные, тогда ∠1 = ∠3 = 43°27′
Углы 1 и 2 — смежные, тогда ∠1 + ∠2 = 180° ⇒ ∠2 = 180° — ∠1 = 180° — 43°27′ = 136°33′
Углы 2 и 4 — вертикальные, тогда ∠2 = ∠4 = 136°33′
О т в е т. а) ∠1 = ∠3 = 63°, ∠4 = 117°; б) ∠1 = 43°27′, ∠2 = ∠4 = 136°33′.
ГДЗ. Ответы по геометрии. 7 класс. Учебник. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И.
Геометрия. 7 класс
А.В. Погорелов. Геометрия. 7 класс. §2. Контрольные вопросы, ответы — Решебник
Вопрос 1. Какие углы называются смежными?
Ответ. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
На рисунке 31 углы (a1b) и (a2b) смежные. У них сторона b общая, а стороны a1 и a2 являются дополнительными полупрямыми.
Вопрос 2. Докажите, что сумма смежных углов равна 180°.
Ответ. Теорема 2.1. Сумма смежных углов равна 180°.
Доказательство. Пусть угол (a1b) и угол (a2b) — данные смежные углы (см. рис.31). Луч b проходит между сторонами a1 и a2 развёрнутого угла. Поэтому сумма углов (a1b) и (a2b) равна развёрнутому углу, т. е. 180°. Что и требовалось доказать.
Вопрос 3. Докажите, что если два угла равны, то смежные с ними углы также равны.
Ответ.
Из теоремы 2.1 следует, что если два угла равны, то смежные с ними углы равны.
Допустим, углы (a1b) и (c1d) равны. Нам нужно доказать, что углы (a2b) и (c2d) тоже равны.
Сумма смежных углов равна 180°. Из этого следует, что a1b + a2b = 180° и c1d + c2d = 180°. Отсюда, a2b = 180° — a1b и c2d = 180° — c1d. Так как углы (a1b) и (c1d) равны, то мы получаем, что a2b = 180° — a1b = c2d. По свойству транзитивности знака равенства следует, что a2b = c2d. Что и требовалось доказать.
Вопрос 4. Какой угол называется прямым (острым, тупым)?
Ответ. Угол, равный 90°, называется прямым углом.
Угол, меньший 90°, называется острым углом.
Угол, больший 90° и меньший 180°, называется тупым.
Вопрос 5. Докажите, что угол, смежный с прямым, есть прямой угол.
Ответ. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом, есть прямой угол: x + 90° = 180°, x= 180° — 90°, x = 90°.
Вопрос 6. Какие углы называются вертикальными?
Ответ. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого.
Вопрос 7. Докажите, что вертикальные углы равны.
Ответ. Теорема 2.2. Вертикальные углы равны.
Доказательство. Пусть (a1b1) и (a2b2)- данные вертикальные углы (рис. 34). Угол (a1b2) является смежным с углом (a1b1) и с углом (a2b2). Отсюда по теореме о сумме смежных углов заключаем, что каждый из углов (a1b1) и (a2b2) дополняет угол (a1b2) до 180°, т.е. углы (a1b1) и (a2b2) равны. Что и требовалось доказать.
Вопрос 8. Докажите, что если при пересечении двух прямых один из углов прямой, то остальные три угла тоже прямые.
Ответ. Предположим, что прямые AB и CD пересекают друг друга в точке O. Предположим, что угол AOD равен 90°. Так как сумма смежных углов равна 180°, то получаем, что AOC = 180°-AOD = 180°- 90°=90°. Угол COB вертикален углу AOD, поэтому они равны. То есть угол COB = 90°. Угол COA вертикален углу BOD, поэтому они равны. То есть угол BOD = 90°. Таким образом, все углы равны 90°, то есть они все – прямые. Что и требовалось доказать.
Вопрос 9. Какие прямые называются перпендикулярными? Какой знак используется для обозначения перпендикулярности прямых?
Ответ. Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Перпендикулярность прямых обозначается знаком \(\perp\). Запись \(a\perp b\) читается: «Прямая a перпендикулярна прямой b».
Вопрос 10. Докажите, что через любую точку прямой можно провести перпендикулярную ей прямую, и только одну.
Ответ. Теорема 2.3. Через каждую прямую можно провести перпендикулярную ей прямую, и только одну.
Доказательство. Пусть a — данная прямая и A — данная точка на ней. Обозначим через a1 одну из полупрямых прямой a с начальной точкой A (рис. 38). Отложим от полупрямой a1 угол (a1b1), равный 90°. Тогда прямая, содержащая луч b1, будет перпендикулярна прямой a.
Допустим, что существует другая прямая, тоже проходящая через точку A и перпендикулярная прямой a. Обозначим через c1 полупрямую этой прямой, лежащую в одной полуплоскости с лучом b1.
Углы (a1b1) и (a1c1), равные каждый 90°, отложены в одну полуплоскость от полупрямой a1. Но от полупрямой a1 в данную полуплоскость можно отложить только один угол, равный 90°. Поэтому не быть другой прямой, проходящей через точку A и перпендикулярной прямой a. Теорема доказана.
Вопрос 11. Что такое перпендикуляр к прямой?
Ответ. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов их точку пересечения. Этот конец отрезка называется основанием перпендикуляра.
Этот конец отрезка называется основанием перпендикуляра.
Вопрос 12. Объясните, в чём состоит доказательство от противного.
Ответ. Способ доказательства, который мы применили в теореме 2.3, называется доказательством от противного. Этот способ доказательства состоит в том, что мы cначала делаем предположение, противоположное тому, что утверждается теоремой. Затем путем рассуждений, опираясь на аксиомы и доказанные теоремы, приходим к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме. На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы.
Вопрос 13. Что называется биссектрисой угла?
Ответ. Биссектрисой угла называется луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам.
Мини — проект по геометрии 7 класс
Введение
В этом году мы начали изучать новый предмет – геометрию.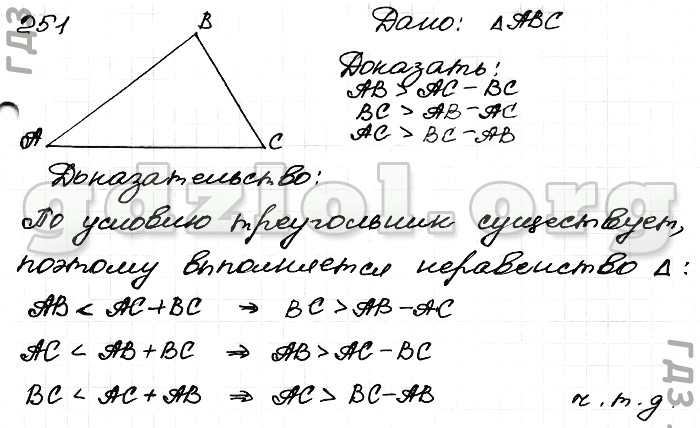 Все время, когда мы имеем дело с формой, размером, положением предмета в пространстве, мы вовлечены в геометрию. Когда доисторические люди занимались ткачеством или отделкой зданий, они пользовались геометрией, не зная ее. Древним египтянам была нужна геометрия, чтобы измерить участки земли, подвергавшиеся затоплению во время разливов Нила. Им была нужна геометрия в строительных целях, когда религия заставила их строить могилы для умерших — пирамиды. Само слово «геометрия» произошло от греческих слов «Земля» и «измерять» и, вероятно, является переводом египетского слова.
Все время, когда мы имеем дело с формой, размером, положением предмета в пространстве, мы вовлечены в геометрию. Когда доисторические люди занимались ткачеством или отделкой зданий, они пользовались геометрией, не зная ее. Древним египтянам была нужна геометрия, чтобы измерить участки земли, подвергавшиеся затоплению во время разливов Нила. Им была нужна геометрия в строительных целях, когда религия заставила их строить могилы для умерших — пирамиды. Само слово «геометрия» произошло от греческих слов «Земля» и «измерять» и, вероятно, является переводом египетского слова.
Сначала геометрия была интуитивной. Это означает, что факты признавались существующими без попытки доказать это или продемонстрировать, что это действительно так. Но в 600 году до н.э. греческий ученый Фалес развил идею, что должны существовать пути, доказывающие, что геометрические факты истинны. В геометрии такая истина называется теоремой. Фалес открыл доказательства теорем, которые люди принимали на веру до этого времени. Это послужило началом доказательной геометрии.
Это послужило началом доказательной геометрии.
В результате люди накапливали знания, опыт, формулировались правила, связанные с геометрическими измерениями и построениями, потом выдвигались гипотезы, формулировались и доказывались теоремы.
Меня очень заинтересовала геометрия и мне захотелось самой решить практическую задачу по геометрии и на ее основе выдвинуть и доказать гипотезу. Моя работа построена по следующей схеме:
- Задача.
Найти угол между биссектрисами двух смежных углов.
- Постановка проблемы.
Зависит ли значение угла между биссектрисами двух смежных углов от выбора угла и его значения?
- Разбор частных случаев.
Берется несколько частных случаев значений одного из смежных углов и вычисляется угол между биссектрисами. Рассматриваются случаи:
.
- Оформление результатов исследования.
Полученные результаты исследования оформляются в виде таблицы.
- Выдвижение гипотезы.
Возникает гипотеза о том, что угол между биссектрисами двух смежных углов равен .
- Доказательство или проверка гипотезы.
Доказательство данной гипотезы.
- Применение результатов исследования.
Задачи, в которых может применяться данное утверждение.
Глава 1
- Задача
Найти угол между биссектрисами двух смежных углов.
- Постановка проблемы
Зависит ли значение угла между биссектрисами двух смежных углов от выбора угла и его значения?
- Разбор частных случаев
а)
Пусть =140о, тогда смежный с ним угол равен 40о. Поэтому угол между биссектрисами равен: 20о + 70о = 90о
б)
Пусть =70о, а смежный с ним угол равен 110о. Поэтому угол между биссектрисами равен: 35о +55о = 90о
в)
Пусть и смежный с ним угол равен 90о. Поэтому угол между биссектрисами равен: 45о + 45о = 90о
г)
Пусть =41о, а смежный с ним угол равен 139о. Поэтому угол между биссектрисами равен: 20,5о + 69,5о = 90о
Поэтому угол между биссектрисами равен: 20,5о + 69,5о = 90о
- Оформление результатов исследования
Полученные результаты отобразим в таблице.
|
Угол между биссектрисами двух смежных углов |
|
|
а) =140о |
90о |
|
б) =70о |
90о |
|
в) =90о |
90о |
|
с) =41о |
90о |
- Выдвижение гипотезы
У меня получилось, что во всех случаях угол между биссектрисами равен 90о. Значит можно выдвинуть гипотезу – угол между биссектрисами двух смежных углов равен 90о.
- Доказательство или проверка гипотезы
Обозначим один из смежных углов , тогда другой угол – 180°–.
1=, так как биссектриса делит угол пополам
2= .
Нам надо найти угол между биссектрисами, значит
+ = – + 90° = 90°.
В общем случае я получила, что угол между биссектрисами равен 90о, также как и в частных случаях. Следовательно, угол между биссектрисами 2-х смежных углов действительно равен 90°.
- Применение результатов исследования
Результаты данной работы могут найти применение в задачах различного вида. Например, такой:
На биссектрисах двух смежных углов взяты произвольные точки А и В.
- Определить большую сторону треугольника АВС.
- Найти сумму углов САВ и АВС.
- Найти сторону ВС, если известно, что, АВ=с.
- Найти сторону АВ, если известно, что ,ВС=.
- Найти расстояние от точки В до прямой АС, от точки А до прямой ВС.
Решение
Т.к. треугольник АВС – прямоугольный, то больший угол = 90°( по теореме о сумме углов треугольника), а против большего угла лежит большая сторона, т. е. АВ — большая сторона треугольника АВС.
е. АВ — большая сторона треугольника АВС.
САВ + АВС= 90°( по теореме о сумме углов треугольника).
ВС=1/2 АВ=1/2с, т.к. в прямоугольном треугольнике против угла 30° лежит катет, равный половине гипотенузы. Отсюда же и АВ= 2.
Т.к. длина перпендикуляра, проведенного из точки к прямой, называется расстоянием от этой точки до прямой, то в данном случае расстояние от точки В до прямой АС будет равно ВС, а расстояние от точки А до прямой ВС будет равно АС.
Заключение
В ходе исследования данной задачи я убедилась в том, угол между биссектрисами любых смежных углов равен 90°.
На основе полученных данных мы можем решать задачи, используя свойства прямоугольного треугольника, построенного на биссектрисах смежных углов:
- Сумма острых углов прямоугольного треугольника равна 90°.
- Катет прямоугольного треугольника, лежащий против угла 30°,
равен половине гипотенузы.
- Если катет прямоугольного треугольника равен половине
гипотенузы, то угол, лежащий против этого катета, равен 30°.
А также различные задачи, где используются другие свойства прямоугольного треугольника.
Список литературы
- Геометрия, 7-9:учеб. для общеобразоват.учреждений/Л.С. Атанасян, В.Ф.Бутузов и др.
- Энциклопедия для школьников. Математика. Гл.ред. М. Аксенова. Изд. «Аванта»
Урок геометрии в 7-м классе по теме «Свойства прямоугольного треугольника. Решение задач»
- Попова Наталия Владимировна
Разделы:
Математика
Цели урока:
- дидактические – совершенствование навыков решения задач на применение свойств прямоугольного треугольника;
- развивающие – развитие специального учебного навыка решения геометрических задач;
- воспитательные – воспитание интереса к математике.

1. Орг. момент.
Французский писатель Анатоль Франс однажды заметил: «Учиться можно только весело, чтобы переваривать знания, надо поглощать их с аппетитом». Так вот, давайте сегодня на уроке будем следовать этому совету писателя, будем активны, внимательны, будем поглощать знания с большим желанием.
Сегодня у нас заключительный урок по теме «Свойства прямоугольного треугольника».
Перед вами стоит задача – закрепить умение применять свойства прямоугольного треугольника при решении задач; проверить свои знания в ходе выполнения самостоятельной работы.
2. Актуализация опорных знаний.
Работа с буклетами( напротив каждого пункта «Памятки» записать правильный ответ)
- Сумма двух острых углов прямоугольного треугольника равна 90°.
- Катет прямоугольного треугольника, лежащий против угла в 30° равен половине гипотенузы.
- Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.

- В прямоугольном треугольнике медиана, проведенная из вершины прямого угла, равна половине гипотенузы.
- Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
3. Решение задач.
а) по готовым чертежам ( готовые чертежи в буклетах и на интерактивной доске).
Устно.
1. Найти: N
2. АВ=12см. Найти: ВС
3. PD = 1,2cм. Найти: PQ
Возле доски с решением.
4. АВ = 4,2см. ВС = 8,4см. Найти: B
5.DCM = 70° Найти: DAM
6. C = 90°, PC = СM; CA = 8 см Найти: MP.
б) Решение текстовых задач.
7. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего катета равна 18 см. Найдите гипотенузу и меньший катет.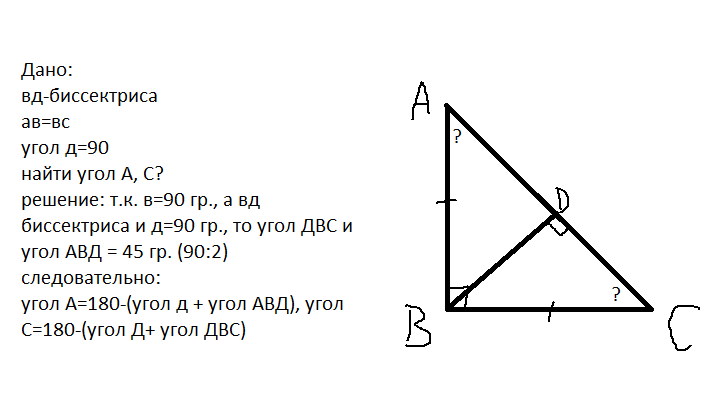
| Дано: ΔАВС, С=90°, А=60°, АВ+АС=18см Найти: АВ, АС. Решение: В=90° – 60°=30°, значит, АС – меньший катет, тогда АС=0,5АВ АВ+0,5АВ=18 АВ=12см, АС=6см Ответ: АВ=12см, АС=6см. |
8. В прямоугольном треугольнике АВС С=90° и А=30°, проведена медиана СМ и биссектриса MD ΔСМА. Найдите MD, если ВС=23см.
| Дано: ΔАВС, С=90°, А=30°, СМ-медиана С, МD – биссектриса ΔСМА, ВС=23см. Найти: MD. Решение: Т.к. СМ – медиана, то СМ-ВМ=МА=0,5АВ Т.к. А=30° и ВС=24см, то АВ=46см и = СМ=ВМ=МА=23см. Т.к. СМ=МА, то ΔСМА равнобедренный, следовательно, МD – высота. 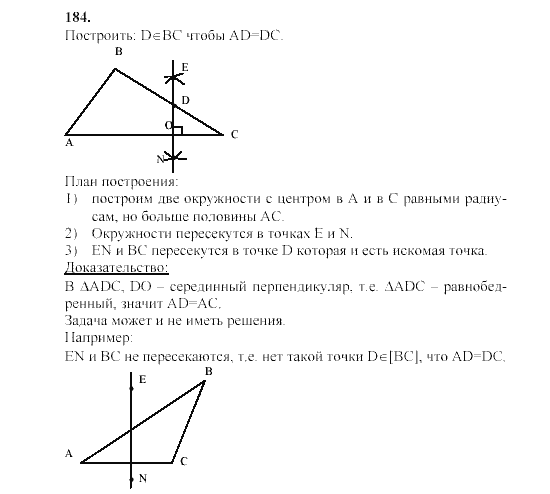 Т.к. А=30°, АDM= 90° и МА=23см, то MD=0,5МА= 11,5см. Ответ: MD=11,5см. |
Физ.пауза
- разминка шейного отдела позвоночника;
- разминка для глаз.
4. Самостоятельная работа.
Прежде чем приступить к этой работе, запишем домашнее задание.
П.34, №259, №260, №265.
| Самостоятельная работа | |
| Вариант 1.
1. Найти: 2. В прямоугольном треугольнике СDЕ с прямым углом Е проведена высота ЕF. Найдите СF и FD, если CD=18см, а DCE=30°. |
Вариант 2
1. Найти: 2. |
5. Итог урока.
Чем мы сегодня занимались на уроке?
Какие свойства применяли при решении задач?
Приложение.
NCERT Solutions for Class 7 Math Chapter 10
-
Решения НЦЭРТ
-
Класс 7
-
Математика
- практическая геометрия
Математика NCERT 7 класс, глава 10: Практическая геометрия . Он охватывает все основы рисования параллельных линий и некоторые типы треугольников . Сначала в главе рассказывается о построении линии, параллельной заданной линии. Есть два способа сделать то же самое:
Он охватывает все основы рисования параллельных линий и некоторые типы треугольников . Сначала в главе рассказывается о построении линии, параллельной заданной линии. Есть два способа сделать то же самое:
1. Через складывание бумаги , когда точка не лежит на линии
2. С помощью линейки и циркуля 9Только 0014
Тема объясняется поэтапно с хорошо маркированным схематическим описанием.
Упражнение 10.1 основано на той же концепции.
Позже основное внимание будет уделено понятиям, связанным с построением треугольников.
Всестороннее объяснение следующих тем с помощью полезных рисунков:
- Построение треугольника по известным длинам трех его сторон (критерий SSS).
- Построение треугольника по известным длинам двух сторон и величине угла между ними (критерий САС).
- Построение треугольника по двум его углам и длине стороны, заключенной между ними (критерий ASA).

- Построение прямоугольного треугольника по длине катета и его гипотенузе (критерий RHS).
Всего дается пять нерешенных упражнений, из которых последние четыре упражнения основаны на теме, связанной с построением треугольников.
В конце приведен краткий обзор главы для быстрого ознакомления.
Страница № 196:
Вопрос 1:
Нарисуйте линию, скажем, AB, возьмите точку C вне ее. Через С проведите линию, параллельную АВ, используя только линейку и циркуль.
Ответ:
Этапы построения следующие.
(i)Проведите линию AB. Поставьте на нем точку P. Возьмем точку С вне этой прямой. Соедините C с P.
(ii) Приняв P за центр и с удобным радиусом, проведите дугу, пересекающую линию AB в точке D и PC в точке E.
(iii) Приняв C за центр и с тем же радиусом, что и раньше, нарисуйте дугу FG, пересекающую PC в точке H.
(iv) Отрегулируйте циркуль до длины DE. Не меняя отверстия циркуля и приняв H за центр, начертите дугу, пересекающую ранее проведенную дугу FG в точке I.
Не меняя отверстия циркуля и приняв H за центр, начертите дугу, пересекающую ранее проведенную дугу FG в точке I.
(v) Соедините точки C и I, чтобы провести линию ‘ l ’.
Это искомая линия, параллельная линии AB.
Видео Решение по практической геометрии (Страница: 196 , Q.No.: 1)
NCERT Решение по математике для 7 класса — Практическая геометрия 196 , Вопрос 1
Страница № 196:
Вопрос 2:
Нарисуй
линия л . Проведите перпендикуляр к l в любой точке l .
На этом перпендикуляре выберите точку X, отстоящую на 4 см от l .
Через Х провести линию м параллельно м .
Ответ:
Шаги
конструкции заключаются в следующем.
(i) Проведите линию l и возьмите точку P на линии l . Затем,
провести перпендикуляр в точке P.
(ii) Отрегулировав циркуль до длины 4 см, нарисуйте дугу, чтобы
пересекают этот перпендикуляр в точке X.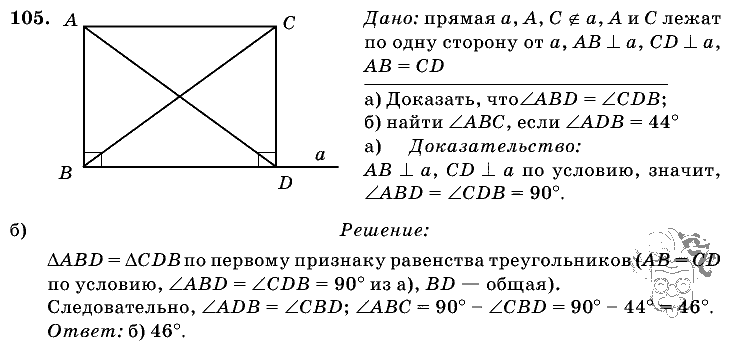 Выберите любую точку Y на прямой
Выберите любую точку Y на прямой
л . Присоедините X к Y.
(iii) Взяв Y за центр и с удобным радиусом, нарисуйте дугу
пересечение l в точке A и XY в точке B.
(iv) Приняв X за центр и с тем же радиусом, что и раньше, нарисуйте
дуга CD резка XY по E.
(v) Отрегулируйте компасы до длины АВ. Без
изменив апертуру циркуля и взяв Е за центр, нарисуйте
дуга, пересекающая ранее проведенную дугу CD в точке F.
(vi) Присоединиться
точки X и F провести линию м .
Линия м – это требуемая линия, параллельная линии 9.0087 л .
Страница № 196:
Вопрос 3:
Let l
быть линией и P быть точкой не на l . Через Р провести линию м
параллельно л . Теперь присоедините P к любой точке Q на l . Выбирать
любая другая точка R на м . Через R провести линию, параллельную PQ.
Пусть это встретит l в точке S. Какую форму имеют два набора параллельных
Какую форму имеют два набора параллельных
линии заключают?
Ответ:
Этапы построения следующие.
(i)Нарисуйте линию l и отметьте на ней точку А. Возьмите точку P не на l и соедините A с P.
(ii) Взяв A за центр и с удобным радиусом, нарисуйте дугу, пересекающую l в B и AP в C.
(iii) Приняв P за центр и с тем же радиусом, что и раньше, нарисуйте дугу DE, пересекающую AP в точке F.
(iv) Отрегулируйте компас до длины BC. Не меняя отверстия циркуля и приняв F за центр, проведите дугу, пересекающую ранее проведенную дугу DE в точке G.
(v) Соедините P и G, чтобы нарисовать линию м . Линия м будет параллельна линии l .
(vi) Соедините P с любой точкой Q на линии l . Выберите другую точку R на линии м . Точно так же можно провести прямую через точку R и параллельно PQ.
Пусть пересекается с прямой l в точке S.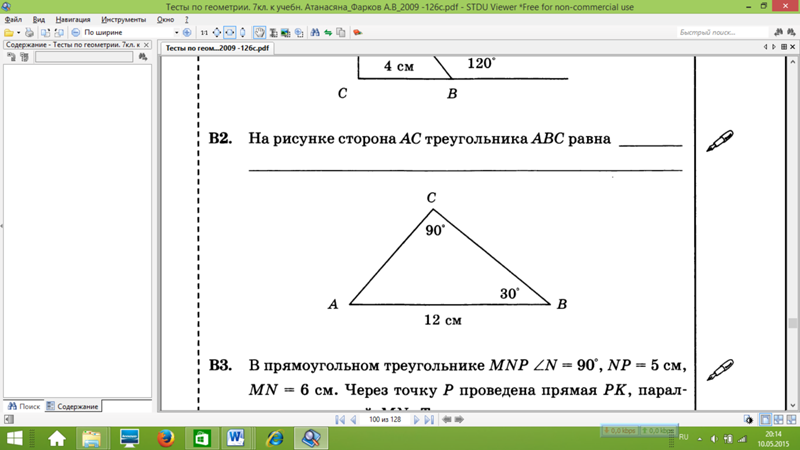
В четырехугольнике PQSR противоположные прямые параллельны друг другу.
ПК || РС и ПР || КС
Таким образом, четырехугольник PQSR является параллелограммом.
Страница № 199:
Вопрос 1:
Конструкция
ΔXYZ, где XY = 4,5 см,
YZ = 5 см и ZX = 6 см.
Ответ:
Грубое
фигура этого треугольника выглядит следующим образом.
искомый треугольник строится следующим образом.
(i) Рисовать a
отрезок YZ длиной 5 см.
(ii) Точка X находится на расстоянии 4,5 см от точки Y. Следовательно,
взяв за центр точку Y, нарисуйте дугу радиусом 4,5 см.
(iii) Точка X находится на расстоянии 6 см от точки Z. Следовательно,
взяв за центр точку Z, нарисуйте дугу радиусом 6 см. Отметьте точку
пересечения дуг как X. Соедините XY и XZ.
XYZ является обязательным
треугольник.
Страница № 199:
Вопрос 2:
Конструкция
равносторонний треугольник со стороной 5,5 см.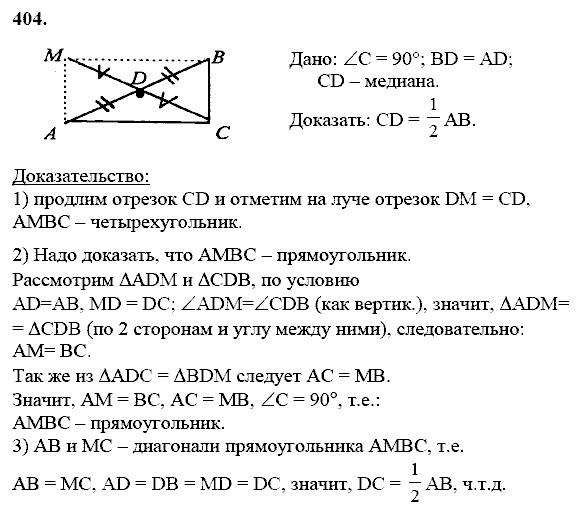
Ответ:
Ан
Нужно построить равносторонний треугольник со стороной 5,5 см. Мы знаем
что все стороны равностороннего треугольника имеют одинаковую длину.
Следовательно, необходимо построить треугольник ABC, где AB = BC = CA =
5,5 см.
Ступени
конструкции заключаются в следующем.
(i) Рисовать a
отрезок ВС длиной 5,5 см.
(ii) Взятие
точку B как центр, нарисуйте дугу радиусом 5,5 см.
(iii) Взяв точку С за центр, начертите дугу радиусом 5,5 см,
предыдущая дуга в точке A.
(iv) Присоединиться
от А до В и С.
ABC – искомый равносторонний треугольник.
Страница № 199:
Вопрос 3:
Начертите ΔPQR с PQ = 4 см, QR = 3,5 см и PR = 4 см. Какой это треугольник
?
Ответ:
Этапы построения следующие.
(i) Нарисуйте отрезок QR длиной 3,5 см.
(ii) Приняв точку Q за центр, начертите дугу радиусом 4 см.
(iii) Приняв точку R за центр, начертите дугу радиусом 4 см, пересекающую предыдущую дугу в точке P.
(iv) Соедините P с Q и R.
ΔPQR — искомый треугольник. Поскольку две стороны этого треугольника имеют одинаковую длину (PQ = PR), следовательно, ΔPQR — равнобедренный треугольник.
Видео Решение по практической геометрии (Страница: 199 , Q.No.: 3)
NCERT Решение по математике для 7 класса — Практическая геометрия 199 , Вопрос 3
Страница № 199:
Вопрос 4 :
Постройте ∆ABC так, чтобы AB
= 2,5 см, ВС = 6 см и АС = 6,5 см. Измерьте ∠B.
Ответ:
Шаги
конструкции заключаются в следующем.
(i) Рисовать a
отрезок ВС длиной 6 см.
(ii) Взятие
точку С как центр, нарисуйте дугу радиусом 6,5 см.
(iii) Приняв точку В за центр, начертите дугу радиусом 2,5 см до пересечения
предыдущая дуга в точке A.
(iv) Присоединиться
от А до В и С.
ΔABC – это
требуемый треугольник. ∠B может быть
измеряется транспортиром. Доходит до 90º.
Страница № 200:
Вопрос 1:
Конструкция
ΔDEF такой, что DE = 5 см, DF
= 3 см и m∠EDF = 90°.
Ответ:
Грубое
эскиз требуемого ΔDEF
составляет.
Ступени
конструкции заключаются в следующем.
(i)Ничья
отрезок DE длиной 5 см.
(ii) В
В точке D провести луч DX, образующий с DE угол 90°.
(iii) Взяв D за центр, начертите дугу радиусом 3 см. Так и будет
пересекают DX в точке F.
(iv) Присоединиться
от F до E. ΔDEF – требуемый
треугольник.
Страница № 200:
Вопрос 2:
Конструкция
равнобедренный треугольник, у которого длины каждой из равных сторон
6,5 см
а угол между ними равен 110°.
Ответ:
Ан
равнобедренный треугольник PQR должен быть построен с PQ = QR = 6,5 см. А
Набросок необходимого треугольника можно нарисовать следующим образом.
Ступени
конструкции заключаются в следующем.
(i) Розыгрыш
отрезок QR длиной 6,5 см.
(ii) В
точки Q, проведите луч QX, образующий с QR угол 110°.
(iii) Взятие
В качестве центра начертите дугу радиусом 6,5 см. Он пересекает QX в точке
стр.
(iv) Присоединиться
P на R, чтобы получить требуемый треугольник PQR.
Страница № 200:
Вопрос 3:
Постройте ΔABC, где BC = 7,5 см, AC = 5 см и m∠C = 60°.
Ответ:
Грубый набросок требуемого треугольника выглядит следующим образом.
Этапы строительства следующие.
(i) Нарисуйте отрезок BC длиной 7,5 см.
(ii) В точке C проведите луч CX, составляющий 60º с BC.
(iii) Приняв С за центр, начертите дугу радиусом 5 см. Он пересекает CX в точке A.
(iv) Соедините A с B, чтобы получить треугольник ABC.
Видео Решение для практической геометрии (Страница: 200 , Q.No.: 3)
NCERT Решение для 7 класса математика — практическая геометрия 200 , Вопрос 3
Страница № 202:
Вопрос 1:
Построить ΔABC, учитывая m∠A = 60°, m∠B = 30° и AB = 5,8 см .
Ответ:
Грубый набросок требуемого ΔABC выглядит следующим образом.
Этапы строительства следующие.
(i) Нарисуйте отрезок АВ длиной 5,8 см.
(ii) В точке A проведите луч AX, образующий с AB угол 60º.
(iii) В точке B проведите луч BY, составив угол 30º с AB.
(iv) Точка C должна лежать на обоих лучах, AX и BY. Следовательно, С является точкой пересечения этих двух лучей.
Это искомый треугольник ABC.
Страница № 202:
Вопрос 2:
Постройте ΔPQR, если PQ = 5 см, m∠PQR = 105° и m∠QRP = 40°.
(Подсказка: вспомните свойство суммы углов треугольника).
Ответ:
Грубый набросок требуемого ΔPQR выглядит следующим образом.
Чтобы построить ΔPQR, необходимо рассчитать показатель ∠RPQ.
в соответствии с свойством угловой суммы треугольников,
Ϫpqr + Ϫprq + Ϫrpq = 180º
105º + 40º + ↑rpq = 180 °
145º + retrpq = 180º
° С. ° = 35°
° = 35°
Этапы построения следующие.
(i) Нарисуйте отрезок PQ длиной 5 см.
(ii) В точке P проведите луч PX, образующий угол 35º с PQ.
(iii) В точке Q проведите луч QY, составляющий угол 105º с PQ.
(iv) Точка R должна лежать на обоих лучах, PX и QY. Следовательно, R — точка пересечения этих двух лучей.
Это искомый треугольник PQR.
Видео Решение по практической геометрии (Страница: 202 , Q.No.: 2)
NCERT Решение по математике для 7 класса — Практическая геометрия 202 , Вопрос 2
Страница № 202:
Вопрос 3:
Изучить
можно ли построить ΔDEF
такое, что EF = 7,2 см, m∠E =
110°
и m∠F = 80°.
Обосновать ответ.
Ответ:
Дано
то,
м∠E
= 110° и м∠F = 80°
Следовательно,
м∠E
+ м∠F = 110° + 80° =
190°
Однако,
согласно свойству суммы углов треугольников, мы должны получить
m∠E
+ м∠F + м∠D
= 180°
Следовательно,
за свойством суммы углов не следует данный треугольник. А также
А также
таким образом, мы не можем построить ΔDEF
с заданными измерениями.
Кроме того, это
можно заметить, что точка D должна лежать на обоих лучах, EX и FY, для
построить нужный треугольник. Однако оба луча не
пересекая друг друга. Следовательно, искомый треугольник не может быть
сформировался.
Страница № 203:
Вопрос 1:
Постройте прямоугольный ΔPQR, где m∠Q = 90°, QR = 8 см и PR = 10 см.
Ответ:
Грубый набросок ΔPQR выглядит следующим образом.
Этапы строительства следующие.
(i) Нарисуйте отрезок QR длиной 8 см.
(ii) В точке Q проведите луч QX, составляющий 90º с QR.
(iii) Приняв R за центр, нарисуйте дугу радиусом 10 см, чтобы пересечь луч QX в точке P.
(iv) Соедините P с R. ΔPQR — искомый прямоугольный треугольник.
Видео Решение по практической геометрии (Страница: 203 , Q.No.: 1)
NCERT Решение по математике для 7 класса — Практическая геометрия 203 , Вопрос 1
Страница № 203:
Вопрос 2:
Постройте прямоугольный треугольник, длина гипотенузы которого 6 см, а длина одного из катетов 4 см.
Ответ:
Нужно построить прямоугольный треугольник ABC с гипотенузой 6 см и одним катетом 4 см. Грубый набросок ΔABC выглядит следующим образом.
Этапы строительства следующие.
(i) Нарисуйте отрезок BC длиной 4 см.
(ii) В точке B проведите луч BX, образующий угол 90º с БК.
(iii) Приняв С за центр, начертите дугу радиусом 6 см, пересекающую луч ВХ в точке А.
(iv) Соедините А с С, чтобы получить требуемое ΔABC.
Страница № 203:
Вопрос 3:
Построить равнобедренный прямоугольный треугольник ABC, где m∠ACB
= 90° и АС = 6 см.
Ответ:
В равнобедренном треугольнике длины любых двух сторон равны.
Пусть в ΔABC, AC = BC = 6 см. Грубый набросок этого ΔABC
составляет.
Этапы строительства следующие.
(i) Нарисуйте отрезок AC длиной 6 см.
(ii) В точке C проведите луч CX, образующий угол 90º с
переменного тока.
(iii) Приняв точку C за центр, проведите дугу радиусом 6 см к
пересекают CX в точке B.
(iv) Соедините A с B, чтобы получить требуемое ΔABC.
Практическая геометрия Класс 7 Дополнительные вопросы Математика Глава 10
Дополнительные вопросы для 7 класса по математике, глава 10. Практическая геометрия
Практическая геометрия, 7 класс Дополнительные вопросы Очень короткий тип ответа
Вопрос 1.
Укажите, можно ли построить треугольник, если
(a) В ΔABC m∠A = 80°, m∠B = 60°, AB = 5,5 см
(б) In ΔPQR, PQ = 5 см, QR = 3 см, PR = 8,8 см
Решение:
(а) m∠A = 80°, м ∠B = 60°
м∠A + m∠B = 80° + 60° = 140° < 180°
Таким образом, можно построить ΔABC.
(б) PQ = 5 см, QR = 3 см, PR = 8,8 см
PQ + QR = 5 см + 3 см = 8 см < 8,8 см
или PQ + QR < PR
Таким образом, ΔPQR построить невозможно.
Вопрос 2.
Нарисуйте равносторонний треугольник, каждая сторона которого равна 4,5 см.
Решение:
Шаги построения:
(i) Нарисуйте АВ = 4,5 см.
(ii) Нарисуйте две дуги с центрами A и B и одинаковым радиусом 4,5 см, чтобы они встретились в точке C.
(iii) Соедините CA и CB.
(iv) ΔCAB — искомый треугольник.
Вопрос 3.
Нарисуйте ΔPQR, где QR = 3,5 см, m∠Q = 40°, m∠R = 60°.
Решение:
Шаги построения:
(i) Нарисуйте QR = 3,5 см.
(ii) Нарисуйте ∠Q = 40°, ∠R = 60°, которые пересекаются в точке P.
(iii) ΔPQR — искомый треугольник.
Вопрос 4.
Есть четыре варианта, из которых один правильный. Выберите правильный:
(i) Треугольник может быть построен с данным размером.
(a) 1,5 см, 3,5 см, 4,5 см
(b) 6,5 см, 7,5 см, 15 см
(c) 3,2 см, 2,3 см, 5,5 см
(d) 2 см, 3 см, 6 см
( ii) (а) m∠P = 40°, m∠Q = 60°, AQ = 4 см
(б) м∠В = 90°, м∠С = 120° , АС = 6,5 см
(в) м∠L = 150°, м∠N = 70°, MN = 3,5 см
(г) м∠ P = 105°, м∠Q = 80°, PQ = 3 см
Решение:
(i) Вариант (а) можно построить.
1,5 см + 3,5 см > 4,5 см
(ii) Вариант (а) правильный.
m∠P + m∠Q = 40° + 60° = 100° < 180°
Вопрос 5.
Чему равны другие углы прямоугольного равнобедренного треугольника?
Решение:
В прямоугольном равнобедренном треугольнике ABC ∠B = 90°
∠A + ∠C = 180° – 90° = 90°
Но ∠A = ∠B
∠A = ∠C = \(\frac { 90 }{ 2 }\) = 45°
Следовательно, искомые углы равны ∠A = ∠C = 45°
Вопрос 6.
Чему равен внешний угол равностороннего треугольника?
Решение:
Мы знаем, что мера каждого внутреннего угла = 60°
Внешний угол = 180° – 60° = 120°
Вопрос 7.
В ΔABC ∠A = ∠B = 50°. Назовите пару сторон, которые равны.
Решение:
∠A = ∠B = 50°
AC = BC [∵ Стороны, противоположные равным углам равны]
Следовательно, искомые стороны равны AC и BC.
Вопрос 8.
Если один из других углов прямоугольного треугольника тупой, то можно ли построить треугольник.
Решение:
Мы знаем, что углы, отличные от прямого угла прямоугольного треугольника, являются острыми углами.
Значит, такой треугольник построить невозможно.
Вопрос 9.
Укажите, равны ли данные пары треугольников.
Решение:
Здесь AB = PQ = 3,5 см
AC = PR = 5,2 см
∠BAC = ∠QPR = 70°
ΔABC = ΔPQR [по правилу SAS]
Практическая геометрия, класс 7 Дополнительные вопросы Тип краткого ответа
Вопрос 10.
Нарисуйте ΔABC, в котором BC = 5 см, AB = 4 см и м∠В = 50°.
Решение:
Шаги построения:
(i) Нарисуйте ВС = 5 см.
(ii) Начертите ∠B = 50° и отрежьте AB = 4 см.
(iii) Присоединяйтесь к AC.
(iv) ΔABC — искомый треугольник.
Вопрос 11.
Нарисуйте ΔPQR, где QR = 5,4 см, ∠Q = 40° и PR = 6,2 см.
Решение:
Шаги построения:
(i) Нарисуйте QR = 5,4 см.
(ii) Нарисуйте ∠Q = 40°.
(iii) Возьмите R за центр и с радиусом 6,2 см нарисуйте дугу, чтобы пересечь прежнюю угловую линию в точке P.
(iv) Соедините PR.
(v) ΔPQR — искомый треугольник.
Вопрос 12.
Постройте ΔPQR, в котором m∠P = 60° и m∠Q = 30°, QR = 4,8 см.
Решение:
м∠Q = 30°, м∠P = 60°
м∠Q + m∠P + m∠R = 180° (свойство суммы углов треугольника)
30° + 60° + m∠R = 180°
90° + м∠R = 180°
м∠R = 180° – 90°
м∠R = 90°
Шаги построения:
(i) Нарисуйте QR = 4,8 см.
(ii) Нарисуйте ∠Q = 30°.
(iii) Начертите ∠R = 90°, который пересекает прежнюю линию угла в точке P.
(iv) ∠P = 180° – (30° + 90°) = 60°
(v) ΔPQR – искомый треугольник.
Практическая геометрия Класс 7 Дополнительные вопросы Навыки мышления высшего порядка [HOTS] Тип
Вопрос 13.
Начертите равнобедренный прямоугольный треугольник, гипотенуза которого равна 5,8 см.
Решение:
Прямоугольный треугольник является равнобедренным треугольником
Каждый из его острых углов = \(\frac { 90 }{ 2 }\) = 45°
Этапы построения:
(i) Нарисуйте AB = 5,8 см.
(ii) Построить ∠A = 45° и ∠B = 45°, чтобы они встретились в точке C.
(iii) ∠C = 180° – (45° + 45°) = 90°
(iv) ΔACB искомый равнобедренный прямоугольный треугольник.
Вопрос 14.
Постройте ΔABC так, что AB = 6,5 см, AC = 5 см и высота AP до BC равна 4 см.
Решение:
Шагов построения:
(i) Проведите прямую l и возьмите на ней любую точку P.
(ii) Постройте перпендикуляр к l в точке P.
(iii) Отрежьте AP = 4 см.
(iv) Начертите две дуги с центром А и радиусами 6,5 см и 5 см, чтобы пересечь линию l в точках В и С соответственно.
(v) Соедините AB и AC.
(vi) ΔABC — искомый треугольник.
Вопрос 15.
Постройте равносторонний треугольник, высота которого равна 4,5 см.
Решение:
Шаги построения:
(i) Проведите любую прямую l и отметьте на ней точку D.
(ii) Постройте перпендикуляр к l в точке D и отрежьте AD = 4,5 см.
(iii) Начертите угол 30° по обе стороны от AD так, чтобы линия l пересекалась в точках B и C.
(iv) ΔABC — искомый равносторонний треугольник.
Дополнительные вопросы по математике для 7-го класса
Решения NCERT для 7-го класса по математике
Практическая геометрия для 7-го класса, дополнительные вопросы по математике, глава 10
Практическая геометрия, 7-й класс, дополнительные вопросы по математике, глава 10 Геометрия
Практическая геометрия Класс 7 Дополнительные вопросы Очень короткий ответ Тип
Вопрос 1.
Укажите, можно ли построить треугольник, если
(а) В ΔABC m∠A = 80°, m∠B = 60°, AB = 5,5 см
(b) В ΔPQR, PQ = 5 см, QR = 3 см, PR = 8,8 см
Решение:
(a) m∠A = 80°, m∠B = 60°
m∠A + m∠B = 80° + 60° = 140° < 180 °
Итак, ΔABC можно построить.
(b) PQ = 5 см, QR = 3 см, PR = 8,8 см
PQ + QR = 5 см + 3 см = 8 см < 8,8 см
или PQ + QR < PR
Итак, ΔPQR построить невозможно .
Присоединяйтесь к программе регулярных занятий Infinity Learn!
Загрузите БЕСПЛАТНО PDF-файлы, решенные вопросы, работы за предыдущий год, викторины и головоломки!
+91
Проверьте код OTP (обязательно)
класс
— Класс 6CLASS 7CLASS 8CLASS 9CLASS 10CLASS 11CLASS 12
КУРС
— CBSEIIT-JEENEET
ШКОЛА/Колледж.
НетДа
Я согласен с условиями и политикой конфиденциальности.
Вопрос 2.
Нарисуйте равносторонний треугольник, каждая сторона которого равна 4,5 см.
Решение:
Шаги построения:
(i) Нарисуйте АВ = 4,5 см.
(ii) Нарисуйте две дуги с центрами A и B и одинаковым радиусом 4,5 см, чтобы они встретились в точке C.
(iii) Соедините CA и CB.
(iv) ΔCAB — искомый треугольник.
Вопрос 3.
Нарисуйте ΔPQR, где QR = 3,5 см, m∠Q = 40°, m∠R = 60°.
Решение:
Шаги построения:
(i) Нарисуйте QR = 3,5 см.
(ii) Нарисуйте ∠Q = 40°, ∠R = 60°, которые пересекаются в точке P.
(iii) ΔPQR — искомый треугольник.
Вопрос 4.
Есть четыре варианта, из которых один правильный. Выберите правильный:
(i) Треугольник может быть построен с данным размером.
(a) 1,5 см, 3,5 см, 4,5 см
(b) 6,5 см, 7,5 см, 15 см
(c) 3,2 см, 2,3 см, 5,5 см
(d) 2 см, 3 см, 6 см
( ii) (а) m∠P = 40°, m∠Q = 60°, AQ = 4 см
(б) m∠B = 90°, m∠C = 120°, AC = 6,5 см
(в) м ∠L = 150°, м∠N = 70°, MN = 3,5 см
(г) м∠P = 105°, м∠Q = 80°, PQ = 3 см
Решение:
(i) Вариант (а) построить можно.
1,5 см + 3,5 см > 4,5 см
(ii) Вариант (а) правильный.
m∠P + m∠Q = 40° + 60° = 100° < 180°
Вопрос 5.
Чему равны другие углы прямоугольного равнобедренного треугольника?
Решение:
В прямоугольном равнобедренном треугольнике ABC ∠B = 90°
∠A + ∠C = 180° – 90° = 90°
Но ∠A = ∠B
∠A = ∠C = \(\frac { 90 }{ 2 }\) = 45°
Отсюда искомые углы равны ∠A = ∠C = 45°
Вопрос 6.
Чему равен внешний угол равностороннего треугольника?
Решение:
Мы знаем, что мера каждого внутреннего угла = 60°
Внешний угол = 180° – 60° = 120°
Вопрос 7.
В ΔABC ∠A = ∠B = 50°. Назовите пару сторон, которые равны.
Решение:
∠A = ∠B = 50°
AC = BC [∵ Стороны, противоположные равным углам, равны]
Следовательно, искомые стороны равны AC и BC.
Вопрос 8.
Если один из других углов прямоугольного треугольника тупой, то можно ли построить треугольник.
Решение:
Мы знаем, что углы, отличные от прямого угла прямоугольного треугольника, являются острыми углами.
Значит, такой треугольник построить невозможно.
Вопрос 9.
Укажите, равны ли данные пары треугольников.
Решение:
Здесь AB = PQ = 3,5 см
AC = PR = 5,2 см
∠BAC = ∠QPR = 70°
ΔABC = ΔPQR [по правилу SAS]
Практическая геометрия, класс 7 Дополнительные вопросы Тип короткого ответа
Вопрос 10.
Начертите ΔABC, где BC = 5 см, AB = 4 см и m∠B = 50°.
Решение:
Шаги построения:
(i) Нарисуйте ВС = 5 см.
(ii) Начертите ∠B = 50° и отрежьте AB = 4 см.
(iii) Присоединяйтесь к AC.
(iv) ΔABC — искомый треугольник.
Вопрос 11.
Нарисуйте ΔPQR, где QR = 5,4 см, ∠Q = 40° и PR = 6,2 см.
Решение:
Шаги построения:
(i) Нарисуйте QR = 5,4 см.
(ii) Нарисуйте ∠Q = 40°.
(iii) Возьмите R за центр и с радиусом 6,2 см нарисуйте дугу, чтобы пересечь прежнюю угловую линию в точке P.
(iv) Присоединяйтесь к PR.
(v) ΔPQR — искомый треугольник.
Вопрос 12.
Постройте ΔPQR, в котором m∠P = 60° и m∠Q = 30°, QR = 4,8 см.
Решение:
м∠Q = 30°, м∠P = 60°
м∠Q + m∠P + m∠R = 180° (свойство суммы углов треугольника)
30° + 60° + m∠R = 180 °
90° + м∠R = 180°
м∠R = 180° – 90°
м∠R = 90°
Шаги построения:
(i) Нарисуйте QR = 4,8 см.
(ii) Нарисуйте ∠Q = 30°.
(iii) Начертите ∠R = 90°, который пересекает прежнюю угловую линию в точке P.
(iv) ∠P = 180° – (30° + 90°) = 60°
(v) ΔPQR – искомый треугольник.
Практическая геометрия Класс 7 Дополнительные вопросы Навыки мышления высшего порядка [HOTS] Тип
Вопрос 13.
Начертите равнобедренный прямоугольный треугольник, гипотенуза которого равна 5,8 см.
Решение:
Прямоугольный треугольник является равнобедренным треугольником
Каждый из его острых углов = \(\frac { 90 }{ 2 }\) = 45°
Этапы построения:
(i) Нарисуйте АВ = 5,8 см.
(ii) Постройте ∠A = 45° и ∠B = 45° так, чтобы они встречались друг с другом в точке C.
(iii) ∠C = 180° – (45° + 45°) = 90°
(iv) ΔACB – искомый равнобедренный прямоугольный треугольник.
Вопрос 14.
Постройте ΔABC так, что AB = 6,5 см, AC = 5 см и высота AP до BC равна 4 см.
Решение:
Шаги построения:
(i) Проведите прямую l и возьмем на ней любую точку P.
(ii) Постройте перпендикуляр к l в точке P.
(iii) Отрежьте AP = 4 см.
(iv) Начертите две дуги с центром А и радиусами 6,5 см и 5 см, чтобы пересечь линию l в точках В и С соответственно.
(v) Соедините AB и AC.
(vi) ΔABC — искомый треугольник.
Вопрос 15.
Постройте равносторонний треугольник, высота которого равна 4,5 см.
Решение:
Шаги построения:
(i) Проведите любую прямую l и отметьте на ней точку D.
(ii) Постройте перпендикуляр к l в точке D и отрежьте AD = 4,5 см.
(iii) Начертите угол 30° по обе стороны от AD так, чтобы линия l пересекалась в точках B и C.
(iv) ΔABC — искомый равносторонний треугольник.
Сопутствующее содержимое
Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 4 Geometry Ex 4.1 — Samacheer Kalvi
пересмотреть полную новую программу Совета штата Тамилнаду и получить больше баллов на экзаменах.
Вопрос 1.
Могут ли 30°, 60° и 90° быть углами треугольника?
Решение:
Даны углы 30°, 60° и 90°
Сумма углов = 30° + 60° + 90° = 180°
∴ Данные углы образуют треугольник.
Вопрос 2.
Можете ли вы нарисовать треугольник с углами 25°, 65° и 80°?
Решение:
Даны углы 25°, 65° и 80°.
Сумма углов = 25° + 65° + 80° = 170° ≠ 180
∴ Мы не можем построить треугольник с этими мерами.
Найдите значение x в каждом из данных треугольников.
Вопрос 3.
В каждом из следующих треугольников найдите значение x.
Решение:
(i) Пусть ∠G = x
По свойству суммы углов мы знаем, что
∠E + ∠F + ∠G = 180°
80° + 55° + x = 180°
135° + x = 180°
x = 45°
(ii) Пусть ∠M = x
По свойству суммы углов треугольников имеем
∠M + ∠M + ∠O = 180°
x + 96° + 22° = 180°
x + 118° = 180°
X = 180° – 118° = 620
(iii) Пусть ∠Z = (2x + 1)° и ∠Y = 90°
По свойству суммы треугольников имеем
∠ x + ∠y + ∠z = 180°
29° + 90° + (2x + 1)° = 180° 9{\circ}}{6}\) = 27°
x = 27°
Вопрос 4.
Два отрезка \(\overline{A D}\) и \(\overline{BC}\) пересекаются в O. Соединяя \(\overline{A B}\) и \(\overline{D C}\), мы получаем два треугольника, ∆AOB и ∆DOC, как показано на рисунке. Найдите ∠A и ∠B.
Решение:
В ∆AOB и ∆DOC,
∠AOB = ∠DOC [∵ Вертикально противоположные углы равны]
Пусть ∠AOB = ∠DOC = y
По свойству суммы углов треугольника имеем
∠A + ∠ B + ∠AOB = ∠D + ∠C + ∠DOC = 180° 9{\circ}}{5}\) = 20°
∠A = 3x = 3 × 20 = 60°
∠B = 2x = 2 × 20 = 40°
∠A = 60°
∠B = 40°
Вопрос 5.
Посмотрите на рисунок и найдите значение
∠A + ∠N + ∠G + ∠L + ∠E + ∠S.
Решение:
На рисунке у нас есть два треугольника, а именно ∆AGE и ∆NLS.
По свойству суммы углов треугольников,
Сумма углов ∆AGE = ∠A + ∠G + ∠E = 180° …(1)
Также сумма углов ∆NLS = ∠N + ∠L + ∠S = 180 ° … (2)
(1) + (2) ∠A + ∠G + ∠E + ∠N + ∠L + ∠S = 180° + 180° 9{\circ}}{12}\)
x = 15°
∴ Угол равен 3x = 3 × 15° = 45°
5x = 5 × 15° = 75°
4x = 4 × 15° = 60°
Три угла треугольника равны 45°, 75°, 60°
Вопрос 7.
В ∆RST ∠S на 10° больше, чем ∠R, а ∠T на 5° меньше, чем ∠S, найдите три угла треугольник.
Решение:
In ∆RST. Пусть ∠R = х.
Тогда данное S на ∠10° больше, чем ∠R
∴ ∠S = x + 10°
Также задано, что ∠T на 5° меньше, чем ∠S.
Итак, ∠T = ∠S – 5° = (x + 10)° – 5° = x + 10° – 5° 9{\circ}}{3}\) = 55°
∠R = x = 55°
∠S = x + 10° = 55° + 10° = 65°
∠T = x + 5° = 55° + 5° = 60°
∴ ∠R = 55°
∠S = 65°
∠T = 60°
Вопрос 8.
В ∆ABC , если ∠B в 3 раза больше ∠A, а ∠C в 2 раза больше ∠A , то найти углы.
Решение:
В ABC, пусть ∠A = x,
тогда ∠B = 3 раза ∠A = 3x
∠C = 2 раза ∠A = 2x
По свойству суммы углов треугольников,
Сумма трех углов ∆ АВС =180°.
∠А + ∠В + ∠С = 180
х + 3х + 2х = 180°
х (1 + 3 + 2) = 180° 9{\circ}}{6}\) = 30°
∠A = x = 30°
∠B = 3x = 3 × 30° = 90°
∠C = 2x = 2 × 30° = 60°
∴ ∠ A = 30°
∠B = 90°
∠C = 60°
Вопрос 9.
В ∆XYZ, если ∠X : ∠Z равно 5 : 4 и ∠Y = 72°. Найдите ∠X и ∠Z.
Решение:
Дано в ∆XYZ, ∠X : ∠Z = 5 : 4
Пусть ∠X = 5x; и ∠Z = 4x, учитывая ∠Y = 72°
По свойству суммы углов треугольников сумма трех углов треугольника равна 180°.
∠X + ∠Y + ∠Z = 180°
5x + 72 + 4x = 180°
5x + 4x = 180° – 72° 9{\circ}}{9}\) = 12°
∠X = 5x = 5 × 12° = 60°
∠Z = 4x = 4 × 12° = 48°
∴ ∠X = 60°
∠Z = 48°
Вопрос 10.
В прямоугольном треугольнике ABC угол ∠B прямой, ∠A равен x + 1, а ∠C равен 2x + 5. Найдите ∠A и ∠C.
Найдите ∠A и ∠C.
Решение:
Дано в ∆ABC ∠B = 90°
∠A = x + 1
∠B = 2x + 5
По свойству суммы углов треугольников
Сумма трех углов ∆ABC = 180°
∠A + ∠B + ∠C = 180°
(x + 1) + 90° + (2x + 5) = 180°
x + 2x + 1° + 90° + 5° = 180° 9{\circ}}{3}\) = 28°
∠A = x + 1 = 28 + 1 = 29
∠C = 2x + 5 = 2 (28) + 5 = 56 + 5 = 61
∴ ∠A = 29°
∠C = 61°
Вопрос 11.
В прямоугольном треугольнике MNO ∠N = 90°, MO продолжается в P. Если ∠NOP = 128°, найдите два других угла ∆ МНО.
Решение:
Дано ∠N = 90°
МО продолжается до P, внешний угол ∠NOP = 128°
Внешний угол равен сумме внутренних противоположных углов.
∴ ∠M + ∠N = 128°
∠M + 90° = 128°
∠M = 128° – 90°
∠M = 38°
По свойству суммы углов треугольников,
∴ ∠M + ∠N + ∠O = 180°
38° + 90° + ∠O = 180°
∠ O = 180° – 128°
∠O = 52°
∴ ∠M = 38° и ∠O = 52°
Вопрос 12.
Найдите значение x в каждом из данных треугольников. {\circ} {11}\) = 11° 9{\circ}}{5}\) = 21°
{\circ} {11}\) = 11° 9{\circ}}{5}\) = 21°
x = 21°
Вопрос 14.
Используя данную цифру, найдите значение x.
Решение:
В ∆EDC сторона DE продолжается до B, образуя внешний угол ∠CEB = x.
Мы знаем, что внешний угол равен сумме противолежащих внутренних углов
∠CEB = ∠CDE + ∠ECD
x = 50° + 60°
x = 110°
Вопрос 15.
Используя схему, найдите значение х.
Решение:
Данный треугольник является равносторонним, так как три стороны равны. У равностороннего треугольника все три угла равны и равны 60°. Также внешний угол равен сумме противоположных внутренних углов.
х = 60° + 60°.
x = 120°
Вопросы типа цели
Вопрос 16.
Углы треугольника относятся как 2:3:4. Тогда углы равны
(i) 20,30,40
(ii) 40, 60, 80
(iii) 80, 20, 80
(iv) 10, 15, 20
Ответ:
(ii) 40, 60 , 80
Вопрос 17.
Один из углов треугольника равен 65°. Если разница двух других углов равна 45°, то два угла равны
(i) 85°, 40°
(ii) 70°, 25°
(iii) 80°, 35°
(iv) 80° , 135°
Ответ:
(iii) 80°, 35°
Вопрос 18.
На данном рисунке AB параллельна CD. Тогда значение b равно
(i) 112°
(ii) 68°
(iii) 102°
(iv) 62° A
Ответ:
(ii) 68°
Вопрос 19.
В данном рисунок, какое из следующих утверждений верно?
(i) x + y + z = 180°
(ii) x + y + z = a + b + c
(iii) x + y + z = 2(a + b + c)
(iv) х + у + г = 3 (а + б + с)
Ans :
(iii) x + y + z = 2(a + b + c)]
Вопрос 20.
Внешний угол треугольника равен 70°, а два внутренних противоположных угла равны. Тогда мера каждого из этих углов будет
(i) 110°
(ii) 120°
(iii) 35°
(iv) 60°
Ответ:
(iii) 35°
Вопрос 21.
В ∆ABC AB = AC. Значение х равно _____.
(i) 80°
(ii) 100°
(iii) 130°
(iv) 120°
Ответ:
(iii) 130°
Вопрос 22.
Если внешний угол треугольника равен 115°, а один из внутренних противоположных углов равен 35°, то два других угла треугольника равны
(i) 45°, 60°
(ii) 65°, 80°
(iii) 65°, 70°
(iv) 115°, 60°
Ответ:
(ii) 65°, 80°
Как найти угол в прямоугольном треугольнике
Все ресурсы по базовой геометрии
9 Диагностика Тесты
164 практических теста
Вопрос дня
Карточки
Учитесь по концепции
← Предыдущая 1 2 3 Следующая →
Справка по базовой геометрии »
Плоская геометрия »
Треугольники »
Прямоугольные треугольники »
How to find an angle in a right triangle
Find angle C.
Possible Answers:
C=72
C=65
None of these
C=53
C=70
Правильный ответ:
C=65
Пояснение:
Во-первых, знайте, что сумма всех углов треугольника составляет 180 градусов.
У каждого треугольника 3 угла. Таким образом, у нас есть сумма трех углов, как показано на рисунке:
, где у нас есть углы A, B и C. В нашем прямоугольном треугольнике один угол равен 25 градусам, и мы назовем этот угол A. Другой известный угол равен 90 градусов, и мы назовем этот угол B. Таким образом, у нас есть
Упростите и решите для C.
Сообщить об ошибке
Что из следующего может быть двумя мерами угла прямоугольного треугольника ?
Возможные ответы:
Правильный ответ:
Пояснение:
В прямоугольном треугольнике не может быть тупого угла; это исключает выбор между 100 и 10.
Сумма острых углов прямоугольного треугольника должна составлять 90 градусов. По этому критерию можно исключить три варианта:
Оставшийся вариант правильный:
Сообщить об ошибке
Прямоугольный треугольник имеет угол, который в 15 раз больше, чем угол другого треугольника. Чему равен меньший угол?
Возможные ответы:
Правильный ответ:
Пояснение:
Сумма углов треугольника равна 180. В прямоугольном треугольнике один угол равен 90. Таким образом, сумма двух других углов будет равна 90.
Пусть = первый угол и = второй угол
Итак уравнение для решения становится или
Таким образом, первый угол и второй угол .
Таким образом, меньший угол равен
Сообщить об ошибке
Угол в показанном ниже треугольнике (не в масштабе) равен 35 градусам. Что такое угол?
Что такое угол?
Возможные ответы:
градусов
градусов
градусов
градусов
Правильный ответ:
градусов
.
Пояснение:
Сумма внутренних углов треугольника всегда равна 180 градусам. Нам дан угол и, поскольку указано, что это прямоугольный треугольник, мы знаем, что угол равен 90 градусов. Таким образом, мы знаем 2 из 3 и можем определить третий угол.
Угол равен 55 градусам.
Сообщить об ошибке
Что из следующего не может быть верным для прямоугольного треугольника?
Возможные ответы:
Один из катетов может быть длиннее гипотенузы.
Прямоугольный треугольник может иметь тупой угол.
Прямоугольный треугольник может быть равносторонним.
Ни одно из других утверждений не может быть верным для прямоугольного треугольника.
Меры углов прямоугольного треугольника могут суммироваться.
Правильный ответ:
Ни одно из других утверждений не может быть верным для прямоугольного треугольника.
Объяснение:
Все из этих утверждений ложны.
Прямоугольный треугольник может быть равносторонним.
Неверно: Равносторонний треугольник должен иметь три угла, каждый из которых измеряется.
Один катет может быть длиннее гипотенузы.
Ложь: Каждый катет на короче гипотенузы.
Прямоугольный треугольник может иметь тупой угол.
Ложь: Оба угла прямоугольного треугольника, которые не являются прямыми , должны быть острыми.
Меры углов прямоугольного треугольника могут суммироваться.
Ложь: Меры любой суммы треугольников .
Сообщить об ошибке
Какова мера угла треугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Формула для нахождения всех углов треугольника:
Чтобы найти меру угла , мы подставляем значения и . Поскольку угол прямой, мы знаем, что мера будет равна .
Сообщить об ошибке
Найдите градусную меру недостающего угла.
Возможные ответы:
Правильный ответ:
Пояснение:
Сумма всех углов треугольника равна 180º.
Чтобы найти значение остаточного угла, вычтите известные углы из 180º:
Следовательно, третий угол равен 43º.
Сообщить об ошибке
Прямоугольный треугольник имеет два равных угла, какова их мера?
Возможные ответы:
Правильный ответ:
Пояснение:
Внутренние углы треугольника всегда составляют в сумме 180 градусов, и было дано, что треугольник прямоугольный, а это означает, что один из углов равен 90 градусов.
Это оставляет 90 градусов, чтобы равномерно разделить два оставшихся угла, как было показано в вопросе.
Следовательно, каждый из двух равных углов имеет размер 45 градусов.
Сообщить об ошибке
Какого угла не хватает в этом прямоугольном треугольнике?
Возможные ответы:
Правильный ответ:
Пояснение:
Сумма всех углов треугольника равна .
Это означает, что .
Используя тот факт, что 90 составляет половину от 180, мы можем вычислить, что недостающий угол x плюс 34 добавляется к оставшимся 90, и мы можем просто вычесть
.
Сообщить об ошибке
Решить:
Возможные ответы:
Правильный ответ:
Пояснение:
Сумма углов треугольника составляет 180 градусов. Мы уже знаем, что один из углов равен 90 градусов, поэтому мы можем вычесть 90 из 180: два других угла должны прибавиться к 90 градусам.
Теперь мы можем вычесть, чтобы получить x:
Сообщить об ошибке
← Предыдущая 1 2 3 Следующая →
Уведомление об авторских правах
Все ресурсы по базовой геометрии
9 Диагностические тесты
164 практических теста
Вопрос дня
Карточки
Learn by Concept
30-60-90 Треугольник — Правила, Формула, Теорема, Стороны, Примеры
Треугольник 30-60-90 является особым прямоугольным треугольником, поскольку отношение углов треугольника равно 1. :2:3. Существуют различные типы треугольников, такие как тупоугольные, равнобедренные, остроугольные, равносторонние и так далее. Но только несколько типов треугольников считаются особыми треугольниками. Эти треугольники особенные, поскольку их стороны и углы постоянны и предсказуемы. Их свойства можно использовать для решения различных задач геометрии или тригонометрии. А 30-60-90-треугольник — произносится как «тридцать шестьдесят девяносто» — действительно является одним из таких очень особых типов треугольников.
:2:3. Существуют различные типы треугольников, такие как тупоугольные, равнобедренные, остроугольные, равносторонние и так далее. Но только несколько типов треугольников считаются особыми треугольниками. Эти треугольники особенные, поскольку их стороны и углы постоянны и предсказуемы. Их свойства можно использовать для решения различных задач геометрии или тригонометрии. А 30-60-90-треугольник — произносится как «тридцать шестьдесят девяносто» — действительно является одним из таких очень особых типов треугольников.
В этом уроке мы изучим концепцию треугольника 30-60-90 и узнаем все о нем, включая его формулу, определение, стороны, площадь и правила, применимые к этому треугольнику.
| 1. | Что такое треугольник 0-60-90? |
| 2. | 30-60-90 Стороны треугольника |
| 3. | 30-60-90-Теорема о треугольнике |
| 4. | 30-60-90 Треугольная защита |
5. |
30-60-90 Правило треугольника |
| 6. | Площадь треугольника 30-60-90 |
| 7. | Часто задаваемые вопросы по треугольнику 30-60-90 |
Что такое треугольник 30-60-90?
30-60-90 называется особым прямоугольным треугольником, так как углы этого треугольника находятся в уникальном соотношении 1:2:3. Здесь под прямоугольным треугольником понимается любой треугольник, содержащий угол 90°. Треугольник 30-60-90 — это особый прямоугольный треугольник, углы которого всегда равны 30°, 60° и 90°. Вот несколько вариантов треугольника 30-60-90. Треугольники ABC и PQK составляют 30-60-90 треугольников.
Здесь в треугольнике ABC ∠ C = 30°, ∠ A = 60° и ∠ B = 90° и в треугольнике PQK ∠ P = 30°, ∠ K = 60° и ∠ Q = 90°
30-60-90 Стороны треугольника
Треугольник 30-60-90 является особым треугольником, поскольку длины его сторон всегда находятся в постоянном соотношении друг с другом.
В приведенном ниже треугольнике ABC 30-60-90 ∠ C = 30°, ∠ A = 60° и ∠ B = 90°. Мы можем понять отношения между каждой из сторон из следующих определений:
- Сторона, лежащая против угла 30°, AB = y, всегда будет наименьшей, так как 30° — наименьший угол в этом треугольнике
- Сторона, противоположная углу 60°, BC = y × √ 3 = y √ 3 будет средней длиной, потому что 60° — средний угол в градусах в этом треугольнике
- На стороне, противоположной углу 90°, гипотенуза AC = 2y будет наибольшей стороной, поскольку 90° является наибольшим углом.
Стороны треугольника 30-60-90 всегда находятся в соотношении 1:√3:2. Это также известно как формула треугольника 30-60-90 для сторон y: y√3: 2y. Давайте изучим вывод этого отношения в разделе доказательства треугольника 30-60-90. Эту формулу можно проверить с помощью теоремы Пифагора.
Рассмотрим несколько примеров треугольника 30-60-90 градусов со следующими длинами сторон:
|
Здесь, в треугольнике 30-60-90 DEF ∠ F = 30°, ∠ D = 60° и ∠ E = 90°
|
Здесь, в треугольнике 30-60-90 PQR ∠ R = 30°, ∠ P = 60° и ∠ Q = 90°
|
30-60-90-Теорема о треугольнике
Формулировка теоремы 30-60-90-треугольника дается как,
Утверждение: Длина гипотенузы в два раза больше длины самой короткой стороны, а длина другой стороны в √3 раза больше длины самой короткой стороны в треугольнике 30-60-90.
Формула треугольника 30-60-90
Вышеупомянутая теорема может быть математически записана как Формула треугольника 30-60-90 в виде 1:√3:2, что является отношением трех сторон треугольника 30-60-. 90-треугольник. Другая формула для этого особого треугольника 1:2:3, которая является отношением трех углов треугольника 30-60-90.
30-60-90-Triangle Proof
Рассмотрим равносторонний треугольник ABC с длиной стороны, равной ‘a’.
Теперь проведите перпендикуляр из вершины A на сторону BC в точке D треугольника ABC. Перпендикуляр в равностороннем треугольнике делит другую сторону пополам.
Треугольники ABD и ADC — это два треугольника 30-60-90. Оба треугольника подобны и прямоугольные треугольники. Следовательно, мы можем применить теорему Пифагора, чтобы найти длину AD.
(AB) 2 = (AD) 2 + (BD) 2
A 2 = (AD) 2 + (A/2) 2
A 2 001000 2
A 2 00100100 — (a/2) 2 = (AD) 2
3a 2 /4 = (AD) 2
(a √ 3)/2 = AD 90a (57 AD 90a) √ 3)/2
BD = a/2
AB = a
Эти стороны также подчиняются тому же соотношению a/2 : (a√3)/2: a
Умножьте на 2 и разделите на ‘ а’,
(2а)/(2а) : (2а√3)/(2а): (2а/а)
Получаем 1:√3:2. Это теорема треугольника 30-60-90.
Это теорема треугольника 30-60-90.
30-60-90 Правило треугольника
В треугольнике 30-60-90 меру любой из трех сторон можно узнать, зная меру хотя бы одной стороны треугольника. Это называется правилом треугольника 30-60-90. В приведенной ниже таблице показано, как найти стороны треугольника 30-60-90, используя правило треугольника 30-60-90:
| База дается | Дан перпендикуляр | Гипотенуза дана |
|---|---|---|
|
Предполагается, что основание треугольника BC равно ‘a’. |
Предполагается, что перпендикуляр DE треугольника равен ‘a’. |
Предполагается, что гипотенуза PR треугольника равна ‘a’. |
|
Перпендикуляр треугольника ABC равен AB = (a /√3) Гипотенуза треугольника ABC равна AC = (2a)/√3 |
Основание треугольника DEF равно EF = √3a. Гипотенуза треугольника DEF равна DF = 2a. |
Основание треугольника PQR равно QR = (√3a)/2. Перпендикуляр треугольника PQR равен PQ = (a/2). |
Площадь треугольника 30-60-90
Формула для вычисления площади треугольника: = (1/2) × основание × высота. В прямоугольном треугольнике высота есть перпендикуляр треугольника. Таким образом, формула для вычисления площади прямоугольного треугольника = (1/2) × основание × перпендикуляр
Давайте узнаем, как применить эту формулу, чтобы найти площадь треугольника 30-60-90.
Основание BC треугольника принимается равным а, а гипотенуза треугольника ABC равна АС. В предыдущем разделе мы узнали, как найти гипотенузу, зная основание.
Применим изученную формулу.
Таким образом, перпендикуляр треугольника = a/√3
Площадь треугольника = (1/2) × основание × перпендикуляр
Площадь = 1/2 × a × a/√3
Таким образом, площадь треугольника 30-60-90, когда основание (сторона средней длины) обозначена как «а», составляет: Треугольники
Важные примечания о треугольнике 30-60-90
Вот несколько моментов, которые следует помнить при изучении треугольника 30-60-9. 0 треугольников:
0 треугольников:
- Треугольник 30-60-90 называется особым прямоугольным треугольником, так как углы этого треугольника находятся в уникальном отношении 1:2:3, а стороны находятся в соотношении 1:√3:2
- Треугольник 30-60-90 — это особый прямоугольный треугольник, углы которого всегда равны 30°, 60° и 90°
- Все стороны треугольника 30-60-90 можно вычислить, если известна любая сторона. Это называется правилом треугольника 30-60-90.
Часто задаваемые вопросы по телефону 30-60-90 Треугольник
Что такое треугольник 30-60-90?
Треугольник 30-60-90 называется особым прямоугольным треугольником, так как углы этого треугольника находятся в уникальном соотношении 1:2:3. Треугольник 30-60-90 — это особый прямоугольный треугольник, углы которого всегда равны 30°, 60° и 90°.
Каков периметр треугольника 30-60-90?
Периметр треугольника 30 60 90 с наименьшей стороной, равной а, является суммой всех трех сторон. Две другие стороны равны a√3 и 2a. Периметр треугольника равен а+а√3+2а = 3а+а√3 = а√3(1+√3).
Две другие стороны равны a√3 и 2a. Периметр треугольника равен а+а√3+2а = 3а+а√3 = а√3(1+√3).
Есть ли какие-нибудь советы по запоминанию правил треугольника 30-60-90?
Этот метод можно использовать для запоминания правила треугольника 30-60-90. Можно запомнить его как 1, 3, 2; это может напоминать соотношение сторон, все, что нужно помнить, это то, что средний член равен √3
. Каковы длины сторон треугольника 30-60-90?
Стороны треугольника 30-60-90 имеют заданный узор. Сторона, противоположная углу 30°, y всегда будет наименьшей, так как 30° — наименьший угол в этом треугольнике. Сторона, противоположная углу 60°, y√3, будет средней длиной, потому что 60° — это средний угол в градусах в этом треугольнике. Сторона, лежащая напротив 9.Угол 0 °, 2y будет наибольшей стороной, потому что 90 ° — самый большой угол.
Каковы правила для треугольника 45-45-90?
Треугольник 45-45-90 имеет прямой угол и два угла по 45 градусов. Две стороны треугольника 45-45-90 всегда равны, а гипотенуза треугольника всегда противоположна прямому углу.
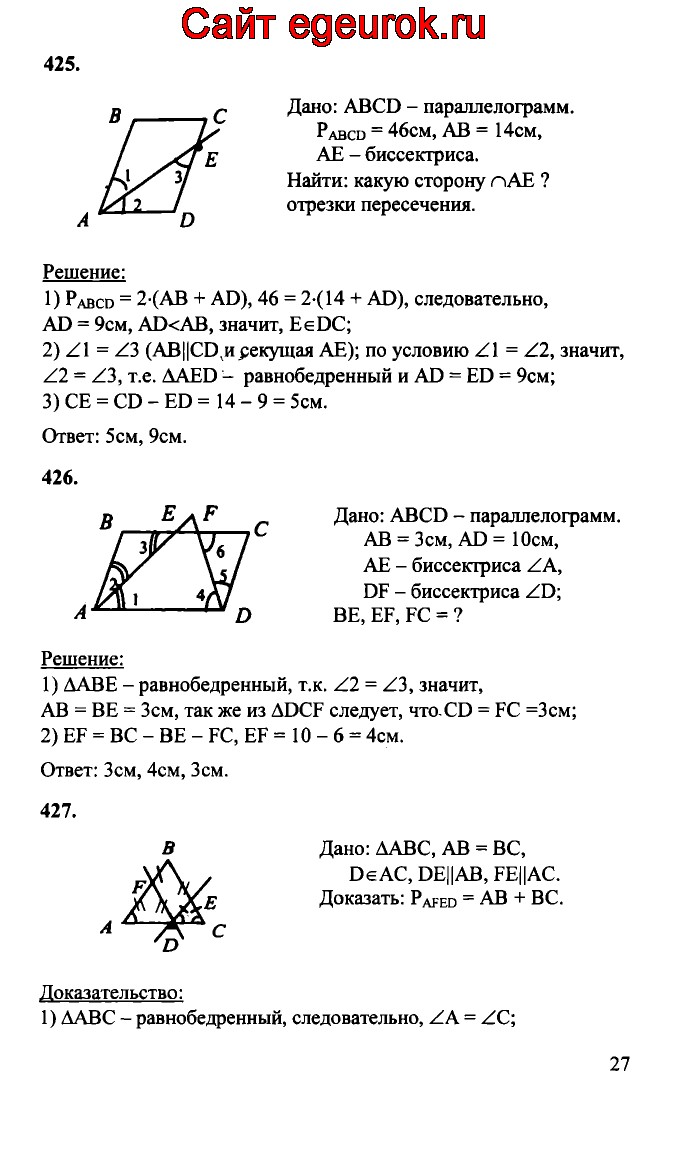 В прямоугольном треугольнике MNK с гипотенузой MN и углом M равным 60° проведена высота KН. Найдите MH и NН, если MН=6см.
В прямоугольном треугольнике MNK с гипотенузой MN и углом M равным 60° проведена высота KН. Найдите MH и NН, если MН=6см.