ГДЗ по Алгебре 7 класс Задачник Мордкович Базовый уровень
Решебник по алгебре, это отличная дополнительная информация, помогающая в полной мере разобраться с новой темой. Здесь А.Г. Мордкович собрал материал по решению всех упражнений из учебника 7 класса. Все сорок глав книги разобраны подробно, в соответствии с оригинальным изданием. Алгоритмы решений из сборника ГДЗ не противоречат нормативам общеобразовательных учреждений.
ГДЗ по алгебре за 7 класс Мордкович состоит из сорока глав, последняя из которых, глава на повторение, помогает ученику закрепить весь пройденный материал. Каждое задание имеет свою нумерацию, поэтому долго его искать не придется. Такой систематизированный материал понравится как самим семиклассникам, так и их родителям.
Чтобы ни одна линейная функция не была упущена; чтобы все арифметические операции над одночленами проводились в два счёта; и чтобы ни одна из степеней не ввела школьника в заблуждение, специалисты разработали этот новый сборник ГДЗ. Книга помогает понять особенности математического языка, разъясняет семикласснику суть координатной плоскости, повышает уровень знаний о методах подстановки и алгебраического сложения. В конце решебника авторы не забыли решить задания на повторение пройденного. Такой подход закрепит полученную информацию в памяти семиклассника до конца учёбы. А краткий справочный материал даст возможность быстро вспомнить все определения и правила.
Книга помогает понять особенности математического языка, разъясняет семикласснику суть координатной плоскости, повышает уровень знаний о методах подстановки и алгебраического сложения. В конце решебника авторы не забыли решить задания на повторение пройденного. Такой подход закрепит полученную информацию в памяти семиклассника до конца учёбы. А краткий справочный материал даст возможность быстро вспомнить все определения и правила.
ГДЗ к контрольным работам по алгебре за 7 класс Александрова Л.А. (базовый уровень) можно посмотреть
здесь.
ГДЗ к самостоятельным работам по алгебре за 7 класс Александрова Л.А. (базовый уровень) можно посмотреть
здесь.
ГДЗ к тестам по алгебре за 7-9 классы Мордкович А. Г. (базовый уровень) можно посмотреть
здесь.
ГДЗ к рабочей тетради по алгебре за 7 класс Ключникова Е.М. (Экзамен) можно посмотреть
здесь.
ГДЗ к дидактическим материалам по алгебре за 7 класс Попов М.А. (Экзамен) можно посмотреть
здесь.
ГДЗ к учебнику по алгебре за 7 класс Мордкович А.Г. (задачник) можно посмотреть
здесь.
ГДЗ к тематическим проверочным работам по алгебре за 7 класс Александрова Л. А. можно посмотреть
А. можно посмотреть
здесь.
ГДЗ к учебнику по алгебре за 7 класс Мордкович А.Г. (Просвещение) можно посмотреть
здесь.
ГДЗ к сборнику задач по алгебре за 7 класс Рурукин А.Н. можно посмотреть
здесь.
ГДЗ к контрольным и самостоятельным работам по алгебре за 7 класс Попов М.А. можно посмотреть
здесь.
Алгебра. 7 класс. Задачник. Мордкович А.Г. и др
ОГЛАВЛЕНИЕ (2009, 13-е изд. , 270с.)
, 270с.)
Предисловие для учителя 3
Глава 1. МАТЕМАТИЧЕСКИЙ ЯЗЫК. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
§ 1. Числовые и алгебраические выражения 5
§ 2. Что такое математический язык 12
§ 3. Что такое математическая модель 15
§ 4. Линейное уравнение с одной переменной 22
§ 5. Координатная прямая 27
Домашняя контрольная работа № 1 31
Глава 2. ЛИНЕЙНАЯ ФУНКЦИЯ
§ 6. Координатная плоскость 34
§ 7. Линейное уравнение с двумя переменными и его график 40
§ 8. Линейная функция и ее график 44
§ 9. Линейная функция y = kx 52
§10. Взаимное расположение графиков линейных функций 57
Домашняя контрольная работа № 2 61
Глава 3. СИСТЕМЫ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ
§11. Основные понятия 63
§12. Метод подстановки 66
§13. Метод алгебраического сложения 70
§ 14. Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций 75
Домашняя контрольная работа № 3 79
Глава 4. СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ И ЕЕ СВОЙСТВА
СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ И ЕЕ СВОЙСТВА
§15. Что такое степень с натуральным показателем 82
§16. Таблица основных степеней 86
§ 17. Свойства степени с натуральными показателями … 89
§ 18. Умножение и деление степеней с одинаковыми показателями 92
§ 19. Степень с нулевым показателем 95
Домашняя контрольная работа № 4 97
Глава 5. ОДНОЧЛЕНЫ. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД ОДНОЧЛЕНАМИ
§ 20. Понятие одночлена. Стандартный вид одночлена … 99
§21. Сложение и вычитание одночленов 101
§ 22. Умножение одночленов. Возведение одночлена в натуральную степень 106
§23. Деление одночлена на одночлен 110
Домашняя контрольная работа № 5 111
Глава 6. МНОГОЧЛЕНЫ. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД МНОГОЧЛЕНАМИ
§24. Основные понятия 113
§25. Сложение и вычитание многочленов 117
§26. Умножение многочлена на одночлен 119
§ 27. Умножение многочлена на многочлен 124
§ 28. Формулы сокращенного умножения 126
Формулы сокращенного умножения 126
§29. Деление многочлена на одночлен 132
Домашняя контрольная работа № 6 135
Глава 7. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ
§ 30. Что такое разложение многочленов на множители и зачем оно нужно 137
§31. Вынесение общего множителя за скобки 139
§ 32. Способ группировки 141
§ 33. Разложение многочленов на множители с помощью формул сокращенного умножения 144
§ 34. Разложение многочленов на множители с помощью комбинации различных приемов 149
§ 35. Сокращение алгебраических дробей 151
§ 36. Тождества 157
Домашняя контрольная работа № 7 159
Глава 8. ФУНКЦИЯ у = х2
§37. Функция у = х2 и ее график 161
§38. Графическое решение уравнений 169
§39. Что означает в математике запись у — f(х) 171
Домашняя контрольная работа № 8 182
Глава 9. ИТОГОВОЕ ПОВТОРЕНИЕ 184
Приложение 207
Ответы 238
Справочный материал 267
ОГЛАВЛЕНИЕ (2001, 4-е изд. , 160с.)
, 160с.)
Предисловие для учителя 3
Глава 1. МАТЕМАТИЧЕСКИЙ ЯЗЫК. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
§ 1. Числовые и алгебраические выражения 5
§ 2. Что такое математический язык 12
§ 3. Что такое математическая модель 15
Глава 2. СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ И ЕЕ СВОЙСТВА
§ 4. Что такое степень с натуральным показателем 20
§ 5. Таблица основных степеней 24
§ 6. Свойства степеней с натуральным показателем 26
§ 7. Умножение и деление степеней с одинаковыми показателями ., 30
§ 8. Степень с нулевым показателем 32
Глава 3. ОДНОЧЛЕНЫ. ОПЕРАЦИИ НАД ОДНОЧЛЕНАМИ
§ 9. Понятие одночлена. Стандартный вид одночлена 34
§ 10. Сложение и вычитание одночленов 36
§ 11. Умножение одночленов. Возведение одночлена в натуральную степень 41
§ 12. Деление одночлена на одночлен 45
Глава 4. МНОГОЧЛЕНЫ. ОПЕРАЦИИ НАД МНОГОЧЛЕНАМИ
§ 13. Основные понятия 47
Основные понятия 47
§ 14. Сложение и вычитание многочленов 50
§ 15. Умножение многочлена на одночлен 52
§ 16. Умножение многочлена на многочлен 57
§ 17. Формулы сокращенного умножения 59
§ 18. Деление многочлена на одночлен 64
Глава 5. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ
§ 19. Что такое разложение многочленов на множители и зачем оно нужно 67
§ 20. Вынесение общего множителя за скобки 68
§ 21. Способ группировки 70
§ 22. Разложение многочлена на множители с помощью формул сокращенного умножения 72
§ 23. Разложение многочлена на множители с помощью комбинации различных приемов 76
§ 24. Сокращение алгебраических дробей 78
§ 25. Тождества 84
Глава 6. ЛИНЕЙНАЯ ФУНКЦИЯ
§ 26. Координатная прямая 86
§ 27. Координатная плоскость 90
§ 28. Линейное уравнение с двумя переменными и его график 95
§ 29. Линейная функция и ее график 100
§ 30. Прямая пропорциональность и ее график 107
Прямая пропорциональность и ее график 107
§ 31. Взаимное расположение графиков линейных функций 113
Глава 7. ФУНКЦИЯ У = Х2
§ 32. Функция у = х2 и ее график 116
§ 33. Графическое решение уравнений 122
§34. Что означает в математике запись у = f(x) 123
Основные результаты 144
Глава 8. СИСТЕМЫ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ
§ 35. Основные понятия 133
§ 36. Метод подстановки 136
§ 37. Метод алгебраического сложения 139
§ 38. Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций 142
Ответы 147
Решебник (гдз) по задачнику алгебра 7 класс Мордкович, Николаев
Задачник по алгебре 7 класс Мордкович А.
 Г.
Г.
Задачник по алгебре для седьмого класса в двух частях, составленный Мордковичем А.Г. и Николаевым Н.П., предназначен для учащихся, которые изучают математику на базовом уровне. Задачник соответствует государственным образовательным стандартам и рекомендован к использованию Министерством образования и наук Российской Федерации. Задачник прекрасно подходит к учебнику алгебры для седьмого класса разработанным, как Мордковичем, так и другими авторами, которые ориентируются на стандартную программу образования.
Задачник состоит из восьми глав. В самом начале пособия приведено руководство для учителя, в котором авторы излагают свои требования и рекомендации к провидению занятии и использованию пособия. В пособие приведены задания по следующим темам: математический язык, математическая модель, одночлен и способы работы с ним, многочлен и способы работы с ним, линейная функция и применение их в решение задач, степени и особенности работы с ними. Каждая глава включает в себя насколько параграфов, которые нацелены на более детальное усвоение темы. Каждый параграф начинается со схематического описания теоретического материала, который нацелен на повторение пройденного, дальше приведен пример разбора задачи с комментариями к нему. После этого приведены упражнения разбитые на три уровня сложности, что соответствует принципу дифференцированного подхода к учащимся.
Материал в задачнике изложен в форме диалога с учащимся, в виде непрерывных попыток заинтересовать школьника, вырастить в нем стремление к постоянному развитию математической логики и интуиции. Пособие может прекрасно использоваться при подготовке к экзаменам, зачетам, а также при самостоятельном повышении уровня знаний по математике. Задания из пособия активно применяются преподавателями при разработке к поурочному контролю учащихся, проверке их знаний и самостоятельной работы.
Предлагаем вам список ссылок на источники в интернете по которым возможно скачать готовое домашнее задание по задачнику алгебры 7 класс Мордкович А.Г., Николаев Н.П. для помощи в решении и подготовки уроков. Мы искренне надеемся, что это онлайн гдз будет использоваться вами для самоконтроля и проверки домашних заданий, а не для машинального списывания. Если же в ссылке для скачивания присутствует ошибка или вы знаете где можно ещё бесплатно скачать готовые ответы и решения за седьмой класс по задачнику алгебры от автора Мордкович А.Г., Николаев Н.П., то сообщите нам об этом в комментариях.
Мы искренне надеемся, что это онлайн гдз будет использоваться вами для самоконтроля и проверки домашних заданий, а не для машинального списывания. Если же в ссылке для скачивания присутствует ошибка или вы знаете где можно ещё бесплатно скачать готовые ответы и решения за седьмой класс по задачнику алгебры от автора Мордкович А.Г., Николаев Н.П., то сообщите нам об этом в комментариях.
ГДЗ по задачнику алгебра 7 класс Мордкович А.Г., Николаев Н.П.
Комментарии
▶▷▶ решебник алгебра задачник 7 класс мордкович николаев 2013
▶▷▶ решебник алгебра задачник 7 класс мордкович николаев 2013
| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 09-11-2018 |
решебник алгебра задачник 7 класс мордкович николаев 2013 — Yahoo Search Results Yahoo Web Search Sign in Mail Go to Mail» data-nosubject=»[No Subject]» data-timestamp=’short’ Help Account Info Yahoo Home Settings Home News Mail Finance Tumblr Weather Sports Messenger Settings Yahoo Search query Web Images Video News Local Answers Shopping Recipes Sports Finance Dictionary More Anytime Past day Past week Past month Anytime Get beautiful photos on every new browser window Download ГДЗ по алгебре 7 класс задачник, углубленный уровень АГ megareshebaru/gdz/algebra/ 7 -klass/mordkovich Cached Если ваш семиклассник учится в классе с углубленным изучением алгебры, то ему необходимо иметь дополнительную вспомогательную литературу, а именно ГДЗ по алгебре за 7 класс углубленное изучение Мордкович ГДЗ, Решебник Алгебра 7 класс АГ Мордкович (Задачник) 2013 г vse-gdzinfo/ 7 /algebra- 7 /gdz-reshebnik-algebra- 7 Cached Готовые Домашние Задания Решебник по Алгебре 7 класс АГ Мордкович ( Задачник ) 2013 г Учебник Алгебра 8 класс АГ Мордкович, НП Николаев 2013 vklasseonline … Алгебра Первая часть учебника уже на сайте На нашем сайте уже размещен Учебник Алгебра 8 класс АГ Мордкович , НП Николаев Часть 1 2013 года ГДЗ по алгебре задачник, углубленный уровень 7 класс АГ reshebacom/gdz/algebra/ 7 -klass/uglublennoe Cached Качественные решения и подробные гдз по алгебре для учеников 7 класса задачник , углубленный уровень, авторы учебника:АГ Мордкович , НП Николаев ГДЗ по алгебре 7 класс Мордкович (Решебник задачника) gdzputinainfo/reshebniki/ 7 -klass/algebra/ Cached Авторы: Алгебра 7 класс Часть 2 Задачник для учащихся общеобразовательных учреждений / АГ гдз по алгебре 7 класс задачник мордкович николаев 2009года wwwboomleru/гдз-по-алгебре- 7 Cached Алгебра 7 класс Решебник Мордкович АГ Решебник по Алгебре Задачник Углубленный уровень для 7 класса, авторы учебника : Мордкович АГ, Николаев НП на 2017-2018 год ГДЗ по алгебре 7 класс Мордкович — онлайн решебник uchimorg/gdz/po-algebre- 7 -klass-mordkovich Cached ГДЗ по алгебре 7 класс Мордкович — онлайн решебник Здесь вы можете бесплатно воспользоваться ГДЗ по алгебре за 7 класс по учебнику Мордковича Решебник (ГДЗ) Алгебра 7 класс АГ Мордкович 2013 Часть 2 vklasseonline … Алгебра Решебник по алгебре для каждого ученика На нашем сайте уже размещен решебник Алгебра 7 класс АГ Мордкович Часть 2 2013 года Решебник по алгебре 7 класс Мордкович megareshebaru/publ/reshebnik/algebra/ 7 _klass Cached Готовые домашние задания и решебник по алгебре за 7 класс автор АГ Мордкович 2016 Алгебра наверное самый сложный предмет в 7 классе Решебник задачник, углубленный уровень по алгебре 7 класс АГ gdzguru Алгебра Решебник задачник , углубленный уровень по алгебре 7 класс АГ Мордкович , НП Николаев ФГОС ГДЗ 7 класс Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 29,600 results Settings Help Suggestions Privacy (Updated) Terms (Updated) Advertise About ads About this page Powered by Bing™
- Николаев НП Углубленный уровень на 2017-2018 год Читать ещё ГДЗ по Алгебре 7 класс Задачник Углубленный уровень авторы: Мордкович АГ
- а Читать ещё Решебник задачника части 2 по алгебре 7 класс Мордкович Курс алгебры за 7 класс отличается достаточной сложностью В итоге не все дети способны в классе понять
- автор: АГ Мордкович
а именно ГДЗ по алгебре за 7 класс углубленное изучение Мордкович В его содержание входит восемь глав Первая глава подробно расскажет
как проводятся действия с многочленами или как решить простую систему из двух уравнений В итоге они допускают ошибки в домашней работе
- углубленный уровень по алгебре 7 класс АГ Мордкович
- углубленный уровень по алгебре 7 класс АГ Мордкович
- углубленный уровень
решебник алгебра задачник 7 класс мордкович николаев 2013 — Все результаты ГДЗ по Алгебре за 7 класс задачник, углубленный уровень АГ › › 7 класс › Алгебра › Мордкович углубленное изучение Похожие Подробный решебник (ГДЗ) по Алгебре для 7 класса задачник , углубленный уровень, часть 2 Авторы учебника: АГ Мордкович , НП Николаев ГДЗ по алгебре 7 класс Мордкович › ГДЗ › 7 класс › Алгебра › АГ Мордкович Похожие ГДЗ к задачнику за 7 класс , автор АГ Мордкович по алгебре Подробные решения и пояснения с рисунками ГДЗ по Алгебре за 7 класс: Мордкович АГ Решебник Задачник › ГДЗ › 7 класс › Алгебра › Мордкович АГ ГДЗ: Спиши готовые домашние задания задачник по алгебре за 7 класс , решебник АГ Мордкович , Базовый Авторы: Мордкович АГ, Николаев НП Видео 1:44 решебник по алгебре 7 класс мордкович Ozoke Ozoke YouTube — 16 сент 2015 г 4:07 Задача №413 Алгебра 7 класс Мордкович Дядя Андрей YouTube — 12 сент 2014 г 8:16 Задача №435 Алгебра 7 класс Мордкович Дядя Андрей YouTube — 13 сент 2014 г Все результаты ГДЗ решебник по алгебре 7 класс Мордкович — Mathcomua wwwmathcomua/gdz-reshebnik/algebra-7-klass/mordkovichhtml Похожие Рейтинг: 3,8 — 12 голосов Если вы учитесь в 7 классе и вам нужна помощь в решении задач по алгебре из учебника « Алгебра 7 класс Часть 2 Задачник » Мордкович АГ, или вы ГДЗ по алгебре для 7 класс от Путина Похожие Алгебра 7 класс Мордкович для углубленного изучения Алгебра 7 класс задачник , углубленный уровень авторы: АГ Мордкович НП Николаев ГДЗ по алгебре 7 класс Мордкович — онлайн решебник — uchimorg Здесь вы можете бесплатно воспользоваться ГДЗ по алгебре за 7 класс по учебнику Мордковича Помните, что решебник создавался для родителей ГДЗ по алгебре 7 класс — АГ Мордкович wwwggdzru/class-7/algebra/mordkovich-7-klass/ Похожие Выберите из задачника номер упражнения, чтобы просмотреть решение Содержание гдз алгебра 7 класс мордкович николаев 2013 · алгебра 7 Решебник задачник, углубленный уровень (гдз) по Алгебре для 7 Онлайн решебник задачник , углубленный уровень по Алгебре для 7 класса А Г Мордкович , НП Николаев , гдз и ответы к домашнему заданию Алгебра, 7 класс Часть 2 Задачник (А Г Мордкович, Н П Алгебра , 7 класс Часть 2 Задачник (А Г Мордкович , Н П Николаев ) 2009 Это раздел УЧЕБНИКОВ, раздел решебников в другом месте Решебник 7 класса мордкович александрова мишустина wwwbioverru//reshebnik-7-klassa-mordkovich-aleksandrova-mishustina-tulchinskay 13 нояб 2015 г — ГДЗ по алгебре 7 класс Мордкович , Александрова, Мишустина, Тульчинская Глава 1 мордкович николаев задачник решебник решебник алгебра 7 николаев 2013 решебник путина 7 класс алгебра мордкович ГДЗ по алгебре 7 класс Мордкович, Александрова, Мишустина › Алгебра › 7 класс Похожие Решебник по алгебре за 7 класс авторы Мордкович , Александрова, Мишустина издательство Мнемозина ГДЗ по алгебре для 7 класса задачник, углубленный уровень › ГДЗ › 7 класс › Алгебра › Мордкович углубленное изучение Похожие ГДЗ по алгебре задачник , углубленный уровень 7 класс АГ Мордкович Углубленный уровень ГДЗ · 7 класс · Алгебра Алгебра 7 класс Мордкович для углубленного изучения авторы: АГ Мордкович , НП Николаев На начальном Решебник по Алгебре для 7 класса АГ Мордкович ГДЗ задачник Похожие ГДЗ (Готовые домашние задания) по Алгебре задачник 7 класс АГ Мордкович , решенные задания и онлайн ответы из решебника Гдз по Алгебре задачник за 7 класс, авторы АГ Мордкович Похожие Подробные гдз и решебник по Алгебре для 7 класса задачник , авторы учебника: АГ Мордкович на 2017-2018 год Картинки по запросу решебник алгебра задачник 7 класс мордкович николаев 2013 «cb»:6,»id»:»1Fa999gep8UXeM:»,»ml»:»600″:»bh»:90,»bw»:57,»oh»:253,»ou»:» «,»ow»:160,»pt»:»wwwmathcomua/gdz-reshebnik/algebra-7-klass/mord»,»rh»:»mathcomua»,»rid»:»ZIq0cHzrrm0DfM»,»rt»:0,»ru»:» «,»st»:»Mathcomua»,»th»:105,»tu»:» \u003dtbn:ANd9GcRKVb5juAbIahF_tG_6P4qkFn8chUW98MDVMb870L4gCqdSe2OGngoKRw»,»tw»:66 «id»:»8ObYrsZJzk4hTM:»,»ml»:»600″:»bh»:90,»bw»:109,»oh»:588,»ou»:» «,»ow»:720,»pt»:»gdzru/attachments/images/tasks/000/005/963/0002/5″,»rh»:»gdzru»,»rid»:»zLEab3rTslYfWM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»GDZru»,»th»:90,»tu»:» \u003dtbn:ANd9GcS9LObfRJIeFaTuMd36_vCykq1ljxGuTPWPKgzJJXGz496HjIvcn0HjyZU»,»tw»:110 «id»:»Ha9Ksmy-aoNQIM:»,»ml»:»600″:»bh»:90,»bw»:119,»oh»:474,»ou»:» «,»ow»:720,»pt»:»gdzru/attachments/images/tasks/000/005/963/0002/5″,»rh»:»gdzru»,»rid»:»A4D5V3iyhl0FOM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»GDZru»,»th»:90,»tu»:» \u003dtbn:ANd9GcRbLxPpKPz4pcGHuiCv_NovddgqV4m4_KnJx6Hx8X6mxeDI3NMi5-iMEO4-«,»tw»:137 «cb»:3,»id»:»I2zP1oiciSTsAM:»,»ml»:»600″:»bh»:90,»bw»:64,»oh»:313,»ou»:» «,»ow»:222,»pt»:»uchimorg/img/gdz-po-algebre-8-klass-mordkovich-mi»,»rh»:»uchimorg»,»rid»:»gg85OB1ukLk34M»,»rt»:0,»ru»:» «,»st»:»uchimorg»,»th»:99,»tu»:» \u003dtbn:ANd9GcSIbSlL5jTU1AYWwkBZUWzWDmmPmyCDOpkJ60j-btJAwhZXyAj6vhCLxjs»,»tw»:70 «id»:»FZDRPKmZVPc4wM:»,»ml»:»600″:»bh»:90,»bw»:119,»oh»:522,»ou»:» «,»ow»:720,»pt»:»gdzru/attachments/images/tasks/000/005/963/0002/5″,»rh»:»gdzru»,»rid»:»L-SPI6HyVLpUjM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»GDZru»,»th»:90,»tu»:» \u003dtbn:ANd9GcTujR058rs287qdhDft4-qt1sZ_bitNHAjR8x7W6yD0GoF4h2o_75D8D8E»,»tw»:124 «id»:»lc-3O9Nwk9RjUM:»,»ml»:»600″:»bh»:90,»bw»:112,»oh»:577,»ou»:» «,»ow»:720,»pt»:»gdzru/attachments/images/tasks/000/005/963/0002/5″,»rh»:»gdzru»,»rid»:»Dx75Tivjy14X7M»,»rt»:0,»ru»:» «,»sc»:1,»st»:»GDZru»,»th»:90,»tu»:» \u003dtbn:ANd9GcRV3FZr3COsJ7OIM_166haTxabWQmE7DBpWGNGthu1l5XegBpP1AS6bXg»,»tw»:112 Другие картинки по запросу «решебник алгебра задачник 7 класс мордкович николаев 2013» Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Пояснения к фильтрации результатов Мы скрыли некоторые результаты, которые очень похожи на уже представленные выше (30) Показать скрытые результаты Вместе с решебник алгебра задачник 7 класс мордкович николаев 2013 часто ищут гдз по алгебре 7 класс мордкович николаев гдз по алгебре 7 класс мордкович домашняя контрольная работа гдз по алгебре 7 класс мордкович николаев учебник алгебра 7 класс мордкович учебник решебник по алгебре седьмой класс задачник мордкович николаев гдз по алгебре 7 класс мордкович от путина гдз по алгебре 7 класс мордкович николаев бесплатно гдз по алгебре 7 класс макарычев Ссылки в нижнем колонтитуле Россия — Подробнее… Справка Отправить отзыв Конфиденциальность Условия Аккаунт Поиск Карты YouTube Play Новости Почта Контакты Диск Календарь Google+ Переводчик Фото Ещё Документы Blogger Hangouts Google Keep Подборки Другие сервисы Google
Яндекс Яндекс Найти Поиск Поиск Картинки Видео Карты Маркет Новости ТВ онлайн Музыка Переводчик Диск Почта Коллекции Все Ещё Дополнительная информация о запросе Показаны результаты для Нижнего Новгорода Москва 1 ГДЗ по Алгебре 7 класс АГ Мордкович , НП Николаев eurokime › gdz/algebra/7class/mordkovich…izuchenie Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Здесь вы найдете ГДЗ с подробным и полным решением упражнений (номеров) по Алгебре задачник , углубленный уровень за 7 класс , автор: АГ Мордкович , НП Николаев Издательство: Мнемозина ФГОС Показать решебники Видеорешения Классы 1 2 3 4 5 6 7 8 9 10 11 Математика 1 2 3 4 5 6 7 8 9 10 11 Читать ещё Здесь вы найдете ГДЗ с подробным и полным решением упражнений (номеров) по Алгебре задачник , углубленный уровень за 7 класс , автор: АГ Мордкович , НП Николаев Издательство: Мнемозина ФГОС Показать решебники Видеорешения Классы 1 2 3 4 5 6 7 8 9 10 11 Математика 1 2 3 4 5 6 7 8 9 10 11 Английский язык 1 2 3 4 5 6 7 8 9 10 11 Скрыть 2 ГДЗ Задачник алгебра 7 класс АГ Мордкович MegaReshebaru › gdz/algebra/7-klass/mordkovich… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте ГДЗ по алгебре 7 класс задачник , углубленный уровень АГ Мордкович Углубленный уровень часть 2 Если ваш семиклассник учится в классе с углубленным изучением алгебры , то ему необходимо иметь дополнительную Читать ещё ГДЗ по алгебре 7 класс задачник , углубленный уровень АГ Мордкович Углубленный уровень часть 2 авторы: АГ Мордкович , НП Николаев Если ваш семиклассник учится в классе с углубленным изучением алгебры , то ему необходимо иметь дополнительную вспомогательную литературу, а именно ГДЗ по алгебре за 7 класс углубленное изучение Мордкович В его содержание входит восемь глав Первая глава подробно расскажет, что такое математический язык и математическая модель Скрыть 3 ГДЗ по Алгебре за 7 класс Задачник Мордкович GDZ-Putinacom › 7 класс › Алгебра › mordkovich-nikolaev… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Алгебра 7 класс Решебник Мордкович АГ Авторы: Мордкович АГ, Николаев НП Решебник по Алгебре Задачник Углубленный уровень для 7 класса , авторы учебника : Мордкович АГ, Николаев НП на 2017-2018 год 4 Решебник и ГДЗ по Алгебре за 7 класс задачник , авторы gdz-putinanet › 7…mordkovich-nikolaev…zadachnik Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте ГДЗ по Алгебре 7 класс Задачник Углубленный уровень Решебник и ГДЗ по Алгебре для 7 класса задачник , авторы учебника: Мордкович АГ, Николаев НП Углубленный уровень на 2017-2018 год Читать ещё ГДЗ по Алгебре 7 класс Задачник Углубленный уровень авторы: Мордкович АГ, Николаев НП Решебник и ГДЗ по Алгебре для 7 класса задачник , авторы учебника: Мордкович АГ, Николаев НП Углубленный уровень на 2017-2018 год §-1 11 12 13 14 15 16 1 7 18 19 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 §-2 21 22 23 24 25 26 2 7 28 29 210 211 212 213 214 215 216 217 218 219 220 221 222 223 Скрыть 5 ГДЗ по Алгебре за 7 класс : Мордкович АГ Задачник GDZru › class-7/algebra/mordkovich-14/ Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте ГДЗ: Спиши готовые домашние задания задачник по алгебре за 7 класс , решебник АГ Мордкович , Базовый уровень ФГОС, часть 2 ГДЗ по алгебре к упомянутому задачнику рассчитано на поздний выпуск книги, а значит, что он содержит в себе больше ответов, которые подходят к обеим вариантам изданий Читать ещё ГДЗ: Спиши готовые домашние задания задачник по алгебре за 7 класс , решебник АГ Мордкович , Базовый уровень ФГОС, часть 2 онлайн ответы на GDZRU ГДЗ по алгебре к упомянутому задачнику рассчитано на поздний выпуск книги, а значит, что он содержит в себе больше ответов, которые подходят к обеим вариантам изданий В решебнике разобраны все разновидности уравнений, системы уравнений, виды графиков и дополнительные задания, которые автор добавил лично Поэтапное описание решений позволяет работать с материалом самостоятельно, поможет быстро догнать пропущенные уроки и повысить успеваемость Школьники ценят именно это издание ГДЗ за полные ответы и обилие примеров Скрыть 6 Гдз по Алгебре задачник за 7 класс , авторы Мордкович GdzPutinacom › Гдз за 7 класс › Алгебра › mordkovich-nikolaev… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Алгебра 7 класс Мордкович АГ Задачник Подробные гдз и решебник по Алгебре для 7 класса задачник , авторы учебника: Мордкович АГ, Николаев НП на 2017-2018 год Читать ещё Алгебра 7 класс Мордкович АГ Задачник Подробные гдз и решебник по Алгебре для 7 класса задачник , авторы учебника: Мордкович АГ, Николаев НП на 2017-2018 год ГДЗ к учебнику по алгебре за 7 класс Мордкович АГ (теория) можно скачать здесь ГДЗ контрольным работам по алгебре за 7 -9 классы Мордкович АГ (углублённый уровень) можно скачать здесь ГДЗ к задачнику по алгебре за 7 класс Мордкович АГ (углублённый уровень) можно скачать здесь ГДЗ к самостоятельным работам по алгебре за 7 класс Александрова ЛА (углублённый уровень) можно скачать здесь ГДЗ к учебнику по алгебре за 7 класс Мордкович Скрыть 7 ГДЗ решебник по Алгебре Задачник 7 класс Мордкович GdzMonsternet › 7-klass/gdz…zadachnik-mordkovich-1/ Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Выберите подходящее издание решебника Алгебра 7 класс Контрольные работы Дудницин Тульчинская 2006 Рабочая тетрадь по Алгебре 7 класс Ключникова Комиссарова Мордкович 2013 Алгебра 7 класс Задачник Мордкович 2015-2016 Читать ещё Выберите подходящее издание решебника Алгебра 7 класс Контрольные работы Дудницин Тульчинская 2006 Алгебра 7 класс Контрольные работы Дудницын Тульчинская 2009 Рабочая тетрадь по Алгебре 7 класс Ключникова Комиссарова Мордкович 2013 Рабочая тетрадь по Алгебре 7 класс Ключникова Комиссарова Мордкович 2013 Алгебра 7 класс Задачник Мордкович 2015-2016 Алгебра 7 класс Контрольные работы Мордкович 2016-2017 Алгебра 7 класс Задачник Мордкович Мишустина Тульчинская Часть 2 Алгебра 7 класс Задачник Мордкович Часть 2 Готовые задания Скрыть 8 ГДЗ по алгебре 7 класс Мордкович ( Решебник задачника ) gdzputinainfo › Решебники › 7 класс › Алгебра › Мордкович Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Решебник задачника части 2 по алгебре 7 класс Мордкович Курс алгебры за 7 класс отличается достаточной сложностью В итоге не все дети способны в классе понять, как проводятся действия с многочленами или как решить простую систему из двух уравнений В итоге они допускают ошибки в домашней работе, а Читать ещё Решебник задачника части 2 по алгебре 7 класс Мордкович Курс алгебры за 7 класс отличается достаточной сложностью В итоге не все дети способны в классе понять, как проводятся действия с многочленами или как решить простую систему из двух уравнений В итоге они допускают ошибки в домашней работе, а не уясненная до конца тема становится причиной сложностей в изучении алгебры в последующих классах Родители также не всегда могут помочь своему чаду – не все помнят свойства степеней и график квадратично функции Скрыть 9 Решебник по Алгебре 7 класс задачник Мордкович zoobrilkaorg › load…7…mordkovich_nikolaev…zadachnik Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Зубрилкаорг — подробные гдз и решебник по Алгебре для 7 класса задачник Мордкович АГ, Николаев НП Спиши Зубрилкаорг — самые качественные гдз к учебникам по алгебре за 7 класс , авторы : Мордкович АГ, Николаев НП на 2018 год Спиши решения онлайн и бесплатно с любого устройства Читать ещё Зубрилкаорг — подробные гдз и решебник по Алгебре для 7 класса задачник Мордкович АГ, Николаев НП Спиши решения онлайн с любого устройства Зубрилкаорг — самые качественные гдз к учебникам по алгебре за 7 класс , авторы : Мордкович АГ, Николаев НП на 2018 год Спиши решения онлайн и бесплатно с любого устройства Задания § 1 11 12 13 14 15 16 1 7 18 19 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 § 2 21 22 23 24 25 26 2 7 28 29 210 211 212 213 214 215 216 217 218 219 220 221 222 223 § 3 Скрыть 10 Решебник Алгебра задачник 7 класс Мордкович Николаев 2013 — смотрите картинки ЯндексКартинки › решебник алгебра задачник 7 класс мордкович Пожаловаться Информация о сайте Ещё картинки ГДЗ по Алгебре для 7 класса АГ Мордкович задачник gdzotputinaorg › algebra/7-class/mordkovich… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте авторы: АГ Мордкович , НП Николаев ГДЗ по Алгебре для 7 класса задачник , углубленный уровень часть 2 Содержит правильные ответы на все упражнения и номера из учебного издания автора: АГ Мордкович , НП Николаев Читать ещё авторы: АГ Мордкович , НП Николаев ГДЗ по Алгебре для 7 класса задачник , углубленный уровень часть 2 Содержит правильные ответы на все упражнения и номера из учебного издания автора: АГ Мордкович , НП Николаев Издательство: Мнемозина ФГОС 2016 ГДЗ к дидактическим материалам по алгебре за 7 класс Попов МА можно скачать здесь ГДЗ контрольным работам по алгебре за 7 -9 классы Мордкович АГ(углублённый уровень) можно скачать здесь ГДЗ к задачнику по алгебре за 7 класс Мордкович АГ (углублённый уровень) можно скачать здесь ГДЗ к самостоятельным работам по алгебре за 7 класс Алексан Скрыть Алгебра 7 класс Учебник и задачник (комплект из 2 Доставка Акции Книги Канцтовары chitai-gorodru › Алгебра-7-класс-Учеб Не подходит по запросу Спам или мошенничество Мешает видеть результаты Информация о сайте реклама Литература для образования Программа бонусов – копите и оплачивайте! Контактная информация +7 (495) 444-84-44 пн-вс 9:00-21:00 Магазин на Маркете 18+ Вместе с « решебник алгебра задачник 7 класс мордкович николаев 2013 » ищут: решебник алгебра 8 класс мерзляк решебник алгебра 10 класс колягин решебник алгебра 11 класс колягин решебник алгебра 7 класс мерзляк решебник алгебра 9 класс макарычев решебник алгебра и начала математического анализа 10 класс колягин решебник алгебра 10 класс алимов решебник алгебра 8 класс колягин решебник алгебра 9 класс мордкович решебник алгебра 7 класс мерзляк полонский якир 1 2 3 4 5 дальше Браузер Интересное в ленте рекомендаций лично для вас 0+ Установить
Решебник ГДЗ Алгебра 7 класс А.
 Г. Мордкович, Е. Е. Тульчинская, Т. Н. Мишустина, 2003 г.
Г. Мордкович, Е. Е. Тульчинская, Т. Н. Мишустина, 2003 г.
Алгебра для многих семиклассником является новым предметом. Конечно, она может изучаться раньше, так как все зависит от школы, но в большинстве средних учебных заведений математика именно в этот года разделяется на алгебру и геометрию. Ах, сколько эмоций у школьников вызывает неведомый ранее предмет. Одним детям он дается легко, а другие с ужасом ждут уроков по нему. Если первой категории учеников регулярная помощь не нужна, то второй пригодятся ГДЗ по алгебре, 7 класс, Мордкович. Поверьте, что пособие является настоящей находкой, учитывая сложность современной программы по данной науке в школе.
Решебник по алгебре, 7 класс, Мордкович — действительно нужен?
Стоит отметить, что решебник полезен для школьников с различным уровнем успеваемости. Для детей, которые совершенно не могут понять алгебру, он будет в качестве шпаргалки на уроке и дома. А для подростков, которые с алгеброй на «Ты» ГДЗ позволят самостоятельно практиковаться на примере аналогичных заданий.
Не сомневайтесь, что пособие положительно отразиться на среднем балле по алгебре:
-
Все домашние задания будут решены правильно и в срок.
-
Станет легче справляться с самостоятельными и контрольными работами, так как всегда можно скачать решебник по алгебре, 7 класс, Мордкович.
Желательно, чтобы во время процесса списывания готовых домашних заданий школьник вникал в алгоритм решения. Таким образом, в памяти будет автоматически откладываться порядок действий, что поможет решать без затруднений аналогичные примеры в школе. Если домашняя задача стала для вас понятной, то попробуйте осилить ряд типовых заданий, которых в решебнике большое количество.
ГДЗ алгебра, 7 класс, Мордкович прост в использовании
Для того чтобы работать с пособием, достаточно иметь под рукой доступ в интернет. На компьютере, ноутбуке, планшете, мобильном телефоне следует нажать мышкой на выбранную книгу, определиться с темой, параграфом и нажать на номер задания. Эти незамысловатые действия в течение нескольких секунд приведут к готовому решению необходимого домашнего задания. Остается только списать пример или сверить его со своим алгоритмом решения. При желании пособие можно скачать.
Эти незамысловатые действия в течение нескольких секунд приведут к готовому решению необходимого домашнего задания. Остается только списать пример или сверить его со своим алгоритмом решения. При желании пособие можно скачать.
Жизнь школьника благодаря решебнику станет намного проще. Во-первых, всегда под рукой будет подсказка относительно решения любого домашнего упражнения по алгебре. Во-вторых, появится больше свободного времени на хобби и увлечения. В-третьих, улыбку на лице подростка можно будет увидеть значительно чаще, так как его не будут обременять непонятные домашние задания по алгебре.
Решебник по алгебре, 7 класс, Мордкович, 2007 поможет побороть страх перед точной наукой
Не секрет, что алгебра понятна далеко не всем детям. Однако изучать этот предмет в школе должны все без исключения. Пригодится наука в жизни или нет – это вопрос времени, но в седьмом классе плохая успеваемость по ней может отразиться на общем балле. Лучше воспользоваться ГЗД, чтобы облегчить учебу по алгебре.
Не стесняйтесь пользоваться книгой и не думайте, что к ней обращаются только двоечники. Если вы не знали, то учителя частенько прибегают к помощи к ГДЗ, чтобы сверить ответы на контрольных срезах. Бывает так, что сложность заданий не дает возможность решить пример даже отличнику. А решебник позволяет одним глазком взглянуть на пример, чтобы понять, в чем заключалась ошибка. Таким образом, пособие готовых домашних заданий незаменимо для всех школьников. Одни будут бездумно списывать решенные задачи, а другие контролировать свои знания по алгебре. В любом случае ГДЗ – это путь к хорошей успеваемости по алгебре.
График cos x. Синус (sin x) и косинус (cos x)
В этом уроке мы подробно рассмотрим функцию y = cos x, ее основные свойства и график. В начале урока дадим определение тригонометрической функции y=cost на координатной окружности и рассмотрим график функции на окружности и прямой. Покажем периодичность этой функции на графике и рассмотрим основные свойства функции. В конце урока мы решим несколько простых задач, используя график функции и ее свойства.
В конце урока мы решим несколько простых задач, используя график функции и ее свойства.
Тема: Тригонометрические функции
Урок: Функция y=cost, ее основные свойства и график
Функция – это закон, согласно которому каждому значению независимого аргумента соответствует единственное значение функции.
Вспомним определение функции Пусть будет t — любое вещественное число.Он имеет единственную точку M на числовом круге. В точке М проходит одна абсцисса. Он называется косинусом числа t. Каждому значению аргумента t соответствует только одно значение функции (рис. 1).
Центральный угол численно равен величине дуги в радианах, т.е. числу. Следовательно, аргументом может быть действительное число или угол в радианах.
Если мы можем определить для каждого значения, то мы можем построить функцию
График функции можно получить и другим способом. По формулам приведения график косинуса представляет собой синусоиду, сдвинутую по оси х влево (рис. 2).
По формулам приведения график косинуса представляет собой синусоиду, сдвинутую по оси х влево (рис. 2).
Функциональные свойства
1) Объем:
2) Диапазон значений:
3) Функция четная:
4) Наименьший положительный период:
5) Координаты точек пересечения с осью абсцисс:
6) Координаты точки пересечения с осью Y:
7) Интервалы, на которых функция принимает положительные значения:
8) Интервалы, на которых функция принимает отрицательные значения:
9) Восходящие интервалы:
10) Убывающие интервалы:
11) Минимум баллов:
12) Минимальная функция:.
13) Максимальное количество баллов:
14) Максимальная функция:
Мы рассмотрели основные свойства и график функции. В дальнейшем они будут использоваться при решении задач.
Библиография
1. Алгебра и начало анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень), изд. А. Г. Мордкович. -М.: Мнемосина, 2009.
А. Г. Мордкович. -М.: Мнемосина, 2009.
2. Алгебра и начало анализа, 10 класс (в двух частях).Сборник задач для общеобразовательных учреждений (профильный уровень), изд. А. Г. Мордкович. -М.: Мнемосина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебник для учащихся школ и классов с углубленным изучением математики).- М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для абитуриентов в высшие учебные заведения (под ред. М. И. Сканави).- М.: Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и принципам анализа (пособие для учащихся 10-11 классов общеобразовательных учреждений).- М.: Просвещение, 2003.
8. Карп А. П. Сборник задач по алгебре и принципам анализа: учеб. пособие за 10-11 классы с углублением изучения математики.-М.: Просвещение, 2006.
П. Сборник задач по алгебре и принципам анализа: учеб. пособие за 10-11 классы с углублением изучения математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начало анализа, 10 класс (в двух частях). Сборник задач для общеобразовательных учреждений (профильный уровень), изд. А. Г. Мордкович. -М.: Мнемосина, 2007.
№№ 16.6, 16.7, 16.9.
Дополнительные веб-ресурсы
3. Образовательный портал для подготовки к ЕГЭ ().
Урок и презентация на тему: «Функция y = cos(x). Определение и график функции»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания.Все материалы проверены антивирусной программой.
Учебные пособия и тренажеры в интернет-магазине Интеграл для 10 класса
Алгебраические задачи с параметрами, 9-11 классы
Программная среда «1С:Математический конструктор 6.1»
Что будем изучать:
1. Определение.
Определение.
2. График функций.
3. Свойства функции Y = cos(X).
4. Примеры.
Определение функции косинуса y = cos(x)
Ребята, мы уже познакомились с функцией Y = sin(X).
Вспомним одну из формул призрака: sin(X + π/2) = cos(X).
Благодаря этой формуле можно утверждать, что функции sin(X + π/2) и cos(X) идентичны, а их графики функций совпадают.
График функции sin(X + π/2) получается из графика функции sin(X) параллельным сдвигом на π/2 единиц влево. Это будет график функции Y = cos(X).
График функции Y = cos(X) также называют синусоидой.
Свойства функции cos (x)
- Напишем свойства нашей функции:
- Домен представляет собой набор действительных чисел.
- Функция четная. Вспомним определение четной функции. Функция вызывается, даже если выполняется равенство y(-x) = y(x). Как мы помним из формул призрака: cos(-x) = — cos(x), определение выполнено, значит косинус — четная функция.
- Функция Y = cos(X) убывает на отрезке и возрастает на отрезке [π; 2π].
 Мы можем видеть это на графике нашей функции.
Мы можем видеть это на графике нашей функции. - Функция Y = cos(X) ограничена снизу и сверху. Это свойство следует из того, что
-1 ≤ cos (X) ≤ 1 - Наименьшее значение функции равно -1 (при x = π + 2πk). Наибольшее значение функции равно 1 (при x = 2πk).
- Функция Y = cos (X) является непрерывной функцией. Посмотрим на график и убедимся, что наша функция не имеет разрывов, а значит непрерывность.
- Сегмент диапазона значений [- 1; 1].Это также хорошо видно из графика.
- Функция Y = cos (X) является периодической функцией. Посмотрим еще раз на график и увидим, что функция через промежутки времени принимает одни и те же значения.
Примеры с функцией cos(x)
1. Решить уравнение cos(X) = (x — 2π) 2 + 1
Решение: Построим 2 графика функции: y = cos(x) и y = (x — 2π) 2 + 1 (см. рисунок).
y = (x — 2π) 2 + 1 — парабола, сдвинутая вправо на 2π и вверх на 1.Наши графики пересекаются в одной точке A (2π; 1), это и есть ответ: x = 2π.
2. Построить график функции Y = cos (X) при x ≤ 0 и Y = sin (X) при x ≥ 0
Решение: Для построения нужного графика построим два графика функции «срезы». Первый срез: y = cos(x) для x ≤ 0. Второй срез: y = sin(x)
для x ≥ 0. Нарисуем оба «кусочка» на одном графике.
3. Найти наибольшее и наименьшее значение функции Y = cos(X) на отрезке [π; 7π/4]
Решение: Построим график функции и рассмотрим наш отрезок [π; 7π/4].На графике видно, что наибольшее и наименьшее значения достигаются на концах отрезка: в точках π и 7π/4 соответственно.
Ответ: cos (π) = -1 — наименьшее значение, cos (7π / 4) = наибольшее значение.
4. Построить график функции y = cos (π / 3 — x) + 1
Решение: cos(-x) = cos(x), то искомый график получается смещением графика функции y = cos(x) на π/3 единицы вправо и на 1 единицу вверх.
Задания для самостоятельного решения
1) Решить уравнение: cos(x) = x — π/2.
2) Решите уравнение: cos (x) = — (x — π) 2 — 1.
3) Постройте график функции y = cos (π / 4 + x) — 2.
4) Постройте график функции y = cos (-2π/3+x)+1.
5) Найти наибольшее и наименьшее значение функции y=cos(x) на отрезке.
6) Найдите наибольшее и наименьшее значение функции y = cos(x) на отрезке [- π/6; 5π/4].
В этом уроке мы подробно рассмотрим функцию y = cos x, ее основные свойства и график. В начале урока дадим определение тригонометрической функции y=cost на координатной окружности и рассмотрим график функции на окружности и прямой.Покажем периодичность этой функции на графике и рассмотрим основные свойства функции. В конце урока мы решим несколько простых задач, используя график функции и ее свойства.
Тема: Тригонометрические функции
Урок: Функция y=cost, ее основные свойства и график
Функция – это закон, согласно которому каждому значению независимого аргумента соответствует единственное значение функции.
Вспомним определение функции Пусть будет t — любое вещественное число. Он имеет единственную точку M на числовом круге. В точке М проходит одна абсцисса. Он называется косинусом числа t. Каждому значению аргумента t соответствует только одно значение функции (рис. 1).
Центральный угол численно равен величине дуги в радианах, т.е. числу. Следовательно, аргументом может быть действительное число или угол в радианах.
Если мы можем определить для каждого значения, то мы можем построить функцию
График функции можно получить и другим способом. По формулам приведения график косинуса представляет собой синусоиду, сдвинутую по оси х влево (рис. 2).
Функциональные свойства
1) Объем:
2) Диапазон значений:
3) Функция четная:
4) Наименьший положительный период:
5) Координаты точек пересечения с осью абсцисс:
6) Координаты точки пересечения с осью Y:
7) Интервалы, на которых функция принимает положительные значения:
8) Интервалы, на которых функция принимает отрицательные значения:
9) Восходящие интервалы:
10) Убывающие интервалы:
11) Минимум баллов:
12) Минимальная функция:.
13) Максимальное количество баллов:
14) Максимальная функция:
Мы рассмотрели основные свойства и график функции. В дальнейшем они будут использоваться при решении задач.
Библиография
1. Алгебра и начало анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень), изд. А. Г. Мордкович. -М.: Мнемосина, 2009.
2. Алгебра и начало анализа, 10 класс (в двух частях).Сборник задач для общеобразовательных учреждений (профильный уровень), изд. А. Г. Мордкович. -М.: Мнемосина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебник для учащихся школ и классов с углубленным изучением математики).- М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для абитуриентов в высшие учебные заведения (под ред. М. И. Сканави).- М.: Высшая школа, 1992.
М. И. Сканави).- М.: Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и принципам анализа (пособие для учащихся 10-11 классов общеобразовательных учреждений).- М.: Просвещение, 2003.
8. Карп А.П. Сборник задач по алгебре и принципам анализа: учеб. пособие за 10-11 классы с углублением изучения математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начало анализа, 10 класс (в двух частях). Сборник задач для общеобразовательных учреждений (профильный уровень), изд. А. Г. Мордкович. -М.: Мнемосина, 2007.
№№ 16.6, 16.7, 16.9.
Дополнительные веб-ресурсы
3. Образовательный портал для подготовки к ЕГЭ ().
Система уравнений методом сложения.Линейные уравнения. Решение систем линейных уравнений.
 Метод добавления
Метод добавления
На этом уроке мы продолжим изучение метода решения систем уравнений, а именно: метода алгебраического сложения. Сначала рассмотрим применение этого метода на примере линейных уравнений и его сущность. Давайте также вспомним, как уравнивать коэффициенты в уравнениях. И мы решим ряд задач по применению этого метода.
Тема: Системы уравнений
Урок: Алгебраический метод сложения
1. Метод алгебраического сложения на примере линейных систем
Рассмотрим метод алгебраического сложения на примере линейных систем.
Пример 1. Решить систему
Если мы сложим эти два уравнения, то у сократится, а уравнение для х останется.
Если из первого уравнения вычесть второе, x взаимно аннулируются, и мы получим уравнение для y.В этом смысл метода алгебраического сложения.
Мы решили систему и вспомнили метод алгебраического сложения. Повторим его суть: мы можем складывать и вычитать уравнения, но при этом необходимо добиться того, чтобы получилось уравнение только с одним неизвестным.
2. Метод алгебраического сложения с предварительным уравниванием коэффициентов
Пример 2. Решить систему
Член присутствует в обоих уравнениях, поэтому удобен метод алгебраического сложения.Вычтем из первого уравнения второе.
Ответ: (2;-1).
Таким образом, проанализировав систему уравнений, можно увидеть, что она удобна для метода алгебраического сложения, и применить ее.
Рассмотрим еще одну линейную систему.
3. Решение нелинейных систем
Пример 3. Решить систему
Мы хотим избавиться от y, но коэффициенты y в двух уравнениях разные. Уравняем их, для этого умножаем первое уравнение на 3, второе — на 4.
Пример 4. Решить систему
Уравняем коэффициенты при х
Можно по другому — уравнять коэффициенты при y.
Мы решили систему, дважды применив метод алгебраического сложения.
Метод алгебраического сложения также применим для решения нелинейных систем.
Пример 5. Решить систему
Добавьте эти уравнения, и мы избавимся от y.
Одну и ту же систему можно решить, дважды применив метод алгебраического сложения.Прибавим и вычтем из одного уравнения другое.
Пример 6. Решить систему
Ответ:
Пример 7. Решить систему
Избавимся от члена xy, используя метод алгебраического сложения. Умножим первое уравнение на .
Первое уравнение остается без изменений, вместо второго пишем алгебраическую сумму.
Ответ:
Пример 8.Решить систему
Умножьте второе уравнение на 2, чтобы найти идеальный квадрат.
Наша задача сводилась к решению четырех простейших систем.
4. Заключение
Мы рассмотрели метод алгебраического сложения на примере решения линейных и нелинейных систем. На следующем уроке мы рассмотрим метод введения новых переменных.
1. Мордкович А.Г. и соавт.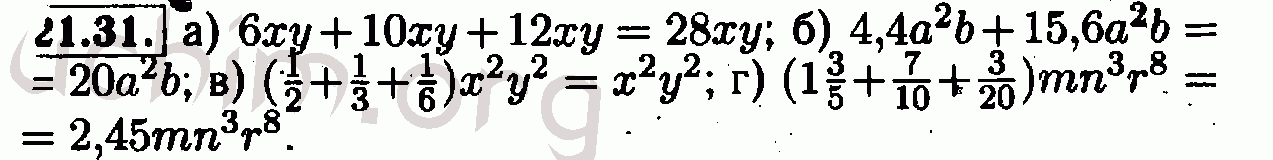 Алгебра 9 класс: Учебник. Для общего образования. Учреждения.- 4-е изд. — М.: Мнемосина, 2002. — 192 с.: ил.
Алгебра 9 класс: Учебник. Для общего образования. Учреждения.- 4-е изд. — М.: Мнемосина, 2002. — 192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 класса: Сборник задач для учащихся общеобразовательных учреждений / А.Г. Мордкович, Т.Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002. — 143 с.: ил.
3. Макарычев Ю.В. Н. Алгебра. 9 класс: учеб. для учащихся общеобразовательных школ. учреждений / Ю. Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, И.Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемосина, 2008.
4. Алимов Ш.А., Колягин Ю. М., Сидоров Ю. В. Алгебра. 9 класс. 16-е изд. – М., 2011. – 287 с.
5. Мордкович А.Г. Алгебра. 9 класс. В 14 ч. Часть 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. – М.: 2010. – 224 с.: ил.
.
6. Алгебра. 9 класс. В 2 часа, ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Эд. А. Г. Мордкович.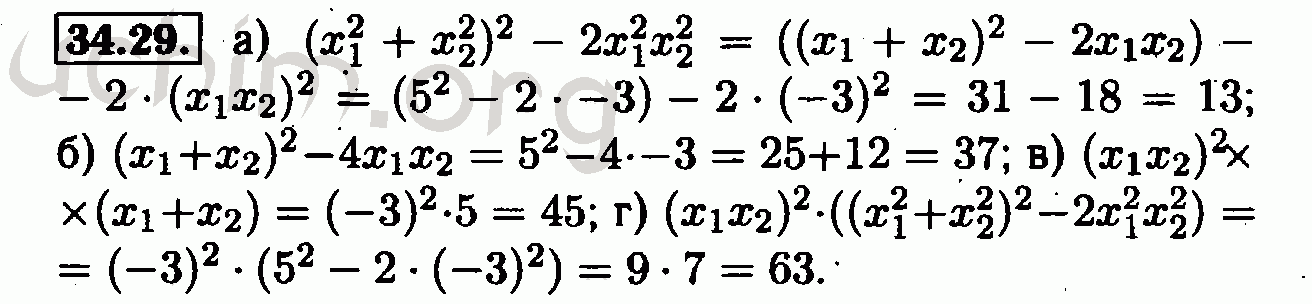 — 12-е изд., испр. — М.: 2010. — 223 с.: ил.
— 12-е изд., испр. — М.: 2010. — 223 с.: ил.
1. Раздел колледжа. ру по математике.
2. Интернет-проект «Задачи».
3. Образовательный портал «РЕШАЮ ЕГЭ».
1. Мордкович А.Г. и соавт. Алгебра 9 класс: Задача для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. – М.: Мнемозина, 2002. – 143 с.: ил. № 125 — 127.
Вам необходимо скачать план урока по теме » Алгебраический метод сложения ?
Система линейных уравнений с двумя неизвестными – это два или более линейных уравнения, для которых необходимо найти все их общие решения.Будем рассматривать системы двух линейных уравнений с двумя неизвестными. Общий вид системы двух линейных уравнений с двумя неизвестными показан на рисунке ниже:
(а1 * х + b1 * у = с1,
(а2 * х + b2 * у = с2
Здесь x и y — неизвестные переменные, a1, a2, b1, b2, c1, c2 — некоторые действительные числа. Решением системы двух линейных уравнений с двумя неизвестными является пара чисел (x, y) такая, что если эти числа подставить в уравнения системы, то каждое из уравнений системы превратится в истинное равенство. Существует несколько способов решения системы линейных уравнений. Рассмотрим один из способов решения системы линейных уравнений, а именно метод сложения.
Существует несколько способов решения системы линейных уравнений. Рассмотрим один из способов решения системы линейных уравнений, а именно метод сложения.
Алгоритм решения методом сложения
Алгоритм решения системы линейных уравнений с двумя неизвестными методами сложения.
1. При необходимости с помощью эквивалентных преобразований уравнять коэффициенты при одной из неизвестных в обоих уравнениях.
2. Сложив или вычитая полученные уравнения, получить линейное уравнение с одним неизвестным
3.Решите полученное уравнение с одним неизвестным и найдите одну из переменных.
4. Подставить полученное выражение в любое из двух уравнений системы и решить это уравнение, получив вторую переменную.
5. Проверьте решение.
Пример решения с помощью сложения
Для большей наглядности решим методом сложения следующую систему линейных уравнений с двумя неизвестными:
(3 * x + 2 * y = 10;
(5 * x + 3 * y = 12;
) Так как ни одна из переменных не имеет одинаковых коэффициентов, приравняем коэффициенты переменной y. Для этого умножьте первое уравнение на три, а второе уравнение на два.
Для этого умножьте первое уравнение на три, а второе уравнение на два.
(3 * х + 2 * у = 10 | * 3
(5 * х + 3 * у = 12 | * 2
Получаем следующую систему уравнений:
(9 * x + 6 * y = 30;
(10 * x + 6 * y = 24;
) Теперь из второго уравнения вычтем первое. Приведем аналогичные члены и решим полученное линейное уравнение.
10*х+6*у — (9*х+6*у) = 24-30; х = -6;
Подставляем полученное значение в первое уравнение нашей исходной системы и решаем полученное уравнение.
(3 * (- 6) + 2 * у = 10;
(2 * у = 28; у = 14;
Результатом является пара чисел x = 6 и y = 14. Проверяем. Делаем замену.
(3 * х + 2 * у = 10;
(5 * х + 3 * у = 12);
{3*(-6) + 2*(14) = 10;
{5*(-6) + 3*(14) = 12;
{10 = 10;
{12=12;
Как видите, у нас получилось два верных равенства, значит, мы нашли правильное решение.
Очень часто учащиеся затрудняются с выбором метода решения систем уравнений.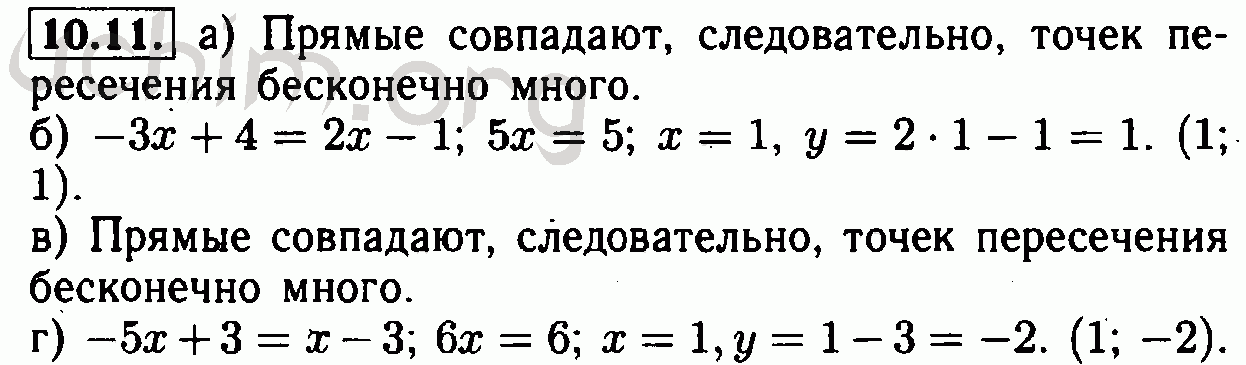
В этой статье мы рассмотрим один из способов решения систем — метод подстановки.
Если найдено общее решение двух уравнений, то говорят, что эти уравнения образуют систему. В системе уравнений каждое неизвестное обозначает одно и то же число во всех уравнениях. Чтобы показать, что эти уравнения образуют систему, их обычно записывают одно под другим и объединяют фигурными скобками, например
Обратите внимание, что для x = 15 и y = 5 оба уравнения системы верны.Эта пара чисел является решением системы уравнений. Каждая пара значений неизвестных, одновременно удовлетворяющая обоим уравнениям системы, называется решением системы.
Система может иметь одно решение (как в нашем примере), бесконечно много решений и не иметь решений.
Как решать системы методом подстановки? Если коэффициенты при каком-то неизвестном в обоих уравнениях равны по модулю (если не равны, то уравниваем), то сложив оба уравнения (или вычитая одно из другого), можно получить уравнение с одним неизвестным.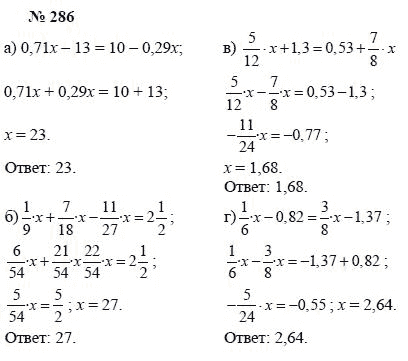 Затем решаем это уравнение. Определим одно неизвестное. Подставляем полученное значение неизвестного в одно из уравнений системы (в первое или второе). Находим еще одно неизвестное. Рассмотрим примеры применения этого метода.
Затем решаем это уравнение. Определим одно неизвестное. Подставляем полученное значение неизвестного в одно из уравнений системы (в первое или второе). Находим еще одно неизвестное. Рассмотрим примеры применения этого метода.
Пример 1. Решить систему уравнений
Здесь коэффициенты при y равны по модулю друг другу, но противоположны по знаку. Попробуем сложить уравнения системы почленно.
Получившееся значение x = 4, подставляем его в какое-нибудь уравнение системы (например, в первое) и находим значение y:
2 * 4 + у = 11, у = 11 — 8, у = 3.
Наша система имеет решение x = 4, y = 3. Как вариант, ответ можно записать в скобках, как координаты точки, в первом месте x, во втором y.
Ответ: (4; 3)
Пример 2 … Решить систему уравнений
Приравняем коэффициенты при переменной x, для этого умножаем первое уравнение на 3, а второе на (-2), получаем
Будьте осторожны при добавлении уравнений
Тогда у = — 2.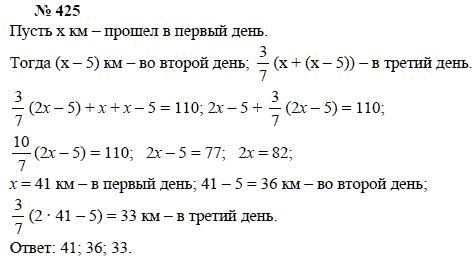 Подставляем в первое уравнение вместо y число (-2), получаем
Подставляем в первое уравнение вместо y число (-2), получаем
4x + 3 (-2) = — 4. Решите это уравнение 4x = — 4 + 6, 4x = 2, x = ½.
Ответ: (1/2; — 2)
Пример 3. Решить систему уравнений
Умножить первое уравнение на (-2)
Решаем систему
получаем 0 = — 13.
Система не имеет решений, так как 0 не равно (-13).
Ответ: Решений нет.
Пример 4. Решить систему уравнений
Обратите внимание, что все коэффициенты второго уравнения делятся на 3,
давайте разделим второе уравнение на три и получим систему, состоящую из двух одинаковых уравнений.
Эта система имеет бесконечно много решений, так как первое и второе уравнения совпадают (мы получили только одно уравнение с двумя переменными).Как представить решение этой системы? Выразим переменную y из уравнения x + y = 5. Получим y = 5 — x.
Тогда ответ будет записан так: (х;5-х), х — любое число.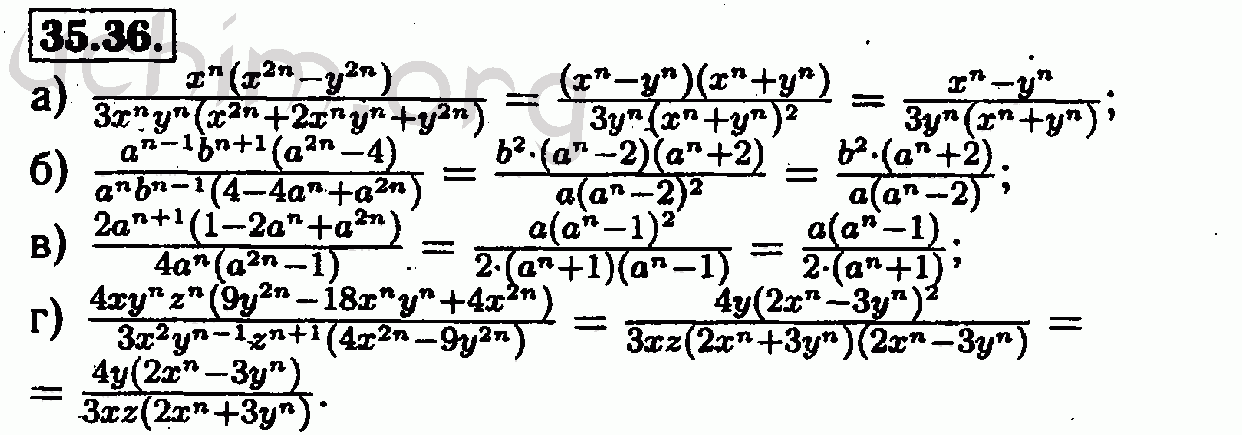
Мы рассмотрели решение систем уравнений методом сложения. Если у вас остались вопросы или что-то непонятно, записывайтесь на урок и мы вместе с вами исправим все неполадки.
сайта, при полном или частичном копировании материала ссылка на первоисточник обязательна.
ОГБОУ «Центр образования детей с особыми образовательными потребностями г. Смоленска»
Центр дистанционного образования
Урок алгебры в 7 классе
Тема урока: Метод алгебраического сложения.
-
-
- Тип урока: Урок первичного изложения новых знаний.
-
Цель занятия: контроль уровня усвоения знаний и умений по решению систем уравнений методом подстановки; формирование навыков и умений решать системы уравнений методом сложения.
Цели урока:
Тема: научиться решать системы уравнений с двумя переменными методом сложения.
Метапредмет: Познавательный УУД : анализировать (выделять главное), определять понятия, обобщать, делать выводы. Нормативное УУД : для определения цели, задачи в образовательной деятельности. Коммуникативное УУД : высказывать свое мнение, аргументируя его. Персональный УУД:ф формировать положительную мотивацию к обучению, формировать положительное эмоциональное отношение учащегося к занятию и предмету.
Нормативное УУД : для определения цели, задачи в образовательной деятельности. Коммуникативное УУД : высказывать свое мнение, аргументируя его. Персональный УУД:ф формировать положительную мотивацию к обучению, формировать положительное эмоциональное отношение учащегося к занятию и предмету.
Форма работы: индивидуальная
Этапы занятия:
1) Организационный этап.
организовать работу учащегося по теме через создание установки на целостность мышления и понимания темы.
2. Опрос студента по материалу, выданному на дому, уточнение знаний.
Цель: проверить знания учащегося, полученные в ходе выполнения домашнего задания, выявить ошибки, работать над ошибками.Повторить материал предыдущего урока.
3. Изучение нового материала.
1). формировать умение решать системы линейных уравнений методом сложения;
2). развивать и совершенствовать имеющиеся знания в новых ситуациях;
3). воспитывать навыки контроля и самоконтроля, развивать самостоятельность.
http://zhakulina200
.blogspot.ru/2011/06/blog-post_25.html
Назначение: сохранение зрения, снятие усталости с глаз при работе на уроках.
5. Закрепление изученного материала
Цель: проверка знаний, умений и навыков, полученных на уроке
6. Конспект урока, информация домашнего задания, рефлексия.
Ход урока (работа в электронном документе Google):
1. Сегодня я хотел начать урок с философской загадки Уолтера.
Что самое быстрое, но и самое медленное, самое большое, но и самое маленькое, самое длинное и самое короткое, самое дорогое, но и самое дешевое мы ценим?
Время
Вспомним основные понятия по теме:
Перед нами система двух уравнений.
Давайте вспомним, как мы решали системы уравнений на прошлом уроке.
Методом подстановки
Еще раз обратите внимание на решаемую систему и скажите, почему мы не можем решить каждое уравнение в системе, не прибегая к методу подстановки?
Потому что это уравнения системы с двумя переменными.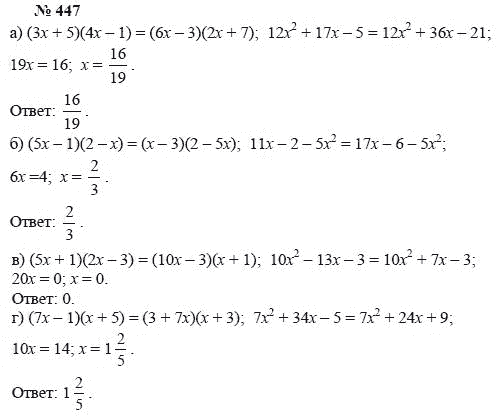 Мы можем решить уравнение только с одной переменной.
Мы можем решить уравнение только с одной переменной.
Только получив уравнение с одной переменной, мы смогли решить систему уравнений.
3. Приступим к решению следующей системы:
Выберем уравнение, в котором удобно выразить одну переменную через другую.
Такого уравнения нет.
Тех. в этой ситуации ранее изученный метод нам не подходит. Каков выход из этой ситуации?
Найдите новый метод.
Попробуем сформулировать цель урока.
Научитесь решать системы новым методом.
Что нам нужно сделать, чтобы научиться решать системы по-новому?
знать правила (алгоритм) решения системы уравнений, выполнять практические задания
Приступим к выводу нового метода.
Обратите внимание на вывод, который мы сделали после решения первой системы. Решить систему удалось только после того, как мы получили линейное уравнение с одной переменной.
Посмотрите на систему уравнений и подумайте, как из двух заданных уравнений получить одно уравнение с одной переменной.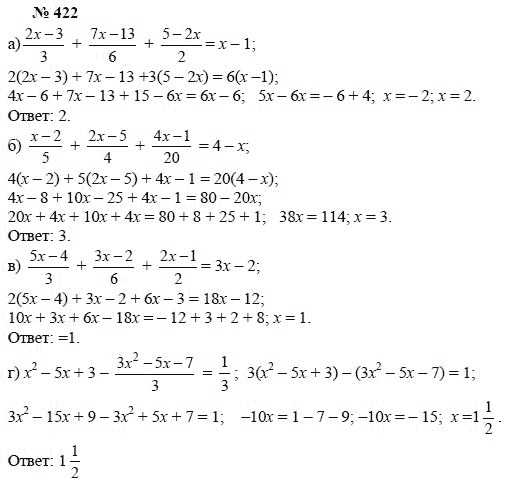
Добавить уравнения.
Что значит складывать уравнения?
Отдельно составить сумму левых частей, сумму правых частей уравнений и полученные суммы равными.
Попробуем. Мы работаем вместе со мной.
13x + 14x + 17y-17y = 43 + 11
Получили линейное уравнение с одной переменной.
Вы решили систему уравнений?
Решением системы является пара чисел.
Как тебя найти?
Подставить найденное значение x в уравнение системы.
Имеет ли значение, в какое уравнение мы подставим значение x?
Это означает, что найденное значение x можно подставить в …
любое уравнение системы.
Мы познакомились с новым методом — методом алгебраического сложения.
Решая систему, мы рассказали об алгоритме решения системы этим методом.
Мы рассмотрели алгоритм. Теперь применим его к решению задач.
Умение решать системы уравнений может пригодиться на практике.
Рассмотрим задачу:
На ферме есть куры и овцы.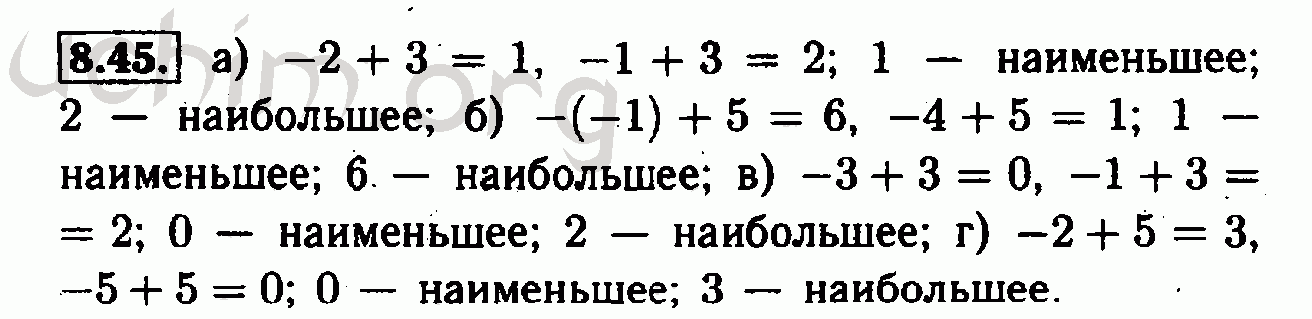 Сколько тех и других, если у них 19 голов и 46 ног вместе?
Сколько тех и других, если у них 19 голов и 46 ног вместе?
Зная, что всего кур и овец 19, составим первое уравнение: x + y = 19
4x — количество ног у овцы
2y — количество ног у кур
Зная, что есть всего 46 ножек, составляем второе уравнение: 4x + 2y = 46
Составим систему уравнений:
Решим систему уравнений с помощью алгоритма сложения.
Проблема! Коэффициенты перед х и у не равны и не противоположны! Что делать?
Возьмем другой пример!
Добавим к нашему алгоритму еще один шаг и поставим его на первое место: Если коэффициенты перед переменными не одинаковы и не противоположны, то надо уравнять модули по какой-то переменной! А дальше будем действовать по алгоритму.
4. Электронная физкультура для глаз: http://zhakulina200
.blogspot.ru/2011/06/blog-post_25.html
5. Завершаем задачу методом алгебраического сложения, закрепляя новый материал и выясняем, сколько кур и овец было на ферме.
Дополнительные задания:
6.
Отражение.
За работу на уроке ставлю оценку — …
6. Использованные интернет-ресурсы:
Сервисы Google для образования
Учитель математики Соколова Н.Н.
Системы уравнений широко используются в экономической отрасли при математическом моделировании различных процессов.Например, при решении задач управления и планирования производства, логистических маршрутов (транспортная задача) или размещения оборудования.
Системы уравнений применяются не только в области математики, но и в физике, химии и биологии, при решении задач нахождения численности населения.
Системой линейных уравнений называют два или более уравнений с несколькими переменными, для которых необходимо найти общее решение. Такая последовательность чисел, для которой все уравнения становятся истинными равенствами или доказывают, что последовательности не существует.
Линейное уравнение
Уравнения вида ax + by = c называются линейными. Обозначения x, y – неизвестные, значение которых необходимо найти, b, a – коэффициенты при переменных, c – свободный член уравнения.
Обозначения x, y – неизвестные, значение которых необходимо найти, b, a – коэффициенты при переменных, c – свободный член уравнения.
Решение уравнения при построении его графика будет иметь вид прямой линии, все точки которой являются решением многочлена.
Типы систем линейных уравнений
Простейшими примерами считаются системы линейных уравнений с двумя переменными X и Y.
F1 (x, y) = 0 и F2 (x, y) = 0, где F1,2 — функции, а (x, y) — функциональные переменные.
Решить систему уравнений —
означает нахождение таких значений (х, у), при которых система превращается в истинное равенство, или установление отсутствия подходящих значений для х и у.
Пара значений (x, y), записанная как координаты точки, называется решением системы линейных уравнений.
Если системы имеют одно общее решение или такое решение не существует, они называются эквивалентными.
Однородные системы линейных уравнений – это системы, правая часть которых равна нулю.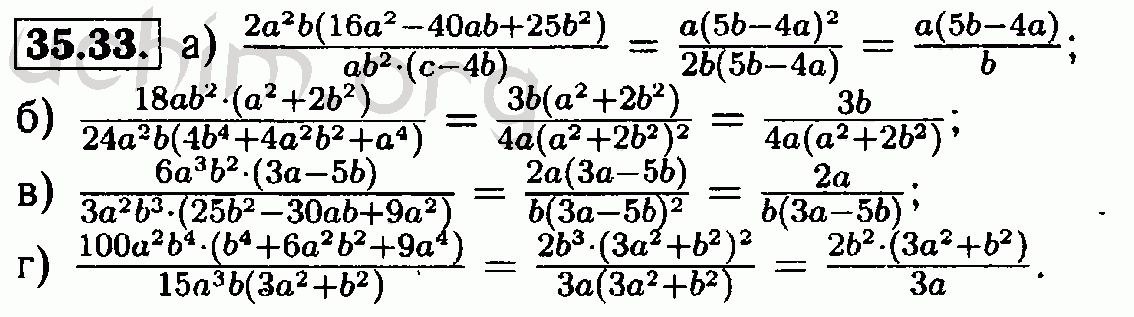 Если правая часть после знака «равно» имеет значение или выражается функцией, такая система неоднородна.
Если правая часть после знака «равно» имеет значение или выражается функцией, такая система неоднородна.
Количество переменных может быть намного больше двух, тогда следует говорить о примере системы линейных уравнений с тремя и более переменными.
Столкнувшись с системами, школьники предполагают, что количество уравнений обязательно должно совпадать с количеством неизвестных, но это не так.Количество уравнений в системе не зависит от переменных; их может быть сколько угодно.
Простые и сложные методы решения систем уравнений
Общего аналитического способа решения таких систем не существует; все методы основаны на численных решениях. В школьном курсе математики подробно описаны такие методы, как перестановка, алгебраическое сложение, подстановка, а также графический и матричный метод, решение методом Гаусса.
Основная задача в обучении методам решения — научить правильно анализировать систему и находить оптимальный алгоритм решения для каждого примера. Главное не запомнить систему правил и действий по каждому методу, а понять принципы применения того или иного метода
Главное не запомнить систему правил и действий по каждому методу, а понять принципы применения того или иного метода
Решение примеров систем линейных уравнений 7 класса общешкольной программы достаточно просто и объяснил очень подробно. В любом учебнике по математике этому разделу уделяется достаточно внимания. Решение примеров систем линейных уравнений методом Гаусса и Крамера более подробно изучается на первых курсах высших учебных заведений.
Решение систем методом подстановки
Действия метода подстановки направлены на выражение значения одной переменной через вторую. Выражение подставляется в оставшееся уравнение, затем приводится к виду с одной переменной. Действие повторяется в зависимости от количества неизвестных в системе
Приведем пример решения системы линейных уравнений 7 класса методом подстановки:
Как видно из примера, переменная x была выражена через F (X) = 7 + Y.Полученное выражение, подставленное во 2-е уравнение системы вместо X, помогло получить одну переменную Y во 2-м уравнении. Решение этого примера не вызывает затруднений и позволяет получить значение Y. Последним шагом является проверка полученных значений.
Решение этого примера не вызывает затруднений и позволяет получить значение Y. Последним шагом является проверка полученных значений.
Не всегда возможно решить пример системы линейных уравнений подстановкой. Уравнения могут быть сложными и выражение переменной через вторую неизвестную будет слишком громоздким для дальнейших вычислений.При наличии в системе более 3-х неизвестных решение подстановкой также нецелесообразно.
Решение примера системы линейных неоднородных уравнений:
Решение алгебраического сложения
При поиске решения систем методом сложения выполняются почленное сложение и умножение уравнений на различные числа . Конечной целью математических операций является уравнение с одной переменной.
Этот метод требует практики и наблюдения.Решить систему линейных уравнений методом сложения с числом переменных 3 и более непросто. Алгебраическое сложение полезно, когда в уравнениях присутствуют дроби и десятичные числа.
Алгоритм действий решения:
- Умножить обе части уравнения на некоторое число.
 В результате арифметического действия один из коэффициентов переменной должен стать равным 1.
В результате арифметического действия один из коэффициентов переменной должен стать равным 1. - Сложить полученное выражение почленно и найти одно из неизвестных.
- Подставьте полученное значение во второе уравнение системы, чтобы найти оставшуюся переменную.
Решение путем введения новой переменной
Введение новой переменной допускается, если системе необходимо найти решение не более двух уравнений, число неизвестных также должно быть не более двух.
Метод используется для упрощения одного из уравнений путем ввода новой переменной. Новое уравнение решается относительно введенного неизвестного, и полученное значение используется для определения исходной переменной.
Пример показывает, что введением новой переменной t удалось привести 1-е уравнение системы к стандартному квадратному трехчлену. Вы можете решить многочлен, найдя дискриминант.
Необходимо найти значение дискриминанта по известной формуле: D = b2 — 4 * a * c, где D — искомый дискриминант, b, a, c — множители многочлена. В данном примере a = 1, b = 16, c = 39, следовательно, D = 100.Если дискриминант больше нуля, то решения два: t = -b ± √D/2*a, если дискриминант меньше нуля, то решение одно: x = -b/2*a.
В данном примере a = 1, b = 16, c = 39, следовательно, D = 100.Если дискриминант больше нуля, то решения два: t = -b ± √D/2*a, если дискриминант меньше нуля, то решение одно: x = -b/2*a.
Решение полученных систем находится методом сложения.
Визуальный метод решения систем
Подходит для систем с 3 уравнениями. Метод заключается в построении по оси координат графиков каждого уравнения, входящего в систему. Координаты точек пересечения кривых и будут общим решением системы.
Графический метод имеет ряд нюансов. Рассмотрим несколько примеров решения систем линейных уравнений наглядным способом.
Как видно из примера, для каждой прямой построены две точки, значения переменной x выбраны произвольно: 0 и 3. На основании значений x получены значения для y были найдены: 3 и 0. Точки с координатами (0, 3) и (3, 0) были отмечены на графике и соединены линией.
Действия необходимо повторить для второго уравнения.Точка пересечения прямых является решением системы.
В следующем примере необходимо найти графическое решение системы линейных уравнений: 0,5xy + 2 = 0 и 0,5xy-1 = 0.
Как видно из примера, система имеет решения нет, так как графики параллельны и не пересекаются по всей своей длине.
Системы из примеров 2 и 3 похожи, но при построении становится очевидно, что их решения разные.Следует помнить, что не всегда можно сказать, имеет система решение или нет, всегда необходимо строить граф.
Матрица и ее разновидности
Матрицы используются для краткой записи системы линейных уравнений. Матрица — это таблица особого вида, заполненная числами. n * m имеет n — строк и m — столбцов.
Матрица является квадратной, если количество столбцов и строк равно друг другу. Векторная матрица — это одностолбцовая матрица с бесконечным числом строк.Матрица с единицами вдоль одной из диагоналей и нулевыми остальными элементами называется единичной матрицей.
Обратная матрица это такая матрица, при умножении на которую исходная превращается в единичную матрицу, такая матрица существует только для исходной квадратной.
Правила преобразования системы уравнений в матрицу
Применительно к системам уравнений коэффициенты и свободные члены уравнений записываются в виде чисел матрицы, одно уравнение — одна строка матрицы.
Строка матрицы называется отличной от нуля, если хотя бы один элемент строки не равен нулю. Поэтому, если в каком-либо из уравнений количество переменных отличается, то необходимо вместо отсутствующих неизвестных писать ноль.
Столбцы матрицы должны строго соответствовать переменным. Это означает, что коэффициенты при переменной х можно записывать только в один столбец, например, первый, коэффициент при неизвестной у — только во второй.
При умножении матрицы все элементы матрицы последовательно умножаются на число.
Варианты нахождения обратной матрицы
Формула нахождения обратной матрицы достаточно проста: K -1 = 1 / | K |, где K -1 — обратная матрица, а | К | является определителем матрицы. | К | не должен быть равен нулю, то система имеет решение.
Определитель легко вычисляется для матрицы два на два, нужно просто перемножить элементы по диагонали друг на друга. Для варианта «три на три» есть формула | К | = а 1 б 2 с 3 + а 1 б 3 с 2 + а 3 б 1 с 2 + а 2 б 3 с 1 + а 2 б 1 с 3 + а 3 б 2 с 1.Можно воспользоваться формулой, а можно запомнить, что нужно брать по одному элементу из каждой строки и каждого столбца, чтобы номера столбцов и рядов элементов не повторялись в произведении.
Решение примеров систем линейных уравнений матричным методом
Матричный метод поиска решения позволяет сократить громоздкие записи при решении систем с большим количеством переменных и уравнений.
В примере a nm — коэффициенты уравнений, матрица — вектор x n — переменные, b n — свободные члены.
Гауссово решение систем
В высшей математике метод Гаусса изучается совместно с методом Крамера, а процесс нахождения решения систем называется методом Гаусса-Крамера. Эти методы используются для нахождения переменных систем с большим количеством линейных уравнений.
Метод Гаусса очень похож на решения подстановки и алгебраического сложения, но более систематичен. В школьном курсе решение Гаусса используется для систем из 3 и 4 уравнений.Цель метода — сделать систему похожей на перевернутую трапецию. Значение одной переменной в одном из уравнений системы находится путем алгебраических преобразований и подстановок. Второе уравнение представляет собой выражение с 2-мя неизвестными, а 3 и 4 — соответственно с 3 и 4 переменными.
После приведения системы к описанному виду дальнейшее решение сводится к последовательной подстановке известных переменных в уравнения системы.
В школьных учебниках для 7 класса пример решения методом Гаусса описан так:
Как видно из примера, на шаге (3) были получены два уравнения: 3x 3 -2x 4 = 11 и 3x 3 + 2x 4 = 7.Решение любого из уравнений позволит узнать одну из переменных x n.
Теорема 5, упомянутая в тексте, утверждает, что если одно из уравнений системы заменить эквивалентным, то полученная система также будет эквивалентна исходной.
Метод Гаусса сложен для понимания старшеклассниками, но это один из самых интересных способов развития интеллекта детей на продвинутых уроках математики и физики.
Для удобства записи расчетов принято делать следующее:
Коэффициенты уравнений и свободные члены записываются в виде матрицы, где каждая строка матрицы связана с одним из уравнения системы. отделяет левую часть уравнения от правой. Римскими цифрами обозначены номера уравнений в системе.
Сначала записывают матрицу, с которой предстоит работать, затем все действия, проводимые с одной из строк.Полученную матрицу записывают после знака стрелки и продолжают необходимые алгебраические действия до достижения результата.
В результате должна получиться матрица, у которой одна из диагоналей равна 1, а все остальные коэффициенты равны нулю, то есть матрица приведена к единому виду. Не забудьте произвести расчеты с числами в обеих частях уравнения.
Этот способ записи менее громоздкий и позволяет не отвлекаться на перечисление многочисленных неизвестных.
Бесплатное применение любого решения потребует осторожности и определенного опыта. Не все методы носят прикладной характер. Одни способы поиска решений более предпочтительны в этой другой области человеческой деятельности, а другие существуют для образовательных целей.
Алгебраический способ решения системы уравнений. Видеоурок «Алгебраический метод сложения
»
Метод алгебраического сложения
Систему уравнений с двумя неизвестными можно решить разными способами — графическим методом или методом замены переменных.
В этом уроке мы познакомимся с еще одним способом решения систем, который вам наверняка понравится — это метод алгебраического сложения.
А откуда пришла идея — добавить что-то в системы? При решении систем основной проблемой является наличие двух переменных, потому что мы не умеем решать уравнения с двумя переменными. Это означает, что один из них должен быть исключен каким-либо законным способом. И такими юридическими средствами являются математические правила и свойства.
Одно из этих свойств звучит так: сумма противоположных чисел равна нулю. Это означает, что если для одной из переменных будут противоположные коэффициенты, то их сумма будет равна нулю и мы сможем исключить эту переменную из уравнения. Понятно, что мы не имеем права добавлять только термы с нужной нам переменной. Добавлять уравнения нужно целиком, т.е. добавлять подобные члены отдельно в левую часть, затем в правую. В результате мы получаем новое уравнение, содержащее только одну переменную.Рассмотрим сказанное на конкретных примерах.
Мы видим, что в первом уравнении стоит переменная у, а во втором противоположное число у. Следовательно, это уравнение может быть решено методом сложения.
Одно из уравнений оставлено как есть. Какой вам больше нравится.
Но второе уравнение будет получено путем сложения этих двух уравнений почленно. Те. Прибавьте 3x к 2x, прибавьте y к -y, прибавьте 8 к 7.
Получаем систему уравнений
Второе уравнение этой системы является простым уравнением с одной переменной.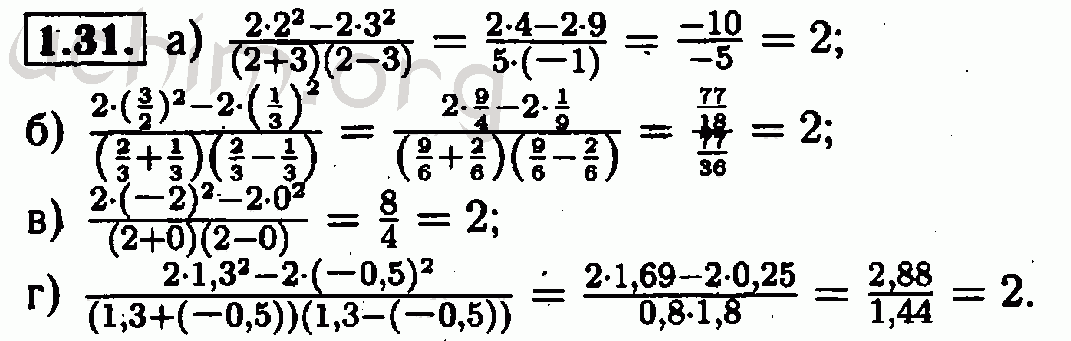 Из него находим x = 3. Подставляя найденное значение в первое уравнение, находим y = -1.
Из него находим x = 3. Подставляя найденное значение в первое уравнение, находим y = -1.
Ответ: (3; — 1).
Образец регистрации:
Решите систему уравнений методом алгебраического сложения
В этой системе нет переменных с противоположными коэффициентами. Но мы знаем, что обе части уравнения можно умножить на одно и то же число. Умножим первое уравнение системы на 2.
Тогда первое уравнение примет вид:
Теперь мы видим, что переменная x имеет противоположные коэффициенты.Это значит, что мы поступим так же, как и в первом примере: оставим одно из уравнений без изменений. Например, 2у + 2х = 10. А второе получаем сложением.
Теперь у нас есть система уравнений:
Легко находим из второго уравнения y = 1, а затем из первого уравнения x = 4.
Образец регистрации:
Подведем итоги:
Мы научились решать системы двух линейных уравнений с двумя неизвестными методом алгебраического сложения.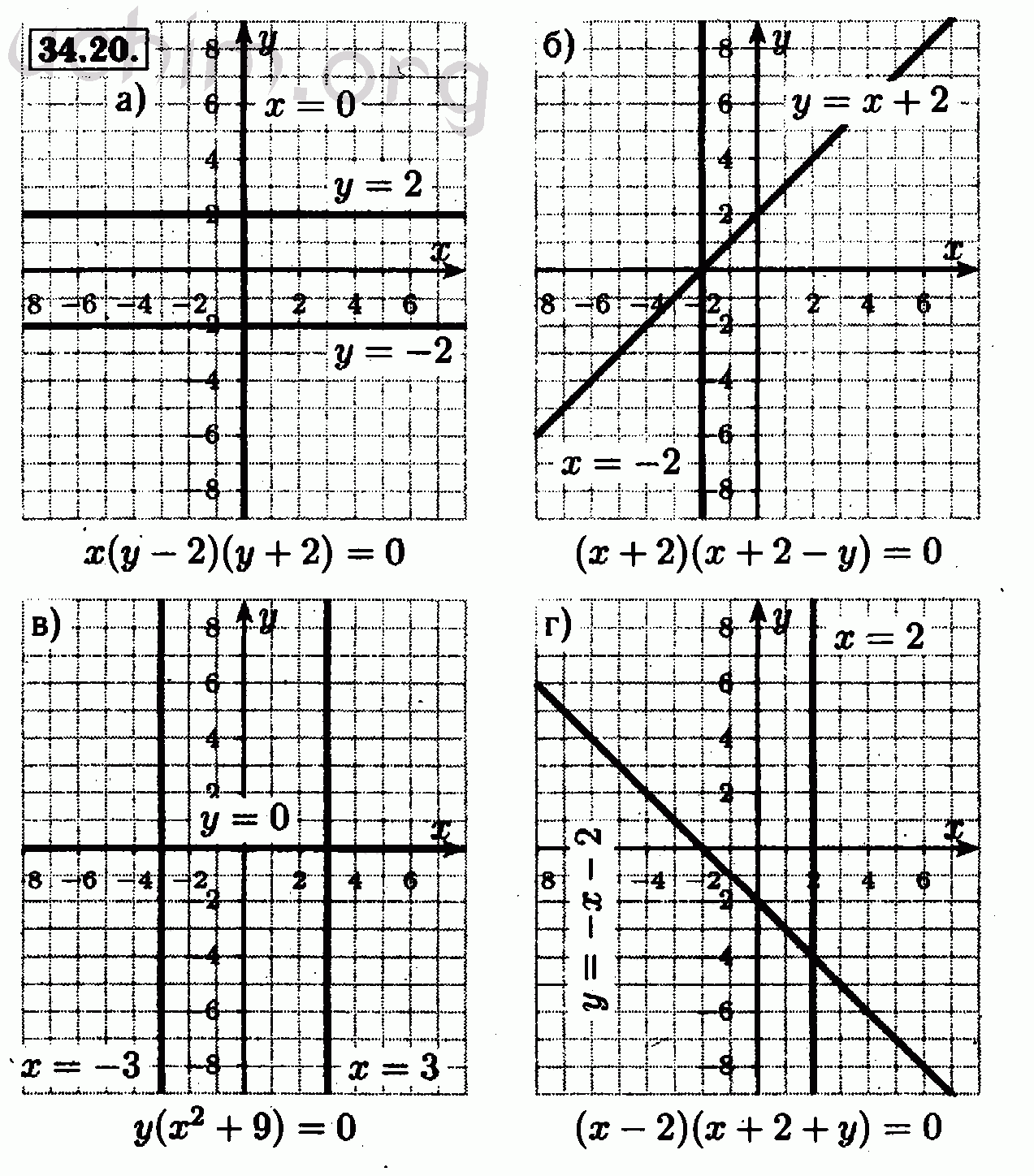 Таким образом, теперь мы знаем три основных метода решения таких систем: графический, замена переменных и сложение. Этими методами можно решить почти любую систему. В более сложных случаях используется комбинация этих методов.
Таким образом, теперь мы знаем три основных метода решения таких систем: графический, замена переменных и сложение. Этими методами можно решить почти любую систему. В более сложных случаях используется комбинация этих методов.
Список использованной литературы:
- Мордкович А.Г., Алгебра 7 класс в 2-х частях, ч.1, Учебник для общеобразовательных учреждений / А.Г. Мордкович. — 10-е изд., перераб. — М., «Мнемозина», 2007.
- Мордкович А.Г., Алгебра 7 класс в 2-х частях, часть 2, Задача для общеобразовательных учреждений / [А.Г. Мордкович и др.]; под редакцией А.Г. Мордковича — 10-е издание, переработанное — Москва, «Мнемозина», 2007.
- ЕЕ. Тульчинская, Алгебра 7 класс. Блиц-опрос: пособие для учащихся общеобразовательных учреждений, 4-е издание, исправленное и дополненное, Москва, «Мнемозина», 2008.
- Александрова Л.А., Алгебра 7 класс. Тематические тесты в новой форме для учащихся общеобразовательных учреждений под редакцией А.Г. Мордковича, Москва, «Мнемозина», 2011.

- Александрова Л.А. Алгебра 7 класс.Самостоятельная работа для учащихся общеобразовательных учреждений под редакцией Мордковича А.Г. — 6-е издание, шаблонное, Москва, «Мнемозина», 2010.
Методом сложения уравнения системы складываются почленно, при этом 1 или оба (несколько) уравнений могут быть умножены на любое число. В результате приходим к эквивалентному СЛУ, в котором одно из уравнений содержит только одну переменную.
Для решения системы почленное сложение (вычитание) выполните следующие действия:
1.Выберите переменную, для которой будут сделаны одинаковые коэффициенты.
2. Теперь нужно сложить или вычесть уравнения и получить уравнение с одной переменной.
Системное решение являются точками пересечения графиков функций.
Давайте рассмотрим несколько примеров.
Пример 1.
Учитывая систему:
Проанализировав эту систему, можно увидеть, что коэффициенты при переменной равны по величине и различны по знаку (-1 и 1). В этом случае уравнения легко сложить почленно:
В этом случае уравнения легко сложить почленно:
Действия, обведенные красным, выполняются в уме.
Результатом почленного сложения стало исчезновение переменной y … Именно в этом и в этом, собственно, смысл метода — избавиться от 1-й из переменных .
-4 —
у + 5 = 0 →
у = 1,
В виде системы решение выглядит примерно так:
Ответ: х =
-4
,
у =
1.
Пример 2.
Учитывая систему:
В этом примере можно использовать «школьный» метод, но он имеет довольно большой недостаток — при выражении любой переменной из любого уравнения вы получите решение в обыкновенных дробях. А решение дробей занимает достаточно времени и вероятность ошибок возрастает.
Поэтому лучше использовать почленное сложение (вычитание) уравнений. Проанализируем коэффициенты соответствующих переменных:
Вам нужно выбрать число, которое можно разделить на 3
и на 4
, при этом необходимо, чтобы это число было минимально возможным. Это наименьшее общее кратное … Если вам трудно подобрать подходящее число, то можно умножить коэффициенты: .
Это наименьшее общее кратное … Если вам трудно подобрать подходящее число, то можно умножить коэффициенты: .
Следующий шаг:
1-е уравнение умножается на
3-е уравнение умножается на
Системы уравнений получили широкое применение в экономической отрасли при математическом моделировании различных процессов. Например, при решении задач управления и планирования производства, логистических маршрутов (транспортная задача) или размещения оборудования.
Системы уравнений применяются не только в области математики, но и в физике, химии и биологии, при решении задач нахождения численности населения.
Системой линейных уравнений называют два или более уравнений с несколькими переменными, для которых необходимо найти общее решение. Такая последовательность чисел, при которой все уравнения становятся истинными равенствами или доказывают, что последовательности не существует.
Линейное уравнение
Уравнения вида ax + by = c называются линейными.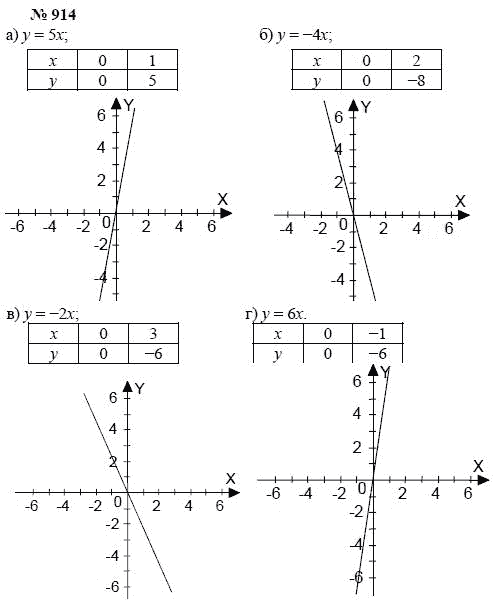 Обозначения x, y – неизвестные, значение которых необходимо найти, b, a – коэффициенты при переменных, c – свободный член уравнения.
Обозначения x, y – неизвестные, значение которых необходимо найти, b, a – коэффициенты при переменных, c – свободный член уравнения.
Решение уравнения при построении его графика будет иметь вид прямой линии, все точки которой являются решением многочлена.
Типы систем линейных уравнений
Простейшими примерами считаются системы линейных уравнений с двумя переменными X и Y.
F1 (x, y) = 0 и F2 (x, y) = 0, где F1 ,2 — функции, а (x, y) — функциональные переменные.
Решить систему уравнений —
это означает нахождение таких значений (x, y), при которых система превращается в истинное равенство, или установление отсутствия подходящих значений для x и y.
Пара значений (x, y), записанная как координаты точки, называется решением системы линейных уравнений.
Если системы имеют одно общее решение или такое решение не существует, они называются эквивалентными.
Однородные системы линейных уравнений – это системы, правая часть которых равна нулю. Если правая часть после знака «равно» имеет значение или выражается функцией, такая система неоднородна.
Если правая часть после знака «равно» имеет значение или выражается функцией, такая система неоднородна.
Количество переменных может быть намного больше двух, тогда следует говорить о примере системы линейных уравнений с тремя и более переменными.
Столкнувшись с системами, школьники предполагают, что количество уравнений обязательно должно совпадать с количеством неизвестных, но это не так. Количество уравнений в системе не зависит от переменных; их может быть сколько угодно.
Простые и сложные методы решения систем уравнений
Не существует единого аналитического способа решения подобных систем, все методы основаны на численном решении. В школьном курсе математики подробно описаны такие методы, как перестановка, алгебраическое сложение, подстановка, а также графический и матричный метод, решение методом Гаусса.
Основная задача в обучении методам решения — научить правильно анализировать систему и находить оптимальный алгоритм решения для каждого примера.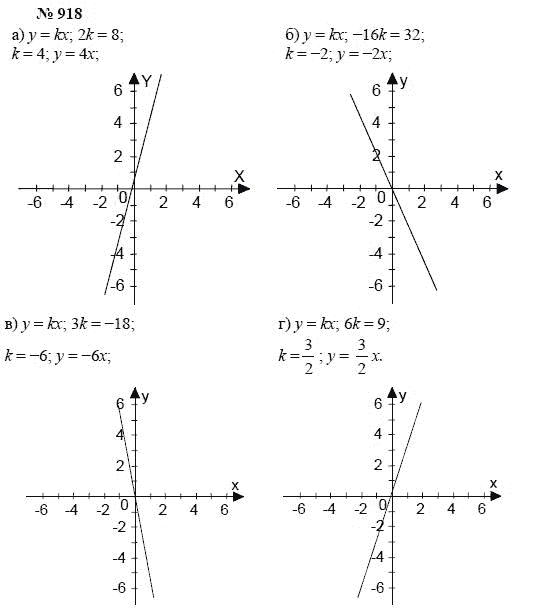 Главное не запомнить систему правил и действий для каждого метода, а понять принципы применения того или иного метода
Главное не запомнить систему правил и действий для каждого метода, а понять принципы применения того или иного метода
Решение примеров систем линейных уравнений для 7 класса общешкольной программы достаточно просто и объяснил очень подробно. В любом учебнике по математике этому разделу уделяется достаточно внимания. Решение примеров систем линейных уравнений методом Гаусса и Крамера более подробно изучается на первых курсах высших учебных заведений.
Решение систем методом подстановки
Действия метода подстановки направлены на выражение значения одной переменной через вторую. Выражение подставляется в оставшееся уравнение, затем приводится к виду с одной переменной. Действие повторяется в зависимости от количества неизвестных в системе
Приведем пример решения системы линейных уравнений 7 класса методом подстановки:
Как видно из примера, переменная x была выражена через F (X) = 7 + Y.Полученное выражение, подставленное во 2-е уравнение системы вместо X, помогло получить одну переменную Y во 2-м уравнении. Решение этого примера не вызывает затруднений и позволяет получить значение Y. Последним шагом является проверка полученных значений.
Решение этого примера не вызывает затруднений и позволяет получить значение Y. Последним шагом является проверка полученных значений.
Не всегда возможно решить пример системы линейных уравнений подстановкой. Уравнения могут быть сложными, и выражение переменной через вторую неизвестную будет слишком громоздким для дальнейших вычислений.При наличии в системе более 3-х неизвестных решение подстановкой также нецелесообразно.
Решение примера системы линейных неоднородных уравнений:
Решение алгебраического сложения
При поиске решения систем методом сложения выполняются почленное сложение и умножение уравнений на различные числа . Конечной целью математических действий является уравнение с одной переменной.
Для применения этого метода необходимы практика и наблюдение.Непросто решить систему линейных уравнений методом сложения с 3 и более переменными. Удобно использовать алгебраическое сложение, когда в уравнениях присутствуют дроби и десятичные числа.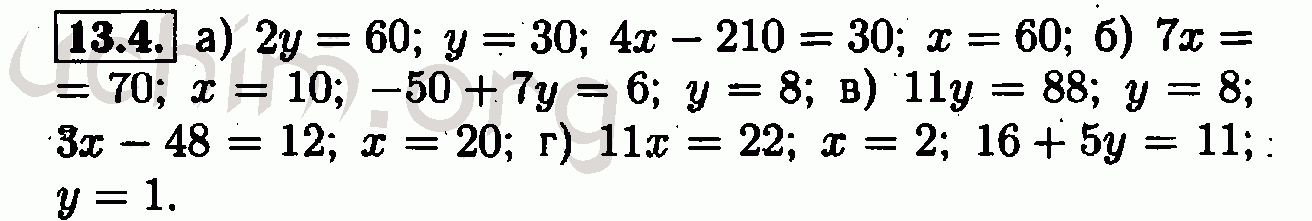
Алгоритм действий решения:
- Умножить обе части уравнения на некоторое число. В результате арифметического действия один из коэффициентов переменной должен стать равным 1.
- Сложить полученное выражение почленно и найти одно из неизвестных.
- Подставьте полученное значение во второе уравнение системы, чтобы найти оставшуюся переменную.
Решение путем введения новой переменной
Введение новой переменной допускается, если системе необходимо найти решение не более двух уравнений, число неизвестных также должно быть не более двух.
Метод используется для упрощения одного из уравнений путем введения новой переменной. Новое уравнение решается относительно введенного неизвестного, и полученное значение используется для определения исходной переменной.
Пример показывает, что введением новой переменной t удалось привести 1-е уравнение системы к стандартному одноквадратичному трехчлену. Решить многочлен можно, найдя дискриминант.
Необходимо найти значение дискриминанта по известной формуле: D = b2 — 4 * a * c, где D — искомый дискриминант, b, a, c — множители многочлена. В данном примере a = 1, b = 16, c = 39, следовательно, D = 100.Если дискриминант больше нуля, то решения два: t = -b ± √D/2*a, если дискриминант меньше нуля, то решение одно: x = -b/2*a.
Решение полученных систем находится методом сложения.
Визуальный метод решения систем
Подходит для систем с 3 уравнениями. Метод заключается в построении по оси координат графиков каждого уравнения, входящего в систему. Координаты точек пересечения кривых и будут общим решением системы.
Графический метод имеет ряд нюансов. Рассмотрим несколько примеров решения систем линейных уравнений наглядным способом.
Как видно из примера, для каждой прямой построены две точки, значения переменной x выбраны произвольно: 0 и 3. На основании значений x получены значения для y были найдены: 3 и 0. Точки с координатами (0, 3) и (3, 0) были отмечены на графике и соединены линией.
Действия необходимо повторить для второго уравнения.Точка пересечения прямых является решением системы.
В следующем примере требуется найти графическое решение системы линейных уравнений: 0,5xy + 2 = 0 и 0,5xy-1 = 0.
Как видно из примера, система не имеет решения, поскольку графики параллельны и не пересекаются на всем протяжении.
Системы из примеров 2 и 3 похожи, но при построении становится очевидно, что их решения разные.Следует помнить, что не всегда можно сказать, имеет система решение или нет, всегда необходимо строить граф.
Матрица и ее разновидности
Матрицы используются для краткой записи системы линейных уравнений. Матрица — это таблица особого вида, заполненная числами. n * m имеет n — строк и m — столбцов.
Матрица является квадратной, если количество столбцов и строк равно друг другу. Векторная матрица — это одностолбцовая матрица с бесконечным числом строк.Матрица с единицами вдоль одной из диагоналей и нулевыми остальными элементами называется единичной матрицей.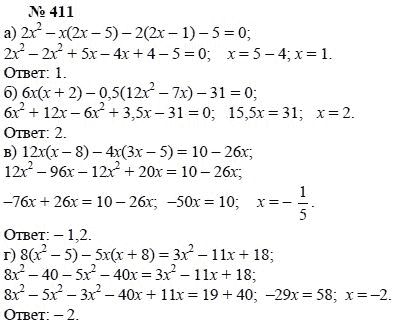
Обратная матрица это такая матрица, при умножении на которую исходная превращается в единичную матрицу, такая матрица существует только для исходной квадратной.
Правила преобразования системы уравнений в матрицу
Применительно к системам уравнений коэффициенты и свободные члены уравнений записываются в виде чисел матрицы, одно уравнение — одна строка матрицы.
Строка матрицы называется отличной от нуля, если хотя бы один элемент строки не равен нулю. Поэтому, если в каком-либо из уравнений количество переменных отличается, то необходимо вместо отсутствующих неизвестных писать ноль.
Столбцы матрицы должны строго соответствовать переменным. Это означает, что коэффициенты при переменной х можно записывать только в один столбец, например, первый, коэффициент при неизвестной у — только во второй.
При умножении матрицы все элементы матрицы последовательно умножаются на число.
Варианты нахождения обратной матрицы
Формула нахождения обратной матрицы достаточно проста: K -1 = 1 / | K |, где K -1 — обратная матрица, а | К | является определителем матрицы.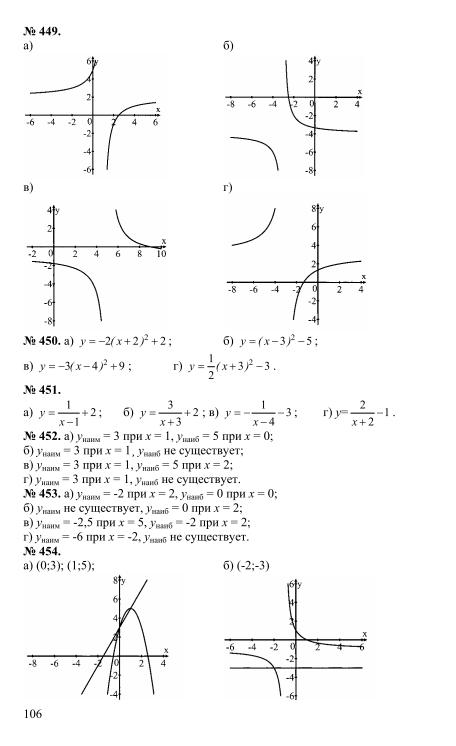 | К | не должен быть равен нулю, то система имеет решение.
| К | не должен быть равен нулю, то система имеет решение.
Определитель легко вычисляется для матрицы два на два; вам просто нужно умножить элементы по диагонали друг на друга. Для варианта «три на три» есть формула | К | = а 1 б 2 с 3 + а 1 б 3 с 2 + а 3 б 1 с 2 + а 2 б 3 с 1 + а 2 б 1 с 3 + а 3 б 2 с 1.Можно воспользоваться формулой, а можно запомнить, что нужно брать по одному элементу из каждой строки и каждого столбца, чтобы номера столбцов и рядов элементов не повторялись в произведении.
Решение примеров систем линейных уравнений матричным методом
Матричный метод поиска решения позволяет сократить громоздкие записи при решении систем с большим количеством переменных и уравнений.
В примере a nm — коэффициенты уравнений, матрица — вектор x n — переменные, b n — свободные члены.
Гауссово решение систем
В высшей математике метод Гаусса изучается совместно с методом Крамера, а процесс нахождения решения систем называется методом Гаусса — Крамера.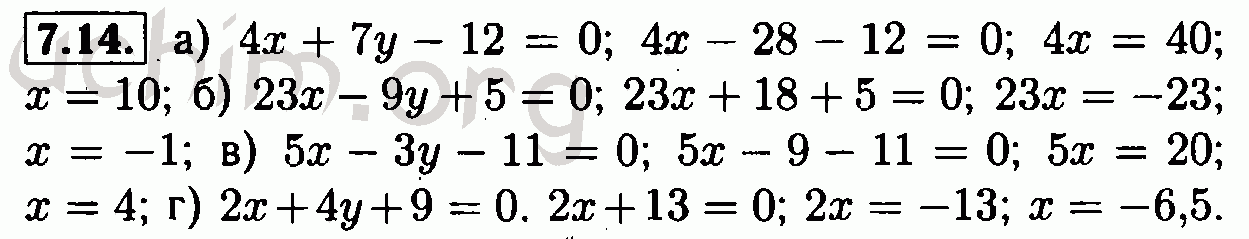 Эти методы используются при нахождении переменных систем с большим количеством линейных уравнений.
Эти методы используются при нахождении переменных систем с большим количеством линейных уравнений.
Метод Гаусса очень похож на решения подстановки и алгебраического сложения, но более систематичен. В школьном курсе решение Гаусса используется для систем из 3 и 4 уравнений.Цель метода — сделать систему похожей на перевернутую трапецию. Путем алгебраических преобразований и подстановок значение одной переменной находится в одном из уравнений системы. Второе уравнение представляет собой выражение с 2-мя неизвестными, а 3 и 4 — соответственно с 3 и 4 переменными.
После приведения системы к описанному виду дальнейшее решение сводится к последовательной подстановке известных переменных в уравнения системы.
В школьных учебниках для 7 класса пример решения методом Гаусса описан так:
Как видно из примера, на шаге (3) были получены два уравнения: 3x 3 -2x 4 = 11 и 3x 3 + 2x 4 = 7.Решение любого из уравнений позволит узнать одну из переменных x n.
Теорема 5, упомянутая в тексте, утверждает, что если одно из уравнений системы заменить эквивалентным, то полученная система также будет эквивалентна исходной.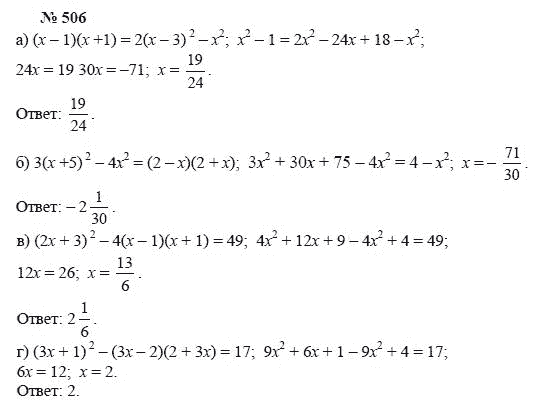
Метод Гаусса сложен для восприятия старшеклассниками, но является одним из самых интересных способов развития интеллекта детей на продвинутых уроках математики и физики.
Для удобства записи расчетов принято делать следующее:
Коэффициенты уравнений и свободные члены записываются в виде матрицы, где каждая строка матрицы связана с одним из уравнения системы. отделяет левую часть уравнения от правой. Римскими цифрами обозначены номера уравнений в системе.
Сначала записывают матрицу, с которой предстоит работать, затем все действия, проводимые с одной из строк.Полученную матрицу записывают после знака стрелки и продолжают необходимые алгебраические действия до достижения результата.
В результате должна получиться матрица, у которой одна из диагоналей равна 1, а все остальные коэффициенты равны нулю, то есть матрица приведена к единому виду. Не забудьте произвести расчеты с числами в обеих частях уравнения.
Этот способ записи менее громоздкий и позволяет не отвлекаться на перечисление многочисленных неизвестных.
Бесплатное применение любого решения потребует осторожности и определенного опыта. Не все методы носят прикладной характер. Одни способы поиска решений более предпочтительны в этой другой области человеческой деятельности, а другие существуют для образовательных целей.
Очень часто учащиеся затрудняются с выбором метода решения систем уравнений.
В этой статье мы рассмотрим один из способов решения систем — метод подстановки.
Если найдено общее решение двух уравнений, то говорят, что эти уравнения образуют систему.В системе уравнений каждое неизвестное обозначает одно и то же число во всех уравнениях. Чтобы показать, что эти уравнения образуют систему, их обычно записывают одно под другим и объединяют фигурными скобками, например
Обратите внимание, что для x = 15 и y = 5 оба уравнения системы верны. Эта пара чисел является решением системы уравнений. Каждая пара значений неизвестных, одновременно удовлетворяющая обоим уравнениям системы, называется решением системы.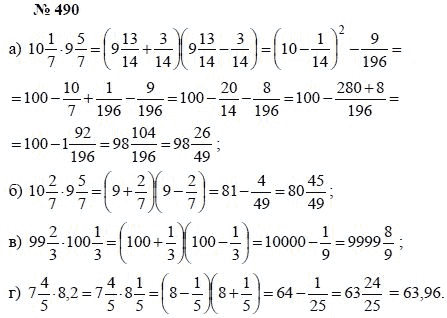
Система может иметь одно решение (как в нашем примере), бесконечно много решений и не иметь решений.
Как вы решаете системы подстановкой? Если коэффициенты при каком-то неизвестном в обоих уравнениях равны по абсолютной величине (если не равны, то уравниваем), то сложив оба уравнения (или вычитая одно из другого), можно получить уравнение с одним неизвестным. Затем решаем это уравнение. Определим одно неизвестное. Подставляем полученное значение неизвестного в одно из уравнений системы (в первое или во второе). Находим еще одно неизвестное. Рассмотрим примеры применения этого метода.
Пример 1. Решить систему уравнений
Здесь коэффициенты при y равны по модулю друг другу, но противоположны по знаку. Попробуем сложить уравнения системы почленно.
Получившееся значение x = 4, подставляем его в какое-нибудь уравнение системы (например, в первое) и находим значение y:
2 * 4 + у = 11, у = 11 — 8, у = 3.
Наша система имеет решение x = 4, y = 3. Как вариант, ответ можно записать в скобках, как координаты точки, во первых х, во вторых у.
Как вариант, ответ можно записать в скобках, как координаты точки, во первых х, во вторых у.
Ответ: (4; 3)
Пример 2 … Решить систему уравнений
Приравняем коэффициенты при переменной x, для этого умножаем первое уравнение на 3, а второе на (-2), получаем
Будьте осторожны при добавлении уравнений
Тогда у = — 2.Подставляем в первое уравнение вместо y число (-2), получаем
4x + 3 (-2) = — 4. Решите это уравнение 4x = — 4 + 6, 4x = 2, x = ½.
Ответ: (1/2; — 2)
Пример 3. Решить систему уравнений
Умножить первое уравнение на (-2)
Решаем систему
получаем 0 = — 13.
Система не имеет решений, так как 0 не равно (-13).
Ответ: Решений нет.
Пример 4. Решить систему уравнений
Обратите внимание, что все коэффициенты второго уравнения делятся на 3,
давайте разделим второе уравнение на три и получим систему, состоящую из двух одинаковых уравнений.
Эта система имеет бесконечно много решений, так как первое и второе уравнения совпадают (мы получили только одно уравнение с двумя переменными).Как представить решение этой системы? Выразим переменную y из уравнения x + y = 5. Получим y = 5 — x.
Тогда ответ будет записан так: (х;5-х), х — любое число.
Мы рассмотрели решение систем уравнений методом сложения. Если у вас остались вопросы или что-то непонятно, записывайтесь на урок и мы вместе с вами исправим все неполадки.
сайта, при полном или частичном копировании материала ссылка на первоисточник обязательна.
.