Решение олимпиадных задач по математике (6-7 класс) (детям)
1. Введение. (2 часа)
2. Делимость чисел (14 часов)
Цифры и числа. Запись цифр у разных народов. Числа- великаны. Натуральные числа. Некоторые виды натуральных чисел и их свойства. Построение математиками фигурных чисел. Признаки делимости на 4,6,7,8,11. Нахождение НОД и НОК способом Евклида. Решение задач на нахождение НОК и НОД чисел.
2. Сложные задачи на движение (10 часов)
Основные понятия (скорость, время, расстояние) и формулы, по которым они находятся. Задачи на “одновременное” движение. Задачи на движение в одном направлении. Задачи на движение в разных направлениях. Задачи на движение по воде (по течению и против течения). Решение всех типов задач на движение.
· движение из разных пунктов на встречу друг другу;
· движение из одного пункта в одном направлении;
· движение из одного пункта в различных направлениях;
· движение из разных пунктов в различных направлениях;
· движение из разных пунктов в одном направлении;
· движение по реке;
· решение всех типов задач на движение.
3. Пропорции, проценты, совместная работа (8 часов)
Проценты. Нахождение процента от числа. Процентное отношение. Решение задач на нахождение части числа и числа по части. Решение текстовых задач по теме «Процентные вычисления в жизненных ситуациях». Задачи на смеси, растворы, сплавы. Последовательное снижение (повышение) цены товара. Задачи на последовательное выпаривание и высушивание.
· прямая пропорциональность;
· обратная пропорциональность;
· разные задачи;
· нахождение процента от числа.
· нахождение целого по части и числа по части;
· процентное отношение;
· задачи на смеси и сплавы;
· задачи на последовательное повышение и понижение цены;
· задачи на банковские проценты;
· задачи на сложные проценты;
· задачи на последовательное выпаривание и высушивание.
4. Различные логические задачи (16 часов)
Логические задачи и методы их решения.
5. Задачи по математическим ребусам и головоломкам и с геометрическим содержанием (12 часов)
Задачи на вычисление площадей нестандартными способами.
Задачи на разрезание фигур, расположение, размещение, разбиение и составление геометрических фигур. Моделирование геометрических фигур.
Задачи с использованием координатной плоскости.
6. Основы комбинаторики (8часов)
Правила сложения и умножения в комбинаторике. Перестановки. Размещения. Сочетания. Применение формул в решении задач.
7. Подведение итогов (2 часа)
Олимпиадные задачи отборочного тура образовательного центра «Сириус».
xn--47-kmc.xn--80aafey1amqq.xn--d1acj3b
Страница 11 №8-15 ГДЗ к учебнику «Математика» 6 класс Бунимович, Кузнецова, Минаева
Задание 8. Приведите к наименьшему общему знаменателю дроби:
а) $\frac{3}{5}$ и $\frac{1}{4}$;
б) $\frac{3}{7}$ и $\frac{2}{5}$;
в) $\frac{3}{16}$ и $\frac{3}{2}$;
г) $\frac{3}{20}$ и $\frac{7}{10}$;
д) $\frac{3}{4}$ и $\frac{5}{6}$;
е) $\frac{7}{12}$ и $\frac{5}{8}$.
Решение
а) $\frac{3}{5}$ и $\frac{1}{4}$ − приведем к знаменателю 20:
$\frac{3}{5} = \frac{3 * 4}{5 * 4} = \frac{12}{20}$;
$\frac{1}{4} = \frac{1 * 5}{4 * 5} = \frac{5}{20}$.б) $\frac{3}{7}$ и $\frac{2}{5}$ − приведем к знаменателю 35:
$\frac{3}{7} = \frac{3 * 5}{7 * 5} = \frac{15}{35}$;
$\frac{2}{5} = \frac{2 * 7}{5 * 7} = \frac{14}{35}$.в) $\frac{3}{16}$ и $\frac{3}{2}$ − приведем к знаменателю 16:
$\frac{3}{2} = \frac{3 * 8}{2 * 8} = \frac{24}{16}$.г) $\frac{3}{20}$ и $\frac{7}{10}$ − приведем к знаменателю 20:
$\frac{7 * 2}{10 * 2} = \frac{14}{20}$.д) $\frac{3}{4}$ и $\frac{5}{6}$ − приведем к знаменателю 12:
$\frac{3}{4} = \frac{3 * 3}{4 * 3} = \frac{9}{12}$;
$\frac{5}{6} = \frac{5 * 2}{6 * 2} = \frac{10}{12}$.е) $\frac{7}{12}$ и $\frac{5}{8}$ − приведем к знаменателю 24:
$\frac{7}{12} = \frac{7 * 2}{12 * 2} = \frac{14}{24}$;
$\frac{5}{8} = \frac{5 * 3}{8 * 3} = \frac{15}{24}$.
Сравнение дробей
Задание 9. Сравните дроби и запишите результат с помощью знаков >,
Решение
а) $\frac{4}{5} = \frac{4 * 2}{5 * 2} = \frac{8}{10}$;
$\frac{8}{5} > \frac{7}{10}$;
$\frac{8}{10} > \frac{7}{10}$.б) $\frac{5}{12} = \frac{5 * 3}{12 * 3} = \frac{15}{36}$;
$\frac{7}{18} = \frac{7 * 2}{18 * 2} = \frac{14}{36}$;
$\frac{15}{36} > \frac{14}{36}$;
$\frac{5}{12} > \frac{7}{18}$.в) $\frac{5}{6} = \frac{5 * 4}{6 * 4} = \frac{20}{24}$;
$\frac{7}{8} = \frac{7 * 3}{8 * 3} = \frac{21}{24}$;
$\frac{20}{24} < \frac{21}{24}$;
$\frac{5}{6} < \frac{7}{8}$.г) $\frac{3}{8} = \frac{3 * 2}{8 * 2} = \frac{6}{16}$;
$\frac{6}{16} > \frac{5}{16}$;
$\frac{3}{8} > \frac{5}{16}$.д) $\frac{9}{8} = 1\frac{1}{8}$
е) $1\frac{7}{20} = \frac{27}{20} = \frac{27 * 9}{20 * 9} = \frac{243}{180}$;
$\frac{11}{9} = \frac{11 * 20}{9 * 20} = \frac{220}{180}$;
$\frac{243}{180} > \frac{220}{180}$;
$1\frac{7}{20} > \frac{11}{9}$.
Задание 10. Запишите в порядке возрастания дроби
$\frac{3}{4}, \frac{11}{12}, \frac{2}{5}, \frac{5}{6}$.
Ответ 7 гуру
$\frac{3}{4} = \frac{3 * 15}{4 * 15} = \frac{45}{60}$;
$\frac{11}{12} = \frac{11 * 5}{12 * 5} = \frac{55}{60}$;
$\frac{2}{5} = \frac{2 * 12}{5 * 12} = \frac{24}{60}$;
$\frac{5}{6} = \frac{5 * 10}{6 * 10} = \frac{50}{60}$.
$\frac{24}{60} < \frac{45}{60} < \frac{50}{60} < \frac{55}{60}$, значит:
$\frac{2}{5} < \frac{3}{4} < \frac{5}{6} < \frac{11}{12}$.
Задание 11. Запишите в порядке убывания дроби
$\frac{1}{2}, \frac{17}{20}, \frac{2}{5}, \frac{3}{4}$.
Ответ
$\frac{1}{2} = \frac{1 * 10}{2 * 10} = \frac{10}{20}$;
$\frac{2}{5} = \frac{2 * 4}{5 * 4} = \frac{8}{20}$;
$\frac{3}{4} = \frac{3 * 5}{4 * 5} = \frac{15}{20}$.
$\frac{17}{20} > \frac{15}{20} > \frac{10}{20} > \frac{8}{20}$, значит:
$\frac{17}{20} > \frac{3}{4} > \frac{1}{2} > \frac{2}{5}$.
Задание 12. На тренировке Оля пробежала стометровку за $\frac{1}{3}$ мин, Галя − за $\frac{17}{60}$ мин, Вера − за $\frac{3}{10}$ мин, Зоя − за $\frac{4}{15}$ мин. В каком порядке девочки пришли к финишу?
Решение задачи
1) $\frac{1}{3} = \frac{1 * 20}{3 * 20} = \frac{20}{60}$ (мин) = 20 (с) − результат Оли;
2) $\frac{17}{60}$ (мин) = 17 (с) − результат Гали;
3) $\frac{3}{10} = \frac{3 * 6}{10 * 6} = \frac{18}{60}$ (мин) = 18 (с) − результат Веры;
4) $\frac{4}{15} = \frac{4 * 4}{15 * 4} = \frac{16}{60}$ (мин) = 16 (с) − результат Зои;
5) 16 < 17 < 18 < 20 − значит девочки пришли в следующем порядке:
Зоя, Галя, Вера, Оля.
Ответ:
1) Зоя;
2) Галя;
3) Вера;
4) Оля.
Задание 13. Не приводя дроби к общему знаменателю, установите, какая из них наибольшая:
а) $\frac{10}{11}, \frac{9}{10}, \frac{8}{9}$;
б) $\frac{11}{20}, \frac{21}{40}, \frac{31}{60}$;
в) $\frac{23}{48}, \frac{17}{36}, \frac{35}{72}$.
Решение
а) $\frac{10}{11} > \frac{9}{10} > \frac{8}{9}$
Ответ: $\frac{10}{11}$б) $\frac{11}{20} > \frac{21}{40} > \frac{31}{60}$
Ответ: $\frac{11}{20}$в) $\frac{35}{72} > \frac{23}{48} > \frac{17}{36}$
Ответ: $\frac{35}{72}$
Задание 14. Найдите несколько чисел, которые:
а) больше $\frac{1}{7}$, но меньше $\frac{2}{7}$;
б) больше $\frac{4}{9}$, но меньше $\frac{5}{9}$.
Ответ
а) $\frac{1}{7} = \frac{1 * 10}{7 * 10} = \frac{10}{70}$;
$\frac{2}{7} = \frac{2 * 10}{7 * 10} = \frac{20}{70}$;
$\frac{10}{70} < \frac{11}{70} < \frac{13}{70} < \frac{19}{70} < \frac{20}{70}$;
$\frac{1}{7} < \frac{11}{70} < \frac{13}{70} < \frac{19}{70} < \frac{2}{7}$.б) $\frac{4}{9} = \frac{4 * 10}{9 * 10} = \frac{40}{90}$;
$\frac{5}{9} = \frac{5 * 10}{9 * 10} = \frac{50}{90}$;
$\frac{40}{90} < \frac{41}{90} < \frac{43}{90} < \frac{47}{90} < \frac{50}{90}$;
$\frac{4}{9} < \frac{41}{90} < \frac{43}{90} < \frac{47}{90} < \frac{5}{9}$.
Задание 15. ЗАДАЧА−ИССЛЕДОВАНИЕ
1) Дана правильная дробь $\frac{2}{3}$. Запишите обратную ей дробь и определите, какая из этих двух дробей ближе к 1.
2) Запишите какую−нибудь правильную дробь и дробь, обратную ей. Какая из них ближе к 1? Проведите такой эксперимент еще раз.
3) Сделайте вывод о том, какая из дробей ближе к 1 − правильная или обратная ей неправильная. Поясните свой вывод.
Решение
1) Дробь, обратная $\frac{2}{3}$ есть дробь $\frac{3}{2}$.
К единице ближе та дробь, разница которой с единицей меньше.
$\frac{1}{3}$ до единицы у дроби $\frac{2}{3}$;
$\frac{3}{2} = 1\frac{1}{2}$, значит $\frac{1}{2}$ до единицы у дроби $\frac{3}{2}$.
$\frac{1}{3} < \frac{1}{2}$, значит дробь $\frac{2}{3}$ ближе к единице.2) Дробь, обратная $\frac{2}{5}$ есть дробь $\frac{5}{2}$.
К единице ближе та дробь, разница которой с единицей меньше.
$\frac{3}{5}$ до единицы у дроби $\frac{2}{5}$;
$\frac{5}{2} = 2\frac{1}{2}$, значит $1\frac{1}{2}$ до единицы у дроби $\frac{5}{2}$.
$\frac{3}{5} < 1\frac{1}{2}$, значит дробь $\frac{2}{5}$ ближе к единице.Дробь, обратная $\frac{3}{7}$ есть дробь $\frac{7}{3}$.
К единице ближе та дробь, разница которой с единицей меньше.
$\frac{4}{7}$ до единицы у дроби $\frac{3}{7}$;
$\frac{7}{3} = 2\frac{1}{3}$, значит $1\frac{1}{3}$ до единицы у дроби $\frac{7}{3}$.
$\frac{4}{7} < 1\frac{1}{3}$, значит дробь $\frac{3}{7}$ ближе к единице.3) К единице ближе правильная дробь, чем обратная ей неправильная. Пусть дана дробь $\frac{a}{b}$, где a < b (то есть данная дробь правильная).
Дробь обратная данной есть $\frac{b}{a}$. К единице ближе та дробь, разница которой с единицей меньше. Найдем разницу с единицей данных дробей:
$1 — \frac{a}{b} = \frac{b}{b} — \frac{a}{b} = \frac{(b — a)}{b}$;
$\frac{b}{a} — 1 = \frac{b}{a} — \frac{a}{a} = \frac{(b — a)}{a}$.
Из двух дробей с одинаковыми числителями больше та дробь, знаменатель которой меньше, a < b, значит:
$\frac{(b — a)}{b} < \frac{(b — a)}{a}$, поэтому дробь $\frac{a}{b}$ ближе к единице.
7gy.ru
Страница 8 №1-7 ГДЗ к учебнику «Математика» 6 класс Дорофеев, Шарыгин
Глава 1. Дроби и проценты
Ответы к разделу учебника 1.1 Что мы знаем о дробях
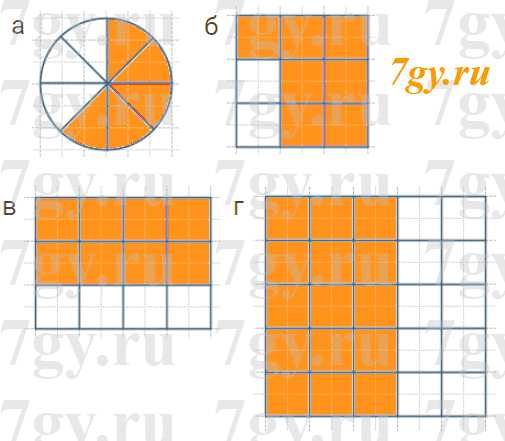
Задание 1. Изобразите какую−нибудь геометрическую фигуру (прямоугольник, круг или отрезок) и закрасьте ее часть, которая соответствует дроби:
а) $\frac{5}{8}$; б) $\frac{7}{9}$; в) $\frac{8}{12}$; г) $\frac{15}{25}$.
Ответ 7 гуру
Задание 2. 1) Приведите дроби:
а) $\frac{4}{9}$, $\frac{5}{6}$, $\frac{7}{2}$ к знаменателю 18; б) $\frac{7}{8}$, $\frac{5}{16}$, $\frac{21}{40}$ к знаменателю 80.
2) Приведите к наименьшему общему знаменателю дроби:
а) $\frac{1}{3}$ и $\frac{1}{4}$; б) $\frac{5}{8}$ и $\frac{3}{16}$; в) $\frac{5}{8}$ и $\frac{3}{20}$; г) $\frac{2}{9}$ и $\frac{7}{24}$.
Решение
1)
а) $\frac{4}{9} = \frac{4 * 2}{9 * 2} = \frac{8}{18}$;
$\frac{5}{6} = \frac{5 * 3}{6 * 3} = \frac{15}{18}$;
$\frac{7}{2} = \frac{7 * 9}{2 * 9} = \frac{63}{18}$.б) $\frac{7}{8} = \frac{7 * 10}{8 * 10} = \frac{70}{80}$;
$\frac{5}{16} = \frac{5 * 5}{16 * 5} = \frac{25}{80}$;
$\frac{21}{40} = \frac{21 * 2}{40 * 2} = \frac{42}{80}$.2)
а) $\frac{1}{3} = \frac{1 * 4}{3 * 4} = \frac{4}{12}$;
$\frac{1}{4} = \frac{1 * 3}{4 * 3} = \frac{3}{12}$.
Ответ: $\frac{4}{12}$ и $\frac{3}{12}$б) $\frac{5}{8} = \frac{5 * 2}{8 * 2} = \frac{10}{16}$;
$\frac{3}{16}$.
Ответ: $\frac{10}{16}$ и $\frac{3}{16}$в) $\frac{5}{8} = \frac{5 * 5}{8 * 5} = \frac{25}{40}$;
$\frac{3}{20} = \frac{3 * 2}{20 * 2} = \frac{6}{40}$.
Ответ: $\frac{25}{40}$ и $\frac{6}{40}$г) $\frac{2}{9} = \frac{2 * 8}{9 * 8} = \frac{16}{72}$;
$\frac{7}{24} = \frac{7 * 3}{24 * 3} = \frac{21}{72}$.
Ответ: $\frac{16}{72}$ и $\frac{21}{72}$
Задание 3. В Древнем Риме при измерении величин применялись дроби со знаменателем 12. Вместо $\frac{1}{12}$ говорили «одна унция», вместо $\frac{5}{12}$ − «пять унций» и т.п. Выразите в унциях: половину, треть, четверть, пять шестых, три четверти.
Решение
Половина = $\frac{1}{2} = \frac{1 * 6}{2 * 6} = \frac{6}{12}$ = шесть унций;
треть = $\frac{1}{3} = \frac{1 * 4}{3 * 4} = \frac{4}{12}$ = четыре унции;
четверть = $\frac{1}{4} = \frac{1 * 3}{4 * 3} = \frac{3}{12}$ = три унции;
пять шестых = $\frac{5}{6} = \frac{5 * 2}{6 * 2} = \frac{10}{12}$ = десять унций;
три четверти = $\frac{3}{4} = \frac{3 * 3}{4 * 3} = \frac{9}{12}$ = девять унций.
Задание 4. Сократите дробь:
а) $\frac{24}{30}$; б) $\frac{12}{48}$; в) $\frac{20}{36}$; г) $\frac{14}{56}$; д) $\frac{44}{100}$; е) $\frac{36}{60}$.
Решение
а) $\frac{24}{30} = \frac{24 : 6}{30 : 6} = \frac{4}{5}$
б) $\frac{12}{48} = \frac{12 : 12}{48 : 12} = \frac{1}{4}$
в) $\frac{20}{36} = \frac{20 : 4}{36 : 4} = \frac{5}{9}$
г) $\frac{14}{56} = \frac{14 : 14}{56 : 14} = \frac{1}{4}$
д) $\frac{44}{100} = \frac{44 : 4}{100 : 4} = \frac{11}{25}$
е) $\frac{36}{60} = \frac{36 : 12}{60 : 12} = \frac{3}{5}$
Задание 5. Сравните дроби и запишите результат сравнения с помощью знаков >, < или =. В каждом случае расскажите, каким способом вы действовали.
Решение
а) $\frac{4}{5} = \frac{4 * 2}{5 * 2} = \frac{8}{10}$
$\frac{8}{10} > \frac{7}{10}$
$\frac{4}{5} > \frac{7}{10}$
Привел дроби к наименьшему общему знаменателю.б) $\frac{5}{12} = \frac{5 * 6}{12 * 6} = \frac{30}{72}$
$\frac{7}{8} = \frac{7 * 9}{8 * 9} = \frac{63}{72}$
$\frac{30}{72} < \frac{63}{72}$
$\frac{5}{12} < \frac{7}{8}$
Привел дроби к наименьшему общему знаменателю.в) $\frac{5}{6} = \frac{5 * 4}{6 * 4} = \frac{20}{24}$
$\frac{7}{8} = \frac{7 * 3}{8 * 3} = \frac{21}{24}$
$\frac{20}{24} < \frac{21}{24}$
$\frac{5}{6} < \frac{7}{8}$
Привел дроби к наименьшему общему знаменателю.г) $\frac{6}{16} = \frac{6 : 2}{16 : 2} = \frac{3}{8}$
$\frac{3}{8} = \frac{3}{8}$
$\frac{3}{8} = \frac{6}{16}$
Сократил дробь $\frac{6}{16}$.д) $1\frac{1}{8} = \frac{8 * 1 + 1}{8} = \frac{9}{8}$
$\frac{9}{8} = \frac{9}{8}$
$\frac{9}{8} = 1\frac{1}{8}$
Преобразовал смешанное число в неправильную дробь.е) $1\frac{8}{20} = 1\frac{8 : 4}{20 : 4} = 1\frac{2}{5}$
$1\frac{2}{5} > 1\frac{2}{9}$
$1\frac{8}{20} > 1\frac{2}{9}$
Сократил дробь $1\frac{8}{20}$.ж) $\frac{5}{9} < \frac{9}{5}$
Неправильная дробь больше правильной дроби.з) $\frac{12}{11} > \frac{11}{12}$
Неправильная дробь больше правильной дроби.
Задание 6. Запишите дроби в порядке возрастания:
а) $\frac{3}{4}, \frac{11}{12}, \frac{2}{3}, \frac{5}{6}$;
б) $\frac{1}{15}, \frac{2}{5}, \frac{7}{15}, \frac{1}{3}$;
в) $\frac{1}{2}, \frac{17}{20}, \frac{2}{5}, \frac{3}{4}$;
г) $\frac{7}{10}, \frac{4}{5}, \frac{63}{100}, \frac{1}{2}$.
Решение
а) $\frac{3}{4} = \frac{3 * 3}{4 * 3} = \frac{9}{12}$;
$\frac{2}{3} = \frac{2 * 4}{3 * 4} = \frac{8}{12}$;
$\frac{5}{6} = \frac{5 * 2}{6 * 2} = \frac{10}{12}$;
$\frac{8}{12} < \frac{9}{12} < \frac{10}{12} < \frac{11}{12}$;
$\frac{2}{3} < \frac{3}{4} < \frac{5}{6} < \frac{11}{12}$.б) $\frac{2}{5} = \frac{2 * 3}{5 * 3} = \frac{6}{15}$;
$\frac{1}{3} = \frac{1 * 5}{3 * 5} = \frac{5}{15}$;
$\frac{1}{15} < \frac{5}{15} < \frac{6}{15} < \frac{7}{15}$;
$\frac{1}{15} < \frac{1}{3} < \frac{2}{5} < \frac{7}{15}$.в) $\frac{1}{2} = \frac{1 * 10}{2 * 10} = \frac{10}{20}$;
$\frac{2}{5} = \frac{2 * 4}{5 * 4} = \frac{8}{20}$;
$\frac{3}{4} = \frac{3 * 5}{4 * 5} = \frac{15}{20}$;
$\frac{8}{20} < \frac{10}{20} < \frac{15}{20} < \frac{17}{20}$;
$\frac{2}{5} < \frac{1}{2} < \frac{3}{4} < \frac{17}{20}$.г) $\frac{7}{10} = \frac{7 * 10}{10 * 10} = \frac{70}{100}$;
$\frac{4}{5} = \frac{4 * 20}{5 * 20} = \frac{80}{100}$;
$\frac{1}{2} = \frac{1 * 50}{2 * 50} = \frac{50}{100}$;
$\frac{50}{100} < \frac{63}{100} < \frac{70}{100} < \frac{80}{100}$;
$\frac{1}{2} < \frac{63}{100} < \frac{7}{10} < \frac{4}{5}$.
Задание 7. а) На тренировке Оля пробежала стометровку за $\frac{1}{3}$ мин, Галя − за $\frac{17}{60}$ мин, Вера − за $\frac{3}{10}$ мин, Зоя − за $\frac{4}{15}$ мин. В каком порядке девочки пришли к финишу, если они стартовали одновременно?
б) На путь от школы до стадиона Толя и три его друга затрачивают разное время:
Толя − $\frac{2}{5}$ ч;
Саша − $\frac{1}{2}$ ч;
Коля − $\frac{3}{10}$ ч;
Петя − $\frac{7}{12}$ ч.
Ребята вышли из школы одновременно. В каком порядке они придут на стадион?
Решение
а) 1) $\frac{1}{3} = \frac{1 * 20}{3 * 20} = \frac{20}{60}$ мин = 20 (с) − время, за которое пробежала Оля;
2) $\frac{17}{60}$ мин = 17 (с) − время, за которое пробежала Галя;
3) $\frac{3}{10} = \frac{3 * 6}{10 * 6} = \frac{18}{60}$ мин = 18 (с) − время, за которое пробежала Вера;
4) $\frac{4}{15} = \frac{4 * 4}{15 * 4} = \frac{16}{60}$ мин = 16 (с) − время, за которое пробежала Зоя;
5) 16 < 17 < 18 < 20 − значит, первой прибежала Зоя, второй Галя, третьей Вера, четвертой Оля.
Ответ: 1 место − Зоя; 2 место − Галя; 3 место − Вера; 4 место − Оля.б) 1) $\frac{2}{5} = \frac{2 * 12}{5 * 12} = \frac{24}{60}$ ч = 24 (мин) − затратит на путь Толя;
2) $\frac{1}{2} = \frac{1 * 30}{2 * 30} = \frac{30}{60}$ ч = 30 (мин) − затратит на путь Саша;
3) $\frac{3}{10} = \frac{3 * 6}{10 * 6} = \frac{18}{60}$ ч = 18 (мин) − затратит на путь Коля;
4) $\frac{7}{12} = \frac{7 * 5}{12 * 5} = \frac{35}{60}$ ч = 35 (мин) − затратит на путь Петя;
5) 18 < 24 < 30 < 35 − значит, первым придет Коля, вторым − Толя, третьим − Саша, четвертым − Петя.
Ответ: ребята придут в следующем порядке: Коля, Толя, Саша, Петя.
7gy.ru
Страница 47 №286-295 ГДЗ к учебнику «Математика» 6 класс Виленкин, Жохов, Чесноков
Задание № 286. На какое число надо умножить 24; 8; 16; 6; 12, чтобы получить 48?
Решение
24 * 2 = 48;
8 * б = 48;
16 * 3 = 48;
6 * 8 = 48;
12 * 4 = 48.
Задание № 287. С помощью транспортира разделите одну окружность на 6, а другую − на 3 равные дуги. Постройте многоугольники, изображённые на рисунке 14. У каждого из этих многоугольников равны стороны и равны углы. Такие многоугольники называют правильными. Подумайте, является ли правильным многоугольником прямоугольник; квадрат.
Ответ 7 гуру

Прямоугольник не является правильным многоугольником, потому что у него стороны попарно равны. Квадрат − правильный многоугольник, у него равны все углы и все стороны.
Задание № 288. Сократите: 75/90,150/120,140/210,330/495.
Решение
Задание № 289. Найдите наибольший общий делитель числителя и знаменателя и сократите дробь:
а) 168/160;
б) 880/1008;
в) 3240/972;
г) 2835/7425.
Решение
а) НОД(168; 160) = НОД(2 * 2 * 2 * 3 * 7; 2 * 2 * 2 * 2 * 2 * 5) = 2 * 2 * 2 * 2 = 8,
168/160=21/20.
б) НОД(880; 1008) = НОД(2 * 2 * 2 * 2 * 5 * 11; 2 * 2 * 2 * 2 * 5 * 63) = 2 * 2 * 2 * 2 * 2 = 16,
880/1008=55/63.
в) НОД(3240; 972) = НОД(3240 = 2 * 2 * 2 * 3 * 3 * 3 * 35; 2 * 2 * 3 * 3 * 3 * 3 * 3) = 2 * 2 * 3 * 3 * 3 * 3 = 324,
3240/972=10/3
г) НОД(2835; 7425) = НОД(3 * 3 * 3 * 3 * 5 * 7; 3 * 3 * 3 * 5 * 5 * 11) = 3 * 3 * 3 * 5 = 135,
2835/7425=21/55.
Задание № 290. При каком значении х верно равенство:
а) 15/35=х/7;
б) х/6=40/48;
в) 26/65=2/х;
г) 6/х=30/35?
Решение
Задача № 291. Жук ползёт вверх по стволу дерева (рис. 15) со скоростью 6 см/с. По тому же дереву ползёт вниз гусеница. Сейчас она находится на 60 см ниже жука. С какой скоростью ползёт гусеница, если через 5 с расстояние между ней и жуком будет 100 см?
Решение задачи
1 способ.
1) 100 — 60 = 40 (см) — на столько увеличилось расстояние за 5 с.
2) 40 : 5 = 8 (см/с) — скорость удаления.
3) 8 — 6 = 2 (см/с) — скорость гусеницы.
Ответ: 2 см/с.2 способ
6 * 5 = 30 (см) — проползет жук за 5 с.
100 − 60 = 40 (см) — на таком расстоянии находится жук от гусеницы через 5 с.
40 − 30 = 10 (см) — проползет гусеница за 5 с.
10 : 5 = 2 (см/с) — скорость гусеницы.
Ответ: 2 см/с.
Задача № 292. Космический корабль «Вега−1» двигался к комете Галлея со скоростью 34 км/с, а сама комета двигалась ему навстречу со скоростью 46 км/с. Какое расстояние было между ними за 15 мин до встречи?
Решение задачи
Задачу можно решить двумя способами.
1 способ.
1) 34 + 46 = 80 (км/с) — скорость сближения.
2) 15 мин = 15 * 60 = 900 (с) — до встречи.
3) 80 * 900 = 72000 (км)
Ответ: 72 000 км.2 способ.
1) 15 мин = 15 * 60 = 900 (с) — до встречи.
2) 46 * 900 = 41400 (км) — пролетит комета.
3) 34 * 900 = 30600 (км) — пролетит космический корабль.
4) 41400 + 30600 = 72 000 (км)
Ответ: 72 000 км.
Задание № 293. Сколько чётных пятизначных чисел можно составить из цифр 0, 3, 5, 6, 8? Есть ли среди них числа, кратные трём? кратные девяти?
Решение
Одну из цифр 3, 5, 6, 8 можно поставить на первое место. 0, 3, 5, 6, 8 − можно поставить на второе место.
На третье и четвёртое места одну из неиспользованных цифр. На пятое место можно поставить − 0, 6, 8.
Всего можно поставить 4 * 5 * 5 * 5 * 3 = 1500 чисел.
Да, есть кратные трём, например, 3336. Да, есть кратные девяти − 3366.
Задание № 294. Сократите:
1) 15 * 17−15 * 6
15 * 17+15 * 6;
2) 81 * 17−15 * 81
81 * 17+81 * 4.
Решение
Задание № 295. Найдите значение выражения:
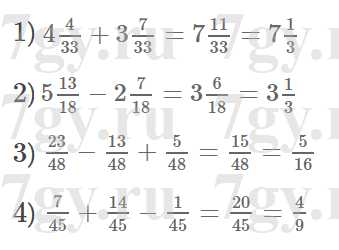
7gy.ru
Страница 19 №42-48 ГДЗ к учебнику «Математика» 6 класс Бунимович, Кузнецова, Минаева
Задание 42. а) Размеры макета дома составляют $\frac{1}{12}$ его реальных размеров. На макете окно имеет ширину 60 мм. Какова ширина окна в действительности?
б) Размеры участка земли на плане составляют $\frac{3}{1000}$ его действительных размеров. Чему равна одна из сторон участка, если на плане она равна 9 см?
Решение
а) $60 : \frac{1}{12} = 60 * 12 = 720$ (мм) = 72 (см) − ширина окна в действительности.
Ответ: 72 см.б) $9 : \frac{3}{1000} = 9 * \frac{1000}{3} = 3 * 1000 = 3000$ (см) = 30 (м) − длина одной из сторон участка.
Ответ: 30 м.
Задание 43. Сергей заполнил $\frac{5}{8}$ тетради по математике, и у него осталось 36 чистых листов. Сколько листов в тетради?
Решение задачи
1) $1 — \frac{5}{8} = \frac{3}{8}$ (т.) − осталось чистой;
2) $36 : \frac{3}{8} = 36 * \frac{8}{3} = 12 * 8 = 96$ (л.) − всего в тетради.
Ответ: 96 листов.
Задание 44. По рецепту молочного коктейля молоко составляет $\frac{7}{10}$ его массы, фруктовый сироп − $\frac{1}{4}$, а ванилин − $\frac{1}{20}$. Для приготовления коктейля взяли 350 г молока. Рассчитайте, сколько граммов сиропа и сколько граммов ванилина надо взять.
Решение задачи от 7 гуру
1) $350 : \frac{7}{10} = 350 * \frac{10}{7} = 50 * 10 = 500$ (г) − масса коктейля;
2) $500 * \frac{1}{4} = 125$ (г) − масса сиропа;
3) $500 * \frac{1}{20} = 25$ (г) − масса ванилина.
Ответ: 125 г сиропа и 25 г ванилина.
Какую часть одно число составляет от другого
Задание 45. а) Какую часть от 1 кг составляют 500 г? 260 г? 30 г? 25 г?
б) Какую часть от 1 ч составляют 30 мин? 15 мин? 10 мин? 6 мин?
в) Какую часть суток составляет 1 ч? 2 ч? 5 ч?
Ответы
а) 1 кг = 1000 г
$500 : 1000 = \frac{500}{1000} = \frac{1}{2}$ (кг) − составляют 500 г;
$260 : 1000 = \frac{260}{1000} = \frac{13}{50}$ (кг) − составляют 260 г;
$30 : 1000 = \frac{30}{1000} = \frac{3}{100}$ (кг) − составляют 30 г;
$25 : 1000 = \frac{25}{1000} = \frac{1}{40}$ (кг) − составляют 25 г.б) 1 ч = 60 мин
$30 : 60 = \frac{30}{60} = \frac{1}{2}$ (ч) − составляют 30 мин;
$15 : 60 = \frac{15}{60} = \frac{1}{4}$ (ч) − составляют 15 мин;
$10 : 60 = \frac{10}{60} = \frac{1}{6}$ (ч) − составляют 10 мин;
$6 : 60 = \frac{6}{60} = \frac{1}{10}$ (ч) − составляют 6 мин.в) 1 сутки = 24 ч
$1 : 24 = \frac{1}{24}$ (сут) − составляет 1 ч;
$2 : 24 = \frac{2}{24} = \frac{1}{12}$ (сут) − составляет 2 ч;
$5 : 24 = \frac{5}{24}$ (сут) − составляет 5 ч.
Задание 46. а) Из 30000 избирателей, включенных в списки, пришли голосовать 24000 человек. Какая часть избирателей приняла участие в голосовании?
б) В школе 900 учащихся. На уроках 15 декабря отсутствовали 60 учащихся. Какая часть учащихся в этот день пропустила уроки?
Решение
а) $24000 : 30000 = \frac{24000}{30000} = \frac{4}{5}$ (часть) − избирателей приняла участия в голосовании.
Ответ: $\frac{4}{5}$ часть всех избирателей.б) $60 : 900 = \frac{60}{900} = \frac{1}{15}$ (часть) − учащихся 15 декабря пропустила уроки.
Ответ: $\frac{1}{15}$ часть всех учащихся.
Задание 47. Решите задачу двумя способами.
а) Стакан вмещает 200 г молока. В него налили 160 г молока. Какая часть стакана осталась незаполненной?
б) Человек спит в среднем 8 ч в сутки. Какую часть суток человек бодрствует?
Подсказка. К пункту а).
Первый способ: сначала найдите, какая часть стакана заполнена; второй способ: сначала найдите, сколько граммов молока еще может поместиться в стакан.
Решение
а) Способ 1.
1) $160 : 200 = \frac{160}{200} = \frac{4}{5}$ (стакана) − заполнено;
2) $1 — \frac{4}{5} = \frac{1}{5}$ (стакана) − осталось незаполненной.
Ответ: $\frac{1}{5}$ стакана.Способ 2.
1) 200 − 160 = 40 (г) − молока не долили;
2) $40 : 200 = \frac{40}{200} = \frac{1}{5}$ (стакана) − осталось незаполненной.
Ответ: $\frac{1}{5}$ стакана.б) Способ 1.
1) $8 : 24 = \frac{8}{24} = \frac{1}{3}$ (суток) − человек бодрствует;
2) $1 — \frac{1}{3} = \frac{2}{3}$ (суток) − человек бодрствует.
Ответ: $\frac{2}{3}$ сутокСпособ 2.
1) 24 − 8 = 16 (ч) − человек бодрствует;
2) $16 : 24 = \frac{16}{24} = \frac{2}{3}$ (суток) − человек бодрствует.
Ответ: $\frac{2}{3}$ суток.
Задание 48. Два спортсмена стреляют по летящей мишени. Они договорились, что побеждает тот, у кого выше доля попаданий. Первый стрелок сделал 80 выстрелов и попал в цель 60 раз, второй сделал 60 выстрелов и попал 50 раз. Кто из них победил?
Решение
1) $60 : 80 = \frac{60}{80} = \frac{3}{4}$ (всех выстрелов) − попал в цель первый стрелок;
2) $50 : 60 = \frac{5}{6} $ (всех выстрелов) − попал в цель второй стрелок;
3) $\frac{3}{4} = \frac{9}{12}$;
$\frac{5}{6} = \frac{10}{12}$;
$\frac{9}{12} < \frac{10}{12}$;
$\frac{3}{4} < \frac{5}{6}$, значит доля попаданий второго спортсмена выше.
Ответ: победил второй спортсмен.
7gy.ru
Страница 6 №1-17 ГДЗ к учебнику «Математика» 6 класс Мерзляк, Полонский, Якир
Задание № 1. Верно ли утверждение:
1) число 6 является делителем числа 24; верно
2) число 6 кратно числу 24; неверно
3) число 5 является делителем числа 51; неверно
4) число 9 является делителем числа 99; верно
5) число 18 кратно числу 3; верно
6) число 28 кратно числу 8. неверно
Задание № 2. Какие из чисел 2, 3, 4, 6, 8, 9, 10, 12, 15, 16, 18, 30 являются:
1) делителями 24;
2) кратными 6;
3) делителями 20 и 24;
4) делителями 24 и кратными 4?
Ответ 7 гуру
1) 2, 3, 4, 6, 8, 12.
2) 6, 12, 18, 30.
3) 2, 4.
4) 4, 8, 12.
Задание № 3. Чему равняется:
1) наибольший делитель числа 19735;
2) наименьший делитель числа 19735;
3) наименьшее кратное числа 19735?
Ответ
1) 19735
2) 1
3) 19735
Задание № 4. Запишите все делители числа:
1) 18;
2) 8;
3) 13;
4) 56.
Ответ
1) 18, 9, 6, 3, 2, 1.
2) 1, 2, 4, 8.
3) 13, 1.
4) 56, 28, 14, 8, 7, 4, 2, 1.
Задание № 5. Запишите все делители числа:
1) 30;
2) 12;
3) 23;
4) 72.
Ответ
1) 30, 15, 10, 6, 5, 3, 2, 1.
2) 12, 6, 4, 3, 2, 1.
3) 23, 1.
4) 72, 36, 24, 18, 12, 9, 8, 6, 4, 3, 2, 1.
Задание № 6. Запишите пять чисел, кратных числу:
1) 7;
2) 30;
3) 100;
4) 34.
Ответ
1) 7, 14, 21, 28, 35.
2) 30, 60, 90, 120, 150.
3) 100, 200, 300, 500, 1000.
4) 34, 68, 102, 136, 170.
Задание № 7. Запишите четыре числа, кратных числу:
1) 16;
2) 12;
3) 150;
4) 47.
Ответ
1) 16, 32, 48, 64.
2) 12, 24, 36, 48.
3) 150, 300, 450, 600.
4) 47, 94, 141, 188.
Задание № 8. Из чисел 28, 36, 48, 64, 92, 100, 108, 110 выпишите те, которые:
1) кратны 4;
2) не кратны 6.
Решение
1) 28, 36, 48, 64, 92, 100, 108.
2) 28, 64, 92, 100, 110.
Задание № 9. Запишите все числа, являющиеся делителями каждого из чисел:
1) 15 и 20;
2) 7 и 21;
3) 24 и 36;
4) 20 и 21.
Ответ
1) 5, 1.
2) 7, 1.
3) 1, 2, 3, 4, 6, 12.
4) 1
Задание № 10. Запишите все числа, являющиеся делителями каждого из чисел:
1) 12 и 18;
2) 60 и 90;
3) 22 и 35;
4) 9 и 27.
Ответ
1) 2, 3, 6.
2) 1, 2, 3, 6, 10, 15, 30.
3) 1.
4) 1, 3, 9.
Задание № 11. Запишите какое−либо число, кратное каждому из чисел:
1) 3 и 4;
2) 6 и 12;
3) 4 и 6.
Ответ
1) 12
2) 72
3) 24
Задание № 12. Запишите какое−либо число, кратное каждому из чисел:
1) 5 и 9;
2) 8 и 32;
3) 8 и 12.
Ответ
1) 45
2) 32
3) 96
Задание № 13. Запишите все двузначные числа, кратные 19;
1) все двузначные числа, кратные 19;
2) все трёхзначные числа, кратные 105.
Ответ
1) 19, 38, 57, 76, 95.
2) 105, 210, 315, 420, 525, 630, 735, 840, 942.
Задание № 14. Запишите все двузначные числа, кратные 23.
Ответ
23, 46, 69, 92.
Задание № 15. Запишите все значения x, кратные числу 4, при которых верно неравенство 18 < x < 36.
Ответ
20, 24, 28, 32.
Задание № 16. Запишите все значения x, кратные числу 6, при которых верно неравенство 25 < x < 60.
Ответ
30, 36, 42, 48, 54.
Задание № 17. Запишите все значения x, являющиеся делителями числа 80, при которых верно неравенство 7 < x < 40.
Ответ
8, 10, 16, 20.
7gy.ru
Конспект урока по математике на тему: Деление на 6
Конспект урока по математике
Учитель: Куршева Ю.В.
Класс: 2 «в»
Тема занятия: Деление на 6
Оборудование: учебник, презентация.
Цель: Познакомить с табличными случаями деления на 6; повторить таблицу деления на 2-5; совершенствовать умения решать задачи изученных видов.
Предметные:
Формировать умения моделировать задачи, отрабатывать навыки устного и письменного счета.
Метапредметные:
Личностные:
Уметь проводить оценку и самооценку работы на основе критерия успешности учебной деятельности.
Познавательные:
Уметь обобщать полученные знания
Регулятивные
Выполнять задания в рамках учебного диалога.
Коммуникативные :
Умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации
Актуализация знаний
Сообщение темы урока:
1)Повторение табличного умножения и деления на 5.
Ребята, а сейчас выполним математический диктант. Открыли тетради , отступили от предыдущей работы 4 клетки, записали число сегодня у нас 14 декабря , классная работа. Я буду диктовать вам пример. Вы его записываете и решаете.
15:5=
3*5=
10:5=
5:5=
5*1=
5*2=
Теперь посмотрите на экране записаны ответы. У кого все правильно ставит оценку-5, у кого одна ошибка-4, две ошибки-3, три ошибки –оценка 2.
3) Игра «Цепочка» (Ученики выходят к доске ставят правильный ответ в окошке)
4) Работа по карточкам в парах
Задание №1
Сравни, поставь знаки «<» ,«>», или «=».
12-6 14-5 12+10 10+12
15-9 13-3 16-8 11-3
Задание №2
Укажи порядок действий и вычисли
7*2+3 18-16:2
2+2*8 15:15*6
5) Решение логических задач в стихах
У деда Архипа большая семья.
Детей всего 8,
И все сыновья.
У каждого сына по паре ребят-
Внучата Архипа.
Их сколько внучат?
Подарил утятам ежик
8 кожаных сапожек,
Сколько ж маленьких утят
Ежика благодарят?
Хомячок по полю шел.
Девять зерен он нашел.
Посмотрел-к нему спешат
Трое маленьких мышат.
Возле них остановился.
И находкой поделила.
Девять зерен на троих
Разделил он в тот же миг
Молодцы , ребята!
Сегодня на уроке мы с вами познакомимся с табличными случаями деления на 6, а так же повторим таблицу деления на 2-5.
3
15
2
1
5
10
ставят оценку карандашом
16
4
3
Основная часть урока
Для того что бы познакомиться с таблицей деления на 6, вы сегодня на урок должны были принести счетные палочки.
1)Работа с раздаточным материалом (счетные палочки).
Возьмите 6 палочек и разделите по 6, сколько кучек получилось?
Какой пример можно составить?
Отступите от предыдущей записи 2 клеточки запишите пример в тетрадь и его ответ.
Теперь возьмите 12 палочек, и разделите по 6, сколько кучек получилось? (2)
Значит какой пример можем составить?
Запишите пример и его решение в тетрадь.
Затем возьмите 18 палочек, и разделите по 6, сколько кучек получилось? (3)
Какой пример можем составить?
Запишите его в тетрадь.
Ребята посмотрите на экран, на экране у меня записаны примеры на умножение, самостоятельно их решите и ответы запишите в тетрадь.
1*6=6
2*6=12
3*6=18
Теперь к каждому их этих примеров на умножение составим по два примера на деление.
6:6=1
6:1=6
12:6=2
12:2=6
18:6=3
18:3=6
Ребята, откройте учебник на стр. 101 и прочитайте про себя задание под №3, выполните задание самостоятельно, затем проверим.
Какой ответ получился в 1 примере?
Какой ответ получился во втором примере?
Какой ответ получился в 3 примере?
Молодцы, ребята!
Выполним задание под №4 устно.
Прочитайте первое задание про себя, затем в слух
Анализ текста.
О ком идет речь?(о ленте) Что показывает число 12?(длину ленты) число 6 ?(сколько равных частей получилось) Прочитайте вопрос задачи.
Поиск решения.
Зная длину ленты (12 дм) и сколько частей получилось, что мы можем узнать? (Какой длины получилась каждая часть).
Каким действием? (Делением)
Почему?
Какой длины получилась каждая часть? (2)
Анализ текста.
Прочитайте вторую задачу. Сначала про себя затем в слух
О ком говорится в задаче? (о солдатиках),
Что показывает число 18? (количество солдатиков), что показывает число 6? (сколько солдатиков в каждом ряду). Прочитайте вопрос задачи еще раз
Поиск решения.
Зная сколько солдатиков было (18) и зная что по 6 солдатиков в каждом ряду, что мы можем узнать? (сколько рядов получилось)
Каким действием? (делением)
Почему?
Какое решение ?
Какой ответ?
Задача №6
Анализ краткой записи:
Прочитайте задание.
Составь и реши задачи по краткой записи.
Рассмотрим первую краткую запись. Прочитайте, какие опорные слова выделены?(было, взяли, осталось).
Что известно?(что было 15 кг, Взяли 6 кг), а что не известно?(сколько осталось кг). Расскажите по этой краткой записи задачу.(слушаю одного или 2-х учеников)
Поиск решения:
Зная что было 15 кг, а взяли 6 кг. что мы можем узнать?(сколько кг осталось). Каким действием? (вычитанием).Почему?(потому что взяли)
Оформление решения:
Записываем только решение и ответ.(один ученик на доске)
15-6=9(кг)
Ответ:9 кг осталось.
Рассмотрим вторую краткую запись. Прочитайте, какие опорные слова выделены?(было, взяли, осталось).
Что известно?(что было 15 кг, осталось 9 кг.), а что не известно?(сколько взяли кг). Расскажите по этой краткой записи задачу.(слушаю одного или 2-х учеников)
Поиск решения:
Зная что было 15 кг, а осталось 8 кг что мы можем узнать?(сколько кг осталось). Каким действием? (вычитанием).Почему?
Оформление решения:
Записываем только решение и ответ.(один ученик на доске)
15-9=6(кг)
Ответ:6 кг взяли.
Рассмотрим третью краткую запись. Прочитайте, какие опорные слова выделены?(было, взяли, осталось).
Что известно?(взяли 6кг и осталось 9 кг), а что не известно?(сколько было). Расскажите по этой краткой записи задачу.(слушаю одного или 2-х учеников)
Поиск решения:
Зная что взяли 6кг и осталось 9 кг, что мы можем узнать?(сколько кг было). Каким действием? (сложением).Почему?
Оформление решения:
Записываем только решение и ответ.(один ученик на доске)
6+9=15(кг)
Ответ:15 кг было.
Как называются такие задачи?(Все эти задачи взаимообратные).
Далее мы с вами выполним задание №5
Прочитайте задание про себя, затем в слух.
Задание будем выполнять с комментированием у доски, начиная по цепочки в первого ряда.
3*5-4=11
9+8:2=13
8+18:3=14
9+12:6=11
19-4*4=3
11+14:2=18
6*3-12=6
7+15:3=12
6:6+17=18
20-20:5=16
18-12:2=12
3+5*2=13
РЕзерв №7.
Прочитаем задание.
Поставь вместо кружков знаки «<»,«>» или « =» , чтобы получились верные записи.
1 ряд-1 выражение.
2ряд-2 выражение.
3 ряд-3 выражение.
К доске от каждого ряда по одному учащемуся. Докажите почему поставили именно эти знаки.
6:6=1
2
12:6=2
3
18:6=3
1
2
3
потому что в 1 и 2 мы находим часть, а в третьей мы находим целое
каждую часть разделить еще на 2 части.
3
2 раза
6
2*3=6
12см
2
3
12:2:3=2
1) -, +
2) -,+
3) +, —
3*5-4=11
9+8:2=13
8+18:3=14
9+12:6=11
19-4*4=3
11+14:2=18
6*3-12=6
7+15:3=12
6:6+17=18
20-20:5=16
18-12:2=12
3+5*2=13
Итоги урока
Что сегодня на уроке мы с вами делали? Что нового узнали? Возникли ли у вас трудности.
Домашнее задание
Учебник Стр. 101, 102 №6 и №8
Записывают домашнее задание в дневник
infourok.ru