Математика гдз за 6 класс зубарева – Страница 12 №25-30 ГДЗ к учебнику «Математика» 6 класс Дорофеев, Шарыгин

Страница 12 №25-30 ГДЗ к учебнику «Математика» 6 класс Дорофеев, Шарыгин

Задание 25. Найдите значение выражения:
а) $25 * (\frac{7}{10} + \frac{3}{5} + \frac{1}{2})$;
б) $(\frac{5}{12} + \frac{1}{6} + \frac{3}{8}) : \frac{15}{16}$;
в) $5 : 1\frac{1}{4} + 7 : 1\frac{1}{3}$;
г) $\frac{1}{2} + \frac{3}{4} * \frac{8}{15} — \frac{3}{10}$.

Решение

а) $25 * (\frac{7}{10} + \frac{3}{5} + \frac{1}{2}) = \frac{25}{1} * \frac{7 * 1 + 3 * 2 + 1 * 5}{10} = \frac{25}{1} * \frac{7 + 6 + 5}{10} = \frac{25}{1} * \frac{18}{10} = \frac{25 * 18}{1 * 10} = \frac{5 * 9}{1} = 45$

б) $(\frac{5}{12} + \frac{1}{6} + \frac{3}{8}) : \frac{15}{16} = \frac{5 * 2 + 1 * 4 + 3 * 3}{24} * \frac{16}{15} = \frac{10 + 4 + 9}{24} * \frac{16}{15} = \frac{23 * 16}{24 * 15} = \frac{23 * 2}{3 * 15} = \frac{46}{45} = 1\frac{1}{45}$

в) $5 : 1\frac{1}{4} + 7 : 1\frac{1}{3} = \frac{5}{1} : \frac{5}{4} + \frac{7}{1} : \frac{4}{3} = \frac{5}{1} * \frac{4}{5} + \frac{7}{1} * \frac{3}{4} = \frac{5 * 4}{5} + \frac{7 * 3}{4} = \frac{1 * 4}{1} + \frac{21}{4} = 4 + 5\frac{1}{4} = 9\frac{1}{4}$

г) $\frac{1}{2} + \frac{3}{4} * \frac{8}{15} — \frac{3}{10} = \frac{1}{2} + \frac{3 * 8}{4 * 15} — \frac{3}{10} = \frac{1}{2} + \frac{1 * 2}{1 * 5} — \frac{3}{10} = \frac{1}{2} + \frac{2}{5} — \frac{3}{10} = \frac{1 * 5 + 2 * 2 — 3}{10} = \frac{5 + 4 — 3}{10} = \frac{6}{10} = \frac{3}{5}$

Задание 26. Решите задачу и прокомментируйте свои действия.
а) В субботу Толя покрасил $\frac{1}{2}$ забора. В воскресенье три друга пришли ему помочь. Вместе с Толей они разделили непокрашенную часть забора поровну и докрасили забор. Какую часть забора покрасил каждый из них в воскресенье?
б) Три школьницы решили написать поздравительные открытки к празднику. Они разделили всю работу поровну. Одна из девочек, Таня, нашла себе трех помощниц, с которыми разделила свою часть работы поровну. Какую часть всей работы выполнила Таня?

Решение

а) Так как Толя покрасил $\frac{1}{2}$ забора, то:
1) $1 — \frac{1}{2} = \frac{1}{2}$ (забора) − осталось покрасить;
Так как пришло три друга, то:
2) 1 + 3 = 4 (ч.) − красило забор в воскресенье;
Так как 4 человека поровну окрасили половину забора, то:
3) $\frac{1}{2} : 4 = \frac{1}{2} * \frac{1}{4} = \frac{1}{8}$ (забора) − покрасил каждый из ребят в воскресенье.
Ответ: $\frac{1}{8}$ забора

б) Пусть вся работа равна 1, и раз каждой из трех девочек осталось работы поровну, то:
1) $1 : 3 = \frac{1}{3}$ (открыток) − нужно было написать каждой из трех девочек;
Так как, к Тане пришло 3 помощницы, то:
2) 1 + 3 = 4 (д.) − писали Танины открытки;
Так как каждая из четырех девочек написали Танины открытки поровну, то:
3) $\frac{1}{3} : 4 = \frac{1}{3} * \frac{1}{4} = \frac{1}{12}$ (открыток) − написала Таня.
Ответ: $\frac{1}{12}$ часть всех открыток.

Задание 27. Решите задачу и прокомментируйте свои действия.
а) У Андрея два аквариума. Длина, ширина и высота одного из них $\frac{9}{10}$ м, $\frac{2}{5}$ м и $\frac{1}{2}$ м, а другого − $\frac{4}{5}$ м, $\frac{3}{4}$ м и $\frac{3}{10}$ м. В какой из аквариумов вмещается больше воды?
б) Сколько потребуется проволоки для изготовления каркасной модели параллелепипеда с измерениями $\frac{4}{5}$ дм, $1\frac{1}{5}$ дм и $1\frac{2}{5}$ дм?

Решение

а) Объем аквариума равен произведению его длины, ширины и высоты, тогда:
1) $\frac{9}{10} * \frac{2}{5} * \frac{1}{2} = \frac{9 * 1 * 1}{10 * 5 * 1} = \frac{9}{50} (м^3)$ − объем первого аквариума;
2) $\frac{4}{3} * \frac{3}{4} * \frac{3}{10} = \frac{1 * 3 * 3}{5 * 1 * 10} = \frac{9}{50} (м^3)$ − объем второго аквариума;
3) $\frac{9}{50} = \frac{9}{50}$ − объемы аквариумов равны.
Ответ: в оба аквариума вмещается одинаковое количество воды.

б) Найдем сумму длину ребер прямоугольного параллелепипеда, у него 4 тройки равных ребер:
$4 * (\frac{4}{5} + 1\frac{1}{5} + 1\frac{2}{5}) = 4 * 2\frac{7}{5} = 4 * 3\frac{3}{5} = \frac{4}{1} * \frac{17}{5} = \frac{68}{5} = 13\frac{3}{5}$ (дм) − проволоки потребуется.
Ответ: $13\frac{3}{5}$ дм

Задание 28. а) Брат может прополоть грядку за 30 мин, а его младшая сестра − за 60 мин. За сколько минут они могут прополоть грядку, работая вместе?
1) Какую часть грядки пропалывает каждый из них за 1 мин?
2) Какую часть грядки пропалывают они за 1 мин, работа вместе?
3) За сколько минут брат с сестрой пропалывают грядку, работая вместе?
б) Мама может почистить картофель для обеда за 16 мин, а сыну на эту работу потребуется 48 мин. За сколько минут они почистят весь картофель, работая вместе?
Сравните задачу с задачей а) и решите ее по такому же плану.

Решение

а) Пусть вся грядка равна 1, тогда:
1) $1 : 30 = \frac{1}{30}$ (грядки) − пропалывает брат за 1 минуту;
$1 : 60 = \frac{1}{60}$ (грядки) − пропалывает сестра за 1 минуту;
2) $\frac{1}{30} + \frac{1}{60} = \frac{2 + 1}{60} = \frac{3}{60} = \frac{1}{20}$ (грядки) − пропалывают брат с сестрой вместе за 1 минуту;
3) $1 : \frac{1}{20} = 1 * \frac{20}{1} = 20$ (мин) − требуется брату с сестрой, чтобы прополоть всю грядку.
Ответ: за 20 минут.

б) Пусть весь картофель равен 1, тогда:
1) $1 : 16 = \frac{1}{16}$ (картофеля) − чистит мама за 1 минуту;
$1 : 48 = \frac{1}{48}$ (картофеля) − чистит сын за 1 минуту;
2) $\frac{1}{16} + \frac{1}{48} = \frac{3 + 1}{48} = \frac{4}{48} = \frac{1}{12}$ (картофеля) − чистят мама и сын за 1 минуту вместе;
3) $1 : \frac{1}{12} = 1 * \frac{12}{1} = 12$ (минут) − потребуется маме и сыну, чтобы почистить весь картофель.
Ответ: за 12 минут.

Задание 29. Располодите в порядке возастания следующие суммы:
$\frac{1}{3} + \frac{1}{8}$;
$\frac{1}{4} + \frac{1}{7}$;
$\frac{1}{5} + \frac{1}{6}$;
$\frac{1}{2} + \frac{1}{9}$.

Решение

$\frac{1}{3} + \frac{1}{8} = \frac{1 * 8 + 1 * 3}{24} = \frac{11}{24}$;
$\frac{1}{4} + \frac{1}{7} = \frac{1 * 7 + 1 * 4}{28} = \frac{11}{28}$;
$\frac{1}{5} + \frac{1}{6} = \frac{6 + 5}{30} = \frac{11}{30}$;
$\frac{1}{2} + \frac{1}{9} = \frac{1 * 9 + 1 * 2}{18} = \frac{11}{18}$.
Ответ:
$\frac{11}{30} < \frac{11}{28} < \frac{11}{24} < \frac{11}{18}$

Задание 30. Выполните действия:
а) $6\frac{6}{11} * \frac{3}{4} : 2\frac{2}{5} * 2\frac{1}{5}$;
б) $9 : 6\frac{1}{4} * 2\frac{1}{2} : \frac{3}{5}$;
в) $9\frac{1}{3} : \frac{7}{8} * \frac{9}{16} : \frac{14}{27}$;
г) $1\frac{5}{6} : 2\frac{1}{3} * 3\frac{3}{4} * 4\frac{1}{5}$.

Решение

а) $6\frac{6}{11} * \frac{3}{4} : 2\frac{2}{5} * 2\frac{1}{5} = \frac{72}{11} * \frac{3}{4} : \frac{12}{5} * \frac{11}{5} = \frac{72}{11} * \frac{3}{4} * \frac{5}{12} * \frac{11}{5} = \frac{72 * 3 * 5 * 11}{11 * 4 * 12 * 5} = \frac{6 * 3 * 1 * 1}{1 * 4 * 1 * 1} = \frac{3 * 3}{2} = \frac{9}{2} = 4\frac{1}{2}$

б) $9 : 6\frac{1}{4} * 2\frac{1}{2} : \frac{3}{5} = \frac{9}{1} : \frac{25}{4} * \frac{5}{2} * \frac{5}{3} = \frac{9 * 4 * 5 * 5}{25 * 2 * 3} = \frac{3 * 2 * 1 * 1}{1 * 1 * 1} = 6$

в) $9\frac{1}{3} : \frac{7}{8} * \frac{9}{16} : \frac{14}{27} = \frac{28}{3} * \frac{8}{7} * \frac{9}{16} * \frac{27}{14} = \frac{2 * 1 * 3 * 27}{1 * 7 * 2 * 1} = \frac{3 * 27}{7} = \frac{81}{7} = 11\frac{4}{7}$

г) $1\frac{5}{6} : 2\frac{1}{3} * 3\frac{3}{4} * 4\frac{1}{5} = \frac{11}{6} : \frac{7}{3} * \frac{15}{4} * \frac{21}{5} = \frac{11}{6} * \frac{3}{7} * \frac{15}{4} * \frac{21}{5} = \frac{11}{6} * \frac{3}{7} * \frac{15}{4} * \frac{21}{5} = \frac{11 * 3 * 15 * 21}{6 * 7 * 4 * 5} = \frac{11 * 1 * 3 * 3}{2 * 1 * 4 * 1} = \frac{99}{8} = 12\frac{3}{8}$

7gy.ru

Страница 16 №46-51 ГДЗ к учебнику «Математика» 6 класс Дорофеев, Шарыгин

Задание 46. Найдите значение выражения:
а) $\frac{1 — \frac{1}{5}}{2}$;
б) $\frac{6}{1 — \frac{1}{3}}$;
в) $\frac{\frac{2}{3} + \frac{1}{6}}{3}$;
г) $\frac{1 — \frac{1}{6}}{2 + \frac{1}{6}}$;
д) $\frac{\frac{17}{100} — \frac{1}{10}}{10}$;
е) $\frac{\frac{1}{4} + \frac{2}{3}}{2 — \frac{1}{6}}$.

Решение 7 гуру

а) $\frac{1 — \frac{1}{5}}{2} = \frac{\frac{4}{5}}{2} = \frac{4}{5} * \frac{1}{2} = \frac{2}{5} * \frac{1}{1} = \frac{2}{5}$

б) $\frac{6}{1 — \frac{1}{3}} = \frac{6}{\frac{2}{3}} = 6 * \frac{3}{2} = 3 * 3 = 9$

в) $\frac{\frac{2}{3} + \frac{1}{6}}{3} = \frac{\frac{4 + 1}{6}}{3} = \frac{5}{6} * \frac{1}{3} = \frac{5}{18}$

г) $\frac{1 — \frac{1}{6}}{2 + \frac{1}{6}} = \frac{\frac{5}{6}}{2\frac{1}{6}} = \frac{\frac{5}{6}}{\frac{13}{6}} = \frac{5}{6} * \frac{6}{13} = \frac{5}{1} * \frac{1}{13} = \frac{5}{13}$

д) $\frac{\frac{17}{100} — \frac{1}{10}}{10} = \frac{\frac{17 — 10}{100}}{10} = \frac{7}{100} * \frac{1}{10} = \frac{7}{1000}$

е) $\frac{\frac{1}{4} + \frac{2}{3}}{2 — \frac{1}{6}} = \frac{\frac{3 + 8}{12}}{1\frac{5}{6}} = \frac{\frac{11}{12}}{\frac{11}{6}} = \frac{11}{12} * \frac{6}{11} = \frac{1}{2} * \frac{1}{1} = \frac{1}{2}$

Задание 47. Что может означать запись $\frac{\frac{3}{2}}{3}$? Примите по очереди каждую дробную черту за «основную» и запишите соответствующие выражения. Найдите значение каждого из этих выражений.

Решение

$\frac{\frac{3}{2}}{3} = \frac{3}{2} : 3 = \frac{3}{2} * \frac{1}{3} = \frac{1}{2}$;
$\frac{\frac{3}{2}}{3} = 3 : \frac{2}{3} = 3 * \frac{3}{2} = \frac{9}{2} = 4\frac{1}{2}$.

Задание 48. Разделить некоторое число на 2 − это все равно что умножить его на $\frac{1}{2}$. Поэтому $\frac{3 — \frac{1}{4}}{2} = (3 — \frac{1}{4}) * \frac{1}{2}$. Рассуждая таким же образом, представьте в виде произведения выражение:
а) $\frac{\frac{1}{2} + \frac{1}{3}}{2}$;
б) $\frac{1 — \frac{5}{6}}{3}$;
в) $\frac{\frac{4}{5} — \frac{1}{2}}{10}$;
г) $\frac{2 + \frac{5}{8}}{5}$.

Решение

а) $\frac{\frac{1}{2} + \frac{1}{3}}{2} = (\frac{1}{2} + \frac{1}{3}) * \frac{1}{2}$

б) $\frac{1 — \frac{5}{6}}{3} = (1 — \frac{5}{6}) * \frac{1}{3}$

в) $\frac{\frac{4}{5} — \frac{1}{2}}{10} = (\frac{4}{5} — \frac{1}{2}) * \frac{1}{10}$

г) $\frac{2 + \frac{5}{8}}{5} = (2 + \frac{5}{8}) * \frac{1}{5}$

Задание 49. Запишите выражение в виде частного, используя черту дроби:
а) $(8 — 6\frac{1}{4}) * \frac{1}{4}$;
б) $(\frac{5}{6} — \frac{1}{2}) * \frac{1}{2}$;
в) $(\frac{3}{10} + \frac{3}{100}) * \frac{1}{100}$.

Решение

а) $(8 — 6\frac{1}{4}) * \frac{1}{4} = \frac{8 — 6\frac{1}{4}}{4}$

б) $(\frac{5}{6} — \frac{1}{2}) * \frac{1}{2} = \frac{\frac{5}{6} — \frac{1}{2}}{2}$

в) $(\frac{3}{10} + \frac{3}{100}) * \frac{1}{100} = \frac{\frac{3}{10} + \frac{3}{100}}{100}$

Задание 50. Найдите значение выражения:
а) $\frac{6 — \frac{1}{\frac{1}{2} — \frac{1}{3}}}{6 + \frac{1}{\frac{1}{2} — \frac{1}{3}}}$;
б) $2 + \frac{1}{1 + \frac{2}{1 + \frac{1}{3}}}$;
в) $\frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{3}}}}$.

Решение

а) $\frac{6 — \frac{1}{\frac{1}{2} — \frac{1}{3}}}{6 + \frac{1}{\frac{1}{2} — \frac{1}{3}}} = \frac{6 — \frac{1}{\frac{3 — 2}{6}}}{6 + \frac{1}{\frac{3 — 2}{6}}} = \frac{6 — 1 : \frac{1}{6}}{6 + 1 : \frac{1}{6}} = \frac{6 — 1 * 6}{6 + 1 * 6} = \frac{6 — 6}{6 + 6} = \frac{0}{12} = 0$

б) $2 + \frac{1}{1 + \frac{2}{1 + \frac{1}{3}}} = 2 + \frac{1}{1 + 2 : 1\frac{1}{3}} = 2 + \frac{1}{1 + 2 : \frac{4}{3}} = 2 + \frac{1}{1 + 2 * \frac{3}{4}} = 2 + \frac{1}{1 + \frac{3}{2}} = 2 + \frac{1}{1 + 1\frac{1}{2}} = 2 + \frac{1}{2\frac{1}{2}} = 2 + 1 : \frac{5}{2} = 2 + 1 * \frac{2}{5} = 2 + \frac{2}{5} = 2\frac{2}{5}$

в) $\frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{3}}}} = \frac{1}{1 + \frac{1}{1 + \frac{1}{1\frac{1}{3}}}} = \frac{1}{1 + \frac{1}{1 + 1 : \frac{4}{3}}} = \frac{1}{1 + \frac{1}{1 + 1 * \frac{3}{4}}} = \frac{1}{1 + \frac{1}{1\frac{3}{4}}} = \frac{1}{1 + 1 : 1\frac{3}{4}} = \frac{1}{1 + 1 : \frac{7}{4}} = \frac{1}{1 + 1 * \frac{4}{7}} = \frac{1}{1 + \frac{4}{7}} = \frac{1}{1\frac{4}{7}} = 1 : 1\frac{4}{7} = 1 : \frac{11}{7} = 1 * \frac{7}{11} = \frac{7}{11}$

Задание 51. Найдите значение выражения:
а) $\frac{9 * 5 * 4}{20 * 8 * 15}$;
б) $\frac{4}{9} : \frac{7}{10} : \frac{8}{3}$;
в) $\frac{9}{10} * \frac{5}{33} : \frac{9}{16}$.

Решение

а) $\frac{9 * 5 * 4}{20 * 8 * 15} = \frac{3 * 1 * 1}{1 * 8 * 5} = \frac{3}{40}$

б) $\frac{4}{9} : \frac{7}{10} : \frac{8}{3} = \frac{4}{9} * \frac{10}{7} * \frac{3}{8} = \frac{4 * 10 * 3}{9 * 7 * 8} = \frac{1 * 5 * 1}{3 * 7 * 1} = \frac{5}{21}$

в) $\frac{9}{10} * \frac{5}{33} : \frac{9}{16} = \frac{9}{10} * \frac{5}{33} * \frac{16}{9} = \frac{9 * 5 * 16}{10 * 33 * 9} = \frac{1 * 1 * 16}{2 * 33 * 1} = \frac{16}{66} = \frac{8}{33}$

7gy.ru

Страница 56 №142-151 ГДЗ к учебнику «Математика» 6 класс Бунимович, Кузнецова, Минаева

Ответы к упражнениям

Равные десятичные дроби

Задание 142. Есть ли среди данных чисел равные? Если есть, укажите их:
а) 3,001; 3,010; 3,100; 3,1;
б) 6,800; 6,080; 6,880; 6,08;
в) 0,4; 0,40; 0,004; 0,400;
г) 1,05; 1,0505; 1,500; 1,5050.

Ответы 7 гуру

а) 3,100 = 3,1

б) 6,080 = 6,08

в) 0,4 = 0,40 = 0,400

г) Среди данных чисел равных нет.

Задание 143. Верно ли, что:
а) 12,40 = 12,4;
б) 25 = 25,0;
в) 1,03 = 1,30;
г) 1,500 = 1,50;
д) 160 = 16;
е) 2,01 = 2,0100000?

Решение

а) 12,40 = 12,4 − верно

б) 25 = 25,0 − верно

в) 1,03 = 1,30 − неверно

г) 1,500 = 1,50 − верно

д) 160 = 16 − неверно

е) 2,01 = 2,0100000 − верно

Задание 144. Замените данную десятичную дробь равной наиболее простого вида:
а) 3,6000;
б) 70,0200;
в) 0,8700;
г) 0,0030.

Решение

а) 3,6000 = 3,6

б) 70,0200 = 70,02

в) 0,8700 = 0,87

г) 0,0030 = 0,003

Задание 145. а) Выразите в метрах: 17 м 30 см; 70 м 50 см.
б) Выразите в килограммах: 3 кг 430 г; 5 кг 80 г.

Решение

а) 17 м 30 см = $17\frac{30}{100} = 17,30 = 17,3$ м;
70 м 50 см = $70\frac{50}{100} = 70,50 = 70,5$ м.

б) 3 кг 430 = $3\frac{430}{1000} = 3,430 = 3,43$ кг;
5 кг 80 г = $5\frac{80}{1000} = 5,080 = 5,08$ кг.

Задание 146. К числу приписывают справа один нуль, два нуля, три нуля и т.д. Что происходит с этим числом, если оно является:
а) натуральным числом;
б) десятичной дробью?

Ответы

а) Если к натуральному числу приписывают справа один нуль, два нуля, три нуля и т.д., то оно увеличивается в 10 раз, 100 раз, 1000 раз и т.д.

б) Если к десятичной дроби приписывают справа один нуль, два нуля, три нуля и т.д., то она не меняется.

Сравнение и упорядочивание десятичных дробей

Задание 147. Сравните числа:
а) 0,6 и 0,4;
б) 0,2 и 0,1;
в) 0,30 и 0,3;
г) 2,55 и 2,65;
д) 1,21 и 1,28;
е) 4,75 и 4,05;
ж) 1,99 и 10,9;
з) 7,0191 и 7,1;
и) 2,44 и 2,404.

Ответы

а) 0,6 > 0,4

б) 0,2 > 0,1

в) 0,30 = 0,3

г) 2,55 < 2,65

д) 1,21 < 1,28

е) 4,75 > 4,05

ж) 1,99 < 10,9

з) 7,0191 < 7,1

и) 2,44 > 2,404

Задание 148. Сравните числа:
а) 50,001 и 50,01;
б) 17,183 и 17,09;
в) 29,5 и 29,53;
г) 7 и 6,99;
д) 0,89 и 1,5;
е) 0,00041 и 0,0005.

Ответы

а) 50,001 < 50,01

б) 17,183 > 17,09

в) 29,5 < 29,53

г) 7 > 6,99

д) 0,89 < 1,5

е) 0,00041 < 0,0005

Задание 149. Какое из трех данных чисел наибольшее и какое наименьшее:
а) 0,016; 0,044; 0,031;
б) 2,601; 2,610; 2,061;
в) 0,5; 0,6; 0,56;
г) 3,215; 32,15; 0,3215?

Решение

а) 0,016 < 0,031 < 0,044;
0,016 − наименьшее число;
0,044 − наибольшее число.

б) 2,061 < 2,601 < 2,610;
2,061 − наименьшее число;
2,610 − наибольшее число.

в) 0,5 < 0,56 < 0,6;
0,5 − наименьшее число;
0,6 − наибольшее число.

г) 0,3215 < 3,215 < 32,15;
0,3215 − наименьшее число;
32,15 − наибольшее число.

Задание 150. Расположите в порядке возрастания числа:
а) 7,34; 7,4; 7,3;
б) 10,2; 10,1; 10,16;
в) 2,356; 2,35; 2,36;
г) 0,007; 0,008; 0,0073.

Ответ

а) 7,3 < 7,34 < 7,4

б) 10,1 < 10,16 < 10,2

в) 2,35 < 2,356 < 2,36

г) 0,007 < 0,0073 < 0,008

Задание 151. Расположите в порядке убывания числа:
а) 22,86; 23,01; 22,68; 21,99;
б) 0,93; 0,853; 0,914; 0,94;
в) 0,09; 0,111; 0,1; 0,091;
г) 3,099; 3,909; 3,99; 3,9009.

Ответ

а) 23,01 > 22,86 > 22,68 > 21,99

б) 0,94 > 0,93 > 0,914 > 0,853

в) 0,111 > 0,1 > 0,091 > 0,09

г) 3,99 > 3,909 > 3,9009 > 3,099

7gy.ru

Страница 18 №34-41 ГДЗ к учебнику «Математика» 6 класс Бунимович, Кузнецова, Минаева

Ответы к упражнениям

Нахождение части от числа

Задание 34. Прочитайте предложения и вставьте нужные слова.
а) Чтобы найти половину некоторого числа, нужно это число разделить на … или умножить на … .
б) Чтобы найти четверть некоторого числа, нужно это число разделить на … или умножить на … .

Ответ

а) Чтобы найти половину некоторого числа, нужно это число разделить на 2 или умножить на $\frac{1}{2}$.

б) Чтобы найти четверть некоторого числа, нужно это число разделить на 4 или умножить на $\frac{1}{4}$.

Задание 35. а) $\frac{1}{4}$ от 8 кг;
б) $\frac{1}{10}$ от 30 км;
в) $\frac{3}{4}$ от 12 ч;
г) $\frac{2}{5}$ от 20 см.

Решение

а) $8 * \frac{1}{4} = 2$ (кг) − составляют $\frac{1}{4}$ от 8 кг.

б) $30 * \frac{1}{10} = 3$ (км) − составляют $\frac{1}{10}$ от 30 км.

в) $12 * \frac{3}{4} = 3 * 3 = 9$ (ч) − составляет $\frac{3}{4}$ от 12 ч.

г) $20 * \frac{2}{5} = 4 * 2 = 8$ (см) − составляет $\frac{2}{5}$ от 20 см.

Задание 36. а) $\frac{1}{2}$ от $\frac{3}{4}$ м;
б) $\frac{1}{10}$ от $\frac{1}{2}$ г;
в) $\frac{3}{4}$ от $\frac{1}{10}$ кг;
г) $\frac{2}{5}$ от $\frac{1}{4}$ ч.

Решение

а) $\frac{3}{4} * \frac{1}{2} = \frac{3}{8}$ (м) − составляет $\frac{1}{2}$ от $\frac{3}{4}$ м.

б) $\frac{1}{2} * \frac{1}{10} = \frac{1}{20}$ (г) − составляет $\frac{1}{10}$ от $\frac{1}{2}$ г.

в) $\frac{1}{10} * \frac{3}{4} = \frac{3}{40}$ (кг) − составляет $\frac{3}{4}$ от $\frac{1}{10}$ кг.

г) $\frac{1}{4} * \frac{2}{5} = \frac{1}{2} * \frac{1}{5} = \frac{1}{10}$ (ч) − составляет $\frac{2}{5}$ от $\frac{1}{4}$ ч.

Задание 37. а) Стакан вмещает 160 г крупы. Крупой наполнили $\frac{2}{5}$ стакана. Сколько граммов крупы насыпали в стакан?
б) Общая площадь окон, которые надо вымыть, составляет 24 $м^2$. За час вымыли $\frac{5}{8}$ этой площади. Определите площадь окон, вымытых за это время.

Решение задач

а) $160 * \frac{2}{5} = 32 * 2 = 64$ (г) − крупы насыпали в стакан.
Ответ: 64 г.

б) $24 * \frac{5}{8} = 3 * 5 = 15 (м^2)$ − вымыли за 1 час.
Ответ: 15 $м^2$ .

Задание 38. а) От веревки длиной 2 м 40 см отрезали $\frac{3}{8}$ ее длины. Найдите длину оставшейся части.
б) Занятия в школе длятся 5 ч 30 мин. Перемены занимают $\frac{3}{11}$ этого времени. Сколько часов длятся уроки?

Решение задач

а) 2 м 40 см = 240 см
1) $240 * \frac{3}{8} = 30 * 3 = 90$ (см) − веревки отрезали;
2) 240 − 90 = 150 см = 1 м 50 см − длина оставшейся части веревки.
Ответ: 1 м 50 см

б) 5 ч 30 мин = (5 * 60 + 30) мин = 330 мин
1) $330 * \frac{3}{11} = 30 * 3 = 90$ (мин) − длятся перемены;
2) 330 − 90 = 240 (мин) = 4 (ч) − длятся уроки.
Ответ: 4 ч.

Задание 39. Ученик взял в библиотеке интересную книгу. В ней 75 страниц. В первый день он прочитал $\frac{3}{5}$ всей книги, во второй − $\frac{2}{5}$ оставшихся страниц. Сколько страниц ему осталось прочитать?

Решение задач

1) $75 * \frac{3}{5} = 15 * 3 = 45$ (страниц) − прочитал ученик в первый день;
2) 75 − 45 = 30 (страниц) − осталось прочитать после первого дня;
3) $30 * \frac{2}{5} = 6 * 2 = 12$ (страниц) − прочитал ученик во второй день;
4) 30 − 12 = 18 (страниц) − осталось прочитать ученику.
Ответ: 18 страниц.

Задание 40. Учащиеся шестых классов составляют $\frac{1}{14}$ всех учащихся школы, причем $\frac{2}{5}$ из них − девочки. Сколько девочек в шестых классах, если всего в школе 910 учащихся?

Решение

1) $910 * \frac{1}{14} = 65$ (учащихся) − всего в шестых классах;
2) $65 * \frac{2}{5} = 13 * 2 = 26$ (девочек) − в шестых классах.
Ответ: 26 девочек.

Нахождение числа по его части

Задание 41. Найдите длину отрезка, если:
а) $\frac{2}{5}$ его длины равны 12 м;
б) $\frac{3}{4}$ его длины равны 9 см;
в) $\frac{3}{5}$ его длины равны 15 дм;
г) $\frac{2}{7}$ его длины равны 8 мм.

Ответы 7 гуру

а) $12 : \frac{2}{5} = 12 * \frac{5}{2} = 6 * 5 = 30$ (м) − длина отрезка.

б) $9 : \frac{3}{4} = 9 * \frac{4}{3} = 3 * 4 = 12$ (см) − длина отрезка.

в) $15 : \frac{3}{5} = 15 * \frac{5}{3} = 5 * 5 = 25$ (дм) − длина отрезка.

г) $8 : \frac{2}{7} = 8 * \frac{7}{2} = 4 * 7 = 28$ (мм) − длина отрезка.

7gy.ru

Страница 8 №1-7 ГДЗ к учебнику «Математика» 6 класс Дорофеев, Шарыгин

Глава 1. Дроби и проценты

Ответы к разделу учебника 1.1 Что мы знаем о дробях

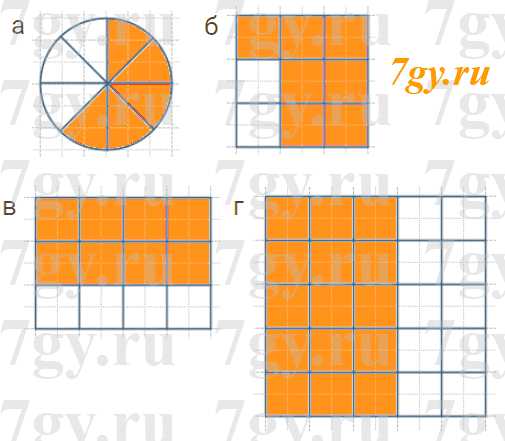
Задание 1. Изобразите какую−нибудь геометрическую фигуру (прямоугольник, круг или отрезок) и закрасьте ее часть, которая соответствует дроби:
а) $\frac{5}{8}$; б) $\frac{7}{9}$; в) $\frac{8}{12}$; г) $\frac{15}{25}$.

Ответ 7 гуру

Задание 2. 1) Приведите дроби:
а) $\frac{4}{9}$, $\frac{5}{6}$, $\frac{7}{2}$ к знаменателю 18;  б) $\frac{7}{8}$, $\frac{5}{16}$, $\frac{21}{40}$ к знаменателю 80.
2) Приведите к наименьшему общему знаменателю дроби:
а) $\frac{1}{3}$ и $\frac{1}{4}$; б) $\frac{5}{8}$ и $\frac{3}{16}$; в) $\frac{5}{8}$ и $\frac{3}{20}$; г) $\frac{2}{9}$ и $\frac{7}{24}$.

Решение

1)
а) $\frac{4}{9} = \frac{4 * 2}{9 * 2} = \frac{8}{18}$;
$\frac{5}{6} = \frac{5 * 3}{6 * 3} = \frac{15}{18}$;
$\frac{7}{2} = \frac{7 * 9}{2 * 9} = \frac{63}{18}$.

б) $\frac{7}{8} = \frac{7 * 10}{8 * 10} = \frac{70}{80}$;
$\frac{5}{16} = \frac{5 * 5}{16 * 5} = \frac{25}{80}$;
$\frac{21}{40} = \frac{21 * 2}{40 * 2} = \frac{42}{80}$.

2)
а) $\frac{1}{3} = \frac{1 * 4}{3 * 4} = \frac{4}{12}$;
$\frac{1}{4} = \frac{1 * 3}{4 * 3} = \frac{3}{12}$.
Ответ: $\frac{4}{12}$ и $\frac{3}{12}$

б) $\frac{5}{8} = \frac{5 * 2}{8 * 2} = \frac{10}{16}$;
$\frac{3}{16}$.
Ответ: $\frac{10}{16}$ и $\frac{3}{16}$

в) $\frac{5}{8} = \frac{5 * 5}{8 * 5} = \frac{25}{40}$;
$\frac{3}{20} = \frac{3 * 2}{20 * 2} = \frac{6}{40}$.
Ответ: $\frac{25}{40}$ и $\frac{6}{40}$

г) $\frac{2}{9} = \frac{2 * 8}{9 * 8} = \frac{16}{72}$;
$\frac{7}{24} = \frac{7 * 3}{24 * 3} = \frac{21}{72}$.
Ответ: $\frac{16}{72}$ и $\frac{21}{72}$

Задание 3. В Древнем Риме при измерении величин применялись дроби со знаменателем 12. Вместо $\frac{1}{12}$ говорили «одна унция», вместо $\frac{5}{12}$ − «пять унций» и т.п. Выразите в унциях: половину, треть, четверть, пять шестых, три четверти.

Решение

Половина = $\frac{1}{2} = \frac{1 * 6}{2 * 6} = \frac{6}{12}$ = шесть унций;
треть = $\frac{1}{3} = \frac{1 * 4}{3 * 4} = \frac{4}{12}$ = четыре унции;
четверть = $\frac{1}{4} = \frac{1 * 3}{4 * 3} = \frac{3}{12}$ = три унции;
пять шестых = $\frac{5}{6} = \frac{5 * 2}{6 * 2} = \frac{10}{12}$ = десять унций;
три четверти = $\frac{3}{4} = \frac{3 * 3}{4 * 3} = \frac{9}{12}$ = девять унций.

Задание 4. Сократите дробь:
а) $\frac{24}{30}$; б) $\frac{12}{48}$; в) $\frac{20}{36}$; г) $\frac{14}{56}$; д) $\frac{44}{100}$; е) $\frac{36}{60}$.

Решение

а) $\frac{24}{30} = \frac{24 : 6}{30 : 6} = \frac{4}{5}$

б) $\frac{12}{48} = \frac{12 : 12}{48 : 12} = \frac{1}{4}$

в) $\frac{20}{36} = \frac{20 : 4}{36 : 4} = \frac{5}{9}$

г) $\frac{14}{56} = \frac{14 : 14}{56 : 14} = \frac{1}{4}$

д) $\frac{44}{100} = \frac{44 : 4}{100 : 4} = \frac{11}{25}$

е) $\frac{36}{60} = \frac{36 : 12}{60 : 12} = \frac{3}{5}$

Задание 5. Сравните дроби и запишите результат сравнения с помощью знаков >, < или =. В каждом случае расскажите, каким способом вы действовали.

Решение

а) $\frac{4}{5} = \frac{4 * 2}{5 * 2} = \frac{8}{10}$
$\frac{8}{10} > \frac{7}{10}$
$\frac{4}{5} > \frac{7}{10}$
Привел дроби к наименьшему общему знаменателю.

б) $\frac{5}{12} = \frac{5 * 6}{12 * 6} = \frac{30}{72}$
$\frac{7}{8} = \frac{7 * 9}{8 * 9} = \frac{63}{72}$
$\frac{30}{72} < \frac{63}{72}$
$\frac{5}{12} < \frac{7}{8}$
Привел дроби к наименьшему общему знаменателю.

в) $\frac{5}{6} = \frac{5 * 4}{6 * 4} = \frac{20}{24}$
$\frac{7}{8} = \frac{7 * 3}{8 * 3} = \frac{21}{24}$
$\frac{20}{24} < \frac{21}{24}$
$\frac{5}{6} < \frac{7}{8}$
Привел дроби к наименьшему общему знаменателю.

г) $\frac{6}{16} = \frac{6 : 2}{16 : 2} = \frac{3}{8}$
$\frac{3}{8} = \frac{3}{8}$
$\frac{3}{8} = \frac{6}{16}$
Сократил дробь $\frac{6}{16}$.

д) $1\frac{1}{8} = \frac{8 * 1 + 1}{8} = \frac{9}{8}$
$\frac{9}{8} = \frac{9}{8}$
$\frac{9}{8} = 1\frac{1}{8}$
Преобразовал смешанное число в неправильную дробь.

е) $1\frac{8}{20} = 1\frac{8 : 4}{20 : 4} = 1\frac{2}{5}$
$1\frac{2}{5} > 1\frac{2}{9}$
$1\frac{8}{20} > 1\frac{2}{9}$
Сократил дробь $1\frac{8}{20}$.

ж) $\frac{5}{9} < \frac{9}{5}$
Неправильная дробь больше правильной дроби.

з) $\frac{12}{11} > \frac{11}{12}$
Неправильная дробь больше правильной дроби.

Задание 6. Запишите дроби в порядке возрастания:
а) $\frac{3}{4}, \frac{11}{12}, \frac{2}{3}, \frac{5}{6}$;
б) $\frac{1}{15}, \frac{2}{5}, \frac{7}{15}, \frac{1}{3}$;
в) $\frac{1}{2}, \frac{17}{20}, \frac{2}{5}, \frac{3}{4}$;
г) $\frac{7}{10}, \frac{4}{5}, \frac{63}{100}, \frac{1}{2}$.

Решение

а) $\frac{3}{4} = \frac{3 * 3}{4 * 3} = \frac{9}{12}$;
$\frac{2}{3} = \frac{2 * 4}{3 * 4} = \frac{8}{12}$;
$\frac{5}{6} = \frac{5 * 2}{6 * 2} = \frac{10}{12}$;
$\frac{8}{12} < \frac{9}{12} < \frac{10}{12} < \frac{11}{12}$;
$\frac{2}{3} < \frac{3}{4} < \frac{5}{6} < \frac{11}{12}$.

б) $\frac{2}{5} = \frac{2 * 3}{5 * 3} = \frac{6}{15}$;
$\frac{1}{3} = \frac{1 * 5}{3 * 5} = \frac{5}{15}$;
$\frac{1}{15} < \frac{5}{15} < \frac{6}{15} < \frac{7}{15}$;
$\frac{1}{15} < \frac{1}{3} < \frac{2}{5} < \frac{7}{15}$.

в) $\frac{1}{2} = \frac{1 * 10}{2 * 10} = \frac{10}{20}$;
$\frac{2}{5} = \frac{2 * 4}{5 * 4} = \frac{8}{20}$;
$\frac{3}{4} = \frac{3 * 5}{4 * 5} = \frac{15}{20}$;
$\frac{8}{20} < \frac{10}{20} < \frac{15}{20} < \frac{17}{20}$;
$\frac{2}{5} < \frac{1}{2} < \frac{3}{4} < \frac{17}{20}$.

г) $\frac{7}{10} = \frac{7 * 10}{10 * 10} = \frac{70}{100}$;
$\frac{4}{5} = \frac{4 * 20}{5 * 20} = \frac{80}{100}$;
$\frac{1}{2} = \frac{1 * 50}{2 * 50} = \frac{50}{100}$;
$\frac{50}{100} < \frac{63}{100} < \frac{70}{100} < \frac{80}{100}$;
$\frac{1}{2} < \frac{63}{100} < \frac{7}{10} < \frac{4}{5}$.

Задание 7. а) На тренировке Оля пробежала стометровку за $\frac{1}{3}$ мин, Галя − за $\frac{17}{60}$ мин, Вера − за $\frac{3}{10}$ мин, Зоя − за $\frac{4}{15}$ мин. В каком порядке девочки пришли к финишу, если они стартовали одновременно?
б) На путь от школы до стадиона Толя и три его друга затрачивают разное время:
Толя − $\frac{2}{5}$ ч;
Саша − $\frac{1}{2}$ ч;
Коля − $\frac{3}{10}$ ч;
Петя − $\frac{7}{12}$ ч.
Ребята вышли из школы одновременно. В каком порядке они придут на стадион?

Решение

а) 1) $\frac{1}{3} = \frac{1 * 20}{3 * 20} = \frac{20}{60}$ мин = 20 (с) − время, за которое пробежала Оля;
2) $\frac{17}{60}$ мин = 17 (с) − время, за которое пробежала Галя;
3) $\frac{3}{10} = \frac{3 * 6}{10 * 6} = \frac{18}{60}$ мин = 18 (с) − время, за которое пробежала Вера;
4) $\frac{4}{15} = \frac{4 * 4}{15 * 4} = \frac{16}{60}$ мин = 16 (с) − время, за которое пробежала Зоя;
5) 16 < 17 < 18 < 20 − значит, первой прибежала Зоя, второй Галя, третьей Вера, четвертой Оля.
Ответ: 1 место − Зоя; 2 место − Галя; 3 место − Вера; 4 место − Оля.

б) 1) $\frac{2}{5} = \frac{2 * 12}{5 * 12} = \frac{24}{60}$ ч = 24 (мин) − затратит на путь Толя;
2) $\frac{1}{2} = \frac{1 * 30}{2 * 30} = \frac{30}{60}$ ч = 30 (мин) − затратит на путь Саша;
3) $\frac{3}{10} = \frac{3 * 6}{10 * 6} = \frac{18}{60}$ ч = 18 (мин) − затратит на путь Коля;
4) $\frac{7}{12} = \frac{7 * 5}{12 * 5} = \frac{35}{60}$ ч = 35 (мин) − затратит на путь Петя;
5) 18 < 24 < 30 < 35 − значит, первым придет Коля, вторым − Толя, третьим − Саша, четвертым − Петя.
Ответ: ребята придут в следующем порядке: Коля, Толя, Саша, Петя.

7gy.ru

Страница 11 №17-24 ГДЗ к учебнику «Математика» 6 класс Дорофеев, Шарыгин

Ответы к разделу учебника 1.2 Вычисления с дробями

Задание 17. Найдите сумму или разность:
а) $\frac{5}{24} + \frac{3}{8}$;
б) $\frac{7}{10} — \frac{2}{5}$;
в) $\frac{7}{9} — \frac{5}{7}$;
г) $\frac{2}{3} + \frac{7}{8}$;
д) $\frac{3}{4} — \frac{1}{6}$;
е) $\frac{5}{6} + \frac{1}{9}$;
ж) $\frac{8}{25} + \frac{17}{20}$;
з) $\frac{4}{45} — \frac{1}{30}$;
и) $\frac{17}{18} — \frac{11}{12}$;
к) $\frac{11}{15} + \frac{5}{12}$;
л) $\frac{1}{3} + \frac{1}{6}$;
м) $\frac{3}{4} — \frac{2}{5}$.

Решение

а) $\frac{5}{24} + \frac{3}{8} = \frac{5 * 1 + 3 * 3}{24} = \frac{5 + 9}{24} = \frac{14}{24} = \frac{7}{12}$

б) $\frac{7}{10} — \frac{2}{5} = \frac{7 * 1 — 2 * 2}{10} = \frac{7 — 4}{10} = \frac{3}{10}$

в) $\frac{7}{9} — \frac{5}{7} = \frac{7 * 7 — 5 * 9}{63} = \frac{49 — 45}{63} = \frac{4}{63}$

г) $\frac{2}{3} + \frac{7}{8} = \frac{2 * 8 + 7 * 3}{24} = \frac{16 + 21}{24} = \frac{37}{24} = 1\frac{13}{24}$

д) $\frac{3}{4} — \frac{1}{6} = \frac{3 * 3 — 1 * 2}{12} = \frac{9 — 2}{12} = \frac{7}{12}$

е) $\frac{5}{6} + \frac{1}{9} = \frac{5 * 3 + 1 * 2}{18} = \frac{15 + 2}{18} = \frac{17}{18}$

ж) $\frac{8}{25} + \frac{17}{20} = \frac{8 * 4 + 17 * 5}{100} = \frac{32 + 85}{100} = \frac{117}{100} = 1\frac{17}{100}$

з) $\frac{4}{45} — \frac{1}{30} = \frac{4 * 2 — 1 * 3}{90} = \frac{8 — 3}{90} = \frac{5}{90} = \frac{1}{18}$

и) $\frac{17}{18} — \frac{11}{12} = \frac{17 * 2 — 11 * 3}{36} = \frac{34 — 33}{36} = \frac{1}{36}$

к) $\frac{11}{15} + \frac{5}{12} = \frac{11 * 4 + 5 * 5}{60} = \frac{44 + 25}{60} = \frac{69}{60} = 1\frac{9}{60} = 1\frac{3}{20}$

л) $\frac{1}{3} + \frac{1}{6} = \frac{1 * 2 + 1 * 1}{6} = \frac{2 + 1}{6} = \frac{3}{6} = \frac{1}{2}$

м) $\frac{3}{4} — \frac{2}{5} = \frac{3 * 5 — 2 * 4}{20} = \frac{15 — 8}{20} = \frac{7}{20}$

Задание 18. Двум дежурным было поручено вымыть парты в классе. Когда они закончили работу, то первый сказал, что вымыл $\frac{3}{5}$ всех парт, а второй сказал, что вымыл $\frac{2}{3}$ всех парт. Их товарищ заметил, что кто−то из них ошибся в расчетах. Как он догадался?

Решение

Все парты в классе должны составить единицу, тогда:
$\frac{3}{5} + \frac{2}{3} = \frac{3 * 3 + 2 * 5}{15} = \frac{9 + 10}{15} = \frac{19}{15} = 1\frac{4}{15} ≠ 1$ − значит, кто−то ошибся в расчетах.

Задание 19. Выполните вычисления:
а) $4 + 5\frac{1}{4}$;
б) $1\frac{1}{2} + 3\frac{1}{3}$;
в) $1\frac{3}{5} + 2\frac{2}{3}$;
г) $5\frac{3}{4} — 2$;
д) $3 — \frac{5}{7}$;
е) $4 — 1\frac{7}{9}$;
ж) $3\frac{2}{5} — \frac{3}{5}$;
з) $4\frac{1}{3} — 1\frac{1}{2}$.

Решение

а) $4 + 5\frac{1}{4} = 9\frac{1}{4}$

б) $1\frac{1}{2} + 3\frac{1}{3} = (1 + 3) + (\frac{2}{9} + \frac{1}{3}) = 4 + \frac{2 * 1 + 1 * 3}{9} = 4 + \frac{2}{3} = 4 + \frac{5}{9} = 4\frac{5}{9}$

в) $1\frac{3}{5} + 2\frac{2}{3} = (1 + 2) + (\frac{3}{5} + \frac{2}{3}) = 3 + \frac{3 * 3 + 2 * 5}{15} = 3 + \frac{9 + 10}{15} = 3 + \frac{19}{15} = 4\frac{4}{15}$

г) $5\frac{3}{4} — 2 = 3\frac{3}{4}$

д) $3 — \frac{5}{7} = 2\frac{7}{7} — \frac{5}{7} = 2\frac{2}{7}$

е) $4 — 1\frac{7}{9} = 3 — \frac{7}{9} = 2\frac{9}{9} — \frac{7}{9} = 2\frac{2}{9}$

ж) $3\frac{2}{5} — \frac{3}{5} = 2\frac{7}{5} — \frac{3}{5} = 2\frac{4}{5}$

з) $4\frac{1}{3} — 1\frac{1}{2} = 3\frac{1}{3} — \frac{1}{2} = 2 + 1\frac{1}{3} — \frac{1}{2} = 2 + (\frac{4}{3} — \frac{1}{2}) = 2 + \frac{4 * 2 — 1 * 3}{6} = 2 + \frac{8 — 3}{6} = 2 + \frac{5}{6} = 2\frac{5}{6}$

Задание 20. Найдите произведение или частное:
а) $\frac{9}{10} * \frac{5}{12}$;
б) $\frac{3}{5} : \frac{11}{15}$;
в) $\frac{9}{22} * \frac{2}{3}$;
г) $\frac{7}{8} : \frac{7}{16}$;
д) $\frac{27}{40} : \frac{18}{35}$;
е) $\frac{8}{9} : 6$;
ж) $15 * \frac{5}{6}$;
з) $1 : \frac{3}{7}$;
и) $\frac{2}{3} * 12$;
к) $\frac{2}{3} : 18$;
л) $\frac{8}{27} * 36$;
м) $10 : \frac{4}{15}$.

Решение

а) $\frac{9}{10} * \frac{5}{12} = \frac{9 * 5}{10 * 12} = \frac{3 * 1}{2 * 4} = \frac{3}{8}$

б) $\frac{3}{5} : \frac{11}{15} = \frac{3}{5} * \frac{15}{11} = \frac{3 * 15}{5 * 11} = \frac{3 * 3}{1 * 11} = \frac{9}{11}$

в) $\frac{9}{22} * \frac{2}{3} = \frac{9 * 2}{22 * 3} = \frac{3 * 1}{11 * 1} = \frac{3}{11}$

г) $\frac{7}{8} : \frac{7}{16} = \frac{7}{8} * \frac{16}{7} = \frac{7 * 16}{8 * 7} = \frac{1 * 2}{1 * 1} = 2$

д) $\frac{27}{40} : \frac{18}{35} = \frac{27}{40} * \frac{35}{18} = \frac{27 * 35}{40 * 18} = \frac{3 * 7}{8 * 2} = \frac{21}{16} = 1\frac{5}{16}$

е) $\frac{8}{9} : 6 = \frac{8}{9} * \frac{1}{6} = \frac{8 * 1}{9 * 6} = \frac{4 * 1}{9 * 3} = \frac{4}{27}$

ж) $15 * \frac{5}{6} = \frac{15 * 5}{6} = \frac{5 * 5}{2} = \frac{25}{2} = 12\frac{1}{2}$

з) $1 : \frac{3}{7} = 1 * \frac{7}{3} = \frac{7}{3} = 2\frac{1}{3}$

и) $\frac{2}{3} * 12 = \frac{2 * 12}{3} = \frac{2 * 4}{1} = \frac{8}{1} = 8$

к) $\frac{2}{3} : 18 = \frac{2}{3} * \frac{1}{18} = \frac{2 * 1}{3 * 18} = \frac{1 * 1}{3 * 9} = \frac{1}{27}$

л) $\frac{8}{27} * 36 = \frac{8 * 36}{27} = \frac{8 * 4}{3} = \frac{32}{3} = 10\frac{2}{3}$

м) $10 : \frac{4}{15} = 10 * \frac{15}{4} = \frac{10 * 15}{4} = \frac{5 * 15}{2} = \frac{75}{2} = 37\frac{1}{2}$

Задание 21. Пирог разделили на 6 равных частей. Одну из них разделили еще на 3 равные части. Какую часть пирога составляет одна маленькая часть? Выберите правильный ответ.
1) $\frac{1}{3}$;
2) $\frac{1}{9}$;
3) $\frac{1}{12}$;
4) $\frac{1}{18}$.

Решение

1) $1 : 6 = \frac{1}{6}$ (пирога) − составляет одна большая часть;
2) $\frac{1}{6} : 3 = \frac{1}{6} * \frac{1}{3} = \frac{1}{18}$ (пирога) − составляет одна маленькая часть.
Ответ: 4) $\frac{1}{18}$

Задание 22. Вычислите:
а) $2\frac{7}{9} * 15$;
б) $28 * 1\frac{3}{4}$;
в) $1\frac{3}{5} * 2\frac{1}{2}$;
г) $3\frac{1}{3} * \frac{3}{5}$;
д) $3\frac{1}{3} : 30$;
е) $6 : 1\frac{1}{2}$;
ж) $1\frac{3}{4} : 10\frac{1}{2}$;
з) $5\frac{1}{5} : \frac{13}{15}$.

Решение

а) $2\frac{7}{9} * 15 = \frac{25}{9} * \frac{15}{1} = \frac{25 * 5}{3 * 1} = \frac{125}{3} = 41\frac{2}{3}$

б) $28 * 1\frac{3}{4} = \frac{28}{1} * \frac{7}{4} = \frac{28 * 7}{1 * 4} = \frac{7 * 7}{1 * 1} = \frac{49}{1} = 49$

в) $1\frac{3}{5} * 2\frac{1}{2} = \frac{8}{5} * \frac{5}{2} = \frac{8 * 5}{5 * 2} = \frac{4 * 1}{1 * 1} = \frac{4}{1} = 4$

г) $3\frac{1}{3} * \frac{3}{5} = \frac{10}{3} * \frac{3}{5} = \frac{10 * 3}{3 * 5} = \frac{2 * 1}{1 * 1} = \frac{2}{1} = 2$

д) $3\frac{1}{3} : 30 = \frac{10}{3} * \frac{1}{30} = \frac{10 * 1}{3 * 30} = \frac{10 * 1}{3 * 30} = \frac{1 * 1}{3 * 3} = \frac{1}{9}$

е) $6 : 1\frac{1}{2} = \frac{6}{1} : \frac{3}{2} = \frac{6}{1} * \frac{2}{3} = \frac{6 * 2}{1 * 3} = \frac{2 * 2}{1 * 1} = \frac{4}{1} = 4$

ж) $1\frac{3}{4} : 10\frac{1}{2} = \frac{7}{4} : \frac{21}{2} = \frac{7}{4} * \frac{2}{21} = \frac{7 * 2}{4 * 21} = \frac{1 * 1}{2 * 3} = \frac{1}{6}$

з) $5\frac{1}{5} : \frac{13}{15} = \frac{26}{5} : \frac{13}{15} = \frac{26}{5} * \frac{15}{13} = \frac{26 * 15}{5 * 13} = \frac{2 * 3}{1 * 1} = \frac{6}{1} = 6$

Задание 23. Найдите значение степени:
$(\frac{3}{4})^2$;
$(\frac{2}{3})^3$;
$(1\frac{1}{2})^3$;
$(2\frac{1}{2})^2$.

Решение

$(\frac{3}{4})^2 = \frac{3}{4} * \frac{3}{4} = \frac{3 * 3}{4 * 4} = \frac{9}{16}$;
$(\frac{2}{3})^3 = \frac{2}{3} * \frac{2}{3} * \frac{2}{3} = \frac{2 * 2 * 2}{3 * 3 * 3} = \frac{8}{27}$;
$(1\frac{1}{2})^3 = (\frac{3}{2})^3 = \frac{3}{2} * \frac{3}{2} * \frac{3}{2} = \frac{3 * 3 * 3}{2 * 2 * 2} = \frac{27}{8} = 3\frac{3}{8}$;
$(2\frac{1}{2})^2 = (\frac{5}{2})^2 = \frac{5}{2} * \frac{5}{2} = \frac{5 * 5}{2 * 2} = \frac{25}{4} = 6\frac{1}{4}$.

Задание 24. Выполните действия:
а) $\frac{9 * 7 * 5}{10 * 8 * 6}$;
б) $\frac{17 * 26 * 8}{13 * 51 * 9}$;
в) $\frac{3}{25} * \frac{5}{6} * \frac{10}{9}$;
г) $8 * \frac{9}{16} * \frac{7}{12}$;
д) $\frac{3}{8} * \frac{2}{15} : \frac{7}{20}$;
е) $\frac{4}{9} : \frac{8}{9} * \frac{10}{7}$.

Решение

а) $\frac{9 * 7 * 5}{10 * 8 * 6} = \frac{3 * 7 * 1}{2 * 8 * 2} = \frac{21}{32}$

б) $\frac{17 * 26 * 8}{13 * 51 * 9} = \frac{1 * 2 * 8}{1 * 3 * 9} = \frac{16}{27}$

в) $\frac{3}{25} * \frac{5}{6} * \frac{10}{9} = \frac{3 * 5 * 10}{25 * 6 * 9} = \frac{1 * 1 * 10}{5 * 2 * 9} = \frac{1}{9}$

г) $8 * \frac{9}{16} * \frac{7}{12} = \frac{8 * 9 * 7}{1 * 16 * 12} = \frac{1 * 3 * 7}{2 * 4} = \frac{21}{8} = 2\frac{5}{8}$

д) $\frac{3}{8} * \frac{2}{15} : \frac{7}{20} = \frac{3}{8} * \frac{2}{15} * \frac{20}{7} = \frac{3 * 2 * 20}{8 * 15 * 7} = \frac{1 * 1 * 20}{4 * 5 * 7} = \frac{5}{5 * 7} = \frac{1}{7}$

е) $\frac{4}{9} : \frac{8}{9} * \frac{10}{7} = \frac{4}{9} * \frac{9}{8} * \frac{10}{17} = \frac{4 * 9 * 10}{9 * 8 * 17} = \frac{1 * 1 * 10}{1 * 2 * 17} = \frac{5}{1 * 17} = \frac{5}{17}$

7gy.ru

Страница 71 ГДЗ к учебнику «Математика» 6 класс Дорофеев, Шарыгин

Продолжение ответов к теме «Чему вы научились, стр. 71. Начало на стр. 70

Задание 3. 1) Представьте в виде обыкновенной дроби:
а) 0,7;
б) 1,23;
в) 0,085.
2) запишите в виде десятичной дроби:
а) $\frac{27}{100}$;
б) $4\frac{39}{1000}$;
в) $\frac{305}{100}$.

Ответы 7 гуру

1) а) $0,7 = \frac{7}{10}$;
   б) $1,23 = 1\frac{23}{100}$;
   в) $0,085 = \frac{85}{1000} = \frac{17}{200}$.

2) а) $\frac{27}{100} = 0,27$;
   б) $4\frac{39}{1000} = 4,039$;
   в) $\frac{305}{100} = 3,05$.

Задание 4. Представьте в виде десятичных дробей числа, для которых это возможно:
$\frac{1}{2}; \frac{1}{3}; \frac{3}{4}; \frac{2}{5}; \frac{5}{6}; \frac{1}{8}; \frac{3}{20}; \frac{4}{25}; \frac{1}{30}; \frac{7}{50}$.

Ответы

$\frac{1}{2} = \frac{5}{10} = 0,5$;
$\frac{1}{3}$ − нельзя представить;
$\frac{3}{4} = \frac{75}{100} = 0,75$;
$\frac{2}{5} = \frac{4}{10} = 0,4$;
$\frac{5}{6}$ − нельзя представить;
$\frac{1}{8} = \frac{125}{1000} = 0,125$;
$\frac{3}{20} = \frac{15}{100} = 0,15$;
$\frac{4}{25} = \frac{16}{100} = 0,16$;
$\frac{1}{30}$ − нельзя представить;
$\frac{7}{50} = \frac{14}{100} = 0,14$.

Задание 5. Сравните числа:
а) 1,001 и 0,999;
б) 8,54 и 8,455;
в) 0,305 и 0,3050.

Ответ

а) 1,001 > 0,999

б) 8,54 > 8,455

в) 0,305 = 0,3050

Задание 6. Запишите в порядке возрастания десятичные дроби:
0,28;
0,218;
0,281.

Ответ

0,218 < 0,28 < 0,281

Задание 7. Умею сравнивать десятичную дробь и обыкновенную.
Сравните числа:
а) 0,2 и $\frac{1}{3}$;
б) $\frac{1}{4}$ и 0,3.

Решение

а) $0,2 = \frac{2}{10} = \frac{1}{5} = \frac{3}{15}$;
$\frac{1}{3} = \frac{5}{15}$;
$\frac{3}{15} < \frac{5}{15}$;
$0,2 < \frac{1}{3}$.

б) $\frac{1}{4} = \frac{25}{100}$;
$0,3 = \frac{3}{10} = \frac{30}{100}$;
$\frac{25}{100} < \frac{30}{100}$;
$\frac{1}{4} < 0,3$.

Задание 8. Выразите:
а) 6 м 37 см в метрах;
б) 150 м в километрах;
в) 1040 г в килограммах.

Ответы

а) 6 м 37 см = 6,37 м

б) 150 м = 0,15 км

в) 1040 г = 1,04 кг

Задание 9. Выразите:
а) 3,8 см в сантиметрах и миллиметрах;
б) 4,05 кг в килограммах и граммах.

Решение

а) 3,8 см = 3 см 8 мм

б) 4,05 кг = 4 кг 50 г

7gy.ru