Рабочая программа по математике, 6 класс, ФГОС, УМК Н. Я. Виленкина
Управление образования администрации
Амурского муниципального района Хабаровского края
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 9
г. Амурска Амурского муниципального района Хабаровского края
|
СОГЛАСОВАНО Заместитель директора по УВР _________/________________ «____»____________ 20____г. |
|
УТВЕРЖДЕНА Приказом директора учреждения от ___________г. №_____ |
Рабочая программа
по математике
6 класс
Разработала:
Пономарева И. А.,
А.,
учитель математики
высшей квалификационной категории
2018 год
Пояснительная записка
Рабочая программа по математике разработана на основе ФГОС ООО, требований к результатам освоения основной образовательной программы основного общего образования муниципального бюджетного общеобразовательного учреждения средней общеобразовательной школы №9 г. Амурска Амурского муниципального района Хабаровского края с учётом Примерной программы основного общего образования по математике, и с учетом авторской программы по математике Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд – сборник рабочих программ 5-6 классы (составитель В. И. Жохов) – 2-е изд., стер. М.:Мнемозина, 2010
Общие цели учебного предмета.
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
систематическое развитие понятия числа;
выработка умений выполнять устно и письменно арифметические действия над числами, переводить практические задачи на язык математики; подготовка обучающихся к изучению систематических курсов алгебры и геометрии.
В ходе изучения курса учащиеся развивают навыки вычислений с натуральными числами, овладевают навыками действий с обыкновенными и десятичными дробями, получают начальные преставления об использовании букв для записи выражений и свойств арифметических действий, составлении уравнений, продолжают знакомство с геометрическими понятиями, приобретают навыки построения геометрических фигур и измерения геометрических величин.
Усвоенные знания и способы действий необходимы не только для дальнейшего успешного изучения математики и других школьных дисциплин, но и для решения многих практических задач во взрослой жизни.
Согласно учебному плану на изучение математики отводится в 6 классе 170 часов в год. Количество контрольных работ – 14.
Количество контрольных работ – 14.
Рабочая программа ориентирована на УМК Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд, «Математика, 6» рекомендованного Министерством образования и науки Российской Федерации – М.:Мнемозина, 2012
Срок реализации рабочей программы 1 год.
Планируемые результаты изучения учебного предмета, курса
В ходе преподавания математики в 6 классе, работы над формированием у обучающихся перечисленных в программе знаний и умений следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
Программа обеспечивает достижение обучающимися следующих личностных, метапредметных и предметных результатов.
Личностные результаты
Чувство гордости за свою Родину, российский народ и историю России;
Осознание роли своей страны в мировом развитии, уважительное отношение к семейным ценностям, бережное отношение к окружающему миру.
Целостное восприятие окружающего мира.
Развитую мотивацию учебной деятельности и личностного смысла учения, заинтересованность в приобретении и расширении знаний и способов действий, творческий подход к выполнению заданий.
Рефлексивную самооценку, умение анализировать свои действия и управлять ими.
Навыки сотрудничества со взрослыми и сверстниками.
Установку на здоровый образ жизни, наличие мотивации к творческому труду, к работе на результат.
Метапредметные результаты
Способность принимать и сохранять цели и задачи учебной деятельности, находить средства и способы её осуществления.
Овладение способами выполнения заданий творческого и поискового характера.
Умения планировать, контролировать и оценивать учебные действия в соответствии с поставленной задачей и условиями её выполнения, определять наиболее эффективные способы достижения результата.
Способность использовать знаково-символические средства представления информации для создания моделей изучаемых объектов и процессов, схем решения учебно-познавательных и практических задач.
Использование речевых средств и средств информационных и коммуникационных технологий для решения коммуникативных и познавательных задач.
Овладение логическими действиями сравнения, анализа, синтеза, обобщения, классификации по родовидовым признакам, установления
аналогий и причинно-следственных связей, построения рассуждений, отнесения к известным понятиям.
Готовность слушать собеседника и вести диалог; готовность признать возможность существования различных точек зрения и права каждого иметь свою; излагать своё мнение и аргументировать свою точку зрения.
Определение общей цели и путей её достижения: умение договариваться о распределении функций и ролей в совместной деятельности, осуществлять взаимный контроль в совместной деятельности, адекватно оценивать собственное поведение и поведение окружающих.
Овладение начальными сведениями о сущности и особенностях объектов и процессов в соответствии с содержанием учебного предмета «математика».
Овладение базовыми предметными и межпредметными понятиями, отражающими существенные связи и отношения между объектами и процессами.
Предметные результаты
Использование приобретённых математических знаний для описания и объяснения окружающих предметов, процессов, явлений, а также для
оценки их количественных и пространственных отношений.
Овладение основами логического и алгоритмического мышления,
пространственного воображения и математической речи, основами счёта, измерения, прикидки результата и его оценки, наглядного представления данных в разной форме (таблицы, схемы, диаграммы), записи и выполнения алгоритмов.
Умения выполнять устно и письменно арифметические действия с числами и числовыми выражениями, решать текстовые задачи, выполнять и строить алгоритмы и стратегии в игре, исследовать, распознавать и изображать геометрические фигуры, работать с таблицами, схемами, графиками и диаграммами, цепочками, представлять, анализировать и интерпретировать данные.
Приобретение первоначальных навыков работы на компьютере (набирать текст на клавиатуре, работать с меню, находить информацию по заданной теме, распечатывать её на принтере).
В результате изучения курса математики 6 класса учащиеся должны:
знать/понимать
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения; примеры их применения для решения математических и практических задач;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
уметь
выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;
переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты — в виде дроби и дробь — в виде процентов;
выполнять арифметические действия с рациональными числами, находить значения числовых выражений;
округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и с избытком, выполнять оценку числовых выражений;
пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;
решать текстовые задачи, включая задачи, связанные дробями и процентами;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера;
устной прикидки и оценки результата вычислений; проверки результата вычисления с использованием различных приемов;
интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений.
Содержание учебного предмета, курса
Делимость чисел (20 ч)
Делители и кратные. Признаки делимости на 2, 3, 5, 9, 10. Простые и составные числа. Разложение числа на простые множители. Наибольший общий делитель. Наименьшее общее кратное.
Основная цель — завершить изучение натуральных чисел, подготовить основу для освоения действий с обыкновенными дробями.
В данной теме завершается изучение вопросов, связанных с натуральными числами. Основное внимание должно быть уделено знакомству с понятиями «делитель» и «кратное», которые находят применение при сокращении обыкновенных дробей и при их приведении к общему знаменателю. Упражнения полезно выполнять с опорой на таблицу умножения прямым подбором. Понятия «наибольший общий делитель» и «наименьшее общее кратное» вместе с алгоритмами их нахождения можно не рассматривать.
Определенное внимание уделяется знакомству с признаками делимости, понятиям простого и составного чисел. При их изучении целесообразно формировать умения проводить простейшие умозаключения, обосновывая свои действия ссылками на определение, правило.
При их изучении целесообразно формировать умения проводить простейшие умозаключения, обосновывая свои действия ссылками на определение, правило.
Учащиеся должны уметь разложить число на множители. Вопрос о разложении числа на простые множители не относится к числу обязательных.
Сложение и вычитание дробей с разными знаменателями (22 ч)
Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю. Сравнение дробей. Сложение и вычитание чисел с разными знаменателями.
Основная цель — выработать прочные навыки преобразования дробей, сложения и вычитания дробей.
Одним из важнейших результатов обучения является усвоение основного свойства дроби, применяемого для преобразования дробей: сокращения, приведения к новому знаменателю. При этом рекомендуется излагать материал без опоры на понятия НОД и НОК. Умение приводить дроби к общему знаменателю используется для сравнения дробей.
При рассмотрении действий с дробями используются правила сложения и вычитания дробей с одинаковыми знаменателями, понятие смешанного числа. Важно обратить внимание на случай вычитания дроби из целого числа. Что касается сложения и вычитания смешанных чисел, которые не находят активного применения в последующем изучении курса, то учащиеся должны лишь получить представление о принципиальной возможности выполнения таких действий.
Умножение и деление обыкновенных дробей (31 ч)
Умножение дробей. Взаимно обратные числа. Деление дробей. Нахождение части числа и числа по его части.
Основная цель — выработать прочные навыки арифметических действий с обыкновенными дробями и решения основных задач на дроби.
В этой теме завершается работа над формированием навыков арифметических действий с обыкновенными дробями. Навыки должны быть достаточно прочными, чтобы учащиеся не испытывали затруднений в вычислениях с рациональными числами, чтобы алгоритмы действий с обыкновенными дробями могли стать в дальнейшем опорой для формирования умений выполнять действия с алгебраическими дробями.
Расширение аппарата действий с дробями позволяет решать текстовые задачи, в которых требуется найти дробь от числа или число по данному значению его дроби, выполняя соответственно умножение или деление на дробь.
Отношения и пропорции (18 ч)
Отношения. Пропорции. Основное свойство пропорции. Прямая и обратная пропорциональная зависимость. Масштаб, Длина окружности. Площадь круга. Шар
Основная цель — сформировать понятия пропорции, прямой и обратной пропорциональностей величин.
Необходимо, чтобы учащиеся усвоили основное свойство пропорции, так как оно находит применение на уроках математики, химии, физики. В частности, достаточное внимание должно быть уделено решению с помощью пропорции задач на проценты.
Понятия о прямой и обратной пропорциональностях величин можно сформировать как обобщение нескольких конкретных примеров, подчеркнув при этом практическую значимость этих понятий, возможность их применения для упрощения решения соответствующих задач.
В данной теме даются представления о длине окружности и площади круга. Соответствующие формулы к обязательному материалу не относятся. Рассмотрение геометрических фигур завершается знакомством с шаром.
Положительные и отрицательные числа (13 ч)
Положительные и отрицательные числа. Противоположные числа. Модуль числа. Целые числа. Изображение чисел точками координатной прямой. Координаты точки. Сравнение чисел. Изменение величин.
Основная цель — расширить представления учащихся о числе путем введения отрицательных чисел.
Целесообразность введения отрицательных чисел показывается на содержательных примерах. Учащиеся должны научиться изображать положительные и отрицательные числа на координатной прямой, с тем чтобы она могла служить наглядной основой для правил сравнения чисел, сложения и вычитания чисел, рассматриваемых в следующей теме.
Специальное внимание должно быть уделено усвоению вводимого здесь понятия модуля числа, прочное знание которого необходимо для формирования умения сравнивать отрицательные числа, а в дальнейшем для овладения и алгоритмами арифметических действий с положительными и отрицательными числами.
Сложение и вычитание положительных и отрицательных чисел (11 ч)
Сложение положительных и отрицательных чисел; вычитание положительных и отрицательных чисел. Свойства арифметических действий.
Основная цель — выработать прочные навыки сложения и вычитания положительных и отрицательных чисел.
Действия с отрицательными числами вводятся на основе представлений об изменении величин: сложение и вычитание чисел иллюстрируется соответствующими перемещениями точек числовой оси. При изучении данной темы целенаправленно отрабатываются алгоритмы сложения и вычитания при выполнении действий с целыми и дробными числами.
Умножение и деление положительных и отрицательных чисел (12 ч)
Умножение положительных и отрицательных чисел. Свойства умножения. Деление положительных и отрицательных чисел. Рациональные числа. Десятичное приближение обыкновенной дроби. Периодическая дробь. Свойства действий с рациональными числами.
Основная цель — выработать прочные навыки арифметических действий с положительными и отрицательными числами.
Навыки умножения и деления положительных и отрицательных чисел отрабатываются сначала при выполнении отдельных действий, а затем в сочетании с навыками сложения и вычитания при вычислении значений числовых выражений.
При изучении данной темы учащиеся должны усвоить, что для обращения обыкновенной дроби в десятичную достаточно разделить числитель на знаменатель. В каждом конкретном случае они должны знать, в какую десятичную дробь обращается данная обыкновенная дробь — конечную или бесконечную. При этом необязательно акцентировать внимание на том, что бесконечная десятичная дробь оказывается периодической.
При этом необязательно акцентировать внимание на том, что бесконечная десятичная дробь оказывается периодической.
Решение уравнений (15 ч)
Раскрытие скобок. Коэффициент. Приведение подобных слагаемых. Уравнение. Корень уравнения. Решение линейных уравнений. Нахождение неизвестных компонентов арифметических действий.
Основная цель — подготовить учащихся к выполнению преобразований выражений, решению уравнений.
Преобразования буквенных выражений путем раскрытия скобок и приведения подобных слагаемых отрабатываются в той степени, в которой они необходимы для решения несложных уравнений.
Введение арифметических действий над отрицательными числами позволяет ознакомить учащихся с общими приемами решения линейных уравнений с одним неизвестным.
Координаты на плоскости (13 ч)
Построение перпендикуляра к прямой и параллельных прямых с помощью угольника и линейки. Прямоугольная система координат на плоскости, абсцисса и ордината точки. Примеры графиков, диаграмм.
Прямоугольная система координат на плоскости, абсцисса и ордината точки. Примеры графиков, диаграмм.
Основная цель — познакомить учащихся с прямоугольной системой координат на плоскости.
Учащиеся должны научиться распознавать и изображать перпендикулярные и параллельные прямые. Основное внимание следует уделить отработке навыков их построения с помощью линейки и угольника, не требуя воспроизведения точных определений.
Основным результатом знакомства учащихся с координатной плоскостью должны явиться знания порядка записи координат точек плоскости и их названий, умения построить координатные оси, отметить точку по заданным ее координатам, определить координаты точки, отмеченной на координатной плоскости.
Формированию вычислительных и графических умений способствует построение столбчатых диаграмм. При выполнении соответствующих упражнений найдут применение изученные ранее сведения о масштабе и округлении чисел.
Повторение. Решение задач (15 ч)
Повторение, обобщение и систематизация знаний, умений и навыков за курс математики 6 класса.
Тематическое планирование
|
№ раздела п/п |
Название темы раздела |
Всего часов |
Из них |
||||
|
Теория |
Контрольные работы |
||||||
|
1 |
Обыкновенные дроби |
91 |
83 |
8 |
|||
|
2 |
Рациональные числа |
64 |
58 |
6 |
|||
|
3 |
Повторение. |
15 |
14 |
1 |
|||
|
Итого |
170 |
155 |
15 |
||||
Календарно – тематическое планирование
|
№ п/п |
Дата |
Тема урока |
Кол-во часов |
Примечание Причина корректировки |
|
|
план |
факт |
||||
|
Раздел I. |
|||||
|
п. 1. Делимость чисел – 20 часов |
|||||
|
1 |
Делители и кратные |
1 |
|||
|
2 |
Делители и кратные |
1 |
|||
|
3 |
Делители и кратные |
1 |
|||
|
4 |
Признаки делимости на 10, на 5 и на 2 |
1 |
|||
|
5 |
Признаки делимости на 10, на 5 и на 2 |
1 |
|||
|
6 |
Признаки делимости на 10, на 5 и на 2 |
1 |
|||
|
7 |
Признаки делимости на 9 и на 3 |
1 |
|||
|
8 |
Признаки делимости на 9 и на 3 |
1 |
|||
|
9 |
Простые и составные числа |
1 |
|||
|
10 |
Простые и составные числа |
1 |
|||
|
11 |
Разложение на простые множители |
1 |
|||
|
12 |
Разложение на простые множители |
1 |
|||
|
13 |
Наибольший общий делитель. |
1 |
|||
|
14 |
Наибольший общий делитель. Взаимно простые числа |
1 |
|||
|
15 |
Наибольший общий делитель. Взаимно простые числа |
1 |
|||
|
16 |
Наименьшее общее кратное |
1 |
|||
|
17 |
Наименьшее общее кратное |
1 |
|||
|
18 |
Наименьшее общее кратное |
1 |
|||
|
19 |
Наименьшее общее кратное |
1 |
|||
|
20 |
Контрольная работа №1 по теме «Делимость чисел» |
1 |
|||
|
п. |
|||||
|
21 |
Анализ контрольной работы №1. Основное свойство дроби |
1 |
|||
|
22 |
Основное свойство дроби |
1 |
|||
|
23 |
Сокращение дробей |
1 |
|||
|
24 |
Сокращение дробей |
1 |
|||
|
25 |
Сокращение дробей |
1 |
|||
|
26 |
Приведение дробей к общему знаменателю |
1 |
|||
|
27 |
Приведение дробей к общему знаменателю |
1 |
|||
|
28 |
Приведение дробей к общему знаменателю |
1 |
|||
|
29 |
Сравнение, сложение и вычитание дробей с разными знаменателями |
1 |
|||
|
30 |
Сравнение, сложение и вычитание дробей с разными знаменателями |
1 |
|||
|
31 |
Сравнение, сложение и вычитание дробей с разными знаменателями |
1 |
|||
|
32 |
Сравнение, сложение и вычитание дробей с разными знаменателями |
1 |
|||
|
33 |
Сравнение, сложение и вычитание дробей с разными знаменателями |
1 |
|||
|
34 |
Сравнение, сложение и вычитание дробей с разными знаменателями |
1 |
|||
|
35 |
Контрольная работа №2 по теме «Сравнение, сложение и вычитание дробей с разными знаменателями» |
1 |
|||
|
36 |
Анализ контрольной работы №2. Сложение и вычитание смешанных чисел |
1 |
|||
|
37 |
Сложение и вычитание смешанных чисел |
1 |
|||
|
38 |
Сложение и вычитание смешанных чисел |
1 |
|||
|
39 |
Сложение и вычитание смешанных чисел |
1 |
|||
|
40 |
Сложение и вычитание смешанных чисел |
1 |
|||
|
41 |
Сложение и вычитание смешанных чисел |
1 |
|||
|
42 |
Контрольная работа №3 по теме «Числовые и буквенные выражения» |
1 |
|||
|
п. |
|||||
|
43 |
Анализ контрольной работы №3. Умножение дробей |
1 |
|||
|
44 |
Умножение дробей |
1 |
|||
|
45 |
Умножение дробей |
1 |
|||
|
46 |
Умножение дробей |
1 |
|||
|
47 |
Умножение дробей |
1 |
|||
|
48 |
Нахождение дроби от числа |
1 |
|||
|
49 |
Нахождение дроби от числа |
1 |
|||
|
50 |
Нахождение дроби от числа |
1 |
|||
|
51 |
Нахождение дроби от числа |
1 |
|||
|
52 |
Применение распределительного свойства умножения |
1 |
|||
|
53 |
Применение распределительного свойства умножения |
1 |
|||
|
54 |
Применение распределительного свойства умножения |
1 |
|||
|
55 |
Применение распределительного свойства умножения |
1 |
|||
|
56 |
Применение распределительного свойства умножения |
1 |
|||
|
57 |
Контрольная работа №4 по теме «Умножение обыкновенных дробей» |
1 |
|||
|
58 |
Анализ контрольной работы №4. Взаимно обратные числа |
1 |
|||
|
59 |
Взаимно обратные числа |
1 |
|||
|
60 |
Деление |
1 |
|||
|
61 |
Деление |
1 |
|||
|
62 |
Деление |
1 |
|||
|
63 |
Деление |
1 |
|||
|
64 |
Деление |
1 |
|||
|
65 |
Контрольная работа №5 по теме «Деление обыкновенных дробей» |
1 |
|||
|
66 |
Анализ контрольной работы №5. Нахождение числа по его дроби |
1 |
|||
|
67 |
Нахождение числа по его дроби |
1 |
|||
|
68 |
Нахождение числа по его дроби |
1 |
|||
|
69 |
Нахождение числа по его дроби |
1 |
|||
|
70 |
Дробные выражения |
1 |
|||
|
71 |
Дробные выражения |
1 |
|||
|
72 |
Дробные выражения |
1 |
|||
|
73 |
Контрольная работа №6 по теме «Умножение и деление обыкновенных дробей» |
1 |
|||
|
п. |
|||||
|
74 |
Анализ контрольной работы №6 Отношения |
1 |
|||
|
75 |
Отношения |
1 |
|||
|
76 |
Отношения |
1 |
|||
|
77 |
Отношения |
1 |
|||
|
78 |
Отношения |
1 |
|||
|
79 |
Пропорции |
1 |
|||
|
80 |
Пропорции |
1 |
|||
|
81 |
Пропорции |
1 |
|||
|
82 |
Прямая и обратная пропорциональные зависимости |
1 |
|||
|
83 |
Прямая и обратная пропорциональные зависимости |
1 |
|||
|
84 |
Прямая и обратная пропорциональные зависимости |
1 |
|||
|
85 |
Контрольная работа №7 по теме «Отношения и пропорции» |
1 |
|||
|
86 |
Анализ контрольной работы № 7 Масштаб |
1 |
|||
|
87 |
Масштаб |
1 |
|||
|
88 |
Длина окружности и площадь круга |
1 |
|||
|
89 |
Длина окружности и площадь круга |
1 |
|||
|
90 |
Шар |
1 |
|||
|
91 |
Контрольная работа №8 по теме «Длина окружности и площадь круга» |
1 |
|||
|
Раздел II. |
|||||
|
п.5. Положительные и отрицательные числа – 13 часов |
|||||
|
92 |
Анализ контрольной работы № 7 Координаты на прямой |
1 |
|||
|
93 |
Координаты на прямой |
1 |
|||
|
94 |
Координаты на прямой |
1 |
|||
|
95 |
Противоположные числа |
1 |
|||
|
96 |
Противоположные числа |
1 |
|||
|
97 |
Модуль числа |
1 |
|||
|
98 |
Модуль числа |
1 |
|||
|
99 |
Сравнение чисел |
1 |
|||
|
100 |
Сравнение чисел |
1 |
|||
|
101 |
Сравнение чисел |
1 |
|||
|
102 |
Изменение величин |
1 |
|||
|
103 |
Изменение величин |
1 |
|||
|
104 |
Контрольная работа №9 по теме «Положительные и отрицательные числа» |
1 |
|||
|
п. |
|||||
|
105 |
Анализ контрольной работы №9. Сложение чисел с помощью координатной прямой |
1 |
|||
|
106 |
Сложение чисел с помощью координатной прямой |
1 |
|||
|
107 |
Сложение отрицательных чисел |
1 |
|||
|
108 |
Сложение отрицательных чисел |
1 |
|||
|
109 |
Сложение чисел с разными знаками |
1 |
|||
|
110 |
Сложение чисел с разными знаками |
1 |
|||
|
111 |
Сложение чисел с разными знаками |
1 |
|||
|
112 |
Вычитание |
1 |
|||
|
113 |
Вычитание |
1 |
|||
|
114 |
Вычитание |
1 |
|||
|
115 |
Контрольная работа №10 по теме «Сложение и вычитание положительных и отрицательных чисел» |
1 |
|||
|
п. |
|||||
|
116 |
Анализ контрольной работы № 10 Умножение |
1 |
|||
|
117 |
Умножение |
1 |
|||
|
118 |
Умножение |
1 |
|||
|
119 |
Деление |
1 |
|||
|
120 |
Деление |
1 |
|||
|
121 |
Деление |
1 |
|||
|
122 |
Рациональные числа |
1 |
|||
|
123 |
Рациональные числа |
1 |
|||
|
124 |
Контрольная работа №11 по теме «Умножение и деление положительных и отрицательных чисел» |
1 |
|||
|
125 |
Анализ контрольной работы №11 Свойства действий с рациональными числами |
1 |
|||
|
126 |
Свойства действий с рациональными числами |
1 |
|||
|
127 |
Свойства действий с рациональными числами |
1 |
|||
|
п. |
|||||
|
128 |
Раскрытие скобок |
1 |
|||
|
129 |
Раскрытие скобок |
1 |
|||
|
130 |
Раскрытие скобок |
1 |
|||
|
131 |
Коэффициент |
1 |
|||
|
132 |
Коэффициент |
1 |
|||
|
133 |
Подобные слагаемые |
1 |
|||
|
134 |
Подобные слагаемые |
1 |
|||
|
135 |
Подобные слагаемые |
1 |
|||
|
136 |
Контрольная работа №12 по теме «Раскрытие скобок. |
1 |
|||
|
137 |
Анализ контрольной работы №12. Решение уравнений |
1 |
|||
|
138 |
Решение уравнений |
1 |
|||
|
139 |
Решение уравнений |
1 |
|||
|
140 |
Решение уравнений |
1 |
|||
|
141 |
Решение уравнений |
1 |
|||
|
142 |
Контрольная работа №13 по теме «Решение уравнений» |
1 |
|||
|
п. |
|||||
|
143 |
Анализ контрольной работы №13 Перпендикулярные прямые |
1 |
|||
|
144 |
Перпендикулярные прямые |
1 |
|||
|
145 |
Параллельные прямые |
1 |
|||
|
146 |
Параллельные прямые |
1 |
|||
|
147 |
Координатная плоскость |
1 |
|||
|
148 |
Координатная плоскость |
1 |
|||
|
149 |
Координатная плоскость |
1 |
|||
|
150 |
Столбчатые диаграммы |
1 |
|||
|
151 |
Столбчатые диаграммы |
1 |
|||
|
152 |
Графики |
1 |
|||
|
153 |
Графики |
1 |
|||
|
154 |
Графики |
1 |
|||
|
155 |
Контрольная работа №14 по теме «Координаты на плоскости» |
1 |
|||
|
Раздел III. |
|||||
|
156 |
Анализ контрольной работы №14 Повторение по теме «Обыкновенные дроби» |
1 |
|||
|
157 |
Повторение по теме «Обыкновенные дроби» |
1 |
|||
|
158 |
Повторение по теме «Обыкновенные дроби» |
1 |
|||
|
159 |
Повторение по теме «Рациональные числа» |
1 |
|||
|
160 |
Повторение по теме «Рациональные числа» |
1 |
|||
|
161 |
Повторение по теме «Рациональные числа» |
1 |
|||
|
162 |
Повторение по теме «Рациональные числа» |
1 |
|||
|
163 |
Повторение по теме «Рациональные числа» |
1 |
|||
|
164 |
Повторение по теме «Рациональные числа» |
1 |
|||
|
165 |
Контрольная работа №15 (итоговая) |
1 |
|||
|
166 |
Анализ контрольной работы №15 Повторение по теме «Проценты. |
1 |
|||
|
167 |
Повторение по теме «Проценты. Решение задач на проценты» |
1 |
|||
|
168 |
Повторение по теме «Проценты. Решение задач на проценты» |
1 |
|||
|
169 |
Повторение по теме «Проценты. Решение задач на проценты» |
1 |
|||
|
170 |
Заключительный урок |
1 |
|||
Страница 14 №61-67 ГДЗ к учебнику «Математика» 6 класс Виленкин, Жохов, Чесноков
Решебник к теме 3.
 Признаки делимости на 9 и на 3
Признаки делимости на 9 и на 3
Задание № 61. Какие из чисел 75432, 2772825, 5402070 делятся на 3? Какие из них делятся на 9?
Решение
Сумма чисел: 7 + 5 + 4 + 3 + 2 = 21 делится на 3, следовательно и число 75432 делится на 3;
2 + 7 + 7 + 2 + 8 + 2 + 5 = 33 делится на 3, и число 2772825 делится на 3;
5 + 4 + 0 + 2 + 0 + 7 + 0 = 18 делится на 3 и на 9, а следовательно число 5402070 делится на 3 и на 9.
Задание № 62. Запишите какие−нибудь три четырёхзначных числа, которые делятся на 9.
Ответ 7 гуру
1116, 2223, 8001.
Задание № 63. Какие цифры следует поставить вместо звёздочек в записи 25, 46, *14, чтобы получившиеся числа делились на 3?
Ответ
2*5 − 225, 255, 285;
46* − 462, 465, 468;
*14 − 114, 414, 714.
Задание № 64. Напишите три числа, записанные только с помощью:
а) цифры 1, которые делятся на 3;
б) цифры 6, которые делятся на 9.
Ответ
а) 111, 111111, 111111111.
б) 666, 666666, 666666666.
Задание № 65. Любое ли число, которое оканчивается цифрой 3, делится на 3?
Ответ
Нет. Например 13, 23 не делятся на 3.
Задание № 66. Мама принесла детям три одинаковых подарка. Может ли быть, что во всех подарках было 25 конфет? 75 конфет? 63 конфеты?
Решение
В подарках может быть только 75 (7 + 5 = 12) или 63 (6 + 3 = 9) конфеты, так как эти числа делятся на 3.
Задание № 67. В каждом стойле коровника 9 коров. Может ли быть, что всего в коровнике 542 коровы? 288 коров?
Решение
В коровнике может быть только 288 (2 + 8 + 8 = 18) коров, так как это число делится на 9.
Поурочные разработки по Математике 6 класс
ГЛАВА I. ОБЫКНОВЕННЫЕ ДРОБИ
§ 1. ДЕЛИМОСТЬ ЧИСЕЛ (20 ч)
ДЕЛИМОСТЬ ЧИСЕЛ (20 ч)
ДЕЛИТЕЛИ И КРАТНЫЕ (3 ч)
Урок 1. Делители и кратные
Урок 2. Делители и кратные
Урок 3. Делители и кратные
ПРИЗНАКИ ДЕЛИМОСТИ НА 10, НА 5, НА 2 (3 ч)
Урок 4. Признаки делимости на 10, на 5, на 2
Урок 5. Признаки делимости на 10, на 5, на 2
Урок 6. Признаки делимости на 10, на 5, на 2
ПРИЗНАКИ ДЕЛИМОСТИ НА 9 И НА 3 (2 ч)
Урок 7. Признаки делимости на 9 и на 3
Урок 8. Признаки делимости на 9 и на 3
ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА (2 ч)
Урок 9. Простые и составные числа
Урок 10. Простые и составные числа
РАЗЛОЖЕНИЕ НА ПРОСТЫЕ МНОЖИТЕЛИ (2 ч)
Урок 11. Разложение на простые множители
Урок 12. Разложение на простые множители
НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ. ВЗАИМНО ПРОСТЫЕ ЧИСЛА (3 ч)
Урок 13. Наибольший общий делитель
Урок 14. Наибольший общий делитель. Взаимно простые числа
Урок 15. Наибольший общий делитель. Взаимно простые числа
НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ (4 ч)
Урок 16. Наименьшее общее кратное
Наименьшее общее кратное
Урок 17. Наименьшее общее кратное
Урок 18. Наименьшее общее кратное
Урок 19. Наименьшее общее кратное
Урок 20. Контрольная работа № 1
§ 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ (22 ч)
ОСНОВНОЕ СВОЙСТВО ДРОБИ (2 ч)
Урок 21. Основное свойство дроби
Урок 22. Основное свойство дроби
СОКРАЩЕНИЕ ДРОБЕЙ (3 ч)
Урок 23. Сокращение дробей
Урок 24. Сокращение дробей
Урок 25. Сокращение дробей
ПРИВЕДЕНИЕ ДРОБЕЙ К ОБЩЕМУ ЗНАМЕНАТЕЛЮ (3 ч)
Урок 26. Приведение дробей к общему знаменателю
Урок 27. Приведение дробей к общему знаменателю
Урок 28. Приведение дробей к общему знаменателю
СРАВНЕНИЕ, СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ (6 ч)
Урок 29. Сравнение дробей с разными знаменателями
Урок 30. Сравнение дробей с разными знаменателями
Урок 31. Сравнение, сложение и вычитание дробей с разными знаменателями
Урок 32. Сравнение, сложение и вычитание дробей с разными знаменателями
Сравнение, сложение и вычитание дробей с разными знаменателями
Урок 33. Сравнение, сложение и вычитание дробей с разными знаменателями
Урок 34. Сравнение, сложение и вычитание дробей с разными знаменателями
Урок 35. Контрольная работа № 2
СЛОЖЕНИЕ И ВЫЧИТАНИЕ СМЕШАННЫХ ЧИСЕЛ (6 ч)
Урок 36. Сложение и вычитание смешанных чисел
Урок 37. Сложение и вычитание смешанных чисел
Урок 38. Сложение и вычитание смешанных чисел
Урок 39. Сложение и вычитание смешанных чисел
Урок 40. Сложение и вычитание смешанных чисел
Урок 41. Сложение и вычитание смешанных чисел
Урок 42. Контрольная работа № 3
§ 3. УМНОЖЕНИЕ И ДЕЛЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ (32 ч)
УМНОЖЕНИЕ ДРОБЕЙ (5 ч)
Урок 43. Умножение дробей
Урок 44. Умножение дробей
Урок 45. Умножение дробей
Урок 46. Умножение дробей
Урок 47. «Счастливый случай» (урок-игра)
НАХОЖДЕНИЕ ДРОБИ ОТ ЧИСЛА (4 ч)
Урок 48. Нахождение дроби от числа
Урок 49. Нахождение дроби от числа
Нахождение дроби от числа
Урок 50. Нахождение дроби от числа
Урок 51. Нахождение дроби от числа
ПРИМЕНЕНИЕ РАСПРЕДЕЛИТЕЛЬНОГО СВОЙСТВА УМНОЖЕНИЯ (5 ч)
Урок 52. Применение распределительного свойства умножения
Урок 53. Применение распределительного свойства умножения
Урок 54. Применение распределительного свойства умножения
Урок 55. Применение распределительного свойства умножения
Урок 56. Применение распределительного свойства умножения
Урок 57. Контрольная работа № 4
ВЗАИМНО ОБРАТНЫЕ ЧИСЛА (2 ч)
Урок 58. Взаимно обратные числа
Урок 59. Взаимно обратные числа
ДЕЛЕНИЕ (5 ч)
Урок 60. Деление
Урок 61. Деление
Урок 62. Деление
Урок 63. Деление
Урок 64. Деление
Урок 65. Контрольная работа № 5
НАХОЖДЕНИЕ ЧИСЛА ПО ЕГО ДРОБИ (5 ч)
Урок 66. Нахождение числа по его дроби
Урок 67. Нахождение числа по его дроби
Урок 68. Нахождение числа по его дроби
Урок 69. Нахождение числа по его дроби
Нахождение числа по его дроби
Урок 70. Нахождение числа по его дроби
ДРОБНЫЕ ВЫРАЖЕНИЯ (3 ч)
Урок 71. Дробные выражения
Урок 72. Дробные выражения
Урок 73. Дробные выражения
Урок 74. Контрольная работа № 6
§ 4. ОТНОШЕНИЯ И ПРОПОРЦИИ (19 ч)
ОТНОШЕНИЯ (3 ч)
Урок 75. Отношения
Урок 76. Отношения
Урок 77. Отношения
ПРОПОРЦИИ (4 ч)
Урок 78. Пропорции
Урок 79. Пропорции
Урок 80. Пропорции
Урок 81. Пропорции
Урок 82. Повторение, обобщение и закрепление материала, пройденного за I полугодие
ПРЯМАЯ И ОБРАТНАЯ ПРОПОРЦИОНАЛЬНАЯ ЗАВИСИМОСТИ (3 ч)
Урок 83. Прямая и обратная пропорциональная зависимости
Урок 84. Прямая и обратная пропорциональная зависимости
Урок 85. Прямая и обратная пропорциональная зависимости
Урок 86. Контрольная работа № 7
МАСШТАБ (2 ч)
Урок 87. Масштаб
Урок 88. Масштаб
ДЛИНА ОКРУЖНОСТИ И ПЛОЩАДЬ КРУГА (2 ч)
Урок 89. Длина окружности и площадь круга
Длина окружности и площадь круга
Урок 90. Длина окружности и площадь круга
ШАР (2 ч)
Урок 91. Шар
Урок 92. Шар
Урок 93. Контрольная работа № 8
ГЛАВА II. РАЦИОНАЛЬНЫЕ ЧИСЛА
§ 5. ПОЛОЖИТЕЛЬНЫЕ И ОТРИЦАТЕЛЬНЫЕ ЧИСЛА (13 ч)
КООРДИНАТЫ НА ПРЯМОЙ (3 ч)
Урок 94. Координаты на прямой
Урок 95. Координаты на прямой
Урок 96. Координаты на прямой
ПРОТИВОПОЛОЖНЫЕ ЧИСЛА (2 ч)
Урок 97. Противоположные числа
Урок 98. Противоположные числа
МОДУЛЬ ЧИСЛА (2 ч)
Урок 99. Модуль числа
Урок 100. Модуль числа
СРАВНЕНИЕ ЧИСЕЛ (3 ч)
Урок 101. Сравнение чисел
Урок 102. Сравнение чисел
Урок 103. Сравнение чисел
ИЗМЕНЕНИЕ ВЕЛИЧИН (2 ч)
Урок 104. Изменение величин
Урок 105. Изменение величини
Урок 106. Контрольная работа № 9
§ 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ПОЛОЖИТЕЛЬНЫХ И ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ (11 ч)
СЛОЖЕНИЕ ЧИСЕЛ С ПОМОЩЬЮ КООРДИНАТНОЙ ПРЯМОЙ (2 ч)
Урок 107. Сложение чисел с помощью координатной прямой
Сложение чисел с помощью координатной прямой
Урок 108. Сложение чисел с помощью координатной прямой
СЛОЖЕНИЕ ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ (2 ч)
Урок 109. Сложение отрицательных чисел
Урок 110. Сложение отрицательных чисел
СЛОЖЕНИЕ ЧИСЕЛ С РАЗНЫМИ ЗНАКАМИ (3 ч)
Урок 111. Сложение чисел с разными знаками
Урок 112. Сложение чисел с разными знаками
Урок 113. Сложение чисел с разными знаками
ВЫЧИТАНИЕ (3 ч)
Урок 114. Вычитание
Урок 115. Вычитание
Урок 116. Вычитание
Урок 117. Контрольная работа № 10
§ 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ ПОЛОЖИТЕЛЬНЫХ И ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ (12 ч)
УМНОЖЕНИЕ (3 ч)
Урок 118. Умножение
Урок 119. Умножение
Урок 120. Умножение
ДЕЛЕНИЕ (3 ч)
Урок 121. Деление
Урок 122. Деление
Урок 123. Деление
РАЦИОНАЛЬНЫЕ ЧИСЛА (2 ч)
Урок 124. Рациональные числа
Урок 125. Рациональные числа
СВОЙСТВА ДЕЙСТВИЙ С РАЦИОНАЛЬНЫМИ ЧИСЛАМИ (3 ч)
Урок 126. Свойства действий с рациональными числами
Свойства действий с рациональными числами
Урок 127. Свойства действий с рациональными числами
Урок 128. Свойства действий с рациональными числами
Урок 129. Контрольная работа № 11
§ 8. РЕШЕНИЕ УРАВНЕНИЙ (15 ч)
РАСКРЫТИЕ СКОБОК (3 ч)
Урок 130. Раскрытие скобок
Урок 131. Раскрытие скобок
Урок 132. Раскрытие скобок
Урок 133. Повторение и обобщение материала за III четверть (урок-игра)
КОЭФФИЦИЕНТ (2 ч)
Урок 134. Коэффициент
Урок 135. Коэффициент
ПОДОБНЫЕ СЛАГАЕМЫЕ (3 ч)
Урок 136. Подобные слагаемые
Урок 137. Подобные слагаемые
Урок 138. Подобные слагаемые
Урок 139. Контрольная работа № 12
РЕШЕНИЕ УРАВНЕНИЙ (4 ч)
Урок 140. Решение уравненийк
Урок 141. Решение уравнений
Урок 142. Решение уравнений
Урок 143. Решение уравнений
Урок 144. Контрольная работа № 13
§ 9. КООРДИНАТЫ НА ПЛОСКОСТИ (13 ч)
ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ (2 ч)
Урок 145. Перпендикулярные прямые
Перпендикулярные прямые
Урок 146. Перпендикулярные прямые
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ (2 ч)
Урок 147. Параллельные прямые
Урок 148. Параллельные прямые
КООРДИНАТНАЯ ПЛОСКОСТЬ (3 ч)
Урок 149. Координатная плоскость
Урок 150. Координатная плоскость
Урок 151. Координатная плоскость
СТОЛБЧАТЫЕ ДИАГРАММЫ (2 ч)
Урок 152. Столбчатые диаграммы
Урок 153. Столбчатые диаграммы
ГРАФИКИ (3 ч)
Урок 154. Графики
Урок 155. Графики
Урок 156. Графики
Урок 157. Контрольная работа № 14
Виленкин Н.И. 6. Принципы эффективной самоподготовки
Среди школьных предметов особняком стоит математика. Действительно, его изучению посвящено очень много времени. При этом математика начинается уже в первом классе и заканчивается только в конце одиннадцатого. Кроме того, в конце 9 и 11 годов обучения именно по математике предстоит пройти итоговые аттестации, именуемые ОГЭ и ЕГЭ соответственно.
Требуются выпускные экзамены, т.е.е. их нельзя избежать ни при каких обстоятельствах. При этом математические способности разных детей сильно отличаются. Не всем предмет дается без труда. В последнем случае будет полезно использовать вспомогательную литературу, например, онлайн-решатель Виленкина с содержанием правильных ответов.
Учебно-методический комплекс Н.Я. Виленкина, В.И. Жохов, А.С. Чесноковой и С.И. Шварцбурд распространяется издательством «Мнемозина» с 2015 по 2019 год.Используется во многих школах. Российская Федерация. Соответствующие руководства также довольно легко получить в публичных библиотеках. Многие преподаватели формируют собственные рабочие программы по данному предмету.
За что школьники любят ВЛЕНКИН ГДЗ по математике?
В зависимости от врожденных способностей к точным наукам у разных людей изучение алгебры требует разного уровня усилий и вложенного времени. Оснащенный большим количеством полезных прикладных материалов сборник для 6 класса, авторы которого Виленкин, Жохов, Чесноков, имеет ряд преимуществ:
- содержание заданий полностью соответствует ФГОС;
- просто используйте смартфон, планшет или компьютер с выходом в интернет;
- можно выбрать наиболее понятное решение из нескольких предложенных;
- поиск нужного упражнения осуществляется с помощью индекса в виде таблицы.

Ответы, данные в Госдуме по математике, нельзя просто так переписать. Их следует тщательно изучить, найти закономерности и полезные решения. Интенсивная работа поможет повысить успеваемость, легко справиться с контрольными и проверочными работами.
Почему ученик Виленкина и Жохова для 6 класса может заменить репетитора?
Если школьник будет стараться на протяжении всей школьной жизни, то с большой вероятностью он получит высокие баллы на выпускном экзамене и сможет поступить в хороший вуз.При изучении математики особенно важно избегать пробелов. В шестом классе нужно серьезно подойти к разработке абзацев, решению задач, отработке практических навыков:
- простые дроби. Числитель и знаменатель;
- приведение к общему основанию. Сложение, вычитание, умножение, деление;
- линейных уравнений. Правило пропорции;
- наибольший общий делитель. Наименее кратное.
Достаточная практика в решении примеров и упражнений, а также своевременное заполнение пропусков убережет ученика от проблем в старшей школе. Поэтому ГДЗ онлайн можно рекомендовать любому шестикласснику, который сталкивается с непонятными темами на уроках или в домашних заданиях. Пособие с готовыми решениями соответствует требованиям ФГОС.
Поэтому ГДЗ онлайн можно рекомендовать любому шестикласснику, который сталкивается с непонятными темами на уроках или в домашних заданиях. Пособие с готовыми решениями соответствует требованиям ФГОС.
Если школьник хочет действительно разобраться в сложном предмете, ему придется правильно использовать ГДЗ по математике 6 класс Виленкин:
- Всегда пытайтесь сначала решить все домашние номера самостоятельно. Когда не получается, внимательно смотрите на правильное решение и разбирайтесь с каждым шагом.
- Для выполненных задач и примеров проверьте ответы. Если они не совпали, то сначала попытайтесь найти ошибку в своих рассуждениях и только потом вникайте в показания поселенца.
- Когда совсем нет времени делать качественные уроки, лучше списать работу, стараясь запомнить ход решения, а не полагаться на «а вдруг учитель не спросит».
Работать нужно только с теми ГДЗ, которые написаны опытными преподавателями, не содержат опечаток даже самых сложных понятий. На ГДЗ-онлайн есть именно такой решатель по математике для 6 класса Виленкин. С ним шестиклассник действительно разберется в дисциплине и повысит успеваемость.
На ГДЗ-онлайн есть именно такой решатель по математике для 6 класса Виленкин. С ним шестиклассник действительно разберется в дисциплине и повысит успеваемость.
- Математика в 6 классе включает в себя большой объем знаний. Именно в 6 классе осуществляется переход от простых математических задач к более сложным. Учащийся уже начинает понимать различия между алгеброй и геометрией; он должен хорошо разбираться в задачах и формулах.Учебник имеет различные блоки, которые включают в себя задания и примеры по двум предметам.
- Математический решатель Виленкина помогает школьнику привести все в порядок. Большой объем материала не всегда хорошо усваивается учащимися в школе. Бывает, что студент понимает теорию, но не может понять практику. На конкретных примерах, имеющихся в расчетной книжке, учащиеся сравнивают и перепроверяют свои знания. Благодаря домашнему заданию у них есть возможность досконально разобраться в теме, поэтапно рассмотреть решение той или иной задачи.
- Благодаря ГДЗ значительно облегчается процесс выполнения домашнего задания, и у ученика вырабатываются навыки самоподготовки, теоретический материал находит свое практическое применение, ученик начинает лучше учиться, у него проявляется стремление к знаниям.
 Еженедельное выполнение упражнений из учебника поможет ученику закрепить пройденный материал, подготовиться к контрольной работе и закрыть задание на отлично.
Еженедельное выполнение упражнений из учебника поможет ученику закрепить пройденный материал, подготовиться к контрольной работе и закрыть задание на отлично. - Шестиклассники продолжают углубленно изучать математику.Классические основы этой дисциплины изучаются в 6 классе. В прошлом году уже с 7-го класса у школьников предмет разделится на два самостоятельных — геометрию и алгебру. Для успешного обучения, хорошей подготовки к текущей и итоговой, диагностической работе, ВПР шестиклассникам необходимо заранее настроиться на ответственную и планомерную работу. В помощь студентам качественные учебные материалы, пособия и решатели к ним. Вы можете планировать свою работу самостоятельно или обратившись за помощью к учителям, репетиторам и родителям.Для того чтобы самостоятельная работа по ГДЗ была эффективной, необходимо:
— разработать грамотную систему, план работы, исходя из базового уровня знаний шестиклассника по математике, его интересов, задач и целей. Например, для углубления имеющихся знаний или для участия в математических олимпиадах и конкурсах и т.п.;
Например, для углубления имеющихся знаний или для участия в математических олимпиадах и конкурсах и т.п.;
— придерживаться разработанной схемы, периодически контролируя достигнутые достижения, выявляя и исправляя недостатки. Динамику подготовки можно отслеживать после изучения блока либо — назначая конкретные даты наблюдения;
— Скорректировать полученные результаты, изменив и дополнив программу тренировок. - В качестве полезного и интересного исходника многие учителя, репетиторы и сами шестиклассники называют Н.Я. Виленкина по математике для 6 класса, в котором подробно и полно рассмотрены трудные темы, для их тщательного и всестороннего изучения имеются различные задания. Среди тем, вызывающих наибольшие трудности при изучении математики шестиклассниками, которые подробно рассматриваются в данном пособии, можно выделить:
— делимость чисел и их знаки;
— кратность и действия с дробями, имеющими разные знаменатели;
— пропорции и отношения как математические величины;
— зависимости прямые и обратные;
— шкала — раздел, вызывающий наибольшее количество затруднений у шестиклассников;
— шар, круг, его длина и площадь круга.
- Для лучшего освоения и закрепления материала желательно дополнить основной учебник практикумами того же автора. Для тех студентов, которые находятся на семейной форме обучения, можно дополнительно к методическим материалам использовать рабочие программы.
Принципы эффективного самообучения
Решатель по математике для 6 класса Виленкину — это сборник готовых решений и ответов, в основе которого лежит учебник математики для шестиклассников, составленный группой российских авторов — Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.
Решебник к учебнику по математике 6 класс от Виленкина
ГДЗ по математике за 6 класс позволяет проверить правильность выполнения домашнего задания учащимися. С его помощью им удается понять алгоритм решения. сложные задачи самостоятельно.
Более того, готовые решения и ответы являются подсказкой для родителей, стремящихся оказать своим детям посильную помощь в подготовке домашнего задания по математике.
Ресечник позволяет снизить нагрузку на шестиклассников, которые не всегда успевают разобраться в решении примера или задачи на уроке.
Интерфейс нашего сайта делает пользование учебником максимально удобным для детей и родителей:
- База ответов доступна с телефона, планшета и компьютера;
- Таблица номеров позволяет быстро перейти к нужному ответу;
- Регулярное обновление резольверов исключает возможность ошибок при подготовке домашних заданий.
Такие опции позволяют сделать процесс выполнения работы по математике максимально эффективным, как с точки зрения результата, так и с точки зрения экономии времени.
Учебник по математике для 6 класса от Виленкина, Жохова, Чеснокова и Шварцбурга
На нашем сайте представлены готовые решения и ответы к заданиям учебника для 6 класса от Н. Виленкина. В настоящее время в большинстве школ используется учебник 30-го издания, выпущенный в 2013 году.
Учебное пособие Подробно рассмотрены два основных раздела арифметики:
- Свойства и действия с натуральными числами;
- Знаки, характеристики и математические операции с дробными числами.

В учебнике также приводится информация о таких арифметических понятиях, как НОЦ (наименьшее общее кратное) и НОД (наибольший общий делитель), приводится порядок их вычисления, а также особенности составления пропорций.
Книга знакомит шестиклассников с особенностями координат на плоскости, а также с понятием масштаба. Подробно описаны различия между положительными и отрицательными числами, а также правила математических действий с ними.
Н.Я. Виленкин 6. Принципы эффективной самоподготовки
Математика стоит особняком среди школьных предметов… Действительно, ее изучению уделяется очень много времени. При этом математика начинается уже в первом классе и заканчивается только в конце одиннадцатого класса. Кроме того, в конце 9 и 11 годов обучения именно по математике вам предстоит пройти итоговые аттестации, называемые ОГЭ и ЕГЭ соответственно.
Выпускные экзамены обязательны, т.е. их нельзя избежать ни при каких обстоятельствах. При этом математические способности разных детей сильно отличаются. Не всем предмет дается без труда. В последнем случае будет полезно использовать вспомогательную литературу, например, онлайн-решатель Виленкина с содержанием правильных ответов.
При этом математические способности разных детей сильно отличаются. Не всем предмет дается без труда. В последнем случае будет полезно использовать вспомогательную литературу, например, онлайн-решатель Виленкина с содержанием правильных ответов.
Учебно-методический комплекс Н.Я. Виленкина, В.И. Жохова, А.С. Чеснокова и С.И. Шварцбурда распространяется издательством «Мнемозина» с 2015 по 2019 год.Он используется во многих школах Российской Федерации. Соответствующие пособия также довольно легко получить в публичных библиотеках. Многие преподаватели формируют на их основе собственные рабочие программы по предмету.
Почему школьники любят ГДЗ Виленкина по математике?
В зависимости от врожденной склонности к точным наукам у разных людей изучение алгебры требует разного уровня усилий и затрат времени. Запасен большим количеством полезных прикладных материалов, сборник для 6 класса, авторы которого Виленкин, Жохов, Чесноков имеет ряд достоинств:
- содержание заданий полностью соответствует ФГОС;
- достаточно смартфона, планшета или компьютера с выходом в интернет;
- можно выбрать наиболее понятное решение из нескольких предложенных;
- поиск нужного упражнения осуществляется с помощью числового указателя в виде таблицы.
Ответы, данные в ГДЗ по математике, нельзя просто переписать. Их следует тщательно изучить, найти закономерности и полезные решения. Интенсивная работа поможет повысить успеваемость, легко решать контрольные и проверочные работы, тесты.
Почему учитель Виленкина и Жохова для 6 класса может заменить репетитора?
Если ученик будет стараться на протяжении всей школьной жизни, то с большой вероятностью он получит высокие баллы на выпускном экзамене и сможет поступить в хороший университет… При изучении математики особенно важно избегать пробелов. В шестом классе нужно серьезно относиться к освоению абзацев, решению задач, отработке практических навыков:
- простые дроби. Числитель и знаменатель;
- приведение к общей основе. Сложение, вычитание, умножение, деление;
- линейных уравнений. правило пропорции;
- наибольший общий делитель… Наименьшее кратное.
Достаточная практика в решении примеров и упражнений, а также своевременное устранение пропусков убережет ученика от проблем в старшей школе. Поэтому ГДЗ онлайн можно рекомендовать любому шестикласснику, который сталкивается с непонятными темами на уроках или при выполнении домашних заданий. Пособие с готовыми решениями соответствует требованиям ФГОС.
Поэтому ГДЗ онлайн можно рекомендовать любому шестикласснику, который сталкивается с непонятными темами на уроках или при выполнении домашних заданий. Пособие с готовыми решениями соответствует требованиям ФГОС.
Если школьник хочет действительно разобраться в сложном предмете, ему придется грамотно использовать ГДЗ по математике 6 класс Виленкин:
- Всегда старайтесь сначала решить все домашние номера самостоятельно. Когда не получается, внимательно следите за правильным решением и разбирайтесь с каждым этапом.
- Проверьте ответы на выполненные задания и примеры. Если они не совпадают, то сначала попытайтесь найти ошибку в своих рассуждениях и только потом вникайте в доказательства Резервера.
- Когда совсем нет времени хорошо делать уроки, лучше списать работу, стараясь запомнить ход решения, а не надеяться, что учитель может не спросить.
Работать нужно только с теми ГДЗ, которые написаны опытными преподавателями, не содержат опечаток, подробно и понятно объясняют даже самые сложные понятия. .. На ГДЗ-онлайн есть как раз такое решение по математике для Виленкина 6 класса. С ним шестиклассник действительно разберется в дисциплине и повысит успеваемость.
.. На ГДЗ-онлайн есть как раз такое решение по математике для Виленкина 6 класса. С ним шестиклассник действительно разберется в дисциплине и повысит успеваемость.
- Математика в 6 классе включает в себя большой объем знаний. Именно в 6 классе осуществляется переход от простых математических задач к более сложным. Учащийся уже начинает понимать различия между алгеброй и геометрией, он должен хорошо разбираться в задачах и формулах.В учебнике есть различные блоки, включающие задания и примеры по двум предметам.
- Учебник по математике Виленкина помогает школьнику расставить все по полочкам. Большой объем материала не всегда хорошо усваивается учащимися в школе. Бывает, что студент понимает теорию, но не может разобраться на практике. На конкретных примерах, которые имеются в Решебнике, студенты проверяют и перепроверяют свои знания. Выполняя домашнее задание, они имеют возможность досконально разобраться в теме, шаг за шагом рассмотреть решение той или иной проблемы.

- Благодаря ГДЗ значительно облегчается процесс выполнения домашних заданий, и у ученика вырабатываются навыки самоподготовки, теоретический материал находит себе практическое применение, ученик начинает лучше учиться, у него проявляется стремление к знаниям. Еженедельное выполнение упражнений учебника, поможет учащемуся закрепить пройденный материал, подготовиться к контрольной работе и закрыть тему на отлично.
- Шестиклассники продолжают углубленно изучать курс математики.Классические основы этой дисциплины преподаются в 6 классе. В прошлом году уже с 7-го класса школьники разделят предмет на два самостоятельных – геометрию и алгебру. Чтобы добиться успеха в учебе, хорошо подготовиться к текущей и итоговой, диагностической работе, ВПР, шестиклассникам необходимо заранее настроиться на ответственную и систематическую работу. В помощь школьникам качественные учебные материалы, пособия и ответы к ним. Вы можете спланировать работу самостоятельно или обратившись за помощью к учителям, репетиторам и родителям.
 Для того, чтобы самостоятельная работа по ГДЗ была эффективной, необходимо:
Для того, чтобы самостоятельная работа по ГДЗ была эффективной, необходимо:
— разработать грамотную систему, план работы, исходя из базового уровня знаний шестиклассника по математике, его интересов, задач и целей. Например, для углубления имеющихся знаний или участия в математических олимпиадах и олимпиадах и т.п.;
— придерживаться разработанной схемы, периодически контролируя достигнутые достижения, выявляя и исправляя недостатки. Динамику подготовки можно отслеживать после изучения блока тем, либо — назначить конкретные даты контроля;
— скорректировать полученные результаты, изменив и дополнив программу тренировок. - В качестве полезного и интересного базового источника многие учителя, репетиторы и сами шестиклассники называют учебник Виленкина Н.Я. по математике для 6 класса, в котором подробно и полно рассмотрены сложные темы, для их тщательного и всестороннего изучения , есть разные задачи. К числу тем, вызывающих наибольшие трудности при изучении математики шестиклассниками, которые подробно рассматриваются в данном пособии, относятся:
— делимость чисел и их знаки;
— кратность и действия с дробями с разными знаменателями;
— пропорции и отношения как математические величины;
— прямые и обратные зависимости;
— шкала — раздел, вызывающий наибольшее количество затруднений у шестиклассников;
— шар, длина окружности, его длина и площадь круга.
- Для лучшего усвоения и закрепления материала целесообразно дополнять базовый учебник мастер-классами того же автора. Для тех студентов, которые находятся на семейной форме обучения, можно дополнительно к методическим материалам использовать рабочие программы.
Принципы эффективного самообучения
Решебник по математике для 6 класса Виленкину — это сборник готовых решений и ответов, который составлен на основе учебника по математике для шестиклассников, составленного группой российских авторов — Виленкина Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.
Решебник к учебнику математики 6 класса от Виленкина
ГДЗ по математике за 6 класс позволяет проверить правильность выполнения домашнего задания учащимися. С его помощью им удается самостоятельно разобраться в алгоритме решения сложных задач.
Более того, готовые решения и ответы являются подсказкой родителям, стремящимся оказать своим детям посильную помощь в подготовке домашних заданий по математике.
Решебник позволяет снизить учебную нагрузку на шестиклассников, которые не всегда успевают разобраться в решении примера или задачи на уроке.
Интерфейс нашего сайта делает использование учебника максимально удобным для детей и родителей:
- База ответов доступна с телефона, планшета и компьютера;
- Таблица чисел позволяет быстро перейти к нужному ответу;
- Регулярное обновление решебников исключает вероятность ошибок при подготовке домашних заданий.
Такие варианты позволяют сделать процесс выполнения работы по математике максимально эффективным, как с точки зрения результата, так и с точки зрения экономии времени.
Учебник по математике 6 класс от Виленкина, Жохова, Чеснокова и Шварцбурга
На нашем сайте представлены готовые решения и ответы к заданиям учебника для 6 класса от Виленкина Н.Я. В настоящее время в большинстве школ используется книга 30-го издания, выпущенная в 2013 году.
В учебном пособии подробно рассмотрены два больших раздела по арифметике:
- Свойства и действия с натуральными числами;
- Знаки, характеристики и математические операции с дробными числами.

В учебнике также приведены сведения о таких арифметических понятиях, как НОК (наименьшее общее кратное) и НОД (наибольший общий делитель), порядке их вычисления, а также особенностях составления пропорций.
Книга знакомит шестиклассников с особенностями координат на плоскости, а также понятием масштаба.Подробно объясняет различия между положительными и отрицательными числами и правила математических действий с ними.
Гдз по математике виленкин 6. Принципы эффективной самоподготовки
Решебник по математике для 6 класса Виленкину — это сборник готовых решений и ответов, который составлен на основе учебника по математике для шестиклассников, составленного группой российских авторов — Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.I.
Решебник к учебнику математики за 6 класс от Виленкина
ГДЗ по математике за 6 класс позволяет проверить правильность выполнения домашнего задания учащимися. С его помощью им удается самостоятельно понять алгоритм решения сложных задач.
Более того, готовые решения и ответы являются подсказкой родителям, стремящимся оказать своим детям посильную помощь в подготовке домашних заданий по математике.
Решебник позволяет снизить учебную нагрузку на шестиклассников, которые не всегда успевают разобраться в решении примера или задачи на уроке.
Интерфейс нашего сайта делает использование учебника максимально удобным для детей и родителей:
- База ответов доступна с телефона, планшета и компьютера;
- Таблица чисел позволяет быстро перейти к нужному ответу;
- Регулярное обновление решебников исключает вероятность ошибок при подготовке домашних заданий.
Такие варианты позволяют сделать процесс выполнения работы по математике максимально эффективным, как с точки зрения результата, так и с точки зрения экономии времени.
Учебник по математике 6 класс от Виленкина, Жохова, Чеснокова и Шварцбурга
На нашем сайте представлены готовые решения и ответы к заданиям учебника для 6 класса от Виленкина Н. Я. В настоящее время в большинстве школ используется учебник 30-го издания, выпущенный в 2013 году.
Я. В настоящее время в большинстве школ используется учебник 30-го издания, выпущенный в 2013 году.
Учебник подробно охватывает два основных раздела арифметики:
- Свойства и операции с натуральными числами;
- Знаки, характеристики и математические операции с дробными числами.
В учебнике также приведены сведения о таких арифметических понятиях, как НОК (наименьшее общее кратное) и НОД (наибольший общий делитель), порядке их вычисления, а также особенностях составления пропорций.
Книга знакомит шестиклассников с особенностями координат на плоскости, а также понятием масштаба. Подробно представлены отличия положительных и отрицательных чисел, а также правила математических действий с ними.
Математика выделяется среди школьных предметов. Действительно, его изучению посвящено очень много времени. При этом математика начинается уже в первом классе и заканчивается только в конце одиннадцатого класса. Кроме того, в конце 9 и 11 годов обучения именно по математике вам предстоит пройти итоговые аттестации, называемые ОГЭ и ЕГЭ соответственно.
Выпускные экзамены обязательны, т.е. их нельзя избежать ни при каких обстоятельствах. При этом математические способности разных детей сильно отличаются.Не всем предмет дается без труда. В последнем случае будет полезно использовать вспомогательную литературу, например, онлайн-решатель Виленкина с содержанием правильных ответов.
Учебно-методический комплекс Н.Я. Виленкина, В.И. Жохова, А.С. Чеснокова и С.И. Шварцбурда распространяется издательством «Мнемозина» с 2015 по 2019 год. Используется во многих школах Российской Федерации. Соответствующие руководства также довольно легко получить в публичных библиотеках.Многие преподаватели формируют на их основе собственные рабочие программы по предмету.
Почему школьники любят ГДЗ Виленкина по математике?
В зависимости от врожденной склонности к точным наукам у разных людей изучение алгебры требует разного уровня усилий и затрат времени. Оснащенный большим количеством полезных прикладных материалов сборник для 6 класса, авторы которого Виленкин, Жохов, Чесноков, имеет ряд преимуществ:
- содержание заданий полностью соответствует ФГОС;
- достаточно смартфона, планшета или компьютера с выходом в интернет;
- можно выбрать наиболее понятное решение из нескольких предложенных;
- поиск нужного упражнения осуществляется с помощью числового указателя в виде таблицы.

Ответы, данные в ГДЗ по математике, нельзя просто переписать. Их следует тщательно изучить, найти закономерности и полезные решения. Интенсивная работа поможет повысить успеваемость, легко решать контрольно-ревизионные работы, зачеты.
Почему учитель Виленкина и Жохова для 6 класса может заменить репетитора?
Если ученик будет стараться на протяжении всей школьной жизни, то велика вероятность, что он получит высокие оценки на выпускном экзамене и сможет поступить в хороший университет.При изучении математики особенно важно избегать пробелов. В шестом классе нужно серьезно относиться к освоению абзацев, решению задач, отработке практических навыков:
- простые дроби. Числитель и знаменатель;
- приведение к общей основе. Сложение, вычитание, умножение, деление;
- линейных уравнений. правило пропорции;
- наибольший общий делитель. Наименее кратное.
Достаточная практика в решении примеров и упражнений, а также своевременное устранение пропусков убережет ученика от проблем в старшей школе. Поэтому ГДЗ онлайн можно рекомендовать любому шестикласснику, который сталкивается с непонятными темами на уроках или при выполнении домашних заданий. Пособие с готовыми решениями соответствует требованиям ФГОС.
Поэтому ГДЗ онлайн можно рекомендовать любому шестикласснику, который сталкивается с непонятными темами на уроках или при выполнении домашних заданий. Пособие с готовыми решениями соответствует требованиям ФГОС.
В шестом классе происходит процесс разделения предмета математики на алгебру и геометрию. Это приводит к тому, что учащимся необходимо осваивать новые сложные понятия и задачи. Однако не каждый школьник сможет самостоятельно освоить такой материал, и здесь на помощь придет решение, созданное автором. Н.Я. Виленкин … Учебник по математике 6 класс станет более доступным, если использовать ГДЗ … Это позволит учащемуся лучше понять новые темы и задачи к ним, на решенном примере.
С помощью данного пособия школьник может снизить сложность домашней подготовки к занятиям. Это также позволяет учащимся самостоятельно решать задачи в будущем без каких-либо подсказок. ГДЗ способствует пониманию учащимися языка математики, углубляет их навыки об общих принципах решения математических примеров.
ГДЗ на рабочую тетрадь по математике для 6 класса Рудницкая В.Н. можно скачать.
ГДЗ к учебнику математики 6 класса Виленкин Н.Я. (2018) можно скачать.
ГДЗ для тестов по математике за 6 класс Жохов В.И. можно скачать.
ГДЗ на дидактические материалы по математике для 6 класса Попова М.А. можно скачать
Если школьник хочет действительно разобраться в сложном предмете, ему придется грамотно использовать ГДЗ по математике 6 класс Виленкин:
- Всегда старайтесь сначала решить все домашние номера самостоятельно.Когда не получается, внимательно следите за правильным решением и разбирайтесь с каждым этапом.
- Проверьте ответы на выполненные задания и примеры. Если они не совпадают, то сначала попытайтесь найти ошибку в своих рассуждениях и только потом вникайте в доказательства Резервера.
- Когда совсем нет времени хорошо делать уроки, лучше списать работу, стараясь запомнить ход решения, а не надеяться, что учитель может не спросить.

Работать необходимо только с теми ГДЗ, которые написаны опытными преподавателями, не содержат опечаток, подробно и понятно объясняют даже самые сложные понятия.На ГДЗ-онлайн есть как раз такое решение по математике для Виленкина 6 класса. С ним шестиклассник действительно разберется в дисциплине и повысит успеваемость.
ГДЗ по математике за 6 класс Виленкина — онлайн-сборник готовых ответов (от Решебника) к задачам одноименного учебника по математике, составленный Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. Она позволяет учащимся проверить правильность выполнения домашнего задания и разобраться со сложными задачами, а родителям — оказать своим детям посильную помощь в подготовке домашнего задания по математике.
Ассистент по изучению математики в 6 классе — решебник Виленкин Н.Я. 2013 год
Курс математики для 6 класса общеобразовательной школы Российской Федерации включает широкий круг тем, связанных с натуральными и дробными числами. Высокий уровень сложности отдельных задач часто не позволяет ребенку на занятии разобраться в алгоритме решения примера.
Высокий уровень сложности отдельных задач часто не позволяет ребенку на занятии разобраться в алгоритме решения примера.
Решить эту задачу может решатель по математике 6 класса N.Я. Виленкина, которая представлена на нашем сайте в онлайн-доступе. Каковы его преимущества?
- Благодаря удобному интерфейсу достаточно вбить в строку поиска номер домашнего задания или пример условия (необязательно) — и система предложит список заданий с похожими условиями;
- К каждому примеру дается не только готовый ответ, но и подробный алгоритм его решения.
Такие варианты позволяют ученикам самостоятельно разобраться, как решить ту или иную задачу, а родителям — адекватно проверить домашнее задание учеников.Кроме того, таким образом можно сэкономить много времени.
Что входит в решение по математике 6 класса: Виленкин, Жохов, Чесноков, Шварцдурд?
Представленное на сайте решение составлено на основе учебника математики для 6 класса под редакцией Н. Я. Виленкин. в 30-м издании (2013 г.). Но это вовсе не означает, что невозможно найти решения для более ранних и более поздних редакций: на самом деле нужно вбить в строку поиска условия примера — и система найдет требуемую проблему.
Я. Виленкин. в 30-м издании (2013 г.). Но это вовсе не означает, что невозможно найти решения для более ранних и более поздних редакций: на самом деле нужно вбить в строку поиска условия примера — и система найдет требуемую проблему.
Учебник Виленкин Н.Я. включает две основные главы:
- Обыкновенные дроби — их понятие, свойства, операции с ними;
- Рациональные числа — сущность, роль в осуществлении вычислений, математические операции с ними.
В первой части учебника подробно описаны понятие и признаки делимости чисел, механизм вычисления наименьшего общего короткого (НОК) и наибольшего общего делителя (НОД), а также алгоритм составления и решения пропорций.
Во второй части подробно описаны правила выполнения математических действий с положительными и отрицательными числами, а также порядок решения уравнений с учетом расположения координат на плоскости.
Наш сайт готовых домашних заданий – это не только помощь в решении домашних заданий для учащихся 6-х классов и их родителей, но и полноценное практическое пособие, позволяющее самостоятельно постигать азы математики.
Deoma — Продукты — Алгебра
Электронный учебник «Интерактивная математика», 6 класс, предназначен для использования
Возможности компьютера в обучении математике в 6 классе.Ты можешь выбрать
конфигурация электронного учебника, соответствующая печатной
учебник, которым пользуется учитель. Адаптация электронного учебника
обеспечены печатными книгами авторов: Виленкина, Зубаревой и Мордкович,
Шарыгин. Электронное приложение включает в себя интерактивные разработки для
преподавание основ математики, в частности, таких тем, как: целые числа и
отрицательные целые числа, делимость, пропорции, десятичные дроби, основы выражений
упрощение, координатная прямая, координатная плоскость, понятие математического
модель; используются математические игры.
Последняя версия продукта от 12 августа 2015 г.:
.
Скачать «Интерактивная математика», 6 класс v1.4.3.21 для Windows
Скриншоты программы приведены ниже.
Вы можете увеличить цифры ↓
Версия 1. 4.3.21 из 12 августа 2015 г. (последняя)
4.3.21 из 12 августа 2015 г. (последняя)
Показать предыдущие версии
Версия 1.4.3.20 от 11 августа 2015
версия 1.4.3.19 от 11 августа 2015
версия 1.4.3.18 от 17 ноября 2012 г.
версия 1.4.3.17 от 9 октября 2011 г.
версия 1.4.3.16 от 28 июня 2011
версия 1.4.3.15 от 6 мая 2011 г. 6 мая 2011 г.
Версия 1.4.3.14 от 18 апреля 2011 г.
Версия 1.4.3.12 от 23 января 2011 года
версия 1.4.3.11 от 4 января 2011 г.
версия 1.4.3.10 от 4 ноября 2010 г.
Версия 1.4.3.9 от 4 ноября 2010
версия 1.4.3.8 от 5 сентября 2010 г.
Версия 1.4.3.7 от 5 сентября 2010 г. 5 сентября 2010 г.
Версия 1.4.3.6 от 24 августа 2010 г.
Версия 1.4.3.5 от 16 августа 2010 г.
версия 1.4.3.4 от 13 июня 2010 г.
версия 1.4.3.3 от 10 мая 2010 г.
Версия 1.4.3.2 от 10 мая 2010
версия 1.4.3.0 от 23 марта 2010 г.
версия
версия 1.4.2.0 от 17 марта 2010 г.
Версия 1.4.1.0 от 1 марта 2010 г.
Версия 1.4.0.0 от 20 февраля 2010 г.
версия 1.3.15.0 от 10 февраля 2010 г.
версия
от 4 февраля 2010
версия 1.3.13 от 10 января 2010
версия 1.3.12 от 5 января 2010 г.
версия 1.3.11 от 25 декабря 2009 г. 25 декабря 2009 г.
Версия 1.3.10 от 24 декабря 2009 г.
Версия 1.3.9 от 15 декабря 2009 г.
версия 1.3.8 от 14 декабря 2009 г.
Версия 1.3.6 от 11 октября 2009 г.
Версия 1.3.59 от 9 октября 2009 г.
версия 1.3.4 от 2 октября 2009 г.
версия
от 1.3.3 от 27 сентября 2009 г.
Версия 1.3.2 от 20 сентября 2009 г.
Версия 1.3.1 от 13 сентября 2009
версия 1.3.0
от 25 августа 2009 г.
версия 1.0.2 от 12 апреля 2009 г.
Версия 1.0.1 от 16 марта 2009 г.
Скрыть предыдущие версии
Умножаем значение в скобках. Как репетитор по математике дает тему «умножение многочленов
На этом уроке вы узнаете, как преобразовать выражение, содержащее скобки, в выражение, не содержащее скобок.Вы узнаете, как раскрывать круглые скобки, которым предшествуют знаки плюс и минус. Вспомним, как раскрывать скобки с помощью распределительного закона умножения. Рассмотренные примеры позволят связать новый и ранее изученный материал в единое целое.
Тема: Решение уравнений
Урок: Раскрытие скобок
Как раскрыть круглые скобки, перед которыми стоит знак «+». Применение комбинационного закона сложения.
Если вам нужно прибавить к числу сумму двух чисел, то вы можете сначала прибавить к этому числу первое слагаемое, а потом второе.
Слева от знака стоит выражение со скобками, а справа — выражение без скобок. Это означает, что при переходе от левой части равенства к правой скобки раскрывались.
Давайте рассмотрим несколько примеров.
Пример 1.
Раскрыв скобки, мы изменили порядок действий.Считать стало удобнее.
Пример 2.
Пример 3.
Обратите внимание, что во всех трех примерах мы просто удалили круглые скобки. Сформулируем правило:
Комментарий.
Если первый член в круглых скобках беззнаковый, то он должен быть записан со знаком плюс.
Вы можете шаг за шагом следовать этому примеру. Сначала прибавьте 445 к 889. Это действие можно проделать в уме, но оно не очень простое.Раскроем скобки и увидим, что измененный порядок действий значительно упростит расчеты.
Сначала прибавьте 445 к 889. Это действие можно проделать в уме, но оно не очень простое.Раскроем скобки и увидим, что измененный порядок действий значительно упростит расчеты.
Если следовать указанному порядку действий, то из 512 нужно сначала вычесть 345, а затем к результату прибавить 1345. Раскрыв скобки, мы изменим порядок действий и значительно упростим расчеты.
Наглядный пример и правило.
Рассмотрим пример:. Вы можете найти значение выражения, сложив 2 и 5, а затем взяв полученное число с обратным знаком.Получаем -7.
С другой стороны, тот же результат можно получить, сложив противоположные числа.
Сформулируем правило:
Пример 1.
Пример 2.
Правило не меняется, если в скобках не два, а три и более условия.
Пример 3.
Комментарий. Знаки меняются местами только перед терминами.
Чтобы раскрыть скобки, в этом случае нужно помнить о свойстве распределения.
Сначала умножьте первую скобку на 2, а вторую на 3.
Перед первой скобкой стоит знак «+», что означает, что знаки нужно оставить без изменений. Перед вторым стоит знак «-«, поэтому все знаки надо поменять на противоположные
Библиография
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемосина, 2012.
- Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия, 2006.
- Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — Образование, 1989.
- Рурукин А.Н., Чайковский И.В. Задания по курсу математики 5-6 класс — ЗШ МИФИ, 2011.
- Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6 классов заочной школы МИФИ. — ЗШ МИФИ, 2011.
- Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-учебник для 5-6 классов средней школы. Библиотека учителя математики. — Образование, 1989.

.
- Онлайн тесты по математике ().
- Вы можете скачать указанные в п.1.2. книги ().
Домашнее задание
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемосина, 2012. (ссылку см. 1.2)
- Домашнее задание: Нет.1254, № 1255, № 1256 (б, г)
- Другие присвоения: № 1258 (в), № 1248
В этой статье мы подробно рассмотрим основные правила такой важной темы курса математики, как открывающие скобки. Знание правил раскрытия скобок необходимо для того, чтобы правильно решать уравнения, в которых они используются.
Как правильно расширять скобки дополнительно
Раскрыть скобки перед знаком «+»
Это самый простой случай, потому что если перед скобками стоит знак сложения, то знаки внутри них не меняются при раскрытии скобок.Пример:
(9 + 3) + (1 — 6 + 9) = 9 + 3 + 1 — 6 + 9 = 16.
Как расширить круглые скобки, которым предшествует «-»
В этом случае нужно переписать все термины без скобок, но при этом изменить все знаки внутри них на противоположные. Знаки меняются только у терминов из тех скобок, перед которыми стоял знак «-». Пример:
Знаки меняются только у терминов из тех скобок, перед которыми стоял знак «-». Пример:
(9 + 3) — (1 — 6 + 9) = 9 + 3 — 1 + 6 — 9 = 8.
Как раскрыть скобки при умножении
Скобкам предшествует множитель
В этом случае нужно каждое слагаемое умножить на коэффициент и раскрыть скобки, не меняя знаки.Если у множителя стоит знак «-», то умножение меняет знаки слагаемых на противоположные. Пример:
3 * (1 — 6 + 9) = 3 * 1 — 3 * 6 + 3 * 9 = 3 — 18 + 27 = 12.
Как расширить две скобки со знаком умножения между ними
В этом случае нужно умножить каждое слагаемое из первых скобок на каждое слагаемое из вторых скобок, а затем сложить результаты. Пример:
(9 + 3) * (1 — 6 + 9) = 9 * 1 + 9 * (- 6) + 9 * 9 + 3 * 1 + 3 * (- 6) + 3 * 9 = 9 — 54 + 81 + 3 — 18 + 27 = 48.2) * 12 = 1728.
Как расширить 3 кронштейна
Существуют уравнения, в которых умножаются сразу 3 скобки. В этом случае необходимо сначала умножить члены первых двух скобок, а затем умножить сумму этого умножения на члены третьей скобки. Пример:
Пример:
(1 + 2) * (3 + 4) * (5 — 6) = (3 + 4 + 6 + 8) * (5 — 6) = — 21.
Эти правила раскрытия скобок в равной степени применимы к решению как линейных, так и тригонометрических уравнений.3 + 5x + 1 \)
Сумма нескольких многочленов может быть преобразована (упрощена) в стандартный многочлен.
Иногда члены полинома необходимо разделить на группы, заключив каждую группу в круглые скобки. Поскольку скобки противоположны раскрытию скобок, то легко сформулировать правил раскрытия скобок:
Если перед скобками ставится знак «+», то члены, заключенные в скобки, записываются с теми же знаками.3\)
Произведение монома на многочлен тождественно равно сумме произведений этого монома и каждого из членов многочлена.
Этот результат формулируется как правило.
Чтобы умножить одночлен на многочлен, нужно этот одночлен умножить на каждый из членов многочлена.
Мы уже много раз использовали это правило для умножения на сумму.
Произведение многочленов. Преобразование (упрощение) произведения двух многочленов
В общем случае произведение двух многочленов тождественно равно сумме произведений каждого члена одного многочлена и каждого члена другого.2 = (а — b) (а + b) \) — разность квадратов равна произведению разности на сумму.
Эти три тождества позволяют при преобразованиях заменить их левые части на правые и наоборот — правые части на левые. Самое сложное — увидеть соответствующие выражения и понять, что заменяет в них переменные a и b. Давайте рассмотрим несколько примеров использования формул сокращенного умножения.
Скобки используются для указания порядка выполнения действий в числовых, буквенных и переменных выражениях.Удобно переходить от выражения со скобками к тождественно равному выражению без скобок. Этот метод называется расширением скобок.
Раскрыть скобки означает избавиться от выражения из этих скобок.
Отдельного внимания заслуживает еще один момент, который касается особенностей записи решений при открытии скобок. Мы можем записать исходное выражение со скобками и результат, полученный после раскрытия скобок, как равенство.Например, после раскрытия скобок вместо выражения
Мы можем записать исходное выражение со скобками и результат, полученный после раскрытия скобок, как равенство.Например, после раскрытия скобок вместо выражения
3−(5−7) мы получим выражение 3−5 + 7. Оба эти выражения можно записать в виде равенства 3−(5−7) = 3− 5 + 7.
И еще один важный момент. В математике для сокращения записей принято не писать плюсик, если он стоит первым в выражении или в скобках. Например, если мы сложим два положительных числа, например, семь и три, то запишем не + 7 + 3, а просто 7 + 3, несмотря на то, что семь — тоже положительное число.Аналогично, если вы видите, например, выражение (5+х) — знайте, что перед скобкой стоит плюс, который не пишется, а перед пятеркой стоит плюс + (+5+х) .
Правило расширения скобок дополнительно
При раскрытии скобок, если перед скобками стоит плюс, то этот плюс вместе со скобками опускается.
Пример. Раскрыть скобки в выражении 2 + (7 + 3) Перед скобками плюс, поэтому знаки перед цифрами в скобках не меняются.
2 + (7 + 3) = 2 + 7 + 3
Правило раскрытия скобок при вычитании
Если перед скобками стоит минус, то этот минус вместе со скобками опускается, но слагаемые, которые были в скобках, меняют знак на противоположный. Отсутствие знака перед первым слагаемым в круглых скобках подразумевает наличие знака +.
Пример. Раскрыть скобки в выражении 2 — (7 + 3)
Перед скобками стоит минус, значит надо поменять знаки перед цифрами из скобок.Знака в скобках перед цифрой 7 нет, это означает, что семерка положительная, считается, что перед ней стоит знак +.
2 — (7 + 3) = 2 — (+ 7 + 3)
При раскрытии скобок убираем из примера минус, который был перед скобками, а самих скобок 2 — (+7+3), а знаки, которые были в скобках, меняем местами.
2 — (+ 7 + 3) = 2 — 7 — 3
Раскрывающие скобки при умножении
Если перед скобками стоит знак умножения, то каждое число внутри скобок умножается на множитель перед скобками.
При этом умножение минуса на минус дает плюс, а умножение минуса на плюс, как и умножение плюса на минус, дает минус.
Таким образом, скобки в произведениях раскрываются в соответствии с распределительным свойством умножения.
Пример. 2 (9 — 7) = 2 9 — 2 7
При умножении скобки на скобку каждый элемент первой скобки умножается на каждый член второй скобки.
(2 + 3) (4 + 5) = 2 4 + 2 5 + 3 4 + 3 5
На самом деле нет необходимости запоминать все правила, достаточно запомнить только одно, это: c(a-b) = ca-cb. Почему? Потому что если вместо с подставить в него единицу, то получится правило (а — b) = а — b. А если подставить минус единицу, то получится правило — (a — b) = — a + b. Ну а если вместо c подставить другую скобку, то можно получить последнее правило.
Раскрывающие скобки при делении
Если после скобок стоит знак деления, то каждое число внутри скобок делится на делитель после скобок, и наоборот.
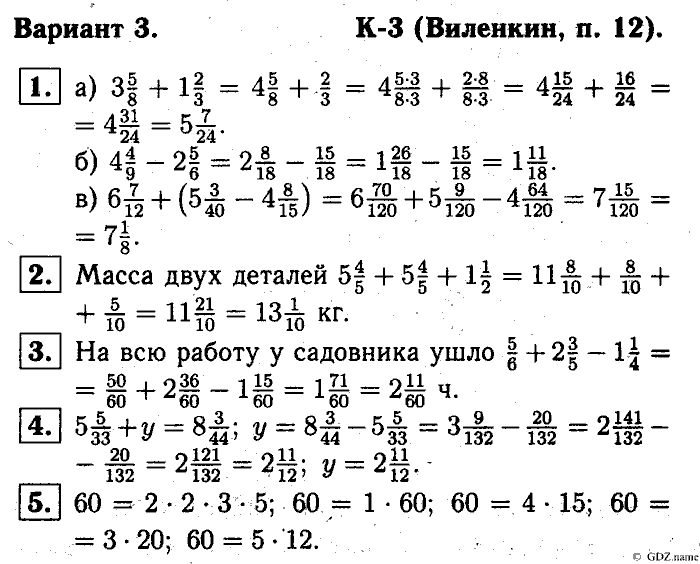
Пример. (9 + 6): 3 = 9: 3 + 6: 3
Как расширить вложенные скобки
Если выражение содержит вложенные скобки, то они раскрываются по порядку, начиная с внешних или внутренних.
При этом, открывая одну из скобок, важно не трогать остальные скобки, просто переписав их как есть.
Пример. 12 — (а + (6 — Ь) — 3) = 12 — а — (6 — Ь) + 3 = 12 — а — 6 + Ь + 3 = 9 — а + Ь
«Раскрывающие скобки» — Учебник по математике 6 класс (Виленкин)
Краткое описание:
В этом разделе вы узнаете, как раскрывать скобки в примерах.Для чего это? Все для того же, что и раньше – чтобы вам было легче и легче считать, чтобы меньше ошибаться, а в идеале (мечта вашей учительницы математики) чтобы вообще все решить без ошибок.
Вы уже знаете, что скобки в математической записи ставятся, если два математических знака идут подряд, если мы хотим показать объединение чисел, их перестановку. Раскрытие скобок означает избавление от лишних символов. Например: (-15) + 3 = -15 + 3 = -12, 18 + (- 16) = 18-16 = 2. Помните распределительное свойство умножения относительно сложения? Ведь в том примере мы тоже избавились от скобок для упрощения вычислений. Названное свойство умножения можно применить и к четырем, трем, пяти и более терминам. Например: 15 * (3 + 8 + 9 + 6) = 15 * 3 + 15 * 8 + 15 * 9 + 15 * 6 = 390. Вы замечали, что при раскрытии скобок числа в них не меняют знак, если число перед скобками положительное? Ведь пятнадцать — положительное число.А если решить этот пример: -15 * (3 + 8 + 9 + 6) = — 15 * 3 + (- 15) * 8 + (- 15) * 9 + (- 15) * 6 = -45 + ( — 120) + (- 135) + (- 90) = — 45-120-135-90 = -390. Перед скобками у нас стояло отрицательное число минус пятнадцать, когда мы раскрывали скобки, все числа начинали менять свой знак на другой — противоположный — с плюса на минус.
Например: (-15) + 3 = -15 + 3 = -12, 18 + (- 16) = 18-16 = 2. Помните распределительное свойство умножения относительно сложения? Ведь в том примере мы тоже избавились от скобок для упрощения вычислений. Названное свойство умножения можно применить и к четырем, трем, пяти и более терминам. Например: 15 * (3 + 8 + 9 + 6) = 15 * 3 + 15 * 8 + 15 * 9 + 15 * 6 = 390. Вы замечали, что при раскрытии скобок числа в них не меняют знак, если число перед скобками положительное? Ведь пятнадцать — положительное число.А если решить этот пример: -15 * (3 + 8 + 9 + 6) = — 15 * 3 + (- 15) * 8 + (- 15) * 9 + (- 15) * 6 = -45 + ( — 120) + (- 135) + (- 90) = — 45-120-135-90 = -390. Перед скобками у нас стояло отрицательное число минус пятнадцать, когда мы раскрывали скобки, все числа начинали менять свой знак на другой — противоположный — с плюса на минус.
Исходя из вышеприведенных примеров, можно выделить два основных правила раскрытия скобок:
1. Если у вас перед скобками стоит положительное число, то после раскрытия скобок все знаки чисел в скобках не меняются, но остаются точно такими же, как и были.
2. Если у вас перед скобками стоит отрицательное число, то после раскрытия скобок знак минус уже не пишется, а знаки всех абсолютно чисел в скобках резко меняются местами.
Например: (13 + 8) + (9-8) = 13 + 8 + 9-8 = 22; (13+8)-(9-8)=13+8-9+8=20. Немного усложним наши примеры: (13+8)+2(9-8)=13+8+2*9- 2 * 8 = 21 + 18-16 = 23. Вы заметили, что когда мы раскрывали вторые скобки, мы умножали на 2, но знаки оставались прежними.А вот пример: (3+8)-2*(9-8)=3+8-2*9+2*8=11-18+16=9, в данном примере число два отрицательное, это стоит перед скобками со знаком минус, поэтому при их раскрытии мы поменяли местами знаки чисел (девять было с плюсом, было с минусом, восемь было с минусом, было с плюсом).
.
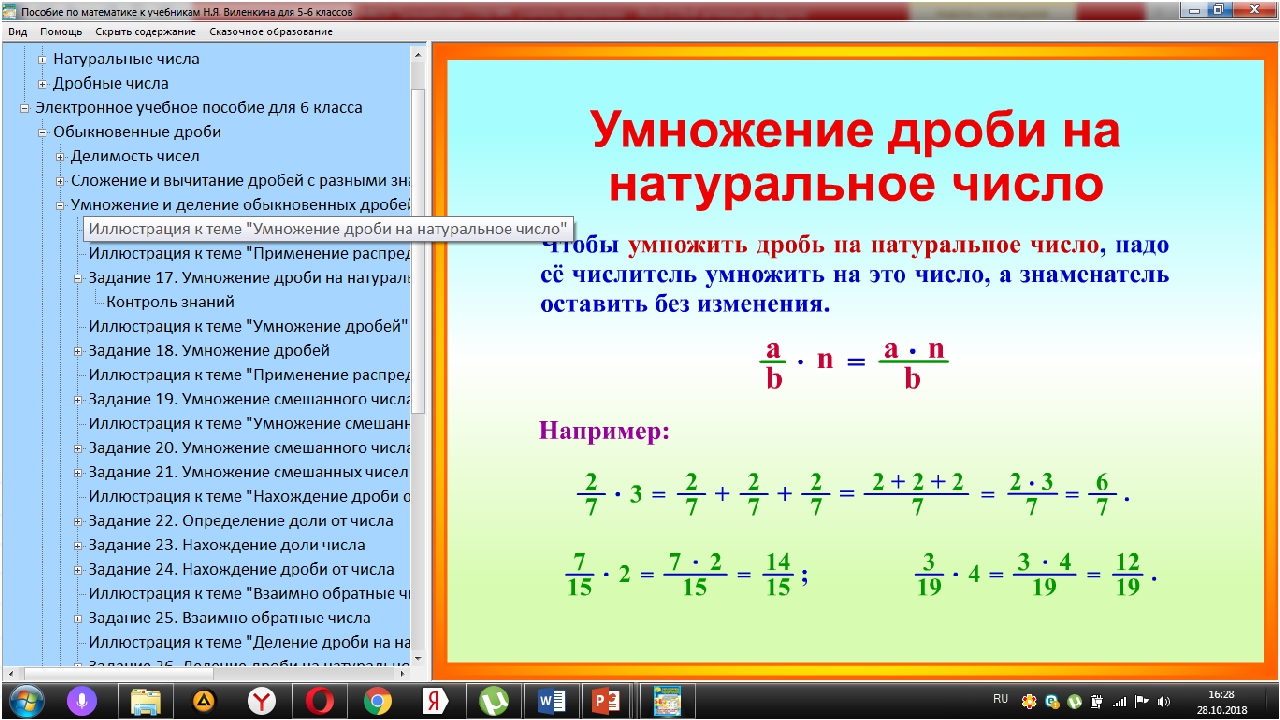 Решение задач
Решение задач Обыкновенные дроби – 91 час
Обыкновенные дроби – 91 час Взаимно простые числа
Взаимно простые числа 2. Сложение и вычитание дробей с разными знаменателями – 22 часа
2. Сложение и вычитание дробей с разными знаменателями – 22 часа
 3. Умножение и деление обыкновенных дробей – 31 час
3. Умножение и деление обыкновенных дробей – 31 час

 4. Отношения и пропорции – 18 часов
4. Отношения и пропорции – 18 часов Рациональные числа – 64 часа
Рациональные числа – 64 часа 6. Сложение и вычитание положительных и отрицательных чисел – 11 часов
6. Сложение и вычитание положительных и отрицательных чисел – 11 часов 7. Умножение и деление положительных и отрицательных чисел – 12 часов
7. Умножение и деление положительных и отрицательных чисел – 12 часов 8. Решение уравнений – 15 часов
8. Решение уравнений – 15 часов Подобные слагаемые»
Подобные слагаемые» 9 Координаты на плоскости – 13 часов
9 Координаты на плоскости – 13 часов Повторение. Решение задач – 15 часов
Повторение. Решение задач – 15 часов Решение задач на проценты»
Решение задач на проценты»