Поиск материала «Математика. 6 класс. Сборник задач и заданий для тематического оценивания. Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. 2010» для чтения, скачивания и покупки
Ниже показаны результаты поиска поисковой системы Яндекс. В результатах могут быть показаны как эта книга, так и похожие на нее по названию или автору.
Search results:
- А. Г. Мерзляк, В. Б. Полонский, E. M. Рабинович, М. С. Якир
Харьков «Гимназия». удк 51(075) 74.262. Одобрено к использованию в учебно-воспитательно.и процессе Министерством образования и науки Украины. от 10.08.2006 г.) Полонский В. Якир М. С. Сборник задач и заданий для тематического оценивания по математике для 6 класса. Гимназия. 2010. илл. ISBN 966-8319-45-1. Сборник является составной частью учебно-методического комплекта к учебнику «Математика. 6 класс» (авторы Мерзляк А. Лкир. содержит тренировочные задания, соответствующие представленным в учебнике темам.

cmiso.ru
- Скачать бесплатно Математика. Дидактические материалы.
6 класс — А. Г. Мерзляк, В. Б. Полонский, Е. М. Рабинович, М. С. Якир. cкачать в PDF. Дидактические материалы содержат упражнения для самостоятельных и контрольных работ. Используются в комплекте с учебником «Математика. 6 класс» (авт. А. Г. Мерзляк, В. Б. Полонский, М. С. Якир) системы «Алгоритм успеха». Соответствует Федеральному государственному образовательному стандарту основного общего образования (2010 г.).
fizikadlyvas.net
-
Купить эту книгу - Канцтовары
Канцтовары: бумага, ручки, карандаши, тетради.
Ранцы, рюкзаки, сумки.
И многое другое.
my-shop.ru
- Математика. Дидактические материалы. 6 класс — А.
 Г. Мерзляк…
Г. Мерзляк…
Дидактические материалы содержат упражнения для самостоятельных и контрольных работ. Используются в комплекте с учебником «Математика. 6 класс» (авт. А. Г. Мерзляк, В. Б. Полонский, М. С. Якир) системы «Алгоритм успеха».
6 класс» (авт. А. Г. Мерзляк, В. Б. Полонский, М. С. Якир) системы «Алгоритм успеха». Соответствует Федеральному государственному образовательному стандарту основного общего образования (2010 г.).
11klasov.net
- Сборники задач и заданий для тематического оценивания по…
Сборники являются составной частью учебно-методического комплекта к учебникам «Математика» (авторы Мерзляк А. Г., Полонский В. Б., Якир М. С). Они содержат тренировочные задания, соответствующие темам, которые представлены в учебнике. Их можно использовать для работы в классе и дома, а также во время самостоятельных работ.
 Также в сборнике приведены задания для тематического оценивания знаний учащихся в двух вариантах.
Также в сборнике приведены задания для тематического оценивания знаний учащихся в двух вариантах.b-ok.xyz
- Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир…
Сборник является составной частью учебно-методического комплекта к учебникам «Математика» (авторы Мерзляк А. Г., Полонский В. Б., Якир М. С). Он содержит тренировочные задания, соответствующие темам, которые представлены в учебнике. Их можно использовать для работы в классе и дома, а также во время самостоятельных работ. Также в сборнике приведены задания для тематического оценивания знаний учащихся в двух вариантах.
www.studmed.ru
- Домашние зачётные работы по математике 6 класс…
Сборник задач и заданий для тематического оценивания по. математике для 6 класса.- Харьков: Гимназия,2005. • А.П. Ершов, В.В. Голобородько.
 Самостоятельные и.
Самостоятельные и.Мнемозина, 1996. • А.Г. Мерзляк, В.Б. Полонский, Е.М. Рабинович, М.С. Якир. Математика: 6 класс: дидактические материалы: пособие для.
uchitelya.com
- Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир…
Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. Сборник задач и заданий для тематического оценивания по математике для 6 класса скачать (3814.7 kb.)
nashaucheba.ru
- Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир…
(Популярное пособие для родителей и педагогов) 5 класс: 120 стр. 6 класс: 128 стр. Сборники являются составной частью учебно-методического комплекта к учебникам «Математика» (авторы Мерзляк А. Г., Полонский В. Б., Якир М. С). Они содержат тренировочные задания, соответствующие темам, которые представлены в учебнике.
 Их можно использовать для работы в классе и дома, а также во время самостоятельных работ. Также в сборнике приведены задания для тематического оценивания знаний учащихся в двух вариантах.
Их можно использовать для работы в классе и дома, а также во время самостоятельных работ. Также в сборнике приведены задания для тематического оценивания знаний учащихся в двух вариантах.www.studmed.ru
- Математика Сборник задач и заданий 6 класс Мерзляк.
Математика Сборник задач 6 класс Мерзляк 2010. 32. Автори:Мерзляк А.Г., Полонский В.Б., Рабинович Е.М. Видавництво:Гімназія, Харьков. Рік видання:2010.
4book.org
- Мерзляк дидактические материалы 6 класс математика 2017
Просмотров: 39782. Инфо. Читать онлайн. Автор: А.Г. Мерзляк. Предмет (категория): Дидактические материалы по математике. Класс: 6. Читать онлайн: Да. Скачать бесплатно: Да. Формат книги: jpg.
 Размер книги/ГДЗ: 9,03 Мб. Год публикации (выпуска): 2017. Читать онлайн или скачать дидактические материалы по математике для 6 класса Мерзляка 2017 года:
Размер книги/ГДЗ: 9,03 Мб. Год публикации (выпуска): 2017. Читать онлайн или скачать дидактические материалы по математике для 6 класса Мерзляка 2017 года:gdz-online.ws
- Сборники задач и заданий для тематического оценивания по…
Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. Скачать книгу бесплатно (djvu, 3.77 Mb) | Читать «Сборники задач и заданий для тематического оценивания по математике для 5 и 6 класса.
bookscat.org
- Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир…
Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. Сборники задач и заданий для тематического оценивания по математике для 5-6 класса (Документ). Решения с комментариями к итоговым контрольным работам (Лабораторная работа).

Жафяров А.Ж., Созоненко Р.С. Сборник подготовительных задач по математике для поступающих в ВУЗы (Документ). Сергеев И.С., Панферов B.C. ЕГЭ: 1000 задач с ответами и решениями по математике. Все задания группы С (Документ).
nashaucheba.ru
- Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир…
Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. Сборники задач и заданий для тематического оценивания по математике для 5-6 класса скачать (7948.8 kb.)
nashaucheba.ru
- Сборники задач и заданий для тематического оценивания по…
Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. Скачать книгу бесплатно (djvu, 3.99 Mb) | Читать «Сборники задач и заданий для тематического оценивания по математике для 5 и 6 класса.

bookscat.org
- 6 класс. Математика. Дидактические материалы. А. Г. Мерзляк
Дидактические материалы содержит упражнения для самостоятельных и контрольных работ. Они используется в комплекте с учебником «Математика. 6 класс» (авт. А.Г. Мерзляк, В.Б. Полонский, М.С. Якир) системы «Алгоритм успеха».Соответствуют федеральному государственному.
А.Г. Мерзляк, В.Б. Полонский, М.С. Якир) системы «Алгоритм успеха». Соответствуют федеральному государственному образовательному стандарту основного общего образования (2010 г.).
multiurok.ru
- Контрольные работы по математике 6 класс (Мерзляк) скачать
учебник Математика. 6 класс. Мерзляк А.Г., Полонский В.Б., Якир М.С. Контрольная работа №1. Делимость натуральных чисел.
Тренажёр «Решаем задачи» 1 класс.
 Сборник контрольных работ по математике для ППССЗ. Контрольная работа «Средняя линия треугольника. Трапеция. Вписанные и описанные четырёхугольники» 7 класс (Мерзляк).
Сборник контрольных работ по математике для ППССЗ. Контрольная работа «Средняя линия треугольника. Трапеция. Вписанные и описанные четырёхугольники» 7 класс (Мерзляк).uchitelya.com
- Математика. 6 класс — Мерзляк А.Г., Полонский В.Б., Якир М.С.
6 класс — Мерзляк А.Г., Полонский В.Б., Якир М.С. Учебник предназначен для изучения математики в 6 классе общеобразовательных учреждений. В нем предусмотрена уровневая дифференциация, позволяющая формировать у школьников познавательный интерес к математике. Содержит большой дидактический материал: задания для подготовки к изучению нового материала, задания для повторения. Учебник входит в систему «Алгоритм успеха».
11klasov.net
- А. Г. Мерзляк, В. Б. Полонский, Е. М. Рабинович, М. С. Якир.
 ..
..
Автор: А. Г. Мерзляк, В. Б. Полонский, Е. М. Рабинович, М. С. Якир Название: Математика. Дидактические материалы. 6 класс. Формат: PDF Размер: 1,09 Мб Язык: Русский. Скачать по прямой ссылке. Дидактические материалы содержат упражнения для самостоятельных и контрольных работ. Используются в комплекте с учебником «Математика. 6 класс» (авт. А. Г. Мерзляк, В. Б. Полонский, М. С. Якир) системы «Алгоритм успеха».
www.psyoffice.ru
- А. Г. Мерзляк, В. Б. Полонский, E. M. Рабинович, М. С. Якир
Якир М. С. Сборник задач и заданий для тематического оценивания по математике для 5 класса. Гимназия, 2010. ISBN 966-8319-36-2. Сборник является составной частъю учебно-методического комплекта к учебнику «Математика. 5 класс» (авторы Мерзляк А. Г., Полонский В. Б., Якир М. С.). Он содержит тренировочные задания, соответствующие темам, которые представлены в учебнике. Их можно использовать для работы в классе и дома, а также во время самостоятельных работ.

cmiso.ru
- Математика. 6 класс. Дидактические материалы. Мерзляк…
Готовые домашние задания к рабочей тетради c дидактическими материалами включающие в себя самостоятельные и контрольные работы по математике за шестой класс — помогут тебе ответить и решить работы на оценку «отлично». Авторы: Мерзляк, Полонский, Якир, издательство: вентана-граф. С помощью нашего гдз вы всегда сможете найти правильное решение, с тщательными разъяснениями. А родители, в частности, смогут показать алгоритмическое решение, пользуясь нашим сайтом.
dnsis.ru
- Математика. Дидактические материалы. 6 класс — А. Г. Мерзляк…
Дидактические материалы. 6 класс — А. Г. Мерзляк, В. Б. Полонский, Е. М. Рабинович, М. С. Якир. Дидактические материалы содержат упражнения для самостоятельных и контрольных работ.
 Используются в комплекте с учебником «Математика. 6 класс» (авт. А. Г. Мерзляк, В. Б. Полонский, М. С. Якир) системы «Алгоритм успеха».
Используются в комплекте с учебником «Математика. 6 класс» (авт. А. Г. Мерзляк, В. Б. Полонский, М. С. Якир) системы «Алгоритм успеха».cdnpdf.com
- ГДЗ Дидактические материалы по Математике 6 класс Мерзляк…
ГДЗ решебник Математика 6 класс дидактические материалы Мерзляк А.Г. Вентана-граф 2017 ФГОС с ответами онлайн бесплатно!
ГДЗ Математика Дидактические материалы Алгоритм успеха за 6 класс Мерзляк
Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С.
gdz.moda
- ГДЗ: Математика 6 класс Мерзляк — Дидактические материалы
«Дидактические материалы по математике 6 класс» Мерзляка, Полонского, Рабиновича издательства Вентана-Граф позволяют закрепить изученный по учебнику «Математика. 6 класс» Мерзляка материал, поскольку в нем собраны 4 варианта упражнений по 229 номеров заданий в каждом, которые, в свою очередь, разделены по изучаемым темам.
 В конце книги даны 2 варианта контрольных работ, которые также разделены по темам.
В конце книги даны 2 варианта контрольных работ, которые также разделены по темам.gdzbezmoroki.com
- ГДЗ Математика 6 класс Мерзляк, Полонский, Рабинович…
Математика – это числа. Какие бывают, что можно с ними делать, отношения, пропорции, проценты и многое другое нужно будет изучить и закрепить на уроках в 6 классе . Чтобы изученные темы оставались в памяти надолго, нужны практические навыки.
Авторы всегда делают все, чтобы этого не произошло. Созданный учебник «Математика 6 класс дидактические материалы Мерзляк, Полонский, Рабинович Вентана-Граф» позволит учащимся потренироваться и выполнить самостоятельные и контрольные работы.
megashpora.com
- ГДЗ решебник по математике 6 класс Мерзляк, Полонский.
 ..
..
«ГДЗ по математике 6 класс дидактические материалы Мерзляк (Вентана-Граф)» окажет твердую поддержку шестиклассникам в освоении «царицы наук». Учебное пособие разработано в соответствии с требованиями Федерального государственного образовательного стандарта признанными авторами в данной области. Решебник включает верные ответы на все номера заданий основного издания. В шестом классе программа по математике значительно усложняется, и включает элементы геометрии.
spishi.ltd
- Математика 6 класс Мерзляк А.Г., Полонский В.Б., Якир М.С.
Для каждого параграфа подобраны задачи для самостоятельного решения, приступать к которым советуем только после усвоения теоретического материала. Среди заданий есть как простые и средние по сложности, так и трудные задачи. Каждый параграф заканчивается особой задачей, которую мы назвали «Задачей от мудрой совы».
 Для её решения следует проявить изобретательность и смекалку. Кроме того, в рубрике «Когда сделаны уроки» вы можете узнать о важных математических объектах — числах и фигурах, об истории их возникновения.
Для её решения следует проявить изобретательность и смекалку. Кроме того, в рубрике «Когда сделаны уроки» вы можете узнать о важных математических объектах — числах и фигурах, об истории их возникновения.znayka.win
- Контрольные работы по математике 6 класс УМК Мерзляк…
Контрольные работы по математике 5 классУМК Мерзляк А.Г., Полонский В.Б., Якир М.С…. Контрольная работа по математике. 6 класс. Отношения и пропорции. УМК Мерзляк А.Г., Полонский В.Б., Якир М.С.
nsportal.ru
- Решебник (ГДЗ) Математика 6 класс А.Г. Мерзляк… | Вшколе
Каждый школьник изучает математику по учебнику для шестого класса. Все задания очень объемные и сложные. Плюс ко всему дети учатся выполнять задания самостоятельно. Для этого авторы создали сборники задач и контрольных работ по математике.
 Ответы к дополнительным задачам и примерам. Найти ответы к заданиям поможет решебник математика 6 клас А.Г. Мерзляк, В.Б. Полонський, Ю.М. Рабінович, М.С. Якір Збірник задач і контрольних робіт 2014 года, который уже опубликован на нашем сайте и готов помочь всегда.
Ответы к дополнительным задачам и примерам. Найти ответы к заданиям поможет решебник математика 6 клас А.Г. Мерзляк, В.Б. Полонський, Ю.М. Рабінович, М.С. Якір Збірник задач і контрольних робіт 2014 года, который уже опубликован на нашем сайте и готов помочь всегда.vshkole.com
- Математика 6 класс. УМК Мерзляк и др. (2014-2017)
Учебник / А.Г.Мерзляк, В.Б.Полонский, М.С. Якир — М.: Вентана-Граф, 2014» . Учебник включен в федеральный перечень учебников. В нём предусмотрена уровневая дифференциация, позволяющая формировать у школьников познавательный интерес к математике.
Ниже представлена ознакомительная версия с цитатами в учебных целях для учащихся на самообучении (семейное образование, домашнее обучение). После ознакомления рекомендуем КУПИТЬ книгу: «Мерзляк, Полонский, Якир: Математика.
xn--6-8sb3ae5aa.xn--p1ai
- ГДЗ по Математике 6 класс: Мерзляк.
 Решебник с подробными…
Решебник с подробными…
Решебник математики шестого класса к учебнику А.Г. Мерзляка. В этом сборнике готовых домашних заданий представлены две версии учебника математики от Мерзляка – старый за 2014 год и новый за 2019 год. Они немного отличаются между собой по структуре, количеству страниц, порядку практических заданий. Версия 2014 года содержит 1346 номеров, а в 2019 году их 1446. Наш решебник содержит подробные ответы к обеим версиям, чтобы школьник не путался в нумерации параграфов и задач.
otvetkin.info
- Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир…
Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. Сборник задач и заданий для тематического оценивания по математике для 6 класса (Документ). Решения с комментариями к итоговым контрольным работам (Лабораторная работа). Белошистая А.В. Тетрадь по математике и конструированию для 1 класса коррекционно-развивающего обучения (Документ).

nashaucheba.ru
- Математика 6 класс Мерзляк А.Г., Полонский В.Б., Якир М.С.
Для каждого параграфа подобраны задачи для самостоятельного решения, приступать к которым советуем только после усвоения теоретического материала. Среди заданий есть как простые и средние по сложности, так и трудные задачи. Каждый параграф заканчивается особой задачей, которую мы назвали «Задачей от мудрой совы». Для её решения следует проявить изобретательность и смекалку. Кроме того, в рубрике «Когда сделаны уроки» вы можете узнать о важных математических объектах — числах и фигурах, об истории их возникновения.
uchebniksonline.ru
На данной странице Вы можете найти лучшие результаты поиска для чтения, скачивания и покупки на интернет сайтах материалов, документов, бумажных и электронных книг и файлов похожих на материал «Математика. 6 класс. Сборник задач и заданий для тематического оценивания. Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. 2010»
6 класс. Сборник задач и заданий для тематического оценивания. Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. 2010»
Для формирования результатов поиска документов использован сервис Яндекс.XML.
Нашлось 17 млн ответов. Показаны первые 32 результата(ов).
Дата генерации страницы:
Сборник задач по математике 6 класс в категории «Подарки, хобби, книги»
Розв’язання до збірника задач з математики Мерзляка. 6 клас. Щербань П.
На складе
Доставка по Украине
95 грн
Купить
Znai Bilshe
Розв’язання до збірника задач з математики Мерзляка. 6 клас. Щербань П
Доставка по Украине
99 грн
Купить
Шкільна література
Розв’язання до збірника задач і контрольних робіт з математики 6 клас. Щербань П.
На складе
Доставка по Украине
100 грн
Купить
Інтернет-магазин «Schoolbooks»
Збірник задач і контрольних робіт з математики 6клас А. Г.Мерзляк,В.Б.Полонський, Ю.М.Рабінович, М.С.Якір
Г.Мерзляк,В.Б.Полонський, Ю.М.Рабінович, М.С.Якір
Доставка по Украине
70 грн
Купить
Книжковий Почайна
Збірник задач і контрольних робіт з математики 6 клас. А.Г. Мерзляк, В.Б. Полонський та ін.
Доставка по Украине
100 грн
Купить
Інтернет-магазин «Schoolbooks»
Сборник задач и контрольных работ по математике, 6 класс. Мерзляк А.Г
Доставка по Украине
60 грн
Купить
Учебные книги и не только
6 клас Розв’язання до збірника задач з математики Мерзляка Щербань П. Гімназія
Доставка из г. Киев
100 грн
Купить
Интернет-магазин «КНИЖЕЧКА»
Решения к сборнику задач и контрольных работ по математике, 6 класс. Щербань П.
Доставка по Украине
80 грн
Купить
Bookshelf
Сборник задач и контрольных работ по математике, 6 класс. Мерзляк А.Г и др.
Доставка по Украине
108 грн
Купить
Bookshelf
Розв’язання до збірника задач і контрольних робіт з математики, 6 клас. Щербань П.
Щербань П.
Доставка по Украине
80 грн
Купить
Bookshelf
Решения к сборнику задач и контрольных работ по математике, 6 класс. Щербань П
На складе
Доставка по Украине
100 грн
Купить
Інтернет-магазин «Schoolbooks»
Сборник задач и контрольных работ по математике, 6 класс. Мерзляк А.Г., Полонский В.Б., и др.
На складе
Доставка по Украине
100 грн
Купить
Інтернет-магазин «Schoolbooks»
Математика 1 класс СБОРНИК Задачи упражнения тесты с цветной вкладкой кубик Рубика НУШ Будна Богдан
На складе
Доставка по Украине
70 грн
Купить
Portfel4ik.com «С нами учиться легче!»
Математика 2 класс СБОРНИК Задачи упражнения тесты НУШ Будна Богдан
На складе
Доставка по Украине
60 грн
Купить
Portfel4ik.com «С нами учиться легче!»
Математика 3 класс СБОРНИК Задачи упражнения тесты НУШ Будна Богдан
На складе
Доставка по Украине
60 грн
Купить
Portfel4ik. com «С нами учиться легче!»
com «С нами учиться легче!»
Смотрите также
Математика 4 класс СБОРНИК Задачи упражнения тесты НУШ Будна Богдан
На складе
Доставка по Украине
60 грн
Купить
Portfel4ik.com «С нами учиться легче!»
Математика 1 класс СБОРНИК Задачи упражнения тесты НУШ Будна Богдан
На складе
Доставка по Украине
60 грн
Купить
Portfel4ik.com «С нами учиться легче!»
Математика 6 клас. Збірник задач і контрольних робіт. Аркадій Мерзляк
На складе в г. Киев
Доставка по Украине
95 грн
Купить
Znai Bilshe
Математика 6 клас.Збірник задач і контрольних робіт.Мерзляк, Полонський, Рабінович, Якір.
На складе в г. Киев
Доставка по Украине
80 грн
Купить
Школяр
Розв’язання до збірника задач і контрольних робіт Мерзляка 6 клас Математика. Авт. Щербань.
На складе в г. Киев
Доставка по Украине
90 грн
Купить
Школяр
Розв’язання до Збірника задач і контрольних робіт Математика 6 клас. Щербань П.
На складе в г. Киев
Доставка по Украине
95 грн
Купить
Znai Bilshe
Математика 5 клас. Збірник задач і контрольних робіт. Мерзляк, Полонський, Рабінович, Якір.
На складе в г. Киев
Доставка по Украине
80 грн
Купить
Школяр
Математика 11 клас. Збірник задач і контрольних робіт. Мерзляк, Полонський, Рабінович, Якір.
На складе в г. Киев
Доставка по Украине
80 грн
Купить
Школяр
Математика 10 клас. Збірник задач і контрольних робіт. Мерзляк, Полонський, Рабінович, Якір.
На складе в г. Киев
Доставка по Украине
80 грн
Купить
Школяр
6 клас. Математика. Збірник задач і контрольних робіт.Мерзляк, Полонський, Рабінович. Видавництво Гімназія
Математика. Збірник задач і контрольних робіт.Мерзляк, Полонський, Рабінович. Видавництво Гімназія
На складе в г. Киев
Доставка по Украине
80 грн
Купить
Моя Книга
Відповіді та розв’язання до збірника задач і контрольних робіт Мерзляка 6 клас Математика.
На складе в г. Киев
Доставка по Украине
100 грн
Купить
Моя Книга
Математика. Збірник задач і контрольних робіт 6 клас. Мерзляк А.Г.
На складе
Доставка по Украине
80 грн
Купить
Шкільна література
Збірник задач і контрольних робіт з математики, 6 клас. А.Г. Мерзляк та ін.
Доставка по Украине
108 грн
Купить
Bookshelf
Розв’язання до Збірника задач і контрольних робіт Математика 5 клас. Щербань П.
На складе в г. Киев
Доставка по Украине
95 грн
Купить
Znai Bilshe
| Табличка на дверь |
Учебное пособие по анализу растительности Hyperion EO-1
Учебное пособие по индексам растительности Hyperion EO-1
В этом учебном пособии используются гиперспектральные изображения EO-1 Hyperion для определения участков умирающих хвойных деревьев, вызванных повреждением насекомыми. Вы узнаете, как предварительно обрабатывать изображения и как создавать индексы растительности, которые используют определенные диапазоны длин волн, чтобы выделить области стрессовой растительности.
Вы узнаете, как предварительно обрабатывать изображения и как создавать индексы растительности, которые используют определенные диапазоны длин волн, чтобы выделить области стрессовой растительности.
Расчетное время прохождения этого урока составляет два часа. Используйте ENVI 5.2 или более позднюю версию.
См. следующие разделы:
- Файлы, используемые в этом учебном пособии
- Предварительная обработка
- Индексы растительности
- Ссылки
Файлы, используемые в этом учебном пособии
Файлы учебного пособия доступны на нашей веб-странице учебных пособий по ENVI или на DVD-диске с ресурсами ENVI в гиперспектральном каталоге. Скопируйте файлы на локальный диск.
Скопируйте файлы на локальный диск.
|
Файл |
Описание |
HyperionForest.dat |
Изображение Hyperion EO-1 в растровом формате ENVI с 242 спектральными каналами и пространственным разрешением 30 м, полученное 20 июля 2013 г. |
Серый многоугольник на следующей карте показывает приблизительную зону охвата изображения. Он охватывает небольшую территорию национальных лесов Сент-Джо и Клируотер в восточном Айдахо, США.
Эта конкретная сцена Гипериона была выбрана для урока, потому что она показывает свидетельства широко распространенного повреждения насекомыми от горного соснового жука и западного бальзамического короеда.
Предварительная обработка
Перед выполнением любого научного анализа изображения выполните следующие действия предварительной обработки.
Открытие и отображение изображения
- В строке меню ENVI выберите Файл > Открыть .
- Выберите файл HyperionForest.dat. Щелкните Открыть .
- Нажмите клавишу F12 на клавиатуре, чтобы просмотреть изображение в полном размере.

- Более подробно изучите изображение с помощью инструментов навигации на панели инструментов. В полноцветном отображении мертвая и поврежденная растительность окрашена в серый или красно-серый цвет. Ущерб от жуков, вероятно, является причиной гибели хвойных деревьев в этом регионе. Здоровая растительность окрашена в зеленый цвет.
Это изображение является пространственным подмножеством более крупного изображения Hyperion, которое было загружено с веб-сайта USGS EarthExplorer в формате HDF4 (Level-1R). Мы определили пространственное подмножество и сохранили его в растровом формате ENVI, чтобы создать файл меньшего размера для этого руководства. Мы также сократили названия групп в соответствующем заголовочном файле.
Если для параметра Auto Display Method for Multispectral Files установлено значение True Color , изображение отображается с использованием каналов 29 (красный), 20 (зеленый) и 12 (синий), чтобы получить приблизительное представление в истинном цвете:
Просмотр метаданных
- В диспетчере слоев щелкните правой кнопкой мыши имя файла HyperionForest.dat и выберите Просмотр метаданных .
- Щелкните категорию Spectral в левой части средства просмотра метаданных.
- Прокрутите вправо, пока не увидите поля Radiance Gains и Radiance Offsets . Полосы 1-70 — это диапазоны видимого/ближнего инфракрасного диапазона (VNIR). Позже, когда вы откалибруете данные, инструмент радиометрической калибровки ENVI умножит значение усиления 0,025 на каждый пиксель в этом диапазоне каналов, что равносильно делению каждого пикселя на 40.
 Полосы 71–242 относятся к коротковолновому инфракрасному диапазону (SWIR). группы. Инструмент «Радиометрическая калибровка» будет умножать значение усиления 0,0125 на каждый пиксель в этом диапазоне полос, что эквивалентно делению значения каждого пикселя на 80.
Полосы 71–242 относятся к коротковолновому инфракрасному диапазону (SWIR). группы. Инструмент «Радиометрическая калибровка» будет умножать значение усиления 0,0125 на каждый пиксель в этом диапазоне полос, что эквивалентно делению значения каждого пикселя на 80.
Примечание: Этот конкретный файл относится к 2013 году и используется с ENVI 5.2. Порядок полос будет другим в ENVI 5.3 и более поздних версиях. Файлы Hyperion HDF4 будут иметь следующий порядок полос: полосы 1-59 и 71-81 имеют значения усиления 0,025, а полосы 60-70 и 82-242 имеют значения усиления 0,0125.
- Щелкните категорию Время в левой части средства просмотра метаданных и запишите Время получения . Это должно быть 2013-07-20T17:36:52Z . Эта дата и время понадобятся вам позже во FLAASH.
- Щелкните Система координат , затем категории Geo Points .
 Система координат изображения — географическая широта/долгота WGS-84, но это не означает, что изображение имеет правильную географическую привязку. Категория Geo Points указывает, что известны только четыре угловые точки изображения. ENVI рассматривает это как псевдо 9.Проекция 0007. Он применяет преобразование аффинной карты для деформации изображения на основе четырех угловых точек и коэффициентов Kx/Ky. Он пытается вычислить географические координаты для каждого пикселя. Этот тип прогноза содержит высокую степень изменчивости и не является географически точным. У ENVI нет инструментов для ортотрансформирования данных Hyperion. Одним из вариантов является использование инструмента Регистрация изображения на карте для создания наземных опорных точек для регистрации изображения на карте. Вы не будете выполнять эти шаги в этом руководстве.
Система координат изображения — географическая широта/долгота WGS-84, но это не означает, что изображение имеет правильную географическую привязку. Категория Geo Points указывает, что известны только четыре угловые точки изображения. ENVI рассматривает это как псевдо 9.Проекция 0007. Он применяет преобразование аффинной карты для деформации изображения на основе четырех угловых точек и коэффициентов Kx/Ky. Он пытается вычислить географические координаты для каждого пикселя. Этот тип прогноза содержит высокую степень изменчивости и не является географически точным. У ENVI нет инструментов для ортотрансформирования данных Hyperion. Одним из вариантов является использование инструмента Регистрация изображения на карте для создания наземных опорных точек для регистрации изображения на карте. Вы не будете выполнять эти шаги в этом руководстве. - Закройте средство просмотра метаданных.
Анимация каналов
Вы можете анимировать все 242 канала, чтобы увидеть, какие из них имеют неверные данные. Вы удалите эти полосы позже.
Вы удалите эти полосы позже.
- В диспетчере слоев щелкните правой кнопкой мыши файл HyperionForest.dat и выберите Band Animation . Появится диалоговое окно Band Animation, и анимация начнется резко.
- Во время воспроизведения видео нажмите кнопку Без задержки раскрывающееся меню и выберите время задержки 0,5 сек для замедления анимации.
- Переместите ползунок назад к началу анимации (влево), затем нажмите кнопку Воспроизвести . В диалоговом окне Band Animation указан номер канала, отображаемый в данный момент в каждом кадре.
Датчик Hyperion видимого и ближнего инфракрасного (VNIR) имеет 70 полос, а коротковолновый инфракрасный (SWIR) датчик имеет 172 полосы. Следующие полосы уже установлены на нулевые значения (Барри, 2001):
- 1-7
- 58-76
- 225-242
Другие полосы на этом изображении имеют сильный шум, соответствующий сильному поглощению водяного пара; эти полосы обычно удаляются из обработки (Dat et al. , 2003):
, 2003):
- 121-126
- 167-180
- 222-224
Обозначить плохие полосы
- На панели инструментов введите edit . Дважды щелкните имя инструмента Edit ENVI Header , которое появляется.
- В диалоговом окне выбора входного файла выберите HyperionForest.dat и нажмите OK .
- В диалоговом окне «Редактировать метаданные растра» перейдите к полю Bad Bands List .
- Нажмите кнопку Выбрать все .
- Перейдите к началу списка диапазонов.
- Удерживайте нажатой клавишу Ctrl на клавиатуре.
- Нажмите, чтобы отменить выбор следующих диапазонов полос (чтобы они были окрашены в белый цвет).
 Когда вы отмените выбор последней полосы в группе, отпустите клавишу Ctrl . При необходимости прокрутите список групп вниз. Затем снова удерживайте клавишу Ctrl и отмените выбор следующей группы плохих полос.
Когда вы отмените выбор последней полосы в группе, отпустите клавишу Ctrl . При необходимости прокрутите список групп вниз. Затем снова удерживайте клавишу Ctrl и отмените выбор следующей группы плохих полос.
- 1-7
- 58-76
- 121-126
- 167-180
- 222-242
На следующем снимке экрана показан пример отмены выбора плохих полос:
Количество выбранных элементов (хорошие полосы, выделенные синим цветом) должно быть 175.
- Нажмите OK в диалоговом окне «Редактировать значения списка плохих полос», а затем еще раз в диалоговом окне «Информация о заголовке». Файл закрывается и удаляется с экрана.
- Выберите «Файл » > «Открыть » в строке меню и снова откройте файл HyperionForest.dat.
Некоторые из оставшихся полос имеют эффект вертикальных полос, что является известной проблемой, возникающей из-за плохой калибровки детектора на сканере с веерным сканированием Hyperion. Доступны и описаны в литературе по дистанционному зондированию различные алгоритмы дестрайпинга. В этом уроке мы не будем исправлять эти вертикальные полосы.
Доступны и описаны в литературе по дистанционному зондированию различные алгоритмы дестрайпинга. В этом уроке мы не будем исправлять эти вертикальные полосы.
Следующим шагом является калибровка изображения по спектральной яркости.
Калибровка изображения
- На панели инструментов введите радио . Дважды щелкните появившееся имя инструмента Radiometric Calibration .
- В диалоговом окне «Выбор файла» уже выбран файл HyperionForest.dat. Поле Spectral Subset показывает 175 из 242 каналов, что подтверждает распознавание плохих каналов. Нажмите OK .
- В диалоговом окне «Радиометрическая калибровка» нажмите «Применить настройки FLAASH» . Это создаст изображение яркости с чередованием полос (BIL) со значениями с плавающей запятой в правильных единицах, необходимых для инструмента коррекции атмосферы FLAASH.
- Нажмите кнопку Browse и перейдите в каталог, в котором вы хотите сохранить выходные данные.
- Введите имя выходного файла Radiance.dat.
- Отключите параметр Показать результат .
- Щелкните OK . Процесс калибровки может занять несколько минут, так как это большой файл со 175 полосами для обработки.
Примечание: Не изменяйте поле Масштабный коэффициент . Значения пикселей HyperionForest.dat указаны в единицах Вт/(м2 * ср * мкм). Инструмент «Радиометрическая калибровка» применит значения усиления, указанные в разделе «Просмотр метаданных» выше, затем умножит значения пикселей на 0,1, чтобы они были выражены в единицах мкВт/(см2 * ср * нм), что требуется для ввода в ВСПЫШКА.
Значения пикселей HyperionForest.dat указаны в единицах Вт/(м2 * ср * мкм). Инструмент «Радиометрическая калибровка» применит значения усиления, указанные в разделе «Просмотр метаданных» выше, затем умножит значения пикселей на 0,1, чтобы они были выражены в единицах мкВт/(см2 * ср * нм), что требуется для ввода в ВСПЫШКА.
Коррекция атмосферных эффектов
Дальнейшая калибровка изображения по видимому коэффициенту отражения поверхности дает наиболее точные результаты при использовании спектральных индексов. Это особенно важно для гиперспектральных датчиков, таких как AVIRIS и EO-1 Hyperion. Калибровка изображений по коэффициенту отражения поверхности также обеспечивает согласованность при сравнении показателей во времени и с разных датчиков.
Это особенно важно для гиперспектральных датчиков, таких как AVIRIS и EO-1 Hyperion. Калибровка изображений по коэффициенту отражения поверхности также обеспечивает согласованность при сравнении показателей во времени и с разных датчиков.
На этих этапах вы будете использовать FLAASH для удаления атмосферных эффектов с изображения и создания изображения кажущейся отражательной способности поверхности.
FLAASH — это основанная на моделях программа переноса излучения, разработанная компанией Spectral Sciences, Inc. Она использует код переноса излучения MODTRAN4 для корректировки изображений с учетом атмосферного водяного пара, кислорода, углекислого газа, метана, поглощения озона, а также молекулярного и аэрозольного рассеяния. Для запуска FLAASH необходимо приобрести отдельную лицензию на модуль коррекции атмосферы: FLAASH и QUAC.
Выполните следующие действия:
- В панели инструментов введите flaash . Дважды щелкните FLAASH Атмосферная коррекция Появляющееся название инструмента.

- Нажмите кнопку Input Radiance Image .
- В диалоговом окне «Входной файл FLAASH» выберите Radiance.dat и нажмите OK .
- В диалоговом окне Radiance Scale Factors выберите параметр Использовать единый масштабный коэффициент для всех полос и оставьте значение по умолчанию 1,0 для Единый масштабный коэффициент . Инструмент «Радиометрическая калибровка» уже применил правильные значения усиления и коэффициенты масштабирования, поэтому здесь не требуется никаких дополнительных настроек.
- Щелкните OK .
Определение выходных файлов
-
В поле Output Reflectance File введите полный путь к каталогу, в который вы хотите записать выходной файл отражения. В качестве имени файла введите SurfaceReflectance.dat.
- В поле Выходной каталог для файлов FLAASH введите полный путь к каталогу, в который вы хотите записать все остальные выходные файлы FLAASH.
 К ним относятся изображение водяного пара в столбце, карта классификации облаков, файл журнала и (необязательно) файл шаблона.
К ним относятся изображение водяного пара в столбце, карта классификации облаков, файл журнала и (необязательно) файл шаблона. - В поле Корневое имя для файлов FLAASH введите корневое имя, которое будет префиксом для выходных файлов FLAASH.
Выбор сцены и опций сенсора
-
FLAASH автоматически определяет географические координаты центра сцены, поэтому вам не нужно вводить эти значения.
- В раскрывающемся меню Sensor Type выберите Hyperspectral > Hyperion .
- Заполните остальные поля следующим образом:
- Датчик Высота (км): 705 для КА ЭО-1
- Высота над уровнем моря (км): 1 , средняя высота сцены, рассчитанная с использованием картографической службы Google Earth™
- Размер пикселя (м): 30
- Дата отправки: см.
 дату, которую вы отметили ранее в шагах просмотра метаданных. Введите 20 июля 2013 г. .
дату, которую вы отметили ранее в шагах просмотра метаданных. Введите 20 июля 2013 г. . - Время полета (GMT): см. время, которое вы отметили ранее в шагах просмотра метаданных. Введите 17:36:52 .
Выберите параметры модели атмосферы
Гиперспектральные датчики обычно содержат достаточно информации, необходимой для оценки водяного пара и аэрозолей в атмосфере. Таким образом, вы извлечете водяной пар и аэрозоли в следующих шагах.
- В раскрывающемся меню Модель атмосферы выберите Стандарт США .
- Нажмите кнопку-переключатель Сбор воды , чтобы выбрать Да .
- Примите значение по умолчанию 1135 нм для Функция поглощения воды . Если вы выберете 1135 нм или 940 нм, а функция будет насыщена из-за очень влажной атмосферы (что маловероятно для этого места), то вместо нее будет использоваться функция 820 нм.

- Примите значение по умолчанию Rural для Aerosol Model . Это хороший вариант для расположения нашей сцены, где на аэрозоли не сильно воздействуют городские или промышленные источники. Выбор модели в данном случае не критичен, так как видимость обычно превышает 40 км.
- Примите значения по умолчанию для всех остальных полей.
- Настройки, доступные под кнопкой Hyperspectral Settings в нижней части диалогового окна FLAASH, необходимы только в том случае, если вы работаете с гиперспектральным датчиком, который широко не известен. Вы можете использовать эти настройки, чтобы выбрать, как выбираются полосы для поиска водяного пара и/или аэрозоля. Поскольку наши данные получены от именованного датчика (Hyperion), вам не нужно определять эти настройки.
- Щелкните Применить .
- : Закройте оба диалоговых окна FLAASH.
Обработка FLAASH может занять несколько минут. По завершении обработки появится диалоговое окно FLAASH Atmospheric Correction Results со сводкой результатов обработки. FLAASH создает несколько выходных файлов в указанном вами каталоге: изображение маски облаков, изображение водяного пара, файл журнала с результатами обработки, файл шаблона с заданными вами параметрами и файл отражательной способности.
По завершении обработки появится диалоговое окно FLAASH Atmospheric Correction Results со сводкой результатов обработки. FLAASH создает несколько выходных файлов в указанном вами каталоге: изображение маски облаков, изображение водяного пара, файл журнала с результатами обработки, файл шаблона с заданными вами параметрами и файл отражательной способности.
Отображение изображения отражения
- Откройте диспетчер данных и прокрутите вниз до файла SurfaceReflectance.dat. Щелкните правой кнопкой мыши имя файла и выберите Load CIR . Изображение отображается в комбинации искусственных цветов. На следующем рисунке показан пример северной части изображения:
- Нажмите кнопку Spectral Profile на панели инструментов.
- В поле Перейти к на панели инструментов введите следующие координаты в пикселях: 10, 762 .
 Этот пиксель представляет собой здоровую растительность, которая ярко-розового цвета на дисплее в искусственных цветах. Обратите внимание на форму кривой отражения с резким увеличением коэффициента отражения от 680 до 730 нм (обозначается как красный край ). Этот диапазон длин волн часто анализируют более подробно при изучении факторов стресса растительности. Две особенности сильного поглощения, отражающие содержание воды в растительности, очевидны при 1450 нм и 1950 нм. Вы также можете увидеть пик в зеленой области длин волн около 550 нм.
Этот пиксель представляет собой здоровую растительность, которая ярко-розового цвета на дисплее в искусственных цветах. Обратите внимание на форму кривой отражения с резким увеличением коэффициента отражения от 680 до 730 нм (обозначается как красный край ). Этот диапазон длин волн часто анализируют более подробно при изучении факторов стресса растительности. Две особенности сильного поглощения, отражающие содержание воды в растительности, очевидны при 1450 нм и 1950 нм. Вы также можете увидеть пик в зеленой области длин волн около 550 нм. - Закройте спектральный профиль для подготовки к следующему упражнению.

.
В поле Перейти к на панели инструментов введите следующие координаты в пикселях: 227, 342 . В этом месте растут нездоровые хвойные деревья. Обратите внимание на форму кривой отражения. В целом, наклон красного края значительно уменьшился, а характеристика поглощения воды при 1450 нм не так заметна, что указывает на более низкое содержание влаги.
В то время как спектральные профили могут помочь найти пиксели с нездоровой растительностью, спектральные индексы могут дать нам более точную оценку подверженной стрессу растительности.
Индексы растительности
Спектральные индексы представляют собой комбинации коэффициентов отражения поверхности на двух или более длинах волн, которые указывают на относительное изобилие интересующих объектов. Индексы растительности, полученные по спутниковым снимкам, являются одним из основных источников информации для мониторинга состояния растительности. Обнаружение стресса растительности с помощью методов дистанционного зондирования основано на предположении, что факторы стресса мешают фотосинтезу или физической структуре растительности и влияют на поглощение световой энергии и, таким образом, изменяют спектр отражения растительности (Riley, 19).89; Пинтер и Хэтфилд, 2003 г.).
Спектральное разрешение снимков Hyperion позволяет более детально исследовать красный спектр в ближней инфракрасной области, что помогает выявить участки растительности, подверженные стрессу. ENVI предлагает несколько узкополосных индексов растительности , которые показывают общее количество и качество фотосинтетического материала и содержание влаги в растительности.
ENVI предлагает несколько узкополосных индексов растительности , которые показывают общее количество и качество фотосинтетического материала и содержание влаги в растительности.
Выполните следующие действия, чтобы создать различные индексы растительности:
- В наборе инструментов разверните Band Algebra 9Папка 0121.
- Дважды щелкните инструмент Spectral Index .
- В поле Входной растр уже должен быть указан SurfaceReflectance.dat. Если нет, нажмите кнопку Browse и найдите этот файл.
- В раскрывающемся списке Индекс выберите Индекс влажности .
- В поле Выходной растр назовите выходной файл MSI.dat.
- Включите параметр Показать результат и нажмите OK , чтобы создать изображение индекса влажности.
- По завершении обработки более подробно изучите изображение индекса влажности.
 Спектральные индексы не дают точных количественных показателей спектральных свойств; они лишь обеспечивают относительное изобилие интересующей функции. Более яркие значения пикселей указывают на больший дефицит воды. Индекс влагостойкости — это показатель отражательной способности, чувствительный к увеличению содержания воды в листьях. По мере увеличения содержания воды в растительности сила поглощения составляет около 1599 нм увеличивается. Поглощение при 819 нм почти не зависит от изменения содержания воды, поэтому эта длина волны используется в качестве эталонной длины волны (Hunt, Jr. and Rock, 1989): 90 367
Спектральные индексы не дают точных количественных показателей спектральных свойств; они лишь обеспечивают относительное изобилие интересующей функции. Более яркие значения пикселей указывают на больший дефицит воды. Индекс влагостойкости — это показатель отражательной способности, чувствительный к увеличению содержания воды в листьях. По мере увеличения содержания воды в растительности сила поглощения составляет около 1599 нм увеличивается. Поглощение при 819 нм почти не зависит от изменения содержания воды, поэтому эта длина волны используется в качестве эталонной длины волны (Hunt, Jr. and Rock, 1989): 90 367
White et al (2007) обнаружили существенную корреляцию между значениями индекса влагостойкости и уровнями поражения сосновым жуком.
Далее вы создадите растровый цветной фрагмент, который выделяет самые высокие значения пикселей в изображении MSI.
Цветные фрагменты
- Щелкните правой кнопкой мыши слой MSI.
 dat в диспетчере слоев и выберите Новый растровый цветовой фрагмент .
dat в диспетчере слоев и выберите Новый растровый цветовой фрагмент . - Выберите имя диапазона Moisture Stress Index в диалоговом окне File Selection и нажмите OK .
- Нажмите кнопку Очистить цветовые фрагменты в диалоговом окне «Редактировать цветные фрагменты растра». Вместо этого вы создадите новый цветной фрагмент растра.
- Нажмите кнопку Добавить цветной фрагмент . Добавляется новый цветовой фрагмент, который охватывает весь диапазон значений пикселей (от -245 до 14,08). Вы выделите самые высокие значения пикселей, которые соответствуют концу отображаемой узкой гистограммы.
- Сохраните значение Slice Max как есть и введите значение 1 для Slice Min . Нажмите клавишу Enter , чтобы принять значение. Значения индекса влагостойкости выше 1,0 выделены красным цветом:
- Щелкните правой кнопкой мыши папку Slices в диспетчере слоев и выберите Export Color Slices > Shapefile .

- Введите имя выходного файла HighMSI.shp и нажмите OK .
- Дождитесь завершения процесса ExportVector в диспетчере процессов, затем нажмите OK , чтобы закрыть диалоговое окно «Редактировать цветовые фрагменты растра».
- Снимите отметку со слоя MSI.dat в диспетчере слоев, чтобы скрыть этот слой. Срез красного цвета растра отображается поверх исходного изображения коэффициента отражения поверхности.
- Выделите слой Raster Color Slice в Диспетчере слоев, затем отрегулируйте ползунок Transparency на панели инструментов, чтобы видеть сквозь цветной фрагмент изображение отражательной способности поверхности под ним.
- Снимите отметку с фрагмента растрового цвета слой, чтобы скрыть его.
Далее вы будете использовать инструмент «Здоровье леса» для поиска областей с высоким стрессом.
Инструмент «Здоровье леса»
Инструмент «Анализ растительности леса» создаст пространственную карту, показывающую общее состояние и жизнеспособность лесного региона. Он хорош для обнаружения вредителей и болезней в лесу, а также для оценки площадей заготовки древесины. Лес в условиях сильного стресса имеет признаки сухого или отмирающего растительного материала, очень густой или очень редкий полог и неэффективное использование света. Инструмент использует следующие категории вегетационного индекса:
-
Широкополосная и узкополосная зелень, чтобы показать распределение зеленой растительности.
-
Пигменты листьев, чтобы показать концентрацию каротиноидов и антоциановых пигментов при стрессе.
-
Содержание воды в куполе, чтобы показать концентрацию воды.
-
Эффективность использования света, чтобы показать скорость роста леса.

Чтобы создать карту здоровья леса, выполните следующие действия:
- В окне поиска панели инструментов введите forest .
- Дважды щелкните имя инструмента Анализ состояния растительности леса .
- В диалоговом окне «Входной файл» выберите SurfaceReflectance.dat и нажмите ОК .
- В раскрывающемся списке Индекс зелени в диалоговом окне Параметры здоровья леса выберите Модифицированный индекс нормализованной разницы красной кромки .
- Из раскрывающегося списка Leaf Pigment Index выберите Carotenoid Reflectance Index 2 .
- В раскрывающемся списке Canopy Water or Light Use Efficiency Index выберите Структурно-нечувствительный пигмент, индекс .
- Введите имя выходного файла Forest Health.
 dat и нажмите OK .
dat и нажмите OK . - Результирующее изображение не отображается автоматически. Откройте диспетчер данных, прокрутите список файлов до конца и выберите полосу Forest Health . Щелкните Загрузить данные , чтобы отобразить изображение.
- В диспетчере слоев отключите все классы, кроме 1 и 2:
Изображение «Здоровье леса» не дает никаких количественных показателей нагрузки на растительность; вместо этого он показывает относительное количество здоровья лесной растительности от 1 (нездоровый) до 9 (здоровый). Вы можете увидеть артефакты с вертикальными полосами от датчика Hyperion.
Эти пиксели представляют участки с растительностью, подверженной стрессу. Сравните это с изображениями вегетационного индекса, которые вы создали ранее.
Полевые исследования и аэрофотосъемка также необходимы для проверки того, соответствуют ли участки повреждениям насекомыми. Однако методы, которые вы изучили в этом руководстве, показывают, что дистанционное зондирование и гиперспектральные изображения являются эффективными инструментами для выявления нездоровой и отмирающей растительности в лесах.
Ссылки
Barry, P. Руководство пользователя EO-1/Hyperion Science Data . Редондо-Бич, Калифорния: TRW Space, Defense & Information Systems (2001).
Чеккато, П. и др. «Определение содержания воды в листьях растительности с использованием коэффициента отражения в оптической области». Дистанционное зондирование окружающей среды 77 (2001): 22-33.
Datt, B. et al. «Предварительная обработка гиперспектральных данных EO-1 Hyperion для поддержки применения сельскохозяйственных индексов». IEEE Transactions on Geoscience and Remote Sensing 41, № 6 (2003): 1246-1259.
Датт, Б. «Новый индекс отражения для дистанционного определения содержания хлорофилла в высших растениях: тесты с использованием листьев эвкалипта». Журнал физиологии растений 154 (1999): 30-36.
«Новый индекс отражения для дистанционного определения содержания хлорофилла в высших растениях: тесты с использованием листьев эвкалипта». Журнал физиологии растений 154 (1999): 30-36.
Хант-младший, Э. и Б. Рок. «Обнаружение изменений в содержании воды в листьях с использованием коэффициентов отражения в ближнем и среднем инфракрасном диапазоне». Дистанционное зондирование окружающей среды 30 (1989): 43-54.
Мерзляк Дж. и др. «Неразрушающее оптическое обнаружение изменений пигмента во время старения листьев и созревания плодов». Physiologia Plantarum 106 (1999): 135-141.
Пинтер П. и Дж. Хэтфилд. «Дистанционное зондирование для управления посевами». Фотограмметрическая инженерия и дистанционное зондирование 69, Vol. 6 (2003): 647-664.
Райли, Дж. «Дистанционное зондирование в энтомологии». Ежегодный обзор энтомологии 34 (1989): 247-271.
Симс, Д. и Дж. Гамон. «Взаимосвязь между содержанием пигмента в листьях и спектральной отражательной способностью у широкого круга видов, структур листьев и стадий развития».

 Расширение скобки
Расширение скобки
 .. » [Википедия, «Апории Зенона»]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.
.. » [Википедия, «Апории Зенона»]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.  Если применить к этой ситуации понятие «бесконечность», то правильно будет сказать «Ахиллес бесконечно быстро догонит черепаху».
Если применить к этой ситуации понятие «бесконечность», то правильно будет сказать «Ахиллес бесконечно быстро догонит черепаху». 


 ..
.. 
 Что мы наделали? Мы преобразовали число в числовой графический символ. Это не математическая операция.
Что мы наделали? Мы преобразовали число в числовой графический символ. Это не математическая операция.  Посмотрим на результат.
Посмотрим на результат. 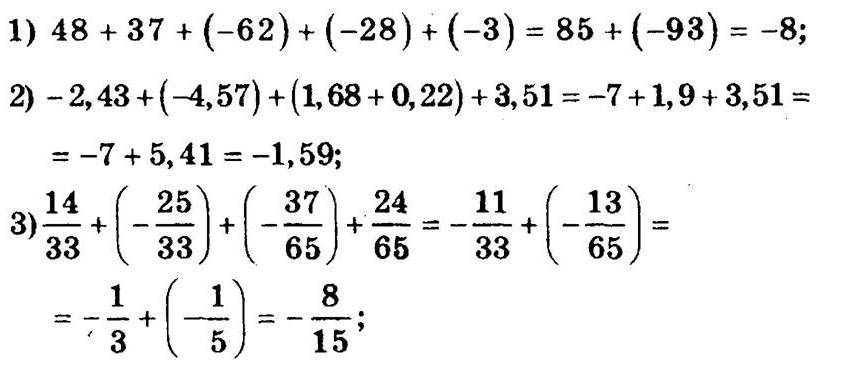
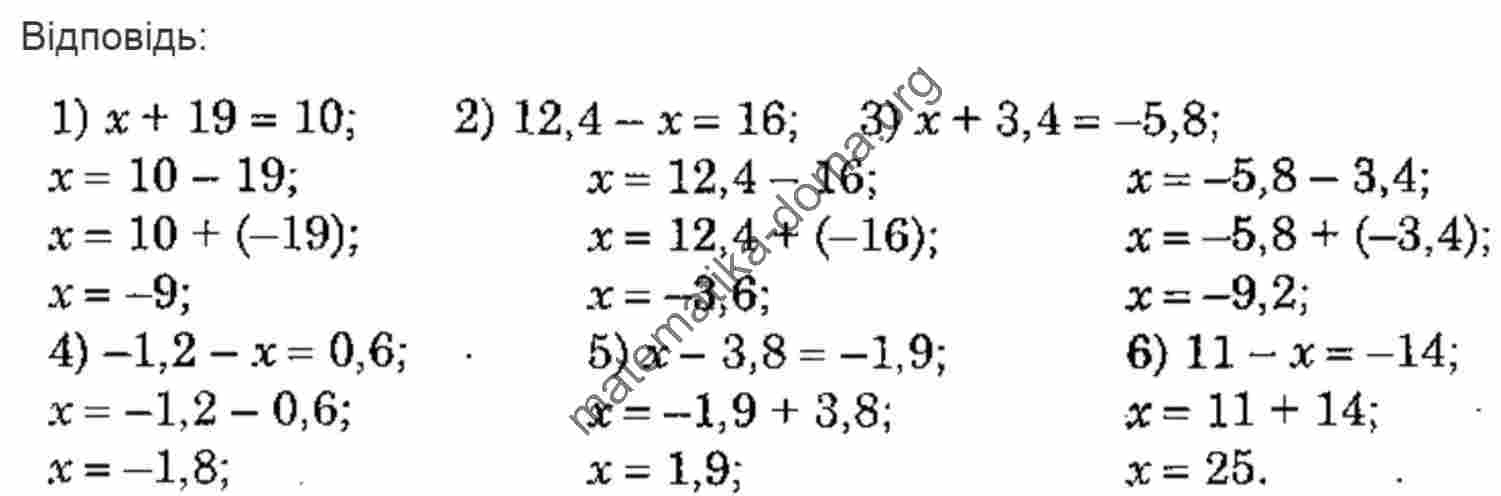 И математики учат нас этому все время. Вот пример.
И математики учат нас этому все время. Вот пример.  2 \) — это, конечно, не просто квадрат суммы, а квадрат суммы а и б. Однако квадрат суммы а и b встречается не так часто, как правило, вместо букв а и Ь в нем содержатся различные, иногда довольно сложные выражения. 92 = (a — b)(a + b) \) — разность квадратов равна произведению разности на сумму.
2 \) — это, конечно, не просто квадрат суммы, а квадрат суммы а и б. Однако квадрат суммы а и b встречается не так часто, как правило, вместо букв а и Ь в нем содержатся различные, иногда довольно сложные выражения. 92 = (a — b)(a + b) \) — разность квадратов равна произведению разности на сумму.  Раскрыть скобки означает избавиться от лишних символов. Например: (-15)+3=-15+3=-12, 18+(-16)=18-16=2. Вы помните распределительное свойство умножения по отношению к сложению? Ведь в том примере мы тоже избавились от скобок для упрощения вычислений. Названное свойство умножения можно применить и к четырем, трем, пяти и более терминам. Например: 15*(3+8+9+6)=15*3+15*8+15*9+15*6=390. Вы замечали, что при раскрытии скобок числа в них не меняют знак, если число перед скобками положительное? Ведь пятнадцать — положительное число. А если решить этот пример: -15*(3+8+9+6)=-15*3+(-15)*8+(-15)*9+(-15)*6=-45+( — 120)+(-135)+(-90)=-45-120-135-90=-390. Перед скобками у нас стояло отрицательное число минус пятнадцать, когда мы раскрывали скобки все числа начинали менять свой знак на другой — противоположный — с плюса на минус.
Раскрыть скобки означает избавиться от лишних символов. Например: (-15)+3=-15+3=-12, 18+(-16)=18-16=2. Вы помните распределительное свойство умножения по отношению к сложению? Ведь в том примере мы тоже избавились от скобок для упрощения вычислений. Названное свойство умножения можно применить и к четырем, трем, пяти и более терминам. Например: 15*(3+8+9+6)=15*3+15*8+15*9+15*6=390. Вы замечали, что при раскрытии скобок числа в них не меняют знак, если число перед скобками положительное? Ведь пятнадцать — положительное число. А если решить этот пример: -15*(3+8+9+6)=-15*3+(-15)*8+(-15)*9+(-15)*6=-45+( — 120)+(-135)+(-90)=-45-120-135-90=-390. Перед скобками у нас стояло отрицательное число минус пятнадцать, когда мы раскрывали скобки все числа начинали менять свой знак на другой — противоположный — с плюса на минус. 
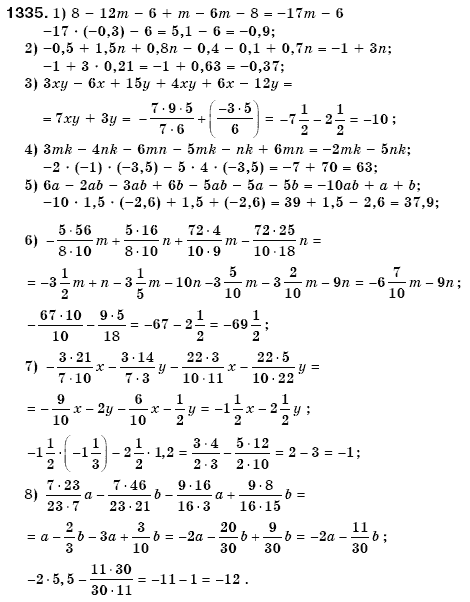 к. если перед скобками стоит знак сложения, то при раскрытии скобок знаки внутри них не меняются. Пример:
к. если перед скобками стоит знак сложения, то при раскрытии скобок знаки внутри них не меняются. Пример:  Пример: 92) * 12 = 1728.
Пример: 92) * 12 = 1728. 
 Раскрыв скобки, мы изменим порядок действий и значительно упростим расчеты.
Раскрыв скобки, мы изменим порядок действий и значительно упростим расчеты.  Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика: 6. — Математика. Мнемозина, 2012.
Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика: 6. — Математика. Мнемозина, 2012.