Задача (условие, вопрос, схема, выражение, ответ). 1-й класс
Разделы:
Начальная школа
Класс:
1
Цели:
- Закрепление навыков устного счёта в пределах 10.
- Повторить составление выражений по рисункам, соотношение
между целым и его частями. - Уточнить термины, связанные с понятием «задача»: условие,
вопрос, выражение, решение, ответ. - Научить делать краткую запись в виде схем, познакомить с
записью решения в тетради. - Учить составлять задачи по схемам и числовым выражениям.
- Развивать мышление, речь, творческие способности.
Оборудование:
- наглядность к устному счёту: ромашки, поезд, зайчик,
Великий Математик; - иллюстрация к задаче;
- плакаты: условие, вопрос, схема, выражение, решение,
ответ; - схемы к задачам;
- плакат (проверка № 5 с. 45).
Ход урока
I. Организационный момент.
II. Вводная беседа.
— Ребята, сегодня на уроке мы отправляемся с вами
путешествовать в страну Математики и нас будет сопровождать Великий Математик.
Математика – это точная наука, требующая хороших знаний, чёткого выполнения всех
арифметических действий.
— Какие действия мы с вами уже знаем? (Сложение и
вычитание.)
— Во 2 классе мы познакомимся с умножением и делением.
— Сегодня на уроке мы будем заниматься наблюдениями,
открывать математические закономерности, изучать новый материал.
III. Устный счёт.
1) Путешествовать мы с вами отправляемся на поезде, но
прежде, чем наш поезд тронется, мы должны получить билеты. Для этого разделимся
на команды и поиграем в игру «Кто быстрее?»
(Учащиеся выходят к доске и дописывают нужные числа.)
I ряд – 1 команда.
II ряд – 2 команда.
III ряд – 3 команда.
2) А теперь надо узнать № поезда. Для этого решим цепочку
примеров:
Проверка (у каждого учащегося цифры, ответ показывает каждый
с места).
(На доске картинка с зайчиком).
— Зайчик тоже хочет отправиться с нами путешествовать, но он
не знает номер поезда, ему достался трудный пример. Он записан под цепочкой.
(Учащиеся записывают пример в тетради и решают.)
| 3 + 4 – 2 + 3 – 4 + 5 = ? |
— Что вы заметили? (В примере выполнены те же действия,
что и в цепочке. Значит ответ будет такой же 9.)
Значит Зайка едет в нашем поезде – берём его с собой.
Наш поезд отправился, давайте сосчитаем:
— Сколько пассажиров в каждом вагоне?
| 9-6 | 3 | 4+5 | 9 | 8-4 | 4 |
| 3+3 | 6 | 7-5 | 2 | 3+4 | 7 |
(Ответы в тетради.)
— Прочитаем ответы.
— Запишите их в порядке возрастания и вы отгадаете слово.
(На доске все картинки перемешаны, выходит ученик и
располагает их в порядке возрастания.)
| 2 | 3 | 4 | 6 | 7 | 9 |
| З | А | Д | А | Ч | А |
— Какое слово получилось? (Дети отвечают хором.)
IV. Знакомство с новым материалом.
Тема сегодняшнего урока: Задача.
Наш поезд делает I остановку в лесу. Рассмотрите иллюстрацию.
Составьте задачу про детей.
«Мальчик и девочка пошли в лес за грибами. Мальчик нашёл 2
гриба, а девочка 4.Сколько всего грибов нашли дети?»
— Правильно. Без чего нет задачи? (Без вопроса.)
— В задаче всегда о чём-то спрашивается, без вопроса нет
задачи. Это нужно хорошо понять и запомнить.
— Задачу можно разбить на 2 части:
- Условие – то, что известно.
- Вопрос – то, что неизвестно.
(На доске постепенно открываются плакаты: условие, вопрос,
схема, выражение, решение, ответ.)
— Давайте повторим условие нашей задачи, вопрос.
— А теперь запишем в тетради: Задача.
— Ниже запишите выражение: 4 + 2.
— Найдите его значение: 4 + 2 = 6(гр.)
— Полученное равенство называют решением задачи, а значение
выражения 6 грибов – ответом задачи.
Ответ: 6 грибов. (На доске записан образец записи.)
— Разобраться в этом помогает рисунок, но если числа большие
то делать рисунок неудобно – слишком много предметов надо рисовать. На помощь
приходит схема-отрезок, разбитый на части. Разбивая отрезок на части, мы
получаем те же самые соотношения между частью и целым, что и при разбиении
совокупностей предметов.
(На доске схема.)
— Какой мы делаем вывод? (Наглядно представить содержание
задачи можно сопоставив целое всему отрезку, а части – частям отрезка.)
— Что такое целое? (Отрезок.)
— Что обозначает весь отрезок? (Число грибов, собранных детьми.)
— Что такое части? (Части отрезка.)
— Что обозначают части отрезка? (Грибы, собранные
мальчиком и девочкой.)
— Что показывает знак вопроса? (Находят целое.)
— Каким действием решаем задачу? (Сложением.)
— Почему? (Находим целое.)
V. Закрепление.
1) Следующая остановка нашего поезда «Поиграй-ка».
— А сейчас мы с вами немного поиграем.
— Великий Математик прислал конверты с задачами.
(Работа в группах).
— Каждой группе нужно определить, что относится к условию,
вопросу, найти схему, записать выражение, решение, назвать ответ.
Проверка:
А) Условие. Во дворе играли 6 ребят. Двое ушли домой.
Вопрос. Сколько ребят осталось во дворе?
Схема:
На доске выражение: 6 – 2.
Решение: 6 – 2 = 4(р.)
Ответ: 4 ребят.
Б) Условие. В хоре пело 4 мальчика и 6 девочек.
Вопрос. Сколько детей пело в хоре?
Схема:
Выражение: 6 + 4.
Решение: 6 + 4 = 10(д.)
Ответ: 10 детей.
В) Условие. Из клетки улетело сначала 2 попугая, а потом ещё
3.
Вопрос. Сколько попугаев улетело из клетки?
Схема:
Выражение: 2 + 3.
Решение: 2 + 3 = 5(п.)
Ответ: 5 птиц.
Физкультурная минутка.
2) Наш поезд продолжает путешествие.
— Следующая остановка: «Объясни-ка».
— Откройте учебник с. 44 урок 23 № 2.
— Что нужно сделать? (Соотнести записи в рамках с
соответствующими терминами.)
— Выполните самостоятельно.
— Назовите условие, вопрос, выражение, решение.
— Что обозначает весь отрезок? (Число конфет у девочки.)
— Его части? (Число конфет, которые она подарила и число
конфет, которые у неё остались.)
— Почему задача решается вычитанием? (Ищем части.)
— Как найти часть? (Из целого вычитаем другую часть.)
3) Перейдём к №3. Составьте задачу по рисунку.
На столе лежали яблоки в 2-х вазах. В 1 вазе – 5 яблок, во 2
– 2 яблока.
— Сколько всего яблок лежало в двух вазах?
— Назовите условие, вопрос, выражение, решение.
— Что обозначает весь отрезок? (Все яблоки, лежащие на 1 и
2 вазе.)
— Его части? (1 ваза с яблоками, 2 – с яблоками.)
— Почему задача решается сложением? (Находим целое.)
4) Путешествие наше продолжается, но нам надо забрать багаж в
камере хранения ( №5).
Расшифруем записи – код ячеек.
— Что нужно выполнить? (Составить выражение с заданным
числовым значением и дорисовать картинки.) Выполните самостоятельно.
Проверка (плакат на доске).
№ 6
— Наше путешествие подходит к концу.
— И в последнем задании Великий Математик зашифровал слово.
— Если вы правильно выполните действие и сосчитаете, то
узнаете слово (умница).
— Великий Математик считает, что вы все умницы, так как
хорошо работали на уроке и правильно отвечали на все вопросы, и выполнили все
задания.
VI. Итог урока.
— Что нового узнали, чем занимались на уроке?
— Где можно использовать эти знания?
14.02.2011
urok.1sept.ru
Знакомство с задачей и её составными частями. Видеоурок. Математика 1 Класс
На данном уроке вы познакомитесь с задачей и ее логическими частями.
Среди данных текстов найдите текст задачи (рис. 1).

Рис. 1. Варианты текстов
Чтобы выполнить это задание, необходимо знать, чем отличается текст задачи от других текстов (рис. 2).
Текст задачи включает в себя две части – то, что известно – условие, то, что необходимо найти – вопрос.
Рис. 2. Из чего состоит задача
Прочитайте первый текст.
Ваня поймал 4 рыбки, а Саша – 2 рыбки.
В этом тексте есть только условие, из которого мы узнали, сколько рыбок поймали мальчики. Вопроса в тексте нет, значит, это не задача (рис. 3).
Рис. 3. Текст без вопроса не является задачей
Прочитайте второй текст.
Ваня поймал 4 рыбки, а Саша – 2 рыбки. Сколько рыбок у Саши и Вани вместе?
В этом тексте нам известно, сколько рыбок поймал каждый мальчик, значит, есть условие. Еще в этом тексте записано, что надо найти, значит, есть вопрос. Значит, этот текст является задачей (рис. 4).

Рис. 4. Текст задачи
Прочитайте третий текст.
На сколько яблок больше, чем груш?
В тексте есть вопрос, но нет условия, следовательно, этот текст не является задачей (рис. 5).

Рис. 5. Текст без условия не является задачей
Второй текст – это задача, так как в нем есть 2 части: условие и вопрос.
Сделаем рисунок к задаче (рис. 6).

Рис. 6. Рисунок к задаче
Рисунок помогает установить, что неизвестно – целое или часть. Но если числа большие, то делать рисунки неудобно: слишком много предметов нужно рисовать. В этом случае на помощь приходит схема-отрезок, поделенная на части (рис. 7).
Рис. 7. Схема-отрезок
Схема – это часть задачи, которая поможет правильно установить взаимосвязь между условием и вопросом задачи.
Составим выражение к этой задаче и найдем его значение.
Чтобы составить выражение по рисунку или схеме, необходимо еще раз перечитать вопрос задачи.
Сколько рыбок у Вани и Саши вместе?
Мы знаем, сколько рыбок поймал Ваня и сколько рыбок поймал Саша, то есть нам известны части, а найти нам нужно целое (рис. 8).
Рис. 8. Что нужно найти
Чтобы найти целое, нужно части сложить: к 4 прибавим 2.
Мы составили выражение к данной задаче. Выражение – это еще одна часть задачи.
Найдем значение этого выражения. К 4 прибавим 2, получим 6.
В скобках запишем сокращенно слово «рыбки». Сокращаем до первой буквы гласного звука.
Полученное равенство называется решением задачи. Решение – это часть задачи.
Полученное значение выражения, 6 рыбок, является ответом. Ответ – это последняя часть задачи (рис. 9).
interneturok.ru
Методика решения текстовых задач в 5-6 классах

Методика решения текстовых задач в 5-6 классах
Автор: Сидорова А.В., учитель математики
МБОУ г. Мурманска СОШ № 31

Математическая задача
– это связанный лаконический рассказ, в котором введены значения некоторых величин и предлагается отыскать другие неизвестные значения величин, зависимые от данных и связанные с ними определенными соотношениями, указанными в условии.

Структура задачи
Любая текстовая задача состоит из двух частей: условия и требования (вопроса).
- В условии соблюдаются сведения об объектах и некоторых величинах, характеризующих данные объекта, об известных и неизвестных значениях этих величин, об отношениях между ними.
- Требования задачи – это указание того, что нужно найти. Оно может быть выражено предложением в повелительной или вопросительной форме («Найти площадь треугольника.» или «Чему равна площадь прямоугольника?»).
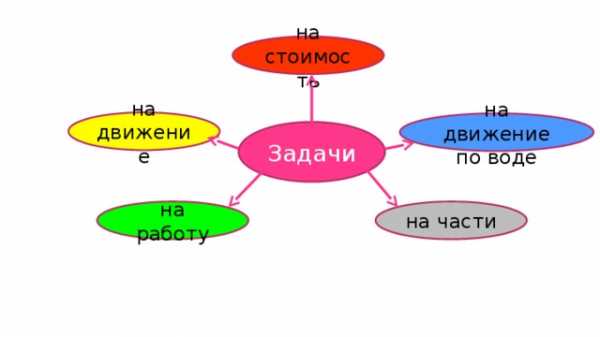
на стоимость
на движение
на движение по воде
Задачи
на работу
на части
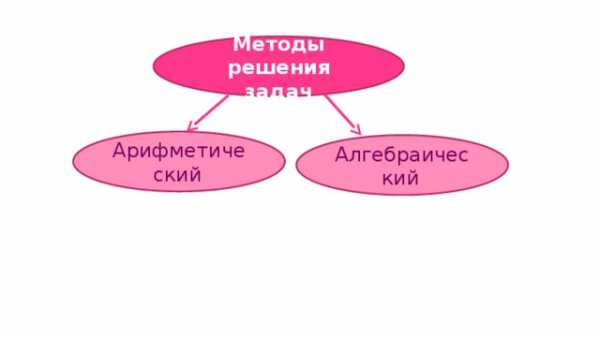
Методы решения задач
Арифметический
Алгебраический

Арифметический
- Найти ответ на требование задачи посредством выполнения арифметических действий над числами.
- Одну и ту же задачу можно решить различными способами. Они отличаются друг от друга логикой рассуждений, выполняемых в процессе решения задачи.
- Все арифметические задачи по числу действий, выполняемых для их решения, делятся на простые и составные.

Алгебраический
- Найти ответ на требование задачи, составив и решив уравнение или систему уравнений.
- Если для одной и той же задачи можно составить различные уравнения (системы уравнений), то это означает, что данную задачу можно решить различными алгебраическими способами.

Этапы решения задачи
- Анализ задачи
- Поиск плана решения задачи
- Осуществление плана решения задачи
- Проверка решения задачи

Анализ задачи
- Анализ — это метод рассуждений от искомых к данным.
- Основное назначение этого этапа – понять в целом ситуацию, описанную в задаче; выделить условия и требования; назвать известные и искомые объекты, выделить все отношения (зависимости) между ними.

Специальные вопросы:
- О чём задача, т.е. о каком процессе (явлении, ситуации) идёт речь в задаче, какими величинами характеризуется этот процесс?
- Что требуется найти в задаче?
- Что обозначают те или иные слова в тексте задачи?
- Что в задаче известно о названных величинах?
- Что неизвестно?
- Что является искомым?
 , чем На автобусе — ? км, на 128 км ? км О какой ситуации идёт речь в задаче ? Что в задаче известно о названных величинах? Что неизвестно? Что требуется найти в задаче? «
, чем На автобусе — ? км, на 128 км ? км О какой ситуации идёт речь в задаче ? Что в задаче известно о названных величинах? Что неизвестно? Что требуется найти в задаче? «
Группа туристов прошла пешком 72 км, проехала на поезде в 5 раз больше, чем прошла пешком, а на автобусе проехала на 128 км меньше, чем на поезде. Сколько километров прошли и проехали туристы?
Пешком – 72 км
На поезде — ? км, в 5 раз , чем
На автобусе — ? км, на 128 км
? км
О какой ситуации идёт речь в задаче ?
Что в задаче известно о названных величинах?
Что неизвестно?
Что требуется найти в задаче?

План решения задачи
- Как искать план решения текстовой задачи? Односложного ответа на этот вопрос нет.
- Одним из наиболее известных приёмов поиска плана решения задачи арифметическим способом является разбор задачи по тексту или по её вспомогательной модели.
- Разбор задачи проводится в виде цепочки рассуждений, которая может начинаться как от данных задачи, так и от её вопросов.
 , чем На автобусе — ? км, на 128 км ? км 1) 72 ∙ 5 = 360 (км) – проехали на поезде Что надо знать, чтобы ответить на вопрос задачи? 2) 360 – 128 = 232 (км) – проехали на автобусе Что можно найти по условию задачи? Составим план действий. 3) 72 + 360 + 232 = 664 (км) Ответ: туристы прошли и проехали 664 км. «
, чем На автобусе — ? км, на 128 км ? км 1) 72 ∙ 5 = 360 (км) – проехали на поезде Что надо знать, чтобы ответить на вопрос задачи? 2) 360 – 128 = 232 (км) – проехали на автобусе Что можно найти по условию задачи? Составим план действий. 3) 72 + 360 + 232 = 664 (км) Ответ: туристы прошли и проехали 664 км. «
Группа туристов прошла пешком 72 км, проехала на поезде в 5 раз больше, чем прошла пешком, а на автобусе проехала на 128 км меньше, чем на поезде. Сколько километров прошли и проехали туристы?
Каким образом можно проверить
правильность найденного решения?
Пешком – 72 км
На поезде — ? км, в 5 раз , чем
На автобусе — ? км, на 128 км
? км
1) 72 ∙ 5 = 360 (км) – проехали на поезде
Что надо знать, чтобы ответить на вопрос задачи?
2) 360 – 128 = 232 (км) – проехали на автобусе
Что можно найти по условию задачи?
Составим план действий.
3) 72 + 360 + 232 = 664 (км)
Ответ: туристы прошли и проехали 664 км.
 , чем ? орехов на 23 , чем О какой ситуации идёт речь в задаче ? Что в задаче известно о названных величинах? Что неизвестно? Как можно перефразировать текст задачи? Что требуется найти в задаче? «
, чем ? орехов на 23 , чем О какой ситуации идёт речь в задаче ? Что в задаче известно о названных величинах? Что неизвестно? Как можно перефразировать текст задачи? Что требуется найти в задаче? «
Три бельчонка Рыжик, Пушистик и Ушастик собирали орехи. Рыжик собрал 38 орехов, что на 16 меньше, чем Пушистик, а Ушастик на 23 ореха больше, чем Рыжик. Сколько всего орехов они собрали?
Рыжик – 38 ор.,
Пушистик — ? ор.
Ушастик — ? ор.,
на 16
, на 16 , чем
? орехов
на 23 , чем
О какой ситуации идёт речь в задаче ?
Что в задаче известно о названных величинах?
Что неизвестно?
Как можно перефразировать текст задачи?
Что требуется найти в задаче?
 ? г (х + 100 + 400) г , на 400 г ? г Что в задаче известно о количестве шерсти, израсходованной на каждую вещь? О какой ситуации идёт речь в задаче ? Каким способом будем решать задачу? Сколько всего израсходовали шерсти? Что обозначим за х? Зная, что всего израсходовали 1200 г шерсти, составляем уравнение: х + (х + 100) + (х + 500) = 1200 3х = 600 х + 500 = 200 + 500 = 700 (г) 3х + 600 = 1200 х = 600 : 3 Ответ: 700 г пошло на свитер. х = 200 3х = 1200 — 600 «
? г (х + 100 + 400) г , на 400 г ? г Что в задаче известно о количестве шерсти, израсходованной на каждую вещь? О какой ситуации идёт речь в задаче ? Каким способом будем решать задачу? Сколько всего израсходовали шерсти? Что обозначим за х? Зная, что всего израсходовали 1200 г шерсти, составляем уравнение: х + (х + 100) + (х + 500) = 1200 3х = 600 х + 500 = 200 + 500 = 700 (г) 3х + 600 = 1200 х = 600 : 3 Ответ: 700 г пошло на свитер. х = 200 3х = 1200 — 600 «
На шапку , шарф и свитер израсходовали 1200 г шерсти. Известно, что на шарф израсходовали на 100 грамм больше, чем на шапку, а на свитер – на 400 г больше, чем на шарф. Сколько граммов шерсти израсходовали на свитер?
Пусть х г израсходовали на шапку.
Шапка —
Шарф —
Свитер —
? г
х г
1200 г
1200 г
(х + 100) г
, на 100 г
? г
(х + 100 + 400) г
, на 400 г
? г
Что в задаче известно о количестве шерсти, израсходованной на каждую вещь?
О какой ситуации идёт речь в задаче ?
Каким способом будем решать задачу?
Сколько всего израсходовали шерсти?
Что обозначим за х?
Зная, что всего израсходовали 1200 г шерсти, составляем уравнение:
х + (х + 100) + (х + 500) = 1200
3х = 600
х + 500 = 200 + 500 = 700 (г)
3х + 600 = 1200
х = 600 : 3
Ответ: 700 г пошло на свитер.
х = 200
3х = 1200 — 600
 , чем 2х 2х + 10 Зная, что в ящике стало в 5 раз больше, составляем уравнение: 3х = 60 2х = 2 ∙ 20 = 40(яб.) – было в ящике 5(х – 10) = 2х + 10 х = 60 : 3 5х – 50 = 2х + 10 Ответ: 20 и 40 яблок. х = 20 5х – 2х = 10 + 50 «
, чем 2х 2х + 10 Зная, что в ящике стало в 5 раз больше, составляем уравнение: 3х = 60 2х = 2 ∙ 20 = 40(яб.) – было в ящике 5(х – 10) = 2х + 10 х = 60 : 3 5х – 50 = 2х + 10 Ответ: 20 и 40 яблок. х = 20 5х – 2х = 10 + 50 «
В корзине было в 2 раза меньше яблок, чем в ящике. После того, как из корзины переложили в ящик 10 яблок, в ящике их стало в 5 раз больше, чем в корзине. Сколько яблок было в корзине и сколько в ящике?
Пусть х яблок было в корзине первоначально.
Корзина
Было
Изменилось
Ящик
Стало
х
х — 10
-10
+10
, в 5 раз , чем
2х
2х + 10
Зная, что в ящике стало в 5 раз больше, составляем уравнение:
3х = 60
2х = 2 ∙ 20 = 40(яб.) – было в ящике
5(х – 10) = 2х + 10
х = 60 : 3
5х – 50 = 2х + 10
Ответ: 20 и 40 яблок.
х = 20
5х – 2х = 10 + 50

Задачи на движение
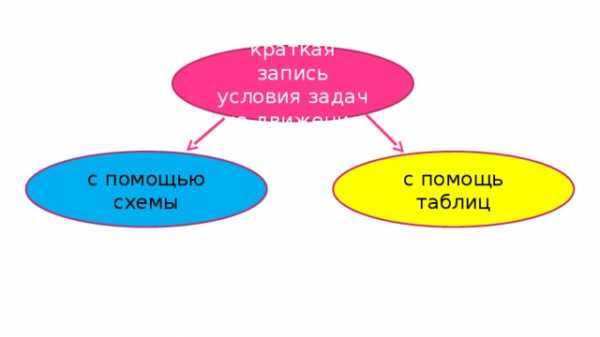
краткая запись условия задач на движение
с помощью схемы
с помощь таблиц

Алгоритм решения задач на движение
- Читаем задачу
- Выясняем, на какой вид движения эта задача
- По вопросу определяем, какой формулой эталона будем пользоваться
 6 ? 156 О какой ситуации идёт речь в задаче ? Что требуется найти в задаче? Как, зная путь и время, найти скорость? 1) 276 : 4 = 69 (км/ч) – скорость ступы Как, зная путь и время, можно найти скорость? 2) 156 : 6 = 26 (км/ч) – скорость сапог — скороходов Какими величинами характеризуется этот процесс? 3) 69 – 26 = 43 (км/ч) Что в задаче известно о названных величинах? Что неизвестно? Ответ: на 43 км/ч скорость ступы больше. «
6 ? 156 О какой ситуации идёт речь в задаче ? Что требуется найти в задаче? Как, зная путь и время, найти скорость? 1) 276 : 4 = 69 (км/ч) – скорость ступы Как, зная путь и время, можно найти скорость? 2) 156 : 6 = 26 (км/ч) – скорость сапог — скороходов Какими величинами характеризуется этот процесс? 3) 69 – 26 = 43 (км/ч) Что в задаче известно о названных величинах? Что неизвестно? Ответ: на 43 км/ч скорость ступы больше. «
Отправившись в гости к Змею Горынычу, Баба-яга пролетела в своей ступе 276 км за 4 ч, а остальные 156 км за 6 ч в сапогах-скороходах. На сколько скорость движения ступы больше, чем скорость движения сапог-скороходов?
v = s : t
Вид транспорта
Ступа
S (км)
t (ч)
Сапоги-скороходы
v (км/ч)
?
4
276
на ?
6
?
156
О какой ситуации идёт речь в задаче ?
Что требуется найти в задаче?
Как, зная путь и время, найти скорость?
1) 276 : 4 = 69 (км/ч) – скорость ступы
Как, зная путь и время, можно найти скорость?
2) 156 : 6 = 26 (км/ч) – скорость сапог — скороходов
Какими величинами характеризуется этот процесс?
3) 69 – 26 = 43 (км/ч)
Что в задаче известно о названных величинах?
Что неизвестно?
Ответ: на 43 км/ч скорость ступы больше.
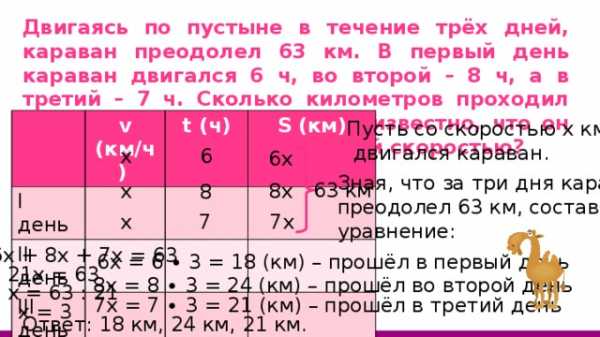
Двигаясь по пустыне в течение трёх дней, караван преодолел 63 км. В первый день караван двигался 6 ч, во второй – 8 ч, а в третий – 7 ч. Сколько километров проходил караван каждый день, если известно, что он двигался все дни с постоянной скоростью?
I день
v (км/ч)
t (ч)
II день
S (км)
III день
Пусть со скоростью х км/ч
двигался караван.
6
х
6х
Зная, что за три дня караван
преодолел 63 км, составляем
уравнение:
63 км
х
8х
8
х
7х
7
6х + 8х + 7х = 63
6х = 6 ∙ 3 = 18 (км) – прошёл в первый день
21х = 63
8х = 8 ∙ 3 = 24 (км) – прошёл во второй день
х = 63 : 21
7х = 7 ∙ 3 = 21 (км) – прошёл в третий день
х = 3
Ответ: 18 км, 24 км, 21 км.
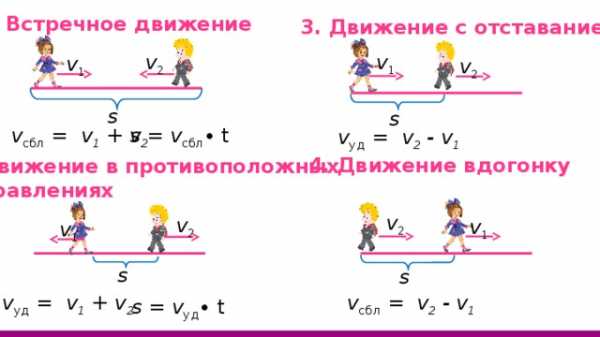
1. Встречное движение
3. Движение с отставанием
v 1
v 2
v 1
v 2
s
s
v сбл = v 1 + v 2
s = v сбл ∙ t
v уд = v 2 — v 1
4. Движение вдогонку
2. Движение в противоположных
направлениях
v 2
v 2
v 1
v 1
s
s
v уд = v 1 + v 2
v сбл = v 2 — v 1
s = v уд ∙ t
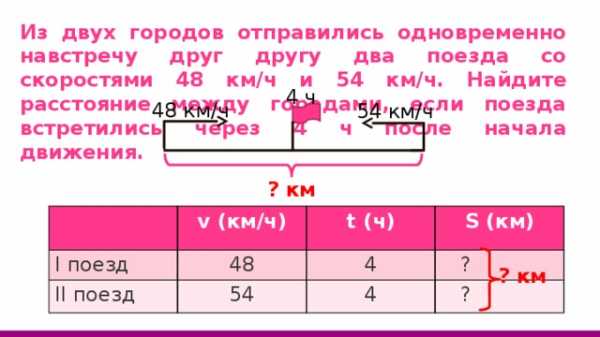
Из двух городов отправились одновременно навстречу друг другу два поезда со скоростями 48 км/ч и 54 км/ч. Найдите расстояние между городами, если поезда встретились через 4 ч после начала движения.
4 ч
48 км/ч
54 км/ч
? км
I поезд
v (км/ч)
II поезд
t (ч)
48
S (км)
4
54
?
4
?
? км

Из пунктов А и В, расстояние между которыми 60 км, одновременно навстречу друг другу отправились пешеход и велосипедист. Скорость пешехода 5 км/ч, а велосипедиста в 3 раза больше скорости пешехода. Какое расстояние будет между ними через 2 часа?
? км/ч
5 км/ч
? км
В
А
2 ч
2 ч
60 км
О какой ситуации идёт речь в задаче?
1) 5 ∙ 2 = 10 (км) – прошёл за 2 часа пешеход
2) 5 ∙ 3 = 15 (км/ч) – скорость велосипедиста
Что известно о скорости пешехода и велосипедиста?
3) 15 ∙ 2 = 30 (км) – проехал за 2 часа велосипедист
Сколько часов они были в пути?
4) 10 + 30 = 40 (км) – преодолели вместе за 2 часа
Что надо найти в задаче?
Ответ: 20 км.
5) 60 — 40 = 20 (км) будет между ними через 2 часа
 Что требуется найти в задаче? О какой ситуации идёт речь в задаче? 1) 5 ∙ 3 = 15 (км/ч) – скорость велосипедиста Какими величинами характеризуется этот процесс? 2) 5 + 15 = 20 (км/ч) – скорость сближения Они сближаются или удаляются? 3) 60 : 20 = 3 (ч) Сколько километров преодолел каждый до встречи? Как найти скорость сближения при встречном движении? Что известно про скорости пешехода и велосипедиста? Как можно найти время, через которое они встретятся? Ответ: они встретятся через 3 часа. Что можно сказать про время движения пешехода и велосипедиста? «
Что требуется найти в задаче? О какой ситуации идёт речь в задаче? 1) 5 ∙ 3 = 15 (км/ч) – скорость велосипедиста Какими величинами характеризуется этот процесс? 2) 5 + 15 = 20 (км/ч) – скорость сближения Они сближаются или удаляются? 3) 60 : 20 = 3 (ч) Сколько километров преодолел каждый до встречи? Как найти скорость сближения при встречном движении? Что известно про скорости пешехода и велосипедиста? Как можно найти время, через которое они встретятся? Ответ: они встретятся через 3 часа. Что можно сказать про время движения пешехода и велосипедиста? «
Из пунктов А и В, расстояние между которыми 60 км, одновременно навстречу друг другу отправились пешеход и велосипедист. Скорость пешехода 5 км/ч, а велосипедиста в 3 раза больше скорости пешехода. Через сколько часов они встретились?
S (км)
пешеход
v (км/ч)
велосипедист
t (ч)
5
?
?
одинаковое
60
?
?
?, в 3 р.
Что требуется найти в задаче?
О какой ситуации идёт речь в задаче?
1) 5 ∙ 3 = 15 (км/ч) – скорость велосипедиста
Какими величинами характеризуется этот процесс?
2) 5 + 15 = 20 (км/ч) – скорость сближения
Они сближаются или удаляются?
3) 60 : 20 = 3 (ч)
Сколько километров преодолел каждый до встречи?
Как найти скорость сближения при встречном движении?
Что известно про скорости пешехода и велосипедиста?
Как можно найти время, через которое они встретятся?
Ответ: они встретятся через 3 часа.
Что можно сказать про время движения пешехода и велосипедиста?

Из одного пункта одновременно в противоположных направлениях отправились пешеход и велосипедист. Скорость велосипедиста в 3 раза больше скорости велосипедиста. Через 3 часа расстояние между ними стало 60 км. Найдите скорости пешехода и велосипедиста .
Пусть х км/ч скорость пешехода.
Тогда скорость велосипедиста – 3х км/ч.
Скорость удаления – (х + 3х) км/ч.
Зная, что они удалялись друг от друга за 3 ч,
на 60 км составляем уравнение:
3х км/ч
х км/ч
3 ч
3 ч
60 км
(х + 3х) ∙ 3 = 60
х = 5
4х ∙ 3 = 60
3х = 3 ∙ 5 = 15 (км/ч) – скорость велосипедиста
12х= 60
Ответ: 5 км/ч и 15 км/ч.
х = 60 : 12
 2) 1050 + 840 = 1890 (км) – пролетел самолёт за 3 ч 3) 1890 : 3 = 630 (км/ч) – скорость самолёта Ответ: 630 км/ч. «
2) 1050 + 840 = 1890 (км) – пролетел самолёт за 3 ч 3) 1890 : 3 = 630 (км/ч) – скорость самолёта Ответ: 630 км/ч. «
С аэродрома вылетел вертолёт со скоростью 210 км/ч. Через 2 ч с этого же аэродрома вылетел вслед за вертолётом самолёт, который через 3 ч после своего вылета перегнал вертолёт на 840 км. Найдите скорость самолёта.
? км/ч
210 км/ч
840 км
2 ч
3 ч
3 ч
v (км/ч)
вертолёт
210
t (ч)
самолёт
S (км)
?
- 210 ∙ 5 = 1050 (км) – пролетел
вертолёт за 5 ч
5
?
3
?, на 840
2) 1050 + 840 = 1890 (км) –
пролетел самолёт за 3 ч
3) 1890 : 3 = 630 (км/ч) – скорость самолёта
Ответ: 630 км/ч.
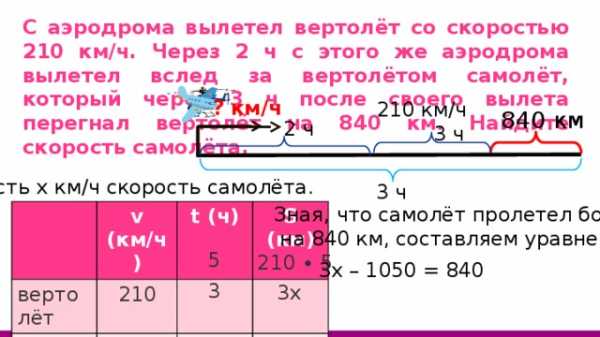
С аэродрома вылетел вертолёт со скоростью 210 км/ч. Через 2 ч с этого же аэродрома вылетел вслед за вертолётом самолёт, который через 3 ч после своего вылета перегнал вертолёт на 840 км. Найдите скорость самолёта.
? км/ч
210 км/ч
840 км
2 ч
3 ч
Пусть х км/ч скорость самолёта.
3 ч
Зная, что самолёт пролетел больше
на 840 км, составляем уравнение:
v (км/ч)
вертолёт
самолёт
t (ч)
210
S (км)
х
5
210 ∙ 5
3х – 1050 = 840
3
3х

Из двух пунктов навстречу друг другу выехали два автолюбителя, скорость одного из них 72 км/ч, а другого – 64 км/ч. Встретились они через 3 часа, а затем продолжили своё движение каждый по своему направлению. На каком расстоянии друг от друга будут автолюбители через 2 часа после встречи?
3 ч
72 км/ч
64 км/ч
- Какие данные в условии лишние?
- Поставьте другой вопрос к задаче и найдите на него ответ.
- Какой из автолюбителей будет ближе к своему конечному пункту от момента начала их движения?
- Какой из них будет ближе к своему конечному пункту от момента их встречи?

Движение по водному пути

Формулы
v по теч = v соб + v теч
v пр теч = v соб – v теч
v соб = ( v по теч + v пр теч ) : 2
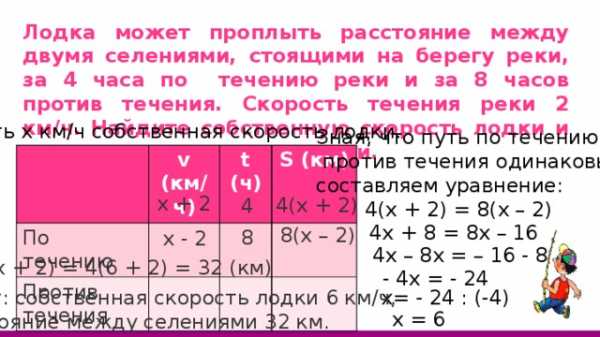
Лодка может проплыть расстояние между двумя селениями, стоящими на берегу реки, за 4 часа по течению реки и за 8 часов против течения. Скорость течения реки 2 км/ч. Найдите собственную скорость лодки и расстояние между селениями.
Пусть х км/ч собственная скорость лодки.
Зная, что путь по течению и
против течения одинаковый,
составляем уравнение:
v (км/ч)
По течению
t (ч)
Против течения
S (км)
х + 2
4(х + 2)
4
4(х + 2) = 8(х – 2)
4х + 8 = 8х – 16
8(х – 2)
8
х — 2
4х – 8х = – 16 — 8
4(х + 2) = 4(6 + 2) = 32 (км)
— 4х = — 24
х= — 24 : (-4)
Ответ: собственная скорость лодки 6 км/ч,
расстояние между селениями 32 км.
х = 6

Памятка по решению текстовых задач
- Прочитайте задачу, попросите ребёнка представить себе то, о чём говорится в ней.
- Выясните у ребёнка, как он думает, что показывает каждое число, и попросите его выделить вопрос задачи.
- Предложите ему составить вспомогательную краткую запись условия задачи или зарисовать условие.
- Спросите его, можно ли сразу ответить на вопрос задачи. Если нет, то почему?
- Что нужно узнать сначала? Что потом?
- Предложите составить план решения задачи.
- Посоветуйте записать и выполнить решение.
- Проверить решение и записать ответ задачи предложите самостоятельно.

Из двух пунктов, расстояние между которыми 7 км 500 м, одновременно в одном направлении вышел пешеход со скоростью 6 км/ч и выехал автобус. Определите скорость автобуса, если он догнал пешехода через 15 минут.

Расстояние между двумя станциями 784 км. С этих станций одновременно навстречу друг другу вышли два поезда. Они встретились через 8 ч. Найдите скорость каждого поезда, если скорость первого на 10 км/ч больше скорости второго?
videouroki.net
«Задачи на части». 5-й класс
Разделы:
Математика, Конкурс «Презентация к уроку»
Класс:
5
Презентация к уроку
Загрузить презентацию (2,2 МБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Тип урока: урок «открытия» новых знаний
Деятельностная цель: формирование у учащихся умений реализации новых способов действия (составление алгоритма решения задач на части)
Образовательная цель: расширение понятийной базы за счет включения в нее новых элементов (задачи на части)
Планируемые результаты:
Личностные УУД: Формировать учебную мотивацию, адекватную самооценку, необходимость приобретения новых знаний
Метапредметные УУД:
- Регулятивные: понимать учебную задачу урока, осуществлять решение учебной задачи под руководством учителя, определять цель учебного задания, контролировать свои действия в процессе его выполнения, обнаруживать и исправлять ошибки, отвечать на итоговые вопросы и оценивать свои достижения
- Познавательные: формировать навыки решения простейших задач на части арифметическим методом; формировать умения применять полученные знания при решении более сложных задач на части.
- Коммуникативные: воспитывать любовь к математике, коллективизм, уважение друг к другу, умение слушать, дисциплинированность, самостоятельность мышления.
Методы обучения: Репродуктивный. Наглядный. Проблемно – поисковый. Эвристическая беседа. Подводящий диалог.
Оборудование: проектор, презентация, карточки для самостоятельной работы, алгоритм решения задач, листок для самооценки своей УД.
Технологическая карта урока (таблица).
Приложение.
14.02.2013
Поделиться страницей:
urok.1sept.ru
Разработка урока по математике 5 класс «Задачи на части»
Конспект урока
Предмет: математика
Класс: 5
Тема урока: Задачи на части
Для учащихся
Цель урока: научиться решать задачи на части
Задачи урока:
-
Отличать задачи на части от задач другого вида
-
Составлять схему или краткую запись
-
Составлять план решения задачи
Для учителя
Цель урока: научить учащихся решать задачи на части
Задачи урока:
-
Научить видеть и отличать задачи на части от других видов задач
-
Разобрать решение основных задач на части: нахождение одной величины через другую, нахождение двух величин через их сумму,
-
Углубить, упрочить полученные знания и навыки в решении задач на части, выработать алгоритм решения таких задач.
-
Развивать познавательную активность, творческие способности, смекалку и сообразительность у учащихся.
-
Формирование умения работать в паре
-
Формирование навыков работы с компьютером (презентация)
-
Формирование навыков самооценки, взаимооценки
План урока
-
Орг момент – 2 мин
-
Проверка д/з – 3 мин
-
Устная работа – 5 мин
-
Целеполагание (Вывод темы, цели и задач урока) – 4 мин
-
Изучение нового материала + закрепление знаний– 25 мин
-
Физминутка – 1-2 мин
-
Подведение итогов урока – 4 мин
-
Рефлексия – 1 мин
ХОД УРОКА
Учитель сообщает план урока
Проверка д/з, Устная работа, Целеполагание (Вывод темы, цели и задач урока), Изучение нового материала, Физминутка, Подведение итогов урока, Рефлексия. За урок вы получите одну оценку за домашнее задание и еще одну оценку вы можете получить, если будете активно работать при изучении новой темы.
Назначим двух статистов, которые будут вести учет устных ответов одноклассников.
Помимо этого у вас на парте лежат листы самооценки, в которых вы будете вести учет баллов за весь урок, критерии я сообщу дополнительно на каждом из этапов.
Мы продолжаем учиться работать в паре.
Проверяют готовность к уроку, слушают учителя
Назначаются статисты.
Проверка домашнего задания
Обменяйтесь с соседом по парте тетрадями, в которых вы выполняли домашнее задание. На 1-ом слайде презентации у Вас есть критерии и ответы к домашнему заданию. Оценка поставленная вами соседу идет в журнал.
По критериям, представленным в презентации дети проверяют домашнее задание соседа по парте.
Демонстрируют навыки взаимооценки, умение работать с компьютером.
Устная работа + вывод темы
Выходят к доске 6 человек, им раздаются листы с выражениями, которые нужно вычислить и расставить в порядке возрастания.
Далее к доске выходят еще 5 человек, им раздаются листы, на которых именнованные единицы измерения, которые нужно расставить в порядке убывания.
Таким образом у нас получилось выражение, которое является темой нашего урока.
З —
А —
Д —
А —
Ч —
И —
Ч – 3 т
А – 20 ц
С – 3750 гр
Т – 2 кг
И – 1008 гр
Постановка цели и задач урока
Тема нашего урока «Задачи на части». А какова цель нашего урока?
А как же понять, что вы научились решать задачи на части. Давайте уточним нашу цель, составив для этой цели задачи урока.
На следующем слайде презентации есть несколько задач, конкретизирующих нашу цель. (Работа в паре за компьютером)
Критерии оценок: (ставим в лист самооценки количество правильно выбранных вами ответов)
Цель: научиться решать задачи на части
Работая в паре, выбирают на слайде задачи урока
Заполняют лист самооценки
Оценивают свою работу по количеству правильно выбранных задач урока
Изучение нового материала
-
Выбор задач на части среди представленных на слайде задач
Прочитайте задачи, представленные на слайде. Нажав клавишу ESC, вы выйдете из режима демонстрации презентации. Теперь вы можете удалить со слайда те задачи, которые не являются задачами на части.
Проверим какие задачи вы оставили.
Почему? Скажите, пожалуйста, что общего в этих задачах?
Задача № 7 не содержит слово часть, но тоже относится к типу задач на части.
Эту задачу я взяла из книги для подготовки к ОГЭ 9 класс.
-
Составление краткой записи или схемы к задаче
Решим задачу № 2 со слайда (учебник стр 90 № 342 (а))
С чего начинается решение любой задачи?
Попробуйте составить самостоятельно то с чем вам удобнее работать либо краткую запись, либо схему.
Если вам сложно это сделать можете обратиться к учебнику.
-
Составление плана решения задачи
Как вы думаете как эту задачу решить, какие действия необходимо выполнить Давайте составим план решения задачи:
Решите задачу по составленному плану.
Далее работаем с № 343 (в) на стр 91 учебник.
Работают в паре с презентацией, удаляют лишние задачи.
№ 2, № 5, № 6, № 7
В этих задачах встречается слово ЧАСТЬ
Вывод: задачи на части содержат слова часть, отношение.
С составления краткой записи или схемы.
Работают самостоятельно в тетради, затем выходят 2 человека к доске записывают свой вариант записи.
Предлагают способы решения задачи
-
Узнаем, сколько всего частей;
-
Найдем, сколько граммов приходится на одну часть;
-
Узнаем массу каждого продукта.
Решают задачу.
Физминутка
После того как вы выполните задание, возьмите стикер на вашем столе и приклейте его к плакату на доске в нужный столбик
Понял суть, нужно еще потренироваться решать задачи на части
На уроке всё было понятно, умею решать задачи на части
Выходят к доске, приклеивают стикер
Закрепление знаний
По приклеенным стикерам формируются пары
1 столбик + 2 столбик. Решение № 346 (а)
3 столбик – составьте свою задачу на части и решите её.
Подведение итогов урока
Итак подведем итоги урока. Какие задачи мы сегодня рассмотрели?
Какие цели были перед нами?
-
Отличать задачи на части от других видов задач
-
Составлять схему или краткую запись
-
Составлять план решения задачи
Молодцы!
Статисты оглашают количество баллов для каждого ученика.
Урок окончен.
Задачи на части
Мы научились видеть задачи на части среди других видов задач. Такие задачи содержат слово ЧАСТЬ, ОТНОШЕНИЕ.
Схема и краткая запись на доске
Для решения задач на части нужно сначала найти общее количество частей, затем найти сколько составляет 1 часть. Далее вычислить те части, о которых спрашивается в задаче.
Считают количество баллов, полученных за урок, по критериям на листе самооценки выставляют оценки за урок.
Записывают домашнее задание
№ 342 (б), № 344(а), 346(б)
infourok.ru
Презентация к уроку по математике (5 класс) на тему: Задачи на части 5 класс
Слайд 1
5 класс Задачи на части
Слайд 2
День Варенья
Слайд 3
К лассический рецепт варенья из ягод На 3 части ягод берут 2 части сахара. Сколько килограммов сахара и ягод надо купить, чтобы сварить 10 кг варенья? + = 3 части 2 части 10 кг
Слайд 4
Сахар Ягоды 2 части 3 части 1) 2+3= 5 (частей) – всего 2) 10:5 = 2 (кг) – составляет одна часть Ответ: 4 кг, 6 кг 3) 2 * 2 = 4 (кг) – нужно купить сахара 4) 2 * 3 = 6 (кг) – нужно купить ягод 10 кг варенья На 3 части ягод берут 2 части сахара. Сколько килограммов сахара и ягод надо купить, чтобы сварить 10 кг варенья?
Слайд 5
Для варенья из вишни на 2 части ягод берут 3 части сахара. Сколько сахара требуется на 4 кг ягод? Ягоды Сахар 2 части – 4 кг 3 части – ? кг 1) 4 : 2 = 2 (кг) – составляет одна часть 2) 2 · 3 = 6 (кг) – нужно взять сахара Ответ: 6 кг
Слайд 6
Подумайте и ответьте: какое важное условие (которое не оговаривается, но принимается по умолчанию) должно выполняться в задачах на части ? Все части, о которых идет речь в задаче, равные . ПОДУМАЙ!
Слайд 7
Подумайте и ответьте: что первым делом необходимо найти при решении задачи на части? Нужно узнать, сколько составляет одна часть. ПОДУМАЙ!
Слайд 8
«Необыкновенное» варенье из моркови Для этого варенья необходимо взять 2 части моркови, 1 часть воды и 1 часть сахара. Сколько моркови надо собрать Маше, чтобы приготовить 8 кг варенья ? Морковь Вода 2 части 1 часть 8 кг варенья 1 часть Сахар
Слайд 9
Для этого варенья берут 2 части огурцов, 3 части крыжовника и 4 части сахара. Сколько надо взять огурцов и сколько крыжовника, если у Маши 3 килограмма сахара? «Необыкновенное» в аренье из огурцов и крыжовника Огурцы Крыжовник 2 части — ? кг 3 части — ? кг Сахар 4 части – 3 кг
Слайд 10
Для приготовления варенья из шишек в сироп, содержащий 3 части сахара, добавляют 2 части сосновых шишек. Сколько сахара надо взять на 400 граммов шишек? «Необыкновенное» в аренье из шишек
Слайд 11
«Необыкновенное» варенье из грибов Для приготовления варенья из грибов необходимо взять 2 части воды, 2 части грибов и 1 часть сахара. Сколько варенья сварит Маша, если ежики принесли ей 6 кг сыроежек?
Слайд 12
Придумайте по схеме свой рецепт «Необыкновенного» варенья 15 ? ПОДУМАЙ!
Слайд 13
Интернет-ресурсы Рецепты: http://elite-life.narod.ru/jams44.htm http ://conservirovanie.ru/wps/archives/1539 http :// vizhevske.ru/blog/dom-hitrosti/13121.html http:// www.vashaibolit.ru/5497-celebnye-svoystva-varenya-iz-sosnovyh-shishek.html Видео: http:// vk.com/mashaimedvedtv
nsportal.ru
План-конспект урока по математике (5 класс) на тему: «Задачи на части»
- Индивидуальное задание для учащихся (1 учащихся на доске)
Вычислите , выбирая удобный порядок действий:
- 42+ 61+ 28+ 39 + 30=
- 4*9*5*2*25 =
- Сначала поработаем устно (задания для устной работы показываются на проекционном экране).
1.Найдите значение выражения, вынося за скобки общий множитель:
Самостоятельная работа (с самопроверкой).
(Проверить у учащихся умения видеть свои ошибки, оценивать свою работу, делать выводы)
- 3*52 = 75
- (76-66) *18 = 180
- Найдите площадь прямоугольника со сторонами 4см и 9 см.
- Выразите приближенно 16 381 г в килограммах
5) Выразите приближенно 5 743 м в километрах
Критерии оценок: (оценку ставим по количеству правильных ответов)
0 — ошибок-«5», 1 — ошибка-«4», 2 — ошибки-«3»
- Работа в группах(2 группы по 5 человек).Постановка проблемы.
С помощью создания проблемной ситуации подвести учащихся к новому виду задачи.Работа с текстом(каждой группе выдан текст)
- Прочитайте задачу:
- Ответьте устно на вопросы:а) Возможно в задачнике опечатка и Витя верно решил задачу?б) Предложите свой вариант решения.
- После обсуждения в группах, по 1 ученику из каждой группы на доскезаписывают своё решение.
- После чего рассматриваются все варианты решения, обсуждаются (принимаются/нет).
- Затем смотрим слайд, на котором показана краткая запись задачи в виде схемы и сравним с вашими решениями.
—————————————————————————————
«Мальчик и девочка рвали в лесу орехи. Они сорвали всего 120 штук. Девочка сорвала в два раза меньше мальчика. Сколько орехов было у мальчика и сколько у девочки?»
(Оказывается, Витя смог решить задачу лишь тогда, когда нарисовал девочку в переднике с одним карманом, а мальчика в курточке с двумя карманами. «Все 120 орехов теперь лежали у них в трех карманах: в двух карманах у мальчика и в одном кармане у девочки, а всего, значит, в трех.
И вдруг у меня в голове, будто молния, блеснула мысль: «Все 120 орехов надо делить на три части!»
1) Этот рисунок соответствует условию задачи?
2) Что мы видим по рисунку? На что, на какие элементы можно разделить условно все орехи? (все орехи можно условно разделить на равные части).
3) Сколько частей приходится на 120 орехов? (три части)
4) Что мы можем узнать из этого? (Сколько орехов приходится на одну часть, то есть у девочки, а значит и количество орехов у мальчика).
5) Какое действие будет следующим? (Узнаем, сколько орехов у девочки).
6) Ответив на все поставленные вопросы, смогли мы решить задачу? (Да).
В чем сходство решений? (Схематический рисунок, деление на части, нахождение количества объекта, приходящегося на одну часть).
В таком случае, можно сделать вывод, что вы самостоятельно смогли правильно придумать способ решения задач на части.
Итак, ребята, смогли мы с вами решить задачу, с решением которой возникли вначале затруднения? (Да)
А сейчас я предлагаю вам немного отдохнуть и выполнить упражнения для снятия утомляемости.
Физкультминутка
Мотивация учебной деятельности учащихся. Объявление темы урока, постановка цели и задач урока
Что нового встретилось вам при решении задач? (Понятие части, распределение всех объектов на части).
Как же мы можем сформулировать тему урока?
Запишите тему урока:«Задачи на части».
Какие цели и задачи мы с вами поставим к уроку?
Для чего мы рассматриваем новый тип задач? (Чтобы научиться их решать)
Итак, наша цель:-научиться решать задачи на части!
В повседневной жизни человеку нередко приходится сталкиваться с «рецептами» приготовления (или изготовления чего-либо), в составе которых указаны части.
Многие средства бытовой химии, используемые в домашних условиях, продают в концентрированном виде, чтобы их использовать, их надо развести (обычно водой).Например
Рецепт приготовления состава для полировки:
Нашатырный спирт — 5 частей,
Мел — 2 части,
Вода — 10 частей.
Рецепт приготовления настойки для полоскания рта:
Ромашка — 3 части,
Календула — 2 части,
Шалфей — 4 части.
1столовую ложку смеси залить 1 стаканом воды, настоять, полоскать рот
При приготовлении пищи мы берём продукты в частях, например, при варке варенья необходимо на 1 кг красной смородины взять 2 кг сахарного песка. Т.е. другими словами: на 1 часть ягод берём 2 части песка.
— А что ещё, кроме кг можно взять за часть?
1). Поработаем с частями:
(слайд)
= Масса трех частей ягод 15 кг . Как узнать какова масса одной части?
= Масса одной части ягод 12 кг . Какова масса трех частей?
Задача 1
Для варенья из вишни на 2 части ягод берут 3 части сахара. Сколько сахара требуется на 4 кг ягод?
Предлагает составить план решения задачи:
- Узнаем, сколько кг ягод приходится на 1 часть.
- Узнаем, сколько кг сахара приходится на 3 части.
Предлагает записать решение с вопросами в тетрадь.
Решение:
1. Сколько кг ягод приходится на 1 часть? 4:2=2(кг).
2. Сколько кг сахара приходится на 3 части? 2*3=6(кг).
Ответ: 6 кг.
— Одну из задач на части мы с вами решили. Что помогло нам в решении задачи?? (схема – краткое условие)
— Как вы думаете, поможет нам рисунок (кр.усл.) при решении других задач такого вида? (Да)
Задача: Добиться умения определять вид задачи, отработать навыки их решения.
Закрепить у учащихся знания и умения, которые они получили на уроке для выполнения письменной работы. Стимулировать учащихся к самоанализу, самоконтролю.
— Вы любите праздники?
— Вы участвуете в приготовлении к празднику. Не сомневаюсь, что если нужна помощь, то не отказываетесь. Например, в приготовлении САЛАТОВ.
Следующая часть нашего урока: Приготовление салатов.
(запись в тетрадях):«Вкусные салаты».
САЛАТЫ:
- Нужно приготовить салат «Венеция»,
который состоит из: 5 частей
колбасы 5 частей огурцов, 5 частей сыра, 3 частей моркови и 10 частей кукурузы.
Сколько грамм каждого ингредиента нужно взять, если колбасы взяли 100 г?
К — 5ч 100 г
О-5 ч — ?
С – 5 ч — ?
М – 3 ч — ?
Кук – 10 ч — ?
Предлагает:
Ответить на вопросы.
- Сколько частей колбасы надо взять для приготовления салата?
2. Сколько частей огурцов надо взять для приготовления салата?
3. Сколько граммов сыра, моркови, кукурузы?
4.Сколько граммов колбасы приходится на одну часть? Как найти?
5. Сколько граммов О, С, М, К необходимо? Как найти?
Предлагает записать решение задачи с вопросами в тетрадь.
Ответ:100гр-колбасы,огурца,сыра; 200гр-кукурузы;60гр-моркови.
Первичное усвоение новых знаний. (решают в парах с последующей проверкой)
- Салат «Креветочный»
Первичная проверка понимания (решают задачу самостоятельно)с дальнейшей взаимопроверкой
- Салат «Прибалтийский»
По истечении времени предлагается учащимся поменяться работами для проверки работ друг друга, на экране даются ответы самостоятельной работы. На проверку отводится 3 минуты. Учащиеся берут простые карандаши, проверяют письменные работы. Оценивают.
(Проверить у учащихся умения видеть чужие ошибки, оценивать работу, делать выводы)
Научились делать салаты.
С каким типом задач мы познакомились?
Помогает краткое условие при решении задачи?
А сейчас предлагаю выполнить Самостоятельную работу (на 6 минут).
Предлагает записать цифровой диктант
- Самая низкая отметка в школе (1).
- 3² (9).
- 7* 38 – 7* 37= 7
- 0 : 153 (0).
1970- год основания нашей школы
- 3*52 =
- (76-66) *18 =
7. Найдите площадь прямоугольника со сторонами 4см и 9 см.
8.Выразите приближенно 16 381 г в килограммах
9. Выразите приближенно 5 743 м в километрах
Задачи: сообщить учащимся домашнее задание, дать краткий инструктаж по его выполнению.
Предлагает
ответить на вопрос «Где мы в жизни встречаем задачи на части и кто умеет их решать?» (область деятельности человека, профессия, «рецепт»).
Составить минипроект по теме «Вкусные салаты»:
- Составить две задачи
- Оформить их решение
Итоги урока. Выставление оценок.
- Незаконченное предложение…
- Ребята, давайте вернемся к целям и задачам, которые мы ставили на урок и посмотрим, что мы должны были сделать и что сделали? (что ещё предстоит сделать?
Предлагает дополнить предложения:
- Я узнал, что…
- Я научился…
Благодарит за урок
nsportal.ru