Математика 5 Виленкин — Жохов
Контрольные работы по математике 5 класс Виленкин (автор — Жохов)
Математика 5 Виленкин — Жохов — это контрольные работы (цитаты) из учебного пособия «Математика. 5 класс. Контрольные работы для учащихся общеобразовательных учреждений / В. И. Жохов, Л. Б. Крайнева. — 5-е изд., стер. — М. : Мнемозина, 2012».
Цитаты из вышеуказанного учебного пособия использованы на сайте в незначительных объемах, исключительно в учебных и информационных целях (пп. 1 п. 1 ст. 1274 ГК РФ): цитаты переработаны в удобный формат (каждая работа на 1-й странице), что дает экономию денежных средств учителю и образовательному учреждению я в использовании бумаги и ксерокопирующего оборудования.
При постоянном использовании контрольных работ по математике в 4 классе рекомендуем купить книгу:
Математика. 5 класс. Контрольные работы для учащихся общеобразовательных учреждений / В. И. Жохов, Л. Б. Крайнева, в которой кроме представленных контрольных работ есть еще 2 варианта КР (итого 4 варианта контрольных работ), а также задания на карточках и проверочные работы. В пособии содержатся карточки для проведения диагностических и проверочных работ по математике в классах, обучающихся по учебнику «Математика 5 класс» Н. Я. Виленкина, В. И. Жохова, А. С. Чеснокова, С. И. Шварцбурда. Соответствует ФГОС основного общего образования.
Для увеличения изображения — нажмите на картинку !
Контрольная работа № 1
Математика 5 класс Виленкин — Жохов. Контрольная работа 1
Контрольная работа № 2
Математика 5 класс Виленкин — Жохов. Контрольная работа 2
Контрольная работа № 3
Математика 5 класс Виленкин — Жохов. Контрольная работа 3
Контрольная работа № 4
Математика 5 класс Виленкин — Жохов. Контрольная работа 4
Контрольная работа № 5
Математика 5 класс Виленкин — Жохов. Контрольная работа 5
Контрольная работа № 6
Математика 5 класс Виленкин — Жохов. Контрольная работа 6
Контрольная работа № 7
Математика 5 класс Виленкин — Жохов. Контрольная работа 7
Контрольная работа № 8
Математика 5 класс Виленкин — Жохов. Контрольная работа 8
Контрольная работа № 9
Математика 5 класс Виленкин — Жохов. Контрольная работа 9
Контрольная работа № 10
Математика 5 класс Виленкин — Жохов. Контрольная работа 10
Контрольная работа № 11
Математика 5 класс Виленкин — Жохов. Контрольная работа 11
Контрольная работа № 12
Математика 5 класс Виленкин — Жохов. Контрольная работа 12
Контрольная работа № 13
Математика 5 класс Виленкин — Жохов. Контрольная работа 13
Контрольная работа № 14
Математика 5 класс Виленкин — Жохов. Контрольная работа 14
Контрольная работа № 15. ИТОГОВАЯ.
Математика 5 класс Виленкин — Жохов. Контрольная работа 15
Вы смотрели Математика 5 Виленкин — Жохов контрольные работы (цитаты) из пособия для учащихся «Математика. 5 класс. Контрольные работы для учащихся общеобразовательных учреждений / В. И. Жохов, Л. Б. Крайнева. — 5-е изд., стер. — М. : Мнемозина, 2012».
Ответов нет !
Просмотры: 4 433
xn--b1agatflbfbtgq5jm.xn--p1ai
Тест (5 класс) по теме: годовая контрольная работа по математике 5 класс Виленкин
Итоговая контрольная работа по математике
учени_________5__«____»___класса_______________
(фамилия, имя)
____ « » мая 20 г.
2 вариант
Часть I
При выполнении заданий 1-6 в строке ответов обведите номер, который соответствует номеру выбранного вами ответа
1. Найти сумму чисел 2,59 и 4
1) 6,59 2) 2,99 3) 2,63 4) 42,59
2. Найти разность чисел 18,6 и 6
1) 18 2) 12,6 3) 24,6 4) 19,2
3. Найти частное чисел 20,4 и 0,3
1) 0,68 2) 68 3) 6,8 4) 6,12
4. Найти произведение чисел 6,8 и 0,6
1) 40,8 2) 7,4 3) 6,2 4) 4,08
5. Найдите 22% от 600.
1) 130 2) 120 3) 220 4) 132
6. Среди чисел 0,043 0,004 0,0049 0,04 укажите наибольшее
1) 0,043 2) 0,004 3) 0,0049 4) 0,04
7. Выполни действия
1) 2) 3) 11 4)
8. Найдите корень уравнения: 32х – 46 = 50
1) 30 2) 3 3) 52 4) 8
Часть II
При выполнении заданий 1 и 2 запишите номер выполняемого задания, подробное решение и ответ
9. Лодка шла по течению 3 часа, а против течения 2 часа. Собственная скорость лодки 3,8 км/ч, а скорость течения реки 2 км/ч. Какой путь прошла лодка за это время?
10. Начертите угол КМN равный 70º. Разделите угол KMN лучом ME пополам. Вычислите градусную меру образовавшихся углов.
11*. Продолжи ряд чисел 4 ; 9 ; 16 ; __ ; __ .
Итоговая контрольная работа по математике
учени_________5_ «____»___класса_______________
(фамилия, имя)
____ « » мая 20 г.
1вариант
Часть I
При выполнении заданий 1-6 в строке ответов обведите номер, который соответствует номеру выбранного вами ответа
1. Найти сумму чисел 7 и 5,23
1) 5,30 2) 12,23 3) 5,93 4) 75,23
2. Найти разность чисел 29,8 и 8
1) 19,8 2) 12,6 3) 21,8 4) 29,0
3. Найти частное чисел 16,6 и 0,2
1) 0,83 2) 130,3 3) 16,4 4) 83
4. Найти произведение чисел 7,5 и 0,4
1) 0,30 2) 3 3) 7,9 4) 7,1
5. Найдите 15% от 800.
1) 60 2) 120 3) 12 4) 6
6. Среди чисел 0,0072 0,013 0,009 0,0017 укажите наименьшее.
1) 0,0072 2) 0,013 3) 0,009 4) 0,0017.
7. Выполни действия
1) 2) 3) 7 4)
8. Найдите корень уравнения: 25х + 49 = 149
1) 2500 2) 4 3) 792 4) 40
Часть II
При выполнении заданий 9 – 11 запишите номер выполняемого задания, подробное решение и ответ
9. Катер шёл по течению 4 часа, а против течения 3 часа. Собственная скорость катера 40,4 км/ч, а скорость течения реки 2 км/ч. Какой путь прошёл катер?
10. Начертите угол КМN равный 70º. Разделите угол KMN лучом ME пополам. Вычислите градусную меру образовавшихся углов.
11*. Продолжи ряд чисел 36 ; 25 ; 16 ; __ ; __ .
Решения 5 класс
Вариант 1.
Часть 1.
Номер задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Верный ответ | 2 | 3 | 4 | 2 | 2 | 4 | 3 | 2 |
Часть 2.
№ 9.
- 40,4 + 2 = 42,4 (км/ч)- скорость катера по течению
- 42,4 ∙ 4 = 169,6 (км) – путь, пройденный по течению
- 40,4 – 2 = 38,4 (км/ч)- скорость катера против течения
- 38,4 ∙ 3 = 115,2 (км) – путь, пройденный против течения
- 169,6 + 115,2 = 284,8 (км) – весь путь
Ответ . 284,8 км путь, который прошёл катер.
№ 10. К
E 70 : 2 = 35° градусная мера образовавшихся углов
М N
№ 11.
36, 25, 16, 9, 4
Вариант 2.
Часть 1.
Номер задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Верный ответ | 1 | 2 | 2 | 4 | 4 | 1 | 1 | 2 |
№ 9.
- 3,8 + 2 = 5,8 (км/ч)- скорость лодки по течению
- 5,8 ∙ 3 = 17,4 (км) – путь, пройденный по течению
- 3,8 – 2 = 1,8 (км/ч)- скорость лодки против течения
- 1,8 ∙ 2 = 3,6 (км) – путь, пройденный против течения
- 17,4 + 3,6 = 21 (км) – весь путь
Ответ . 21 км — путь, который прошла лодка
№ 11.
4 9 16 25 36
nsportal.ru
Элективный курс по алгебре (5 класс) по теме: Контрольные работы по математике 5 класс (учеб. компл. Виленкин Н. Я.)
Математика 5 класс. Контрольная работа № 11. 1 вариант.
1. Выполите действия: а) 4,125 * 1,6 ; б) 0,042 * 7,3 ;
в) 29,64 : 7,6 ; г) 7,2 : 0,045 .
2. Найдите значение выражения: ( 18 – 16,9) * 3,3 – 3 : 0,5 .
3. Найдите среднее арифметическое чисел 23,6 ; 24,1 ; 22,8 и 23,9 .
4. Решите задачу: «С кондитерской фабрики отгрузили мармелад: 20 коробок по 1,3 кг в коробке и 30 коробок по 1,1 кг . Какова средняя масса одной коробки?»
5. Как изменится число, если его умножить на 0,5? Приведите три примера.
6 *. Решите задачу: «Среднее арифметическое двух чисел 1,68. Одно число в 3,2 раза больше другого. Найдите эти числа».
………………………………………………………………………………………………..
Математика 5 класс. Контрольная работа № 11. 2 вариант.
1. Выполните действия: а) 3,2 * 5,125 ; б) 0,084 * 6,9 ;
в) 60,03 : 8,7 ; г) 36,4 : 0,065 .
2. Найдите значение выражения: (21 – 18,3) * 6,6 + 3 : 0,6 .
3. Найдите среднее арифметическое чисел 23,12 ; 24,23 ; 22,11 и 25,06 .
4. Решите задачу: «В магазин привезли 10 ящиков яблок по 3,6 кг в ящике и 40 ящиков яблок по 3,2 кг в ящике. Сколько в среднем килограммов яблок в одном ящике?»
5. Как изменится число, если его умножить на 0,25? Приведите три примера.
6 *. Решите задачу: «Среднее арифметическое двух чисел 1,68. Одно число в 3,2 раза больше другого. Найдите эти числа».
Математика 5 класс. Контрольная работа №11. 3 вариант.
1. Вычислите: а) 3,8 * 6,95 ; б) 0,24 * 3,5 ; в) 16,45 : 4,7 4 г) 6 : 3,75 .
2 Найдите значение выражения: (9,5 : 0,25 – 29,4) * 6,5 .
3. Найдите среднее арифметическое чисел 1,11 ; 1,12 ; 1,19 и 1,48 .
4. Решите задачу « Чему равна скорость катера, если он прошел 3,6 км за 0,2 часа?»
5. Решите уравнение: а) х : 0,03 =2,4 ; б) 0,05 х = 2,45 .
……………………………………………………………………………………………………….
Математика 5 класс. Контрольная работа №11. 3 вариант.
1. Вычислите: а) 3,8 * 6,95 ; б) 0,24 * 3,5 ; в) 16,45 : 4,7 4 г) 6 : 3,75 .
2 Найдите значение выражения: (9,5 : 0,25 – 29,4) * 6,5 .
3. Найдите среднее арифметическое чисел 1,11 ; 1,12 ; 1,19 и 1,48 .
4. Решите задачу « Чему равна скорость катера, если он прошел 3,6 км за 0,2 часа?»
5. Решите уравнение: а) х : 0,03 =2,4 ; б) 0,05 х = 2,45 .
…………………………………………………………………………………………….
Математика 5 класс. Контрольная работа №11. 3 вариант.
1. Вычислите: а) 3,8 * 6,95 ; б) 0,24 * 3,5 ; в) 16,45 : 4,7 4 г) 6 : 3,75 .
2 Найдите значение выражения: (9,5 : 0,25 – 29,4) * 6,5 .
3. Найдите среднее арифметическое чисел 1,11 ; 1,12 ; 1,19 и 1,48 .
4. Решите задачу « Чему равна скорость катера, если он прошел 3,6 км за 0,2 часа?»
5. Решите уравнение: а) х : 0,03 =2,4 ; б) 0,05 х = 2,45 .
nsportal.ru
ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА ПО МАТЕМАТИКЕ ученика(цы) 5 ______ класса Ф.И. ____________________ ________________________ Вариант 1 Инструкция по выполнению работы Контрольная работа состоит из трех частей, включающих в себя 15 заданий. На выполнение работы отводится 45 минут. Внимательно читайте задание. Первая часть содержит 9 заданий с выбором одного ответа и одно задание на соответствие. За каждый верный ответ Вы получаете 1 балл. Вторая часть включает два задания с кратким ответом. За каждый верный ответ Вы получаете 2 балла. При выполнении заданий третьей части требуется запись полного решения. За выполнение каждого задания третьей части Вы можете получить от 0 до 3 баллов в зависимости от правильности и полноты записи решения. При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы. Если Вы ошиблись, можно исправить свой ответ: зачеркните уже отмеченную цифру и обведите нужную или запишите рядом новый ответ. Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов. Желаем успеха!
| Часть А. В заданиях А1-А10 отметьте один правильный, по вашему мнению, ответ. А1. Представьте число в виде неправильной дроби. 2) 3) 4) А2. Установите соответствие между выражением и их числовыми значениями
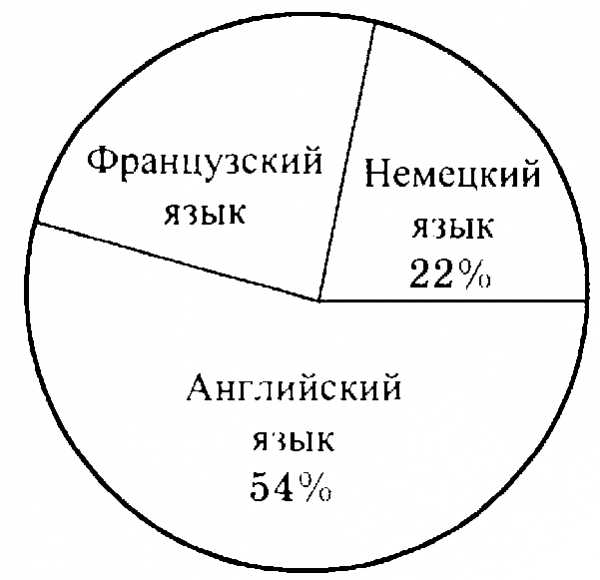
Впишите в таблицу ответов под каждой буквой соответствующий номер ответа. Ответ А3. Старинная русская мера массы – пуд равна 16,38 кг. Округлите его значение до десятых. 17 кг 2) 16,5 кг 3) 20 кг 4) 16,4 кг А4. Расположите числа 2,453; 24,35; 2,543 и 2,54 в порядке возрастания. 24,53; 2,543; 2,54; 2,453 3) 2,453; 2,543; 2,54; 24,35 2,453; 2,54; 2,543; 24,35 4) 2,54; 24,35; 2,453; 2,543 А5. Решите уравнение 2) 3) 4) А6. Упростите выражение 6,47а + 2,2а – 4,8а и найдите его значение при а=0,01 387 2) 0,387 3) 0,0387 4) 0,00387 А7. Найдите объем прямоугольного параллелепипеда, высота которого равна 6 см, длина 4см, а ширина является средним арифметическим высоты и длины. 120 см3 2) 240 см 3) 240 см3 4) 120 см2 А8. Запишите в виде процентов десятичную дробь . 72% 2) 3,5 % 3) 35% 4) 7% | А9. Длина первого куска ткани м, а второго на 0,3 м меньше. Сколько метров ткани в двух кусках? 2) 3) 4) А10. В магазин привезли 250 кг сахара. В первый день было продано 60% завезенного сахара,а во второй день продали остатки. Сколько килограммов сахара было продано во второй день? 250 кг 2) 100 кг 3) 200 кг 4) 150 кг Часть В. В заданиях В1-В2 запишите краткий ответ к задаче. В1. На диаграмме показано, как распределились учащиеся в зависимости от изучаемого ими иностранного языка. Используя диаграмму, найдите, сколько учащихся школы изучают французский язык, если всего в школе обучается 400 учеников, и каждый учащийся изучает только один иностранный язык. Ответ: __________________________ В2. В автобусе можно рассадить 35 детей. Сколько потребуется таких автобусов для перевозки 329 детей? Ответ: _______________________________ Часть С. Задания С1, С2, С3,С4, С5 выполняется с полной записью решения. С1. От двух пристаней навстречу друг другу одновременно отошли два катера. Скорость одного катера 42,5 км/ч, второго на 6 км/ч больше. Какое расстояние будет между катерами через 2 часа, если расстояние между пристанями 140,5 км? | С2. Среднее арифметическое четырех чисел равно 3,16. Первое число равно 3,6 и оно в 1,5 раза больше, чем второе число. Третье число составляет 40 % первого числа. Найдите четвертое число. С3. Решите уравнение С4. Начертите треугольник АВС, у которого АВ=4см, ˪А=1100, ˪В=400 Измерьте величину угла С. С5. Имеется шаблон с помощью которого можно построить только угол в 110 и никакой другой. Как с помощью этого шаблона построить угол в 40? | ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА ПО МАТЕМАТИКЕ ученика(цы) 5 ______ класса Ф.И. ____________________ ________________________ Вариант 2 Инструкция по выполнению работы Контрольная работа состоит из трех частей, включающих в себя 15 заданий. На выполнение работы отводится 45 минут. Внимательно читайте задание. Первая часть содержит 9 заданий с выбором одного ответа и одно задание на соответствие. За каждый верный ответ Вы получаете 1 балл. Вторая часть включает два задания с кратким ответом. За каждый верный ответ Вы получаете 2 балла. При выполнении заданий третьей части требуется запись полного решения. За выполнение каждого задания третьей части Вы можете получить от 0 до 3 баллов в зависимости от правильности и полноты записи решения. При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы. Если Вы ошиблись, можно исправить свой ответ: зачеркните уже отмеченную цифру и обведите нужную или запишите рядом новый ответ. Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов. Желаем успеха!
| Часть А. В заданиях А1-А10 отметьте один правильный, по вашему мнению, ответ. А1. Представьте число в виде неправильной дроби. 2) 3) 4) А2. Установите соответствие между выражением и их числовыми значениями
Впишите в таблицу ответов под каждой буквой соответствующий номер ответа. Ответ А3. Старинная русская мера длины – сажень равна 2,13 м. Округлите его значение до десятых. 2,1 м 2) 2 м 3) 2,2 м 4) 2,14 м А4. Расположите числа 7,481; 7,81; 71,84 и 7,418 в порядке убывания. 7,481; 7,418; 71,84; 7,81 3) 71,84; 7,81; 7,481; 7,418 71,84; 7,481; 7,418; 7,81 4) 71,84; 7,81; 7,418; 7,481 А5. Решите уравнение 2) 3) 4) А6. Упростите выражение 6,47с + 2,5с – 4,4с и найдите его значение при с=0,001 1) 457 2) 0,457 3) 0,00457 4) 0,0457 А7. Найдите объем прямоугольного параллелепипеда, высота которого равна 10 см, ширина 6 см, а длина является средним арифметическим высоты и ширины. 480 см3 2) 4800 см3 3) 960 см3 4) 3600 см3 А8. Запишите в виде процентов десятичную дробь 0,327. 32,7% 2) 3,27 % 3) 327% 4) 0,327% | А9. Дыня весит кг, а арбуз – на 1,8 кг больше. Сколько весят дыня и арбуз вместе? 2) 3) 4) А10. В стаде 200 животных, из них 34% составляют овцы, остальные коровы. Сколько коров было в стаде? 68 2) 132 3) 130 4) 54 Часть В. В заданиях В1-В2 запишите краткий ответ к задаче. В1. На диаграмме показано, чем занимаются дети, посещающие школу искусств. Используя диаграмму, найдите сколько детей занимаются танцами, если в школе 300 учащихся и каждый учащийся занимается одним видм искусств? Ответ: __________________________ В2. В коробку входит 14 кг конфет. Сколько такимх коробок потребуется, чтобы разложить 163 кг конфет? Ответ: _______________________________ Часть С. Задания С1, С2, С3, выполняется с полной записью решения. С1. Из двух городов навстречу друг другу одновременно вышли два автомобиля. Скорость одного автомобиля 60,5 км/ч второго на 4 км/ч больше. Какое расстояние будет между автомобилями через 4 часа, если расстояние между городами 400 км? | С2. Среднее арифметическое четырех чисел равно 1,35. Первое число равно 1,8 и оно в 1,2 раза больше, чем второе число. Третье число составляет 60 % второго числа. Найдите четвертое число. С3. Решите уравнение С4. Начертите треугольник АВС, у которого АВ=3см, ˪А=550, ˪В=300 Измерьте величину угла С. С5. Имеется шаблон с помощью которого можно построить только угол в 130 и никакой другой. Как с помощью этого шаблона построить угол в 20? |
xn--j1ahfl.xn--p1ai
Тест (5 класс) на тему: годовая контрольная работа по математике 5 класс Виленкин
По теме: методические разработки, презентации и конспекты
Контрольные работы по математике 5 класс, Н.Я. Виленкин и др.
Все контрольные работы по математике за курс 5 класса в двуз вариантах по Н.Я. Виленкину….
годовая контрольная работа по математике 5 класс
годовая контрольная работа по математике для 5 класса (комбинированная работа: 1 часть — в форме теста, 2 часть — развернутый ответ)…
Годовые контрольные работы по математике 5-6 класс УМК Виленкин
Контрольные работы по математике 5-6 класс. В двух вариантах с решениями и таблицами для записи ответов. По учебнику Виленкина….
Годовые контрольные работы по математике 5-6 класс УМК Виленкин
Контрольные работы по математике 5-6 класс. В двух вариантах с решениями и таблицами для записи ответов. По учебнику Виленкина….
годовая контрольная работа по математике 5 класс Виленкин
Контрольная работа состоит из тестовых заданий….
Итоговая контрольная работа по математике 5 класс (Виленкин Н.Я.)
Итоговая контрольная работа 5 класс (Виленкин Н.Я.)_углубленное изучение математики…
Методическая разработка годовой контрольной работы по математике, 5 класс, коррекционная школа VIII вида
Методическая разработка годовой контрольной работы 5 класса коррекционной школы VIII вида включает в всебя 4 варианта, разработанных по типогруппам обучающихся….
nsportal.ru
Контрольные работы по математике 5 класс
Контрольные работы из дидактических материалов и пособий для учителя. Программа обеспечивается УМК А.Г. Мерзляка, в состав которого входит:
1. Математика: 5 класс: учебник для учащихся общеобразовательных учреждений / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.: Вентана-Граф, 2015
2. Математика: 5 класс: дидактические материалы: сборник задач и контрольных работ / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.: Вентана-Граф, 2015.
3. Математика: 5 класс: рабочая тетрадь №1, №2 / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.: Вентана-Граф, 2015.
Просмотр содержимого документа
«Контрольные работы по математике 5 класс»
Контрольные работы по математике 5 класс
УМК Мерзляк А.Г., Полонский В.Б., Якир М.С.
Контрольная работа № 1
Натуральные числа
Вариант 1
Запишите цифрами число:
шестьдесят пять миллиардов сто двадцать три миллиона девятьсот сорок одна тысяча восемьсот тридцать семь;
восемьсот два миллиона пятьдесят четыре тысячи одиннадцать:
тридцать три миллиарда девять миллионов один.
Сравните числа: 1) 5 678 и 5 489; 2) 14 092 и 14 605.
Начертите координатный луч и отметьте на нём точки, соответствующие числам 2, 5, 7, 9.
Начертите отрезок FK, длина которого равна 5 см 6 мм, отметьте на нём точку C. Запишите все отрезки, образовавшиеся на рисунке, и измерьте их длины.
Точка К принадлежит отрезку МЕ, МК = 19 см, отрезок КЕ на 17 см больше отрезка МК. Найдите длину отрезка МЕ.
Запишите цифру, которую можно поставить вместо звёздочки, чтобы образовалось верное неравенство (рассмотрите все возможные случаи):
3 78* 3 784; 2) 5 8*5 5 872.
На отрезке CD длиной 40 см отметили точки P и Q так, что CP = 28 см, QD =26 см. Чему равна длина отрезка PQ?
Сравните: 1) 3 км и 2 974 м; 2) 912 кг и 8 ц.
Вариант 2
Запишите цифрами число:
семьдесят шесть миллиардов двести сорок два миллиона семьсот восемьдесят три тысячи сто девяносто пять;
четыреста три миллиона тридцать восемь тысяч сорок девять;
сорок восемь миллиардов семь миллионов два.
Сравните числа: 1) 6 894 и 6 983; 2) 12 471 и 12 324.
Начертите координатный луч и отметьте на нём точки, соответствующие числам 3, 4, 6, 8.
Начертите отрезок АВ, длина которого равна 4 см 8 мм, отметьте на нём точку D. Запишите все отрезки, образовавшиеся на рисунке, и измерьте их длины.
Точка T принадлежит отрезку МN, МT = 19 см, отрезок TN на 18 см меньше отрезка МT. Найдите длину отрезка МN.
Запишите цифру, которую можно поставить вместо звёздочки, чтобы образовалось верное неравенство (рассмотрите все возможные случаи):
2 *14 2 316; 2) 4 78* 4 785.
На отрезке SK длиной 30 см отметили точки A и B так, что SA = 14 см, BK =19 см. Чему равна длина отрезка AB?
Сравните: 1) 3 986 г и 4 кг; 2) 586 см и 6 м.
Вариант 3
Запишите цифрами число:
сорок семь миллиардов двести девяносто три миллиона восемьсот пятьдесят шесть тысяч сто двадцать четыре;
триста семь миллионов семьдесят восемь тысяч двадцать три;
восемьдесят пять миллиардов шесть миллионов пять.
Сравните числа: 1) 7 356 и 7 421; 2) 17 534 и 17 435.
Начертите координатный луч и отметьте на нём точки, соответствующие числам 2, 4, 6, 9.
Начертите отрезок MN, длина которого равна 6 см 4 мм, отметьте на нём точку A. Запишите все отрезки, образовавшиеся на рисунке, и измерьте их длины.
Точка E принадлежит отрезку CK, CE = 15 см, отрезок EK на 24 см больше отрезка CE. Найдите длину отрезка CK.
Запишите цифру, которую можно поставить вместо звёздочки, чтобы образовалось верное неравенство (рассмотрите все возможные случаи):
3 344 3 34*; 2) 2 724 * 619.
На отрезке AC длиной 60 см отметили точки E и F так, что AE = 32 см, FC =34 см. Чему равна длина отрезка EF?
Сравните: 1) 6 т и 5 934кг; 2) 4 м и 512 см.
Вариант 4
Запишите цифрами число:
восемьдесят шесть миллиардов пятьсот сорок один миллион триста семьдесят две тысячи триста сорок два;
шестьсот пять миллионов восемьдесят три тысячи десять;
сорок четыре миллиарда девять миллионов три.
Сравните числа: 1) 9 561 и 9 516; 2) 18 249 и 18 394.
Начертите координатный луч и отметьте на нём точки, соответствующие числам 2, 5, 8, 10.
Начертите отрезок АВ, длина которого равна 7 см 8 мм, отметьте на нём точку D. Запишите все отрезки, образовавшиеся на рисунке, и измерьте их длины.
Точка A принадлежит отрезку BM, BA = 25 см, отрезок AM на 9 см меньше отрезка BA. Найдите длину отрезка BM.
Запишите цифру, которую можно поставить вместо звёздочки, чтобы образовалось верное неравенство (рассмотрите все возможные случаи):
5 64* 5 646; 2) 1 4*2 1 431.
На отрезке OP длиной 50 см отметили точки M и N так, что OM = 24 см, NP =38 см. Чему равна длина отрезка M N?
Сравните: 1) 8 км и 7 962 м; 2) 60 см и 602 мм.
Контрольная работа № 2
Сложение и вычитание натуральных чисел. Числовые и буквенные выражения. Формулы.
Вариант 1
Вычислите: 1) 15 327+ 496 383; 2) 38 020 405 – 9 497 653.
На одной стоянке было 143 автомобиля, что на 17 автомобилей больше, чем на второй. Сколько автомобилей было на обеих стоянках?
Выполните сложение, выбирая удобный порядок вычислений:
(325 + 791) + 675; 2) 428 + 856 + 572 + 244.
Проверьте, верно ли неравенство:
1 674 – (736 + 328) 2 000 – (1 835 – 459).
Найдите значение 𝑎 по формуле 𝑎 = 4𝑏 – 16 при 𝑏 = 8.
Упростите выражение 126 + 𝒙 + 474 и найдите его значение при 𝒙 = 278.
Вычислите:
4 м 73 см + 3 м 47 см; 2) 12 ч 16 мин – 7 ч 32 мин.
Найдите значение выражения, выбирая удобный порядок вычислений:
(713 + 529) – 413; 2) 624 – (137 + 224).
Вариант 2
Вычислите: 1) 17 824+ 128 356; 2) 42 060 503 – 7 456 182.
На одной улице 152 дома, что на 18 домов меньше, чем на другой. Сколько всего домов на обеих улицах?
Выполните сложение, выбирая удобный порядок вычислений:
(624 + 571) + 376; 2) 212 + 497 + 788 + 803.
Проверьте, верно ли неравенство:
1 826 – (923 + 249) 3 000 – (2 542 – 207).
Найдите значение 𝑝 по формуле 𝑝= 40 – 7𝑞 при 𝑞 = 4.
Упростите выражение 235 + y + 465 и найдите его значение при y = 153.
Вычислите:
6 м 23 см + 5 м 87 см; 2) 14 ч 17 мин – 5 ч 23 мин.
Найдите значение выражения, выбирая удобный порядок вычислений:
(837 + 641) – 537; 2) 923 – (215 + 623).
Вариант 3
Вычислите: 1) 26 832 + 573 468; 2) 54 073 507 – 6 829 412.
В одном классе 37 учащихся, что на 9 человек больше, чем во втором. Сколько всего учащихся в обоих классах?
Выполните сложение, выбирая удобный порядок вычислений:
(736 + 821) + 264; 2) 573 + 381 + 919 + 627.
Проверьте, верно ли неравенство:
2 491 – (543 + 1 689) 1 000 – (931 – 186).
Найдите значение 𝑦 по формуле 𝑦 = 3𝑥 + 18 при 𝑥 = 5.
Упростите выражение 433 + 𝑎 + 267 и найдите его значение при 𝑎 = 249.
Вычислите:
7 м 23 см + 4 м 81 см; 2) 6 ч 38 мин – 4 ч 43 мин.
Найдите значение выражения, выбирая удобный порядок вычислений:
(674 + 245) – 374; 2) 586 – (217 + 186).
Вариант 4
Вычислите: 1) 19 829 + 123 471; 2) 61 030 504 – 8 695 371.
На одной книжной полке стоят 23 книги, что на 5 книг меньше, чем на другой. Сколько всего книг стоит на обеих полках?
Выполните сложение, выбирая удобный порядок вычислений:
(349 + 856) + 651; 2) 166 + 452 + 834 + 748.
Проверьте, верно ли неравенство:
1 583 – (742 + 554) 1 000 – (883 – 72).
Найдите значение 𝑥 по формуле 𝑥 = 16 + 8𝑧 при 𝑧 = 7.
Упростите выражение 561 + 𝑏 + 139 и найдите его значение при 𝑏 = 165.
Вычислите:
9 м 41 см + 4 м 72 см; 2) 18 ч 18 мин – 5 ч 24 мин.
Найдите значение выражения, выбирая удобный порядок вычислений:
(563 + 721) – 363; 2) 982 – (316 + 582).
Контрольная работа № 3
Уравнение. Угол. Многоугольники.
Вариант 1
Постройте угол МКА, величина которого равна 74. Проведите произвольно луч КС между сторонами угла МКА. Запишите образовавшиеся углы и измерьте их величины.
Решите уравнение: 1) 𝑥 +37 = 81 2) 150 – 𝑥 = 98.
Одна из сторон треугольника равна 24 см, вторая – в 4 раза короче первой, а третья – на 16 см длиннее второй. Вычислите периметр треугольника.
Решите уравнение: 1) (34 + 𝑥) – 83 = 42 2) 45 – (𝑥 – 16) = 28.
Из вершины развёрнутого угла АВС (см рис.) проведены два луча ВD и ВЕ так, что ∠АВЕ = 154, ∠DВС = 128. Вычислите градусную меру угла DВЕ.
Какое число надо подставить вместо 𝑎, чтобы корнем уравнения
52 – (𝑎 – 𝑥) = 24 было число 40?
Вариант 2
Постройте угол ABC, величина которого равна 168. Проведите произвольно луч BM между сторонами угла ABC. Запишите образовавшиеся углы и измерьте их величины.
Решите уравнение: 1) 21 + 𝑥 = 58 2) 𝑥 – 135 = 76.
Одна из сторон треугольника равна 32 см, вторая – в 2 раза короче первой, а третья – на 6 см короче первой. Вычислите периметр треугольника.
Решите уравнение: 1) (96 – 𝑥) – 15 = 64 2) 31 – (𝑥 + 11) = 18.
Из вершины прямого угла MNK (см рис.) проведены два луча ND и NE так, что ∠MND = 73, ∠KNF = 48. Вычислите градусную меру угла DNF.
Какое число надо подставить вместо 𝑎, чтобы корнем уравнения
64 – (𝑎 – 𝑥) = 17 было число 16?
Вариант 3
Постройте угол FDK, величина которого равна 56. Проведите произвольно луч DT между сторонами угла FDK. Запишите образовавшиеся углы и измерьте их величины.
Решите уравнение: 1) 𝑥 + 42 = 94 2) 284 – 𝑥 = 121.
Одна из сторон треугольника равна 12 см, вторая – в 3 раза длиннее первой, а третья – на 8 см короче второй. Вычислите периметр треугольника.
Решите уравнение: 1) (41 + 𝑥) – 12 = 83 2) 62 – (𝑥 – 17) = 31.
Из вершины развёрнутого угла FAN (см рис.) проведены два луча AK и AP так, что ∠NAP = 110, ∠FAK = 132. Вычислите градусную меру угла PAK.
Какое число надо подставить вместо 𝑎, чтобы корнем уравнения
(69 – 𝑎) – 𝑥 = 23 было число 12?
Вариант 4
Постройте угол NMC, величина которого равна 58. Проведите произвольно луч MB между сторонами угла NMC. Запишите образовавшиеся углы и измерьте их величины.
Решите уравнение: 1) 𝑥 + 53 = 97 2) 142 – 𝑥 = 76.
Одна из сторон треугольника равна 30 см, вторая – в 5 раза короче первой, а третья – на 22 см длиннее второй. Вычислите периметр треугольника.
Решите уравнение: 1) (58 + 𝑥) – 23 = 96 2) 54 – (𝑥 – 19) = 35.
Из вершины прямого угла DMK (см рис.) проведены два луча MB и MC так, что ∠DMB = 51, ∠KMC = 65. Вычислите градусную меру угла BMC.
Какое число надо подставить вместо 𝑎, чтобы корнем уравнения
(𝑎 – 𝑥) – 14 = 56 было число 5?
Контрольная работа № 4
Умножение и деление натуральных чисел. Свойства умножения.
Вариант 1
Вычислите:
36 ∙ 2 418; 3) 1 456 : 28;
175 ∙ 204; 4) 177 000 : 120.
Найдите значение выражения: (326 ∙ 48 – 9 587) : 29.
Решите уравнение:
𝑥 ∙ 14 = 364; 2) 324 : 𝑥 = 9; 3) 19𝑥 — 12𝑥 = 126.
Найдите значение выражения наиболее удобным способом:
25 ∙ 79 ∙ 4; 2) 43 ∙ 89 + 89 ∙ 57.
Купили 7 кг конфет и 9 кг печенья, заплатив за всю покупку 1 200 р. Сколько стоит 1 кг печенья, если 1 кг конфет стоит 120 р?
С одной станции одновременно в одном направлении отправились два поезда. Один из поездов двигался со скоростью 56 км/ч, а второй – 64 км/ч. Какое расстояние будет между поездами через 6 ч после начала движения?
Сколькими нулями оканчивается произведение всех натуральных чисел от 19 до 35 включительно?
Вариант 2
Вычислите:
24 ∙ 1 246; 3) 1 856 : 32;
235 ∙ 108; 4) 175 700 : 140.
Найдите значение выражения: (625 ∙ 25 – 8 114) : 37.
Решите уравнение:
𝑥 ∙ 28 = 336; 2) 312 : 𝑥 = 8; 3) 16𝑥 — 11𝑥 = 225.
Найдите значение выражения наиболее удобным способом:
2 ∙ 83 ∙ 50; 2) 54 ∙ 73 + 73 ∙ 46.
Для проведения ремонта электрической проводки купили 16 одинаковых мотков алюминиевого и 11 одинаковых мотков медного провода. Общая длина купленного провода составляла 650 м. Сколько метров алюминиевого провода было в мотке, если медного провода в одном мотке было 30 м?
Из одного города одновременно в одном направлении выехали два автомобиля. Один из них двигался со скоростью 74 км/ч, а второй – 68 км/ч. Какое расстояние будет между автомобилями через 4 ч после начала движения?
Сколькими нулями оканчивается произведение всех натуральных чисел от 23 до 42 включительно?
Вариант 3
Вычислите:
32 ∙ 1 368; 3) 1 664 : 26;
145 ∙ 306; 4) 216 800 : 160.
Найдите значение выражения: (546 ∙ 31 – 8 154) : 43.
Решите уравнение:
𝑥 ∙ 22 = 396; 2) 318 : 𝑥 = 6; 3) 19𝑥 — 7𝑥 = 144.
Найдите значение выражения наиболее удобным способом:
5 ∙ 97 ∙ 20; 2) 68 ∙ 78 — 78 ∙ 58.
В автомобиль погрузили 5 одинаковых мешков сахара и 3 одинаковых мешка муки. Оказалось, что общая масса груза равна 370 кг. Какова масса одного мешка муки, если масса одного мешка сахара равна 50 кг?
Из одного села одновременно в одном направлении отправились пешеход и велосипедист. Пешеход двигался со скоростью 3 км/ч, а велосипедист – 12 км/ч. Какое расстояние будет между ними через 3 ч после начала движения?
Сколькими нулями оканчивается произведение всех натуральных чисел от 34 до 53 включительно?
Вариант 4
Вычислите:
28 ∙ 2 346; 3) 1 768 : 34;
185 ∙ 302; 4) 220 500 : 180.
Найдите значение выражения: (224 ∙ 46 – 3 232) : 34.
Решите уравнение:
𝑥 ∙ 16 = 384; 2) 371 : 𝑥 = 7; 3) 22𝑥 — 14𝑥 = 112.
Найдите значение выражения наиболее удобным способом:
2 ∙ 87 ∙ 50; 2) 167 ∙ 92 — 92 ∙ 67.
В школьную столовую завезли 8 одинаковых ящиков яблок и 6 одинаковых ящиков апельсинов. Сколько килограммов апельсинов было в одном ящике, если всего было 114 кг яблок и апельсинов, а яблок в каждом ящике было 9 кг?
От одной пристани одновременно в одном направлении отплыли лодка и катер. Лодка плыла со скоростью 14 км/ч, а катер – 21 км/ч. Какое расстояние будет между ними через 5 ч после начала движения?
Сколькими нулями оканчивается произведение всех натуральных чисел от 41 до 64 включительно?
Контрольная работа № 5
Деление с остатком. Площадь прямоугольника. Прямоугольный параллелепипед и его объем. Комбинаторные задачи.
Вариант 1
Выполните деление с остатком: 478 : 15.
Найдите площадь прямоугольника, одна сторона которого равна 14 см, а вторая сторона в 3 раза больше первой.
Вычислите объем и площадь поверхности куба с ребром 3 см.
Длина прямоугольного параллелепипеда равна 18 см, ширина – в 2 раза меньше длины, а высота – на 11 см больше ширины. Вычислите объем параллелепипеда.
Чему равно делимое, если делитель равен 11, неполное частное – 7, а остаток – 6?
Поле прямоугольной формы имеет площадь 6 га. Ширина поля 150 м. Вычислите периметр поля.
Запишите все трёхзначные числа, для записи которых используются только цифры 5, 6 и 0 (цифры не могут повторяться).
Сумма длин всех рёбер прямоугольного параллелепипеда равна 116 см, а два его измерения – 12 см и 11 см. Найдите третье измерение параллелепипеда.
Вариант 2
Выполните деление с остатком: 376 : 18.
Найдите площадь прямоугольника, одна сторона которого равна 21 см, а вторая сторона в 3 раза меньше первой.
Вычислите объем и площадь поверхности куба с ребром 4 дм.
Ширина прямоугольного параллелепипеда равна 6 см, длина – в 5 раз больше ширины, а высота – на 5 см меньше длины. Вычислите объем параллелепипеда.
Чему равно делимое, если делитель равен 17, неполное частное – 5, а остаток – 12?
Поле прямоугольной формы имеет площадь 3 га, его длина – 200 м. Вычислите периметр поля.
Запишите все трёхзначные числа, для записи которых используются только цифры 0, 9 и 4 (цифры не могут повторяться).
Сумма длин всех рёбер прямоугольного параллелепипеда равна 80 см, а два его измерения – 10 см и 4 см. Найдите третье измерение параллелепипеда.
Вариант 3
Выполните деление с остатком: 516 : 19.
Найдите площадь прямоугольника, одна сторона которого равна 17 см, а вторая сторона в 2 раза больше первой.
Вычислите объем и площадь поверхности куба с ребром 5 дм.
Высота прямоугольного параллелепипеда равна 20 см, длина – на 4 см больше высоты, а ширина – в 2 раза меньше длины. Вычислите объем параллелепипеда.
Чему равно делимое, если делитель равен 14, неполное частное – 8, а остаток – 9?
Поле прямоугольной формы имеет площадь 7 га, его длина – 350 м. Вычислите периметр поля.
Запишите все трёхзначные числа, для записи которых используются только цифры 1, 2 и 0 (цифры не могут повторяться).
Сумма длин всех рёбер прямоугольного параллелепипеда равна 100 дм, а два его измерения – 8 дм и 13 дм. Найдите третье измерение параллелепипеда.
Вариант 4
Выполните деление с остатком: 610 : 17.
Найдите площадь прямоугольника, одна сторона которого равна 45 см, а вторая сторона в 5 раз меньше первой.
Вычислите объем и площадь поверхности куба с ребром 2 см.
Длина прямоугольного параллелепипеда равна 20 см, высота – в 4 раза меньше длины, а ширина – на 7 см больше высоты. Вычислите объем параллелепипеда.
Чему равно делимое, если делитель равен 15, неполное частное – 6, а остаток – 14?
Поле прямоугольной формы имеет площадь 4 га, его ширина – 50 м. Вычислите периметр поля.
Запишите все трёхзначные числа, для записи которых используются только цифры 7, 0 и 8 (цифры не могут повторяться).
Сумма длин всех рёбер прямоугольного параллелепипеда равна 72 см, а два его измерения – 6 см и 8 см. Найдите третье измерение параллелепипеда.
Контрольная работа № 6
Обыкновенные дроби
Вариант 1
Сравните числа:
и ; 2) и 1; 3) и 1.
Выполните действия:
+ ; 3) ;
+ 5 ; 4) .
В саду растёт 72 дерева, из них составляют яблони. Сколько яблонь растёт в саду?
Кирилл прочёл 56 страниц, что составило книги. Сколько страниц было в книге?
Преобразуйте в смешанное число дробь:
; 2) .
Найдите все натуральные значения 𝑥, при которых верно неравенство .
Каково наибольшее натуральное значение n, при котором верно неравенство n ?
Найдите все натуральные значения 𝑎, при которых одновременно выполняются условия: дробь правильная, а дробь неправильная.
Вариант 2
Сравните числа:
и ; 2) и 1; 3) и 1.
Выполните действия:
+ ; 3) ;
+ 1 ; 4) .
В гараже стоят 63 машины, из них составляют легковые. Сколько легковых машин стоит в гараже?
В классе 12 учеников изучают французский язык, что составляет всех учеников класса. Сколько учеников в классе?
Преобразуйте в смешанное число дробь:
; 2) .
Найдите все натуральные значения 𝑥, при которых верно неравенство .
Каково наименьшее натуральное значение n, при котором верно неравенство n ?
Найдите все натуральные значения 𝑎, при которых одновременно выполняются условия: дробь правильная, а дробь неправильная.
Вариант 3
Сравните числа:
и ; 2) и 1; 3) и 1.
Выполните действия:
+ ; 3) ;
+ 7 ; 4) .
В классе 36 учеников, из них занимаются спортом. Сколько учеников занимаются спортом?
Ваня собрал 16 вёдер картофеля, что составляет всего урожая. Сколько вёдер картофеля составляет урожай?
Преобразуйте в смешанное число дробь:
; 2) .
Найдите все натуральные значения 𝑥, при которых верно неравенство .
Каково наибольшее натуральное значение n, при котором верно неравенство n ?
Найдите все натуральные значения 𝑎, при которых обе дроби и одновременно будут неправильными.
Вариант 4
Сравните числа:
и ; 2) и 1; 3) и 1.
Выполните действия:
+ ; 3) ;
+ 2 ; 4) .
В пятых классах 64 ученика, из них составляют отличники. Сколько отличников в пятых классах?
Мама приготовила вареники с творогом, а Коля съел 9 штук, что составляет всех вареников. Сколько вареников приготовила мама?
Преобразуйте в смешанное число дробь:
; 2) .
Найдите все натуральные значения 𝑥, при которых верно неравенство 2 .
Каково наименьшее натуральное значение n, при котором верно неравенство n ?
Найдите все натуральные значения 𝑎, при которых одновременно выполняются условия: дробь будет неправильная, а дробь правильная.
Контрольная работа № 7
Понятие о десятичной дроби. Сравнение, округление, сложение и вычитание десятичных дробей.
Вариант 1
Сравните: 1) 14,396 и 14,4; 2) 0,657 и 0, 6565.
Округлите: 1) 16,76 до десятых; 2) 0,4864 до тысячных.
Выполните действия: 1) 3,87 + 32,496; 2) 23,7 – 16,48; 3) 20 – 12,345.
Скорость катера по течению реки равна 24,2 км/ч, а собственная скорость катера – 22,8 км/ч. Найдите скорость катера против течения реки.
Вычислите, записав данные величины в килограммах:
3,4 кг + 839 г; 2) 2 кг 30 г – 1956 г.
Одна сторона треугольника равна 5,6 см, что на 1,4 см больше второй стороны и на 0,7 см меньше третьей. Найдите периметр треугольника.
Напишите три числа, каждое из которых больше 5,74 и меньше 5,76.
Найдите значение выражения, выбирая удобный порядок вычислений:
(8,63 + 3,298) – 5,63; 2) 0,927 – (0,327 + 0,429).
Вариант 2
Сравните: 1) 17,497 и 17,5; 2) 0,346 и 0, 3458.
Округлите: 1) 12,88 до десятых; 2) 0,3823 до сотых.
Выполните действия: 1) 5,62 + 43,299; 2) 25,6 – 14,52; 3) 30 – 14,265.
Скорость катера против течения реки равна 18,6 км/ч, а собственная скорость
катера – 19,8 км/ч. Найдите скорость катера по течению реки.
Вычислите, записав данные величины в метрах:
8,3 м + 784 см; 2) 5 м 4 см – 385 см.
Одна сторона треугольника равна 4,5 см, что на 3,3 см меньше второй стороны и на 0,6 см больше третьей. Найдите периметр треугольника.
Напишите три числа, каждое из которых больше 3,82 и меньше 3,84.
Найдите значение выражения, выбирая удобный порядок вычислений:
(5,94 + 2,383) – 3,94; 2) 0,852 – (0,452 + 0,214).
Вариант 3
Сравните: 1) 12,598 и 12,6; 2) 0,257 и 0, 2569.
Округлите: 1) 17,56 до десятых; 2) 0,5864 до тысячных.
Выполните действия: 1) 4,36 + 27,647; 2) 32,4 – 17,23; 3) 50 – 22,475.
Скорость катера по течению реки равна 19,6 км/ч, а собственная скорость катера – 18,3 км/ч. Найдите скорость катера против течения реки.
Вычислите, записав данные величины в центнерах:
6,7 ц + 584 кг; 2) 6 ц 2 кг – 487 кг.
Одна сторона треугольника равна 3,7 см, что на 0,9 см больше второй стороны и на 1,2 см меньше третьей. Найдите периметр треугольника.
Напишите три числа, каждое из которых больше 7,87 и меньше 7,89.
Найдите значение выражения, выбирая удобный порядок вычислений:
(6,73 + 4,594) – 2,73; 2) 0,791 – (0,291 + 0,196).
Вариант 4
Сравните: 1) 16,692 и 16,7; 2) 0,745 и 0, 7438.
Округлите: 1) 24,87 до десятых; 2) 0,8653 до тысячных.
Выполните действия: 1) 6,72 + 54,436; 2) 27,6 – 15,72; 3) 40 – 11,825.
Скорость катера против течения реки равна 17,8 км/ч, а собственная скорость
катера – 19,4 км/ч. Найдите скорость катера по течению реки.
Вычислите, записав данные величины в метрах:
2,8 м + 524 см; 2) 4 м 6 см – 257 см.
Одна сторона треугольника равна 5,1 см, что на 2,1 см меньше второй стороны и на 0,7 см больше третьей. Найдите периметр треугольника.
Напишите три числа, каждое из которых больше 1,34 и меньше 1,36.
Найдите значение выражения, выбирая удобный порядок вычислений:
(7,86 + 4,183) – 2,86; 2) 0,614 – (0,314 + 0,207).
Контрольная работа № 8
Умножение и деление десятичных дробей
Вариант 1
Вычислите:
0,024 ∙ 4,5; 3) 2,86 : 100; 5) 0,48 : 0,8;
29,41 ∙ 1 000; 4) 4 : 16; 6) 9,1 : 0,07.
Найдите значение выражения: (4 – 2,6) ∙ 4,3 + 1,08 : 1,2.
Решите уравнение: 2,4 (𝑥 + 0,98) = 4,08.
Моторная лодка плыла 1,4 ч по течению реки и 2,2 ч против течения. Какой путь преодолела лодка за всё время движения, если скорость течения равна 1,7 км/ч, а собственная скорость лодки – 19,8 км/ч?
Если в некоторой десятичной дроби перенести запятую вправо через одну цифру, то она увеличится на 14,31. Найдите эту дробь.
Вариант 2
Вычислите:
0,036 ∙ 3,5; 3) 3,68 : 100; 5) 0,56 : 0,7;
37,53 ∙ 1 000; 4) 5 : 25; 6) 5,2 : 0,04.
Найдите значение выражения: (5 – 2,8) ∙ 2,4 + 1,12 : 1,6.
Решите уравнение: 0,084 : (6,2 – 𝑥) = 1,2.
Катер плыл 1,6 ч против течения реки и 2,4 ч по течению. На сколько больше проплыл катер, двигаясь по течению реки, чем против течения, если скорость течения реки равна 2,1 км/ч, а собственная скорость катера – 28,2 км/ч?
Если в некоторой десятичной дроби перенести запятую влево через одну цифру, то она уменьшится на 23,76. Найдите эту дробь.
Вариант 3
Вычислите:
0,064 ∙ 6,5; 3) 4,37 : 100; 5) 0,63 : 0,9;
46,52 ∙ 1 000; 4) 6 : 15; 6) 7,2 : 0,03.
Найдите значение выражения: (6 – 3,4) ∙ 1,7 + 1,44 : 1,6.
Решите уравнение: 1,6 (𝑥 + 0,78) = 4,64.
Теплоход плыл 1,8 ч против течения реки и 2,6 ч по течению. Какой путь преодолел теплоход за всё время движения, если скорость течения равна 2,5 км/ч, а собственная скорость теплохода – 35,5 км/ч?
Если в некоторой десятичной дроби перенести запятую вправо через одну цифру, то она увеличится на 15,93. Найдите эту дробь.
Вариант 4
Вычислите:
0,096 ∙ 5,5; 3) 7,89 : 100; 5) 0,76 : 0,4;
78,53 ∙ 100; 4) 6 : 24; 6) 8,4 : 0,06.
Найдите значение выражения: (7 – 3,6) ∙ 2,8 + 1,32 : 2,2.
Решите уравнение: 0,144 : (3,4 – 𝑥) = 2,4.
Моторная лодка плыла 3,6 ч против течения реки и 1,8 ч по течению. На сколько километров больше проплыла лодка, двигаясь против течения , чем по течению, если скорость течения реки равна 1,2 км/ч, а собственная скорость лодки – 22,4 км/ч?
Если в некоторой десятичной дроби перенести запятую влево через одну цифру, то она уменьшится на 29,52. Найдите эту дробь.
Контрольная работа № 9
Среднее арифметическое. Проценты.
Вариант 1
Найдите среднее арифметическое чисел: 32,6; 38,5; 34; 35,3.
Площадь поля равна 300 га. Рожью засеяли 18 % поля. Сколько гектаров поля засеяли рожью?
Петя купил книгу за 90 р., что составляет 30 % всех денег, которые у него были. Сколько денег было у Пети?
Лодка плыла 2 ч со скоростью 12,3 км/ч и 4 ч со скоростью 13,2 км/ч. Найдите среднюю скорость лодки на всём пути.
Турист прошёл за три дня 48 км. В первый день он прошёл 35 % всего маршрута. Путь пройденный в первый день, составляет 80 % расстояния , пройденного во второй день. Сколько километров прошёл турист в третий день?
В первый день Петя прочитал 40 % всей книги, во второй – 60 % остального, а в третий — оставшиеся 144 страницы. Сколько всего страниц в книге?
Вариант 2
Найдите среднее арифметическое чисел: 26,3; 20,2; 24,7; 18.
В школе 800 учащихся. Сколько пятиклассников в этой школе, если известно, что их количество составляет 12 % количества всех учащихся?
Насос перекачал в бассейн 42 воды, что составляет 60 % объёма бассейна. Найдите объём бассейна.
Автомобиль ехал 3 ч со скоростью 62,6 км/ч и 2 ч со скоростью 65 км/ч. Найдите среднюю скорость автомобиля на всём пути.
Токарь за три дня изготовил 80 деталей. В первый день он выполнил 30 % всей работы. Известно, что количество деталей, изготовленных в первый день, составляет 60 % количества деталей , изготовленных во второй день. Сколько деталей изготовил токарь в третий день?
В первый день тракторная бригада вспахала 30 % площади всего поля, во второй – 75% остального, а в третий — оставшиеся 14 га. Найдите площадь поля.
Вариант 3
Найдите среднее арифметическое чисел: 26,4; 42,6; 31,8; 15.
В магазин завезли 600 кг овощей. Картофель составляет 24% всех завезённых овощей. Сколько килограммов картофеля завезли в магазин?
За первый день турист прошёл расстояние 18 км, что составляет 40 % всего пути, который он должен преодолеть. Найдите длину пути, который должен пройти турист.
Катер плыл 1,5 ч со скоростью 34 км/ч и 2,5 ч со скоростью 30 км/ч. Найдите среднюю скорость катера на всём пути.
За три дня оператор набрал на компьютере 60 страниц. В первый день было выполнено 35 % всей работы. Объём работы, выполненной в первый день, составляет 70 % работы, выполненной во второй день. Сколько страниц было набрано в третий день?
За первый час было продано 84 % всего мороженого, за второй – 78 % остального, а за третий – оставшиеся 44 порции. Сколько порций мороженого было продано за три часа?
Вариант 4
Найдите среднее арифметическое чисел: 43,6; 21,8; 32,4; 11.
Площадь парка равна 40 га. Площадь озера составляет 15 % площади парка. Найдите площадь озера.
За первый час движения автомобиль преодолел расстояние 72 км, что составляет 24 % длины всего пути, который ему надо проехать. Найдите общий путь, который преодолел автомобиль.
Черепаха ползла 2 ч со скоростью 15,3 м/ч и 3 ч со скоростью 12, 4 м/ч. Найдите среднюю скорость черепахи на всём пути.
Три насоса наполнили водой бассейн объёмом 320 . Первый насос заполнил бассейн на 30 %, что составляет 80 % объёма воды, которую перекачал второй насос. Найдите объём воды, которую перекачал третий насос.
В первый день турист прошёл 20% всего пути, во второй – 60 % остального, а в третий – оставшиеся 24 км. Найдите длину пути, который прошёл турист за три дня.
Контрольная работа № 10
Обобщение и систематизация знаний учащихся
за курс математики 5 класса
Вариант 1
Найдите значени
multiurok.ru
