Гдз по математике за 5 класс виленкин н я решебник – Страница 9 №12-14 ГДЗ к учебнику «Математика» 5 класс Дорофеев, Шарыгин, Суворова

Страница 14 №14-20 ГДЗ к учебнику «Математика» 5 класс Бунимович, Дорофеев, Суворова

Упражнения

Прямая. Части прямой

Задание 14. Отметьте в тетради точки A и C. Проверьте через них прямую. Отметьте на прямой AC еще три точки и обозначьте их. Отметьте четыре точки, не лежащие на прямой AC; обозначьте их.

Задание 15. Начертите две пересекающиеся прямые a и b и обозначьте точку их пересечения буквой D. Проведите через точку D еще одну прямую, отличную от a и b. Сколько получилось лучей с началом в точке D? Сколько можно построить прямых, проходящих через точку D?

Решение

Получилось 6 лучей с началом в точке D.
Можно построить бесконечное количество прямых, проходящих через точку D.

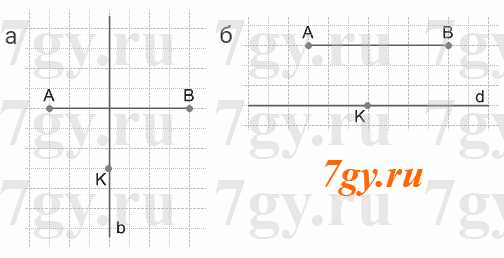
Задание 16. Проведите прямую a и отметьте на ней точки A, B, C, D, K так, чтобы:
а) точка C принадлежала отрезку с концами в точках A и B;
б) точка D принадлежала лучу AB и не принадлежала отрезку AB;
в) точка K принадлежала лучу BA и не принадлежала отрезку AB.

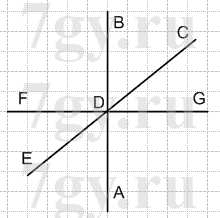
Задание 17. Рассмотрите рисунок 1.19. Верно ли утверждение:
а) точка A лежит на отрезке CB;
б) точка A лежит на луче CB;
в) точка A лежит на луче BD;
г) точка D лежит между точками A и C;
д) точка B лежит на луче AC и луче CA;
е) точки D и C лежат на одном и том же луче с началом в точке B?

Решение

а) Нет, неверно. Точка A не лежит на отрезке CB.
б) Да, верно. Точка A лежит на луче CB.
в) Да, верно. Точка A лежит на луче BD.
г) Нет, неверно. Точка D не лежит между точками A и C.
д) Да, верно. Точка B лежит на луче AC и луче CA
е) Нет, неверно. Точки D и C лежат на разных лучах с началом в точке B.

Отрезок

Задание 18. В узле квадратной сетки тетради отметьте точку O. Постройте:
1) точку A, расположенную на 5 клеток правее и на 4 клетки выше точки O;
2) точку B, расположенную на 3 клетки правее и на 2 клетки ниже точки O;
3) точку C, расположенную на 4 клетки левее и на 1 клетку ниже точки O.
4) Соедините каждую из точек A, B, C с точкой O. Назовите получившиеся отрезки.

Решение

Получилось 3 отрезка:
1) OA;
2) OB;
3) OC.

Задание 19. Начертите отрезок AB. Отметьте точку K так, чтобы точки A, B и K не принадлежали одной прямой. Проведите через точку K:
а) прямую b, пересекающую отрезок AB;
б) прямую d, не пересекающую отрезок AB.

Задание 20. Отметьте три точки, не лежащие на одной прямой. Обозначьте их. Проведите все отрезки, концами которых являются пары этих точек. Сколько получилось отрезков?

Решение

Получилось 3 отрезка: AB, BC, AC.

7gy.ru

Страница 11 ГДЗ к учебнику «Математика» 5 класс Дорофеев, Шарыгин, Суворова

1. 2 Прямая. Части прямой. Ломаная

Задание № 15. Начертите две пересекающиеся прямые и обозначьте точку пересечения буквой D. Проведите через точку D еще одну прямую. Закончите предложение: Через одну точку можно провести . . . . Сколько лучей с началом в точке D? Обозначьте лучи буквами.

Решение

Через одну точку можно провести бесконечное множество прямых.
C началом в точке D 6 лучей: DA, DB, DC, DE, DF, DG.

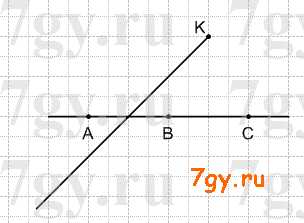
Задание № 16. Отметьте в тетради точки A и C. Проведите через них прямую. Отметьте точку B, лежащую на прямой AC, и точку K, не лежащую на прямой AC. Проведите луч с началом в точке K, пересекающий отрезок AB.

Задание № 17. Рассмотрите рисунок 1. 15. и скажите, верно ли утверждение:

1) Точка A лежит на отрезке BC.
2) Точка A лежит на луче BD.
3) Точка D не лежит между точками A и C.
4) Точки D и C лежат на одном и том же луче с началом в точке B.

Решение

1) неверно
2) верно
3) верно
4) неверно

Задание № 18. Проведите прямую и отметьте на ней точки A и B. Отметьте на прямой AB точку C так, чтобы она принадлежала отрезку AB; точку D так, чтобы она не принадлежала отрезку AB.

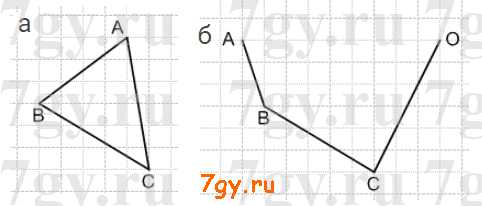
Задание № 19. Перечертите в тетрадь ломаную (рис. 1. 16). Запишите её звенья.

Решение

Звенья ломаной: AB, BC, CD.

Задание № 20. 1) Что такое алгоритм? Найдите в словаре значение этого слова.
2) Постройте в тетради ломаную по следующему алгоритму:
Шаг 1. Отметьте в одном из узлов квадратной сетки точку A.
Шаг 2. От точки A отсчитайте 7 клеток влево и 1 клетку вниз. Отметьте точку B.
Шаг 3. От точки B отсчитайте 5 клеток вправо и 3 клетки вниз. Отметьте точку C.
Шаг 4. От точки C отсчитайте 3 клетки вправо и 6 клеток вверх. Отметьте точку O.
Шаг 5. Соедините точки по линейке в том порядке, в котором вы их строили.
3) Начертите в тетради ломаную с вершинами в узлах сетки и продиктуйте её соседу по парте. Сравните построенные с вами ломаные.

Решение

Алгоритм − последовательность операций.

Задание № 21. Начертите в тетради:
а) замкнутую ломаную, состоящую из трёх звеньев;
б) незамкнутую ломаную, состоящую из четырёх звеньев.

7gy.ru

Страница 23 №134-142 ГДЗ к учебнику «Математика» 6 класс Виленкин, Жохов, Чесноков

Задание № 134. а) Книга на 100% дороже альбома. На сколько процентов альбом дешевле книги?
б) Масса гуся на 25% больше массы утки. На сколько процентов масса утки меньше массы гуся?

Решение 7 гуру

а) Пусть х − стоимость альбома. Тогда цена книги равна: х + х = 2х.
Альбом дешевле книги на:
 х * 100% = 50%.
2х
Ответ: на 50%.

б) Пусть х − масса утки. Масса гуся: х + 0,25х = 1,25х.
Утка легче гуся на: 1,25 − х = 0,25х.
0,25x * 100% = 20%.
1,25x
Ответ: на 20%.

Задание № 135. Для какого числового выражения составлена программа вычислений на микрокалькуляторе:
а) 7,46 |+| 8,7 |÷| 0,016 |+| 6,9 |=|;
б) 10,2 |+| 8,83 |−| 20 |↔| |=|?

Решение

а) (7,46 + 8,7) : 0,016 + 6,9
б) 20 − (10,2 + 8,83)

Задание № 136. Стороны треугольника 12 см, 17 см и х см:
а) составьте выражение для вычисления периметра этого треугольника;
б) подумайте, каким может быть значение х и каким быть не может.

Решение

а) P = 12 + 17 + x, где Р − периметр прямоугольника
б) у треугольника сумма двух любых сторон всегда больше третьей стороны, поэтому 12 + 17 > х => х < 29 и х + 12 > 17 => х > 5.
Из двух неравенств получаем условие: 5 < х < 29.

Задание № 137. Сколько чётных четырёхзначных чисел можно составить из цифр 0, 2, 3, 4, 5?

Решение

В разряд тысяч можно поставить цифры 2, 2, 4, 5;
в разряд сотен и десятков места можно поставить 0, 2, 3, 4, 5;
в разряд единиц можно поставить 0, 2, 4 (число чётное).
Всего имеем 4 * 5 * 5 * 3 = 300 чисел.

Задание № 138. Решите задачу:
1) Две бригады хлопкоробов собрали вместе 20,4 ц хлопка за день. При этом первая бригада собрала на 1,52 ц больше второй. Сколько центнеров хлопка собрала каждая бригада?
2) Два комбайнера убрали пшеницу с 64,2 га. Сколько гектаров убрал каждый комбайнер, если первый убрал на 2,8 га меньше, чем второй?

Решение задач

1)
1-я бригада _ ? на 1,52 ц >
2-я бригада — ?                         } 20,4 ц

Пусть первая бригада собрала х ц хлопка за день, тогда:
х + 1,52 (ц) — хлопка за день собрала вторая бригада.
х + х + 1,52 = 20,4
x = (20,4 − 1,52) : 2
х = 9,44 (ц) — собрала первая бригада.
9,44 + 1,52 = 10,96 (ц) — собрала вторая бригада.
Ответ: 9,44 ц, 10,96 ц.

2) Пусть первый комбайн убрал х га, тогда:
х + 2,8 (га) убрал второй комбайн.
x + x + 2,8 = 64,2
2х = 61,4
х = 30,7 (га) — убрал первый комбайнёр.
30,7 + 2,8 = 33,5 (га) — убрал второй комбайнёр.
Ответ: 30,7 га, 33,5 га.

Задание № 139. Найдите значение выражения:
1) (13 − 9,5 : 3,8) * 0,3;
2) (16,1 : 4,6 − 3,07) * 0,2;
3) (1,3 * 2,8 + 1) : 0,8;
4) (3,7 * 2,3 − 5) : 0,3.

Решение

1) (13 − 9,5 : 3,8) * 0,3 = (13 − 2,5) * 0,3 = 10,5 * 0,3 = 3,15
2) (16,1 : 4,6 − 3,07) * 0,2 = (3,5 − 3,07) * 0,2 = 0,43 * 0,2 = 0,086
3) (1,3 * 2,8 + 1) : 0,8 = (3,64 + 1) : 0,8 = 4,64 : 0,8 = 5,8
4) (3,7 * 2,3 − 5) : 0,3 = (8,51 − 5) : 0,3 = 3,51 : 0,3 = 11,7

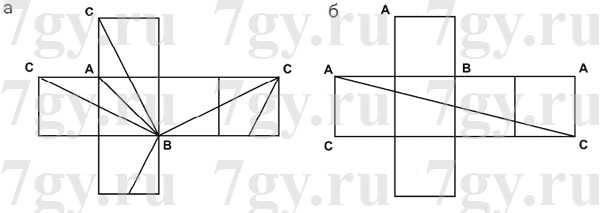
Задание № 140. На поверхности куба (рис. 6) найдите кратчайший путь:
а) из точки А в точку С через точку В;
б) из точки А в точку С, который пересекал бы все боковые рёбра куба, кроме ребра АС.

Решение

Задание № 141. Разложите на простые множители числа:
а) 54; 65; 99; 162; 10 000;
б) 1500; 7000; 3240; 4608.

Решение

а) 54 = 2 * 27 = 2 * 3 * 9 = 2 * 3 * 3 * 3;
65 = 5 * 13;
99 = 3 * 33 = 3 * 3 * 11;
162 = 2 * 81 = 2 * 3 * 27 = 2 * 3 * 3 * 9 = 2 * 3 * 3 * 3 * 3;
10000 = 2 * 5000 = 2 * 2 * 2500 = 2 * 2 * 2 * 1250 = 2 * 2 * 2 * 2 * 625 = 2 * 2 * 2 * 2 * 5 * 125 = 2 * 2 * 2 * 2 * 5 * 5 * 25 = 2 * 2 * 2 * 2 * 5 * 5 * 5 * 5.

б) 1500 = 2 * 750 = 2 * 2 * 375 = 2 * 2 * 3 * 125 = 2 * 2 * 3 * 5 * 25 = 2 * 2 * 3 * 5 * 5 * 5;
7000 = 2 * 3500 = 2 * 2 * 1750 = 2 * 2 * 2 * 875 = 2 * 2 * 2 * 5 * 175 = 2 * 2 * 2 * 5 * 5 * 35 = 2 * 2 * 2 * 5 * 5 * 5 * 7;
3240 = 2 * 1620 = 2 * 2 * 810 = 2 * 2 * 2 * 405 = 2 * 2 * 2 * 3 * 135 = 22 * 2 * 3 * 3 * 45 = 2 * 2 * 2 * 3 * 3 * 315 = 2 * 2 * 2 * 3 * 3 * 3 * 3 * 5;
4608 = 2 * 2304 = 2 * 2 * 1152 = 2 * 2 * 2 * 576 = 2 * 2 * 2 * 2 * 288 = 2 * 2 * 2 * 2 * 2 * 144 = 2 * 2 * 2 * 2 * 2 * 2 * 72 = 2 * 2 * 2 * 2 * 2 * 2 * 2 * 36 = 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 18 = 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 29 = 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 3 * 3.

Задание № 142. Выполните действия:

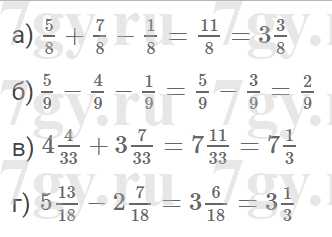
7gy.ru

Страница 42 №260-269 ГДЗ к учебнику «Математика» 6 класс Виленкин, Жохов, Чесноков

Задание № 260. Разделите числитель и знаменатель дроби:
а) 15/10 на 5;
б) 12/18k на 6;
в) 6а/9 на 3;
г) 21х/14y на 7.

Решение

Задание № 261. Умножьте числитель и знаменатель дроби:
а) 2/7 на 7;
б) 5/a на 4;
в) 2n/9 на 8;
г) 3x/5y на 2.

Решение

Задание № 262. Сколько пятизначных чисел можно составить из чётных цифр, если цифры в записи числа не повторяются?

Решение

На первое место можно поставить 2, 4, 6 или 8 (4 варианта). На второе место можно поставить одну цифру из любых неиспользованных или ноль (4 варианта). На третье место − одну из трёх оставшихся (3 варианта).
На четвёртое − одну из двух оставшихся (2 варианта) и на пятое место − последнюю оставшеюся (1 вариант).
Всего получается 4 * 4 * 3 * 2 * 1 = 96 чисел.

Задание № 263. Собственная скорость катера 12,8 км/ч. Скорость течения реки 1,7 км/ч. Найдите скорость катера по течению и против течения.

Дано:
v_{собств.} = 12,8 км/ч
v_теч. = 1,7 км/ч
______________
v_{по теч.} — ?
v_{против теч.} — ?

Решение:
v_{по теч.} = v_{собств.} + v_теч.
v_{по теч.} = 12,8 + 1,7 = 14,5 (км/ч)
v_{против теч.} = v_{собств.} — v_теч.
v_{против теч.} = 12,8 − 1,7 = 11,1 (км/ч)
Ответ: v_{по теч.} = 14,5 км/ч, v_{против теч.} = 11,1 (км/ч)

Задание № 264. Скорость движения теплохода по течению реки 22,7 км/ч. Скорость течения 1,9 км/ч. Найдите собственную скорость теплохода и его скорость против течения.

Дано:
v_{по теч.} = 22,7 км/ч
v_теч. = 1,9 км/ч
_______________
v_{собств.} — ?
v_{против теч.} — ?

Решение:
v_{по теч.} = v_{собств.} + v_теч.
v_{собств.} = v_{по теч.} — v_теч.
v_{собств.} = 22,7 − 1,9 = 20,8 (км/ч)
v_{против теч.} = v_{собств.} — v_теч.
v_{против теч.} = 20,8 − 1,9 = 18,9 (км/ч)
Ответ: v_{собств.} = 20,8 км/ч, v_{против теч.} = 18,9 км/ч.

Задание № 265. Бригада изготовила за 3 дня 6000 деталей при плане 5100 деталей. Причём в первый день была изготовлена треть всех выпущенных деталей, а во второй день − 2/5 плана. Сколько деталей изготовила бригада в третий день?

Дано:
3 дн. — 6000 д.
План — 5100 д.
1-й день — 1/3 всех д.
2-й день — 2/5 плана
3-й день — ?

Решение:
6000 * 1 = 6000 = 2000 (д.) — было изготовлено в первый день
            3        3
5100 * 2 = 5100 * 2 = 2040 (д.) — было изготовлено во второй день
            5           5
6000 − 2000 − 2040 = 1960 (д.) — было изготовлено в третий день
Ответ: 1960 деталей.

Задание № 266. Найдите значение выражения:

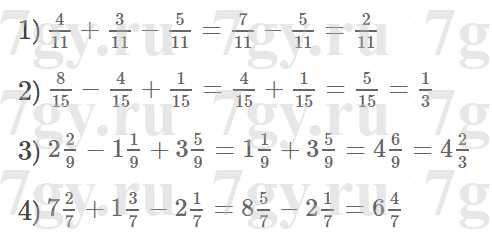
Задание № 267. Решите задачу:
1) Путешественник проплыл против течения реки на моторной лодке 3 ч. Обратно он вернулся на плоту. Сколько времени путешественник затратил на обратный путь, если собственная скорость лодки 24 км/ч, а скорость течения 3 км/ч?
2) Путешественник проплыл по реке на плоту 75 км за 25 ч. Обратно он вернулся на моторной лодке, собственная скорость которой 28 км/ч. Сколько времени затратил путешественник на обратный путь?

Решение

1) Дано:
    t_{против теч.} = 3 ч.
    v_{собств.} = 24 км/ч
    v_теч. = 3 км/ч
     ___________
     t_{по теч.}  ?

    Решение:
    v_{против теч.} = 24 − 3 = 21 (км/ч)
    S = 21 * 3 = 63 (км)
    t_{по теч.} = 63 : 3 = 21 (ч)
    Ответ: 21 ч.

2) Дано:
   S = 75 км
   t_{по теч.} = 25 ч
   v_{собств.}  = 28 км/ч
  ______________
   t_{против теч} — ?
   
   Решение:
   v_теч. = 75 : 25 = 3 (км/ч) 
   v_{против теч.} = 28 − 3 = 25 (км/ч)
   t_{против теч} =  75 : 25 = 3 (ч)
   Ответ: t_{против теч} = 3 ч.

Задание № 268. Сократите дроби:
а) 4/10,8/12,6/9,9/12;
б) 2/8,3/12,10/2,6/30;
в) 15/60,88/33,2/100,50/100.

Решение

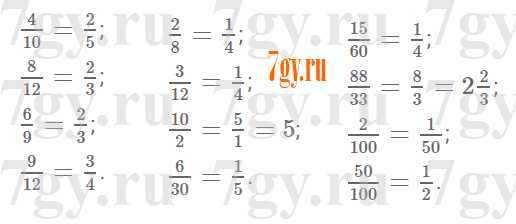
Задание № 269. Сократите:

7gy.ru

Страница 9 №9-20 ГДЗ к учебнику «Математика» 5 класс Никольский, Потапов, Решетников

Задание № 9. Сколько знаков используют для записи натуральных чисел в десятичной системе? Как называют эти знаки?

Решение

В десятичной системе используют 10 знаков для записи натуральных чисел. Эти знаки называют цифрами.

Задание № 10. Какие цифры могут стоять в лбом разряде числа кроме высшего?

Решение

Все цифры, кроме нуля. Цифра 0 может стоять в любом разряде числа кроме высшего.

Задание № 11. Какие цифры могут стоять в высшем разряде числа?

Решение

Цифры 1,2,3,4,5,6,7,8,9 могут стоять в высшем разряде числа.

Задание № 12. Прочитайте следующие числа:
10, 100, 1000, 10000, 100000, 1000000, 10000000.

Решение

10 − десять,
100 − сто,
1 000 − тысяча,
10 000 − десять тысяч,
100 000 − сто тысяч,
1 000 000 − миллион,
10 000 000 − десть миллионов.

Задание № 13. Запишите следующие числа: сто тысяч, миллион, десять тысяч, сто миллионов, миллиард, десять миллионов, сто миллиардов, десять миллиардов.

Решение

сто тысяч − 100 000,
миллион − 1 000 000,
десять тысяч − 10 000,
сто миллионов − 100 000 000,
миллиард − 1 000 000 000,
десять миллионов − 10 000 000,
сто миллиардов − 100 000 000 000,
десять миллиардов − 10 000 000 000.

Задание № 14. Запишите и прочитайте число:
а) двузначное;
б) трёхзначное;
в) четырёхзначное;
г) семизначное.

Решение

а) 28 − двадцать восемь
б) 359 − триста пятьдесят девять
в) 2891 − две тысячи восемьсот девяносто один
г) 8 567 394 − восемь миллионов пятьсот шестьдесят семь триста девяносто четыре

Задание № 15. Запишите первое и последнее в натуральном ряду число:
а) двузначное;
б) трёхзначное;
в) четырёхзначное.

Решение

а) первое двузначное число в натуральном ряду 10, последнее двузначное число в натуральном ряду 99.
б) первое трёхзначное число в натуральном ряду 100, последнее трёхзначное число в натуральном ряду 999.
в) первое четырёхзначное число в натуральном ряду 1000, последнее четырёхзначное число в натуральном ряду 9999.

Задание № 16. Сколько натуральных чисел:
а) однозначных;
б) двузначных;
в) трёхзначных?

Решение

а) Однозначных чисел всего 9, от 1 до 9.
б) Двузначных натуральных чисел всего 90, от 10 до 99.
в) Трёхзначных натуральных чисел всего 900, от 100 до 999.

Задание № 17. В записи каждого из чисел назовите цифры разрядов единиц, десятков, сотен, тысяч, десятков тысяч, сотен тысяч и т.д.
а) 123;
б) 1240;
в) 102;
г) 4397;
д) 13 487 905;
е) 2 000 009.

Решение

а) 123: цифра разряда единиц 3, десятков 2, сотен 1;
б) 1240: цифра разряда единиц 0, десятков 4, сотен 2, тысяч 1;
в) 102: цифра разряда единиц 2, десятков 0, сотен 1;
г) 4397: цифра разряда единиц 7, десятков 9, сотен 3, тысяч 4;
д) 13 487 905: цифра разряда единиц 5, десятков 0, сотен 9, тысяч 7, десятков тысяч 8, сотен тысяч 4, миллионов 3, десятков миллионов 1;
е) 2 000 009: цифра разряда единиц 9, десятков 0, сотен 0, тысяч 0, десятков тысяч 0, сотен тысяч 0, миллионов 2.

Задание № 18. Запишите число, состоящее из:
а) 1 тысячи, 2 сотен, 3 десятков и 5 единиц;
б) 5 десятков тысяч, 9 тысяч, 7 сотен и 4 единиц;
в) 8 сотен и 6 десятков;
г) 7 сотен тысяч и 3 десятков.

Решение

а) 1235
б) 59704
в) 860
г) 700030

Задание № 19. Прочитайте следующие числа, запишите их в виде суммы разрядных слагаемых:
а) 48;
б) 159;
в) 2945;
г) 34 196;
д) 102;
е) 150;
ж) 4067;
з) 10504;
и) 6401;
к) 5060;
л) 12007;
м) 104090.

Решение

а) 48: сорок восемь 48 = 40 + 8.
б) 159: сто пятьдесят девять 159 = 100 + 50 + 9.
в) 2945: две тысячи девятьсот сорок пять 2945 = 2000 + 900 + 40 + 5.
г) 34 196: тридцать четыре тысячи сто девяносто шесть 34196 = 30000 + 4000 + 100 + 90 + 6.
д) 102: сто двадцать 102 = 100 + 2.
е) 150: сто пятьдесят 150 = 100 + 50.
ж) 4067: четыре тысячи шестьдесят семь 4067 = 4000 + 60 + 7.
з) 10504: десять тысяч пятьсот четыре 10504 = 10000 + 500 + 4.
и) 6401: шесть тысяч четыреста один 6401 = 6000 + 400 + 1.
к) 5060: пять тысяч шестьдесят 5060 = 5000 + 60.
л) 12007: двенадцать тысяч семь 12007 = 10000 + 2000 + 7.
м) 104090: сто четыре тысячи девяносто 104090 = 100000 + 4000 + 90.

Задание № 20. Запишите числа:
а) триста двадцать;
б) сто тридцать тысяч пятьдесят;
в) двести восемь тысяч двадцать четыре;
г) два миллиона три тысячи;
д) одиннадцать миллионов двенадцать.

Решение

а) триста двадцать: 320.
б) сто тридцать тысяч пятьдесят: 130050.
в) двести восемь тысяч двадцать четыре: 208024.
г) два миллиона три тысячи: 2003000.
д) одиннадцать миллионов двенадцать: 11000012.

7gy.ru

Страница 20 №69-75 ГДЗ к учебнику «Математика» 5 класс Никольский, Потапов, Решетников

Задача № 69. Торговец купил некий товар за 7 р., продал его за 8 р., потом вновь купил за 9 р. и опять продал его за 10 р. Какую прибыль он получил?

Решение задачи с пояснениями

Торговец покупает товар по цене меньше, чем продает. Найти разницу между ценой покупки и ценой продажи можно с помощью действия вычитания.
Сначала найдем прибыль от первой продажи. Для этого вычтем из цены, по которой торговец продал товар впервые цену, по которой он его купил впервые.
1) 8 − 7 = 1 (р.) − прибыль после первой продажи;
Теперь найдем прибыль от второй продажи. Для этого вычтем из цены, по которой торговец продал товар во второй раз цену, по которой он его купил во второй раз.
2) 10 − 9 = 1 (р.) − прибыль после второй продажи;
Чтобы найти общую прибыль, надо к прибыли от первой сделки прибавить прибыль от второй сделки.
3) 1 + 1 = 2 (р.) − общая прибыль.
Ответ: торговец получил 2 р. прибыли.

Записываем решение задачи в тетради:

1) 8 − 7 = 1 (р.) − прибыль после первой продажи.
2) 10 − 9 = 1 (р.) − прибыль после второй продажи.
3) 1 + 1 = 2 (р.) − общая прибыль.
Ответ: 2 рубля.

Задание № 70. а) в коллекции имеется 128 марок. Из них 93 российские, а остальные иностранные. Каких марок больше в коллекции и на сколько?
б) За две недели бригада собрала 113 т картофеля. Из них за первую неделю − 54 т. В какую неделю картофеля собрано больше и на сколько?
в) За сентябрь и октябрь завод выпустил 193 станка, причем за сентябрь 98 станков. В какой из этих месяцев было выпущено больше станков и на сколько?

Решение задач с объяснением

а) Чтобы найти, каких марок больше в коллекции и на сколько, надо сначала вычислить, сколько в коллекции иностранных марок.
Для этого из общего количества марок надо вычесть количество российских.
1) 128 − 93 = 35 (шт.) − иностранных марок в коллекции;
Чтобы определить разницу, на сколько одних марок больше, чем других, надо из большего количества вычесть меньшее.
2) 93 − 35 = 58 (шт.) − российских марок больше.
Ответ: в коллекции российских марок больше на 58 штук.

б) Чтобы найти, в какую неделю картофеля собрано больше и на сколько, для начала надо найти, сколько собрано картофеля во 2−ю неделю. Для этого необходимо из общего количества собранного картофеля вычесть картофель, собранный в первую неделю.
1) 113 − 54 = 59 (т) − собрано картофеля во 2−ую неделю;
Чтобы определить разницу, на сколько в одну неделю было собрано картофеля больше, чем в другую, надо из большего количества вычесть меньшее.
2) 59 − 54 = 5 (т) − картофеля собрано больше во 2−ую неделю.
Ответ: во вторую неделю собрано картофеля больше на 5 т.

в) Чтобы найти, в какой месяц было выпущено больше станков и на сколько, сначала надо найти, сколько станков выпущено в октябре. Для этого надо из общего количества выпущенных станков вычесть количество станков, выпущенных в сентябре.
1) 193 − 98 = 95 (ст.) − выпущено в октябре;
Чтобы определить разницу, на сколько в одном месяце было выпущено станков больше, чем в другом, надо из большего количества вычесть меньшее.
2) 98 − 95 = 3 (ст.) − выпущено больше в сентябре.
Ответ: за сентябрь было выпущено больше станков на 3 шт.

Записываем в тетради:

а) 1) 128 − 93 = 35 (м.) − иностранных.
    2) 93 − 35 = на 58 (м.) − российских больше.
    Ответ: на 58 марок российских больше, чем иностранных.

б)  1) 113 − 54 = 59 (т) − собрано картофеля во 2−ую неделю.
     2) 59 − 54 = на 5 (т) − картофеля собрано больше во 2−ую неделю.
    Ответ: во вторую неделю собрано картофеля больше на 5 т.

в) 1) 193 − 98 = 95 (ст.) − выпущено в октябре.
    2) 98 − 95 = 3 (ст.) − выпущено больше в сентябре.
    Ответ: за сентябрь было выпущено на 3 станка больше.

Задание № 71. а) Туристы планировали за три дня пройти 65 км. В первый день они прошли 24 км, во второй − на 3 км меньше. Сколько километров им осталось пройти в третий день?
б) В швейной мастерской было 900 м ткани, за первый месяц израсходовали 225 м ткани, за второй − на 23 м больше. Сколько ткани осталось в швейной мастерской к концу второго месяца?

Решение 7 гуру с пояснениями

а) Чтобы найти, сколько километров осталось пройти туристам в третий день, сначала надо найти, сколько км прошли туристы во 2−й день. Во второй день туристы прошли на 3 км меньше, чем в первый. Найти это расстояние можно с помощью действия вычитания. Из количества км, пройденных в 1−й день надо вычесть 3.
1) 24 − 3 = 21 (км) − прошли туристы во 2−й день;
Теперь найдём, сколько прошли туристы в 1−й и 2−й день всего, для этого сложим количество км, пройденных в 1−й день и количество км, пройденных во 2−й день.*
2) 24 + 21 = 45 (км) − прошли туристы в 1−й и 2−й день всего;
Теперь найдем, сколько км осталось туристам пройти в 3−й день. Для этого из запланированного пути вычтем пройденное расстояние.
3) 65 − 45 = 20 (км) − осталось пройти в 3−й день.
Ответ: в третий день туристам осталось пройти 20 км.

б) Чтобы найти, сколько ткани осталось в швейной мастерской к концу второго месяца, сначала найдём сколько ткани израсходовано за 2−й месяц. Во второй месяц израсходовали ткани на 23 м больше, чем в первый. Найти, сколько ткани израсходовали во второй месяц, можно сложением.
Надо прибавить к количеству ткани, израсходованной в 1−й месяц, 23 м.
1) 225 + 23 248 (м) − ткани израсходовано за 2−й месяц;
Теперь прибавим к количеству ткани, израсходованной в 1−й месяц количество ткани, израсходованной во 2−месяц.
2) 225 + 248 = 473 (м) − ткани израсходовано за 1−й и 2−й месяц всего;
Далее из общего количества ткани вычтем израсходованную за 2 месяца.
3) 900 − 473 = 427 (м) − ткани осталось к концу 2−го месяца.
Ответ: к концу 2−го месяца осталось 427 м ткани.

Пишем:

а) 1) 24 − 3 = 21 (км) − прошли туристы во 2−й день.
    2) 24 + 21 = 45 (км) − прошли туристы в 1−й и 2−й день всего.
    3) 65 − 45 = 20 (км) − осталось пройти в 3−й день.
    Ответ: 20 км.

б) 1) 225 + 23 248 (м) − ткани израсходовано за 2−й месяц.
     2) 225 + 248 = 473 (м) − ткани израсходовано за 1−й и 2−й месяц всего.
     3) 900 − 473 = 427 (м) − ткани осталось к концу 2−го месяца.
     Ответ:  427 м ткани.

Задание № 72. Из «Арифметики» Л.Н.Толстого.
а) У одного мужика 23 овцы, а у другого на 7 больше. Сколько у них овец вместе?
б) У одного мужика 26 овец, а у другого на 5 овец меньше. Сколько у них вместе овец?
в) У двух мужиков 50 овец, а у одного 15. На сколько овец у него меньше против другого?

Решение

а) Чтобы найти, сколько овец у 2−х мужиков вместе, надо сначала найти, сколько овец у другого мужика.
У другого мужика на 7 овец больше, чем у первого. Найти это количество можно сложением.
Прибавляем к количеству овец первого мужика 7.
1) 23 + 7 = 30 (ов.) − у второго мужика;
Теперь к количеству овец первого мужика прибавим количество овец второго мужика.
2) 23 + 30 = 53 (ов.) − всего у двух мужиков.
Ответ: у мужиков вместе 53 овцы.
б) Чтобы найти, сколько овец у 2−х мужиков вместе, надо сначала найти, сколько овец у другого мужика.
У другого мужика на овец меньше, чем у первого. Найти это количество можно вычитанием:
Вычтем из количества овец первого мужика 5.
1) 26 − 5 = 21 (ов.) − у второго мужика;
Теперь к количеству овец первого мужика прибавим количество овец второго мужика.
2) 26 + 21 = 47 (ов.) − всего у двух мужиков.
Ответ: у мужиков вместе 47 овец.
в) Чтобы найти, на сколько овец у одного мужика меньше, чем у другого, для начала надо найти, сколько овец у второго мужика. Для этого из общего числа овец вычтем количество овец первого мужика.
1) 50 − 15 = 35 (ов.) − у второго мужика;
Чтобы найти разницу, на сколько у одного мужика овец меньше, чем у другого, надо из большего количества вычесть меньшее.
2) 35 − 15 = 20 (ов.) − меньше у одного против другого.
Ответ: у одного мужика на 20 овец меньше, чем у другого.

Записываем решение задач в тетради:

а) 1) 23 + 7 = 30 (ов.) − у второго мужика.
   2) 23 + 30 = 53 (ов.) − всего у двух мужиков.
   Ответ:53 овцы.

б) 1) 26 − 5 = 21 (ов.) − у второго мужика.
   2) 26 + 21 = 47 (ов.) − всего у двух мужиков.
   Ответ:  47 овец.

в) 1) 50 − 15 = 35 (ов.) − у второго мужика.
   2) 35 − 15 = 20 (ов.) − меньше у одного против другого.
   Ответ:  на 20 овец .

Задание № 73. Задача С.А.Рачинского. Летом у меня целые сутки было открыто окно. В первый час влетел 1 комар, во второй − 2, в третий − 3 и т.д. Сколько комаров налетело за сутки?

Решение

В сутках 24 часа, поэтому можно представить все суточные часы в виде ряда натуральных чисел, каждое из которых соответствует порядковому номеру часа, а также соответствует количеству влетевших комаров в этот час. Для того, чтобы найти общее количество комаров, надо сложить количество комаров каждого часа. Получаем следующее уравнение:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16 + 17 + 18 + 19 + 20 + 21 + 22 + 23 + 24 = 300 (к.) − налетело комаров за сутки.
Ответ: за сутки налетело 300 комаров.

Задача № 74. Первая бригада собрала за смену 5 прибора, вторая − на 9 приборов меньше, чем первая, а третья − на 12 приборов больше, чем вторая. Сколько всего приборов собрали три бригады за смену?

Решение задачи с пояснениями

Чтобы узнать, сколько всего приборов собрали три бригады за смену, надо для начала узнать, сколько собрала 2−я бригада.
Вторая бригада собрала на 9 приборов меньше первой. Найти это количество можно вычитанием. Надо из количества приборов, собранных 1−й бригадой, вычесть 9.
1) 52 − 9 = 43 (пр.) − собрала 2−я бригада;
Третья бригада собрала на 12 приборов больше, чем первая. Найти это количество можно сложением. Надо количества приборов, собранных 1−й бригадой, прибавить 12.
2) 43 + 12 = 55 (пр.) − собрала 3−я бригада;
Теперь прибавим к результату 1−й бригады результаты 2−й и 3−й бригады;
3) 52 + 43 + 55 = 150 (пр.) − собрали все три бригады.
Ответ: три бригады за смену собрали 150 приборов.

Запишем:

1) 52 − 9 = 43 (пр.) − собрала 2−я бригада.
2) 43 + 12 = 55 (пр.) − собрала 3−я бригада.
3) 52 + 43 + 55 = 150 (пр.) − собрали все три бригады.
Ответ: 150 приборов.

Задание № 75. а) Учащиеся 5 класса собрали 220 кг яблок, учащиеся 6 класса на 60 кг больше, а учащиеся 7 класса на 190 кг меньше, чем учащиеся 5 и 6 классов вместе. Сколько килограммов яблок собрали учащиеся трёх классов вместе?
б) За первый день старшеклассники собрали 312 ящиков огурцов, а за второй − на 120 ящиков больше. За третий день собрали на 218 ящиков меньше, чем за первые два дня вместе. Сколько ящиков огурцов собрали старшеклассники за три дня?

Решение

а) Чтобы узнать, сколько килограммов яблок собрали учащиеся трёх классов, сначала надо найти, сколько собрали учащиеся 6 класса.
Учащиеся 6 класса собрали на 60 кг больше яблок, чем учащиеся 5 класса. Найти это количество можно сложением.
1) 220 + 60 = 280 (кг) − собрали учащиеся 6 класса;
Теперь к количеству, которые собрал 5 класс, прибавим количество яблок, которое собрал 6 класс.
2) 220 + 280 = 500 (кг) − собрали учащиеся 5 и 6 классов вместе;
Теперь найдем, сколько яблок собрали учащиеся 7 класса.
Учащиеся 7 класса собрали на 190 кг меньше, чем учащиеся 5 и 6 классов вместе. Найти это количество можно вычитанием.
Из количества яблок, которое собрали 5 и 6 классы, вычтем 190 кг;
3) 500 − 190 = 310 (кг) − собрали учащиеся 7 класса;
Теперь прибавим к количеству яблок, которое собрали 5 и 6 классы, количество яблок, которое собрал 7 класс:
4) 500 + 310 = 810 (кг) − собрали учащиеся 5, 6 и 7 классов вместе.
Ответ: учащиеся трёх классов вместе собрали 810 кг яблок.
б) Чтобы найти, сколько ящиков огурцов собрали старшеклассники за три дня, для начала надо найти, сколько огурцов собрали во 2−й день.
За второй день старшеклассники собрали на 120 ящиков больше, чем за 1−й. Найти это количество можно сложением.
К количеству огурцов, собрали старшеклассники за три дня, для начала надо найти, сколько огурцов собрали во 2−й день.
За второй день старшеклассники собрали на 120 ящиков больше, чем за 1−й. Найти это количество можно сложением.
К количеству огурцов, собранных в 1−й день, прибавим 120.
1) 312 + 120 = 432 (ящ.) − огурцов собрали во 2−й день;
Теперь прибавим к количеству огурцов, собранных в 1−й день количество огурцов, собранных во второй день.
2) 312 + 432 = 744 (ящ.) − огурцов собрали в 1−й и 2−й вместе;
За третий день они собрали на 218 ящиков меньше, чем за первые дня вместе. Найти это количество можно вычитанием.
Вычтем из количества огурцов, собранных в первый и второй дни 218.
3) 744 − 218 = 526 (ящ.) − огурцов собрали в 3−й день;
Теперь прибавим к количеству огурцов, собранных в 1−й и 2−й день, количество, собранное в 3 день.
4) 744 + 526 = 1270 (ящ.) − огурцов собрали за 3 дня.
Ответ: старшеклассники за 3 дня собрали 1270 ящиков огурцов.

Пишем решение в тетради:

а) 1) 220 + 60 = 280 (кг) − яблок собрали учащиеся 6 класса.
   2) 220 + 280 = 500 (кг) − собрали учащиеся 5 и 6 классов вместе.
   3) 500 − 190 = 310 (кг) − собрали учащиеся 7 класса.
   4) 500 + 310 = 810 (кг) − яблок собрали учащиеся 5, 6 и 7 классов вместе.
   Ответ: 810 кг яблок.

б) 1) 312 + 120 = 432 (ящ.) − огурцов собрали во 2−й день.
   2) 312 + 432 = 744 (ящ.) − огурцов собрали в 1−й и 2−й вместе.
   3) 744 − 218 = 526 (ящ.) − огурцов собрали в 3−й день;
   4) 744 + 526 = 1270 (ящ.) − огурцов собрали за 3 дня.
   Ответ: 1270 ящиков огурцов.

7gy.ru

Страница 10 №31-34 ГДЗ к учебнику «Математика» 6 класс Виленкин, Жохов, Чесноков

Решебник к теме 2. Признаки делимости на 10, на 5 и на 2

Задание № 31. Запишите натуральные числа от 1 до 30 в порядке возрастания и подчеркните красным карандашом каждое второе число, а синим − каждое пятое. Какие числа окажутся подчёркнуты красным карандашом, какие − синим?
Какие числа подчёркнуты обоими цветами? Назовите числа, не делящиеся ни на 2, ни на 5.

Решение

Красным карандашом подчёркнуты числа: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30.
Синим карандашом подчёркнуты числа: 5, 10, 15, 20, 25, 30.
Подчёркнуты и обоими карандашами: 10, 20, 30, − эти числа делятся на 10.
На 2 или на 5 не делятся числа: 1, 3, 7, 9, 11, 13, 17, 19, 21, 23, 27, 29.

Задание № 32. Назовите три числа, которые:
а) делятся на 2;
б) делятся на 5;
в) делятся на 2 и на 5;
г) не делятся ни на 2 и ни на 5.

Ответ 7 гуру

а) 2, 4, 6 делятся на 2
б) 5, 10, 15 делятся на 5
в) 10, 20, 30 делятся на 2 и на 5
г) 3, 7, 9 не делятся ни на 2 ни на 5

Задание № 33. Назовите:
а) два чётных числа, кратных 5;
б) два нечётных числа, кратных 5;
в) два чётных числа, которые не делятся на 5;
г) два нечётных числа, которые не делятся на 5.

Ответы к заданию

а) 10 и 20
б) 15 и 25
в) 12 и 22
г) 7 и 9

Задание № 34. Какие из чисел 200, 320, 3000, 50000, 861, 76540 делятся на 100?
Какие из них делятся на 1000?
Сформулируйте признаки делимости на 100, на 1000.

Решение

На 100 делятся числа: 200, 3000, 50 000.
На 1000 делятся: 3000, 50000.
На 100 делятся числа, оканчивающиеся двумя и более нулями.
На 1000 делятся числа, оканчивающиеся тремя и более нулями.

7gy.ru