Страница 13 №54-60 ГДЗ к учебнику «Математика» 6 класс Виленкин, Жохов, Чесноков
Задание № 54. Решите задачу:
1) Я задумал число. Если его увеличить в 11 раз и результат уменьшить на 2,75, то получится 85,25. Какое число я задумал?
2) Я задумал число. Если его увеличить на 9,2 и результат увеличить в 11 раз, то получится 110. Какое число я задумал?
Решение
1. Пусть задуманное число х, тогда:
х * 11 − 2,75 = 85,25
x = (85,25 + 2,75) : 11 = 88 : 11 = 8
Ответ: 8.2. Пусть задуманное число х, тогда:
(x + 9,2) * 11 = 110
х = 110 : 11 − 9,2 = 0,8
Ответ: 0,8.
Задание № 55. Найдите среди чисел 154, 161, 174, 178, 191, 315, 320, 346, 425, 475 числа:
а) кратные 2;
б) кратные 5;
в) кратные 10;
г) нечётные.
Ответы 7 гуру
а) 154, 174, 178, 320, 346.
б) 315, 320, 425, 475.
в) 320
г) 161, 191, 315, 425, 475.
Задание № 56. Напишите:
а) все чётные числа, большие 10 и меньшие 21;
б) все нечётные числа, большие 12, но меньшие 23.
Ответы
а) 12, 14, 16, 18, 20.
б) 13, 17, 19, 21.
Задание № 57. Напишите три четырёхзначных числа, кратных 5.
Ответ
1000, 1050, 5555.
Задание № 58. Выберите из дробей 5/7,8/9,13/19,18/18,5/4,4/5,125/126,384/383 сначала все правильные дроби, а затем неправильные.
Ответ
Правильные дроби: 5/7,8/9,13/19,4/5,125/126;
Неправильные дроби: 18/18,5/4,384/383.
Задание № 59. Решите уравнение:
а) (4,9 − х) : 1,2 − 3;
б) 3,8 * (х − 0,2) = 2,28.
Решение
а) (4,9 − x) : 1,2 = 3
4,9 − x = 3 * 1,2
4,9 − x = 3,6
х = 4,9 − 3,6 = 1,3б) 3,8 * (x − 0,2) = 2,28
x − 0,2 = 2,28 : 3,8
х − 0,2 = 0,6
х = 0,6 + 0,2 = 0,8
Задание № 60. Найдите значение выражения:
а) (93 * 7 + 141) : 72;
б) (357 − 348 : 6) * 4;
в) 7091 + 9663 − (243 916 + 75 446) : 527 : 3;
г) 8607 + 7605 + (376 012 − 83 314) : 414 : 7.
Решение
а) (93 * 7 + 141) : 72 = (651 + 141) : 72 = 792 : 72 = 11
б) (357 − 348 : 6) * 4 = (357 − 58) * 4 = 299 * 4 = 1196
в) 7091 + 9663 − (243916 + 75446) : 527 : 3 = 16 574 − 319362 : 527 : 3 = 16574 − 606 : 3 = 16574 − 202 = 16552
г) 8607 + 7605 + (376012 − 83314) : 414 : 7 = 16212 + 292698 : 414 : 7 = 16212 + 707 : 7 = 16212 + 101 = 16313
7gy.ru
Страница 32 №195-205 ГДЗ к учебнику «Математика» 6 класс Виленкин, Жохов, Чесноков
Задание № 195. Запишите в виде дроби частные:
3 : 7;
5 : 11;
23 : 34.
Ответы 7 гуру
3 , 5 , 23 .
7 11 24
Задание № 196. Запишите в виде частного дроби: 6/11; 19/9; 37/10; 0,6; 0,13.
Ответ
6 : 11;
19 : 9;
37 : 10;
6 : 10;
13 : 100.
Задание № 197. Запишите в виде обыкновенной дроби частные:
18 : 7;
23 : 8;
16 : 5;
343 : 14 и выделите целые части.
Решение
Задание № 198. Найдите среднее арифметическое чисел: 3,8; 4,2; 3,5; 4,1.
Решение
(3,8 + 4,2 + 3,5 + 4,1) : 4 = 15,6 : 4 = 3,9.
Задание № 199. Среднее арифметическое двух чисел равно 54. Одно число в 2 раза больше другого. Найдите эти числа.
Решение
Пусть х − первое число, тогда второе число 2х.
Составим и решим уравнение:
(х + 2х) : 2 = 54
3х : 2 = 54
3х = 108
х = 36
2х = 2 * 36 = 72.
Ответ: 36, 72.
Задание № 200. Решите задачу:
1) В цистерне было 38 т керосина. В первый день израсходовали в 2,4 раза больше керосина, чем во второй день. К утру третьего дня в цистерне осталось 9,1 т керосина. Сколько тонн керосина израсходовали в первый день?
2) Утром на базе было 19 т муки. До обеда с базы выдали в 3,2 раза больше муки, чем после обеда. К вечеру на базе осталось 4,3 т муки. Сколько тонн муки выдали с базы до обеда?
Решение задач
1) Пусть во второй день израсходовали х т керосина, тогда:
2,4х т керосина израсходовали в первый день.
Составим и решим уравнение:
2,4x + х + 9,1 = 38
3,4х = 38 − 9,1
х = 28,9 : 3,4 = 8,5
2,4х = 2,4 * 8,5 = 20,4 (т) керосина было израсходовано в первый день.
Ответ: 20,4 т.2) Пусть после обеда выдали х т муки, тогда:
3,2х т муки выдали до обеда.
Составим и решим уравнение:
х + 3,2x + 4,3 = 1
4,2x = 19 − 4,3
4,2x = 14,7
х = 14,7 : 4,2 = 3,5 (т) муки выдали после обеда.
3,2x = 3,2 * 3,5 = 11,2 (т) муки было выдано до обеда.
Ответ: 11,2 т.
Задание № 201. По таблице простых чисел (см. форзац) подсчитайте, сколько простых чисел в каждой из первых десяти сотен (т. е. среди чисел от 1 до 100, от 101 до 200 и т. д.). Заметили ли вы какие−либо закономерности в расположении простых чисел?
Два простых числа, разность которых равна 2, называют близнецами. Найдите в таблице все пары чисел−близнецов. Какие из них самые большие? Сколько таких пар среди первых 500 натуральных чисел? среди чисел от 500 до 1000? Учёные до сих пор не знают, есть ли самая большая пара чисел−близнецов.
Решение
1−я сотня − 25, 2−я сотня − 21, 3−я сотня − 16 и далее: 16, 17, 14. 16, 14, 15, 14.
Какой−либо закономерности в расположении простых чисел не наблюдается.
В таблице всего 35 пар чисел−близнецов: (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), (101, 103), (107, 109), (137, 139), (149, 151), (179, 181), (191, 193), (197, 199), (227, 229), (239, 241), (269, 271), (281, 283), (311, 313), (347, 349), (419, 421), (431, 433), (461, 463), (521, 523), (569, 571), (599, 601), (617, 619), (641, 643), (659, 661), (809, 811), (821, 823), (827, 829), (857, 859), (881, 883).
Самая большая пара чисел−близнецов 881 и 883. Среди первых 500 натуральных чисел 24 пары чисел−близнецов, среди чисел от 500 до 1000 − 11 пар.
Задание № 202. Найдите наименьшее общее кратное чисел:
а) 18 и 45;
б) 30 и 40;
в) 210 и 350;
г) 20, 70 и 15.
Решение
а) HOK(18; 45) = HOK(2 * 3 * 3; 3 * 3 * 5) = 2 * 3 * 3 * 5 = 90
б) НОК(30; 40) = НОК(30 = 2 * 3 * 5; 2 * 2 * 2 * 5) = 2 * 2 * 2 * 3 * 5 = 120
в) НОК(210; 350) = = НОК(2 * 3 * 5 * 7; 2 * 5 * 5 * 7) = 2 * 3 * 5 * 5 * 7 = 1050
г) НОК(20; 70; 15) = НОК(2 * 2 * 5; 2 * 5 * 7; 3 * 5) = 2 * 2 * 3 * 5 * 7 = 420
Задание № 203. Найдите наименьшее общее кратное чисел а и b, если:
а) а = 5 * 5 * 7 * 13, b = 5 * 7 * 7 * 13;
б) а = 504, b = 540.
Решение
а) НОК(а,b) = 5 • 5 • 7 • 7 • 13 = 15925
б) НОК(а,b) = НОК(504, 540) = НОК(2 * 2 * 2 * 3 * 3 * 7,2 * 2 * 3 * 3 * 3 * 5) = 2 * 2 * 2 * 3 * 3 * 3 * 5 * 7 = 7560
Задание № 204. Саша, Коля и Серёжа собрали 51 стакан малины. Серёжа собрал в 2 раза больше малины, чем Саша, а Коля − на 3 стакана больше, чем Саша. Сколько стаканов малины собрал каждый из мальчиков?
Решение
Пусть Саша собрал х стаканов малины, тогда Серёжа 2х стаканов, а Коля х + 3.
Все вместе мальчики собрали 51 стакан.
Составим и решим уравнение:
х + 2х + 3 + х = 51
4х = 51 − 3
4х = 48
х = 48 : 4
х = 12 (стаканов) — собрала Саша.
2х = 2 * 12 = 24 (стакана) — собрал Сережа
х + 3 = 12 + 3 = 15 (стаканов) — собрал Коля
Ответ: 12, 24 и 15 стаканов.
Задание № 205. Масса первых трёх искусственных спутников Земли, запущенных в 1957−1958 гг., была равна 1918,9 кг. Найдите массу каждого из этих спутников, если масса второго была больше массы первого на 424,7 кг, а масса третьего больше массы второго на 818,7 кг.
Решение задачи
Пусть х кг масса первого спутника. Тогда масса второго спутника х + 424,7 кг, а масса третьего х + 424,7 + 818,7 кг.
Масса всех трёх спутников − 1918,9 кг.
Составим и решим уравнение:
х + х + 424,7 + х + 424,7 + 818,7 = 1918,9
3х = 250,8
х = 250,8 : 3
х = 83,6 (кг) − масса первого спутника.
x + 424,7 = 83,6 + 424,7 = 508,3 (кг) — масса второго спутника
х + 424,7 + 818,7 = 83,6 + 424,7 + 818,7 = 1327 (кг) — масса третьего спутника
Ответ: 83,6 кг, 508,3 кг, 1327 кг.
7gy.ru
Страница 35 №211-212 ГДЗ к учебнику «Математика» 6 класс Виленкин, Жохов, Чесноков
- Категория: ГДЗ Математика учебник 6 класс Виленкин, Жохов, Чесноков
Решебник к параграфу 2. Сложение и вычитание дробей с разными знаменателями. Тема 8. Основное свойство дроби
Задание № 211. Используя рисунок 9, объясните, почему равны дроби:
1. Круг разбили на 5 равных частей и закрасили 3. Затем каждую часть разбили на 3 равных части. Получилось 15 частей, из которых 9 закрашены. Значит дробь три пятых равна дроби девять пятнадцатых.
2. Квадрат разбили на 4 равных части и закрасили 3 из них. Затем каждую часть разбили еще на 4 равных части, получилось 16 частей, из которых 12 закрашены. Значит дроби три четвертых и двенадцать шестнадцатых равны.
3. Прямоугольник разбили на 7 равных частей и закрасили 5 из них. Затем каждую часть разбили еще на 2 части, получилось 14 частей. Закрашены 10 из них. Значит дроби равны.
Задание № 212. По рисунку 10 объясните, почему равны дроби:
а) 1/4=3/12=15/60;
б) 1/2=6/12=30/60;
в) 3/4=9/12=45/60;
г) 1/3=4/12=20/60.
Решение
а) В четверти часа (1/4 часа) содержится 3 раза по 5 минут (3/12 часа) или 15 минут (15/60 часа),
б) в получасе (1/2 часа) содержится 6 раз по 5 минут (6/12 часа) или 30 минут (30/60 часа),
в) в трёх четвертях часа (3/4 часа) содержится 9 раз по 5 минут (9/12 часа) или 45 минут (45/60 часа),
г) в одной трети часа (1/3 часа) содержится 4 раза по 5 минут (4/12 часа) или 20 минут (20/60 часа).
© Копирование допустимо только с прямой активной ссылкой на страницу с оригиналом статьи.
При любых заболеваниях не занимайтесь диагностикой и лечением самостоятельно, необходимо обязательно обратиться к врачу — специалисту.
Изображения обложек учебной литературы приведены на страницах сайта исключительно в качестве иллюстративного материала (ст. 1274 п. 1 части четвертой Гражданского кодекса РФ)
7gy.ru
Страница 19 №108-115 ГДЗ к учебнику «Математика» 6 класс Виленкин, Жохов, Чесноков
Задание № 108. Сколько нечётных четырёхзначных чисел можно составить из цифр 0, 1, 2, 3, 4?
Решение
На первом месте в записи числа может стоять любая цифра, кроме нуля, − 4 варианта. На втором и на третьем местах − любая из этих пяти цифр. Так как число нечётное, на последнем месте могут быть только цифры 1 или 3 − т. е. имеем ещё два варианта. В соответствии с правилом умножения получаем, что нечётных четырёхзначных чисел можно составить 4 * 5 * 5 * 2 = 200.
Задание № 109. Какую цифру нужно приписать к числу 10 слева и справа, чтобы получилось четырёхзначное число, делящееся:
а) на 9;
б) на 3;
в) на 6?
Решение
а) 4104 (4 + 1 + 0 + 4 = 9)
б) 1101 (1 + 1 + 0 + 1 = 3),
4104 (4 + 1 + 0 + 4 = 9),
7107 (7 + 1 + 0 + 7 = 15).
в) 4104 (4 + 1 + 0 + 4 = 9).
Задание № 110. Выпишите из чисел 215 783, 3 289 775, 21112 221, 44 856, 555 444, 757 575, 835 743 те, которые:
а) кратны 3;
б) кратны 9;
в) делятся без остатка на 3 и на 5;
г) кратны 9 и 2.
Решение
а) 21112 221 (2 + 1 + 1 + 1 + 2 + 2 + 2 + 1 = 12)
44856 (4 + 4 + 8 + 5 + 6 = 27)
757 575 (7 + 5 + 7 + 5 + 7 + 5 = 36)
835 743 (8 + 3 + 5 + 7 + 4 + 3 = 30)б) 44856 (4 + 4 + 8 + 5 + 6 = 27)
757 575 (7 + 5 + 7 + 5 + 7 + 5 = 36)
в) 835 743 (8 + 3 + 5 + 7 + 4 + 3 = 30)
г) 757 575 (7 + 5 + 7 + 5 + 7 + 5 = 36)
Задание № 111. а) Верно ли, что если число оканчивается цифрой 6, то оно делится на 6?
б) Верно ли, что если число делится на 6, то его запись оканчивается цифрой 6?
в) Может ли нечётное число делиться на чётное число?
г) Может ли чётное число делиться на нечётное число?
Решение
а) нет неверно, 16 не делится нацело на 6.
б) нет неверно, 18 : 6 = 3, деление без остатка.
в) нет не может по определению.
г) да может, например, 12 : 3 = 4.
Задание № 112. Какие цифры можно поставить вместо звёздочки, чтобы число делилось без остатка на 3 и на 5:
а) 241;
б) 1734;
в) 43*5?
Ответы 7 гуру
а) 2415
б) 17340
в) 4305, 4335, 4365, 4395.
Задание № 113. Стакан вмещает 210 г крупы. Крупой наполнили 5/7 стакана. Сколько граммов крупы насыпали в стакан?
Решение
210 : 7 * 5 = 150 (г).
Ответ: 150 г.
Задание № 114. Дочь пообещала: «Я схожу в булочную и вымою посуду». Можно ли обещание считать выполненным, если дочь:
а) вымыла посуду, но не сходила в булочную;
б) сходила в булочную, но не вымыла посуду;
в) и вымыла посуду, и сходила в булочную;
г) не вымыла посуду и не была в булочной?
Подумайте, в чём сходство этой задачи с задачей нахождения решений неравенства 2 < х < 6 среди чисел 1; 3; 5; 7.
Решение
а) нет (выполнено только одно условие)
б) нет (выполнено только одно условие)
в) да (выполнены оба условия)
г) нет (выполнено только одно условие)
Для неравенства 2 < x < 6 тоже должно быть выполнено два условия x > 2 и x < 6.
Неравенство 2 < x < 6 будет верным при х = 3 и х = 5.
Задание № 115. Докажите, что числа 575, 10 053, 3627, 565 656 являются составными.
Решение
575 делится на 1, 5, 575;
10053 делится на 1, 3, 10053;
3627 делится на 1, 3, 3627;
565 656 делится на 1, 3, 565 656;
У всех чисел больше двух делителей, значит они составные.
7gy.ru
Страница 43 №270-274 ГДЗ к учебнику «Математика» 6 класс Виленкин, Жохов, Чесноков
Задание № 270. Представьте в виде обыкновенной несократимой дроби следующие десятичные дроби:
0,875; 0,75; 0,035.
Задание № 271. Выполните действие и сократите результат:
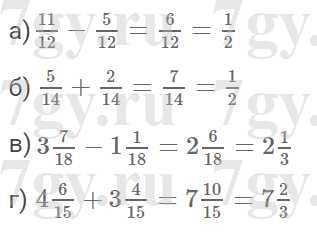
Задание № 272. Турист плыл на теплоходе сначала 1,2 ч по озеру, а затем 3,6 ч по реке, которая впадает в это озеро. Собственная скорость теплохода 22,4 км/ч, а скорость течения реки 1,7 км/ч. Найдите длину всего пути туриста на теплоходе.
Дано:
tо = 1,2 ч
tр = 3,6 ч
vсобств. = 22,4 км/ч
vтеч. = 1,7 км/ч
___________
S -?Решение:
S = Sо + Sр
Sо = vсобств. * tо
Sо = 22,4 * 1,2 = 26,88 (км)
vпротив теч. = vсобств. — vтеч.
vпротив теч. = 22,4 − 1,7 = 20,7 (км/ч)
Sр = vпротив теч. * tр
Sр = 20,7 * 3,6 = 74,52 (км)
S = 26,88 + 74,52 = 101,4 (км)
Ответ: S = 101,4 км.
Задача № 273. В четырёх больших и трёх маленьких коробках с цветными карандашами всего 132 карандаша. В двух больших и трёх маленьких таких же коробках всего 84 карандаша. Сколько карандашей в одной маленькой коробке?
Решение задачи
132 − 84 = 48 (к.) — в двух больших коробках.
84 − 48 = 36 (к.) — в трех маленьких коробках .
36 : 3 = 12 (к.) — одной маленькой коробке.
Ответ: 12 карандашей.
Задание № 274. Выполните действия:
а) (867 000 : 2125 − 396,4) * 2,15;
б) (26,16 : 6 + 2,6 * 1,4) : 0,4 − 0,4.
Решение
а) (867000 : 2125 − 396,4) * 2,15 = (408 − 396,4) * 2,15 = 11,6 * 2,15 = 24,94
б) (26,16 : 6 + 2,6 * 1,4) : 0,4 − 0,4 = (4,36 + 3,64) : 0,4 − 0,4 = 8 : 0,4 − 0,4 = 20 − 0,4 = 19,6
7gy.ru
Страница 6 №8-16 ГДЗ к учебнику «Математика» 6 класс Виленкин, Жохов, Чесноков
Задание № 8. В спортивном празднике участвовали 90 школьников. Могут ли они на заключительном параде построиться:
− в две одинаковые шеренги?
− в пять одинаковых шеренг?
− в одиннадцать одинаковых шеренг?
− в колонну по шесть человек в ряд?
Решение
Школьники могут построиться:
по 90 : 2 = 45 школьников в две шеренги;
по 90 : 5 = 18 школьников в 5 шеренг;
90 не делится на 11 без остатка;
по 90 : 6 = 15 школьников в 6 рядах.
Задание № 9. Докажите, что число 70525 кратно числу 217, а число 729 является делителем числа 225261.
Решение
Задание № 10. На координатном луче отмечено число а (рис. 1). Отметьте на этом луче четыре числа, кратных числу а.
Решение
Числа а, 2а, 3а, 4а, 5а, 6а кратны числу а.
Задание № 11. Проверьте, что каждое из чисел 6, 28, 496 равно сумме всех его делителей, не считая самого числа.
Решение
Делители числа 6: 1, 2, 3, 6, их сумма делителей не считая самого числа: 1 + 2 + 3 = 6;
число 28: 1, 2, 4, 7, 14, 28; 1 + 2 + 4 + 7 + 14 = 28;
число 496: 1, 2, 4, 8, 16, 31, 62, 124, 248, 496; 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496.
Задание № 12. Проверьте, что каждое из чисел 220 и 284 равно сумме делителей другого числа, не считая его самого.
Решение
Делители числа 220: 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110, 220;
1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284.
Делители числа 284: 1, 2, 4, 71, 142, 284;
1 + 2 + 4 + 71 + 142 = 220.
Задание № 13. Докажите, что произведение двух натуральных чисел кратно каждому из множителей.
Решение
Пусть a и b натуральные числа, тогда их произведение a * b, и,
a * b = b,
aa * b = a,
b
то есть a * b кратно a и b.
Задание № 14. На рисунке 2 изображён в натуральную величину один кадр фотоплёнки. Каких размеров получится фотография при пятикратном увеличении? Уместится ли изображение этого кадра при десятикратном увеличении на листе бумаги, размер которого 24 х 30 см?
Решение
Ширина кадра на рисунке а = 2,8 см, а высота b = 4,3 см; после увеличения в 5 раз они будут равны:
a * 5 = 2,8 * 5 = 14 см, b * 5 = 4,3 * 5 = 21,5 см, соответственно;
после увеличения в 10 раз они будут равны:
a * 10 = 2,8 * 10 = 28 см, 6 * 10 = 4,3 * 10 = 43 см, соответственно.
Следовательно при десятикратном увеличении изображение кадра не уместятся на листе бумаги, так как лист имеет размеры − 24 х 30 см.
Ответ: не уместится.
Задание № 15. Вычислите устно:
а) 5 + 0,8; 0,23 + 7; 0,48 + 0,2; 0,6 + 0,34; 2,7 + 1,12;
б) 0,76 − 0,3; 2,54 − 2; 0,82 − 0,02; 0,63 − 0,6; 0,8 − 0,25;
в) 0,2 * 4; 2,1 * 3; 0,7 * 10; 0,5 * 2; 0,25 * 4;
г) 6 : 10; 0,8 : 2; 2,1 : 7; 0,5 : 10; 4,1 : 2.
Решение
а) 5,8; 7,23; 0,68; 0,94; 3,82.
б) 0,46; 0,54; 0,8; 0,03; 0,55.
в) 0,8; 6,3; 7; 1; 1.
г) ,6; 0,4; 0,3; 0,05; 2,05.
Задание № 16. Найдите пропущенные числа:
Решение
а)128 : 2 = 64,
128 : 4 = 32,
128 : 8 = 16,
128 : 16 = 8,
128 : 32 = 4,
128 : 64 = 2.б) 6 + 6 = 12;
12 + 6 = 18;
18 + 6 = 24;
24 + 6 = 30;
6 * 5 = 30;
6 * 3 = 18.
7gy.ru
Страница 11 №35-43 ГДЗ к учебнику «Математика» 6 класс Виленкин, Жохов, Чесноков
Задание № 35. Напишите все трёхзначные числа, в запись которых входят лишь цифры 0, 2, 5 и которые:
а) делятся на 2;
б) делятся на 5.
Ответы 7 гуру
а) 200, 202, 220, 222, 250, 252, 500, 502, 520, 522, 550, 552.
б) 200, 205, 220, 225, 250, 255, 500, 505, 520, 525, 550, 555.
Задание № 36. Коля принёс несколько коробок с яйцами, по 10 яиц в каждой коробке.
Может ли быть, что он принёс 35 яиц? 43 яйца? 50 яиц?
Решение
Коля мог принести только 50 яиц, 50 делиться на 10 без остатка 50 : 10 = 5.
Задание № 37. Купили 5 одинаковых коробок цветных карандашей. Может ли в них оказаться:
всего 92 карандаша?
90 карандашей?
75 карандашей?
Решение
92 карандаша быть не может, так как не делится на 5 без остатка.
90 и 75 карандаша может быть, так как 90 : 5 = 18; 75 : 5 = 15.
Задание № 38. Подставьте в таблицу подходящие значения а и b и сделайте вывод о чётности или нечётности результата действия:
Решение
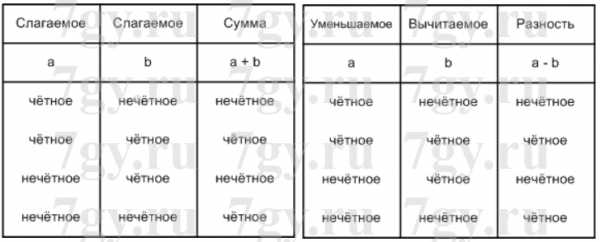
Задание № 39. Можно ли, используя только цифры 3 и 4, записать:
а) число, которое делится на 10;
б) чётное число;
в) число, кратное 5;
г) нечётное число?
Ответы к заданию
а) Нет нельзя, число должно оканчиваться нулём.
б) Да можно, число должно оканчиваться 4.
в) Нет нельзя, число должно оканчиваться 0 или 5.
г) Да можно, число должно оканчиваться 3.
Задание № 40. Какие числа, кратные 5, удовлетворяют неравенству:
а) 64 < х < 78;
б) 405 < х < 450;
в) 24 < у < 49;
г) 1 < у < 30?
Ответы
а) 65, 70, 75.
б) 410, 415, 420, 425, 430, 435, 440, 445.
в) 25, 30, 35, 40, 45.
г) 5, 10, 15, 20, 25.
Задание № 41. Вычислите устно:
а) 17 + 0,3; 0,05 + 25; 0,37 + 2,03; 3,84 + 0,2; 1,27 + 2,3;
б) 0,728 − 0,7; 0,8 − 0,25; 1 − 0,6; 0,7 − 0,07; 3 − 0,85;
в) 0,2 * 5; 4 * 2,5; 0,5 * 20; 0,24 * 1000; 2,7 * 100;
г) 2,6 : 2; 1,8 : 9; 3,7 : 10; 5,3 : 0,1; 6 : 0,3.
Ответы
а) 17,3; 25,05; 2,4; 4,04; 3,57.
б) 0,028; 0,55; 0,4; 0,63; 2,15.
в) 1; 10; 10; 240; 270.
г) 1,3; 0,2; 0,37; 53.
Задание № 42. Какие различные натуральные числа надо вписать в кружки (рис. 4), чтобы произведение каждых двух чисел, помещённых в кружках, соединённых отрезком, равнялось 70? Подумайте, как можно назвать набор чисел, оказавшихся в кружках.
Ответы
Эти числа 1, 2, 5, 7, 10, 14, 35, 70 − делители числа 70.
Задание № 43. Если к числу прибавить 4, то полученное число разделится без остатка на 6. Чему равен остаток от деления первого числа на 6?
Решение
Пусть это некоторое число х, тогда, если к нему прибавить 4, то получится число х + 4. Так как оно нацело делится на 6, то оно кратно 6.
Пусть х + 4 = 6, тогда:
х = 6 − 4 = 2_2 |6
0 |0
2Таким образом, остаток от деления первого числа на 6 будет равен 2.
Ответ: 2.
7gy.ru