Конспект урока по математике «Решение неравенства» (4 класс)
Урок по математике на тему: «Решение неравенства»
Учитель начальных классов
МБОУ Гимназии №17 г. Королев
Афанасьева Анастасия Викторовна
Цели урока:
-
Учить решать неравенства.
-
Тренировать вычислительные навыки, умение решать текстовые задачи на движение.
-
Развивать мышление, внимание, речь.
Оборудование: игра «Танграм», игра «Внимание».
Ход урока
I. Организационный момент
Чтоб водить корабли, Чтобы в небо взлететь, Надо многое знать, Надо много уметь. И при этом, и при этом, Вы заметьте-ка, Очень важная наука -А-риф-ме-ти-ка!
II. Актуализация знаний
-
Игра «Внимание».
Учитель показывает детям полоску с рисунками, цифрами, или знаками, а ученики, рассматривая ее 3 секунды, должны запомнить и зарисовать в своих тетрадях.
2. Запись на доске:
— В таблице указан рост учащихся. Чем похожи фамилии детей? {Фамилии принадлежат мальчикам. Последние буквы -ов. Образованы от имен мальчиков: Максим, Иван, Федор.)
-
Какое число можно считать лишним? (134 — четное, 111 — состоит из цифры 1, 111 — сумма цифр равна 3, а в остальных числах сумма цифр равна 8.)
-
Назовите фамилии в порядке возрастания их роста. (Федоров, Иванов, Максимов.)
-Докажите (111 меньше 125; 125 меньше 134.) Запись на доске:
111 < 125 125<134
-
Как называются высказывания, в записи которых используются знаки « > » или « < »? (Неравенствами.)
-
Что же такое неравенство?
Неравенство — это высказывание, в записи которого используются знаки « < » или « > ».
-
Индивидуальные задания (дети работают у доски). Сравнить:
с + 42*(>)с+27 6 • 4-6 • 1 * (<)6 • 5
a + 45 * (>)а — 45
-
Верно ли, что:
а) 23 • 27 < 630.
Высказывание 23 • 27 < 630 верно, т.к. 23 • 27 = 621, а 621 < 630, т.к. 621 при счете называют меньше, чем число 630.
б) 1288 :56 >40.
Высказывание 1288 : 56 > 40 неверно, т.к. 1288 : 56 = 23, а число 23 при счете называют меньше числа 40.
у< 9.
Высказывание с переменной у < 9 верно при у = 0, 1, 2, 3, 4, 5, 6, 7, 8, т.к. эти числа при счете называются раньше, чем число 9, но неверно при у = 10, 11, 12, и т.д., потому что эти числа называются при счете позже числа 9.
г)у> 9.
Высказывание с переменной у> 9 верно при у — 10, 11, 12, 13 и т.д., и неверно при у= 0,1, 2, 3,4, 5, 6, 7, 8. (Учитель приходит на помощь, если ученики испытывают затруднения.)
III. Постановка проблемы
-
Что интересного заметили при выполнении неравенств у < 9, у > 9? (Эти высказывания могут быть ложными и истинными.)
-
От чего зависит истинность высказывания с переменной? (От значения переменной.)
-
Что называют значением переменной? (То, что подставляют вместо переменной.)
-
Сегодня нам надо на уроке научиться находить такие значения переменной, при которых неравенство было бы истинным высказыванием — это и есть цель нашего урока.
На доске открывается тема урока:
«Решение неравенства»
IV. «Открытие» детьми нового знания
Дети записывают в тетради свои значения переменной, и по цепочке сообщают классу.
Учитель записывает на доске:
у < 9 верно при у = 0, 1, 2, 3, 4, 5, 6, 7, 8.
-
Почему в этом неравенстве нельзя написать число 9 или 10? (Эти значения не подходят этому неравенству.)
-
Ученые говорят: «число не удовлетворяет этому неравенству».
-
Какие значения переменной удовлетворяют неравенству у < 9? (0, 1, 2, 3, 4, 5, 6, 7, 8.)
-
Следовательно, эти числа являются решением неравенства.
-
Что мы можем назвать решением неравенства? (Решением неравенства мы можем назвать значение переменной, удовлетворяющее этому неравенству.)
-
Сравните свой вывод с выводом учебника на с. 1 (учебник-тетрадь № 1).
Упр. 1, с. 1 — фронтально. Главная мысль подчеркивается красным карандашом.
V. Физкультминутка
-
Для улучшения мозгового кровообращения.
-
Исходное положение (и. п.) — сидя на стуле, «раз, два» — отвести голову назад и плавно наклонить назад; «три, четыре» — голову наклонить вперед, плечи не поднимать. Повторить 4-6 раз. Темп медленный.
-
Для снятия утомления с плечевого пояса и рук. И.п. — стоя или сидя, руки на поясе.
«Раз» — правую руку вперед, левую вверх. «Два» — переменить положение рук. Повторить 3-4 раза, затем расслабленно опустить вниз и потрясти кистями, голову наклонить вперед. Темп средний.
-
Гимнастика для глаз.
Крепко зажмурить глаза (сосчитать до трех), открыть их и посмотреть вдаль (считать до пяти). Повторить 4-5 раз.
VI. Первичное закрепление
Учащиеся выполняют с контролированием:
а) упр. 2, с. 1 — фронтально;
б) упр. 5, с. 2 — в парах;
в) упр. 3, с. 1 — фронтально (обоснование и исправление ошибок).
VII. Самостоятельная работа с самопроверкой в классе
1. Упр. 4, с. 1 выполняются по вариантам:
1вариант — верхняя строка; II вариант — нижняя строка. Записать в тетрадь неравенства, решением которых будет число 6. Проверка проводится по записи на доске, которая открывается после самостоятельной работы:
/ вариант:
54 :1 > 1, т.к. а + а < 20, т.к.
54:6 = 9, а 6 + 6=12, а
9>1. 12 < 20.
// вариант:
2+у<9в, т.к.
2+ 6 = 8, а 8<96
2. Дополнительно (для детей, которые не испытывают затруднений): одна из задач упр. 6 или упр. 7, с. 2 (по выбору).
— Что называется решением неравенства?
VIII. Повторение
1. Упр. 8, с. 2.
Задача читается по частям и заполняется таблица:
Можем ли мы сразу ответить на вопросы задачи? (Нет.)
Почему? (Нужно сравнить скорости зайца и сокола, а они неизвестны. )
Как найти скорость? (Расстояние разделить на время.)
Решите задачу
(Задача выполняется в учебнике-тетради по вопросам, предложенным автором).
-
Как найти скорость? (V = х : t)
-
Как найти расстояние? (S=v*t)
-
Как найти время? T=s:v
-
Как узнать, во сколько раз одно число больше, или меньше другого? (Большее число разделить на меньшее.)
-
Как узнать, на сколько одно число больше или меньше другого? (Из большего числа вычесть меньшее.)
2. а) Упр. 9, с. 3 выполняется самостоятельно. (Один ученик у доски решает задачу, но так, чтобы дети не видели его записи.) Решение:
-
14-6 = 8 (км) — прошли после привала.
-
(14 + 8) • 3 = 66 (км) — осталось пройти.
-
14 + 8 + 66 = 88 (км) — намеченный путь. Ответ: 88 км.
Взаимопроверка: ученики меняются тетрадями и проверяют решение по записям на доске, правильность которых проверил учитель.
-
Кто справился с заданием?
-
У кого вычислительные ошибки? Будьте внимательны!
-
Можно ли сразу ответить на вопрос задачи? (Нет.)
-
Почему? (Чтобы найти целое, нужно сложить его части, а они неизвестны.)
-
Объясните знак вычитания в первом действии. (В условии сказано: «на 6 км меньше».)
-
Объясните знак умножения во втором действии. (В условии сказано: «в 3 раза больше».)
-
Объясните знак сложения во втором действии. (В условии сказано: «чем они прошли», а шли они до привала и после привала.)
б) Во время выполнения упражнения 9 на с. 3, сильные дети выполняли логическую задачу: «Муравьишка и Муравьин нашли 3 пшеничных зернышка. Муравьин понес два зернышка, а Муравьишка -одно. Муравьин может донести до муравейника 2 зерна за 12 минут. Муравьишка же с 1 зернышком, или без него, вдвое быстрее. Если Муравьин понесет 1 зерно, то он будет двигаться с такой же скоростью, как и Муравьишка с одним. У муравьев строго: только солнышко сядет, муравьи все ходы и выходы закроют и спать. А кто опоздал, тот
будет ночевать на улице. До закрытия муравейника осталось 11 минут. Каким образом Муравьишке и Муравьину успеть в муравейник до закрытия?» Решение:
12:2 = 6 (мин.) — Муравьишка донесет зернышко до муравейника. В это же время Муравьин пройдет с 2-мя зернышками половину расстояния до муравейника. Ему останется идти с такой же скоростью 12-6 = 6 (мин.).
В то время как Муравьин с 2-мя зернышками пройдет один отрезок пути, Муравьишко без груза пройдет навстречу вдвое больше, т.е. 2 таких отрезка. На это им понадобится 6:3 = 2 (мин.).
После этого Муравьишка и Муравьин понесут по 1-му зернышку в течении 2 минут до муравейника. Всего понадобилось 6 + 2+2=10 (мин.). Значит, Муравьишка и Муравьин успеют в муравейник до его закрытия.
3. Упр. 10, с. 3 (а) или б) — по выбору). Составить программу действий и вычислить:
а) Программа: 1, 3, 6, 2, 4, 7, 5. Ответ: 3354.
б) Программа: 1, 3, 5, 6, 4, 2. Ответ: 9094812.
IX. Итоги урока
-
Чему учились на уроке? (Находить решения неравенств.)
-
К какому выводу пришли? (Значение переменной, удовлетворяющее неравенству, называется решением неравенства.)
-
У кого не было затруднений в новой теме?
-
Как оцениваете свою работу?
Домашнее задание
-
Составить неравенство и найти его решение.
-
Решить по выбору одно из упр. 12 или 13, с. 3.
Дополнительно: упр. 11.
infourok.ru
Презентация к уроку математики в 4 классе по теме «Множество решений неравенства» (Петерсон, 1 часть)

Презентация к уроку математики
(4 класс, Петерсон, 1 часть)
МНОЖЕСТВО РЕШЕНИЙ НЕРАВЕНСТВА
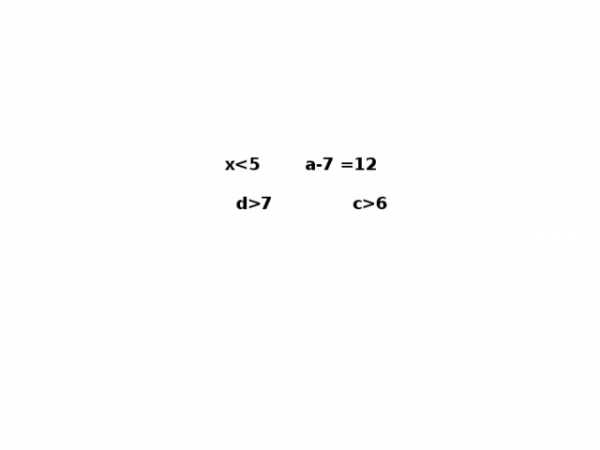 7 с6″
7 с6″
х d7 с6

7 4 8 {7,4,8}

Множество – объекты, собранные вместе.

{7,4,8}
х7
 6″
6″
{7,4,8}
с6

МНОЖЕСТВО РЕШЕНИЙ НЕРАВЕНСТВА

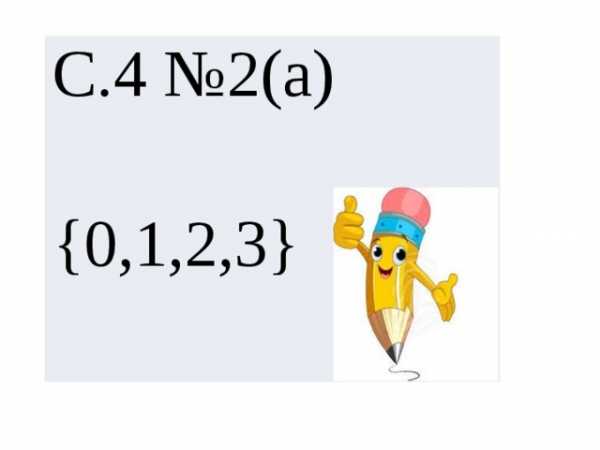
С.4 №2(а)
{0,1,2,3}
С.4 №2(б)
{5,6,7…}

— Над чем нам еще надо поработать?
— Какое новое открытие вы сделали сегодня на уроке?
— Что называется множеством решений неравенства?
-У всех ли неравенств есть решения?
- Как называется такое множество решений?
- Над чем ещё предстоит поработать?
compedu.ru
Урок математики по теме: «Решение неравенства», 4-й класс
Разделы:
Математика
Класс:
4
Тип урока: Изучение нового материала.
Цели: Образовательные:
Сформировать представление о понятии
«решение неравенства», способность
устанавливать, является данное число решением
неравенства или нет.
решение задач и примеров на порядок действий.
Развивающие:
- Вывести алгоритм конспектирования учебного
текста. - Развивать различные виды внимания, памяти, речи.
Воспитательные:
- Формировать систему ценностей, направленную на
максимальный личный вклад в коллективную
деятельность в процессе урока.
Оборудование: плакаты, картинки: «заяц»,
«человек», сборник загадок, учебник математики
Л.Г. Петерсон.
Ход урока
I. Самоопределение к деятельности.
На доске написано число, «классная работа».
— Давайте, ребята, вспомним, какие задания вы
выполняли в прошлом году на уроках математики?
Какие задания казались наиболее интересными?
Трудными? (Ответы детей.)
— С помощью каких математических знаков вы
могли решить задачи, примеры, составить
выражения ? (Ответы детей.)
— Правильно, невозможно представить себе
математику без чисел и знаков. А как вы думаете,
какие задания вы будете выполнять в 4 классе? (Ответы
детей. )
— Действительно, ребята, в этом году вы еще
больше узнаете нового, необычного и интересного.
II. Актуализация знаний и фиксация затруднения в
деятельности.
Угадайте, ребята, кто пришел к нам сегодня на
урок и принес интересные задания?
Много бед таят леса,
Волк, медведь там и лиса!
Наш зверек живет в тревоге,
От беды уносит ноги.
Ну-ка, быстро отгадай-ка,
Как зверек зовется? ( Зайка)
На доске карточки:
|
140 х 3 |
365 — ( 20 + 65 ) |
( 160 + 40 ) — 70 |
|
10< 9 |
19 + 9 = 28 |
960 : 3 |
|
( 30 + 243 ) + 17 |
У > 920 |
А – 15 = 17 |
— На какие группы можно разбить данные записи? (Например:
буквенные и числовые; выражения, равенства и
неравенства.)
Дети расставляют карточки по группам:
|
Равенства |
Неравенства |
Выражения |
В это время с классом обсуждаются вопросы:
— Какое высказывание называют равенством,
неравенством? (Высказывание, в котором есть
знак «=», знак > или < .)
— А выражения, которые являются высказываниями?
(О них нельзя сказать, верные они или неверные.)
Затем учащиеся проверяют, как выставлены
карточки на доске. Должны появиться следующие 3
столбца:
|
140 х 3 |
19 + 9 = 28 |
10 < 9 |
|
960 : 3 |
A -15 = 17 |
y>920 |
| ( 30 + 243 ) + 17 | ||
| 365 – ( 20 + 65 ) | ||
|
(160 + 40) — 70 |
1. Вычисление удобным способом значений
выражений в 1 столбике.
Дети сигналят ответы: 420, 320, 290, 280, 130. (Приемы
вычислений проговариваются, устанавливаются
верные варианты.)
2. Запишите в тетрадь полученные числа в
порядке возрастания. (130, 280, 290, 320, 420)
Один ученик читает ответы, остальные
сравнивают их со своими записями, ошибки
исправляются.
— Что интересного вы заметили? (Все числа
круглые, в разряде сотен и десятков разные числа.)
3. С доски убираются выражения.
— Как одним словом назвать все записи, которые
остались? (Высказывания.)
— На какие группы их можно разбить? (Уравнения
и неравенства; высказывания с переменной и
без переменной.)
Оставшиеся на доске записи разбиваются на
группы: «высказывания» и «высказывания с
переменной»
|
10 < 9
19 + 9 = 28 |
У > 920
а – 15 = 17 |
— Какое из высказываний неверное, а какое
верное?
(10 < 9 – неверное, а 19 + 9 = 28– верное.)
Записи высказываний 1 столбика убираются с
доски.
— Найдите решение уравнения. (а = 32)
— Как проверить, верно ли оно найдено? (Надо
подставить число 32 в уравнение, 32 – 15 = 17 – верное
равенство.)
— Как еще называют решение уравнения? (Корнем
уравнения.)
III. Индивидуальное задание.
— Из составленного ряда чисел выберите и
запишите на листках решение неравенства
у < 260.
Варианты детей фиксируются на доске, например:
160, 240, 260.
— Кто же прав? (Мы не знаем.)
— Какое задание выполняли? (Искали решение
неравенства у < 260.)
— Почему не можем обосновать свои ответы? (Не
знаем, как определить, является число решением
или нет.)
— Поставьте перед собой цель. (Научиться
определять, является число решением неравенства
или нет.)
— Предложите название темы урока («Решение
неравенства».)
Тема урока выставляется на доске. Решение
неравенства.
IV. Построение проекта выхода из затруднения.
— Каким способом вы предлагаете обосновать,
является число решением неравенства или нет? (Надо
знать, что такое – «решение неравенства».)
— Предложите свои версии? (Варианты детей.)
— Сравните с текстом учебника.
— Итак, что такое «решение неравенства»?
— Как вы поняли, «решение неравенства» — это
действие или число? (Это число.)
— Какие же числа из вашего ряда являются
решением неравенства у < 260? (160,240)
— Почему число 260 не является решением? (Неверно,
что 260< 260.)
— Итак, какой первый шаг при ответе на данный
вопрос? Второй шаг?
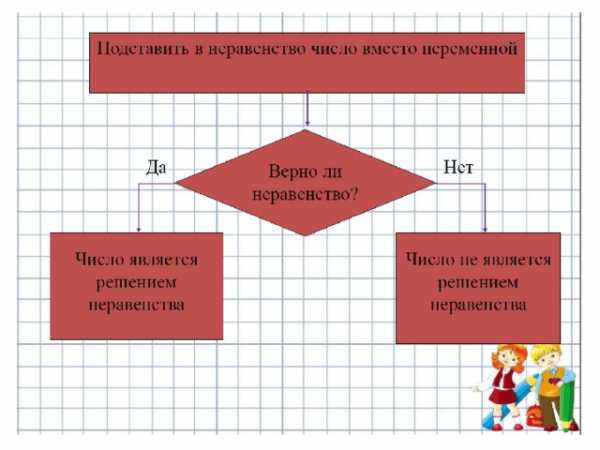
Алгоритм поиска решений неравенства с
переменной фиксируем в виде блок-схемы:
(Скобки вокруг У обозначают, что число
должно подставляться вместо переменной, а буквы
внизу — что нужно проверить, верно или неверно
полученное числовое неравенство.)
Физкультминутка: « Все имеет смысл, пока мы
здоровы».
- Крепко зажмурить глаза на 3-5 секунд, а затем
открыть их на 3-5 секунд. Продолжительность 6-8 раз.
(Укрепляет мышцы век, способствует
кровообращению и расслаблению мышц глаз). - «Написать цифры». Стоя, плечевым суставом,
(сначала правым, потом левым) написать поочередно
цифры от единицы до 8. Руки опущены. - Активный массаж мизинца (8-10 секунд) -
способствует снятию психического напряжения,
нервного переутомления - Активный массаж большого пальца (8-10 секунд) –
повышает функциональную активность головного
мозга.
V. Первичное закрепление во внешней речи.
1. № 1, стр 1.
На доске выставлены карточки, напротив которых
во время беседы отмечаются соответствующие
символы.
Вводная часть — 1
Главная мысль – W
Примеры — µ
Беседа: «Текст, который мы прочитали, как и
любой учебный текст, состоит из нескольких
частей: вводной, которая подготавливает
понимание смысла; главной мысли – смысла
нового; примеров, которые иллюстрируют
главную мысль. Найдите в тексте эти части и
догадайтесь, какими значками они обозначены? Так
устроен любой учебный текст. Почему важно уметь
его понимать?
— Для этого мы будем конспектировать текст,
т.е. кратко излагать его смысл.
— Какая из главных частей должна войти в
конспект? (Главная мысль.) Учитель выставляет
на доску карточки.
|
Отметить части текста |
Выписать главные мысли | Прочитать текст |
— Расставьте шаги алгоритма
конспектирования текста и обсудите в группах.
| Прочитать текст | Отметить части текста | Выписать главные мысли |
— Какие шаги у нас уже сделаны? (Первые два)
Что осталось? (Выписать главную мысль.)
— Подчеркните карандашом текст, который надо
выписать в конспект. ( Значение переменной,
удовлетворяющее неравенству, называют решением
неравенства.)
2. №2 , стр 1.
— Прочитайте задание.
— Какие числа вы подчеркнули? (Все числа,
которые больше 56. Это 91 и 318.)
— Как можно назвать эти числа? (Решения
неравенства.)
— Почему не выбрали письмо 56? (Потому что неверно
56>56.)
3. № 3, стр 1.
Рассмотрите картинку и раскрасьте числа,
которые являются решением данного неравенства. (
Дети «цепочкой» комментируют: «Число 75 не
является решением, так как неверно, что 75 –75 >4».)
4. № 5, стр 2. — работа в парах.
Соревнование — чья пара быстрее и правильнее
выберет нужные числа.
а) 8 х в – 7 > (30,72) б) к : 3 + 9 < 12 (6)
VI. Самостоятельная работа с самопроверкой по
эталону.
№ 4, стр 1.
— Выберите одну любую строчку и подчеркните
только то неравенство, решением которого будет
число 6.
Затем через готовую запись на доске дети
сверяют свой выбор, пользуясь алгоритмом.
(Если задание выполнено правильно, то рядом
дети ставят знак «+», если была допущена ошибка,
то они выявляют и называют ошибку.)
VII. Повторение.
1. №8, стр 2
На доске таблица. (Один ученик работает над
закрытой частью доски.)
— Прочитайте задачу. Заполните таблицу.
— Рассмотрите запись в тетради. Что необычного? (
Записаны вопросы.)
— Для чего нужны вопросы? ( Чтобы определить
порядок решения задачи.)
— Как ответить на первый вопрос? (Надо
расстояние разделить на время.)
— Надо ли писать пояснение? (Нет, в вопросе все
объяснено.)
— Узнайте самостоятельно скорость зайца. Чему
она равна? (7км\ч.)
— Ответьте самостоятельно на все следующие
вопросы.
После окончания работы дети сверяют свое
решение с записью на доске.
2. № 10, стр 3. – работа в парах.
— Здесь первый пример легче, а второй сложнее.
Выберите и решите один пример по желанию.
Проверка с доски.
VIII. Итог урока. Рефлексия деятельности.
— Назовите тему урока? (Решение неравенства.)
— Что означает термин «решение неравенства» -
действие или число? (Число.)
— Как узнать, является число решением
неравенства или нет? (Поставить его вместо
буквы и определить, верное неравенство или нет.)
— Посигнальте мне, кому нужна еще помощь? Кто уже
разобрался?
— А что еще нового узнали? ( Как составлять
конспект, записывать задачи с вопросами.)
— Для чего надо уметь конспектировать текст?
— А записывать задачи с вопросами?
— Как вы думаете, что нужно потренировать дома?
— Д/з: закончить конспект текста и выучить
опорный конспект; потренироваться в решении
неравенств № 6, стр 2 и попробовать записать
решение задачи с помощью вопросов № 9, стр 3.
Дополнительно по желанию -№ 12* или № 13*, стр 3.
9.02.2005
urok.1sept.ru
Презентация на тему Решение неравенства (4 класс) Петерсон
Презентацию на тему Решение неравенства (4 класс) Петерсон можно скачать абсолютно бесплатно на нашем сайте.
Предмет презентации : Математика. Красочные слайды и илюстрации помогут вам заинтересовать своих одноклассников или аудиторию.
Для просмотра содержимого презентации воспользуйтесь плеером, или если вы хотите скачать презентацию — нажмите на соответствующий текст под плеером.
Презентация содержит 8 слайдов.
скачать презентацию
Слайды презентации
Слайд 1
Математика 4 класс
http://aida.ucoz.ru
Тема «Решение неравенства»
Слайд 2
На какие группы можно разбить эти записи?
170 * 2 585-(10+85) (380+90)-80 4 › 5 17+9=26 580:2 (384+40) +16 х ‹ 290 12-а=8
12.12.2017
Выражения Равенства Неравенства
Слайд 3
Выражения равенства неравенства 170*2 17+9=26 4›5 580:2 12-а=8 х‹290 (384+40)+16 (380+90)-80 585-(10+85)
Вычислите удобным способом значения выражений
Слайд 4
Как одним словом назвать все записи, которые остались?
17+9=26 4›5 12-а=8 х‹290 Высказывания
На какие группы их можно разбить?
Слайд 5
высказывания высказывания с переменной 17+9=26 12-а=8 4›5 х‹290 Какое из высказываний верное, а какое — нет?
Слайд 6
Запишите решение неравенства
Х‹290 ?
Слайд 7
Слайд 8
Наталия Аркадьевна Полянцева 2011
Молодцы!
Список похожих презентаций
prezentacii.org
Презентация «Знаки « > » и «
Знаки « > » и « < »
3 урок
«Математика – это больше, чем наука, это язык».
х
<
(
)
≥
5
≤
Из знаков на доске составьте высказывание, записанное на математическом языке.
х
<
5
Как называется это высказывание?
На сегодняшнем уроке вы ещё узнаете новое о неравенствах. Как вы будете узнавать новое?
Прежде чем узнавать новое, что необходимо сделать?
А зачем вам повторять?
А почему смайлик не все шарики собирает в корзинку?
(Он берёт только те шарики, которые ему потребуются сегодня.)
Значит, вы будете повторять всё, что изучили раньше?
Множеством решений неравенства
x < 5
является множество: {0, 1, 2,3,4}.
Что называется множеством решений неравенства?
(Полный список решений конкретного неравенства.)
Что называется решением неравенства?
(Число, которое превращает неравенство в истинное высказывание.)
Какой еще смысл имеет слово «решение»?
(Процесс поиска множества решений.)
Решите неравенство, которое мы составили в начале урока: х < 5.
Работа по учебнику стр.7
Количество пассажиров в лифте должно быть меньше или равно пяти.
Строгие неравенства
Строгие неравенства
Нестрогие неравенства
Работа по учебнику стр.7
Работа по учебнику стр.7
Работа по учебнику стр.8
Работа по учебнику стр.8
Отметит закрашенным кружком на числовом луче число а
Знак ?
Отметить закрашенными кружками числа слева от числа а
Отметить закрашенными кружками числа справа от числа а
Записать множество решений неравенства
(числа слева от числа а)
Записать множество решений
неравенства
(числа справа от числа а)
Да
Нет
Работа по учебнику стр.8
Работа в парах
Самостоятельно
Работа по учебнику стр.9
Работа по учебнику стр.9
Работа по учебнику стр.9
Наш урок подошёл к концу, и я хочу сказать …
- Меня удивило…
- Для меня было открытием то, что …
- Мне больше всего удалось …
- Я могу похвалить одноклассников за…
- Я могу себя похвалить за…
Домашнее задание:
стр.9, №13, №14(а)
uchitelya.com
План-конспект урока по математике (4 класс) по теме: Урок математики в 4 классе по теме «Решение неравенств»
Тема: «Решение неравенства».
Основные цели:
Сформировать представление о понятии «решение неравенства», способность устанавливать, является данное число решением неравенства или нет;
1. Мотивация к учебной деятельности:
Учитель открывает на доске запись:
Хорошее начало – залог успеха
– Прочитайте высказывание на доске. Согласны ли вы с ним? (…)
– Докажите, что это высказывания! (…)
– Ребята, а побудительные предложения, такие как «Внимание!», «Стой!», «Докажите!» являются высказываниями? (Нет, так как о таких предложениях нельзя сказать, истинны они или ложны.)
– Что вы можете сказать о высказывании: «В школу вы приходите учиться». (Это высказывание истинное.)
– Докажите, что это высказывание истинное. (…)
– А что вы можете сказать о высказывании: «Вы умеете учиться». (…)
2. Актуализация знаний и фиксация затруднения в пробном действии.
— Чтобы узнать, что вы не знаете, что надо сначала сделать? (Надо повторить, что мы уже знаем.)
— А где эти знания могут вам помочь? (При открытии новых знаний.)
. На доске открываются расположенные под ними карточки с математическими записями:
170 ∙ 2 585 – (10 + 85) (380 + 90) – 80
4 5 17 + 9 = 26 580 : 2
(384 + 40) +16 х 7 12 – а = 8
— Какие виды математических записей представлены на доске? (Равенства, неравенства и выражения.)
— Вспомните, что вы знаете о равенствах, неравенствах, выражениях. (…)
— Какие из записанных на доске предложений являются высказываниями? Докажите. (Неравенство 4 5 – ложно; равенство 17 + 9 = 26 – истинно.)
— А математические выражения являются высказываниями? Почему? (Не являются, так как о них нельзя сказать, истинны они или ложны.)
— Передвиньте карточки на доске по группам: выражения, равенства, неравенства.
Трое учащихся работают у доски, остальные – фронтально. На доске должны получиться следующие три столбика:
170 ∙ 2 17 + 9 = 26 4 5
580 : 2 12 – а = 8 х 7
(384 + 40) + 16
(380 + 90) – 80
585 – (10 + 85)
— Что можно сделать с выражениями в первом столбике? (Можно найти значения этих выражений.)Дети находят значения выражений.
— Что вы сейчас повторили? (Способы нахождения значений числовых выражений)
— Я вам предлагаю следующее задание: запишите маркером на обратной стороне своих сигнальных карточек решения неравенства х 7.
— Прежде выполнять задание сравните предложенное задание с предыдущими заданиями, и определите, что в этом задании нового?
— Сформулируйте свою цель и тему урока. (Цель: найти решение неравенства, тема: решение неравенств.)
Тема записывается на доске: «Решение неравенства».
— Выполните задание.
Учащиеся самостоятельно выполняют задание.
— У кого нет ответов?
— Сформулируйте своё затруднение. (Мы не смогли найти решение неравенства.)
— Прикрепите на доску карточки те, у кого есть ответы.
Учитель фиксирует разные позиции, отсутствие единого мнения.
— Что же получилось? (Мнения разделились.)
— Вы можете объяснить, почему получились разные ответы? (…)
— Сформулируйте своё затруднение. (Мы не можем объяснить, почему получились разные ответы.)
— Что же делать? (Надо подумать, почему так получилось.)
3. Выявление места и причины затруднения.
— Какое задание вы выполняли? (Найти решение неравенства х 7.)
— Каким правилом вы пользовались при выполнении задания? (…)
-Почему не удалось всем выполнить это задание? (Не знаем, что такое решения неравенства; не знаем способа их нахождения.)
4. Построение проекта выхода из затруднения.
— Поставьте перед собой цель. (Нам надо согласовать, что такое «решение неравенства» и научиться находить их.)
— Что вы сначала должны сделать? (Выяснить, что такое решение неравенств.)
Учитель на доске фиксирует первый пункт плана:
1. Выяснить, что такое решение неравенства.
— А что после этого надо сделать? (Найти способы нахождения решений неравенств.)
Учитель на доске фиксирует второй шаг плана:
2. Найти способ решения неравенств.
5. Построение проекта выхода из затруднения.
Один из учеников читает текст учебника вслух.
— Так что же такое «решение неравенства» – действие или число? (Это число, которое подставляют вместо переменной и получают верное неравенство.)
— Какие числа являются решениями неравенства х 7
— Почему же число 7 не является решением этого неравенства? (7 7 – ложное высказывание.)
— Первый шаг плана вы выполнили? Что теперь надо сделать? (…)
— Давайте составим алгоритм поиска решения неравенства. Эту работу я вам предлагаю выполнить в группах
— Я вам предлагаю шаги алгоритма, вам необходимо из предложенных блоков построить алгоритм нахождения решения неравенства, обосновав свой вариант, на работу отводится 2 минуты.
Учащиеся выполняют задание в группах.
—
Учащиеся выполняют задание в группах.
— Запишем алгоритм в виде опорного конспекта на листах бумаги.
— Покажите, что у вас получилось?
Варианты, предложенные группами, обсуждаются и записываются в тетради для опорных конспектов.
Учитель вывешивает карточку с опорным конспектом на доску:
-Что нужно проверить?
-Истинно или ложно получившееся числовое неравенство.
— Вы достигли поставленной цели, что вы узнали? (Да, цель достигнута, мы узнали, что такое решение неравенства, и построили алгоритм нахождения решений неравенств.)
— Что надо сделать? (Надо потренироваться в нахождении решений неравенств.)
6. Первичное закрепление во внешней речи.
— Для тренировки я вам предлагаю выполнить № 2, стр. 1.
— Подчеркните числа, удовлетворяющие данному неравенству.
Учащиеся работают в учебниках-тетрадях.
— Какие числа подчеркнули? (91 и 38.)
— Как называются эти числа? (Решениями неравенства.)
— Почему не выбрали число 56? (Потому что высказывание 56 56 – ложно.)
— Что ещё надо сделать, чтобы каждый из вас мог сказать истинным или ложным является высказывание «Мы научились решать неравенства»? (Надо проверить себя.)
7. Самостоятельная работа с самопроверкой по эталону.
— Переделайте ее так, чтобы получилось истинное высказывание. (Мы будем выполнять самостоятельную работу; в самостоятельной работе все задания мне понятны и т. д.).
— Прочитайте задание № 4, стр. 1.
Учащиеся читают задание про себя.
— Что нужно сделать? (Проверить, является ли число 6 решением неравенства.)
— Выберите любое неравенство верхней строчки и выполните задание самостоятельно, обведя неравенство в случае, если число 6 является решением неравенства и подчеркните неравенство, если не является решением.
Учащиеся выполняют самостоятельную работу, по окончании которой учитель на доске выставляет эталон для самопроверки.
— Проверяем первый шаг.
— Как вы выполняли шаг?
— У кого этот шаг вызвал затруднение?
— Почему вы допустили ошибку?
— Зафиксируйте результат проверки при помощи знаков «+» или «?».
— Что нам поможет исправить ошибки? (Эталон.)
— Проверяем второй шаг.
— Как вы выполняли второй шаг?
— У кого второй шаг вызвал затруднение?
— Почему вы допустили ошибку?
— Зафиксируйте результат проверки при помощи знаков «+» или «?».
— Исправьте ошибки.
— Проверяем третий шаг.
— Как вы выполняли третий шаг?
— У кого шаг вызвал затруднение?
— Почему вы допустили ошибку?
— Зафиксируйте результат проверки при помощи знаков «+» или «?».
— Исправьте ошибки.
— Поднимите руки, у кого все верно. Вы молодцы!
8. Рефлексия учебной деятельности на уроке.
— Назовите тему урока. (Решение неравенств.)
— Какова была цель урока? (Определить, что такое решение неравенств и найти способ для нахождения способа решения неравенства.)
— Вы достигли поставленной цели? (Да.)
— Как узнать, является ли число решением неравенства? (Поставить его вместо переменной и определить, верно неравенство или нет.)
— У кого остались вопросы на конец урока?
— Кто хорошо разобрался в теме? Молодцы!
— Как вы думаете, с какими заданиями надо поработать дома? (…)
Домашнее задании
№ 6 (в, г), стр. 2; № 9
nsportal.ru
Математика 4 класс Петерсон Номер 1
Математика 4 класс Петерсон
авторы: Петерсон Л.Г. .
издательство: «Фгос» 2013 год
Раздел:
- Часть 1
- 2 урок. Множество решений
У неравенства может быть несколько решений. Числа 1, 3, 5 являются решениями неравенства x < 6. Но это не все его решения: кроме них решениями являются числа 0, 2, 4. Если мы напишем числа 0, 1, 2, 3, 4, 5, то получим все решения неравенства x < 6. Других решений у него нет.
Полный список решений неравенства называют множеством решений этого неравенства. Так, множеством решений неравенства x < 6 является множество {0, 1, 2, 3, 4, 5}.
Неравенство y + 8 < 6 не имеет ни одного решения. Множество его решений является пустым: ∅.
Решениями неравенства z > 6 являются любые числа, большие 6. Это неравенство имеет бесконечное множество решений: {7, 8, 9, 10, …}.
Найди в тексте, выделенном рамкой вводную часть, главную мысль, примеры. Обозначь эти части текста знаками соответственно |, w и S. Придумай свои примеры неравенств, множество решений которых являются:
а) конечным;
б) бесконечным;
в) пустым.
Сделай конспект.
Решениями неравенства z > 6 являются любые числа, большие 6. Это неравенство имеет бесконечное множество решений: {7, 8, 9, 10, …}.
Найди в тексте, выделенном рамкой вводную часть, главную мысль, примеры. Обозначь эти части текста знаками соответственно |, w и S. Придумай свои примеры неравенств, множество решений которых являются:
а) конечным;
б) бесконечным;
в) пустым.
Сделай конспект.
Решение
1) Вводная часть − 1 абзац − выделяем знаком |.
2) Главная мысль − 2 абзац − знаком w.
3) Примеры − 3, 4 абзацы − знаком S.
Примеры неравенств:
а) x < 3 {0, 1, 2};
б) x > 4 {5, 6, 7, 8, …}.
в) x + 9 < 3 − не имеет ни одного решения ∅.
Конспект:
1) У неравенства может быть несколько решений. y < 4 {0, 1, 2, 3}.
2) Множество решений − полный список решений неравенства.
3) Примеры:
y + 10 < 5 − не имеет ни одного решения.
y > 5 {6, 7, 8, …}.
×
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
Отправить
reshalka.com