Как решить задачу по математике 3 класса часть 1: Страница 34 — ГДЗ Математика 3 класс. Моро, Бантова. Учебник часть 1

Страница 44 (учебник Моро 1 часть 3 класс) ответы по математике

1.
1) Увеличь в 6 раз числа: 3, 5, 7, 9, 10, 1.
2) Уменьши в 6 раз числа: 12, 24, 48, 42, 60, 6.

1)
3 * 6 = 18       9 * 6 = 54
5 * 6 = 30       10 * 6 = 60
7 * 6 = 42       1 * 6 = 6

2)
12 : 6 = 2       42 : 6 = 7
24 : 6 = 4       60 : 6 = 10
48 : 6 = 8       6 : 6 = 1

2.

6 * 8 = 48       54 : 9 = 6       24 : 8 = 3
7 * 6 = 42       48 : 6 = 8       18 : 6 = 3
6 * 6 = 36       42 : 7 = 6       42 : 6 = 7

52 — 20 : 5 = 52 — 4 = 48
49 + 30 : 6 = 49 + 5 = 54
18 : 9 + 58 = 2 + 58 = 60
36 — 4 * 9 = 36 — 36 = 0
40 + 7 * 5 = 40 + 35 = 75
60 — 8 * 4 = 60 — 32 = 28

3. Запиши выражение. Найди знамение частного чисел 24 и с, если с = 3, с = 4, с = 24, с = 1.

24 : 3 = 8
24 : 4 = 6
24 : 24 = 1
24 : 1 = 24

4. Найди ошибки и реши уравнения правильно.

5. Тетрадь в клетку стоит 10 р., альбом на 10 р. дороже, чем тетрадь, а ручка на 5 р. дешевле, чем альбом.
Дополни условие задачи и поставь вопрос так, чтобы задача решалась двумя действиями.

Сколько стоит ручка?

1) 10 + 10 = 20 р. стоит альбом.
2) 20 — 5 = 15 р. стоит ручка.
Ответ: 15 р.

6. В школьной столовой было 50 кг сахару. Его расходовали 6 дней, по 2 кг каждый день. Сколько килограммов сахару осталось?

1) 6 * 2 = 12 кг сахара израсходовали.
2) 50 — 12 = 38 кг сахара осталось.
Ответ: 38 кг.

Задание под знаком вопроса.
Вычисли значение выражения 4 * b, если b = 3, b = 5, b = 6, b = 10.

4 * 3 = 12
4 * 5 = 20
4 * 6 = 24
4 * 10 = 40

Задание на полях.
Занимательные рамки.

ПНШ 3 класс. Математика. Учебник № 1, с. 139

Составные задачи на все действия

Ответы к с. 139

465. Сформулируй дополнительные промежуточные требования, которые помогают решить данную задачу.
До полудня на станции разгрузили 10 вагонов с удобрениями, а после полудня — на 5 вагонов меньше. Во сколько раз меньше вагонов разгрузили после полудня, чем за весь день?
Реши задачу. Вычисли и запиши ответ.

Дополнительное промежуточное требование — необходимо найти, сколько вагонов разгрузили после полудня.
1. 10 — 5 = 5 (в.) — разгрузили после полудня
2. 10 : 5 = 2
О т в е т: разгрузили в 2 раза меньше вагонов.

466. Составь задачу, решением которой было бы выражение (18 — 10) • 3 : 4 + 5.
Вычисли и запиши ответ задачи.

В детском саду в коробке с игрушками было 18 кукол, пупсиков было на 10 меньше, чем кукол. Солдатиков было в 3 раза больше, чем пупсиков, а клоунов в 4 раза меньше, чем солдатиков. Машинок было на 5 больше, чем клоунов. Сколько машинок было в коробке с игрушками?
(18 -10) • 3 : 4 + 5 = 11 (м.)
О т в е т: в коробке было 11 машинок.

467. Для решения некоторой задачи была составлена следующая схема:

Чтобы упростить построение схемы, мы не стали изображать некоторые стрелки.
Запиши решение этой задачи.
Начерти другую схему (упрощённый вариант), которая соответствует задаче, решаемой с помощью двух действий вычитания.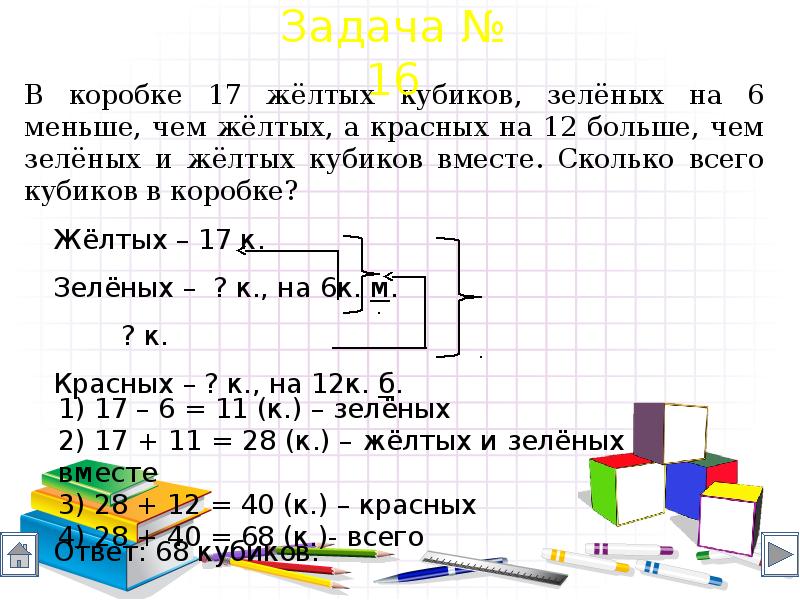

1. 150 — 20 = 130
2. 300 — 130 = 170

1. 100 — 50 = 50
2. 150 — 50 = 100

Ответы к заданиям. Математика. Учебник. Часть 1. Чекин А.Л. 2013 г.

Математика. 3 класс. Чекин А.Л.

4.1
/
5
(
16

голосов
)

Урок по математике «Решение задач разными способами. Закрепление изученного материала» (3 класс)

Тема: Решение задач разными способами. Закрепление изученного материала

Тип урока: закрепление изученного материала

Основные цели:

1. сформировать умение решать задачу двумя способами

2. сформировать умение составлять выражения для решения текстовых задач.

3. тренировать мыслительные операции, закрепить умение действовать по установленному правилу, развивать память, внимание, речь, мелкую моторику рук; воспитывать коммуникативные умения, познавательный интерес, веру в свои силы.

 Оборудование:  презентация, учебники, тетради

                                              Ход урока.

1. Оргмомент.

— Откройте, пожалуйста, тетрадки. Запишите сегодняшнее число, подчеркните орфограммы.  

2. Мотивация к учебной деятельности.

— Какой раздел мы изучаем на уроках математики? («Математические законы»)

— Для чего нужны математические законы? Где мы их используем? (В решении задач, примеров, выражений. Благодаря им можно ЛЕГКО решить даже самые трудные примеры)

3. Актуализация знаний.

Математическая разминка. (слайд из презентации)

Решите пример и вы узнаете, какой зверь самый чистоплотный.

658+174

723 медведь

832 барсук

858 лиса

— Самый чистоплотный зверёк — барсук . У его нор нет пищевых остатков, вблизи жилища находится специальная «уборная» ямка.

4. Минутка красивого письма

832

4. Закрепление изученного материала.

Какое животное самое умное?

217+361

578 Дельфин

687 Обезьяна

587 Жираф

-Мозг дельфина по величине почти такой же, как у человека, однако объем знаний он способен усвоить в 1,5 раза больший, чем мы с вами.
Таким образом, дельфины заслуженно, считаются самыми умными животными на земле.

-Определите доли (устно)

-Решите лесенку примеров

20·8=

5·70=

3·300=

8·40=

60:20=

7·100=

800:200=

Какое самое злое животное на планете?

1000-65

925 волк

935 тасманийский дьявол

835 лиса

-Это животное имеет соответствующее название — «дьявол» и водится в Австралии и на острове Тасмания.

5. Работа по учебнику

Стр. 28 № 4(а)

— Прочитайте задачу.

— Что известно в задаче?

— Что нужно найти?

— Можем ли мы сразу ответить на вопрос задачи?

— Во сколько действий будет решаться задача?

— Запишем краткую запись в тетрадь.

— Расскажите о своем способе решения.

— Запишем три способа решения задачи.

№ 4 (б)

1 день – 50 бел. и 20 чёрн.

7 дней — ? буханок хлеба

1-й способ

(50+20) ·7=490 (б)

2-й способ

50·7+20·7=490 (б)

3-й способ

1) 50·7=350 (бел)

2) 20·7=140 (чёрн)

3) 350+140=490 (б)

— Что общего в этих способах? Чем различаются?

Какое самое большое животное на планете?

456-321

235 слон

153 кашалот

135 синий кит

-Самое большое животное в мире из ныне существующих это, безусловно, голубой кит. Он является морским млекопитающим. В длину особи достигают 30-ти метров, вес чудища – около 180 тонн.

6. Самостоятельная работа  

Дан прямоугольник со сторонами 5 см и 3 см. Найдите периметр и площадь фигуры.

Проверка :

Р= 5+3+5+3=16 см

Р= (5+3) · 2= 16 см

Р= 5·2+3·2=16 см

S= 5·3=15 см²

Ответ: 16см, 15 см²

Какая самая большая птица на земле ?

574+254

828 страус

728 индюк

815 кондор

— Крупнейшая птица в мире не умеет летать. Страус – обитатель равнин Аравии и Африки. Особи мужского пола вырастают до 2,8 метров и весят от 150 килограммов.

№ 2 на доске

Решение примеров с комментированием.

8. Рефлексия учебной деятельности.

— Какую тему урока изучали сегодня на уроке?

— Что нового узнали в решении задач?

— Каким образом математические законы помогают в решении задач?

— Что было особенно тяжело понять, выполнить?

— С чем легко справились?

9. Домашнее задание.

Стр. 28 № 5, № 7

мыслительных блоков | Моделирование и решение математических словесных задач

Детский сад

1 класс

2 класс

3 класс

4 класс

5 класс

6 класс

Веселые игры для детей

Представляем новые и улучшенные блоки мышления®

Мы переработали Thinking Blocks и наполнили его новыми функциями!

задачи на чтение вслух — визуальные подсказки — улучшенные модели — увлекательные темы — мобильная версия

Thinking Blocks хорошо работает на всех устройствах.

Распечатайте задачи из блоков мышления

Блоки мышления для детей

Блоки мышления Дополнение

Умножение мыслительных блоков

Дроби мыслительных блоков

Соотношения мыслительных блоков

Инструмент «Мыслительные блоки»

Видео сложения и вычитания

Часть-Целое A

Часть-Целое B

Два шага

Сравните А

Сравните B

Сравнить C

Видео умножения и деления

Умножить

Разделить

Смешанные операции

Сравните А

Сравните B

Критическое мышление

Фракции Видео

Часть набора A

Часть набора B

Часть набора C

Сложение и вычитание А

Сложение и вычитание B

Умножить и разделить

Десятичные и процентные видео

Десятичные числа А

Десятичные B

% от числа

Налоги, чаевые, продажи

% Вызов А

% Задача B

Соотношение и пропорции видео

Сравните А

Сравните B

Сравнить C

Частичная сумма

Три количества

Критическое мышление

Видео по алгебре

Проблема 1

Проблема 2

Проблема 3

Проблема 4

Проблема 5

Проблема 6

МАТЕМАТИЧЕСКАЯ ПЛОЩАДКА
Игры для 1-го класса
Игры для 2-го класса
Игры для 3-го класса
Игры для 4-го класса
Игры для 5-го класса
Игры для 6-го класса
Блоки мышления
Математические видео

МАТЕМАТИЧЕСКИЕ ИГРЫ
Игры на сложение
Игры на вычитание
Игры на умножение
Игры на деление
Игры на дроби
Игры на соотношения
Игры на преалгебру
Игры на геометрию

ОБУЧАЮЩИЕ ИГРЫ
Логические игры
Классические игры
Правописание
Грамматические игры
Печатание
География
Математические головоломки
Пространственное мышление

FUN KIDS GAMES
Fun Games
Приключенческие игры
Car Games
Спортивные игры
Endless Runner Games
Игры Perfect Time
Игры для двоих
Все игры

FRACTION FOREST
Фракции единиц 1
Фракции единиц 2
Игровая площадка 1
Равные фракции 1
Равные фракции 2
Игровая площадка 2
Добавление фракций 1
Добавление фракций 2
Игровая площадка 3

МЫСЛИТЕЛЬНЫЕ БЛОКИ
TB Junior
TB Сложение
TB Умножение
TB Дроби
TB Соотношения
Инструмент моделирования
Печатная версия
Видео
Словесные задачи

ЧИСЛОВЫЕ ЗАГАДКИ
Суммарные стеки
Числовая последовательность
Суммарные связи
Суммарные блоки
Суммы цепочек
Суммы растяжения
Суммы обмена
Суммы перекрытий

ОБУЧЕНИЕ МАТЕМАТИКЕ
Головоломки по алгебре
Стратегическое умножение
Задания на дроби
Решение задач
Математика для 3-го класса
Наглядные математические инструменты
Задания на моделирование слов

Реклама | Перейти без рекламы

О нас
Политика конфиденциальности
Условия использования
Условия оплаты
Получить помощь

Copyright © 2022 Math Playground LLC • Все права защищены

Проверьте эти 50 задач дня по математике для третьего класса

Начните свой ежедневный урок математики со словесной задачи дня по математике — это отличный способ подготовить почву для обучения. Все мы знаем, что юным ученикам трудно понять текстовые задачи, даже если часть задачи, связанная с математическими операциями, является базовой.

Включайте эти задачи по математике для третьего класса один день за раз в начале вашего математического блока, чтобы укрепить уверенность, навыки критического мышления и обучающееся сообщество. Студенты привыкнут читать медленно, чтобы понять смысл, а также определять ключевую информацию. Предложите учащимся записывать уравнения и рисовать картинки, чтобы объяснить свое мышление, так как это помогает им увидеть свет, когда они застряли!

Рассматриваемые темы включают сложение, вычитание, умножение, деление, смешанные операции, дроби, площадь и периметр, а также измерения! Все, что вам нужно сделать, это опубликовать одну из этих математических задач третьего класса на доске или экране проектора.Тогда пусть дети взять его оттуда.

Если вы хотите еще математических задач, мы ежедневно публикуем их на нашем удобном для детей сайте: Daily Classroom Hub. Обязательно добавьте ссылку в закладки!

Хотите весь этот набор текстовых задач в одном простом документе? Получите бесплатный пакет PowerPoint, отправив сообщение электронной почты здесь.

50 задач по математике для третьего класса

1. Гейдж пошел в магазин и купил 19 кексов, 18 яблочных пирогов и 47 глазированных пончиков. Сколько вещей он купил всего?

2.Приют заботится о 384 кошках. прибывают еще 176 человек. Сколько кошек сейчас в приюте?

3. У Габби на книжной полке 42 книги. Отец подарил ей еще 23 на день рождения. Сколько книг сейчас у Габби?

4. На футбольном матче присутствовало 823 человека, а ушли 37 человек. Сколько человек было на игре до того, как люди ушли?

5. У мистера Вашингтона 44 карандаша. Он нашел в ящиках 37 карандашей и открыл новую пачку из 60 карандашей.Сколько всего карандашей у мистера Вашингтона?

6. Джефф играет в Minecraft.

В понедельник он отыграл 67 минут. Во вторник он отыграл 32 минуты. В среду он отыграл 43 минуты. Сколько минут Джефф играл в течение недели?

7. В начальной школе Смита учатся 286 мальчиков и 241 девочка. Каково общее количество учеников, посещающих начальную школу Смита?

8. Эшли каждый день ездит в школу на велосипеде. Поездка от ее дома до школы занимает 21 минуту.Если она уже катается на велосипеде 17 минут, сколько еще ей осталось ехать, прежде чем она прибудет в школу?

9. Джейсон испек 93 печенья для продажи на школьной распродаже выпечки. Он планирует забрать домой любое печенье, которое не продает. Если он продал 77 печенек, сколько печенек он заберет домой?

10. Школа собирает деньги на футболки. Третьеклассники собрали 327 долларов. Четвертый класс собрал на 138 долларов меньше. Сколько денег собрал четвертый класс?

11.У Хайдена 610 наклеек. 250 штук в белой коробке и несколько в желтой.

Сколько в желтом ящике?

12. В таблице указаны классовые баллы учащихся. Какие два студента имеют разницу в 15 баллов?

13. У г-жи Брейди 356 кустов помидоров. Она продает 91 растение и отдает 49 растений. Сколько кустов томатов осталось у мисс Брейди?

14. Мама Дэвида покупает яблоки для его класса. Есть 5 рядов по 4 зеленых яблока.В 1 ряду 4 красных яблока. Заполните пропуски, чтобы закончить выражения.

15. В коробке конфет 14 рядов. В каждом ряду по 6 шоколадок. Сколько кусочков шоколада в коробке?

16. Кристи и Ян играют в карты. У Кристи 4 карты, а у Яна в 4 раза больше карт. Сколько карт у них вместе?

17. Эмерсон отвечает за сбор баскетбольных мячей в конце урока физкультуры.Есть 6 корзин, и в каждой может поместиться 7 баскетбольных мячей. Сколько баскетбольных мячей, если все корзины полны?

18. У Луз было две страницы домашнего задания.

На каждой странице было по пять задач. Сколько всего задач она должна была решить?

19. Кианна рисовала на скрап-бумаге. На каждой странице она могла уместить семь рисунков. Если у нее есть три листа бумаги, сколько рисунков она может сделать?

20. Пекарня продает одно сахарное печенье за ​​2 доллара.00. Сколько будет стоить дюжина сахарного печенья?

21. Миссис Смит готовит свой класс к первому учебному дню. В ее классе 25 учеников. Она хочет, чтобы за каждым столом сидело 5 студентов. Сколько столов ей понадобится?

22. Алекс собирает школьные принадлежности. У него 141 каталожная карточка. Он хочет разделить их на 3 стопки. Сколько карт будет в каждой стопке?

23. Класс миссис Блэкли играет в обзорную игру.Класс получает 5 баллов каждый раз, когда правильно отвечает на вопрос. В понедельник класс зарабатывает 50 очков, играя в игру. На сколько вопросов класс ответил правильно?

24.

У Марии 56 мармеладных мишек. Она отдаст всех мармеладных мишек 8 своим друзьям. Каждый друг получит одинаковый номер. Сколько мармеладных мишек получит каждый друг?

25. У Даниэля 63 монеты и 9 копилок. Если в каждой копилке одинаковое количество монет, сколько монет в каждой копилке?

26.У Лесли 32 куклы в 4 корзинах. В каждой корзине одинаковое количество кукол. Сколько кукол в каждой корзине?

27. В аквариуме Леви 10 рыбок. 4 рыбки — золотые рыбки, остальные — гольяны. Какую часть рыб составляют золотые рыбки?

28. У Мелани 8 цветных карандашей. 3 зеленые, 2 желтые и 3 синие. Какая часть карандашей синяя?

29. У Ханны есть пакет M&M’s. В упаковке 24 M&M’s.8 красных, 6 зеленых, 7 желтых и 3 коричневых. Какая часть M&M’s коричневого цвета?

30. Мистеру Брауну нужно заказать пиццу для 18 студентов. Он хочет, чтобы каждый ученик получил ¼ пиццы. Сколько пицц он должен заказать?

31.

Класс провел опрос о любимых животных. ¼ студентов выбрали своим любимым животным львов, а ½ студентов выбрали слонов. Остальные студенты выбрали либо акул, либо китов. Разделите круговую диаграмму, чтобы показать эти результаты.

32. Джон хотел шоколадный торт на день рождения. Задув свечи, он разрезал торт. Из 12 гостей вечеринки только 6 ели торт. Джон позволил своему другу Джексону забрать домой половину оставшегося торта. Какая часть пирога осталась?

33. Площадь прямоугольника 72 квадратных единицы. Одна сторона имеет длину 9 единиц. Какова длина другой стороны?

34. Монико нарисовала фигуру. Это был четырехугольник, и все стороны были одинаковой длины.Какую фигуру нарисовала Монико?

35. Глория покупает новый ковер на пол в свою спальню. Если размер пола 12 футов на 12 футов, ковер какого размера ей нужен?

36. Площадь Хэппитауна составляет 42 квадратных мили. Если длина 7 миль, каков периметр города?

37.

Эйден читал по 2 страницы в своей книге глав каждый день в течение 7 дней. Всего в книге 32 страницы. Сколько страниц осталось прочитать Эйдену?

38.У Софии есть двадцатидолларовая купюра. Она покупает шесть игрушек-поп-ит по 2 доллара каждая. Сколько денег осталось у Софьи?

39. На пикнике 10 человек. Каждый человек съест 2 хот-дога. В упаковке 8 хот-догов. Сколько пакетов нужно?

40. Миссис Поттер купила 160 каталожных карточек. Она дала первому ряду 55 учетных карточек, затем второму ряду 72 учетные карточки. Сколько ей осталось отдать в последний ряд?

41.У Саманты 38 маркеров, она дает 29 маркеров своим одноклассникам. Затем она открывает новую упаковку из 15 маркеров. Сколько маркеров у нее сейчас?

42. В сумке было 18 волейбольных мячей, а в корзине – 13 волейбольных мячей. 10 из них использовались на переменах. Сколько волейбольных мячей не было использовано?

43.

У миссис Хортон 1 галлон молока. Она налила 3 ​​стакана молока. Сколько чашек молока у нее осталось?

44. Марку нужно купить пряжу для 5 друзей, чтобы заняться наукой.Каждому другу нужно 2 фута зеленой пряжи и 1 фут фиолетовой пряжи. Сколько метров пряжи нужно купить Марку?

45. Новая скакалка Надин на 4 дюйма длиннее ее старой скакалки. Ее старая скакалка была 32 дюйма в длину. Какой длины новая скакалка Надин?

46. Дервин выстроил скрепки в два ряда. Каждый ряд был длиной 18 футов. Сколько футов скрепок было у Дервина, если он сложил два ряда вместе?

47. Лондон начал искать пропавшую собаку в 14:10.Ей понадобилось 43 минуты, чтобы найти его. В какое время Лондон нашел свою собаку?

48. Деймон сел на поезд из своего дома в центр города. Поезд отправился со станции в 13:08 и проехал 33 минуты, прежде чем прибыл в центр города. Во сколько прибыл поезд?

49. Ханна работала над домашним заданием 37 минут.

Если она начала в 19:14, во сколько она закончила домашнее задание?

50. Кевин начал убирать свою комнату в 18:03. Если он наконец закончил в 18:40, сколько времени Нед потратил на уборку своей комнаты?

Нравятся эти задачи по математике в третьем классе? Посетите наш центр третьего класса, чтобы получить еще больше ресурсов.

Получите версию этих текстовых задач в формате PPT.

Математика 3-го класса. Часть 2: Умножение и деление, часть 1

Обзор блока

Модуль 2 открывает учащимся глаза на некоторые из наиболее важных предметов, которые учащиеся изучают в 3 классе, — умножение и деление. В этом разделе «учащиеся начинают развивать эти понятия, работая с числами, с которыми они более знакомы, такими как 2, 5 и 10, в дополнение к числам, которые легко пропустить, таким как 3 и 4», позволяя когнитивным требуют опираться на сами понятия умножения и деления, а не на числа (CCSS Toolbox, Sequenced Units for the Common Core State Standards in Mathematics Grade 3). Затем в Блоке 3 учащиеся будут работать над более сложными блоками 0, 1, 6–9 и числами, кратными 10. 

Во 2-м классе учащиеся научились считать объекты в массивах, используя многократное сложение (2.OA.4), чтобы получить основы умножения. Они также проделали большую работу над одно- и двухэтапными задачами на сложение и вычитание, освоив все типы задач, включающие эти операции (2.OA.1). Таким образом, учащиеся развили сильную склонность к решению проблем и получили базовое содержание, необходимое для того, чтобы сразу приступить к умножению и делению в этом разделе.

В начале этого раздела учащиеся получают представление об умножении и делении в контексте задач на равные группы и массивы в теме A. Чтобы сосредоточиться на концептуальном понимании умножения и деления (3.OA.1, 3. OA.2), Тема A не обсуждает конкретные стратегии решения, поэтому учащиеся могут пересчитать все объекты (стратегия 1-го уровня) или вспомнить свой пропуск счета и многократное сложение (стратегии 2-го уровня) из 2-го класса, чтобы найти произведение. Однако в темах B и C основное внимание уделяется разработке более эффективных стратегий для решения задач умножения и деления, включая пропуск счета и многократное сложение (стратегии уровня 2), а также «просто знание» фактов, которое работает на достижение цели. «к концу 3 класса [учащиеся] знают наизусть все произведения двух однозначных чисел и связанные с ними факты деления» (3.ОА.7). Как говорится в разделе «Операции и развитие алгебраического мышления», «освоение этого материала и достижение беглости в умножении однозначных чисел и связанном с ним делении может занять довольно много времени, потому что не существует общих стратегий умножения или деления всех однозначных чисел, как для сложения или сложения». вычитание» (OA Progression, стр. 22). Таким образом, поскольку «существует много шаблонов и стратегий, зависящих от конкретных чисел», они сначала работают с факторами 2, 5 и 10 в Теме B, так как они выучили эти последовательности с пропуском счета во 2-м классе.Затем в Теме С они работают с новыми факторами 3 и 4. Только тогда, когда учащиеся лучше познакомятся с этими факторами, учащиеся будут решать с ними более сложные и/или абстрактные задачи, в том числе определение неизвестного целого числа в виде числа. уравнение умножения или деления, связывающее три целых числа (3.OA.4) и решение двухшаговых задач со словами с использованием всех четырех операций (3.OA.3, 3.OA.8), оценивая обоснованность их ответов для множества типы задач в теме D. 

На протяжении всего модуля учащиеся выполняют различные математические упражнения.Модуль уделяет особое внимание абстрактным и количественным рассуждениям, поскольку учащиеся начинают понимать значение умножения и деления и абстрактных символов, используемых для их представления (MP.2). Далее учащиеся моделируют с помощью математики эти новые операции, решая с их помощью одно- и двухшаговые уравнения (МН.4).

Это введение в умножение и деление углубляется в Разделе 3, когда учащиеся изучают более сложные множители 0, 1, 6–9 и числа, кратные 10. Затем, в Разделе 4, учащиеся будут исследовать площадь как приложение умножения. В 4 классе их понимание умножения и деления станет еще более тонким, когда они начнут понимать мультипликативное сравнение и решать текстовые задачи, связанные с ним (4.OA.1, 4.OA.2). Кроме того, они будут решать многоэтапные текстовые задачи, включающие все четыре операции, иногда с необходимостью интерпретации остатка в контексте задачи (4.OA.3). Наконец, учащиеся станут более свободно выполнять умножение и деление, умножая целое число до четырех цифр на однозначное целое число и два двузначных числа, а также деля до четырехзначных делимых на однозначное число. делитель (4.НБТ.5, 4.НБТ.6). Умножение и деление обеспечивают основу для множества алгебраических и геометрических тем, от линейных функций до тригонометрии, и, таким образом, это содержание имеет решающее значение для всего будущего изучения математики.

Темп: 19 учебных дней (16 уроков, 2 гибких дня, 1 оценочный день)

Для получения рекомендаций по корректировке темпа на 2021–2022 учебный год см. Рекомендуемые корректировки объема и последовательности для 3-го класса.

Часть-Часть-Целое со Сложением и Вычитанием

Обучение отношениям часть-часть-целое имеет решающее значение при обучении сложению и вычитанию.Чтобы учащиеся хорошо понимали сложение и вычитание, им необходимо понимать, что представляет каждый из них. Хотя это полезно при работе с уравнениями с неизвестными во всех областях, крайне важно, чтобы учащиеся хорошо понимали сложение и вычитание, чтобы они могли применять оба навыка в реальных сценариях. Понимание части-части-целого — гораздо более эффективная стратегия обучения решению проблем, чем ключевые слова, хотя они все же имеют свое место.

НЕИЗВЕСТНЫЙ

Одной из первых частей обучения части-части-целому является неизвестное; вопрос.Учащиеся должны часто знакомиться с неизвестными различных типов — переменными, вопросительными знаками, пустыми строками, прямоугольниками и т. д., чтобы понять, что все они означают одно и то же. Крайне важно, чтобы неизвестное находилось в разных положениях, особенно слева от знака равенства ( x = 6 + 2), чтобы учащиеся усвоили его значение. Неизвестное следует определить как ЦЕЛОЕ или ЧАСТЬ на раннем этапе, чтобы они могли позже перенести свое обучение на текстовые задачи.

Здесь вступают в действие ключевые слова. Студенты могут использовать ключевые слова, чтобы идентифицировать что-либо как «часть» или «неизвестное».Однако всегда следует возвращаться к «части» или «целому», поскольку это помогает построить фундаментальное понимание операций. Ключевые слова не должны преподаваться как основа понимания проблемы и не должны представлять собой ряд категорически заученных терминов. Тем не менее, они относятся к части и целому и могут помочь учащимся понять контекст. Подробнее читайте в моем посте «Почему студенты борются со словесными задачами».

Вы можете скачать приведенный выше постер частично, частично, целиком в формате pdf, нажав на него.

ДОПОЛНЕНИЕ ПОЛНОСТЬЮ НЕИЗВЕСТНО

Сложение — это соединение частей, чтобы найти общее или целое. Дети строят это понимание, считая группы объектов вместе, чтобы найти их общее количество. Ключевые слова словесных задач, указывающие на то, что целое неизвестно: во всем, вместе, в совокупности и в сумме. Учащиеся изучают суммы, используя манипуляции, и строят свое понимание сложения, а также своих фактов посредством практических исследований.

Один из моих любимых инструментов для сложения моделей для учащихся — это большая магнитная десятичная рамка от Learning Resources.Поскольку магниты бывают двух цветов, вы можете представить обе части уравнения. Я использую их в качестве моделей во время уроков, но мои ученики также любят использовать их, когда они работают в центрах или играют во время Fun Friday. Десять кадров — это идеальные визуальные модели для «часть-часть-целое», потому что учащиеся могут легко увидеть, что каждый цвет — это отдельная часть.

Вы можете купить их на Amazon, нажав на ссылку здесь или на картинку выше. Я также создал уменьшенные версии для студентов, используя скотч Scotch Expressions, листы для печенья, магниты и цветные точки. Я разделил каждый лист печенья на четыре десятка рамок из-за размера, но одну или две можно было бы легко использовать на них. Каждая сторона магнита представляет собой цветную точку (стороны разные), и я помещаю их в небольшие контейнеры в наборах по 10 штук. Они доступны для использования учащимися во время самостоятельной работы, чтобы помочь им моделировать и решать уравнения, и они могут занять больше времени. чем один контейнер, если они нужны для большего числа.

У меня также есть ресурс цифровых десятков кадров. Он работает через 10 со сложением и вычитанием.Всего 16 видов деятельности. Прибавление к 10, вычитание из 10, пропущенные сложения в пределах 10 и вычитание в пределах 10 действий представлены в 4 разных темах. Вы можете более подробно ознакомиться с моим цифровым сложением и вычитанием из 10 десятков кадров ниже. Вас также может заинтересовать мой пост в блоге с 44 Free Tens Frames Activity.

Учащиеся также могут использовать блоки с основанием 10, чтобы найти способы сложения. Блокирующие кубы также можно легко использовать для отработки того же навыка.Студенты исследуют связанные числа, которые являются «частями», составляющими «целое». У вас может быть заранее определенное количество кубиков, уже разделенных, или пусть учащиеся возьмут несколько кубиков и исследуют числа, которые можно соединить, чтобы получить это число.

ВЫЧИТАНИЕ ЯВЛЯЕТСЯ ЧАСТЬЮ НЕИЗВЕСТНОЙ

Вычитание — это взятие целого и разбиение на части. Это понимание строится так же, как и дополнение — через исследование с группами предметов. Предоставление учащимся группы объектов для разделения на более мелкие части помогает сформировать это понимание. Работа с базовыми десятью кубами или связывающими кубами выше помогает учащимся увидеть, что одно и то же количество объектов может быть разделено на части разных размеров, а также что размеры двух частей обратно пропорциональны. Ключевые слова задачи Word, указывающие на то, что часть неизвестна: осталось, меньше, отнять и минус. Проблемы сравнения — это вычитание, поскольку две части — это известное число и число, которое необходимо добавить, чтобы получить другое число (сумму). Ключевые слова «насколько больше» и «насколько меньше» представляют задачи сравнения.Десять рамок — отличные модели для построения задач на сравнение, поскольку учащиеся видят, сколько еще нужно, чтобы получить общее количество.

Мне нравится использовать разделенные тарелки для работы в режиме часть-часть-целое. Для вычитания я помещаю все манипуляции (M&M’s и Skittles немного хитовые!) в большую часть тарелки, а затем перемещаю заданное количество в одну из меньших частей, чтобы соответствовать уравнению. Вы также можете писать на пластиковых тарелках сухостираемыми маркерами и маркировать «части» и «целое».Тарелки и любые виды счетчиков, которые у вас уже есть под рукой, являются идеальным ресурсом для студентов, поскольку они работают со сложением и вычитанием независимо друг от друга во время центров.

ФАКТ СЕМЬИ СОСТАВЛЯЮТ ЧАСТЬ-ЧАСТЬ-ЦЕЛОЕ

Учебные семьи фактов также должны быть укоренены в части-части-целом. Семейные треугольники фактов помогают учащимся визуально увидеть частичные и целые отношения. При обучении семьям фактов я использую изображение дома, изображенное ниже. Я всегда помещаю уравнения сложения и вычитания, связанные с частью и целым в треугольнике для крыши, чтобы помочь учащимся сосредоточиться на отношениях между ними и помочь им понять факт семейных треугольников.

Щелкните изображение выше, чтобы загрузить плакат в формате pdf.

Когда мы работаем с семействами фактов, мы также используем наши руки, чтобы построить треугольник и помочь добавить кинестетические движения в наше обучение. Мы соединяем руки вместе над головой для целого и вытягиваем руки в каждую сторону для каждой части (как треугольник выше). Кинестетические движения помогают учащимся сохранить знания и дают им простой инструмент, который можно использовать позже, когда это необходимо.

МОДЕЛИ ЧАСТЬ-ЧАСТЬ-ЦЕЛОЕ

Существует множество различных моделей отношений часть-часть-целое.Двумя наиболее распространенными являются стержневые модели и числовые связи. Я считаю, что столбчатые модели наиболее полезны при работе с текстовыми задачами, поскольку учащиеся могут визуально видеть части, относящиеся к целому, и какая часть является неизвестной. Связи чисел, на мой взгляд, более уместны при рассмотрении фактов как суммы и построении понимания числовых отношений и семейств фактов. Десять кадров также являются отличными инструментами, помогающими учащимся визуализировать частичные и целые отношения, особенно когда учащиеся работают с числами до 10.

Я собрал 12 страниц печатных форм, которые вы можете использовать для работы с моделями «часть-часть-целое» со счетчиками, десятью частями, блокирующими кубиками или чем-то еще, что у вас есть в вашем классе.

Есть страницы для числовых связей, десяти фреймов и семейств фактов. Страницы включают в себя практику как для сложения, так и для вычитания. Знак равенства стоит слева от уравнения на некоторых страницах. Две половинчатые страницы также включены для работы в центрах. Все страницы черно-белые, поэтому вы можете распечатать их на цветной бумаге и заламинировать или сразу распечатать и использовать.Вы можете щелкнуть здесь, чтобы загрузить печатные формы «Часть-часть-целое».

ЗАДАЧИ СЛОВА

Понимание учащимися операций сложения, вычитания и части-части-целого проявляется в их понимании текстовых задач. С помощью сюжетных задач учащиеся демонстрируют, что они могут использовать контекст для определения используемой операции и могут применять ее независимо. Именно с помощью текстовых задач мы определяем, могут ли учащиеся по-настоящему понять и распознать отношения часть-часть-целое.Специально для практики часть-часть-целое у меня есть эти цифровые словесные задачи «часть-часть-целое» для 1-го класса. Они практикуют сложение и вычитание в пределах 20 в реальном контексте. Учащиеся читают задачу, строят уравнение и решают, используя встроенные числовые линии и десятки кадров, чтобы смоделировать сценарий.

Вы можете более подробно ознакомиться с моими задачами на часть части целого слова для 1-го класса. Включены 4 разных типа задач: набор для идентификации неизвестного как части или целого; набор для всего неизвестного; набор на неизвестную деталь; и набор для обеих частей неизвестен.

У меня также есть бесплатная версия для добавления 3 чисел. Каждый из этих сценариев представлен в отношениях часть-целое. Набор задач «Добавление 3 чисел» дает вам представление о том, как настроен набор «Часть-Часть-Целое».

В дополнение к отработке конкретных типов задач, когда это является предметом нашего обучения, важно дать студентам возможность попрактиковаться вне этого. Я каждый день решаю задачу-рассказ вне моей учебной программы по математике, чтобы убедиться, что учащиеся сталкиваются с различными типами задач и последовательно отрабатывают навыки в течение года, а не работают с одним навыком за раз.Это помогает учащимся не просто полагаться на «содержание недели» при решении; они действительно должны использовать контекст для решения.

Моя задача дня для 1-го класса состоит из двух задач на странице. Существует два разных формата: последовательные страницы рядом и одна и та же страница дублируется рядом. У моих учеников есть задача с рассказом в ежедневном переплете, поэтому я предпочитаю, чтобы они были у них последовательно. Если вы хотите продублировать их для учащихся, вам может подойти альтернативный формат. В ходе ежедневной работы со словесными задачами учащиеся заполняют таблицы «часть-часть-целое», таблицы «начало-изменение-конец», пишут уравнения, моделируют задачи и записывают свои ответы полными предложениями. Учащиеся строят свое глубокое понимание математических центров 1-го класса посредством ежедневной практики и спирали. Учащиеся работают с различными типами задач и хорошо понимают, что такое часть-часть-целое, а также сложение и вычитание. Вы можете увидеть весь годовой пакет в моем магазине TpT Word Word Problem of the Day для 1-го класса или щелкнув изображение ниже.Пакет разбит на месячные наборы и может быть приобретен отдельно.

Для более подробного ознакомления со всеми форматами задач на сложение и вычитание, в дополнение к задаче «часть-часть-целое», ознакомьтесь с моей записью в блоге «Сценарии задач со словами на сложение и вычитание».

НАЧАТЬ-ИЗМЕНИТЬ-КОНЕЦ С СЛОЖЕНИЕМ И ВЫЧИТАНИЕМ

В дополнение к обучению своих студентов части-части-целому, я также учу начинать-изменять-конец сложением и вычитанием. В реальных сценариях сложение и вычитание — это либо (а иногда и то, и другое) начало-изменение-конец или часть-часть-целое. Я учу и тому, и другому в явном виде со своими 1-м и 2-м классом, и мы говорим о наших текстовых задачах в связи с обоими. Вы можете прочитать о типах проблем start-change-end в этом посте.

УМНОЖЕНИЕ И ДЕЛЕНИЕ С ЧАСТИ-ЧАСТЬ-ЦЕЛОЕ

Будучи учителем третьего класса, когда я знакомлю учащихся с умножением и делением, я связываю их обратно с частью-частью-целым.Мы меняем «часть» на «количество групп» и «количество в каждой группе». Если учащиеся имеют четкое представление о частях и целом, они намного легче понимают отношения умножения и деления, когда они вводятся и связаны обратно с частью и целым. При работе со словесными задачами на умножение и деление основное внимание уделяется тому, неизвестно ли целое, чтобы определить, какая операция используется. Четыре операции могут быть идентифицированы в текстовых задачах, когда учащиеся идентифицируют неизвестную и данную информацию, поскольку они относятся к части-части-целому и группам.

После того, как учащиеся получат четкое представление о сценариях «часть-часть-целое» и «начало-изменение-конец», мы продолжаем развивать их мастерство сложения и вычитания и беглость фактов посредством постоянной игры и практики. Я люблю использовать игры и центры, чтобы развить беглость сложения и вычитания моих учеников, потому что ученики не испытывают стресса, который они испытывают в сценариях с временными интервалами. Они могут использовать манипуляторы, такие как числовые линии и десятки кадров, а также выполнять увлекательную деятельность.Ниже я выделил некоторые из моих любимых ресурсов по практике сложения и вычитания.

У меня есть другие статьи по математике, идеально подходящие для учителей 1-го класса, ссылки на которые приведены ниже. Просто нажмите на изображения, чтобы перейти к сообщениям.

Решение математических задач в классах третьего класса на JSTOR

Абстрактный

Авторы проводили проектные или классные эксперименты (Р. Gersten, S. Baker, & J. W. Lloyd, 2000) в двух местах (Пенсильвания и Флорида) для проверки эффективности обучения на основе схем (SBI) перед проведением формальных экспериментальных исследований. Результаты исследования 1, проведенного в 2 классах для учащихся 3-х классов с низкими способностями и в 1 классе специального образования, показали улучшение среднего балла от предварительного к итоговому тесту по решению текстовых задач и показателям беглости вычислений. Кроме того, восприятие учащимися SBI в соответствии с опросником удовлетворенности стратегией показало, что SBI эффективен в решении текстовых задач.Результаты исследования 2, которое включало неоднородную (высокую, среднюю и низкую успеваемость) выборку учащихся 3-х классов, также выявили улучшение учащихся в решении текстовых задач и показателях беглости вычислений. Однако результаты исследования 2 были не такими положительными, как результаты исследования 1. Уроки, извлеченные из двух исследований, обсуждаются в отношении преподавания и обучения решению математических задач для различных групп учащихся.

Информация о журнале

The Journal of Educational Research — это хорошо известный и уважаемый периодический журнал, который выходит на международную аудиторию педагогов и других лиц, занимающихся передовыми теориями и предложениями.На протяжении 100 лет журнал вносит свой вклад в развитие образовательной практики в начальных и средних школах путем тщательного изучения последних тенденций, изучения новых процедур, оценки традиционных практик и повторения предыдущих исследований. Журнал является бесценным ресурсом для учителей, консультантов, супервайзеров, администраторов, специалистов по планированию учебных программ и исследователей в области образования, поскольку они обдумывают структуру учебных программ завтрашнего дня. В специальных выпусках подробно рассматриваются основные проблемы образования.Тематические темы включают методологию, мотивацию, грамотность и профессиональное развитие.

Информация об издателе

Основываясь на двухвековом опыте, Taylor & Francis быстро выросла за последние два десятилетия и стала ведущим международным академическим издателем. отпечатки Routledge, Carfax, Spon Press, Psychology Press, Martin Dunitz и Taylor & Francis.Тейлор и Фрэнсис полностью привержены публикации и распространению научной информации самого высокого качества, и сегодня это остается основной целью.

Богатые задачи — Часть 1 — Математика для всех

• Ожидание, что учащийся сможет изложить свои идеи и защитить свой подход.
• Возможность для учащихся выбирать из ряда инструментов и стратегий для решения проблемы на основе их собственных сильных сторон в развитии нервной системы.
• Возможность изучить новую математику (математический остаток) в процессе работы над задачей.
• Возможность отработать рутинные навыки для решения сложной проблемы.
• Возможность для учителя углубить свое понимание своих учеников как учеников и построить новые уроки на основе того, что знают ученики, их уровня развития, а также их сильных и слабых сторон в развитии нервной системы.

Почему насыщенные задачи?

Все взрослые нуждаются в математических знаниях для решения задач в повседневной жизни.Большинство взрослых используют калькуляторы и компьютеры для выполнения рутинных вычислений, выходящих за рамки того, что они могут сделать в уме. Однако они должны достаточно понимать математику, чтобы знать, что вводить в машины и как оценивать то, что выходит. Наше личное финансовое положение сильно зависит от нашего понимания схем ценообразования на вещи, которые мы покупаем, ипотечных кредитов, которые мы держим, и сборов, которые мы платим. Как граждане, понимание математики может помочь нам оценивать политику правительства, понимать политические опросы и принимать решения.Строительство и проектирование наших домов, а также масштабирование рецептов для толпы также требуют математики. Особенно сейчас математическое понимание имеет решающее значение для понимания политики, связанной с пандемией. Решения о закрытии, лечении и вакцинах основаны на математике. По всем этим причинам важно, чтобы учащиеся развивали свои способности рассуждать о математике. Исследования показали, что опыт решения сложных задач улучшает математическое мышление детей (Hattie, Fisher, & Frey, 2017).

Где найти расширенные задачи

Несколько типов сложных задач доступны онлайн, готовые к использованию или адаптации. Сайты ниже являются одними из многих мест, где можно найти богатые задачи:

• Какой из них не принадлежит — эти задачи состоят из квадратов, разделенных на 4 квадранта с числами, фигурами или графиками. В каждой задаче есть по крайней мере один способ, которым каждый из квадрантов «не принадлежит». Таким образом, можно утверждать, что любой квадрант отличается от других.
• Задачи «Открытая середина» — это задачи с одним ответом, но с множеством способов получить ответ. Они организованы как по темам, так и по классам.
• NRICH Maths — это многогранный сайт Кембриджского университета в Великобритании. В нем есть как статьи, так и готовые задачи. На сайте представлены задачи для 1–5 классов (листайте до раздела «Сборники») и задачи для детей младшего возраста. Мы также рекомендуем вам более полно изучить NRICH. На сайте много познавательных статей и обсуждений.
• Расширенные задачи из Вирджинии — это задачи, опубликованные Департаментом образования Вирджинии. Они поставляются с полными планами уроков, а также примерами ожидаемых ответов учащихся.
• Расширенные задания из Джорджии. Этот сайт содержит полную систему заданий, разработанных для соответствия всем стандартам для всех классов. Они включают в себя задачи 3-Act, задачи YouCubed и многие другие задачи с открытым концом или подходом с открытой серединой.

Задачи можно использовать «как есть» или адаптировать к конкретным сильным сторонам развития нервной системы и проблемам ваших учащихся.Тщательно адаптированные, они могут вовлечь ВСЕХ ваших учеников в размышления о математических идеях различными способами, тем самым не только улучшая их навыки, но и их способности мыслить гибко и глубоко.