▶▷▶▷ схемы к задачам по математике 2 класс петерсон на умножение
▶▷▶▷ схемы к задачам по математике 2 класс петерсон на умножение
| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 21-03-2019 |
схемы к задачам по математике 2 класс петерсон на умножение — Yahoo Search Results Yahoo Web Search Sign in Mail Go to Mail» data-nosubject=»[No Subject]» data-timestamp=’short’ Help Account Info Yahoo Home Settings Home News Mail Finance Tumblr Weather Sports Messenger Settings Want more to discover? Make Yahoo Your Home Page See breaking news more every time you open your browser Add it now No Thanks Yahoo Search query Web Images Video News Local Answers Shopping Recipes Sports Finance Dictionary More Anytime Past day Past week Past month Anytime Get beautiful photos on every new browser window Download Самоучка — Задачи на умножение и деление Интерактивные samouchkacomua/_matematika_peterson/13 Cached На этой странице помещены 24 простые задачи на умножение и деление к курсу математики по ЛГ Петерсон Ученики учатся выбирать действие умножения или деления для решения задачи Задачи по математике для 2 класса, Моро, России, Петерсон mathematics-testscom/zadachi-i-zadaniya-po Cached Задачи для 2 класса по математике к учебникам Моро, Петерсон , –» Умножение на числа 2 и 3″ Математика, 1-4 класс, В схемах и таблицах, Марченко ИС, 2011 nasholcom … Книги по математике Пособие окажет неоценимую помощь в учебе, систематизируя полученные знания, а также будет полезным при подготовке к итоговому тестированию по математике за курс начальной школы Простые задачи 2 класс на умножение и деление | Школа XXI век irina-secom/prostye-zadachi- 2 -klass Cached Простые задачи 2 класс Простые задачи на УМНОЖЕНИЕ и Простые задачи по математике на Готовое домашнее задание ГДЗ по математике 2 класс Петерсон Л Г ne-hochuru/gotovoe-domashnee-zadanie-gdz-po-matematike Cached Скачать ГДЗ на НЕ ХОЧУ ру, ответы, решения и готовые домашние задания по математике , 2 класс Петерсон Л Г, 1 часть, 2 часть, 3 часть Схемамы к задачам 2 класс — exeltano’s blog tabsorighhatenablogcom/entry/2017/05/26/231958 Cached схемы к задачам по математике 3 класс составление схем к задачам 2 класс как правильно записать условия задачи по математике 2 класс решение задач с помощью схемы 3 класс Самостоятельные для 3 класса по Моро по математике mathematics-testscom/matematika-3-klass-new/z Cached В каждый класс поставили по 4 стола В скольких классах поставили новые столы? Самостоятельная работа №5 «Текстовые задачи и примеры на умножение и деление чисел» 1 Реши примеры Задачи для 3 класса по математике: занимательные текстовые logiclikecom/math-logic/3-klass Cached Задачи для 3 класса по математике : занимательные задания, примеры, тесты Интересные задания и примеры на умножение и деление, текстовые задачи на логику, наглядная геометрия… Схемы-опоры краткой записи задач к урокам математики по easyenru/load/m/1_klass/skhemy_opory_kratkoj Cached Содержит раздаточный материал формата А4 в двух листах Первый лист содержит с 1 по 14 схемы краткой записи задач с решением в 1 действие и используется как памятка на уроках математики в 1- 2 классах Презентация к уроку по математике (2 класс) по теме: Задачи nsportalru/nachalnaya-shkola/matematika/2013/10/ Cached Презентация к уроку по математике ( 2 класс ) по теме: Задачи на кратное сравнение Презентация к уроку математики по учебнику Л Г Петерсон Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 1,960 results Settings Help Suggestions Privacy (Updated) Terms (Updated) Advertise About ads About this page Powered by Bing™
- Составить и выучить таблицу деления на 2.
( Отв.: При делении 6 на 2 получается число 3, которое при - умножении на 2 даёт число 6)
Древние единицы измерения: А. 2. Презентация: Уравнения 2 класс, Урок: Математика, Класс: 2. «Школа 2100» Тренажер по математике, 2 класс Тема: Решение уравнений.
Физик - : Математика, Класс: 2. «Школа 2100» Тренажер по математике, 2 класс Тема: Решение уравнений.
Физико-математический лицей № 239. Об учебной жизни лицея, условия поступления, задачи вступительных олимпиад. Лекции по математике.
Вторая Санкт-Петербургская гимназия. История, учебный процесс, коллектив, лаборатория. Математика 2 класс.
Похожие на quot;Математика. Взяли на лето между 2 и 3 классом. Задачи на пропорциональное деление. Учим таблицу умножения 2 рец.
Интегрированный урок познания мира и трудового обучения направлен на развитие познавательной активности и творческих способностей учащихся 2 класса с задержкой психического развития, на лучшее понимание учебного материала.
Данная презентация разработана для учащихся 2-го класса при изучении темы quot;Безударные гласные в корне слова.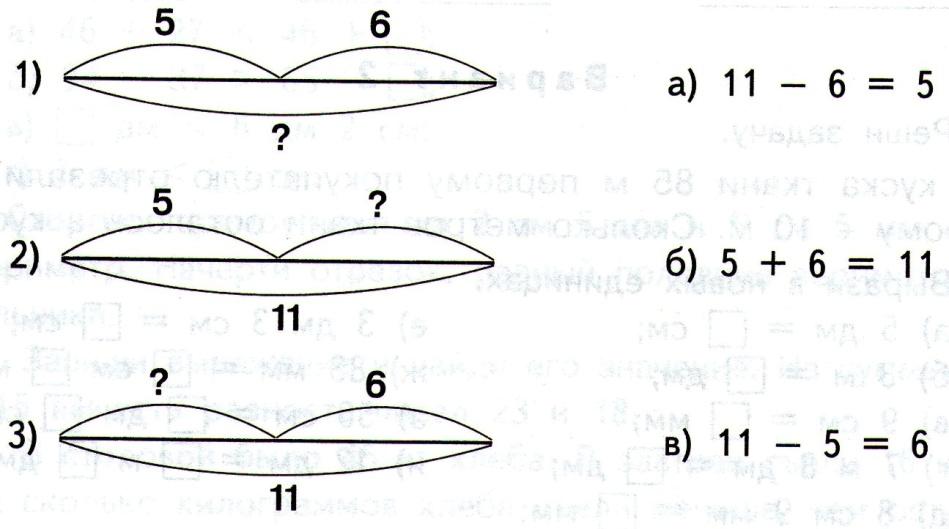 quot;С её помощью дети легко выходят на тему урока,повторяют основные понятия темы quot;кореньquot;,quot;однокоренные словаquot;,наблюдают за гласной в корне слова и выводят алгоритм проверки безударных гласных….
Перечень направлений выпускаемой литературы: педагогические журналы, книги по и педагогике, учебные пособия, справочные издания. Каталог продукции, прайс-лист.
( Отв.: При делении 6 на 2 получается число 3, которое при
quot;С её помощью дети легко выходят на тему урока,повторяют основные понятия темы quot;кореньquot;,quot;однокоренные словаquot;,наблюдают за гласной в корне слова и выводят алгоритм проверки безударных гласных….
справочные издания. Каталог продукции
- smarter
- 2 часть
- примеры
Составить и выучить таблицу деления на 2. ( Отв.: При делении 6 на 2 получается число 3, которое при умножении на 2 даёт число 6)
Древние единицы измерения: А. 2. Презентация: Уравнения 2 класс, Урок: Математика, Класс: 2. «Школа 2100» Тренажер по математике, 2 класс Тема: Решение уравнений.
Физико-математический лицей № 239. Об учебной жизни лицея, условия поступления, задачи вступительных олимпиад. Лекции по математике.
Вторая Санкт-Петербургская гимназия. История, учебный процесс, коллектив, лаборатория.
Математика 2 класс.
Похожие на quot;Математика. Взяли на лето между 2 и 3 классом. Задачи на пропорциональное деление. Учим таблицу умножения 2 рец.
Интегрированный урок познания мира и трудового обучения направлен на развитие познавательной активности и творческих способностей учащихся 2 класса с задержкой психического развития, на лучшее понимание учебного материала.
Данная презентация разработана для учащихся 2-го класса при изучении темы quot;Безударные гласные в корне слова.quot;С её помощью дети легко выходят на тему урока,повторяют основные понятия темы quot;кореньquot;,quot;однокоренные словаquot;,наблюдают за гласной в корне слова и выводят алгоритм проверки безударных гласных….
Перечень направлений выпускаемой литературы: педагогические журналы, книги по и педагогике, учебные пособия, справочные издания. Каталог продукции, прайс-лист.
ГДЗ по математике 2 класс учебник Петерсон 1 часть
- Тип: ГДЗ, Решебник.
- Автор: Л. Г. Петерсон.
- Год: 2021.
- Серия: Учись Учиться.
- Издательство: Просвещение/Бином.
Петерсон.
Подготовили готовое домашнее задание к упражнениям на 67
странице по предмету математика за 2 класс. Ответы на задания: 7, 8, 9, 10, 11 и 12.
Учебник 1 часть — Страница 67.
Ответы 2021 года.
Номер 7.
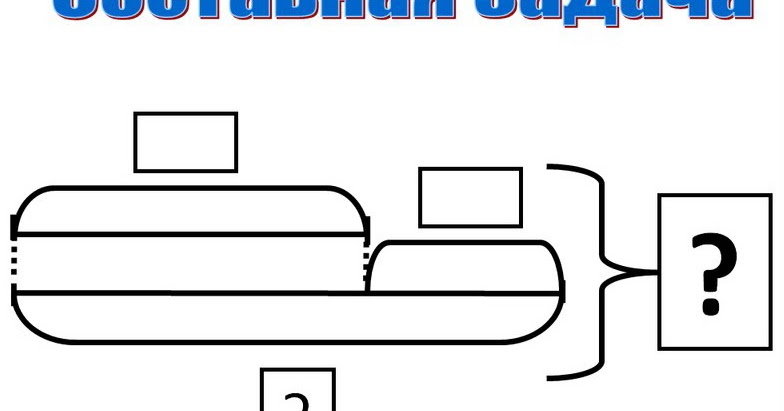
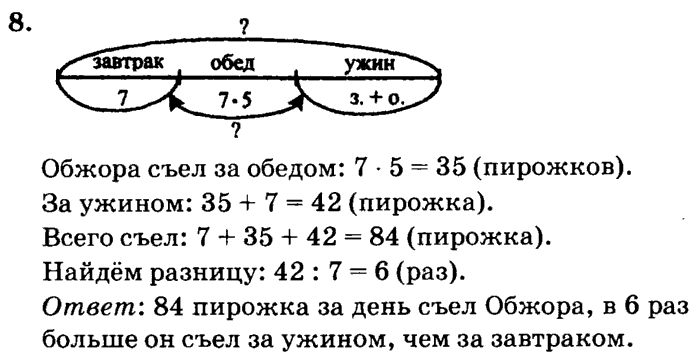
Задача-ловушка
Во 2 «А» классе 25 учеников, а во 2 «Б» – 24 ученика. Сколько учеников во 2 «В»?
Ответ:
На вопрос ответить нельзя – нет данных в условии.
Номер 8.
а) На чемпионате школы по футболу Ваня забил 5 голов, Саша – на 2 гола меньше, чем Ваня, а Дима забил столько голов, сколько Ваня и Саша вместе. Сколько голов забили на чемпионате школы все три мальчика?
б) Придумай и реши аналогичную задачу.
Ответ:
– Чтобы узнать, сколько голов забили на чемпионате школы все три мальчика, надо сложить количество голов, которые забил каждый из них.
(Ищем целое.) Сразу мы не можем ответить на вопрос задачи, так как не известно, сколько голов забили Саша и Дима. Но мы можем это найти. По условию, Саша забил на 2 гола меньше, чем Ваня, то есть 5 – 2. (Ищем меньшее число по большему и разности.) Чтобы узнать, сколько голов забил Дима, надо сложить количества голов, которые забили Саша и Ваня. (Ищем целое.)
1) 5 – 2 = 3 (г.) – забил Саша;
2) 5 + 3 = 8 (г.) – забил Дима;
3) 8 + 8 = 16 (г.)
Ответ: все три мальчика забили вместе 16 голов.
На клумбе росло 5 тюльпанов, пионов – на 2 меньше, чем тюльпанов, а нарциссов столько, сколько тюльпанов и пионов вместе. Сколько цветов росло на клумбе?»
Так как схемы у задач одинаковые, то и решения, и ответы будут также одинаковыми. Значит, в решении поменяются только наименования, а ответ будет – 16 цветов.
Номер 9.
По клеточкам нарисуй в тетради фигуры, равные данным.
Ответ:
Номер 10.
Двое друзей, чтобы ехать вместе, договорились сесть в пятый вагон поезда.
Но один сел в пятый вагон этого поезда с конца, а другой – в пятый вагон с начала. Сколько должно быть всего в этом поезде вагонов, чтобы друзья действительно оказались в одном вагоне?
Ответ:
Номер 11.
Врач назначил больному три укола, по одному через каждый час. За какое время будут сделаны все уколы?
Ответ:
Все уколы будут сделаны за 2 часа.
Номер 12.
Построй замкнутую ломаную линию, состоящую из трёх звеньев и проходящую через 4 данные точки.
Ответ:
Приведем несколько возможных вариантов решения:
Номер 13.
Какое из следующих слов лишнее:
РОДНИК РЕКА РУЧЕЙ РЕДИСКА ВОДОПАД
Ответ:
Возможно несколько решений:
1) ВОДОПАД – начинается с буквы «В», а не с «Р».
2) РИСУНОК – не является природной водой.
3) РЕДИСКА – никакого отношения к воде не имеет.
Номер 14.
Найди закономерность и продолжи ряд.
Ответ:
Рейтинг
← Выбрать другую страницу ←
Иллюстративная математика
Иллюстративная математика
Класс
2
2 класс
- Карандаш и наклейка
- Экономия денег 2
- Стремление к беглости
- Удар по целевому номеру
- Запоздалое признание
- Кнопки нечетные и четные
- Красные и синие плитки
- Подсчет точек в массивах
- Разбиение прямоугольника на единичные квадраты
2.
ОА. 2 класс — Операции и алгебраическое мышление
2.ОА.А. Представлять и решать задачи на сложение и вычитание.
2.ОА.А.1. Используйте сложение и вычитание в пределах 100 для решения одно- и двухшаговых задач со словами, включающих ситуации сложения, взятия, сложения, разъединения и сравнения с неизвестными во всех позициях, например, с помощью рисунков и уравнений с символом для неизвестного числа, представляющего проблему. См. Глоссарий, Таблица 1.
2.ОА.Б. Сложите и вычтите в пределах 20.
2.ОА.Б.2. Свободно складывать и вычитать в пределах 20, используя умственные стратегии. Список умственных стратегий см. в стандарте 1.OA.6. К концу 2 класса знать наизусть все суммы двух однозначных чисел.
2.ОА.С. Работайте с равными группами объектов, чтобы получить основу для умножения.
2.ОА.С.3. Определите, имеет ли группа объектов (до 20) нечетное или четное количество членов, например, путем объединения объектов в пары или подсчета их по 2; Напишите уравнение, выражающее четное число в виде суммы двух равных слагаемых.
2.ОА.С.4. Используйте сложение, чтобы найти общее количество объектов, расположенных в прямоугольных массивах до 5 строк и до 5 столбцов; напишите уравнение, выражающее сумму в виде суммы равных слагаемых.
- Коробки и коробки карандашей
- Объединение и разделение
- Подсчет марок
- Игра с наибольшим числом
- Глядя на числа в любом направлении
- Изготовление 124
- Один, десять и сто больше и меньше
- Перегруппировка
- Десять 10 долларов составляют 100 долларов.
- Три задачи на композицию/декомпозицию
-
Пока нет задач, иллюстрирующих этот стандарт.
- Экономия денег 2
- Глядя на числа в любом направлении
- Сравнения 1
- Сравнения 2
- Цифры 2-5-7
- Сравнение числовых строк
- Заказ 3-значных номеров
- Использование изображений для объяснения сравнения чисел
- Форд и Логан Добавляют 45+36
- Банка пенни Джамира
- Экономия денег 1
- Экономия денег 2
- Головоломка с платным мостом
- Сколько дней до летних каникул?
- Много способов сделать дополнение 2
- Пейтон и Пресли обсуждают дополнение
- Хоровой счет
- Пейтон и Пресли обсуждают дополнение
2.НБТ. 2 класс — Числа и операции с основанием десять
2.НБТ.А. Поймите значение места.
2.НБТ.А.1. Поймите, что три цифры трехзначного числа представляют количество сотен, десятков и единиц; например, 706 равно 7 сотням, 0 десяткам и 6 единицам.
Под особыми случаями следует понимать следующее:
2.НБТ.А.1.б. Числа 100, 200, 300, 400, 500, 600, 700, 800, 900 относятся к одной, двум, трем, четырем, пяти, шести, семи, восьми или девяти сотням (и 0 десяткам и 0 единицам).
2.НБТ.А.2. Считать в пределах 1000; пропуск счета на 5, 10 и 100 секунд.
2.НБТ.А.3. Читать и записывать числа до 1000, используя десятичные числа, имена чисел и расширенную форму.
2.НБТ.А.4. Сравните два трехзначных числа на основе значений цифр сотен, десятков и единиц, используя символы $>$, = и $
<$ для записи результатов сравнения.
2.НБТ.Б. Используйте понимание значения разряда и свойства операций сложения и вычитания.
2.НБТ.Б.5. Свободно складывать и вычитать в пределах 100, используя стратегии, основанные на разрядности, свойствах операций и/или отношениях между сложением и вычитанием.
2.НБТ.Б.6. Сложите до четырех двузначных чисел, используя стратегии, основанные на разрядности и свойствах операций.
2.НБТ.Б.7. Складывать и вычитать в пределах 1000, используя конкретные модели или чертежи и стратегии, основанные на позиционном значении, свойствах операций и/или отношениях между сложением и вычитанием; связать стратегию с письменным методом. Поймите, что при сложении или вычитании трехзначных чисел прибавляются или вычитаются сотни и сотни, десятки и десятки, единицы и единицы; а иногда надо составить или разложить десятки или сотни.
2.НБТ.Б.8. Мысленно прибавьте 10 или 100 к заданному числу 100–900 и мысленно вычтите 10 или 100 из заданного числа 100–900.
2.НБТ.Б.9. Объясните, почему стратегии сложения и вычитания работают, используя позиционное значение и свойства операций.
Объяснения могут быть подкреплены рисунками или предметами.
- Насколько велик фут?
- Определение длины
-
Пока нет задач, иллюстрирующих этот стандарт.
- Определение длины
- Определение длины
- Соревнования по прыжкам в высоту
- Лягушка и жаба на числовой прямой
- Запоздалое признание
- Время заказа
- Александр, который был богат в прошлое воскресенье
- Выбор, выбор, выбор
- Банка пенни Джамира
- Зоомагазин
- Экономия денег 1
- Выбор Сьюзен
- Посещение Аркады
- Выращивание бобовых растений
- Измерения размаха рук
- Самая длинная прогулка
- Любимый вкус мороженого
2.МД. 2 класс — Измерения и данные
2.МД.А. Измерьте и оцените длину в стандартных единицах.
2.МД.А.1. Измерьте длину объекта, выбрав и используя соответствующие инструменты, такие как линейки, линейки, измерительные рейки и измерительные ленты.
2.МД.А.2. Дважды измерьте длину объекта, используя для двух измерений единицы длины разной длины; опишите, как два измерения соотносятся с размером выбранной единицы измерения.
2.МД.А.3. Оцените длину, используя единицы измерения: дюймы, футы, сантиметры и метры.
2.МД.А.4.
Измерьте, чтобы определить, насколько длиннее один объект, чем другой, выражая разницу в длине с точки зрения стандартной единицы длины.
2.МД.Б. Свяжите сложение и вычитание с длиной.
2.МД.Б.5. Используйте сложение и вычитание в пределах 100 для решения текстовых задач с длинами, заданными в одних и тех же единицах, например, с помощью рисунков (например, рисунков линеек) и уравнений с символом неизвестного числа для представления задачи.
2.МД.Б.6. Представляйте целые числа как длины от 0 на диаграмме числовых линий с равноотстоящими точками, соответствующими числам 0, 1, 2, …, и представляйте суммы и разности целых чисел в пределах 100 на диаграмме числовых линий.
2.МД.К. Работа со временем и деньгами.
2.
MD.C.7. Говорите и записывайте время по аналоговым и цифровым часам с точностью до ближайших пяти минут, используя время до и после полудня.
2.MD.C.8. Решайте словесные задачи с участием долларовых банкнот, четвертаков, десятицентовиков, пятицентовых монет и пенни, используя соответствующие символы \$ и $¢$. Пример: Если у вас есть 2 цента и 3 пенни, сколько у вас центов?
2.МД.Д. Представлять и интерпретировать данные.
2.МД.Д.9. Генерируйте данные измерений, измеряя длину нескольких объектов с точностью до целой единицы или выполняя повторные измерения одного и того же объекта. Покажите измерения, построив линейный график, где горизонтальная шкала отмечена в целых числах.
2.МД.Д.10. Нарисуйте графическое изображение и столбчатую диаграмму (с единичной шкалой), чтобы представить набор данных с четырьмя категориями. Решайте простые задачи на сборку, разборку и сравнение См. Глоссарий, Таблицу 1, используя информацию, представленную в виде гистограммы.
- Полигоны
- Разбиение прямоугольника на единичные квадраты
- Представление половины прямоугольника
- Какие картинки представляют одну половину?
2.Г. 2 класс — Геометрия
2.Г.А. Рассуждайте о формах и их атрибутах.
2.Г.А.1. Распознавать и рисовать фигуры с заданными атрибутами, такими как заданное количество углов или заданное количество равных граней. Размеры сравниваются непосредственно или визуально, а не путем измерения. Определите треугольники, четырехугольники, пятиугольники, шестиугольники и кубы.
2.Г.А.2. Разделите прямоугольник на строки и столбцы квадратов одинакового размера и посчитайте, чтобы найти их общее количество.
2.Г.А.3. Разделите круги и прямоугольники на две, три или четыре равные доли, опишите доли, используя слова
половин , третей , половину , треть и т. д., и опишите целое как две половины, три трети, четыре четверти. Признайте, что равные части одинаковых целых не обязательно должны иметь одинаковую форму.
По данным Национального центра образовательной статистики (2018 г.), около 59% детей в возрасте от трех до пяти лет, охваченных дошкольными программами, принадлежат к разным культурным и/или языковым группам, и ожидается, что этот процент будет расти в ближайшие несколько лет. Культурно-поддерживающая практика — это педагогическая педагогика, которая сосредоточена на соединении опыта учащихся в классе с их домом, культурой и языком (Gay, 2000; Howard, 2003; Ladson-Billings, 2014; Paris, 2012). Ладсон-Биллингс (2014) утверждает, что эта практика способствует «интеллектуальному росту» учащихся, помогает учащимся «прославлять свою собственную культуру, приобретая знания и свободное владение какой-либо другой культурой» и помогает учащимся понимать, распознавать, «анализировать и решать реальные проблемы». мировые проблемы» (с. 75). Пэрис (2012) утверждает, что эти практики должны быть не только актуальными для жизни и опыта учащихся, но также должны поддерживаться во времени, что позволит разнообразить всех учащихся, включая все языки, культуры и индивидуальные различия. Из-за большого количества контента и учебных программ, ориентированных на навыки, учителя часто имеют ограниченное время для включения дополнительных проектов для учащихся. Лучший способ интеграции — это начать с очень малого и задач, основанных на жизненном опыте учащихся, резонирующих с культурой и сообществом учащихся (Gutstein & Peterson, 2013). Выбор контекста в задаче должен быть таким, чтобы он был значим для учащихся и чтобы они чувствовали себя включенными в процесс обучения. Аллекссахт-Снайдер и Харт (2001) отмечают, что чувство включенности или принадлежности имеет решающее значение в изучении математики, поскольку оно способствует уверенности учащихся в себе и мотивации к изучению математики. Не менее важно, чтобы учителя создавали задания, чтобы познакомить детей с мировым обществом, разными культурами и языками; такая практика способствует развитию у детей культурных и глобальных компетенций (Durden et al., 2015). Дерден и др. (2015) предполагают, что учителя могут использовать такие ресурсы, как книги, семейные фотографии и т. д., чтобы вовлекать детей в изучение различных обществ по всему миру с самого раннего возраста. Полезность использования контекстов в учебной программе по математике хорошо изучена (Meyer et al., 2001; Peterson, 2012; Tate, 2013). Наиболее успешными контекстами являются те, которые основаны на домашней культуре учащихся и родном языке. Нет никаких сомнений в пользе контекстных задач при тщательном их выполнении. Однако это требует серьезного рассмотрения учителями, которые планируют использовать контексты в своих классах. Салливан, Зевенберген и Моусли (2003) утверждают, что, во-первых, учителя должны знать своих учеников; затем им нужно проверить математическую пригодность контекста, релевантность и значимость контекста для учащихся; и, наконец, они должны знать о положительных и отрицательных последствиях для учащихся, если таковые имеются. К негативным последствиям часто относится исключение определенных групп учащихся из математического обучения. Тейт (2013) отмечает, что большая часть школьного опыта в американских школах сосредоточена на истории и взглядах белых. Это ставит студентов из других культурных слоев в невыгодное положение. Тейт обсуждает один случай в классе второго класса, когда ученик-учитель использовал контекст, который был препятствием для изучения математики для афроамериканского ребенка. Учитель использовал тыквенный пирог на День Благодарения, чтобы решить задачу «часть-часть-целое». Учитель задал следующую задачу: «У Джо пять тыквенных пирогов. У Карен шесть тыквенных пирогов. Сколько тыквенных пирогов у Карен и Джо вместе?» (стр. 46). Из пяти учеников четверо белых были в восторге от процесса решения задач; один афроамериканец молчал. У учителя сложилось впечатление, что афроамериканскому ребенку не нравилась математика. Позже, после того как исследователь попросил учителя спросить детей, ели ли они тыквенный пирог в День Благодарения, они обнаружили, что тыквенный пирог действительно был десертом для белых детей, но не для афроамериканцев. Подводя итог, можно сказать, что контексты полезны при изучении математики, и их следует использовать в качестве вспомогательного средства, помогающего учащимся изучать математику. Тем не менее, учителя должны иметь четкую «цель» и хорошо продуманные «последствия» использования контекстов, а также должны иметь несколько способов сделать контекст «ясным и явным» для учащихся (Sullivan et al., 2003, стр. 111). Учителя должны предпринять соответствующие шаги не только для того, чтобы сделать математику актуальной, интересной и увлекательной для учащихся, но и не исключать некоторых учащихся, которые уже оказались в процессе маргинализации. Учителя должны выбрать контекст, который подходит как для математического содержания, так и для опыта всех учащихся.  | |
Следовательно, сейчас как никогда важно, чтобы учителя обладали знаниями и навыками для поддержки учащихся из разных культур. Это требует от учителей внедрения методов преподавания и учебных программ, которые «культурно чувствительны» и соответствуют опыту учащихся (Durden, Escalante, & Blitch, 2015, стр. 223).
Чтобы создать такую практику в классе, учителя должны иметь намерение поддерживать учащихся как из доминирующих, так и из маргинализированных групп (Бобёф-ЛаФонтан, 19).99, как указано в Durden et al., 2015). Поскольку действия определяются убеждениями, очень важно, чтобы учителя твердо верили в то, что эти виды практики важны для качественного обучения учащихся, принадлежащих к разным культурам (Gay, 2000; Ladson-Billings, 2014; Paris, 2012).
Они также обсудили, как чувство принадлежности связано с участием учащихся в классе и насколько оно может быть связано с культурой и языком, используемым в классе. Учащиеся, скорее всего, будут вовлечены в работу в классе, если они знакомы с контекстом заданий, которые им предлагаются. Это также укрепит их чувство принадлежности к математическому сообществу. Следовательно, преподаватели должны знать о культурной принадлежности детей, но также должны находить способы поддерживать обучение детей тем, что каждый ученик привносит в класс (Smith, Gilmore, Goldman, & McDermott, 19).93).
При тщательном рассмотрении и обдумывании контекстуальные задачи и культурно-устойчивые методы обучения могут способствовать интеллектуальному росту детей и пониманию глобального общества.
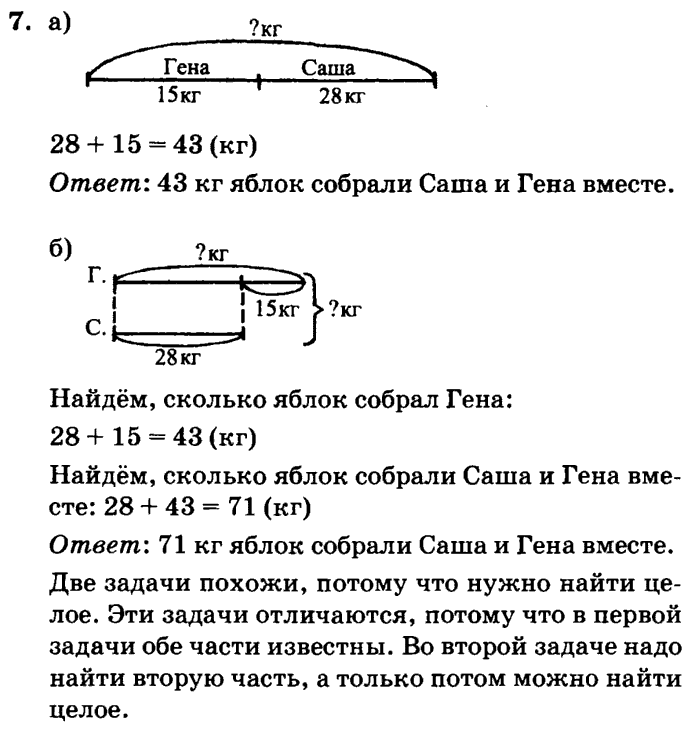
Таким образом, контекст «Тыквенный пирог на День Благодарения» был совершенно неактуален для ребенка, который не испытал этого дома. тем ученикам ей не удалось связаться со студентом, чей опыт не соответствовал контексту Это говорит о том, что выбор математических задач может привести к разным результатам, если не выбирать их тщательно9.0003