|
1) Обведи кружком числа, в которых десятков больше, чем единиц, на 2. 97, 20, 68, 53, 79, 97, 42, 13, 31. 2) Заполни пропуски, чтобы в ответах получилось 10. 92 – … = 10 34 + 6 – … = 10 1 + 5 + 16 – … = 10 3) Реши примеры. (94 + 4) – (45 + 45)= 57 – (90 – 83)= (44 + 44) – (90 – 2)= 4) Вставь пропущенные числа: 1.__ , 23, 28, 33,__ , 43,__ , 53 2. 99, 90,__ , 72, 63,__ , 3. 3, 6, 10, 13,__ , 20,__ , 31 5) Реши задачу. Мама испекла 24 пирожка. После обеда осталось столько же пирожков, сколько съели. Сколько пирожков съели? ________________________________________ 6) Найди вычитаемое. 40 – = 20 90 – = 45 60 – = 30 30 – = 15 80 – = 40 50 – = 25 70 – = 35 100 – = 50 7) Реши задачу. В гараже 17 легковых машин, а грузовых на 3 меньше. Сколько всего машин в гараже? _________________________________________ 8) Начерти ломаную из трёх звеньев так, чтобы первое звено было на 1 см короче второго, а третье на 2 см длиннее первого. 9) Вычисли только разности. 100 – 25= 45 – 36= 100 – 54= 28 + 56= 45 – 5 – 23= 48 + 12= 45 + 45= 49 + 13 – 35= 10) Запиши цифрами числа. семь десятков и три единицы____________ четыре десятка и ноль единиц____________ десять десятков_________ восемь десятков и шесть единиц_______ девять десятков и одна единица_________ 11) Найди периметр квадрата со стороной 3 см _________________________________________ |
1) Вычисли +46 -92 +73 -56 +28 27 44 29 19 28 2) Поставь знак (+) или (–) и скобки, чтобы равенства стали верными. 23 … 6 …5 = 12 48 … 12 … 36 = 0 65 … 50 … 15 = 100 72 … 7 … 65 = 0 56 … 9 … 29 = 46 29 … 19 … 1 = 9
3) Вставь пропущенные числа.
4) Вставь пропущенные числа.
5) Запиши и реши. а) К сумме чисел 34 и 5 прибавить 8 _____________________________________________ б) Из числа 56 вычесть разность чисел 45 и 9 _____________________________________________ в) К 67 прибавить разность чисел 67 и 67 _____________________________________________ 6) Реши задачу. На речке купались 7 ребят, а на озере на 4 больше. Сколько всего ребят купалось на озере и на речке? ______________________________________________ 7) Реши задачу. На фабрике игрушек за 1 день изготовили 15 кукол, машинок на 7 больше, а погремушек столько, сколько кукол и машинок вместе. Сколько изготовили погремушек? _____________________________________________ 8) Вычисли +36 -58 +64 -80 + 54 27 23 28 29 36
9) Продолжи ряд чисел. 97, 89,__ , 73,__ ,__ , 49,__ ,__ ,__ ,17,__ ,1 10) Найди периметр прямоугольника со сторонами 7 и 4 см. _______________________________________________ 11) Сравни 12) Вырази 9дм 4 см … 92 см 67см = …дм…см 32 см… 3 дм 8 дм = … см 46 см…6дм 4см 79см = …дм…см 90 см …9дм 105 см = …дм…см |
Тесты онлайн по математике для 2 класса
Здесь выложены онлайн тесты по математике за 2 класс на тему «Математические задачи, Сложение и вычитание до 100, и Умножение и деление» и другие. Тесты составлены с учетом школьной программы по математике для 2 класса на основе того, что должен знать и уметь ребенок в этом возрасте. А именно:
Математические задачи для 2 класса. Задачи на нахождение неизвестного слагаемого, неизвестного уменьшаемого и неизвестного вычитаемого. Решение задач в 2 действия на сложение и вычитание. Решение задач в одно действие на умножение и деление (с числами 2 и 3 из таблицы умножения). Порядок выполнения действий в выражениях, содержащих 2-3 действия (со скобками и без них). При этом, кроме простых выражений из программы 1 класса, в этих задачах используются новые (более сложные) выражения: прибавление одноцифрового числа к двухцифровому (45+7), отнимание одноцифрового числа от двухцифрового (45-7), прибавление и отнимание двухцифровых чисел (45+27, 45-27). Также в этих задачах используются меры длины (миллиметры, сантиметры, дециметры, метры), разменная монета (рубли, копейки), единицы измерения веса (киллограмм, центнер), единицы измерения ёмкости (литр).
Сложение и вычитание до 100 для 2 класса. Новая счетная единица – десяток.. Счет десятками. Образование и названия чисел, их десятичный состав. Запись и чтение чисел. Числа однозначные и двузначные. Порядок следования чисел при счете. Сравнение чисел. Единицы длины: сантиметр, дециметр, миллиметр, метр. Соотношения между ними. Единицы времени: час, минута. Соотношение между ними. Определение времени по часам с точностью до минуты. Монеты (набор и размен). Задачи на нахождение неизвестного слагаемого, неизвестного уменьшаемого и неизвестного вычитаемого. Решение задач в 2 действия на сложение и вычитание. Устные и письменные приемы сложения и вычитания чисел в пределах 100. Числовое выражение и его значение. Порядок действий в выражениях, содержащих 2 действия (со скобками и без них). Сочетательное свойство сложения. Использование переместительного и сочетательного свойств сложения для рационализации вычислений.
Умножение и деление для 2 класса. Конкретный смысл и названия действий умножения и деления. Знаки умножения • (точка) и деления : (две точки). (В тестах знак умножения заменяется на «х»). Названия компонентов и результата умножения (деления), их использование при чтении и записи выражений. Переместительное свойство умножения. Взаимосвязи между компонентами и результатом действия умножения; их использование при рассмотрении деления с числом 10 и при составлении таблиц умножения и деления с числами 2, 3. Порядок выполнения действий в выражениях, содержащих 2-3 действия (со скобками и без них). Периметр прямоугольника (квадрата). Решение задач в одно действие на умножение и деление.
Дальше вы можете пройти по порядку (или вразброс) тесты по математике за 2 класс. Желаем успехов!
Тесты
В этом тесте тебе нужно решить 10 математических задач на нахождение суммы для 2 класса.
В этом тесте тебе нужно решить 10 математических задач на нахождение суммы для 2 класса.
В этом тесте тебе нужно решить 10 математических з
Олимпиада по математике 2 класс, уравнения, задачи и загадки с ответами
Проводя в своем образовательном учреждении дистанционную олимпиаду, вы сможете привить ученикам 2-го класса любовь и познавательный интерес к изучению математики. Задания для проведения олимпиады во втором классе должны быть не слишком сложны и вместе с этим достаточно разнообразными и интересными. Именно поэтому в составлении заданий стоит довериться профессионалам, работающим в этом направлении.
На этой странице представлены примеры олимпиадных заданий с готовыми ответами. Этот материал может быть использован учителями в качестве тренажера для подготовки учеников к олимпиаде.
Скачайте задания, заполнив форму!
После того как укажете данные, кнопка скачивания станет активной
Уравнения для 2-го класса
1. Решите уравнения:
45 – х = 25
х + 7 = 17
28 – х = 13
2. Решите уравнения:
22 + x = 28
x – 12 = 13
х – 15 = 15
3. Решите уравнения:
13 + х = 20
x – 16 = 13
x – 6 = 10
4. Определите уравнение, решение которого равно 7
a) 19 — х = 10
b) х + 5 = 12
c) x — 5 = 2
5. Решите уравнения:
70 — x = 38
x + 37 = 49
x — 35 = 59
6. Найдите решение уравнений:
22 + x = 48
100 — x = 67
7. Решите предложенные уравнения
x + 25 = 49
x — 23 = 45
x + 13 = 37
8. Найдите решения данных уравнений
x — 18 = 34
x + 36 = 65
9. Решите уравнения
12 + x = 25
x – 18 = 30
х – 18 = 18
10. Верно ли решено уравнение
99 — 18 = x + 59
x = 22
Задачи для олимпиад в 2 классе
Задача №1
В бочке 26 ведер воды. Из нее забрали 17 ведер. Сколько необходимо ведер воды долить, чтобы в бочке стало 30 ведер воды?
Задача №2
Начало сказки «Снежная королева» на 20 странице, а конец – на 50. Сколько страниц нужно прочитать?
Задача №3
Катя, Галя и Оля, играя, спрятали по игрушке. Они играли с медвежонком, зайчиком и слоником. Известно, что Катя не прятала зайчика, а Оля не прятала ни зайчика, ни медвежонка. У кого какая игрушка?
Задача №4
В поезде 22 вагона. Класс расположился в 11 вагоне. Сколько вагонов перед ними и сколько за ними?
Задача №5
Написано 99 чисел: 1, 2, 3, …98, 99. Сколько раз в записи чисел встречается цифра 5?
Задача №6
В кастрюле одновременно варились 5 морковок. Сварились они за 20 минут. За сколько минут сварилась одна морковка?
Задача №7
Какое число меньше 29, от которого можно отнять 3 раза по 9?
Задача №8
Рыбаки выловили за один улов 46 кг рыбы. Сколько ещё надо выловить рыбы, если по плану нужно 90 кг?
Задача №9
Механик отремонтировал за месяц 67 мотоциклов. Сколько ему ещё осталось отремонтировать, если всего в мастерской 77 мотоциклов?
Задача №10
В лагерь приехали отдыхать 15 групп детей. Хотя лагерь может принять на отдых ещё 8 групп. Сколько групп всего может принять лагерь на отдых?
Математические загадки
Загадка №1
Мельник пошел на мельницу и увидел в каждом углу по 3 кошки. Сколько ног на мельнице?
Загадка №2
Термометр показывает плюс 15 градусов. Сколько градусов покажут два таких термометра?
Загадка №3
Около столовой, где обедали лыжники, пришедшие из похода, стояли 20 лыж, а в снег было воткнуто 20 палок. Сколько лыжников ходило в поход?
Загадка №4
Дед, баба, внучка, Жучка, кошка и мышка тянули-тянули репку и, наконец, вытянули. Сколько глаз смотрело на репку?
Загадка №5
В 9-этажном доме есть лифт. На первом этаже живет 2 человека, на втором — 4 человека, на третьем — 8 человек, на четвертом — 16, на пятом — 32 и так далее. Какая кнопка в лифте этого дома нажимается чаще других?
Ответы к уравнениям
| Уравнение | № 1 | № 2 | № 3 | № 4 | № 5 |
| Ответ | x=20 x=10 x=15 |
x=6 x=25 x=30 |
x=7 x=29 x=16 |
b) c) |
x=32 x=12 x=24 |
| Уравнение | № 6 | № 7 | № 8 | № 9 | № 10 |
| Ответ | x=26 x=33 |
x=24 x=68 x=24 |
x=52 x=29 |
x=13 x=48 x=36 |
да |
Ответы к задачам
Задача 1
21 ведро
Задача 2
31 страницу
Задача 3
У Оли — слоник, у Кати — медвежонок, у Гали — зайчик
Задача 4
10 и 11 вагонов
Задача 5
20 раз
Задача 6
за 20 минут
Задача 7
27
Задача 8
44 кг
Задача 9
10 мотоциклов
Задача 10
23 группы
Ответы на загадки
Загадка 1
3*4*4+2=50
Загадка 2
15 градусов
Загадка 3
10 лыжников
Загадка 4
12 глаз
Загадка 5
Кнопка первого этажа
Скачайте задания, заполнив форму!
После того как укажете данные, кнопка скачивания станет активной
Другие классы
Обновлено: , автор: Валерия Токарева
Урок 10. задачи, обратные данной — Математика — 2 класс
Математика, 2 класс
Урок № 10. Задачи, обратные данной
Перечень вопросов, рассматриваемых в теме:
- Что такое задачи, обратные данной?
- Как составлять и решать обратные задачи?
Глоссарий по теме:
Задачи, обратные данной — считаются те задачи, в которых говорится об одних и тех же предметах, но известное и неизвестное меняются местами.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.26, 27
2. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова А.Д.-М.: Просвещение, 2017, с. 16, 17
3. Математика. Рабочая тетрадь. 2 кл. 1 часть: учебное пособие для общеобразовательных организаций/ Волкова С.И.-М.: Просвещение, 2017.-с.31
Теоретический материал для самостоятельного изучения
Решим три задачи.
Составим по рисунку первую задачу.

В классе 10 девочек и 8 мальчиков. Сколько всего детей в классе?
Составим схематический рисунок.

Решим задачу:
10 + 8 = 18 (д.)
Ответ: 18 детей в классе.
Составим вторую задачу.

В классе 18 детей. Девочек 10, остальные-мальчики. Сколько мальчиков в классе?

Решим задачу:
18 – 10 = 8 (м.)
Ответ: 8 мальчиков в классе.
Составим третью задачу.

В классе 18 детей. Мальчиков 8, остальные — девочки. Сколько девочек в классе?

Решим задачу:
18 – 8 = 10 (д.)
Ответ: 10 девочек в классе.
Посмотрим еще раз на схемы к каждой задаче. Обратим внимание на то, что во всех задачах одинаковый сюжет, но то, о чем спрашивается в первой задаче стало известным во второй и третьей задачах, а узнать во второй задаче, сколько мальчиков и в третьей задаче сколько девочек в классе надо то, что известно в первой задаче.
Задачи, в которых известно то, о чем спрашивается в первой задаче и надо узнать то, что в первой задаче известно, называют обратными первой.
Сделаем вывод: задачи, обратные данной — считаются те задачи, в которых говорится об одних и тех же предметах, но известное и неизвестное меняются местами.
Тренировочные задания.
1. Решите задачу. Выберите задачи, обратные данной.
Кате подарили 8 воздушных шариков красного и синего цвета. Красных шариков было 5. Сколько синих шариков у Кати?
Варианты ответов:
1. Кате подарили 5 шариков красного цвета и 3 шарика синего цвета. Сколько шариков у Кати?
2. У Кати было 8 шариков. 3 шарика она подарила. Сколько шариков осталось у Кати?
3. Кате подарили 8 воздушных шариков красного и синего цвета. Синих шариков было 3. Сколько красных шариков у Кати?
Правильные варианты:
1. Кате подарили 5 шариков красного цвета и 3 шарика синего цвета. Сколько шариков у Кати?
3. Кате подарили 8 воздушных шариков красного и синего цвета. Синих шариков было 3. Сколько красных шариков у Кати?
2 . Восстановите пропуски в задачах.
1.В июне было 10 пасмурных дней и 20 ясных дней. Сколько дней в ________?
2. В июне ____ дней. Из них 10 дней были пасмурными. Сколько______ дней было в июне?
3. В июне 30 дней. Ясными были ____ дней. Сколько ____ дней было в июне?
Варианты ответов:
30, 20, ясных, пасмурных, июне
Правильный вариант:
1. В июне было 10 пасмурных дней и 20 ясных дней. Сколько дней в июне?
2. В июне 30 дней. Из них 10 дней были пасмурными. Сколько ясных дней было в июне?
3. В июне 30 дней. Ясными были 20 дней. Сколько пасмурных дней было в июне?
Как решить два уравнения с двумя неизвестными — I
Не могли бы вы напомнить, как решить два уравнения с двумя неизвестными? Если да, или если вы никогда не знакомы с этой концепцией, я приглашаю вас посмотреть это видео и следующее видео, которое является второй частью этой серии.
Два уравнения с двумя переменными. До сих пор при изучении алгебраических уравнений мы рассматривали решение отдельных уравнений только с одной переменной. Например, что-то вроде 2x + 7 = 15.
Что произойдет, если в уравнении есть более одной переменной? Предположим, у нас есть что-то вроде 2x + 3y = 15.
Итак, что бы значило для кого-то прийти и сказать нам, решить это уравнение? Как найти значения, которые работают в этом уравнении? Ну, конечно, одно возможное значение, если x = 0, тогда y может быть равно 5, так что это было бы решением. Другими словами, если x = 3 и y = 3, x = 6 и y = 1, это также значения, которые заставляют его работать.
Конечно, нет ограничений на то, что любая переменная должна быть положительной, поэтому другие решения включают (x = 9, y = -1) или (x = -3 и y = +7).И, как вы понимаете, мы могли бы сделать x все более и более отрицательным, а y — все более и более положительным — или наоборот. Так что мы могли бы получить довольно много подобных решений. Также нет ограничения, что переменные должны быть целыми числами, поэтому другие решения включают такие вещи, как x = 7 1/2 y = 0 или x = 4 и y = 2 1/3.
Итак, только на этой странице обратите внимание, что у нас есть одно, два, три, четыре, пять, шесть, семь решений для этого. И, конечно же, ясно, что мы можем получить намного больше. Фактически, одно уравнение с двумя переменными обычно имеет бесконечное количество решений.Обратите внимание, что все эти решения, если их нанести на график x-y, лежали бы на прямой линии.
Чтение диаграммы
Итак, семь упомянутых нами решений — это семь точек на этой диаграмме. И все они лежат на прямой. Теперь по причинам, которые мы обсудим позже в модуле координатной геометрии, любое отдельное уравнение только с x и y (ни одна из переменных не возведена в степень или дробь) может быть представлено линией в плоскости x-y. Так что прямо сейчас вам не нужно беспокоиться об их графическом отображении.Вам не нужно беспокоиться о том, как вы найдете наклон линии или что-то еще.
Все, что вам нужно сделать, это просто иметь эту идею, только эту ассоциацию — что уравнение с x и y представлено линией. Это все, что вам нужно знать для этого обсуждения.
Большая идея номер один
Итак, первая большая идея заключается в том, что никто не может попросить вас решить одно уравнение с двумя переменными, потому что у него будет бесконечное количество решений. Линия проходит через бесконечное количество точек, и каждая из этих точек является решением.
Итак, никто не может законно попросить вас решить, потому что они просят вас решить бесконечное количество вещей одновременно.
Теперь предположим, что у нас есть два уравнения, каждое с двумя переменными. Это называется системой уравнений. Значения x и y должны одновременно удовлетворять обоим уравнениям. Что ж, это интересно.
Если каждое уравнение является линией, то имеет смысл, что единственная точка, где эти две линии пересекаются, будет единственной точкой, которая удовлетворяет обоим уравнениям.Итак, вы выбираете одну случайную линию и выбираете другую случайную линию, очень велики шансы, что они собираются где-то пересекаться, и они пересекаются в одной точке, и эта одна точка будет решением.
Большая идея номер два
С алгебраической точки зрения, когда мы находим это решение, мы геометрически находим точку, в которой они пересекаются. Итак, большая идея №2 состоит в том, что если у нас есть система двух уравнений с двумя неизвестными, мы обычно можем решить для уникальных значений x и y.Как решить систему уравнений для этих значений? Есть две стратегии.
Один — это подстановка, а другой — либо исключение, некоторые источники также называют это линейной комбинацией. Я назову их заменой и устранением . Цель обоих этих методов — свести ситуацию с двумя уравнениями и двумя неизвестными к ситуации с одним уравнением и одним неизвестным, в которой мы уже знаем, как найти решение.
Метод замены
Итак, что мы делаем, и это часто верно в отношении математики, мы превращаем проблему, которую не знаем, как решить, в проблему, которую мы действительно знаем, как решить.Это очень типично для математики. Итак, метод подстановки. В этом методе мы сначала решаем одно уравнение, либо одно для одной из переменных.
Изображение с digitalconsumator
В этом уравнении мы получим одну переменную на одной стороне уравнения. Итак, я привел два уравнения, одно из которых было x + 2y = 11. И это уравнение, в котором особенно легко получить x само по себе. Что я собираюсь сделать, так это вычесть 2y с обеих сторон, и я получу x = 11-2y.Так что задержитесь на секунду, x = 11-2y. Теперь давайте посмотрим на другое уравнение.
Мы можем заменить x в другом уравнении выражением, которое x равно. Это потому, что x = 11-2y означает, что где бы ни был x, мы можем удалить x и заменить его тем, что он равен. Итак, вот другое уравнение, и мы просто снова напишем то же уравнение, но мы заменим это x на 11 минус 2y. Где теперь у нас есть одно уравнение с y.
Итак, теперь мы просто используем наше обычное решение, мы распределим, объединим
Image by CLS Digital Art
как термины, вычтем 22 с обеих сторон, мы получим -y = -7 умножить на -1 получаем y = 7.Итак, теперь мы решили для одного из двух значений, мы решили для y, нам все еще нужно решить для x. Теперь мы подставляем это значение и возвращаем y обратно в уравнение, которое было решено для x.
Итак, у нас было x = 11-2y, теперь мы знаем, что y = 7. Итак, мы просто вставим это, 11-14 равно -3. Таким образом, точка x равна -3, y равна положительному 7, что является решением. Обратите внимание, что метод подстановки наиболее полезен, когда в одном из двух уравнений коэффициенты одной из переменных равны положительной единице или отрицательной единице.
Дроби и метод исключения
Если все коэффициенты при x и y в двух уравнениях не равны положительному или отрицательному, то решение для любой переменной приведет к дробям, что сделает решение более громоздким. Так, например, предположим, что это наша система. Предположим, мы пытаемся решить первое уравнение относительно x. Хорошо, если мы можем распределить 5y в обе стороны, тогда делим на 4.
Сразу попадаем в дроби. Заменить это было бы неинтересно.Да, математически мы могли бы решить уравнение таким образом — и после разбиения на дроби, но мы предпочитаем не делать этого. В системах, в которых замена не удобна, мы будем использовать исключение. Мы рассмотрим метод исключения в следующем уроке.
Таким образом, система уравнений, два уравнения с двумя переменными, обычно имеют единственное уникальное решение, и снова это будет место, где две линии пересекаются. Это то, что мы находим. Мы можем решить либо заменой, либо устранением.Замена работает лучше всего, когда одна из переменных имеет коэффициент плюс или минус 1.
И снова в следующем уроке мы поговорим об устранении.
О Майке MᶜGarry
Майк создает уроки для экспертов и практические вопросы, чтобы помочь студентам GMAT добиться успеха. У него есть степень бакалавра физики и магистра религии в Гарварде, а также более 20 лет опыта преподавания, специализирующегося на математике, естественных науках и стандартизированных экзаменах. Майк любит разбивать футбольные мячи на орбите, и, несмотря на отсутствие очевидной черепно-мозговой недостаточности, он настаивает на том, чтобы болеть за Нью-Йорк Метс.
,2 = 1
у = х
[по одному в строке]
х
Y
[по одному в строке]
Решить
ГРАФИЧЕСКИЕ РЕШЕНИЯ
Часто мы хотим найти одну упорядоченную пару, которая является решением двух различных линейных
уравнения.Один из способов получить такую упорядоченную пару — построить график двух уравнений
на одном наборе осей и определение координат точки, где они
пересекаются.
Пример 1
Постройте уравнения
х + у = 5
х — у = 1
на том же наборе осей и определите упорядоченную пару, которая является решением для каждого
уравнение.
Решение
Используя метод построения графика с перехватом, мы обнаруживаем, что две упорядоченные пары, которые
решения x + y = 5 равны
(0, 5) и (5, 0)
И две упорядоченные пары, которые являются решениями
x — y = 1
(0, -1) и (1,0)
Показаны графики уравнений.
Точка пересечения — (3, 2). Таким образом,
(3, 2) должны удовлетворять каждому уравнению.
Фактически,
3 + 2 = 5 и 3 — 2 = 1
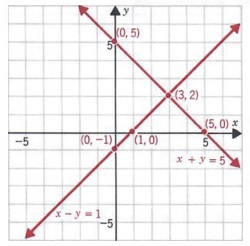
В целом, графические решения являются приблизительными. Разработаем методы
для точных решений в следующих разделах.
Считается, что линейные уравнения, рассматриваемые вместе таким образом, образуют систему
уравнения. Как и в приведенном выше примере, решение системы линейных уравнений
может быть одной упорядоченной парой. Компоненты этой упорядоченной пары удовлетворяют каждому из
два уравнения.
Некоторые системы не имеют решений, в то время как другие имеют бесконечное количество решений.
ЦИИ. Если графики уравнений в системе не пересекаются, то есть если линии
параллельны (см. рис. 8.1a) — уравнения считаются несовместимыми , и
не является упорядоченной парой, которая удовлетворяла бы обоим уравнениям. Если графики уравнений имеют вид
на той же линии (см. рисунок 8.1b), уравнения считаются зависимыми от , и каждое
упорядоченная пара, которая удовлетворяет одному уравнению, будет удовлетворять обоим уравнениям.Заметь
когда система несовместима, наклон линий тот же, но
y-перехваты разные. Когда система зависима, наклоны и пересечения по оси Y
одинаковые.
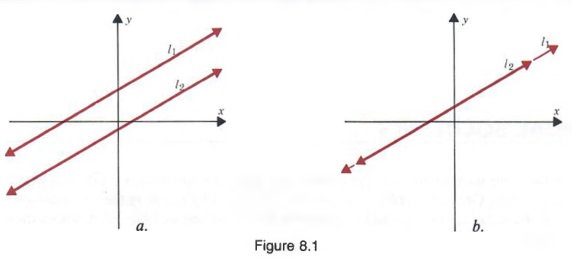
В нашей работе нас в первую очередь будут интересовать системы, имеющие один-единственный
решение, которые считаются непротиворечивыми и независимыми. График такой
система показана в решении Примера 1.
РЕШЕНИЕ СИСТЕМ ДОПОЛНЕНИЕМ I
Мы можем решать системы уравнений алгебраически.Более того, решения, которые мы
получить алгебраическими методами точны.
Система в следующем примере — это система, которую мы рассматривали в разделе 8.1.
на странице 335.
Пример 1
Решить
х + у = 5 (1)
х — у = 1 (2)
Решение
Мы можем получить уравнение с одной переменной, сложив уравнения (1) и (2)

Решение полученного уравнения относительно x дает
2х = 6, х = 3
Теперь мы можем заменить x на 3 либо в уравнении (1), либо в уравнении (2), чтобы получить
соответствующее значение y.В этом случае мы выбрали уравнение (1) и получили
(3) + у = 5
г = 2
Таким образом, решение x = 3, y = 2; или (3, 2).
Обратите внимание, что мы просто применяем свойство сложения равенства, чтобы мы могли
получить уравнение, содержащее единственную переменную. Уравнение с одной переменной,
вместе с любым из исходных уравнений, то образует эквивалентную систему
решение которого легко получить.
В приведенном выше примере мы смогли получить уравнение с одной переменной с помощью
сложение уравнений (1) и (2), поскольку члены + y и -y являются отрицательными значениями каждого
Другой.Иногда необходимо умножить каждый член одного из уравнений
на -1, чтобы члены одной переменной имели противоположные знаки.
Пример 2
Решить
2a + b = 4 (3)
а + Ь = 3 (4)
Решение
Начнем с умножения каждого члена уравнения (4) на -1, чтобы получить
2a + b = 4 (3)
-a — b = — 3 (4 ‘)
, где + b и -b отрицательны друг другу.
Символ ‘, называемый «простым», указывает на эквивалентное уравнение; то есть
уравнение, которое имеет те же решения, что и исходное уравнение.Таким образом, уравнение (4 ‘)
эквивалентно уравнению (4). Теперь складывая уравнения (3) и (4 ‘), получаем

Подставляя 1 вместо a в уравнении (3) или уравнении (4) [скажем, в уравнении (4)], мы получаем
1 + b = 3
б = 2
и наше решение — a = 1, b = 2 или (1, 2). Когда переменные a и b,
упорядоченная пара задается в виде (a, b).
РЕШЕНИЕ СИСТЕМ ДОПОЛНЕНИЕМ II
Как мы видели в разделе 8.2, решение системы уравнений сложением зависит от
одна из переменных в обоих уравнениях с коэффициентами, отрицательными
друг друга.Если это не так, мы можем найти эквивалентные уравнения, которые действительно имеют
переменные с такими коэффициентами.
Пример 1
Решите систему
-5x + 3y = -11
-7x — 2y = -3
Решение
Если мы умножим каждый член уравнения (1) на 2 и каждый член уравнения
(2) на 3, получаем эквивалентную систему
(2) (-5x) + (2) (3y) = (2) (- ll)
(3) (-7x) — (3) (2y) = (3) (- 3)
или
-10x + 6y = -22 (1 ‘)
-21x — 6y = -9 (2 ‘)
Теперь, сложив уравнения (1 ‘) и (2’), мы получим
-31x = -31
х = 1
Подстановка 1 вместо x в уравнении (1) дает
-5 (1) + 3у = -11
3y = -6
у = -2
Решение: x = 1, y = -2 или (1, -2).
Обратите внимание, что в уравнениях (1) и (2) члены, включающие переменные, находятся в
левый член, а постоянный член находится в правом члене. Мы будем ссылаться
таким договоренностям, как стандартный бланк для систем. Удобно расположить
системы в стандартной форме, прежде чем приступить к их решению. Например, если мы
хочу решить систему
3у = 5х — 11
-7x = 2 года — 3
мы сначала напишем систему в стандартной форме, добавив -5x к каждому члену
уравнения (3) и добавлением -2y к каждому члену уравнения (4).Таким образом, получаем
-5x + 3y = -11
-lx — 2y = -3
, и теперь мы можем продолжить, как показано выше.
РЕШЕНИЕ СИСТЕМ ЗАМЕНЫ
В разделах 8.2 и 8.3 мы решали системы уравнений первой степени с двумя вариациями.
способностей методом сложения. Другой метод, называемый методом подстановки,
также могут быть использованы для решения таких систем.
Пример 1
Решите систему
-2x + y = 1 (1)
х + 2у = 17 (2)
Решение
Решая уравнение (1) относительно y через x, получаем
y = 2x + 1 (1 ‘)
Теперь мы можем заменить y 2x + 1 в уравнении (2), чтобы получить
х + 2 (2x + 1) = 17
х + 4х + 2 = 17
5x = 15
x = 3 (продолжение)
Подставляя 3 вместо x в уравнении (1 ‘), мы получаем
у = 2 (3) + 1 = 7
Таким образом, решение системы: x = 3, y = 7; или (3, 7).
В приведенном выше примере было легко выразить y явно через x, используя
Уравнение (1). Но мы также могли бы использовать уравнение (2) для явной записи x в терминах
из
х = -2у + 17 (2 ‘)
Теперь подставляя — 2y + 17 вместо x в уравнении (1), мы получаем
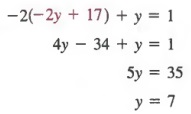
Подставляя 7 вместо y в уравнение (2 ‘), мы получаем
х = -2 (7) + 17 = 3
Решение системы снова (3, 7).
Обратите внимание, что метод подстановки полезен, если мы можем легко выразить одну переменную
с точки зрения другой переменной.
ПРИЛОЖЕНИЯ, ИСПОЛЬЗУЮЩИЕ ДВЕ ПЕРЕМЕННЫЕ
Если две переменные связаны одним уравнением первой степени, существует бесконечно
много упорядоченных пар, которые являются решениями уравнения. Но если две переменные
связанных двумя независимыми уравнениями первой степени, может быть только одна упорядоченная
пара, которая является решением обоих уравнений. Поэтому для решения задач с помощью двух
переменных, мы должны представить два независимых отношения с помощью двух уравнений .
Часто мы можем легче решать проблемы с помощью системы уравнений, чем с помощью
используя одно уравнение с одной переменной.Мы будем следовать указанным шести шагам
на стр. 115, с небольшими изменениями, как показано в следующем примере.
Пример 1
Сумма двух чисел равна 26. Чем больше число, тем больше 2 больше, чем в три раза
меньшее количество. Найдите числа.
Решение
Шаги 1-2
Мы представляем то, что хотим найти, в виде двух словесных фраз. Тогда мы
представляют словосочетания в терминах двух переменных.
Меньшее число: x
Большее число: y
Шаг 3 Эскиз не применим.
Шаг 4 Теперь мы должны написать два уравнения, представляющих указанные условия.
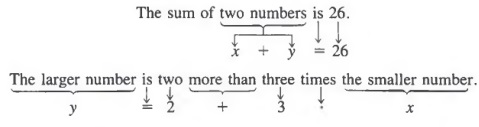
Сумма двух чисел равна 26.
Шаг 5 Чтобы найти числа, решаем систему
х + у = 26 (1)
у = 2 + 3х (2)
Поскольку уравнение (2) явно показывает y через x, мы решим систему следующим образом:
метод подстановки. Подставляя 2 + 3x вместо y в уравнение (1), мы получаем
х + (2 + 3х) = 26
4x = 24
х = 6
Подставляя 6 вместо x в уравнении (2), мы получаем
у = 2 + 3 (6) = 20
Шаг 6 Меньшее число — 6, большее — 20.
РЕЗЮМЕ ГЛАВЫ
-
Два уравнения, рассматриваемые вместе, образуют систему уравнений . Решение
обычно одна упорядоченная пара. Если графики уравнений представляют собой параллельных линий ,
уравнения считаются несогласованными ; если графики представляют собой ту же линию , уравнения
считаются зависимыми . -
Мы можем решить систему уравнений методом сложения , если сначала напишем
системы в стандартной форме , в которой термины, включающие переменные, находятся в
левый член, а постоянный член находится в правом члене. -
Мы можем решить систему уравнений методом подстановки , если одна переменная в
по крайней мере, одно уравнение системы сначала явно выражается через другое
переменная. -
Мы можем решать текстовые задачи, используя две переменные, представляя два независимых
отношения двумя уравнениями.
,
Область задачи умножения слов 2-й класс
Добро пожаловать на нашу страницу задач на умножение слов для второго класса.
Здесь вы найдете наш диапазон печатных задач умножения.
которые помогут вашему ребенку применить и практиковать свои навыки умножения и умножения для решения ряда «реальных» проблем.
Здесь вы найдете ряд рабочих листов для решения задач, связанных с умножением.
Каждый лист предполагает решение ряда письменных задач на умножение.
Для каждого рабочего листа ниже есть 3 уровня сложности: A, B и C.
Рабочий лист A — самый простой уровень, подходящий для детей в начале их класса.
Рабочий лист B — это рабочий лист среднего уровня для детей, которые работают на ожидаемом уровне в своем классе.
Рабочий лист C установлен на более сложном уровне и подходит для более способных математиков.
Задачи на каждом листе похожи по формулировке, но их числа становятся сложнее по мере того, как уровень становится сложнее.
Чтобы способствовать развитию навыков тщательной проверки и мышления, на каждом листе есть один «хитрый» вопрос, который не является задачей умножения.
Детям необходимо определить эту словесную проблему и решить, какую операцию им необходимо решить.
Использование этих листов поможет вашему ребенку:
- применить свои навыки умножения и умножения;
- применять свои знания таблицы умножения для выяснения связанных фактов;
- распознает проблемы с умножением и пытается обнаружить «хитрые» проблемы;
- решить ряд «реальных» проблем.
Некоторые листы имеют версию для Великобритании с написанием для Великобритании.
В нашей области задач на умножение слов для 3-го класса вы найдете ряд задач на умножение слов, предназначенных для учеников 3-го класса.
Охватываются следующие области:
- базовых информационных бюллетеней по умножению;
- фактов умножения до 10х10;
- задач, для решения которых требуются письменные методы умножения (TU x U)
Взгляните на еще несколько наших рабочих листов, похожих на эти.
У нас есть ряд реальных проблем, связанных с различными измерениями,
типа самых быстрых насекомых или длины разных динозавров!
Охватывается целый ряд различных навыков, от округления и разложения до использования сложения, вычитания и умножения.
Здесь вы найдете подборку таблиц времени умножения.
до 10×10 или 12×12, чтобы помочь вашему ребенку в изучении
факты умножения.
Существует широкий выбор таблиц умножения, включая
цветные и черно-белые, диаграммы меньшего размера, диаграммы с заливкой
и пустые диаграммы.
Использование этих таблиц поможет вашему ребенку:
- Узнайте их факты умножения на 10х10 или 12х12;
- Попрактикуйтесь в их таблице умножения.
Все бесплатные печатные математические таблицы в этом разделе основаны на тестах Elementary Math Benchmarks.
Здесь вы найдете ряд бесплатных печатных игр на умножение.
Следующие игры развивают математические навыки умножения в увлекательной и мотивирующей форме.
Использование этих листов поможет вашему ребенку:
- узнают их факты умножения;
- попрактиковаться и улучшить отзыв таблицы умножения;
- развивают навыки стратегического мышления.
Саламандры по математике надеются, что вам понравятся эти бесплатные распечатываемые рабочие листы по математике.
и все другие наши математические игры и ресурсы.
Мы приветствуем любые комментарии о нашем сайте или рабочие листы в поле комментариев Facebook внизу каждой страницы.
,
Решайте неравенства с помощью программы «Пошаговое решение математических задач»
Введите уравнение вместе с переменной, для которой вы хотите его решить, и нажмите кнопку «Решить».
В этой главе мы разработаем определенные методы, которые помогут решить проблемы, сформулированные на словах. Эти методы включают переписывание задач в виде символов. Например, заявленная проблема
«Найдите число, которое при добавлении к 3 дает 7»
можно записать как:
3+? = 7, 3 + n = 7, 3 + x = 1
и так далее, где символы?, N и x обозначают число, которое мы хотим найти.Мы называем такие сокращенные версии поставленных задач уравнениями или символическими предложениями. Такие уравнения, как x + 3 = 7, являются уравнениями первой степени, поскольку переменная имеет показатель степени 1. Члены слева от знака равенства составляют левую часть уравнения; те, что справа, составляют правую часть. Таким образом, в уравнении x + 3 = 7 левый член равен x + 3, а правый член равен 7.
РЕШЕНИЕ УРАВНЕНИЙ
Уравнения могут быть истинными или ложными, так же как словесные предложения могут быть истинными или ложными.Уравнение:
3 + х = 7
будет ложным, если вместо переменной подставлено любое число, кроме 4. Значение переменной, для которой верно уравнение (4 в этом примере), называется решением уравнения. Мы можем определить, является ли данное число решением данного уравнения, подставив число вместо переменной и определив истинность или ложность результата.
Пример 1 Определите, является ли значение 3 решением уравнения
4x — 2 = 3x + 1
Решение Мы подставляем значение 3 вместо x в уравнение и смотрим, равен ли левый член правому члену.
4 (3) — 2 = 3 (3) + 1
12 — 2 = 9 + 1
10 = 10
Отв. 3 — решение.
Уравнения первой степени, которые мы рассматриваем в этой главе, имеют не более одного решения. Решения многих таких уравнений можно определить путем осмотра.
Пример 2 Найдите решение каждого уравнения путем осмотра.
а. х + 5 = 12
б. 4 · х = -20
Решения а. 7 — решение, так как 7 + 5 = 12.
b. -5 — решение, поскольку 4 (-5) = -20.
РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИТАНИЯ
В разделе 3.1 мы решили несколько простых уравнений первой степени путем проверки. Однако решения большинства уравнений не сразу видны при осмотре. Следовательно, нам нужны некоторые математические «инструменты» для решения уравнений.
ЭКВИВАЛЕНТНЫЕ УРАВНЕНИЯ
Эквивалентные уравнения — это уравнения, которые имеют идентичные решения. Таким образом,
3x + 3 = x + 13, 3x = x + 10, 2x = 10 и x = 5
являются эквивалентными уравнениями, потому что 5 — единственное решение каждого из них.Обратите внимание, что в уравнении 3x + 3 = x + 13 решение 5 не очевидно при осмотре, но в уравнении x = 5 решение 5 очевидно при осмотре. Решая любое уравнение, мы преобразуем данное уравнение, решение которого может быть неочевидным, в эквивалентное уравнение, решение которого легко заметить.
Следующее свойство, иногда называемое свойством сложения-вычитания , является одним из способов создания эквивалентных уравнений.
Если одинаковое количество прибавляется или вычитается из обоих элементов
уравнения, полученное уравнение эквивалентно исходному
уравнение.
в символах,
a — b, a + c = b + c и a — c = b — c
— эквивалентные уравнения.
Пример 1 Напишите уравнение, эквивалентное
х + 3 = 7
путем вычитания 3 из каждого члена.
Решение Если вычесть 3 из каждого члена, получим
х + 3 — 3 = 7 — 3
или
х = 4
Обратите внимание, что x + 3 = 7 и x = 4 — эквивалентные уравнения, поскольку решение одинаково для обоих, а именно 4.В следующем примере показано, как мы можем генерировать эквивалентные уравнения, сначала упростив один или оба члена уравнения.
Пример 2 Напишите уравнение, эквивалентное
4x- 2-3x = 4 + 6
, объединив одинаковые термины, а затем добавив по 2 к каждому члену.
Объединение одинаковых терминов дает
х — 2 = 10
Добавление 2 к каждому члену дает
х-2 + 2 = 10 + 2
х = 12
Чтобы решить уравнение, мы используем свойство сложения-вычитания, чтобы преобразовать данное уравнение в эквивалентное уравнение вида x = a, из которого мы можем найти решение путем проверки.
Пример 3 Решить 2x + 1 = x — 2.
Мы хотим получить эквивалентное уравнение, в котором все члены, содержащие x, находятся в одном члене, а все члены, не содержащие x, — в другом. Если мы сначала добавим -1 (или вычтем 1 из) каждого члена, мы получим
2x + 1- 1 = x — 2-1
2х = х — 3
Если мы теперь прибавим -x к каждому члену (или вычтем x из него), мы получим
2х-х = х — 3 — х
х = -3
, где решение -3 очевидно.
Решением исходного уравнения является число -3; однако ответ часто отображается в виде уравнения x = -3.
Поскольку каждое уравнение, полученное в процессе, эквивалентно исходному уравнению, -3 также является решением 2x + 1 = x — 2. В приведенном выше примере мы можем проверить решение, подставив — 3 вместо x в исходном уравнении.
2 (-3) + 1 = (-3) — 2
-5 = -5
Симметричное свойство равенства также помогает при решении уравнений. В этом объекте указано
Если a = b, то b = a
Это позволяет нам менять местами члены уравнения в любое время, не беспокоясь о каких-либо изменениях знака.Таким образом,
Если 4 = x + 2, то x + 2 = 4
Если x + 3 = 2x — 5, то 2x — 5 = x + 3
Если d = rt, то rt = d
Может быть несколько разных способов применить свойство сложения, указанное выше. Иногда один метод лучше другого, а в некоторых случаях также полезно симметричное свойство равенства.
Пример 4 Решите 2x = 3x — 9. (1)
Решение Если мы сначала добавим -3x к каждому члену, мы получим
2x — 3x = 3x — 9 — 3x
-x = -9
, где переменная имеет отрицательный коэффициент.Хотя при осмотре мы можем видеть, что решением является 9, поскольку — (9) = -9, мы можем избежать отрицательного коэффициента, добавив -2x и +9 к каждому члену уравнения (1). В этом случае получаем
2x-2x + 9 = 3x- 9-2x + 9
9 = х
, из которого решение 9 очевидно. При желании мы можем записать последнее уравнение как x = 9 по симметричному свойству равенства.
РЕШЕНИЕ УРАВНЕНИЙ С СВОЙСТВОМ DIVISION
Рассмотрим уравнение
3x = 12
Решение этого уравнения — 4.Также обратите внимание, что если мы разделим каждый член уравнения на 3, мы получим уравнения
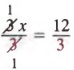
, решение которого также равно 4. В общем, мы имеем следующее свойство, которое иногда называют свойством деления.
Если оба члена уравнения делятся на одно и то же (ненулевое)
количество, полученное уравнение эквивалентно исходному уравнению.
в символах,
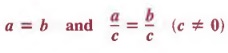
— эквивалентные уравнения.
Пример 1 Напишите уравнение, эквивалентное
-4x = 12
, разделив каждый член на -4.
Решение Если разделить оба элемента на -4, получим
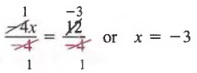
При решении уравнений мы используем указанное выше свойство для создания эквивалентных уравнений, в которых переменная имеет коэффициент 1.
Пример 2 Решите 3y + 2y = 20.
Сначала мы объединяем одинаковые термины, чтобы получить
5лет = 20
Тогда, разделив каждый член на 5, получим
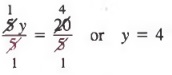
В следующем примере мы используем свойство сложения-вычитания и свойство деления для решения уравнения.
Пример 3 Решить 4x + 7 = x — 2.
Решение
Сначала мы добавляем -x и -7 к каждому члену, чтобы получить
4x + 7 — x — 7 = x — 2 — x — 1
Далее, объединяя одинаковые термины, получаем
3x = -9
Наконец, мы разделим каждый член на 3, чтобы получить
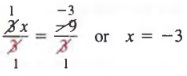
РЕШЕНИЕ УРАВНЕНИЙ С СВОЙСТВОМ УМНОЖЕНИЯ
Рассмотрим уравнение
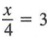
Решение этого уравнения — 12. Также обратите внимание, что если мы умножим каждый член уравнения на 4, мы получим уравнения
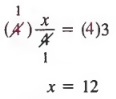
, решение которого также равно 12.В общем, мы имеем следующее свойство, которое иногда называют свойством умножения.
Если оба члена уравнения умножаются на одну и ту же ненулевую величину, полученное уравнение эквивалентно исходному уравнению.
в символах,
a = b и a · c = b · c (c ≠ 0)
— эквивалентные уравнения.
Пример 1 Напишите уравнение, эквивалентное
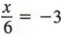
путем умножения каждого члена на 6.
Решение Умножение каждого члена на 6 дает
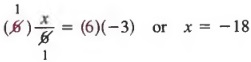
При решении уравнений мы используем указанное выше свойство для создания эквивалентных уравнений, не содержащих дробей.
Пример 2 Решить 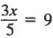
Решение Сначала умножьте каждый член на 5, чтобы получить
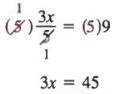
Теперь разделите каждого члена на 3,
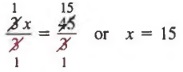
Пример 3 Решить 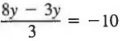 .
.
Решение
Сначала упростите над дробной чертой, чтобы получить
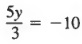
Затем умножьте каждый член на 3, чтобы получить
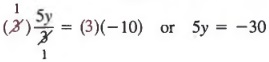
Наконец, разделив каждого члена на 5, получим
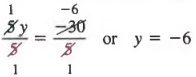
ДАЛЬНЕЙШИЕ РЕШЕНИЯ УРАВНЕНИЙ
Теперь мы знаем все методы, необходимые для решения большинства уравнений первой степени.Не существует определенного порядка, в котором следует применять свойства. Может оказаться подходящим любой один или несколько из следующих шагов, перечисленных на странице 102.
Шаги по решению уравнений первой степени:
- Объедините одинаковые члены в каждом члене уравнения.
- Используя свойство сложения или вычитания, запишите уравнение со всеми членами, содержащими неизвестное в одном члене, и всеми членами, не содержащими неизвестное в другом.
- Объедините одинаковые термины в каждом элементе.
- Используйте свойство умножения для удаления дробей.
- Используйте свойство деления, чтобы получить коэффициент 1 для переменной.
Пример 1 Решите 5x — 7 = 2x — 4x + 14.
Решение
Сначала мы объединяем одинаковые члены, 2x — 4x, чтобы получить
5x — 7 = -2x + 14
Затем мы добавляем + 2x и +7 к каждому члену и объединяем одинаковые термины, чтобы получить
5x — 7 + 2x + 7 = -2x + 14 + 2x + 1
7x = 21
Наконец, мы разделим каждый член на 7, чтобы получить
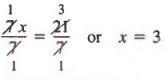
В следующем примере мы выполняем упрощение над полосой дроби перед применением свойств, которые мы изучали.
Пример 2 Решить 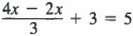
Решение Сначала мы объединяем одинаковые термины, 4x — 2x, чтобы получить
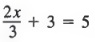
Затем мы добавляем -3 к каждому члену и упрощаем
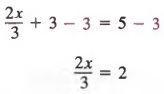
Затем мы умножаем каждый член на 3, чтобы получить

Наконец, мы делим каждый член на 2, чтобы получить
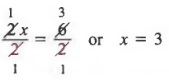
РЕШЕНИЕ ФОРМУЛ
Уравнения, в которых используются переменные для измерения двух или более физических величин, называются формулами.Мы можем найти любую одну из переменных в формуле, если известны значения других переменных. Мы подставляем известные значения в формулу и решаем неизвестную переменную методами, которые мы использовали в предыдущих разделах.
Пример 1 В формуле d = rt найти t, если d = 24 и r = 3.
Решение Мы можем найти t, заменив 24 на d и 3 на r. То есть
d = rt
(24) = (3) т
8 = т
Часто бывает необходимо решить формулы или уравнения, в которых есть более одной переменной для одной из переменных в терминах других.Мы используем те же методы, что и в предыдущих разделах.
Пример 2 В формуле d = rt найдите t через r и d.
Решение Мы можем решить для t в терминах r и d, разделив оба члена на r, чтобы получить
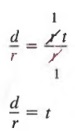
из которых по закону симметрии
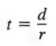
В приведенном выше примере мы решили для t, применив свойство деления для создания эквивалентного уравнения. Иногда необходимо применить более одного такого свойства.
Пример 3 В уравнении ax + b = c решите относительно x через a, b и c.
Решение Мы можем решить для x, сначала добавив -b к каждому члену, чтобы получить
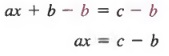
, затем разделив каждый член на a, мы получим
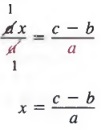
,