Пример по алгебре 10 класса – 10 класс. Алгебра

Производная. Алгебра, 10 класс: уроки, тесты, задания.

Вход на портал

Вход на портал

Регистрация

Начало

Поиск по сайту

ТОПы

Учебные заведения

Предметы

Проверочные работы

Обновления

Подписка Я+

Новости

Переменка

Отправить отзыв

• Предметы
• Алгебра
• 10 класс

1. 
   

   
   Числовые последовательности и их свойства
   

   
   
   
   
   
   
   
   

2. 
   

   
   Предел числовой последовательности
   

   
   
   
   
   
   
   
   

3. 
   

   
   Cумма бесконечной геометрической прогрессии
   

   
   
   
   
   
   
   
   

4. 
   

   
   Предел функции
   

   
   
   
   
   
   
   
   

5. 
   

   
   Определение производной
   

   
   
   
   
   
   
   
   

6. 
   

   
   Вычисление производных
   

   
   
   
   
   
   
   
   

7. 
   

   
   Уравнение касательной к графику функции
   

   
   
   
   
   
   
   
   

8. 
   

   
   Применение производной для исследования функций на монотонность и экстремумы
   

   
   
   
   
   
   
   
   

9. 
   

   
   Построение графиков функции
   

   
   
   
   
   
   
   
   

10. 
    

    
    Применение производной для отыскания наибольших и наименьших величин
    

    
    
    
    
    
    
    
    

Отправить отзыв

Нашёл ошибку?

Сообщи нам!

Copyright © 2019 ООО ЯКласс

Контакты

Пользовательское соглашение

www.yaklass.ru

Примеры вычисления основных производных. Типовые задачи

Производная функции  в точке :

Геометрический смысл производной

Если задан график функции , то производная в точке  – это тангенс угла наклона касательной к данной функции в точке c абсциссой  (или угловой коэффициент касательной).

Физический смысл производной

Если в качестве функции мы берем перемещение, зависящее от , – , то , где  – перемещение,  – время, а  – мгновенная скорость в данной точке.

И сегодня мы попробуем вычислить некоторые производные по определению.

Начнем с самого простого – с линейной функции.

Пусть , где  и  – некоторые числа, а  – переменная.

Тогда:

Итак, выясняется, что  для любого . Значит, можно утверждать, что .

О чем это говорит?

Во-первых, мы подтвердили несколько фактов про линейную функцию, которые нам, возможно, уже были известны.

1. Так, исходя из геометрического смысла производной, тангенс угла наклона прямой совпадает с ее угловым коэффициентом (он равен производной в соответствующей точке).

Кроме этого, мы видим, что раз производная постоянна, то угол наклона постоянен, это вполне соответствует нашим представлениям о прямой.

2. Если предположить, что материальная точка движется прямолинейно равномерно, то ее координата в данный момент времени описывается функцией: , где  – начальная координата, а  – скорость. Рассмотрим это утверждение.

Предположим, что есть некоторая материальная точка, которая двигается по закону . Найти его производную.

Решение

Для удобства предположим, что точка движется равномерно, то есть  в каждой точке одинаково. Тогда с точки зрения физического смысла мы получим:

.

Физический смысл производной: производная от координаты равна мгновенной скорости точки в данный момент времени.

Но для равномерного движения мгновенная скорость в любой момент времени одна и та же и равна скорости движения тела . Получаем, что должно выполняться равенство: .

Во-первых, . Это следует из наших выкладок просто в силу того, что мы подставили ; .

Далее, . Итак, производная от константы равна нулю.

Дальше рассмотрим производную функции .

В силу того что  – произвольна, имеем:

Где это может нам пригодиться? В дальнейшем с помощью производных мы будем исследовать свойства функций, говорить об их монотонности и т.  д. Пока же мы можем говорить лишь о физическом и геометрическом смыслах. Разберем по примеру на каждый из них.

Тело движется по закону  ( – в секундах,  – в метрах). Какой будет скорость тела через 3 секунды после начала движения? Через какое время после начала движения скорость тела будет равна ?

Дано: , .

Найти: 1. , 2.

Прежде всего вспомним, что .

Отсюда мы можем вывести, что скорость через три секунды, то есть при , будет равна .

А  скорость будет равна через 5 секунд ().

Ответ: , .

В качестве небольшого упражнения попробуйте сами вывести производную функции .

А сделав это, вы сможете решать физические задачи на равноускоренное движение. , где  – ускорение.

В какой точке графика  его касательная параллельна прямой ?

Дано: , .

Решение

Раз прямые параллельны, то их угловые коэффициенты равны, то есть угловой коэффициент касательной (он же тангенс угла наклона) должен быть равен 1. Но мы помним, что тангенс угла наклона касательной как раз равен производной в точке касания (в абсциссе точки касания) (см. рис. 1).

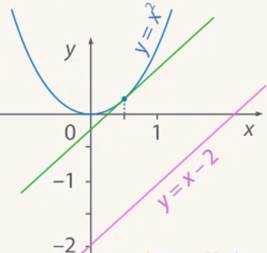
Рис. 1. Иллюстрация к примеру 1

Приравнивая  имеем , значит, речь идет о касательной в точке .

Ответ: в точке .

Теперь рассмотрим кубическую функцию .

В силу того, что  произволен, имеем:

.

На этом уроке мы с вами применяли определение производной на конкретных примерах. Мы вычислили производную линейной функции, производную  и , а также пока без доказательства познакомились с производной от . Кроме этого, мы разобрали несколько примеров, увидели, где применяется производная.

Доказательство

.

По формуле бинома Ньютона:

interneturok.ru

Предел функции. Алгебра, 10 класс: уроки, тесты, задания.

www.yaklass.ru

Сайт учителя математики — Алгебра 10-11 классы

	Рабочие программы
10-11 классы		Рабочая программа по алгебре и началам анализа для 10-11 классов к УМК А.Г. Мордковича (профильный уровень) 5 часов
10-11 классы		Рабочая программа по алгебре и началам анализа для 10-11 классов к УМК А.Г. Мордковича (профильный уровень) 4 часа
10-11 классы		Рабочая программа по математике для 10-11 классов к УМК А.Г. Мордковича, Л.С. Атанасяна (базовый уровень) 5 часов
10 класс		Рабочая программа по алгебре и началам анализа для 10 класса к УМК А.Г. Мордковича (профильный уровень) 5 часов
11 класс		Рабочая программа по алгебре и началам анализа для 11 класса к УМК А.Г. Мордковича (профильный уровень) 5 часов
10 класс		Рабочая программа по математике для 10 класса к УМК А.Г. Мордковича, Л.С. Атанасяна (базовый уровень) 5 часов
	Презентации к урокам
10 класс		Действительные числа
10 класс		Модуль и его приложения
10 класс		Понятие функции. Свойства функций
10 класс		Функции, их свойства и графики
10 класс		Числовые последовательности
10 класс		Понятие производной
10 класс		Производная и ее применение
10 класс		Применение производной
10 класс		Числовая окружность
10 класс		Тригонометрия
10 класс		Построение графиков тригонометрических функций
10 класс		Обратные тригонометрические функции
10 класс		Решение тригонометрических уравнений и неравенств
10 класс		Решение тригонометрических уравнений и неравенств с примерами
10 класс		Преобразование графиков тригонометрических функций
10 класс		Методы решения тригонометрических уравнений
11 класс		Корень n-ой степени. Степень с рациональным показателем
11 класс		Первообразная. Интеграл
11 класс		Многочлены
11 класс		Показательная функция, ее свойства и график. Показательные уравнения и неравенства
11 класс		Логарифмическая функция, ее свойства и график. Логарифмические уравнения и неравенства
11 класс		Комплексные числа
1  2

semenova-klass.moy.su

Основные тригонометрические формулы — Математика 10 класс — Школьная математика — Каталог статей

free-math.ru

Олимпиада по математике 10 класс, задания, уравнения, задачи с ответами

Часто ученики 10 класса относятся к занятиям с легким пренебрежением, ведь ГИА уже позади, а ЕГЭ кажется  . На уроках математики в 10 классе учащиеся знакомятся с такими темами, как «Числовые функции и их свойства», «Тригонометрические функции» и «Тригонометрические уравнения», «Производная». Для закрепления изученного материала, школьникам нужно много и упорно заниматься решением задач разной сложности.

Олимпиадные задания по математике помогают ученикам 10 класса закрепить полученные знания, а также расширить и углубить их.

На этой странице собраны примеры уравнений и задач с ответами и решениями, а также математические загадки, решение которых требует нестандартного мышления. Данный материал может использоваться на уроках или во время самостоятельной подготовки. Рекомендован учителям, репетиторам, родителям и учащимся.

Уравнения

1. Решите уравнение: 

2. Решите уравнение: 

3. Решите уравнение: 

4. Решите уравнение: 

5. Решите уравнение: 

6. Решите уравнение: 

7. Решите уравнение: 

8. Решите уравнение: 

9. Решите уравнение: 

10. Решите уравнение: 

Задачи

Задача №1
Учащиеся 10 «а» и 10«б» классов отправились на экскурсию. Юношей было 16, учащихся 10«б» класса – 24, девушек 10«а» столько, сколько юношей из 10«б» класса. Сколько всего учащихся побывали на экскурсии?

Задача №2
Четырехугольник ABCD вписан в окружность диаметра 17. Диагонали АС и ВD перпендикулярны. Найдите стороны АВ, ВС, CD, если известно, что AD = 8 и AB : CD = 3 : 4

Задача №3
Через диагональ прямоугольного параллелепипеда и точку, лежащую на боковом ребре, не пересекающем эту диагональ, проведена плоскость так, чтобы площадь сечения параллелепипеда этой плоскостью была наименьшей. Найдите длины сторон основания параллелепипеда, если известно, что диагонали сечения равны 6 и 2√3 , а угол между ними 30°.

Задача №4
Найти множество значений параметра a, при которых дискриминант уравнения  + + 1 = 0, в 9 раз больше квадрата разности двух его различных корней?

Задача №5
Известно, что tga  и tg3a  целые. Найдите все возможные значения  tga

Математические загадки

Загадка №1

Можно ли провести в городе 10 автобусных маршрутов и установить на них остановки так, что для любых 8 маршрутов найдётся остановка, не лежащая ни на одном из них, а любые 9 маршрутов проходят через все остановки?

Загадка №2

Сколько существует четырехзначных чисел, не делящихся на 1000, у которых первая и последняя цифры чётны?

Загадка №3

На доске через запятую выписаны числа 1, 2, 3, … 99. Двое играющих по очереди заменяют одну из имеющихся запятых на знак «+» или «*» (умножить). После того как запятых не останется, игроки вычисляют значение полученного выражения. Если результат является нечётным числом, то выигрывает первый, а если чётным – второй. Кто выигрывает при правильной игре?

Загадка №4

Расположите натуральные числа от 1 до 100 в строку так, чтобы разность между  любыми двумя соседними числами была равна 2 или 3.

Загадка №5

На какое наибольшее число натуральных  слагаемых можно разложить число 96 так, чтобы все слагаемые были больше 1 и попарно взаимно просты?

Ответы к уравнениям

Ответы к задачам

Задача 1
40 учащихся.

Задача 2
AB = 10,2; CD = 13,6; ВС = 15.

Задача 3
1; √3

Задача 4
a ∈ {−3}

Задача 5
−1; 0 или 1.

Ответы на загадки

Загадка 1

Ответ: можно.

Решение. Рассмотрим, например, 10 прямых  плоскости. Никакие  две из  которых не параллельны и никакие три не пересекаются в одной точке. Будем считать, что прямые – это автобусные маршруты, а их точки пересечения – остановки. При этом  с каждой остановки можно проехать на любую другую: если остановки лежат на одной прямой, то без пересадки, а если нет, то с одной пересадкой. Далее, если даже отбросить в этой схеме одну прямую, то всё ещё останется возможность проехать с каждой остановки на любую другую, сделав в пути не больше одной пересадки. Однако если отбросить две прямые, то одна остановка (точка пересечения этих прямых) уже вовсе не будет обслуживаться оставшимися маршрутами и с неё будет невозможно проехать на какую- либо другую.

Загадка 2

Ответ: 1996.

Решение. Первая цифра  числа может быть любой из четырёх (2,4,6 или 8), вторая и третья – любой из десяти каждая, а четвёртая, если отказаться от условия « не делящихся на тысячу», — любой из пяти ( 0,2, 4,6 или 8). Следовательно, четырёхзначных чисел, в записи которых первая и последняя цифры чётны, всего имеется 4+10+10+5= 2000; так как среди них четыре числа (2000, 4000, 6000, 8000) делятся на 1000, то чисел, удовлетворяющих условию задачи, окажется 2000 – 4 = 1996.

Загадка 3

Ответ: выигрывает второй игрок.

Решение. Для достижения успеха второй игрок может пользоваться симметричной стратегией: если первый ставит  какой – то знак между числами к и к+1, то второй ставит такой же знак между числами 99-к и 100-к. Выражение, которое получится в конце игры, будет содержать несколько слагаемых – произведений, причём слагаемое,  содержащее число 50, является чётным, а остальные слагаемые естественным образом разобьются на пары «симметричных» слагаемых одинаковой чётности. Таким образом, выражение, полученное в конце игры, окажется чётным.

Загадка 4
Решение. Например, так:1, 3, 5, 2, 4, 6, 8,10, 7, 9 , 11, … , 96, 98, 100,97, 99 (в каждой пятёрке порядок расположения чисел 5к+1,  5к+3, 5к+5, 5к+2,  5к+4).

Загадка 5

Ответ: на  семь слагаемых.

Решение. Приведём пример разбиения числа 96 на семь слагаемых:

96 = 2 + 5 + 7 + 11 + 13 + 17 + 41.

Если слагаемых больше, то среди них не менее восьми нечётных ( если их семь, то сумма нечётна). Заменим каждое из них на наименьший простой сомножитель. При этом сумма не увеличится, и все слагаемые будут различны.  Но сумма  восьми  наименьших нечётных  простых  чисел равна 98.

Другие классы

Обновлено: 26/02/2015 , автор: Валерия Токарева

ruolimpiada.ru

Алгебра, 11 класс: уроки, тесты, задания

www.yaklass.ru