|
РАЗРАБОТКИ |
10 классВ категории разработок: 62 Фильтр по целевой аудитории — Целевая аудитория -для 1 классадля 2 классадля 3 классадля 4 классадля 5 классадля 6 классадля 7 классадля 8 классадля 9 классадля 10 классадля 11 классадля учителядля классного руководителядля дошкольниковдля директорадля завучейдля логопедадля психологадля соц.педагогадля воспитателя План — конспект и презентация к двум урокам алгебры и начала анализа в 10 классе по теме «Способы решения логарифмических уравнений» . На этих уроках учащиеся знакомятся с девятью способами решения уравнений и закрепляют их в ходе выполнения упражнений. Закрепление изученного материала учитель может организовать по-разному: фронтально, в ходе парной или групповой работы(в зависимости от уровня подготовленности класса). На слайдах презентации отражены: определение логарифма, свойства логарифмов, примеры для устных упражнений, способы решения уравнений, уравнения, которые учитель объясняет в ходе изучения нового материала, и примеры для закрепления изученного. К этим примерам приведены ответы, а их решения разобраны в плане — конспекте. При подведении итогов урока учащимся предлагается определить способ решения того или иного уравнения.
Целевая аудитория: для 10 класса Основные цели данного урока — это закрепление знаний о применении производной для нахождения наибольшего и наименьшего значения функции, непрерывной на отрезке; введение нового материала о нахождении наибольшего и наименьшего значения функции на незамкнутом промежутке и рассмотрение математической модели решения задач на оптимизацию, связь с профессией. Урок сопровождается презентацией.
Целевая аудитория: для 10 класса Урок алгебры в 10 классе по теме «Решение простейших тригонометрических уравнений». Цель урока: изучить решение простейших тригонометрических уравнений. Планируемый результат: формирование положительной мотивации, знания определения термина «тригонометрическое уравнение», запись формул решения простейших тригонометрических уравнений, формирование у учащихся первичные умения и навыки решения простейших тригонометрических уравнений; развитие коммуникативных умений. На данном уроке используются электронные образовательные ресурсы.
Целевая аудитория: для 10 класса Урок относится к нетрадиционному типу- урок –исследование. Целевая аудитория: для 10 класса Это урок по изучению, закреплению и систематизации знаний на уроке «Геометрии» в 10 классе по теме «Параллельность прямой и плоскости». Целевая аудитория: для 10 класса Урок алгебры и начала анализа в 10 классе физико – математического профиля. Цель урока: обобщение и систематизация знаний по теме. Подготовка учащихся к ЕГЭ. В заданиях Единого государственного экзамена имеется довольно много уравнений, при решении которых необходимо выбрать такой способ решения, который позволяет решить уравнения проще, быстрее. На уроке учащиеся анализируют различные методы решения иррациональных уравнений. Этот материал можно использовать при обобщении темы «Решение иррациональных уравнений» в 10 классе, а также при повторении в 11 классе — обучение, закрепление и фактические проверки навыков в данной теме, чтобы в короткие сроки и в полном объеме повторить тему «Решение иррациональных уравнений». Это особенно ценно при подготовке к ЕГЭ. Целевая аудитория: для 10 класса Тип урока-изучение нового материала. В начале урока повторяется понятие предела функции на бесконечности и предела функции в точке. Затем дается небольшая историческая справка об ученых — основоположниках дифференциального исчисления. Вводится понятие производной, понятие дифференцирования функции. Рассматриваются две задачи, приводящие к понятию производной. подчеркивается физический и геометрический смысл производной. Урок разработан учителем математики ГБОУ МООШИ с ПЛП Егоровой И. Г.
Целевая аудитория: для 10 класса Урок проводится в форме урока-погружения (не менее 90 минут), обеспечивающей повторение учебного материала, контроль знаний учащихся, их коррекцию. Каждый блок состоит из учебных элементов (УЭ). УЭ — это последовательные шаги, алгоритм работы учащихся, с которым школьник работает непосредственно:
Целевая аудитория: для 10 класса Урок по теме: «Методы решения тригонометрических уравнений». В ходе урока вводится метод универсальной тригонометрической подстановки. Целевая аудитория: для 10 класса Разработка содержит конспект урока и презентацию к уроку алгебры и начала анализа в 10 классе. Материал подобран так, чтобы учащиеся рассмотрели один из способов решений тригонометрических уравнений. Удобно применять данный способ при решении заданий В5 (решение тригонометрических уравнений с отбором корней), Целевая аудитория: для 10 класса |
Конкурсы Диплом и справка о публикации каждому участнику! |
www.uchportal.ru
Презентация «Первые уроки алгебры и начал анализа в 10 классе»


Что означает название предмета «Алгебра и начала анализа?»
Алгебра – один из разделов математики, изучающий свойства
величин, выраженных буквами, независимо от их конкретного
числового значения.
Математический анализ – это совокупность частей математики,
в которых главным объектом исследования является функция, а
оперативная часть опирается на выполнение операций
дифференцирования и интегрирования.
Основоположники математического анализа:


Тригономе́трия (от греч. τρίγονο (треугольник) и греч. μετρειν (измерять),
то есть измерение треугольников) — раздел математики,
в котором изучаются тригонометрические функции и их приложения к геометрии.
Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса (Bartholomäus Pitiscus, 1561—1613),
а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, геодезии и архитектуре .

Эти ученые внесли свой вклад в развитие тригонометрии
Архимед
Жозеф Луи
Лагранж
Фалес

Тригонометрия возникла и развивалась в древности как один из разделов астрономии, как ее вычислительный аппарат, отвечающий практическим нуждам человека. С ее помощью можно определить расстояние до недоступных предметов и существенно упрощать процесс геодезической съемки местности для составления географических карт. Общепринятые понятия тригонометрии, а также обозначения и определения тригонометрических функция сформировались в процессе долгого исторического развития. Тригонометрические сведения были известны древним вавилонянам и египтянам, но основы этой науки заложены в Древней Греции встречающиеся уже в III веке до н.э.
в работах великих математиков– Евклида, Архимеда, Апполония Пергского. Древнегреческие астрономы успешно решали вопросы из тригонометрии, связанные с астрономией.

Тригонометрия – математическая дисциплина, изучающая зависимость между сторонами и углами треугольника.
Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела, при измерении расстояний до недалёких звёзд в астрономии, между ориентирами в географии, при контроле системы навигации, в теории музыки, акустике, оптике, электронике, теории вероятностей, статистике, биологии, медицине (включая ультразвуковое исследование (УЗИ) и компьютерную томографию), фармацевтике, химии, сейсмологии, метеорологии, океанологии, картографии, архитектуре, экономике, электронной технике, машиностроении, компьютерной графике.
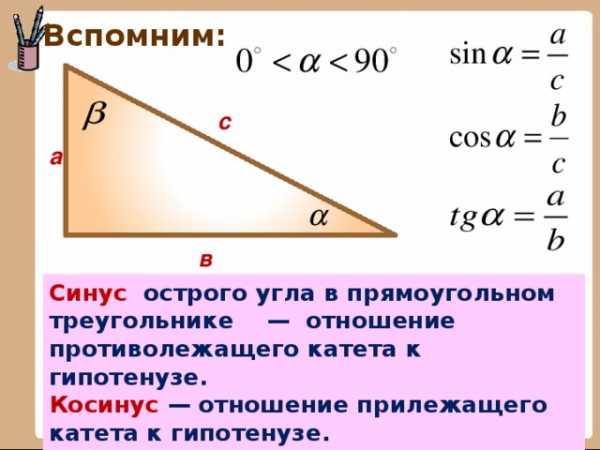
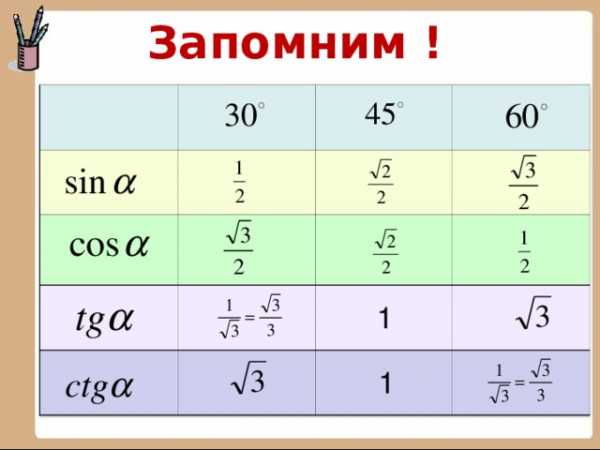
Вспомним:
с
а
в
Синус острого угла в прямоугольном треугольнике — отношение противолежащего катета к гипотенузе.
Косинус — отношение прилежащего катета к гипотенузе.
Тангенс — отношение противолежащего катета к прилежащему.

В XVIII веке Леонард Эйлер дал современные, более общие определения, расширив область определения этих функций на всю числовую ось.
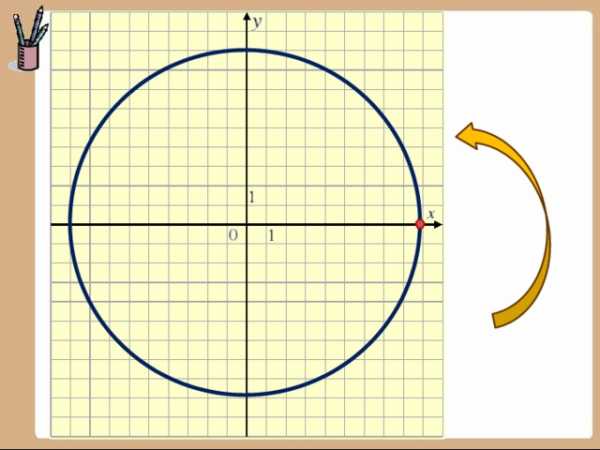
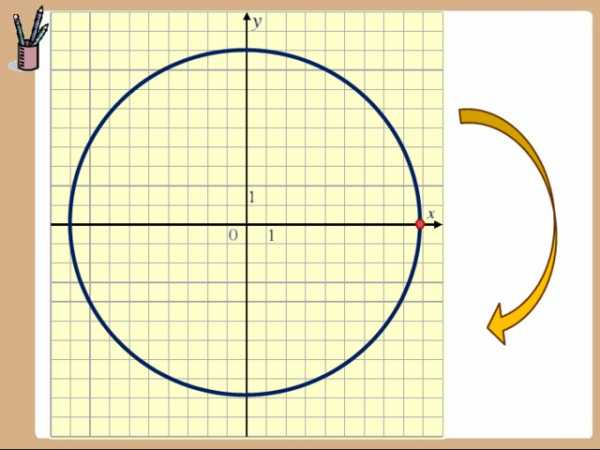

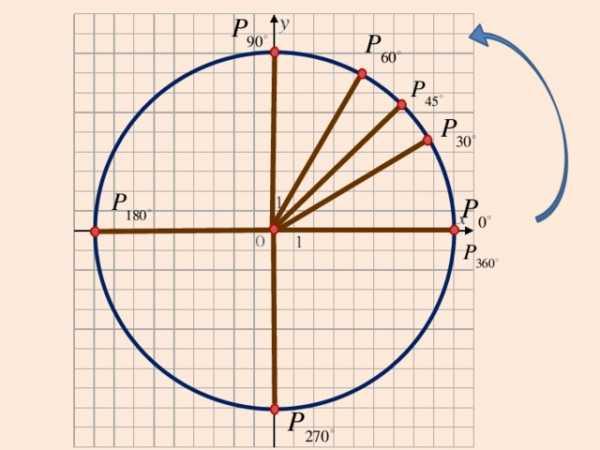
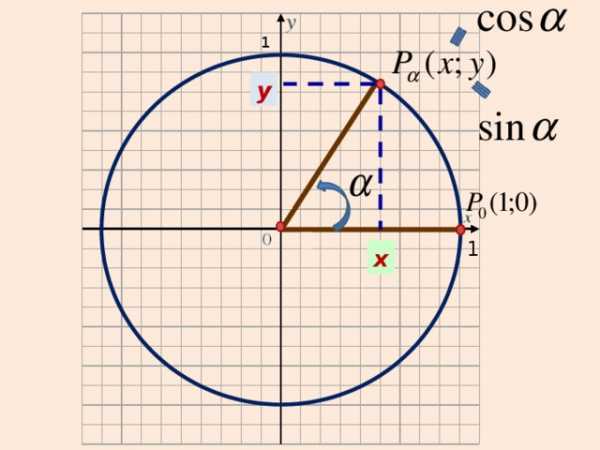
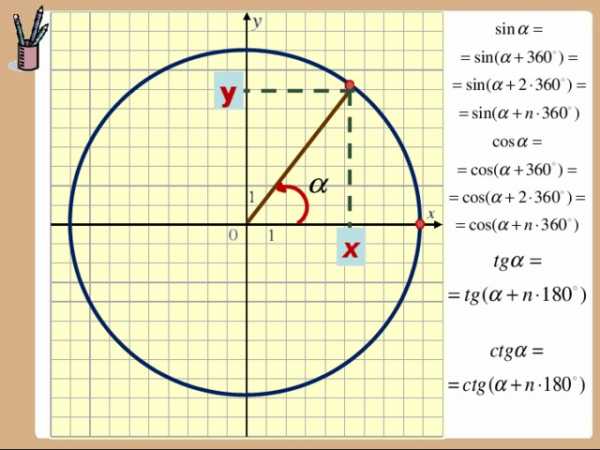
Рассмотрим в прямоугольной системе координат окружность единичного радиуса и отложим от горизонтальной оси угол
(если величина угла положительна, то откладываем против часовой стрелки, иначе по часовой стрелке). Точку пересечения построенной стороны угла с окружностью обозначим Р.
Р
1
1
у
1
х

Синус угла определяется как ордината
точки
Косинус — абсцисса точки
Тангенс – отношение ординаты к абсциссе
точки
Котангенс – отношение абсциссы к ординате
точки

Понятие синуса встречается уже в III в. до н. э.
и имел название джива (тетева лука) ,
в IX в. заменено на арабское слово
джайб (выпуклость) , XII в. заменено на латинское
синус (изгиб, кривизна) .
Косинус – это дополнительный синус.
Тангенс переводится с латинского
как «касающийся»
1
-1
1
-1
Запомним !
1
1
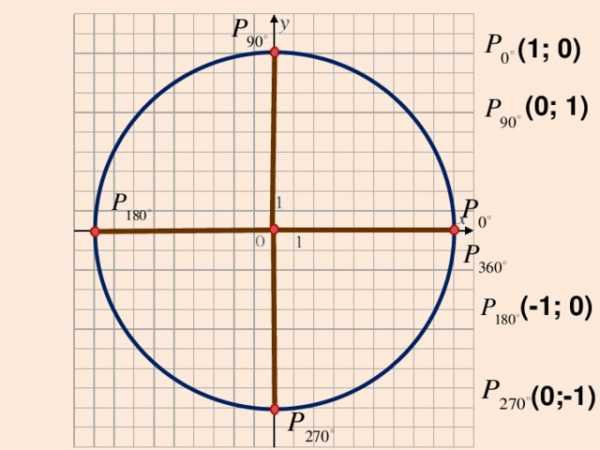
(1; 0)
(0; 1)
(-1; 0)
(0;-1)
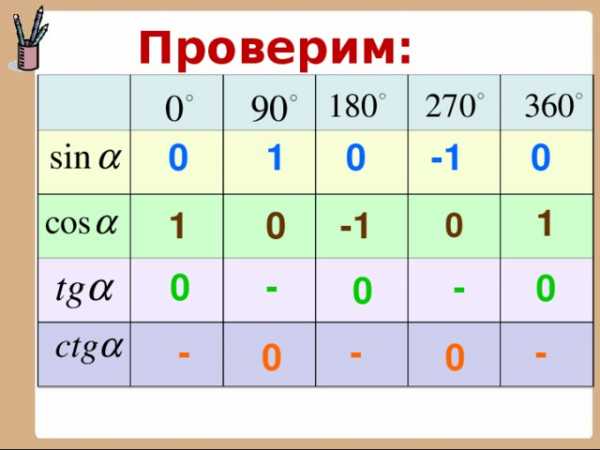
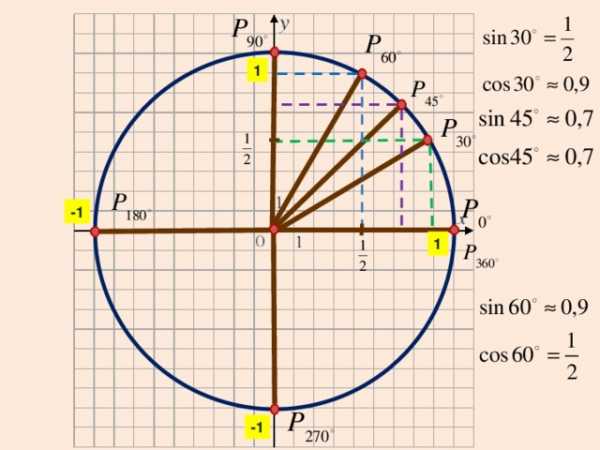
Проверим:
0
-1
0
1
0
1
1
0
-1
0
—
0
—
0
0
—
—
—
0
0
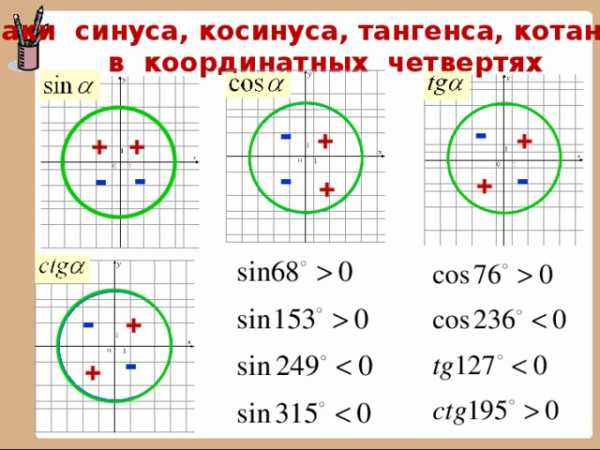
Знаки синуса, косинуса, тангенса, котангенса
в координатных четвертях
—
—
+
+
+
+
—
—
—
—
+
+
—
+
—
+

Четность, нечетность синуса, косинуса,
тангенса, котангенса
Нечетные функции
Четная функция

Периодичность тригонометрических
функций
При изменении угла на целое число оборотов
значения синуса, косинуса, тангенса, котангенса
не изменяются
у
х
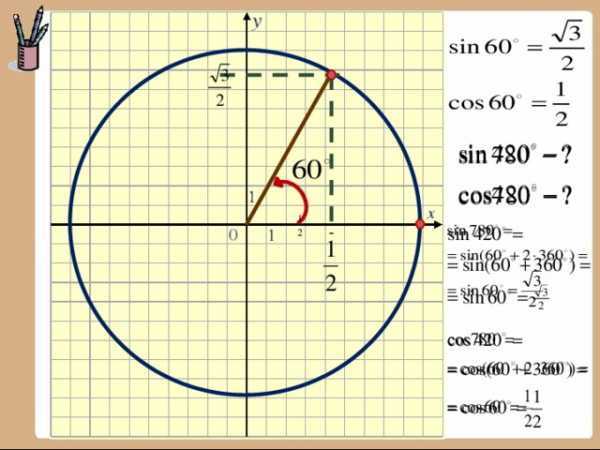
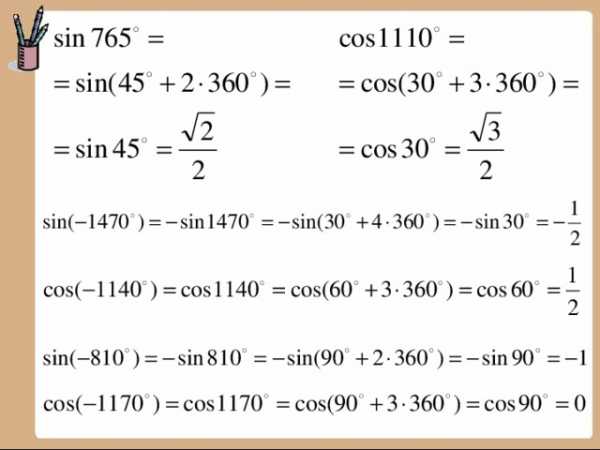
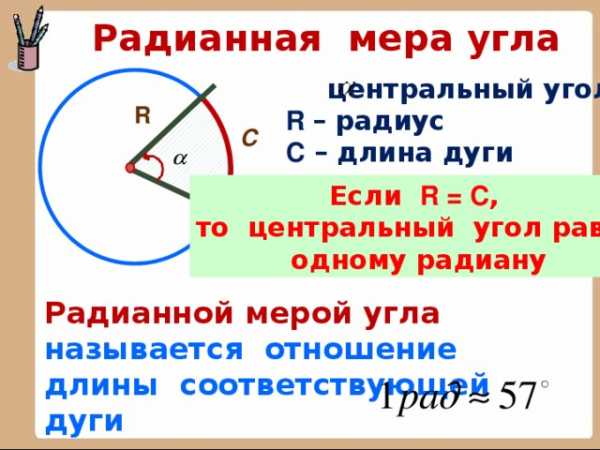
Радианная мера угла
центральный угол
R – радиус
С – длина дуги
R
С
Если R = C ,
то центральный угол равен
одному радиану
Радианной мерой угла называется отношение длины соответствующей дуги
к радиусу окружности
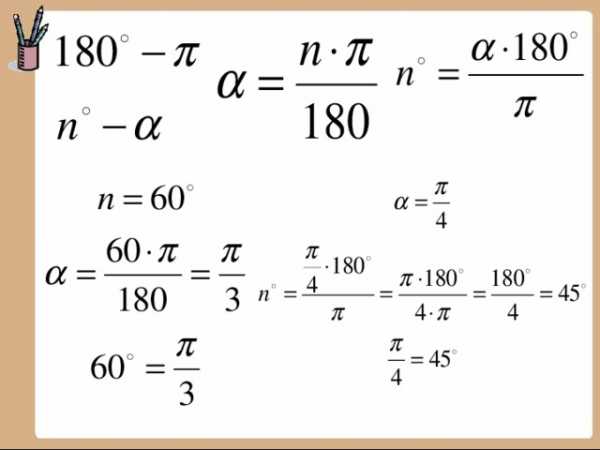
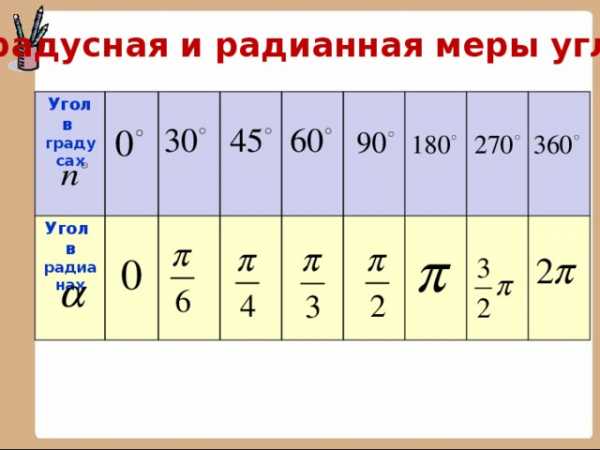
Градусная и радианная меры углов
Угол
в градусах
Угол
в
радианах
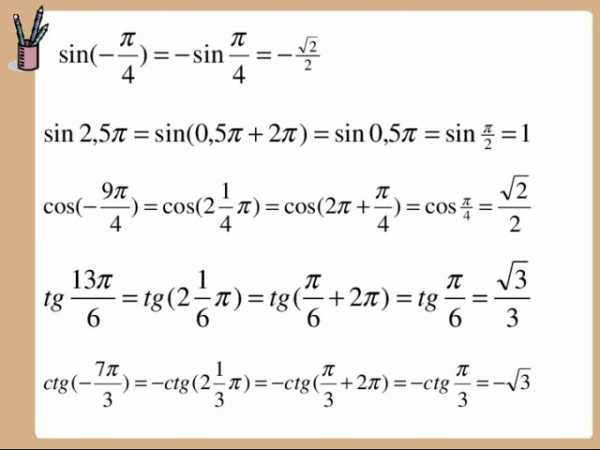
kopilkaurokov.ru
Открытый урок по математике 10 класс
10-класс
Тип урок:Обобщения и систематизация знаний
Тема: Производная функций,ее геометрический и физический смысл.Уравнение касательной .
Задачи:
Обучающие: Обобщить и систематизировать свой знания умения и навыки нахождения производных функции ,ее геометрическом и физическом смысле и применить их к решению задач ЕНТ
Развивающие:Развитие познавательных интересов ,вычислительных навыков ,навыков устного счета , использование рациональных способов решения ,умения взаймопроверки и самооценки знаний
Воспитывающие: воспитание трудолюбия,чувства ответственности, рационального использование урочного времени
План урока.
I.Оганизационный момент
II.Проверка домашнего задания :
Работа в группах.
1.Проверить и оценить работу;
2. Разминка- знание формул 3 мин. нахождение соответствия « Найди пару».
III.Основной этап урока.
1. Повторение теоритического материала;
2.Выполнение задач ЕНТ, решаемых устно ;
3.Задание на соответствие;
4. Задание-2;
5. Тест
IV.Заверщающий этап
Домашнее задание.
Оценка знаний
Итог урока
Самооценочная карта
Ход урока.
1.Организационный момент-(3-4мин)
-приветствие
-Девиз урока :
Урок начнем с девиза «Никогда не беритесь за последующее ,не усвоив предыдущее»
И.П. Павлов
Так как нам предстоит изучение темы «Применение производной,которая важна,так же как сама производная при подготовке и сдаче ЕНТ-ы,поэтому необходимо обобщить и закрепить наши знания по теме производная функций
И так тема урока:Производная функций,ее геометрический и физический смысл. Уравнение касательной в заданиях ЕНТ
Задачи урока:
Обучающие: Обобщить и систематизировать свой знания умения и навыки нахождения производных функции ,ее геометрическом и физическом смысле и применить их к решению задач ЕНТ
Развивающие:Развитие познавательных интересов ,вычислительных навыков ,навыков устного счета , использование рациональных способов решения ,умения взаймопроверки и самооценки знаний
Воспитывающие: воспитание трудолюбия,чувства ответственности, рационального использование урочного времени
2.Проверка домашнего задания-на дом были заданы 10 тестовых заданий из сборников ЕНТ-ы 2015
-«Проверь себя”
Ответы домашнего задания (3мин.)
3.А теперь разминка.(5мин)
-раздаточный материал
Найдите соответствие между функцией и ее производным.Напишите ответ. Например: 1функция – ? производная.
Ответы на соответствие:
Ответы: 1-9; 6-3; 11-14;
16-19; 2-4; 7-18; 12-19;
17-13; 3-5; 8-17; 4-19;
5-19; 15-16; 10-20.
Вопросы теоретического материала(7мин)
-
1.Определение производной функций и алгоритм ее нахождения
-
2.Правила вычисления производных
-
3.Физический смысл производной
-
4.Геометрический смысл производной
-
5.Уравнение касательной к графику функций в точке с абциссой х
-
6.Как найти уравнение касательной ,проведенной к графику функций у= f(x) параллельно прямой y=кх+в
-
7.Нахождение координаты точек пересечения производной и касательной проведенной в точку касания
-
8.Как найти уравнение касательной, если она пересекает ось ординат и ось абцисс
-
9.Как найти угол наклона между касательной и графиком функций
-
10.Как найти угловой коэффициент
-
11.Как найти скорость ,ускорение, силу и кинетическую энергию с помощью производной функций
Устные задания (5мин)
Некоторые задания ЕНТ расчитаны на устные выполнения,что позволяет сэкономить время для решения более сложных заданий:
1.у=
2. у=(х2+1) (х2-1)
3. у=-
4.у=cos2x+sin2x
5 y=cos2x-sin2x
6.y=(x-2) (x2+2х+4)
7.y=
Ответы:
1. y´=4x3— 3x2 2. y´=4x3 3. у/= 4. y´=0 5. y´=-2sin2x
6. y´=3x2 7. у/=
Тест
1.Найдите производную функций: f(x)=sin(x3+2)
A)3cos(x3+2) B)3sin(x3+2) C)x2(x3+2) D)3x2(x3+2) E) 3x2cos(x3+2)
2.В каких точках касательная,проведенная к графику функций у=
cостовляет с осью абцисс угол 60 0
A) ( ; ) B) ( 😉 C) (1 ; 1 ) D) ( ) E) ( )
3. Найдите производную функций f(x)=(x5+2x3)95
A)95(x5+2x3)94 B)95(x5+2x3)94 C)95(5x4+6x2)(x5+2x3)94
D) (x5+2x3)95 E)96(x5+2x3)96
4. Найдите производную функций: f(x)= (-5x2)32
A) -160(-5x2)32 B)-160(-5x2)32 C)-320(-5x2)32 D)8(-5x2)32 E)32(-5x2)32
5.Дана функция: у=найдите у/(х)
A) B — C) — D) E)
6. Найдите производную функций: f(x)=
A) B) C) D) E) —
7. Найдите производную функций:f(x)=(5x+6)8
A)5(5x+6)7 B)-8(5x+6)7 C)40(5x+6)7 D)13(5x+6)7 E)8(5x+6)8
8. Если y(x)=sin3x cos5x-cos3x sin5x,то y/() равно:
A)-1 B)- C) D)1 E) —
9. Если f(x)=sin3 . f/()
A) B) C)1 D)2 E)
10. Тело движется прямолинейно по закону S(t)=4t-t2 найдите скорость движения тела в момент времени t=1.75сек.
A)2,5м/с B)1м/с C)0,5м/с D)2м/с E)1,5м/с
Коды ответов:
Задачи :
Домашнее задание:задачи ЕНТ-2015год
Итог:
-
Изучение свойств и способов вычисления производных и их применение играет большую роль в развитий науки и техники.Это основа предмета ВУЗа –дифференциальное исчисления,механика.Необходимо для решения задач ЕНТ по физике, геометрии.
-
Материал этого урока поможет вам успешно выполнить задания при подготовке к ЕНТ.а также успешному усвоению следующего раздела: «Применение производных функций».
-
Урок окончен,
-
Спасибо за внимание!
-
Сегодня на уроке я узнал…»
-
«Сегодня на уроке я научился…»
-
«Сегодня на уроке я познакомился…»
-
«Сегодня на уроке я повторил…»
-
«Сегодня на уроке я закрепил…»
Письменная работа
Карточка №1 (уровень сложности А)
1 Найдите производную функции:
-
у = 4х4 — х5 + х2 -3х
-
у = (х + 4)3
-
у =
Карточка №2 (уровень сложности В)
1 Найдите производную функции:
-
у = —
-
у = sin(2х2 + 3)
3. Решите уравнение: f ‘ (x) = 0, если f (x) = —
Карточка №3 (уровень сложности С)
Найдите производную функции:
-
у =
-
у =
-
у = arctg 2x
Самооценочная карта
Самооценочная карта
Самооценочная карта
Карточка №1 (уровень сложности А)
1 Найдите производную функции:
-
у = 4х4 — х5 + х2 -3х
-
у = (х + 4)3
-
у =
——————————————————
Карточка №1 (уровень сложности А)
1 Найдите производную функции:
-
у = 4х4 — х5 + х2 -3х
-
у = (х + 4)3
-
у =
——————————-
Карточка №1 (уровень сложности А)
1 Найдите производную функции:
-
у = 4х4 — х5 + х2 -3х
-
у = (х + 4)3
-
у =
Карточка №1 (уровень сложности А)
1 Найдите производную функции:
-
у = 4х4 — х5 + х2 -3х
-
у = (х + 4)3
-
у =
——————————————
Карточка №1 (уровень сложности А)
1 Найдите производную функции:
-
у = 4х4 — х5 + х2 -3х
-
у = (х + 4)3
-
у =
infourok.ru
Открытый урок математики в 10 классе
Муниципальное бюджетное общеобразовательное учреждение
Песчано-Ковалинская средняя общеобразовательная школа
Лаишевского муниципального района
Республики Татарстан
Конспект фрагмента
открытого урока математики
в 10 классе
«Методы решений тригонометрических уравнений»
в рамках программы стажировки
руководителей общеобразовательных организаций
муниципальных районов Республики Татарстан
«Повышение качества образования через создание эффективной образовательно-воспитательной среды»
Учитель математики: Копцева Н. И.
30.01.2017 г.
Орг. момент. Здравствуйте, ребята! Я рада Вас приветствовать на уроке математики. Посмотрите друг на друга, улыбнитесь и присаживайтесь за парты. Наш сегодняшний урок мне хотелось бы начать словами французского писателя Анатоля Франса, который однажды заметил: «… Чтобы переварить знания, надо поглощать их с аппетитом». Давайте будем следовать этому совету писателя, будем активны, внимательны, всё будем делать с удовольствием и большим желанием (слайд 1).
А еще в начале нашего урока мне бы хотелось процитировать слова великого ученого Альберта Эйнштейна: «Мне приходится делить время между политикой и уравнениями. Однако уравнения гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно» (слайд 2).
—Скажите, пожалуйста, чем мы занимались на последних уроках математики (изучали формулы тригонометрии, применяли их при решении уравнений).
-А только ли в математике применяются формулы тригонометрии и умение решать тригонометрические уравнения? (слайд 3), (нет, во многих областях: геодезия, астрономия, электротехника, акустика и др.) (слайд 4)
-Молодцы! На прошлом уроке вы разделились на пары, каждая из которых получила задание. Итак, первое задание, рассказать другим группам об одной из областей применения тригонометрии (выступления учащихся).
-А где еще в недалеком будущем вам пригодятся знания по тригонометрии и умение решать тригонометрические уравнения? (ЕГЭ, задание 13 (С1)), (слайд 5)
Итак, тема сегодняшнего урока «Методы решения тригонометрических уравнений». Повторяем, обобщаем, приводим в систему изученные виды, типы, методы и приёмы решения тригонометрических уравнений (слайд 6).
Перед вами задача – показать свои знания и умения по решению тригонометрических уравнений.
-Что нужно знать, что бы решать тригонометрические уравнения? (формулы тригонометрии, алгебры, решение простейших тригонометрических уравнений, уметь находить значения обратных тригонометрических функций).
Устная работа. Насколько вы это умеете делать, мы сейчас проверим.
-
Найти ошибки в ответах (слайд 7)

-
Установи соответствие (слайд 8), (математическое лото)

На прошлом уроке мы с Вами выделили три класса тригонометрических уравнений по способу их решения(слайд 9).

На дом было задания парам: разобрать свой класс тригонометрических уравнений, привести пример тригонометрического уравнения данного класса из банка заданий ЕГЭ, дать задание другим парам на дом.
1 пара. Решение алгебраических уравнений. Решение алгебраических уравнений заключается в том, что все тригонометрические функции, которые входят в уравнение, выражают через какую-нибудь одну тригонометрическую функцию, зависящую от одного и того же аргумента.
Например:
2 пара. Решение однородных уравнений (уравнения, в которых у всех слагаемых сумма показателей одинакова) и приводимых к ним сводится к решению алгебраических относительно tgx путём деления обеих частей уравнения на cosx≠0 и cos2x≠0 соответственно.
Например:
3 пара. Решение с помощью разложения на множители сводится к решению двух или нескольких простейших тригонометрических уравнений.
Например:
|
1) sin x = |
|
|
2) cos x = |
|
|
3) tg x = -1 |
|
|
4) ctg x = — |
|
|
5) sin t = -2 |
|
|
6) cos t = 1 |
|
|
7) tg t = |
|
|
8) ctg t = 5 |
|
|
9) cos a =1,3 |
|
|
10) sin y = — |
|
|
11) sin a = 1 |
|
|
12) cos y = — |
|
|
1. — + , nZ |
|
|
2., nZ |
|
|
3. (-1)k +, kZ |
|
|
4.arctg+ ,nZ |
|
|
5.+ + 2, nZ |
|
|
6.+ , nZ |
|
|
7. нет корней |
|
|
8.(-1)k+1 +,kZ |
|
|
9. + + 2,nZ |
|
|
10. arcсtg5+,nZ |
|
|
7. нет корней |
11. + 2, nZ |
|
1 |
7 |
|
2 |
8 |
|
3 |
9 |
|
4 |
10 |
|
5 |
11 |
|
6 |
7 |
multiurok.ru