|
РАЗРАБОТКИ |
10 классВ категории разработок: 20 Фильтр по целевой аудитории — Целевая аудитория -для 1 классадля 2 классадля 3 классадля 4 классадля 5 классадля 6 классадля 7 классадля 8 классадля 9 классадля 10 классадля 11 классадля учителядля классного руководителядля дошкольниковдля директорадля завучейдля логопедадля психологадля соц.педагогадля воспитателя Представлено 4 варианта экзаменационной работы. Цель экзамена: проверка уровня предметной компетентности учащихся 10 класса по математике за курс 10 класса в рамках проведения промежуточной аттестации. Целевая аудитория: для 10 класса Представлена контрольная работа по алгебре для учеников 10 класса по учебнику Алимова Целевая аудитория: для 10 класса В работе представлены 4 варианта. Работа составлена в форме теста с кратким ответом и состоит из двух частей: Часть1 – 7 заданий базового уровня сложности с кратким ответом, часть 2 – 3 задания повышенного уровня сложности. Структура теста аналогична структуре КИМ ЕГЭ, что позволит не только проверить знания, умения и навыки учащихся за курс 10 класса, но и постепенно подготовить к работе с подобным материалом при подготовке и сдаче экзамена. На выполнение работы отводится 45 минут. Целевая аудитория: для 10 класса
Итоговая контрольная работа по алгебре и началам математического анализа за курс 10 класса составлена в соответствии с учебником: Целевая аудитория: для 10 класса
Итоговая контрольная работа по геометрии за курс 10 класса составлена в соответствии с учебником: Геометрия, 10-11: учебник для общеобразовательных учреждений. / Атанасян Л.С., Бутузов В.Ф. и др. – М.: Просвещение, 2009 — 2013. Целевая аудитория: для 10 класса 4 варианта + демонстрационный вариант. Ко всем вариантам даны ответы. Целевая аудитория: для 10 класса Данный материал содержит 9 теоретических самостоятельных работ по геометрии за курс 10 класса, к учебнику Л.С.Атанасян. Данные работы рекомендуется проводить на второй урок после изучения нового. Такая работа займет не много времени, 5-7 минут. Задания подобраны с разным уровнем сложности. Целевая аудитория: для 10 класса
В дидактических материалах предоставлены теоретические материалы по теме «Показательные уравнения», рассмотрены методы решения уравнений, предложены задания для самостоятельного изучения и закрепления новых знаний и умений. Это пособие поможет подготовиться к ЕГЭ по математике. Цель работы направлена на обучение решения показательных уравнений стандартного вида. При подготовке к ЕГЭ эти задачи входят в группы А и В. Целевая аудитория: для 10 класса Данная контрольная работа выполнена в форме малого ЕГЭ, содержит 15 различных вариантов по 15 вопросов в каждом. Каждый вариант разбит на 2 части. Часть 1: Задания B1 — B10 Часть 2: Задания B11 — B15. Ко всем вариантам есть ответы и критерии оценивания. Целевая аудитория: для 10 класса Планирование,контрольные работы,справочный материал по учебнику Мордковича,алгебра-10 Целевая аудитория: для 10 класса |
Конкурсы Диплом и справка о публикации каждому участнику! |
www.uchportal.ru
Тест по математике (10 класс) на тему: Итоговая контрольная работа по математике 10 класс.
Промежуточная аттестация по алгебре и началам анализа для 10 класса
2016-2017учебный год.
ВАРИАНТ 1.
- Найдите значение выражения : 24.
- Найдите производную функции:
а) f(x)= x3+x2+2x; б) h(x)=.
- Найдите угловой коэффициент касательной, проведенной к графику
функции у = 5х3+2х — 5 в его точке с абсциссой х = 3.
4. Решите уравнение : .
5. Дано Cos . Вычислить sin 2.
6. Найдите точки экстремума и определите их характер:
у = х3 + 3х2 – 9х – 2.
7. Решите уравнение: 2cos2 x + 3cos x + 1=0.
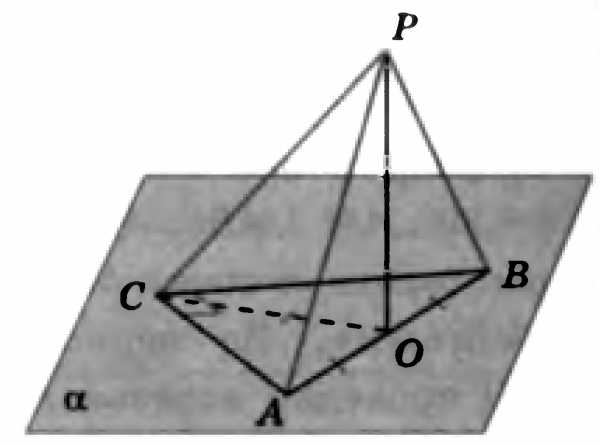
8. Боковое ребро правильной треугольной пирамиды равно 5 см, а высота √13 см. Найдите площадь боковой поверхности пирамиды.
ВАРИАНТ 2.
- Найдите значение выражения : 46.
- Найдите производную функции:
а) f(x)= — x3+2×2 — x; б) h(x)=.
- Найдите угловой коэффициент касательной, проведенной к графику
функции у = 7х3 + 6х — 5 в его точке х = 2.
- Решить уравнение 2sin ()=1.
- Дано Sin = , 000 .Вычислить sin (300+).
- Найдите точки экстремума и определите их характер:
у = 2х3 — 10х2 + 6х.
- Решите уравнение : 5sin2 x — 12sin x + 4=0.
- Сторона правильной треугольной пирамиды равна 6 см, а высота √13 см. Найдите площадь боковой поверхности пирамиды.
ВАРИАНТ 3.
- Найдите значение выражения :
- Найдите производную функции:
а) f(x)= x3+ 3×2+ x; б) h(x)=.
- Найдите угловой коэффициент касательной, проведенной к графику
функции у = х3- 2х2 + 3 в его точке с абсциссой х = — 1.
4. Решите уравнение : .
5. Найти
6. Найдите точки экстремума и определите их характер:
7. Решите уравнение : 2cos2 3x — 5cos 3x — 3=0.
8. Найдите площадь поверхности правильной четырехугольной пирамиды
Стороны основания которой равны 6 см и высота равна 4 см.
ВАРИАНТ 4.
- Найдите значение выражения : .
- Найдите производную функции:
а) f(x)= — x3+3×2 — x; б) h(x)=.
- Найдите угловой коэффициент касательной, проведенной к графику
функции у = х3 — 3х + 5 в его точке х = — 1.
- Решить уравнение : sin .
- Найти
- Найдите точки экстремума и определите их характер:
у = — х3 + 7 + 12х.
- Решите уравнение : 2sin2 x + 3 cos x =0.
- В правильной треугольной пирамиде SABC точка M – середина ребра AB, S – вершина. Известно, что BC = 3, а площадь боковой поверхности пирамиды равна 45. Найдите длину отрезка SM.
ВАРИАНТ 5.
- Найдите значение выражения :
- Найдите производную функции:
а) f(x)= ; б) h(x)=.
- Найдите угловой коэффициент касательной, проведенной к графику
функции в его точке с абсциссой х = 1.
4. Решите уравнение : .
5. Найти
6. Найдите точки экстремума и определите их характер:
7. Решите уравнение : 6cos2 x + cos x — 1=0.
8. Найдите площадь поверхности правильной четырехугольной
пирамиды, стороны основания которой равны 80 и высота равна 9.
ВАРИАНТ 6.
- Найдите значение выражения : .
- Найдите производную функции:
а) f(x)= — x4+5×2 — 7; б) h(x)=.
- Найдите угловой коэффициент касательной, проведенной к графику
функции у = в его точке х = 1.
- Решить уравнение : sin .
- Найти
- Найдите точки экстремума и определите их характер:
у = 8 + 2х2 – х4.
- Решите уравнение : 5cos2 x + 6 sin x — 6=0.
- В правильной треугольной пирамиде SABC точка M – середина ребра AB, S – вершина. Известно, что BC = 4, а площадь боковой поверхности пирамиды равна 48. Найдите длину отрезка SM.
ВАРИАНТ 7.
- Найдите значение выражения :
- Найдите производную функции:
а) f(x)= x4 + 2 x2+cos x; б) h(x)=.
- Найдите угловой коэффициент касательной, проведенной к графику
функции у = х2 — х + 5 в его точке с абсциссой х = 1.
4. Решите уравнение : .
5. Дано sin . Вычислить cos 2.
6. Найдите точки экстремума и определите их характер:
у = x3 – 12 x – 5.
7. Решите уравнение: sin2 x + 3cos x sin x + 2 cos2x=0.
8. Боковое ребро правильной треугольной пирамиды равно 5 см, а высота √13 см. Найдите площадь боковой поверхности пирамиды.
ВАРИАНТ 8.
- Найдите значение выражения :
- Найдите производную функции:
а) f(x)= ; б) h(x)=.
- Найдите угловой коэффициент касательной, проведенной к графику
функции у = 3х3 — х2 + x +1 в его точке х = 1.
- Решить уравнение 2 cos () =1.
- Дано sin = — 0,6 , 9000 .Вычислить — 2 cos .
- Найдите точки экстремума и определите их характер:
у = х3 — 3х – 5 .
- Решите уравнение : sin2 x — 3sin x cos x + 2 cos2x=0.
В правильной треугольной пирамиде SABC точка M – середина ребра AB, S – вершина. Известно, что BC = 4, а площадь боковой поверхности пирамиды равна 48. Найдите длину отрезка SM.
nsportal.ru
Контрольные работы по математике 10 класс со спецификациями
2. Упростите выражение: .
3. Вычислить .
4. Вычислить:
5. Упростить выражение:
6. Доказать тождество:
7. Решить уравнение
Контрольная работа по теме «Тригонометрические формулы»
Форма контрольной работы: контрольная работа
Вид контроля: тематический
Спецификация контрольной работы по математике
по теме «Тригонометрические уравнения» для обучающихся 10 классов
1.Назначение контрольно-измерительных материалов контрольной работы.
Контрольно-измерительные материалы позволяют оценить уровень подготовки по математике обучающихся 10 классов МБОУО лицей №6 в объеме, установленном обязательным минимумом содержания образования
2.Документы, определяющие содержание контрольно-измерительных материалов контрольной работы.
Содержание работы определяется на основе следующих документов:
Федеральный компонент государственного стандарта общего образования. Математика. Среднее (полное) общее образование (приказ Минобразования России №1089 от 05.03.2004) .Содержание контрольной работы по математике рассчитано на обучающихся 10 классов общеобразовательных учреждений, изучающих математику, в соответствии с Федеральным компонентом государственного стандарта среднего (полного) общего образования по математике, по учебнику (Ю.М Колягин, Ю.В.Сидоров и др. «Алгебра и начала анализа-10»,М. «Мнемозина) и учебно-методическим комплексом к ним, имеющими гриф Министерства образования и науки Российской Федерации.
3.Структура контрольной работы.
Работа состоит из одной части, которая направлена на проверку овладения содержанием курса математики на уровне углубленной подготовки. Эта работа содержит 5 заданий и предусматривает развернутый ответ с записью решения. Работа включает задания по темам «Показательная функция», «Показательные уравнения», «Показательные неравенства».
4.Обобщенный план варианта контрольно-измерительных материалов контрольной работы по математике для обучающихся 10 классов.
5.Оценивание работы
Для оценивания результатов выполненных работ обучающихся используется общий балл. Максимальный балл работу в целом – 10. Задание оценивается в 1 балл и считается выполненными верно, если приведено верное решение и записан верный ответ
6.Дополнительные материалы и оборудование: не используются.
7.Инструкция по выполнению работы.
Время выполнение работы-45 минут (1урок). Все задания выполняются с полным пояснением
Контрольная работа по теме «Тригонометрические уравнения»
Вариант 1
1. Решите уравнение:
2. Найдите решение уравнения на отрезке .
3. Решите уравнение:
; в)
4. Решите уравнение:
а)
в)
5.Решите систему уравнений:
Контрольная работа по теме «Тригонометрические уравнения»
Вариант 2
1. Решите уравнение:
а)
2. Найдите решение уравнения на отрезке .
3. Решите уравнение:
в)
4. Решите уравнение:
а)
в)
Решите систему уравнений:
.
Контрольная работа по теме «Тригонометрические функции»
Форма контрольной работы: контрольная работа
Вид контроля: тематический
Спецификация контрольной работы по математике
по теме «Тригонометрические функции» для обучающихся 10 классов
1.Назначение контрольно-измерительных материалов контрольной работы.
Контрольно-измерительные материалы позволяют оценить уровень подготовки по математике обучающихся 10 классов МБОУО лицей №6 в объеме, установленном обязательным минимумом содержания образования
2.Документы, определяющие содержание контрольно-измерительных материалов контрольной работы.
Содержание работы определяется на основе следующих документов:
Федеральный компонент государственного стандарта общего образования. Математика. Среднее (полное) общее образование (приказ Минобразования России №1089 от 05.03.2004) .Содержание контрольной работы по математике рассчитано на обучающихся 10 классов общеобразовательных учреждений, изучающих математику, в соответствии с Федеральным компонентом государственного стандарта среднего (полного) общего образования по математике, по учебнику (Ю.М Колягин, Ю.В.Сидоров и др. «Алгебра и начала анализа-10»,М. «Мнемозина) и учебно-методическим комплексам к ним, имеющими гриф Министерства образования и науки Российской Федерации.
3.Структура контрольной работы.
Работа состоит из одной части, которая направлена на проверку овладения содержанием курса математики на уровне углубленной подготовки. Эта работа содержит 6 заданий и предусматривает развернутый ответ с записью решения. Работа включает задания по темам «Тригонометрические функции, их графики и свойства»
4.Обобщенный план варианта контрольно-измерительных материалов контрольной работы по математике для обучающихся 10 классов.
5.Оценивание работы
Для оценивания результатов выполненных работ обучающихся используется общий балл. Максимальный балл работу в целом – 6. Задание оценивается в 1 балл и считается выполненными верно, если приведено верное решение и записан верный ответ
6.Дополнительные материалы и оборудование
Калькуляторы не используются.
7.Инструкция по выполнению работы.
Время выполнение работы-45 минут (1урок). Все задания выполняются с полным пояснением
Контрольная работа по теме «Тригонометрические функции»
Вариант 1
-
Найдите область определения функции .
-
Найдите область значений функции . Укажите, при каких значениях аргумента функция достигает наибольшего и наименьшего значения (если таковые существуют).
-
Какие из указанных ниже функций являются четными: какие нечетными и какие не являются ни четными, ни нечетными:
-
-
а) ; б) ; в) .
-
-
Постройте график функции . Опишите ее свойства (D(f), E(f), нули функции, промежутки знакопостоянства, промежутки возрастания и убывания).
-
Запишите все решения уравнения , принадлежащие промежутку .
-
Запишите все решения неравенства , принадлежащие промежутку .
-
-
Контрольная работа по теме «Тригонометрические функции»
-
Вариант 2
-
Найдите область определения функции .
-
-
2. Найдите область значений функции . Укажите, при каких значениях аргумента функция достигает наибольшего и наименьшего значения (если таковые существуют).
-
3. Какие из указанных ниже функций являются четными: какие нечетными и какие не являются ни четными, ни нечетными:
-
а) ; б) ; в) .
-
Постройте график функции . Опишите ее свойства (D(f), E(f), нули функции, промежутки знакопостоянства, промежутки возрастания и убывания)
-
Запишите все решения уравнения , принадлежащие промежутку .
-
Запишите все решения неравенства , принадлежащие промежутку .
-
-
Контрольная работа по теме «Параллельность в пространстве»
-
Форма контрольной работы: контрольная работа
-
Вид контроля: тематический
-
Спецификация контрольной работы по математике
-
по теме «Параллельность в пространстве» для обучающихся 10 классов
-
1.Назначение контрольно-измерительных материалов контрольной работы.
-
Контрольно-измерительные материалы позволяют оценить уровень подготовки по математике обучающихся 10 классов МБОУО лицей №6 в объеме, установленном обязательным минимумом содержания образования
-
2.Документы, определяющие содержание контрольно-измерительных
-
материалов контрольной работы.
-
Содержание работы определяется на основе следующих документов:
-
Федеральный компонент государственного стандарта общего образования. Математика. Среднее (полное) общее образование (приказ Минобразования России №1089 от 05.03.2004) .Содержание контрольной работы по математике рассчитано на обучающихся 10 классов общеобразовательных учреждений, изучающих математику, в соответствии с Федеральным компонентом государственного стандарта среднего (полного) общего образования по математике, по учебнику (Геометрия, 10-11: учебник для общеобразовательных учреждений/ Л.С. Атанасян, В.Ф, Бутузов, С.Б. Кадомцев и др. – Москва: Просвещение, 2010) и учебно-методическим комплексам к ним, имеющими гриф Министерства образования и науки Российской Федерации.
-
3.Структура контрольной работы.
-
Работа состоит из одной части, которая направлена на проверку овладения содержанием курса математики на уровне углубленной подготовки. Эта работа содержит 3 заданий и предусматривает развернутый ответ с записью решения. Работа включает задания по темам «Параллельность прямых», «Параллельность прямой и плоскости», «Параллельность плоскостей».
-
4.Обобщенный план варианта контрольно-измерительных материалов контрольной работы по математике для обучающихся 10 классов.
5.Оценивание работы
-
Для оценивания результатов выполненных работ обучающихся используется общий балл. Максимальный балл работу в целом – 3. Задание оценивается в 1 балл и считается выполненными верно, если приведено верное решение и записан верный ответ .
6.Дополнительные материалы и оборудование: не используются.
-
7.Инструкция по выполнению работы.
-
Время выполнение работы-45 минут (1урок). Все задания выполняются с полным пояснением
-
Контрольная работа ПО ТЕМЕ «пАРАЛЛЕЛЬНОСТЬ В ПРОСТРАНСТВЕ»
-
Вариант I
-
1. Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А2В2, если А1В1 = 12 см, В1О : ОВ2 = 3 : 4.
-
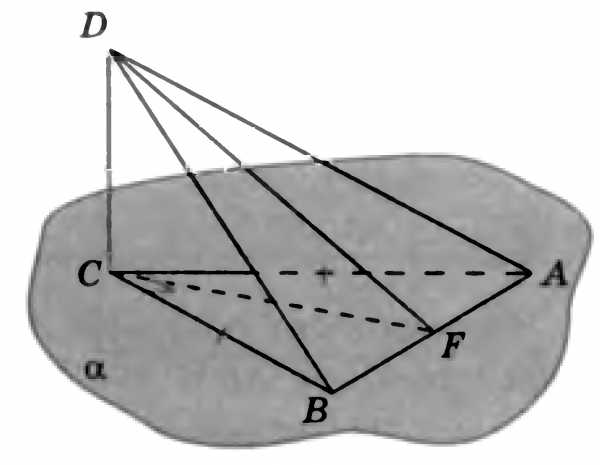
2. В тетраэдре DABC точки М и N-середины ребер DA и DВ. Постройте сечение тетраэдра, проходящей через точки M, N параллельно прямой DС. Определите вид построенного сечения.
-
3.Найдите площадь сечения единичного куба ABCDA1B1C1D1 плоскостью, проходящей через вершины A1, C1 и середину ребра DС.
-
Контрольная работа ПО ТЕМЕ «пАРАЛЛЕЛЬНОСТЬ В ПРОСТРАНСТВЕ»
-
Вариант II
-
1. Через точку О, не лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А1В1, если А2В2 = 15 см, ОВ1 : ОВ2 = 3 : 5.
-
2. В тетраэдре DABC точки М и К-середины ребер DA и ВС соответственно. Постройте сечение тетраэдра, проходящей через точки M, К параллельно прямой DС. Определите вид построенного сечения.
-
3.Найдите площадь сечения единичного куба ABCDA1B1C1D1 плоскостью, проходящей через вершины A, C и середину ребра A1D1
-
Контрольная работа по теме «Перпендикулярность в пространстве»
-
Форма контрольной работы: контрольная работа
-
Вид контроля: тематический
-
Спецификация контрольной работы по математике
-
по теме «Перпендикулярность в пространстве» для обучающихся 10 классов
-
1.Назначение контрольно-измерительных материалов контрольной работы.
-
Контрольно-измерительные материалы позволяют оценить уровень подготовки по математике обучающихся 10 классов МБОУО лицей №6 в объеме, установленном обязательным минимумом содержания образования
-
2.Документы, определяющие содержание контрольно-измерительных материалов контрольной работы.
-
Содержание работы определяется на основе следующих документов:
-
Федеральный компонент государственного стандарта общего образования. Математика. Среднее (полное) общее образование (приказ Минобразования России №1089 от 05.03.2004) .Содержание контрольной работы по математике рассчитано на обучающихся 10 классов общеобразовательных учреждений, изучающих математику, в соответствии с Федеральным компонентом государственного стандарта среднего (полного) общего образования по математике, по учебнику (Геометрия, 10-11: учебник для общеобразовательных учреждений/ Л.С. Атанасян, В.Ф, Бутузов, С.Б. Кадомцев и др. – Москва: Просвещение, 2010) и учебно-методическим комплексам к ним, имеющими гриф Министерства образования и науки Российской Федерации.
-
3.Структура контрольной работы.
-
Работа состоит из одной части, которая направлена на проверку овладения содержанием курса математики на уровне углубленной подготовки. Эта работа содержит 2 задания и предусматривает развернутый ответ с записью решения. Работа включает задания по темам «Перпендикулярность прямых», «Перпендикулярность прямой и плоскости», «Перпендикулярность плоскостей», «Угол между прямыми, прямой и плоскостью, плоскостями».
-
4.Обобщенный план варианта контрольно-измерительных материалов контрольной работы по математике для обучающихся 10 классов.
Геометрическая задача на нахождение:
-
а)измерений параллелепипеда (куба)
-
б)синуса (косинуса) угла между прямой и плоскостью
-
-
2
-
-
-
2
-
-
-
2
-
-
-
Геометрическая задача на нахождение:
-
а)расстояния от точки до плоскости
-
б)линейный угол двугранного угла
-
в)синуса угла между плоскостями
-
-
-
3
-
-
5.Оценивание работы
Для оценивания результатов выполненных работ обучающихся используется общий балл. Максимальный балл работу в целом – 5. Задание оценивается в 1 балл и считается выполненными верно, если приведено верное решение и записан верный ответ
6.Дополнительные материалы и оборудование: нет
7.Инструкция по выполнению работы.Время выполнение работы-45 минут (1урок). Все задания выполняются с полным пояснением
Контрольная работа теме «Перпендикулярность в пространстве»
Вариант 1
1. Диагональ куба равна 6 см. Найдите:
а) ребро куба;
б) косинус угла между диагональю куба и плоскостью одной из его граней.
2. Сторона АВ ромба ABCD равна a, один из углов равен 60°. Через сторону АВ проведена плоскость α на расстоянии от точки D.
а) Найдите расстояние от точки С до плоскости α.
б) Покажите на рисунке линейный угол двугранного угла DABM,
М α.
в) Найдите синус угла между плоскостью ромба и плоскостью α.
Контрольная работа теме «Перпендикулярность в пространстве»
Вариант 1
1. Основанием прямоугольного параллелепипеда служит квадрат; диагональ параллелепипеда равна 2 см, а его измерения относятся как 1 : 1 : 2. Найдите:
а) измерения параллелепипеда;
б) синус угла между диагональю параллелепипеда и плоскостью его основания.
2. Сторона квадрата ABCD равна а. Через сторону AD проведена плоскость α на расстоянии от точки В.
а) Найдите расстояние от точки С до плоскости α.
б) Покажите на рисунке линейный угол двугранного угла BADM,
М α.
в) Найдите синус угла между плоскостью квадрата и плоскостью α.
Итоговая контрольная работа
Форма контрольной работы: контрольная работа
Вид контроля: итоговый
Спецификация итоговой контрольной работы по математике
для обучающихся 10 классов
1.Назначение контрольно-измерительных материалов контрольной работы.
Контрольно-измерительные материалы позволяют оценить уровень подготовки по математике обучающихся 10 классов МБОУО лицей №6 в объеме, установленном обязательным минимумом содержания образования
2.Документы, определяющие содержание контрольно-измерительных
материалов контрольной работы.
Содержание работы определяется на основе следующих документов:
Федеральный компонент государственного стандарта общего образования. Математика. Среднее (полное) общее образование (приказ Минобразования России №1089 от 05.03.2004) .Содержание контрольной работы по математике рассчитано на обучающихся 10 классов общеобразовательных учреждений, изучающих математику, в соответствии с Федеральным компонентом государственного стандарта среднего (полного) общего образования по математике, по учебнику (Ю.М Колягин, Ю.В.Сидоров и др. «Алгебра и начала анализа-10»,М. «Мнемозина; Геометрия, 10-11: учебник для общеобразовательных учреждений/ Л.С. Атанасян, В.Ф, Бутузов, С.Б. Кадомцев и др. – Москва: Просвещение, 2010) и учебно-методическим комплексам к ним, имеющими гриф Министерства образования и науки Российской Федерации.
3.Структура контрольной работы.
Работа состоит из двух частей, которые направлены на проверку овладения содержанием курса математики на уровне углубленной подготовки. Первая часть содержит 12 заданий базового уровня. К каждому заданию 1-6 и 8-12 требуется дать краткий ответ, при выполнении задания 7 необходимо сделать выбор верных утверждений. Вторая часть включает 2 задания (13,14) повышенного уровня и 1 задание (15) высокого уровня сложности с развернутым ответом. Работа включает задания по темам «Выражения и преобразования», «Уравнения и неравенства», «Функции и их свойства», «Геометрические задачи»
4.Обобщенный план варианта контрольно-измерительных материалов контрольной работы по математике для обучающихся 10 классов.
5.Оценивание работы
Для оценивания результатов выполненных работ обучающихся используется общий балл. Максимальный балл работу в целом – 19. Верное выполнение заданий 1-12 оценивается 1 баллом. Выполнение заданий с развернутым ответом повышенного уровня (13, 14) в зависимости от полноты решения и правильности ответа оценивается от 0 до 2 баллов, а высокого уровня (15) – от 0 до 3 баллов
6.Дополнительные материалы и оборудование
Калькуляторы не используются.
7.Инструкция по выполнению работы.
Время выполнение работы-90минут (2урока). Все задания выполняются с полным пояснением
Итоговая контрольная работа по математике
Вариант 1
1. Вычислите + 0,5-1.
2. Упростите выражение .
3. Найдите значение выражения .
4. На одной из граней двугранного угла величиной 30о взята точка, находящаяся на расстоянии 56 см от ребра данного двугранного угла. Найдите расстояние от указанной точки до другой грани этого двугранного угла.
5. Найдите корень уравнения log3(x + 2) = log3(2x2 — 8) .
6. Найдите , если .
7. Выберите верные утверждения.
1) Через любые две точки пространства можно провести прямую.
2) Через любые три точки пространства можно провести плоскость.
3) Через любые четыре точки пространства можно провести плоскость.
4) Для любых двух плоскостей в пространстве найдутся две параллельные прямые, каждая из которых содержится ровно в одной из указанных плоскостей.
8. Решите уравнение 2x-1 + 2x+1 = 2,5.
9. Найти область определения функции .
10. Упростите выражение .
11. Упростите выражение .
12. На рисунке изображен график функции y = f(x) ,
определенной на (-4;8). Найдите сумму точек экстремума функции f(x)
13. Решите уравнение
14. В правильной четырёхугольной призме площадь основания 16 см2, а высота 2 см. Найдите диагональ призмы и угол между прямой, содержащей эту диагональ, и плоскостью боковой грани.
15. Решите неравенство:
Итоговая контрольная работа по математике
Вариант 2
1. Вычислите — 0,25-2
2. Упростите выражение .
3. Найдите значение выражения 44.
4. На одной из граней двугранного угла величиной 30о взята точка, находящаяся на расстоянии 38 см от другой грани данного двугранного угла. Найдите расстояние от указанной точки до ребра этого двугранного угла.
5. Найдите корень уравнения log3(x2 + 4) = log3(2x + 7).
6. Найдите , если .
7. Выберите венные утверждения.
1) Любая прямая в пространстве имеет общую точку хотя бы с одной плоскостью.
2) Любые две непараллельные прямые в пространстве имеют общую точку.
3) Любые две непараллельные плоскости в пространстве имеют общую точку.
4) Для любых двух прямых в пространстве найдутся две параллельные плоскости, каждая из которых содержит ровно одну из данных прямых.
8. Решите уравнение 41-x + 42—x = 1,25.
9. Найдите область определения функции у=.
10. Упростите выражение .
11. Упростите выражение .
12. На рисунке изображен график функции y = f(x), определенной на (-7;5) . Найдите сумму точек экстремума функции f(x).
13. Решить уравнение
14. В основании прямой треугольной призмы АВСА1В1С1 лежит прямоугольный треугольник с прямым углом С и катетами 8 и 6 см. Площадь боковой поверхности призмы 120 см 2 . Найдите длину бокового ребра призмы и угол между прямой С1М , где М – середина АВ, и плоскостью основания призмы.
15. Решите неравенство:
infourok.ru
Итоговая контрольная работа по математике (10 класс)
Вариант 1
А1 Упростить: 5sin 2α – 4 + 5cos2α
1) 1 2) 9 3) -9 4) -4
А2 Найти все решения уравнения:
-
 + 2πn , где n; 2) 2πn , где n; 3) πn , где n; 4) π +2πn , где n
+ 2πn , где n; 2) 2πn , где n; 3) πn , где n; 4) π +2πn , где n
А3 Указать множество значений функции: y = 2 cos x – 1
1) [-1; 1 ] 2) ( -∞; ∞) 3) [-1; 3 ] 4) [-3; 1 ]
А4 Найти значение выражения: 5cos2x + 1 , если sin2x = 0,3
1) 2,5 2) 5,55 3) 4,5 4) 7, 5
А5 Найти значение выражения: 2 – tg2x∙ cos2 x, если sin x = 0,2
1) 1,2 2) 1,96 3) 1,04 4) 1,6
А6. Укажите производную функции у = х4 – 
1)4х —  2) 4х3 —
2) 4х3 —  3) 4х3 +
3) 4х3 +  4) 4х +
4) 4х + 
А7. Найдите производную функции у = 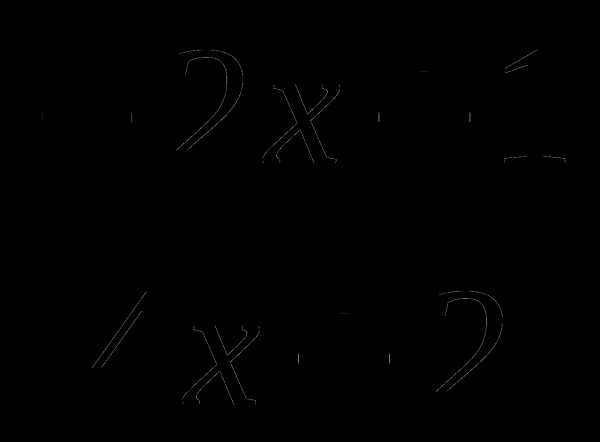
1) – 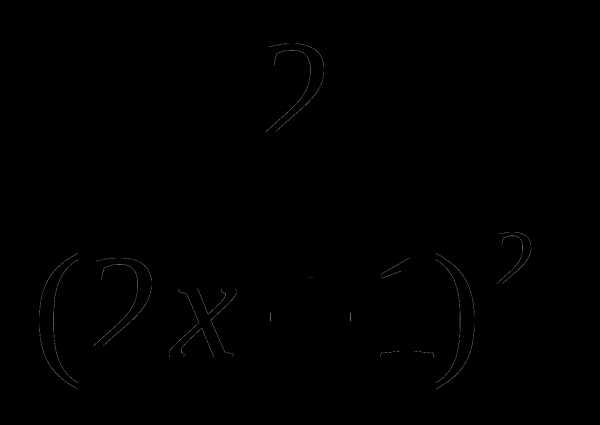 2)
2) 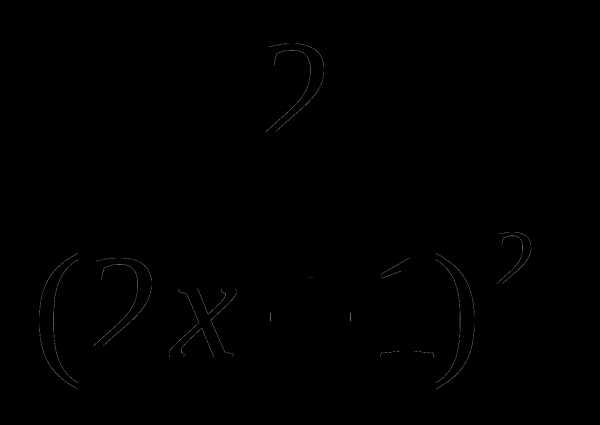 3)
3) 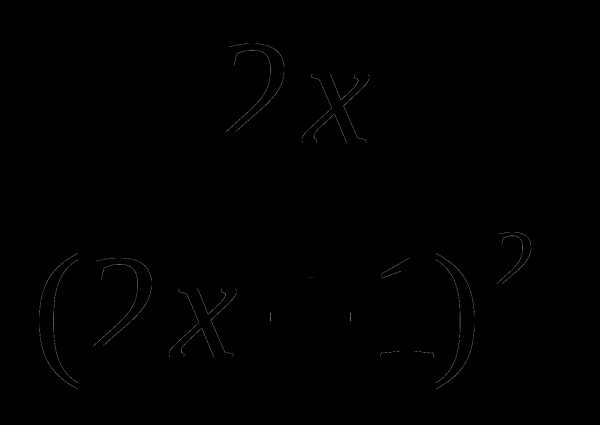 4) —
4) — 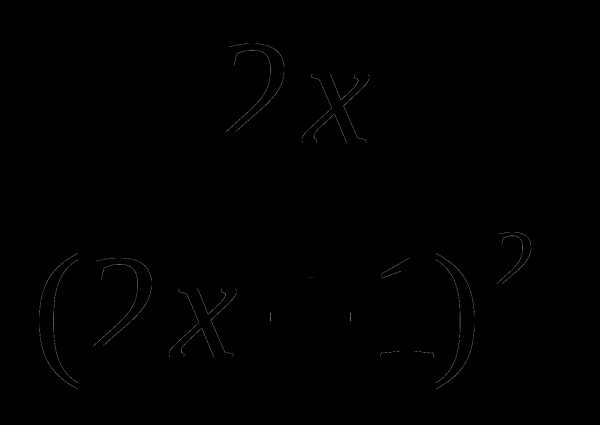
А8. Найдите тангенс угла наклона касательной, проведенной к графику функции у = 4 – х2 в точке с абсциссой х0 = — 3
1) 0 2)6 3) -6 4) -5
А9. Найдите производную функции у = х3 + sin x
1) y‘ =3x2+cosx 2) y‘= x2 + cos x 3) y‘=x2-sinx 4) y‘=3x2-cosx
А10. Найдите точку максимума функции у = х3 – 2х2
1) -1 2) 2 3) -2 4) 0
— — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — —
В1. Найдите наибольшее значение функции f(x) = x3 – 3x на отрезке [0;3].
В 2.
За время t тело перемещается по прямой на расстояние S(t) = 2,5t2 – 11t +17. Через сколько секунд скорость точки будет равна 14?
В 3. Найдите значение выражения: 21 ∙ sinα ∙ ctg(π-α), если cosα =
∙ sinα ∙ ctg(π-α), если cosα =
B4. На рисунке изображен 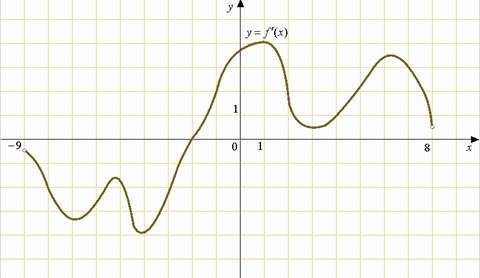 график производной функции , определенной на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней.
график производной функции , определенной на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней.
В5. Найти сумму корней уравнения 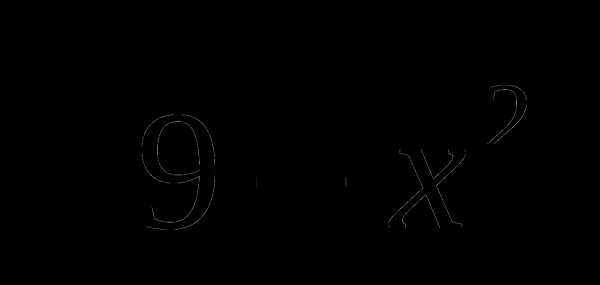 ∙ sin2x = 0
∙ sin2x = 0
В6. Найдите минимум функции g(x) = 3х5 – 5х3.
В7
С1. Решите уравнение
С2. Определите размеры бассейна с квадратным дном и объёмом 32 м3 таким образом,
чтобы сумма площади боковой поверхности и площади дна была минимальной. В
ответе укажите площадь боковой поверхности.
С3
Вариант 2
А1 Упростить:
1) 1 2 ) ctg2α 3) tg2α 4) 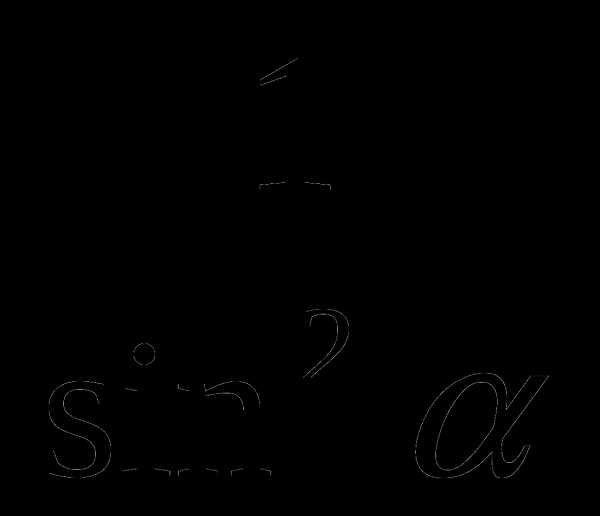
А2 Найти все решения уравнения: (tg2х + 1)∙ tg х =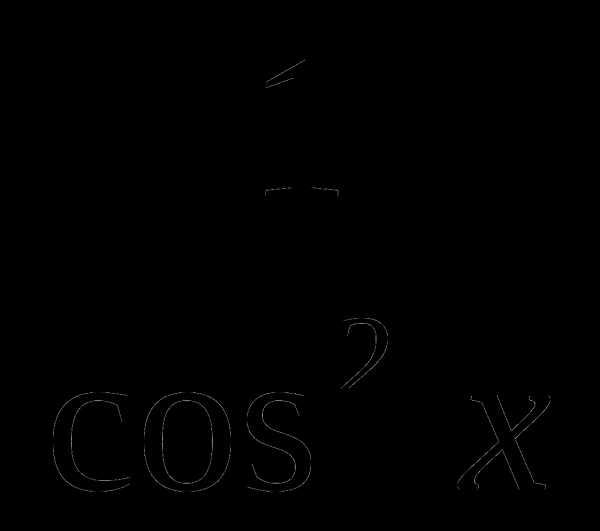
1)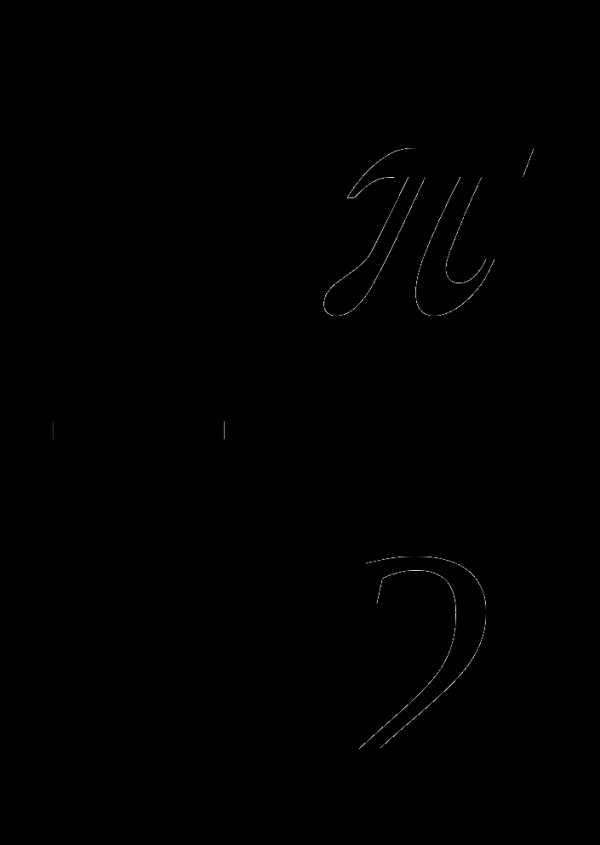 + 2πn , где n; 2) πn , где n ; 3)
+ 2πn , где n; 2) πn , где n ; 3)  + πn , где n; 4) —
+ πn , где n; 4) — + πn, где n
+ πn, где n
А3 Указать множество значений функции: y = sin x – 3
1) [-4; -2 ] 2) [-10; 4 ] 3 )[-4; 4 ] 4) [-10; 10 ]
А4 Найти значение выражения: 3 sin2x – 1, если cos2 х = 0,5
1) 0,5 2) 1,25 3) -1,5 4) -0,5
А5 Найти значение выражения : 3 + 2tg2 x∙ cos2 x, если sin x = 0,3
1) 4,82 2) 3,6 3)4,8 4) 3,18
А6. Укажите производную функции : у = х2 + cosx.
1) 2х+sin x 2) 2x – sin x 3) x – sin x 4) x + sin x
А7. Найдите производную функции : у = 3х2 ∙ cosx.
1) -6xsinx 2) x3cosx + 3x2sinx 3) 6xcosx + 3x2sinx 4) 6xcosx – 3x2sinx
А8. Найдите тангенс угла наклона касательной, проведенной к графику функции у = 2х – х2 в его точке с абсциссой х0 = -2
1) 0 2) 6 3) -2 4) -8
А9. Найдите производную функции: у = (х+1)(х+2) – (х-1)(х-3)
1) 7 2) — 7 3) -1 4) 1
А10. Найдите точку минимума функции: у = х2 – 1.
1) 0 2) 0,5 3) 1 4) -1
В1. Найдите наименьшее значение функции : f(х) = х3 – 3х на отрезке [-3;3].
В2. За время t тело перемещается по прямой на расстояние S(t) = 3t2 — 4,5t + 5.
Через сколько секунд скорость будет 13,5?
В3. Найти значение выражения : 3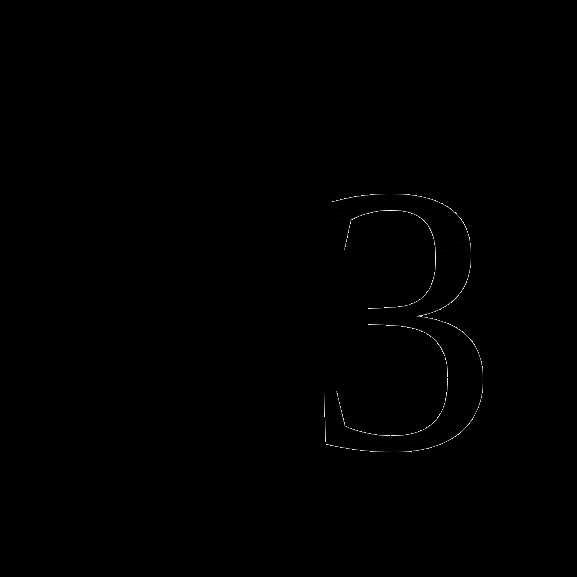 ∙ tgα ∙ cos2(π-α), если sin2α =
∙ tgα ∙ cos2(π-α), если sin2α = 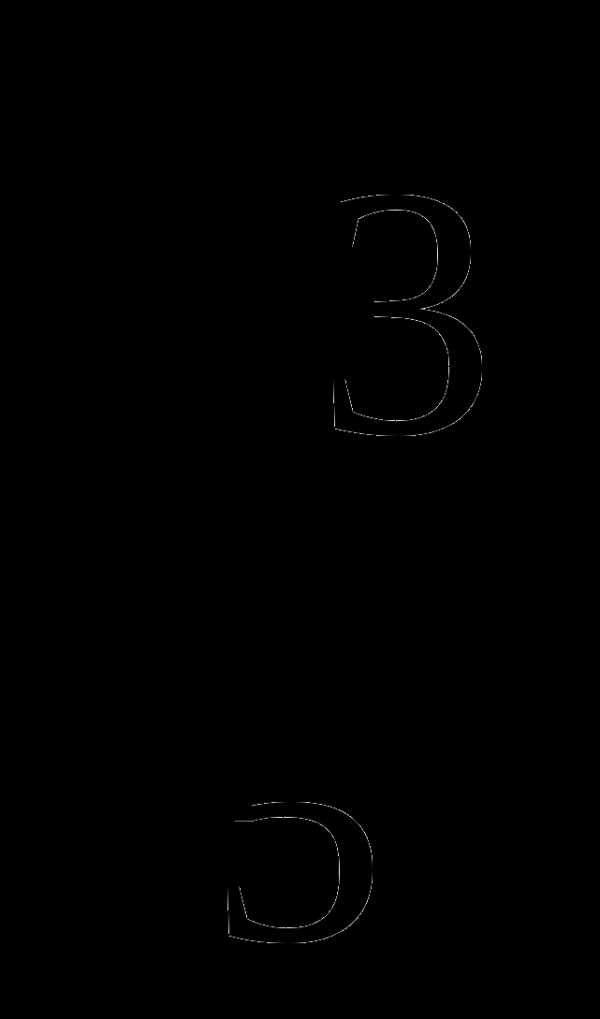 .
.
В4. Функция у = f (х) определена на промежутке (-8;8). График её производной изображен на рисунке. Укажите число промежутков возрастания функции.
В5. Найти сумму корней уравнения 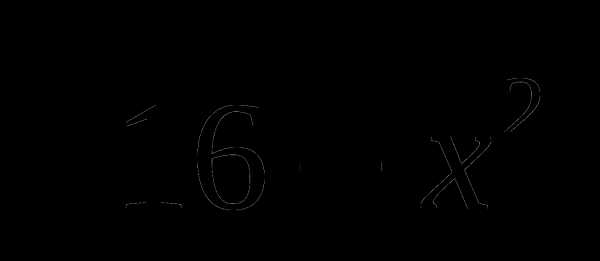 ∙ cos2x = 0
∙ cos2x = 0
В6. Найдите максимум функции у =  +
+ — 2х — 2
— 2х — 2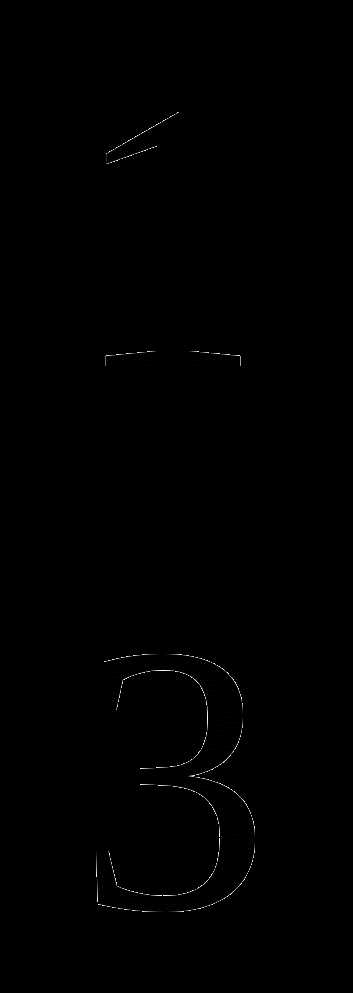 .
.
В7
С1. Решите уравнение :
С2. Рассматриваются всевозможные прямоугольные параллелепипеды, объём каждого
из которых равен 32 см3, а одна из боковых граней является квадратом. Найдите среди них параллелепипед с наименьшим периметром основания. В ответе укажите этот периметр.
С3

Вариант 3.
А1. Упростить: cos4x + sin2x ∙ cos2x
1) cos2x 2) 2sin2x 3) cos4x. 4) cos2x
А2. Найдите все решения уравнения: 2sinx ∙( tg2x + 1) = 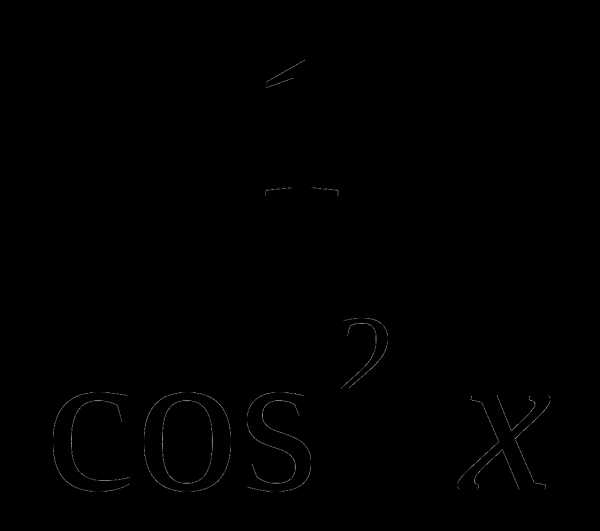
1) πn, n z 2)(-1)n
z 2)(-1)n  + πn, n
+ πn, n z 3)
z 3)  +
+  n, n
n, n z 4)
z 4)  + 2
+ 2 n, n
n, n z
z
А3. Найдите множество значений функции: у = cosх -10
1) 2)
2)  3)
3)  4)( -∞; + ∞)
4)( -∞; + ∞)
А4. Найдите значение выражения: 3 – 2tg2x ∙ cos2x, если sinx = 0,1
1) 2,98 2) 1,02 3) 2,8 4) 3,02
А5. Найдите значение выражения: 3cos2x – 2, если sin2x = 0,1
1) 1,3 2) 0,7 3) — 0,5 4) –1,7
А6. Укажите производную функции : у = х2 –sinx
1) 2x — cosx 2) 2x + cosx 3)  + cosx 4)
+ cosx 4)  — cosx
— cosx
А7. Найдите производную функции: у = -3,6х2 ∙ cosx
1) -7,2xcosx — 3,6x2sinx 2) -7,2xcosx +3,6x2sinx 3) -1,2x3cosx + 3,6x2sinx
4) 7,2xsinx
А8. Найдите тангенс угла наклона касательной, проведённой к графику функции у = -0,5х2 в его точке с абсциссой х0 = -3.
1) -3 2) 3 3) -4,5 4) 0.
А9. Найдите производную функции: у = 9 – 9х8 —  х5
х5
1) у’ = 9х – х9 —  х6 2) у’ = 9х – 72х7 – 5х4 3) у’ = -17х7 — 6х4 4) у’ = -72х7 – 6х4
х6 2) у’ = 9х – 72х7 – 5х4 3) у’ = -17х7 — 6х4 4) у’ = -72х7 – 6х4
А10. Найдите точку максимума функции: у = х3 – 3х + 2
1) 1 2) 0 3) -1 4) 4.
В1. Найдите наименьшее значение: f(x) = х3 + 3х на отрезке  .
.
В2
Точка движется по координатной прямой согласно закону х(t) = t2 — 5t – 7, где х(t)-координата точки в момент времени t. Найдите её скорость при t = 3.
t2 — 5t – 7, где х(t)-координата точки в момент времени t. Найдите её скорость при t = 3.
В3. Найдите значение выражения
18 ∙ sinα ∙ ctg(
∙ sinα ∙ ctg( — α), если cosα =
— α), если cosα =  .
.
В4. Функция у = f(х) определена на промежутке (-10;2). График её производной изображён на рисунке. Сколько точек экстремума имеет функция у = f(х) на этом промежутке?
В5. Сколько корней имеет уравнение: 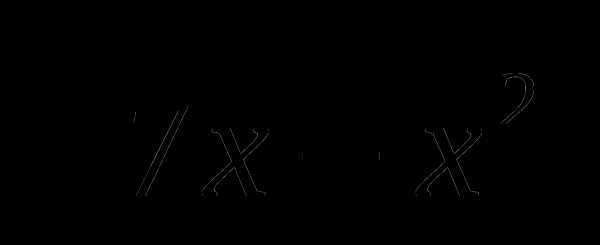 ∙ (2cosx – 1) = 0.
∙ (2cosx – 1) = 0.
В6. Найдите минимум функции: f(х) =  .
.
В7
С1. Решите уравнение :
С2. Рассматриваются всевозможные прямоугольные параллелепипеды, объем каждого
из которых равен 4 см3, а одна из боковых граней является квадратом. Найдите
среди них параллелепипед с наименьшим периметром основания. В ответе укажите
этот периметр.
С3

Вариант 4.
А1. Упростить: 1 – sinα ∙ ctgα ∙ cosα
1) 0 2) cos2α 3) sin2α 4) 1 – sin2α
А2. Найдите все решения уравнения: ctg2x ∙ (1 — cos2x) = 0
1)  +
+ n, n
n, n z. 2)
z. 2)  n, n
n, n z 3)
z 3)  n, n
n, n z 4)
z 4)  +
+  n, n
n, n z
z
А3. Найдите множество значений функции: у = 6cos3x
1)  2)
2) 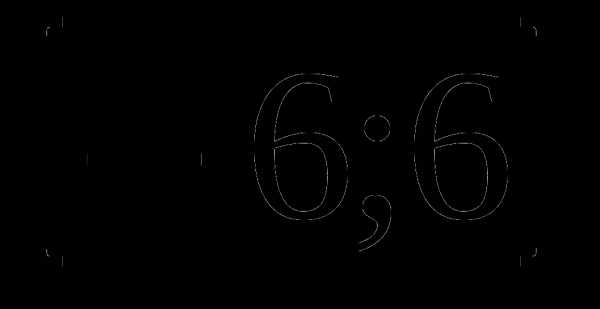 3)
3) 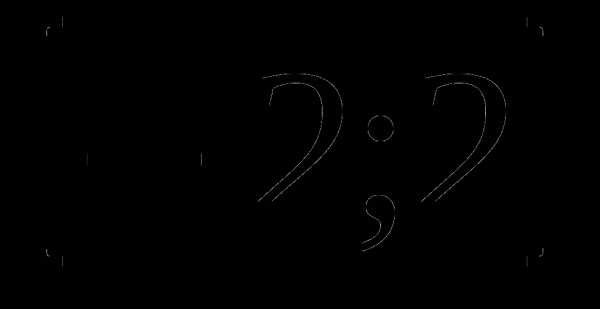 4)
4) 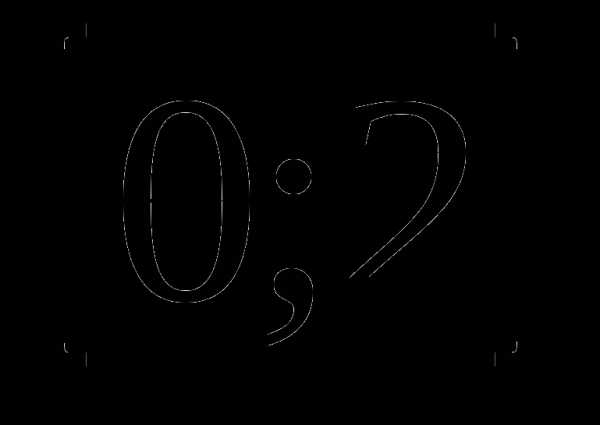
А4. Найдите значение выражения: 4 + 5tg2x ∙ cos2x, если sinx = 0,4
1) 6 2) 4,8 3) 4,4 4) 9,2
А5. Найдите значение выражения: 14sin2x – 3, если cos2x = 0,7
1)-2,58 2) 39 3) 1,2 4) 6,8.
А6. Укажите производную функции: у = х2 + cosx
1) 2x + sinx 2)  — sinx 3)
— sinx 3)  + sinx 4) 2x – sinx
+ sinx 4) 2x – sinx
А7. Найдите производную функции : у = 5х2 sinx
1) y’ = 10xcosx 2) y’=10xsinx — 5x2cosx 3) y’=10xsinx + 5x2cosx
4) y’ = 10xcosx + 5x2sinx
А8. Найдите тангенс угла наклона касательной, проведенной к графику функции у = 2х2 в его точке с абсциссой х0 = -1
1) 4 2) 2 3) -2 4) — 4
А9. Найдите производную функции: у = 8 -5х4 + 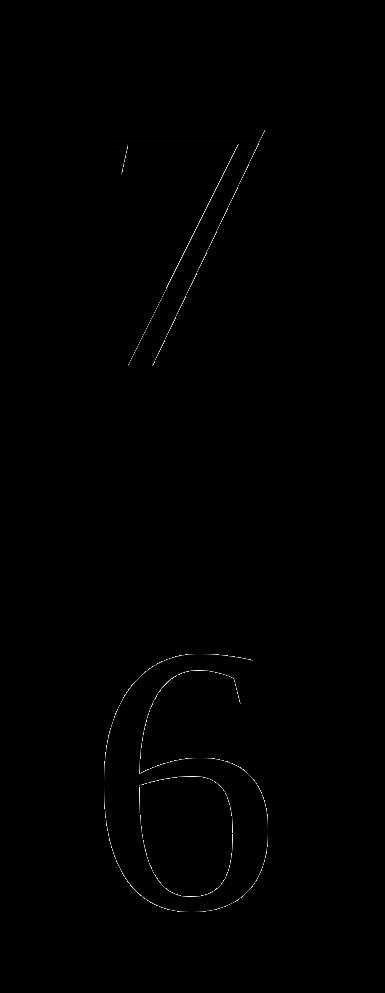 х6
х6
1) у’ = -20х3 + 7х5 2) у’ = 8х – 20х5 + 7х7 3) у’ = 8х – х5 + х7
х7
4) у’ = -20х3 + 7х4.
А10. Найдите точку максимума функции: у = 4х – х4
1) 1 2) -1 3) 0 4) -2.
В1. Найдите наибольшее значение функции: f(x) = -х3 – 3х на отрезке 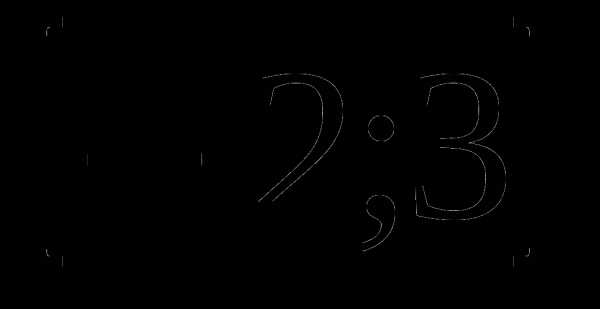 .
.
В2.
За время t тело перемещается по прямой на расстояние S(t) = 0,5t2 – 7t + 23. Через сколько секунд скорость точки будет равна 6?
В3. Найдите значение выражения: 6 ∙ tgα ∙ cos2(
∙ tgα ∙ cos2( — α), если sin2α =
— α), если sin2α =  .
.
В4. Функция у = f(x) определена на промежутке (-4;10). График её производной изображён на рисунке. Укажите наибольшую длину промежутка возрастания функции
у = f(х).
В5. Сколько корней имеет уравнение ( sinx + cosx )2 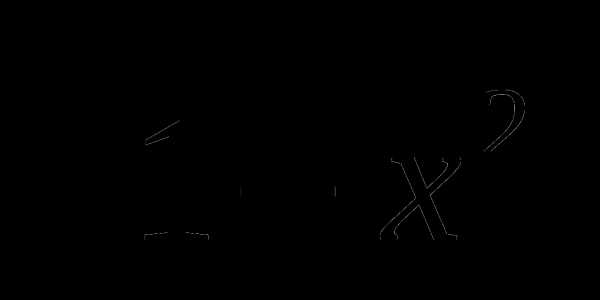 =0 ?
=0 ?
В6. Найдите максимум функции у = х3 – 2х2 – 7х + 3.
В7 Найдите наибольшее значение функции у=9х – 8 sin х +7 на отрезке
С1. Решите уравнение.
С2. Закрытый металлический бак с квадратным дном должен иметь объём 216 м3.
При каких размерах на его изготовление пойдет наименьшее количество материала?
С3 
infourok.ru
Методическая разработка по алгебре (10 класс) по теме: Итоговая контрольная работа по математике за курс 10 класса
Итоговая контрольная работа по математике
за курс 10 класса
Вариант№1
Блок I. Корень n- ой степени. Иррациональные уравнения.
№1. Найдите значение выражения:
- 2) 3)
№2. Найдите корень уравнения:
- 2)
- Если уравнение имеет более одного корня, в ответе запишите меньший из них.
Блок II. Степень с рациональным показателем. Показательные уравнения.
№1. Найдите значение выражения:
- при 2) 3)
№2. Найдите корень уравнения:
- 2) 3)
Блок III Логарифмы. Логарифмические уравнения.
№1. Найдите значение выражения:
- 2) 3)
№2. Найдите корень уравнения:
Блок IV. Тригонометрия.
№1. Найдите значение выражения:
- 2)
- ,если
№2. Найдите корень уравнения:
В ответе запишите наибольший отрицательный корень.
В ответе напишите наибольший отрицательный корень.
В ответе напишите наименьший положительный корень.
№3. а) Решите уравнение .
б) Укажите корни этого уравнения, принадлежащие
отрезку
Блок V. Стереометрия.
№1. Основанием прямой треугольной
призмы служит прямоугольный
треугольник с катетами 6 и 8, высота
призмы равна 10. Найдите площадь
ее поверхности.
№2. В прямоугольном параллелепипеде известны длины рёбер , , . Найдите синус угла между прямыми и
№3. Ребра тетраэдра равны 33. Найдите площадь сечения,
проходящего через середины четырех его ребер.
№4. В правильной шестиугольной призме все ребра равны 48. Найдите расстояние между точками и
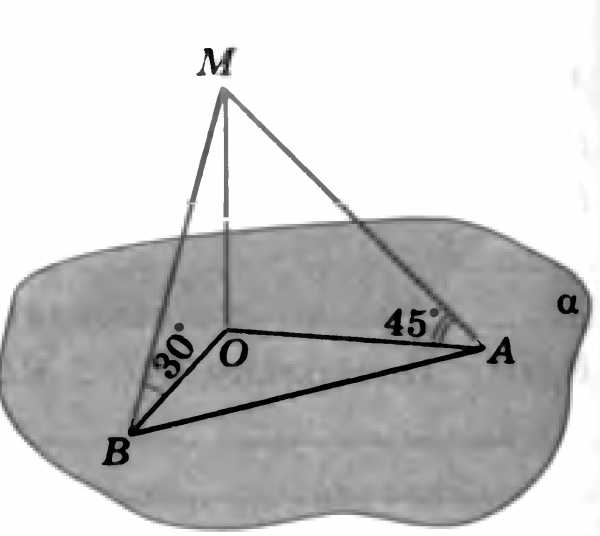
№5. В правильной четырехугольной пирамиде точка — центр основания, вершина, , . Найдите боковое ребро
№6. В прямоугольном параллелепипеде известно, что , , . Найдите длину ребра .
№7. Стороны основания правильной шестиугольной пирамиды равны 72, боковые рёбра равны 85. Найдите площадь боковой поверхности этой пирамиды.
№8. Во сколько раз увеличится площадь поверхности куба, если все его рёбра увеличить в 2 раза?
№9. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
№10. В кубе найдите угол между прямыми и . Ответ дайте в градусах.
nsportal.ru
Переводная контрольная работа по математике 10 класс 2 вариант
Вариант
1. Найдите значение выражения
2. Найдите значение выражения
3. Оптовая цена учебника 150 рублей. Розничная цена на 15% выше оптовой. Какое наибольшее число таких учебников можно купить по розничной цене на 4550 рублей?
4. Мощность постоянного тока (в ваттах) вычисляется по формуле где U — напряжение (в вольтах), R — сопротивление (в омах). Пользуясь этой формулой, найдите P (в ваттах), если R = 6 Ом и U = 12 В.
5. Найдите значение выражения при .
6. Таксист за месяц проехал 7000 км. Цена бензина 30 рублей за литр. Средний расход бензина на 100 км составляет 7 литров. Сколько рублей потратил таксист на бензин за этот месяц?
7. Найдите корень уравнения .
8. План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ дайте в квадратных метрах.
9. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
А) длина хоботка мухи
Б) длина экватора
В) длина товарного поезда
Г) тормозной путь автомобиля
1) 40 000 км
2) 100 м
3) 0,2 см
4) 1,5 км
10. В среднем из 2000 садовых насосов, поступивших в продажу, 12 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
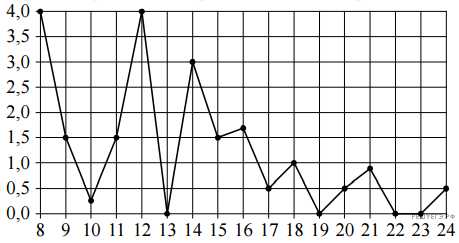
11. На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней выпадало более 2 миллиметров осадков.
12. Для обслуживания международного семинара необходимо собрать группу переводчиков. Сведения о кандидатах представлены в таблице. Пользуясь таблицей, соберите хотя бы одну группу, в которой переводчики вместе владеют всеми четырьмя языками: английским, немецким, испанским и французским, — а суммарная стоимость их услуг не превышает 12 000 рублей в день. В ответе укажите какой-нибудь один набор номеров переводчиков без пробелов, запятых и других дополнительных символов.
- Номер
переводчикаЯзыки
Стоимость услуг
(рублей в день)1
английский, испанский
5850
2
английский
3000
3
испанский, французский
6800
4
немецкий
2000
5
английский, немецкий
5950
6
французский
4050
13. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
14. На рисунке точками показан прирост населения Китая в период с 2004 по 2013 годы. По горизонтали указывается год, по вертикали — прирост населения в процентах (увеличение численности населения относительно прошлого года). Для наглядности точки соединены линией.
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику прироста населения.
ИНТЕРВАЛЫ
ХАРАКТЕРИСТИКИ ДВИЖЕНИЯ
А) 2005–2007 гг.
Б) 2007–2009 гг.
В) 2009–2011 гг.
Г) 2011–2013 гг.
1) Падение прироста остановилось.
2) Наибольшее падение прироста населения.
3) Прирост населения находился в пределах от 0,5% до 0,52%.
4) Прирост населения увеличивался.
15. В треугольнике , высота равна 4, . Найдите .
16. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
17. Поставьте в соответствие каждому неравенству множество его решений.
НЕРАВЕНСТВА
РЕШЕНИЯ
А)
Б)
В)
Г)
1)
2)
3)
4)
18. Когда учитель физики Николай Дмитриевич ведёт урок, он обязательно отключает свой телефон. Выберите утверждения, которые верны при приведённом условии.
1) Если телефон Николая Дмитриевича включён, значит, он не ведёт урок.
2) Если телефон Николая Дмитриевича включён, значит, он ведёт урок.
3) Если Николай Дмитриевич проводит на уроке лабораторную работу по физике, значит, его телефон выключен.
4) Если Николай Дмитриевич ведёт урок физики, значит, его телефон включён.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
19. Найдите трёхзначное натуральное число, которое при делении на 4 и на 15 даёт равные ненулевые остатки и средняя цифра которого является средним арифметическим крайних цифр. В ответе укажите какое-нибудь одно такое число.
20. Хозяин договорился с рабочими, что они копают колодец на следующих условиях: за первый метр он заплатит им 3500 рублей, а за каждый следующий метр — на 1600 рублей больше, чем за предыдущий. Сколько денег хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 9 метров?
infourok.ru
Контрольная работа по математике 10 класс. Базовый уровень. 1 полугодие.
Контрольная работа по математике за 1 полугодие, 10 класс (базовый уровень)
Вариант 1
Вариант 2
-
Вычислите
а), б), в), г), д), е), ж),
з)
-
Вычислите
а), б), в), г), д), е), ж),
з)
-
При каких значениях имеет смысл выражение
а), б), в) ?
-
При каких значениях имеет смысл выражение
а), б), в) ?
-
Упростите выражение
а), б)
при х6
-
Упростите выражение
а), б)
при х
-
Решите уравнение
а) х3-5х2-5х+1=0
б) 6х3-х2-20х+12=0
-
Решите уравнение
а) 2х3+3х2+3х+2=0
б) 6х3-13х2+4=0
-
Плоскость проходит через середины боковых сторон AB и CD трапеции ABCD – точки М и К.
а)Докажите, что AD параллельна .
б)Найдите ВС, если AD=10см, МК=8см.
-
Плоскость проходит через основание AD трапеции ABCD. М и К — середины боковых сторон трапеции.
а)Докажите, что МК параллельна .
б)Найдите AD, если ВС=4см, МК=6см.
-
Прямая а параллельна плоскости , а прямая в лежит в плоскости .
Определите, могут ли прямые а и в
а)быть параллельными, б)пересекаться,
в)быть скрещивающимися.
-
Прямая а параллельна плоскости , а прямая в пересекает плоскость .
Определите, могут ли прямые а и в
а)быть параллельными,
б)пересекаться,
в) быть скрещивающимися.
-
Решите неравенства
а)
б) 
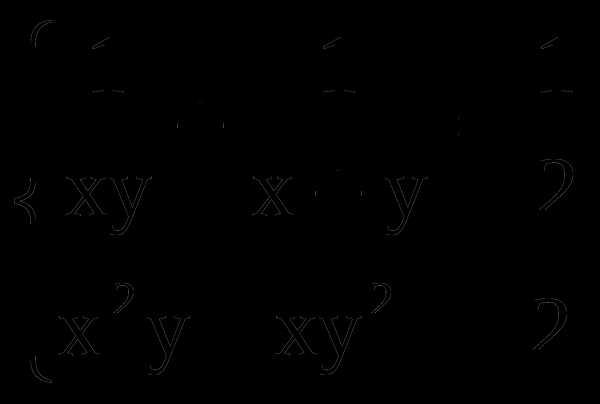
-
Решите неравенства
а)
в)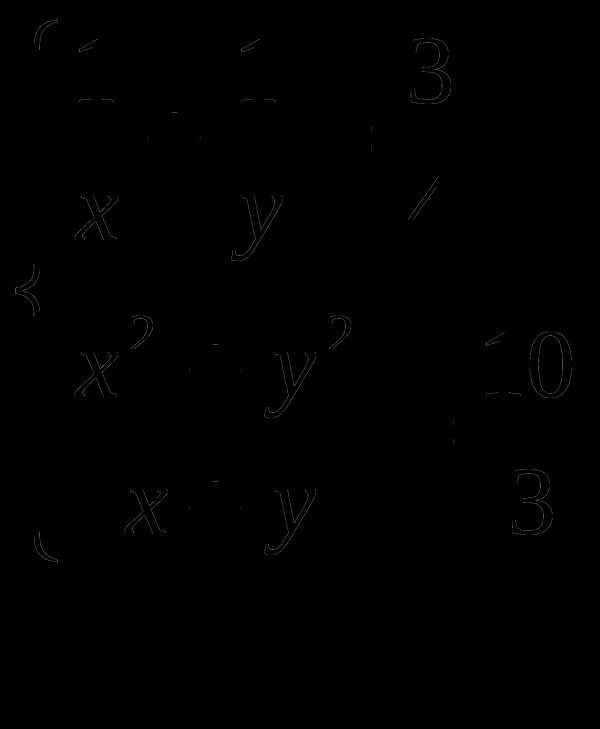
-
Выполните действия
-
Выполните действия

-
Решить графически уравнение
-
Решить графически уравнение
Подготовительный вариант контрольной работы по математике за 1 полугодие,
10 класс
В классе
Д/з
-
Вычислите
а), б), в), г), д), е), ж),
з)
-
Вычислите
а), б), в), г), д), е), ж),
з)
-
При каких значениях имеет смысл выражение
а), б), в) ?
-
При каких значениях имеет смысл выражение
а), б), в) ?
-
Упростите выражение
а), б)
при х8
-
Упростите выражение
а), б)
при х
-
Решите уравнение
а), б),
в), г) ,
д) 4
-
Решите уравнение
а), б),
в), г),
д) 6
-
Плоскость проходит через середины боковых сторон AB и CD трапеции ABCD – точки М и К.
а)Докажите, что BC параллельна .
б)Найдите AD, если BC=6см, МК=8см.
-
Плоскость проходит через основание ВС трапеции ABCD. М и К — середины боковых сторон трапеции.
а)Докажите, что МК параллельна .
б)Найдите ВС, если AD=8см, МК=6см.
-
Прямая а параллельна плоскости , и прямая в параллельна плоскости .
Определите, могут ли прямые а и в
а) быть параллельными, б) пересекаться,
в) быть скрещивающимися.
-
Прямая а пересекает плоскость и прямая в пересекает плоскость .
Определите, могут ли прямые а и в
а)быть параллельными,
б)пересекаться,
в) быть скрещивающимися.
-
Решите неравенства
а), б)
-
Решите неравенства
а), б)
-
Выполните действия
-
Выполните действия
-
Решить графически уравнение
-
Решить графически уравнение
infourok.ru