Учебно-методический материал по алгебре (10 класс) на тему: Контрольные работы по алгебре иначалам анализа 10 класс
Контрольная работа №3
Свойства и графики тригонометрических функций
Вариант 1
А1. Постройте график функции: .
А2. Найдите множество значений функции .
А3. Выяснить, является ли данная функция четной или нечетной:
А4. Докажите, что функция является периодической с периодом .
В1. Сравните числа: .
В2. Найдите наибольшее и наименьшее значение функции на отрезке .
С1. Построить график функции у = |sin x| +1
Нормы оценок: «3»- любые 3А, «4» — 3А + 1В, «5» — 2А + 2В или 2А + 1В + 1С.
_________________________________________________________________________
Контрольная работа №3
Свойства и графики тригонометрических функций
Вариант 2
А1. Постройте график функции: .
А2. Найдите множество значений функции .
А3. Выясните, является ли данная функция четной или нечетной: .
А4. Докажите, что функция у = tg 3x является периодической с периодом .
В1. Сравните числа:
В2. Найдите наибольшее и наименьшее значение функции на отрезке .
С1. Постройте график функции .
Нормы оценок: «3»- любые 3А, «4» — 3А + 1В, «5» — 2А + 2В или 2А + 1В + 1С.
nsportal.ru
Контрольные работы по алгебре, 10 класс
10 класс. Диагностическая контрольная работа по алгебре
№
Задание
№
Задание
І вариант
ІІ вариант
1.
Сравнить числа х и у, если разность х – у равна (-7).
1.
Сравнить числа х и у, если разность х – у равна (+9).
А. х > у Б. х = у В. х < у Г. Другой ответ
2.
Решить систему неравенств:
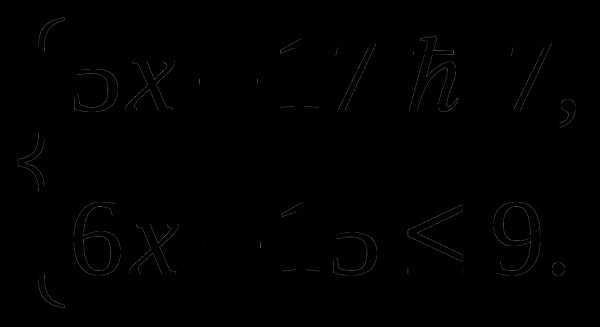
2.
Решить систему неравенств:
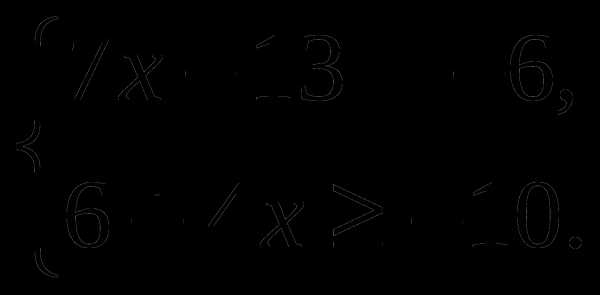
А. (-3; 7] Б. (-2; 4] В. [-4; 1) Г. (-2; -4]
3.
Указать точку, через которую проходит график функции: у = 2х² + 5х -1
3.
Указать точку, через которую проходит график функции: у = 2х² + 3х -5
А. (-1; -6) Б. (1; 6) В. (3; 0) Г. (2; 11)
4.
Указать координаты вершины параболы
у = (х +1)² — 3?
4.
Указать координаты вершины параболы
у = (х -1)² + 3?
А. (-2; 3) Б. (1; 3) В. (-1; -3) Г. (2; -3)
5.
Решить графически систему уравнений:
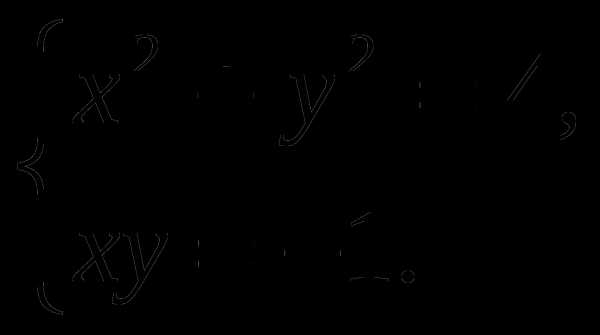
5.
Решить графически систему уравнений:
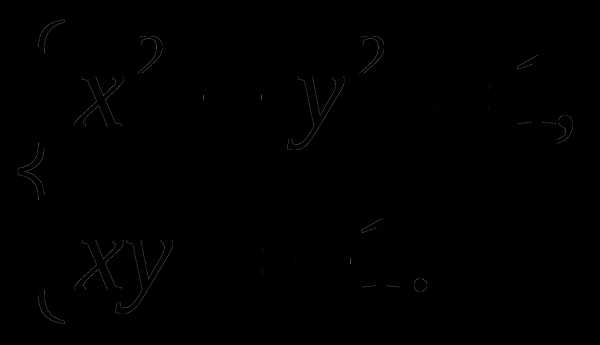
6.
Постройте график функции у = -х² + 2х + 8. Используя график: а) решите неравенство
-х² + 2х + 8 0;
0;
б) определите промежутки возрастания и убывания функции.
6.
Постройте график функции у = х² + 2х — 3. Используя график: а) решите неравенство х² + 2х — 3 0;
0;
б) определите промежутки возрастания и убывания функции.
7.
В геометрической прогрессии (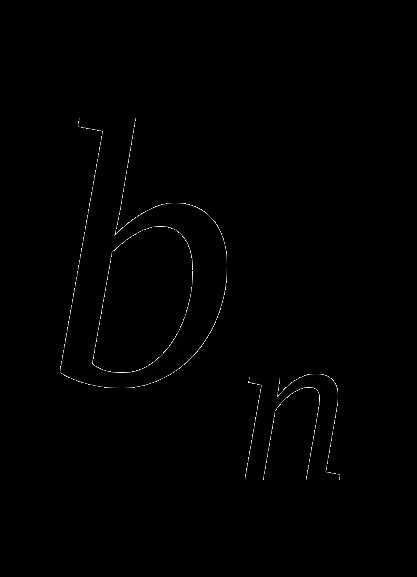 )
) 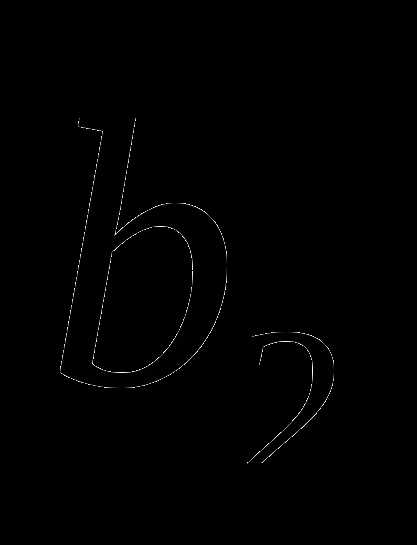 =6,
=6,  =486, q>0. Найдите
=486, q>0. Найдите .
.
7.
В геометрической прогрессии (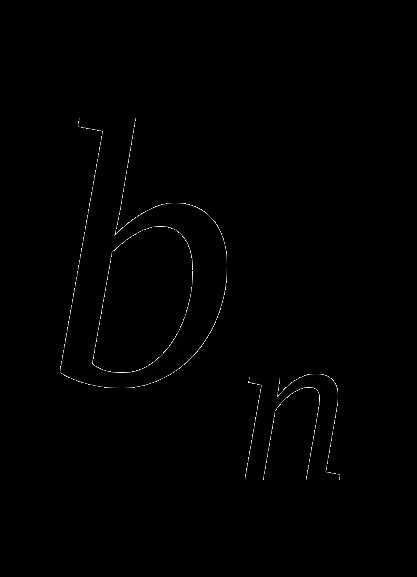 )
) 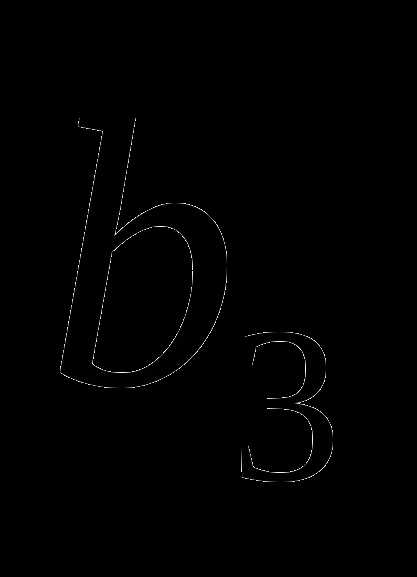 =18,
=18, 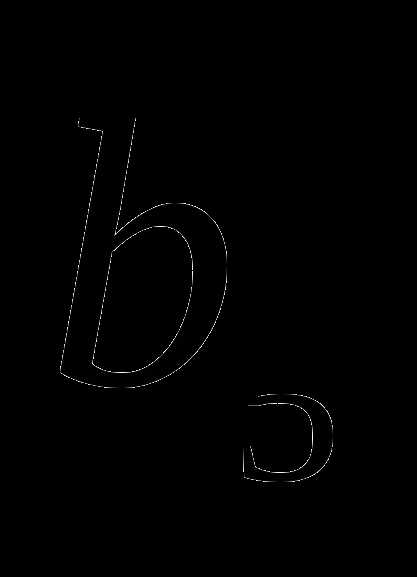 =162, q<0. Найдите
=162, q<0. Найдите 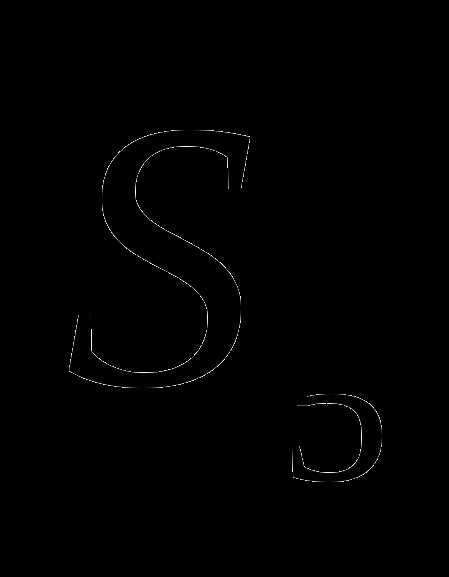 .
.
8.
Сумма первого и второго членов арифметической прогрессии равна 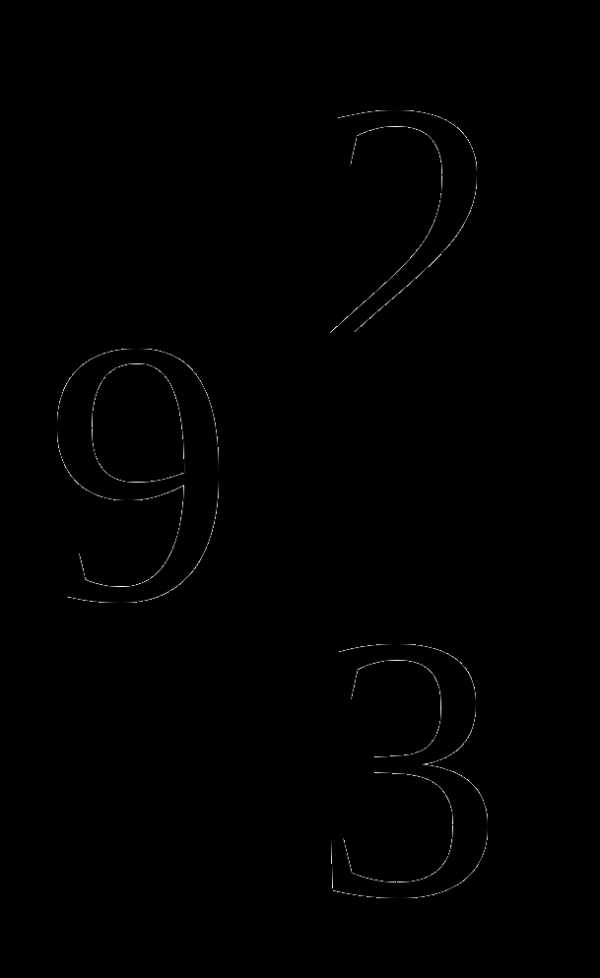 , а разность между первым членом и разностью d этой арифметической прогрессии равна
, а разность между первым членом и разностью d этой арифметической прогрессии равна  . Найдите третий член и номер члена, который равен
. Найдите третий член и номер члена, который равен
(-3).
8.
Сумма первого и третьего членов арифметической прогрессии равна 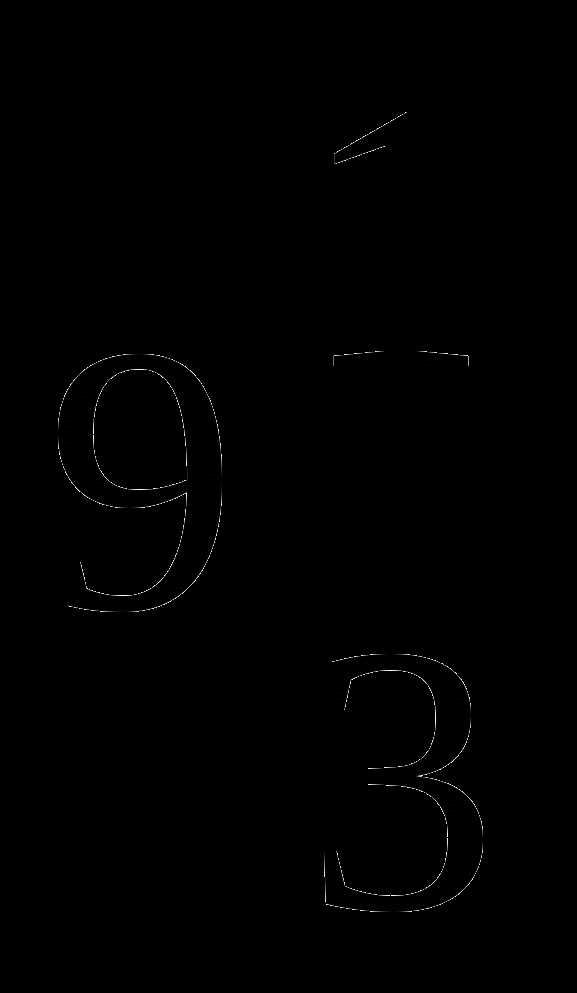 , а разность между первым и третьим членами этой арифметической прогрессии равна
, а разность между первым и третьим членами этой арифметической прогрессии равна  . Найдите четвертый член и номер члена, который равен (-6).
. Найдите четвертый член и номер члена, который равен (-6).
Оценивание: 1-5 по 1 баллу; 6,7 по 2 балла; 8 – 3 балла.
10 класс. Тематическая контрольная работа по алгебре «Числовые множества. Функции».
№
Задание
1 вариант
№
Задание
2 вариант
1
Записать множество способом перечисления его элементов:
а) правильные дроби со знаменателем 7;
б) решения уравнения х² + 6х -7 = 0;
в) гласные буквы украинского алфавита.
1
а) неправильные дроби, числитель которых равен 6;
б) решения уравнения х² +х – 12 = 0;
в) дни недели.
2
Записать все подмножества множества
В = {m, n, k}.
2
Записать все подмножества множества
С = {5, 6, 7}.
3
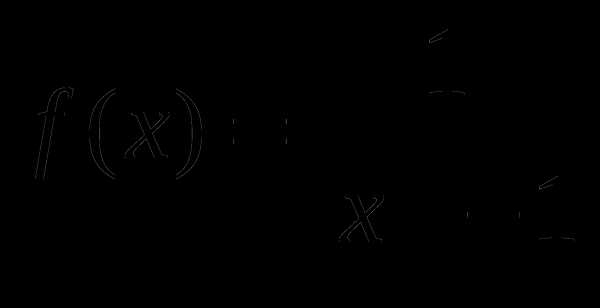 , найти f(-2), f(-1), f(0), f(1), f(2).
, найти f(-2), f(-1), f(0), f(1), f(2).
3
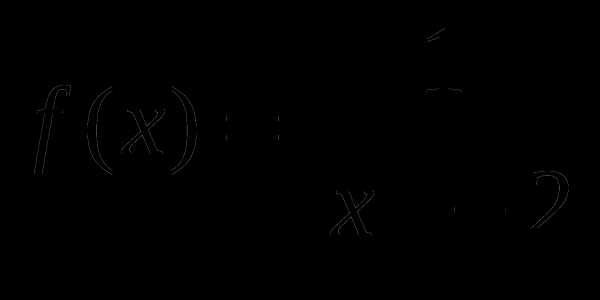 , найти f(-2), f(-1), f(0), f(1), f(2).
, найти f(-2), f(-1), f(0), f(1), f(2).
4
Найти область определения функций:
а) у = 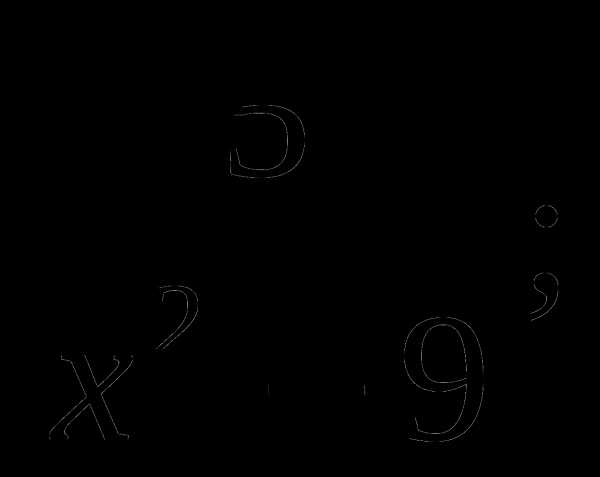 б) у =
б) у = 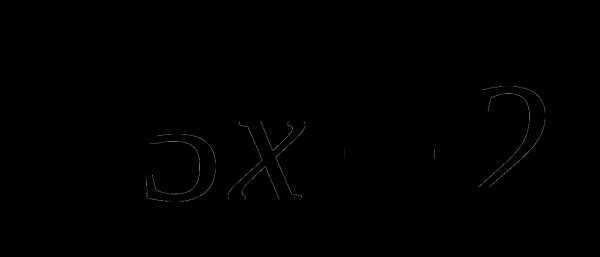 .
.
4
Найти область определения функций:
а) у = 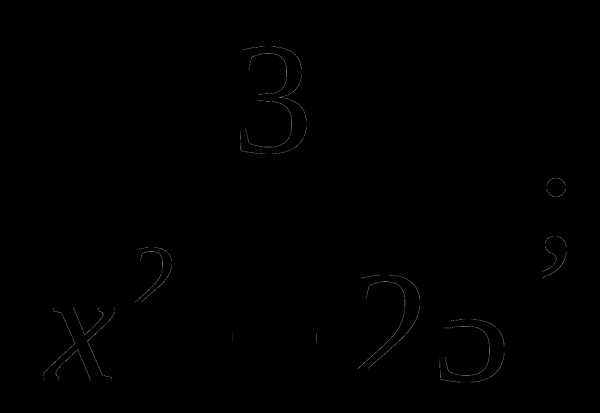 б) у =
б) у = 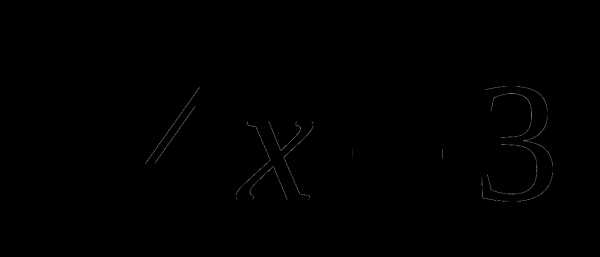 .
.
5
Указать множество значений функций:
а) у = 16х – 5; б) у = 23; в) у = х² — 9.
5
Указать множество значений функций:
а) у = -5х + 7; б) у = 32; в) у = х² — 7.
6
Доказать, что функция у = 7х – 3 возрастает на всей области определения.
6
Доказать, что функция у = -2х + 5 убывает на всей области определения.
7
Определить четность или нечетность функций: а) у = |х| + х²; б) у = х³·|х|.
7
Определить четность или нечетность функций: а) у = х (5 -|х|) ; б) у =  .
.
8
Построить графики функций: а) у = |х| — 5;
б) у = 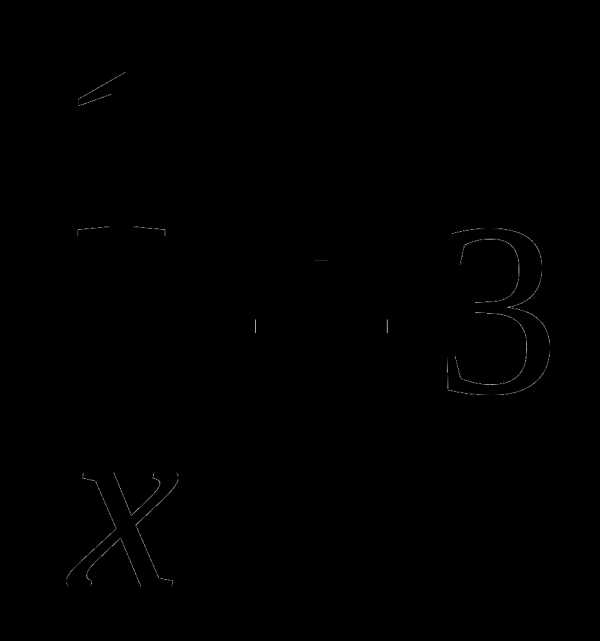 .
.
8
Построить графики функций: а) у = 5 — |х|;
б) у =  .
.
Оценивание: 1 – 4 задания – по 1 баллу;
5 – 8 задания – по 2 балла.
10 класс. Тематическая контрольная работа по алгебре №3 «Уравнения и неравенства» (учебник Е.П.Нелин, 10 класс, §3,4,5).
№
Задание
1 вариант
№
Задание
2 вариант
1
Какие из уравнений равносильны уравнению 3 —  =0?
=0?
А) 1–3х=0, Б) 
В)  Г) 3х–1=0.
Г) 3х–1=0.
1
Какие из уравнений равносильны уравнению  -7 =0?
-7 =0?
А) 1–7х=0, Б) 
В) 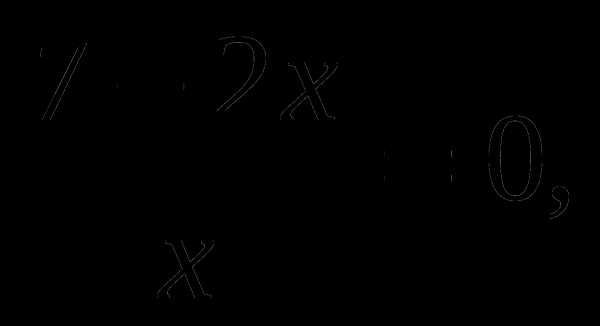 Г) 7х–2=0.
Г) 7х–2=0.
2
Решите уравнение и укажите, какое преобразование могло бы привести к нарушению равносильности.
.
2
Решите уравнение и укажите, какое преобразование могло бы привести к нарушению равносильности.
.
3
Применяя свойства функций, решите уравнения:
а)
б) |х²+4х-21| +|49-х²| +|2х+14| = 0;
в) х +  + х³ = 70.
+ х³ = 70.
3
Применяя свойства функций, решите уравнения:
а)
б) |х²-х-20| +|25-х²| +|2х-10| = 0;
в) х +  + х² = 93.
+ х² = 93.
4
Решить неравенство методом интервалов:
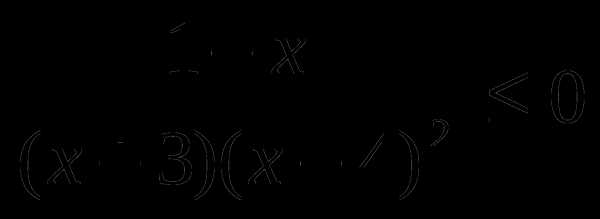
4
Решить неравенство методом интервалов:
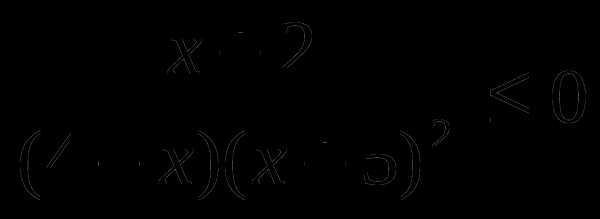
5
Решить уравнения:
а) |12-х| = 5;
б) | х-3 | — | 2х + 4 | = 2.
5
Решить уравнения:
а) |х — 7| = 8;
б) | х +3 | — | 6 – 3х | = 1.
Оценивание: 1 – 1 балл;
2 – 2 балла;
3,4,5 – по 3 балла.
10 класс. Контрольная работа №4 «Уравнения и неравенства с параметрами. Графики уравнений и неравенств».
№
І вариант
№
ІІ вариант
1
Решить уравнение с параметром а относительно переменной х:
|х² -6|х|| = а.
1
Решить уравнение с параметром а относительно переменной х:
|х² -8|х|| = а.
2
Решить неравенство с параметром а относительно переменной х:
4х + 3а≥ 6 – ах.
2
Решить неравенство с параметром а относительно переменной х:
2ах — 3≤ а – х.
3
Построить график неравенства:
(х-2)² + у² ≤16.
3
Построить график неравенства:
х² + (у-1)² ≥36.
4
Выполнить деление многочлена
А(х) = на В(х)=.
4
Выполнить деление многочлена
А(х) = на В(х)=.
5
Используя схему Горнера, проверить являються ли числа 1 и (-2) корнями многочлена: х³ + х² — 3х – 2.
5
Используя схему Горнера, проверить являються ли числа (-1) и 2 корнями многочлена: х³ — х² — 5х – 3.
10 класс. Контрольная работа по алгебре и началам анализа №5 «Метод математической индукции. Корень п-ой степени».
№
І вариант
№
ІІ вариант
1
Используя метод математической индукции, доказать:
1
Используя метод математической индукции, доказать:
1 + 2 + 3 +…+ n = 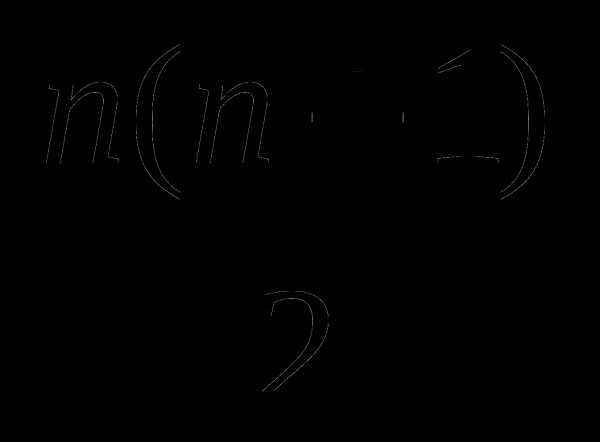
2
Установить соответствие:
1.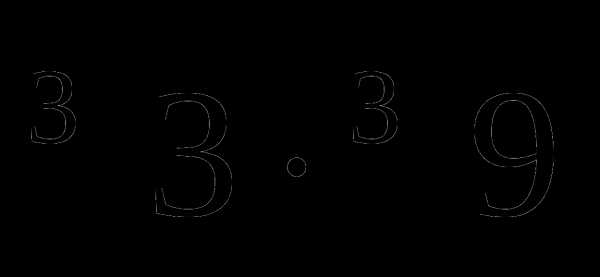 А 1
А 1
2.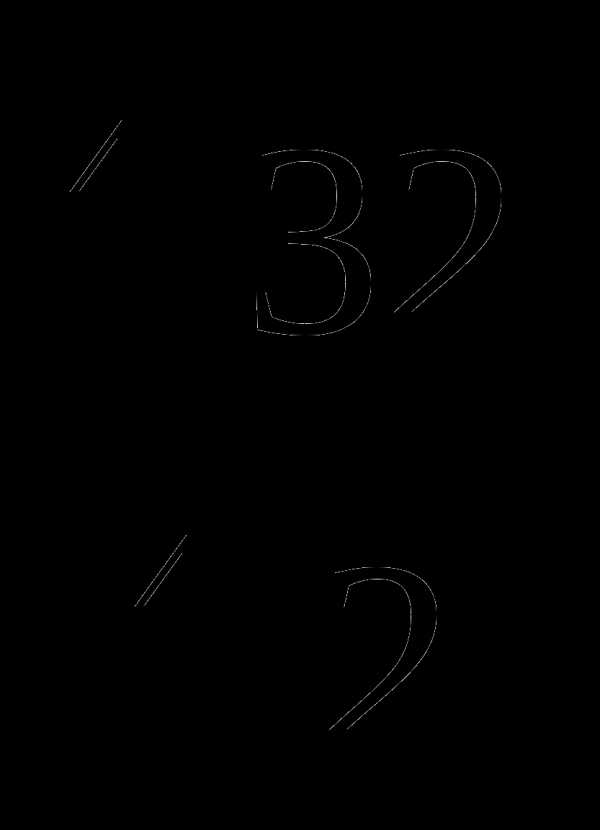 Б 2
Б 2
3. 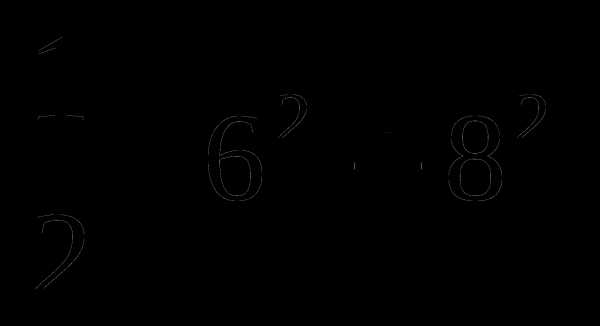 В 3
В 3
4. 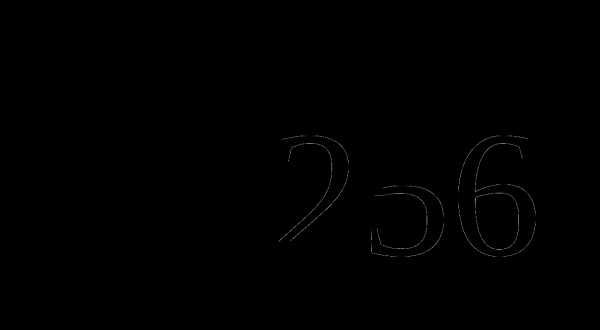 Г 4
Г 4
Д 5
2
Установить соответствие:
1. А 1
А 1
2. 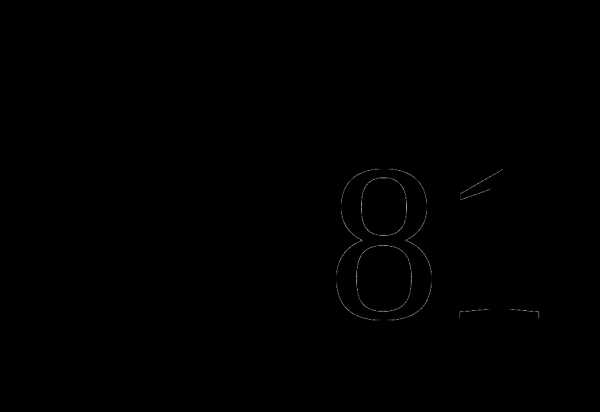 Б 2
Б 2
3. 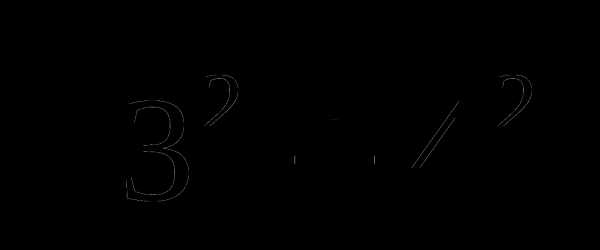 В 3
В 3
4.  Г 4
Г 4
Д 5
3
Разместить числа в порядке убывания:  ;
;  ;
; 
3
Разместить числа в порядке возрастания:
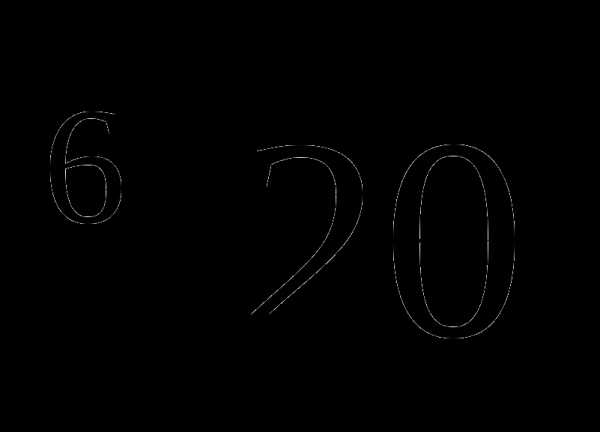 ;
; 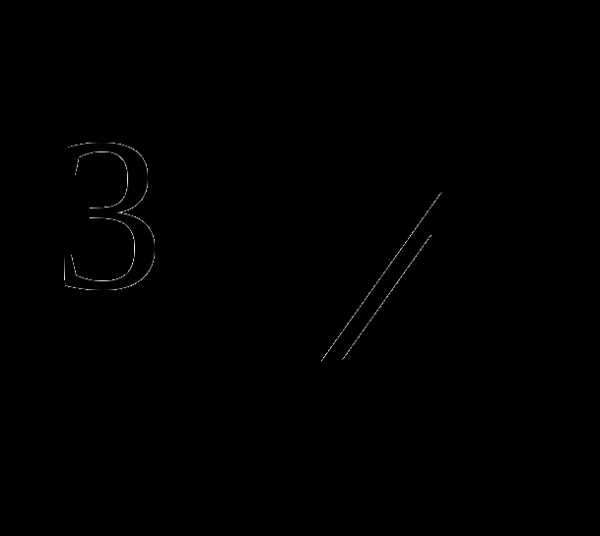 ;
; 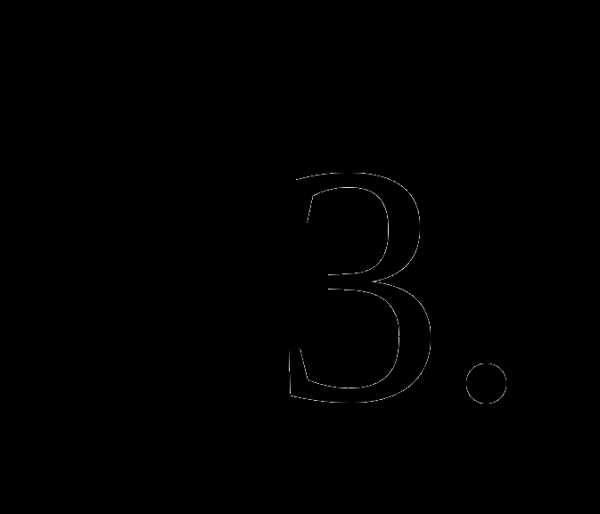
4
Вычислить:
4
Вычислить:
5
Сравнить:  и
и  .
.
5
Сравнить: 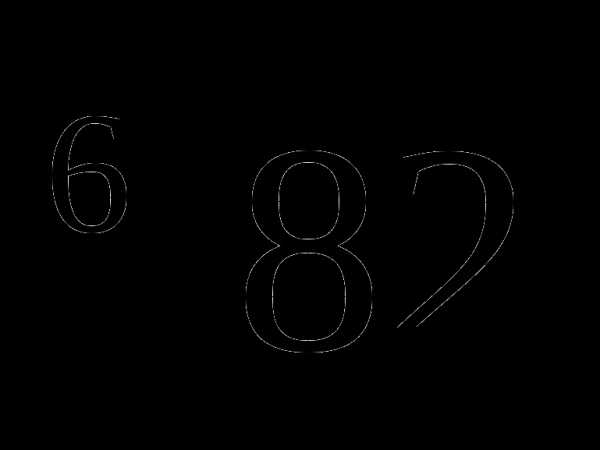 и
и 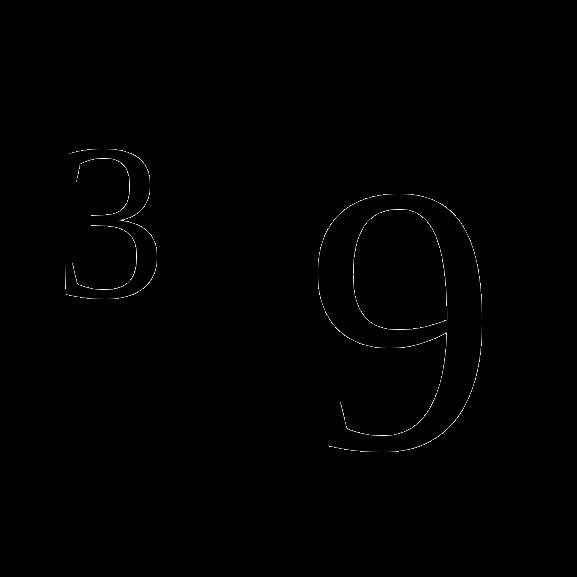 .
.
10 класс. Контрольная работа по алгебре и началам анализа №6
№
І вариант
№
ІІ вариант
1.
Вычислить: а) 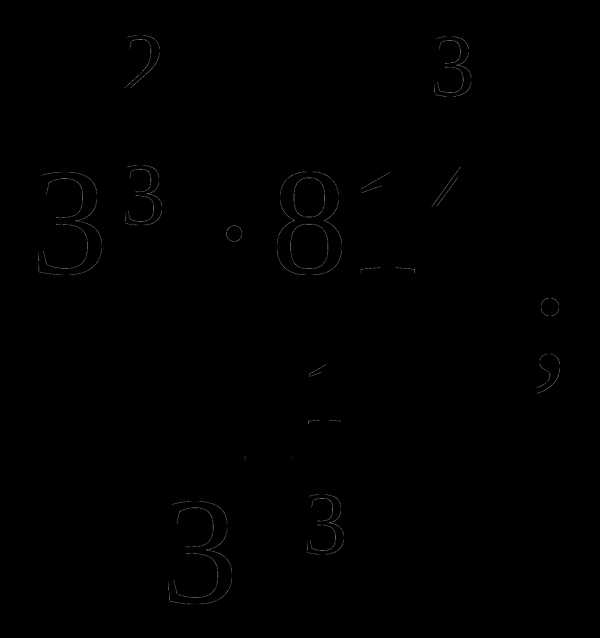 б)
б) 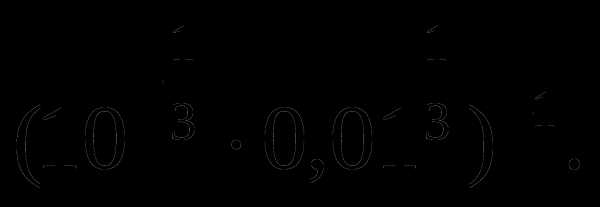
1.
Вычислить: а) 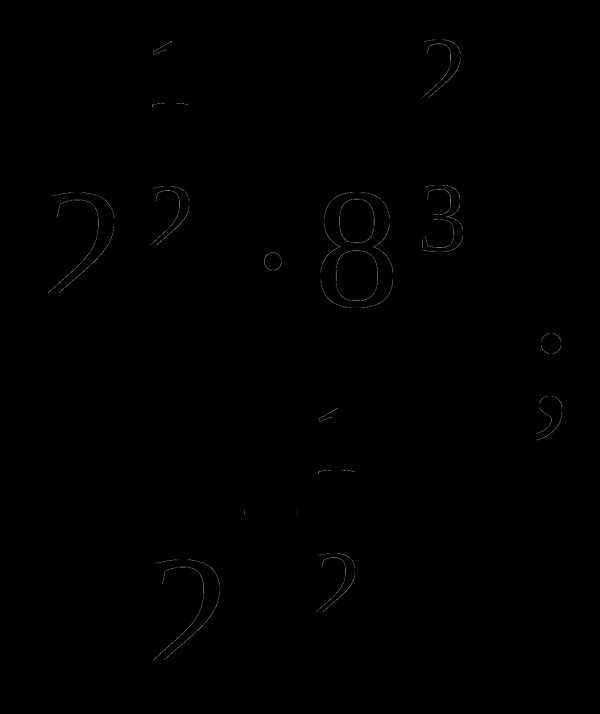 б)
б) 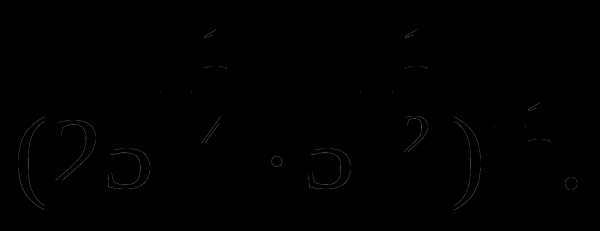
2.
Решить уравнение: х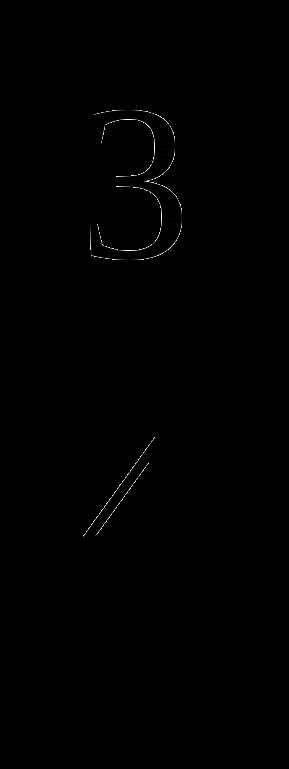 = 81.
= 81.
2.
Решить уравнение: х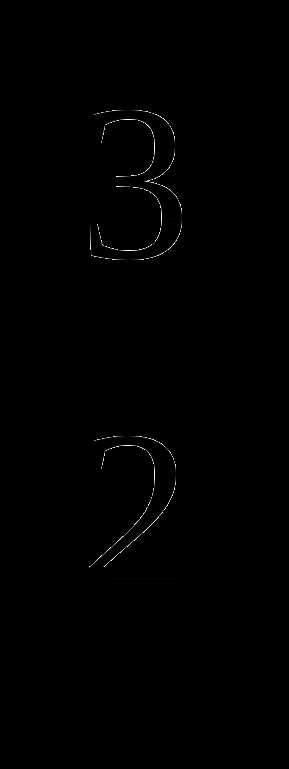 = 64.
= 64.
3.
Установить соответствие между функциями, заданными формулами, (1 – 4) и их графиками (А – Д).
1) у = х
2) у = х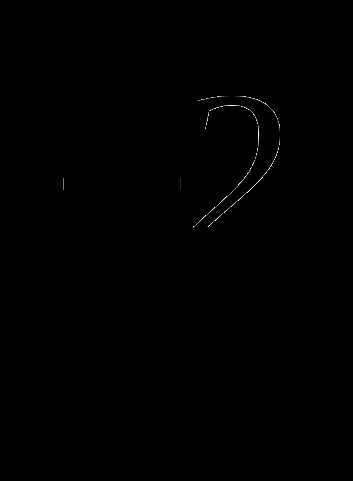
3) у = х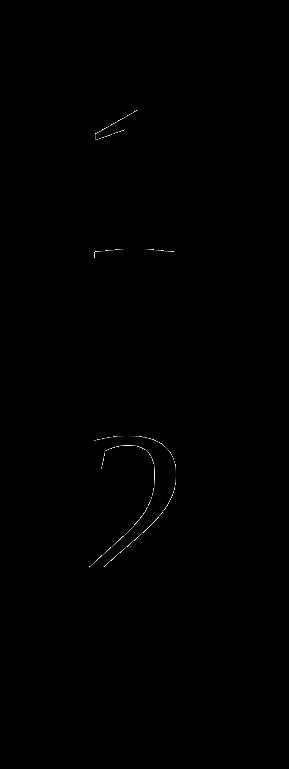
4) у = х
3.
Установить соответствие между функциями, заданными формулами, (1 – 4) и их графиками (А – Д).
1) у = х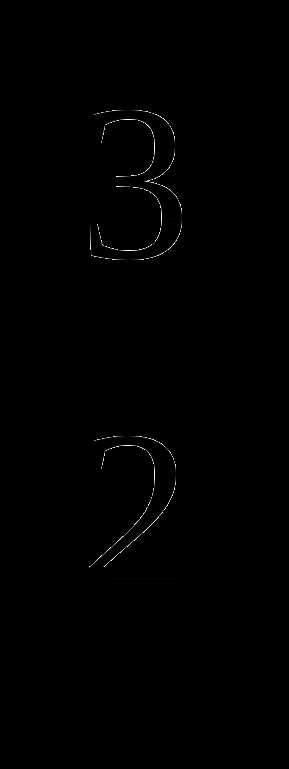
2) у = х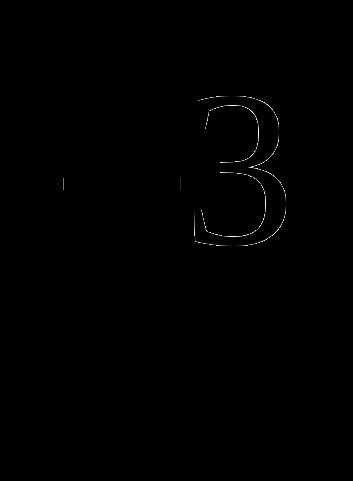
3) у = х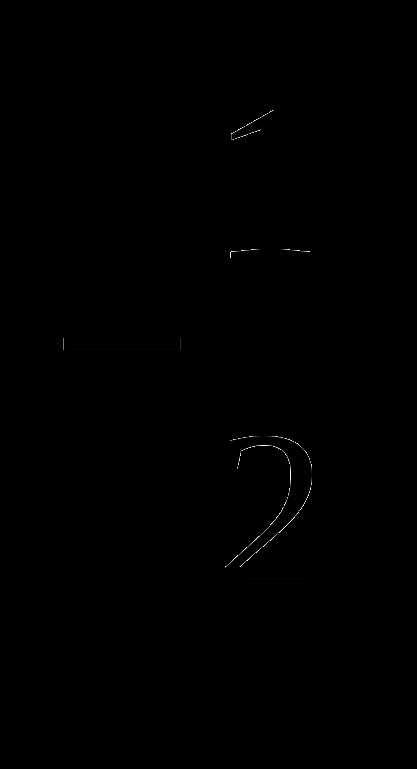
4) у = х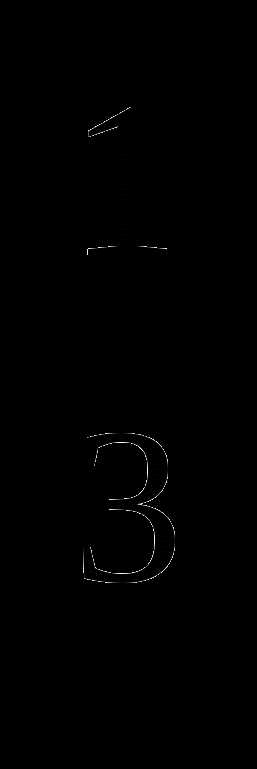
4.
Сократить дробь:
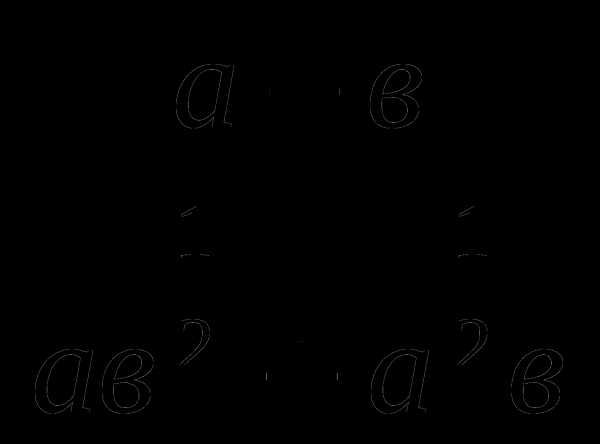
4.
Сократить дробь:
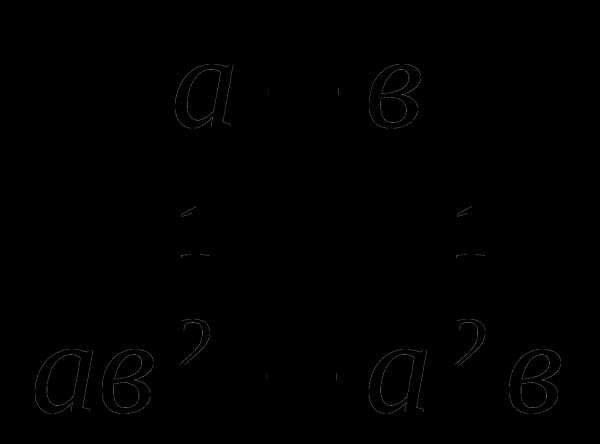
5.
Упростить:
5.
Упростить: .
10 класс. Контрольная работа по алгебре и началам анализа №6
№
І вариант
№
ІІ вариант
1.
Вычислить: 27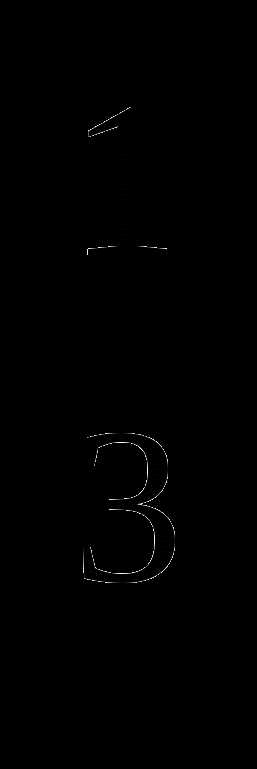
1.
Вычислить: 8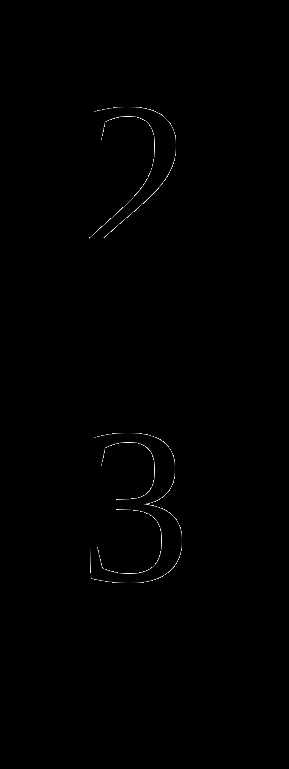
2.
Решить уравнение: х = 81.
= 81.
2.
Решить уравнение: х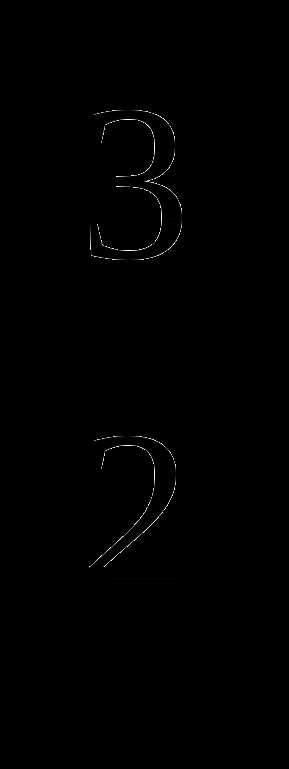 = 64.
= 64.
3.
Установить соответствие между функциями, заданными формулами, (1 – 4) и их графиками (А – Д).
1) у = х
2) у = х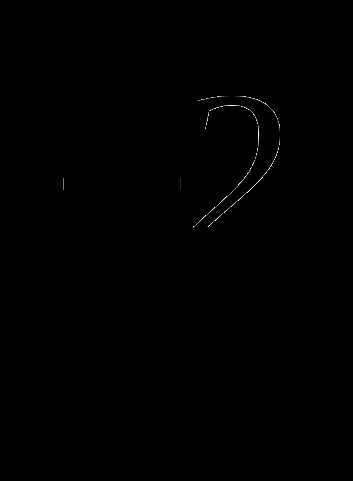
3) у = х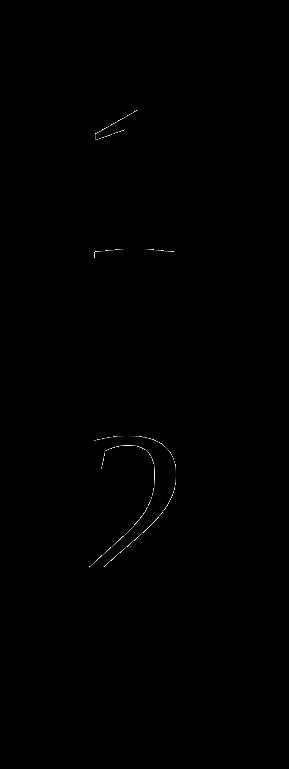
4) у = х
3.
Установить соответствие между функциями, заданными формулами, (1 – 4) и их графиками (А – Д).
1) у = х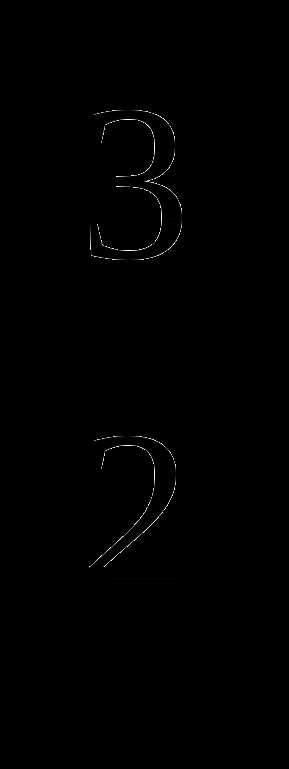
2) у = х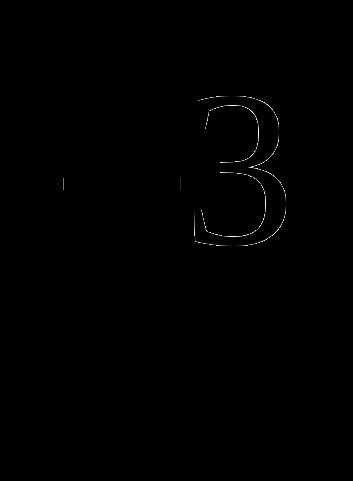
3) у = х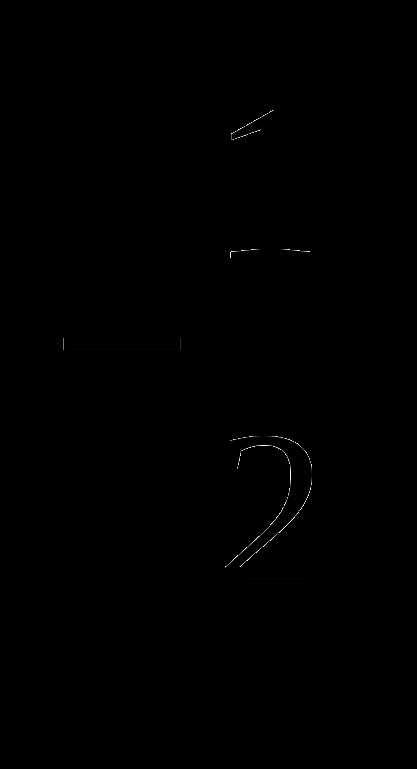
4) у = х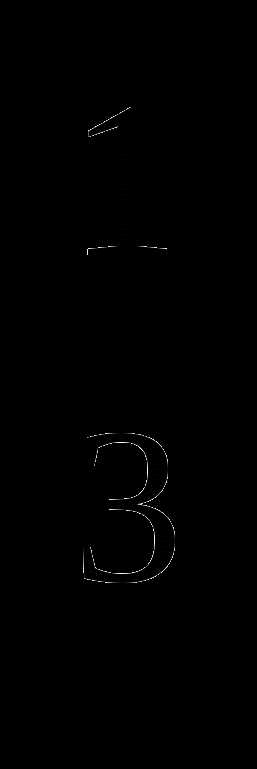
4.
Сократить дробь:
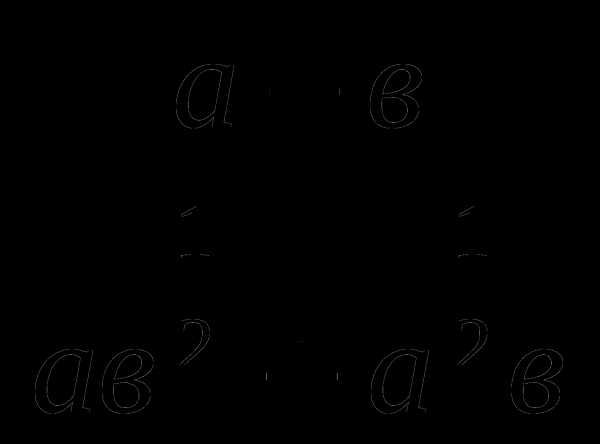
4.
Сократить дробь:
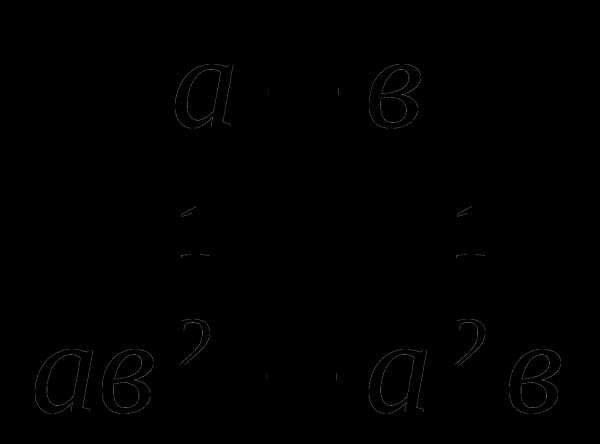
5.
Решить уравнение:
5.
Решить уравнение:
6.
Решить неравенство:
6.
Решить неравенство:
10 класс. Алгебра. Контрольная работа №7 «Иррациональные уравнения и неравенства»
№
І вариант
№
ІІ вариант
1
Сколько корней имеет уравнение .
1
Сколько корней имеет уравнение .
2
Установить соответствие между функциями, заданными формулами (1-4), и их областями определения (А-Д):
1. у = 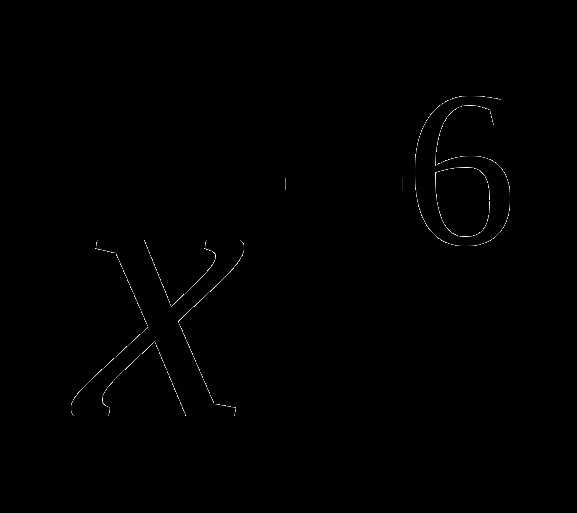 А. (-∞; 0)
А. (-∞; 0)
2. у =  Б. [0; +∞)
Б. [0; +∞)
3. у = 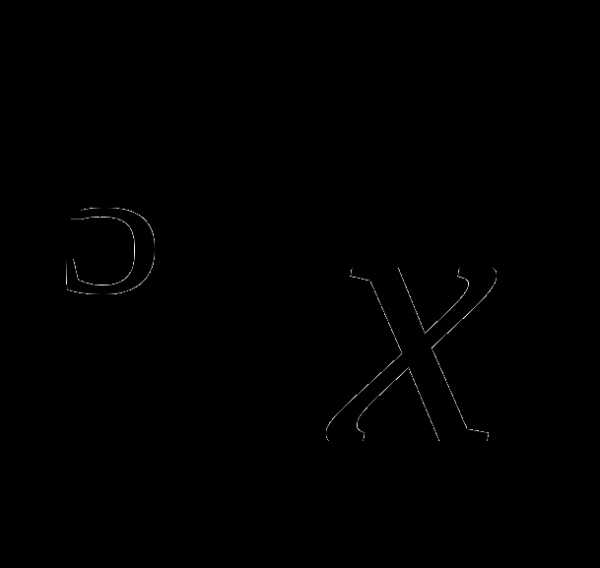 В. (0; +∞)
В. (0; +∞)
4. у =  Г. (-∞; +∞)
Г. (-∞; +∞)
Д. (-∞; 0) U (0; +∞)
2
Установить соответствие между функциями, заданными формулами (1-4), и их областями определения (А-Д):
1. у = 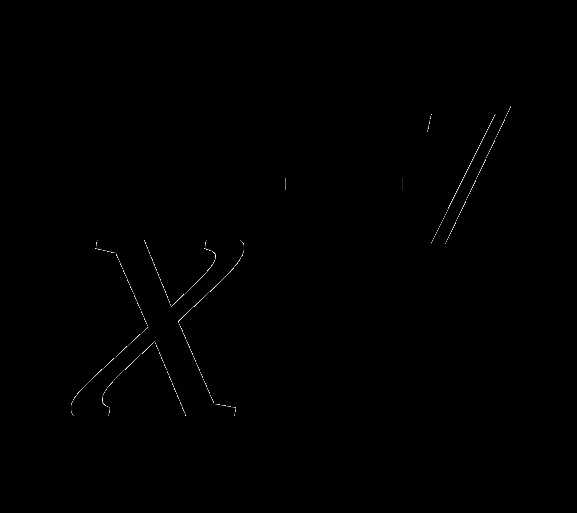 А. (-∞; 0)
А. (-∞; 0)
2. у =  Б. (0; +∞)
Б. (0; +∞)
3. у = 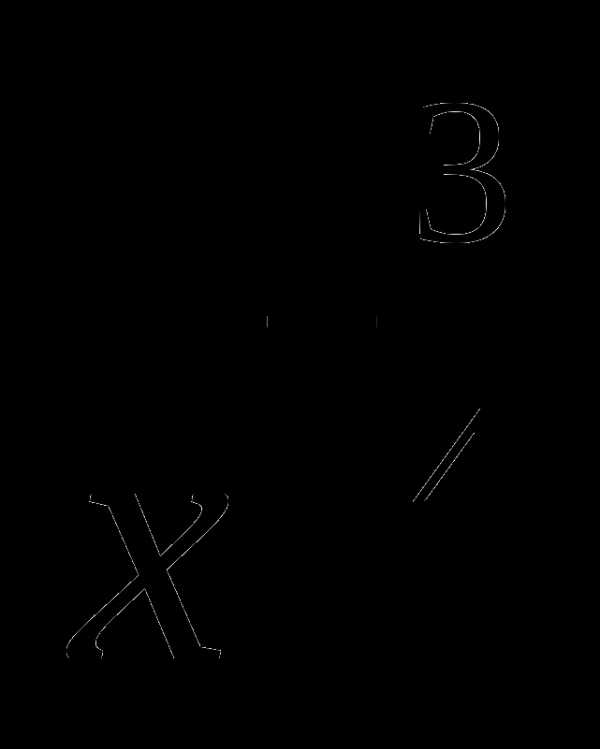 В. [0; +∞)
В. [0; +∞)
4. у = 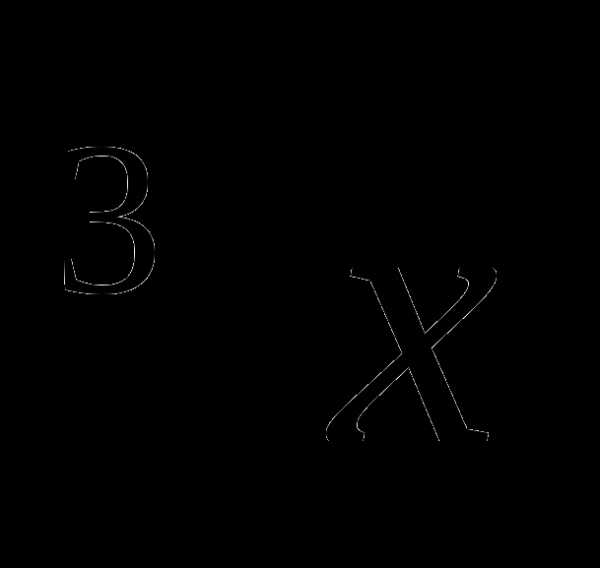 Г. (-∞; +∞)
Г. (-∞; +∞)
Д. (-∞; 0) U (0; +∞)
3
Решить уравнения:
.
3
Решить уравнения:
.
4
Решить систему уравнений:
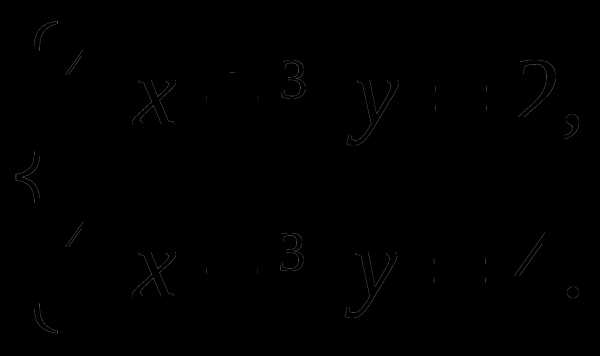
4
Решить систему уравнений:
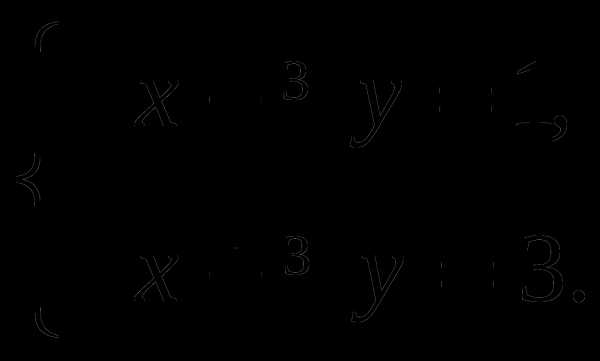
5
Решить неравенства:
а) ;
б) 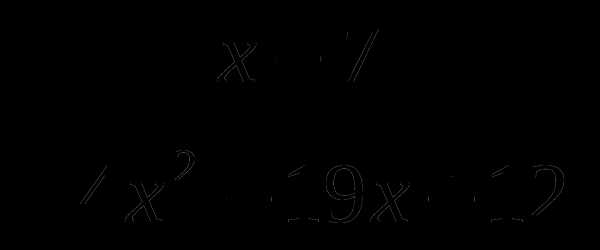 < 0.
< 0.
5
Решить неравенства:
а) ;
б) 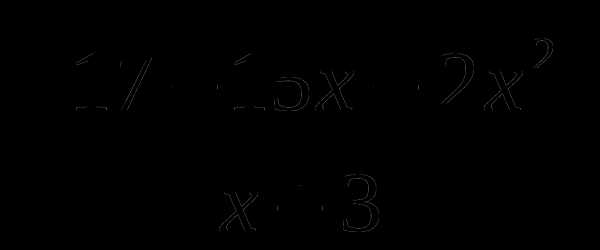 > 0.
> 0.
Оценивание: 1, 2 – по 0,5 балла; 3, 4 – по 1 баллу; 5 – 2 балла.
10 класс. Контрольная работа №8 «Тригонометрические функции и их графики»
№
І вариант
№
ІІ вариант
1
Записать в порядке возрастания:
sin(-1), sin , sin 135º, sin(-30º).
, sin 135º, sin(-30º).
Записать в порядке убывания:
cos , cos(-1), cos(-30º), cos 135º.
, cos(-1), cos(-30º), cos 135º.
2
Построить график функции 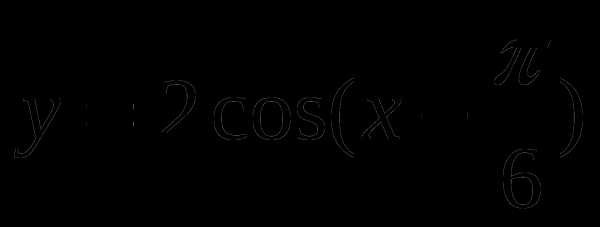 . Записать промежутки возрастания и убывания функции.
. Записать промежутки возрастания и убывания функции.
2
Построить график функции 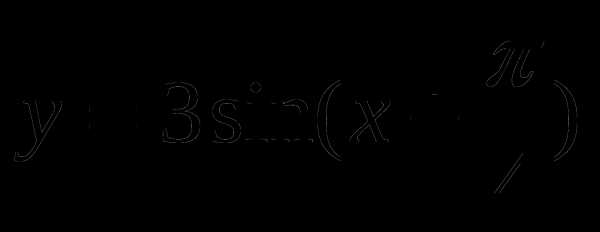 . Записать промежутки возрастания и убывания функции.
. Записать промежутки возрастания и убывания функции.
3
Найти значение выражения 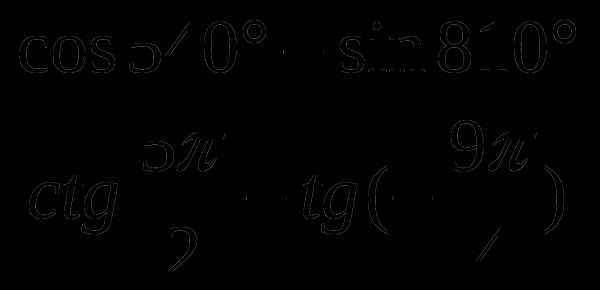
3
Найти значение выражения 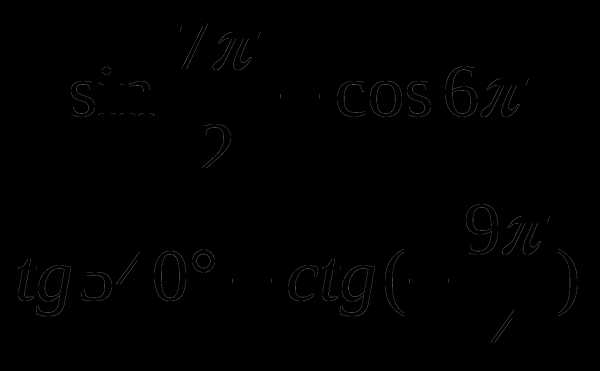
10 класс. Годовая контрольная работа.
І вариант
ІІ вариант
1.
Известно, что множество А=, В=.
Найти 1) АUВ; 2)А∩В.
1.
Известно, что множество А=, В=.
Найти 1) АUВ; 2)А∩В.
2.
Определить четность или нечетность функции у =  .
.
2.
Определить четность или нечетность функции у = х (4 -|х|).
3.
Решить неравенство методом интервалов:
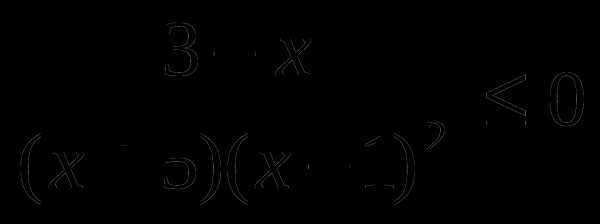
3.
Решить неравенство методом интервалов:
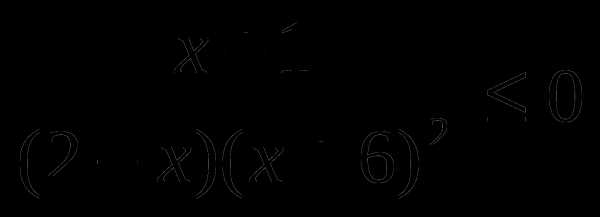
4.
Решить уравнение:
а) 2| х-3 | — | 3 — х | = 5.
б) .
4.
Решить уравнение:
а) 5| х – 4 | — 2| 4 – х | = 4.
б) .
5.
Докажите тождество:
.
5.
Докажите тождество:
.
infourok.ru
Контрольные работы по алгебре, 10 класс.
Контрольная работа №1 по теме:
«Действительные числа»
Вариант №1. Обязательная часть
-
Бесконечно убывающая геометрическая прогрессия. Формула суммы.
-
Вычислите:
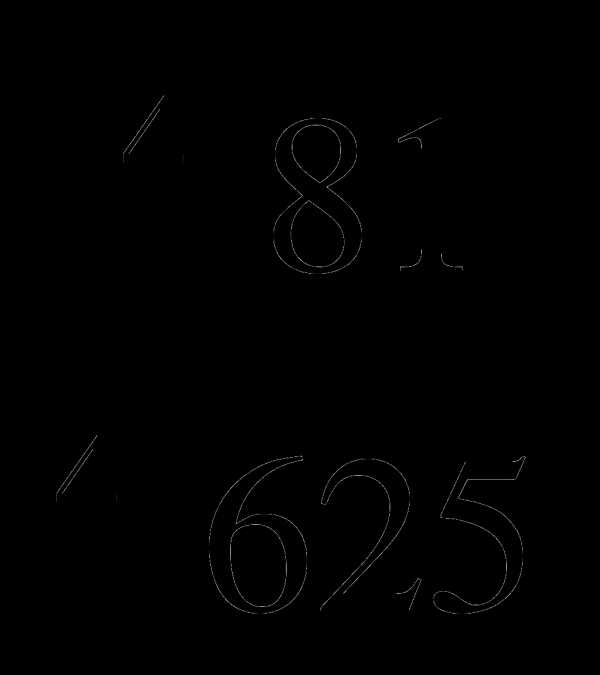
в)
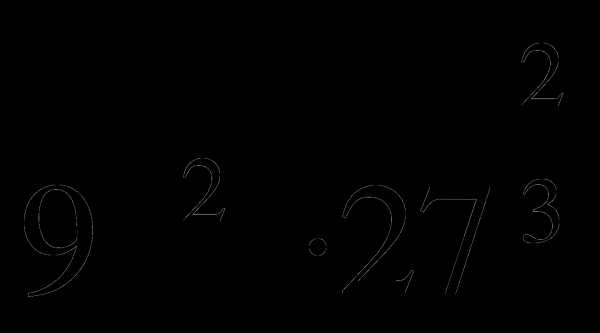
б)
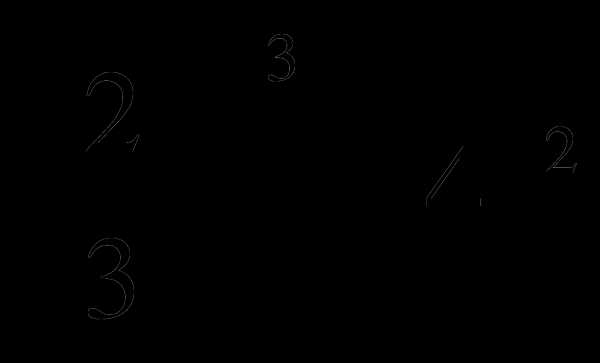
г)
-
Упростите выражения:
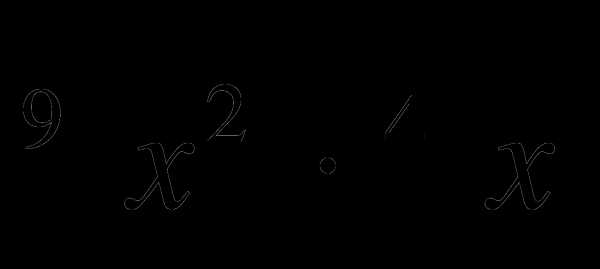
б)
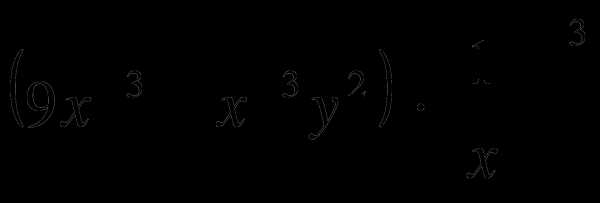
в)
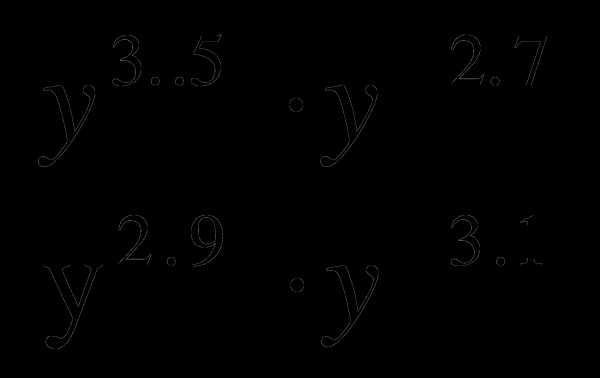
-
Разложите на множители: a – 4.
-
Сократите дробь:
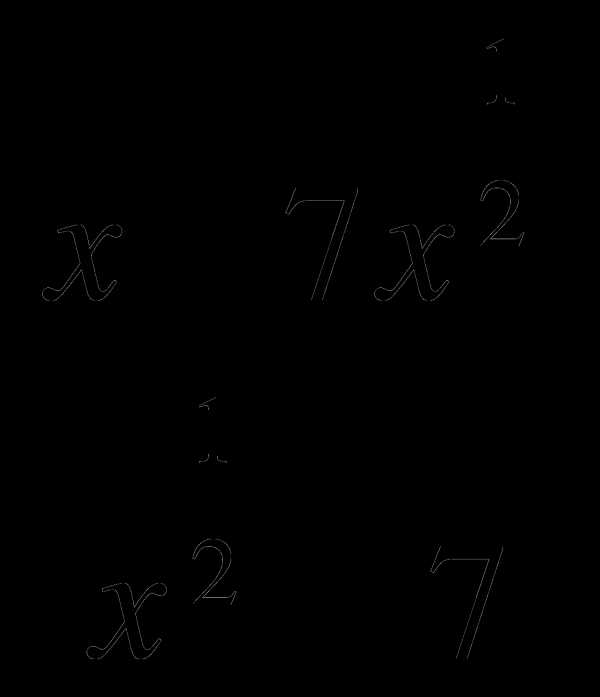
Дополнительная часть
-
Сравните числа a и b, если:
-
Упростите выражение:
Вариант №2. Обязательная часть
-
Арифметический корень натуральной степени. Свойства.
-
Вычислите:
в)

б)
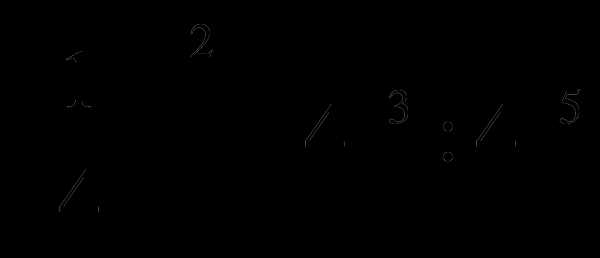
г)
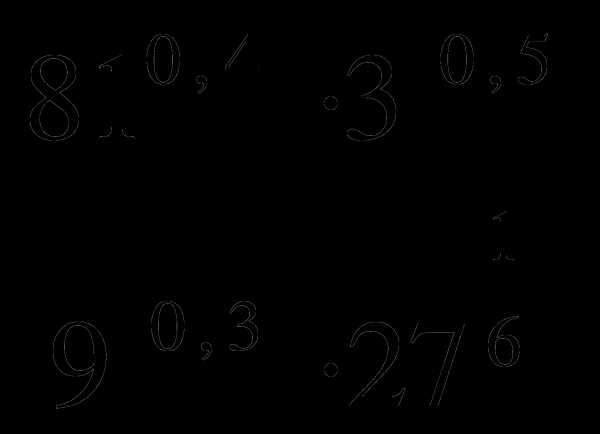
-
Упростите выражения:
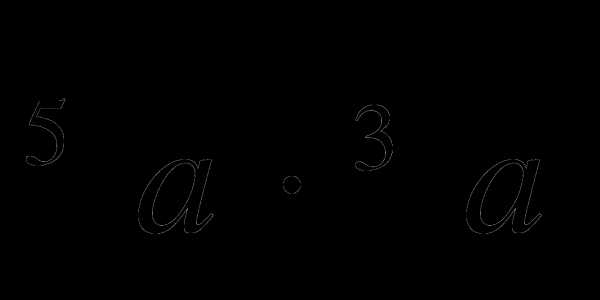
б)
в)
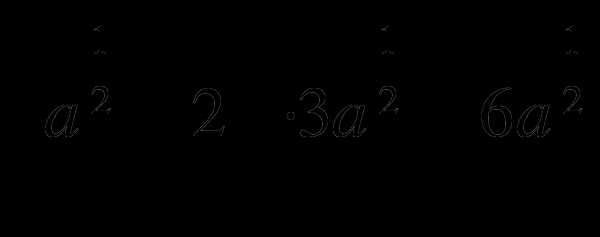
-
Разложите на множители:
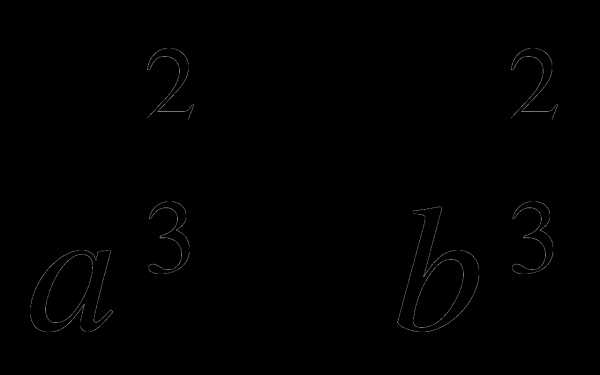
-
Сократите дробь:
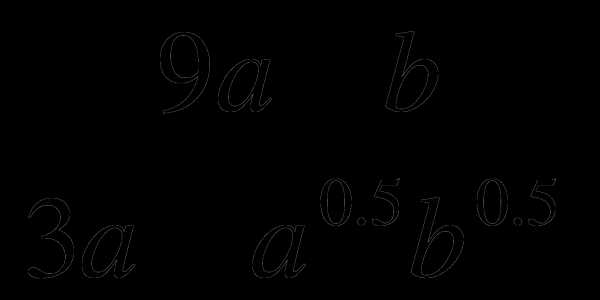
Дополнительная часть
-
Сравните числа a и b, если:
-
Упростите выражение:
Контрольная работа №2 по теме:
«Степенная функция»
Вариант №1.
1. Найти область определения функции  .
.
2. Изобразить эскиз графика функции 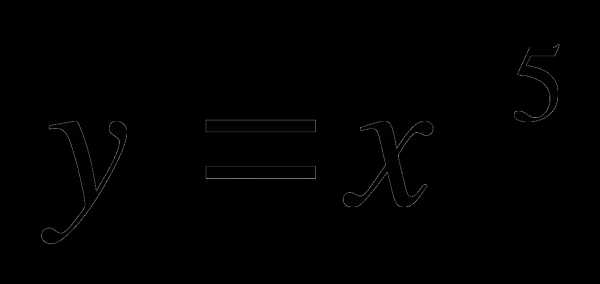 .
.
-
Указать область определения и множество значений функции.
-
Выяснить, на каких промежутках функция убывает.
-
Сравнить числа
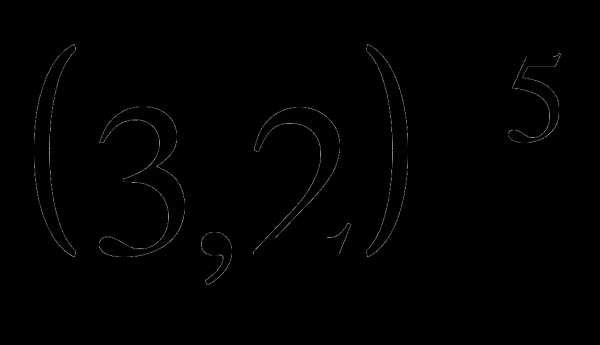 и
и 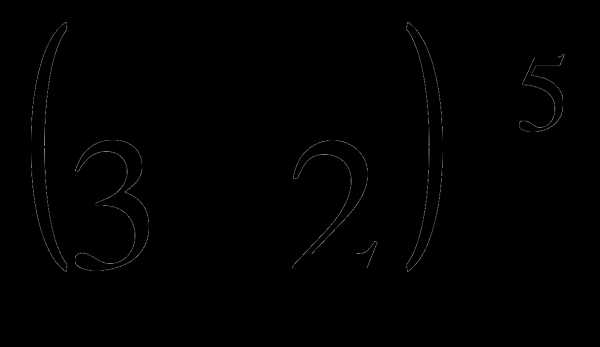 .
.
-
Решить уравнение:
1)
2)
3)
-
Решить неравенство: .
-
Найти функцию, обратную к ; указать её область определения и множество значений. На одном рисунке построить графики данной функции и функции, обратной к данной.
Вариант №2
-
Найти область определения функции
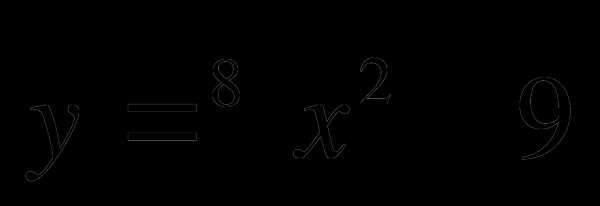 .
. -
Изобразить эскиз графика функции
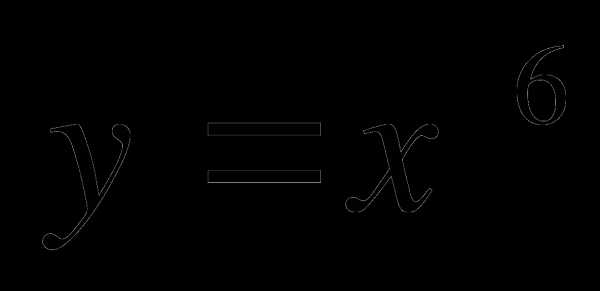 .
.
-
Указать область определения и множество значений функции.
-
Выяснить, на каких промежутках функция возрастает.
-
Сравнить числа
 и
и  .
.
-
Решить уравнение:
1)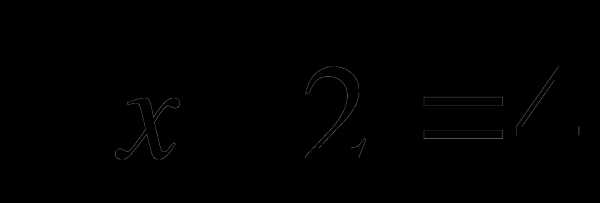 ;
;
2);
3);
-
Решить неравенство: .
-
Найти функцию, обратную к ; указать её область определения и множество значений. На одном рисунке построить графики данной функции и функции, обратной к данной.
Контрольная работа №3 по теме:
«Показательная функция»
Вариант №1
-
Решить уравнение:
 ; 2).
; 2). -
Решить неравенство
 .
. -
Решить систему уравнений
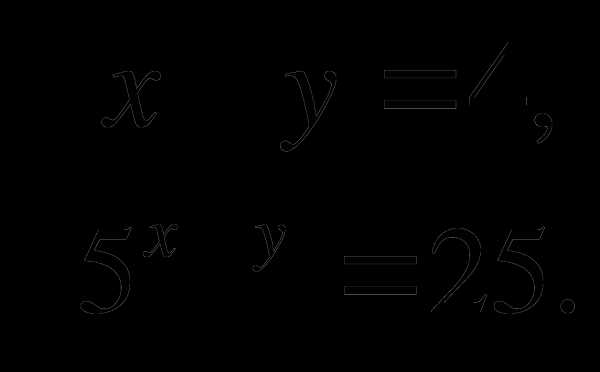
-
Решить неравенство:
1)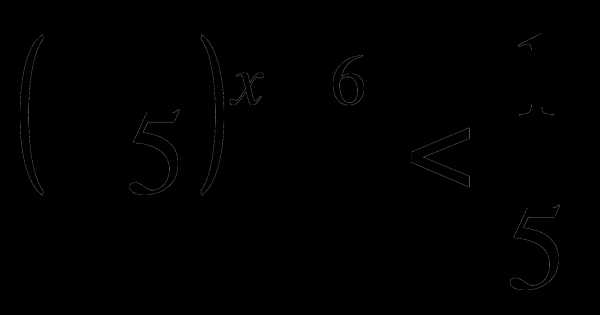 ; 2)
; 2)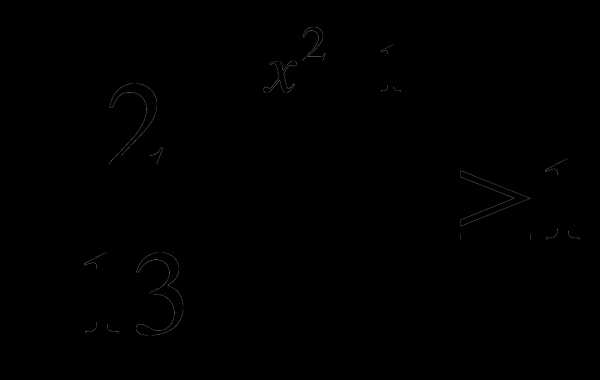 .
.
-
Решить уравнение .
-
Решите уравнение: .
В ответе укажите корень уравнения или сумму корней, если их несколько.
Контрольная работа №3 по теме:
«Показательная функция»
Вариант №2
1. Решить уравнение:
; 2).
2. Решить неравенство  .
.
3. Решить систему уравнений 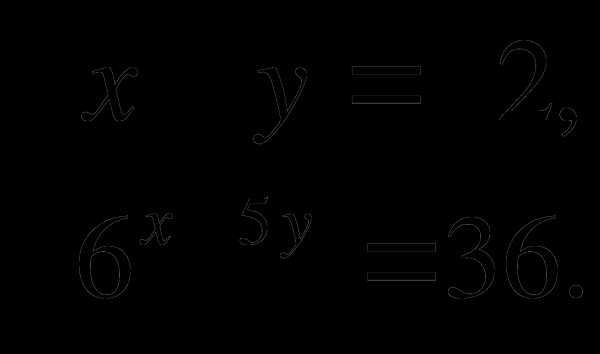
_ 4. Решить неравенство:
1)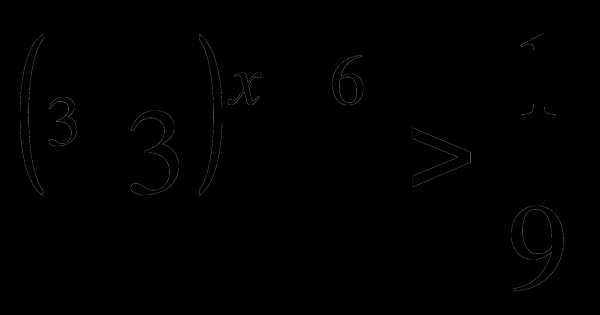 ; 2)
; 2)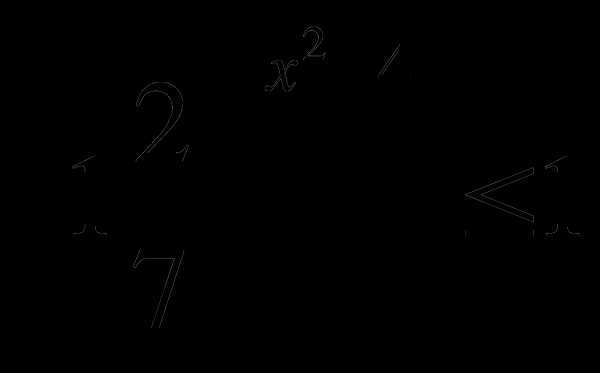 .
.
5. Решить уравнение .
6. Решите уравнение: .
В ответе укажите корень уравнения или сумму корней, если их несколько.
Контрольная работа №4 по теме:
«Логарифмическая функция»
Вариант №1
1. Вычислите:.
2. При каких значениях х имеет смысл выражение:
а);
б)
3. Решите уравнение:
4. Упростите: a0,a1.
5. Дано:. Найти: 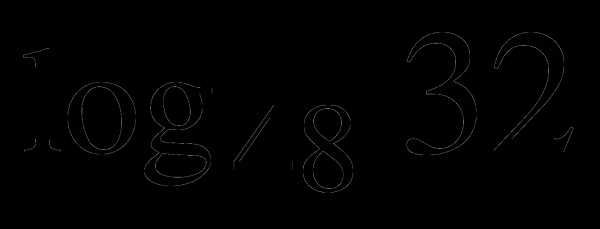 .
.
Контрольная работа №4 по теме:
«Логарифмическая функция»
Вариант №2
1. Вычислите: .
2. При каких значениях x имеет смысл выражение:
а) б)
3. Решите уравнение:
4. Упростите: a0,a1.
5. Дано: Найти: 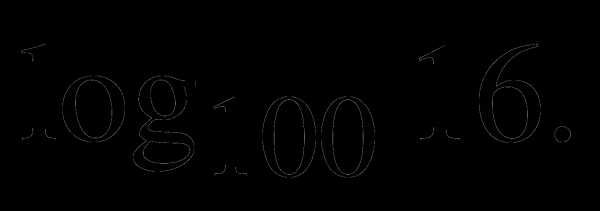
Контрольная работа №5 по теме:
«Тригонометрические формулы»
Вариант №1
1. Решите уравнение:
.
2. Упростите выражение:
а);
б);
в).
3. Пусть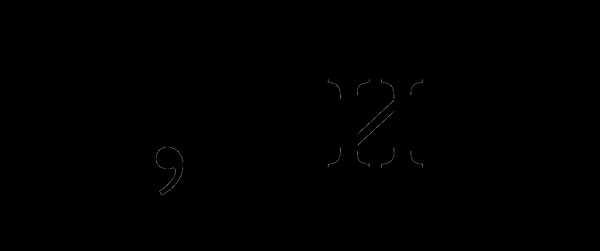 углы треугольника. Докажите тождество:
углы треугольника. Докажите тождество:
.
Контрольная работа №5 по теме:
«Тригонометрические формулы»
Вариант №2
1. Решите уравнение:
.
2. Упростите выражение:
а);
б);
в).
3. Пусть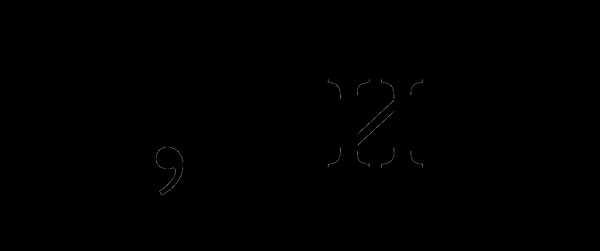 углы треугольника. Докажите тождество:
углы треугольника. Докажите тождество:
.
Контрольная работа №6 по теме:
«Тригонометрические уравнения»
Вариант №1
1. Решите уравнение: sin x —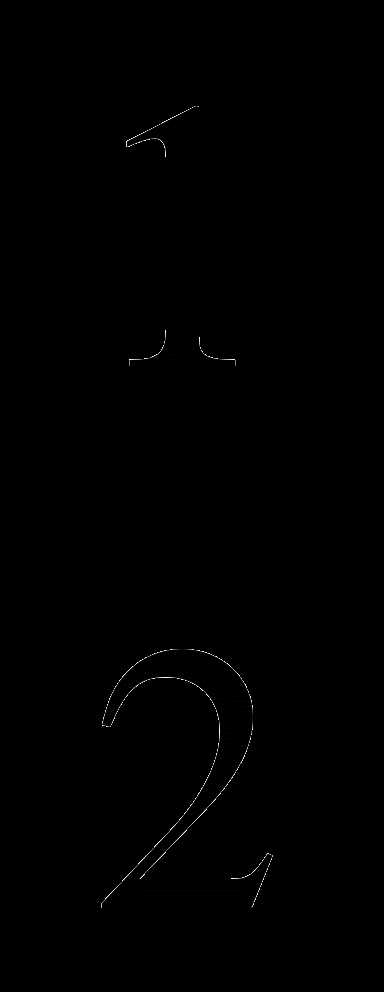 =0
=0
2. Решите уравнение: cos 2x=1
3. Укажите уравнение, которому соответствует решение: :
1) tg x = 1; 2) cos x = 0; 3) sin x = -1; 4) ctg x = .
.
4. На каком из рисунков показано решение неравенства: cos x < ?
?
1) 2) 3) 4)
5. Решите неравенство: tg x ≥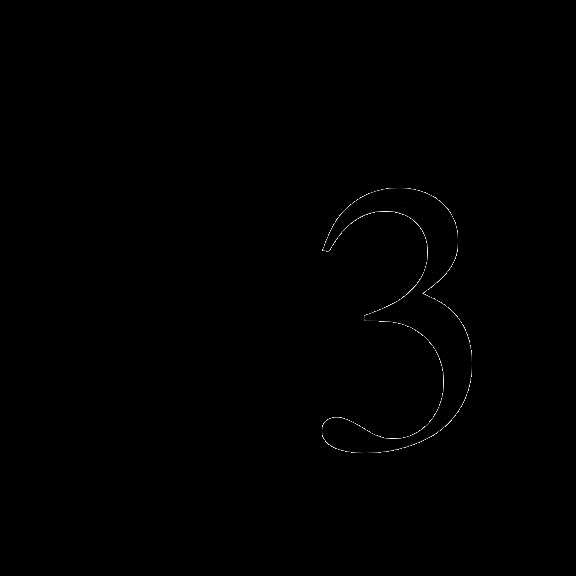 :
:
6. Решите уравнение: 6sin2 x + sin x – 1 = 0
7. Решите уравнение: 2sin2 x —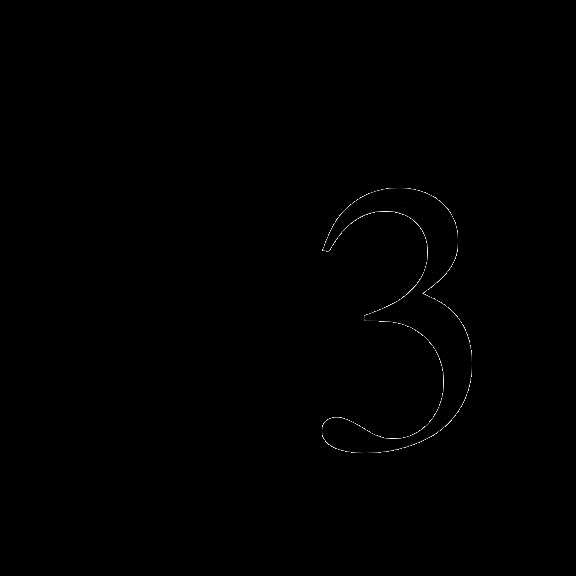 sin 2x =0
sin 2x =0
Контрольная работа №6 по теме:
«Тригонометрические уравнения»
Вариант №2
1. Решите уравнение: sin x + =0
=0
2. Решите уравнение: ctg (x+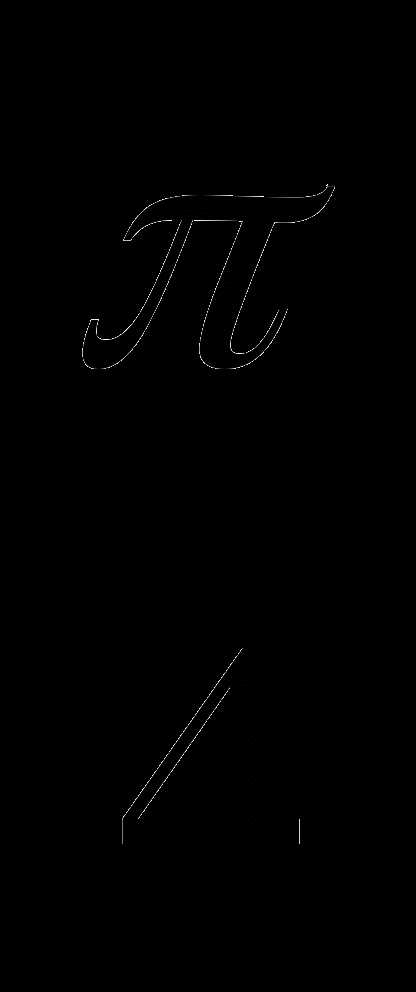 )=
)=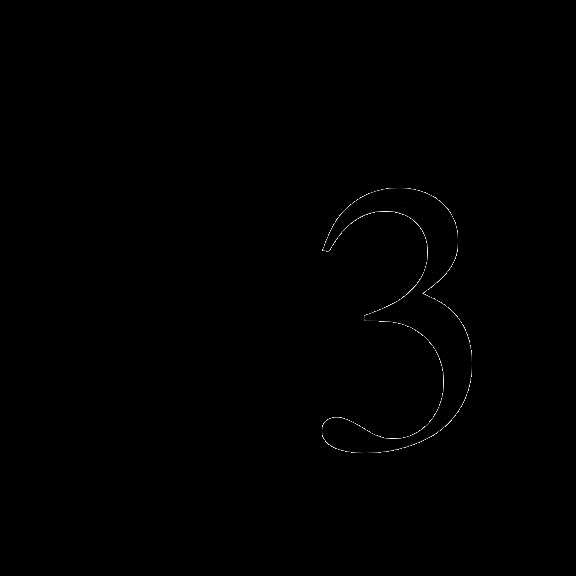
3. Укажите уравнение, которому соответствует решение:  :
:
1) ctg x = -1; 2) cos x = 0; 3) cos x = -1; 4) tg x = 1.
4. На каком из рисунков показано решение неравенства: sin x ≥ ?
?
1) 2) 3) 4) 4)
5. Решите неравенство: ctg x ≥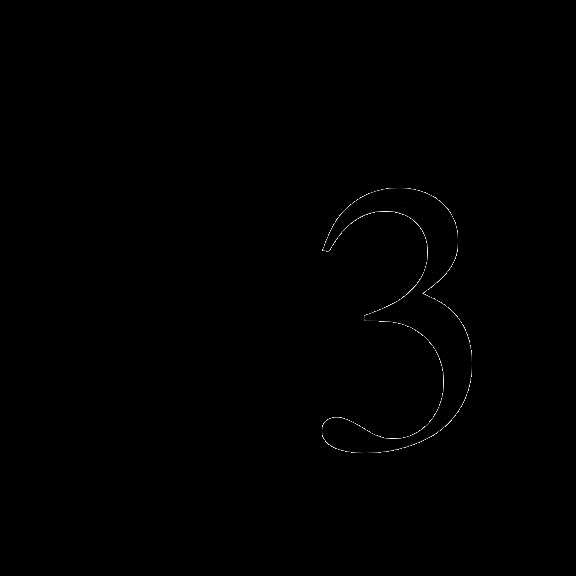
6. Решите уравнение: cos2 x — 4sin x + 3 = 0
7. Решите уравнение: 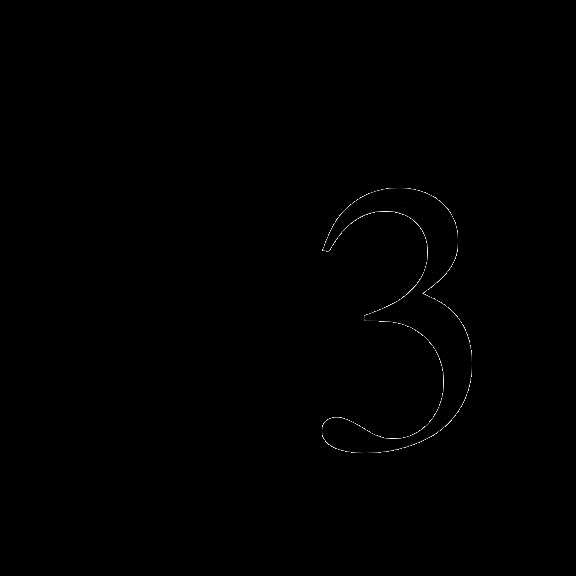 sin2 x -3sin x cos x =0
sin2 x -3sin x cos x =0
infourok.ru
Контрольная работа по алгебре 10 класс «Производная. Геометрический и механический смысл производной»
1 вариант
-
Найдите производные функций:
а) f(x) = 5х4 + 3х2 – 8х – 9; б) g(x) =  ;
;
в) q(x) = 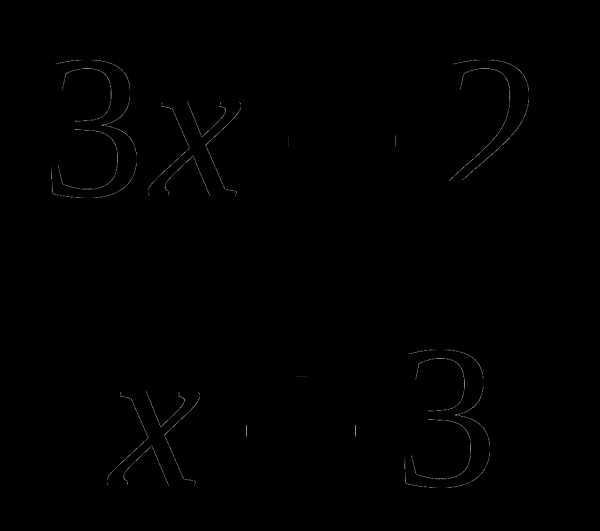 ; г) u(x) = sin 5x
; г) u(x) = sin 5x
2. Точка движется по закону х(t)=3t3+2t+1 Найдите ускорение точки в момент времени 2сек.
3. Найдите угол наклона касательной к графику функции f(x)=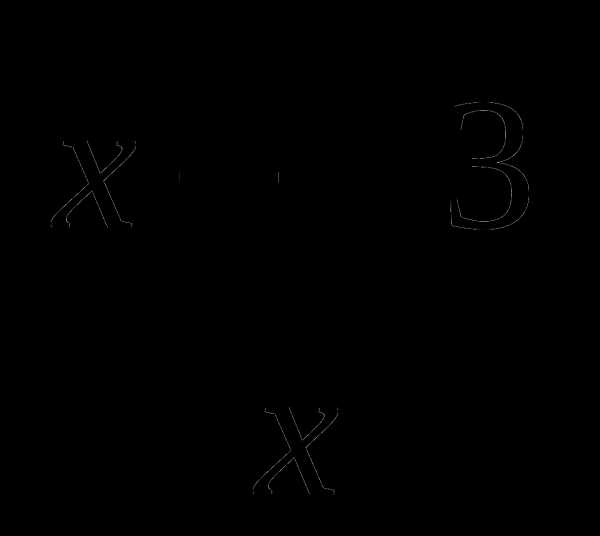 в точке х0=-1
в точке х0=-1
4. напишите уравнение касательной к графику функции f(x) = x2-2x в точке х0=2. Сделайте рисунок
5.На рисунке изображены график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке
6. Решите неравенство: 2х(х2-4)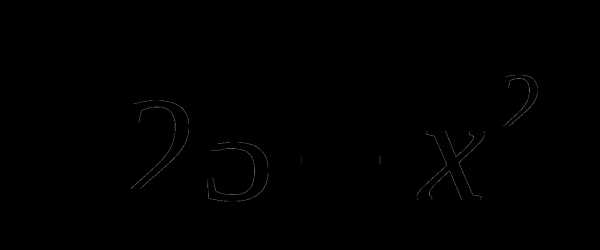 < 0
< 0
2 вариант
1. Найдите производные функций:
а) f(x) = 3х5 + 2х3 – 4х – 3; б)g(x) = 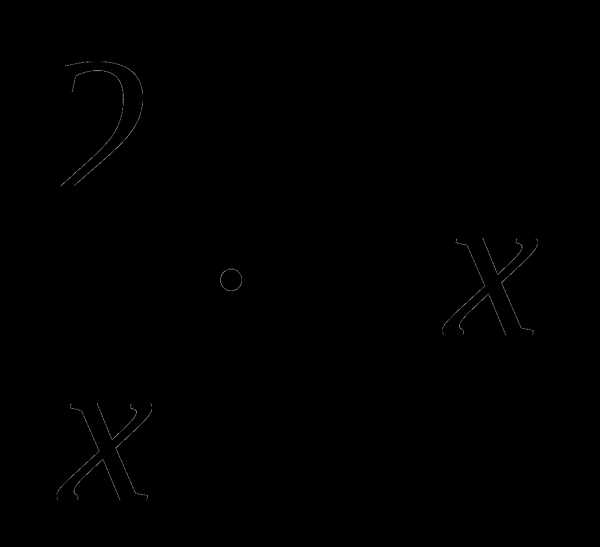 ;
;
в) q(x) = 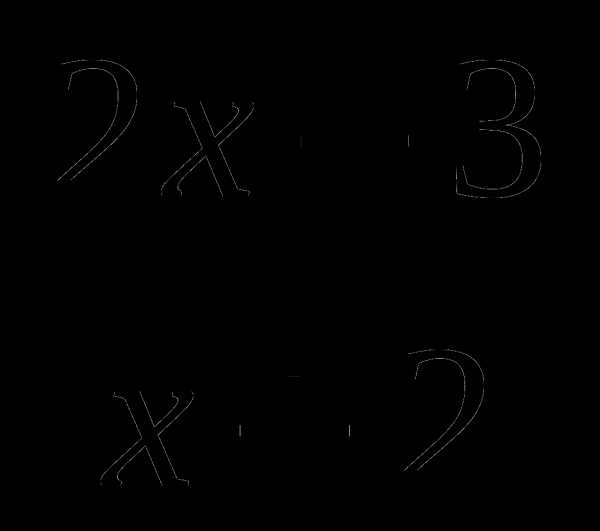 ; г) u(x) = cos 4x.
; г) u(x) = cos 4x.
2. Точка движется по закону х(t)=2t2+1 Найдите скорость точки в момент времени 2сек.
3. Найдите угол наклона касательной к графику функции f(x)= в точке х0=-2
в точке х0=-2
4. напишите уравнение касательной к графику функции f(x) = x2-1 в точке х0=-1. Сделайте рисунок
5. На рисунке изображены график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке
6.Решите неравенство: х(х2-2х+1)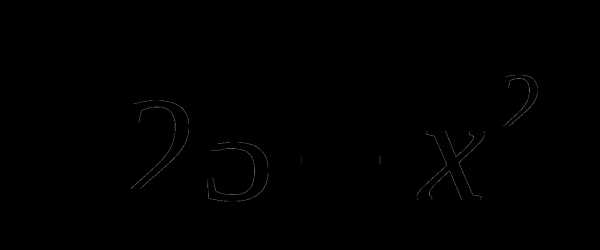 ≥ 0
≥ 0
3 вариант
1. Найдите производные функций:
а) f(x) =  х5 + 3х3 – х – 4; б) g(x) =
х5 + 3х3 – х – 4; б) g(x) = 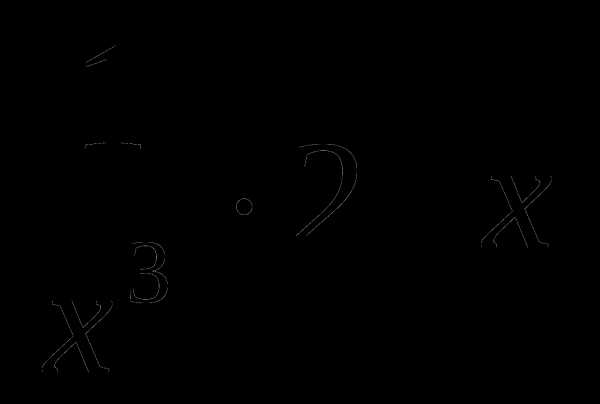 ;
;
в) q(x) = 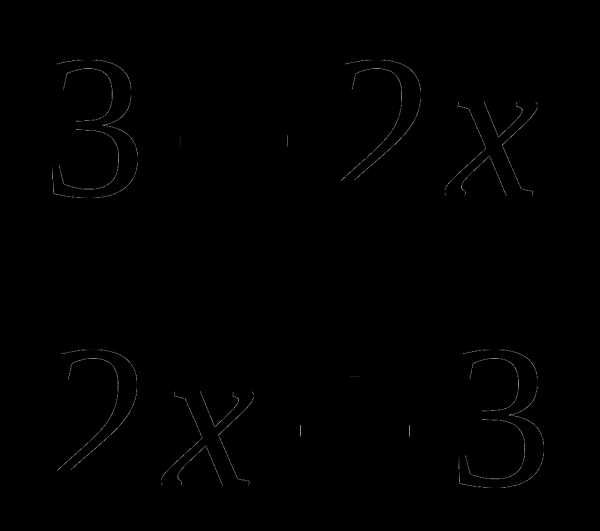 ; г) u(x) =
; г) u(x) =  sin 5x
sin 5x
2. Точка движется по закону х(t)=2t3+4t Найдите ускорение точки в момент времени 2сек.
3. Найдите угол наклона касательной к графику функции f(x)=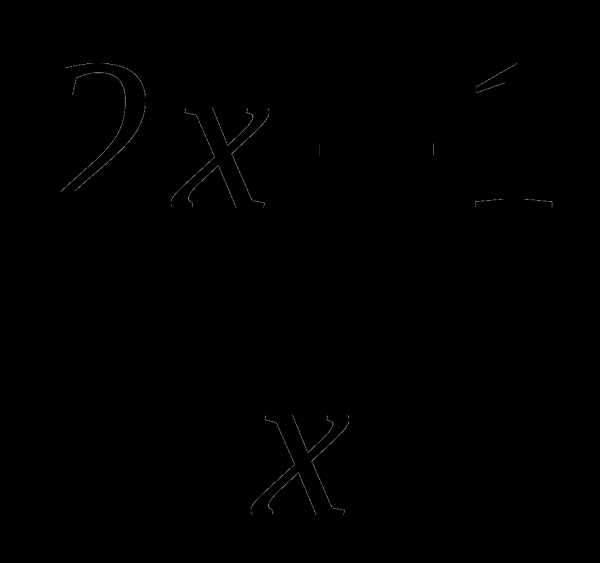 в точке х0=2
в точке х0=2
4. напишите уравнение касательной к графику функции f(x) = x2-4 в точке х0=3. Сделайте рисунок
5. На рисунке изображены график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке
6. Решите неравенство: (х2-2х)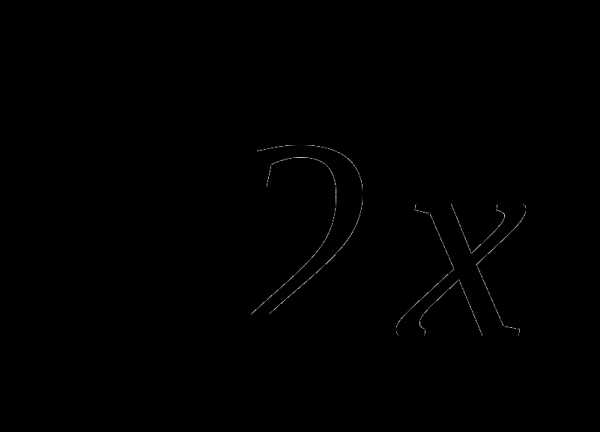 ≤ 0
≤ 0
4 вариант
1. Найдите производные функций:
а) f(x) = — 2х6 + 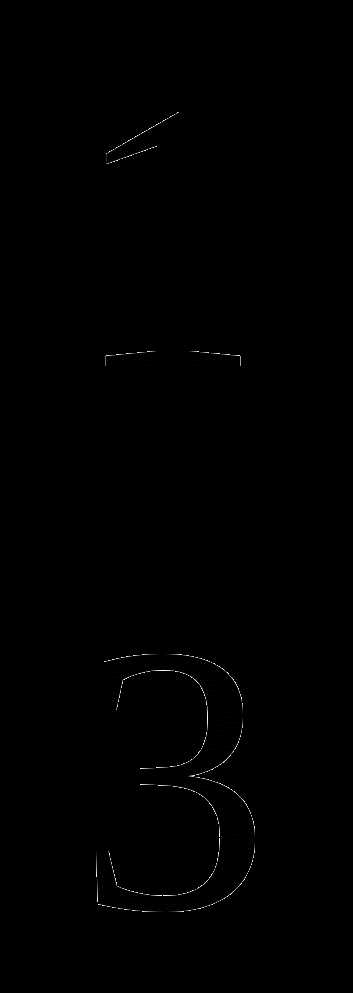 х9 – 3; б)g(x) =
х9 – 3; б)g(x) = ;
;
в) q(x) = 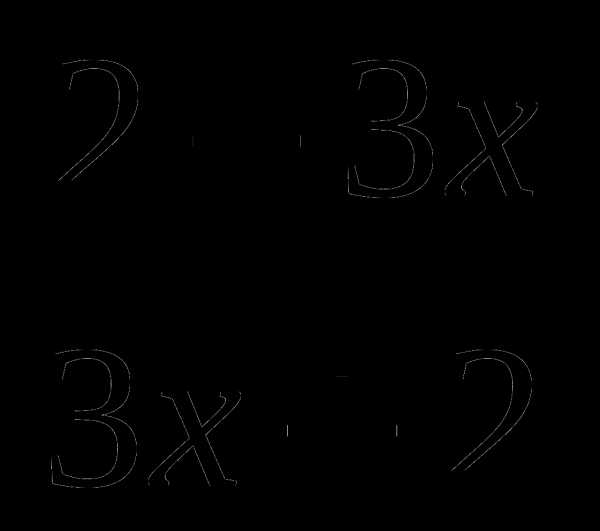 ; г) u(x) =
; г) u(x) =  cos 4x.
cos 4x.
2. Точка движется по закону х(t)=t3+1 Найдите скорость точки в момент времени 3сек.
3. Найдите угол наклона касательной к графику функции f(x)=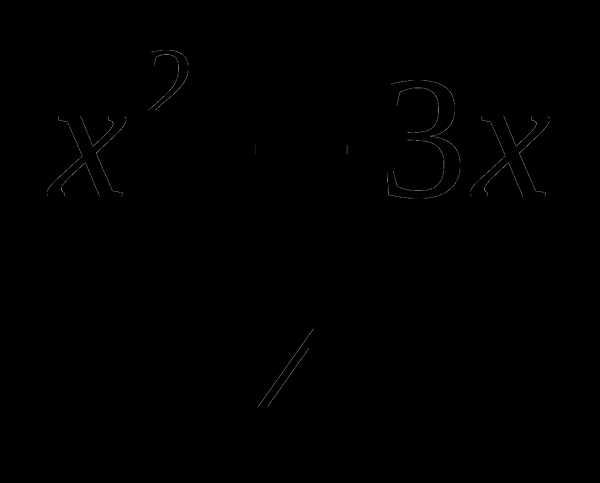 в точке х0=1
в точке х0=1
4. напишите уравнение касательной к графику функции f(x) = x2+5 в точке х0=2. Сделайте рисунок
5. На рисунке изображены график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке
6. Решите неравенство: (-х2+1) > 0
> 0
5 вариант
1. Найдите производные функций:
а) f(x) = 5х4 + 3х2 – 8х – 9; б) g(x) =  ;
;
в) q(x) = 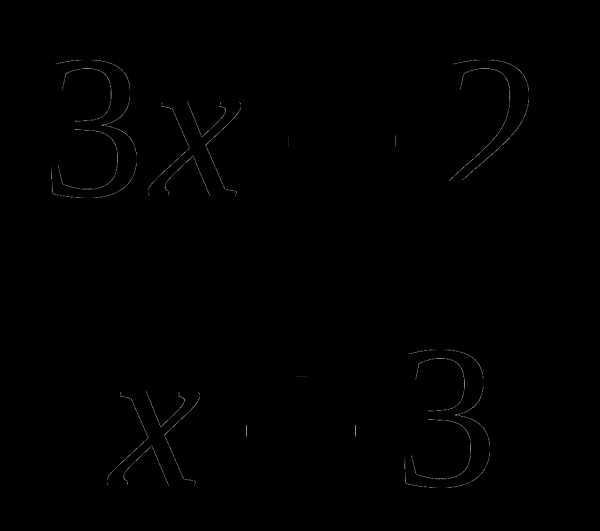 ; г) u(x) = sin 5x
; г) u(x) = sin 5x
2. Точка движется по закону х(t)=t3-1 Найдите ускорение точки в момент времени 2сек.
3. Найдите угол наклона касательной к графику функции f(x)=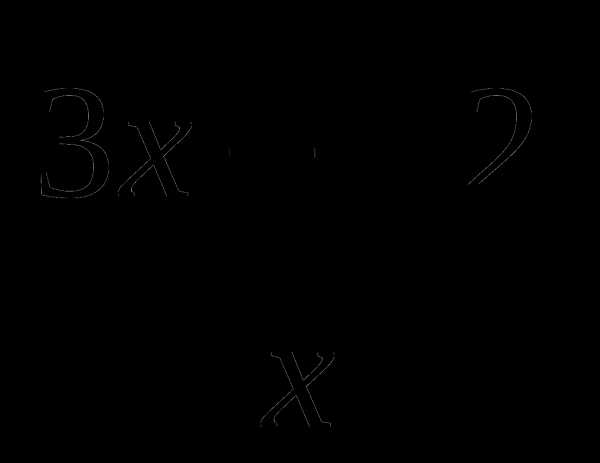 в точке х0=2
в точке х0=2
4. напишите уравнение касательной к графику функции f(x) = x2-1 в точке х0=-1. Сделайте рисунок
5. На рисунке изображены график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке
6.Решите неравенство:(х2+х-6)< 0
6 вариант
1. Найдите производные функций:
а) f(x) = 3х5 + 2х3 – 4х – 3; б)g(x) = 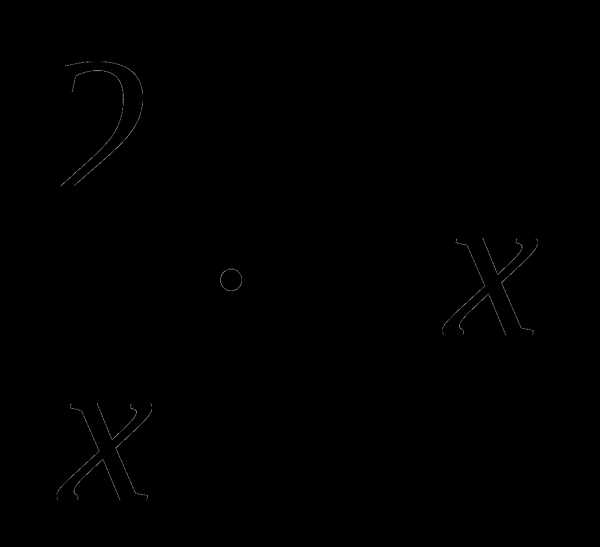 ;
;
в) q(x) = 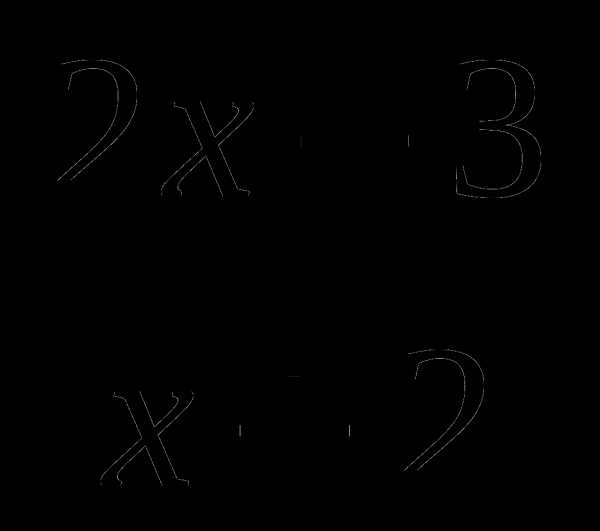 ; г) u(x) = cos 4x 2. Точка движется по закону х(t)= t3+5t Найдите, в какой момент времени скорость была равна 32м/с
; г) u(x) = cos 4x 2. Точка движется по закону х(t)= t3+5t Найдите, в какой момент времени скорость была равна 32м/с
3. Найдите угол наклона касательной к графику функции f(x)=sinx-7 в точке х0=2π
4. напишите уравнение касательной к графику функции f(x) = x2+2x в точке х0=1. Сделайте рисунок
5. На рисунке изображены график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке
6. Решите неравенство: (х2-1) ≥ 0
≥ 0
7 вариант
1. Найдите производные функций:
а) f(x) =  х5 + 3х3 – х – 4; б) g(x) =
х5 + 3х3 – х – 4; б) g(x) = 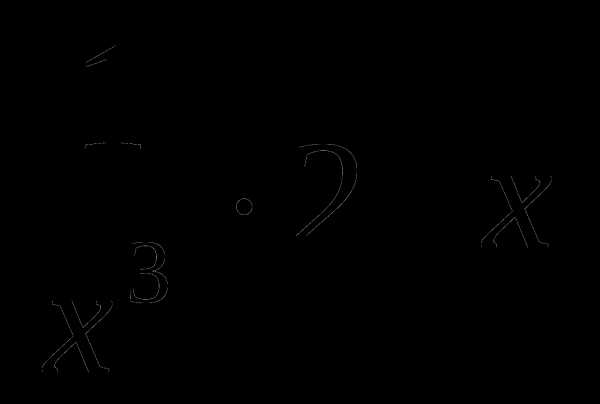 ;
;
в) q(x) = 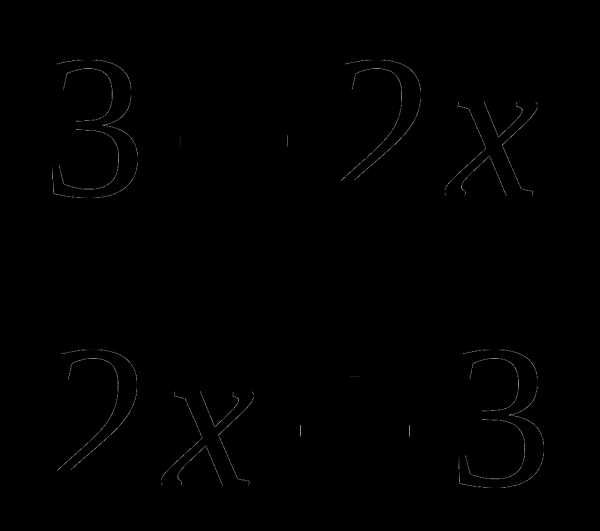 ; г) u(x) =
; г) u(x) =  sin 5x
sin 5x
2. Точка движется по закону х(t)= t4+1 Найдите скорость точки в момент времени 1сек.
3. Найдите угол наклона касательной к графику функции f(x)=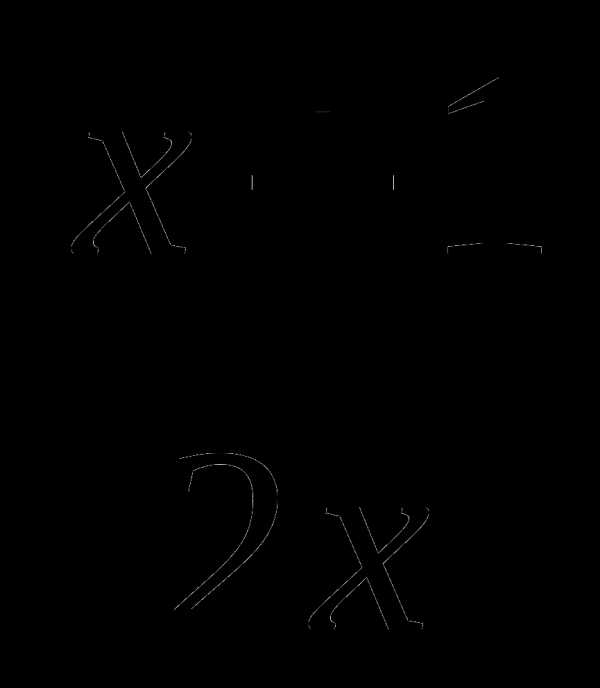 в точке х0=1
в точке х0=1
4. напишите уравнение касательной к графику функции f(x) = x2+3 в точке х0=1. Сделайте рисунок
5. На рисунке изображены график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке
6. Решите неравенство: (х+1)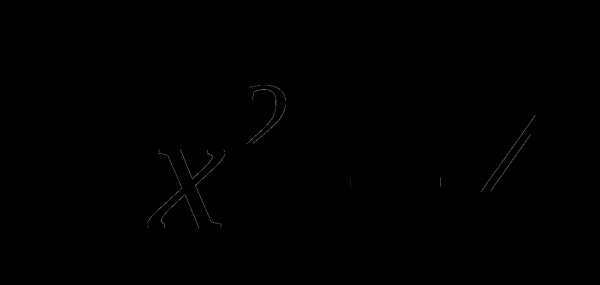 < 0
< 0
8 вариант
1. Найдите производные функций:
а) f(x) = — 2х6 +  х9 – 3; б)g(x) =
х9 – 3; б)g(x) = ;
;
в) q(x) = 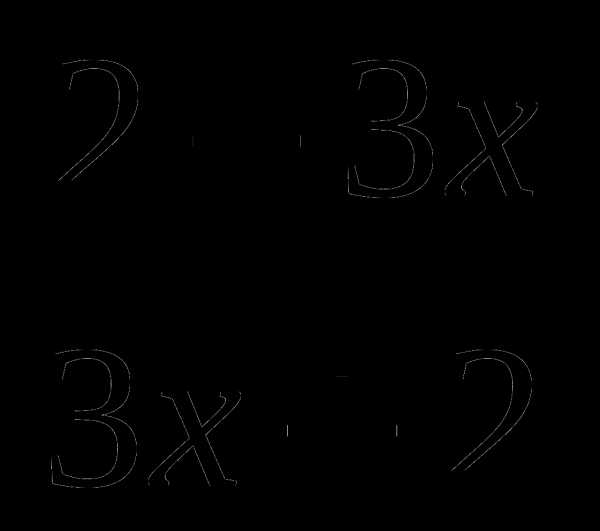 ; г) u(x) =
; г) u(x) =  cos 4x
cos 4x
2. Точка движется по закону х(t)=2t3+1 Найдите в какой момент времени ускорение было 48м/с2
3. Найдите угол наклона касательной к графику функции f(x)=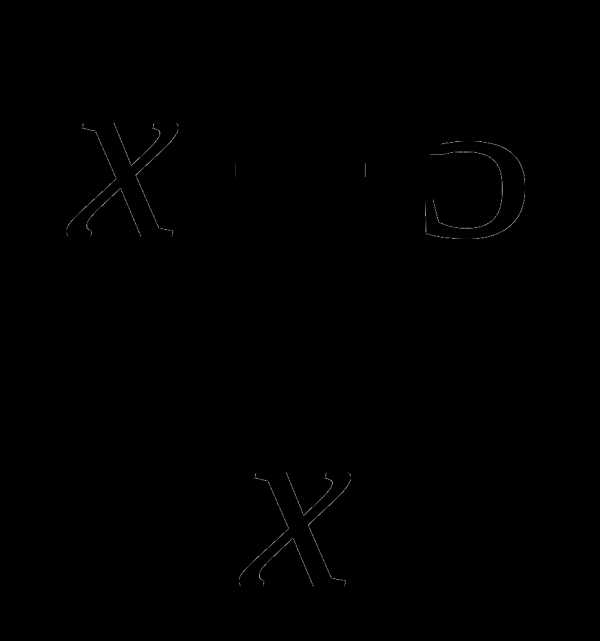 в точке х0=3
в точке х0=3
4. напишите уравнение касательной к графику функции f(x) = 0,5x2-2x в точке х0=1. Сделайте рисунок
5. На рисунке изображены график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке
6. Решите неравенство: (х+1)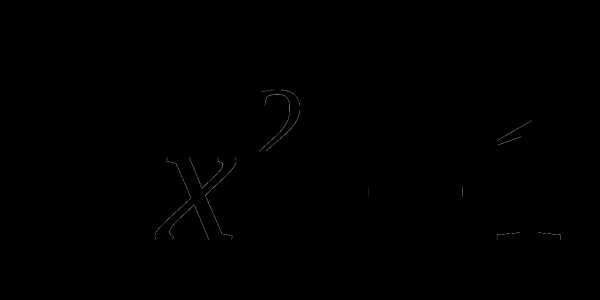 ≤ 0
≤ 0
9 вариант
1. Найдите производные функций:
а) f(x) = 5х4 + 3х2 – 8х – 9; б) g(x) =  ;
;
в) q(x) = 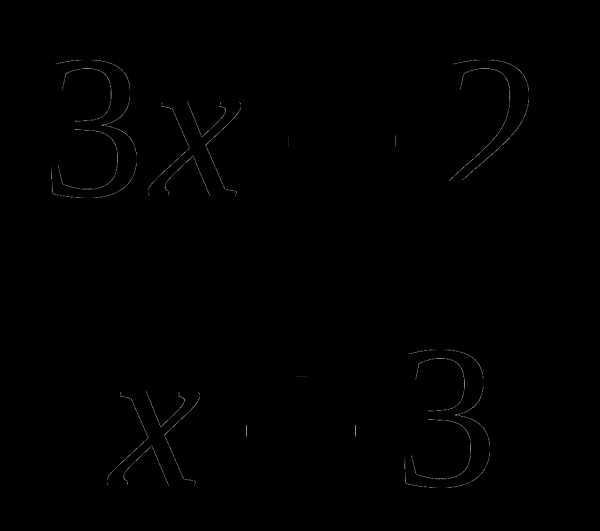 ; г) u(x) = sin 5x
; г) u(x) = sin 5x
2. Точка движется по закону х(t)=t3-4t Найдите скорость точки в момент времени 4сек.
3. Найдите угол наклона касательной к графику функции f(x)= в точке х0=-1
в точке х0=-1
4. напишите уравнение касательной к графику функции f(x) = 2x2+1 в точке х0=-1. Сделайте рисунок
5. На рисунке изображены график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке
6. Решите неравенство: х(х2+2х+1)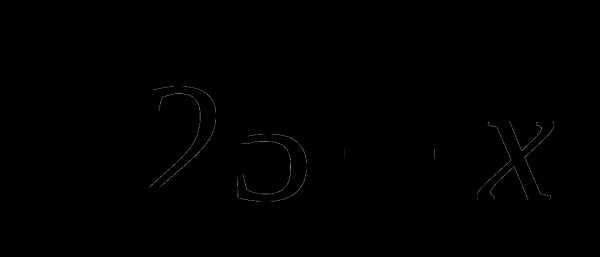 < 0
< 0
10 вариант
1. Найдите производные функций:
а) f(x) = 3х5 + 2х3 – 4х – 3; б)g(x) = 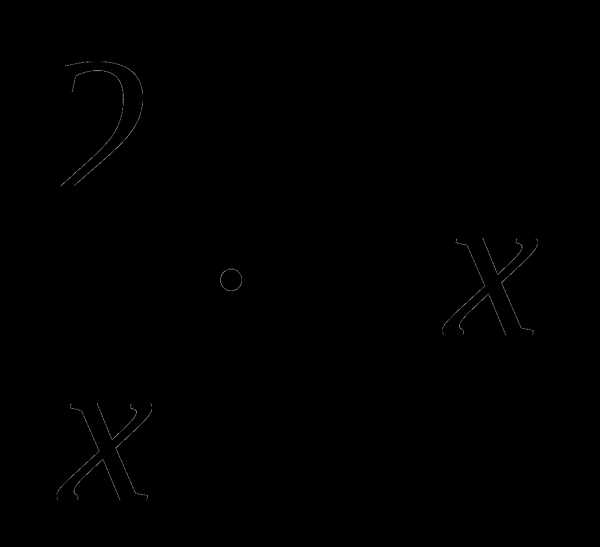 ;
;
в) q(x) = 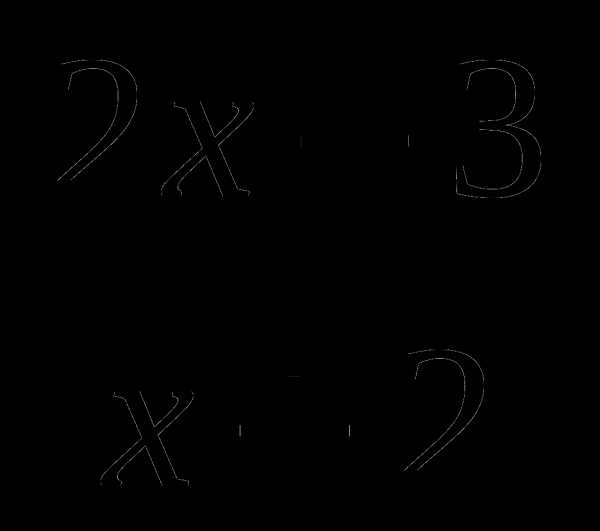 ; г) u(x) = cos 4x.
; г) u(x) = cos 4x.
2. Точка движется по закону х(t)=3t3+2. Найдите в какой момент времени ускорение было 27м/с2
3. Найдите угол наклона касательной к графику функции f(x)=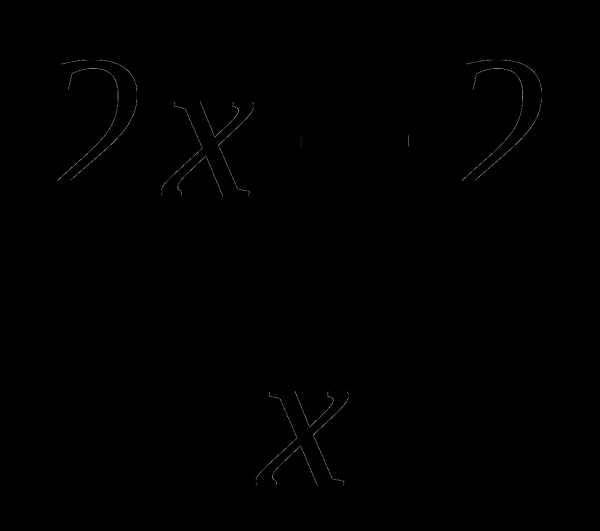 в точке х0=2
в точке х0=2
4. напишите уравнение касательной к графику функции f(x) = x2+x в точке х0=1. Сделайте рисунок
5. На рисунке изображены график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке
6. Решите неравенство: (х+1)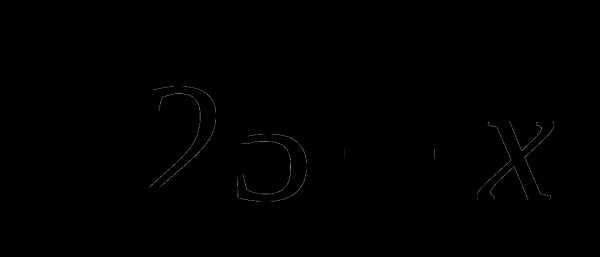 < 0
< 0
11 вариант
1. Найдите производные функций:
а) f(x) =  х5 + 3х3 – х – 4; б) g(x) =
х5 + 3х3 – х – 4; б) g(x) = 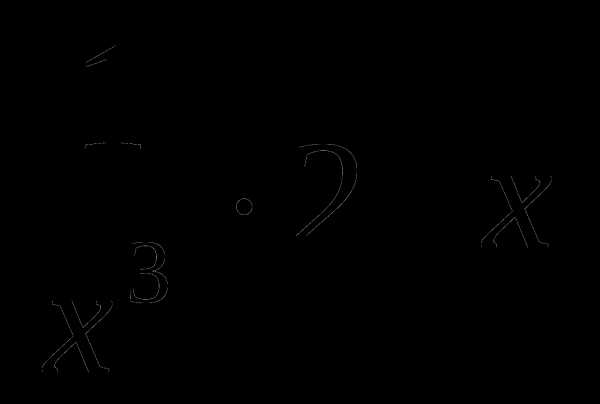 ;
;
в) q(x) = 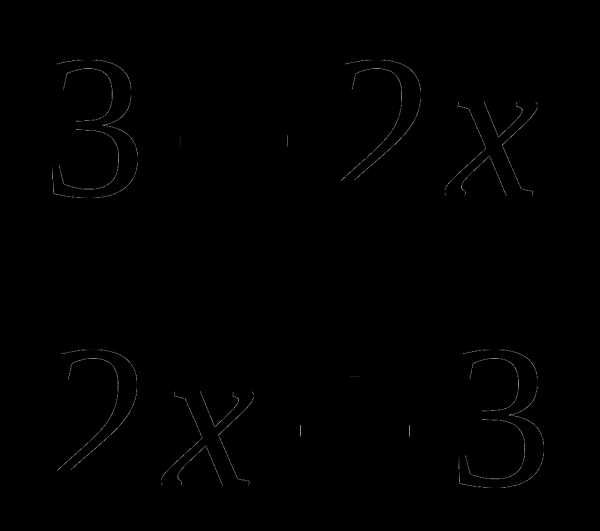 ; г) u(x) =
; г) u(x) =  sin 5x
sin 5x
2. Точка движется по закону х(t)= t2+2t Найдите в какой момент времени скорость была 68м/с
3. Найдите угол наклона касательной к графику функции f(x)=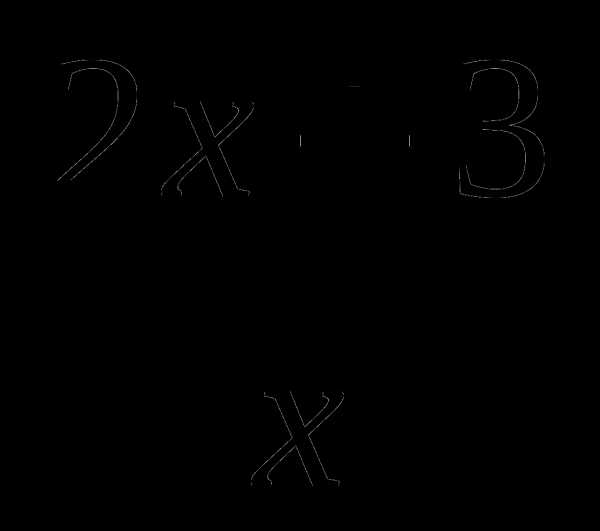 в точке х0=1
в точке х0=1
4. напишите уравнение касательной к графику функции f(x) = x2-x в точке х0=2. Сделайте рисунок
5. На рисунке изображены график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке
6. Решите неравенство: (х2-4х+4) < 0
< 0
12 вариант
1. Найдите производные функций:
а) f(x) = — 2х6 +  х9 – 3; б)g(x) =
х9 – 3; б)g(x) = ;
;
в) q(x) = 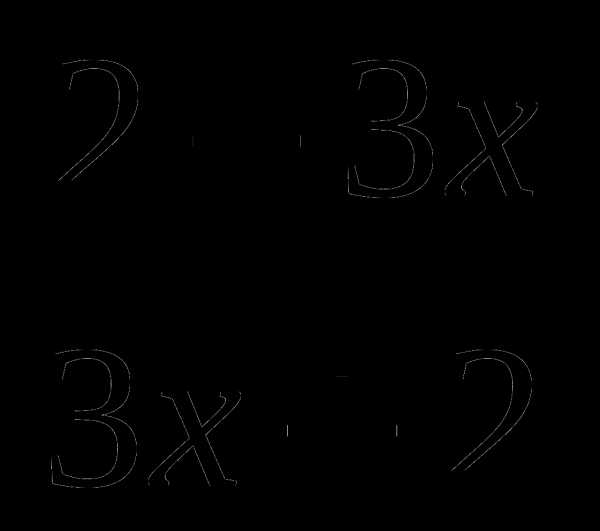 ; г) u(x) =
; г) u(x) =  cos 4x 2. Точка движется по закону х(t)=t2+5. Найдите в какой момент времени скорость была 74м/с
cos 4x 2. Точка движется по закону х(t)=t2+5. Найдите в какой момент времени скорость была 74м/с
3. Найдите угол наклона касательной к графику функции f(x)=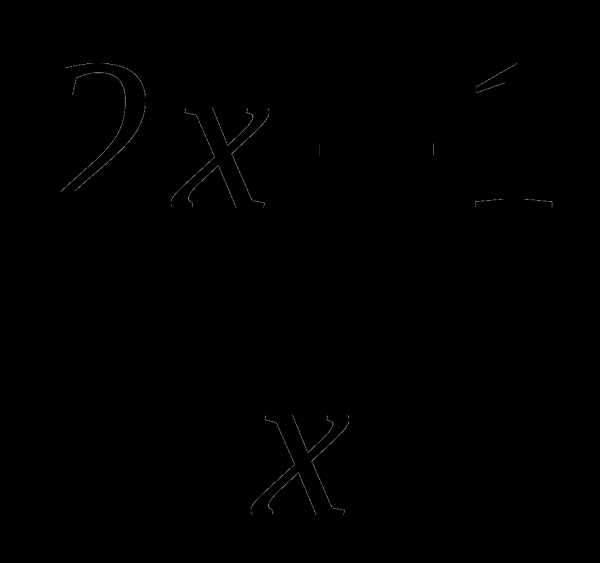 в точке х0=-1
в точке х0=-1
4. напишите уравнение касательной к графику функции f(x) = x2+1 в точке х0=1. Сделайте рисунок
5. На рисунке изображены график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке
6. Решите неравенство: х(х2+4х+4)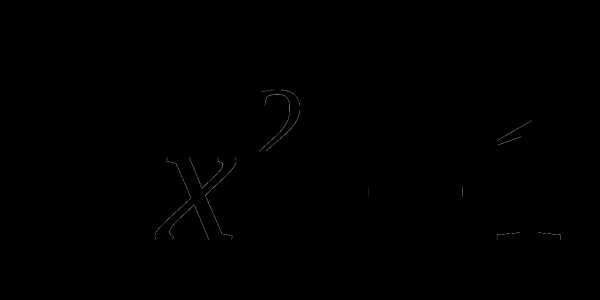 < 0
< 0
13 вариант
1. Найдите производные функций:
а) f(x) = 5х4 + 3х2 – 8х – 9; б) g(x) =  ;
;
в) q(x) = 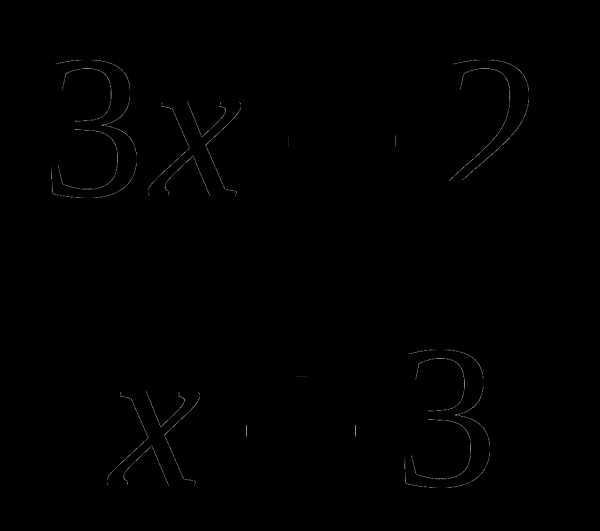 ; г) u(x) = sin 5x
; г) u(x) = sin 5x
2. Точка движется по закону х(t)=2t3+1 .Найдите в какой момент времени скорость точки была 54м/с
3. Найдите угол наклона касательной к графику функции f(x)=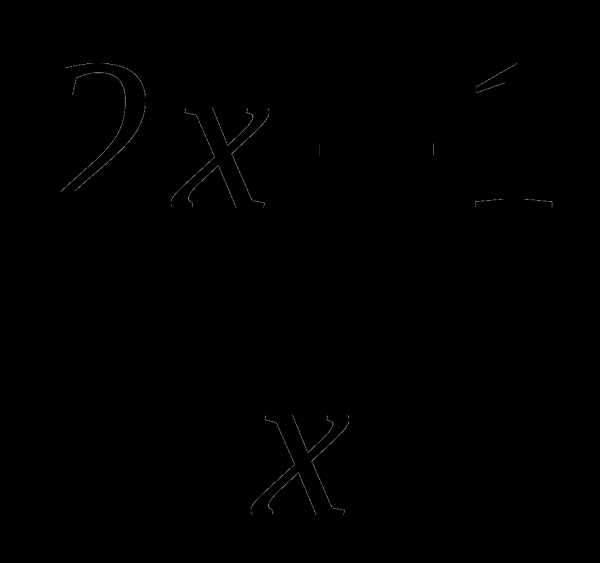 в точке х0=2
в точке х0=2
4. напишите уравнение касательной к графику функции f(x) = x2-3x в точке х0=-1. Сделайте рисунок
5. На рисунке изображены график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке
6. Решите неравенство: (х+4) < 0
< 0
14 вариант
1. Найдите производные функций:
а) f(x) =  х5 + 3х3 – х – 4; б) g(x) =
х5 + 3х3 – х – 4; б) g(x) = 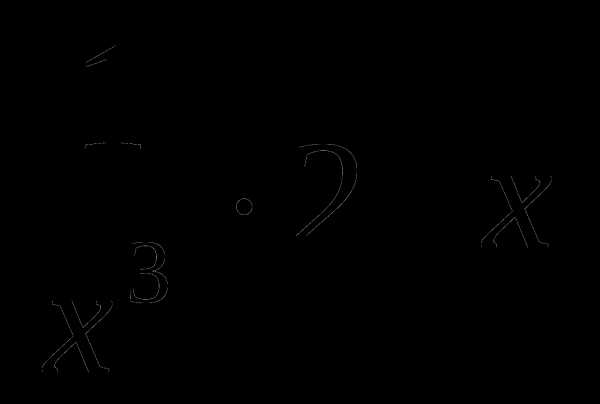 ;
;
в) q(x) = 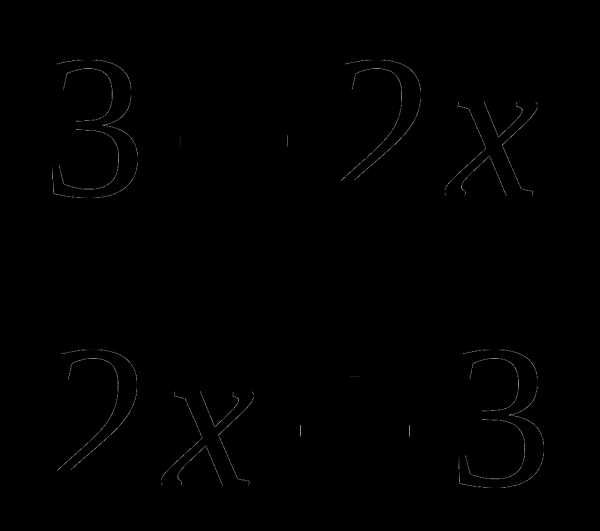 ; г) u(x) =
; г) u(x) =  sin 5x
sin 5x
2. Точка движется по закону х(t)= t3+2t+3 Найдите ускорение точки в момент времени 1сек.
3. Найдите угол наклона касательной к графику функции f(x)=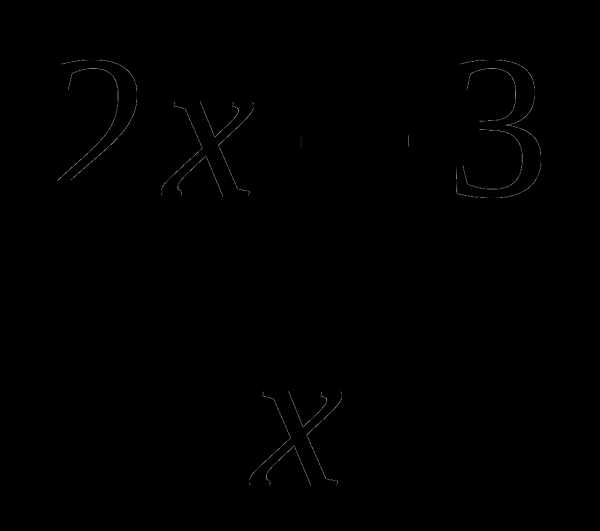 в точке х0=-1
в точке х0=-1
4. напишите уравнение касательной к графику функции f(x) = x2+2 в точке х0=-1. Сделайте рисунок
5. На рисунке изображены график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке
6. Решите неравенство: х(х+4)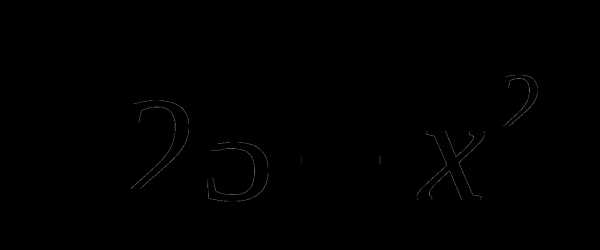 ≥ 0
≥ 0
infourok.ru
Контрольная работа по алгебре, 10 класс.
Просмотр содержимого документа
«Контрольная работа по алгебре, 10 класс.»
Контрольная работа №5. Тригонометрия.
I вариант
1. Вычислите:
а) ;
б) .
в)
2. Упростите выражение:
а) ;
б)
3. Вычислите:
а)
б) Известно, что. Вычислите: .
|
4 Доказать тождество: 5 Расположите в порядке убывания sin3,4 cos1, cos0,2, sin3,8 |
Контрольная работа №5. Тригонометрия.
II вариант
1. Вычислите:
а)
б)
в) .
2. Упростите выражение:
а)
б)
3. Вычислите: а)
б) Известно, что. Вычислите: .
4 Доказать тождество:
5 Расположите в порядке возрастания
sin 3 cos 3, sin 6 , sin2
Контрольная работа №5. Тригонометрия.
III вариант
1. Вычислите:
а)
б)
в)
2. Упростите выражение:
а)
б)cos(α–β)–2sinαsinβ в)
г)
3. Вычислите:
а)
б) Известно, что . Вычислите: .
4 Доказать тождество:
5 Расположите в порядке убывания
sin6 cos6, cos5, sin5
Контрольная работа №5. Тригонометрия.
IV вариант
1. Вычислите:
а)
б)
в)
2. Упростите выражение:
а)
в)
б)
г) sin(α–β)–sin(α+β)
3. Вычислите:
а)
б) Известно, что . Вычислите: .
4 Доказать тождество:
5 Расположите в порядке возрастания
sin 2,8 cos 4, sin 2,5 , sin2
multiurok.ru