|
Контрольная работа № 1 |
|
|
1 вариант 1). Для функции f (х) = х3 + 2х2 – 1. Найти f (0), f (1), f (-3), f (5). 2). Найти D(у), если:
3). Построить график функции: а). у = – х + 5 б). у = х2 – 2 По графику определить : а). Монотонность функции; б). Ограниченность функции; в). Минимальное ( максимальное ) значение функции 4). Для заданной функции найти обратную:
|
2 вариант 1). Для функции f (х) = 3х2 – х3 + 2. Найти f (0), f (1), f (-3), f (5). 2). Найти D(у), если:
3). Построить график функции: а). у = х – 7 б). у = – х2 + 2 По графику определить : а). Монотонность функции; б). Ограниченность функции; в). Минимальное ( максимальное ) значение функции 4). Для заданной функции найти обратную:
|
|
Контрольная работа № 2 |
|
|
1 вариант 1). Вычислите:
2). Упростите: 3). Известно, что: Вычислить 4). Решите уравнение: 5). Докажите тождество: |
2 вариант 1). Вычислите:
2). Упростите:
3). Известно, что:
Вычислить 4). Решите уравнение:
5). Докажите тождество:
|
|
Контрольная работа № 3 |
|
|
1 вариант 1). Найти наименьшее и наибольшее значения функций:
2). Упростить выражение:
3). Исследуйте функцию на четность: 4). Постройте график функции:
5). Известно, что |
2 вариант 1). Найти наименьшее и наибольшее значения функций:
2). Упростить выражение:
3). Исследуйте функцию на четность: 4). Постройте график функции:
5). Известно, что |
|
Контрольная работа № 4 |
|
|
1 вариант 1). Решить уравнение:
2). Найти корни уравнения 3). Решить уравнение:
4). Найти корни уравнения |
2 вариант 1). Решить уравнение:
2). Найти корни уравнения 3). Решить уравнение:
4). Найти корни уравнения |
|
Контрольная работа № 5 |
|
|
1 вариант 1). Вычислить:
2). Упростить выражение:
3). Доказать тождество:
4). Решить уравнение а).
5). Зная, что |
2 вариант 1). Вычислите:
2). Упростить выражение:
3). Доказать тождество:
4). Решить уравнение а).
5). Зная, что |
|
Контрольная работа № 6 |
|
|
1 вариант 1). Найдите производную функции: а). в). д). 2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции 3). Прямолинейное движение точки описывается законом 4). Дана функция Найдите: а). Промежутки возрастания и убывания функции; б). Точки экстремума; в). Наибольшее и наименьшее значения функции на отрезке |
2 вариант 1). Найдите производную функции: а). в). д). 2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции 3). Прямолинейное движение точки описывается законом 4). Дана функция Найдите: а). Промежутки возрастания и убывания функции; б). Точки экстремума; в). Наибольшее и наименьшее значения функции на отрезке |
|
Контрольная работа № 7 ( итоговая ) |
|
|
1 вариант 1). Дана функция 2). Решите уравнение:
3). Упростите выражение: а). б). 4). Постройте график функции с полным исследованием функции |
2 вариант 1). Дана функция 2). Решите уравнение:
3). Упростите выражение: а). б). 4). Постройте график функции с полным исследованием функции |
|
Контрольная работа № 1 |
|
|
1 вариант 1). Для функции f (х) = х3 + 2х2 – 1. Найти f (0), f (1), f (-3), f (5). 2). Найти D(у), если: 3). Построить график функции: а).у = – х + 5 б).у = х2 – 2 По графику определить : а). Монотонность функции; б). Ограниченность функции; в). Минимальное ( максимальное ) значение функции 4). Для заданной функции найти обратную: |
2 вариант 1). Для функции f (х) = 3х2 – х3 + 2. Найти f (0), f (1), f (-3), f (5). 2). Найти D(у), если: 3). Построить график функции: а).у = х – 7 б).у = – х2 + 2 По графику определить : а). Монотонность функции; б). Ограниченность функции; в). Минимальное ( максимальное ) значение функции 4). Для заданной функции найти обратную: |
|
Контрольная работа № 2 |
|
|
1 вариант 1). Вычислите: 2). Упростите: 3).Известно, что: Вычислить . 4). Решите уравнение: 5). Докажите тождество: |
2 вариант 1). Вычислите: 2). Упростите: 3). Известно, что: . Вычислить . 4). Решите уравнение: . 5). Докажите тождество:
|
|
Контрольная работа № 3 |
|
|
1 вариант 1). Найти наименьшее и наибольшее значения функций:
2). Упростить выражение: 3). Исследуйте функцию на четность: 4). Постройте график функции: 5). Известно, что . Докажите, что . |
2 вариант 1). Найти наименьшее и наибольшее значения функций:
2). Упростить выражение: 3). Исследуйте функцию на четность: 4). Постройте график функции: 5). Известно, что . Докажите, что . |
|
Контрольная работа № 4 |
|
|
1 вариант 1). Решить уравнение: 2). Найти корни уравнения 3). Решить уравнение: 4). Найти корни уравнения |
2 вариант 1). Решить уравнение: 2). Найти корни уравнения 3). Решить уравнение: 4). Найти корни уравнения |
|
Контрольная работа № 5 |
|
|
1 вариант 1). Вычислить: 2). Упростить выражение: 3). Доказать тождество: 4). Решить уравнение а). 5). Зная, что |
2 вариант 1). Вычислите: 2). Упростить выражение: 3). Доказать тождество: 4). Решить уравнение а). 5). Зная, что |
|
Контрольная работа № 6 |
|
|
1 вариант 1). Найдите производную функции: а). ; б). в). д). . 2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции 3). Прямолинейное движение точки описывается законом 4). Дана функция Найдите: а). Промежутки возрастания и убывания функции; б). Точки экстремума; в). Наибольшее и наименьшее значения функции на отрезке |
2 вариант 1). Найдите производную функции: а). ; б). в). д). . 2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции в точке х0 = 1. 3). Прямолинейное движение точки описывается законом 4). Дана функция Найдите: а). Промежутки возрастания и убывания функции; б). Точки экстремума; в). Наибольшее и наименьшее значения функции на отрезке . |
|
Контрольная работа № 7( итоговая ) |
|
|
1 вариант 1). Дана функция 2). Решите уравнение: 3). Упростите выражение: а). б). 4). Постройте график функции с полным исследованием функции |
2 вариант 1). Дана функция 2). Решите уравнение: 3). Упростите выражение: а). б). . 4). Постройте график функции с полным исследованием функции . |
|
+Контрольная работа № 1 |
|
|
1 вариант 1). Для функции f (х) = х3 + 2х2 – 1. Найти f (0), f (1), f (-3), f (5). 2). Найти D(у), если: 3). Построить график функции: а). у = – х + 5 б). у = х2 – 2 По графику определить : а). Монотонность функции; б). Ограниченность функции; в). Минимальное ( максимальное ) значение функции 4). Для заданной функции найти обратную: |
2 вариант 1). Для функции f (х) = 3х2 – х3 + 2. Найти f (0), f (1), f (-3), f (5). 2). Найти D(у), если: 3). Построить график функции: а). у = х – 7 б). у = – х2 + 2 По графику определить : а). Монотонность функции; б). Ограниченность функции; в). Минимальное ( максимальное ) значение функции 4). Для заданной функции найти обратную: |
|
Контрольная работа № 2 |
|
|
1 вариант 1). Вычислите: 2). Упростите: 3). Известно, что: . Вычислить . 4). Решите уравнение: . 5). Докажите тождество: . |
2 вариант 1). Вычислите: 2). Упростите: 3). Известно, что: . Вычислить . 4). Решите уравнение: . 5). Докажите тождество: . |
|
Контрольная работа № 3 |
|
|
1 вариант 1). Найти наименьшее и наибольшее значения функций: на отрезке ; на отрезке . 2). Упростить выражение: 3). Исследуйте функцию на четность: 4). Постройте график функции: 5). Известно, что . Докажите, что . |
2 вариант 1). Найти наименьшее и наибольшее значения функций: на отрезке ; на отрезке . 2). Упростить выражение: 3). Исследуйте функцию на четность: 4). Постройте график функции: 5). Известно, что . Докажите, что . |
|
Контрольная работа № 4 |
|
|
1 вариант 1). Решить уравнение: 2). Найти корни уравнения на отрезке . 3). Решить уравнение: 4). Найти корни уравнения , принадлежащие отрезку . |
2 вариант 1). Решить уравнение: 2). Найти корни уравнения на отрезке . 3). Решить уравнение: 4). Найти корни уравнения , принадлежащие отрезку . |
|
Контрольная работа № 5 |
|
|
1 вариант 1). Вычислить: 2). Упростить выражение: 3). Доказать тождество: 4). Решить уравнение а). 5). Зная, что и , найти . |
2 вариант 1). Вычислите: 2). Упростить выражение: 3). Доказать тождество: 4). Решить уравнение а). 5). Зная, что и , найти . |
|
Контрольная работа № 6 |
|
|
1 вариант 1). Найдите производную функции: а). ; б). ; в). ; г). ; д). . 2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции в точке х0 = 1. 3). Прямолинейное движение точки описывается законом . Найдите ее скорость в момент времени с. 4). Дана функция . Найдите: а). Промежутки возрастания и убывания функции; б). Точки экстремума; в). Наибольшее и наименьшее значения функции на отрезке . |
2 вариант 1). Найдите производную функции: а). ; б). ; в). ; г). ; д). . 2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции в точке х0 = 1. 3). Прямолинейное движение точки описывается законом . Найдите ее скорость в момент времени t = 2с. 4). Дана функция . Найдите: а). Промежутки возрастания и убывания функции; б). Точки экстремума; в). Наибольшее и наименьшее значения функции на отрезке . |
|
Контрольная работа № 7 ( итоговая ) |
|
|
1 вариант 1). Дана функция. Составить уравнение касательной к графику в точке с абсциссой . Установить, в каких точках промежутка касательная к графику данной функции составляет с осью Ох угол 600. 2). Решите уравнение: 3). Упростите выражение: а). ; б). . 4). Постройте график функции с полным исследованием функции . |
2 вариант 1). Дана функция. Составить уравнение касательной к графику в точке с абсциссой . Установить точки минимума и максимума, а также наибольшее и наименьшее значение на промежутке . 2). Решите уравнение: 3). Упростите выражение: а). ; б). . 4). Постройте график функции с полным исследованием функции . |
ГДЗ Алгебра 10 класс Глизбург
Алгебра 10 класс
Контрольные работы (Базовый и углубленный уровень)
Глизбург
Мнемозина
Тем кто отважился все же перейти в десятый класс, предстоит пережить вскоре самое изматывающее событие в жизни — ЕГЭ. Впрочем, эти испытания не так страшны, как им приписывают. На самом деле непонятно ради чего создавать такой ажиотаж, если с аналогичными проверками школьники вполне успешно справляются в повседневности, решая задачи на контрольных. И хотя в этом году они значительно усложняются, но все же при должной подготовке с ними вполне можно справиться. В этом подросткам поможет решебник к учебнику «Алгебра. Контрольные работы 10 класс (базовый и углубленный уровень)» Глизбург, где представлен полноценный материал по всему курсу.
Основные моменты в решебнике
В данном издании представлено девять контрольных работ, каждая рассчитана на шесть вариантов. Основным аспектом является пометка времени, что поможет учащимся сориентироваться в том, сколько же им отведут на выполнение того или иного задания. ГДЗ по алгебре 10 класс Глизбург содержит проверенные и детализированные ответы по всем пунктам.
Почему его стоит применять
Если у ребенка есть математический талант — это прекрасно. А когда подростки больше тянуться к гуманитарным наукам, то данный предмет начинает представлять для них определенную проблему. Так как тематика этого курса включает в себя и тригонометрию, то воспринять все необходимые знания будет совсем непросто. Так же сложна и подготовка к контрольным работам, хотя после нее материал систематизируется таким образом, что его легко применить в дальнейшем. Поэтому стоит потратить время на то, чтобы во время настоящих испытаний не испытывать никаких затруднений. В этом начинании хорошо поможет решебник к учебнику «Алгебра. Контрольные работы 10 класс (базовый и углубленный уровень)» Глизбург. «Мнемозина», 2014 г.
Похожие ГДЗ Алгебра 10 класс
Пояснительная записка
к тексту годовой контрольной работы
по алгебре за курс 10 класса (уч. Мордкович А.Г.).
Базовый уровень
Годовая контрольная работа составлена в соответствии с программным материалом курса «Алгебра и начала анализа» и требованиями федеральных государственных образовательных стандартов. Задания данной работы отражают следующие основные темы курса алгебры: «Тригонометрические выражения», «Тригонометрические уравнения», «Производная», «Применение производной».
Работа составлена в форме теста с кратким ответом и состоит из двух частей: Часть1 – 7 заданий базового уровня сложности с кратким ответом, часть 2 – 3 задания повышенного уровня сложности. Структура теста аналогична структуре текстов в формате ЕГЭ, что позволит не только проверить знания, умения и навыки учащихся за курс 10 класса, но и постепенно подготовить к работе с подобным материалом при подготовке и сдаче экзамена. Использованы задания из открытого банка задач ЕГЭ по математике. На выполнение работы отводится 40 минут.
Элементы анализа:
Часть В.
-
Нахождение значения тригонометрического выражения.
-
Решение тригонометрического уравнения и нахождение наименьшего положительного корня.
-
Нахождение значения тригонометрического выражения. Применение формулы косинуса двойного угла.
-
Нахождение значения тригонометрической функции по известной кофункции
-
Нахождение значения производной рациональной функции в точке.
-
Нахождение значения производной тригонометрической функции в точке.
-
Применение производной. Нахождение точек экстремума.
Часть С
-
Применение производной. Нахождение абсциссы точки касания.
-
а) Решение тригонометрического уравнения методом замены и сведением к квадратному
б) Нахождение корней уравнения, принадлежащих данному отрезку.
Несмотря на то, что всего в работе 9 заданий, элементов анализа всего 10. Поэтому критерии оценивания следующие:
«3» — верно выполнено 5-6 заданий
«4» — верно выполнено 7-8 заданий
«5» — верно выполнено 9-10 заданий
Итоговая контрольная работа 10 класс.
I вариант
Часть В.
-
Найдите значение выражения: 24.
-
Решить уравнение — = 0 и укажите наименьший положительный корень уравнения в градусах.
-
Найдите значение выражения:
-
Найдите и
-
Найдите значение производной функцииу = х2 – 6х + 1 в точке х0=-1.
-
Найдите значение производной функции в точке:
у = -3 + 2, х0 = .
-
Найдите точки экстремума и определите их характер: у = х3 + 3х2 – 9х – 2.
Часть С.
-
Прямая у = 4х + 13 параллельна касательной к графику функции у = х2 – 3х + 5. Найдите абсциссу точки касания.
-
а) Решите уравнение:
2
б) Укажите корни, принадлежащие отрезку
Итоговая контрольная работа 10 класс.
II вариант
Часть В.
-
Найдите значение выражения: 46.
-
Решить уравнение: — = 0 и укажите наименьший положительный корень уравнения в градусах.
-
Найдите значение выражения: .
-
Найдите и
-
Найдите значение производной функции в точке у = х2 – 5х + 2 в точке х0=-2.
-
Найдите значение производной функции в точке:
у = 3 -, х0 = .
-
Найдите точки экстремума и определите их характер: у = 2х3 — 10х2 + 6х.
Часть С.
-
Прямая у = 6х + 9 параллельна касательной к графику функции у = х2 + 7х — 6. Найдите абсциссу точки касания.
-
а) Решите уравнение:
б) Укажите корни, принадлежащие отрезку
Итоговая контрольная работа 10 класс.
III вариант
Часть В.
-
Найдите значение выражения: 37
-
Решить уравнение — = 0 и укажите наименьший положительный корень уравнения в градусах.
-
Найдите значение выражения: .
-
Найдите и
-
Найдите значение производной функции у = х3 + 4х2 – 1 в точке х0=-1.
-
Найдите значение производной функции в точке: у = — 2, х0 = .
-
Найдите точки экстремума и определите их характер: у = х3 + х2 – 5х – 3.
Часть С.
-
Прямая у = -5х — 6 параллельна касательной к графику функции у = х2+ 8х – 7. Найдите абсциссу точки касания.
-
а)Решите уравнение:
б) Укажите корни, принадлежащие отрезку
-
Найдите наибольшее и наименьшее значения функции у = х + на отрезке .
Итоговая контрольная работа 10 класс.
IV вариант
Часть В.
-
Найдите значение выражения: 34.
-
Решить уравнение и укажите наименьший положительный корень уравнения в градусах.
-
Найдите значение выражения: .
-
Найдите и
-
Найдите значение производной функции у = х4 – 2х — 1 в точке х0=-2.
-
Найдите значение производной функции в точке: у = — 2, х0= .
-
Найдите точки экстремума и определите их характер: у = х3— х2 – х +3.
Часть С.
-
Прямая у = -3х + 8 параллельна касательной к графику функции у = х2+ 7х -6. Найдите абсциссу точки касания.
-
а) Решите уравнение:
б) Укажите корни, принадлежащие отрезку
-
Найдите наибольшее и наименьшее значения функции у = х + на отрезке .
ГДЗ — Алгебра и начала анализа 10-11 класс Контрольные работы А.Г. Мордкович, Е.Е. Тульчинская
— М.: Мнемозина, 2000 — 2013 гг.
Пожалуйста выберите номер Контр. раб. в этом окне * →
Контрольные работы 1-13
Контрольная №1 Вариант 1
Контрольная №1 Вариант 2
Контрольная №1 Вариант 3
Контрольная №1 Вариант 4
Контрольная №2 Вариант 1
Контрольная №2 Вариант 2
Контрольная №2 Вариант 3
Контрольная №2 Вариант 4
Контрольная №3 Вариант 1
Контрольная №3 Вариант 2
Контрольная №3 Вариант 3
Контрольная №3 Вариант 4
Контрольная №4 Вариант 1
Контрольная №4 Вариант 2
Контрольная №4 Вариант 3
Контрольная №4 Вариант 4
Контрольная №5 Вариант 1
Контрольная №5 Вариант 2
Контрольная №5 Вариант 3
Контрольная №5 Вариант 4
Контрольная №6 Вариант 1
Контрольная №6 Вариант 2
Контрольная №6 Вариант 3
Контрольная №6 Вариант 4
Контрольная №7 Вариант 1
Контрольная №7 Вариант 2
Контрольная №7 Вариант 3
Контрольная №7 Вариант 4
Контрольная №8 Вариант 1
Контрольная №8 Вариант 2
Контрольная №8 Вариант 3
Контрольная №8 Вариант 4
Контрольная №9 Вариант 1
Контрольная №9 Вариант 2
Контрольная №9 Вариант 3
Контрольная №9 Вариант 4
Контрольная №10 Вариант 1
Контрольная №10 Вариант 2
Контрольная №10 Вариант 3
Контрольная №10 Вариант 4
Контрольная №11 Вариант 1
Контрольная №11 Вариант 2
Контрольная №11 Вариант 3
Контрольная №11 Вариант 4
Контрольная №12 Вариант 1
Контрольная №12 Вариант 2
Контрольная №12 Вариант 3
Контрольная №12 Вариант 4
Контрольная №13 Вариант 1
Контрольная №13 Вариант 2
Контрольная №13 Вариант 3
Контрольная №13 Вариант 4
* для выбора упражнения нажмите на стрелку вниз, чтобы открылся список.
Экзаменационная работа за 1 полугодие. 10 класс.
Вариант 1.
Часть 1.
1.Укажите сколько натуральных чисел входят в область определения функции:
у = -2х+4 +2х+3-3 x2+10х-3.
2.Найдите по графику наименьшее значение функции: y=sin x на [π/3;7π/6]
3. Найдите значение функции: у =2 sin x + cos x, если х = — π/2.
4.В ∆АВС угол С равен 900 , ВС=21, АВ=5. Найдите sin В.
5. Решите уравнение: — cos x= 3х-1.
6.Сколько корней имеет уравнение: cos x=22 на [-π;3π].
7.Вычислите: sin (arccos x+ arccos(- x)).
8.Сколько натуральных чисел входит в область допустимых значений выражения arcsin (5-2x).
9.Вычислите: sin(-7π)+2 cos31π3 — tg7π4.
10.Найдите значение выражения: 27 sinα -15, если cos α=429 и 0
11.Найдите сумму наибольшего отрицательного и наименьшего положительного корней уравнения 4 cos2 2х =2.
12. Сколько корней имеет уравнение 3 cos х +sin х =0 на [0; π].
Часть 2.
1.Найдите значение выражения 3 tg2 х0 -1, где х0 – наименьший положительный корень уравнения 2 cos2 х + 5 sin x -4=0.
2.Точка М не лежит в плоскости параллелограмма АВСД. На отрезке АМ выбрана точка Е так, что МЕ : ЕА = 2:3.
а) постройте точку F –точку пересечения прямой МВ с плоскостью СДЕ;
б) найдите АВ, если EF=10см.
3.При каких а решения системы 3х+2у=7;х-у=а удовлетворяют неравенству х
4.Используя график функции у=f(х), где f(х) = х2 -4х+3 постройте
у=| -f ( |х| ) |.
5.Решите неравенство 6 cos 2 t + sin t > 4.
6. Решите уравнение (2 cos x -1) 4×2- 7 х+3 = 0
Экзаменационная работа за 1 полугодие. 10 класс.
Вариант 2.
Часть 1.
1.Укажите сколько натуральных чисел входят в область определения функции:
у = 2×2-5х+2 +2×2-4х10-2х.
2.Найдите по графику наибольшее значение функции: y= cos x на [π/2;4π/3]
3. Найдите значение функции: у =2 cos (x- π/2)-1, если х = — π/2.
4.В ∆АВС угол С равен 900 , АС=621, АВ=30. Найдите sin А.
5. Решите уравнение: cos x= 2х + 1.
6.Сколько корней имеет уравнение: sin x=- 22 на [-π;2π].
7.Вычислите: cos (arcsin x+ arcsin(- x)).
8.Сколько натуральных чисел входит в область допустимых значений выражения arccos (3-2x).
9.Вычислите: cos(-9π)+2 sin(-49π6) — ctg(-21π4).
10.Найдите значение выражения: 7 — 8 sinα , если cos α=-154 и 3π/2
11.Найдите сумму наибольшего отрицательного и наименьшего положительного корней уравнения 4 sin2 2х =3.
12. Сколько корней имеет уравнение cos х= sinх на [0; π].
Часть 2.
1.Найдите значение выражения 5 tg2 х0 + 2,3 , где х0 – наименьший положительный корень уравнения 6 — 6 cos х — sin2 x =0.
2.Точка М не лежит в плоскости ромба АВСД. На отрезке ВМ выбрана точка F так, что МF : FB = 1:3.
а) постройте точку K –точку пересечения прямой МC с плоскостью AFД;
б) найдите FK, если AД=16см.
3.При каких а решения системы х+ау=3;ах+4у=6 удовлетворяют неравенству х >1, у>0.
4.Используя график функции у=f(х), где f(х) = х2 +4х+3 постройте
у= — | f ( |х| ) |.
5.Решите неравенство 6 cos 2 t + sin t ≤ 4.
6. Решите уравнение (2cos 2 x — 3) 3×2- 7 х+4 = 0.
10-й класс по математике
Распечатайте тест по математике для 10-го класса перед началом обучения. У него 40 вопросов, но он очень исчерпывающий! Для тех, кто любит математику, я обещаю веселье и испытания с этим тестом по математике 10-го класса.
1. Каков периметр и площадь следующей беговой дорожки?
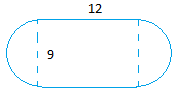
2. Предложение : квадрат — это прямоугольник
a. Напишите предложение как условное и определите гипотезу и заключение.
б. Напишите обратное условие и скажите, является ли предложение бикондиционным.
в. Напишите обратное и противоположное условного и исследуйте правдивость обратного и противоположного.
3. Мера угла в четыре раза больше его дополнения. Какова мера его дополнения?
4. Какая линия или линии перпендикулярны линии y = 6x — 8?
а. у = 6х + 1 б.x — 6y = 9
в. х + 6у = -3 д. у = -6х — 1
5. Найдите два угла, которые являются дополнительными и вертикальными одновременно
6. Какова мера внешнего угла правильного 10-угольника?
7. На рисунке ниже линия n параллельна линии m. Найти меру всех углов внутри линии n и линии m.
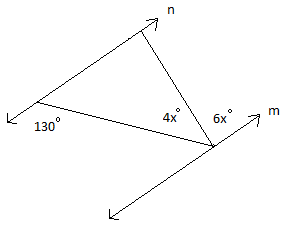
8. Найти объем и площадь поверхности сферы с радиусом 4 см
9. Какой треугольник ниже? Найти все 3 угла.
а. Равносторонний б. Право c. Правые равнобедренные d. Scalene
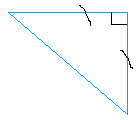
10. В треугольнике UVW, UV = 9, VW = 7 и UW = 11. Какой угол является наибольшим?
а. Угол U б. Угол V c. Угол W
d. недостаточно информации
11. Площадь поверхности сферы A в 4 раза больше площади сферы B.Насколько велик объем сферы A по сравнению со сферой B?
12. График точек A (-3, 3), C (4, -3) и D (4, 3). Назовите рисунок и покажите, что сегмент AD перпендикулярен сегменту CD. Напишите уравнения для всех 3 сегментов.
13. Показать все медианы и все высоты этого треугольника. Никакая конструкция с линейкой и компасом не требуется!
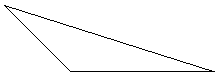
14. Длина гипотенузы равнобедренного прямоугольного треугольника составляет 10 дюймов.Какова длина одной ноги?
15. Найдите объем и площадь поверхности прямоугольной призмы 3 см на 5 см на 10 см.
16.
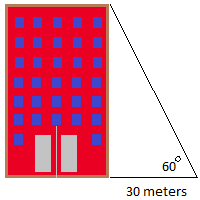
а. Используйте тригонометрическое соотношение, чтобы найти высоту этого здания с точностью до десятых.
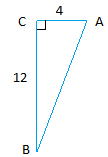
б. Какое выражение даст наибольшее значение?
а. грех А б. cos A c. загар д загар B
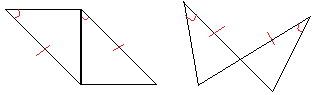
17. Скажите, какой постулат конгруэнтности можно использовать для доказательства конгруэнтности.Запишите SSS, SAS, ASA или AAS под каждым треугольником. Если вы не можете доказать соответствие, напишите N / A.
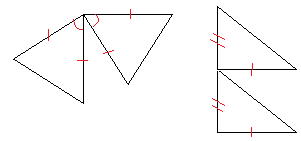
18. Написать уравнение прямой, параллельной и перпендикулярной y = 12x — 4 и проходящей через (1, 0)
19. Что такое стандартное уравнение круга с центром (3, -4) и радиусом 2?
а. (x — 3) 2 + (y — 4) 2 = 4
b. (x — 3) 2 + (y + 4) 2 = 4
c. (x — 4) 2 + (y — 3) 2 = 4
d.(x — 3) 2 + (y + 4) 2 = 2
20.
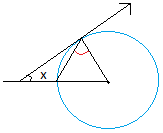
Если угол красного цвета равен 50 градусам, какова мера угла х?
21. Постройте график треугольника X (-2,2), Y (3,2) и Z (5,5)
a. Найдите изображение треугольника XYZ под переводом (x — 3, y — 4)
b. Отразите треугольник XYZ через ось X.
в. Треугольный треугольник XYZ 270 градусов против часовой стрелки о X
d. Расширить треугольник XYZ в 2
раз
22. Какой объем рисунка ниже?
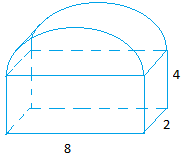
23. Если часы показывают 16:00, какова мера угла, образованного руками?
24. Найти меру угла a
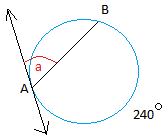
25. Написать уравнение окружности с центром (-4,5) и проходящей через точку (-2, 5)
26. Мужчина ростом 6 футов. Когда его тень достигает 8 футов, тень его сына, стоящего рядом с ним, составляет всего 6 футов. Сделайте рисунок и узнайте, какой рост у сына в футах и дюймах.
27.
Используйте треугольник ниже, чтобы найти длины AB и CD
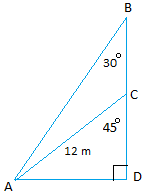
28.
Когда длина одной стороны шестиугольника составляет 3 метра, площадь составляет 23,38 квадратных метра. Какова площадь, если длина шестиугольника составляет 6 метров?
29. Используйте треугольник ниже, чтобы найти y
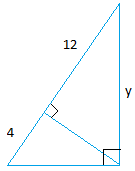
30.
Две стороны треугольника имеют размеры 15 и 20. Если угол между этими сторонами составляет 60 градусов, найдите площадь треугольника.
31. Используйте треугольник ниже, чтобы найти x
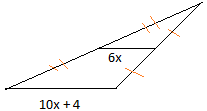
32.
Какое утверждение превратит параллелограмм в ромб?
а. Диагонали делят пополам друг друга.
б. Противоположные углы равны
c. 4 равных стороны
d. Противоположные стороны равны
и
эл. Диагонали перпендикулярны
a и b b и c a и e
c и e b и d
33. Объем конуса составляет одну треть от объема цилиндра. Попытайтесь объяснить, почему это , а не выполняет математических вычислений.
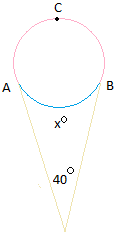
34. Для формы ниже
a. Найти угол х
б. Предположим, что кружок представляет собой 1 шарик мороженого и весит 4 унции. Оцените, сколько мороженого находится внутри конуса. Подсказка: часть, которая находится внутри, показана синей дугой.
35. Лодка плывет на запад по реке со скоростью 50 миль в час.Река течет прямо на юг со скоростью 10 миль в час. Какова результирующая скорость и направление лодки?
36. Сколько линий симметрии в правильном шестиугольнике?
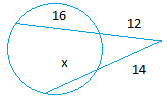
37. Используйте рисунок ниже, чтобы найти x
38. Используйте косвенные доказательства, чтобы показать, что любой треугольник должен иметь не более 1 прямого угла
39. Какая фигура обладает симметрией вращения?
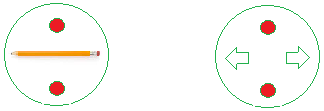
40. Найдите площадь поверхности шестиугольной пирамиды, если одна сторона основания равна 8 дюймам, а высота уклона — 12 дюймов.
Примечание : оценка 35 или более в этом тесте по математике в 10-м классе является хорошим показателем того, что большинство навыков, преподаваемых в 10-м классе, были освоены
Если вы много боролись в этом тесте по математике в 10-м классе, попросите кого-нибудь помочь вам
Хотите решение для этого теста по математике 10-го класса? Добавьте в корзину и приобретите подробное 53-страничное решение и первоклассные пояснения с PayPal.
Я старался изо всех сил, чтобы сделать этот тест по математике 10-го класса в соответствии с национальными стандартами
Чтобы распечатать этот тест по математике 10-го класса, нажмите здесь
Новые уроки математики
Ваша электронная почта в безопасности с нами. Мы будем использовать его только для информирования вас о новых уроках математики.
,
8-й класс по математике
Перед началом теста распечатайте тест по математике для 8-го класса и постарайтесь ответить на все вопросы.
Имя Дата:_____________________
Решить следующие проблемы
1.
a. 5 7 × 5 -10 =
A. 1/3 B. 5 -2 C. 1/125 D. 5 -17
2.
Если 2x 3 = 54, что такое x?
A. 1 B. 5 C. 2 D. 3
3.
a. Ответ для 20000000 × 3,5 × 1000000 в научной нотации:
(Подсказка: сначала поместите 20000000 и 1000000 в научной нотации)
A. 7 × 10 13 B. 3,5 × 10 13 C. 2 × 10 13 D. 7 × 10 12
b. 0,0004 × 4000 в виде десятичной дроби ___________ и в виде дроби ____________
4.
a. Какой набор содержит только рациональные числа?
A. {√ (49), √ (7), 1/2, 9/5}
B. {√ (121), 12/5, √ (169), 0.333333333333}
C {4 × √ (5), 2, √ (100), 0}
b.Вытащите все иррациональные числа из каждого набора выше и запишите их здесь.
_______________________________________________________
5.
Чтобы пойти в школу, вам нужно пройти 6 миль на восток и затем 8 миль на север?
а. Нарисуйте фигуру, изображающую ваш путь от дома до школы
б. Нарисуйте линию, представляющую кратчайшее расстояние, которое вы могли бы пройти. Затем рассчитайте это расстояние _________________
6.
Формула для площади круга показана ниже
A = pi × r 2
a.Что из следующего является правильным выражением для r или радиуса в терминах A и pi?
A. r = √ (A / 2pi) B. r = √ (2A / pi) C. r = √ (pi / A) D. r = √ (A / pi)
б. Используйте правильную формулу, которую вы нашли в части а и пи = 3, чтобы найти г, когда А = 48 квадратных футов.
р = __________________
7.
Компания взимает фиксированную плату в 1500 долларов за аренду яхты.Кроме того, арендаторы должны платить 100 долларов в час.
а. Какое уравнение показывает стоимость C для аренды яхты в час?
A. C = 100 + 1500 × ч B. C = 1500 × ч C. C = 100 × ч + 1 000 D. C = 100 × ч + 1500 × ч
б. Сколько будет стоить аренда яхты на 5 часов?
c. Каков наклон стоимости? что такое y-перехват?
д. Используя ответы для c, наметьте стоимость в системе координат.
8.
Эскалатор 1 имеет подъем 6 и пробег 4. Эскалатор 2 имеет подъем 12 и пробег 6. У эскалаторов одинаковый наклон? Объясните с математическими вычислениями.
9.
У Целиты есть сад в форме квадрата. Как изменяется область, если она утраивает длину каждой стороны?
A. Площадь сада утроена B. Площадь сада не увеличена C. уменьшена вдвое D. sextupled
10.
Найдите объем конуса с радиусом 8 дюймов и высотой 3 дюйма.
(Подсказка: используйте v = 1/3 (pi × r 2 × h)
11.
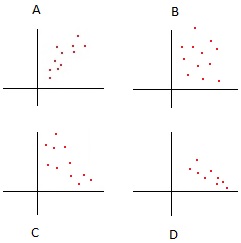
|
а. Посмотрите на рисунок выше, а затем скажите, какие графики показывают следующую корреляцию.
Положительная корреляция. ____________
Отрицательная корреляция _____________
Без корреляции ___________
b.Какая корреляция в следующей ситуации?
Количество галлонов бензина в вашем автомобиле и расстояние, которое вы можете проехать ___________________
Количество апельсинов, которые вы можете съесть, и ваш рост ___________________
Количество учеников, идущих на концерт, и полученный доход. ____________________
c. Если график рассеяния показывает отрицательную корреляцию, какая линия наилучшего соответствия может представлять график рассеяния?
A. y = x — 5 B. y = -1000x + 5000 C. y = 100x — 7 D. y = 5
12.
Какое уравнение линии имеет наклон 3/5 и y перехват 2?
A. 5y + 3x = 10 B. 5x — 3y = 10 C. 5y — 3x = 10 D. 5x + 3y = 10
13.
Треугольник ABC имеет вершины (1,1), (3,5) и (5, 3). Этот треугольник расширен в 3 раза.Какие изображения из 3 вершин. График ABC и изображение A’B’C ‘
14.
Диагональ квадратного экрана компьютера составляет 50 дюймов. Каков периметр этого телевизора? ______________
15.
100 студентов принимают участие в опросе, чтобы узнать, какое мороженое любят есть в Америке.
Что из нижеперечисленного будет наиболее вероятным из ?
A. Некоторые студенты не родились в Соединенных Штатах
B. Учащиеся были недостаточно молоды.
C. В опрос могут не входить люди, которые едут за 50 миль, чтобы получить мороженое.
D. Выберите учеников из разных школ.
16.
Какое утверждение показывает сходство следующих двух графиков?
4y = 2x + 0,5 и 4y = 5x + 1/2
A. Y-точки пересечения одинаковы
B. Графики идентичны
C. X-точки пересечения одинаковы
D. Наклоны одинаковы
17.
Ниже приведены 3 уравнения
1) 4x -2x + 1 = -1 + 2 + 2x
2 ) 2x — 2 = 6 — 4 + 4x
3) 5 + 3x = 2 + 3x + 5
Решить все уравнения и затем сказать
Какое уравнение имеет 1 решение _______________, нет решений _______________, бесконечно много решений ______________
18.
Дерево высотой 8 футов и отбрасывает тень, которая составляет 6 футов.а. Если рост вашего ребенка составляет 4 фута, какое уравнение вы можете использовать, чтобы найти длину его тени?
а. Какую пропорцию вы можете использовать для решения этой проблемы?
A. 8/5 = 6 / x B. 4/6 = x / 8 C. 8/4 = 6 / x D. x / 4 = 8/6
b. Какова длина тени? _______________
19.
Решите следующие силмные уравнения.
2x + 4y = 8
4x — 4y = 6
a.с помощью графика
б. алгебраически
20.
Чаша ниже заполнена на 2/3. Сколько воды может держать чашка? _____________
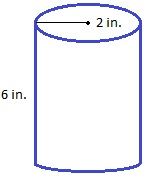
|
Примечание : оценка 16 или более в этом тесте по математике 8-го класса является хорошим показателем того, что большинство навыков, преподаваемых в 8-м классе, были освоены
Если вы много боролись в этом тесте по математике 8-го класса, попросите кого-нибудь помочь вам
Хотите решение этого теста по математике 8-го класса? Добавьте в корзину и приобретите подробное 28-страничное решение и первоклассные пояснения с PayPal.
Я старался изо всех сил, чтобы сделать этот тест по математике 8-го класса в соответствии с национальными стандартами
Чтобы распечатать этот тест по математике 8-го класса, нажмите здесь
Новые уроки математики
Ваша электронная почта в безопасности с нами. Мы будем использовать его только для информирования вас о новых уроках математики.
,
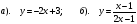
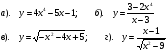
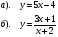
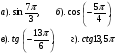
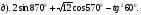
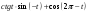
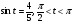 .
.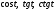 .
.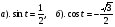 .
.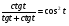 .
.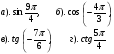
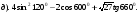
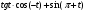
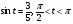 .
. 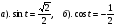 .
.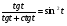 .
.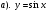 на отрезке
на отрезке 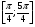 ;
; 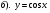 на отрезке
на отрезке 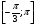 .
.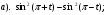
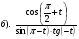
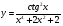
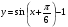
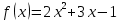 . Докажите, что
. Докажите, что 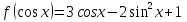 .
.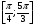 ;
; 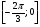 .
.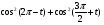
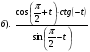
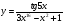
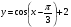
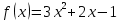 . Докажите, что
. Докажите, что 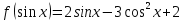 .
.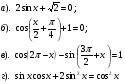
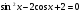 на отрезке
на отрезке 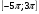 .
.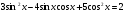
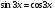 , принадлежащие отрезку
, принадлежащие отрезку 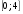 .
.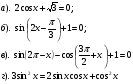
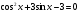 на отрезке
на отрезке 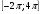 .
.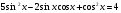
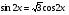 , принадлежащие отрезку
, принадлежащие отрезку 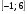 .
.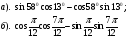
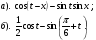
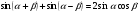
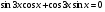
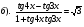
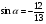 и
и 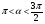 , найти
, найти 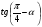 .
.
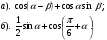
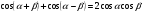
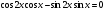
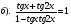
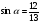 и
и 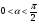 , найти
, найти 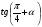 .
.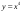 ; б).
; б). 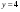 ;
; 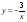 ; г).
; г). 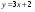 ;
; 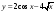 .
.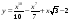 в точке х0 = 1.
в точке х0 = 1.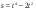 . Найдите ее скорость в момент времени
. Найдите ее скорость в момент времени 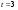 с.
с.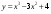 .
. 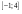 .
.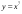 ; б).
; б). 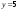 ;
; 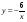 ; г).
; г). 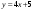 ;
; 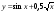 .
.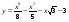 в точке х0 = 1.
в точке х0 = 1.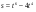 . Найдите ее скорость в момент времени t = 2с.
. Найдите ее скорость в момент времени t = 2с.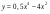 .
. 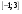 .
.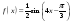 . Составить уравнение касательной к графику в точке с абсциссой
. Составить уравнение касательной к графику в точке с абсциссой 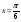 . Установить, в каких точках промежутка
. Установить, в каких точках промежутка 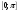 касательная к графику данной функции составляет с осью Ох угол 600.
касательная к графику данной функции составляет с осью Ох угол 600. 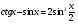
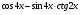 ;
;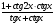 .
.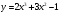 .
.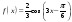 . Составить уравнение касательной к графику в точке с абсциссой
. Составить уравнение касательной к графику в точке с абсциссой 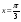 . Установить точки минимума и максимума, а также наибольшее и наименьшее значение на промежутке
. Установить точки минимума и максимума, а также наибольшее и наименьшее значение на промежутке 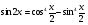
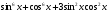 ;
;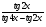 .
.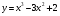 .
.