ГДЗ по алгебре 10 класс самостоятельные работы Александрова Л.А.
автор: Александрова Л.А..
ГДЗ по алгебре 10 класс самостоятельные работы , авторы: , Александрова Л.А., Мнемозина 2019 год.
-
С-0. Варианты
-
1
-
2
-
3
-
4
-
С-1. Варианты
-
1
-
2
-
3
-
4
-
С-2. Варианты
-
1
-
2
-
3
-
4
-
С-3. Варианты
-
1
-
2
-
3
-
4
-
С-4. Варианты
-
1
-
2
-
3
-
4
-
С-5. Варианты
-
1
-
2
-
3
-
4
-
С-6. Варианты
-
1
-
2
-
3
-
4
-
С-7. Варианты
-
1
-
2
gdz.fm
Учебно-методический материал по алгебре (10 класс) на тему: Самостоятельные работы по алгебре для 10 класса
li{counter-increment:lst-ctn-kix_list_4-1}#doc13924714 ol.lst-kix_list_3-1{list-style-type:none}#doc13924714 ol.lst-kix_list_3-2{list-style-type:none}#doc13924714 .lst-kix_list_3-1>li{counter-increment:lst-ctn-kix_list_3-1}#doc13924714 ol.lst-kix_list_3-3{list-style-type:none}#doc13924714 ol.lst-kix_list_3-4.start{counter-reset:lst-ctn-kix_list_3-4 0}#doc13924714 .lst-kix_list_5-1>li{counter-increment:lst-ctn-kix_list_5-1}#doc13924714 ol.lst-kix_list_3-4{list-style-type:none}#doc13924714 .lst-kix_list_2-1>li{counter-increment:lst-ctn-kix_list_2-1}#doc13924714 ol.lst-kix_list_3-0{list-style-type:none}#doc13924714 .lst-kix_list_1-1>li{counter-increment:lst-ctn-kix_list_1-1}#doc13924714 ol.lst-kix_list_2-6.start{counter-reset:lst-ctn-kix_list_2-6 0}#doc13924714 .lst-kix_list_3-0>li:before{content:»» counter(lst-ctn-kix_list_3-0,decimal) «. «}#doc13924714 ol.lst-kix_list_3-1.start{counter-reset:lst-ctn-kix_list_3-1 0}#doc13924714 .lst-kix_list_3-1>li:before{content:»» counter(lst-ctn-kix_list_3-1,lower-latin) «. «}#doc13924714 .lst-kix_list_3-2>li:before{content:»» counter(lst-ctn-kix_list_3-2,lower-roman) «. «}#doc13924714 ol.lst-kix_list_1-8.start{counter-reset:lst-ctn-kix_list_1-8 0}#doc13924714 .lst-kix_list_4-0>li{counter-increment:lst-ctn-kix_list_4-0}#doc13924714 .lst-kix_list_5-0>li{counter-increment:lst-ctn-kix_list_5-0}#doc13924714 ol.lst-kix_list_2-3.start{counter-reset:lst-ctn-kix_list_2-3 0}#doc13924714 .lst-kix_list_3-5>li:before{content:»» counter(lst-ctn-kix_list_3-5,lower-roman) «. «}#doc13924714 .lst-kix_list_3-4>li:before{content:»» counter(lst-ctn-kix_list_3-4,lower-latin) «. «}#doc13924714 ol.lst-kix_list_1-5.start{counter-reset:lst-ctn-kix_list_1-5 0}#doc13924714 .lst-kix_list_3-3>li:before{content:»» counter(lst-ctn-kix_list_3-3,decimal) «. «}#doc13924714 ol.lst-kix_list_3-5{list-style-type:none}#doc13924714 ol.lst-kix_list_3-6{list-style-type:none}#doc13924714 ol.lst-kix_list_3-7{list-style-type:none}#doc13924714 ol.lst-kix_list_3-8{list-style-type:none}#doc13924714 .lst-kix_list_3-8>li:before{content:»» counter(lst-ctn-kix_list_3-8,lower-roman) «. «}#doc13924714 .lst-kix_list_2-0>li{counter-increment:lst-ctn-kix_list_2-0}#doc13924714 ol.lst-kix_list_5-3.start{counter-reset:lst-ctn-kix_list_5-3 0}#doc13924714 .lst-kix_list_2-3>li{counter-increment:lst-ctn-kix_list_2-3}#doc13924714 .lst-kix_list_3-6>li:before{content:»» counter(lst-ctn-kix_list_3-6,decimal) «. «}#doc13924714 .lst-kix_list_4-3>li{counter-increment:lst-ctn-kix_list_4-3}#doc13924714 .lst-kix_list_3-7>li:before{content:»» counter(lst-ctn-kix_list_3-7,lower-latin) «. «}#doc13924714 ol.lst-kix_list_4-5.start{counter-reset:lst-ctn-kix_list_4-5 0}#doc13924714 ol.lst-kix_list_5-0.start{counter-reset:lst-ctn-kix_list_5-0 0}#doc13924714 .lst-kix_list_1-2>li{counter-increment:lst-ctn-kix_list_1-2}#doc13924714 ol.lst-kix_list_3-7.start{counter-reset:lst-ctn-kix_list_3-7 0}#doc13924714 .lst-kix_list_5-2>li{counter-increment:lst-ctn-kix_list_5-2}#doc13924714 ol.lst-kix_list_4-2.start{counter-reset:lst-ctn-kix_list_4-2 0}#doc13924714 .lst-kix_list_3-2>li{counter-increment:lst-ctn-kix_list_3-2}#doc13924714 ol.lst-kix_list_2-2{list-style-type:none}#doc13924714 ol.lst-kix_list_2-3{list-style-type:none}#doc13924714 .lst-kix_list_5-0>li:before{content:»» counter(lst-ctn-kix_list_5-0,decimal) «. «}#doc13924714 ol.lst-kix_list_2-4{list-style-type:none}#doc13924714 ol.lst-kix_list_2-5{list-style-type:none}#doc13924714 .lst-kix_list_5-4>li{counter-increment:lst-ctn-kix_list_5-4}#doc13924714 .lst-kix_list_1-4>li{counter-increment:lst-ctn-kix_list_1-4}#doc13924714 .lst-kix_list_4-4>li{counter-increment:lst-ctn-kix_list_4-4}#doc13924714 ol.lst-kix_list_2-0{list-style-type:none}#doc13924714 ol.lst-kix_list_1-6.start{counter-reset:lst-ctn-kix_list_1-6 0}#doc13924714 ol.lst-kix_list_2-1{list-style-type:none}#doc13924714 .lst-kix_list_4-8>li:before{content:»» counter(lst-ctn-kix_list_4-8,lower-roman) «. «}#doc13924714 .lst-kix_list_5-3>li:before{content:»» counter(lst-ctn-kix_list_5-3,decimal) «. «}#doc13924714 .lst-kix_list_4-7>li:before{content:»» counter(lst-ctn-kix_list_4-7,lower-latin) «. «}#doc13924714 .lst-kix_list_5-2>li:before{content:»» counter(lst-ctn-kix_list_5-2,lower-roman) «. «}#doc13924714 .lst-kix_list_5-1>li:before{content:»» counter(lst-ctn-kix_list_5-1,lower-latin) «. «}#doc13924714 .lst-kix_list_5-7>li:before{content:»» counter(lst-ctn-kix_list_5-7,lower-latin) «. «}#doc13924714 ol.lst-kix_list_5-6.start{counter-reset:lst-ctn-kix_list_5-6 0}#doc13924714 .lst-kix_list_5-6>li:before{content:»» counter(lst-ctn-kix_list_5-6,decimal) «. «}#doc13924714 .lst-kix_list_5-8>li:before{content:»» counter(lst-ctn-kix_list_5-8,lower-roman) «. «}#doc13924714 ol.lst-kix_list_4-1.start{counter-reset:lst-ctn-kix_list_4-1 0}#doc13924714 ol.lst-kix_list_4-8.start{counter-reset:lst-ctn-kix_list_4-8 0}#doc13924714 ol.lst-kix_list_3-3.start{counter-reset:lst-ctn-kix_list_3-3 0}#doc13924714 .lst-kix_list_5-4>li:before{content:»» counter(lst-ctn-kix_list_5-4,lower-latin) «. «}#doc13924714 .lst-kix_list_5-5>li:before{content:»» counter(lst-ctn-kix_list_5-5,lower-roman) «. «}#doc13924714 ol.lst-kix_list_2-6{list-style-type:none}#doc13924714 ol.lst-kix_list_2-7{list-style-type:none}#doc13924714 ol.lst-kix_list_2-8{list-style-type:none}#doc13924714 ol.lst-kix_list_1-0.start{counter-reset:lst-ctn-kix_list_1-0 0}#doc13924714 .lst-kix_list_3-0>li{counter-increment:lst-ctn-kix_list_3-0}#doc13924714 .lst-kix_list_3-3>li{counter-increment:lst-ctn-kix_list_3-3}#doc13924714 ol.lst-kix_list_4-0.start{counter-reset:lst-ctn-kix_list_4-0 0}#doc13924714 .lst-kix_list_3-6>li{counter-increment:lst-ctn-kix_list_3-6}#doc13924714 .lst-kix_list_2-5>li{counter-increment:lst-ctn-kix_list_2-5}#doc13924714 .lst-kix_list_2-8>li{counter-increment:lst-ctn-kix_list_2-8}#doc13924714 ol.lst-kix_list_3-2.start{counter-reset:lst-ctn-kix_list_3-2 0}#doc13924714 ol.lst-kix_list_5-5.start{counter-reset:lst-ctn-kix_list_5-5 0}#doc13924714 .lst-kix_list_2-2>li{counter-increment:lst-ctn-kix_list_2-2}#doc13924714 ol.lst-kix_list_2-4.start{counter-reset:lst-ctn-kix_list_2-4 0}#doc13924714 ol.lst-kix_list_4-7.start{counter-reset:lst-ctn-kix_list_4-7 0}#doc13924714 ol.lst-kix_list_1-3{list-style-type:none}#doc13924714 ol.lst-kix_list_5-0{list-style-type:none}#doc13924714 ol.lst-kix_list_1-4{list-style-type:none}#doc13924714 .lst-kix_list_2-6>li:before{content:»» counter(lst-ctn-kix_list_2-6,decimal) «. «}#doc13924714 .lst-kix_list_2-7>li:before{content:»» counter(lst-ctn-kix_list_2-7,lower-latin) «. «}#doc13924714 .lst-kix_list_2-7>li{counter-increment:lst-ctn-kix_list_2-7}#doc13924714 .lst-kix_list_3-7>li{counter-increment:lst-ctn-kix_list_3-7}#doc13924714 ol.lst-kix_list_5-1{list-style-type:none}#doc13924714 ol.lst-kix_list_1-5{list-style-type:none}#doc13924714 ol.lst-kix_list_5-2{list-style-type:none}#doc13924714 ol.lst-kix_list_1-6{list-style-type:none}#doc13924714 ol.lst-kix_list_1-0{list-style-type:none}#doc13924714 .lst-kix_list_2-4>li:before{content:»» counter(lst-ctn-kix_list_2-4,lower-latin) «. «}#doc13924714 .lst-kix_list_2-5>li:before{content:»» counter(lst-ctn-kix_list_2-5,lower-roman) «. «}#doc13924714 .lst-kix_list_2-8>li:before{content:»» counter(lst-ctn-kix_list_2-8,lower-roman) «. «}#doc13924714 ol.lst-kix_list_1-1{list-style-type:none}#doc13924714 ol.lst-kix_list_1-2{list-style-type:none}#doc13924714 ol.lst-kix_list_5-4.start{counter-reset:lst-ctn-kix_list_5-4 0}#doc13924714 ol.lst-kix_list_4-6.start{counter-reset:lst-ctn-kix_list_4-6 0}#doc13924714 ol.lst-kix_list_5-1.start{counter-reset:lst-ctn-kix_list_5-1 0}#doc13924714 ol.lst-kix_list_3-0.start{counter-reset:lst-ctn-kix_list_3-0 0}#doc13924714 ol.lst-kix_list_5-7{list-style-type:none}#doc13924714 ol.lst-kix_list_5-8{list-style-type:none}#doc13924714 .lst-kix_list_5-7>li{counter-increment:lst-ctn-kix_list_5-7}#doc13924714 ol.lst-kix_list_4-3.start{counter-reset:lst-ctn-kix_list_4-3 0}#doc13924714 ol.lst-kix_list_5-3{list-style-type:none}#doc13924714 ol.lst-kix_list_1-7{list-style-type:none}#doc13924714 .lst-kix_list_4-7>li{counter-increment:lst-ctn-kix_list_4-7}#doc13924714 ol.lst-kix_list_5-4{list-style-type:none}#doc13924714 .lst-kix_list_1-7>li{counter-increment:lst-ctn-kix_list_1-7}#doc13924714 ol.lst-kix_list_1-8{list-style-type:none}#doc13924714 ol.lst-kix_list_3-8.start{counter-reset:lst-ctn-kix_list_3-8 0}#doc13924714 ol.lst-kix_list_5-5{list-style-type:none}#doc13924714 ol.lst-kix_list_5-6{list-style-type:none}#doc13924714 ol.lst-kix_list_2-5.start{counter-reset:lst-ctn-kix_list_2-5 0}#doc13924714 .lst-kix_list_5-8>li{counter-increment:lst-ctn-kix_list_5-8}#doc13924714 .lst-kix_list_4-0>li:before{content:»» counter(lst-ctn-kix_list_4-0,decimal) «. «}#doc13924714 .lst-kix_list_2-6>li{counter-increment:lst-ctn-kix_list_2-6}#doc13924714 .lst-kix_list_3-8>li{counter-increment:lst-ctn-kix_list_3-8}#doc13924714 .lst-kix_list_4-1>li:before{content:»» counter(lst-ctn-kix_list_4-1,lower-latin) «. «}#doc13924714 .lst-kix_list_4-6>li{counter-increment:lst-ctn-kix_list_4-6}#doc13924714 ol.lst-kix_list_1-7.start{counter-reset:lst-ctn-kix_list_1-7 0}#doc13924714 .lst-kix_list_4-4>li:before{content:»» counter(lst-ctn-kix_list_4-4,lower-latin) «. «}#doc13924714 ol.lst-kix_list_2-2.start{counter-reset:lst-ctn-kix_list_2-2 0}#doc13924714 .lst-kix_list_1-5>li{counter-increment:lst-ctn-kix_list_1-5}#doc13924714 .lst-kix_list_4-3>li:before{content:»» counter(lst-ctn-kix_list_4-3,decimal) «. «}#doc13924714 .lst-kix_list_4-5>li:before{content:»» counter(lst-ctn-kix_list_4-5,lower-roman) «. «}#doc13924714 .lst-kix_list_4-2>li:before{content:»» counter(lst-ctn-kix_list_4-2,lower-roman) «. «}#doc13924714 .lst-kix_list_4-6>li:before{content:»» counter(lst-ctn-kix_list_4-6,decimal) «. «}#doc13924714 ol.lst-kix_list_5-7.start{counter-reset:lst-ctn-kix_list_5-7 0}#doc13924714 .lst-kix_list_1-8>li{counter-increment:lst-ctn-kix_list_1-8}#doc13924714 ol.lst-kix_list_1-4.start{counter-reset:lst-ctn-kix_list_1-4 0}#doc13924714 .lst-kix_list_5-5>li{counter-increment:lst-ctn-kix_list_5-5}#doc13924714 .lst-kix_list_3-5>li{counter-increment:lst-ctn-kix_list_3-5}#doc13924714 ol.lst-kix_list_1-1.start{counter-reset:lst-ctn-kix_list_1-1 0}#doc13924714 ol.lst-kix_list_4-0{list-style-type:none}#doc13924714 .lst-kix_list_3-4>li{counter-increment:lst-ctn-kix_list_3-4}#doc13924714 ol.lst-kix_list_4-1{list-style-type:none}#doc13924714 ol.lst-kix_list_4-4.start{counter-reset:lst-ctn-kix_list_4-4 0}#doc13924714 ol.lst-kix_list_4-2{list-style-type:none}#doc13924714 ol.lst-kix_list_4-3{list-style-type:none}#doc13924714 .lst-kix_list_2-4>li{counter-increment:lst-ctn-kix_list_2-4}#doc13924714 ol.lst-kix_list_3-6.start{counter-reset:lst-ctn-kix_list_3-6 0}#doc13924714 .lst-kix_list_5-3>li{counter-increment:lst-ctn-kix_list_5-3}#doc13924714 ol.lst-kix_list_1-3.start{counter-reset:lst-ctn-kix_list_1-3 0}#doc13924714 ol.lst-kix_list_2-8.start{counter-reset:lst-ctn-kix_list_2-8 0}#doc13924714 ol.lst-kix_list_1-2.start{counter-reset:lst-ctn-kix_list_1-2 0}#doc13924714 ol.lst-kix_list_4-8{list-style-type:none}#doc13924714 .lst-kix_list_1-0>li:before{content:»» counter(lst-ctn-kix_list_1-0,decimal) «. «}#doc13924714 ol.lst-kix_list_4-4{list-style-type:none}#doc13924714 ol.lst-kix_list_4-5{list-style-type:none}#doc13924714 .lst-kix_list_1-1>li:before{content:»» counter(lst-ctn-kix_list_1-1,lower-latin) «. «}#doc13924714 .lst-kix_list_1-2>li:before{content:»» counter(lst-ctn-kix_list_1-2,lower-roman) «. «}#doc13924714 ol.lst-kix_list_2-0.start{counter-reset:lst-ctn-kix_list_2-0 0}#doc13924714 ol.lst-kix_list_4-6{list-style-type:none}#doc13924714 ol.lst-kix_list_4-7{list-style-type:none}#doc13924714 .lst-kix_list_1-3>li:before{content:»» counter(lst-ctn-kix_list_1-3,decimal) «. «}#doc13924714 .lst-kix_list_1-4>li:before{content:»» counter(lst-ctn-kix_list_1-4,lower-latin) «. «}#doc13924714 ol.lst-kix_list_3-5.start{counter-reset:lst-ctn-kix_list_3-5 0}#doc13924714 .lst-kix_list_1-0>li{counter-increment:lst-ctn-kix_list_1-0}#doc13924714 .lst-kix_list_4-8>li{counter-increment:lst-ctn-kix_list_4-8}#doc13924714 .lst-kix_list_1-6>li{counter-increment:lst-ctn-kix_list_1-6}#doc13924714 .lst-kix_list_1-7>li:before{content:»» counter(lst-ctn-kix_list_1-7,lower-latin) «. «}#doc13924714 ol.lst-kix_list_5-8.start{counter-reset:lst-ctn-kix_list_5-8 0}#doc13924714 ol.lst-kix_list_2-7.start{counter-reset:lst-ctn-kix_list_2-7 0}#doc13924714 .lst-kix_list_1-3>li{counter-increment:lst-ctn-kix_list_1-3}#doc13924714 .lst-kix_list_1-5>li:before{content:»» counter(lst-ctn-kix_list_1-5,lower-roman) «. «}#doc13924714 .lst-kix_list_1-6>li:before{content:»» counter(lst-ctn-kix_list_1-6,decimal) «. «}#doc13924714 .lst-kix_list_5-6>li{counter-increment:lst-ctn-kix_list_5-6}#doc13924714 .lst-kix_list_2-0>li:before{content:»» counter(lst-ctn-kix_list_2-0,decimal) «) «}#doc13924714 .lst-kix_list_2-1>li:before{content:»» counter(lst-ctn-kix_list_2-1,lower-latin) «. «}#doc13924714 ol.lst-kix_list_2-1.start{counter-reset:lst-ctn-kix_list_2-1 0}#doc13924714 .lst-kix_list_4-5>li{counter-increment:lst-ctn-kix_list_4-5}#doc13924714 .lst-kix_list_1-8>li:before{content:»» counter(lst-ctn-kix_list_1-8,lower-roman) «. «}#doc13924714 .lst-kix_list_2-2>li:before{content:»» counter(lst-ctn-kix_list_2-2,lower-roman) «. «}#doc13924714 .lst-kix_list_2-3>li:before{content:»» counter(lst-ctn-kix_list_2-3,decimal) «. «}#doc13924714 .lst-kix_list_4-2>li{counter-increment:lst-ctn-kix_list_4-2}#doc13924714 ol.lst-kix_list_5-2.start{counter-reset:lst-ctn-kix_list_5-2 0}#doc13924714 ol{margin:0;padding:0}#doc13924714 table td,table th{padding:0}#doc13924714 .c2{margin-left:67.5pt;padding-top:0pt;padding-left:0pt;padding-bottom:0pt;line-height:1.0;orphans:2;widows:2;text-align:justify}#doc13924714 .c7{margin-left:13.5pt;padding-top:0pt;padding-bottom:0pt;line-height:1.0;orphans:2;widows:2;text-align:left;height:10pt}#doc13924714 .c8{margin-left:13.5pt;padding-top:0pt;padding-bottom:0pt;line-height:1.0;orphans:2;widows:2;text-align:left}#doc13924714 .c0{color:#000000;font-weight:400;text-decoration:none;vertical-align:baseline;font-size:12pt;font-family:»Times New Roman»;font-style:normal}#doc13924714 .c4{color:#000000;font-weight:700;text-decoration:none;vertical-align:baseline;font-size:14pt;font-family:»Times New Roman»;font-style:normal}#doc13924714 .c3{color:#000000;font-weight:400;text-decoration:none;vertical-align:baseline;font-size:14pt;font-family:»Times New Roman»;font-style:normal}#doc13924714 .c6{margin-left:31.5pt;padding-top:0pt;padding-bottom:0pt;line-height:1.0;orphans:2;widows:2;text-align:justify}#doc13924714 .c1{margin-left:13.5pt;padding-top:0pt;padding-bottom:0pt;line-height:1.0;orphans:2;widows:2;text-align:center}#doc13924714 .c5{color:#000000;font-weight:400;text-decoration:none;vertical-align:baseline;font-size:20pt;font-family:»Times New Roman»;font-style:normal}#doc13924714 .c11{background-color:#ffffff;max-width:830pt;padding:21.3pt 4.8pt 9.7pt 7.1pt}#doc13924714 .c9{padding:0;margin:0}#doc13924714 .c10{height:10pt}#doc13924714 .title{padding-top:24pt;color:#000000;font-weight:700;font-size:36pt;padding-bottom:6pt;font-family:»Times New Roman»;line-height:1.0;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc13924714 .subtitle{padding-top:18pt;color:#666666;font-size:24pt;padding-bottom:4pt;font-family:»Georgia»;line-height:1.0;page-break-after:avoid;font-style:italic;orphans:2;widows:2;text-align:left}#doc13924714 li{color:#000000;font-size:10pt;font-family:»Times New Roman»}#doc13924714 p{margin:0;color:#000000;font-size:10pt;font-family:»Times New Roman»}#doc13924714 h2{padding-top:24pt;color:#000000;font-weight:700;font-size:24pt;padding-bottom:6pt;font-family:»Times New Roman»;line-height:1.0;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc13924714 h3{padding-top:18pt;color:#000000;font-weight:700;font-size:18pt;padding-bottom:4pt;font-family:»Times New Roman»;line-height:1.0;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc13924714 h4{padding-top:14pt;color:#000000;font-weight:700;font-size:14pt;padding-bottom:4pt;font-family:»Times New Roman»;line-height:1.0;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc13924714 h5{padding-top:12pt;color:#000000;font-weight:700;font-size:12pt;padding-bottom:2pt;font-family:»Times New Roman»;line-height:1.0;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc13924714 h5{padding-top:11pt;color:#000000;font-weight:700;font-size:11pt;padding-bottom:2pt;font-family:»Times New Roman»;line-height:1.0;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc13924714 h6{padding-top:10pt;color:#000000;font-weight:700;font-size:10pt;padding-bottom:2pt;font-family:»Times New Roman»;line-height:1.0;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc13924714 ]]>
Самостоятельная работа по теме
«Показательные уравнения» В – I
- Решите уравнения:
1) ; 2) ; 3) ;
4) ; 5) ; 6) ;
7) ; 8) ;
9) .
……………………………………………….
Самостоятельная работа по теме
Показательные уравнения В – II
- Решите уравнения:
1) ; 2) ; 3) ;
4) ; 5) ; 6) ;
7) ; 8) ;
9) .
……………………………………………….
Самостоятельная работа по теме
Показательные уравнения В – I
- Решите уравнения:
1) ; 2) ; 3) ;
4) ; 5) ; 6) ;
7) ; 8) ;
9) .
………………………
Самостоятельная работа по теме
Показательные уравнения В – II
- Решите уравнения:
1) ; 2) ; 3) ;
4) ; 5) ; 6) ;
7) ; 8) ;
9) .
……………………………………………….
Самостоятельная работа по теме
«Показательные уравнения» В – I
- Решите уравнения:
1) ; 2) ; 3) ;
4) ; 5) ; 6) ;
7) ; 8) ;
9) .
……………………………………………….
Самостоятельная работа по теме
Показательные уравнения В – II
- Решите уравнения:
1) ; 2) ; 3) ;
4) ; 5) ; 6) ;
7) ; 8) ;
9) .
nsportal.ru
Самостоятельные работы по алгебре и начала анализа 10 класс. Учебник Ю.М. Колягин, М.В.Ткачева, Н.Е. Федорова и др.
Самостоятельная работа 4.1
Показательная функция, ее свойства и график
Вариант 1
1. Постройте график функции 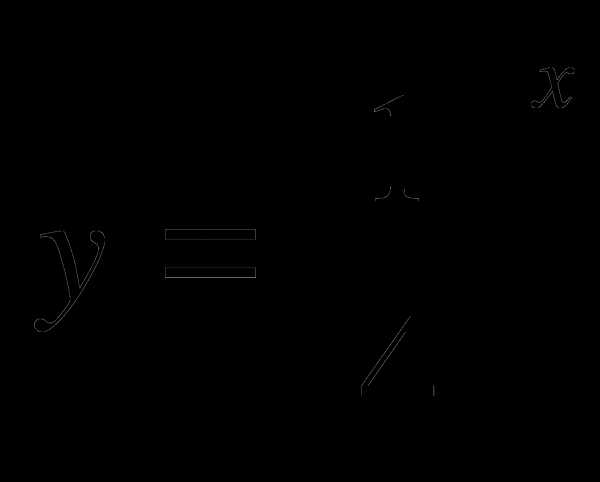 . Используя график функции решите неравенство
. Используя график функции решите неравенство 
2. Сравните с единицей число
3. Найдите наибольшее и наименьшее значения функции 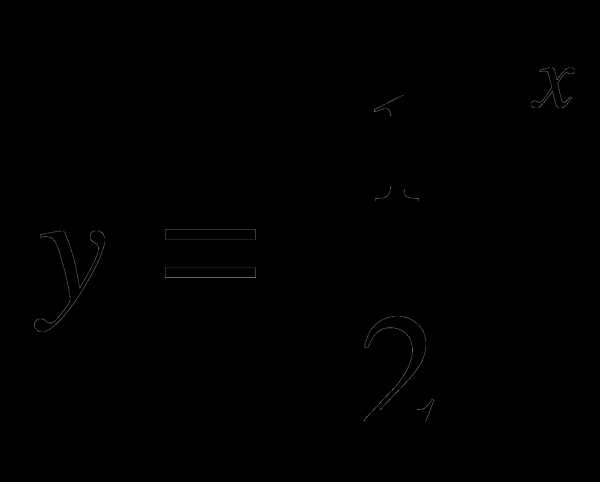 на отрезке [-3;1].
на отрезке [-3;1].
______________________________________________________________________
Самостоятельная работа 4.1
Показательная функция, ее свойства и график
Вариант 2
1. Постройте график функции 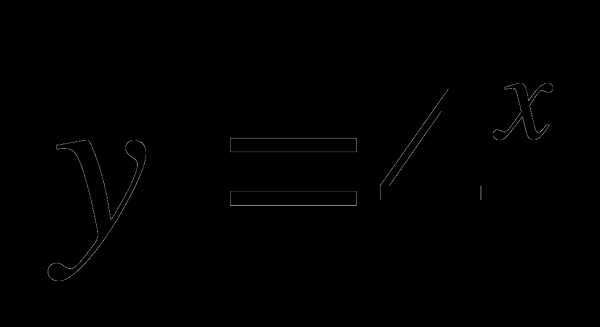 . Используя график функции решите неравенство
. Используя график функции решите неравенство 
2. Сравните с единицей число
3. Найдите наибольшее и наименьшее значения функции 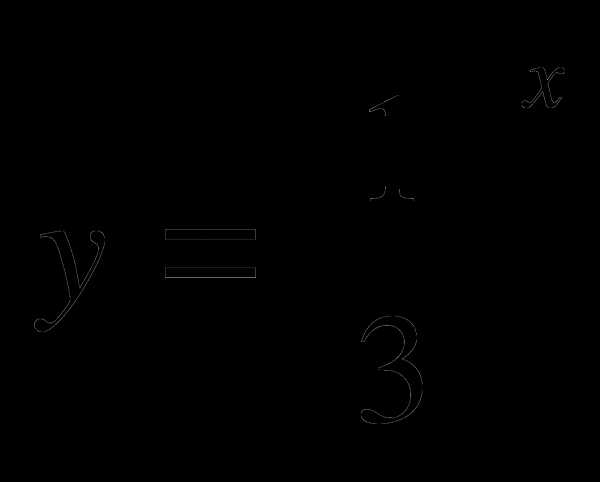 на отрезке [-2;3].
на отрезке [-2;3].
______________________________________________________________________
Самостоятельная работа 4.1
Показательная функция, ее свойства и график
Вариант 3
1. Постройте график функции 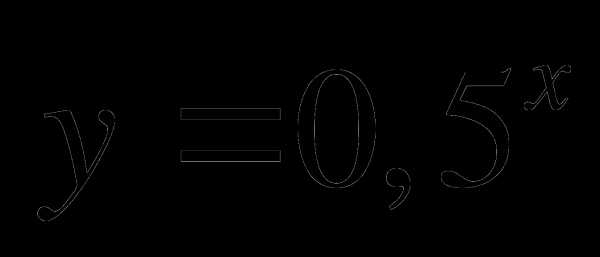 . Используя график функции решите неравенство
. Используя график функции решите неравенство 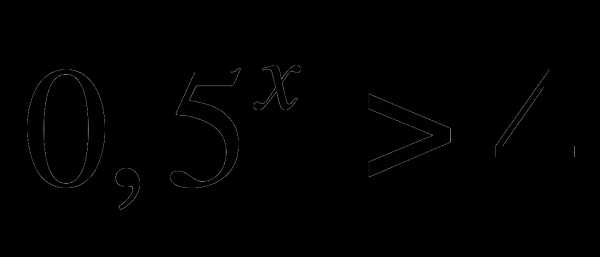
2. Сравните с единицей число
3. Найдите наибольшее и наименьшее значения функции  на отрезке [-1;2].
на отрезке [-1;2].
infourok.ru
Самостоятельная работа по алгебре ( 10 класс)
Самостоятельная работа ( 10 класс)
ВАРИАНТ 1
-
Решите уравнение: А2х-Сх-1х=24
-
Докажите неравенства:
а) (а+2)2>4а в) х2+12х+37>0
б) 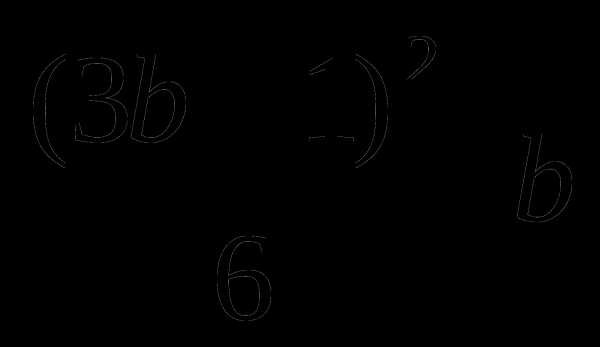 г) а2+b2+8
г) а2+b2+8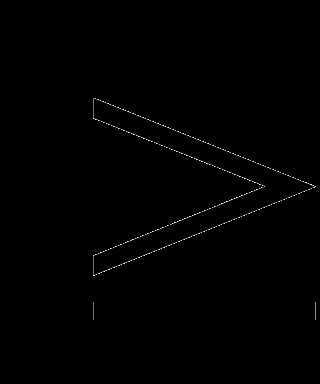 4(a+b)
4(a+b)
Самостоятельная работа ( 10 класс)
ВАРИАНТ 2
-
Решите уравнение: А2х+1+С1х=24
-
Докажите неравенства:
а) (а+6)2>12а в) х2+8х+17>0
б) 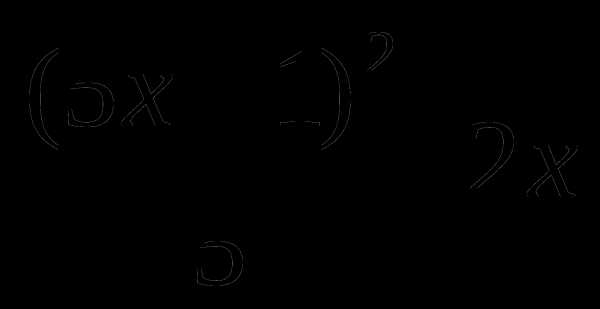 г) х2+у2
г) х2+у2 2(х+у-1)
2(х+у-1)
Самостоятельная работа ( 10 класс)
ВАРИАНТ 1
-
Решите уравнение: А2х-Сх-1х=24
-
Докажите неравенства:
а) (а+2)2>4а в) х2+12х+37>0
б) 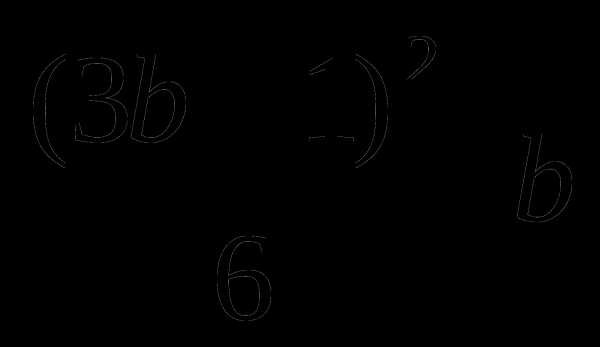 г) а2+b2+8
г) а2+b2+8 4(a+b)
4(a+b)
Самостоятельная работа ( 10 класс)
ВАРИАНТ 2
-
Решите уравнение: А2х+1+С1х=24
-
Докажите неравенства:
а) (а+6)2>12а в) х2+8х+17>0
б) 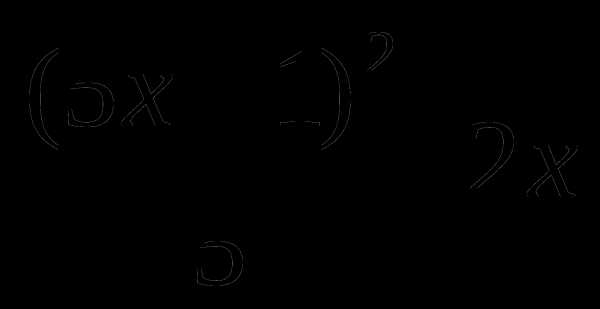 г) х2+у2
г) х2+у2 2(х+у-1)
2(х+у-1)
Самостоятельная работа ( 10 класс)
ВАРИАНТ 1
-
Решите уравнение: А2х-Сх-1х=24
-
Докажите неравенства:
а) (а+2)2>4а в) х2+12х+37>0
б) 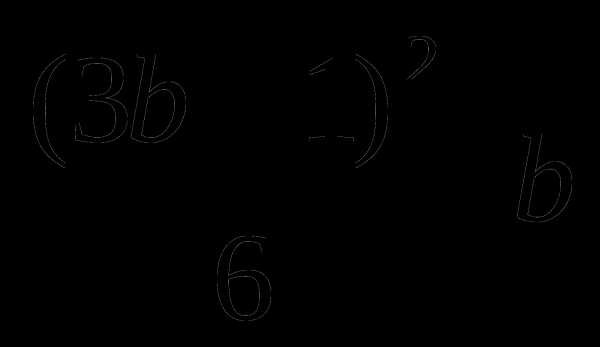 г) а2+b2+8
г) а2+b2+8 4(a+b)
4(a+b)
Самостоятельная работа ( 10 класс)
ВАРИАНТ 2
-
Решите уравнение: А2х+1+С1х=24
-
Докажите неравенства:
а) (а+6)2>12а в) х2+8х+17>0
б) 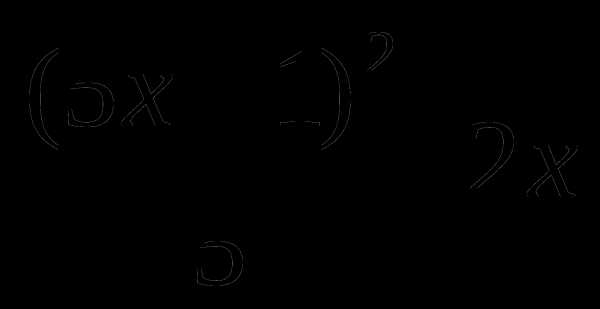 г) х2+у2
г) х2+у2 2(х+у-1)
2(х+у-1)
Самостоятельная работа ( 10 класс)
ВАРИАНТ 1
-
Решите уравнение: А2х-Сх-1х=24
-
Докажите неравенства:
а) (а+2)2>4а в) х2+12х+37>0
б) 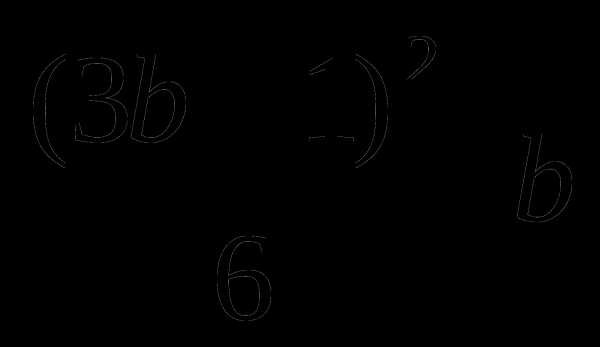 г) а2+b2+8
г) а2+b2+8 4(a+b)
4(a+b)
Самостоятельная работа ( 10 класс)
ВАРИАНТ 2
-
Решите уравнение: А2х+1+С1х=24
-
Докажите неравенства:
а) (а+6)2>12а в) х2+8х+17>0
б) 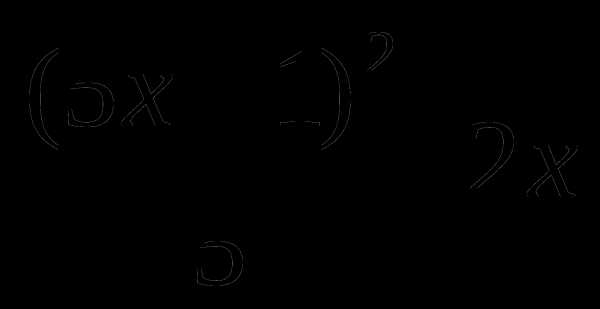 г) х2+у2
г) х2+у2 2(х+у-1)
2(х+у-1)
Самостоятельная работа ( 10 класс)
ВАРИАНТ 1
-
Решите уравнение: А2х-Сх-1х=24
-
Докажите неравенства:
а) (а+2)2>4а в) х2+12х+37>0
б) 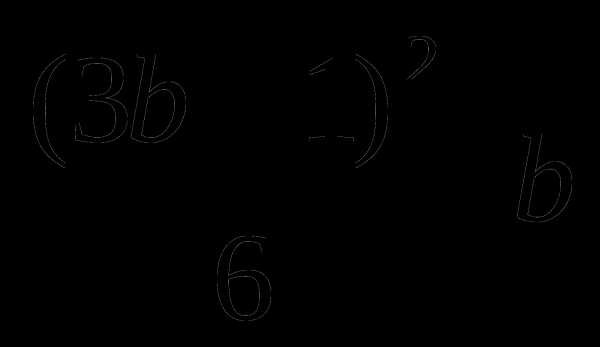 г) а2+b2+8
г) а2+b2+8 4(a+b)
4(a+b)
Самостоятельная работа ( 10 класс)
ВАРИАНТ 2
-
Решите уравнение: А2х+1+С1х=24
-
Докажите неравенства:
а) (а+6)2>12а в) х2+8х+17>0
б) 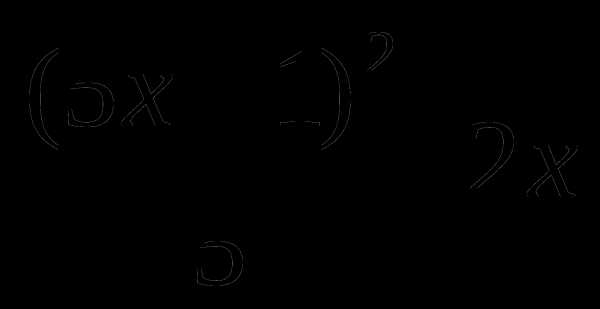 г) х2+у2
г) х2+у2 2(х+у-1)
2(х+у-1)
Самостоятельная работа ( 10 класс)
ВАРИАНТ 1
-
Решите уравнение: А2х-Сх-1х=24
-
Докажите неравенства:
а) (а+2)2>4а в) х2+12х+37>0
б) 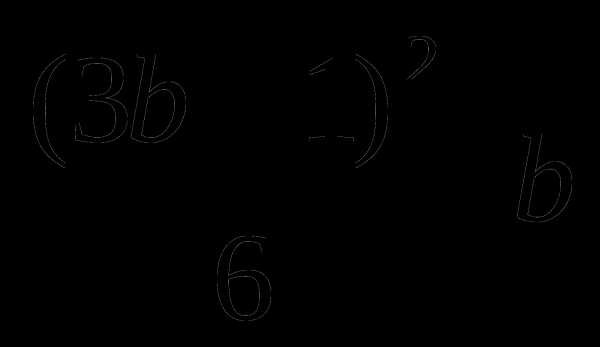 г) а2+b2+8
г) а2+b2+8 4(a+b)
4(a+b)
Самостоятельная работа ( 10 класс)
ВАРИАНТ 2
-
Решите уравнение: А2х+1+С1х=24
-
Докажите неравенства:
а) (а+6)2>12а в) х2+8х+17>0
б) 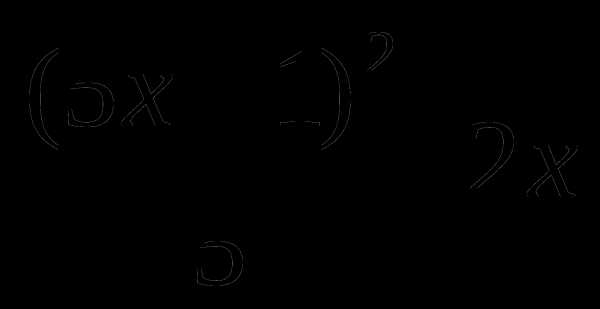 г) х2+у2
г) х2+у2 2(х+у-1)
2(х+у-1)
infourok.ru
Материал по алгебре (10 класс) на тему: Самостоятельная робота по теме «Предел последовательности. Бесконечно убывающая геометрическая прогрессия» 10 класс
B1. 10 класс.
Предел последовательности.
Бесконечно убывающая геометрическая прогрессия.
1.Вычислить предел последовательности:
- Lim 3n+2
n→+∞ n
- Lim 2n²-n+7
n→+∞ n⁵+3n²+2
- Lim 5n²+6n-7
n→+∞ 2n²-3n+4
- Lim 6n³-n+11
n→+∞ n²+7n-5
- Lim 12n⁵+21n²-2n+1
n→+∞ 24n⁵+13n⁶-2
- Lim 4x²-12x+9
x→+∞ x²+4x+4
- Lim (3x+1)²
x→+∞ x²+5x+1
- Lim n²+n³+2n+1
n→+∞ x²+5x+1
- Lim 4n²-20n-3
n→+∞ n³-n+1
- Lim n²-n
n→+∞ n-1
2. Найдите Сумму бесконечно убывающей геометрической прогрессии:
1) 0,4; 0,04; 0,004; 0,0004…
2) 0,17; 0,0017; 0,000017…
3) 0,054; 0,0054; 0,00054…
4) 1 ; 1 ; 1 ; 1 …
3 6 12 36
B2. 10 класс.
Предел последовательности.
Бесконечно убывающая геометрическая прогрессия.
1.Вычислить предел последовательности:
- Lim 5x-7
x→+∞ 2x
- Lim 4x²+3x
x→+∞ 2x⁵-7x³
- Lim 7n²-6n+8
n→+∞ 4n²+2n+6
- Lim 8n³-3n+17
n→+∞ 3n³-61n+1
- Lim 14n⁵-23n²+4n-1
n→+∞ 19n⁵+13n⁴-2n+8
- Lim 6x²-17x+11
x→+∞ 3x²-21x-17
- Lim (5x+1)²
x→+∞ 7x²-x+10
- Lim 3x²-7x²+17x-13
x→+∞ 7x³-8x²+25
- Lim 6x²-11n-3
x→+∞ 7x²-x+5
- Lim 8n²-3n
n→+∞ n-2
2. Найдите сумму бесконечно убывающей геометрической прогрессии:
1) 0,6; 0,006; 0,0006…
2) 0,13; 0,013; 0,0013…
3) 0,045; 0,0045; 0,00045…
4) 1 ; 1 ; 1 ; 1 …
8 16 32 64
B3. 10 класс.
Предел последовательности.
Бесконечно убывающая геометрическая прогрессия.
1.Вычислить предел последовательности:
- Lim x²+x-6
x→+∞ x²-9
- Lim x²-9x+20
x→+∞ x²-12x-15
- Lim 3x²-6x-24
x→+∞ 3x²-9x+12
- Lim 9x⁵-18x⁴+21³-5
x→+∞
- Lim 2+5x-3x²
x→+∞ 21x²+x-2
- Lim 2x²+5x-3
x→+∞ x³-27
- Lim x⁸-7x⁵+21x³-18
x→+∞
- Lim 4x³-8x²+19x-2
x→+∞ 8x³-9x²+21
- Lim 7x²+12x-4
x→+∞ 6x²-x+8
- Lim 9x²-7x
x→+∞ 2x²
2. Найдите Сумму бесконечно убывающей геометрической прогрессии:
1) 0,8; 0,08; 0,008…
2) 0,42; 0,042; 0,0042…
3) 0,168; 0,00168; 0,0000168…
4) 1 ; 1 ; 1 …
4 12 36
B4. 10 класс.
Предел последовательности.
Бесконечно убывающая геометрическая прогрессия.
1.Вычислить предел последовательности:
- Lim 6x-8
x→+∞ 3x+11
- Lim x²-3x-10
x→+∞ x²+5x+6
- Lim 2x²-6x-36
x→+∞ 2x²-16x+24
- Lim 6x²+5x-6
x→+∞ 3x²-8x+4
- Lim x³-12x²+5x⁸-27
x→+∞
- Lim 8x³-1
x→+∞ 4x²+2x+1
- Lim 7
x→+∞ x³-5x+11
- Lim x⁵-5x⁴+2x³+1
x→+∞ x²-5x+1
- Lim 2x
x→+∞ 3x²-13x-16
- Lim 9x²+5x
x→+∞ 12x-11
2. Найдите Сумму бесконечно убывающей геометрической прогрессии:
1) 0,7; 0,07; 0,007…
2) 0,24; 0,0024; 0,000024…
3) 0,008; 0,00008; 0,0000008…
4) 1 ; 1 ; 1 ; 1 …
5 10 20 40
B5. 10 класс.
Предел последовательности.
Бесконечно убывающая геометрическая прогрессия.
1.Вычислить предел последовательности:
- Lim 6n+8
n→+∞ 7n
- Lim 5x²-3x
x→+∞ 3x⁵+7x³
- Lim x²-3x-28
x→+∞ x²+8x-9
- Lim 9n²-12n+4
n→+∞ n²-5n+5
- Lim -3a²+5a+2
a→+∞ 11a²-3a-14
- Lim 4a²-5a³+2
a→+∞ 6a³-21a²-7
- Lim 18a⁸+5a⁶+4a⁴+3a²-5
a→+∞
- Lim 6x-12
x→+∞ 3x²-5x+2
- Lim x⁵
x→+∞ x¹²+3x-18
- Lim 9a²-5a
a→+∞ a-5
2. Найдите Сумму бесконечно убывающей геометрической прогрессии:
1) 0,75; 0,075; 0,0075…
2) 0,16; 0,016; 0,000016…
3) 0,006; 0,0006; 0,00006…
4) 1 ; 1 ; 1 ; …
2 8 32
B6. 10 класс.
Предел последовательности.
Бесконечно убывающая геометрическая прогрессия.
1.Вычислить предел последовательности:
- Lim 6n-5
n→+∞ 7n
- Lim 4x+11
x→+∞ 3x²-2x-1
- Lim 6x²+16x-12
x→+∞ 10x+13-3x²
- Lim 18x⁸-7x⁵+7
x→+∞
- Lim -9n²+12n-4
n→+∞ 16n²+24n+9
- Lim 16-n²
n→+∞ n²+n+12
- Lim 21n⁵+n⁷-n⁸+15
n→+∞
- Lim 5n³-7n²+2n-3
n→+∞ n⁵-6
- Lim 6n²-8n-3
n→+∞ n³-n+1
- Lim 11n²-n
n→+∞ 2n-1
2. Найдите Сумму бесконечно убывающей геометрической прогрессии:
1) 0,82; 0,0082; 0,000082…
2) 0,27; 0,027; 0,0027…
3) 0,0004; 0,00004; 0,000004…
4) 2 ; 2 ; 2 ; …
3 9 27
B7. 10 класс.
Предел последовательности.
Бесконечно убывающая геометрическая прогрессия.
1.Вычислить предел последовательности:
- Lim 10n²-2
n→+∞ 5n²
- Lim 3x²-8x+2
x→+∞ 2x²-16x+3
- Lim x³-3x+3x²-5
x→+∞ x⁵-21
- Lim -2x-1
x→+∞ 10x²-x-2
- Lim 6x²-5x+1
x→+∞ 1-4x²
- Lim 6-7x+5x²
x→+∞ -3x²+1
- Lim 4x³+2x²-4x+5
x→+∞
- Lim x²-6x+8
x→+∞ x-2
- Lim 4x³+8x²-32x+18
x→+∞
- Lim 9n²-19
n→+∞ 19n-5
2. Найдите Сумму бесконечно убывающей геометрической прогрессии:
1) 0,28; 0,028; 0,0028…
2) 0,73; 0,0073; 0,000073…
3) 0,009; 0,00009; 0,0000009…
4) 2 ; 2 ; 2 ; …
9 27 81
B8. 10 класс.
Предел последовательности.
Бесконечно убывающая геометрическая прогрессия.
1.Вычислить предел последовательности:
- Lim 10n-7
n→+∞ 6n
- Lim 3n²-2n-7
n→+∞ n⁶-3n²+2
- Lim 6n²-7n+6
n→+∞ 5n²-6n+3
- Lim 7n³-n²+7
n→+∞ 5n³-7n+8
- Lim 12x⁶-24x-8
x→+∞ (3x-1)²
- Lim 6x²-24x-8
x→+∞ (3x-1)²
- Lim 21x⁵-13x
x→+∞ 2x⁵+8x
- Lim 16x⁸-21x⁶+18x²-2
x→+∞
- Lim 3x³-8x²+2x-2
x→+∞
- Lim 10n²-2n
n→+∞ 5n+2
2. Найдите Сумму бесконечно убывающей геометрической прогрессии:
1) 0,9; 0,009; 0,00009…
2) 0,37; 0,037; 0,0037…
3) 0,171; 0,00171; 0,0000171…
4) 7 ; 7 ; 7 ; …
8 24 72
B9. 10 класс.
Предел последовательности.
Бесконечно убывающая геометрическая прогрессия.
1.Вычислить предел последовательности:
- Lim (1-3m)²
m→+∞ 3m²+5m-2
- Lim 11m-2
m→+∞ 22m
- Lim m-1
m→+∞ m²-2m+5
- Lim 7m-12m²
m→+∞ 4m²-5m+1
- Lim 2x+5
m→+∞ x²+3x-18
- Lim 16m⁵-18m⁴-13m³+16
m→+∞
- Lim 10m²-13m+10
m→+∞ 5m²-3m-18
- Lim 10m⁶+11m⁵-18m⁴+25
m→+∞
- Lim 10m-61
m→+∞ m³+125
- Lim 3m-18
m→+∞ m-5
2. Найдите Сумму бесконечно убывающей геометрической прогрессии:
1) 0,57; 0,057; 0,0057…
2) 0,132; 0,00132 0,0000132…
3) 0,0001; 0,00001; 0,000001…
4) 7 ; 7 ; 7 ; …
12 24 48
B10. 10 класс.
Предел последовательности.
Бесконечно убывающая геометрическая прогрессия.
1.Вычислить предел последовательности:
- Lim 6k-5
k→+∞ 5-k
- Lim 3k²-7k+4
k→+∞ 11k²-3k-14
- Lim k²-2k-10
k→+∞ k²-5+k
- Lim 9k²-1
k→+∞ 4k²-5
- Lim 21k⁵-21k⁴-21k³+1
k→+∞
- Lim 3k³-5k²+10k-2
k→+∞
- Lim (12k-1)²
k→+∞ k²+5k+12
- Lim k²+k³+12k-1
k→+∞ k³+12
- Lim 12k²-20k+3
k→+∞ k³-k+1
- Lim 12k²-k
k→+∞ k-12
2. Найдите Сумму бесконечно убывающей геометрической прогрессии:
1) 0,304; 0,0304; 0,00304…
2) 0,0102; 0,000102; 0,00000102…
3) 1 ; 1 ; 1 ; …
13 26 52
4) 0,34; 0,0034; 0,000034…
B11. 10 класс.
Предел последовательности.
Бесконечно убывающая геометрическая прогрессия.
1.Вычислить предел последовательности:
- Lim 13n-2
n→+∞ 3n
- Lim 13n²-n+8
n→+∞ n²-n+8
- Lim 13x²+6x-7
x→+∞ 2x²-3x+4
- Lim 13x³-x+11
x→+∞ x³-7x-5
- Lim 13x⁵+31x⁴-13x³-5
x→+∞
- Lim 13x²-12x+9
x→+∞ 4x²+4x-4
- Lim (13x+1)²
x→+∞ x²+5x+1
- Lim 31x³-13x²+25
x→+∞
- Lim 13x²-13n-3
x→+∞ x³-x+1
- Lim n³-n
n→+∞ n+1
2. Найдите Сумму бесконечно убывающей геометрической прогрессии:
1) 0,41; 0,041; 0,0041…
2) 0,12; 0,0012; 0,000012…
3) 0,055; 0,0055; 0,00055…
4) 1 ; 1 ; 1 ; …
2 4
B12. 10 класс.
Предел последовательности.
Бесконечно убывающая геометрическая прогрессия.
1.Вычислить предел последовательности:
- Lim 14n+2
n→+∞ n
- Lim 14n²-n-7
n→+∞ n⁵-n²-1
- Lim 5n⁷-3n⁵-2n³+1
n→+∞
- Lim 6n³-13n+14
n→+∞ 14n³-1
- Lim 12n⁵-13n⁸+14n⁹
n→+∞
- Lim 14x²-12x-9
x→+∞ x²-4x+4
- Lim (34x+1)²
x→+∞ x²-14x+1
- Lim 6x
x→+∞ 2x²-5
- Lim 14x²-12x-3
x→+∞ x³-5x+1
- Lim 14n²-n
n→+∞ 2n²
2. Найдите Сумму бесконечно убывающей геометрической прогрессии:
1) 0,14; 0,014; 0,0014…
2) 0,14; 0,0014; 0,000014…
3) 0,041; 0,0041; 0,00041…
4) 2 ; 1 ; 1 ; …
2 8
B13. 10 класс.
Предел последовательности.
Бесконечно убывающая геометрическая прогрессия.
1.Вычислить предел последовательности:
- Lim 15x-4
x→+∞ 4x
- Lim 15x²-5x-8
x→+∞ x⁵-8x+1
- Lim 15x²-7x-8
x→+∞ 3x²+5x-3
- Lim 15x²-7x-5
x→+∞
- Lim 15a²-22a²-2a+1
a→+∞ 25a⁵-13a⁴+a
- Lim 15a²-13a+21
a→+∞ 6a²-5a+1
- Lim (16x+1)²
x→+∞ 2x²
- Lim 2x⁸-7x⁵+15x⁹
x→+∞
- Lim 3x³-x²+15x-13
x→+∞ 2x²-5
- Lim 15k²-5k
k→+∞ 5k+1
2. Найдите Сумму бесконечно убывающей геометрической прогрессии:
1) 0,15; 0,0015; 0,000015…
2) 0,514; 0,0514; 0,00514…
3) 0,045; 0,0045; 0,00045…
4) 10; 1; 0,1…
B14. 10 класс.
Предел последовательности.
Бесконечно убывающая геометрическая прогрессия.
1.Вычислить предел последовательности:
- Lim 16x²+16-1
x→+∞ x²-16
- Lim x²-16x+20
x→+∞ x²-3x+11
- Lim 16x²-6x-11
x→+∞ x²-9x+1
- Lim 16x⁵-10x⁴-24x³+5
x→+∞
- Lim 2-5x²-16x
x→+∞ 2x²-8x+5
- Lim x⁸-16x⁵+13x³-6
x→+∞
- Lim 16x³-8x²-19x+1
x→+∞ 4x³-5
- Lim 16x²-5x
x→+∞ 3x²
- Lim x²-9
x→+∞ x⁵+x⁸
- Lim 6x²-5x-6
x→+∞ x²-3x+4
2. Найдите Сумму бесконечно убывающей геометрической прогрессии:
1) 0,16; 0,0016; 0,000016…
2) 0,061; 0,0061; 0,00061…
3) 0,01; 0,0001; 0,0000001…
4) 1 ; 1 ; 1 ; …
3 9
nsportal.ru
Методическая разработка по алгебре (10 класс) по теме: самостоятельная работа 10 класс
I вариант
- Напишите уравнение касательной к графику функции у = f(х) в точке графика с абсциссой х0, если:
a) f(х)=x2-6x+5, x0=2;
б) f(х)=ln x, x0=e;
в) f(х)= 3x , x0 = 1.
- Дана функция f(х) = х3 + Зх2-2х-2. Напишите уравнение касательной к графику функции у = f(х), параллельной прямой у = — 2х +1.
- Дана функция f(х) = х2-2x-1. Напишите уравнение касательной к графику функции у = f(х), проходящей через точку А(0; -5).
- Даны функции f(х) = -х2 + 2х-3 и g(х) = х2 + 2. Напишите уравнение общей касательной к графикам функций у = f(х) и у = g(х).
II вариант
1. Напишите уравнение касательной к графику функции у = f(х) в точке графика с абсциссой х0, если:
а) f(х)= х2 + 6х-7, х0 = -2; б) f(х) = 1оg3х, х0=1; в) f(х) = ех , х0 = 2.
- Дана функция f(х)= х3-Зх2-Зх + 5. Напишите уравнение касательной к графику функции у = f(х), параллельной прямой у = -Зх + 4.
- Дана функция f(х) = х2 + 2х-2. Напишите уравнение касательной к графику функции у = f(х), проходящей через точку А(0; -6).
- Даны функции f(х) = х2 + 2х + 4 и g(х) = -х2-1. Напишите уравнение общей касательной к графикам функций у = f(х) и у = g(х).
III вариант
1. Напишите уравнение касательной к графику функции у = f(х) в точке графика с абсциссой х0, если:
а) f(х) = Зх2 + 6х+7, х0 = -2; б) f(х )= lgx, х0 =10; в) f(х) = 2x, х0 = 1.
- Дана функция f(х )= x:3 + 6х2 + 7х — 2. Напишите уравнение касательной к графику функции у = f(х), параллельной прямой у = -2х + 7.
- Дана функция f(х) = х2 + 4х + 2. Напишите уравнение касательной к графику функции у = f(х), проходящей через точку А(-1; -5).
- Даны функции f(х) = -х2 + 6х-11 и g(х) = х2-*1х + 6. Напишите уравнение общей касательной к графикам функций у = f(х) и у = g(х).
nsportal.ru
|
I вариант Найдите производные следующих функций: 1. 2. 3. 4. 5. 6. |
II вариант Найдите производные следующих функций: 1. 2. 3. 4. 5. 6. |
|
III вариант Найдите производные следующих функций: 1. 2. 3. 4. 5. 6. |
IV вариант Найдите производные следующих функций: 1. 2. 3. 4. 5. 6. |
|
I вариант Найдите производные следующих функций при х=1: 1. 2. 3. 4. 5. 6. |
III вариант Найдите производные следующих функций при х=1: 1. 2. 3. 4. 5. 6. |
|
II вариант Найдите производные следующих функций при х=1: 1. 2. 3. 4. 5. 6. |
IV вариант Найдите производные следующих функций при х=1: 1. 2. 3. 4. 5. 6. |
|
I вариант Найдите производные следующих функций при х=1: 1. 2. 3. 4. 5. 6. |
III вариант Найдите производные следующих функций при х=1: 1. 2. 3. 4. 5. 6. |
|
II вариант Найдите производные следующих функций при х=1: 1. 2. 3. 4. 5. 6. |
IV вариант Найдите производные следующих функций при х=1: 1. 2. 3. 4. 5. 6. |
nsportal.ru