План-конспект урока по алгебре (11 класс) по теме: Урок-практикум по теме «Общие методы решения уравнений» п.56, «Алгебра и начала анализа 10-11 классы», авт.А.Г. Мордкович и презентации по данной теме.
Тема урока: «Общие методы решения уравнений»
Тип урока: урок обобщения и систематизации знаний.
Форма урока: урок – практикум.
Оборудование:
- компьютер, проектор, экран;
- на магнитной доске размещены таблицы с графиками показательной, логарифмической, степенной функций (см. Приложение 5).
- на столах у учащихся карточки № 1, № 2, № 3, оценочные листы (см. Приложение 4).
Цели:
- Систематизировать, обобщить знания и умения учащихся по применению различных методов решения уравнений.
- Развивать умение наблюдать, обобщать, классифицировать, анализировать математические ситуации.
- Воспитывать такие качества личности, как познавательная активность, самостоятельность, упорство в достижении цели. Побуждать учащихся к взаимоконтролю, самоанализу своей деятельности.
План урока:
- Организационный момент. (2 мин.)
- Приветствие учащихся.
- Формулировка темы урока.
- Формулировка целей урока.
- Знакомство учащихся с этапами урока по оценочным листам.
- Проверка домашнего задания. (1 мин)
- Разминка проводится в форме теста по карточкам № 1 (см. Приложение 1). (10 мин.)
- Фронтальный опрос. (8 мин)
- Решение уравнений с последующим обсуждением. (25 мин)
- Самостоятельная работа по карточкам № 2 (см. Приложение 2). (7 мин.)
- Домашнее задание. (1 мин.)
- Практическая работа по карточкам № 3 из дидактических материалов. (20 мин.) (см. Приложение 3)
- Итог урока. Выставление оценок. (4 мин.)
- Рефлексия урока. (2 мин.)
Ход урока
- Организационный момент.
Приветствие учащихся. Учитель сообщает тему урока, цели урока.
— Ребята, на сегодняшнем уроке мы повторим основные методы решения уравнений. Эпиграфом к уроку будут слова немецкого математика Лейбница.
На экран проецируется слайд № 2 — эпиграф к уроку.
— Действительно, правильно выбранный метод часто позволяет существенно упростить решение, поэтому все изученные нами методы всегда нужно держать в зоне своего внимания, чтобы решать конкретные задачи наиболее подходящим способом.
Далее учитель знакомит учащихся с оценочными листами, порядком их заполнения.
- Проверка домашнего задания.
Консультанты (5 человек), проверившие у учащихся своих групп выполнение домашнего задания на перемене, докладывают учителю о результатах проверки.
- Разминка.
— Решение всех сложных уравнений всегда сводится к решению простейших уравнений. Сейчас мы проверим ваши знания и умения по решению простейших уравнений.
Каждый ученик получает тест (Карточка № 1) (см. Приложение № 1). Решает на листке, сдает учителю. В тетрадь записывает номера правильных ответов.
На экран проецируется слайд № 3 (таблица с правильными ответами).
В оценочный лист ученик выставляет 1 балл за каждое правильное решение.
- Фронтальный опрос.
— Ребята, какие общие методы решения уравнений вы знаете?
— Повторим изученные нами методы более подробно.
На экран проецируется слайд № 4. «Замена уравнения
h(f(x)) = h(g(x)) уравнением f(x) = g(x)» с образцом применения. (Метод 1).
— Когда применяется этот метод?
— Когда нельзя применять этот метод?
На экране слайд № 5. «Метод разложения на множители». (Метод № 2).
— В чем заключается суть данного метода?
— Как правильно отобрать корни?
На экране слайд № 6. «Метод введения новой переменной». (Метод № 3).
— В чем заключается суть данного метода?
— На что важно обратить внимание, если мы ввели новую переменную?
На экране слайд № 7. «Функционально-графический метод». (Метод № 4).
— В чем заключается идея данного метода?
— Существует красивая разновидность функционально-графического метода. Расскажите о ней.
— Когда обязательно нужна проверка?
- Решение уравнений с последующим обсуждением.
На экран проецируется слайд № 8.
Задания:
- определить метод решения уравнений;
- решить уравнения по выбору.
Ученики в тетради записывают номер уравнения, рядом указывают номер метода, которым можно решить данное уравнение.
Правильность классификации уравнений по методам решения проверяется в процессе обсуждения.
3 ученика у доски самостоятельно решают уравнения, которые можно решить I способом. Это уравнения № 2, № 5, № 12. В тетради ученики решают одно уравнение по выбору. По окончании решения каждый ученик объясняет свое решение.
Аналогично решаются остальные 3 группы уравнений:
— методом разложения на множители — № 6, № 8, № 10.
— методом введения новой переменной — № 3, № 4, № 7.
— функционально-графическим методом — № 1, № 9, № 11.
- Самостоятельная работа по карточкам № 2. (4 варианта) (см. Приложение).
Комментарии. Каждый ученик рядом с уравнением указывает номер метода решения. По окончании работы проводится взаимоконтроль.
На экран проецируется Слайд № 9 с правильными ответами.
В оценочный лист за каждый правильный ответ выставляется по одному баллу.
Карточки остаются у учащихся.
- Домашнее задание.
Решить уравнения, записанные на карточках № 2.
- Практическая работа по карточкам № 3 из дидактических материалов. (см. Приложение).
Работу выполняют на листах и сдают учителю.
Ответы записаны в тетради.
Сверяют ответы с ответами на экране. ( Слайд № 10).
В оценочный лист учащиеся вписывают баллы: 1 (а) – 3 балла, 1 (б) – 3 балла, 2- 4 балла. Подводят итог, ставят оценки.
Оценочный лист сдают учителю.
- Итог урока. Выставление оценок.
- Рефлексия урока.
- Какими навыками, умениями вы овладели на сегодняшнем уроке?
- Решение каких задач показалось вам сложным?
- Какие задания вам понравились?
Литература
1.Алгебра и начала анализа 10-11кл. в двух частях. Учебник и задачник для общеобразоват. учреждений. / А. Г. Мордкович – М.: Мнемозина, 2004.
2. Алгебра и начала анализа 11кл. Самостоятельные работы. / Под ред. А. Г. Мордковича – М.: Мнемозина, 2007.
3.Алгебра и начала анализа. Контрольные работы 10-11кл. / А. Г. Мордкович, Е. Е. Тульчинская, 2005.
4.Тесты для промежуточной аттестации 10кл. / Под ред. Ф. Ф. Лысенко – Ростов-на-Дону: Легион, 2007.
5.Алгебра. Открытые уроки (обобщающее повторение в 7,9,10 кл.). /Авт. сост. С.Н. Зеленская – Волгоград: Учитель, 2007.
6.Интернет — ресурсы. http://images.yandex.ru/
nsportal.ru
Конспект урока алгебры в 11 классе по теме «Первоначальное повторение». Урок 1. Свойства функций.
Алгебра 11 класс. Конспект урока по теме «Повторение»
Урок 1. Тема: Свойства числовых функций.
Цель: обобщить и систематизировать знания о следующих свойствах функции:
-
Монотонность;
-
Ограниченность;
-
Четность;
-
Нечетность;
-
Выпуклость;
-
Непрерывность.
2. Монотонность
Опред.1. Функцию у = f(x) называют возрастающей на множестве.
Х Д(f), если для любых точек х1 и х2 множества х, таких, что х1 < х2, выполняется неравенство f(х1) < f (х2).
3. Монотонность
Опред.2. Функцию у = f(x) называют убывающей на множестве Х Д(f), если для любых точек х1 и х2 множества х, таких, что х1 < х2, выполняется неравенство f(х1) > f (х2).
4. Пример 1.
5. Пример 2.
6. Пример 3
7. Пример 4.
8. Пример 5.
9. Ограниченность снизу.
Опред. 3. Функция у = f(х) назначить ограниченной снизу на множестве.
Х Д(f), если все значения этой функции на множестве Х больше некоторого числа. (Иными словами, если существует число m, такое, что для любого значения х Х выполняется неравенство f(х) > m).
10. Ограниченность сверху.
Опред.4. Функция у = f(х) назначить ограниченной сверху на множестве Х Д(f), если все значения этой функции меньше некоторого числа. (Иными словами, если существует число М, такое, что для любого значения х Х выполняется неравенство f(x) М.).
11. Ограниченность.
Опред.5. Если функция ограничена и снизу и сверху на всей области определения, то ее называют ограниченной.
12. Верное и неверное утверждение.
Поддерживаю
мысль
Хотел бы добавить
от себя
А с этим
я бы лично поспорил…
По предложенной схеме разобрать следующие утверждения:
-
Если у функции существует у наименьшее, то она ограничена снизу.
-
Если у функции существует у наибольшее, то она ограничена сверху.
-
Если у функции не существует у наименьшее, то она ограничена снизу.
-
Если функция не ограничена снизу, то у нее не существует наименьшее.
-
Если функция не ограничена сверху, то у нее не существует у наименьшее.
-
Если у функции не существует у наименьшее, то она ограничена сверху.
13. Точка экстремума.
Опред. 6. Точку Х0 назначить точкой максимума функции у = f(х), если у этой точки существует окрестность для всех точек которой (кроме самой точки Х0) выполняется неравенство f(x) < f(x0).
Точку Х0 назначить точкой минимума функции у = f(x), если у этой точки существует окрестность, для всех точек которой (кроме самой точки Х0) выполняется неравенство:
f(х) < f (х0).
14. Выпуклость:
вниз вверх
15. Четность и нечетность.
Опред.7. Функцию y = f(x), х Х, называют четной, если для любого значения Х из множества Х выполняется равенство f(-x) = f (x).
Опред.8. Функцию у = f(x), х Х, называют нечетной, если для любого значения х из множества Х выполняется равенство f(-x) = — f(x).
16. График четных и нечетных функций
17. Алгоритм исследования функции y = f(x), х Х, на четность.
-
Установить, симметрична ли область определения функции. Если нет, то объявить, что функция не является ни четной, ни нечетной. Если да, то перейти ко второму шагу алгоритма.
-
Найти f(-x).
-
Сравнить f(-x) и f(x)
а) если f(-x) = f(x), то функция четная.
б) если f(-x) = — f(x), то функция нечетная
в) если хотя бы в одной точке х Х выполняется соотношение f(-x)f(x) или
f(-x)- f(x), то функция не является ни четной, ни нечетной.
18. Непрерывность.
Непрерывность функции на промежутке Х означает, что график функции на данном промежутке не имеет точек разрыва (т.е. представляет собой сплошную линию).
19. Читаем график функции.
Домашнее задание. Повторение. Конспект учащегося.
Тема
Домашнее задание
1
Функция. Способы задания функции. Основные функциональные термины. Основные свойства функций. Основные элементарные функции и их свойства.
10 класс: §1, 2, с.5-21; №1.18, 1.19, 2.2г, 2.8г, 2.11б, с.13, 21, 22-23
2
Производная функции, физический и геометрический смысл производной. Производные основных элементарных функций
10 класс: §27, 28, 29, с.229-234, 240-249, 257-258; №28.10, 28.23, 28.25, с.252-253
3
Тригонометрические функции. Основные свойства тригонометрических функций. Основные тригонометрические формулы.
10 класс: §6, 7, 8, 9, с.53-55, 59-60, 71-72, 76-79, 82-83; формулы, с. 196, №7.3, 7.14, 8.10, 8.11, 9.12, с.80-81, 86
4
Контрольная работа №1 по теме «Повторение»
Повторить определения и свойства степеней
infourok.ru
Вводный урок по алгебре в 11 классе

Алгебра и начала математического анализа
Лукьянова Екатерина Владимировна
Учитель математики НЧОУ «СОШ им. Н.И. Лобачевского»


Основные темы
- Тригонометрические функции
- Производная и её геометрический смысл
- Применение производной к исследованию функций
- Первообразная и интеграл
- Комбинаторика
- Элементы теории вероятностей

Тригонометрия — это раздел математики, изучающий тригонометрические функции. Сложно представить, но с этой наукой мы сталкиваемся не только на уроках математики, но и в нашей повседневной жизни. Вы могли не подозревать об этом, но тригонометрия встречается в таких науках, как физика, биология, не последнюю роль она играет и в медицине, и, что самое интересное, без нее не обошлось даже в музыке и архитектуре.
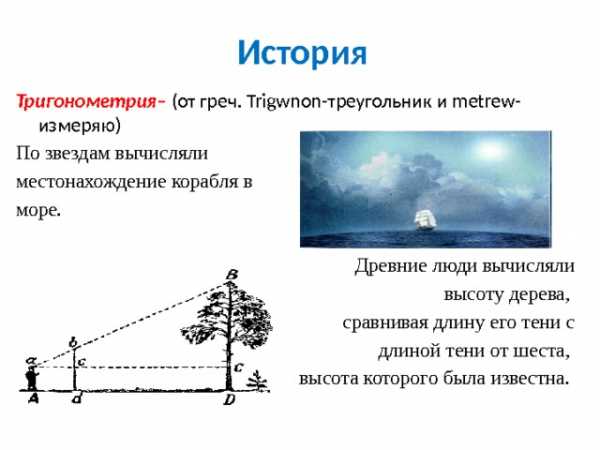
История
Тригонометрия – (от греч. Trigwnon-треугольник и metrew- измеряю)
По звездам вычисляли
местонахождение корабля в
море.
Древние люди вычисляли
высоту дерева,
сравнивая длину его тени с
длиной тени от шеста,
высота которого была известна.

Арабские Зиджи
Улугбек (1394-1449) —
основатель научной школы в
Самарканде.
Первые трактаты о плоской
тригонометрии (X—XI вв.).

Гиппарх

Птолемей

Древняя Греция
Вместо таблиц этих величин они употребляли таблицы: позволяющие отыскать хорду окружности по стягиваемой дуге. Дуги измерялись в градусах и минутах; хорды тоже измерялись градусами (один градус составлял шестидесятую часть радиуса), минутами и секундами.
Это шестидесятеричное подразделение греки заимствовали у вавилонян.

Индия
Индийцы также знали:
- Формулы для кратких углов sin na , cos na, где n=2,3,4,5.
- Первая таблица синусов «Сурья-сиддханте» у Ариабхаты. Она приведена через 3,45.
- Позднее ученые составили более подробные таблицы: например Бхаскара приводит таблицу синусов через 1 .
- Южноиндийские математики в 16 веке добились больших успехов в области суммирования бесконечных числовых рядов. По-видимому, они занимались этими исследованиями, когда искали способы вычисления более точных значений числа

Европа
Ряды для синуса и косинуса вывел И.Ньютон в 1666 г.,
Ряд арктангенса найден Дж.Грегори в 1671 г. И Г.В.Лейбницем в 1673 г.
Теорему тангенсов доказал Региомонтан (латинизированное имя немецкого астронома и математика Иоганна Мюллера (1436-1476)). Региомонтан составил также подробные тригонометрические таблицы;
Дальнейшее развитие тригонометрия получила в трудах выдающихся астрономов Николая Коперника (1473-1543) – творца гелиоцентрической системы мира, Тихо Браге (1546-1601) и Иогана Кеплера (1571-1630), а также в работах математика Франсуа Виета (1540-1603), который полностью решил задачу об определениях всех элементов плоского или сферического треугольника по трем данным .

Россия
Современные обозначения синуса и косинуса знаками sin x и cos x были впервые введены в 1739 году И. Бернулли в письме к петербургскому математику Л. Эйлеру. Последний пришел к выводу, что эти обозначения весьма удобны, и стал употреблять их в своих математических работах.
Кроме того, Эйлер вводит следующие сокращенные обозначения тригонометрических функций угла x : tang x, cos x, sin x, cotg x.
Далее Эйлер установил связь тригонометрических функций с показательными и дал правило для определения знаков функций в различных четвертях круга.

Значимые люди в тригонометрии
- Таблица числовых значений хорд
- Таблица для определения соотношений между элементами треугольников
Гиппарх Никейский
( 180 – 125 г. до н.э.)
- Первая таблица синусов, высчитанная по хордам в окружности
- «Альмагест – самая значимая тригонометрическая работа всей античности
Клавдий Птолемей (90 – 168 г н.э)

- Построил таблицы тангенсов, котангенсов и косекансов
Ал-Батани
( ок. 900 г. н.э)
- Присоединил к линиям синусов и косинусов линии тангенсов, котангенсов, секансов и косекансов
- Установил основные соотношения между этими линиями
- Дал определения функциям
- Установил формулу двойного угла
Абу-ль-Вефа
( 940 – 997 г. н.э)
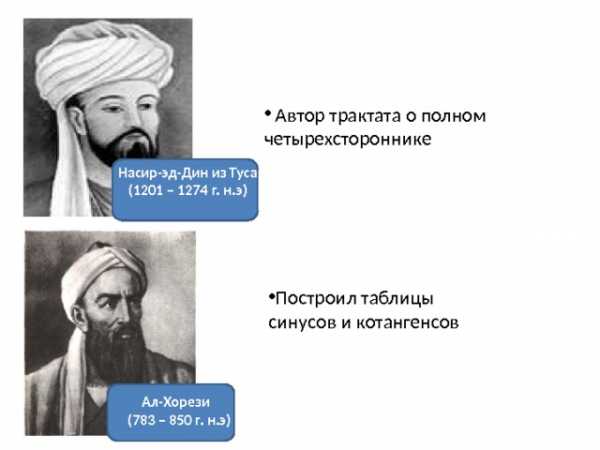
- Автор трактата о полном четырехстороннике
Насир-эд-Дин из Туса
(1201 – 1274 г. н.э)
- Построил таблицы синусов и котангенсов
Ал-Хорези
(783 – 850 г. н.э)

- Ввел понятие функции и принятую в наши дни символику
- Разъяснил вопрос о знаках всех тригонометрических функций любого аргумента
Леонард Эйлер
(1707 – 1783 г. н.э)
- Разработал метод проектирования сложных форм в 1920 году;
- Выразил тригонометрические функции как отношение координат x, y, z к длине элемента.
Ричард Саусвелл (1888-1970)

Тригонометрия в искусстве
cos 2 С + sin 2 С = 1
АС – расстояние от верха статуи до глаз человека,
АН – высота статуи,
sin С — синус угла падения взгляда.
А
А
С
С
Н
Н

Тригонометрия в физике
Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), называются гармоническими колебаниями .
Выражение, стоящее под знаком косинуса или синуса, называется фазой колебания:

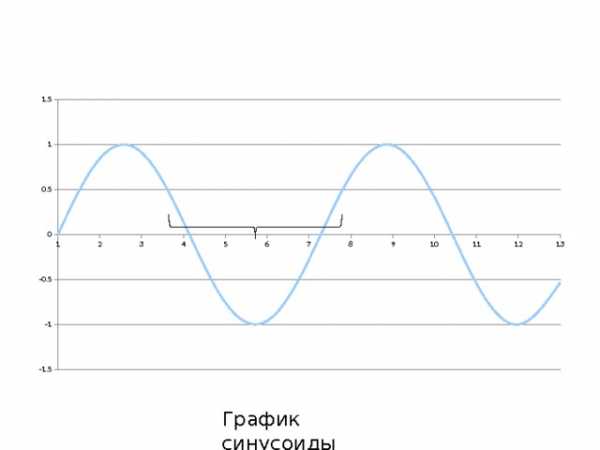
График синусоиды
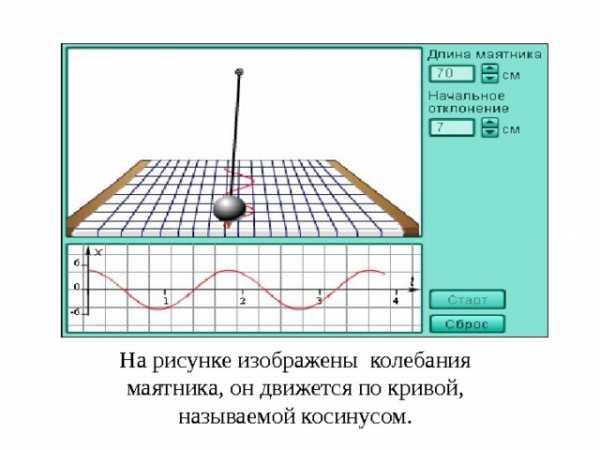
На рисунке изображены колебания маятника, он движется по кривой, называемой косинусом.

Тригонометрия и тригонометрические функции в медицине и биологии.
Одно из фундаментальных свойств живой природы — это цикличность большинства происходящих в ней процессов.
Биологические ритмы, биоритмы – это более или менее регулярные изменения характера и интенсивности биологических процессов.
Основной земной ритм – суточный.
Модель биоритмов можно построить с помощью тригонометрических функций.
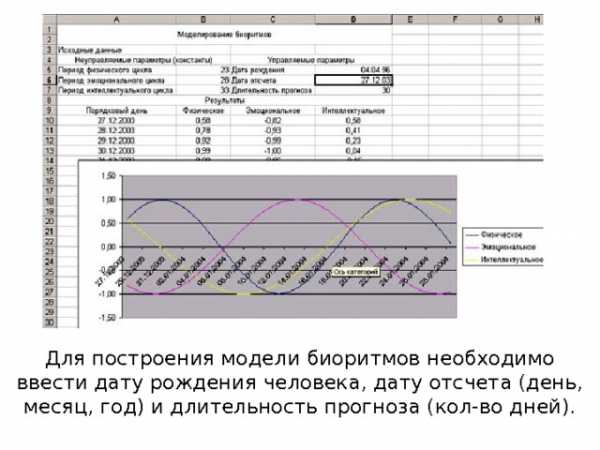
Для построения модели биоритмов необходимо ввести дату рождения человека, дату отсчета (день, месяц, год) и длительность прогноза (кол-во дней).

Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения.
При плавании тело рыбы принимает форму кривой, которая напоминает график функции y=tgx.

Тригонометрия в архитектуре
Детская школа Гауди в Барселоне

Сантьяго Калатрава Винодельня «Бодегас Исиос»

Феликс Кандела Ресторан в Лос-Манантиалесе

Тригонометрия в музыке
- Согласно дошедшим из древности преданиям, первыми, кто попытался сделать это, были Пифагор и его ученики.
- Частоты, соответствующие
одной и той же ноте в первой, второй и т.д. октавах, относятся, как 1:2:4:8…
- диатоническая гамма 2:3:5

Тетраэдр из различных типов аккордов четырех звуков:
синий – малые интервалы;
более теплые тона — более «разряженные» звуки аккорда; красная сфера- наиболее гармоничный аккорд с равными интервалами между нотами.

Теория радуги
Радуга возникает из-за того, что солнечный свет испытывает преломление в капельках воды, взвешенных в воздухе по закону преломления:
n 1 — показатель преломления первой среды n 2 — показатель преломления второй среды
α -угол падения, β -угол преломления света
sin α / sin β = n 1 / n 2

1. Сферическая капля
2. Внутреннее отражение 3. Первичная радуга 4. Преломление 5. Вторичная радуга 6. Входящий луч света 7. Ход лучей при формировании первичной радуги 8. Ход лучей при формировании вторичной радуги 9. Наблюдатель 10-12. Область формирования радуги.

Северное сияние
Проникновение в верхние слои атмосферы планет заряженных частиц солнечного ветра определяется взаимодействием магнитного поля планеты с солнечным ветром.
Сила, действующая на движущуюся в магнитном поле заряженную частицу называется силой Лоренца. Она пропорциональна заряду частицы и векторному произведению поля и скорости движения частицы.

Область определения и множество значений, четность и нечетность, периодичность тригонометрических функций

Удачи!!!
multiurok.ru
План-конспект урока по алгебре (11 класс) по теме: Урок алгебры в 11 классе по теме:»Первообразная»
Урок алгебры в 11 классе по теме «Первообразная»
Три пути ведут к знанию:
путь размышления – это путь
самый благородный,
путь подражания – это путь
самый легкий и
путь опыта – это путь
самый горький.
Конфуций
Тип урока: изучение нового материала.
Оборудование: магнитная доска, папки с приложениями
Цели и задачи урока
Цели:
- повторить понятие производной функции, ее физический смысл, основные формулы дифференцирования; ввести понятие первообразной функции, научить учащихся определять является ли функция F(x) первообразной для функции f(x).
- Способствовать развитию умения сравнивать, обобщать, классифицировать, анализировать, делать выводы.
- Побуждать учащихся само- и взаимоконтролю, воспитывать познавательную активность, самостоятельность, упорство в достижении цели.
Задачи:
а)Обучающая — на основе имеющихся у учащихся знаний по теме: «Производная» подвести учащихся к понятию первообразной, определить вместе с ними это понятие;
б) развивающая — формирование приемов обобщения, алгоритмизации;
в) воспитывающая — воспитывать умение участвовать в диалоге, понимать точку зрения собеседника, признавать право на иное мнении, показ практической применимости математических знаний.
План урока
1. Организационный момент
2. Актуализация прежних знаний
а) фронтальный опрос (по формулам и правилам)
б) вычисление производных (устно)
3. Объяснение нового материала.
4. Первичное закрепление
5. Историческая справка
6. Итог урока
7. Домашнее задание
Ход урока
1.Организационный момент (сообщение темы и цели урока).
2.Актуализация знаний
1) Опорные знания: производная, таблица производных, физический смысл производной.
2) Связь с прошлой темой: на уроке используются таблицы производной, вычисляются производные функций.
Задание классу:
- Вычислить производные следующих функций:
(1)/ = ((2х-3)6)/=
(х)/ = ((х5+20))/=
(30х)/= (Соs 3х)/=
(х3)/= ( 5х10)/=
- Назвать физический смысл производной.
3.Изучение нового материала (Формирование новых понятий и способов действий)
Создание проблемной ситуации.
Задача: При обработке на станке деталь нагреть до 1200. Измерения полагается производить при 200. Скорость охлаждения детали пропорциональна разности температур детали и воздуха в цехе. Сколько же нужно ждать?
Здесь T(t) – температура детали, T/(t) = k(T-180)/- скорость её охлаждения.
Ставится вопрос: зная производную некоторой функции, мы должны найти саму функцию. Как это сделать?
Учащиеся выполняют задания: заполнить пропущенные места в скобках
(…)/ = 2х (…)/ = 0
(…)/ = 4х3 (…)/ = 25
Как можно иначе сформулировать это задание (найти саму функцию, зная её производную; восстановить функцию по производной)?
Восстанавливаемая функция называется первообразной. Дайте определение первообразной функции.
Помощь учителя: если мы обозначим саму функцию через f(x), а её первообразную через F(x) , то куда поставить штрих в равенстве F=f? Или: как проверить, что некоторая функция F(x) является первообразной для f(x)?
Учащиеся обсуждают и дают определение первообразной.
На доске записи:
Производная – «производит» на свет новую функцию, первообразная — первичный образ.
Определение: Функция F(x) называется первообразной для функции f(x) , если F/(x) = f(x) на заданном промежутке.
4. Закрепление нового материала ( Применение знаний и новых способов действий в ситуациях по образцу и в измененных условиях)
1) С целью закрепления определения первообразной выполнить следующие задания:
а) Проверить, что функция F(x) есть первообразная для f(x):
1) F(x) = x3-2x+1 f(x)=3×2-2
2) F(x)= x4-7 f(x)=4×3
3) F(x)=10 f(x)=0
4) F(x)= f(x)=1/2 x€]0;+[
5) F(x) =10×10 f(x)=200×19
б) Найти первообразную для функции f(x):
1) f(x)= x3
2) f(x) = x2
3) f(x) = x
2). После решения второго задания появляется необходимость как-то упорядочить процесс нахождения первообразной; с этой целью учащиеся формулируют алгоритм:
- Подобрать функцию F(x)
- Найти её первообразную F/(x)
- Сравнить полученную производную F/(x) с данной функцией f(x)
- Если они совпадают, то задача решена, если нет, то вернуться к пункту 1).
Задание: Первообразные для следующих функций находим, пользуясь данным алгоритмом.
- f(x) = 1
- f(x) = x3
- f(x) = 0,25
- f(x) = 5x
- f(x) = 6/x
- f(x) = 7×8
- f(x) = 14×10
- f(x) = 20×3
6. Историческая справка.
Математический анализ имеет две главные составляющие его части: дифференциальное и интегральное исчисления. С элементами дифференциального исчисления мы познакомились в 10-м классе, впереди – изучение интегралов.
«Интеграл»- «интегрирование» — «интеграция»… Однокоренные слова, вышедшие за пределы математики и ставшие почти «обиходными». Пожалуй, нет другого математического термина, который использовался бы в обычной жизни так же часто, как термин «интеграл». Музыкальная группа «Интеграл», кафе «Под интегралом», банк «Интеграл-капитал», а слова «интегрирование» и «интеграция» встречаются на каждом шагу. В газетах мы читаем об интеграции наук, культур, интеграции экономики, политики также ведут речь об интеграционных процессах. Почему? Ведь есть масса других красивых математических слов: экспонента, логарифм, синус — звучит ничуть не хуже.
Возможно, здесь играет свою роль красивый знак интеграла или понятный смысл слова: восстановление, целостность, суммирование.
А быть может, привлекает некая таинственность интеграла? Непонятно, почему один и тот же математический инструмент позволяет находить и площади фигур, и формулу скорости по известной формуле ускорения. Почему операция, обратная дифференцированию, оказывается как-то связанной, скажем, с объёмами тел вращения? Конечно, доказаны все необходимые теоремы, но эта эффективность интеграла всё равно завораживает.
7. Итог урока. Рефлексия
Итог урока. «Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию». Ян Амос Коменский
1) С какой операцией, обратной дифференцированию, познакомились;
2) вспоминаем определение первообразной.
Итак, дифференцировать – значит «разделять» процесс, например, находить его мгновенную скорость в каждой отдельно взятой точке; интегрировать – значит «соединять», суммировать бесконечно малые части искомого целого.
Таким образом, операции дифференцирования («разделения») и интегрирования («суммирования») оказываются взаимно обратными (как, например, сложение и вычитание, умножение и деление, возведение в степень и извлечение корня).
Инструментом для вычисления интегралов служит понятие первообразной функции. Операция нахождения первообразной является обратной по отношению к операции дифференцирования функции.
Овладев понятием первообразной функции, а затем и интеграла, мы сможем решать самые разнообразные алгебраические, геометрические и физические задачи.
Рефлексия.
8. Домашнее задание.
1.Прочитать объяснительный текст глава 4 параграф 20, выучить наизусть определение 1. первообразной;
2.Решить № 20.1 -20.5 (в, г) — обязательное задание для всех;
№ 20.6 (б), 20.7 (в, г), 20.8 (б), 20.9 (б)- 4 примера по выбору.
nsportal.ru
Презентация к уроку по алгебре (11 класс) по теме: Помощь в преподавании алгебры 11 класс
Демонстрационный материал для изучения алгебры в 11 классе.
Скачать:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
По теме: методические разработки, презентации и конспекты
nsportal.ru
Алгебра и начала анализа, 11 класс, Поурочные планы по учебнику Мордковича А.Г., 2011
По кнопке выше «Купить бумажную книгу» можно купить эту книгу с доставкой по всей России и похожие книги по самой лучшей цене в бумажном виде на сайтах официальных интернет магазинов Лабиринт, Озон, Буквоед, Читай-город, Литрес, My-shop, Book24, Books.ru.
По кнопке «Купить и скачать электронную книгу» можно купить эту книгу в электронном виде в официальном интернет магазине «ЛитРес», и потом ее скачать на сайте Литреса.
По кнопке «Найти похожие материалы на других сайтах» можно искать похожие материалы на других сайтах.
On the buttons above you can buy the book in official online stores Labirint, Ozon and others. Also you can search related and similar materials on other sites.
Алгебра и начала анализа, 11 класс, Поурочные планы по учебнику Мордковича А.Г., 2011.
Подробные разработки по алгебре и началам математического анализа для 11 класса Мордковича и др. (М.: Мнемозина) и содержит весь необходимый педагогу материал для качественной подготовки к урокам: детальные поурочные планы, методические советы и рекомендации, творческие задания, тесты, подробный разбор контрольных и зачетных работ.
Издание будет полезно как начинающим педагогам, так и преподавателям с опытом работы.
Зачетная работа по теме «Степени и корни. Степенные функции».
Цель: проверка знаний учащихся по вариантам одинаковой сложности.
Ход уроков
I. Сообщение темы и цели уроков
II. Характеристика зачетной работы
Работа составлена в двух равноценных вариантах. По сравнению с контрольной работой увеличено количество заданий. Соответственно, у учащихся возрастает возможность выбора задач. Все задания разбиты на три блока А, В и С. Самые простые задачи находятся в части А, более сложные — в части В, еще сложнее — в части С. Каждая задача из А оценивается в 1 балл, из В — в 2 балла, из С — в 3 балла. Поэтому за правильное решение всех задач блока А можно получить 7 баллов, блока В — 8 баллов и блока С — 9 баллов (всего 24 балла). Оценка 3 ставится за 6 баллов, оценка 4 — за 10 баллов, оценка 5 -за 14 баллов.
Так как эта работа является зачетной, то в нее не включены принципиально новые задачи. Поэтому разбору заданий работы отдельного задания можно и не посвящать (решения задач могут быть вывешены на стенде). Для стендового размещения разбор вариантов приводится.
Оглавление
Предисловие 3
Рекомендации к проведению уроков 5
Тематическое планирование учебного материала 10
I полугодие 12
Глава 6. Степени и корни. Степенные функции 12
Глава 7. Показательные и логарифмические функции 73
Глава 8. Первообразная и интеграл 143
II полугодие 191
Глава 9. Элементы математической статистики, комбинаторики и теории вероятностей 191
Глава 10. Уравнения и неравенства.
Системы уравнений и неравенств 223
Литература 300.
Купить
Дата публикации:
Теги:
поурочные планы по алгебре :: алгебра :: Мордкович :: поурочные планы :: 11 класс
Смотрите также учебники, книги и учебные материалы:
Следующие учебники и книги:
- Поурочные разработки по математике, 6 класс, Выговская В.В., 2010
- Математика, 6 класс, Поурочные планы по учебнику Виленкина Н.Я., 2011
- Математика, 5 класс, Поурочные планы, Ким Е.А., 2008
- Алгебра, Сборник рабочих программ, 7-9 класс, Бурмистрова Т.А., 2011
Предыдущие статьи:
- Алгебра и начала анализа, 11 класс, Поурочные планы по учебнику Колмогорова А.Н., 2009
- Алгебра и начала анализа, 10 класс, Поурочные планы по учебнику Мордковича А.Г., 2008
- Алгебра и начала анализа, 10 класс, Поурочные планы по учебнику Колмогорова А.Н., 2011
- Алгебра и начала анализа, 10 класс, Поурочные планы, Часть 1, Купорова Т.И., 2009
nashol.com
| № урока | Содержание учебного материала | Дата | Примеч. |
|---|---|---|---|
| Глава VI. Степени и корни. Степенные функции | 15 часов. | ||
| Урок 1 | Понятие корня n-й степени из действительного числа | ||
| Урок 2 | Решение упражнений | ||
| Урок 3 | Функции и их свойства и графики | ||
| Урок 4 | Решение упражнений | ||
| Урок 5 | Свойства корня n-й степени | ||
| Урок 6 | Решение упражнений | ||
| Урок 7 | Преобразование выражений, содержащих радикалы | ||
| Урок 8 | Решение упражнений | ||
| Урок 9 | Обобщение понятия о показателе степени | ||
| Урок 10 | Решение иррациональных уравнений и неравенств | ||
| Урок 11 | Решение систем иррациональных уравнений | ||
| Урок 12 | Решение упражнений Самостоятельная работа № 1 |
||
| Урок 13 | Подготовка к контрольной работе № 1 | ||
| Урок 14 | Контрольная работа № 1 | ||
| Урок 15 | Работа над ошибками | ||
| Глава VII. Показательная и логарифмическаяфункции | 24 часа. | ||
| Урок 16 | Показательная функция, ее свойства и график | ||
| Урок 17 | Решение упражнений | ||
| Урок 18 | Решение простейших показательных уравнений | ||
| Урок 19 | Различные способы решения показательных уравнений | ||
| Урок 20 | Решение показательных неравенств | ||
| Урок 21 | Подготовка к контрольной работе № 2 Самостоятельная работа № 2 |
||
| Урок 22 | Контрольная работа № 2 | ||
| Урок 23 | Работа над ошибками | ||
| Урок 24 | Понятие логарифма | ||
| Урок 25 | Функция y = log2 x, ее свойства и график | ||
| Урок 26 | Решение упражнений | ||
| Урок 27 | Свойства логарифмов | ||
| Урок 28 | Решение упражнений | ||
| Урок 29 | Логарифмические уравнения | ||
| Урок 30 | Решение упражнений | ||
| Урок 31 | Самостоятельная работа № 3 | ||
| Урок 32 | Логарифмические неравенства | ||
| Урок 33 | Решение упражнений | ||
| Урок 34 | Переход к новому основанию логарифма | ||
| Урок 35 | Дифференцирование показательной и логарифмической функции | ||
| Урок 36 | Решение упражнений Самостоятельная работа № 4 |
||
| Урок 37 | Подготовка к контрольной работе № 3 | ||
| Урок 38 | Контрольная работа № 3 | ||
| Урок 39 | Контрольная работа № 3 | ||
| Глава VIII. Первообразная и интеграл | 9 часов. | ||
| Урок 40 | Определение первообразной и её общий вид | ||
| Урок 41 | Таблица первообразных. Правила нахождения первообраз-ных. | ||
| Урок 42 | Решение упражнений | ||
| Урок 43 | Задачи, приводящие к понятию определенного интегра-ла.Понятие определенного интеграла | ||
| Урок 44 | Решение упражнений Самостоятельная работа № 5 |
||
| Урок 45 | Вычисление площадей плоских фигур с помощью опреде-ленного интеграла | ||
| Урок 46 | Решение упражнений | ||
| Урок 47 | Подготовка к контрольной работе № 4 | ||
| Урок 48 | Контрольная работа № 4 | ||
| Глава IX. Элементы математической статистики, комбинаторики и теории вероятностей | 11 часов. | ||
| Урок 49 | Статистическая обработка данных | ||
| Урок 50 | Решение задач | ||
| Урок 51 | Простейшие вероятностные задачи | ||
| Урок 52 | Решение задач | ||
| Урок 53 | Сочетания и размещения | ||
| Урок 54 | Решение задач | ||
| Урок 55 | Случайные события и их вероятности | ||
| Урок 56 | Решение задач | ||
| Урок 57 | Решение задач | ||
| Урок 58 | Подготовка к контрольной работе № 5 | ||
| Урок 59 | Контрольная работа № 5 | ||
| Глава X. Уравнения и неравенства. Системы уравнений и неравенств | 17 часов. | ||
| Урок 60 | Равносильность уравнений | ||
| Урок 61 | Решение уравнений | ||
| Урок 62 | Общие методы решения уравнений | ||
| Урок 63 | Решение уравнений Самостоятельная работа № 6 |
||
| Урок 64 | Решение неравенств с одной переменной | ||
| Урок 65 | Решение иррациональных неравенств | ||
| Урок 66 | Решение неравенств с модулями Самостоятельная работа № 7 |
||
| Урок 67 | Уравнения с двумя переменными | ||
| Урок 68 | Решение уравнений | ||
| Урок 69 | Неравенства с двумя переменными | ||
| Урок 70 | Решение неравенств | ||
| Урок 71 | Системы уравнений | ||
| Урок 72 | Решение задач с помощью систем уравнений | ||
| Урок 73 | Решение задач Самостоятельная работа № 8 |
||
| Урок 74 | Уравнения и неравенства с параметрами | ||
| Урок 75 | Подготовка к контрольной работе №9 | ||
| Урок 76 | Контрольная работа №9 | ||
| Повторение | 26 часов. | ||
| Урок 77 | Основы тригонометрии. Преобразование тригонометриче-ских выражений | ||
| Урок 78 | Преобразование тригонометрических выражений | ||
| Урок 79 | Простейшие тригонометрические уравнения | ||
| Урок 80 | Простейшие тригонометрические неравенства | ||
| Урок 81 | Более сложные тригонометрические уравнения | ||
| Урок 82 | Показательная функция. Элементарные показательные урав-нения и неравенства | ||
| Урок 83 | Показательные уравнения и неравенства | ||
| Урок 84 | Логарифмы. Преобразование логарифмических выражений. Логарифмическая функция | ||
| Урок 85 | Логарифмические уравнения и неравенства | ||
| Урок 86 | Функции и их свойства | ||
| Урок 87 | Графики основных элементарных функций | ||
| Урок 88 | Чтение графиков функций | ||
| Урок 89 | Решение упражнений | ||
| Урок 90 | Производная и еегеометрический смысл | ||
| Урок 91 | Вычисление производных | ||
| Урок 92 | Первообразная и интеграл | ||
| Урок 93 | Планиметрия. Треугольники, четырехугольники | ||
| Урок 94 | Планиметрия. Подобие фигур | ||
| Урок 95 | Планиметрия. Окружность и круг. | ||
| Урок 96 | Стереометрия | ||
| Урок 97 | Стереометрия | ||
| Урок 98 | Стереометрия | ||
| Урок 99 | Пробный «экзамен» | ||
| Урок 100 | Работа над ошибками | ||
| Урок 101 | Итоговое повторение | ||
| Урок 102 | Итоговое повторение | ||
www.learn-portal.ru