Контрольные работы по алгебре для 11 класса – Контрольные работы по алгебре и началам анализа, 11 класс

Контрольные работы по алгебре и началам анализа для 11 класса (Колягин Ю.М.)

Контрольные работы по алгебре и началам анализа в 11 классе

Контрольная работа № 1

по теме «Тригонометрические функции»

Вариант 1

1. Найдите область определения и множество значений функции у = 2 cos x.

2. Выясните, является ли функция у = sin x – tg x четной или нечетной.

3. Изобразите схематически график функции у = sin x + 1 на отрезке .

4. Найдите наибольшее и наименьшее значения функции у = 3sin x ∙cos x + 1.

5. Постройте график функции у = 0,5 cos x – 2. При каких значениях х функция возрастает? Убывает?

Контрольные работы по алгебре и началам анализа в 11 классе

Контрольная работа № 1

по теме «Тригонометрические функции»

Вариант 2

1. Найдите область определения и множество значений функции у = 0,5 cos x.

2. Выясните, является ли функция у = cos x – x² четной или нечетной.

3. Изобразите схематически график функции у = cos x — 1 на отрезке .

4. Найдите наибольшее и наименьшее значения функции у = + 1.

5. Постройте график функции у = 2 sin x + 1. При каких значениях х функция возрастает? Убывает?

Контрольные работы по алгебре и началам анализа в 11 классе

Контрольная работа № 1

по теме «Тригонометрические функции»

Вариант 1

1. Найдите область определения и множество значений функции у = 2 cos x.

2. Выясните, является ли функция у = sin x – tg x четной или нечетной.

3. Изобразите схематически график функции у = sin x + 1 на отрезке .

4. Найдите наибольшее и наименьшее значения функции у = 3sin x ∙cos x + 1.

5. Постройте график функции у = 0,5 cos x – 2. При каких значениях х функция возрастает? Убывает?

Контрольные работы по алгебре и началам анализа в 11 классе

Контрольная работа № 1

по теме «Тригонометрические функции»

Вариант 2

1. Найдите область определения и множество значений функции у = 0,5 cos x.

2. Выясните, является ли функция у = cos x – x² четной или нечетной.

3. Изобразите схематически график функции у = cos x — 1 на отрезке .

4. Найдите наибольшее и наименьшее значения функции у = + 1.

5. Постройте график функции у = 2 sin x + 1. При каких значениях х функция возрастает? Убывает?

Контрольная работа № 2

по теме «Производная и ее геометрический смысл»

Вариант 1

1. Найдите производную функции: а) 3х² — б) в) г)

2. Найдите значение производной функции f(x) = в точке х₀ = 8.

3. Запишите уравнение касательной к графику функции f(x) = sin x – 3x + 2 в точке х₀ = 0.

4. Найдите значения х, при которых значения производной функции f(x) = положительны.

5. Найдите точки графика функции f(x)= х³ – 3х², в которых касательная к нему параллельна оси абсцисс.

6. Найдите производную функции f(x) = .

Контрольная работа № 2

по теме «Производная и ее геометрический смысл»

Вариант 2

1. Найдите производную функции: а) 2х³ — б) в) г)

2. Найдите значение производной функции f(x) = в точке х₀ = .

3. Запишите уравнение касательной к графику функции f(x) = 4x — sin x + 1 в точке х₀ = 0.

4. Найдите значения х, при которых значения производной функции f(x) = отрицательны.

5. Найдите точки графика функции f(x)= х³ + 3х², в которых касательная к нему параллельна оси абсцисс.

6. Найдите производную функции f(x) = cos .

Контрольная работа № 3

по теме «Применение производной к исследованию функций»

Вариант 1

1. Найдите стационарные точки функции f(x) = х³— 2х² +х +3.

2. Найдите экстремумы функции: а) f(x) =х³ – 2х² + х + 3; б) f(x) =.

3. Найдите интервалы возрастания и убывания функции f(x) = х³— 2х² +х +3.

4. Постройте график функции f(x) = х³— 2х² +х +3 на отрезке .

5. Найдите наибольшее и наименьшее значения функции f(x) = х³— 2х² +х +3 на отрезке .

6. Среди прямоугольников, сумма длин трех сторон которых равна 20, найдите прямоугольник наибольшей площади.

Контрольная работа № 3

по теме «Применение производной к исследованию функций»

Вариант 2

1. Найдите стационарные точки функции f(x) = х³— х² — х +2.

2. Найдите экстремумы функции: а) f(x) = х³— х² — х +2; б) f(x) =.

3. Найдите интервалы возрастания и убывания функции f(x) = х³— х² — х +2.

4. Постройте график функции f(x) = х³— х² — х +2 на отрезке .

5. Найдите наибольшее и наименьшее значения функции f(x) = х³— х² — х +2 на отрезке .

6. Найдите ромб с наибольшей площадью, если известно, что сумма длин его диагоналей равна 10.

Контрольная работа № 4

по теме «Интеграл»

Вариант 1

1. Докажите, что функция F(x) = 3х + sin x – e^2xявляется первообразной функции f (x) = 3 + cos x – 2e^2x на всей числовой оси.

2. Найдите первообразную F функции f (x) = 2, график которой проходит через точку А(0; ).

3. Вычислите площадь фигуры, изображенной на рисунке.

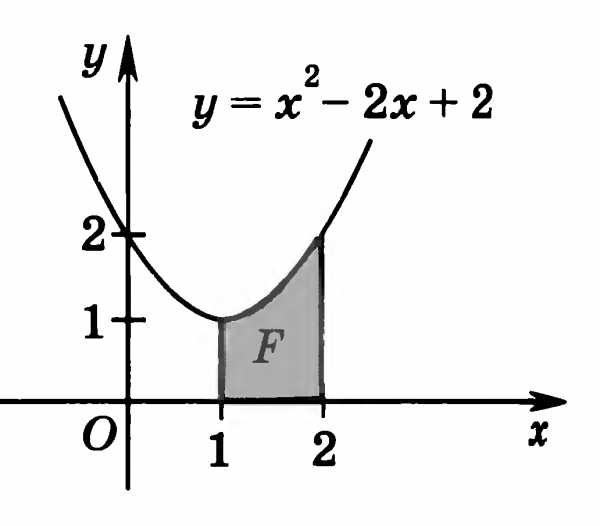
4. Вычислить интеграл: а) dx; б) .

5. Найдите площадь фигуры, ограниченной прямой у = 1 – 2х и графиком функции у = х² – 5х – 3.

Контрольная работа № 4

по теме «Интеграл»

Вариант 2

1. Докажите, что функция F(x) = х + cos x + e^3xявляется первообразной функции f (x) = 1 — sin x + 3e^3x на всей числовой оси.

2. Найдите первообразную F функции f (x) = — 3, график которой проходит через точку А(0; ).

3. Вычислите площадь фигуры, изображенной на рисунке.

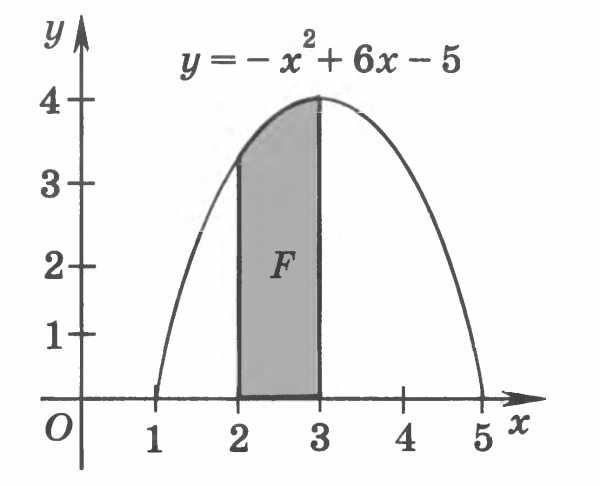
4. Вычислить интеграл: а) dx; б) .

5. Найдите площадь фигуры, ограниченной прямой у = 3 – 2х и графиком функции у = х² + 3х – 3.

infourok.ru

Контрольные работы для 11 класса по алгебре к учебнику Ю.М. Колягина

Контрольная работа №1

В-1,

1. Найти область определения и множество значений функции

у = sinx + 2

2. Выяснить, является ли функция у = х² + cosx чётной или нечётной.

3. Доказать, что функция у = cos x является периодической с периодом Т=3.

4. Найти все принадлежащие отрезку [ -] корни уравнения

sinx = с помощью графика функции.

5. Построить график функции у = sinx 1 и найти значения аргумента, при которых функция возрастает, принимает наибольшее значения.

№ Контрольная работа №1

В-2

1.Найти область определения и множество значений функции

у = 3cosx

2. Выяснить, является ли функция у =х sinx чётной или нечётной.

3. Доказать, что функция у = sin x является периодической с периодом Т=.

4. Найти все принадлежащие отрезку [ 0] корни уравнения

cosx =- с помощью графика функции.

5. Построить график функции у = cos (x + ) и найти значения аргумента, при которых функция убывает, принимает наименьшее значения.

Контрольная работа№2

В – 1

1. Найти производную функции:

а) 3 – ; б) ( + 7)⁶; в) cosx; г) .

2. Найти значение производной функции y = f(x) в точке , если f(x) = 1 – 6 , = 8.

3. Записать уравнение касательной к графику функции

f(x) = sinx – 3x + 2 в точке = 0.

4. Найти значения х, при которых значения производной функции f(x) = положительны.

5. Найти точки графика функции f(x) = x³ – 3x², в которых касательная к нему параллельна оси абсцисс.

___________________________________________________________________

Контрольная работа №2

В – 2,

1. Найти производную функции:

а) 2 – ; б) (4 – 3х)⁷; в) sinx; г) .

2. Найти значение производной функции y = f(x) в точке , если f(x) = 2 – , = .

3. Записать уравнение касательной к графику функции

f(x) = 4х – sinx + 1 в точке = 0.

4. Найти значения х, при которых значения производной функции f(x) = отрицательны.

5. Найти точки графика функции f(x) = x³ + 3x², в которых касательная к нему параллельна оси абсцисс.

Контрольная работа №3

В-1

1. Найти экстремумы функций:

1. f(x)=х³2х²+х+3; 2) f(x)=е^х (5х 3).

2. Найти интервалы возрастания и убывания функции f(x)=х³ 2х²+х+3

3. Построить график функции f(x)=х³2х²+х+3.

4. Найти наибольшее и наименьшее значения функции f(x)=х³ 2х²+ х +3 на отрезке [0; ].

5. Среди прямоугольников, сумма длин трёх сторон у которых равна 20, найти прямоугольник наибольшей площади.

___________________________________________________________

Контрольная работа №3

В-2

1. Найти экстремумы функций:

1) f(x)=х³х²х +2; 2) f(x)= (8 7х) е^х

2. Найти интервалы возрастания и убывания функции f(x)=х³ х² х +2

3. Построить график функции f(x)= х³ х² х +2

4. Найти наибольшее и наименьшее значения функции f(x)= х³ х² х +2 на отрезке [-1; ].

5. Найти ромб с наибольшей площадью, если известно, что сумма длин его диагоналей равна 10.

____________________________________________________________

Контрольная работа №4

В-1

1. Доказать, что функция F(х) = 3х + sinx – e^2х является первообразной функции f(x) = 3 + cosx – 2e^2x на всей числовой оси.

2. Найти первообразную F(x) функции f(x) = 2, график которой проходит через точку А (0; ).

3. Вычислить площадь фигуры, ограниченной линиями у = 3х – х², х = 1, х = 2 и осью Ох.

___________________________________________________________________

Контрольная работа №4

В-2

1. Доказать, что функция F(х) = е^3х + cosx + x является первообразной функции f(x) = 3e^3x — sinx + 1 на всей числовой оси.

2. Найти первообразную F(x) функции f(x) = -3, график которой проходит через точку А (0; ).

3. Вычислить площадь фигуры, ограниченной линиями у = cosx, х = 0, х = и осью Ох.

Контрольная работа №5

В-1

1. Найти

2. Сколькими способами из числа 15 учащихся класса можно выбрать культорга и казначея?

3. Сколько различных шестизначных чисел можно записать с помощью цифр

2, 3, 4, 5, 6, 7 таким образом, чтобы все цифры в числах были различны?

4. Записать разложение бинома (2 – х)⁵.

5. Сколько существует различных кодов, состоящих из двузначного числа, цифры которого выбираются из цифр 1, 2, 3, и следующего за ним трёхбуквенного слова, буквы которого выбираются из гласных букв русского алфавита.

Контрольная работа №5

В-2

1. Найти + .

2. Сколькими способами 7 детей ясельной группы можно рассадить на 7 стульях?

3. Сколькими способами можно составить набор из 5 карандашей, выбирая их из 8 имеющихся карандашей восьми различных цветов.

4. Записать разложение бинома (2х – 1)⁶.

5. Шифр сейфа образуется из двух чисел. Первое, двузначное число, образуется из цифр 1, 2, 3, 4 (цифры в числе могут повторяться). Второе, трёхзначное число, образуется из цифр 7 и 6. Сколько различных шифров можно использовать в таком сейфе?

Контрольная работа №6

В-1

1. Бросают два игральных кубика – большой и маленький. Какова вероятность того, что:

1. На обоих кубиках появится четыре очка;

2. На большом кубике появится 2 очка, а на маленьком – четное число очков.

2. В коробке лежат 3 черных, 2 белых и 4 красных шара. Случайным образом вынимается один шар. Какова вероятность того, что это или белый, или красный шар?

3. Вероятность попадания по мишени стрелков равна . Какова вероятность:

1. непопадания по мишени при одном выстреле?

2. попадания по мишени в каждом из двух последовательных выстрелов?

3. попадания при первом и промахе при втором выстреле?

4. В коробке лежат 4 белых и 3 черных шара. Наугад вынимают два шара. Какова вероятность того, что вынуты белый и черный шары?

5. В вазе стоят 5 гвоздик и 6 нарциссов. Какова вероятность того, что среди трёх случайным образом вынутых цветков окажется по крайней мере одна гвоздика?

________________________________________________________________

Контрольная работа№6

В-2

1. Бросают два игральных кубика – большой и маленький. Какова вероятность того, что:

1. На обоих кубиках появится пять очков;

2. На маленьком кубике появится кратное 3 число очков, а на большом –5 очков.

2. В коробке лежат 3 черных, 2 белых и 4 красных шара. Случайным образом вынимается один шар. Какова вероятность того, что это или черный, или красный шар?

3. Вероятность попадания по мишени стрелков равна . Какова вероятность:

1) непопадания по мишени при одном выстреле?

2) попадания по мишени в каждом из двух последовательных выстрелов?

3. попадания при первом и промахе при втором выстреле

4. В коробке лежат 4 белых и 3 черных шара. Наугад вынимают два шара. Какова вероятность того, что вынуты белый и черный шары?

5. В вазе стоят 5 гвоздик и 6 нарциссов. Какова вероятность того, что среди трёх случайным образом вынутых цветков окажется по крайней мере один нарцисс?

__________________________________________________________________

Контрольная работа №7

В-1

1. Найти множество точек координатной плоскости, удовлетворяющих уравнению:

1. х – у + 2 = 0; 2) (х + 4)² + (у – 1)² = 9.

2. Найти множество точек координатной плоскости, удовлетворяющих неравенству:

1. 2х + у – 1 0; 2) х² + (у – 2)² 4.

3. Найти множество точек координатной плоскости, удовлетворяющих системе неравенств:

_____________________________________________________________

Контрольная работа №7

В-2

1. Найти множество точек координатной плоскости, удовлетворяющих уравнению:

1. х + у — 3 = 0; 2) (х — 3)² + (у + 2)² = 16.

2. Найти множество точек координатной плоскости, удовлетворяющих неравенству:

1. х — 2у + 3 0; 2) (х + 3)² + у² 1.

3. Найти множество точек координатной плоскости, удовлетворяющих системе неравенств:

infourok.ru

ГДЗ к сборнику Ершовой, Голобородько Самостоятельные и контрольные работы по алгебре для 11 класса ОНЛАЙН

Решебник к сборнику задач «Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по алгебре и началам анализа для 11 класса». Рукопись. — 2014.
В решебнике представлены подробные решения задач из сборника «Ершова А. П., Голобородько В. В. Самостоятельные и контрольные работы по алгебре и началам анализа для 10-11 классов.— М.: Илекса, 2005,— 208 с.»
Решены задачи двух уровней сложности: А и Б .
Решебник поможет Вам проверить правильность решения задач и упражнений.
Страницы решебника представлены в виде слайдов. Кликните на нужный слайд, чтобы прочитать содержание страницы.

ВНИМАНИЕ! Варианты В1 и В2 а также домашние самостоятельные работы, содержащие задания повышенной трудности, НЕ РЕШЕНЫ! Учащиеся, претендующие на высокую оценку по математике должны уметь решать их САМОСТОЯТЕЛЬНО!

СОДЕРЖАНИЕ
Начала анализа
С-34. Обобщение понятия модуля. Уравнения и неравенства с модулем
С-35. Вычисление пределов числовых последовательностей и функций. Непрерывность функции
С-36. Определение производной. Простейшие правила вычисления производных
С-37. Производные тригонометрических и сложных функций
С-38. Геометрический и механический смысл производной
К-7. Производная
С-39. Исследование функции на монотонность и экстремумы
С-42. Наибольшее и наименьшее значения функции. Экстремальные задачи
К-8. Применение производной

С-44. Первообразная. Вычисление первообразных
С-45. Определенный интеграл. Вычисление площадей с помощью определенного интеграла
С-46. Применение первообразной и интеграла
К-9. Первообразная и интеграл

С-48. Производная и первообразная показательной функции
С-49. Производная и первообразная логарифмической функции
С-50. Степенная функция
К-10. Производная и первообразная показательной, логарифмической и степенной функции

gdz.math-helper.ru

Учебно-методический материал по алгебре (11 класс) на тему: Контрольные срезы по алгебре для 11 класса (сентябрь)

Контрольный срез по алгебре и началам анализа для 11 класса ( сентябрь ) 45 мин.

3 вариант

В1. Вычислите:       : ( 4,79 – 3,15 · 1,6 )

В2. Упростите:  

В3. Найдите решение уравнения, принадлежащее отрезку

,  х € [ 0; 2п ]

В4. Решите уравнение:  10cos2х + 3сos х = 1

В5. Найдите производную функции:

а) у =  + 3 sin х,  в)  у = х· cos х, г )  у = , д ) у = (3х + 5 )4

В6. Вычислите f’ (  ) , если f (х ) = 2 sinх + 3х2 – 2пх + 3

В7. Решите неравенство  f’ ( х  ) ≤ 0, если f (х ) = 12х – х3

С1.  Решите уравнение: 2sin3х – 3sin2 х – 2sin х = 0

C2. Решите уравнение:   cos х —  cos2х = sin3х

4 вариант

В1. Вычислите:  — 0,81 · ( — ) : ( 1,53 : 1,5 – 1,2 )

В2. Упростите:

В3. Найдите решение уравнения, принадлежащее промежутку

Sinх = — ,  х € (0 ; 2п )

В4. Решите уравнение:  2sin2х + sinх = 1

В5. Найдите производную функции:

а) у = — ,  б)  у = 2cosх — 4,  в)  у = х · sinх,  г) у = , д )  у = ( 2х – 3 )5

В6. Вычислите  f’ (   ), если f (х ) = 1,5 х2 —  + 5 – 4cosх

В7. Решите неравенство f’( х ) > 0, если f ( х ) = 6х2 – х3

С1. Решите уравнение:  2cos3х + 5cos2х + 2cosх = 0

С2. Решите уравнение: cos2х + cosх = sin3х

nsportal.ru

Учебно-методический материал по алгебре (11 класс) на тему: Контрольные работы по алгебре 11 класс

Контрольная работа №1

Первообразная и интеграл

Вариант 1

А1. Найдите общий вид первообразных для функции  :              

 .  

А2. Найдите первообразную для функции , график которой проходит через точку  

А3. Вычислите интеграл:              

 .  

В1. Найдите площадь фигуры, ограниченной линиями   .

В2. Найдите площадь фигуры, ограниченной линиями  . 

С1. Постройте графики функций .  Вычислите площадь фигуры, ограниченной этими линиями.

С2. Найдите площадь фигуры, ограниченной линиями  .

Нормы оценок:   «3»  — любые 4А,   «4»  — 4А + 1В, «5»  — 3А + 1В +1С  или   2А + 2В + 1С.  

Контрольная работа №1

Первообразная и интеграл

Вариант 2

А1. Найдите общий вид первообразных для функции  :              

 .  

А2. Найдите первообразную для функции , график которой проходит через точку  

А3. Вычислите интеграл:              

 .  

В1. Найдите площадь фигуры, ограниченной линиями   .

В2. Найдите площадь фигуры, ограниченной линиями  . 

С1. Постройте графики функций .  Вычислите площадь фигуры, ограниченной этими линиями.

С2. Найдите площадь фигуры, ограниченной линиями  .

Нормы оценок:   «3»  — любые 4А,   «4»  — 4А + 1В, «5»  — 3А + 1В +1С  или   2А + 2В + 1С.  

nsportal.ru

Учебно-методический материал по алгебре (10, 11 класс) на тему: Контрольные работы по алгебре для 10 класса

Контрольная работа № 5.                              А — 10

Вариант № 1.

1. Решите неравенство , где  f(x) = x3 – 12x + 9.

2. Найдите тангенс угла наклона касательной к графику функции

    f(x) = x3+27 в точке пересечения этого графика с осью абсцисс.

3. Найдите скорость точки в момент времени t = 1 с, если она движется  

    прямолинейно по закону x(t) = 5t – t2 – 1 (координата  x(t) измеряется в  

   сантиметрах).  

4. Составьте уравнение касательной к кривой f(x) =  в ее точке с      

    абсциссой х0 = 1.

Контрольная работа № 5.                              А — 10

Вариант № 2.

1. Решите неравенство , где  f(x) = x3 – 6x + 5.

2. Найдите тангенс угла наклона касательной к графику функции

    f(x) = x3 — 64 в точке пересечения этого графика с осью абсцисс.

3. Найдите скорость точки в момент времени t = 2 с, если она движется  

    прямолинейно по закону x(t) = 6t + t2 – 3 (координата  x(t) измеряется в  

   сантиметрах).  

4. Составьте уравнение касательной к кривой f(x) =  в ее точке с      

    абсциссой х0 = 1.

Контрольная работа № 5.                              А — 10

Вариант № 1.

1. Решите неравенство , где  f(x) = x3 – 12x + 9.

2. Найдите тангенс угла наклона касательной к графику функции

    f(x) = x3+27 в точке пересечения этого графика с осью абсцисс.

3. Найдите скорость точки в момент времени t = 1 с, если она движется  

    прямолинейно по закону x(t) = 5t – t2 – 1 (координата  x(t) измеряется в  

   сантиметрах).  

4. Составьте уравнение касательной к кривой f(x) =  в ее точке с      

    абсциссой х0 = 1.

Контрольная работа № 5.                              А — 10

Вариант № 2.

1. Решите неравенство , где  f(x) = x3 – 6x + 5.

2. Найдите тангенс угла наклона касательной к графику функции

    f(x) = x3 — 64 в точке пересечения этого графика с осью абсцисс.

3. Найдите скорость точки в момент времени t = 2 с, если она движется  

    прямолинейно по закону x(t) = 6t + t2 – 3 (координата  x(t) измеряется в  

   сантиметрах).  

4. Составьте уравнение касательной к кривой f(x) =  в ее точке с      

    абсциссой х0 = 1.

Контрольная работа № 5.                              А — 10

Вариант № 1.

1. Решите неравенство , где  f(x) = x3 – 12x + 9.

2. Найдите тангенс угла наклона касательной к графику функции

    f(x) = x3+27 в точке пересечения этого графика с осью абсцисс.

3. Найдите скорость точки в момент времени t = 1 с, если она движется  

    прямолинейно по закону x(t) = 5t – t2 – 1 (координата  x(t) измеряется в  

   сантиметрах).  

4. Составьте уравнение касательной к кривой f(x) =  в ее точке с      

    абсциссой х0 = 1.

Контрольная работа № 5.                              А — 10

Вариант № 2.

1. Решите неравенство , где  f(x) = x3 – 6x + 5.

2. Найдите тангенс угла наклона касательной к графику функции

    f(x) = x3 — 64 в точке пересечения этого графика с осью абсцисс.

3. Найдите скорость точки в момент времени t = 2 с, если она движется  

    прямолинейно по закону x(t) = 6t + t2 – 3 (координата  x(t) измеряется в  

   сантиметрах).  

4. Составьте уравнение касательной к кривой f(x) =  в ее точке с      

    абсциссой х0 = 1.

nsportal.ru

Контрольные работы по алгебре в 11 классе

infourok.ru