По геометрии что задали – Что по геометрии задали

Содержание

31 полезный факт для решения задач ЕГЭ по геометрии

В задаче 16 ЕГЭ по математике (геометрия) пункт (а) – доказательство. Вот 30 полезных фактов, которые надо знать и уметь доказывать. Любой из них может быть таким «пунктом (а)» в задаче ЕГЭ №16. Доказательство таких полезных фактов – первый этап в освоении геометрии.

Углы, треугольники, четырехугольники

1. Биссектрисы смежных углов перпендикулярны.
2. Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.
3. Медианы треугольника пересекаются в одной точке и делятся в ней в отношении 2:1, считая от вершины.
4. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
5. Площадь любого четырехугольника равна половине произведения диагоналей на синус угла между ними.
6. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.
7. Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали – полусумме оснований.
8.Замечательное свойство трапеции. Точка пересечения диагоналей трапеции, точка пересечения продолжений ее боковых сторон и середины оснований лежат на одной линии.

Окружности

9. Диаметр, перпендикулярный хорде, делит ее пополам
10. Произведения отрезков пересекающихся хорд окружности равны.
11. Серединный перпендикуляр к хорде проходит через центр окружности
12. Равные хорды удалены от центра окружности на равные расстояния
13. Дуги окружности, заключенные между параллельными хордами, равны.
14. Теорема о касательной и секущей. Если из одной точки к окружности проведены секущая и касательная, то произведение всей секущей на ее внешнюю часть равно квадрату отрезка касательной.
15. Угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.
16. Угол между пересекающимися хордами равен полусумме противоположных дуг, высекаемых хордами.
17. Угол между двумя секущими равен полуразности дуг, высекаемых секущими на окружности.
18. Радиус окружности, вписанной в прямоугольный треугольник с катетами а и b и гипотенузой с, равен
19. Прямая, проходящая через точки пересечения двух окружностей, делит пополам общую касательную к ним.
20. Если расстояние между центрами окружностей радиусами R и r равно а и а > R+r, то отрезки общих внешних и общих внутренних касательных, заключенные между точками касания, равны соответственно и
21. Если четырехугольник можно вписать в окружность, то сумма его противоположных углов равна 180 градусов.
22. Если в четырехугольник можно вписать окружность, то суммы длин его противоположных сторон равны.
23. Если окружность вписана в равнобедренную трапецию, то боковая сторона трапеции равна ее средней линии.
24. Геометрическое место точек М, из которых отрезок АВ виден под прямым углом (угол АМВ = 90 градусов), есть окружность с диаметром АВ без точек А и В.
25. Геометрическое место точек М, из которых отрезок АВ виден под данным углом, есть две дуги равных окружностей с общей хордой АВ, без точек А и В.
26. Если М – точка касания со стороной АС окружности, вписанной в треугольник АВС, то АМ = р – ВС, где р – полупериметр треугольника АВС.
27. Если окружность касается стороны ВС треугольника АВС и продолжений сторон АВ и АС, то расстояние от вершины А до точки касания окружности с прямой АВ равно полупериметру треугольника АВС.
28. Если окружность, вписанная в треугольник АВС, касается сторон АВ, ВС и АС соответственно в точках K, L, M, а угол ВАС равен φ, то угол KLM равен
29. Если прямые, проходящие через точку А, касаются окружности S в точках В и С, то центр вписанной окружности треугольника АВС лежит на окружности S.
30. Если АМ и СК – высоты треугольника АВС, то треугольник МВК подобен треугольнику АВС, причем коэффициент подобия равен |cos В|.
31. Если площадь треугольника равна S, то площадь треугольника, составленного из его медиан, равна

Доказывайте полезные факты. Запоминайте картинки и схемы решения. Чем больше у вас таких ассоциативных связей – тем проще решаются задачи по геометрии.

При составлении списка полезных фактов использованы учебные пособия Р. К. Гордина.

Звоните нам:
8 (800) 775-06-82 (бесплатный звонок по России)
+7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

ege-study.ru

Техника поиска решений репетитором задач по геометрии

Если Вы регулярно просматриваете решения задач по математике в тех или иных источниках, то, безусловно, обращали внимание на их декларационный характер. То есть последовательность шагов просто сообщается и не разъясняется, почему она именно такая и, самое главное, как до нее догадаться обычному школьнику. При индивидуальном подходе к обучению ситуация, как правило, не улучшается. Приглашенный репетитор по математике попросту повторяет Вашему ребенку то, что написано в книжках. При таком формате работы ценность репетитора неуклонно снижается, ибо на ОГЭ/ЕГЭ обязательно подвернется какая-нибудь незнакомая задача. Кроме того при желании можно и самостоятельно прочесть кучу решений, добиваясь в итоге (с той или иной скоростью) определенного уровня знаний. Конечно, большинство школьников и этого сделать не могут. Им нужен руководитель и проверяющий в одном лице, а также привычные «инфраструктурные условия», в которых привычно вести учебную деятельность: четкое расписание и план освоения предмета, ведение тетрадей, вопросы и ответы и т.д. Но если уж говорить о репетиторе по математике как о максимальном средстве борьбы за знания и развитие, то стоит остановиться на методах обучения поиску решений.

Такое обучение под силу только профессионалу с большой буквы. Мыслительную механику чрезвычайно сложно описывать словами. Одна размытая ориентировка и ученик запутается. Глубокий анализ порой неоднозначно воспринимается и упирается в законы мироздания, но все же попытаемся разобраться в принципах на примере нескольких геометрических задач. Предположим, что ученик знает теорию и не испытывает проблем с реализацией простейших логических операций.

Пример, на котором репетитору легко показать технику поиска

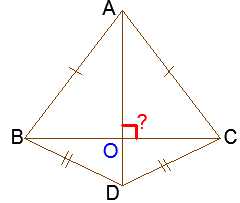
Два равнобедренных треугольника ABC и DBC склеены общим основанием BC. Докажите перпендикулярность прямых BC и AD.

Прежде всего, репетитору важно научить ребенка правильно «брать старт» в решении, а для этого требуется понять, какие факторы влияют на отрезок AD и как вообще можно придти к перпендикулярности. Допустим, что ответ получен: надо придти к углу 90 градусов. Как? Перебираем в голове все известные в 7 классе приемы, теоремы и определения, связанные прямыми углами. Их не так много: 1) определение высоты 2) непосредственный поиск угла через вычисления или через уравнение. Напрягаем мозги. Вычисления нереальны – нет никаких значений в градусах. Для уравнений желательно иметь равные углы, которые можно было бы обозначить одной буквой «икс», либо иметь несколько связующих условий. А у нас только есть вертикальные и смежные углы. Значит надо либо доказывать, что смежные углы AОC и DОC равны, либо брать теорему о высоте, а ей нужен равнобедренный треугольник с медианой, либо биссектрисой. Это в свою очередь потребует объяснить то, что равны отрезки, или равны углы. То есть в любой случае надо получить какие-нибудь равные элементы рисунка. Откуда их взять? Нужно помнить о том, что в 7 классе 80% задач решается через равные треугольники. Вот и возникает с подачи репетитора по математике главный вопрос для старта: «Какие треугольники рассмотреть?»

На старт, внимание, марш

Как правило, ученики видят по рисунку равенство ABО и ACО и зависают над ними. В чем принципиальная ошибка? В разрезании верхнего треугольника на интересующие нас части участвует линия AD, положение которой зависит от точки D. Если в рассмотренных треугольниках не будет вершины D – мы получим произвольное разрезание на части, которое не гарантирует нам их равенство, поэтому доказательство зайдет в тупик. Аналогичная история и с нижней парой треугольников. Здесь уже тупиком будет выброс точки A. Получается, что в паре искомых треугольников должны участвовать обе точки A и D, а значит AD — сторона хотя бы одного из треугольников.
У нас имеется только два треугольника со стороной AD, подозрительно похожих на равные: ABD и ACD. Вот мы и вышли на старт. Любой хорошист укажет репетитору по математике на третий признак в обосновании их равенства.
Далее собираем урожай с нашего поиска – любые соответствующие элементы в треугольниках равны. Какие взять? Помним о том, что нам нужны либо отрезки, либо углы. И то, и другое есть. Например, BO=CO или угол BAD равен углу CAD. В первом случае мы имеем медиану AO, во втором – биссектрису AO. А тогда AO – высота.

«Ясновидение» по математике

Как Вы видите, никакого ясновидения со стороны репетитора. Все действия подкрепляются целесообразностью шагов и логически продиктованы ситуацией. Умению «вскрывать» математику можно и нужно учить, с раннего возраста на систематических занятиях, начиная с подобных простых примеров. В последние годы я резко снизил на своих занятиях процент деклараций решений. Все чаще открываю ученику сам процесс размышлений, озвучивая свои мысли. Говорю: «Если был я не был репетитором и учился математике на твоем месте, то размышлял бы следующим образом …». И начинаю подробно описывать все этапы поиска, вместе с возможными тупиковыми ходами и даже ошибками, то есть ровно так, я должен размышлять обычный человек. Постепенно ученик проникается идеями и каким-то волшебным образом начинает чувствовать математику интуитивно. В каждом человеке живет некое разумное начало, надо только до него достучаться и заставить работать во благо получения знаний. Что я и делаю на своих уроках в Строгино.

С уважением, Колпаков А.Н. Репетитор. Москва.

Метки:
Методики для репетиторов,
Примеры объяснений,
Репетиторам по математике

ankolpakov.ru

Геометрия вокруг нас: основные разделы геометрии

Многие предметы вокруг нас имеют форму, похожую на геометрические фигуры. Альбомный лист имеет форму прямоугольника. Если поставить круглый стакан на лист бумаги и обвести его карандашом, получится линия, изображающая окружность. Кольцо, обруч напоминают своей формой окружность, а арена цирка, дно стакана или тарелка имеют форму круга. Апельсин, футбольный мяч, арбуз похожи на шар. Шестигранный карандаш, египетские пирамиды – это тоже геометрические фигуры.

Геометрия – это наука о свойствах геометрических фигур: треугольника квадрата, круга, пирамиды сферы и др.

Слово «геометрия» греческое, в переводе на русский язык означает «землемерие». Принято считать, что геометрия зародилась в Древней Греции. Но греки переняли у египтян основы землемерия и превратили его в научную дисциплину путём установления общих закономерностей. Главным трудом по геометрии являются «Начала» древнегреческого учёного Евклида, составленные около 300 лет до н.э. Этот труд длительное время считался образцовым. Эвклидова геометрия изучает простейшие геометрические формы: точки, прямые, отрезки, многоугольники, шары, пирамиды и др. Именно этот раздел геометрии изучается в школе.

В 1877 году немецкий математик Феликс Клейн в своей «Эрлангерской программе» предложил классификацию различных разделов геометрии, которая используется и в наши дни: евклидова геометрия, проективная, аффинная, начертательная, многомерная, риманова, неевклидова геометрии, геометрия многообразий, топология.

Евклидова геометрия состоит из двух частей: планиметрии и стереометрии.

Планиметрия – это раздел геометрии, в котором изучаются геометрические фигуры на плоскости.

Стереометрия – это раздел геометрии, в котором изучаются фигуры в пространстве.

Проективная геометрия изучает свойства фигур, которые сохраняются при их проецировании (замене на подобные фигуры другого размера).

Аффинная геометрия исследует постоянные свойства фигур при различных изменениях плоскости и пространства.

Инженерная дисциплина – начертательная геометрия использует для изображения предмета несколько проекций, что позволяет делать трёхмерное изображение объекта.

Многомерная геометрия исследует альтернативное существование четвертого измерения.

Отдельно выделяют инструментальные подразделы: аналитическую геометрию, которая для описания геометрических фигур использует алгебраические методы и дифференциальную геометрию, которая изучает графики различных функций.

blog.tutoronline.ru

Как научиться решать задачи по геометрии? — КиберПедия

Решаем задачи по геометрии

Решение задач

Любой студент или школьник должен запомнить одну простую истину – можно решить любую задачу, какой бы трудной она не казалась на первый взгляд. Ведь задачи составляют для закрепления теоретических знаний и отработки определенных практических навыков, следовательно, для того, чтобы их решали, а не в целях третирования учащихся.

Разумеется, есть такие сверхсложные варианты задач, которые пытаются разрешить столетиями. Однако их количество не так уж и велико, да и награда за найденное решение будет больше «пятерки» за контрольную работу или экзамен. Встретить нечто подобное в школьной программе невозможно.

Следовательно, для того, что бы научиться решать задачи по геометрии необходимо иметь желание, усидчивость и тренированные мозги и воображение. Других путей освоить эту интересную область математики не существует, мы не берем в расчет решебники со 2 по 11 класс и всевозможные ГДЗ, очень сильно облегчающие жизнь студенту. Однако, получив все необходимые навыки и тщательно проштудировав теорию, можно приблизиться к пониманию того, что существует определенная методика решения задач по геометрии, способная упростить процесс решения любой задачи. Для этого необходимо всегда выполнять следующие действия:

1. Изучив условие задачи, сразу же займитесь составление чертежа. Без толковой схемы затруднительно решить даже простую задачу, а сложную – практически невозможно. При этом не жадничайте, экономить место в тетради вы будете в другом случае. Визуализация условия задачи по геометрии требует максимально возможного объема на тетрадном листе. Чем крупнее чертеж, тем нагляднее и доступнее будут решение задачи.

2. Построив чертеж или схему, нанесите на нее все известные данные – прямые и косвенные (которые можно получить путем промежуточных вычислений). Поверьте, решение задачи может «всплыть» сразу же после того, как вы сделаете эту нехитрую работу.

3. Не полагайтесь во всем на интуицию и пространственное воображение, без знания теоретической базы серьезных результатов вам не достигнуть. При этом можно не забираться в дебри формулировок, а запомнить и осмыслить несколько десятков распространенных формул и правил.

4. Помните о небольших хитростях: о задачах, которые решаются методом «первого и второго треугольника», об использовании центра окружности в соответствующих случаях (всегда соединяйте «интересные» точки вписанных и описанных фигур с центром окружности), о правилах суммы углов треугольника и прочих несложных способах вычисления промежуточных величин, которые помогут в поиске искомого значения.

5. Всегда записывайте «полет» вашей мысли. После трех-четырех связок вы можете потерять нить рассуждений и потратить значительное время на попытки вспомнить уже принятое решение. После решения задачи обязательно проверьте себя. Это поможет избежать досадных ошибок, которые могли ускользнуть от вашего внимания, увлеченного удачными поисками варианта решения задачи.

В заключение несколько слов о неудачах и патовых ситуациях, когда все потуги учащегося не приводят к положительным результатам. Для выхода из тупика используйте несколько простых действий:

Во-первых, переверните схему задачи. Посмотрите на чертеж буквально «под другим углом». Вероятно, вы что-то упустили или не заметили, и решение может прийти само собой.

Во-вторых, отложите «затруднительную» задачу в сторону, отвлекитесь на другое дело. Через десять минут мозг «перезагрузится», «накатанная» схема, которая привела вас в тупик, забудется и можно начинать искать новый путь к решению задачи.

В-третьих, примените тактическую хитрость. Вспомните, что вы проходите по программе на данный момент. На контрольной работе вам, как правило, будут задавать задачи с четкой привязкой к изученной теории. Постарайтесь заново оценить условие с точки зрения именно «последних» теоретических материалов. Например, если вы занимались изучением хорды или биссектрисы, постарайтесь «по максимуму» заполнить чертеж именно этими элементами.

Решаем задачи по геометрии

Решение задач

Как научиться решать задачи по геометрии?

Дорогие ребята, Вы начали изучать геометрию. Это новая для вас дисциплина, и вы поначалу можете испытывать трудности в её освоении. Не пугайтесь: пройдет некоторое время, и вы научитесь с легкостью решать любые геометрические задачи. Для приобретения необходимого навыка нужно лишь приложить немного усилий. Итак, как решать задачи по геометрии?

Вам понадобится: учебник, тетрадь, ручка, карандаш, линейка, транспортир, циркуль, ластик.

Инструкция:

Внимательно прочитайте условие задачи.
Сделайте чертеж.
Отметьте на чертеже то, что вам дано: длины сторон, величины углов. Если в условии задачи сказано, что какие-то отрезки равны, поставьте на них одинаковые штрихи. Равные по величине углы отмечайте одинаковыми дужками: одинарными, двойными, волнистыми. Углы разных величин выделяйтеразными

дужками.

Исследуйте фигуры, представленные в задаче. Вспомните их определения и свойства.
Определите тему, к которой относится ваша задача. Освежите в голове теоретический материал по этой теме, повторите основные теоремы.
Рассмотрите примеры решения задач по этой теме. В задачах, приводимых в учебнике в качестве примеров, часто рассматриваются принципиальные вопросы, которые вы должны знать.
Если вы чувствуете себя в теме достаточно уверенно, приступайте к решению задачи. Начните с того, что требуется найти или доказать. Подумайте, каким путем это можно сделать. То есть, решайте задачу «с конца».
Если вы не видите путей решения задачи, попробуйте найти хоть что-нибудь, используя имеющиеся данные. Возможно, так к вам придет идея, как решать задачу.

Полезные советы: не увлекайтесь «устными» доказательствами. Записывайте решение задачи как можно более подробно, если не оговорено иное. Некоторые вещи могут казаться вам очевидными, но всё равно прописывайте их. Так у вас будет отрабатываться навык, вы лучше запомните идею.

Рекомендации от учителя математики Е.В.Жалыбиной

cyberpedia.su

Как решать задачи по геометрии

Геометрия часто вызывает проблемы, потому что непонятно, с какой стороны взяться за задачу. И вроде все теоремы знаешь, но не знаешь, какую из них стоит применить. Поэтому мы составили небольшую
шпаргалку-алгоритм решения задач. Действия, в ней описанные, не обязательно делать все, ты делаешь ровно столько, сколько нужно, чтобы найти решение. А каждый следующий пункт шпаргалки смотришь,
только если предыдущий не сработал.

Итак, когда ты прочитал задачу и сделал чертеж и не понимаешь, как найти ответ, ты:

1. Определяешь
основную фигуру задачи (трапеция, треугольник, параллелограмм).

2. Выясняешь,
является ли она «замечательной», то есть частным случаем какой-нибудь фигуры (прямоугольный или равнобедренный треугольник, равнобедренная трапеция и др)

3. Смотришь вопрос.
Если нужно найти угол или сторону, то обозначаешь их через Х. Если нужно найти площадь или периметр или еще что-то, что рассчитывается по формуле, пишешь формулу и обозначаешь на чертеже нужные
тебе для расчета элементы.

4. Вспоминаешь все
теоремы и свойства, связанные с твоей фигурой. Не нужно бросаться перебирать их по порядку, но стоит хотя бы на секунду задуматься о них, может быть нужная теорема всплывет в памяти. Все время
помни о том, что тебе нужно найти.

5. Еще раз читаешь
условие, медленно и детально. Останавливаешься в каждом месте, где дается новая информация, и вспоминаешь все теоремы и свойства с этой новой информацией связанные (например, на фразе «В
треугольнике ABC проведена биссектриса AD…» нужно вспомнить всё, что известно про биссектрису, и постараться
применить все теоремы о биссектрисе к решению задачи)

6. Находишь все
подряд углы и стороны

7. Пытаешься найти
подобные треугольники и если находишь, то применяешь их свойства (равные углы и пропорциональные стороны)

8. Пытаешься найти
равные треугольники и если находишь, то применяешь их свойства (равные углы и одинаковые стороны).

Не забывай, что ты можешь применять не только теоремы для своего частного случая фигуры, но и более общие. Если у тебя есть прямоугольный треугольник, помни, что он всё же треугольник и к нему,
как и к любому другому треугольнику, применяются все общие теоремы и свойства треугольников.

Но самый главный принцип при решении геометрических задач звучит так: «рисуй чертеж». После первого прочтения – рисуешь чертеж, чтобы лучше понять и представить задачу. Пока ищешь решение, все
записи делаешь только на чертеже, кроме сложных подсчетов, все обозначения делаешь на чертеже. Если какой-то метод решения не дал результата, перерисовываешь чертеж и начинаешь заново. Если
чертеж не похож на условия задачи (отрезки, которые должны быть равны по условию, явно не равны по чертежу и т.д.), то перерисовываешь чертеж. Если дополнительное построение не дало результат,
перерисовываешь чертеж. В общем, чертеж, чертеж, и еще раз чертеж. И не вздумай рисовать его по линейке, такое количество нарисованных по линейке чертежей отнимет столько времени и нервов, что ни
того ни другого уже не хватит на решение задачи. Пока ты в черновике не найдешь решение, всё черти от руки.

И еще одна фишка.

Обычно в геометрии нет четких групп задач, сложно классифицировать задачу и дать рекомендации по поводу её решения. Однако один тип задач мы всё же можем выделить. Если в задаче даны углы, а
найти надо стороны (или наоборот), то нужно рассматривать только те темы, которые позволяют связать углы и стороны, а их по сути всего 4:

1. тригонометрия
(нахождение угла через синус, косинус, тангенс или котангенс)

2. площади (т.к. в
формуле площади есть синус)

3. Теорема синусов

4. Теорема косинусов

Определить, когда какую из них применять, обычно легко. Тригонометрические функции применяются, если есть прямоугольный треугольник или высота. Площади применяются обычно только если они указаны
в условии. Теорема синусов — если есть описанная окружность, косинусов – если известны все стороны треугольника. Конечно это не полный список, но он покрывает примерно 90% задач.

1day1ex.jimdo.com

Как решать задачи по геометрии: практические советы и рекомендации

Как решать задачи по геометрии? Многие учащиеся задаются этим вопросом на протяжении многих лет. Иногда даже сам предмет вызывает страх и отвращение из-за непонимания отдельных тем. Потом бывает очень сложно преодолеть неприязнь к геометрии и снова с заинтересованностью посещать уроки.

В чем причина

Во многом все зависит от того, как преподаватель объясняет свой предмет. Если учитель сможет заинтересовать учеников, дальше дело пойдет по накатанной, и каждый урок будет захватывающим. Дети даже будут оставаться на переменке, чтобы успеть решить как можно больше задач.

Если вам плохо объясняли этот предмет или есть еще какие-то причины, по которым у вас совершенно не получается вникнуть в тему, эта статья поможет разобраться.

Как научиться решать задачи по геометрии?

Для начала нужно понять, что за один день вы вряд ли далеко продвинетесь в своих знаниях, так что настраивайтесь на длительный процесс обучения.

Также нужно определиться с целью. Если вам нужно просто решить задачу по геометрии, чтобы не получить плохую оценку за контрольную работу, достаточно лишь выучить определенную тему и потренироваться в практических аспектах.

Что делать?

Возьмите учебник и пролистайте последние несколько параграфов, которые вы изучили. Постарайтесь вникнуть в информацию, поймите, что от этого зависит то, как будут оценены ваши знания. Теперь можете взять листочек и изучить несколько задач, обязательно смотрите в текст учебника и пытайтесь понять алгоритм решения.

Если что-то не получается, обратитесь к решебнику, который выпущен специально под ваш учебник. Только не списывайте абсолютно все, старайтесь понять, как решать задачи по геометрии.

Вспомните, о чем говорил преподаватель на занятиях, возможно, какая-то информация окажется полезной.

Не стоит пренебрегать и человеческим фактором. Хорошо знающие предмет школьники или студенты не откажут вам в помощи. Некоторые из них могут объяснить гораздо доходчивее преподавателей.

А тем, кто решил не просто разобраться в отдельных темах, а научиться решать задачи и как орешки их щелкать, нужно основательно потрудиться.

Во-первых, главное – это мотивировать себя на дальнейшие занятия. Бывает так, что вопрос о том, как научиться решать задачи по геометрии, встает лишь один раз, а потом начинается просто списывание примеров из интернета. Так делать крайне нежелательно.

Развивайте усидчивость. Посмотреть в решебник намного проще, разумеется, но подумайте, какое наслаждение вы испытаете, когда самостоятельно решите сложную задачку. Поэтому лучше лишние полчаса посидеть за учебником, чем стараться списать побыстрее чье-то решение.

Может быть, геометрия вам понадобится для будущей профессии. Тогда тем более не стоит откладывать дело в долгий ящик, нужно приниматься за задачи прямо сейчас.

Во-вторых, практика, и только она, поможет вам стать на шаг ближе к своей цели!

Заведите привычку узнавать что-то новое каждый день. Просто старайтесь с утра решать одну задачу, а потом проверяйте по ключам ее правильность. Позже заметите, что с каждым днем процесс идет все быстрее и качественнее.

Самое главное здесь – не сдаваться и не обращать внимания на мелкие трудности. Если вы включите в распорядок дня этот совет, то вопрос о том, как решать задачи по геометрии, отпадет сам собой.

В-третьих, обращайтесь за помощью к знакомым.

Не бойтесь в школе лишний раз поднять руку и выйти к доске, чтобы решить сложный пример, который никто не отважился постичь. Даже если что-то пойдет не так, и вам не удастся сделать задание, ничего страшного в этом нет. Преподаватель объяснит решение примера и даже похвалит вас за смелость. Также это неплохой способ показать свои знания одноклассникам.

Ребята могут помочь с выполнением заданий, когда узнают, что вы настроены серьезно в изучении предмета.

Не вешаем нос!

Не отчаивайтесь, если никто не откликнулся на вашу просьбу. Всегда можно обратиться за помощью к репетитору, который точно объяснит, как решить задачу по геометрии. Даже при ограничении в денежных средствах хорошим выходом станут занятия по скайпу, которые ничем не хуже уроков, проходящих при личной встрече.

Вот и все советы. Будем надеяться, что вы все-таки поняли, как решать задачи по геометрии. В любом случае старайтесь применять эти методы на практике, и вы осуществите задуманное!

fb.ru

Как решать задачи по геометрии 7 класса 🚩 как научиться решать геометрию 🚩 Образование 🚩 Другое

5 июня 2011

Автор КакПросто!

Вы начали изучать геометрию. Это новая для вас дисциплина, и вы поначалу можете испытывать трудности в её освоении. Не пугайтесь: пройдет некоторое время, и вы научитесь с легкостью решать любые геометрические задачи. Для приобретения необходимого навыка нужно лишь приложить немного усилий. Итак, как решать задачи по геометрии?

Статьи по теме:

Вам понадобится

Учебник, тетрадь, ручка, карандаш, линейка, транспортир, циркуль, ластик

Инструкция

Внимательно прочитайте условие задачи.

Сделайте чертеж. Отметьте на чертеже то, что вам дано: длины сторон, величины углов. Если в условии задачи сказано, что какие-то отрезки равны, поставьте на них одинаковые штрихи. Равные по величине углы отмечайте одинаковыми дужками: одинарными, двойными, волнистыми. Углы разных величин выделяйте разными дужками.

Исследуйте фигуры, представленные в задаче. Вспомните их определения и свойства.

Определите тему, к которой относится ваша задача. Освежите в голове теоретический материал по этой теме, повторите основные теоремы. Рассмотрите примеры решения задач по этой теме. В задачах, приводимых в учебнике в качестве примеров, часто рассматриваются принципиальные вопросы, которые вы должны знать.

Если вы чувствуете себя в теме достаточно уверенно, приступайте к решению задачи. Начните с того, что требуется найти или доказать. Подумайте, каким путем это можно сделать. То есть, решайте задачу «с конца».

Если вы не видите путей решения задачи, попробуйте найти хоть что-нибудь, используя имеющиеся данные. Возможно, так к вам придет идея, как решать задачу.

Полезный совет

Не увлекайтесь «устными» доказательствами. Записывайте решение задачи как можно более подробно, если не оговорено иное. Некоторые вещи могут казаться вам очевидными, но всё равно прописывайте их. Так у вас будет отрабатываться навык, вы лучше запомните идею.

Источники:

задачи по геометрии 7 класс

Иногда задача по геометрии кажется настолько сложной, что непонятно, с какой стороны к ней подступиться. Начните с четкого чертежа, и часть задачи станет яснее.

Вам понадобится

Карандаш, линейка, циркуль, знание теорем и правил

Инструкция

Успех решения задачи по геометрии на 60% зависит от грамотно изображенного чертежа. Внимательно прочитайте условие, убедитесь, что вы поняли его. Теперь начинайте рисовать чертеж. Не мельчите, на чертеже не должны сливаться точки, буквы, линии, фигуры. Никогда не рисуйте от руки, обязательно пользуйтесь чертежными принадлежностями. Нанесите на чертеж все данные, о которых говорится в условии. Особо выделите то, что необходимо найти. Если найти нужно не отрезок, а абстрактную величину (к примеру, диаметр), то выпишите искомое под условием.

Есть есть необходимость, разбейте задачу на несколько этапов, то есть ряд маленьких подзадач. Решение каждой такой подзадачи будет на шаг приближать вас к решению всей задачи. Получив ответ, проведите проверку – верен ли ваш ответ? Если вы решаете задачу из школьного учебника, то правильный ответ, как правило, указан в конце учебника. Сверьтесь с ним, но если способ решения вам не известен, не пытайтесь «подгонять» задачу под указанный ответ.

Задачи по геометрии — это особая разновидность упражнений, требующая пространственного мышления. Если у вас не получается решить геометрическую задачу, попробуйте следовать нижеприведенным правилам.

Инструкция

Прочитайте очень внимательно условие задачи, если что-то не запомнили или не поняли, перечитайте еще раз.

Начертите чертеж к задаче на черновике. Проставьте на него все известные размеры, это необходимо сделать аккуратно, чтобы вы сами не запутались в этих данных. Постарайтесь определить, к какому виду геометрических задач она относится, так, например: вычислительные, когда нужно узнать какую-нибудь величину, задачи на доказательство, требующие логической цепочки рассуждений, задачи на построение при помощи циркуля и линейки. Еще бывают задачи смешанного типа. Когда вы выяснили тип задачи, постарайтесь рассуждать логически.

Примените необходимую теорему для решения данной задачи, если же есть сомнения или вообще отсутствуют варианты, то постарайтесь вспомнить теорию, которую вы проходили по соответствующей теме.

Оформите решение задачи также на черновике. Попытайтесь применить известные способы проверки верности вашего решения.

Оформите решение задачи аккуратно в тетради, без помарок и зачеркиваний, а главное — напишите ответ.Возможно, на решение первых геометрических задач уйдет много сил и времени. Однако, как только вы освоите этот процесс — начнете щелкать задачи по геометрии, как орешки, получая от этого удовольствие!

По геометрии что задали – Что по геометрии задали — Зубрить.com

31 полезный факт для решения задач ЕГЭ по геометрии

Техника поиска решений репетитором задач по геометрии