Лабораторная работа №119
Содержание
1. Цель работы……………………………………………………………4
2. Теоретическая часть…………………………………………………..4
3. Экспериментальная установка……………………………………….9
4. Порядок выполнения работы………………………………………..10
5. Требования к отчету………………………………………………….11
6. Контрольные вопросы……………………………………………….12
Список литературы……………………………………………………..12
Лабораторная работа № 119
Определение отношения теплоемкостей газа
при постоянном давлении и постоянном объеме
резонансным методом
1. Цель работы
1.1. Изучение процесса распространения звуковых волн в газе.
1.2. Измерение скорости звука в воздухе при различных температурах.
1.3. Определение отношения теплоемкостей воздуха при постоянном давлении и постоянном объеме.
2. Теоретическая часть
2.1. Теплоемкость и коэффициент Пуассона газа
Для характеристики тепловых свойств вещества наряду с другими величинами используют молярную и удельную теплоемкости. Удельная теплоемкость вещества представляет собой количество теплоты, которое необходимо передать единице массы вещества, чтобы нагреть его на один градус Кельвина (или Цельсия), а молярная – количество теплоты, необходимое для нагревания на один градус одного моля вещества. Теплоемкость газа зависит от природы его молекул и от того, как происходит его нагревание. Действительно, по первому закону термодинамики количество теплоты Q, полученное телом, равно сумме изменения его внутренней энергии ΔU и совершенной им работы А:
Q = ΔU + А. (2.1)
Внутренняя энергия идеального газа – это энергия теплового движения его молекул и атомов в молекулах. В общем случае она складывается из кинетических энергий поступательного и вращательного движений молекул и энергии колебательного движения атомов в них. По закону равнораспределения энергии теплового движения по степеням свободы молекулы на каждую ее поступательную и вращательную степень свободы в среднем приходится энергия, равная kT, где k – постоянная Больцмана, T – абсолютная температура газа, а на каждую колебательную степень свободы – энергия, равная в среднем kT. Таким образом, средняя энергия теплового движения одной молекулы идеального числа равна kT, где i – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы, а внутренняя энергия ν молей газа – ν RT, где R – газовая постоянная. Ее изменение при повышении температуры газа на ΔT градусов будет составлять
ΔU = i/2 ν RΔT . (2.2)
При изохорном нагревании газ работы не совершает и его молярная теплоемкость при постоянном объеме CV в соответствии с ее определением оказывается равной
. (2.3)
Во всех остальных процессах нагревание газа сопровождается работой, которая может быть и положительной (при расширении), и отрицательной (при сжатии), при этом разной по величине в зависимости от характера изменения объема газа. Поэтому при увеличении температуры газ может как получать теплоту, так и отдавать ее, а если процесс адиабатный, то не происходит ни того, ни другого. Следовательно, и теплоемкость данного газа в зависимости от вида процесса может принимать различные значения.
При изобарном нагревании газа на ΔT градусов им совершается работа
А = ν RΔT . (2.4)
Значит, при постоянном давлении молярная теплоемкость газа равна
. (2.5)
Отношение теплоемкостей газа при постоянном давлении к теплоемкости при постоянном объеме называют коэффициентом Пуассона или показателем адиабаты газа. Из (2.3) и (2.5) следует, что его значение γ определяется только числом степеней свободы молекул газа:
. (2.6)
2.2. Взаимосвязь коэффициента Пуассона газа со скоростью распространения в нем звуковых волн
Колеблющееся тело, помещенное в упругую среду, будет воздействовать на прилегающие к нему частицы среды и приводить их в колебательное движение. Эти частицы в свою очередь будут воздействовать на соседние частицы и тоже вовлекать их в колебательное движение и т. д. Таким образом колеблющееся тело в упругой среде является источником колебаний, распространяющихся в этой среде. Этот процесс распространения колебаний в упругой среде называется упругой волной. Распространение колебаний происходит со скоростью, определяемой свойствами среды и характером колебаний.
В упругой волне колебания вовлекаемых в движение частиц среды отстают по фазе от колебаний частиц, пришедших в движение ранее, поэтому смещения соседних колеблющихся частиц в один и тот же момент времени являются различными. Значит, отдельные участки среды непрерывно периодически деформируются, т.е. в среде происходит распространение деформации с некоторой скоростью υ. Для определения ее величины рассмотрим простейший случай передачи деформации через упругий твердый стержень.
Допустим, что действуя силой F в течении короткого промежутка времени Δt на основание стержня площадью S, мы сообщим ему некоторый импульс. За указанное время точки торца стержня сместятся на некоторое расстояние Δl (рис. 2.1). Возникшая деформация будет перемещаться от одной части стержня к другой и по нему побежит волна сжатия. Если обозначить длину участка стержня, который охватит сжатие к концу промежутка Δt через l, то
u = (2.7)
представляет собой скорость распространения упругой волны сжатия вдоль стержня. По истечении времени Δt все частицы указанного участка, вначале покоившиеся, приобретут скорость
u = (2.8)
и изменение его импульса составит ρSlu, где ρ – плотность материала стержня. По законам динамики оно равно импульсу внешней силы, действовавшей на стержень:
ρSlu = F Δt. (2.9)
Эта сила по величине равна силе упругости, которая по закону Гука пропорциональна относительной деформации
, (2.10)
где Е – модуль упругости.
Подставляя (2.10) в (2.9), получим:
ρlu. (2.11)
Принимая во внимание (2.7) и (2.8), из (2.11) находим
υ =. (2.12)
В жидкостях и газах деформации сдвига неупруги. Если в них сдвинуть один слой относительно другого, то в противоположность твердым телам сдвинутые слои не будут стремиться вернуться в исходное состояние. Поэтому в жидкостях и газах могут распространяться только продольные упругие волны сжатия и расширения, скорость которых можно вычислить, пользуясь формулой (2.12).
В продольной волне, распространяющейся в газе при одностороннем его сжатии относительное ускорение равно относительному уменьшению объема газа . Изменение объема вызывается увеличением давления на ΔP в данном месте по сравнению с давлением P газа в невозмущенном состоянии. Это увеличение давления играет роль напряжения в твердых телах, поэтому
ΔP =. (2.13)
Для сколь угодно малых изменений давления и объема (2.13) представляется в виде
, (2.14)
где знак минус обусловлен тем, что увеличению давления соответствует уменьшение объема и наоборот.
Пусть в газе распространяется звуковая волна, в которой колебания сжатия и разряжения, происходящие с частотой в пределах 16 Гц – 20 кГц, способны вызвать ощущение звука. Эти колебания происходят достаточно быстро, настолько, что теплообмен между слоями газа с разной температурой не успевает произойти. В этом случае процесс изменения состояния газа в слоях можно считать адиабатным и применить к нему закон Пуассона:. Дифференцируя это уравнение получим:
(2.15)
откуда
. (2.16)
Выразим Р из уравнения Менделеева – Клапейрона:
, (2.17)
где μ – молярная масса газа. Разрешая систему уравнений (2.17), (2.16), (2.14) и (2.12), получим формулу Лапласа для расчета скорости звука в газе:
, (2.18)
из которой
. (2.19)
Таким образом, для определения отношения теплоемкостей газа при постоянном давлении и объеме достаточно измерить его температуру и скорость распространения в нем звуковой волны. Последнее можно сделать с помощью резонансного метода, в котором используется следующее. Звуковая волна, распространяясь в газе, заключенном в закрытой с обоих концов прямой трубе, испытывает многократные отражения от торцевых стенок, в результате чего происходит наложение волн. Если расстояние L между торцами трубы будет равно целому числу n половинок длины волны λ, т.е. если
, (2.20)
то волна, отраженная от одного торца трубы, возвратившись к другому и отражаясь уже от этого торца, будет совпадать по фазе с исходящей от него волной. Такие волны усиливают друг друга. Амплитуда колебаний в этом случае резко возрастает – наступает резонанс.
Выразив длину волны λ через ее скорость υ и частоту колебаний ν (λ = υ ν), условие резонанса (2.20) можно записать в виде:
2 L ν0 = n υ , (2.21)
где ν0 – резонансная частота.
3. Экспериментальная установка
Для определения отношения теплоемкостей воздуха резонансным методом используется экспериментальная установка ФПТ 1 – 7, общий вид которой показан на рис. 3.1.
Рабочий элемент установки представляет собой стеклянную трубу длиной L, на торцах которой размещены телефон и микрофон. Температуру воздуха в трубе можно изменять с помощью нагревательной спирали, навитой на трубу. Мощность нагревателя устанавливается регулятором «Нагрев», находящемся на передней панели блока приборов 1. Температура воздуха в трубе измеряется полупроводниковым термометром и регистрируется на цифровом табло «Температура». В блоке приборов расположен генератор звуковых колебаний, подключенный к телефону, возбуждающему звуковые колебания в трубе. Частота колебаний, звукового генератора регулируется ручками «Грубо» и «Точно» и регистрируется на цифровом индикаторе «Частота». Сигнал микрофона измеряется миллиамперметром, чувствительность которого регулируется ручкой «Усиление». Максимальное значения тока, зарегистрированные миллиамперметром во время плавного изменения частоты колебаний, соответствуют появлению резонанса.
Рис. 3.1. общий вид экспериментальной установки ФПТ 1 – 7:
1 – блок приборов; 2 – блок рабочего элемента;
3 – стойка; 4 – труба с нагревателем
4. Порядок выполнения работы
1. Убедитесь в том, что тумблер «Нагрев» выключен, а регулятор температуры нагрева и ручки «Усиление», «Грубо», «Точно» находятся в крайнем левом положении.
2. Включить установку тумблером «Сеть».
3. Ручкой «Усиление» отрегулировать чувствительность миллиамперметра (стрелка должна быть приблизительно на трети шкалы).
4. Плавно увеличивая с помощью ручек «Грубо» и «Точно» частоту колебаний, задаваемых звуковым генератором, определить частоту первого резонанса по наибольшему отклонению стрелки на шкале миллиамперметра. Результат измерений занести в таблицу. Записать в ней значение температуры t1, указанной на табло «Температура».
5. Постепенно увеличивая ручкой «Усиление» чувствительность миллиамперметра определить частоту второго, третьего,…, седьмого резонансов. Производя измерения при уменьшении частоты, убедиться в повторяемости результатов. Результаты этих измерений также занести в таблицу.
6. Включить тумблер «Нагрев» и регулятором температуры нагрева достичь температуры воздуха в трубе в пределах 40 – 45°С. после стабилизации температуры произвести измерения по пп. 2 – 4.
7. Увеличивая нагрев, достичь температуры воздуха в трубе в пределах 55 – 60°С. После стабилизации температуры произвести измерения по пп. 2 – 4.
8. Регулятор температуры нагрева вывести в крайнее левое положение, выключить тумблер «Нагрев», ручки «Усиление», «Грубо» и «Точно» установить в крайнее левое положение, после чего выключить установку тумблером «Сеть».
9. Построить график зависимости резонансной частоты от номера резонанса νР = f(n) для каждой из температур и определить угловой коэффициент Kα наклона прямой для каждого графика.
10. Для каждого значения температуры воздуха в трубе, используя полученные угловые коэффициенты Kα, определить скорость звука υ по формуле υ = 2L Kα и отношение теплоемкостей γ по формуле (2.19), (молярная масса воздуха μ = 29·10–3 кг/моль, длина трубы L указана на установке).
11. Оценить погрешность результатов измерения.
Таблица
| Номер резонанса | t1 | T2 | T3 | ||||||
| νР, Гц | υ, м/с | γ | νР, Гц | υ, м/с | γ | νР, Гц | υ, м/с | γ | |
5. Требования к отчету
Отчет должен содержать:
1) название, номер и цель работы;
2) краткую теорию метода с расчетными формулами;
3) данные измерений νР, представленные в таблице и на графиках зависимостей резонансной частоты νР от порядкового номера резонанса r для каждой температуры;
4) полученные значения угловых коэффициентов Kα, скорости звука υ и отношения γ для каждой температуры;
5) расчет относительных погрешностей измерения υ и γ;
6) выводы по результатам работы.
6. Контрольные вопросы
1. Что называют молярной и удельной теплоемкостью вещества? Чему равна разность молярных теплоемкостей газа при постоянном давлении и при постоянном объеме?
2. Что такое коэффициент Пуассона? Чем определяется его значение?
3. Сформулируйте закон равнораспределения энергии теплового движения молекул по степеням свободы.
4. Сформулируйте первый закон термодинамики.
5. Какой процесс называют адиабатным? Получите закон Пуассона.
6. Почему процесс изменения состояния слоев газа при распространении в нем звуковой волны можно считать адиабатным?
7. Опишите процесс распространения звуковой волны в газе и выведите формулу для расчета ее скорости.
8. Как зависит скорость звука в воздухе от его температуры?
9. Объясните взаимосвязь коэффициента Пуассона газа со скоростью распространения в нем звуковой волны.
10. В чем заключается резонансный метод определения скорости звука в газе и его коэффициента Пуассона?
11. При каком условии в трубе с воздухом образуются стоячие волны?
Список литературы
1. Савельв И.В. Курс общей физики. – Т.1 – М.: Наука, 1989. – С. 234 – 237, 245 – 248.
2. Зисман Г.А., Тодес О.М. Курс общей физики. – Т.1. – М.: Наука, 1965. – С. 305 – 309.
3. Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высшая школа, 1989. – С. 100 – 103, 318, 323, 329.
fs.nashaucheba.ru
Лабораторная работа по физике
Санкт-Петербургский
национальный исследовательский
университет
информационных
технологий, механики и оптики
Институт холода
и биотехнологий
Измерение
плотности твердых тел простейшей формы
Работу
выполнил
Студент
515 группы
Сатторов
Диловар Эътборович
Преподаватель:
Румп Геннадий Александрович
2013г
Лабораторная
работа №1
Цель
работы
1.Измерить
диаметр и высоту цилиндра, его массу и
по ним рассчитать платность материала.
2.
Представить результаты измерения
плотности материала с указанием
абсолютной и относительной погрешностей.
Перечень
используемого оборудования и средств
измерений:
-образец
цилиндрической формы
-штангенциркуль
-весы
Характеристики
средств измерений представлены в таблице
|
Наименование |
Предел |
Цена |
Класс |
Погрешность, |
|
Штангенциркуль |
150 мм |
0,2мм/дел. |
— |
0,2 мм |
|
Весы электронные |
500гр |
0,1г/дел. |
— |
0,1 г |
Теоретическое
обоснование
-
Измерить
5 раз диаметр D
образца в различных сечениях по высоте
и на разных образующих цилиндра -
Измерить
3 раза высоту цилиндра H
по разным образующим -
Измерить
1 раз массу m
образца
Таблица
данных
|
Диаметр образца |
D1 |
D2 |
D3 |
D4 |
D5 |
|
Значение |
26,1 |
30,1 |
30,1 |
28,1 |
29,1 |
|
Высота образца |
Н1 |
Н2 |
Н3 |
||
|
Значение высоты |
40,6 |
42,1 |
43,1 |
||
|
Масса, гр |
11,0 |
||||
Метод
измерения:
Плотность
вещества равна отношению массы к объему
(1)
Где
m-масса
тела, кг;V-объем
тела,
Объем
цилиндра диаметром D
и высотой H
(2)
Таким
образом, плотность материала цилиндрического
образца
(3)
Используемые
в работе образцы за счет погрешностей
изготовления имеют отклонения от формы
прямого кругового цилиндра: бочкообразность,
прогиб, конусность, эллиптичность
поперечного сечения, а также непараллельность
торцевых поверхностей(см. рис1). Поэтому
диаметры D
образца, измеренные в разных сечениях
и на разных образующих, будут разлицаться.
Также будут различаться и высоты H
на разных продольных сечениях
А)
б)
в) г)
Для
уменьшения случайной погрешности
измерения диаметра D
и высоты H,
будем диаметр D
измерять 5 раз, высоту H—
три раза. Массу образца достаточно
измерить 1 раз.
Для
расчета плотности в формуле (3) будем
использовать средние значения диаметра
D
и высоты H
образца.
Поэтому
окончательная расчетная формула для
плотности примет вид
Примеры
расчетов
-
По
данным таблицы рассчитать средний
диаметр цилиндра D
для пяти измерений
-
Рассчитать
среднее квадратичное отклонение (СКО)
результата измерения диаметра
-
Рассчитать
доверительный интервал случайной
погрешности (случайную погрешность)
измерения диаметра D
для надежности α=0,95
-
Рассчитать
полную и абсолютную погрешность
измерения диаметра
-
Рассчитать
относительную погрешность измерения
диаметра в процентах
-
Записать
результат измерения диаметра в виде
-
По
данным таблицы рассчитать среднюю
высоту цилиндра H
для трех измерений
-
Рассчитать
СКО результата измерения высоты
-
Рассчитать
случайную погрешность измерения высоты
образца для надежности α=0,95
-
Рассчитать
полную абсолютную погрешность измерения
высоты
-
Рассчитать
относительную погрешность измерения
высоты в процентах
-
Записать
результат измерения высоты в виде
-
В
таблице найти инструментальную
погрешность измерения образца, которая
дана для надежности α=1
-
Найти
абсолютную и относительную погрешности
измерения массы в процентах для
надежности α=0,95.
В соответствии с рекомендациями
методических указаний
-
Записать
результат измерения высоты в виде
-
Рассчитать
плотность материала образца
-
Плотность
материала определяется путем косвенных
изменений по формуле, в которую входят
прямо измеряемые величины D,
H,
m.
Формула представляет собой одночлен,
поэтому в соответствии с рекомендациями
методических указаний целесообразно
вначале вычислить относительную
погрешность измерения в процентах
Для этого
в формулу все относительные погрешности
следует поставить в процентах,
а затем рассчитать абсолютную погрешность
-
Записать
результат измерения плотности в виде
Вывод.
Таким
образом, плотность(Р) твердого тела
можно найти с помощью высоты(Н), диаметра(D)
и массы(m)
фигуры.
Плотность
данного твердого тела напрямую зависит
от высоты(Н) и диаметра(D)
цилиндра.
Чем
больше высота цилиндра, тем ниже плотность
тела.
Чем
больше высота цилиндра, тем меньше
плотность тела.
Дата
выполнения:
20 марта 2013 г.
Подпись:
studfiles.net
Лабораторная работа 117
ОПРЕДЕЛЕНИЕ
ОТНОШЕНИЯ ТЕПЛОЕМКОСТЕЙ СР/СV
МЕТОДОМ КЛЕМАНА
– ДЕЗОРМА
ВВЕДЕНИЕ
ПОНЯТИЕ ИДЕАЛЬНОГО
ГАЗА
Идеальный
газ – газ,
при рассмотрении которого пренебрегают
силами межмолекулярного взаимодействия
и размерами молекул. Все реальные газы
при достаточно высоких температурах и
достаточно низких давлениях мало
отличаются по своим свойствам от
идеального газа, поэтому выводы,
полученные для идеального газа, широко
используются для решения практических
задач.
Состояние
газа характеризуют
основными
параметрами состояния: давлением p,
температурой Т, удельным
 или молярнымVm
или молярнымVm
объемом.
Давлением
р называется отношение силы dF,
действующей перпендикулярно поверхности,
к площади dS
этой поверхности:
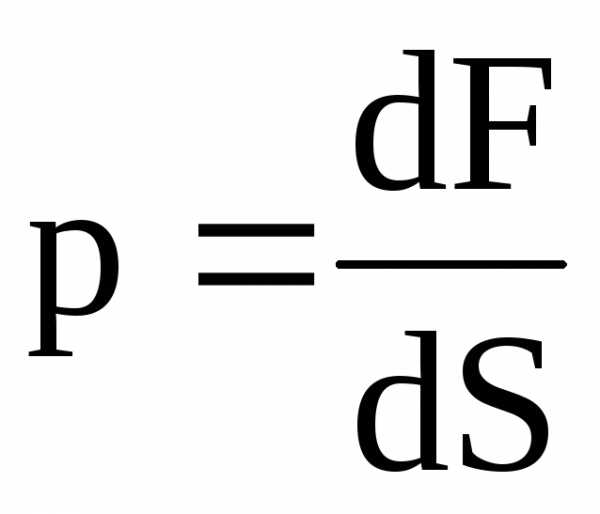 .(1)
.(1)
В
СИ единица давления – паскаль (Па): 1 Па
= 1 Н/м2.
В СГС единица давления – 1дин/см2
= 0,1 Н/м2.
Часто используются внесистемные единицы
измерения давления – 1 бар = 105Па,
физическая атмосфера – 1 атм. = 760 мм рт
ст. = 1,013·105
Па, техническая атмосфера – 1 ат. = 1
кг/см2
= 0,981·105
Па. В области низких давлений обычно
пользуются единицей 1 мм.рт.ст. (торр) =
1/760 атм. = 133,3 Па.
Количество
вещества
ν
– физическая величина, характеризующая
число структурных элементов, содержащихся
в данной системе, Это могут быть атомы,
молекулы, а также ионы, электроны и
другие частицы. Единицей количества
вещества в СИ является 1 моль. 1 моль
равен количеству вещества системы,
содержащей столько же структурных
элементов, сколько содержится атомов
в 0,012 кг изотопа углерода 12С.
В одном моле любого вещества содержится
6,022·1023
структурных элементов (число Авогадро).
Относительной
молекулярной массой
Мr
вещества называется отношение массы
молекулы этого вещества к 1/12 массы атома
12С.
Из определения следует, что молекулярная
масса является безразмерной величиной.
Молярная
масса М
вещества равна отношению массы m
однородной системы к количеству вещества
ν этой системы: М =m/ν. Молярная масса
вещества пропорциональна относительной
молекулярной массе данного вещества:
М = kMr,
где k
– размерный коэффициент пропорциональности,
равный 10-3
кг/моль. Отсюда следует, что молярная
масса, выраженная в граммах на моль,
численно равна относительной молекулярной
массе.
Молярным
объемом Vm
называется объем одного моля вещества.
Объем массы газа можно выразить через
молярный объем:
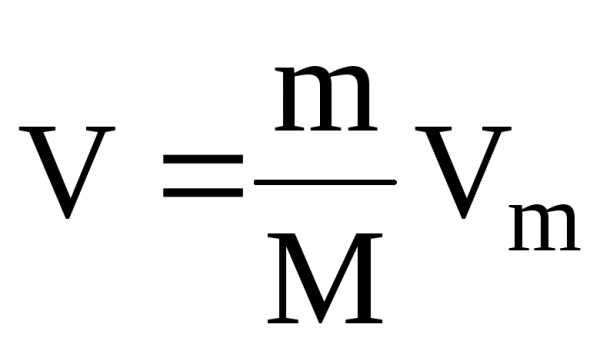 ,(2)
,(2)
где
m/M
= ν
— число молей (количество вещества).
Удельным
объемом υ
называется объем единицы массы вещества:
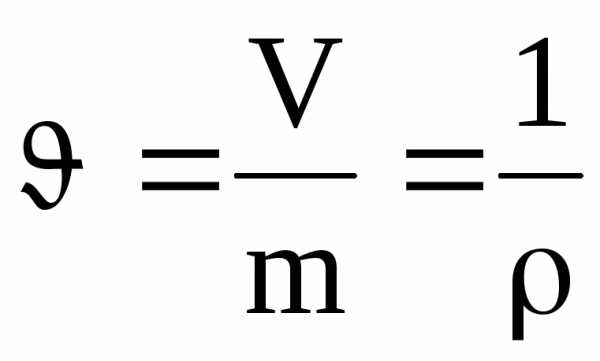 . (3)
. (3)
Температура
характеризует степень нагретости тела.
Для измерения температуры пользуются
Международной практической температурной
шкалой 1968 г. (МПТШ – 1968). По этой шкале
температура измеряется в оС
(градусах Цельсия) и обозначается через
t.
При теоретических выкладках пользуются
абсолютной температурной шкалой, по
которой температура измеряется в К
(кельвинах) и обозначается через Т.
Соотношение между температурами по
любой из этих шкал имеет вид:
Т
= t
+ 273,15.(4)
Температура
Т = 0 (по МПТШ – 1968 t
= — 273,15оС)
называется абсолютным нулем температуры.
Единица измерения температуры 1 градус,
одинаковая для обеих шкал, определяется
как одна сотая часть разности показаний
термометров, помещенных в пары кипящей
воды и тающий лед, при нормальном давлении
(рн
= 1,013·1023Па).
Закон Авогадро.
Соотношения
между макроскопическими (лабораторных
масштабов) и молекулярными (атомных
масштабов) величинами выражаются с
помощью закона и числа Авогадро. Согласно
закону Авогадро, моль
идеального газа при нормальных условиях
(Тн=273,15
К, рн=
= 760 мм. рт.ст. = 1,013·1023
Па) занимает объем Vm
= 22,4·10-3
м3/моль
и содержит постоянное число молекул NA
= 6,022·1023
моль-1,
названное числом Авогадро. Число Авогадро
является универсальной постоянной
(одинаково для моля любого вещества в
любом агрегатном состоянии).
Уравнение
состояния идеального газа.
Равновесное
состояние некоторой массы газа
определяется тремя термодинамическими
параметрами: давлением р, объемом V
и температурой Т. Связь между этими
параметрами может быть выражена
аналитически формулой F(р,V,T)=
0, называемой уравнением состояния тела
или системы.
Уравнением
состояния идеального газа является
уравнение Менделеева – Клапейрона,
которое для одного моля газа имеет вид
PVm
= RT,(5)
где
R
– молярная (универсальная) газовая
постоянная, одинаковая для всех газов.
Численное
значение газовой постоянной рассчитывается
из закона Авогадро по уравнению (5)
.
Уравнение
состояния для произвольной массы m
идеального газа имеет вид
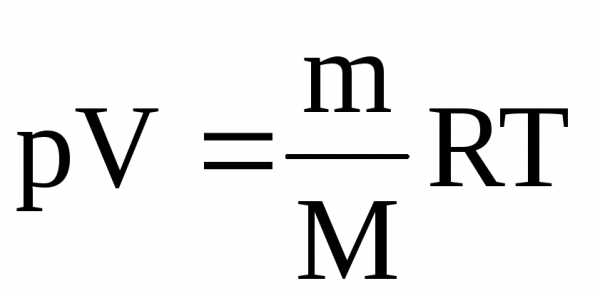 .(6)
.(6)
Отношение
молярной газовой постоянной R
к числу Авогадро NA
называется постоянной Больцмана:
.(7)
Если
в формулу (5) ввести постоянную Больцмана
и учесть, что NA/Vm
= n
– концентрация (число молекул в единице
объема), то можно получить уравнение
состояния идеального газа, выраженное
в другой форме
P
= n*k*T. (8)
Из
соотношения (8) следует, что давление
идеального газа при данной температуре
определяется только концентрацией и
не зависит от рода молекул.
Число
молекул в единице объема идеального
газа в нормальном состоянии называется
числом Лошмидта:
.(9)
Закон
Дальтона.
Давление смеси идеальных газов равно
сумме парциальных давлений газов,
входящих в смесь
р
= р1
+ р2
+ р3
+ … .(10)
Парциальное
давление компонента газовой смеси
— это давление, которое оказывал бы этот
газ, если бы он один занимал весь объем
смеси. Закон Дальтона непосредственно
следует из уравнения (8) при
условии, что n
= n1
+ n2
+ n3
+ … .
studfiles.net
Методические материалы | Кафедра физики наноразмерных систем
Учебные пособия к выполнению лабораторных работ
Механика и молекулярная физика
Электричество и магнетизм
Оптика
Как правильно оформить и представить результаты лабораторных работ по физике
График выполнения лабораторных работ
Поляков А.А. Механика и малекулярная физика: учебное пособие
Рабочие тетради
Бланки для выполнения лабораторных работ по Механике и молекулярной физике
Лабораторная работа 1: Оценка случайной погрешности и доверительной вероятности прямых измерений pdf
Лабораторная работа 2: Проверка закона сохранения импульса pdf
Лабораторная работа 3: Изучение закона динамики вращательного движения pdf
Лабораторная работа 4: Определение момента инерции диска и проверка теоремы Штейнера pdf
Лабораторная работа 5: Определение момента инерции тела, скатывающегося с наклонной плоскости pdf
Лабораторная работа 6: Проверка закона сохранения момента импульса pdf
Лабораторная работа 7: Определение ускорения свободного падения с помощью оборотного маятника pdf
Лабораторная работа 8: Изучение распределения Максвелла на механической модели pdf
Лабораторная работа 9: Изучение распределения термоэлектронов по скоростям pdf
Лабораторная работа 10: Изучение вязкости воздуха pdf
Лабораторная работа 12: Определение отношения теплоемкостей воздуха pdf
Бланки для выполнения лабораторных работ по Электричеству и магнетизму
Лабораторная работа 1: Исследование электростатического поля методом моделирования pdf
Лабораторная работа 2: Определение емкости конденсатора pdf
Лабораторная работа 3: Изучение температурной зависимости сопротивления проводника и полупроводника pdf
Лабораторная работа 4: Определение постоянной времени цепи, содержащей сопротивление и емкость pdf
Лабораторная работа 6: Определение удельного заряда электрона методом магнетрона pdf
Лабораторная работа 9: Изучение зависимости магнитной проницаемости ферромагнетика от напряженности магнитного поля pdf
Лабораторная работа 12: Изучение затухающих электрических колебаний pdf
Лабораторная работа 14: Исследование явления резонанса в электрических цепях pdf
Бланки для выполнения лабораторных работ по Оптике
Лабораторная работа 1: Изучение дисперсии света pdf
Лабораторная работа 2: Определение радиуса кривизны линзы с помощью колец Ньютона pdf
Лабораторная работа 3: Исследование зависимости показателя преломления воздуха с помощью интерферометра pdf
Лабораторная работа 4: Изучение явлений, обусловленных дифракцией света pdf
Лабораторная работа 5: Изучение поляризации света pdf
Лабораторная работа 6: Изучение законов теплового излучения pdf
Лабораторная работа 7: Исследование характеристик вакуумного фотоэлемента pdf
Лабораторная работа 8: Изучение спектров испускания pdf
Уважаемые студенты! Любые вопросы, замечания, предложения по учебным пособиям Вы можете направлять по адресу: [email protected]
physics.susu.ru
Физика — Лабораторная Работа 53
Московский
Энергетический Институт
(Технический
Университет)
Лабораторная
работа №53
«Изучение основных
закономерностей внешнего фотоэффекта»
Группа
С-8-03
Студент
Ильчук М.А
Преподаватель
Спивак В.С
Дата
выполнения
К
работе допущен
Работу
выполнил
Работу
сдал
2005
год.
Цель
работы: изучение
законов внешнего фотоэффекта; исследование
вольтамперных характеристик фотоэлемента;
определение красной границы и работы
выхода материала фотокатода.
Схема
экспериментальной установки.
где
ИС- источник оптического излучения,
ИП1-
блок питания источника излучения,
УМ-2-
монохроматор,
ФЭ-
фотоэлемент,
ИП2,
ИП3- блоки питания фотоэлемента,
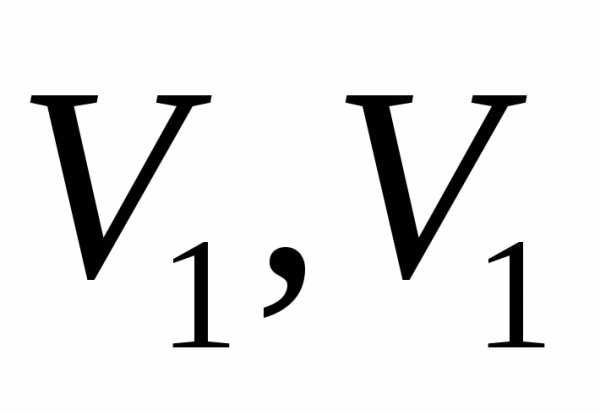 —
—
вольтметры,
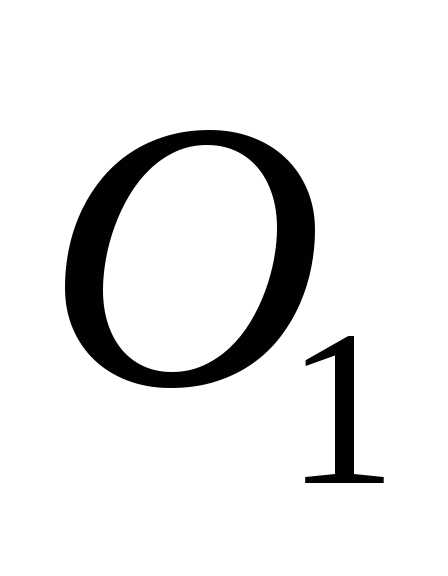 —
—
объектив 1,
Щ1-
входная щель,
 —
—
объектив 2,
ДЭ-
диспергирующий элемент- стеклянная
призма,
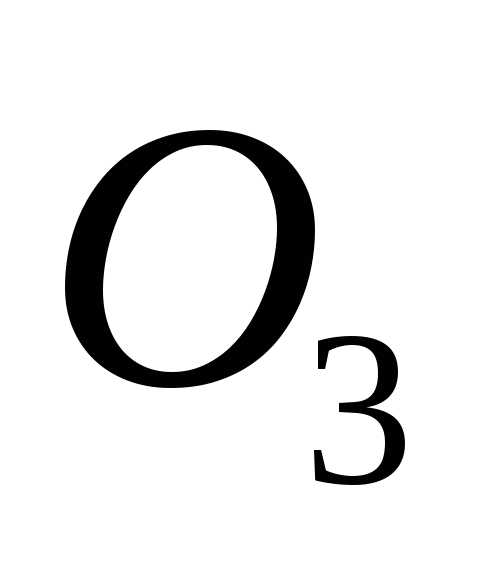 —
—
объектив 3,
Щ2-
выходная щель,
БМ-
барабан монохроматора,
ПС-
призматический столик, раскладывающий
излучение в спектр,
R-
резистор,
ЗК-
защитный корпус,
Таблица
1
|
Название |
Предел |
Цена |
Инструментальная |
|
вольтметр |
-5В- |
0,001В |
|
|
Барабан |
|
|
|
Задание
1:Снятие
зависимости силы фототока от длины
волны света. Определение красной границы
фотоэффекта.
Таблица
2
Зависимость
силы фототока от длины волны.
|
|
|
|
|
|
3450 |
810 |
31,2 |
0,312 |
|
3400 |
800 |
402 |
0,402 |
|
3350 |
790 |
48,1 |
0,481 |
|
3300 |
775 |
52,4 |
0,524 |
|
3250 |
765 |
53,6 |
0,536 |
|
3200 |
755 |
50,8 |
0,508 |
|
3150 |
740 |
46,0 |
0,460 |
|
3100 |
730 |
40,8 |
0,408 |
|
3050 |
720 |
34,4 |
0,344 |
|
3000 |
708 |
29,0 |
0,290 |
|
2950 |
695 |
23,5 |
0,235 |
|
2900 |
685 |
19,1 |
0,191 |
|
2850 |
670 |
15,2 |
0,152 |
|
2800 |
660 |
12,2 |
0,122 |
|
2750 |
650 |
10,0 |
0,100 |
|
2700 |
648 |
7,8 |
0,078 |
|
2650 |
625 |
6,4 |
0,064 |
|
2600 |
615 |
5,2 |
0,052 |
|
2550 |
605 |
4,2 |
0,042 |
|
2500 |
590 |
3,6 |
0,036 |
|
2450 |
580 |
3,0 |
0,030 |
|
2400 |
570 |
2,5 |
0,025 |
|
2350 |
563 |
2,0 |
0,020 |
|
2300 |
554 |
1,7 |
0,017 |
|
2250 |
545 |
1,5 |
0,015 |
|
2200 |
539 |
1,2 |
0,012 |
|
2150 |
530 |
1,0 |
0,010 |
|
2100 |
526 |
0,8 |
0,008 |
|
2050 |
517 |
0,7 |
0,007 |
|
2000 |
510 |
0,6 |
0,006 |
|
1950 |
505 |
0,5 |
0,005 |
|
1900 |
500 |
0,5 |
0,005 |
|
1850 |
495 |
0,4 |
0,004 |
|
1800 |
490 |
0,3 |
0,003 |
|
1750 |
483 |
0,3 |
0,003 |
|
1700 |
479 |
0,2 |
0,002 |
|
1650 |
473 |
0,2 |
0,002 |
|
1600 |
470 |
0,2 |
0,002 |
|
1550 |
465 |
0,1 |
0,001 |
Задание
2: Снятие
вольтамперной характеристики фотоэлемента
и определение задерживающего напряжения
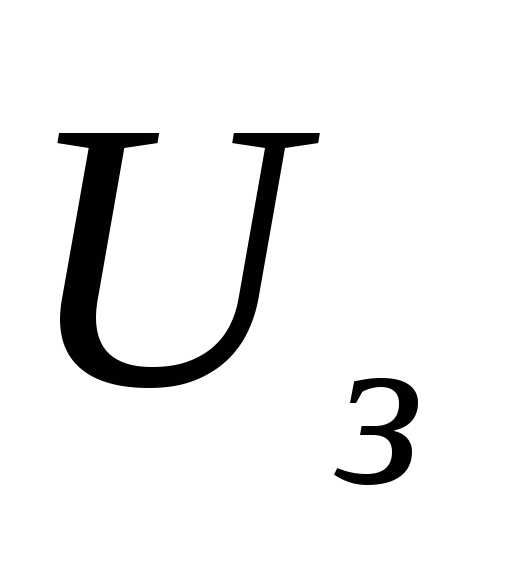 .
.
Таблица
3
Зависимость
силы фототока от напряжения на
фотоэлементе.
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
30,43 |
3,7 |
0,037 |
30,75 |
12,5 |
0,125 |
30,61 |
23,3 |
0,233 |
|
20,29 |
3,6 |
0,036 |
22,34 |
12,5 |
0,125 |
21,85 |
23,2 |
0,232 |
|
10,23 |
3,5 |
0,035 |
14,60 |
12,5 |
0,125 |
18,67 |
22,7 |
0,227 |
|
5,30 |
3,5 |
0,035 |
9,90 |
12,2 |
0,122 |
10,7 |
21,9 |
0,219 |
|
0,35 |
1,3 |
0,013 |
7,90 |
11,9 |
0,119 |
6,3 |
21,8 |
0,218 |
|
-0,0005 |
0,9 |
0,009 |
5,20 |
11,3 |
0,113 |
3,8 |
17,4 |
0,174 |
|
-0,001 |
0,9 |
0,009 |
-0,0005 |
0,8 |
0,008 |
-0,0005 |
0,5 |
0,005 |
|
-0,040 |
0,9 |
0,009 |
-0,114 |
0,6 |
0,006 |
-0,115 |
0,2 |
0,002 |
|
-0,098 |
0,8 |
0,008 |
-0,203 |
0,5 |
0,005 |
-0,228 |
0,1 |
0,001 |
|
-0,136 |
0,7 |
0,007 |
-0,240 |
0,4 |
0,004 |
-0,291 |
0,1 |
0,001 |
|
-0,1711 |
0,7 |
0,007 |
-0,275 |
0,3 |
0,003 |
-0,321 |
0,0 |
0,000 |
|
-0,262 |
0,5 |
0,005 |
-0,344 |
0,2 |
0,002 |
|||
|
-0,358 |
0,4 |
0,004 |
-0,393 |
0,1 |
0,001 |
|||
|
-0,4 |
0,3 |
0,003 |
-0,443 |
0,1 |
0,001 |
|||
|
-0,47 |
0,2 |
0,002 |
-0,492 |
0,0 |
0,000 |
|||
|
-0,57 |
0,1 |
0,001 |
||||||
|
-0,62 |
0,0 |
0,000 |
||||||
Обработка
результатов измерений.
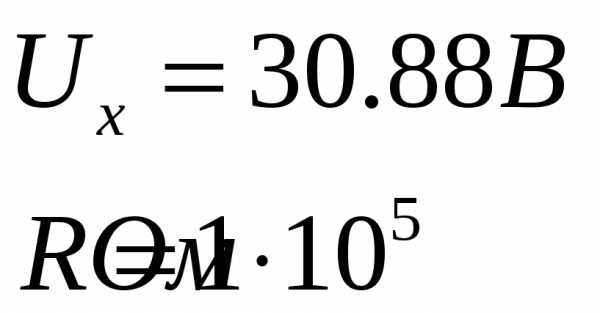
По
графику определили
Рассчитаем
работу выхода электрона:
По
графическим зависимостям определили
значения задерживающих напряжений для
каждого из трех длин волн падающего на
фотокатод излучения:
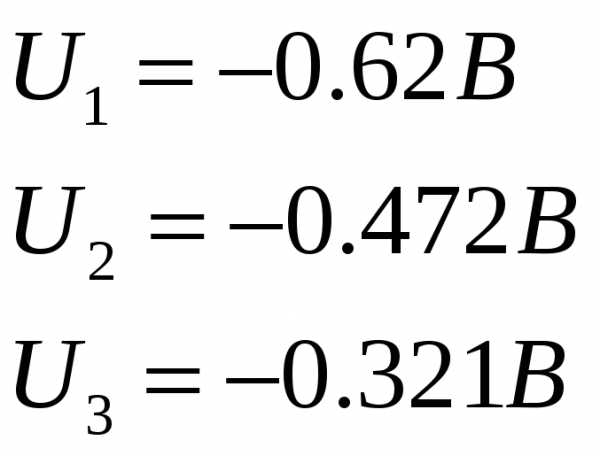
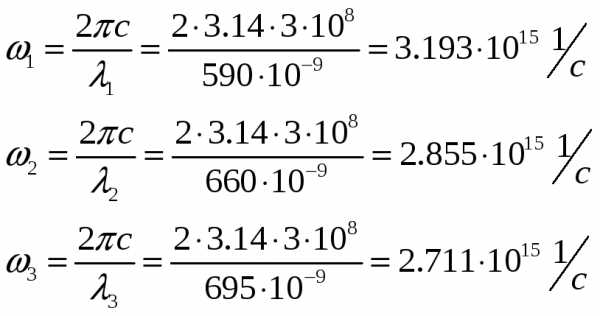
Подсчитаем
погрешности:
-
красной
границы
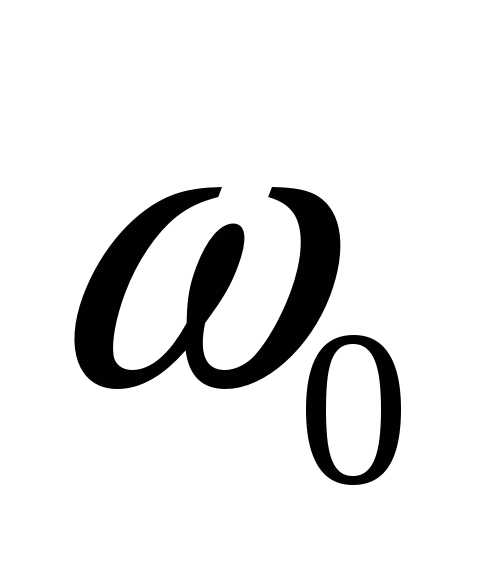 :
:
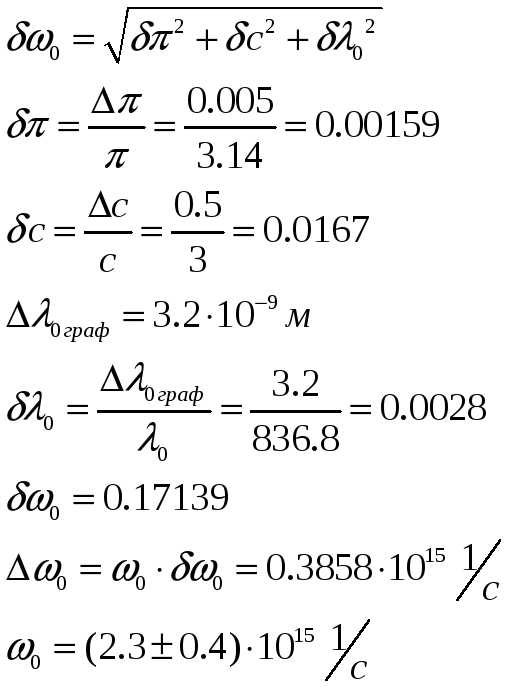
-
работу
выхода


studfiles.net
Физика ЛАБОРАТОРНАЯ РАБОТА 1
ЛАБОРАТОРНАЯ
РАБОТА № 1_4
УПРУГИЕ И НЕУПРУГИЕ
УДАРЫ
ЛАБОРАТОРНАЯ
РАБОТА № 1_4
УПРУГИЕ И НЕУПРУГИЕ
УДАРЫ
Ознакомьтесь с
конспектом лекций и учебником (Савельев,
т. 1, §
27, 28). Запустите программу. Выберите
«Механика» и «Упругие и неупругие
соударения». Нажмите вверху внутреннего
окна кнопку с изображением страницы.
Прочитайте краткие теоретические
сведения. Необходимое запишите в свой
конспект. (Если вы забыли, как работать
с системой компьютерного моделирования,
прочитайте ВВЕДЕНИЕ еще раз.)
ЦЕЛЬ РАБОТЫ:
-
Выбор физических
моделей для анализа взаимодействия
двух тел. -
Исследование
физических характеристик, сохраняющихся
при столкновениях. -
Экспериментальное
определение зависимости тепловыделения
при неупругом столкновении от соотношения
масс при разных скоростях.
КРАТКАЯ ТЕОРИЯ:
СТОЛКНОВЕНИЕ
(удар, соударение) – модель взаимодействия
двух тел, длительность которого равна
нулю (мгновенное событие). Применяется
для описания реальных взаимодействий,
длительностью которых можно пренебречь
в условиях данной задачи.
АБСОЛЮТНО УПРУГИЙ
УДАР – столкновение двух тел, после
которого форма и размеры сталкивающихся
тел восстанавливаются полностью до
состояния, предшествовавшего столкновению.
Суммарные импульс и кинетическая энергия
системы из двух таких тел сохраняются
(после
столкновения такие же, какими были до
столкновения):
;
.
АБСОЛЮТНО НЕУПРУГИЙ
УДАР – столкновение двух тел, после
которого форма и размеры тел не
восстанавливаются, тела «слипаются» и
движутся как одно целое с одной скоростью.
Суммарный импульс двух неупруго
сталкивающихся тел сохраняется, а
кинетическая энергия становится меньше,
так как часть энергии переходит в
конечном итоге в тепловую:
,
.
Используя определение
импульса и определение абсолютно
неупругого удара, преобразуем закон
сохранения импульса, спроектировав его
на ось ОХ,
вдоль которой движутся тела, в следующее
уравнение:
(m1
+ m2)
,
а закон для
кинетической энергии преобразуем в
такое уравнение:
ЕТЕПЛ
=
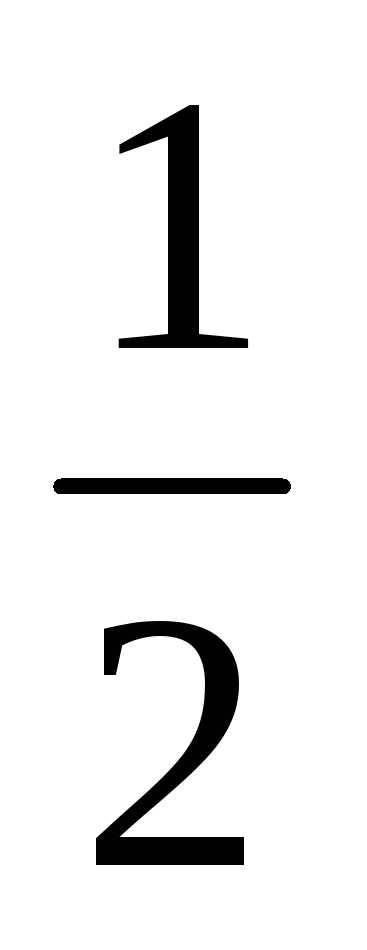 [m1(
[m1(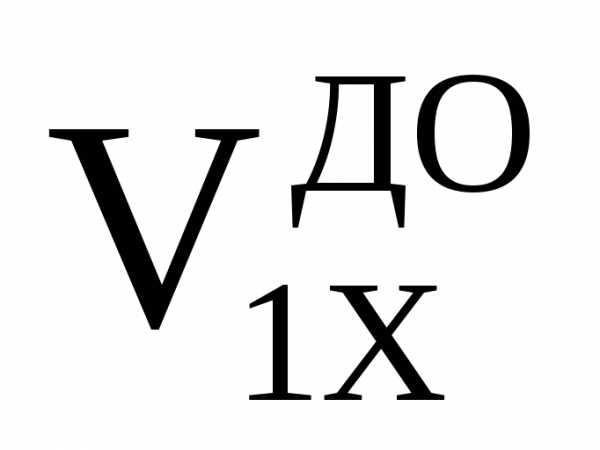 )2+
)2+
m2(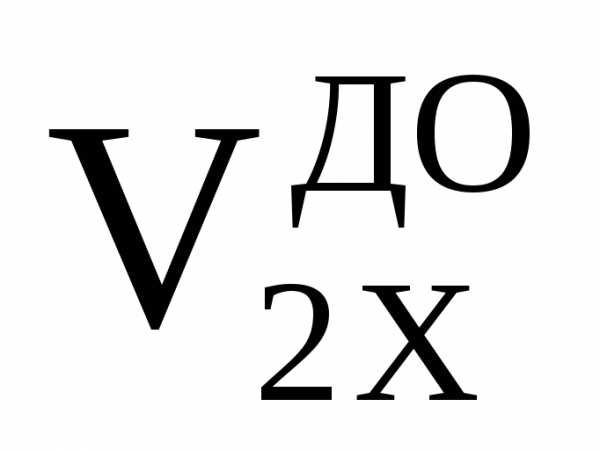 )2
)2
– (m1
+ m2)
(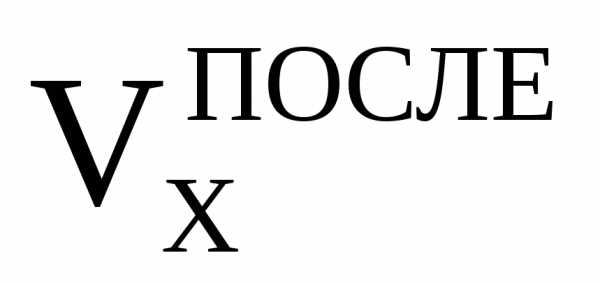 )2].
)2].
Помножив и разделив
второе уравнение на (m1
+ m2)
и используя первое уравнение, получим:
ЕТЕПЛ
=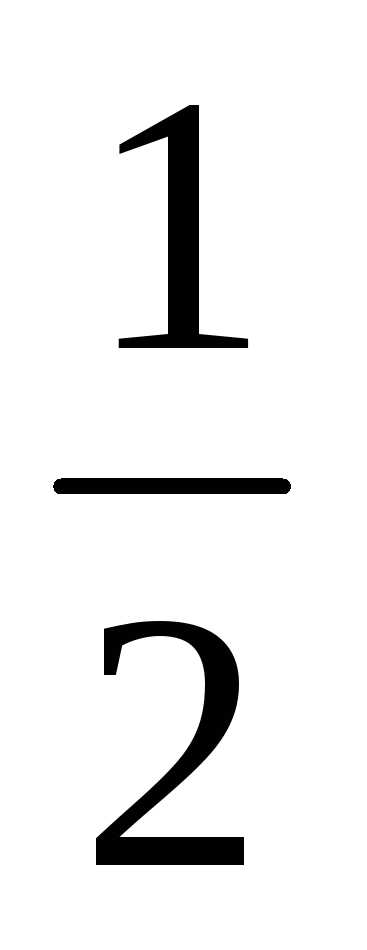 [m1(m1
[m1(m1
+ m2)(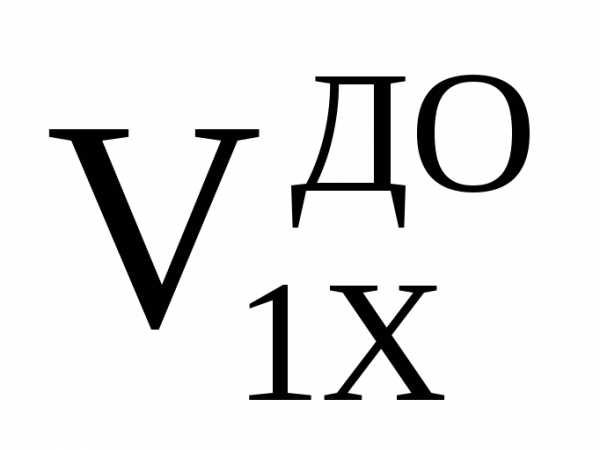 )2
)2
+ m2(m1
+ m2)(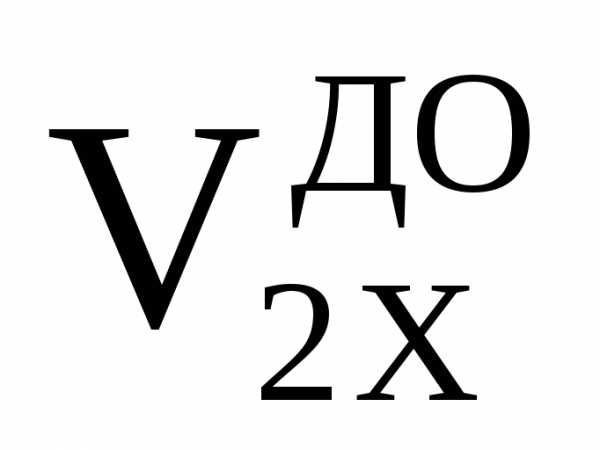 )2
)2
– (m1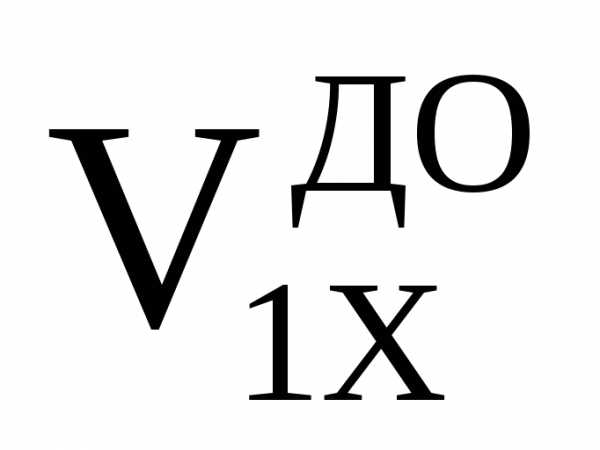 +
+
m2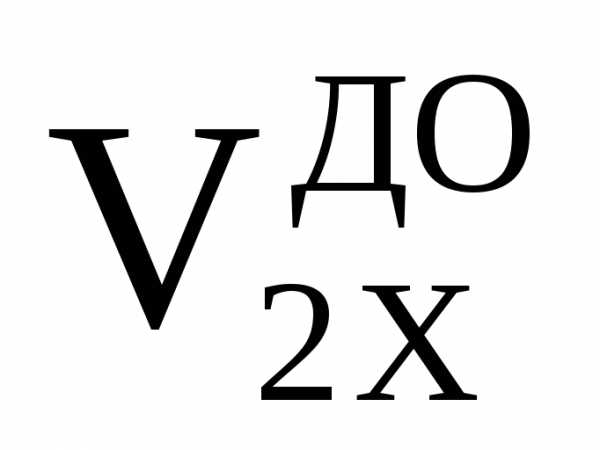 )2]/(m1 + m2)
)2]/(m1 + m2)
Относительная
величина тепловой энергии
равна отношению
=
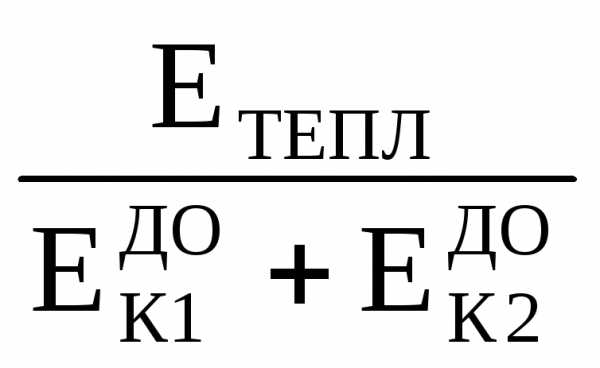
=,
где
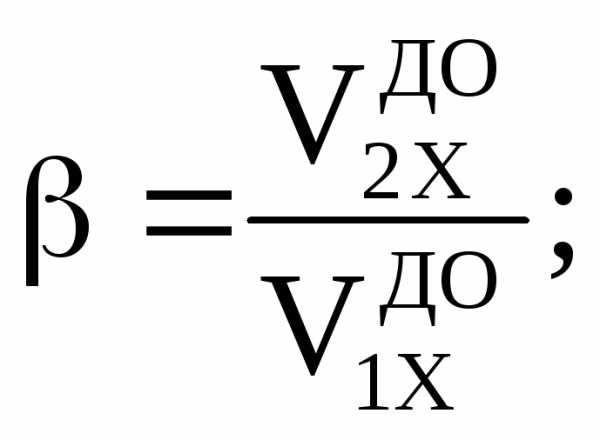
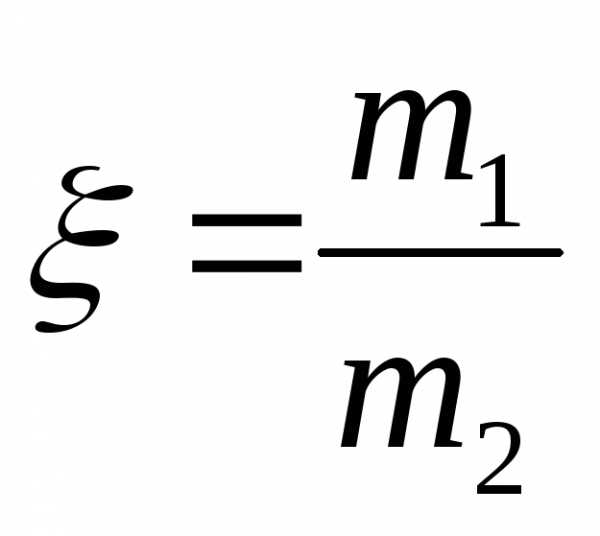 .
.
ЗАДАНИЕ: Выведите
формулу для относительной величины
тепловой энергии в пределе:
1) m1
= m2,
и 2) .
МЕТОДИКА и
ПОРЯДОК ИЗМЕРЕНИЙ
Внимательно
рассмотрите рисунок, найдите все
регуляторы и другие основные элементы
и зарисуйте их в конспект.
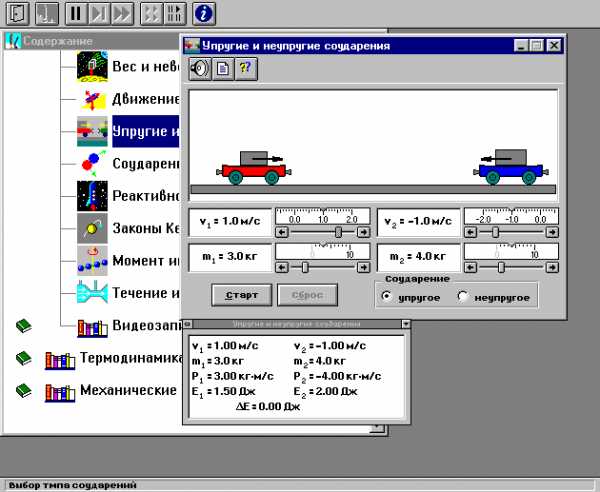
Получите у
преподавателя допуск для выполнения
измерений.
ЭКСПЕРИМЕНТ 1.
Исследование абсолютно упругого удара
Включите кнопку
«Упругий» справа внизу. Установите,
нажимая мышью на кнопки регуляторов,
значение массы первой тележки m1
и ее начальную скорость
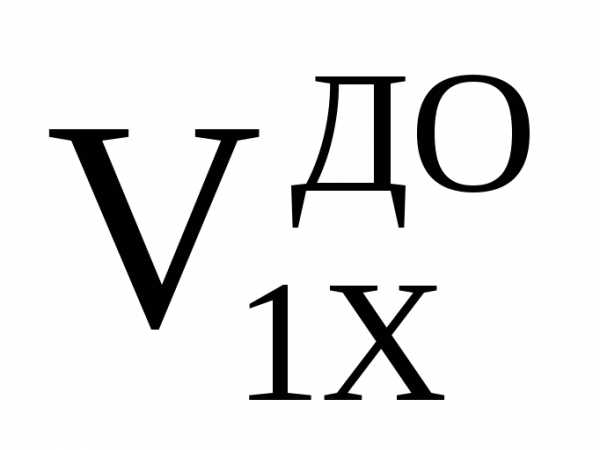 ,
,
указанные в табл. 1 для вашей бригады.
Для массы второй тележки выберите
минимальное значение. Ее начальную
скорость выберите равной
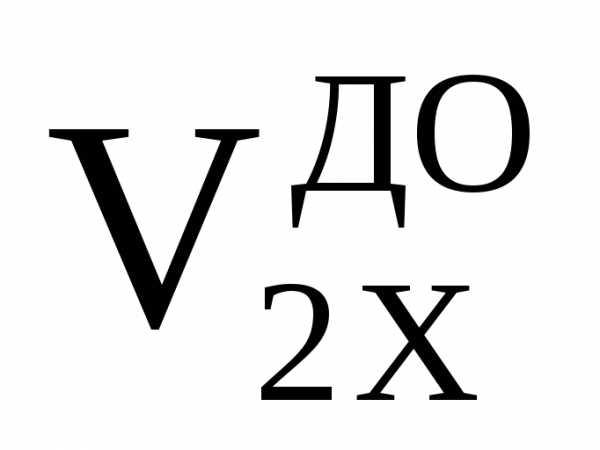 =
=
–
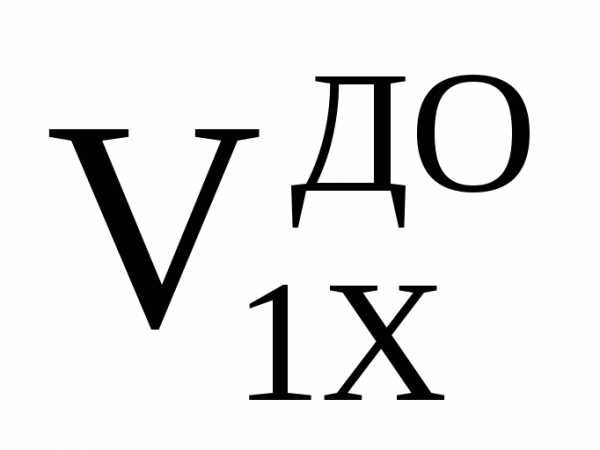 .
.
Нажимая мышью на
кнопку «СТАРТ» на экране монитора,
следите за движением тележек, останавливая
движение после первого столкновения
кнопкой «СТОП». Результаты измерений
необходимых величин записывайте в табл.
2, образец которой приведен ниже. Измените
на 1 кг значение массы второй тележки и
повторите измерения.
ЭКСПЕРИМЕНТ 2.
Исследование абсолютно неупругого
удара
Нажмите кнопку
«Неупругий» справа внизу. Установите,
нажимая мышью на кнопки регуляторов,
значение масс тележек и их начальные
скорости, указанные в табл. 1 для вашей
бригады. Проведите измерения, аналогичные
эксперименту 1. Результаты запишите в
таблицу 3, образец которой приведен
ниже.
Таблица 1. Значения
для первого и второго экспериментов
(не
перерисовывать).
|
Номер бригады |
m1, кг |
м/с |
Номер бригады |
m1, кг |
м/с |
|
|
1 |
1 |
1 |
5 |
5 |
1 |
|
|
2 |
2 |
2 |
6 |
6 |
2 |
|
|
3 |
3 |
1 |
7 |
7 |
1 |
|
|
4 |
4 |
2 |
8 |
8 |
2 |
Таблица 2.
Результаты измерений и расчетов для
абсолютно упругого удара (количество
измерений и строк – 10)
|
Номер |
m1 |
||||
|
измерения |
m2, кг |
м/с |
м/с |
Дж |
Дж |
|
1 |
1 |
||||
|
2 |
2 |
||||
|
… |
|||||
Таблица 3.
Результаты измерений и расчетов для
абсолютно неупругого удара (количество
измерений и строк – 10)
|
Номер |
m1 |
|||||||
|
измерения |
m2, кг |
м/с |
Дж |
Дж |
изм |
РАСЧ |
|
|
|
1 |
1 |
–1 |
||||||
|
2 |
2 |
–1 |
||||||
|
… |
–1 |
|||||||
Таблица 3.
Результаты измерений и расчетов для
абсолютно неупругого удара (количество
измерений и строк – 11)
|
Номер |
m2 |
|||||||
|
измерения |
|
м/с |
Дж |
Дж |
изм |
РАСЧ |
|
|
|
1 |
0 |
1 |
||||||
|
2 |
–0,2 |
1 |
||||||
|
… |
1 |
|||||||
ОБРАБОТКА
РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА:
-
Вычислите требуемые
величины и заполните табл. 2 и 3. -
Постройте графики
зависимостей относительного значения
тепловой энергии
а) от отношения
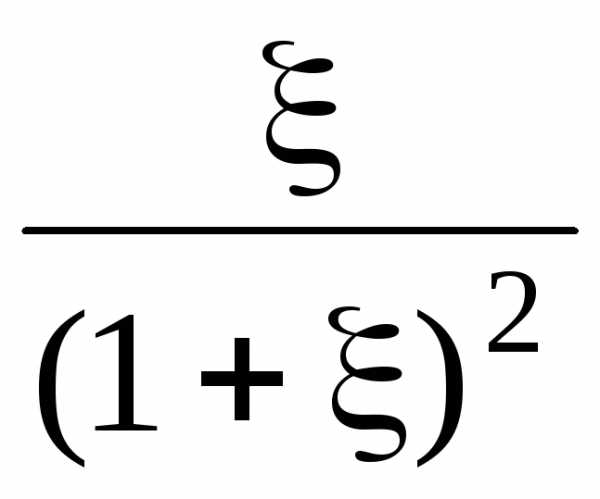
при
= –1 и
б) от отношения
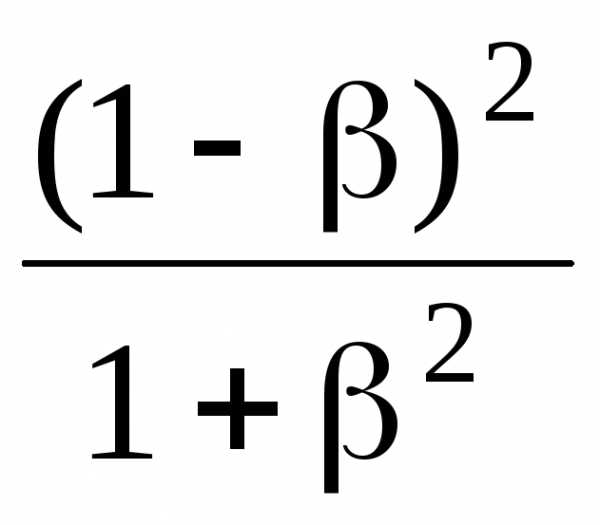
при
= 1.
-
Проанализируйте
графики и сделайте выводы.
Вопросы и задания
для самоконтроля
-
Что такое удар
(столкновение, соударение)? -
Для какого
взаимодействия двух тел можно применять
модель столкновения? -
Какое столкновение
называют абсолютно неупругим? -
Какое столкновение
называют абсолютно упругим? -
При каком
столкновении выполняется закон
сохранения импульса? -
Дайте словесную
формулировку закона сохранения импульса. -
При каком
столкновении выполняется закон
сохранения кинетической энергии? -
Дайте словесную
формулировку закона сохранения
кинетической энергии. -
Дайте определение
кинетической энергии. -
Дайте определение
потенциальной энергии. -
Что такое полная
механическая энергия? -
Что такое замкнутая
система тел? -
Что такое
изолированная система тел? -
При каком
столкновении выделяется тепловая
энергия? -
При каком
столкновении форма тел восстанавливается? -
При каком
столкновении форма тел не восстанавливается?
studfiles.net
10 лабораторных работ по физике
Лабораторная работа №6
«Градуирование пружины и измерение сил динамометром»
Цель: научиться градуировать пружину, получать шкалу с любой заданной ценой деления и с помощью градуированной пружины измерять силы
Оборудование: динамометр с закрытой шкалой, набор грузов по 102 г, штатив с муфтой и перекладиной, листок бумаги, строительная изолента (или чистый листок бумаги и скотч), свинцовый груз.
Ход работы:
1. Повторите назначение и принцип действия динамометра пар.28 стр.65
2. Закрепите строительную изоленту ( или листок бумаги с помощью скотча) на шкале динамометра. Если используется динамометр со скрытой пружиной, то следует заклеить только шкалу.
3. Закрепите муфту на стержне штатива на высоте примерно 35 — 40 см от его основания. Затем в муфте закрепите перекладину, а на неё повесьте динамометр, как показано на рисунке. Сделайте метку напротив указателя динамометра, соответствующую его начальному положению это будет нулевое значение шкалы.
4. Подвесьте к динамометру один груз. После того, как движение пружины прекратится, вновь сделайте метку напротив указателя.
5. Повторите опыт с двумя, тремя грузами, каждый раз отмечая метками положение указателя.
6. Зарисуйте таблицу в тетради и занесите данные из трех опытов.
7. Снимите динамометр со штатива и рядом с каждой меткой напишите соответствующее ей округлённое значение силы. Выше числа 0 напишите Н (Ньютон).
8. Измерьте расстояния между соседними метками и убедитесь, что они одинаковы.
9. Изготовьте шкалу с ценой деления 0,5 Н, проградуировав ее до 5 Ньютонов. Изготовленную шкалу зарисуйте в тетради, изобразив ее в горизонтальном положении.
10. Измерьте динамометром с самодельной шкалой вес свинцового груза = ______, выразите в ньютонах =_______.
Вывод:
infourok.ru
 (0,07+0,02(
(0,07+0,02(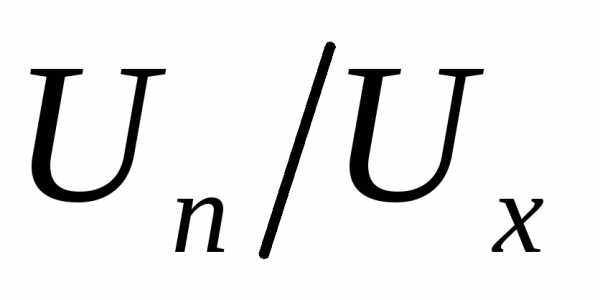 ))
))


 ,
, ,
, = –
= –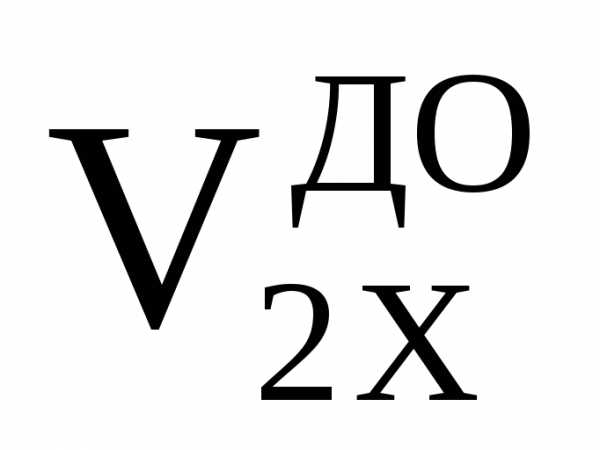
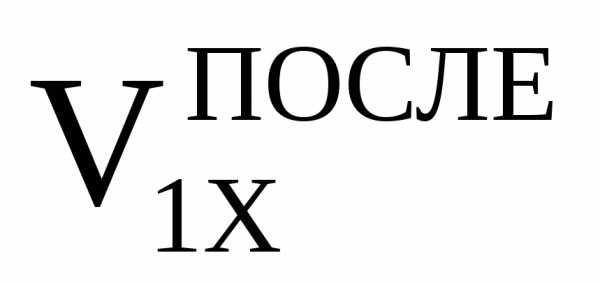 ,
,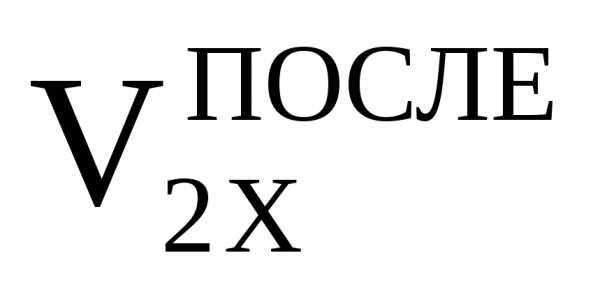 ,
,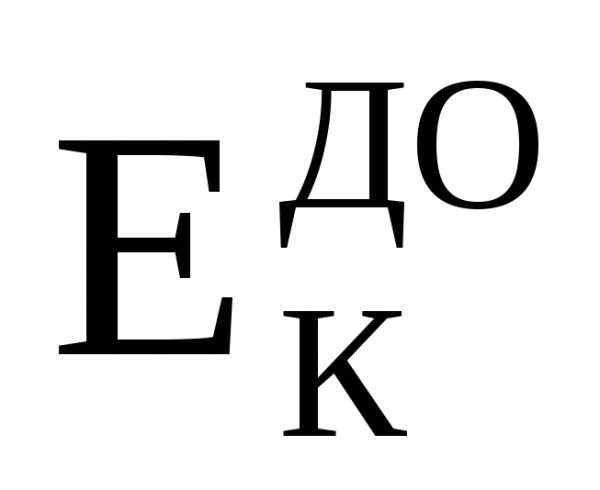 ,
,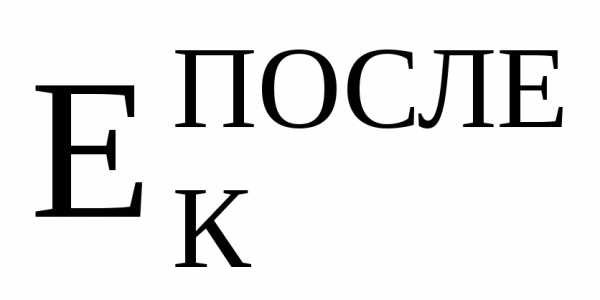 ,
,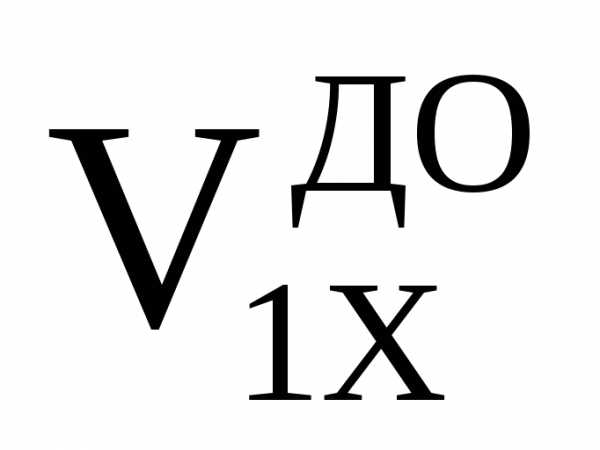 = –
= –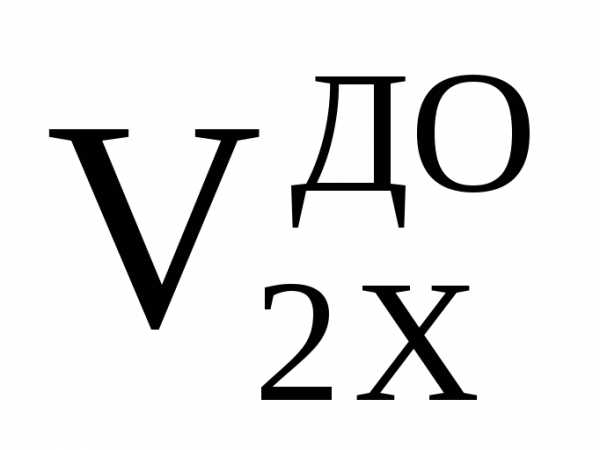 =
=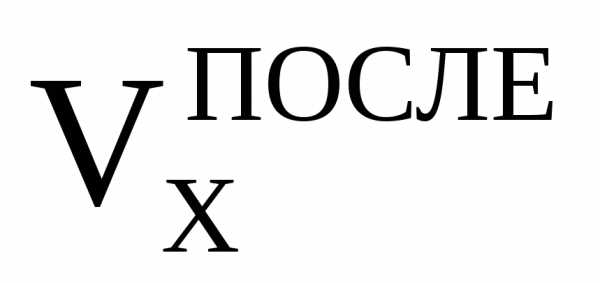 ,
,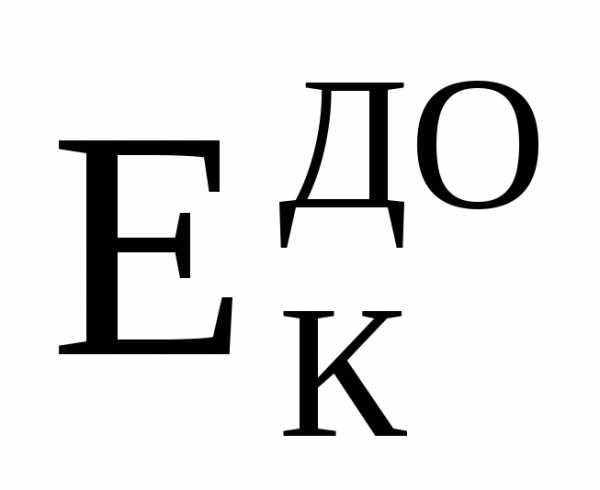 ,
,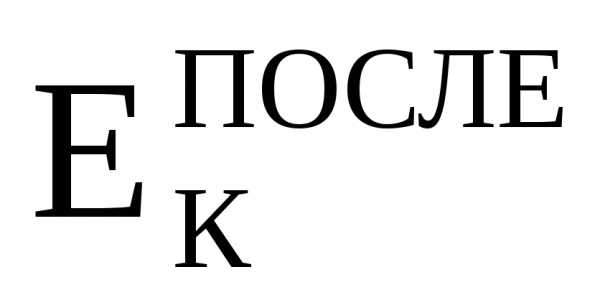 ,
,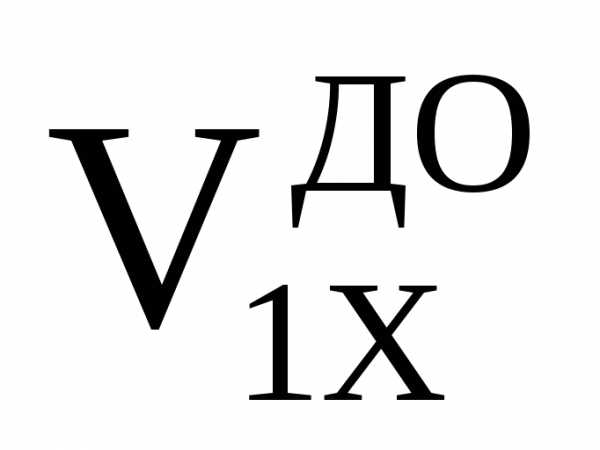 = ___
= ___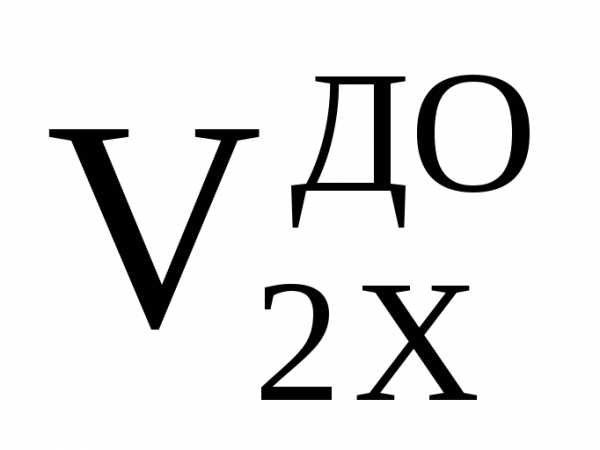 ,
, ,
, ,
, ,
,