Гдз з алгебри 10 клас бурда: Решебник ⏩ ГДЗ Математика 10 класс ⚡ М. И. Бурда, Ю. И. Малеваный, Т. В. Колесник 2018. Уровень стандарта

Решебник ⏩ ГДЗ Математика 10 класс ⚡ М. И. Бурда, Ю. И. Малеваный, Н.А. Тарасенкова, Т. В. Колесник 2010

Авторы:  М. И. Бурда, Ю. И. Малеваный, Н.А. Тарасенкова, Т. В. Колесник

Год:  2010

Рейтинг: 4.4

Оцените книгу

Связанный учебник

Аналоги другого года издания

Самые популярные книги

В 10 классе одним из учебников, популярных во многих школах, является книга под авторством Бурды. Авторы издают не только учебник, но и решебник к своим упражнениям. Можно ли разрешать ученику им пользоваться? Попробуем ответить на вопрос, почему ГДЗ математика, 10 класс, Бурда станет полезным в учебе.

Почему выпускают ГДЗ по математике, 10 класс, Бурда

Много лет выпускаются решебники. Изначально, в советских книгах, в конце прилагался список ответов на задачи по математике. Ученик, делая уроки, мог сверять получившийся результат, но если он не совпадал, приходилось всё переделывать заново. Это отнимало много времени. В 90-х издательства начали выпускать уже расширенные методички, составляемые авторами учебников. В этих готовых домашних заданиях присутствуют развернутые комментарии и решения.

Часто случается, что школьник плохо понял урок. Чтобы сделать домашние задания на пройденную тему, приходилось долго вчитываться в учебник, или просить помощи у родителей. Взрослые могут быть заняты, или вообще не помнят математику старших классов. Как раз в таких случаях методичка послужит бесплатным консультантом.

Еще не так давно надо было на книжных прилавках искать нужные решебники, платить за них и выбрасывать в конце учебного года. Теперь любой старшеклассник запросто найдет методичку в интернете. Главное, пользоваться ею правильно, не списывая постоянно. Иначе похожие задачи на контрольных решить не получится.

Математика, 10 класс, Бурда, ГДЗ онлайн – чем будет полезен

Программа в школе утверждается с расчётом на среднюю успеваемость детей.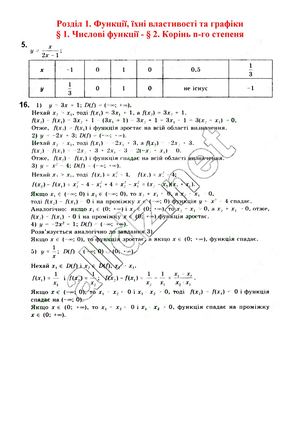 Отличников очень мало, особенно в старших классах. А математика важна для многих, так как по ней будут вступительные экзамены в ВУЗ.

ГДЗ по математике 10 класс, Бурда, Колесник, Мальований, Тарасенкова – бесплатный помощник

Кому-то легче даются точные предметы, кому-то гуманитарные. Если пропустить несколько тем по математика, догнать остальных будет тяжело. Чтобы ребенок не съезжал по оценкам, родителям приходится нанимать репетитора. Вместо этого попробуйте дать ему несколько заданий из учебника, и помогите их решить, держа решебник перед глазами. Через короткое время школьник и сам сможет заниматься с методичкой.

Болезни у школьников – не редкость. Как быть, если подростка отправили домой на лечение и он пропустил несколько недель учебы? Всё верно – индивидуально обучаться с готовыми домашними заданиями. Вернувшись за парту, он не почувствует, что отстал от сверстников.

Больше досуга у ребенка

Вспомните 10 класс, сколько в день уроков и как долго делаются домашние задания. Школьник засиживается до ночи. На домашние обязанности, хобби, игры не остаётся времени. А если подросток еще и занимается спортом, ходит на курсы, однозначно не все уроки будут сделаны. Вместо это лучше быстро и качественно выполнять задания с решебником. И время останется, и знания появятся.

Поэтому у методичек есть много преимуществ:

• нет надобности в репетиторе

• легко наверстать пропущенное или не понятое в школе

• »ГДЗ, 10 класс, математика, Бурда» скачать можно быстро и бесплатно

• родительский контроль за успеваемостью детей

ГДЗ Математика 10 клас Бурда 2010

Формулы алгебры для 10-го класса

Алгебра — важный раздел математики, который имеет важное применение в области техники и технологий. Он имеет дело с символами, называемыми переменными, которые представляют значение любой величины в любом случае, и правилами манипулирования этими символами.

Чтобы учащийся преуспевал в таких темах, как линейные уравнения с двумя переменными, квадратные уравнения и т. д., необходимо тщательно изучить формулу алгебры 10 класса.

Формулы математики для класса 10 Алгебра

класс 10 Алгебраические идентичности

1. (A + B) 2 = A2 + 2AB + B2

2. (A — B) 2 = A2 — 2AB + B2

3. (A — B) 2 = A2 — 2AB + B2

(A — B) 2 = A2 -2AB + B2

(A — B) 2 = A2 — 2

4. (A — B) 2 = A2 — 2

5. (а + b)(a – b) = a2 – b2

6. (x + a)(x + b) = x2 + (a + b)x + ab

7. (x + a) (x – b) = x2 + (a – b)x – ab

8. (x – a)(x + b) = x2 + (b – a)x – ab

9. (x – a) (x – b) = x2 – (a + b)x + ab

10. (а + b)3 = a3 + b3 + 3ab(a + b)

11. (a – b)3 = a3 – b3 – 3ab(a – b)

12. (x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2xz

13. (x + y – z)2 = x2 + y2 + z2 + 2xy – 2yz – 2xz

14. (x – y + z) )2 = x2 + y2 + z2 – 2xy – 2yz + 2xz

15. (x – y – z)2 = x2 + y2 + z2 – 2xy + 2yz – 2xz

16. x3 + y3 + z3 = 3xy3 (x + y + z)(x2 + y2 + z2 – xy – yz − xz)

17. (x + a)(x + b)(x + c) = x3 + (a + b + c)x2 + (ab + bc + ca)x + abc

18. x3 + y3 = (x + y)(x2 – xy + y2)

19. x3 – y3 =(x – y)(x2 + xy + y2)

20. x2 + y2 + z2 – xy – yz – zx = 12[(x − y)2 + (y − z)2 + (z − x)2]

21. x2 + y2 = 1/2[(x + y)2 + (x – y)2]

Формула для квадратных уравнений

Для ax2 + bx + c = 0,

(α, β) = [−b±(b2−4ac)/√2ac

, когда α и β являются корнями уравнения.

1. Если b2 − 4ac > 0, то квадратное уравнение имеет два различных действительных корня.

2. Если b2 − 4ac < 0, то квадратное уравнение имеет два мнимых корня.

3. Если b2 − 4ac = 0, то квадратное уравнение имеет два равных действительных корня.

Формула арифметической прогрессии

1. n-й член арифметической прогрессии: an = a + (n – 1)d 

2. Сумма n членов арифметической прогрессии: Sn = n/2 2a+(n–1)d

3. n-й член геометрической прогрессии: an = a.rn-1

4. Сумма n члены геометрической прогрессии: Sn = a (1 – rn)/ (1 – r), r≠1

5. Сумма бесконечных членов геометрической прогрессии: S = a/ (1 – r)

Важные ключевые слова

Ниже перечислены некоторые важные понятия, используемые в алгебраических формулах, о которых должен знать учащийся:

• Алгебраическое выражение состоит из различных комбинаций констант и переменных, связанных посредством различных символов операций сложения, вычитания, деления и умножения. (+, -, /, x)

• Различные члены составляют алгебраическое выражение.

• Коэффициент относится к числовому коэффициенту, полученному в термине.

• Подобные термины — это термины с одинаковыми алгебраическими факторами. Тогда как непохожие термины — это термины, которые имеют разные алгебраические факторы.

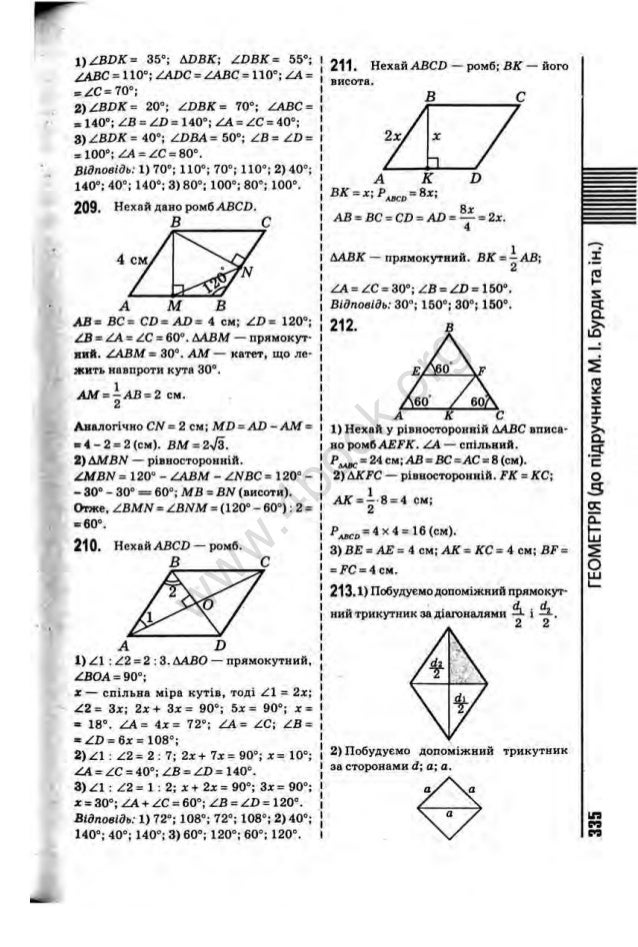
• Алгебраическое выражение, состоящее только из одного члена, называется мономом.

• Алгебраическое выражение, состоящее всего из двух членов, называется биномиальным выражением.

• Алгебраическое выражение, содержащее более двух членов, называется полиномиальным выражением.

• При добавлении двух или более одинаковых терминов получается еще один аналогичный термин с числовым коэффициентом. Этот результирующий числовой коэффициент эквивалентен сумме всех числовых коэффициентов всех соответствующих подобных членов.

• При вычитании двух или более одинаковых терминов получается еще один аналогичный термин с числовым коэффициентом. Этот результирующий числовой коэффициент эквивалентен разности всех числовых коэффициентов всех соответствующих одинаковых членов.

• Все одинаковые члены складываются вместе, а все непохожие не включаются и оставляются как есть в алгебраическом выражении.

Класс 10 Алгебраические задачи с решенными решениями

Ниже перечислены некоторые алгебраические задачи с их решенными решениями, чтобы помочь учащимся лучше понять, как разные алгебраические формулы работают в разных задачах.

1. Выразите следующие утверждения в виде алгебраических выражений, используя соответствующие переменные, константы и арифметические операции.

1. Вычитание x из y.

2. Одна треть суммы чисел a и b.

3. Число r, умноженное само на себя.

4. Половина произведения чисел s и t.

5. Числа c и d, возведенные в квадрат и вычтенные.

6. Число 10 прибавляется к пятикратному произведению чисел v и w

7. Произведение чисел y и x прибавляется к 20.

8. Сумма чисел a, b и c, вычтенная из их соответствующего произведения.

Ответ:

1.  y – x

2.  1/3 (a +b)

3.  r2

4.  ½ (st)

5.  c2 – d2 

6.  10 + 5 (vw)

7. xy + 20

8. abc – (a + b + c)

2. Найдите корни уравнения x2 – 10x – n (n + 10) = 0, где n – константа.

Ответ: 

Нам дано,

x2 – 10x – n (n + 3) = 0

Сравнивая ее с общей формулой алгебраического выражения ax2 + bx + c = 0, получаем:

a = 1, b = -10, c = – n (n + 10)

также знаем, что , D = (b2 – 4ac)

So

D = (- 10)2 – 4(1) [-n(n + 10)]

= 100 + 4n (n + 10)

= 4n2 + 40n + 100

= (2n + 10)2

подставив значение D в формулу квадрата: (α, β) = [–b ± √D]/2ac, получим:

(α, β) = [–10 ± √(2n + 10)2]/2x1x- n (n + 10)

Решив это уравнение, получим

(α, β) = (n + 10, -n)

Итак, корни данного квадратного уравнения равны (n + 10) и -n.

Практические задачи для учащихся

1. Найдите корни уравнения y2 – 5y – p (p + 5) = 0, где p – константа.

2. Если 1 является корнем уравнений az2 + az + 16 = 0 и x2 + x + b = 0, то найдите значение zx.

3. Найдите значение p, чтобы квадратное уравнение px(x – 4) + 16 = 0 имело два одинаковых корня.

4. Найдите значение q, чтобы квадратное уравнение qx (x – 10) + 100 = 0 имело два одинаковых корня.

5. Упростить алгебраическое выражение -2(x – 5) + 4(-3 x + 8)

6. Развернуть и упростить алгебраическое выражение x + 2) (x – 2) – (-x – 4)

7. При каких значениях k уравнение -x2 + 3kx – 9 = 0 имеет одно действительное решение?

8. Если (p2 – q2) = 10 и (p + q) = 2, найти p и q.