Разное

Физика степанов: ГДЗ по физике 10-11 класс Степанова решебник

Содержание

Степанов Сергей Всеволодович

Статус:
Заместитель начальника отдела атомно-масштабных исследований ФГБУ «ГНЦ РФ ИТЭФ»
доцент кафедры «Физика экстремальный состояний вещества» НИЯУ МИФИ
ведущий научный сотрудник кафедры Радиохимия Химфака МГУ

Образование:
1977-1983 физико-химический факультет МИСиС, специальность «Физика металлов»
1983-1986 Аспирантура ИТЭФ, специальность «Экспериментальная физика»

Ученые степени:
1987 г. Кандидат физико-математических наук, специальность (Теоретическая и математическая физика)
2005 г. Доктор физико-математических наук, специальность физика твердого тела

Ученые звания:
1995 г. Старший научный сотрудник

Научные интересы: физика твердого тела, радиационная физика и химия конденсированных сред

Прочитанные курсы лекций:

«Физика конденсированных сред», НИЯУ МИФИ, 2004-2014

Публикации:
Общее количество – более 100, в том числе за последние 5 лет – 20, 2 монографии, 1 патент на изобретения
Радиационная физика и химия, позитронная аннигиляционная спектроскопия
Результаты работ докладывались на многих отечественных и международных конференциях, совещаниях и школах, в том числе как приглашенные обзорные доклады

h-индекс: 8

WEB-site

Общественная научная деятельность, участие в работе научно-технических советов и подготовке специалистов:
с 2002 г. член Международного организационного комитета конференций по аннигиляции позитронов и позитрония (PPC)
с 2013 г. член Международного организационного комитета Азиатско-тихоокеанского симпозиума по радиационной химии (APSRC)
с 2013 г. член Экспертного Совета по аттестации программных средств при Ростехнадзоре (секция №7)
Научный руководитель одной защищенной кандидатской диссертации

    Институт физики имени Б.И. Степанова — НАЦИОНАЛЬНОЙ АКАДЕМИИ НАУК БЕЛАРУСИ


    27 декабря 2021 г. на всенародное обсуждение вынесен проект изменений и дополнений Конституции Республики Беларусь. С проектом изменений и дополнений Конституции Республики Беларусь можно ознакомиться  здесь. Мнения граждан относительно содержания проекта изменений и дополнений, а также возможные предложения по его совершенствованию направляются в Национальный центр правовой информации. Формы сбора предложений размещены здесь. Поступившие материалы будут обобщаться и систематизироваться Национальным центром… Читать далее »







    Уважаемые коллеги! Поздравляем с Днем белорусской науки! Желаем, чтобы каждый новый день был полон креативных и уникальных идей, полезных и великих открытий, интересных и достойных достижений. Пусть наука в нашей стране развивается и влечёт за собой всё больше и больше талантливых, изобретательных, целеустремлённых людей. Дирекция, Профком, СМУ







    По давно сложившейся традиции Степановские чтения проводятся  в день образования Института физики НАН Беларуси — 17 января.  Ежегодно коллектив института заслушивает доклады по завершенным в предыдущем году научным исследованиям и разработкам, выполненным на высоком научном уровне. Заслушивание докладов по выдвинутым работам и присуждение премий на расширенном заседании Ученого совета проводится в Институте ежегодно, начиная с 1958 года. До 1988 года это… Читать далее »







    Федор Иванович Федоров родился 19 июня 1911 г. в семье сельского учителя И.М. Федорова — впоследствии крупнейшего белорусского детского писателя Янки Мавра. В 17 лет окончил среднюю школу в г. Минске, в 20 лет — физико-математическое отделение педагогического факультета Белорусского государственного университета. Самостоятельную трудовую деятельность Федор Иванович начал в 1931г. преподавателем физики и математики педагогического техникума в одном из районных… Читать далее »







    В этом году традиционные Степановские чтения прошли 28 апреля — в День рождения Бориса Ивановича Степанова. Ежегодно коллектив института заслушивает доклады по завершенным в предыдущем году научным исследованиям и разработкам, выполненным на высоком научном уровне. Заслушивание докладов по выдвинутым работам и присуждение премий на расширенном заседании Ученого совета проводится в Институте ежегодно, начиная с 1958 года. До 1988 года это… Читать далее »







    22 апреля 2021 года состоялось торжественное открытие Доски Почета Национальной академии наук Беларуси. В соответствии с Постановлением Бюро Президиума НАН Беларуси от 23.03.2021 № 123 признаны победителями и занесены на Доску почета Национальной академии наук Беларуси за достижение в 2020 году наилучших результатов в научной, научно-технической и инновационной, производственной деятельности следующие организации Национальной академии наук Беларуси:в категории «научные организации»:— государственное… Читать далее »






    Степанов Сергей Васильевич | Сотрудники

    № Наименование работы Форма работы Выходные данные Объем в страницах Соавторы
    1

     

    		 Разработка проекта программы и содержания базисных тем курса физики средних ПТУ машиностроительного и строительного профилей с учетом связи курса физики с общетехнической подготовкой выпускников. Печатная Отчет по НИР № 28/82-3от 1. 04.82 с НИИ Профтехпедагогики АПН СССР. № госрегистрации 01825054749. 136 с. 25 Бобкова М.А.

    Каменецкий С.Е.

    Дунин С.М.

    Пурышева Н.С.
    2 Разработка исходных требований на модернизацию учебных приборов по физике. Печатная Отчет по НИР № 18/84 от 1.01.84 с Главучтехпромом МП РСФСР. № госрегистрации 1840066825. 67с. 45 Анофрикова С.В.

    Павлюков В.К.
    3 Компьютерная дидактическая игра «Баскетбол». Методическая разработка. Печатная Информатика и вычислительная техника. Сборник педагогических программ слушателей ФПК. -М.: МГПИ,1987. С 14-15, 74-76. 4 –
    4 Разработка методического обеспечения курса физики в средних ПТУ, включающего вопросы применения ЭВМ, программу и методику факультативных занятий.   Отчет по НИР. Печатная Отчет по НИР № 2/86 от 1,04.82 с НИИ  Профтехпедагогики АПН СССР. № госрегистрации 01860055810. 150 с. 31 Бобкова М.А.

    Каменецкий С.Е.

    Дунин С.М.

    Пурышева Н.С.
    5 Использование графопроектора для совершенствования учебного эксперимента по физике. Методические рекомендации. Печатная Методика преподавания физики (методические рекомендации для студентов 3-5 курсов)М.: Прометей, 1990. С 53-61. 9 –
    6 Комплексное использование учебного оборудования как один из путей совершенствования школьного физического эксперимента. Печатная Методика преподавания физики (методические рекомендации для студентов 3-5 курсов)М.: Прометей, 1990. С 64-70. 7 –
    7 Опорные конспекты и дидактические материалы по разделу «Молекулярная физика» для средних ПТУ. Методическое руководство. Печатная М.А. Бобкова, С.М. Дунин, С.Е.Каменецкий и др.  Опорные конспекты и дидактические материалы по разделу «Молекулярная физика» для средних ПТУ. Методическое руководство.  Москва,1990. 7 п.л. 15 Бобкова  М.А., Дунин  С.М., Каменецкий  С.Е.,

    Прояненкова Л.А.

    Пурышева Н.С.
    8 Повторение механики с использованием опорных конспектов и дидактических материалов в средних ПТУ. Методическое руководство. Печатная М.А. Бобкова, С.М. Дунин, С.Е.Каменецкий и др.  Повторение механики с использованием опорных конспектов и дидактических материалов в средних ПТУ. Москва,1990. 5,3 п.л. 12 Бобкова  М.А., Дунин  С.М., Каменецкий  С.Е.,

    Прояненкова Л.А.

    Пурышева Н.С.
    9 Спецпрактикум как средство развития интереса студентов к творчеству в области школьного эксперимента. Печатная Журнал «Физика в школе», №3-4,1992. С 42-43 1,5 –
    10 Методические рекомендации к проведению занятий спецпрактикума по методике преподавания физики.

    Материалы к эксперименту.

    		 Печатная Методические рекомендации к проведению занятий спецпрактикума по методике преподавания физики: материалы к эксперименту. М.: Прометей, 1992. 85 с.

    материалы к эксперименту.

    		 85 –
    11 Расширение функциональных возможностей школьных осциллографов. Печатная Дифференциация обучения физике в средней школе и педагогическом университете. М.: МПУ,1992. С 31-33. 2 –
    12 Спецпрактикум по методике преподавания физики как средство совершенствования подготовки студентов для работы в условиях дифференциации школьного обучения. Печатная Дифференциация обучения физике в средней школе и педагогическом университете. М.: МПУ,1992. С 48-50. 3 –
    13 Учебно-материальная база для подготовки студентов к эксплуатации школьных физических кабинетов Печатная Материалы научной сессии по итогам научно-исследовательской работы МПГУ им. В.И.Ленина за 1991г. Серия: Естественные науки. М.: Прометей, 1992. С 90-91. 2 Каменецкий С.Е.

    Смирнов А.В.
    14 Совершенствование подготовки студентов к работе с оборудованием школьного кабинета физики Печатная Материалы научной сессии по итогам научно-исследовательской работы МПГУ им. В.И.Ленина за 1991г. Серия: Естественные науки. М.: Прометей, 1992. С 92-93. 2 Каменецкий С.Е.

    Смирнов А.В.
    15 Спецпрактикум по методике преподавания физики как средство совершенствования подготовки будущих учителей в области школьного физического эксперимента. Печатная Теория и практика обучения физике в современной школе./межвузовский сборник научных трудов. М.: Прометей, 1992. С 97 -104. 6 –
    16 Приставка к графопроектору для моделирования физических явлений. Печатная Журнал «Физика в школе», №5,1993. С 48-50. 2 –
    17 Новый подход к изучению школьных источников электропитания установок. Печатная Образовательный стандарт по физике (средняя школа и педагогический ВУЗ). М.: МПУ, 1993. С 69 -71. 2 –
    18 Подготовка студентов к творческому использованию учебных приборов по физике. Печатная Образовательный стандарт по физике (средняя школа и педагогический ВУЗ). М.: МПУ, 1993. С 134-136. 3 –
    19 Применение графопроектору в демонстрациях по молекулярной физике. Печатная Физика. Приложение к газете «Первое сентября», №11-12, 1993. С 2 1 –
    20 Усилитель и генератор из осциллографа. Печатная Физика. Приложение к газете «Первое сентября», №15-16, 1993. С 8 1 –
    21 Повышение надежности источника электропитания ИЭПП-2. Печатная Физика. Приложение к газете «Первое сентября», №21-22, 1993. С 8 1 –
    22 Простейшие опыты по механическим колебаниям. Печатная Методические советы начинающему учителю физики/ Под ред. С. Е. Каменецкого. –М.: Прометей, 1993. С 87-89. 3 –
    23 Цифровой способ подсчета ионизирующих частиц в опытах по физике. Печатная Методические советы начинающему учителю физики/ Под ред. С.Е. Каменецкого. –М.: Прометей, 1993. С 90-91. 1 –
    24 Автоматизированный комплекс сопровождения лекций по физике. Печатная Использование научно-технических достижений в демонстрационном эксперименте и постановке лабораторных практикумов. Тезисы докладов/ Мордовский Государственный пединститут им. М.Е.Евсевьева. Саранск,1994. С 24 1 Смирнов А.В.
    25 Улучшение видимости результатов опыта в помощью ТСО. Печатная Использование научно-технических достижений в демонстрационном эксперименте и постановке лабораторных практикумов. Тезисы докладов/ Мордовский Государственный пединститут им. М.Е.Евсевьева. Саранск,1994. С 62 1 Смирнов А.В.
    26 Применение элементной базы цифровой техники в учебном физическом эксперименте. Печатная Использование научно-технических достижений в демонстрационном эксперименте и постановке лабораторных практикумов. Тезисы докладов/ Мордовский Государственный пединститут им. М.Е.Евсевьева. Саранск,1994. С 63 1 –
    27 Организация современных кабинетов физики. Печатная Научные труды Московского педагогического государственного университета им. В.И. Ленина. Серия: естественные науки. М.: Прометей, 1994. С 143. 1 Смирнов А.В.
    28 Развитие материальной базы школьного кабинета физики на основе модернизации учебных приборов. Печатная Научные труды Московского педагогического государственного университета им. В.И. Ленина. Серия: естественные науки. М.: Прометей, 1994. С 126. 1 Гуренко Л.В.
    29 Особенности освоения новых приборов в школьных условиях. Печатная Контроль и образовательный стандарт по физике. М.: МПУ, 1994. С 36-38. 2 –
    30 Применение графопроектора в опытах с диапроекцией. Печатная Физика. Приложение к газете «Первое сентября», 5-6, 1994. С 4 1 –
    31 Применение графопроектора в опытах по волновой оптике. Печатная Физика. Приложение к газете «Первое сентября», 9-10, 1994. С 2 1 –
    32 Новые учебно-тренажерные системы для кабинетов физики. Печатная Преподавание физики и астрономии в школе: состояние, проблемы, перспективы./ Тезисы докладов региональной научно-методической конференции (21-22 апреля 1994г.). Н.Новгород, 1994. С 46-47. 1 Смирнов А.В.
    33 Пути использования современных ТСО в школьном физическом эксперименте. Печатная Преподавание физики и астрономии в школе: состояние, проблемы, перспективы./ Тезисы докладов региональной научно-методической конференции (21-22 апреля 1994г.). Н.Новгород, 1994. С 47-48. 1 Смирнов А.В.
    34 Уточнение классификации школьных физических приборов. Печатная Научные труды Московского педагогического государственного университета им. В.И. Ленина. Серия: естественные науки. М.: Прометей, 1995. С 266-267. 2 –
    35 Из опыта использования современной видеотехники в учебном эксперименте по физике. Печатная Научные труды Московского педагогического государственного университета им. В.И. Ленина. Серия: естественные науки. М.: Прометей, 1995. С274-275 1 –
    36 Новый подход к материальному обеспечению школьного физического практикума. Печатная Научные труды Московского педагогического государственного университета им. В.И. Ленина. Серия: естественные науки. М.: Прометей, 1996. С 120-121. 1 Гуренко Л.В.
    37 Подготовка магистров образования по физике к исследовательской работе в области школьного физического эксперимента. Печатная Научные труды Московского педагогического государственного университета им. В.И. Ленина. Серия: естественные науки. М.: Прометей, 1996. С 121-122 1 –
    38 Учет требований техники безопасности как фактор повышения качества самодельных приборов по физике. Печатная Научные труды Московского педагогического государственного университета им. В.И. Ленина. Серия: естественные науки. М.: Прометей, 1996. С 123-124. 1 –
    39 Современные проблемы школьного практикума по физике и возможные пути их решения. Печатная Научные труды Московского педагогического государственного университета им. В.И. Ленина. Серия: естественные науки. М.: Прометей, 1997. С 191-193. 2 –
    40 К вопросу о комплектовании школ учебным оборудованием по физике. Печатная Научные труды Московского педагогического государственного университета им. В.И. Ленина. Серия: естественные науки. М.: Прометей, 1997. С 193-194. 1 –
    41 Цифровые мультиметры в лабораторном эксперименте по физике. Печатная Физика. Приложение к газете «Первое сентября», 36, 1998. С 14-15 2 –
    42 Установка для демонстрации свойств электромагнитных волн. Печатная Приложение к журналу «Наука и школа», №2,1999. С 7 – 10 4 Якушин А.А.
    43  Электронный секундомер для опытов по механике. Печатная Журнал «Физика в школе», №4,1999. С 53-54 2 Якушин А.А.
    44 Учебный эксперимент по физике при дистанционном образовании. Печатная Научные труды МПГУ. Серия: естественные науки. Сборник статей. –М.: Прометей, 2001. С 94 -98. 4,5 –
    45 Практикум по школьному физическому эксперименту. Печатная Научные труды МПГУ. Серия:  естественные науки. Сборник статей. –М.: Прометей, 2001. С 101-104. 3 Каменеций С.Е.
    46 Новый подход к проведению учебного эксперимента по физике. Печатная Научные труды МПГУ. Серия: естественные науки. Сборник статей. –М.: Прометей, 2001. С 125 -126. 2 –
    47 Демонстрационный эксперимент на видеокассете – новая составная часть средств наглядности. Печатная Журнал «Наука и школа», №6,2002. С 34-37 4

     

    		 Разумный Д.В.
    49 Модернизация типовых индивидуальных комплектов малогабаритного школьного лабораторного оборудования ля углубленного изучения физики, химии и биологии.

     

    		 Печатная Отчет по НИР выполненной по НТП «Научное, научно-методическое, материально-техническое обеспечение развития технологий информационного общества и индустрии образования» № 3. 2.21 за 2003 г.

    № госрегистрации 01.20.03 13865 95 с.

    		 31 Евстигнеев В.Е.

    Пичугин В.С.

    Пичугина Г.В.

    Пугал Н.А.
    49 Учебный эксперимент по физике при дистанционном образовании. Печатная Научные труды МПГУ. Серия: Естественные науки. Сборник статей. –М.: Прометей, 2003. С 178-180. 3 Разумный Д.В.
    50 Новая методика проведения лабораторной работы по механике. Печатная Научные труды МПГУ. Серия: Естественные науки. Сборник статей. –М.: Прометей, 2003. С 180 – 181. 2 –
    51 Изучение цепей переменного тока при проведении лабораторных занятий в школе. Печатная Научные труды МПГУ. Серия: Естественные науки. Сборник статей. –М. : Прометей, 2003. С 182 – 187. 5 –
    52 Принципы создания видеозаписей демонстрационных опытов по физике. Печатная Научно-методический журнал «Преподавание физики в высшей школе», №26, 2003. С 73 – 77 4 Разумный Д.В.
    53 О физическом эксперименте на видеокассетах. печатная Журнал «Физика в школе», №8,2004. С 73-75. 2 Разумный Д.В.
    54 Специфика современных учебных измерительных приборов по физике. печатная Научные труды МПГУ. Серия: Естественные науки. Сборник статей. –М.: ГНО Издательство «Прометей» МПГУ, 2005. С 185-188. 4 –
    55 О необходимости модернизации школьных лабораторных весов.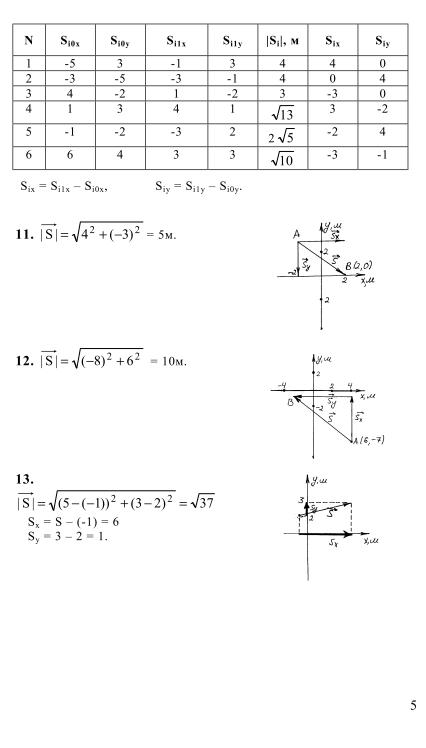 печатная Научные труды МПГУ. Серия: Естественные науки. Сборник статей. –М.: ГНО Издательство «Прометей» МПГУ, 2005. С 189-192. 4 –
    56 Дидактические особенности видеозаписей учебных опытов по физике. печатная Научные труды МПГУ. Серия: Естественные науки. Сборник статей. –М.: ГНО Издательство «Прометей» МПГУ, 2005. С 193-197. 4 Разумный Д.В.
    57 Применение компьютера в качестве осциллографа в учебных опытах по физике. Печатная Научные труды МПГУ. Серия: Естественные науки. Сборник статей. –М.: ГНО Издательство «Прометей» МПГУ, 2006. С 159-161. 3 –
    58  Подготовка студентов к использованию информационных технологий в учебном эксперименте по физике. Печатная Научные труды МПГУ. Серия: Естественные науки. Сборник статей. –М.: ГНО Издательство «Прометей» МПГУ, 2006. С 162-164. 3 –
    59 Один из факторов повышения эффективности учебного эксперимента по физике. печатная Научные труды МПГУ. Серия: Естественные науки. Сборник статей. –М.: ГНО Издательство «Прометей» МПГУ, 2006. С 165-166. 2 –
    60 Особенности новых комплектов электроснабжения кабинета физики. печатная Журнал «Физика в школе», №3,2006. С 62-64. 3 Евстигнеев В.Е.
    61 Комплект электроснабжения для учебных кабинетов малочисленных школ. печатная Журнал «Справочник руководителя сельской школы», № 7, 2006. С 14-17. 4 Евстигнеев В.Е.

    Пичугин В.С.

    Штерн Ю.И.
    62 Технологии обучения инвалидов и лиц с ограниченными возможностями здоровья естественнонаучным дисциплинам с использованием микролабораторий и виртуальных лабораторий в учреждениях общего образования печатная “Школа будущего”  №6, 2010 7 Боридко В.С.

    Корнюшко В.Ф.

    Пичугин В.С.
    63 Учебное оборудование по физике для малокомплектных школ печатная Сборник трудов докладов Всероссийского Съезда учителей физики. М, МГУ, 28-30 июня 2011. 3
    64 Использование для экспериментальных заданий ГИА наборов оборудования для сельских школ печатная В кн.”Физика: ГИА: сборник экспериментальных заданий для подготовки к государственной аттестации в 9 классе” / ГГ Никифоров, ЕЕ Камзеева, МЮ Демидова; под ред. МЮ Демидовой.-М.; СПб.: Просвещение,2012 12
    65 Кабинет “Естествознание” сельской малочисленной школы Электронное приложение к журналу Физика в школе №2, 2012 Пурышева Н.С.
    66 Использование учебного физического  эксперимента для активизации познавательного интереса учеников печатная “Физика” №8, 2012 Издательский дом “1-е сентября
    67 Система ученического эксперимента по теме “Газовые законы”  

    печатная

    		 Материалы Х111 Международной научно-методической конференции “Физическое образование: проблемы и перспективы развития”. Часть 1. -М.:МПГУ, 2014 4 Паутова А.А.
    68 Новые возможности информационных технологий при проведении лабораторных работ по физике печатная Материалы Х111 Международной научно-методической конференции “Физическое образование: проблемы и перспективы развития”. Часть 1. -М.:МПГУ, 2014 3 Степанов А.С.

    Паутова А.А.
    68 Лабораторный комплекс для учебной практической и проектной деятельности по естествознанию  

    печатная

    		 Материалы Х111 Международной научно-методической конференции “Физическое образование: проблемы и перспективы развития”. Часть 2. -М.:МПГУ, 2014 3 Пичугин В.С.

    Паутова А.А.
    70 Реализация системно-деятельностного подхода при проведении учебных опытов по физике печатная Материалы 11 Международной научно-методической конференции “Физикоматематическое и технологическое образование: проблемы и перспективы развития”. Часть 1. -М.:МПГУ, “Onebook.ru”, 2016 4 Пичугин В.С.
    71 Совершенствование системы ученического эксперимента по физике в свете требований ФГОС печатная Материалы 11 Международной научно-методической конференции “Физикоматематическое и технологическое образование: проблемы и перспективы развития”. Часть 1. -М.:МПГУ, “Onebook.ru”, 2016 4
    72 Определение скорости света в веществе печатная “Физика в школе” , 2017, №3 с 44-45.
    73 О наблюдении внешнего фотоэффекта печатная Материалы IV Международной научно-методической конференции «Физико-математическое и технологическое образование: проблемы и перспективы развития» . Часть 1. -М.:МПГУ, 2018.
    74 Учебные приборы для изучения внутреннего фотоэффекта печатная Материалы IV Международной научно-методической конференции «Физико-математическое и технологическое образование: проблемы и перспективы развития» . Часть 1. -М.:МПГУ, 2018.

    Степанов, Борис Иванович (физик) — Wikiwand

    Биография

    Родился 15 (28 апреля) 1913 года в Санкт-Петербурге. После окончания девятилетки учился в ФЗУ, а в 1930 году поступил в Ленинградский университет. С 1934 году одновременно работал в ГОИ. После окончания университета в 1936 году поступил в аспирантуру ГОИ, а через три года защитил кандидатскую диссертацию на тему «Исследование резонансных возмущений в спектрах двухатомных молекул». В июле 1941 году ушёл добровольцем на фронт, воевал в составе 162-го партизанского отряда Ленинградского фронта, а затем и на Сталинградском фронте.

    В январе 1943 года отозван из армии для научной работы в ГОИ, находившемся тогда в эвакуации в Йошкар-Оле. В 1948 году защитил докторскую диссертацию по теме «Расчет частот колебаний сложных органических молекул». До 1953 года работал в ГОИ, с 1951 начальник лаборатории.

    Преподавал в ЛИТМО, являлся одним из создателей инженерно-физического факультета. Доцент, затем профессор кафедры теоретической физики (1946—51).

    В 1953 году приглашён в Институт физики АН БССР, в 1955—1973 годах заведовал лабораторией, в 1957—1985 годах — директор института. Одновременно с 1953 года — профессор БГУ имени В. И. Ленина, до 1963 года возглавлял кафедру спектрального анализа. В 1985—1987 годах являлся членом и советником Президиума АН БССР. С 1964 года и до конца жизни — главный редактор выходящего в Минске всесоюзного «Журнала прикладной спектроскопии».

    Член ВКП(б) с 1939 года, в 1971—86 годах депутат Верховного Совета БССР.

    Создал в Беларуси крупную научную школу, среди его учеников — 11 докторов и 45 кандидатов наук. Его именем назван Институт физики Национальной академии наук Беларуси.

    Научная деятельность

    Работы Степанова посвящены спектроскопии, люминесценции, квантовой электронике, а также нелинейной оптике, лазерной спектроскопии, оптической голографии, вопросам истории оптики.

    Первая работа Степанова, опубликованная в 1935 году, была посвящена теоретическому объяснению тонкого расщепления метастабильных уровней азота, наблюдавшемуся в экспериментах. В 1939 году им была развита теория аномалий в спектрах двухатомных молекул на основе методов численного определения матричных элементов взаимодействия уровней из экспериментальных данных. В 1940-е годы основным направлением деятельности стала разработка теории колебательных спектров многоатомных молекул и её применение для конкретных расчётов. В частности, в 1945 году Степанов исследовал влияние водородных связей на спектры поглощения, а в 1948 году предложил удобные приближённые методы расчёта колебательных спектров сложных органических молекул. Стройная теория спектров многоатомных молекул была изложена в классической монографии «Колебания молекул» (соавторы — М. В. Волькенштейн и М. А. Ельяшевич).

    В 1950-е годы Степанов, отталкиваясь от основополагающих работ С. И. Вавилова, развил квантовомеханическую теорию люминесценции и поглощения света, позволяющую единым образом описать характеристики этих процессов и основные экспериментальные факты. На основе этой теории был получен ряд важных результатов. Так, в 1955 году было впервые показано, что энергетический выход люминесценции системы с тремя уровнями энергии может превышать единицу. В 1956 году Степанов предсказал существование явления отрицательной люминесценции, которая проявляет себя как спектральный провал на фоне широкополосного равновесного теплового излучения. В последующие годы учёный систематически разработал теоретические основы спектроскопии отрицательных световых потоков, в рамках которой получили своё описание новые оптические явления — отрицательная люминесценция и отрицательный фотоэффект. В 1957 году он показал, что спектры поглощения и люминесценции сложных молекул связаны между собой соотношением, не зависящим от индивидуальных свойств молекул (универсальное соотношение Степанова). Обратившись к проблеме классификации вторичного свечения, в 1959 году Степанов совместно со своим учеником П. А. Апанасевичем обосновали в качестве принципиального отличия между люминесценцией и рассеянием наличие промежуточных процессов, происходящих в промежутке между моментами поглощения первичных и испускания вторичных фотонов.

    С начала 1960-х годов основной сферой деятельности Степанова становится лазерная физика и нелинейная оптика. Так, уже в 1960 году совместно с В. П. Грибковским он провёл расчёт зависимости поглощения и люминесценции в трёхуровневой системе от интенсивности возбуждающего излучения. В последующие годы Степановым вместе с учениками были заложены основы инженерных методов расчёта лазерных систем, в частности в 1964 году были предложены простые вероятностные методы расчета энергетических и временных характеристик оптических квантовых генераторов. В этом цикле работ с единых физических позиций были рассмотрены все стороны процесса генерации света (соавторы — В. П. Грибковский, А. С. Рубанов, А. М. Самсон). В статье, написанной в 1965 году совместно с П. А. Апанасевичем, была построена теория внутрирезонаторного вынужденного комбинационного рассеяния; в дальнейшем эта тематика успешно развивалась в институте, возглавлявшемся Степановым.

    Широкое признание получили работы Степанова, связанные с открытием нового класса лазерных сред — органических красителей. Сначала в 1964 году им совместно с А. Н. Рубиновым и В. А. Мостовниковым была предсказана теоретически возможность генерации на растворах ряда красителей, а спустя три года (одновременно с учеными США и ФРГ) они осуществили её экспериментально. В Институте физики АН БССР была создана серия соответствующих лазеров с плавно перестраиваемой частотой излучения в широкой области спектра. В 1972 году эта деятельность была отмечена Государственной премией СССР.

    В работах Степанова и его учеников были заложены основы динамической голографии, разработаны новые методы преобразования световых пучков. В частности, в 1970 году он совместно с А. С. Рубановым и Е. В. Ивакиным обнаружил явление обращения волнового фронта при четырёхволновом взаимодействии.

    Музей университет ИТМО

    Выдающийся ученый и организатор науки, академик АН БССР (1953), Герой Социалистического Труда. Работал в ЛИТМО (1946-51), являлся одним из создателей ИФФ. Доктор физико-математических наук, профессор. Трижды лауреат Государственных премий.

     

    Окончил Ленинградский государственный университет (ЛГУ) (1936). С 1936 г. по 1953 г. работал в ГОИ (аспирант — 1936-39).

    Участник Великой Отечественной войны. Партизан, служил в Рабоче-крестьянской красной армии (РККА) (1941-43).

    Работал в ЛИТМО (1946-51). Являлся одним из создателей инженерно-физического факультета ЛИТМО. Доцент, профессор кафедры теоретической физики (1946-51).

    Кандидат физико-математических наук (1939), старший научный сотрудник (1947), доктор физико-математических наук (1947), профессор кафедры теоретической физики (1950).

    Создал в Минске крупную научную школу в области оптики и лазерной физики. 28 лет был директором Института физики АН БССР, главным редактором журнала «Журнала прикладной спектроскопии». В настоящее время его имя носит Институт физики Национальной академии наук Беларуси.

    Лауреат трех Государственных премий СССР (1950, 1972, 1982) и Государственной премии БССР, лауреат золотой медали им. С.И. Вавилова (1970), заслуженный деятель науки БССР, почетный доктор Сегедского университета (Венгрия) (1971).

    Автор 6 научных монографий и более 350 работ в области спектроскопии, люминесценции, квантовой электроники, нелинейной оптике, голографии.

    Награжден орденами Ленина, Октябрьской Революции, Отечественной войны, Дружбы народов, Знак Почета, двумя орденами Трудового Красного Знамени и многими медалями.

    Информация об академике Б.И. Степанове в Интернет:

    Борис Иванович Степанов (к шестидесятилетию со дня рождения) // Успехи физических наук, 1973. — Том 110, вып 1. — С.154-156

    Степанов, Борис Иванович // Википедия: свободная энциклопедия

    Кафедра общей физики | Радиофизический факультет

    Сайт кафедры

    Кафедра создана в 1934 году. Ее возглавил проф. Г.С. Горелик, впоследствии один из основателей радиофизического факультета и Горьковской (Нижегородской) школы радиофизики. В 1952 году кафедра основной частью вошла в состав радиофизического факультета. Впоследствии кафедрой руководили доцент А.Г. Любина, профессор, член-корр. РАН В.А. Зверев, доцент М.Н. Кром, профессор, заслуженный деятель науки РФ Н.С. Степанов. С 2004 года кафедрой заведует профессор М.И. Бакунов.

    Основная задача кафедры – фундаментальная общефизическая подготовка студентов младших курсов радиофизического факультета. Обучение ведется по оригинальным программам углубленного изучения и сопровождается уникальным лабораторным практикумом. При кафедре имеется Центр физических демонстраций, обеспечивающий демонстрационными опытами все факультеты университета, на которых читаются лекции по общему курсу физики.

    Совместно с ИПФ РАН и ИФМ РАН кафедра организует подготовку бакалавров по академически ориентированному профилю «Фундаментальная радиофизика». Кафедра обеспечивает магистерские программы «Электромагнитные волны в средах», «Квантовая радиофизика и лазерная физика», «Радиофизические методы в нейробиологии» и “Компьютерная радиофизика”.

    Основные научные направления

    • взаимодействие мощных ультракоротких лазерных импульсов с веществом;
    • нелинейно-оптические методы генерации и детектирования терагерцового излучения;
    • терагерцовая спектроскопия и терагерцовый имиджинг;
    • биофотоника и оптический нейроимиджинг;
    • голография;
    • оптика фотополимеризующихся сред;
    • электродинамика нестационарных и движущихся сред.

    Основные курсы

    • Общий курс физики (5 семестров)
    • Нелинейные волны в оптике
    • Сверхсильные световые поля
    • Генерация и регистрация терагерцового излучения ультракороткими лазерными импульсами
    • Оптическая обработка информации
    • Волновые процессы в нестационарных средах
    • Численный эксперимент в оптике
    • Компьютерное моделирование в научных исследованиях
    • Основы программирования
    • Методы математического моделирования
    • Моделирование информационных процессов
    • Параллельное программирование и высокопроизводительные вычисления.

    Ури Шумлак | Воздухоплавание и космонавтика

    Профессор

    Заместитель председателя академического отдела

    Профессор

    Аэронавтика и космонавтика

    Заместитель заведующего кафедрой исследований

    Аэронавтика и космонавтика

    Биография

    Профессор Шумлак завершил свою бакалаврскую работу в Техасе.
    Университет A&M, а затем получил докторскую степень в области ядерной инженерии в
    Калифорнийский университет в Беркли.После окончания аспирантуры он
    был постдокторантом Национального исследовательского совета в ВВС Филлипс.
    Лаборатория в Альбукерке, Нью-Мексико, где он написал MACh4, трехмерный
    зависящий от времени магнитожидкостный код для неидеальной плазмы сложной геометрии.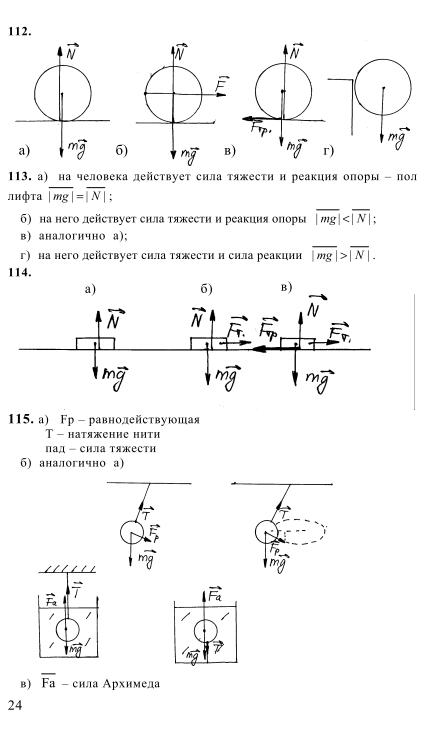
    Профессор Шумлак поступил в Вашингтонский университет после окончания
    Phillips Lab, хотя он по-прежнему поддерживает тесные связи с Исследовательским центром ВВС.
    Lab и часто проводит исследования в поддержку своих приложений.Он
    активно участвует в исследованиях и неоднократно приглашался выступить на
    международные конференции. Он получил множество наград за свое преподавание,
    исследования и наставничество. Профессор Шумлак является членом Американского физического
    Общество, ассоциированный член Американского института аэронавтики и
    космонавтики, старший научный сотрудник Института электротехники и
    Инженеры-электронщики. Он также стал соучредителем Zap Energy — дочерней компании.
    от UW для разработки коммерческих приложений термоядерного синтеза.

    Область исследований профессора Шумлака: физика плазмы,
    теоретическое и расчетное моделирование плазмы, инновационная магнитная плазма
    удержание энергии синтеза и электрическая тяга. Его работа включает
    теоретическое и экспериментальное исследование стабилизирующего эффекта сдвига
    течения в магнитно-удерживаемой плазме. Z-пинч, стабилизированный сдвиговым потоком,
    имеют немедленное применение в качестве краткосрочного термоядерного двигателя для космоса
    разведка и компактный термоядерный источник энергии.Концепция потока
    стабилизация также может применяться к другим магнитным ограничениям.
    приборы и астрофизические плазмы. Концепция проточного Z-пинча также была
    превратился в источник экстремального ультрафиолетового (EUV) света, который применим
    для литографии нового поколения. Профессор Шумлак разрабатывает передовую плазму
    алгоритмы моделирования, использующие приближенный римановский решатель и алгоритмы высокого порядка.
    методы конечных элементов для изучения временной эволюции динамики плазмы. Он
    также исследует электрические двигательные установки.Недавно он разработал роман
    способ изготовления сильноточных источников ионов, основанный на использовании ультразвуковых приводов
    для возбуждения неустойчивых волн в жидкости и применения электрического поля для извлечения
    монодисперсные, заряженные капли. Источник имеет приложения к наночастицам
    напыление, композитное покрытие и электродвигатель.

    Образование

    • Кандидат наук, Калифорнийский университет в Беркли
    • Бакалавр наук, Техасский университет A&M

    Избранные публикации

    1. У.Шумлак. Z-Pinch Fusion. Journal of Applied Physics 127, 200901 (2020) [Избранная статья, статья с приглашенными перспективами]
    2. Э.Л. Клаво, У. Шумлак, Б.А. Нельсон, Э.Г. Forbes, А.Д. Степанов, Т.Р. Вебер, Ю. Чжан и Х.С. Маклин. Выхлоп плазмы в Z-пинче, стабилизированном сдвиговым потоком. Физика плазмы 27, 092510 (2020)
    3. Ю. Чжан, У. Шумлак, Б.А. Нельсон, Р.П. Голинго, Т.Р. Вебер, А.Д. Степанов, Е.Л. Клаво, Э.Г. Форбс, З.Т. Дрейпер, Дж. М. Митрани, Х.С. Маклин, К.К. Таммель, Д.П. Хиггинсон и К.М. Купер. Устойчивое образование нейтронов из Z-пинча, стабилизированного сдвиговым потоком. Письма о физическом обзоре 122, 135001 (2019) [Избранная статья]
    4. К. К. Таммель, Д.П. Хиггинсон, А.Дж. Ссылка, A.E.W. Шмидт, Д.Т. Офферманн, Д.Р. Уэлч, Р.Э. Кларк, У. Шумлак, Б.А. Нельсон, Р.П. Голинго и Х.С. Маклин. Кинетическое моделирование стабилизации сдвигового течения в высокотемпературной плазме Z-пинча. Физика плазмы 26, 062506 (2019) [Приглашенная статья]
    5. А.Хо, И.А.М. Датта и У. Шумлак. Адаптивная модель плазмы, основанная на физике, для высокоточного численного моделирования. Границы физики 6, 105 (2018)
    6. Г.В. Фогман, У. Шумлак и П. Колелла. Консервативный решатель конечного объема Власова-Пуассона четвертого порядка для осесимметричной плазмы в цилиндрических (r, vr, vtheta) координатах фазового пространства. Журнал вычислительной физики 373, 877 (2018)
    7. У. Шумлак, Б.А. Нельсон, Э.Л. Клаво, Э.Г. Forbes, Р.П. Голинго, М.К. Хьюз, Р.Дж. Оберто, член парламента Росс и Т.Р. Вебер. Увеличение параметров плазмы за счет стабилизации сдвигового течения Z-пинча. Physics of Plasmas 24, 055702 (2017) [Приглашенная статья]
    8. М. П. Росс и У. Шумлак. Цифровая голографическая интерферометрия с использованием реконструкции преобразования Френеля для исследования плазмы Z-пинча, стабилизированной сдвигом потока. Обзор научных инструментов 87, 103502 (2016)
    9. Э.М. Соуза и У. Шумлак. Смешанный непрерывно-разрывный метод конечных элементов для решения модели многожидкостной плазмы.Журнал вычислительной физики 326, 56 (2016)
    10. С.Т. Миллер и У. Шумлак. Многокомпонентная 13-моментная модель для умеренно столкновительной плазмы. Физика плазмы 23, 082303 (2016)
    11. Э. М. Соуза, Г. Лин и У. Шумлак. Количественная оценка неопределенности задачи магнитного пересоединения GEM с использованием многоуровневого метода Монте-Карло. Международный журнал по количественной оценке неопределенности 5, 327 (2015)
    12. С.Д. Кнехт, Р.П. Голинго, Б.А. Нельсон и У. Шумлак. Расчет равновесной эволюции Z-пинча потока ЗаП с использованием четыреххордного интерферометра. IEEE Transactions on Plasma Science 43, 2469 (2015)
    13. Г.В. Фогман, П. Колелла и У. Шумлак. Неустойчивость Дори-Геста-Харриса как эталон для непрерывного кинетического моделирования Власова-Пуассона замагниченной плазмы. Журнал вычислительной физики 277, 101 (2014)
    14. С.Д. Кнехт, В. Лоури и У. Шумлак. Влияние проводящей стенки на устойчивость Z-пинча.IEEE Transactions on Plasma Science 42, 1531 (2014)
    15. Э. Канса, Ю. Шумлак, С. Цынков. Дискретные проекции Кальдерона на параллелепипеды и их применение к вычислению внешних магнитных полей для плазмы FRC. Журнал вычислительной физики 234, 172 (2013)
    16. У. Шумлак, Дж. Чадни, Р.П. Голинго, Д.Дж. Ден Хартог, М.К. Хьюз, С.Д. Кнехт, В. Лоури, В.С. Лукин, Б.А. Нельсон, Р.Дж. Оберто, Дж. Л. Рорбах, М.П. Росс и Г.В. Фогман. Z-образный зажим, стабилизированный сдвиговым потоком.Наука и технологии термоядерного синтеза 61, 119 (2012)
    17. И. Т. Мейер и У. Шумлак. Общая нелинейная модель жидкости для реагирующих плазменно-нейтральных смесей. Физика плазмы 19, 072508 (2012)
    18. И.Т. Мейер, А.Х. Глассер, В.С. Лукин и У. Шумлак. Моделирование открытых границ в диссипативном МГД-моделировании. Журнал вычислительной физики 231, 2963 (2012)
    19. У. Шумлак, Р. Лилли, Н. Редделл, Э. Соуза и Б. Шринивасан. Расширенные физические расчеты с использованием модели многожидкостной плазмы.Коммуникации по компьютерной физике 182, 1767 (2011)
    20. Б. Шринивасан и У. Шумлак. Аналитическое и вычислительное исследование модели идеальной полной двухжидкостной плазмы и асимптотических приближений для МГД Холла. Физика плазмы 18, 092113 (2011)
    21. В. Лоури, В.С. Лукин и У. Шумлак. Априорный анализ погрешности метрики качества сетки применительно к методу конечных элементов высокого порядка. Журнал вычислительной физики 230, 5564 (2011)

    Почетные звания и награды

    • Эрна и Якоб Майкл Приглашенные профессора, Научный институт Вейцмана, 2018 г.
    • Научный сотрудник Ливерморской национальной лаборатории им. Лоуренса, 2018 г.
    • Преподаватель года (аэронавтика и астронавтика, Вашингтонский университет, Сиэтл, Вашингтон), 2016 г.
    • Награда новатора факультета (Инженерный колледж Вашингтонского университета), 2011 г.
    • Национальная премия Абэ Зарема для выпускников учебных заведений (Американский институт аэронавтики и астронавтики), 2003 г.
    • Профессор года (аэронавтика и астронавтика, Вашингтонский университет), 2002 г.
    • Свидетельство о признании Программы ALVA по науке и инженерии меньшинств Вашингтонского университета (Союзы обучения и видения для недопредставленных американцев), 2000 г.
    • Профессор года (аэронавтика и астронавтика, Вашингтонский университет), 1999 г.
    • Член Национального исследовательского совета, Национальная академия наук, 1992 г.
    • Член Американского физического общества, 2019 г.
    • Ассоциированный научный сотрудник, Американский институт аэронавтики и астронавтики 2016
    • Старший член Института инженеров по электротехнике и электронике 2020

    Новости

    с.И. Степанов | Физика и механика материалов

    Степанов С.И. | Физика материалов и механика

    МПМ

    С 2000 года

    ISSN 1605-8119

    С.И. Степанов

    • Принадлежность

      Институт Иоффе

    • Санкт-Петербург, Россия
    • Год: 2015
    • Объем: 22
    • Выпуск: 1
    • Год: 2015
    • Объем: 22
    • Выпуск: 1
    • Год: 2015
    • Объем: 22
    • Выпуск: 1
    • Год: 2017
    • Объем: 32
    • Выпуск: 1
    • Год: 2017
    • Объем: 32
    • Выпуск: 2
    • Год: 2020
    • Объем: 46
    • Выпуск: 1
    • Год: 2021
    • Объем: 47
    • Выпуск: 1
    • Год: 2021
    • Объем: 47
    • Выпуск: 4

    Государственное научное учреждение «Б.

    Институт физики им. И.Степанова НАН Беларуси»

    Домой
    » Компании
    » Государственное научное учреждение «Институт физики им. Б.И.Степанова Национальной академии наук Беларуси»

    Беларусь

    Количество сотрудников: 100+

    Годовой оборот: 500000 долларов США

    Беларусь, 220072, Минская область, г. Минск, просп.68-2

    Напишите сообщение

    Основными направлениями деятельности Института физики являются: лазерная физика, нелинейная и квантовая оптика; разработка и создание лазерно-оптических приборов и технологий различного назначения; разработка оптических методов исследования строения и свойств атомно-молекулярных структур и создание на основе этих результатов новых оптических материалов, приборов и технологий; физика плазмы; физика элементарных частиц; физика ядерных реакций и ядерная спектроскопия.

    Товары

    Технологии

    Беларусь

    Оптическое производство Института физики НАН Беларуси специализируется на изготовлении высококачественных прецизионных оптических компонентов и оптико-механического оборудования. ..

    Беларусь

    Компактные лазеры на эрбиевом стекле для условно безопасных дальномеров.

    Беларусь

    Компактные эрбиевые лазеры ИФЛ-Э25-П и ИФЛ-Э45-П.

    Беларусь

    Компактные эрбиевые лазеры IFL-E85-P и IFL-E105-EO.

    Беларусь

    Лазеры Nd:YAG и системы с параметрической генерацией света.

    Беларусь

    Лазеры Nd:YAG с диодной накачкой и системы на их основе.

    Беларусь

    Многоволновой рамановский лидар для оперативного мониторинга окружающей среды и анализа процессов трансграничного переноса загрязнений.

    Беларусь

    Импульсный лазер Nd:YAG с гармониками и энергией в импульсе до 180 мДж.

    Беларусь

    Импульсный лазер Nd:YAG (энергия 200 мДж).

    Беларусь

    Импульсный ультрафиолетовый Nd:YAG-лазер с энергией в импульсе 3 мДж.

    Беларусь

    Мощный лазер Nd:YAG с гармониками для лидарных систем с энергией до 400 мДж.

    Беларусь

    Импульсный лазер Nd:YAG без принудительного охлаждения с энергией в импульсе 40 мДж.

    Беларусь

    Импульсный лазер Nd:YAG без принудительного охлаждения с энергией в импульсе 65 мДж.

    Беларусь

    Портативный двухимпульсный Nd:YAG-лазер для спектрального анализа с энергией в импульсе до 50 мДж.

    Беларусь

    Эрбиевый лазер с активной модуляцией добротности с энергией в импульсе 10 мДж.

    Беларусь

    Оборудование на основе лазерных и светодиодных источников и технологий стимулирующего воздействия оптического излучения на эмбрионы и сперму ценных видов рыб.

    Беларусь

    Многофункциональный комплекс «Тераспектрометр» позволяет проводить бесконтактную диагностику свойств материалов и идентификацию полупроводниковых, керамических, полимерных, композиционных материалов, пористых сред, биохимических. ..

    Олег Степанов

    на самом деле имеет степень по физике.Но пока он еще работал в лаборатории в России, он уже мечтал о танце и театре. Ему посчастливилось попасть в небольшой театральный коллектив танца в Екатеринбурге, где он впервые увидел видеозапись творчества Пины Бауш. Такие видеокассеты были редкостью в России, но Пина Бауш была известной звездой, которой очень восхищались в театральной среде.
    Олег Степанов родился в 1983 году и вырос на Урале, в промышленном регионе на востоке бывшего СССР. У многих жителей была только одна цель – работать на большом металлургическом заводе.Его родители тоже хотели этого для Олега. Учился пять лет в Уральском государственном университете, потом работал на металлургическом заводе. Но он жаждал чего-то другого. До этого его единственным танцевальным опытом были бальные танцы в качестве хобби.
    В возрасте 23 лет он начал посещать танцевальные классы и мастер-классы по классическому и современному танцу — что угодно, кроме работы на фабрике. В конце концов появилась возможность присоединиться к труппе современного танца в Санкт-Петербурге, и он уволился с работы.«Мои родители думали, что я принял неправильное решение. Но я чувствовал телом и разумом, что хочу танцевать, что это моя судьба», — говорит он сегодня.
    Позже он прошел прослушивание в Губернский театр танца в Екатеринбурге и был принят в труппу, наконец вернувшись домой. Он оставался в Екатеринбурге в течение пяти лет, прежде чем переехать в Европу, чтобы работать с более широким кругом хореографов. Его первая работа была в GöteborgsOperans Danskompani в 2013 году. Там он познакомился с Адольфом Биндером, который впоследствии стал художественным руководителем Tanztheater Wuppertal.После того, как она уехала из Гетеборга, он остался в Швеции еще на один год, воспользовавшись шансом пройти прослушивание в Вуппертале в 2016 году.
    С 2016 года он станцевал в девяти пьесах Пины Бауш. Олегу Степанову нравится работать в труппе с танцорами разных поколений. «Здесь роскошь, и вы можете так многому научиться». Он очарован и восхищается своими старшими коллегами «за их качества, их самоотверженность». Теперь, когда его мечта стать частью Tanztheater Wuppertal сбылась, у него появилась новая мечта: выступить с труппой в России.Танцевального театра не было с тех пор, как в 2009 году умерла Пина Бауш.

    Михаил Степанов — Аризонский университет

    • 922
      Цитаты

      Источник: Скопус

    • 14
      h-индекс

      Рассчитано на основе нет. публикаций, хранящихся в Pure, и цитирований из Scopus

    19952016

    Исследовательская деятельность в год

    Если вы внесли какие-либо изменения в Pure, они скоро будут видны здесь.