9 класс алгебра видеоуроки: Видеоуроки. Алгебра. 9 класс. Функции и их свойства.

Видеоурок по алгебре 9 класс тема Нули функции

Квадратичная функция

Уравнения и неравенства с одной переменной

Уравнения и неравенства с двумя переменными

Арифметическая и геометрическая прогрессии

Элементы комбинаторики и теории вероятностей

Показать все темы

Алгебра

7

8

9

10

11

Поделиться

0

0

03:29

Нулями функции называются значение абсциссы, при котором значение функции равно нулю.  

Чтобы найти нули функции, заданной формулой y=f(x), надо решить уравнение f(x)=0.

Если уравнение не имеет корней, нулей у функции нет.

Чтобы найти нули функции, заданной графически, надо найти точки пересечения графика функции с осью абсцисс.

Урок по алгебре 9 класс

Открытый
урок по алгебре в 9 классе

 Учитель
: Романенко И.В.

Тема
урока:
«Арифметическая прогрессия. Формула n-го члена арифметической
прогрессии.

Цель урока: Формировать
умение решать задачи, используя формулы n –ого члена арифметической
прогрессии.  Слайд №1.

Задачи
урока:

—
образовательная: формировать умение применять
теоретические знания при выполнении устных и письменных заданий, а также при выполнении
теста

— развивающая:
продолжить работу над развитием логического мышления, умением анализировать,
сопоставлять и обобщать полученные знания.

—
воспитательная: воспитывать умение слушать своих одноклассников и
учителя, развивать навыки самостоятельной работы, формировать навыки
самоконтроля и взаимоконтроля; подготовка Единому
национальному тестированию по математике. 

Тип урока: урок
формирования умений и навыков.

Техническое
оснащение урока:

• ПК,
• мультимедийный
  проектор;
• экран
  для проекции;
• компьютерная
  презентация.

                                                           
Ход урока:

1.Оргмомент.

Слайд №2.Девиз урока:                     «Закончился   20 век.

              
                           Куда стремится человек ?

                                         
Изучены космос и моря,

                                      
   Строенье звезд и вся Земля.

                                      
   Но математиков зовет

                                      
   Известный лозунг:

                                      
   Прогрессио- движение вперед!»

 Откройте
тетради . Запишите 24,11,17 . Классная работа.

2.Постановка
темы и целей урока.

Вступительное
слово учителя:

– Сегодня
мы проводим урок-аукцион. Что такое аукцион?

Слайд №31.Аукцион – публичная распродажа, при которой
покупателем становится тот, кто предложит более высокую цену.

Аукционер —
участник аукциона.

Аукционист —
человек, ведущий аукцион.

— «Товар» на аукционе – это «лот».
Товаром на уроке сегодня будут задания на арифметическую прогрессию, различные
по сложности. Чтобы «купить» лот — нужны ваши знания.  На
продажу    выставлены поистине бесценные «вещи», купить которые
сможет любая команда (группа) в обмен на знания.

— Помогать вам будут: внимание,
сообразительность и дружная работа в команде.

 Какие задачи поставим на урок?

(Закрепить умение
применять формулы n-ого члена
арифметической прогрессии.)

Работать вы будете
в группах. Каждая группа может заработать смайлы за котрые вы получите оценки:

Слайд №4.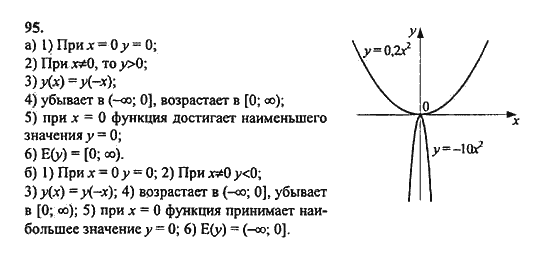

«5» 50-66 смайлов

«4»-40-59 смайлов

«3»- 30-39 смайлов

У вас на партах
лежать оценочные листы. Впишите свои фамилии.

3. Устный
счет:

Чтобы
участвовать в торгах вам необходимо приобрести «Стартовый капитал».
Каждой команде нужно выполнить задание. За которое команда получит «Смайлы».
 У каждой команды есть возможность исправить ошибки другой команды и
получить дополнительные «Смайлы»

 Чья
команда набирает большее количество смайлов, получает возможность выбрать ЛОТ.

Слайд №5. « СТАРТОВЫЙ КАПИТАЛ»

ЗАДАНИЕ №1  Последовательность  задана
формулой:

Укажите
номер члена этой последовательности, если он равен 144? 225? 100? Ответ:
144-12; 225-15; 100-10;

Являются
ли членами этой последовательности числа 48? 49? 168? Ответ: 48- нет; 49-да;
168-нет.  6 смайлов.

Слайд №6.ЗАДАНИЕ №2 О
последовательности  известно, что

Найдите
первые три члена этой последовательности. Ответ: 2; 4; 7

Каким
членом последовательности будут числа:31,46,151 ?.Ответ:11,24,49 6 смайлов.

Слайд №7 ЗАДАНИЕ №
3 О последовательности  известно, что

Найдите
третий  , пятый, восьмой член этой последовательности  Ответ 13, 19, 28

Каким
членом последовательности будут числа: 34;154;304? Ответ: 10,50,100 6
смайлов.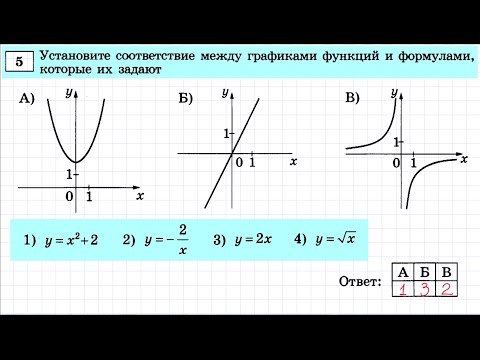

Дополнительные
задания:

 1.
Найдите для каждой последовательности следующие два члена:

                  
— 2; 6; 10; 14; 18; … 22;26.

                 
— 11; 8; 5; 2; -1; … -4;-7

                
— 5; 5; 5; 5; 5; …5;5     6 смайлов

2.) Найдите
член арифметической прогрессии, обозначенный буквой:

       
— …; 6; х; 10; 12; … 8

       
—  …; 11; х; 19; 23; …15

       
—  …; 7; х; 13; 16; …10   3 смайла.

Итак,
подведем итоги.

Слайд №8.

ЛОТ
№1 8 заданий по 7,5 смайлов за каждое. Всего 60смайлов.

ЛОТ
№2  6 заданий по 10смайлов за каждое. Всего 60 смайлов.

ЛОТ№3  
3 задания по 20 смайлов за каждое. Всего 60 смайлов.

  Слайд №9ЛОТ №1

Слайд №10.
ЛОТ№2

ЛОТ№2

1.   Дано:  Найти: .

2.   Дано: . Найти: d,

3.   Дано: Найти номер члена прогрессии, равного 34.

4. Является
   ли число 53 членом арифметической прогрессии -31; -28; …

если да, то определите его порядковый
номер.

5.   Дано: .  Найти: .

6.      Дано:

Слайд №11.ЛОТ№3

Решить и объяснить
решение

1) В угловом
секторе стадиона в первом ряду 7 мест, а в каждом следующем на 2 места больше,
чем в предыдущем. Сколько мест в 26 –ом ряду?

Решение:  а₁
= 7; d = 2; a₂₆ = 7+2*25 = 57    Ответ: в 26 ряду 57 мест.

2) Отдыхающий, следуя
совету врача, в первый день загорал 5 минут. А в каждый последующий день
увеличивал время пребывания на солнце на 5 минут. На какой день время
пребывания на солнце будет равно 40 минут?

Решение: а₁
= 5; d = 5; a_n =
40.      a_{n= а1 +
d (n-1).    40
= 5 + 5(n-1) = 5 +
5n – 5 = 5n.     n = 8.   
Ответ:  на 8 день.}

3): Студенты
должны выложить плиткой мостовую. В 1 день они выложили 3
м. Приобретая опыт, студенты каждый последующий день, начиная со второго,
выкладывали на 2 м больше, чем в предыдущий. Сколько м уложат студенты за 15
дней.

Решение: а₁
= 3; d = 2; a₁₅ = ?.   a₁₅ =  а₁ +
14  d = 3 + 14*2 = 31   Ответ:  31
метр.

Слайд №12

 Тест на
соответствие.   Выполняет каждый ученик индивидуально  .
найдите соответствие вопроса и ответа. Эти тесты я проверю и на следующий урок
объявлю результаты.     

 Ответы: 1-Д; 2-А; 3-В; 4-С;
5-З; 6-Е; 7-Ж. (на интерактивной доске).

Оценивание:
«5» — 0 ошибок; «4» — 1 ошибка; «3» — 2 ошибки, «2» — более 2 ошибок.

 Оценка за
тест заноситься в контрольный лист.

Подведем итоги.
Подсчитайте сколько смайлов заработала каждая команда.?

4.      Рефлексия
урока. 
Оцените урок по 10-бальной системе.

-У вас на партах листочки с
тестами. Ответьте на вопросы .

1. Результатом
своей личной работы считаю, что я …

А. разобрался в
теории; Б. Научился решать задачи.

2. Что вам не
хватало на уроке при решении задач?

А.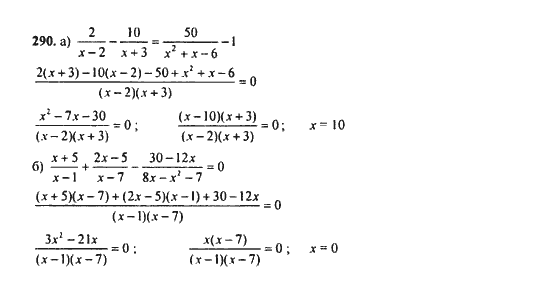 знаний; Б.
времени; В. Желания; Г. Решал нормально.

3. Кто оказывал
вам помощь в преодолении трудностей на уроке?

А. одноклассники;
Б. учитель; В. Учебник.

Самоанализ
урока. Алгебра 9 класс. «Арифметическая прогрессия».

 Учитель
Романенко И.В.

 Тема
урока:
«Арифметическая прогрессия. Формула n-го члена арифметической
прогрессии.

Цель урока: Формировать
умение решать задачи, используя формулы n –ого члена арифметической
прогрессии.

Задачи
урока:

—
образовательная: формировать умение применять теоретические
знания при выполнении устных и письменных заданий, а также при выполнении теста

— развивающая:
продолжить работу над развитием логического мышления, умением анализировать,
сопоставлять и обобщать полученные знания.

— воспитательная:
воспитывать умение слушать своих одноклассников и учителя, развивать навыки
самостоятельной работы, формировать навыки самоконтроля и взаимоконтроля;
подготовка
Единому национальному тестированию по математике. 

Тип урока: урок
формирования умений и навыков.

   Урок алгебры проводила в 9 классе, где обучаются 15
учащихся, из них 4 учащихся на продвинутом уровне обученности, 9 учащихся на
общем уровне обученности и 2учащихся на минимальном уровне обученнности.

          Данный урок является уроком обобщения,
систематизации и контроля знаний по данной теме. Это завершающий урок первой
части  раздела «Числовые последовательности».                   Урок содержал
учебный материал, в соответствии запланированными целями и задачами.              Эффективно
организована деятельность учащихся на протяжении урока. Класс разделен на 3
группы, в каждой группе есть «консультант», который давал рекомендации и
помогал в решении задач своим одноклассникам. Созданы условия для продуктивной
работы проверки знаний и умений по данной теме (дифференцированные задания,
устная  и самостоятельная работы, решение тестовых заданий). Каждый этап урока
содержал  дидактические задачи для полноты и глубины проверки знаний, умений и
навыков по пройденному материалу. Использовались задачи различного типа. В
течение урока ученики класса находились в поле зрения учителя, практически все
девятиклассники были заняты конкретными заданиями.

         При работе по модулю «Новые 
подходы в преподавании и обучении»  я планировала актуализацию знаний
провести в форме диалога: учитель – ученик и ученик-ученик;  ученик – учитель при 
устной работе,   решение тестовых заданий применила индивидуальную и групповую
формы работы.

      Модуль «Обучение критическому
мышлению» прошел через задания на  умение обрабатывать полученную
информацию по данной теме, анализировать ее и делать выводы при выполнение
теста на соответствие.

      При актуализации  темы  и рефлексии
всех этапов урока  применяю  модуль «Использование ИКТ в преподавании».
Данный модуль дает возможность  рационально использовать время на уроке
(экономия времени), красочная наглядность.

      В  «Оценивание для обучения и
оценивание обучения» применила формативное  и суммативное  оценивание,
а также само- и взаимооценивание.  Оценивание осуществляется по контрольным
листам, в листах ответов тестовых заданий, используя  критерии оценивания. По
завершении каждого этапа урока  спикеры групп выставляет оценку за работу
своим  одногруппникам в контрольный лист, где учитывается объективность и
обоснование отметки. Оценивание тестовых заданий проводится индивидуально, по
критериям оценивания.

       Работая в этом классе, с модулем  «Обучение
талантливых и одаренных детей»,  можно проследить работу со способными
учащимися, которые на протяжении всего урока помогали мне в его проведении: 
роль консультанта, роль оценщика, роль координатора в группе; ими оказывалась 
помощь одноклассникам при решение задач.

      В соответствии с модулем «Преподавание
и обучение в соответствии  с  возрастным особенностями учащихся» задания,
используемые в закрепление темы соответствуют возрасту и особенностям учащихся
данного класса.

     Модуль  «Управление и лидерство
в обучении».  На протяжение всего урока при работе в группах, лидерами
являются сильные ученики Итог за урок: «5» —  , «4» —  , «3» -.

Таким образом
поставленные цели и задачи достигнуты полностью.

Иллюстративные обучающие видеоматериалы по математике для 6-9 классов

Обзор

Видеоуроки, представленные ниже, посвящены критической математике для 6, 7, 8 и 9 классов (алгебра I). Уроки были выбраны на основе наиболее важного содержания на уровне класса и содержания, которое многие учащиеся пропустили из-за закрытия школ из-за COVID-19. Эти уроки были созданы в результате сотрудничества между Общественным вещанием Луизианы (LPB), Illustrative Math (IM) и SchoolKit и доступны по запросу на их веб-сайте. Чтобы обеспечить доступность для учащихся с ограниченными возможностями, видео по запросу будут доступны с субтитрами и звуковым описанием.

Видео для 6-х классов

Примечание : смотрите все видео для 6-х классов с размещением здесь .

Знакомство с соотношениями

• (Урок 1) Рецепты и определение эквивалентных соотношений
• (Урок 2) Знакомство с линейными диаграммами с двойным числом
• (Урок 3)  Сколько стоит один? и постоянная скорость
• (Урок 4) Представление соотношений в таблицах и навигация по таблице эквивалентных соотношений

Диапазон единиц и проценты

• (Урок 5) Преобразование единиц
• (Урок 6)    Сравнение скоростей и цен
• (Урок 7)    Проценты и ряды с двойными числами
• (Урок 8)    Нахождение этого процента от этого
• (Урок 9)    Нахождение процента

Выражения и уравнения

• (Урок 10)    Ленточные диаграммы и уравнения
• (Урок 11) Истина и уравнения
• (Урок 12)   Практика решения уравнений и представления ситуаций с помощью уравнений
• (Урок 13)   Напишите выражения, где буквы заменяют цифры
• (Урок 14)   Равен и эквивалентен
• (Урок 15) Распределительное свойство, часть 1
• (Урок 16) Распределительное свойство, часть 2
• (Урок 17)   Два связанных количества, часть 1 и часть 2

Рациональные числа

• (Урок 18) Положительные и отрицательные числа
• (Урок 19) Точки на числовой прямой
• (Урок 20) Сравнение положительных и отрицательных чисел
• (Урок 21) Абсолютное значение чисел
• (Урок 22) Точки на координатной плоскости
• (Урок 23)   Интерпретация точек на координатной плоскости
• (Урок 24) Расстояния на координатной плоскости

Видео для 7-го класса 

Примечание : смотрите все видео для 7-го класса с приспособлениями  здесь .

Знакомство с пропорциональными отношениями

• (Урок 1)   Пропорциональные отношения и уравнения
• (Урок  2)    Использование уравнений для решения задач
• (Урок 3)    Сравнение взаимосвязей с таблицами
• (Урок 4)    Сравнение отношений с уравнениями
• (Урок 5)    Знакомство с графиками пропорциональных отношений
• (Урок 6)   Интерпретация графиков пропорциональных отношений
• (Урок 7) Использование графиков для сравнения отношений

Арифметика рациональных чисел

• (Урок 8)   Интерпретация отрицательных чисел
• (Урок 9)   Изменение отметки
• (Урок 10)   Представление вычитания
• (Урок 11)   Вычитание рациональных чисел
• (Урок 12) Положение, скорость и направление
• (Урок 13)   Умножение рациональных чисел
• (Урок 14)   Деление рациональных чисел
• (Урок 15)   Выражения с рациональными числами и решение задач с рациональными числами

Выражения, уравнения и неравенства

• (Урок 16)   Различные варианты решения одного уравнения
• (Урок 17)    Использование уравнений для решения задач
• (Урок 18)   Вычитание в эквивалентных выражениях
• (Урок 19)  Объединение похожих терминов (часть 1)
• (Урок 20)  Объединение похожих терминов (часть 2)
• (Урок 21)   Объединение похожих терминов (часть 3)
• (Урок 22) Смежные углы
• (Урок 23)   Несмежные углы
• (Урок 24)   Использование уравнений для решения неизвестных углов
   

   Видео для 8-го класса

Примечание : смотрите все видео для 8-го класса с приспособлениями  здесь.

Линейные уравнения и линейные системы

• (Урок 1) Сбалансированные движения
• (Урок 2)    Более сбалансированные движения
• (Урок 3)    Когда они одинаковы?
• (Урок 4)    Системы уравнений
• (Урок 5)    Решение систем уравнений
• (Урок 6)   Написание систем уравнений

Функции и объем

• (Урок 7) Введение в функции и уравнения для функций
• (Урок 8) Таблицы, уравнения
• (Урок 9)  Другие графики функций
• (Урок 10)  Линейные функции
• (Урок 11) Линейные модели

Связи в данных

•   (Урок 12)   Что означает точка на точечной диаграмме
• (Урок 13) Подгонка линии к данным
• (Урок 14)   Описание тенденций на точечных диаграммах
• (Урок 15)   Наклон подобранной линии
• (Урок 16)   Умножение степени десяти
• (Урок 17)   Полномочия числа 10
• (Урок 18)   Деление степени числа 10
• (Урок 19)   Отрицательные показатели со степенью 10 и   А как насчет других оснований?
• (Урок 20) Объединение оснований  
• (Урок 21) Площади квадратов и длины их сторон
• (Урок 22) Длины и площади сторон
• (Урок 23) Рациональные и иррациональные числа
• (Урок 24) Рассуждения о квадратных корнях

9 класс (алгебра 1)   Видео

Примечание : смотрите все видео по алгебре с размещением здесь.

Введение в квадратичные функции

• (Урок 1) Изменение другого типа
• (Урок 2)    Как это меняется?
• (Урок 3)    Построение квадратичных функций из геометрических моделей
• (Урок 4)    Сравнение квадратичных и экспоненциальных функций
• (Урок 5)    Построение квадратичных функций для описания ситуаций    (Часть 1)
• (Урок 6)   Построение квадратичных функций для описания ситуаций    (Часть 2)
• (Урок 7)   Эквивалентные квадратные выражения
• (Урок 8) Стандартная форма и факторизованная форма
• (Урок 9) Графики функций в стандартной и факторизованной формах
• (Урок 10)  Построение графиков из факторизованной формы
• (Урок 11)   Графики, представляющие ситуации  

Квадратные уравнения

• (Урок 12)   Когда и зачем мы пишем квадратные уравнения?
• (Урок 13) Решение квадратных уравнений со свойством нулевого произведения
• (Урок 14)   Сколько решений?
• (Урок 15)    Переписывание квадратных выражений в факторизованной форме    (Часть 1)  
• (Урок 16)    Переписывание квадратных выражений в факторизованной форме    (Часть 2)
• ( Урок 17)    Переписывание квадратных выражений в факторизованной форме    (Часть 3)
• (Урок 18)   Решение квадратных уравнений с использованием факторизованной формы
• (Урок 19)   Что такое идеальные квадраты?
• (Урок 20)   Завершение квадрата (Часть 1)  
• (Урок 21) Завершение квадрата (Часть 2)
• (Урок 22) Квадратные уравнения с иррациональными решениями
• (Урок 23) Квадратичная формула
• (Урок 24)   Применение квадратичной формулы (Часть 1)
   

Алгебра ясно объясняется в бесплатных онлайн-уроках

Перейти к основному содержанию

• Демо MathHelp. com
• Регистрация MathHelp.com
• Логин

Поиск

Purplemath

Нужна помощь по алгебре?
Попробуйте уроки Purplemath ниже!

MathHelp.com

Индивидуальные курсы алгебры с учителем!

Уроки Пурпурной математики составлены таким образом, чтобы их можно было изучать любым удобным для ученика способом. Разные учебники охватывают разные темы в разном порядке. Уроки Purplemath стараются не предполагать какой-либо фиксированный порядок тем, чтобы любой ученик, независимо от учебника, мог извлечь из этого пользу.

Ниже уроки Purplemath перечислены в группах в соответствии с общими значениями алгебры «начальный», «средний» и «продвинутый». Если вы не знаете, где найти нужную тему, воспользуйтесь полем «Поиск» выше.

Перейти к списку уроков «в порядке изучения»

Предварительные темы

• Абсолютное значение
• Номер факторинга
• Дроби
• Геометрические формулы
• LCM и GCF
• Метрические преобразования
• Отрицательные числа

• Основы счисления
  (двоичный, восьмеричный и т. д.)
• Свойства номера
  (дистрибутивная, ассоциативная, коммутативная и т. д.)
• Типы номеров
  (натуральное, целое, действительное и т. д.)

• Преобразование между десятичными дробями, дробями и процентами
• Место Значение
• Римские цифры
• Округление (и значащие цифры)
• Установить обозначение

MathHelp.com

Индивидуальные курсы алгебры с преподавателем!

Начальные темы по алгебре

• Отмена единиц
• Формула расстояния
• Технические обозначения
• Оценка
• Экспоненты:
  • Основные правила
  • Отрицательные показатели
  • Дробные показатели степени
• Обзор графика
• График абсолютного значения
• Графики линейных уравнений
• График радикальных уравнений
• Графики линейных неравенств
  (вида «y < 2x + 3")
• Обзор неравенств
  (три метода решения)
• Перехваты

• Формула средней точки
• Порядок действий
• Многочлены
  (определения и «подобные термины»)
• Полиномы: сложение и вычитание
• Полиномы: умножение
• Многочлены: деление
• Радикалы
  (квадратный корень, кубический корень, рационализирующие знаменатели и т.  д.)
• Соотношение и пропорция
• Диаграммы рассеяния и регрессии
• Научное обозначение
• Простой факторинг
  например «2x + 6 = 2(x + 3)»
• Упрощение с экспонентами

• Упрощение в скобках
• Наклон прямой
• Наклон и график
• Наклон и точка пересечения с осью Y
  (их значение в контексте текстовых задач)
• Решение абсолютных значений
• Решение линейных неравенств
  (например, «2x < 4")
• Уравнения
• Решение линейных уравнений
• Решение буквенных уравнений
• Решение радикальных уравнений
• Уравнения прямых
  (у = мх + б)
• Переменные
• x, y-плоскость
  (точки построения и т. д.)

Темы алгебры среднего уровня

• Заполнение квадрата:
  • круги
  • многоточие
  • решение квадратичных уравнений
  • найти вершину
• Правило знаков Декарта
• Домен и диапазон
• Четные и нечетные функции
• Факторная теорема
• Факторные полиномы
• Факторинг Квадратика
• Нахождение полиномов по их нулям
• Обозначение функций
• Функции
• Преобразование функций

• Квадратичный график
  • Уравнения
  • Получение формулы вершины
• Графические системы линейных неравенств
• Неравенства: абсолютное значение
• Неравенства: Квадратичные
• Линейное программирование
• Численное приближение нулей
• Операции над функциями
• Кусочные функции:
  • определение
  • график
• Полиномиальные графики
• Тест рациональных корней
• Теорема об остатках

• Квадратичная формула
  • Получение квадроцикла. Формула
• Последовательности и серии
• Решение многочленов
• Решение квадратных уравнений
• Решение систем нелинейных уравнений
• Специальные формулы факторинга
  (разность квадратов, суммы и разности кубов и т. д.)
• Симметрия
• Синтетический отдел
• Вариация
  (прямой, инверсный и совместный)
• Тест вертикальной линии

Дополнительные темы по алгебре

• Асимптоты
• Биномиальная теорема
• Сложные дроби
• Комплексные числа
• Состав функций
• Коники: Обзор
  • Параболы
  • Круги
  • Эллипсы
  • Гипербола
• Правило Крамера
• Детерминанты
• Экспоненты
• График экспоненциальных уравнений

• Графические логарифмические уравнения
• Графики рациональных уравнений
• Индукционные доказательства
• Неравенства: Полиномиальное
• Неравенства: рациональные выражения
• Обратные функции
• Логарифмы
• Правила журнала
• Определения матриц
• Матричное сложение и вычитание
• Умножение матриц
• Операции со строками матрицы
• Инверсия матрицы

• Миноры и кофакторы
• Следующий номер в последовательности
• Разложение на неполные дроби
• Рациональные выражения: упрощение
• Рациональные выражения: добавление
• Рациональные выражения: умножение
• Решение экспоненциальных уравнений
• Решение логарифмических уравнений
• Решение рациональных уравнений
• Решающие системы
• Линейные уравнения

Решение словесных задач

Перевод: Как перевести текстовые задачи с английского языка в математические уравнения

• «Возрастные» текстовые задачи
• «площадь/объем/периметр»
  задачи по геометрии
• «монета» (деньги) проблемы

• «расстояние»
  d = rt словесные задачи
• «инвестиции»
  простые проценты I = Prt
• проблемы со «смесью»
• «число» (целое) проблемы
• «рабочие» проблемы
• Решающие задачи со словами

• Экспоненциальные и логарифмические задачи 
• «Процент» словесных задач
  (включая проблемы с увеличением/уменьшением)
• Квадратичные задачи со словами
  (включая движение снаряда)
• Словесные задачи на системы уравнений

Приложение

• «Действительно ли Библия
• сказать «π = 3»
• Коробчатые графики
• Факториалы
• Как может 0,999.