Сборник упражнений по алгебре для 8 класса
Круговые задания
Сборник упражнений по алгебре для 8 класса
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кемерово 2019
 Содержание
Содержание
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Введение
Важным звеном процесса обучения математике является контроль знаний и умений обучающихся. Оттого, как он организован, существенно зависит эффективность учебной работы.
В данном сборнике предложены круговые задания, при выполнении которых на каждом этапе можно проверить себя. Эти задания приучают детей к самостоятельности, быстроте реакции, самоконтролю. Каждое задание включает в себя от 4 до 6 упражнений.
Виды контроля:
1.а) значение выражения есть в другом выражении;
б) корень уравнения есть в другом уравнении.
2. Ответ: номер
а) выражения;
б) уравнения.
3. Модуль ответа равен:
а) номеру выражения;
б) номеру уравнения.
Назначение данного пособия – предоставить в распоряжение учителя разнообразный материал упражнений для дифференцированного обучения путем разумного сочетания фронтальной, групповой и индивидуальной работы с обучающимися.
Сборник, который я предлагаю, можно использовать при опросе учащихся, при самостоятельной работе по закреплению материала, с учетом подготовки учащихся, заинтересованности их математикой, при повторении, на внеклассных занятиях, а также при индивидуальной работе с учениками, проявляющими повышенный интерес к математике.
Цель упражнений – помочь более сознательному и прочному усвоению теории, научить применять пройденный материал, содействовать развитию логического мышления учащихся, их сообразительности, сформировать умения применять полученные знания в нестандартных ситуациях.
Пособие является дидактическим материалом по алгебре для 8 класса. Оно может использоваться, когда преподавание ведется по учебнику «Алгебра, 8» авторов Ю.Н.Макарычев и др. под редакцией С.А.Теляковского.
Глава 1. Рациональные дроби
§1.Сложение и вычитание дробей с одинаковыми знаменателями
№ 1. Найдите значение выражения:
1 вариант.

2 вариант.


§2.Сложение и вычитание дробей с разными знаменателями
№ 2. Найдите значение выражения:
1вариант.

2 вариант


§3. Умножение и деление алгебраических дробей
№ 3. Упростите выражение:
|
|
|
|
|
|
§4. Преобразование рациональных выражений
№ 4. Упростите выражение:


(Значение выражения есть в другом выражении)
№ 5. Упростить и найти числовые значения выражений:





Ответ 1 4 2 3 5
(Ответ номер следующего выражения)
№ 6. Решите уравнение:

(Корень уравнения, номер следующего уравнения)
Глава 2. Квадратные уравнения
§1. Неполные квадратные уравнения
№ 7. Решите уравнение:
1вариант.

№ 8. Решите уравнение:
1вариант.


§2.Формула корней квадратного уравнения
№ 9. Решите уравнение:
1вариант.
1. (2х-1)(2х-3)-(Х-2)2=19+3х.
2. (Х-6)(Х+6)=3(Х-12)
3. (Х+1)2-(Х+1)(1-Х)=2х+50

2вариант.
1. (3х-2)2-(х-4)(5х+1)=100.
2. (1+х)(х-1)-(1+х)2=-2х+22.
3. (4+3х)2-(5+2х)(5-2х)=10+(4х+1)2
4. (х-3)(х+3)=3(х-3)

§3.Дробные рациональные уравнения
№ 10. Решите уравнение:
|
|
|
(Модуль корня, номер следующего уравнения.)
№ 11. Решите уравнение:
1вариант.

(Модуль корня, номер следующего уравнения.)
2вариант.

(Модуль корня, номер следующего уравнения.)
№ 12. Решите уравнение:
1вариант.

2вариант.

Модуль целого корня номер следующего уравнения.
Глава 3. Неравенства
§1.Числовые неравенства
№ 13. Верно ли при любом значении переменной данное неравенство.
-
(с+2)(с+4)>(c+1)(c+5)
-
(3x+2)2>3x(3x+4)
-
(2a+5)(2a-5)<4(a2-5)
-
(3a-1)(3a+1)<9a2
-
5)(4a+1)2-8a>(4a+1)(4a-1)
OTBET:135241
Модуль разности левой и правой части номер следующего
неравенства.
§2.Доказательство неравенств
№ 14. Докажите неравенства:
1вариант.

Модуль разности левой и правой части номер следующего неравенства.
2вариант.

Модуль разности левой и правой части номер следующего неравенства.
Олимпиадные задания по математике 8 класс
Задача 1.
Какой цифрой оканчивается сумма 92007 + 92006 ?
Ответ:
92007 + 92006 = 92006( 9 + 1) = 92006* 10.
Нулем.
Задача 2.
В оранжерее было срезано 360 гвоздик. Причем красных на 80 больше, чем белых, а розовых на 160 штук меньше, чем красных.
Какое наибольшее число одинаковых букетов можно составить из этого количества цветов ?
Сколько и каких цветов было в каждом букете?
Ответ:
Решая уравнение, получаем 40 розовых гвоздик,120 белых гвоздик, 200 красных гвоздик. НОД (40, 120,200) равен 40, следовательно из 360 гвоздик можно составить 40 букетов, причем каждый букет будет состоять из 1 розовой, 3 белых и 5 красных гвоздик.
Задача 3.
Существует ли такой круг, чтобы его площадь и длина окружности выражались одним и тем же числом ?
Ответ:
Да, при радиусе равном 2.
Задача 4.
После семи стирок измерения куска хозяйственного мыла, имеющего форму прямоугольного параллелепипеда, уменьшились в двое.
На сколько еще стирок хватит оставшегося куска мыла ?
Ответ:
Мыла хватит еще на одну стирку, т.к. объем оставшегося мыла составил 1/8 часть первоначального, израсходовано мыла: 1 — 1/8 = 7/8 куска,
значит на каждую стирку расходовалось 1/8 часть куска, именно столько осталось.
Задача 5.
Какими двумя цифрами заканчивается число 13! ?
Ответ:
В произведении 1*2*3…*13 есть множители 2, 5 и 10, значит число 13!
Заканчивается двумя нулями.
Задача 6.
Из 38 учащихся 28 посещают хор и 17 лыжную секцию.
Сколько лыжников посещает хор, если в классе нет учащихся, которые не посещают хор или лыжную секцию ?
Ответ:
7 человек. Хор не посещают 10 человек, все они лыжники.
Лыжников всего 17человек, значит 7 человек надо «взять» из хора.
Задача 7.
Окружность касается квадрата извне и «катится» по нему без скольжения.
Сколько полных оборотов сделает эта окружность около своего центра и какой путь пройдет центр окружности к моменту возвращения в исходную точку, если длина стороны квадрата равна длине окружности и радиус окружности равен а см ?
Те же вопросы, если окружность «катится» по сторонам равностороннего треугольника.
Ответ:
В случае квадрата каждая точка окружности сделает 4 оборота около своего центра.
Центр окружности сделает четверть оборота около каждой вершины квадрата.
За один обход центр окружности совершает путь, равный 5*2Па см.
В случае треугольника — соответственно 3 оборота и 8П а см
Задача 8.
Во время похода палатки расположились в т. А,В, и С.
В каком месте удобно выбрать площадку для проведения общего костра,
чтобы расстояние от него до палаток было одинаковым ?
Ответ:
Точка осей симметрии точек А и В и точек В и С будет искомой.
Задача 9.
Найдите произведение всех целых чисел от (-99) до 99.
Ответ:
0
Задача 10.
Две семьи выехали каждая на машине «Жигули» на прогулку одновременно из одного места.
Обе семьи проехали на машинах одинаковые расстояния и вернулись домой в одно и то же время.
В пути они отдыхали.
Первая семья была в пути в двое больше времени, чем вторая.
Вторая была в пути втрое больше времени. Чем отдыхала первая.
Какая из этих семей двигалась на машине быстрее ?
Ответ:
1-я семья: 2х часов — время на езду, у часов — время на отдых.
2-я семья: 3у часов — время на езду, х часов — время на отдых 2х + у = 3у + х; х = 2у.
Вторая семья отдыхала в два раза больше, чем первая следовательно, она ехала быстрее первой.
Задача 11.
Сосуд имеет форму прямоугольного параллелепипеда.
Как, не делая никаких измерений и не имея других емкостей, наполнить водой ровно половину объема этого сосуда ?
Ответ:
Наклонить параллелепипед так, чтобы уровень воды находился по диагональному сечению параллелепипеда.
Задача № 1 :
В трех кучках лежат соответственно 12, 24 и 19 спичек. За ход можно переложить спичку из одной кучки в другую. За какое наименьшее число ходов можно получить три кучки с 8, 21 и 26 спичками?
Ответ : 4.
Решение :
Менее чем 4 ходами не обойтись: чтобы получить кучку из 8 спичек, придется из любой первоначальной кучки убрать как минимум 4 спички. Четырех ходов достаточно: перекладываем из кучки с 12 спичками по 2 спички в кучки с 19 и 24 спичками.
Задача № 2 :
Сколько всего есть четырехзначных чисел, которые делятся на 19 и оканчиваются на 19?
Ответ : 5 .
Решение :
Пусть — такое число. Тогда N – 19 тоже кратно 19. Но Поскольку 100 и 19 взаимно просты, то двузначное число делится на 19. А таких всего пять: 19, 38, 57, 76 и 95. Легко убедиться, что все числа 1919, 3819, 5719, 7619 и 9519 нам подходят.
Задача № 3 :
У даты 12.04.1961 (то есть 12 апреля 1961 года) сумма цифр равна 24. Найдите ближайшую дату после 01.01.2008, у которой сумма цифр равна: а) 35; б) 7.
Ответ : а) 29.09.2049; б) 03.01.2010.
Решение :
а) Наибольшая сумма цифр числа равна 11 для 29-го числа. Наибольшая сумма цифр месяца равна 9 для сентября, то есть для 09. Значит, наибольшая сумма цифр в текущем году будет у даты 29.09.2008. Она равна 30, что меньше 35. Следовательно, надо менять и год. Последняя цифра года не более 9, и если мы сохраняем первые две цифры, то придется цифру десятилетий увеличить до 4.
б) Для 2008 года сумма цифр года уже больше 27, поэтому год придется изменить. Ближайший год в будущем с меньшей суммой цифр — 2010-й. Соответственно, ближайшая подходящая дата 03.01.2010.
Задача № 4 :
Среди целых чисел от 8 до 17 включительно зачеркните как можно меньше чисел так, чтобы произведение оставшихся было точным квадратом. В ответе укажите сумму всех вычеркнутых чисел.
Ответ : 55.
Решение :
Чтобы произведение было точным квадратом, нужно, чтобы каждый простой множитель входил в него в четной степени. В произведение 8 · 9·…· 17 в нечетной степени входят 2, 7, 11, 13 и 17. Значит, мы обязаны вычеркнуть сомножители 11, 13 и 17. А вот чтобы «убить» лишние простые множители 2 и 7, хватит одного вычеркнутого сомножителя 14. Итого сумма вычеркнутых чисел равна 11 + 13 + 14 + 17 = 55.
Задача № 5 :
На гранях кубика расставлены 6 различных чисел от 6 до 11. Кубик бросили два раза. В первый раз сумма чисел на четырех боковых гранях оказалась равна 36, во второй — 33. Какое число написано на грани, противоположной той, где написана цифра 10?
Ответ : 8.
Решение :
Cумма чисел на всех гранях равна 6 + 7 + 8 + 9 + 10 + 11 = 51. При первом броске сумма на верхней и нижней гранях равна 51 – 36 = 15, при втором — 51 – 33 = 18. Значит, на третьей паре противоположных граней сумма равна 51 – 15 – 18 = 18. Сумму 18 можно получить двумя способами: 11 + 7 или 10 + 8. Значит, на парах граней с суммой 18 напротив 11 находится 7, а напротив 10 — 8.
Задача № 6 :
В конкурсе участвовали 5 человек. На каждый вопрос один из них дал неправильный ответ, остальные — правильный. Число правильных ответов у Пети равно 10 — меньше, чем у любого другого. Число правильных ответов у Васи равно 13 — больше, чем у любого другого. Сколько всего вопросов было в конкурсе?
Ответ : 14 .
Решение :
Так как на каждый вопрос были даны 4 правильных ответа, общее число правильных ответов делится на 4. Поскольку Петя дал 10 верных ответов, Вася — 13, а остальные трое — от 11 до 12, то общее число правильных ответов не меньше, чем 10 + 13 + 3·11 = 56, и не больше, чем 10 + 13 + 3·12 = 59. Из чисел в этих пределах только 56 кратно 4, поэтому число вопросов равно
Задача № 7 :
Команда из Пети, Васи и одноместного самоката участвует в гонке. Дистанция разделена на участки одинаковой длины, их количество равно 42, в начале каждого — контрольный пункт. Петя пробегает участок за 9 мин, Вася — за 11 мин, а на самокате любой из них проезжает участок за 3 мин. Стартуют они одновременно, а на финише учитывается время того, кто пришел последним. Ребята договорились, что один проезжает первую часть пути на самокате, остаток бегом, а другой — наоборот (самокат можно оставить на любом контрольном пункте). Сколько участков Петя должен проехать на самокате, чтобы команда показала наилучшее время?
Ответ : 18
Решение :
Если Петя проедет 18 участков и пробежит оставшиеся 42 – 18 = 24, он затратит 18·3 + 24·9 = 270 мин. При этом Васе, наоборот, достанется проехать 24 участка, а пробежать 18, на что уйдет 24·3 + 18·11 = 270 мин — то же самое время. Если же Петя проедет меньшее число участков, то его время (и, соответственно, время команды) увеличится. Если Петя проедет большее количество участков, то увеличится время Васи (и время команды).
Достаточно обозначить число проезжаемых Петей участков через x и решить уравнение
x·3 + (42 – x)·9 = (42 – x)·3 + 11x.
Задача № 1 :
Нарисуйте на плоскости пять различных прямых так, чтобы они пересекались ровно в семи различных точках.
Решение :
Три возможных ответа изображены на рисунке 1. Можно показать, что других конфигураций из пяти прямых, пересекающихся ровно в семи различных точках, нет.
Задача № 2 :
Мальчик пошел с отцом в тир. Отец купил ему 10 пулек. В дальнейшем отец за каждый промах отбирал у сына одну пульку, а за каждое попадание давал одну дополнительную пульку. Сын выстрелил 55 раз, после чего пульки у него кончились. Сколько раз он попал?
Ответ: 50.
Решение :
Каждый раз, когда мальчик попадал в цель, число имеющихся у него пулек оставалось прежним (одну использовал и одну получил от отца). Каждый раз, когда мальчик промахивался, число имеющихся у него пулек уменьшалось на 2 (одну использовал и одну отобрал отец). Это значит, что сын за 55 выстрелов промахнулся 10 : 2 = 5 раз, стало быть, попал 55 – 5 = 50 раз.
Задача № 3 :
Две биссектрисы треугольника пересекаются под углом 60°. Докажите, что один из углов этого треугольника равен 60°.
Решение :
Пусть биссектрисы AA1 и CC1 треугольника ABC пересекаются в точке I (рис.2). Допустим, что AIC1 = 60°. По теореме о внешнем угле треугольника
откуда
BAC + BCA = 120°
и
ABC = 180°– BAC – BCA = 60°.
Но это еще не все решение: ведь может случиться, что AIC = 60°. Однако тогда
IAC + ICA = 120°,
откуда
BAC + BCA = 240°,
что невозможно.
Задача № 4 :
Когда Винни-Пух пришел в гости к Кролику, он съел 3 тарелки меда, 4 тарелки сгущенки и 2 тарелки варенья, а после этого не смог выйти наружу из-за того, что сильно растолстел от такой еды. Но известно, что если бы он съел 2 тарелки меда, 3 тарелки сгущенки и 4 тарелки варенья или 4 тарелки меда, 2 тарелки сгущенки и 3 тарелки варенья, то спокойно смог бы покинуть нору гостеприимного Кролика. От чего больше толстеют: от варенья или от сгущенки?
Ответ : от сгущенки.
Решение :
По условию
3м + 4с + 2в > 2м + 3с + 4в,
откуда
м + с > 2в. (*)
По условию же
3м + 4с + 2в > 4м + 2с + 3в,
откуда
2с > м + в.
Складывая последнее неравенство с неравенством (*), получаем м + 3с > м + 3в, откуда с > в.
Задача № 5 :
В каждой клетке клетчатой доски размером 50 ? 50 записано по числу. Известно, что каждое число в 3 раза меньше суммы всех чисел, записанных в клетках, соседних с ним по стороне, и в 2 раза меньше суммы всех чисел, записанных в клетках, соседних с ним по диагонали. Докажите, что каждую клетку доски можно покрасить в красный или синий цвет так, что сумма всех чисел, записанных в красных клетках, равна сумме всех чисел, записанных в синих клетках.
Решение :
Покажем, что подойдет раскраска клеток доски в шахматном порядке. Заметим, что сумма данного числа и его соседей по диагоналям равна сумме соседей этого числа по сторонам: обе суммы втрое больше данного числа. Поэтому в квадрате 2 ? 2, находящемся в углу доски, суммы чисел в красных и синих клетках совпадают: обе они втрое больше числа, стоящего в угловой клетке доски. Также совпадают суммы чисел в красных и синих клетках любого прямоугольника 3 ? 2, примыкающего длинной стороной к краю доски: обе они втрое больше числа, стоящего в средней клетке стороны, примыкающей к краю доски. Наконец, совпадают суммы чисел в красных и синих клетках любого квадрата 3 ? 3: обе они втрое больше числа, стоящего в центре квадрата.
Разобьем доску 50 ? 50 на квадрат 48 ? 48, квадрат 2 ? 2 и два прямоугольника 2 ? 48, как показано на рисунке 3. Квадрат 48 ? 48 разобьем на квадраты 3 ? 3, а прямоугольники 2 ? 48 — на прямоугольники 3 ? 2, примыкающие длинной стороной к краю доски. В каждом из этих квадратов и прямоугольников суммы чисел, стоящих в красных и синих клетках, равны. Значит, они равны и на всей доске.
Алгебра 8 класс. Тесты и Тренажеры
Тесты и тренажеры по алгебре
Контрольные работы в 8 классе с ОТВЕТАМИ
Электронные версии учебников и конспекты
Конспекты по математике (5-6 классы) и алгебре (7-9 классы)
Онлайн учебник: Алгебра 8 кл. Макарычев, Миндюк, Суворова (Просвещение 2019)
Онлайн учебник: Алгебра 8 класс. Мордкович, Семенов (Просвещение, 2018)
Онлайн учебник: Алгебра 8 (углубленное изучение). Мерзляк, Поляков (2019)
Рекомендуемые материалы для очного контроля знаний
по предмету «Алгебра 8 класс»:
Контрольно-измерительные материалы по алгебре в 8 классе / В.В.Черноруцкий — М.: ВАКО, 2018
Алгебра. Тематические тесты. 8 класс. Кузнецова Л.В., Минаева С.С., Рослова Л.О. и др. (2014, 142с.)
Алгебра 8 класс. Контрольные работы. Кузнецова Л.В., Минаева С.С., Рослова Л.О., Суворова С.Б. (2016, 80с.)
Алгебра. 7-9 классы. Контрольные работы. Кузнецова Л.В., Минаева С.С., Рослова Л.О. (2011, 110с.)
Алгебра. Дидактические материалы. 8 класс. Евстафьева Л.П., Карп А.П. (2017, 144с.)
Алгебра. 8 класс. Дидактические материалы. Ткачева М.В., Федорова Н.Е., Шабунин М.И. (2013, 96с.)
Алгебра. 8 класс. Тематические тесты. Ткачева М.В. (2014, 80с.)
Алгебра 8 класс. Дидактические материалы. Жохов В.И., Макарычев Ю.Н., Миндюк Н.Г. (2012, 160с.)
Алгебра. 8 класс. Контрольные измерительные материалы. Глазков Ю.А., Гаиашвили М.Я. (2014, 96с.)
Алгебра. 8 класс. Тестовые материалы для оценки качества обучения. Гусева И.Л., Пушкин С.А. и др. (2013, 96с.)
Алгебра. Тематические тесты. 8 класс. Дудницын Ю.П., Кронгауз В.Л. (2012, 128с.)
Алгебра. 8 класс. Дидактические материалы к учебнику Макарычева Ю.Н. — Звавич Л.И., Дьяконова Н.В. (2014, 240с.)
Самостоятельные и контрольные работы по алгебре. 8 класс. К учебнику Макарычева Ю.Н. и др. Глазков Ю.А., Гаиашвили М.Я. (2012, 144с.)
Тесты по алгебре. 8 класс: к учебнику Макарычева Ю.Н. и др. — Глазков Ю.А., Гаиашвили М.Я. (2013, 112с.)
Алгебра. 8 класс. Дидактические материалы к учебнику Макарычева. Углубленное изучение. (2013, 173с.)
Алгебра. Дидактические материалы. 8 класс. Пос. для школ с углубл. изучен. математики. Макарычев Ю.Н., Миндюк Н.Г. (2010, 157с.)
Тесты по алгебре. 8 класс. К учебнику Мордковича А.Г. Ключникова Е.М., Комиссарова И.В. (2011, 96с.)
Алгебра. 7-9 классы. Контрольные работы. Мордкович А.Г. (2011, 127с.)
Алгебра 8 класс. Контрольные работы. Александрова Л.А. (2014, 40с.)
Алгебра. 7-9 классы. Контрольные работы. Мордкович А.Г. (2011, 127с.)
Алгебра. 8 класс. Тематические тесты. Чулков П.В., Струков Т.С. (2012, 95с.)
Тесты по алгебре. 8 класс. К учебнику Никольского С.М. и др. — Журавлев С.Г., Ермаков В.В. и др. (2013, 144с.)
Алгебра. 7-8 классы. Тренажер. Тематические тесты и итоговые работы. Под ред. Лысенко Ф.Ф., Кулабухова С.Ю. (2013, 96с.)
Алгебра. 8 класс. Сборник тестов и контрольных заданий. Дюмина Т.Ю. (2010, 83с.)
Вы смотрели «Тесты по алгебре в 8 классе. Контрольные работы по алгебре 8 класс с ответами». Вернуться
Задачи на логику 8 класс
В одном классе всего 36 учеников. Девочек на 3 больше, чем мальчиков.
Сколько мальчиков и девочек в этом классе?
Ответ: Если разделить 36 пополам, то получим 18, т.е. две половины класса по 18 человек.
Если из первой половины добавить школьника в другую, то получится разница в 2 человека.
Если отнять еще одного и добавить снова в большую часть, то получим превышение на 4 человека. Следовательно задача не имеет решения.
—————————————
Можете ли вы записать число 1000 при помощи только восьми восьмерок и арифметических знаков суммы?
Ответ: Получится равенство : 888 + 88 + 8 + 8 + 8 = 1000.
—————————————
На столе лежат 4 монеты, из которых одна сделана из другого металла и отличается по весу, хотя внешне они все одинаковые.
Как определить эту монету за 2 взвешивания на чашечных весах?
Ответ: Вар-ты взвешиваний : 1) ложем на весы 1 и 2 монеты, если они равны по весу, то одну монету заменяем на третью.
Далее если они равны, то отличная монета 4-я, если не равны, то 3-я монета отличная от остальных. 2) ложем на весы 1 и 2 монеты, если они не равны по весу,
то вместо одной монеты ложем 3-ю. Если уравновешиваются, то отличная убранная монета, если не уравновешиваются,
то отличная от других монет оставшаяся на весах старая монета.
—————————————
Как так могло оказаться, что половина числа 12 стало равно 7
Ответ: Нужно написать число 12 римскими цифрами : IIX , далее провести посередине линию. Верхняя половина будет в виде VII, что соответствует цифре 7.
—————————————
На праздничном столе горят 7 свечей. 3 из них потушили. Сколько свечей останется?
Ответ: Останутся 3 потушенные свечи, т.к. остальные 4 сгорят полностью.
—————————————
Если три десятка умножить на четыре десятка, то сколько получится?
Ответ: Получится не 12 десятков, а 120 десятков. То есть : 30 * 40 = 1200.
—————————————
Можете ли вы обосновать, почему почти во всех странах мира канализационные крышки у люков имеют только круглую форму? (Квадратные крышки люков бывают лишь тогда, когда они дополнительно крепятся шарнирами).
Ответ: Если крышки люков будут квадратными, то они могут легко провалиться в люк, т.к. диагональ квадрата больше стороны квадрата.
Поэтому их если и делают, то только прикрепив к люку шарнирами.
У круглых крышек люков нет диагонали и стороны, а только диаметр, который у крышки всегда больше отверстия люка.
—————————————
Как вы думаете, какой знак следует поставить между 0 и 1, чтобы было получено число больше 0, но меньше 1?
Ответ: Этот знак является запятой. То есть 0,1. Это число больше 0, но меньше 1.
—————————————
Как вы думаете, сколько граней имеет шестигранный карандаш, который ни разу не затачивали?
Ответ: Шестигранный карандаш, если не подвергался заточке будет иметь 8 граней. 6 большие грани и 2 торцевые.
—————————————
Трехлитровый сосуд полностью заполнен тремя литрами воды.
Вам необходимо за 2 переливания заполнить два пустых сосуда на 1 и 2 литра, чтобы в каждом из них было по 1 литру воды.
При этом больше нельзя пользоваться ни чем, кроме этих трех сосудов.
Ответ: Из полного сосуда наливаем в двухлитровый пустой ровно два литра, т.е. до краев.
Далее из этого сосуда выливаем в однолитровый ровно литр воды (т.е. до краев).
—————————————
Как вы думаете, существуют ли линии отличные от окружности, на которых все точки будут равноудалены от какой-то одной точки?
Ответ: Равноудаленностью всех точек обладает любая линя, лежащая на поверхности шара.
—————————————
Как вы думаете, какой предмет будет иметь одинаковое изображение при рисовании его с любой точки зрения?
Ответ: Этим свойством обладает только шар.
—————————————
Попробуйте сообразить, какой из выводов, указанных ниже, верный :
А) Здесь три ложных вывода.
Б) Здесь один ложный вывод.
В) Здесь два ложных вывода.
Г) Здесь пять ложных выводов.
Д) Здесь четыре ложных вывода.
Ответ: Правильный Вар-т Д — здесь четыре ложных вывода. В связи с тем, что один является верным, а остальные не верные.
—————————————
Попробуйте догадаться сколько стоит книга, если книга стоит доллар плюс пол книги.
Ответ: Книга стоит 2 доллара. Решение : полкниги стоит доллар, значит вся книга стоит 2 доллара.
—————————————
Ответьте, сколько сейчас времени, если оставшаяся часть суток в два раза превышает прошедшую?
Ответ: Сейчас восемь часов.
—————————————
Некий бизнесмен захотел привезти в Японию для продажи 10 000 пар первоклассных дорогих кроссовок.
Но в Японии на такие кроссовки накладываются очень большие пошлины.
Подумайте и скажите, как же хитроумный бизнесмен смог ввезти все эти кроссовки в Японию,
при этом заплатил только очень небольшие деньги? Никакой коррупционной и преступной составляющей здесь нет.
Ответ: Бизнесмен поступил очень хитро. Он разделил каждую пару кроссовок и отправил весь объем двумя партиями.
То есть в одной партии были только кроссовки на левую ногу, во второй только на правую ногу. Одну партию он отправил в Токио, другую в Осака.
В каждом из городов бизнесмен не заплатил пошлину и товары были конфискованы и выставлены на аукционе.
В связи с тем, что никому не была нужна партия кроссовок только на одну ногу, то бизнесмен выкупил сам обе партии за мизерные деньги.
—————————————
5 рыбаков съели 5 карпов за 5 дней. Как вы думаете, а за сколько дней 15 рыбаков съедят 15 карпов?
Ответ: 15 рыбаков съедят 15 карпов тоже за 5 дней. Если 5 рыбаков съедают 5 карпов за определенный промежуток времени,
то у 15 рыбаков скорость поедания карпов в 3 раза больше, следовательно за 5 дней они съедят 15 карпов.
—————————————
В мешке имеется 9 кг сахара. Есть также и две гири по 50г и 200г.
Подумайте, как за три взвешивания на чашечных весах отвесить 2кг сахара?
Ответ: Сперва необходимо на чашечных весах разделить содержимое мешка пополам на 4,5кг в каждой чашке.
Далее одну чашу опустошаем, и снова 4,5кг делим пополам и получаем в каждой чаше весов по 2,25кг.
В третье взвешивание уже нужно опустошить обе чаши, но из одной чаши 2,25кг сахара положить в отдельный мешок.
И далее при помощи гирек в 200г и 50г (итого 250г) отвесить из пакета с 2,25кг ровно 250г. Тогда в пакете останется ровно 2 кг.
—————————————
Два колхозника решили узнать, у кого больше овец.
Первый из них сказал : «если ты дашь мне свою козу, то у меня будет их в два раза больше, чем у тебя».
Второй ему говорит : «А давай лучше ты мне дашь свою одну овцу, тогда у меня овец будет столько же, сколько и у тебя».
Сколько же овец у каждого из колхозников? (Передачи овец пока еще не было).
Ответ: У первого колхозника 7 овец, у второго только 5.
Если первый колхозник отдает одну овцу второму и их становится поровну, то значит, что изначально у первого их на 2 больше.
Если же второй колхозник отдает овцу первому, то их становится у первого в 2 раза больше, такое возможно,
только если у первого изначально было 7 овец, а у второго 5.
Дальше: Логические задачи 8 класс с решением
Логические задачи для 8 класса | aaBaby
Логические задачи для 8 класса с ответами
#1
Как вы думаете, какой предмет будет иметь одинаковое изображение при рисовании его с любой точки зрения?
Ответ?
Этим свойством обладает только шар
#2
Если три десятка умножить на четыре десятка, то сколько получится?
Ответ?
Получится не 12 десятков, а 120 десятков. То есть: 30 * 40 = 1200
#3
Ответьте, сколько сейчас времени, если оставшаяся часть суток в два раза превышает прошедшую?
#4
Попробуйте догадаться сколько стоит книга, если книга стоит доллар плюс пол книги.
Ответ?
Книга стоит 2 доллара. Решение: полкниги стоит доллар, значит вся книга стоит 2 доллара
#5
Некий бизнесмен захотел привезти в Японию для продажи 10 000 пар первоклассных дорогих кроссовок.
Но в Японии на такие кроссовки накладываются очень большие пошлины.
Подумайте и скажите, как же хитроумный бизнесмен смог ввезти все эти кроссовки в Японию, при этом заплатил только очень небольшие деньги? Никакой коррупционной и преступной составляющей здесь нет.
Ответ?
Бизнесмен поступил очень хитро. Он разделил каждую пару кроссовок и отправил весь объем двумя партиями.
То есть в одной партии были только кроссовки на левую ногу, во второй только на правую ногу. Одну партию он отправил в Токио, другую в Осака.
В каждом из городов бизнесмен не заплатил пошлину и товары были конфискованы и выставлены на аукционе.
В связи с тем, что никому не была нужна партия кроссовок только на одну ногу, то бизнесмен выкупил сам обе партии за мизерные деньги.
#6
В мешке имеется 9 кг сахара. Есть также и две гири по 50г и 200г.
Подумайте, как за три взвешивания на чашечных весах отвесить 2кг сахара?
Ответ?
Сперва необходимо на чашечных весах разделить содержимое мешка пополам на 4,5кг в каждой чашке.
Далее одну чашу опустошаем, и снова 4,5кг делим пополам и получаем в каждой чаше весов по 2, 25кг.
В третье взвешивание уже нужно опустошить обе чаши, но из одной чаши 2,25кг сахара положить в отдельный мешок.
И далее при помощи гирек в 200г и 50г (итого 250г) отвесить из пакета с 2,25кг ровно 250г. Тогда в пакете останется ровно 2 кг.
#7
5 рыбаков съели 5 карпов за 5 дней. Как вы думаете, а за сколько дней 15 рыбаков съедят 15 карпов?
Ответ?
15 рыбаков съедят 15 карпов тоже за 5 дней. Если 5 рыбаков съедают 5 карпов за определенный промежуток времени, то у 15 рыбаков скорость поедания карпов в 3 раза больше, следовательно за 5 дней они съедят 15 карпов
#8
Два колхозника решили узнать, у кого больше овец.
Первый из них сказал: «если ты дашь мне свою козу, то у меня будет их в два раза больше, чем у тебя». Второй ему говорит: «А давай лучше ты мне дашь свою одну овцу, тогда у меня овец будет столько же, сколько и у тебя». Сколько же овец у каждого из колхозников? (Передачи овец пока еще не было)
Ответ?
У первого колхозника 7 овец, у второго только 5.
Если первый колхозник отдает одну овцу второму и их становится поровну, то значит, что изначально у первого их на 2 больше.
Если же второй колхозник отдает овцу первому, то их становится у первого в 2 раза больше, такое возможно, только если у первого изначально было 7 овец, а у второго 5
#9
Как вы думаете, сколько граней имеет шестигранный карандаш, который ни разу не затачивали?
Ответ?
Шестигранный карандаш, если не подвергался заточке будет иметь 8 граней. 6 большие грани и 2 торцевые.
#10
Можете ли вы обосновать, почему почти во всех странах мира канализационные крышки у люков имеют только круглую форму? (Квадратные крышки люков бывают лишь тогда, когда они дополнительно крепятся шарнирами)
Ответ?
Если крышки люков будут квадратными, то они могут легко провалиться в люк, т.к. диагональ квадрата больше стороны квадрата.
Поэтому их если и делают, то только прикрепив к люку шарнирами.
У круглых крышек люков нет диагонали и стороны, а только диаметр, который у крышки всегда больше отверстия люка
#11
Попробуйте сообразить, какой из выводов, указанных ниже, верный:
А) Здесь три ложных вывода.
Б) Здесь один ложный вывод.
В) Здесь два ложных вывода.
Г) Здесь пять ложных выводов.
Д) Здесь четыре ложных вывода.
Ответ?
Правильный вариант Д — здесь четыре ложных вывода. В связи с тем, что один является верным, а остальные не верные
#12
Можете ли вы записать число 1000 при помощи только восьми восьмерок и арифметических знаков суммы?
Ответ?
Получится равенство: 888 + 88 + 8 + 8 + 8 = 1000
#13
В одном классе всего 36 учеников. Девочек на 3 больше, чем мальчиков. Сколько мальчиков и девочек в этом классе?
Ответ?
Если разделить 36 пополам, то получим 18, т.е. две половины класса по 18 человек.
Если из первой половины добавить школьника в другую, то получится разница в 2 человека.
Если отнять еще одного и добавить снова в большую часть, то получим превышение на 4 человека. Следовательно задача не имеет решения
#14
На столе лежат 4 монеты, из которых одна сделана из другого металла и отличается по весу, хотя внешне они все одинаковые.
Как определить эту монету за 2 взвешивания на чашечных весах?
Ответ?
Варианты взвешиваний :
1) кладем на весы 1 и 2 монеты, если они равны по весу, то одну монету заменяем на третью.
Далее если они равны, то отличная монета 4-я, если не равны, то 3-я монета отличная от остальных.
2) кладем на весы 1 и 2 монеты, если они не равны по весу, то вместо одной монеты ложем 3-ю. Если уравновешиваются, то отличная убранная монета, если не уравновешиваются, то отличная от других монет оставшаяся на весах старая монета
#15
Как вы думаете, какой знак следует поставить между 0 и 1, чтобы было получено число больше 0, но меньше 1?
Ответ?
Этот знак является запятой. То есть 0,1. Это число больше 0, но меньше 1
#16
Как так могло оказаться, что половина числа 12 стало равно 7
Ответ?
Нужно написать число 12 римскими цифрами: IIX, далее провести посередине линию. Верхняя половина будет в виде VII, что соответствует цифре 7
#17
Трехлитровый сосуд полностью заполнен тремя литрами воды.
Вам необходимо за 2 переливания заполнить два пустых сосуда на 1 и 2 литра, чтобы в каждом из них было по 1 литру воды.
При этом больше нельзя пользоваться ничем, кроме этих трех сосудов.
Ответ?
Из полного сосуда наливаем в двухлитровый пустой ровно два литра, т.е. до краев.
Далее из этого сосуда выливаем в однолитровый ровно литр воды (т.е. до краев).
#18
На праздничном столе горят 7 свечей. 3 из них потушили. Сколько свечей останется?
Ответ?
Останутся 3 потушенные свечи, т.к. остальные 4 сгорят полностью.
#19
Как вы думаете, существуют ли линии отличные от окружности, на которых все точки будут равноудалены от какой-то одной точки?
Ответ?
Равноудаленностью всех точек обладает любая линя, лежащая на поверхности шара.
|
|
|
Согласно CCSS, ученики восьмого класса должны сосредоточиться на трех важных областях:
а) формулирование и рассуждение о выражениях и уравнениях, включая моделирование как ассоциацию в двумерных данных с линейным уравнением, решение линейных уравнений и систем линейных уравнений,
б) понимание концепции функции и использование функций для описания отношений,
в) анализ геометрических фигур с использованием расстояния, угла, сходства и конгруэнтности и понимание теоремы Пифагора.
Следующие наборы вопросов по математике предназначены для проверки знаний учащихся восьмого класса. Мы не связаны с Центром передовой практики Национальной ассоциации губернаторов (NGA Center) или Советом старших должностных лиц государственных школ (CCSSO), которые координируют инициативу CCSS.
8-й класс Общие основные функции
8.F: учащиеся должны определить, оценить и сравнить функции и использовать функции для оценки отношений между величинами.
8-я классная базовая система счисления
8.NS: Знайте, что есть числа, которые не рациональны, и приближайте их рациональными числами.
8-й класс Общие основные выражения и уравнения
8.EE: учащиеся должны работать с радикалами и целочисленными показателями, понимать отношения между пропорциональными отношениями, линиями и линейными уравнениями, а также анализировать и решать линейные уравнения.
8-я классная базовая статистика и вероятность
8.SP: Стандарты 8.SP CCS требуют, чтобы учащиеся седьмого класса использовали выборку, чтобы сделать выводы, сделать неофициальные сравнительные выводы о двух популяциях и исследовать случайные процессы, а также разработать, использовать и оценить вероятностные модели.
8-й класс общей базовой геометрии
8.G. Предполагается, что учащиеся седьмого класса смогут понимать соответствие и сходство, понимать и применять теорему Пифагора, а также решать реальные и математические задачи, связанные с объемами сфер, конусов и цилиндров.
,
8-й класс (13 лет) — математические задачи
8 класс (13 лет) — математические задачи
Количество найденных проблем: 2707
- Стоимость велосипеда
Отец дал сыну 100 евро на покупку велосипеда, что составляло 40% от общего количества велосипеда. Сколько стоит велосипед? - Турист
Турист прошел четверть пути в первый день, треть отдыха во второй день и 20 км в последний день.Сколько километров он прошел за три дня? - Золото, серебро, бронза
Сколько способов мы можем разделить золотые, серебряные, бронзовые медали, если соревнуются 6 человек? - Cube surfce2volume
Рассчитайте объем куба, если его поверхность составляет 150 см. 2 . - Траншея
Рассчитайте, сколько кубических метров грунта необходимо извлечь из раскопок в форме равнобедренной трапеции, ширина верха 3 метра, ширина нижнего 1,8 м, глубина раскопок 1 м, и длина составляет 20 м. - Проволочная изгородь
Проволочная изгородь вокруг сада длиной 160 м. Одна сторона сада в три раза длиннее другой. Сколько метров измеряют отдельные стороны сада? - В классе
В классе 30 мальчиков и несколько девочек. За шесть месяцев, 28 мальчиков и все девочки получили пользу, что составляет 95% всех учеников. Сколько учеников в классе? - Высота пирамиды
Пирамида ABCDV имеет длину ребер: AB = 4, AV = 7.Какова его высота? - Длина стороны
В треугольнике ABC высота стороны a составляет 6 см. Высота в сторону b равна 9 см. Сторона «а» на 4 см длиннее, чем сторона «б». Рассчитайте длины сторон a, b. - Воздушный змей
У детей есть воздушный змей на веревке длиной 80 метров, которая плавает над местом в 25 метрах от места, где стоят дети. Как высоко дракон плывет над землей? - Построение трапеции
Построение трапеции, если b = 4см, с = 7см, d = 4,5см, v = 3 см (процедура, обсуждение, эскиз, анализ, построение) - Три примера на миллион
.
Листов 8-го класса по математике
Перво-наперво, расставьте приоритеты по основным темам с нашим печатным сборником математических листов 8-го класса с ключами для ответов. Достигать концептуального понимания таких тем, как системы счисления, выражения и уравнения, работать с радикалами и показателями, решать линейные уравнения и неравенства, оценивать и сравнивать функции, понимать сходство и соответствие, знать и применять теорему Пифагора, находить объем и площадь поверхности, разрабатывать понимание статистики и вероятности и многое другое.Наши бесплатные учебные листы по математике для учеников 8-х классов гарантируют, что они начинают правильно!
Выберите листы математики 8 класса по теме
Изучите 2400+ математических таблиц 8-го класса

Преобразование дробей в десятичные
Преобразуйте каждую дробь с кратным 10 в качестве знаменателя в десятичное число, поместив десятичную точку в нужное место.



Решение многошаговых уравнений
Следуйте порядку операций, переставьте, чтобы сделать неизвестную переменную объектом, и найдите ее целочисленное значение.

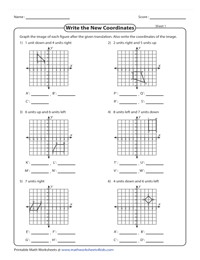
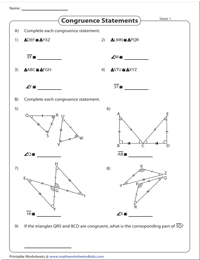
Congruence | Конгруэнтные части
Заполните утверждение конгруэнтности для каждой пары треугольников, написав соответствующую сторону или соответствующий угол.
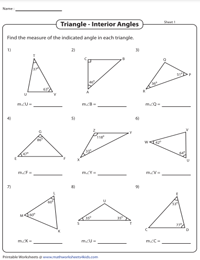
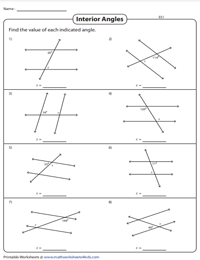
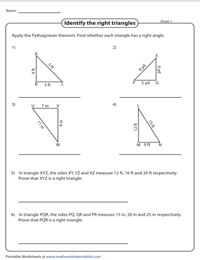
Определение правильных треугольников
Квадрат соседних и противоположных сторон треугольника; взять корень их суммы; если вы достигнете гипотенузы, то это прямоугольный треугольник.
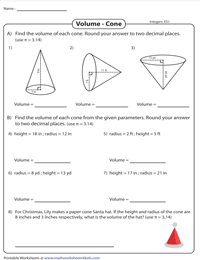
Объем конусов
Вставьте заданный радиус (r) и высоту (h) в формулу V = 1 / 3πr 2 ч и найдите объем конуса.


Преобразование дробей в проценты
Переключите каждую фракцию в процент, умножив числитель на 100, разделив произведение на знаменатель и добавив символ%.

,
Даже если вы не можете выполнять домашнее задание по математике у своего восьмиклассника, вы можете улучшить знания своего ребенка в домашних условиях с помощью этих математических советов для родителей.
-
Обними свой внутренний квадрат!
Хотите убедиться, что ваш ребенок знает некоторые основные квадратные корни? Дай им часы со стены. Каждый номер представляет решение. Используя заметки, замените каждое число на квадратное уравнение. Например, 6 — это √36.Помогите своему ребенку запомнить его идеальные квадраты до 400, чтобы они были готовы выполнять более сложную работу с квадратными корнями.
-
Так иррационально!
Ваш восьмиклассник может связывать иррациональное с необоснованным, но иррациональные числа — это просто числа, которые нельзя записать в виде отношения. Наиболее известным из них является пи, который используется для измерения длины вокруг круга или диаметра. Научите вашего ребенка его полезности, заставив его измерить круглосуточно, круг на баскетбольной площадке или тарелку.
-
Не будь таким дисфункциональным!
Когда ваш восьмиклассник приходит домой и говорит о вводе и выводе, вы знаете, что это функции обучения, одна из ключевых математических концепций для всей математики в старшей школе. Нужна переподготовка? Мы с тобой Посмотрите, как удостоенный наград учитель математики в средней школе объясняет эту идею за 38 секунд!
-
Разбираясь с линейными уравнениями
Ваш восьмиклассник просто выполняет движения или они действительно понимают, что делают, когда занимаются алгеброй? Посмотрите это видео, чтобы понять разницу.
-
Модель для мотивации
Спросите учителя своего ребенка о ряде проблем, которые должны решать восьмиклассники — от простых до дразнящих пеньков. Вы можете решить их самостоятельно? Попросите учителя объяснить каждый из них, а затем отведите их домой и попробуйте их с вашим ребенком. Ваш интерес + решение проблем вместе = гораздо более мотивированный студент-математик.
-
Проблема с проблемами слов
Многие дети, которые могут «сделать математику», борются, когда это означает переходить между чтением описаний случайных ситуаций и вычислять численные расчеты.Новые математические стандарты подчеркивают этот вид математики, потому что он более приближен к тому, как мы используем математику в реальной жизни. Как вы можете помочь своему ребенку с проблемами со словом? Сначала проверьте, как эти дети справляются с проблемами в восьмом классе, а затем используйте некоторые из своих стратегий с вашим ребенком.
-
Обезьяна видит, математическая тревога делает
Если вы один из многих людей, которые страдают от математической тревоги, лучше для вашего ребенка, если вы будете держать этот страх под тайной одеждой. Если вы скажете что-то вроде «Я ненавижу математику» или, что хуже, «У меня просто нет гена математики», ваш ребенок будет хуже в математике.Исследования показывают, что если вы примете математику и покажете своему ребенку, насколько она полезна в повседневной жизни, это положительно скажется на отношении вашего ребенка — и баллах по математике. Узнайте, что должен сказать главный эксперт по математической тревоге, когда ваш ребенок жалуется на математику.
-
Расчетный дизайн
Пусть ваш ребенок задумается о долгосрочной ценности математики. На этой неделе поговорите о том, что вам нужны математические навыки, чтобы создать идеальную пару джинсов, стать архитектором, изобрести видеоигру и даже стать успешным дизайнером сада.Подумайте о страстях вашего ребенка и дайте несколько советов о том, как эта профессия может использовать математику. Затем пусть ваш ребенок спроектирует дом своей мечты.
-
Math музыкально
Хотите помочь вашему восьмикласснику нарастить математические мышцы? Не забывайте, что есть и другие способы, кроме прямой математики. Музыка — одно из многих занятий, которые учат сложному моделированию, ключевой навык для высшей математики. Узнайте о науке, стоящей за связью математики и музыки.
Поделиться на Pinterest

Обновлено: 5 декабря 2019
,




 Математика
Математика
 Реальныe варианты ЕГЭ по математике
Реальныe варианты ЕГЭ по математике
