Тест 3 вариант 3 по геометрии 8 класс – ГДЗ по геометрии 8 класс тесты Фарков к учебнику Атанасяна

Тест по геометрии, 8 класс, УМК Л.С.Атанасян

Вариант 1

Вариант 2

Вариант 3

Вариант 4

Правильные ответы:

Инструкция к выполнению: Тест проводится по итогам обучения геометрии в 8 классе. Перед проведением теста проводится обобщающее занятие. Ученики разбирают обобщающие таблицы, данные в «Геометрия. 8кл. Поурочные планы к учебнику Атанасяна Л.С — 2010 — 365с».

Затем каждый ученик получает распечатанный вариант теста и выполняет его в течении одного урока. Оценивается тест так:

1 вопрос – 3 балла;

2 вопрос – 3 балла;

3 вопрос – 1 балл;

4 вопрос – 1 балл;

5 вопрос – 1 балл;

6 вопрос – 3 балла;

7 вопрос – 1 балл;

8 вопрос – 1 балл;

9 вопрос – 4 балла;

10 вопрос – 1 балл.

Общее количество баллов – 20. Оценка «5» – 17-20 баллов, оценка «4» — 13-17 баллов, оценка «3» — 6-12 баллов.

xn--j1ahfl.xn--p1ai

Тест по геометрии (8 класс) на тему: Итоговый контрольный тест по геометрии за 8 класс

Описание работы

Итоговая аттестация учащихся 8 класса по геометрии проводится в форме тестирования, которое требует от учащихся умения выстраивать логическую цепочку рассуждений, применять изученный материал при решении задач, распознавать на чертежах геометрические фигуры  и их взаимное расположение.     В тесты включены задания двух видов (с выбором ответа и с кратким ответом), которые встречаются в открытом банке задач ГИА и ЕГЭ.

Итоговое тестирование представлено в 2 равносильных вариантах, состоящих из 13 заданий, составленных по принципу основного государственного экзамена.

В заданиях с выбором ответа необходимо верный ответ обвести в кружок.

В заданиях с кратким ответом ответ нужно вписать в отведенное для этого место.

Для получения ответа часто требуется выполнить письменное решение предложенного задания. Решение выполняется на черновике, достаточно аккуратно, четко и разборчиво.

Итоговое тестирование рассчитано на 1 урок (45 минут).

Критерии оценивания

Ответы к итоговой работе по геометрии,  8 класс

Итоговое тестирование составлено на основе следующих источников:

1. Геометрия 7-9: учеб. для общеобразоват. учреждений /Л.С. Атанасян, В.Ф.Бутузов и др. – М.: Просвещение, 2014
2. www. fipi.ru
3. www. matgia.ru

Итоговое тестирование по геометрии, 8 класс

1 вариант

1. АВСД  параллелограмм, . Чему равен  угол С.

а) 80°                  б) 100°             в) 90°

2. Периметр параллелограмма равен 18 см. Чему равна сумма двух соседних       сторон?

Ответ:___________

3. В ромбе АВСД, угол   В равен  150°. Чему равен  угол А?

Ответ:___________

4. В квадрате АВСД диагонали пересекаются в точке О. АО = 7см. Чему равна  диагональ ВД?

а) 7см                б) 49 см             в) 14 см

5. Величина одного из углов равнобедренной трапеции 60° . Найти второй ее острый угол.

Ответ:_____________

6. Найти периметр ромба АВСД, если угол В равен  60°,  АС = 20 см

а) 40 см                б)80 см             в) 60 см

7. Периметр квадрата 16,4 дм. Найдите его сторону.

Ответ:_____________

8. В четырехугольнике АВСД  ∠С = 90°, ∠СВД = 30°, ∠АВД = 60°, ∠ВДА = 30°. Определите вид этого четырехугольника.

а) параллелограмм                        б) трапеция                      в) прямоугольник    

г) ромб                          д) произвольный четырехугольник

9. Периметр прямоугольника 24 см. Одна сторона его на 4 см больше другой.     Найдите площадь этого прямоугольника.

Ответ:_____________

10.  Какие из следующих утверждений верны?

1) Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.

2) Если расстояние от центра окружности до прямой равно диаметру          окружности, то эти прямая и окружность касаются.

3) Если радиус окружности равен 2, а расстояние от центра окружности до          прямой равно 3, то эти прямая и окружность не имеют общих точек.

11.  Одна из сторон параллелограмма равна 12, а опущенная на нее высота равна 10. Найдите площадь параллелограмма.

Ответ:___________

12.  Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см х1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Ответ:___________

13.  Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1см х1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Ответ:_______________

Итоговое тестирование по геометрии, 8 класс

2 вариант

1. АВСД – параллелограмм. Угол В равен 70°. Чему равен угол Д?

а) 70°                           б)110°                             в) 35°

2. Сумма двух соседних сторон параллелограмма равна 10 см. Чему равен его       периметр?

Ответ:___________

3. В параллелограмме МNКР угол N равен 150°. Чему равен угол М?

Ответ:___________

4. В квадрате АВСД диагональ АС = 16 см. Найти длину ВО (O – точка       пересечения диагоналей)

а) 16 см                        б) 24 см                          в) 8 см

5. Величина одного из углов прямоугольной трапеции равна 120°. Найдите      острый угол этой трапеции.

а) 30°                  б) 60 °                в) 45°

6. Один из углов параллелограмма равен 36° . Найдите остальные его углы.

а) 36° , 144° , 144°        б) 36° , 36° , 144 °             в) 36° , 72°, 144°

7. Меньшая сторона прямоугольника АВСД равна 18 см. О — точка       пересечения диагоналей. ∠АОД = 120°. Определите длину диагонали.

а) 36 см                         б) 18 см                             в) 9 см

8. В четырехугольнике АВСД ∠ВАС =40° ,  ∠ВСА = ∠САД = 50°, ∠АСД = 70° . Определите его вид.

а) параллелограмм            б) прямоугольник             в) трапеция    

г) ромб           д) произвольный четырехугольник

9. В прямоугольнике АВСД биссектриса угла Д  делит сторону ВС на отрезки ВК и СК. Найдите длину стороны ДС, если ВК = 6 см, а периметр       прямоугольника равен 48 см.

Ответ:_____________

10.  Какие из следующих утверждений верны?

1) Если дуга окружности составляет , то центральный угол,        опирающийся на эту дугу, равен .

2) Если радиусы двух окружностей равны 3 и 5, а расстояние между их         центрами равно 1, то эти окружности пересекаются.

3) Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность пересекаются.

11.  Одна из сторон параллелограмма равна 20, а опущенная на нее высота равна 23. Найдите площадь параллелограмма.

Ответ:_____________

12.   Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см х1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Ответ:______________

13.  Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см х1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Ответ:____________

nsportal.ru

Тест по геометрии (8 класс) на тему: Тест по геометрии 8 класс (1 полугодие)

Тест по геометрии 8 класс (I полугодие)  

Фамилия ____________________________ Имя________________________________

Город_______________________________ Дата________________________________

1 вариант

   Часть А.    Обведите кружком верный ответ.

      (За каждое верно выполненное задание – 1 балл)

А1.   Один из углов равнобедренной трапеции равен 100. Три оставшихся угла равны:

1. 80, 80,100;     2) 75,75,110;     3) 70,70,120;    4)  другой ответ.

А2.  Смежные стороны прямоугольника равны 6 и 8 см. Диагонали его равны:

1.  и  см;      2) 10 и 10 см;     3)  14 и 14 см;    4) другой ответ.

А3.  Сторона ромба равна 5 см, а одна из его диагоналей 6 см. Площадь ромба равна:

1. 30 ;           2) 24 ;        3) 15 ;          4) другой ответ.

А4.   Диагональ параллелограмма образует с одной из его сторон  угол, равный 54. Найдите величину угла, который эта диагональ образует с противоположной стороной параллелограмма.

1. 126;        2)   27;       3)   54;           4)   другой ответ.

Часть В. Выполните задание  и впишите полученный ответ.

(За каждое верно выполненное задание – 2 балла)

В1.    Стороны параллелограмма 4см и 6см. Меньшая его высота равна 3см. Вычислите вторую высоту параллелограмма.

Ответ:_________________________________________________________

В2.   Вычислите площадь трапеции АВСD с основаниями АD и ВС, если ВС=21 см, АD=27 см, СD=10 см, D=30.

Ответ: ___________________________________________________________

Часть С.  Напишите подробное решение задания.  

 (За верно выполненное задание –  3 балла)

С1.  Трапеция ABCD – прямоугольная (. Ее боковые стороны равны 12 см и 18 см, а диагональ АС равна 15 см. Найдите основания трапеции.

Решение задачи С1

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________

Ответы

Критерии оценок:

Тест по геометрии 8 класс (I полугодие)  

Фамилия ____________________________________ Имя______________________

        Город_______________________________________ Дата______________________

2 вариант

Часть А.   Обведите кружком верный ответ.

  (За каждое верно выполненное задание – 1 балл)

А1.    Один из углов равнобедренной трапеции равен 110. Три оставшихся угла равны:

2. 80, 80, 120;    2)   75,75,110;    3)    70,70,110;    4)    другой ответ.

А2.   Смежные стороны прямоугольника равны 3 и 4 см. Диагонали его равны:

2.  и  см;      2) 5 и 5 см;     3)  7 и 7 см;    4)другой ответ.

А3.   Сторона ромба равна 10 см, а одна из его диагоналей 12 см. Площадь ромба равна:

2. 120 ;           2)   96 ;        3)   48 ;          4)   другой ответ.

А4.   Диагональ параллелограмма образует с одной из его сторон  угол, равный 62. Найдите величину угла, который эта диагональ образует с противоположной стороной параллелограмма.

2. 31;      2)   118;       3)    62;           4) другой ответ.

Часть В.   Выполните задание  и впишите полученный ответ.

(За каждое верно выполненное задание – 2 балла)

В1.   Стороны параллелограмма 6 см и 10 см, а высота, проведенная к меньшей из них, равна 8 см. Найдите высоту, проведенную к другой стороне.

Ответ: ___________________________________________________________

В2.   Вычислите площадь трапеции АВСD с основаниями АD и ВС, если ВС = 16 см, АD = 24 см, D = 90,А = 45.

Ответ:____________________________________________________________

Часть С.  Напишите подробное решение задания.  

 (За верно выполненное задание –  3 балла)

С1.    Трапеция ABCD – прямоугольная (. ЕЕ боковые стороны равны 9 см и 18 см, а диагональ АС равна 15 см. Найдите основания трапеции.

Решение задачи С1

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Ответы

Критерии оценок:

nsportal.ru

Итоговый тест за 8 класс по геометрии

Итоговый тест по геометрии за курс 8 класса

1. Найти < KOM

Ответ:____________

2. Найдите площадь четырёхугольника:

Ответ:____________

3. Найти гипотенузу АВ, если катет АС=5; катет ВС=12:

Ответ:____________

4. Найдите угол ACD, если сторона СА касается окружности,

а дуга AD окружности, заключенная внутри этого угла, равна 116.

5. Используя рисунок найти угол

между диагоналями

2 часть

6. Выберите верные высказывания. Два треугольника называются подобными, если:

1) две стороны одного треугольника равны двум сходственным сторонам другого треугольника

2) стороны одного треугольника пропорциональны сходственным сторонам другого треугольника

3) два угла одного треугольника равны двум углам другого треугольника.

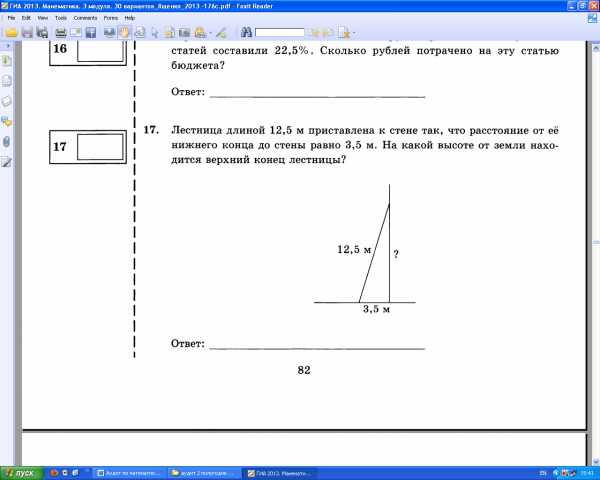
7. Лестница длиной 12,5 м приставлена к стене так, что расстояние от ее

нижнего конца до стены равно 3,5 м. На какой высоте от земли находится

верхний конец лестницы?

8. (2 балла)

infourok.ru

Итоговый тест по геометрии 8 класс

Итоговый тест по геометрии за 8 класс.

Вариант 1.

Часть I. 

1. Площадь прямоугольника АВСD равна 15. Найдите  сторону ВС прямоугольника, если известно, что АВ = 5.

1) 10                      2) 2,5                     3) 3                        4) 5

2. По данным рисунка найти площадь параллелограмма.

4

3

6

1). 18 кв. ед. 2). 24 кв. ед. 3). 12 кв. ед. 4). 9 кв. ед.

3. В ромбе АВСD проведена диагональ АС. Найдите  угол АВС, если известно, что угол АСD равен 35°.

1) 70°                    2) 110°                  3) 145°                  4) 125°

4. РЕ и МF — высоты треугольника МNP. МF пересекает PE в точке О. Какие из высказываний верны: N

1) △ ENP ̴ △FNМ F

2) △ MFP ̴ △ PEM E

3) △ MNP ̴ △MOP

4) △ MEO ̴ △PFO M P

1) 2,3 2) 1,4 3) 1,2 4) 3,4

5. По данным рисунка найдите градусную меру

дуги Х.

120˚ Х

30˚

1). 210˚ 2). 225˚ 3). 180˚ 4). 150˚

6. Укажите, какие из перечисленных ниже утверждений верны:

1) Если диагонали четырехугольника равны, то он прямоугольник.

2) Если противоположные стороны четырехугольника попарно равны, то он параллелограмм.

3) Если диагонали четырехугольника перпендикулярны, то он ромб.

4) Диагонали прямоугольника являются биссектрисами его углов.

7. Сторона ромба равна 5 , а одна из его диагоналей равна 6 . Площадь ромба равна:

1)30 2) 24 3) 15 4) 12

8. Площадь квадрата со стороной 5 равна

1) 50 2) 25 3) 100 4) 20

9. Если sin t =, то

1) cos t = ; tg t = 1 2) cos t = ; tg t = 3) cos t =; tg t = 4) cos t =1; tg t = 0

10. Квадрат вписан в окружность диаметра 8. Периметр квадрата равен:

1) 32 2) 16 3) 16 4) 32

Часть II

1 . В трапеции ABCD (ВC || AD) ВС = 9 см, AD = 16 см, BD = 18 см. Точка О – точка пересечения AC и BD. Найдите ОВ.

2 Хорды AB и CD пересекаются в точке Е так, что АЕ =3, ВЕ = 36, СЕ: DE= 3:4. Найдите CD и наименьшее значение радиуса этой окружности.

Вариант 2.

Часть I. 

1. Площадь прямоугольника АВСD равна 18. Найдите  сторону АВ прямоугольника, если известно, что ВС = 6.

1) 10                      2) 2,5                     3) 3                        4) 5

2. По данным рисунка найти площадь параллелограмма.

3

4

6

1). 18 кв. ед. 2). 24 кв. ед. 3). 12 кв. ед. 4). 9 кв. ед.

3. В ромбе АВСD проведена диагональ АС. Найдите  угол АDС, если известно, что угол АСB равен 35°.

1) 70°                    2) 110°                  3) 145°                  4) 125°

4. РЕ и МF — высоты треугольника МNP. МF пересекает PE в точке О. Какие из высказываний верны: N

1) △ ENP ̴ △FNМ F

2) △ MFP ̴ △ PEM E

3) △ MNP ̴ △MOP

4) △ MEO ̴ △PFO M P

1) 2,3 2) 1,4 3) 1,2 4) 3,4

5. По данным рисунка найдите градусную меру

дуги Х.

120˚ Х

40˚

1). 210˚ 2). 225˚ 3). 180˚ 4). 160˚

6. Укажите, какие из перечисленных ниже утверждений верны:

1) Если диагонали четырехугольника равны, то он прямоугольник.

2) Если противоположные стороны четырехугольника попарно равны, то он параллелограмм.

3) Если диагонали четырехугольника перпендикулярны, то он ромб.

4) Диагонали прямоугольника являются биссектрисами его углов.

7. Сторона ромба равна 5 , а одна из его диагоналей равна 8 . Площадь ромба равна :

1)30 2) 24 3) 15 4) 12

8. Площадь квадрата со стороной 3 равна

1) 36 2) 18 3) 100 4) 12

9. Если sin t =, то

1) cos t = ; tg t = 1 2) cos t = ; tg t = 3) cos t =; tg t = 4) cos t =1; tg t = 0

10. Квадрат вписан в окружность диаметра 4. Периметр квадрата равен:

1) 8 2) 4 3) 16 4) 8

Часть II

1 В △MPK МР = 24 см, DE || МР , причем D € МК, Е € РК. Найти МК, если DM = 6 см, DE = 20 см.

2 Хорды MN и PK пересекаются в точке A так, что АM =3, NA = 16, PA: KA= 1:3. Найдите PK и наименьшее значение радиуса этой окружности.

infourok.ru

Тест по алгебре и геометрии 8 класс

Итоговый тест по алгебре, 8 класс.

Вариант 1.

1. Вычислите:

A) 576 B) 192 C) 24 D)72

2.Решите уравнение: х²=36

A) 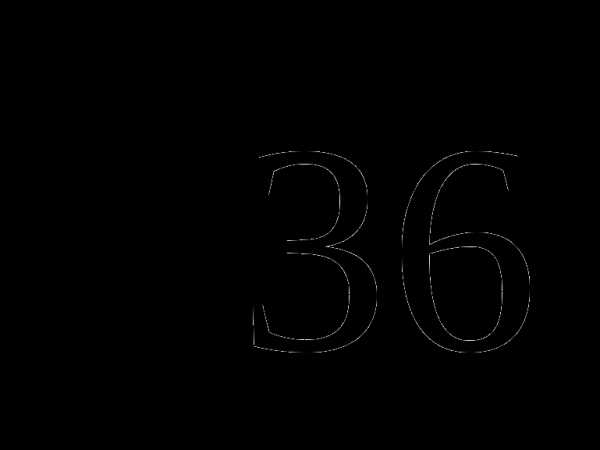B) C) 6 D)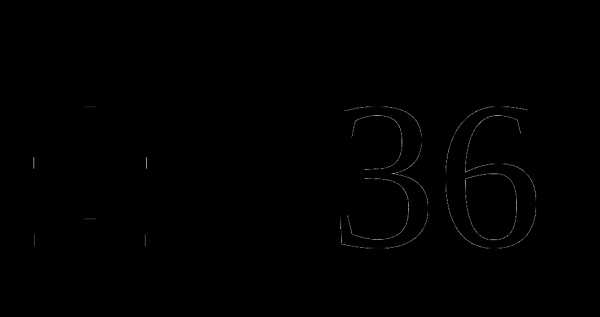

3.Найдите значение выражения:

A) 5 B) 25 C) 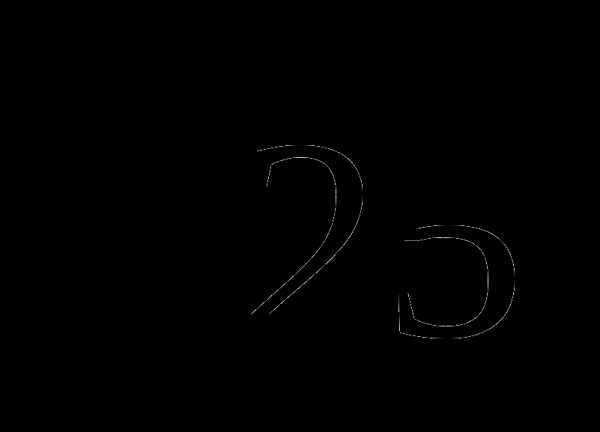D)

4. Один из корней уравнения х ² + kx + 45 = 0 равен 5. Найдите другой корень и коэффициент k

A) 9 и – 14 B) 9 и 14 C) – 9 и – 14 D) – 9 и 14

5.Освободиться от иррациональности в знаменателе дроби:

A) B) 2C) 4D) 2

6.Найдите корни уравнения: 2х²-5х=0

A) -2,5; 0 B) 0;2,5 C) 0; 5 D) 0;2

7.Решите уравнение: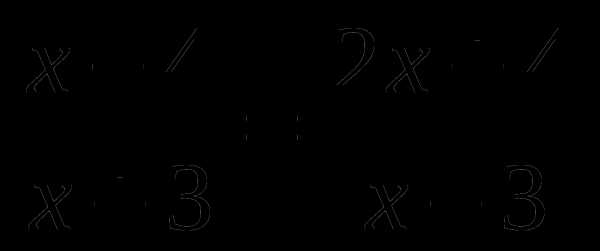

A) 0;17 B) 17;3 C) 0; -3 D) -17;0

8. Найдите корни уравнения: 3х²-6х+3=0

A) 3; 2 B) 3; -3 C) 1;6 D) 1

9.Решите уравнение: (х+3)(х-4)=0

A) 3;4 B) -3;-4 C) -3;4 D)3; -4

10.Найдите корни уравнения с помощью теоремы, обратной теореме Виета: х²-5х+6=0

A) 2;3 B) 5; 1 C) -2;3 D) -2;-3

11.Решите систему уравнений: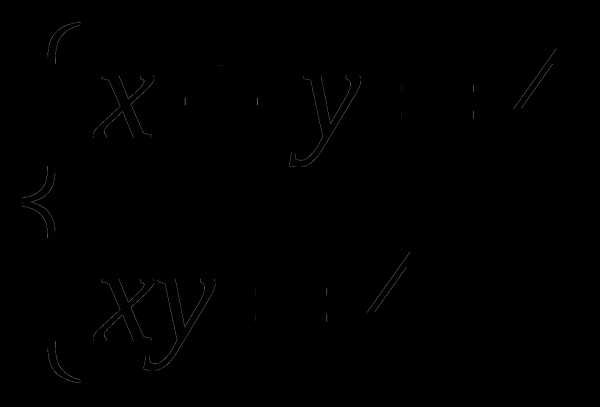

A) 4;1 B) -1;4 C) -2;2 D) 2;2

12.Сколько решений имеет данное уравнение: х²+7х-1=0

A) 1 B) 2 C) не имеет решений D) множество решений

13.Разложите квадратный трехчлен на множители: 5х²-х-42

A) (5х-14)(х+3) B) (х+14)(х-3) C) (5х+14)(х-3) D) (х-14)(х+3)

14.Найдите вершину параболы: у=3(х-2)²+2

A) -2;2 B) 2;-2 C) 2;2 D)-2;-2

15.Пешеход должен был пройти 10 км с некоторой скоростью, но, увеличив скорость на 1 км/ч, он прошел 10 км на 20 мин быстрее. Найдите истинную скорость пешехода.

A) 4км/ч B) 10км/ч C) 6км/ч D) 5 км/ч

16. Вычислите: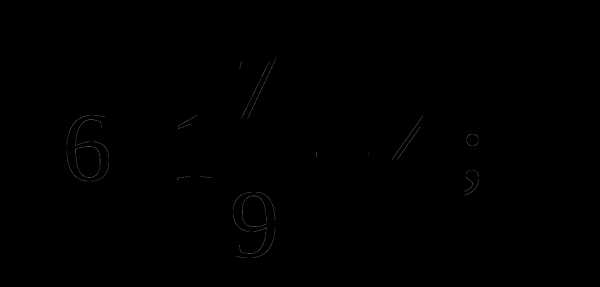

A) 4 B) — 4 C) -2 D) 2

17. Упростите выражение:

A) 9√2 + 6B) 9√2 C) 9√2 + 12D) – 9√2 – 6

18. Решите неравенство: 4х² – 4х – 15 < 0

A) ( — ∞; — 1,5)U( 2,5; + ∞) B) ( — 1,5; 2,5) C) ( — ∞; + ∞) D) [ — 1,5; 2,5]

19. Решите неравенство: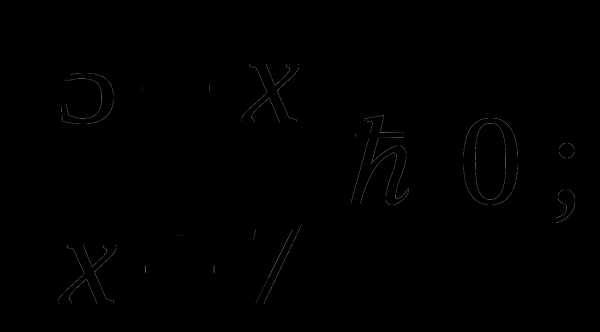

A) ( — ∞; + ∞) B) ( — 7; 5) C) ( — ∞; — 7)U( 5; + ∞) D) ( — ∞; — 7]U[ 5; + ∞)

20. Найдите координаты вершины параболы у = — х ² – 4х + 3.

A) ( -2;5) B) (2; 7) C) (-2; — 7) D) (-2;7)

Итоговый тест по алгебре, 8 класс.

Вариант 2.

1. Вычислите: 5

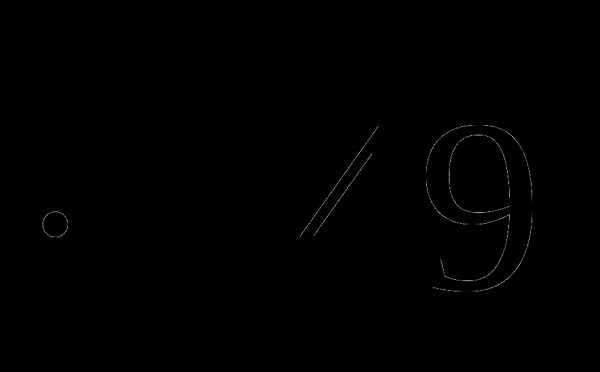
A) 35 B) 245 C) 49 D) 5

2.Решите уравнение: х²=3

A) 3 B)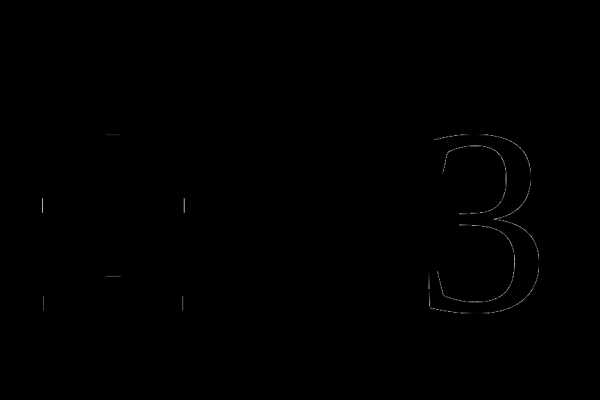C)-3 D)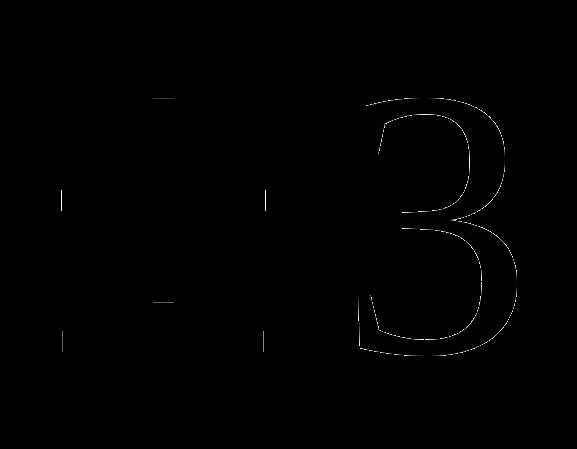

3.Найдите значение выражения: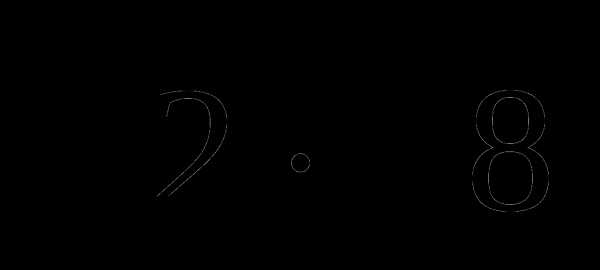

A)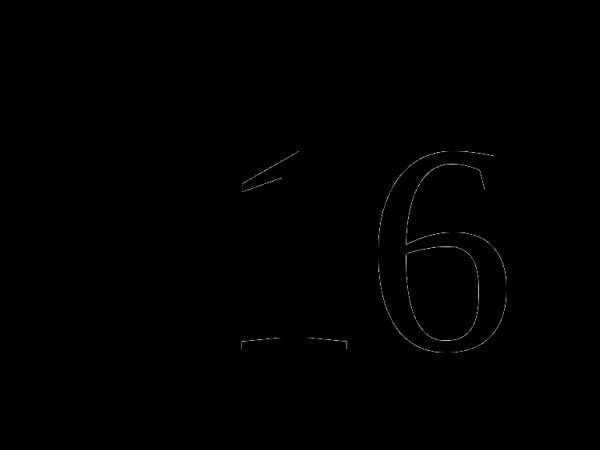B) 18 C) 4 D) 24).

4. Один из корней уравнения х ² + kx + 45 = 0 равен 3. Найдите другой корень и коэффициент k

A) – 15 и 18 B) 15 и 18 C) – 15 и — 18 D) 15 и – 18

5.Освободиться от иррациональности в знаменателе дроби: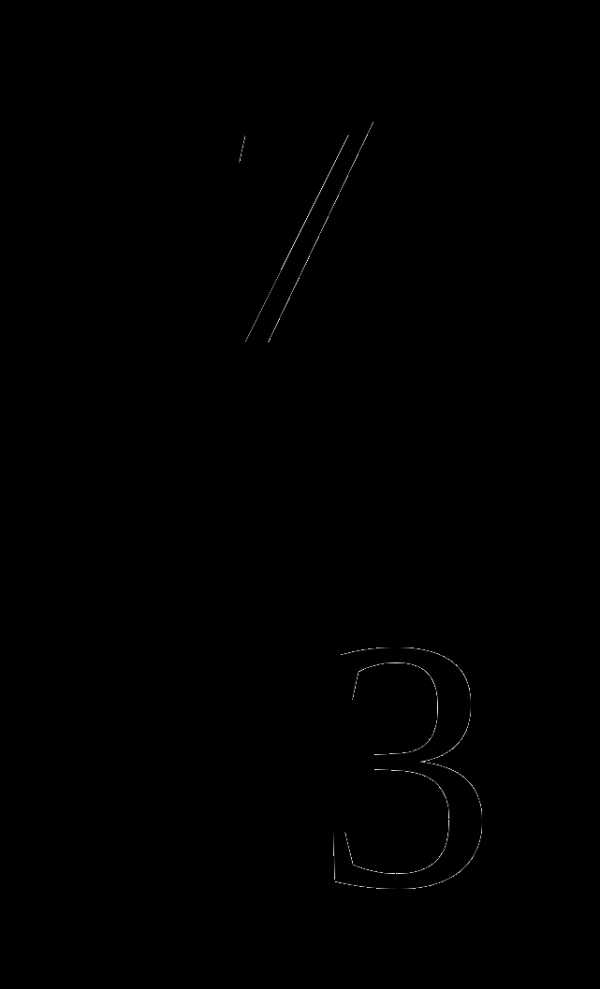

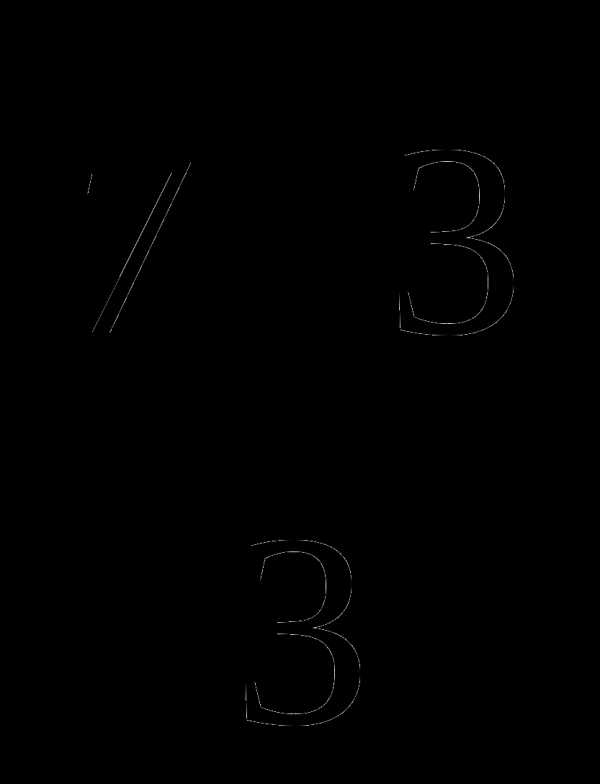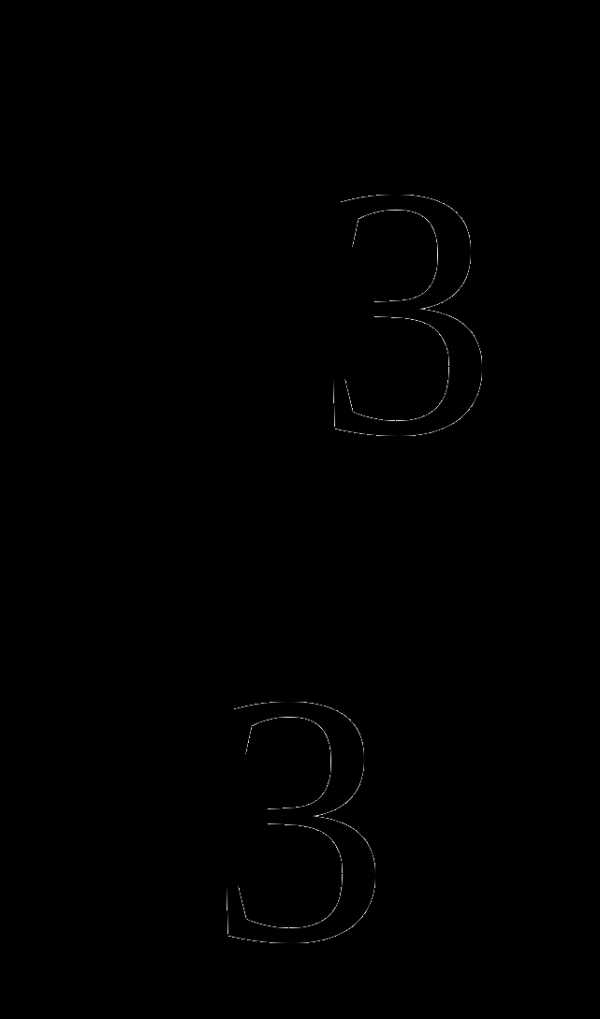A) B)C) D)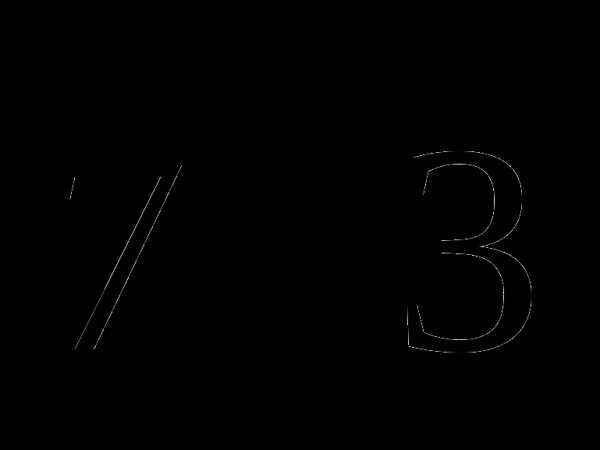

6.Найдите корни уравнения: х²-5х=0

A) -5;0 B) 0;5 C) 0 D)5

7.Решите уравнение: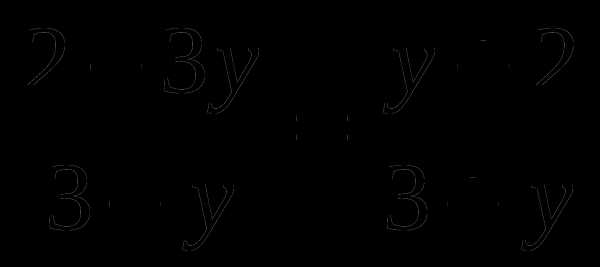

A) 2; 3 B) 4 C) -4; 0 D) 0; 4

8. Найдите корни уравнения: 2х²+3х+1=0

A) -1; 0,5 B)2;3 C)1; -0,5 D) -1;-0,5

9.Решите уравнение: (х+5)(х-1)=0

A) -5; 1 B) 5; 1 C) -5;-1 D) 5;-1

10.Найдите корни уравнения с помощью теоремы, обратной теореме Виета: х²+4х+3=0

A) 3; 1 B)-3;-1 C) -1;3 D) 1;-3

11.Решите систему уравнений: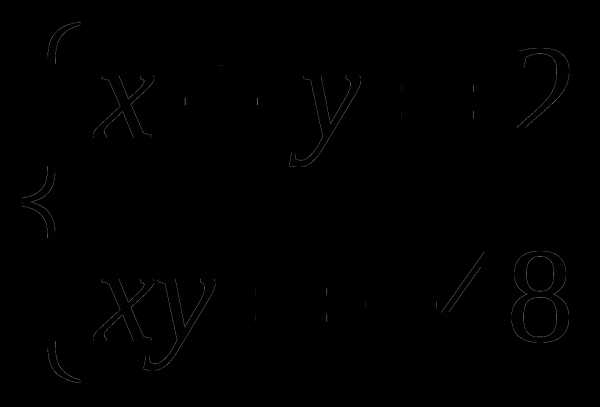

A) 6; 8 B) — 6;-8 C) 6; — 8 D) — 6;8

12.Сколько корней имеет уравнение: х²-2х+1=0

A) 1 B) 2 C) не имеет решений D) множество решений

13.Разложите квадратный трехчлен на множители: 2х²-5х+3

A) (2х+3)(х-1) B) (2х+3)(х+1) C) (2х-3)(х-1) D) (2х-3)(х+1)

14.Найдите вершину параболы: у=(х+3)²+2

A)3;2 B)-3;2 C) -3;-2 D)3;-2

15.Пешеход должен был пройти 9 км с некоторой скоростью, но, увеличив скорость на 2 км/ч, он прошел 9 км на 45 мин быстрее. Найдите истинную скорость пешехода.

A) 6км/ч B) 3км/ч C) 4км/ч D) 7км/ч

16. Вычислите:

A) 35 B) 245 C) 49 D) 75

17. Упростите выражение:

A) 27 — 10√2 B) 27 + 10√2 C) 0 D) 10√2

18. Решите неравенство: х( х + 3 ) – 6 < 3( х + 1 ) .

A) ( — ∞; -3)U( 3; + ∞) B) ( — 3; 3) C) ( — ∞; + ∞) D) [ — 3; 3]

19. Решите неравенство:

A) ( — ∞; — 8]U[0; + ∞) B) ( — 8; 8) C) ( — ∞; — 8)U( 0; 8) D) [ 0; 8]

20. Найдите координаты вершины параболы у = х ² – 4х + 3.

A) ( -2;1) B) (2; 1) C) (2; — 1) D) (-2;- 1)

Итоговый тест по алгебре, 8 класс.

Вариант 3

1. Вычислите:

A) 0,5 B) 5 C) 50 D) 10

2.Решите уравнение: х²=25

A) B) 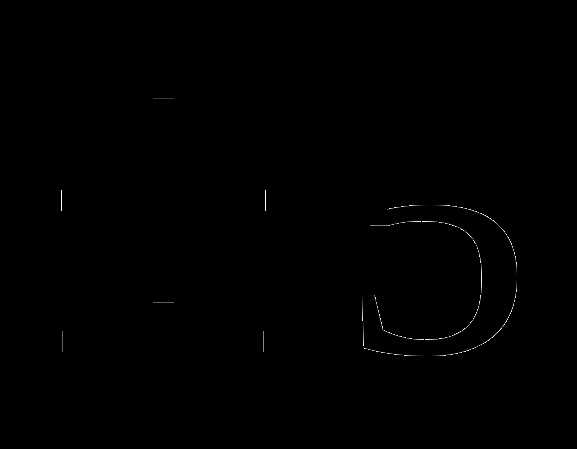C) -5 D)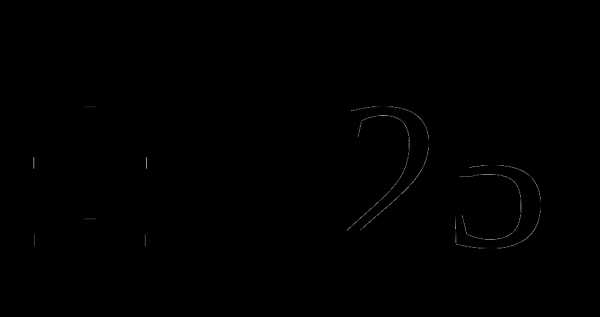

3.Найдите значение выражения: (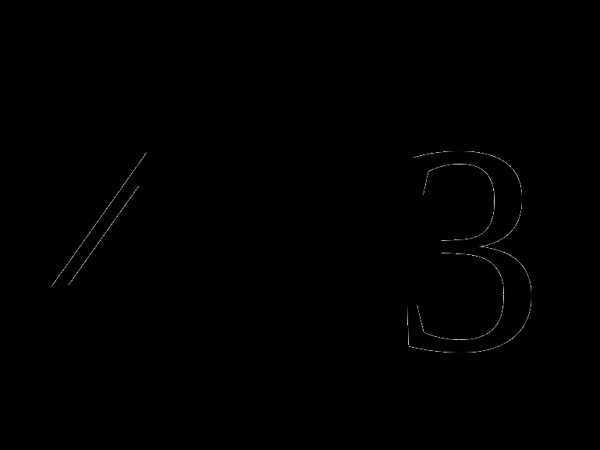)²

А) 12 B) 36 C) 48 D)144

4. Один из корней уравнения х ² – 26x + q = 0 равен 12. Найдите другой корень и свободный член q.

A) 14 и 168 B) – 14 и 168 C) — 14 и — 168 D) 14 и — 168

5.Освободиться от иррациональности в знаменателе дроби:

A) 2B) 2х C) 2хD) х

6.Найдите корни уравнения: 2х²+х=0

A) 2;1 B) -0,5; 0 C) 0,5 D) 0

7.Решите уравнение: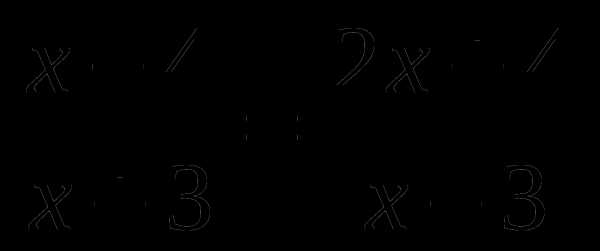

A) 0; 17 B) 17;3 C) 0; -3 D) -17;0

8. Найдите корни уравнения: 2х²+х-3=0

A) 1,5;1 B) -1,5;-1 C)-1,5;1 D)1,5;-1

9.Решите уравнение: (х-5)(х-4)=0

A) 5;-4 B) 5;4 C) -5;-4 D)-5;4

10.Найдите корни уравнения с помощью теоремы, обратной теоремы Виета: х²-5х+4=0

A) 1; 4 B) -1;-4 C)-1;4 D)1;-4

11.Решите систему уравнений: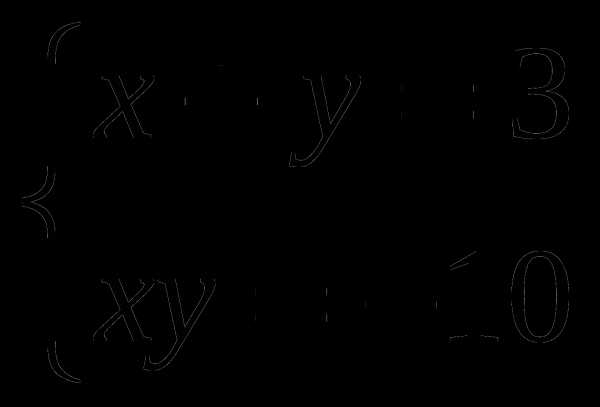

A) -5;-2 B) 5;-2 C) 5;2 D)-5;2

12.Сколько корней имеет уравнение: 2х²-4х +5=0

A) 1 B) 2 C) не имеет решений D) множество решений

13.Разложите квадратный трехчлен на множители: 2х²-7х+6

A) (2х-3)(х-2) B) (2х+3)(х-2) C) (х-3)(х-2) D) (2х+3)(х+2)

14.Найдите вершину параболы: у=0,5(х+3)²-1

A) 3; 1 B) -3;-1 C)-3;1 D)3;-1

15.Велосипедист должен был проехать 40 км с некоторой скоростью, но, увеличив скорость на 6 км/ч, он проехал 40 км на 20 мин быстрее. Найдите истинную скорость велосипедиста.

A) 20 км/ч B) 22 км/ч C) 24 км/ч D) 11 км/ч

16. Вычислите:

A) 0,5 B) 5 C) 50 D) 10

_{17. Упростите выражение:}

A) 21 — 8√2 B) 21 + 8√2 C) 0 D) 8√2

18. Решите неравенство: х ² > 2,3х

A) ( — ∞; + ∞) B) ( 0; 2,3) C) нет решений D) ( — ∞; 0)U(2,3; + ∞)

19. Решите неравенство: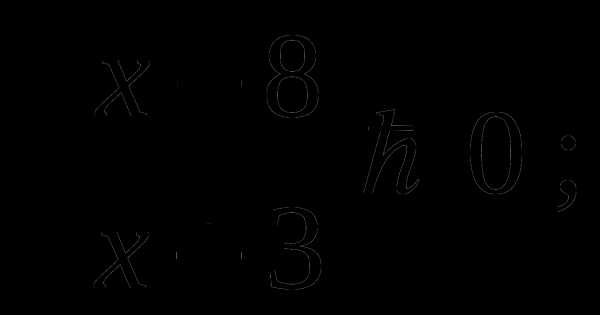

A) ( — ∞; — 3]U[8; + ∞) B) ( — 3; 8) C) ( — ∞; — 3)U( 8; + ∞) D) [ — 3; 8]

20. Найдите координаты вершины параболы у = х ² + 6х — 8.

A) ( — 3;17) B) (- 3; — 17) C) (3; — 17) D) (2; 17)

Итоговый тест по алгебре, 8 класс.

Вариант 4.

1. Вычислите:

A) 0,6 B) 0,2 C) 0,4 D) 4

2.Решите уравнение: х²=81

A) 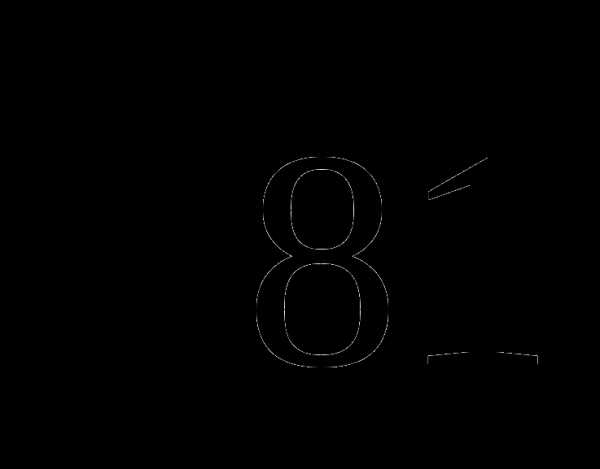B)C) 9 D)

3.Найдите значение выражения:

A) 3 B) 63 C) 21 D)147

4. Один из корней уравнения х ² – 26x + q = 0 равен 13. Найдите другой корень и свободный член q.

A) 13 и 169 B) – 13 и 169 C) — 13 и — 169 D) 13 и — 169

5.Освободиться от иррациональности в знаменателе дроби: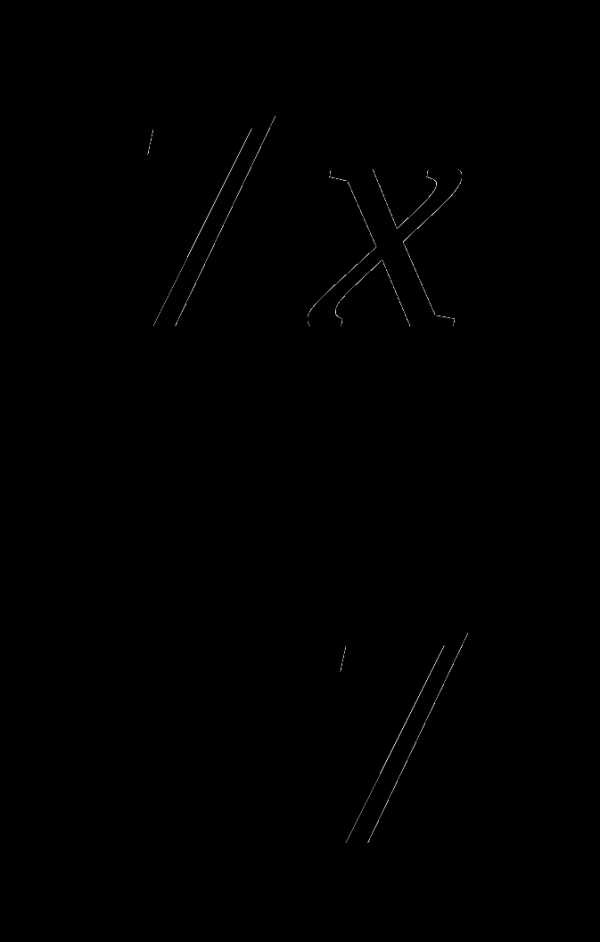

A)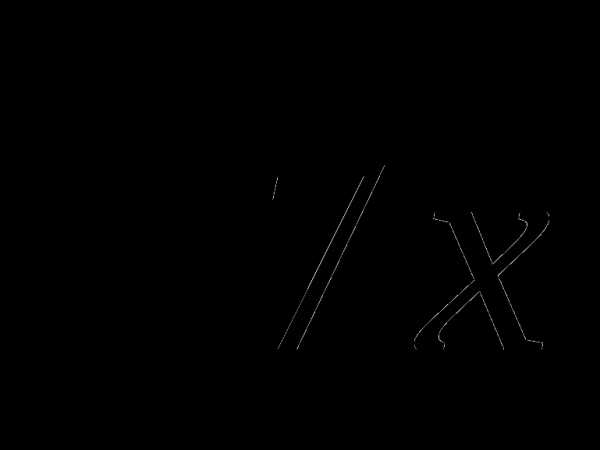B) 7х C) 7хD) 7

6.Найдите корни уравнения: х²-2х=0

A) -2;0 B) 0;2 C) 1;-2 D)-1;-2

7.Решите уравнение: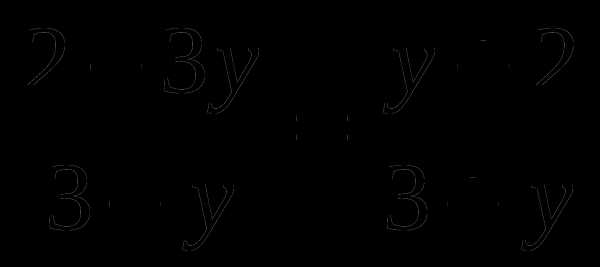

A) 2; 3 B) 4 C) -4; 0 D) 0; 4

8. Найдите корни уравнения: 4х²+4х+1=0

A) 1;4 B) — 0,5 C) -1;-4 D) 0,25

9.Решите уравнение: (х+8)(х+7)=0

A) 8; 7 B) — 7; 8 C) — 8; -7 D) — 8; 7

10.Найдите корни уравнения с помощью теоремы, обратной теоремы Виета: х²+12х+27=0

A) — 9; 3 B) -3; 9 C) 3; 9 D) — 9; — 3

11.Решите систему уравнений: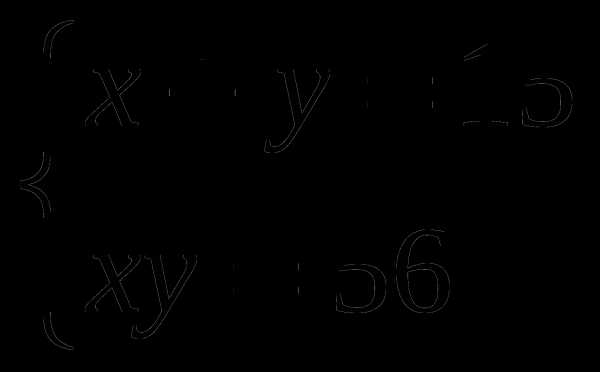

A) 7; 8 B) — 7; 8 C) — 8; — 7 D) — 8; 7

12.Сколько корней имеет уравнение: х²-х-1=0

A) 1 B) 2 C) не имеет решений D) множество решений

13.Разложите квадратный трехчлен на множители: 3х²-10х+3

A) (3х+1)(х-3) B) (х+1)(х+3) C) (3х-1)(х-3) D) (3х-1)(х+3)

14.Найдите вершину параболы: у=(х-5)²+6

A) — 5;6 B) — 6;5 C) — 6;- 5 D) 5; 6

15. Первые 40 км велосипедист проехал со скоростью, на 10км/ч большей, чем вторые 40 км, затратив на весь путь 3ч 20мин. С какой скоростью ехал велосипедист вторые 40км пути?

A) 20км/ч B) 30км/ч C) 25км/ч D) 15км/ч

16. Вычислите: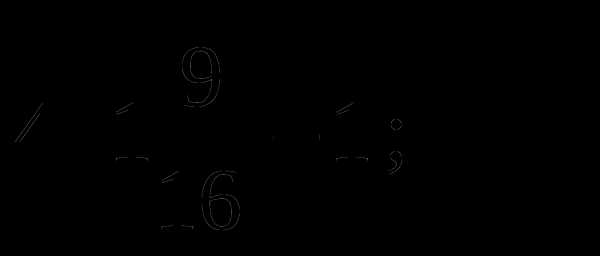

A) 5 B) 1 C) 4 D) 2

_{17. Упростите выражение:}

A) 15 B) 12 C) 14 D) 10

18. Решите неравенство: 2х ² + 5х – 12 > 0

A) ( — ∞; + ∞) B) ( — 1,5; 1) C) ( — ∞; — 1,5)U( 1; + ∞) D) ( — ∞; — 1,5]U[1; + ∞)

19. Решите неравенство:

A) ( — ∞; — 7]U[4; + ∞) B) [ — 7; 4] C) ( — ∞; — 7)U( 4; + ∞) D) ( — 7; 4)

20. Найдите координаты вершины параболы у = – х ² + 6х — 8.

A) ( — 3; — 1) B) ( 3; 1) C) (3; — 1) D) (- 3; 1)

infourok.ru

Тест по геометрии (8 класс) по теме: Итоговый тест по геометрии за курс 8 класса

Итоговый тест по геометрии за 8 класс

Часть 1.

При выполнении заданий с выбором ответа обведите номер выбранного ответа в работе. Если Вы обвели не тот номер, то зачеркните обведённый номер крестиком и затем обведите номер нового ответа.

А1. Вставьте пропущенное слово так, чтобы утверждение было верным. Прямоугольник – это  …, у которого все углы прямые.

1. трапеция
2. четырехугольник  
3. ромб
4. параллелограмм

A2. Вставьте пропущенное слово так, чтобы утверждение было верным. Диагонали ромба являются …  его углов.

1. медианами  
2. высотами
3. средними линиями  
4. биссектрисами

A3. Вставьте пропущенное слово так, чтобы утверждение было верным. Диагонали …  равны.

1. четырехугольника  
2. ромба
3. прямоугольника
4. трапеции    

A4. Найдите площадь трапеции, изображенной на рисунке.

1. 84 ед2
2. 168 ед2
3. 252 ед2
4. 336 ед2

A5.  MPKL – параллелограмм, PMK=45°, MPK=100°. Найти  углы  треугольника MKL.

1. KML=45°, MKL=45°, MLK=100°
2. KML=35°, MKL=45°, MLK=100°
3. KML=45°, MKL=35°, MLK=100°
4. KML=35°, MKL=35°, MLK=100°

A6. Основание равнобедренного треугольника 12 см, а угол при основании 60°. Найти площадь треугольника.

1. 36 см2
2. 72 см2
3. 12 см2
4. 36 см2

A7. Чему равна сумма углов выпуклого пятиугольника?

1. 3600
2. 9000
3. 5400
4. 7200

А8. Вставьте пропущенное слово так, чтобы утверждение было верным. Средняя линия треугольника  параллельна  одной  из  его сторон  и равна …  .

1. половине этой стороны
2. этой стороне
3. удвоенной этой стороне
4. сумме двух сторон треугольника

А9.  В ромбе ABCD  А=700. Чему равен угол АВС?

1. 200
2. 1100
3. 550
4. 700

А10. Смежные стороны прямоугольника равны 6 см и 8 см. Чему равны его диагонали?

1. см и см
2. 10 см и 10 см
3. 7 см и 7 см
4. 14 см и 14 см

А11. Один из углов равнобедренной трапеции равен 1000. Чему равны три оставшихся угла?

1. 800, 800, 1000
2. 750, 750, 1100
3. 700, 700, 1200
4. 600, 600, 1200

А12. В параллелограмме разность смежных сторон равна 5 см, а его периметр равен 38 см. Чему равна меньшая сторона параллелограмма?

1. 7 см
2. 12 см
3. 9 см
4. 9,5 см

А13. Одна из диагоналей ромба равна его стороне. Чему равен наибольший угол ромба?

1. 600
2. 1500
3. 900
4. 1200

А14. Ромб, не являющийся квадратом, имеет n осей симметрии. Чему равно значение n?

1. 3
2. 4
3. 2
4. 1

А15. Чему равна площадь прямоугольного треугольника  с гипотенузой 26 см, один из катетов которого равен 24 см?

1. 120 см2
2. 60 см2
3. 312 см2
4. 240 см2

А16.  Сторона ромба равна 5 см, а одна из его диагоналей – 6 см. Чему равна площадь ромба?

1. 30 см2
2. 24 см2
3. 15 см2
4. 12 см2

А17.  Площадь квадрата равна 48 см2. Чему равен периметр данного квадрата?

1. 12 см
2. 8 см
3. 16 см
4. 144 см

А18.  АВС подобен А1В1С1.  АВ = 4 см, ВС = 6 см, АС = 7 см, А1В1 = 8 см. Чему равна сторона  В1С1?

1. 3 см
2. 12 см
3. 3,5 см
4. 14 см

А19.  АВС подобен А1В1С1.  , SABC = 90 см2. Чему равна площадь треугольника А1В1С1?

1. 250 см2
2. 150 см2
3. 54 см2
4. 32,4 см2

А20.  Чему равен вписанный угол?

1. половине центрального угла, опирающегося на ту же дугу
2. центральному углу, опирающемуся на ту же дугу
3. величине дуги, на которую он опирается
4. удвоенной величине дуги, на которую он опирается

А21.  Центром вписанной в треугольник окружности является ….

1. точка пересечения высот треугольника
2. точка пересечения биссектрис треугольника
3. точка пересечения медиан треугольника
4. точка пересечения серединных перпендикуляров треугольника

А22.  Вписанный угол АВС равен 700. Чему равен центральный угол, опирающийся на дугу АС?

1. 350
2. 700
3. 1400
4. 2900

А23.  На окружности отмечены точки А и В так, что градусные меры образовавшихся дуг относятся как 11 : 7. Чему равны величины данных дуг?

1. 1650; 1050
2. 1100; 700
3. 2200; 1400
4. 2400; 1200

Часть 2.

Полученный ответ на задание  записывается в отведённом для этого месте.  В задаче в ответ запишите только число (наименования указывать не надо).

Если ответ содержит несколько чисел, разделяйте их точкой с запятой (;) и записывайте числа в порядке возрастания. Если ответом является обыкновенная дробь, то переведите ее в десятичную дробь и запишите в ответ десятичную дробь.

В случае записи неверного ответа зачеркните его и запишите рядом новый.

B1. К окружности с центром в точке О проведены касательная АВ и секущая АО. Найдите радиус окружности, если АВ=12 см, АО=13 см.

Ответ:____________________________________

B2. Найдите тангенс угла АОВ, изображенного на рисунке.

Ответ:____________________________________

B3. Проектор полностью освещает экран А высотой 80 см, расположенный на расстоянии 250 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран В высотой 160 см, чтобы он был полностью освещен, если настройки проектора остаются неизменными.

Ответ:____________________________________

B4.  В окружности проведены две хорды АВ и CD, пересекающиеся в точке К,  КС=6 см, АК=8 см, BK+DK=28 см. Найдите произведение ВК и DK.

Ответ:____________________________________

В5. Диагонали АС и BD трапеции ABCD пересекаются в точке О. Площади треугольников AOD и BOC равны соответственно 25 см2 и 16 см2. Найдите площадь трапеции.

Ответ:____________________________________

В6.  В равнобедренном  треугольнике АВС с основанием АС медианы пересекаются в точке О. Найдите площадь треугольника АВС, если ОА=13 см, ОВ=10 см.

Ответ:____________________________________

В7. Радиус окружности с центром в точке O равен 13 см, длина хорды AB равна 24 см. Найдите расстояние от хорды AB до параллельной ей касательной k (см. рисунок).

Ответ:___________________________________

nsportal.ru