Учебно-методическое пособие по геометрии (8 класс) на тему: Теория по геометрии 8 класс
Геометрия 8 класс. Теория.
Свойства параллелограмма. Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны.
1. стороны. Противолежащие стороны параллельны и равны
2.Углы.
Противолежащие углы равны.
Сумма углов, прилежащих к одной стороне равна 1800
3.Диагонали. Диагонали точкой пересечения делятся пополам.
Дополнительные свойства.
1. Биссектриса угла отсекает от параллелограмма равнобедренный треугольник
2. Биссектрисы углов, прилежащих к одной стороне, пересекаются под прямым углом
3. Биссектрисы противолежащих углов параллельны.
4. Связь сторон и диагоналей:
Свойства прямоугольника. Прямоугольник — это параллелограмм, у которого все углы прямые.
1. Сохраняет все свойства параллелограмма
2. Свое свойство. Диагонали прямоугольника равны
Свойства ромба. Ромб – это параллелограмм, у которого все стороны равны
1. Сохраняет все свойства параллелограмма
2. Свое свойство. Диагонали ромба перпендикулярны и являются биссектрисами углов
Свойства квадрата. Квадрат – это прямоугольник, у которого все стороны равны.
1. Сохраняет все свойства прямоугольника.
2. Диагонали квадрата равны, перпендикулярны и являются биссектрисами углов
Свойства равнобедренной трапеции
1.Боковые стороны равны.
2.Углы, прилежащие к основаниям равны ( два острых и два тупых)
3. Сумма углов, прилежащих к боковой стороне равна 1800
4.Бисектрисы углов, прилежащих к боковой стороне, пересекаются под прямым углом
5. Длина средней линии трапеции равна большему отрезку на большем основании, если провести одну высоту
6. При решении задач всегда проводят две высоты. (равные отрезки на большем основании)
7. Средняя линия трапеции параллельна ее основаниям и равна (полусумме оснований – параллельных сторон.)
8.При решении задач. Если диагонали трапеции перпендикулярны, тогда вторую диагональ перенести параллельно к первой. Получим прямоугольный треугольник, гипотенуза = сумме оснований
Средняя линия трапеции – это отрезок, соединяющий середины боковых сторон
Средняя линия треугольника – это отрезок, соединяющий середины двух сторон.
Средняя линия треугольника параллельна одной из сторон и равна ее половине.
Теорема Пифагора. Квадрат гипотенузы равен сумме квадратов катетов.
Гипотенуза = Катет = Гипотенуза больше катета.
Как определить вид треугольника по углам
Большая сторона2 = сторона2 + сторона2 — треугольник прямоугольный
Большая сторона2 2 + сторона2 — треугольник остроугольный
Большая сторона2 > сторона2 + сторона2 — треугольник тупоугольный
сИнус острого угла прямоугольного треугольника равен отношению прОтиволежащего катета к гипотенузе
кОсинус острого угла прямоугольного треугольника равен отношению прИлежащего катета к гипотенузе
Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему катету
Котангенс острого угла прямоугольного треугольника равен отношению прилежащего катета к противолежащему катету
Сумма углов выпуклого многоугольника равна Sn = 1800 (n – 2), где n – количество сторон или углов. Сумма углов правильного многоугольника S = , — угол многоугольника, n – количество сторон или углов
Сумма углов четырехугольника 3600
Сумма внешних углов многоугольника, взятых по одному при каждой вершине равна 3600.
В прямоугольном треугольнике высота проведена к гипотенузе, тогда
- Высота, проведенная к гипотенузе =
- Катет =
Медианы треугольника пересекаются в одной точке и делятся в отношении 2:1, считая от вершины.
- Одна медиана разбивает треугольник на два треугольника равной площади.
- Три медианы разбивают треугольник на 6 треугольников с равными площадями
- Медиана, проведенная к гипотенузе прямоугольного треугольника, является радиусом описанной окружности R и равна половине гипотенузы
Подобие треугольников
- Периметры подобных треугольников пропорциональны коэффициенту подобия.
- Площади подобных треугольников пропорциональны квадрату коэффициенту подобия
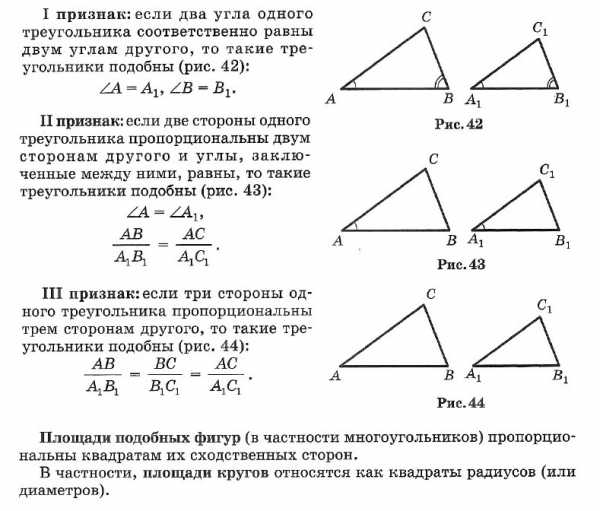
Признаки подобия
- Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами равны, то такие треугольники подобны.
- Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.
Площадь треугольника:
- Площадь треугольника равна половине произведения стороны на высоту, опущенную к ней.
- Площадь треугольника равна половине произведения двух сторон на синус угла между ними
- Площадь треугольника равна произведению полупериметра на радиус вписанной окружности . (Для любого многоугольника)
- Площадь треугольника равна произведение трех сторон деленное на 4 радиуса описанной окружности R.
- – формула Герона, p — полупериметр
- Площадь прямоугольного треугольника равна половине произведения катетов
Площадь параллелограмма, ромба
- Площадь параллелограмма равна произведению стороны на высоту, опущенную к ней.
- Площадь параллелограмма равна произведению двух сторон на синус угла между ними
- Площадь параллелограмма равна половине произведению диагоналей на синус угла между ними
( для любого четырехугольника)
- Площадь ромба равна половине произведению диагоналей (для любого четырехугольника, у которого диагонали перпендикулярны)
Площадь квадрата
- Площадь квадрата равна стороне в квадрате S = a2
- Площадь квадрата равна
Площадь прямоугольника:
- Площадь прямоугольника равна произведению смежных сторон.
- Площадь прямоугольника равна половине произведению диагоналей на синус угла между ними
(для любого четырехугольника)
Площадь трапеции
- Площадь трапеции равна произведению полусумме оснований на высоту
- Площадь трапеции равна произведению средней линии на высоту
- Если в трапеции диагонали перпендикулярны, то ее площадь равна
Касательная к окружности.
- Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки. Это секущая к окружности.
- Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.
- Если расстояние от центра окружности до прямой равно радиуса окружности, то прямая и окружность имеют одну общую точку. Это касательная к окружности. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенных из одной точки равны
АВ = АС, АО — биссектриса
Свойство хорд в окружности
Свойства секущих и касательных
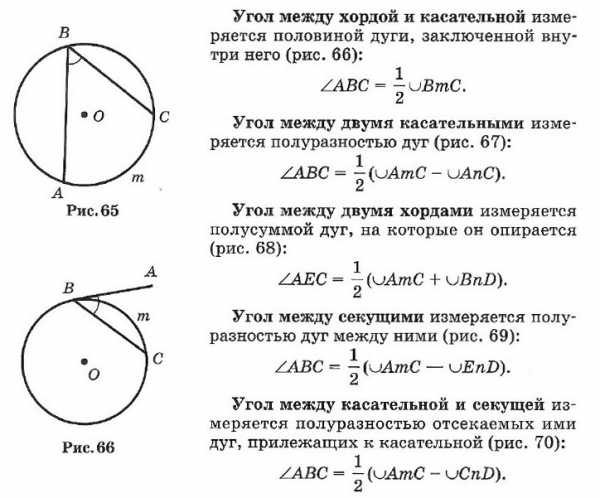
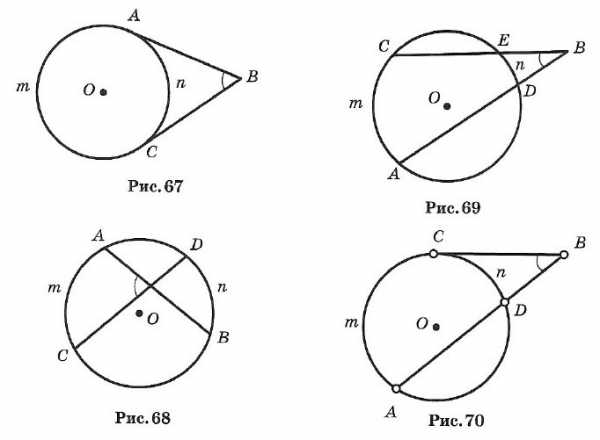
Углы между касательными
Центральные и вписанные углы.
Угол, вершина которого лежит в центре окружности называется центральным.
Центральный угол равен дуге, на которую опирается.
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным.
Вписанный угол равен половине дуги, на которую опирается, (половине соответствующего центрального угла)
Вписанные углы, опирающиеся на одну дугу, равны.
Вписанный угол, опирающийся на диаметр, равен 900
Вписанная и описанная окружность.
Окружность вписана в многоугольник, если она касается всех его сторон.
Окружность описана около многоугольника, если она проходит через все его вершины
Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы. ,
Медиана, проведенная к гипотенузе равна Радиусу описанной окружности ( образуются равнобедренные треугольники) Медиана = ,
радиус окружности вписанной в прямоугольный треугольник
Центр окружности вписанной в треугольник лежит на пересечении Биссектрис.
Центр окружности описанной около треугольника лежит на пересечении серединных перпендикуляров к сторонам.
Окружность можно вписать в четырехугольник, если суммы противоположных сторон равны.
a +b = k + m
Окружность можно описать около четырехугольника, если сумма противоположных углов равна 1800.
nsportal.ru
Конспект «Краткий курс геометрии 8 класс»
«Краткий курс геометрии 8 класс»
«Краткий курс геометрии 8 класс» — это краткие теоретические сведения по курсу геометрии за 8 класс (определения, теоремы, основные свойства). Цитаты взяты в учебных целях из пособия «Геометрия: задачи на готовых чертежах для подготовки к ОГЭ и ЕГЭ (базовый уровень): 8 класс / Э.Н.Бабаян. — Ростов н/Д: Феникс.
Планиметрия
☑ 1. Многоугольник
ABCDE — пятиугольник (рис. 11). Точки А, В, С, D, Е — вершины многоугольника; ∠A, ∠B, ∠C, ∠D, ∠E — углы; АВ, ВС, CD и т. д. — стороны; отрезки АС, AD, BE, BD, СЕ — диагонали; Р = АВ + ВС + … + ЕА — периметр многоугольника.
Многоугольник называется выпуклым (см. рис. 11), если он целиком расположен по одну сторону от каждой прямой, проходящей через две его соседние вершины. В противном случае многоугольник называется невыпуклым (рис. 12).
Свойства
1. Сумма внутренних углов произвольного n-угольника равна 180° • (n — 2).
2. Сумма внешних углов выпуклого n-угольника, взятых по одному при каждой вершине, равна 360°.
3. В выпуклом n-угольнике из каждой вершины можно провести (n — 3) диагоналей, которые разбивают n-угольник на (n — 2) треугольников.
4. В выпуклом n-угольнике число диагоналей равно n(n — 3)/2.
☑ 2. Правильные многоугольники
Выпуклый многоугольник, у которого равны все углы и стороны, называется правильным.
Свойства
1. Каждый угол правильного n-угольника равен аn = 180°(n — 2)/n
2. Около правильного n-угольника можно описать окружность, и притом только одну.
3. В правильный n-угольник можно вписать окружность, и притом только одну.
4. Окружность, вписанная в правильный n-угольник, касается всех сторон n-угольника в их серединах.
5. Центр окружности, описанной около правильного n-угольника, совпадает с центром окружности, вписанной в тот же n-угольник.
6. Длина стороны правильного n-угольника, вписанного в окружность радиуса R, равна а = 2R sin(180°/n).
7. Длина стороны правильного n-угольника, описанного около окружности радиуса r, равна а = 2r tg(180°/n).
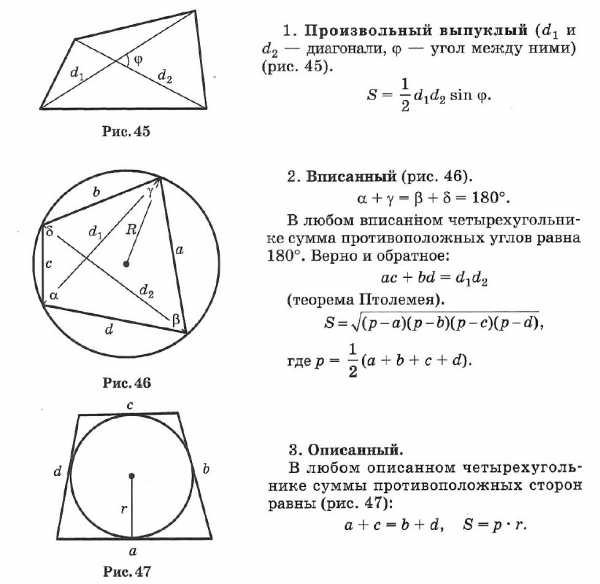
☑ 3. Четырехугольник
☑ 4. Параллелограмм
Признаки параллелограмма (рис. 48)
- Если в четырехугольнике две стороны равны и параллельны (АВ = DC, АВ || CD), то такой четырехугольник — параллелограмм.
- Если в четырехугольнике противоположные стороны попарно равны (АВ = DC, AD = DC), то такой четырехугольник — параллелограмм.
- Если в четырехугольнике противоположные углы попарно равны (∠A = ∠C; ∠B = ∠D), то такой четырехугольник — параллелограмм.
- Если в четырехугольнике диагонали пересекаются и в точке пересечения делятся пополам, то такой четырехугольник — параллелограмм.
☑ 5. Трапеция
Равнобедренная трапеция
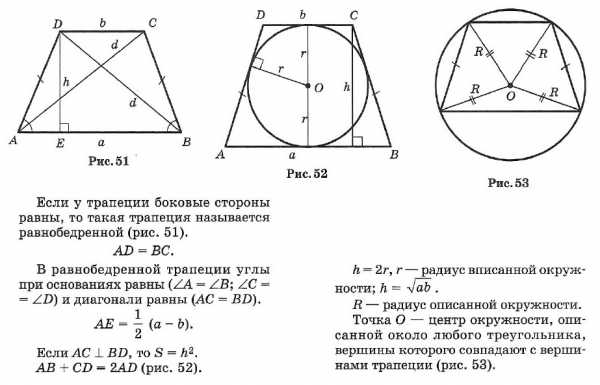
Прямоугольная трапеция
☑ 6. Прямоугольник
☑ 7. Ромб
☑ 8. Квадрат
☑ 9. Теорема Чевы
☑ 10. Теорема Менедая
☑ 11. Теорема синусов
☑ 12. Теорема косинусов
☑ 13. Площадь треугольника
☑ 14. Площадь многоугольников
☑ 15. Равносторонний (правильный) треугольник
☑ 16. Подобные треугольники
☑ 17. Признаки подобия треугольников
☑ 18. Окружность
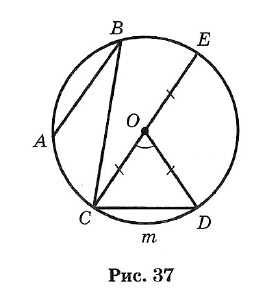Окружностью называется геометрическое место точек плоскости, равноудаленных от одной ее точки (центра) (рис. 37).
Отрезок, соединяющий центр окружности с точкой на окружности, называется радиусом. Обозначение: г или R.
На рисунке ОС = ОЕ = OD = R.
Часть окружности (например, CmD) называется дугой.
Отрезок, соединяющий две точки окружности, называется хордой, а хорда, проходящая через центр, — диаметром.
АВ, ВС, CD и СЕ — хорды окружности. СЕ — наибольшая из хорд — диаметр.
Обозначение: d или D. D = 2R.
Часть плоскости, ограниченная окружностью, называется кругом.
Часть круга, ограниченная дугой (CmD) и стягивающей ее хордой (CD), называется сегментом.
Часть круга, ограниченная двумя радиусами и дугой, называется сектором.
Угол, образованный двумя радиусами, называется центральным (∠COD на рис. 37).
Угол, у которого вершина лежит на окружности, а стороны являются хордами, называется вписанным (например, ∠ABC).
☑ 19. Свойства касательных к окружности
Угол, образованный двумя касательными (СА и СВ), исходящими из одной точки, называется описанным (∠ACB на рис. 38).
1. Радиус, проведенный в точку касания, перпендикулярен касательной.
2. Две касательные, проведенные к окружности из одной точки, равны, и центр окружности лежит на биссектрисе угла между ними.
☑ 20. Окружность и треугольник
1. Около всякого треугольника можно описать окружность; центром окружности является точка пересечения перпендикуляров, проведенных к сторонам через их середины (рис. 39).
2. Во всякий треугольник можно вписать окружность; центром окружности является точка пересечения биссектрис (рис. 40).
☑ 21. Окружность и четырехугольник
☑ 22. Углы и окружность
☑ 23. Метрические соотношения в окружности
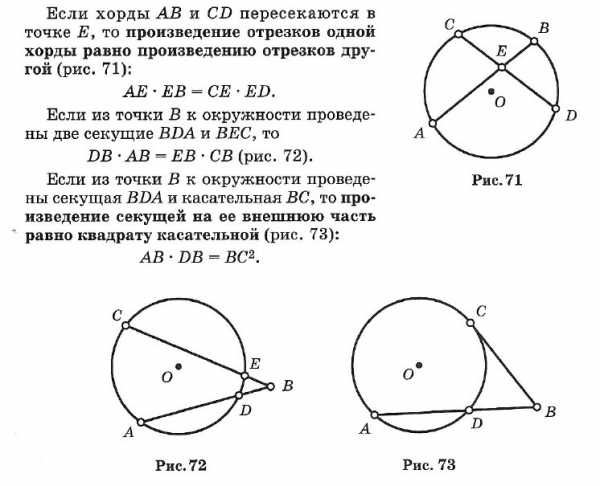
☑ 24. Длина окружности. Площадь круга и его частей
☑ 25. Уравнение окружности
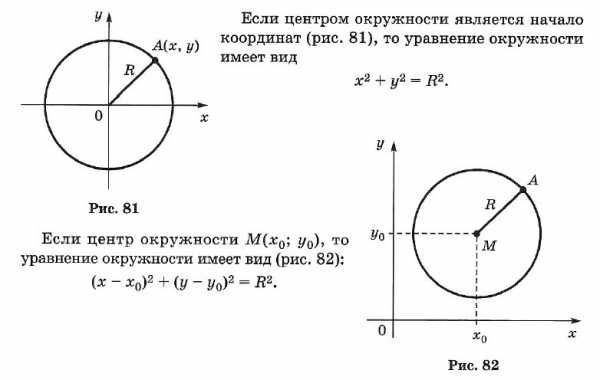
Вы смотрели «Краткий курс геометрии 8 класс» — все определения, теоремы и основные свойства из Геометрии за 8 класс. Выберите дальнейшие действия:
Краткий курс геометрии 8 класс
4.8 (95%) 4 vote[s]
uchitel.pro
Теория по геометрии за курс 8 класса. Вопросы и ответы
Многоугольник. Его элементы.
Выпуклый многоугольник.
Параллелограмм. Определение.
Свойства параллелограмма.
Признаки параллелограмма.
Трапеция.
Виды трапеции.
Основные свойства равнобедренной трапеции.
Особые свойства трапеции.
Прямоугольник. Определение.
Основные свойства прямоугольника.
Признак прямоугольника.
Ромб. Определение.
Основные свойства ромба.
Признак ромба.
Квадрат. Определение.
Основные свойства квадрата.
Осевая симметрия. Определение.
Центральная симметрия. Определение.
Площадь квадрата.
Площадь прямоугольника.
Площадь параллелограмма.
Площадь треугольника.
Площадь прямоугольного треугольника.
Формула Герона для нахождения площади треугольника.
Следствие об отношении площадей треугольников с равными высотами.
Теорема об отношении площадей треугольников, имеющих равные углы.
Площадь трапеции.
Площадь ромба.
Теорема Пика.
Теорема Пифагора.
Пифагоров треугольник. Определение.
Египетский треугольник. Определение.
Подобные треугольники. Определение.
Коэффициент подобия. Определение.
Теорема об отношении площадей подобных треугольников.
Первый признак подобия треугольников.
Второй признак подобия треугольников.
Третий признак подобия треугольников.
Теорема о средней линии треугольника. Определение.
Теорема о точке пересечения медиан треугольника.
Среднее пропорциональное (геометрическое). Определение.
2 теоремы о высоте прямоугольного треугольника, проведённой из вершины прямого угла.
Утверждение о катете прямоугольного треугольника.
Синус острого угла.
Косинус острого угла.
Тангенс острого угла.
Теорема о равных острых углах прямоугольных треугольников.
Основное тригонометрическое тождество.
Значение sin α, cos α, tg α, для углов α равных 300, 450, 600.
Теорема о медиане прямоугольного треугольника, проведённой из вершины прямого угла.
Секущая прямая. Определение.
Касательная прямая. Определение.
В каком случае прямая и окружность не имеют общих точек?
Теорема о свойстве касательной.
Свойство отрезков касательных, проведённых из одной точки.
Признаки касательной.
Полуокружность. Определение.
Центральный угол. Определение.
Градусная мера дуги окружности.
Сумма мер двух дуг окружностей.
Вписанный угол. Определение.
Теорема о вписанном угле.
Вписанный угол, опирающийся на одну и ту же дугу.
Вписанный угол, опирающийся на полуокружность.
Теорема о произведении отрезков пересекающихся хорд.
Теорема о каждой точки биссектрисы.
Теорема обратная теореме о каждой точке биссектрисы.
Точка пересечения биссектрис угла.
Серединный перпендикуляр к отрезку.
Теорема о серединном перпендикуляре к отрезку.
Теорема обратная теореме о серединном перпендикуляре к отрезку.
Следствие о точке пересечения серединных отрезков к сторонам треугольника.
Теорема о пересечении высот треугольника.
Четыре замечательные точки треугольника.
Вписанная окружность. Определение.
Описанный многоугольник. Определение.
Теорема об окружности, вписанной в треугольник.
Сколько окружностей можно вписать в треугольник.
Суммы противоположных сторон в описанном треугольнике.
Описанная окружность. Определение.
Вписанный многоугольник. Определение.
Теорема об окружности, описанной около треугольника.
Какова сумма противоположных углов во вписанном четырёхугольнике.
В каком случае около четырёхугольника можно описать окружность.
Свойство трапеции, в которую можно вписать окружность.
Средняя линия трапеции. Определение.
Теорема о средней линии трапеции.
2) Диагонали параллелограмма точкой пересечения делятся пополам.
2) Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм.
3) Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.
2) Диагонали равнобедренной трапеции равны.
3) Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали – полусумме оснований.
2) Если сумма углов при одном из оснований трапеции равна 900, то отрезок, соединяющий середины оснований трапеции, равен их полуразности.
2) Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
Фигура называется симметричной относительно оси симметрии, если для каждой точки фигуры симметричная ей точка относительно оси симметрии также принадлежит этой фигуре.
Фигура называется симметричной относительно центра симметрии, если для каждой точки фигуры симметричная ей точка относительно центра симметрии также принадлежит этой фигуре.
Площадь квадрата равна квадрату его стороны.
Площадь прямоугольника равна произведению его смежных сторон.
Площадь параллелограмма равна произведению его основания на высоту.
Площадь треугольника равна половине произведения его основания на высоту.
Площадь прямоугольного треугольника равна половине произведения его катетов.
Если высоты двух треугольников равны, то их площади относятся как основания.
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Площадь трапеции равна произведению полусуммы его оснований на высоту.
Площадь ромба равна половине произведения его диагоналей.
Площадь многоугольника, все вершины которого расположены в точках целочисленной решетки, выражается числом , где m – количество точек решетки, находящихся внутри многоугольника, а n — количество точек решетки, лежащих на его границе.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Прямоугольные треугольники, у которых длины сторон выражаются целыми числами,
называются пифагоровыми треугольниками.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
2)Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.
Медиана треугольника, проведённая из вершины прямого угла, равна половине гипотенузы.
Прямая, имеющая с окружностью две общие точки называется секущей к окружности.
Прямая, имеющая с окружностью только одну общую точку называется касательной к окружности.
Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.
Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром окружности.
Угол с вершиной в центре окружности называется её центральным углом.
Если дуга окружности меньше полуокружности или является полуокружностью, то её градусная мера считается равной градусной мере центрального угла. Если дуга больше полуокружности, то её градусная мера считается равной 360º – величина центрального угла.
Сумма градусных мер двух дуг окружности с общими концами равна 360º.
Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Вписанный угол измеряется половиной дуги, на которую он опирается.
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Вписанный угол, опирающийся на полуокружность – прямой.
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон.
Каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе.
Биссектрисы треугольника пересекаются в одной точке.
Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему.
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
Каждая точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему.
Серединные отрезки к сторонам треугольника пересекаются в одной точке.
Высоты треугольника (или их продолжения) пересекаются в одной точке.
Четыре замечательные точки треугольника – это точка пересечения медиан, точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам и точка пересечения высот (или их продолжений).
Если все стороны многоугольника касаются окружности, то окружность называется вписанной.
Описанный многоугольник – это многоугольник, в котором вписана окружность.
В любой треугольник можно вписать окружность.
В треугольник можно вписать только одну окружность.
В любом описанном четырёхугольнике суммы противоположных сторон равны.
Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника.
Многоугольник называется вписанным, если вокруг него описана окружность.
Около любого треугольника можно описать окружность.
В любом вписанном четырёхугольнике сумма противоположных углов равна 180º.
Если сумма противоположных углов равна 1800, то около него можно описать окружность.
Если в трапецию можно вписать окружность, то боковая сторона трапеции видна из центра окружности под прямым углом.
Средняя линия трапеции – это отрезок, соединяющий середины её боковых сторон.
Средняя линия трапеции параллельна основаниям и равна их полусумме.
multiurok.ru
Определения, теоремы и формулы геометрия 8 класс
Геометрия 8 класс
Определения
Многоугольник-геометрическая фигура, составленная из отрезков так, что смежные отрезки не лежат на одной прямой, а несмежные-не имеют общих точек.
Выпуклый многоугольник, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
Параллелограмм-четырехугольник, у которого противоположные стороны попарно параллельны.
Трапеция-четырёхугольник, у которого две стороны параллельны, а две другие-не параллельны.
Основания трапеции-её параллельные стороны, две другие не параллельные-боковые стороны трапеции.
Равнобедренна трапеция, если её боковые стороны равны.
Прямоугольная трапеция, если один из её углов прямой.
Прямоугольник-параллелограмм, у которого все углы прямые.
Ромб-параллелограмм, у которого все стороны равны.
Квадрат-прямоугольник, у которого все стороны равны.
Точки А и А1 симметричны относительно прямой, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему.
Фигура симметрична относительно прямой, если для каждой точки фигуры симметричная ей точка относительно данной прямой также принадлежит этой фигуре(это осевая симметрия).
Ось симметрии-данная прямая, относительно которой происходит симметрия.
Точки А и А1 симметричны относительно точки О, если О середина отрезка АА1.
Фигура симметрична относительно точки, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре(это центральная симметрия).
Отношение отрезков АВ и СD-отношение их длин, т.е. .
Отрезки АВ и СD пропорциональны отрезкам А1В1 и С1D1, если .
Стороны треугольника АВ и А1В1, ВС и В1С1, СА и С1А1 сходственны, если .
Два треугольника подобны, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого
,
где k- коэффициент подобия.
Средняя линия треугольника-отрезок, соединяющий середины двух сторон треугольника.
Синус острого угла прямоугольного треугольника- отношение противолежащего катета к гипотенузе.
Косинус острого угла прямоугольного треугольника- отношение прилежащего катета к гипотенузе.
Тангенс острого угла прямоугольного треугольника – отношение противолежащего катета к прилежащему.
Тангенс острого угла прямоугольного треугольника – отношение синуса к косинусу этого угла.
Касательная к окружности-прямая, имеющая с окружностью только одну общую точку-точку касания прямой и окружности.
Полуокружность-дуга, если отрезок, соединяющий её концы, является диаметром окружности.
Центральный угол-угол с вершиной в центре окружности.
Серединный перпендикуляр к отрезку-прямая, проходящая через середину отрезка и перпендикулярная к нему.
Окружность, вписанная в многоугольник, если все стороны многоугольника касаются окружности. А многоугольник, описанный около этой окружности.
Окружность, описанная около многоугольника, если все вершины многоугольника лежат на окружности. А многоугольник, вписанный в окружность.
Вектор(направленный отрезок)-отрезок, для которого указано, какой его конец является началом, а какой-концом.
Нулевой вектор, если начало совпадает с его концом.
Длина или модуль вектора — длина отрезка АВ.
Векторы коллинеарные , если они лежат либо на одной прямой, либо на параллельных прямых. Нулевой вектор коллинеарен любому вектору.
Векторы сонаправленные , если они направлены в одну сторону.
Векторы противоположно направленные , если они направлены в разные стороны.
Векторы равны, если они сонаправлены и их длины равны.
Сумма двух векторов (правило треугольника)-вектор с началом в начале первого вектора и концом в конце второго вектора.
Сумма n— векторов (правило многоугольника), если А1,А2,…,Аn-произвольные точки плоскости, то , где n_количество векторов.
Разность двух векторов и — вектор , равный сумме векторов и .
Произведение вектора на число k-вектор , длина которого , причем и при и при .
Средняя линия трапеции-отрезок, соединяющий середины её боковых сторон или середины её оснований (вторая средняя линия трапеции).
Правила и теоремы
5.1. Сумма углов выпуклого n-угольника равна , где n-количество сторон многоугольника.
5.2. Сумма углов выпуклого четырехугольника равна 3600.
5.3. Свойства параллелограмма:
10. В параллелограмме противоположные стороны равны и противоположные углы равны.
20. Диагонали параллелограмма точкой пересечения делятся пополам.
5.4. Признаки параллелограмма:
10. Если в четырехугольнике две стороны равны и параллельны, то этот четырёхугольник параллелограмм.
20. Если в четырехугольнике противоположные стороны попарно равны, то этот четырёхугольник параллелограмм.
30. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник параллелограмм.
5.5. Теорема Фалеса. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
5.6. Свойство прямоугольника:
10. Диагонали прямоугольника равны.
5.7. Признак прямоугольника:
10. Если в параллелограмме диагонали равны, значит этот параллелограмм-прямоугольник.
5.8. Свойство ромба:
10. Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
5.9. Свойства квадрата:
10. Все углы квадрата прямые.
20. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
6.1. Свойства суммы многоугольников:
10. Равные многоугольники имеют равные площади.
20. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
30. Площадь квадрата равна квадрату его стороны.
6.2. Теорема (о площади прямоугольника). Площадь прямоугольника равна произведению его смежных сторон.
6.3. Теорема (о площади параллелограмма). Площадь параллелограмма равна произведению его основания на высоту.
6.4. Теорема (о площади треугольника). Площадь треугольника равна половине произведения его основания на высоту.
Следствия из теоремы:
Площадь прямоугольного треугольника равна половине произведения его катетов.
Если высоты двух треугольников равны, то их площади относятся как основания.
6.5. Теорема (о площади двух треугольников). Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
6.6. Теорема (о площади трапеции). Площадь трапеции равна произведению полу суммы её оснований на высоту.
6.7. Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
6.8. Обратная теорема Пифагора. Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
6.9. Свойства биссектрис параллелограмма:
10. Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.
20. Биссектрисы смежных углов параллелограмма пересекаются под прямым углом.
30. Биссектрисы противоположных углов, равны и параллельны.
6.10. Свойства биссектрис трапеции:
10. Биссектриса отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона. .
20. Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом.
30. Точка пересечения биссектрис трапеции, прилежащих к боковой стороне, лежит на средней линии трапеции.
40. Точка пересечения биссектрис тупых углов при основании трапеции принадлежит другому основанию.
6.11. Свойство второй средней линии трапеции: Пусть средняя КN-вторая средняя линия трапеции с основаниями ВС и АD, проходящая через точку пересечения диагоналей трапеции М. Тогда .
7.1. Теорема (об отношение площадей подобных треугольников).Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
7.2. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
7.3. Признаки подобия треугольников:
Теорема 1. Если два угла одного треугольника соответственно равны двум углам другого, то эти треугольники подобны.
Теорема 2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то эти треугольники подобны.
Теорема 3. Если три стороны одного треугольника пропорциональны трём сторонам другого, то эти треугольники подобны.
7.4. Теорема (о средней линии треугольника). Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
7.5. Свойство медианы треугольника:
10. Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношение 2:1, считая от вершины.
7.6. Высота прямоугольного треугольника, проведенная из вершины прямого угла, делит треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
7.7. Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы, косинусы и тангенсы этих углов равны.
8.1. Если расстояние от центра окружности до прямой меньше радиуса окружности (d<r), то прямая и окружность имеют две общие точки.
8.2. Если расстояние от центра окружности до прямой равно радиусу окружности (d=r), то прямая и окружность имеют только одну общую точку.
8.3. Если расстояние от центра окружности до прямой больше радиуса окружности (d>r), то прямая и окружность не имеют общих точек.
8.4. Теорема (о касательной и радиусе). Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
8.5. Отрезки касательных к окружности, проведенные из одной точки. Равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
8.6. Теорема (признак касательной). Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
8.7. Теорема (о касательной и секущей). Если из точки М, лежащей вне окружности, проведены касательная МС и секущая МВ, то квадрат длины касательной равен произведению секущей на ее внешнюю часть
, где А и В-точки пересечения с окружностью секущей соответственно, считая от М.
8.8. Если дуга АВ окружности с центром О меньше полуокружности или является полуокружностью, то её градусная мера считается равной градусной мере центрального угла АОВ. Если же дуга АВ больше полуокружности, то её градусная мера считается равной .
8.9. Сумма градусных мер двух дуг окружности с общими концами равна 3600.
8.10. Теорема (о вписанном угле). Вписанный угол измеряется половиной дуги, на которую он опирается.
Следствия из теоремы:
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Вписанный угол, опирающийся на полуокружность, -прямой.
8.11. Теорема (о произведении отрезков пересекающихся хорд). Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
8.12. Четыре замечательные точки треугольника: точка пересечения медиан, точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам и точка пересечения высот (или их продолжения).
Теорема (о биссектрисе угла). Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон. Обратно: каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе.
Следствие из теоремы: Биссектрисы треугольника пересекаются в одной точке.
Теорема (о серединном перпендикуляре к отрезку). Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Обратно: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
Следствие из теоремы: Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Теорема (о пересечении высот треугольника). Высоты треугольника (или их продолжения) пересекаются в одной точке.
8.13. Теорема (об окружности, вписанной в треугольник). В любой треугольник можно вписать только одну окружность.
8.14. В любом описанном четырехугольнике суммы противоположных сторон равны.
8.15. Теорема (об окружности, описанной около треугольника). Около любого треугольника можно описать только одну окружность.
8.16. В любом вписанном четырехугольнике сумма противоположных углов равна 1800.
8.17. Если сумма противоположных углов четырёхугольника равна 1800, то около него можно описать окружность.
8.18. Свойства равностороннего треугольника:
10. Высота, медиана и биссектриса, проведённые к каждой из сторон равностороннего треугольника, совпадают.
20. Точка пересечения высот, биссектрис и медиан называется центром правильного треугольника и является центром вписанной и описанной окружностей (то есть в равностороннем треугольнике центры вписанной и описанной окружностей совпадают).
30. Расстояние от точки пересечения высот, биссектрис и медиан до любой вершины треугольника равно радиусу описанной окружности.
40. Все высоты равностороннего треугольника равны.
9.1. От любой точки можно отложить только один вектор, равный данному.
9.2. Теорема (правило параллелограмма). Для любых векторов и справедливы равенства:
1. (переместительный закон)
2. (сочетательный закон).
9.3. Теорема (о разности векторов). Для любых векторов и справедливо равенство .
9.4. Произведение любого вектора на 0-это нулевой вектор.
9.5. Векторы и коллинеарны при любых и .
9.6. Свойства произведения вектора на число:
10. (сочетательный закон)
20. (первый распределительный закон)
30. (второй распределительный закон)
9.7. Теорема (о средней линии трапеции). Средняя линия трапеции параллельна основаниям и равна их полу сумме.
9.8. Сумма противолежащих углов трапеции равна 1800.
Формулы
Основное тригонометрическое тождество
Таблица углов
*знать таблицу наизусть для 8 класса (зелёный), для 9 класса (зелёный и жёлтый).
infourok.ru
Теория по геометрии 8 класс — Теория по геометрии за 8 класс по учебнику Л.С. Атанасяна
Теория по геометрии за 8 класс по учебнику Л.С. Атанасяна
Доступные файлы (1):
n1.docx
Составила Аверкова Т.Е.
Теория по геометрии 8 класс.1
Сумма длин всех сторон называется периметром многоугольника.
Многоугольник с n вершинами называется n-угольником; он имеет n сторон.
Две вершины многоугольника, принадлежащие одной стороне, называются соседними.
Отрезок, соединяющий любые две несоседние вершины, называется диагональю многоугольника.
Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней, а другая — внешней областью многоугольника.
Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
Cумма углов выпуклого n-уголника равна (п—2) 180°.
Две несмежные стороны четырехугольника называются противоположными. Две вершины, не
являющиеся соседними, также называются противоположными.
Cумма углов выпуклого четырехугольника равна 360°.
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
Свойства параллелограмма:
1°. В параллелограмме противоположные стороны равны и противоположные углы равны.
2°. Диагонали параллелограмма точкой пересечения делятся пополам.
Признаки параллелограмма:
1°. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник— параллелограмм.
2°. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
3°. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны трапеции называются ее основаниями, а две другие стороны — боковыми сторонами.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Трапеция, один из углов которой прямой, называется прямоугольной.
Теорема Фалеса: если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Прямоугольником называется параллелограмм, у которого все углы прямые.
Так как прямоугольник является параллелограммом, то он обладает всеми свойствами параллелограмма: в прямоугольнике противоположные стороны равны, а диагонали точкой пересечения делятся пополам.
Свойство прямоугольника: Диагонали прямоугольника равны.
Признак прямоугольника: Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.
Ромбом называется параллелограмм, у которого все стороны равны.
Свойство ромба: Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Квадратом называется прямоугольник, у которого все стороны равны.
Прямоугольник является параллелограммом, поэтому и квадрат является параллелограммом, у которого все стороны равны, т. е. ромбом. Отсюда следует, что квадрат обладает всеми свойствами прямоугольника и ромба:
1. Все углы квадрата прямые.
2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. Каждая точка прямой а считается симметричной самой себе.
Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры. Говорят также, что фигура обладает осевой симметрией.
Две точки А и А1называются симметричными относительно точки О, если О— середина отрезка АА1. Точка О считается симметричной самой себе.
Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.
Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.
Так, если за единицу измерения отрезков принят сантиметр, то за единицу измерения площадей принимают квадрат со стороной 1 см. Такой квадрат называется квадратным сантиметром и обозначается см2. Аналогично определяется квадратный метр (м2), квадратный миллиметр (мм2) и т. д.
Основные свойства площадей:
1°. Равные многоугольники имеют равные площади.
2°. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
3°. Площадь квадрата равна квадрату его стороны.
Площадь прямоугольника равна длины на ширину.
Площадь параллелограмма равна произведению его высоты на длину стороны к которой проведена высота.
Площадь треугольника равна половине произведения его высоты на длину стороны к которой проведена высота.
Следствия:
- Площадь прямоугольного треугольника равна половине произведения его катетов.
- Если высоты двух треугольников равны, то их площади относятся как основания.
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Для вычисления площади произвольного многоугольника обычно поступают так: разбивают многоугольник на треугольники и находят площадь каждого треугольника. Сумма площадей этих треугольников равна площади данного многоугольника.
Высотой трапеции называется перпендикуляр, проведенный из любой точки одного из оснований к прямой, содержащей другое основание.
Площадь трапеции равна произведению полусуммы ее оснований на высоту.
Площадь трапеции равна произведению длины средней линии трапеции на высоту.
Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Теорема, обратная теореме Пифагора: Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
Прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются пифагоровыми треугольниками.
Треугольник со сторонами 3, 4, 5 часто называют египетским.
Отношением отрезков АВ и CD называется отношение их длин, т. е.
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
Другими словами, два треугольника подобны, если для них можно ввести обозначения ABC и А1В1С1 так, что:
Число k, равное отношению сходственных сторон подобных
треугольников, называется коэффициентом подобия.
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Признаки подобия треугольников:
- Если два угла одного треугольника соответственно равны двум углам другого, то такие
треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Теорема: Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
Отрезок XY называется средним пропорциональным (или средним геометрическим) для отрезков АВ и CD, если
Свойства:
1°. Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.
2°. Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
т. е. тангенс угла равен отношению синуса к косинусу этого угла.
Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.
Основное тригонометрическое тождество:
Взаимное расположение прямой и окружности в зависимости от соотношения между d и r. Возможны три случая:
- Если расстояние от центра окружности до прямой меньше радиуса окружности (d r), то прямая и окружность имеют две общие точки. В этом случае прямая называется секущей по отношению к окружности.
- Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку.
- Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.
Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
Свойства касательной к окружности:
- Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
- Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Обратная теорема (признак касательной):
Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
Дуга называется полуокружностью, если отрезок, соединяющий ее концы, является диаметром окружности.
- Если дуга АВ окружности с центром в точке О меньше полуокружности или является полуокружностью, то ее градусная мера считается равной градусной мере центрального угла АОВ
- Если же дуга АВ больше полуокружности, то ее градусная мера считается равной (360° — угол АОВ).
Угол с вершиной в центре окружности называется ее центральным углом.
Сумма градусных мер двух дуг окружности с общими концами равна 360°.
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
Если дуга расположена внутри вписанного угла, то говорят, что вписанный угол опирается на эту дугу.
Теорема: Вписанный угол измеряется половиной дуги, на которую он опирается.
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Вписанный угол, опирающийся на полуокружность — прямой.
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Свойства биссектрисы угла: Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.
Обратно: каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе.
Биссектрисы треугольника пересекаются в одной точке.
Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему.
Свойство серединного перпендикуляра к отрезку: Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
Обратно: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Высоты треугольника (или их продолжения) пересекаются в одной точке.
С каждым треугольником связаны четыре замечательные точки:
- точка пересечения медиан,
- точка пересечения биссектрис,
- точка пересечения серединных перпендикуляров к сторонам
- точка пересечения высот (или их продолжений).
Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник — описанным около этой окружности.
В любой треугольник можно вписать окружность.
Не во всякий четырехугольник можно вписать окружность.
В любом описанном четырехугольнике суммы противоположных сторон равны.
Обратное утверждение: Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник — вписанным в эту окружность.
Около любого треугольника можно описать окружность.
Около четырехугольника не всегда можно описать окружность.
В любом вписанном четырехугольнике сумма противоположных углов равна 180°.
Обратно: Если сумма противоположных углов четырехугольника равна 180°, то около него можно описать окружность.
Вектор – направленный отрезок.
Начало нулевого вектора совпадает с его концом, на рисунке такой вектор изображается одной точкой.
Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых;
Нулевой вектор считается коллинеарным любому вектору.
Среди ненулевых коллинеарных векторов выделяют сонаправленные векторы и противоположно направленные векторы.
Векторы называются равными, если они сонаправлены и их длины равны.
От любой точки можно отложить вектор, равный данному вектору, и притом только один.
Правила сложения векторов:
правило треугольника
правило параллелограмма
правило многоугольника
правило треугольника для вычитания векторов
правило №2 для вычитания векторов (сложение с противоположным)
Применение векторов к решению задач:
Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.
Средняя линия трапеции параллельна основаниям и равна их полусумме.
perviydoc.ru
Контроль теоретического материала за курс 8 класса по геометрии
Многоугольник. Его элементы.
Выпуклый многоугольник.
Параллелограмм. Определение.
Свойства параллелограмма.
Признаки параллелограмма.
Трапеция.
Виды трапеции.
Основные свойства равнобедренной трапеции.
Особые свойства трапеции.
Прямоугольник. Определение.
Основные свойства прямоугольника.
Признак прямоугольника.
Ромб. Определение.
Основные свойства ромба.
Признак ромба.
Квадрат. Определение.
Основные свойства квадрата.
Осевая симметрия. Определение.
Центральная симметрия. Определение.
Площадь квадрата.
Площадь прямоугольника.
Площадь параллелограмма.
Площадь треугольника.
Площадь прямоугольного треугольника.
Формула Герона для нахождения площади треугольника.
Следствие об отношении площадей треугольников с равными высотами.
Теорема об отношении площадей треугольников, имеющих равные углы.
Площадь трапеции.
Площадь ромба.
Теорема Пика.
Теорема Пифагора.
Пифагоров треугольник. Определение.
Египетский треугольник. Определение.
Подобные треугольники. Определение.
Коэффициент подобия. Определение.
Теорема об отношении площадей подобных треугольников.
Первый признак подобия треугольников.
Второй признак подобия треугольников.
Третий признак подобия треугольников.
Теорема о средней линии треугольника. Определение.
Теорема о точке пересечения медиан треугольника.
Среднее пропорциональное (геометрическое). Определение.
2 теоремы о высоте прямоугольного треугольника, проведённой из вершины прямого угла.
Утверждение о катете прямоугольного треугольника.
Синус острого угла.
Косинус острого угла.
Тангенс острого угла.
Теорема о равных острых углах прямоугольных треугольников.
Основное тригонометрическое тождество.
Значение sin α, cos α, tg α, для углов α равных 300, 450, 600.
Теорема о медиане прямоугольного треугольника, проведённой из вершины прямого угла.
Секущая прямая. Определение.
Касательная прямая. Определение.
В каком случае прямая и окружность не имеют общих точек?
Теорема о свойстве касательной.
Свойство отрезков касательных, проведённых из одной точки.
Признаки касательной.
Полуокружность. Определение.
Центральный угол. Определение.
Градусная мера дуги окружности.
Сумма мер двух дуг окружностей.
Вписанный угол. Определение.
Теорема о вписанном угле.
Вписанный угол, опирающийся на одну и ту же дугу.
Вписанный угол, опирающийся на полуокружность.
Теорема о произведении отрезков пересекающихся хорд.
Теорема о каждой точки биссектрисы.
Теорема обратная теореме о каждой точке биссектрисы.
Точка пересечения биссектрис угла.
Среднее перпендикулярное к отрезку.
Теорема о серединном перпендикуляре к отрезку.
Теорема обратная теореме о серединном перпендикуляре к отрезку.
Следствие о точке пересечения серединных отрезков к сторонам треугольника.
Теорема о пересечении высот треугольника.
Четыре замечательные точки треугольника.
Вписанная окружность. Определение.
Описанный многоугольник. Определение.
Теорема об окружности, вписанной в треугольник.
Сколько окружностей можно вписать в треугольник.
Суммы противоположных сторон в описанном треугольнике.
Описанная окружность. Определение.
Вписанный многоугольник. Определение.
Теорема об окружности, описанной около треугольника.
Какова сумма противоположных углов во вписанном четырёхугольнике.
В каком случае около четырёхугольника можно описать окружность.
Свойство трапеции, в которую можно вписать окружность.
Средняя линия трапеции. Определение.
Теорема о средней линии трапеции.
2) Диагонали параллелограмма точкой пересечения делятся пополам.
2) Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм.
3) Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.
2) Диагонали равнобедренной трапеции равны.
3) Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали – полусумме оснований.
2) Если сумма углов при одном из оснований трапеции равна 900, то отрезок, соединяющий середины оснований трапеции, равен их полуразности.
2) Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
Фигура называется симметричной относительно оси симметрии, если для каждой точки фигуры симметричная ей точка относительно оси симметрии также принадлежит этой фигуре.
Фигура называется симметричной относительно центра симметрии, если для каждой точки фигуры симметричная ей точка относительно центра симметрии также принадлежит этой фигуре.
Площадь квадрата равна квадрату его стороны.
Площадь прямоугольника равна произведению его смежных сторон.
Площадь параллелограмма равна произведению его основания на высоту.
Площадь треугольника равна половине произведения его основания на высоту.
Площадь прямоугольного треугольника равна половине произведения его катетов.
Если высоты двух треугольников равны, то их площади относятся как основания.
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Площадь трапеции равна произведению полусуммы его оснований на высоту.
Площадь ромба равна половине произведения его диагоналей.
Площадь многоугольника, все вершины которого расположены в точках целочисленной решетки, выражается числом , где m – количество точек решетки, находящихся внутри многоугольника, а n — количество точек решетки, лежащих на его границе.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Прямоугольные треугольники, у которых длины сторон выражаются целыми числами,
называются пифагоровыми треугольниками.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
2)Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.
Медиана треугольника, проведённая из вершины прямого угла, равна половине гипотенузы.
Прямая, имеющая с окружностью две общие точки называется секущей к окружности.
Прямая, имеющая с окружностью только одну общую точку называется касательной к окружности.
Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.
Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром окружности.
Угол с вершиной в центре окружности называется её центральным углом.
Если дуга окружности меньше полуокружности или является полуокружностью, то её градусная мера считается равной градусной мере центрального угла. Если дуга больше полуокружности, то её градусная мера считается равной 360º – величина центрального угла.
Сумма градусных мер двух дуг окружности с общими концами равна 360º.
Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Вписанный угол измеряется половиной дуги, на которую он опирается.
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Вписанный угол, опирающийся на полуокружность – прямой.
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон.
Каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе.
Биссектрисы треугольника пересекаются в одной точке.
Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему.
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
Каждая точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему.
Серединные отрезки к сторонам треугольника пересекаются в одной точке.
Высоты треугольника (или их продолжения) пересекаются в одной точке.
Четыре замечательные точки треугольника – это точка пересечения медиан, точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам и точка пересечения высот (или их продолжений).
Если все стороны многоугольника касаются окружности, то окружность называется вписанной.
Описанный многоугольник – это многоугольник, в котором вписана окружность.
В любой треугольник можно вписать окружность.
В треугольник можно вписать только одну окружность.
В любом описанном четырёхугольнике суммы противоположных сторон равны.
Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника.
Многоугольник называется вписанным, если вокруг него описана окружность.
Около любого треугольника можно описать окружность.
В любом вписанном четырёхугольнике сумма противоположных углов равна 180º.
Если сумма противоположных углов равна 1800, то около него можно описать окружность.
Если в трапецию можно вписать окружность, то боковая сторона трапеции видна из центра окружности под прямым углом.
Средняя линия трапеции – это отрезок, соединяющий середины её боковых сторон.
Средняя линия трапеции параллельна основаниям и равна их полусумме.
videouroki.net
Словарь геометрических понятий 7-8 класс
Геометрия,7-9 Основные определения, теоремы, формулы
7 класс Глава I Начальные геометрические сведения
Первичные понятия: точка, прямая, плоскость, пространство, отрезок, луч, угол, равные фигуры, середина отрезка, биссектриса угла, измерение отрезков, измерение углов
Отрезок-часть прямой, ограниченная двумя точками.
Луч-часть прямой,ограниченная точкой с одной стороны и неограниченная с другой стороны.
Угол-часть плоскости, ограниченная двумя лучами, выходящими из одной точки.
Равные фигуры-фигуры, которые совпадают при наложении друг на друга.
Середина отрезка-точка на отрезке, делящая его пополам.
Биссектриса угла-луч, выходящий из вершины угла и делящий его пополам.
Единицы измерения длины отрезка: миллиметры, сантиметры, дециметры, метры, километры.
Единицы измерения углов: градус, минуты, секунды.
Длина отрезка-количество единиц измерения длины, вмещающихся между двумя концами отрезка.
Градусная мера угла-количество единиц измерения углов, вмещающихся между сторонами угла.
Прямой угол-угол,градусная мера которого равна 900.
Острый угол-угол,градусная мера которого меньше 900.
Тупой угол-угол,градусная мера которого больше 900,но меньше 1800.
Развёрнутый угол-угол,градусная мера которого равна 1800.
Смежные углы – это два угла, у которых одна сторона общая,а две других образуют прямую линию.
Свойство: сумма смежных углов равна 1800.
Вертикальные углы-два угла, у которых стороны одного угла являются продолжением сторон другого.
Свойство: вертикальные углы равны.
Перпендикулярные прямые-прямые, которые при пересечении образуют прямой угол.
Параллельные прямые-прямые, лежащие в одной плоскости и не имеющие общих точек.
Глава II Треугольники
Треугольник-фигура, состоящая из трёх точек, соединённых между собой отрезками.Точки-вершины треугольника, отрезки-стороны треугольника.
Периметр – сумма длин всех сторон.
Теорема(первый признак равенства треугольников): если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Теорема: из точки,не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Медиана треугольника— это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса треугольника— отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Высота треугольника— перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
Равнобедренный треугольник-треугольник, у которого две стороны равные. Равные стороны – боковые, третья сторона – основание.
Равносторонний треугольник— треугольник, у которого все стороны равны.
Свойство:в равнобедренном треугольнике углы при основании равны.
Свойство:в равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Теорема(второй признак равенства треугольников): если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Теорема(третий признак равенства треугольников): если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
Окружность-геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки-центра.
Радиус окружности-отрезок,соединяющий любую точку окружности с её центром.
Хорда-отрезок, соединяющий две любые точки окружности.
Диаметр-хорда, проходящая через центр.
Дуга – часть окружности, ограниченная двумя точками.
Основные задачи на построение циркулем и линейкой:
построение отрезка, равного данному
построение угла, равного данному
построение биссектрисы угла
построение середины отрезка
построение перпендикулярных прямых
Глава III Параллельные прямые
При пересечении двух прямых третьей прямо-секущей образуются следующие виды углов:
накрест лежащие углы
односторонние углы
соответственные углы
Теорема(первый признак параллельности прямых):если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Теорема(второй признак параллельности прямых):если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Теорема(третий признак параллельности прямых):если при пересечении двух прямых секущей сумма внутренних односторонних углов равна углы равна 1800, то прямые параллельны.
Аксиома: через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Теорема:если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
Теорема:если две прямые параллельны третьей прямой, то они параллельны.
Теорема:если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Теорема:если две параллельные прямые пересечены секущей, то соответственные углы равны.
Теорема:если две параллельные прямые пересечены секущей, то сумма внутренних односторонних углов равна 1800.
Глава IV Соотношения между сторонами и углами треугольника
Теорема: сумма внутренних углов треугольника равна 1800.
Внешний угол треугольника-угол, смежный с каким-либо внутренним углом треугольника.
Остроугольный треугольник-это треугольник, все внутренние углы которого острые.
Тупоугольный треугольник-это треугольник, у которого один из углов тупой.
Прямоугольный треугольник-это треугольник, у которого один из углов прямой.
Гипотенуза-это сторона прямоугольного треугольника, лежащая напротив прямого угла.
Катеты-это стороны прямоугольного треугольника, образующие прямой угол.
Теорема:в треугольнике против большей стороны лежит больший угол.
Теорема:в треугольнике против большего угла лежит большая сторона.
Следствие:в прямоугольном треугольнике гипотенуза всегда больше катета.
Теорема(признак равнобедренного треугольника):если в треугольнике два угла равны, то он равнобедренный.
Теорема(неравенство треугольника):каждая сторона треугольника меньше суммы двух других сторон.
Свойство:сумма двух острых углов треугольника равна 900.
Свойство:катет прямоугольного треугольника, лежащий против угла в 300, равен половине гипотенузы.
Свойство:если катет прямоугольного треугольника равен половине гипотенузы, то он лежит напротив угла в 300.
Теорема(признак равенства прямоугольных треугольников):если катеты одного прямоугольного треугольника равны катетам другого прямоугольного треугольника, то такие треугольники равны.
Теорема(признак равенства прямоугольных треугольников):если катет и прилежащий к нему острый угол одного прямоугольного треугольника равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.
Теорема(признак равенства прямоугольных треугольников):если гипотенуза и острый угол одного прямоугольного треугольника равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Теорема(признак равенства прямоугольных треугольников):если катет и гипотенуза одного прямоугольного треугольника равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.
Расстояние от точки до прямой – это длина перпендикуляра, опущенного из этой точки на прямую.
Теорема:все точки каждой из двух параллельных прямых равноудалены от другой прямой.
8 класс. Глава V Четырёхугольники
Многоугольник-фигура, состоящая из нескольких точек плоскости, поочередно соединённых между собой непересекающимися отрезками.
Диагональ-это отрезок, соединяющий две несоседних вершины многоугольника.
Выпуклый многоугольник— это многоугольник, который весь лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
Теорема:Сумма внутренних углов выпуклого n-угольника равна (n-2)*1800.
Параллелограмм— это четырёхугольник, у которого противоположные стороны попарно параллельны.
Свойство:в параллелограмме противоположные стороны равны и противоположные углы равны.
Свойство:диагонали параллелограмма точкой пересечения делятся пополам.
Теорема(признак параллелограмма):Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.
Теорема(признак параллелограмма):Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм.
Теорема(признак параллелограмма):Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.
Трапеция-это четырёхугольник, у которого две стороны параллельны, а две другие не параллельны.Параллельные стороны-основания, непараллельные стороны-боковые.
Равнобедренная трапеция-это трапеция, у которой боковые стороны равны.
Прямоугольная трапеция-это трапеция, у которой один из углов прямой.
Теорема Фалеса: если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пресекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Прямоугольник-это параллелограмм, у которого все углы прямые.
Свойство: диагонали прямоугольника равны.
Теорема(признак прямоугольника):если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.
Ромб-это параллелограмм, у которого все стороны равны.
Свойство: диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Квадрат-это прямоугольник, у которого все стороны равны.
Глава VI Площадь
Площадь плоской фигуры-это количество единичных квадратов, вмещающихся в данную фигуру.
Единицы измерения площади: мм2,см2, дм2, м2, ар=100м2, км2 , га=100км2.
Площадь квадрата равна квадрату его стороны.
Площадь прямоугольника равна произведению его смежных сторон.
Площадь параллелограмма равна произведению его основания на высоту.
Площадь треугольника равна половине произведения его основания на высоту.
Площадь прямоугольного треугольника равна произведению его катетов.
Если высоты двух треугольников равны, то их площади относятся как основания.
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Площадь трапеции равна полусумме её оснований на высоту.
Теорема Пифагора:в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Теорема(обр.):если квадрат одной стороны треугольника равен сумме квадратов двух других его сторон, то треугольник прямоугольный.
Глава VII Подобные треугольники
Отрезки m и n пропорциональны отрезкам m1и n1,если отношения их длин равны m:m1= n: n1.
Подобные треугольники— это треугольники,у которых соответственные углы равны, а сходственные стороны пропорциональны.
Коэффициент подобия- это число, равное отношению сходственных сторон подобных треугольников.
Теорема: Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Свойство биссектрисы тр-ка: биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
Теорема(первый признак подобия треугольников):если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Теорема(второй признак подобия треугольников):если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.
Теорема(первый признак подобия треугольников):если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон.
Теорема:Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
Среднее пропорциональное(среднее геометрическое)двух величин – это квадратный корень из произведения этих величин.
С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
С. Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы,заключённым между катетом и высотой, проведённой из вершины прямого угла.
Синус острого угла прямоугольного треугольника- это отношение противолежащего катета к гипотенузе.
Косинус острого угла прямоугольного треугольника- это отношение прилежащего катета к гипотенузе.
Тангенс острого угла прямоугольного треугольника- это отношение противолежащего катета к прилежащему .
Котангенс острого угла прямоугольного треугольника- это отношение прилежащего катета к противолежащему .
Глава VIII Окружность
Касательная к окружности – это прямая, имеющая с окружностью только одну общую точку.
Т. Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
Т.(обр.) Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
Центральный угол – это угол с вершиной в центре окружности.
Дуга окружности измеряется центральным углом, который на неё опирается.
Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Т.Вписанный угол равен половине дуги, на которую он опирается.
С. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
С. Вписанный угол, опирающийся на полуокружность, — прямой.
Т. Если две хорды окружности пересекаются, произведение отрезков одной хорды равно произведению отрезков другой хорды.
9 класс
Средняя линия трапеции— это отрезок, соединяющий середины её боковых сторон.
Теорема:средняя линия трапеции равна полусумме её оснований и параллельна им.
infourok.ru
