Системы счисления 8 класс презентация босова – Презентация к уроку по информатике и икт (8 класс) на тему: Системы счисления. Общие сведения о системах счисления.

Презентация к уроку по информатике и икт (8 класс) на тему: Системы счисления. Общие сведения о системах счисления.

Слайд 1

Системы счисления Общие сведения о системах счисления

Слайд 2

Определение Система счисления — это знаковая система, в которой приняты определённые правила записи чисел. Цифры — знаки, при помощи которых записываются числа. Алфавит системы счисления — совокупность цифр.

Слайд 3

Виды чисел Узловые – те числа, которые состоят из единичных цифр. Алгоритмические – числа, получаемые в результате каких-либо операций над узловыми. Арабский числа Римские числа 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 I(1), V(5), X(10), L(50), C(100), D(500), M(1000) Арабский числа Римские числа 11, 23, 426 III (3), XIV(14), LXIX (69)

Слайд 4

Виды систем счисления Унарная — простейшая система счисление, где для записи используется всего один символ.

Слайд 5

Виды систем счисления Непозиционная система счисления — значение цифры не изменяется в зависимости от ее расположения. Пример: Римская система чисел Число 242 можно записать ССXLII (т.е. 100+100+(50-10) +1+1).

Слайд 6

Римская система чисел Узловые римские числа Арабские узловые числа I 1 V 5 X 10 L 50 C 100 D 500 M 1000 Алгоритмические римские числа Алгоритмические арабские числа II 2 IV 4 VI 6 IX 9 LXXXIX 89 XC 90 XCIX 99

Слайд 7

Виды систем счисления Позиционная система счисления — это система счисления в которой значение цифры зависит от разряда. Пример: Арабская система чисел 1953 Основание системы счисления – количество цифр её алфавита.

Слайд 8

A =±( a n–1  q n–1 + a n–2  q n–2 +…+ a 0  q 0 + a –1  q –1 +…+ a –m  q –m ) Здесь: А — число; q — основание системы счисления; a i — цифры, принадлежащие алфавиту данной системы счисления; n — количество целых разрядов числа; m — количество дробных разрядов числа; q i — «вес» i -го разряда . Развернутая форма записи позиционных чисел

Слайд 9

Домашнее задание Учебник: Раздел 1.1.1 Рабочая тетрадь: №6, 13, 18, 20 Повторить конспект.

nsportal.ru

Презентация к уроку по информатике и икт (8 класс) по теме: Информатика 8 класс. Презентация по теме «Системы счисления»

Слайд 1

СИСТЕМЫ СЧИСЛЕНИЯ Автор урока: Подкопаева Мария Викторовна ГБОУ СОШ №489 Санкт-Петербург

Слайд 2

ОБЩИЕ СВЕДЕНИЯ Система счисления – это знаковая система, в которой приняты определённые правила записи чисел. Цифры — знаки , при помощи которых записываются числа. Алфавит системы счисления — совокупность цифр .

Слайд 3

ИСТОРИЯ: Египетская система счисления

Слайд 4

ИСТОРИЯ: Вавилонская система счисления

Слайд 5

ИСТОРИЯ: Кириллическая система счисления

Слайд 6

Унарная система счисления Простейшая и самая древняя система В ней для записи любых чисел используется всего один символ: палочка , узелок, зарубка, камушек.

Слайд 7

Непозиционная система счисления Количественный эквивалент цифры в числе (количественное значение) не зависит от её положения в записи числа . Римская система счисления Правило: Каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него. 1 5 10 50 100 500 1000 l V X L C D M

Слайд 8

позиционная система счисления Количественный эквивалент цифры в числе зависит от её положения в записи числа . Основание позиционной с. с. равно количеству цифр, составляющих её алфавит . Десятичная система счисления: основание – 10 алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Слайд 9

позиционная система счисления Двоичная система счисления: основание – 2 алфавит: 0, 1 Троичная система счисления: основание – 3 алфавит: 0, 1, 2 Восьмеричная система счисления: основание – 8 алфавит: 0, 1, 2, 3, 4, 5, 6, 7 1010 2 101100 2 101110001 2 2102 3 101100 3 2002 3 2170 8 206 8 7102 8

Слайд 10

позиционная система счисления Шестнадцатеричная система счисления: основание – 16 алфавит: A5 16 71BA 16 A009B 1 F6 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 8 9 A B C D E F

Слайд 11

Развёрнутая форма числа Для любых чисел A q =±(a n–1  q n–1 + a n–2  q n –2 +…+ a 0  q 0 + a –1  q –1 +…+ a –m  q –m ) Здесь: А — число; q — основание системы счисления; a i — цифры, принадлежащие алфавиту данной системы счисления; n — количество целых разрядов числа ; m — количество дробных разрядов числа ; q i — «вес» i- го разряда.

Слайд 12

Перевод из двоичной в десятичную Пример: Целое положительное четырехзначное число 1101 2 = + ( 1  2 4-1 + 1  2 3-2 + 0  2 4 -3 + 1  2 0 ) = 13 10 i 3 2 1 0 q i 2 3 2 2 2 1 2 0 a i 1 1 0 1 А = 1101 q = 2 a 0 = 1 a 1 = 0 a 2 = 1 a 3 = 1 N = 4

Слайд 13

Пример: Целое положительное четырехзначное число 1101 3 = + ( 1  3 4-1 + 1  3 3-2 + 0  3 4 -3 + 1  3 0 ) = 37 10 i 3 2 1 0 q i 3 3 3 2 3 1 3 0 a i 1 1 0 1 А = 1101 q = 3 a 0 = 1 a 1 = 0 a 2 = 1 a 3 = 1 N = 4 Перевод из троичной в десятичную

Слайд 14

Сравним 1101 3 = + ( 1  3 4-1 + 1  3 3-2 + 0  3 4 -3 + 1  3 0 ) = 37 10 1101 2 = + ( 1  2 4-1 + 1  2 3-2 + 0  2 4 -3 + 1  2 0 ) = 13 10 13 10 ≠ 37 10 1101 2 ≠ 1101 3

Слайд 15

Пример: Целое положительное четырехзначное число 1802 3 = ? 10 Перевод из троичной в десятичную 101 82 11 Ошибка? Ошибка! Троичная система счисления: основание – 3 алфавит: 0, 1, 2

Слайд 16

Домашнее задание Переведите в десятичную систему счисления: 1011 2 10011 2 110110 2 1110011 2 11011000 2 111000111 2 1111010100 2 2018 2 110 3 2010 3 12011 3 2018 3

nsportal.ru

Презентация к уроку по информатике и икт (8 класс) на тему: Презентация к уроку «Системы счисления»

Слайд 1

Системы счисления Виды систем счисления История непозиционных систем счисления Перевод чисел из десятичной СС в двоичную и обратно Самостоятельная работа

Слайд 2

« Мысль – выражать все числа немногими знаками, придавая им не только значение по форме, но еще и значение по месту, настолько проста, что именно из-за этой простоты трудно оценить, насколько она удивительна …» Пьер Симон Лаплас (1 7 49 – 18 27 гг.)

Слайд 3

Система счисления — это совокупность приемов и правил записи чисел с помощью определенного набора символов (некоторый способ кодирования числовой информации).

Слайд 4

Системы счисления непозиционные позиционные Цифры – знаки которые используются для записи чисел

Слайд 5

История развития систем счисления

Слайд 6

Непозиционные системы счисления Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков (бирок): Зарубок черточек точек

Слайд 7

Позже, для облегчения счета, эти значки стали группировать по три или по пять. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу. Отголоски единичной системы счисления встречаются и сегодня. Так, чтобы узнать, на каком курсе учится курсант военного училища, нужно сосчитать, какое количество полосок нашито на его рукаве. Сами того не осознавая, единичной системой счисления пользуются малыши, показывая на пальцах свой возраст, а счетные палочки используется для обучения учеников 1-го класса счету

Слайд 8

Единичная система — не самый удобный способ записи чисел. Записывать таким образом большие количества утомительно, и сами записи при этом получаются очень длинными. С течением времени возникли иные, более удобные, системы счисления .

Слайд 9

Древнеегипетская десятичная непозиционная система счисления. Примерно в третьем тысячелетии до нашей эры древние египтяне придумали свою числовую систему, в которой для обозначения ключевых чисел 1, 10, 100 и т.д. использовались специальные значки — иероглифы. Все остальные числа составлялись из этих ключевых при помощи операции сложения. Система счисления Древнего Египта является десятичной, но непозиционной.

Слайд 10

Древнеегипетская нумерация

Слайд 11

Алфавитные системы счисления

Слайд 12

Славянский цифровой алфавит

Слайд 13

Вавилонская система счисления

Слайд 14

Примером непозиционной системы, которая сохранилась до наших дней, может служить система счисления, которая применялась более двух с половиной тысяч лет назад в Древнем Римскими цифрами пользовались очень долго. Еще 200 лет назад в деловых бумагах числа должны были обозначаться римскими цифрами (считалось, что обычные арабские цифры легко подделать). Римская система счисления сегодня используется, в основном, для наименования знаменательных дат, томов, разделов и глав в книгах.

Слайд 15

Римская система счисления

Слайд 16

В римских числах цифры записываются слева направо в порядке убывания. В таком случае их значения складываются. Если же слева записана меньшая цифра, а справа — большая, то их значения вычитаются. Пример : CCXXXII=100+100+10+10+10+1+1=232 VI=5+1=6 IV=5-1=4 MCMXCVIII= =1000+(-100+1000)+(-10+100)+5+1+1+1=1998

Слайд 17

Позиционные системы счисления Основные достоинства любой позиционной системы счисления — простота выполнения арифметических операций и ограниченное количество символов (цифр), необходимых для записи любых чисел.

Слайд 18

В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Позиция цифры в числе называется разрядом . Каждая позиционная сс имеет определенный алфавит цифр и основание.

Слайд 19

19 Для записи чисел в позиционной системе с основанием п нужно иметь алфавит из п цифр. Обычно для этого при п 10 к десяти арабским добавляют буквы. Вот примеры алфавитов нескольких систем. Система счисления основание Алфавит Десятичная п=10 0,1,2,3,4,5,6,7,8,9 Двоичная п=2 0,1 Восьмеричная п=8 0,1,2,3,4,5,6,7 Шестнадцатеричная п=16 0,1,2,3,4,5,6,7,8,9, А(10), В(11), C(12), D(13),E(14),F(15)

Слайд 20

Развернутой формулой числа называется запись в виде: А q =a n *q n +a n-1 *q n-1 +…+a 0 *q 0 +a -1 *q -1 + …+a -m *q -m где А q = само число q -основание системы счисления а – цифры данной системы счисления п – число разрядов Развернутая форма числа в двоичной сс : А 2 =a n *2 n +a n-1 *2 n-1 +…+a 0 *2 0 +a -1 *2 -1 + …+a -m *2 -m

Слайд 21

Пример: Получить развернутую форму десятичных чисел: 32478 10 =3*10 4 +2*10 3 +4*10 2 +7*10 1 + + 8*10 0

Слайд 22

Для перевода целого числа из СС с основанием 10 в СС с основанием 2 необходимо: Это число разделить на 2 , полученное частное вновь делят на 2 и так до тех пор пока последнее частное не окажется меньше 2 . В результате записать в одну строку последнее частное и все остатки, начиная с последнего. 53 10 = 110101 2 Проверка: 110101 2 =1*2 5 +1*2 4 +0*2 3 +1*2 2 +0*2 1 +1*2 0 + =32+16+4+1=53

Слайд 23

A10 A2 A10 A2 0 0 8 1000 1 1 9 1001 2 10 10 1010 3 11 11 1011 4 100 12 1100 5 101 13 1101 6 110 14 1110 7 111 15 1111 Для удобства запишем начало натурального ряда чисел в десятичной и двоичной системах счисления:

Слайд 24

«ЛОМАЕМ» голову Прочитайте стихотворение А.Н.Старикова: Ей было 1100 лет, Она в 101-й класс ходила, В портфеле по 100 книг носила — Все это правда, а не бред. Когда, пыля десятком ног, Она шагала по дороге, За ней всегда бежал щенок С одним хвостом, зато 100-ногий . Она ловила каждый звук Своими 10-ю ушами, И 10 загорелых рук Портфель и поводок держали. И 10 т емно-синих глаз Рассматривали мир привычно… Но станет все совсем обычным, Когда поймете наш рассказ.

Слайд 25

Занимательные задачи №2 Мартышка висит на хвосте и жует бананы. В каждой руке по 101 банану, а в каждой ноге – на 1 банан больше, чем в руке. Сколько бананов у мартышки? Ответ в 2-й СС

Слайд 26

Ответы к самостоятельной работе XXIII. X. MMX. 100101 2 1110001 2

nsportal.ru

Конспект урока по информатике по Л.Босова 8 класс на тему «Системы счисления»

Конспект урока информатики

Тема: «Системы счисления»

Класс : 8 класс

Учитель: Берёзова Елена Витальевна

Тип урока: объяснение нового материала.

Цель урока: познакомить учащихся с видами систем счисления, с историей непозиционных систем счисления. Научить учащихся переводить числа из десятичной системы счисления в двоичную и обратно. Развивать у школьников теоретическое мышление

Задачи урока:

1. Воспитательная

• развитие познавательного интереса,

• развивать чувство коллективизма, умение выслушивать ответы товарищей;

• прививать интерес к предмету.

2. Учебная

• обсудить разнообразие систем счисления;

• показать на примерах перевод чисел из двоичной системы счисления в десятичную;

• объяснить алгоритм перевода чисел из десятеричной системы в двоичную;

3. Развивающая

• развитие алгоритмического мышления, памяти внимательности;

• развитие познавательного интереса, логического мышления;

• умение выслушивать ответы товарищей.

Формы и методы обучения: словесный, наглядный, практический – индивидуальная робота, работа с классом.

Общее время: 45 минут

Оборудование: Презентация к уроку «Системы счисления», раздаточный материал, карточки с заданиями для индивидуальной работы, проектор, компьютер.

План урока:

1. орг.момент

2. Новый материал

3. Закрепление

4. Самостоятельная работа

5. Подведение итогов

6. Домашнее задание

Ход урока

1. Орг. момент

Здравствуйте ребята! Тема нашего сегодняшнего урока: «Системы счисления». Сегодня мы должны познакомиться с видами систем счисления. Узнать историю непозиционных систем счисления. Научиться переводить числа из десятичной системы счисления в двоичную и обратно. Пользоваться развернутой формулой числа. Также решим несколько занимательных задач, а в конце урока небольшая самостоятельная работа по пройденному материалу.

2. Новый материал

Хочу начать урок со слов известного математика Пьера Симона Лапласа (1749 – 1827гг) «Мысль – выражать все числа немногими знаками, придавая им не только значение по форме, но еще и значение по месту, настолько проста, что именно из-за этой простоты трудно оценить, насколько она удивительна…» .

В тетрадях запишите число и тему урока: «Системы счисления»

Начнем наш урок с определения систем счисления .

Система счисления — это совокупность приемов и правил записи чисел с помощью определенного набора символов (некоторый способ кодирования числовой информации).

Разнообразные системы счисления, которые существовали раньше и используются в наше время, можно разделить на непозиционные и позиционные. Знаки которые используются при записи чисел, называются цифрами. (раздаточный материал Приложение 1)

Сначала рассмотрим непозиционные системы счисления.

Об истории непозиционных систем счисления нам расскажут: Теплова Мария и Романенко Елена.

Итак, вы познакомились с историей непозиционных систем счисления. Остановимся поближе на Римской непозиционной СС.

В Римской системе в качестве цифр используются латинские буквы: (раздаточный материал) Таблица 1

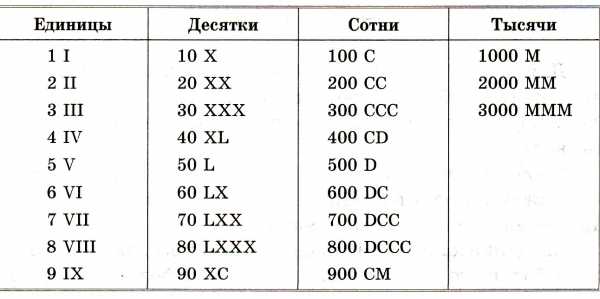
В римских числах цифры записываются слева направо в порядке убывания.

В таком случае их значения складываются.

Если же слева записана меньшая цифра, а справа — большая, то их значения вычитаются.

Пример:

CCXXXII=100+100+10+10+10+1+1=232
VI=5+1=6
IV=5-1=4
MCMXCVIII=

=1000+(-100+1000)+(-10+100)+5+1+1+1=1998 (Раздаточный материал Приложение 2)

В конце урока вам будет предложено несколько примеров для самостоятельного решения.

Теперь поговорим о позиционных системах счисления.

Создание позиционных систем счисления позволили записывать сколь угодно большие числа с помощью небольшого количества цифр, а также возникла возможность упростить выполнение арифметических операций над числами.

Основные достоинства любой позиционной системы счисления — простота выполнения арифметических операций и ограниченное количество символов (цифр), необходимых для записи любых чисел.

В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции. Позиция цифры в числе называется разрядом.

Каждая позиционная сс имеет определенный алфавит цифр и основание.

Основание – это количество используемых цифр. (Раздаточный материал Приложение 3)

СС, применяемая в современной математике, является позиционной десятичной системой. Ее основание равно десяти, т.к. запись любых чисел производится с помощью десяти цифр: 0,1,2,3,4,5,6,7,8,9.

Позиционный характер этой системы легко понять на примере любого многозначного числа. Например в числе 333 первая тройка означает три сотни, вторая – три десятка, третья – три единицы.

Для записи чисел в позиционной системе с основанием п нужно иметь алфавит из п цифр. Обычно для этого при п< 10 используют п первых арабских цифр, а при п>10 к десяти арабским добавляют буквы. Вот примеры алфавитов нескольких систем. (раздаточный материал Таблица2)

Система счисления

основание

Алфавит

Десятичная

п=10

0,1,2,3,4,5,6,7,8,9

Двоичная

п=2

0,1

Восьмеричная

п=8

0,1,2,3,4,5,6,7

Шестнадцатеричная

п=16

0,1,2,3,4,5,6,7,8,9, А(10), В(11), C(12), D(13),E(14),F(15)

Если требуется указать основание системы счисления, к которой относится число, то оно приписывается нижним индексом к этому числу.

Например: 101101₂, 7658₁₀, 3В8А₁₆ (Показать пример на доске)

В системе счисления с основанием q единицами разрядов служат последовательные степени числа q. q единиц какого либо разряда образуют единицу следующего разряда. Для записи числа в q-ричной системе счисления требуется q различных цифр, изображающих числа 0,1,…, q-1.

Развернутой формулой числа называется запись в виде:

А_q=a_n*qⁿ+a_n-1*q^n-1+…+a₀*q⁰+a_-1*q^-1+ …+a_—m*q^—m

где

А_q =само число

q-основание системы счисления

а – цифры данной системы счисления

п – число разрядов

Развернутая форма числа в двоичной сс:

А₂=a_n*2ⁿ+a_n-1*2^n-1+…+a₀*2⁰+a_-1*2^-1+ …+a_-m*2^-m

Пример: Получить развернутую форму десятичных чисел:

32478₁₀=3*10⁴+2*10³+4*10²+7*10¹+8*10⁰

Пример: На доске написать развернутую форму десятичного числа на доске (1 человек) 17368₁₀

Для перевода целого числа из СС с основанием 10 в СС с основанием 2 необходимо:

Это число разделить на 2, полученное частное вновь делят на2 и так до тех пор пока последнее частное не окажется меньше 2.

В результате записать в одну строку последнее частное и все остатки, начиная с последнего.

53₁₀= 110101₂

Проверка: 110101₂=1*2⁵+1*2⁴+0*2³+1*2²+0*2¹+1*2⁰+ =32+16+4+1=53

Решение примеров на доске 2 человека: Перевести из десятичной СС в двоичную числа 27 и 32 и выполнить проверку. Ответ: (11011, 100000)

А теперь с помощью таблицы(3), решим занимательные задачи. Таблица№3 лежит у вас на партах

Пример: Для удобства запишем начало натурального ряда чисел в  десятичной  и  двоичной системах счисления: (Раздаточный материал Таблица3)

А₁₀

А₂

А₁₀

А₂

0

1

2

3

4

5

6

7

0

1

10

11

100

101

110

111

8

9

10

11

12

13

14

15

1000

1001

1010

1011

1100

1101

1110

1111

 

3. Закрепление

А теперь решим несколько занимательных задач пользуясь таблицей.

ДИАЛОГ

1. Вопрос: Какая система счисления используется повсеместно в наше время? Ответ:   Десятичная.

2. Вопрос: Сколько цифр в десятичной системе и в двоичной системе счисления? Ответ:   Десять и две 

3. Вопрос: Какие это цифры? Ответ:   Цифры от 0 до 9, и 0,1

4. Вопрос: Меняется ли десятичное числа, если переставить в нем цифры? Ответ:   Да, меняется

4. Самостоятельная работа обучающего характера.

Индивидуальная работа по карточкам.

5. Подведение итогов. Домашнее задание

Итак, сегодня вы познакомились с понятием СС, с историей непозиционных систем счисления. Научились переводить числа из десятичной СС в двоичную и обратно. Пользоваться развернутой формулой числа.

Домашнее задание: Параграф 4, задание №6 письменно в тетради.

infourok.ru

Презентация по информатике на тему «Системы счисления» (8 класс)

Описание слайда:

Система счисления — способ записи чисел с помощью заданного набора специальных знаков (цифр). Разряд числа — позиция, которую занимает цифра. Рассмотрим три числа: 298, 829 и 982. Эти числа, разумеется, различны, хотя в их записи участвуют одни и те же цифры. Различаются же записи расположением цифр, иными словами, тем, какую позицию занимает та или иная цифра. Отсюда и пошло название такой нумерации — позиционная. Непозиционная система счисления — система счисления, в которой вес цифры не зависит от ее положения. Система счисления — способ записи чисел с помощью заданного набора специальных знаков (цифр). Разряд числа — позиция, которую занимает цифра. Рассмотрим три числа: 298, 829 и 982. Эти числа, разумеется, различны, хотя в их записи участвуют одни и те же цифры. Различаются же записи расположением цифр, иными словами, тем, какую позицию занимает та или иная цифра. Отсюда и пошло название такой нумерации — позиционная. Непозиционная система счисления — система счисления, в которой вес цифры не зависит от ее положения. Система счисления — способ записи чисел с помощью заданного набора специальных знаков (цифр). Разряд числа — позиция, которую занимает цифра. Рассмотрим три числа: 298, 829 и 982. Эти числа, разумеется, различны, хотя в их записи участвуют одни и те же цифры. Различаются же записи расположением цифр, иными словами, тем, какую позицию занимает та или иная цифра. Отсюда и пошло название такой нумерации — позиционная. Непозиционная система счисления — система счисления, в которой вес цифры не зависит от ее положения. Система счисления — способ записи чисел с помощью заданного набора специальных знаков (цифр). Разряд числа — позиция, которую занимает цифра. Рассмотрим три числа: 298, 829 и 982. Эти числа, разумеется, различны, хотя в их записи участвуют одни и те же цифры. Различаются же записи расположением цифр, иными словами, тем, какую позицию занимает та или иная цифра. Отсюда и пошло название такой нумерации — позиционная. Непозиционная система счисления — система счисления, в которой вес цифры не зависит от ее положения. Позиционная система счисления — система счисления, в которой значение числа меняется с изменением положения цифры в данном числе. Основные понятия В системах счисления некоторое число n единиц (например, десять) объединяется в одну единицу 2-го разряда (десяток), то же число единиц 2-го разряда объединяется в единицу 3-го разряда (сотню) и т.д. Число n называется основанием системы счисления, а знаки, употребляемые для обозначения количества едениц каждого разряда, — цифрами.                                              В системах счисления некоторое число n единиц (например, десять) объединяется в одну единицу 2-го разряда (десяток), то же число единиц 2-го разряда объединяется в единицу 3-го разряда (сотню) и т.д. Число n называется основанием системы счисления, а знаки, употребляемые для обозначения количества едениц каждого разряда, — цифрами.                                              В системах счисления некоторое число n единиц (например, десять) объединяется в одну единицу 2-го разряда (десяток), то же число единиц 2-го разряда объединяется в единицу 3-го разряда (сотню) и т.д. Число n называется основанием системы счисления, а знаки, употребляемые для обозначения количества едениц каждого разряда, — цифрами.                                              В системах счисления некоторое число n единиц (например, десять) объединяется в одну единицу 2-го разряда (десяток), то же число единиц 2-го разряда объединяется в единицу 3-го разряда (сотню) и т.д. Число n называется основанием системы счисления, а знаки, употребляемые для обозначения количества едениц каждого разряда, — цифрами.                                             

infourok.ru

Презентация к уроку по информатике и икт (8 класс) по теме: Презентация к уроку информатики в 8 классе по теме «Системы счисления».

Подписи к слайдам:

Перевод чиселв позиционных системах счисления. Система счисления – это способ записи чисел по определенным правилам с помощью специальных знаков – цифр.
Что называется системой счисления? Какие системы счисления существуют?
десятичнаядвоичнаявосьмеричнаяшестнадцатеричнаяи т.д.
Системы счисления
позиционные
непозиционные
римская
Чем они отличаются?
непозиционные – значение цифры не зависит от ее места (позиции) в записи числа;позиционные – зависит…
Непозиционные системы
Унарная – одна цифра обозначает единицу (1 день, 1 камень, 1 баран, …)Римская:I – 1 (палец), V – 5 (раскрытая ладонь, 5 пальцев), X – 10 , L – 50, C – 100 , D – 500, M – 1000
Например: XXX – 30; XLI — 41
Римская система счисления
Недостатки:для записи больших чисел (>3999) надо вводить новые знаки-цифры (V, X, L, C, D, M)как записать дробные числа?как выполнять арифметические действия: CCCLIX + CLXXIV =? Где используется: номера глав в книгах: обозначение веков: «Пираты XX века» циферблат часов
Перевод целых чисел
Двоичная система: Алфавит: 0, 1Основание (количество цифр): 2
10  2
2  10
19
2
9
18
1
2
4
8
1
2
2
4
0
2
1
2
0
2
0
0
1
1910= 100112
система счисления
100112
4 3 2 1 0
разряды
= 1·24 + 0·23 + 0·22 + 1·21 + 1·20 = 16 + 2 + 1 = 1910
Перевести в двоичную систему счисления.
1) 13110 =
2) 7910 =
Проверка
3) 85 10= 4) 12310=
Перевести в десятичную систему счисления.
1)1010112 =
2) 1101102 =
Проверка
3) 101101012 =
4) 10001112 =
И десять темно-синих глаз Рассматривали мир привычно … Но станет все совсем обычным, Когда поймете наш рассказ.
Когда, пыля десятком ног, Она шагала по дороге, За ней всегда бежал щенок С одним хвостом, зато стоногий.
Она ловила каждый звук Своими десятью ушами, и десять загорелых рук Портфель  и поводок держали.
Ей было тысяча сто лет, Она в сто первый класс ходила, В портфеле по сто книг носила. Все это правда, а не бред.
А.Н.Стариков «Необыкновенная девочка»Разгадайте загадку поэта. И двое темно-синих глаз Рассматривали мир привычно … Но станет все совсем обычным, Когда поймете наш рассказ.
Когда, пыля двумя ногами, Она шагала по дороге, За ней всегда бежал щенок С одним хвостом, зато четырехногий.
Она ловила каждый звук Своими двумя ушами, И две загорелые руки Портфель  и поводок держали.
Ей было 12 лет, Она в 5  класс ходила, В портфеле по четыре книги носила. Все это правда, а не бред.
Восьмеричная система
Основание (количество цифр): 8Алфавит: 0, 1, 2, 3, 4, 5, 6, 7
8  10
1448
2 1 0
разряды
= 1·82 + 4·81 + 4·80 = 64 + 32 + 4 = 10010
Перевести в десятичную систему счисления.
1)134 8=
2) 75 8=
Проверка
3) 568 = 4) 1128 =
Шестнадцатеричная система
Основание (количество цифр): 16Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,
16  10
A,10
B,11
C,12
D,13
E,14
F 15
1C516
2 1 0
разряды
= 1·162 + 12·161 + 5·160 = 256 + 192 + 5 = 45310
C
Перевести в десятичную систему счисления.
1) 1BC16 =
2) 22B16 =
Проверка
4АС16 = 5D16 =
ответ 13110 = 100000112 7910 = 10011112 8510 = 10101012 12310 =11110112 ответ 1010112 = 4310 1101102 = 5410 101101012 =18110 10001112 = 7110 ответ 1348 = 9210 758 = 6110 56 8 =4610 1128 = 7410 ответ 1ВС16=4441022В16=555104C16 = 76105D16 = 9310

nsportal.ru

Урок 4. Компьютерные системы счисления

Разработка для проведения урока в 8 классе по теме «Компьютерные системы счисления». УМК Л.Л.Босовой, А.Ю.Босовой.ФГОС.
Планируемые учебные результаты:

Предметные: формирование навыков перевода небольших десятичных чисел в восьмеричную и шестнадцатеричную системы счисления и восьмеричных и шестнадцатеричных чисел в десятичную систему счисления;

Метапредметные: формирование умений анализировать любую позиционную систему счисления как знаковую систему;
Личностные: понимание роли фундаментальных знаний как основы современных информационных технологий

Решаемые учебные задачи:

1) знакомство с восьмеричной системой счисления как знаковой системой;

2) знакомство с правилами перевода восьмеричных чисел в десятичную систему счисления;

3) знакомство с правилами перевода целых десятичных чисел в восьмеричную систему счисления;

4) знакомство с шестнадцатеричной системой счисления как знаковой системой;

5) знакомство с правилами перевода шестнадцатеричных чисел в десятичную систему счисления;

6) знакомство с правилами перевода целых десятичных чисел в шестнадцатеричную систему счисления;

7) характеристика двоичной, восьмеричной и шестнадцатеричной систем счисления с точки зрения их использования в компьютерной технике.

©

Наталья Викторовна Кутепова

Наталья Викторовна Кутепова

Понравилось? Сохраните и поделитесь:

По кнопке ниже вы можете скачать Урок 4. Компьютерные системы счисления категории Информатика 8 класс бесплатно. Будем благодарны, если вы оставите отзыв или посмотрите еще другие материалы на нашем сайте. Документ является презентация, конспект.

Скачать материал 13.8Mb

Загрузка началась…

Понравился сайт? Получайте ссылки
на лучшие материалы еженедельно!

Подарок каждому подписчику!

easyen.ru