Найдите значение дроби при указанных значениях переменных 8 класс дорофеев – Основные понятия. Видеоурок. Алгебра 8 Класс

Основные понятия. Видеоурок. Алгебра 8 Класс

На данном уроке рассматривается понятие алгебраической дроби. С дробями человек встречается в самых простых жизненных ситуациях: когда необходимо разделить некий объект на несколько частей, например, разрезать торт поровну на десять человек. Очевидно, что каждому достанется почасти торта. В указанном случае мы сталкиваемся с понятием числовой дроби, однако возможна ситуация, когда объект делится на неизвестное количество частей, например, на x. В таком случае возникает понятие дробного выражения. С целыми выражениями (не содержащими деление на выражения с переменными) и их свойствами вы уже познакомились в 7 классе.  Далее мы рассмотрим понятие рациональной дроби, а также допустимых значений переменных.

Рациональные выражения делятся на целые и дробные выражения.

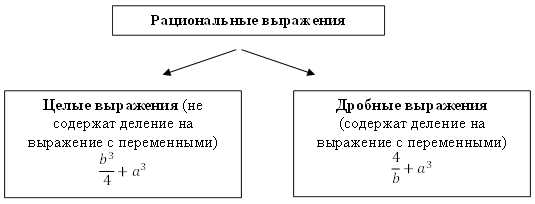
Определение. Рациональная дробь – дробное выражение вида , где  – многочлены.  – числитель,  – знаменатель.

Примеры рациональных выражений:  – дробные выражения;  – целые выражения. В первом выражении, к примеру, в роли числителя выступает , а знаменателя – .

Значение алгебраической дроби, как и любого алгебраического выражения, зависит от численного значения тех переменных, которые в него входят. В частности, в первом примере значение дроби зависит от значений переменных  и , а во втором только от значения переменной .

Рассмотрим первую типовую задачу: вычисление значения рациональной дроби при различных значениях входящих в нее переменных.

Пример 1. Вычислить значение дроби  при а) , б) ,    в)

Решение. Подставим значения переменных в указанную дробь: а) , б) , в)  – не существует (т. к. на ноль делить нельзя).

Ответ: а) 3; б) 1; в) не существует.

Как видим, возникает две типовые задачи для любой дроби: 1) вычисление дроби, 2) нахождение допустимых и недопустимых значений буквенных переменных.

Определение. Допустимые значения переменных – значения переменных, при которых выражение имеет смысл. Множество всех допустимых значений переменных называется ОДЗ или область определения.

Значение буквенных переменных может оказаться недопустимым, если знаменатель дроби при этих значениях равен нулю. Во всех остальных случаях значение переменных являются допустимыми, т. к. дробь можно вычислить.

Пример 2. Установить, при каких значениях переменной не имеет смысла дробь .

Решение. Чтобы данное выражение имело смысл, необходимо и достаточно, чтобы знаменатель дроби не равнялся нулю. Таким образом, недопустимыми будут только те значения переменной, при которых знаменатель будет равняться нулю. Знаменатель дроби , поэтому решим линейное уравнение:

.

Следовательно, при значении переменной  дробь не имеет смысла.

Ответ: -5.

Из решения примера вытекает правило нахождения недопустимых значений переменных – знаменатель дроби приравнивается к нулю и находятся корни соответствующего уравнения.

Рассмотрим несколько аналогичных примеров.

Пример 3. Установить, при каких значениях переменной не имеет смысла дробь.

Решение. .

Ответ. .

Пример 4. Установить, при каких значениях переменной не имеет смысла дробь .

Решение..

Встречаются и другие формулировки данной задачи – найти область определения или область допустимых значений выражения (ОДЗ). Это означает – найти все допустимые значения переменных. В нашем примере – это все значения, кроме . Область определения удобно изображать на числовой оси.

Для этого на ней выколем точку , как это указано на рисунке:

Рис. 1

Таким образом, областью определения дроби будут все числа, кроме 3.

Ответ..

Пример 5. Установить, при каких значениях переменной не имеет смысла дробь .

Решение..

Изобразим полученное решение на числовой оси:

Рис. 2

Ответ..

Пример 6. Установить, при каких значениях переменных не имеет смысла дробь .

Решение.. Мы получили равенство двух переменных, приведем числовые примеры:  или  и т. д.

Изобразим это решение на графике в декартовой системе координат:

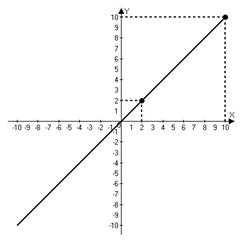
Рис. 3. График функции 

Координаты любой точки, лежащей на данном графике, не входят в область допустимых значений дроби.

Ответ. .

В рассмотренных примерах мы сталкивались с ситуацией, когда возникало деление на ноль. Теперь рассмотрим случай, когда возникает более интересная ситуация с делением типа .

Пример 7. Установить, при каких значениях переменных не имеет смысла дробь .

Решение..

Получается, что дробь не имеет смысла при . Но можно возразить, что это не так, потому что: .

Может показаться, что если конечное выражение равно 8 при , то и исходное тоже возможно вычислить, а, следовательно, имеет смысл при . Однако, если подставить  в исходное выражение, то получим  – не имеет смысла.

Ответ..

Чтобы подробнее разобраться с этим примером, решим следующую задачу: при каких значениях  указанная дробь равна нулю?

 (дробь равна нулю, когда ее числитель равен нулю) . Но необходимо решить исходное уравнение с дробью, а она не имеет смысла при , т. к. при этом значении переменной знаменатель равен нулю. Значит, данное уравнение имеет только один корень .

Таким образом, можем сформулировать точное правило нахождения области допустимых значений дроби: для нахождения ОДЗ дроби необходимо и достаточно приравнять ее знаменатель к нулю и найти корни полученного уравнения.

Мы рассмотрели две основные задачи: вычисление значения дроби при указанных значениях переменных и нахождение области допустимых значений дроби.

Рассмотрим теперь еще несколько задач, которые могут возникнуть при работе с дробями.

Пример 8. Докажите, что при любых значениях переменной дробь .

Доказательство. Числитель – число положительно

interneturok.ru

Обобщающий урок по алгебре в 8-м классе по теме «Алгебраические дроби»

Цели и задачи
урока: повторение и обобщение
изученного ранее материала по данной теме разного уровня сложности; развитие
познавательного интереса учащихся; закрепление навыков работы в коллективе;

Оборудование:
мультимедийный проектор,
номера групп на столах, карточки с заданиями.

ХОД УРОКА

1.
Организация
начала урока

На нашем
сегодняшнем уроке каждый из вас получит возможность не только поработать вместе
с товарищами над одной проблемой, но и научиться отстаивать свою точку зрение,
убедить товарищей в правильности выбранного решения и показать свои знания
теоретического материала.

2.
Сообщение
темы, цели и задач урока

Сегодня на уроке
мы подведём первые итоги работы по теме «Алгебраические дроби», закрепим те
знания, которые уже имеем, познакомимся с различными типами заданий по данной
теме, научимся вести дискуссию, вы попробуете организовать работу в коллективе
и покажите своим одноклассникам результаты это работы.

3.
Устный
опрос

Давайте
вспомним, какие выражения называются алгебраическими дробями?

Ответ:
Алгебраической дробью называется выражение P/Q, где P и Q – многочлены;  P –
числитель алгебраической дроби, Q – знаменатель алгебраической дроби.

Далее вопросы
задаются с использованием  слайда 3 (приложение ). На слайде также даются
верные ответы.

• В чём
  заключается основное свойство дроби?
• Числитель и
  знаменатель дроби можно разделить или умножить на одно и то же число, при
  этом значение дроби не изменится.
• Что
  значит сократить дробь?
• Разделить
  числитель и знаменатель дроби на одно и то же число.
• Какие
  основные формулы сокращённого умножения вы знаете?
• Квадрат суммы
  (разности), разность квадратов, куб суммы (разности).
• Как
  сложить(вычесть) дроби с одинаковыми знаменателями?
• Нужно сложить
  (вычесть) их числители, а знаменатель оставить прежним.
• Как привести
  дроби к общему знаменателю?
• Нужно найти
  НОК знаменателей, затем найти дополнительные множители для числителей,
  выполнить умножение числителей на дополнительный множитель и выполнить
  сложение или вычитание полученных дробей.

4.
Решение
задач

Теперь каждая из
групп получит своё задание (слайд 4). На выполнение данных заданий вам, ребята,
отводится 10 минут. Как только вы справитесь с заданием, один из учащихся
группы должен написать его решение на доске, чтобы остальные могли оценить его правильность 
и задать свои вопросы по предложенному ходу решения. Вопросы можно задавать как
ученику у доски, так и всем остальным членам группы.

Задания для
решения в группах:

1). Сократить
дробь:

а)

б)

2). Указать
допустимые значения переменной x:

а)

б)

3). Представьте
в виде выражения сумму:

4). Упростите
выражение:

.

5.
Работа
у доски

Теперь ребята,
давайте посмотрим, как вы справились со своими заданиями!

Учащиеся по
очереди поясняют решённые ими задания, а участники других групп задают
уточняющие вопросы.

Данные решения
сравниваются с правильными решениями на слайдах 5, 6, 7, 8.

1)Сократить дробь

а) ;

Решение:

 =  = .

б)

Решение:

2) Укажите
допустимые значения переменной х:

a)

Решение:

Выражение не имеет смысла, если знаменатели слагаемых равны ноль. Таким
образом, обращается в ноль при x = ±2.

Знаменатель
второго слагаемого не превращается в ноль ни при каких значениях переменной
x.

Ответ: x = ±2.

б) .

Решение:

Выражение   не имеет смысла, если 1−
 = 0 и x = 0.

1−  =  
Таким образом,  данная дробь обращается в ноль при x−1= 0 , x
= 1.

Ответ: x = 0, x
= 1.

3)
Преобразуйте в выражение сумму:

Решение:

Ответ:

4) Упростите
выражение:

Решение:

Ответ:

6.
Закрепление

И в конце нашего
урока мы проведём небольшой математический диктант.

Текст диктанта
приведён на слайде 9.

Диктант

1.
При каких значениях переменной
выражения не имеют смысла?

2.
При каких значениях
переменной данные выражения обращаются в ноль?

3.
Выполни
действия с дробями:

4.
Сократи
дробь:

В этом диктанте
всего 5 вопросов и количество правильных ответов будет совпадать с вашей
оценкой. Желаю удачи!

После того, как
учащиеся сдадут свои работы, на следующем слайде можно будет увидеть правильные
ответы и оценить выполненную работу самим учеником.

7. Подведение
итогов урока

Какие умения нам
сегодня пришлось применить на уроке?

Умение
работать в коллективе, умение помогать товарищу, отстаивать свою точку зрения,
выбирать правильный ход решения, организовывать совместную работу в группе.

Что, по-вашему,
необходимо для успешной работы вместе с товарищами?

Знание
теоретического материала, владение основными навыками решения аналогичных
заданий, внимание, желание научиться чему-то новому!

Где вам могут
пригодиться полученные навыки и умения?

В организации
своей учебной деятельности, в совместной работе со сверстниками, при подготовке
к экзаменам.

8. Информация
о домашнем задании

Попробуйте дома
самостоятельно приготовить задания разного уровня сложности по теме «Решение
систем уравнений» для работы в группах. Лучшие ваши предложения мы используем
на уроке повторения этой темы.

Список
литературы

1. Алгебра7. Задачник для общеобразовательных 
учреждений  / А.Г. Мордкович, Л.О. Денищева, Т.А. Корешкова, Т.Н. Мишустина,
Е.Е. Тульчинскаи; Под ред. А.Г. Мордковича. – М.: Мненозина, 2003. – 315 с.

2. Авторский коллектив под редакцией Ф.Ф. Лысенко. Математика.
ЕГЭ – 2009. Часть 2.  Учебно – тренировочные  тесты. – Ростов – на – Дону:
Легион, 2009. – 138с.

urok.1sept.ru

Дорофеев Г. В. Алгебра. 8 класс

Алгебраические дроби

Алгебра, 8

Никитина Ольга Владимировна,

МОУ СОШ № 81

г. Волгограда

Цели урока:

— сформировать умение применять
основное свойство дроби, правила действий
с алгебраическими дробями при выполнении
действий с алгебраическими дробями;

— продолжить воспитание
ответственности перед другими;

— способствовать дальнейшему
развитию коммуникативных способностей

личности обучающихся.

Место в учебном плане:
перед темой «Примеры на все действия с
алгебраическими дробями».

Учебник: Дорофеев
Г.В. Алгебра. 8 класс. — М.: Просвещение,
2008.

Ход урока

Работа
в группах

Проверка умений:

— демонстрировать теоретические
знания по теме «Алгебраические дроби»;

— пользоваться алгоритмами
сложения и вычитания дробей с разными
знаменателями, умножения и деления
дробей;

— находить допустимые значения
переменной;

— находить общий знаменатель
нескольких дробей;

— работать в группе, прислушиваться
к другому мнению.

Целевые установки, составление
плана урока (в ходе фронтальной работы).

На доске записан пример (рис. 1).
Используется шторка.

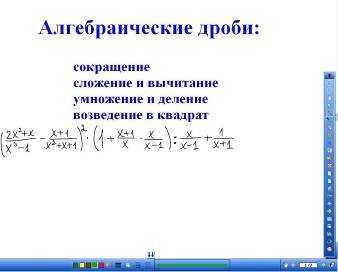
Рис. 1

— Посмотрите на пример (обычно
бурная реакция учащихся)
(открывается шторка).
Красивый?

— Со следующего урока вам предстоит
работать с такими примерами. Но как
говорят: «Чтобы построить крепкое
здание, нужен надежный фундамент». Что
для нас на уроках является таким
фундаментом? (Знания).

— Какие именно знания? (по
мере того как называются — открываем на
интерактивной доске, дублируются на
магнитной доске, где остаются до конца
урока). (Определение
алгебраической дроби. Основное свойство
дроби. Область допустимых значений
переменных. Правила действия с
алгебраическими дробями. Формулы
сокращённого умножения).

— Итак, целью нашего урока мы
можем назвать: (Проверка
теоретических знаний по теме «Алгебраические
дроби», их применение при решении
алгебраических задач).

Демонстрация теоретических
знаний по теме:

Вы работаете сегодня
группами-командами, поэтому результат
зависит от каждого. В конце урока я
возьму одну тетрадь от группы на проверку.

1. Экспресс-опрос
(группам по очереди задаются
вопросы, за верный ответ один балл;
неверный-переход хода к другой команде).

Дать определение:

а) Какая дробь называется
алгебраической?

б) Какие значения переменной
называются допустимыми?

в) Что такое общий знаменатель
дробей?

г) Что значит найти значение
дроби при заданном значении переменной?

2. Составь формулу.
Необходимо составить
формулу и сформулировать правило. Верный
ответ – 1 балл. Если только формула, то
– 0,5 балла (рис. 2-3).

Задания по одному открываются
стиранием белого цвета ластиком, далее
пером записываются результаты справа
от знака «равно».

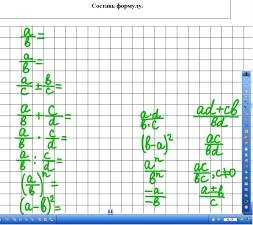
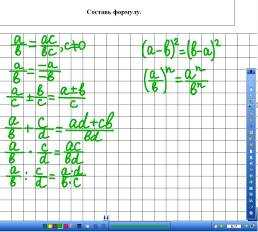
Рис. 2
Рис. 3

Демонстрация умений применять
теоретические знания при решении
примеров

1) «Найди ошибку»
(записаны примеры на интерактивной
доске).

— Определите, в каких примерах
допущены ошибки? (рис. 4). Решите примеры
в тетрадях и исправьте на доске ответы
(задание анализируются всем классом)
(рис. 5).

Рис. 4 Рис.
5

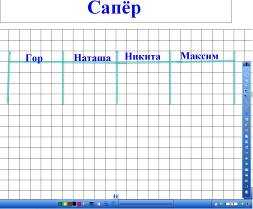
2) «Сапёр»
(рис. 7-9)

— Известно, что сапёры – это люди,
которым нельзя ошибиться. Напоминаю,
что ответ предыдущего примера является
элементом следующего. Конечный ответ
соответствует определённой букве, её
и надо записать на доске.

Контрольные точки — на обороте
вашего листочка (приложение 1) (рис. 6).

.

Рис. 6 Рис. 10

.

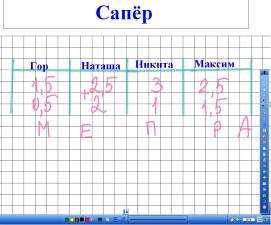
Рис. 7 Рис.
8

Рис. 9

Из этих букв можно сложить фамилию
учёного, которого принято считать
великим физиком, однако он является и
выдающимся математиком. (Ампер).

Историческая пауза

Следует сообщение на французском
языке с переводом на русский язык о
рассеянности Ампера.

Тест

— Я очень хочу, чтобы вы сейчас
не были рассеянными. Ведь предстоит
решить тест, выбрать правильный ответ
(приложение 2) (рис. 10). Используется
шторка.

Собирается по одной тетради
от группы.

— А теперь проверьте свои ответы
и оцените работу с тестом: «5» — нет
ошибок, «4» — одна ошибка, «3» — две ошибки.

Нестандартные задачи

Надо подумать! Задание представлено
на доске (рис. 11).

3 минуты подумать, желающий решает
на интерактивной доске.

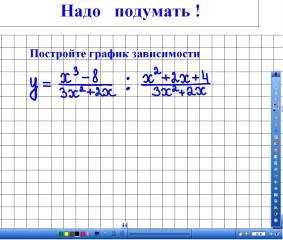
Рис. 11

По гиперссылке осуществляется
переход к видеоролику, на котором записан
процесс выполнения задания. Ученики
выделяют этапы выполнения задания,
сравнивая с работой ученика на доске.

Итоги урока (фронтальная беседа)

Обращаемся к записям на доске,
сделанным в начале урока! Гиперссылка
на первую страницу.

— Какие цели на урок ставили?

— Выполнили?

— Вы готовы к решению примера, с
которого начинали урок?

— Какое правило необходимо
повторить дома?

gigabaza.ru

План-конспект урока алгебры (8 класс) по теме: Алгебраические дроби

Тема урока: “Алгебраические дроби”.

Тип урока: урок повторения, систематизации и обобщения знаний, закрепления умений.

Формы работы на уроке: коллективная, индивидуальная, в диалоге.

Цель методическая: более глубокое усвоение, обобщение и систематизация знаний по теме “Алгебраические дроби” для обеспечения возможности их осмысленного использования учащимися вне урока математики.

Цели образования:

1. Обучения: Закрепление знаний, отработка навыков использования формул сокращенного умножения, приемов разложения многочленов на множители, правил преобразования, совместных действий над алгебраическими дробями. Обобщение материала по теме.
2. Развития: Создание условий, обеспечивающих активную познавательную позицию учеников на уроке путем использования различных видов опроса, самостоятельной работы,  развитие умений объяснять особенности, закономерности, анализировать, сопоставлять, сравнивать.
3. Воспитания: Воспитание самооценки, самоконтроля в ходе самостоятельного выбора уровня сложности заданий. Воспитание общей культуры труда.

4. Ход урока
5. 1. Вступительное слово учителя
6. Сегодня на уроке мы повторим большую тему “Алгебраические дроби”, подготовимся к контрольной работе и постараемся понять, зачем нам нужны знания по данной теме.
7. В ходе работы на уроке каждый из вас может “заработать” баллы за правильно выполненные задания, ответы и получить соответствующую оценку.
8. 2. Презентация по теме: «Алгебраические дроби».
9. 3. Повторение пройденного материала в форме игры «Своя игра»

Оценивание: 100 баллов-1 балл

10. 4. Найди ошибку:

Текст составлен из выполненных упражнений. Задания предъявляются на мобильном экране (ответы – позже). В решении некоторых из них допущены ошибки. Выполненные задания записать в тетрадь. Если задание выполнено правильно, давать краткий ответ: “Да”, если неправильно: “Нет”. Выделять место появления ошибки (карандашом).

Подведение итогов урока

Какие умения нам сегодня пришлось применить на уроке?

Умение работать в коллективе, умение помогать товарищу, отстаивать свою точку зрения, выбирать правильный ход решения.

Что, по-вашему, необходимо для успешной работы?

Знание теоретического материала, владение основными навыками решения аналогичных заданий, внимание, желание научиться чему-то новому!

Где вам могут пригодиться полученные навыки и умения?

В организации своей учебной деятельности, в совместной работе со сверстниками, при подготовке к экзаменам.

Домашнее задание:  дифференцированная самостоятельная работа, выполнив которую вы сможете узнать фамилию известного математика, механика и физика, который является автором данного высказывания.  Он, пожалуй, больше, чем кто-либо другой из отдельных людей, ответствен за рождение современной науки.  Он одним из первых объявил, что у человека есть надежда понять, как устроен мир, и, более того, что этого можно добиться, наблюдая наш реальный мир.

Вариант 1.

1.Укажите значение переменной, при котором алгебраическая дробь не имеет смысла:

а)0  б)0 и 1   в)-1   г)1.

2.Найти значение переменной, при котором алгебраическая дробь равна нулю:

а)4  б)0  в)0 и 4  г)-4

3. Сократите дробь:      к)  л)  м)  н) х.

4.Найти значение алгебраической дроби: при х=-1      г)-0,5  д)1,5  и)-1,5   к)0,5

5.Выполните действия: а)                к)  л) м) н)

б)                                                 в)   г)    д)  е)

в)                                       д)   й)   к)1    л)0

Вариант 2.

1.Укажите значение переменной, при котором алгебраическая дробь не имеет смысла:

а)1  б)2 и 1   в)-1   г)-2.

2.Найти значение переменной, при котором алгебраическая дробь равна нулю

а)-6 и 6  б)6  в)0   г)-6

3. Сократите дробь:             к   л)     м)           н)

4.Найти значение алгебраической дробипри х=-2      г)-1   д)3   и)-     к)

5.Выполните действия: а)                к)   л)-1     м)        н)

б)                                                 в)гд)е)

в)                                     д)   й)-    к)   л)

Вариант 3.          

1.Укажите значение переменной, при котором алгебраическая дробь не имеет смысла

а)-4  б)0 и 4   в)0   г)0 и -4.

2.Найти значение переменной, при котором алгебраическая дробь равна нулю

а)-8 и 0 б)0  в)0 и 8 г)-1

3. Сократите дробь:               к)     л)     м) н) у+5

4.Найти значение алгебраической дроби  при х=-6     г)-  д)3   и)     к)

5.Выполните действия: а)              к)   л)     м)        н)

б)                           в)       г)д)10+3х     е)

в)                                     д) х-6           й)    к)            л)х+6

nsportal.ru

Презентация урока для интерактивной доски по алгебре (8 класс) на тему: 8 класс Алгебра Рациональные выражения Урок 1 и 2

Слайд 1

МсСВУ ФГКОУ Московское суворовское военное училище 06.10.2013 Рациональные выражения Урок 1-2 Преподаватель математики Каримова С.Р.

Слайд 2

Работа над ошибками

Слайд 3

Алгебраическим выражением называется выражение, составленное из чисел и переменных с помощью действий сложения, вычитания, умножения, деления, возведения в степень и с помощью скобок . Целые выражения составлены из чисел и переменных с помощью действий сложения, вычитания и умножения, а также деления на число , отличное от нуля. Дробные выражения помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными

Слайд 4

ВЫРАЖЕНИЯ целые дробные рациональные выражения Рациональными называются целые и дробные выражения.

Слайд 5

Переместите выражения в соответствующие столбцы Дробные выражения Целые выражения

Слайд 6

Параметры / Изделия БМП-2, боевая машина пехоты Масса, кг 14300 Электропитание, В 3 Расчет, чел. 7 (десант) Пушка, тип 30 -мм 2А42 Пулемет 7.62 -мм ПКТ (ПКТМ) Боекомплект, шт: 30 -мм х 500, 7,62 -мм х 2000 Двигатель УТД-20, мощность 300 л.с . по шоссе до 65 на плаву до 7 Запас хода по шоссе, км 600 Параметры / Изделия БМП-3, гусеничная плавающая боевая машина пехоты Масса, кг 18700 Электропитание, В 3 Расчет, чел. 7 Пушка, тип 1х 100 -мм 2А70, 1х 30 -мм 2А72 Пулемет 3х 7,62 -мм ПКТ Боекомплект, шт: 30 х100-мм, в т.ч . 8 УР; 500х 30 -мм; 6000х 7,62 -мм Двигатель УТД-29, дизель по шоссе 70 на плаву 10 Запас хода по шоссе, км 600 Во сколько раз масса БМП-3 больше массы БМП-2? Составить целое выражение.

Слайд 7

Упражнения О б р а з е ц о ф о р м л е н и я: № 5 (а). ; а = –3, b = –1. 1,5. 1) Учебник № 3, № 4, № 5 (а)

Слайд 8

Упражнения Учебник 2) № 7 (а), № 8 3) № 9, № 16.

Слайд 9

Устно: – Какое выражение называется целым? дробным? – Как называются целые и дробные выражения? – Что такое рациональная дробь? – Всякая ли рациональная дробь является дробным выражением? Приведите примеры. – Как найти значение рациональной дроби при заданных значениях входящих в неё переменных?

Слайд 10

Допустимые значения переменных, входящих в дробное выражение Подставьте вместо * какое-нибудь число и назовите полученную дробь: а) ; б) ; в ) ; г) ; д ) ; е) ; ж) ; з) . Устно:

Слайд 11

– Какую дробь называют рациональной? – Всякая ли дробь является дробным выражением? – Как найти значение рациональной дроби при заданных значениях входящих в неё переменных? Устно: З а д а н и е. Найдите значение дроби при указанных значениях переменной: при х = 4; 0; 1.

Слайд 12

при х = 1 невозможно найти значение дроби. Это позволяет сделать следующий вывод : в рациональную дробь нельзя подставлять числа , которые обращают её знаменатель в нуль. Все значения переменных, при которых рациональное выражение имеет смысл, называют допустимыми значениями переменных . !

Слайд 13

Как находить допустимые значения переменных? 1) Если выражение является целым, то все значения входящих в него переменных будут допустимыми. 2) Чтобы найти допустимые значения переменных дробного выражения, нужно проверить, при каких значениях знаменатель обращается в нуль. Найденные числа не будут являться допустимыми значениями.

Слайд 14

Упражнения: О б р а з е ц о ф о р м л е н и я : № 11. г) 4 х ( х + 1) = 0 4 х = 0 или х + 1 = 0 х = 0 х = –1 О т в е т: х ≠ 0 и х ≠ 1 (или все числа, кроме 0 и –1). 1. № 10, № 11.

Слайд 15

Упражнения: 2. № 13. 3. № 14 (а, в), № 15 . 4 . № 17 .

Слайд 16

Решение: № 15. г) х ( х + 3) = 0 2 х + 6 ≠ 0 х = 0 или х = –3 х ≠ –3 О т в е т: х = 0.

Слайд 17

Дополнительно*: № 18 и № 20

Слайд 18

Решение: а ) . Из всех дробей с одинаковым положительным числителем большей будет та, у которой знаменатель является наименьшим. То есть необходимо найти, при каком значении а выражение а 2 + 5 принимает наименьшее значение. Поскольку выражение а 2 не может быть отрицательным ни при каких значениях а , то выражение а 2 + 5 будет принимать наименьшее значение при а = 0. О т в е т: а = 0. б) . Рассуждая аналогично, получим, что необходимо найти то значение а , при котором выражение ( а – 3) 2 + 1 принимает наименьшее значение. О т в е т: а = 3 . № 18.

Слайд 19

Решение: № 20. Дробь будет принимать наибольшее значение, если выражение (2 х + у ) 2 + 9 принимает наименьшее значение. Поскольку (2 х + у ) 2 не может принимать отрицательные значения, то наименьшее значение выражения (2 х + у ) 2 + 9 равно 9. Тогда значение исходной дроби равно = 2.

Слайд 20

Итог урока: – Какие значения называются допустимыми значениями переменных, входящих в выражение? – Каковы допустимые значения переменных целого выражения? – Как найти допустимые значения переменных дробного выражения? – Существуют ли рациональные дроби, для которых все значения переменных являются допустимыми? Приведите примеры таких дробей.

Слайд 21

№ 2, № 5 (б), № 6, № 7 (б ). № 12, № 14 (б, г), № 212. Д о п о л н и т е л ь н о: № 19. Задание на самоподготовку:

Слайд 22

Алгебpа . 8 класс. Учебник. ФГОС. Ю.Н. Макарычев, Н.Г. Миндюк , К.И. Нешков , С.Б. Суворова. Под ред. С.А.Теляковского . 2013г . Алгебра, 8 класс, Поурочные планы, Дюмина Т.Ю., Махонина А.А., 2012: CD; http://www.arms-expo.ru/049049052052124049051054055.html http://s4.goodfon.ru/wallpaper/previews-middle/219776.jp Литература и Интернет–ресурсы :

nsportal.ru

Алгебраические дроби — Алгебра — 8 класс

Просмотр содержимого документа

«Алгебраические дроби»

Вариант 1

№1. Найдите значение выражения при х = 0,4, у = -5.

№2. Сократите дробь .

№3. Выполните действие: .

№4. Упростите выражение:

№5. Представьте выражение в виде степени с основанием х и найдите его значение при х = .

№6. Решите уравнение: .

№7. Решите задачу. От дома до школы Коля обычно едет на велосипеде со скоростью 10 км/ч. Чтобы приехать в школу раньше на 12 мин, ему надо ехать со скоростью 15 км/ч. Чему равно расстояние от дома до школы?

№8. Упростите выражение: .

№9. Расположите в порядке возрастания: .

№10. Сократите дробь: .

Вариант 2.

№1. Найдите значение выражения при х = -2, у = .

№2. Сократите дробь: .

№3. Представьте выражение в виде дроби: х — .

№4. Выполните действие:

№5. Сравните: и 0,015.

№6. Решите уравнение: .

№7. Решите задачу. Все имеющиеся конфеты можно разложить либо в 24 маленькие коробки, либо в 15 больших коробок, если в большую коробку укладывать на 150 г конфет больше, чем в маленькую. Сколько всего имелось килограммов конфет?

№8. Сократите дробь .

№9. Вычислите: .

№10. Решите уравнение:

multiurok.ru

Урок 5. Основные понятия | Поурочные планы по алгебре 8 класс

Урок 5. Основные понятия

25.02.2012

6496

1338

Урок 5.

Основные понятия.

Цели урока: ввести понятие алгебраической
дроби и допустимых значений для дроби; формировать умение определять область
допустимых значений для любой дроби.

Ход урока

                     
IV.     
Организационный момент.

                       
V.     
Устный счет.

                     
VI.     
Объяснение нового материала.

Объяснение темы рассматривается на стр. 9-11 учебника.

Дать определение алгебраической дроби, знаменателя дроби, числителя
дроби. Привести примеры, вписывая в две колонки

Рассмотреть пример № 1 из учебника, показать, как находится
значение алгебраической дроби при некоторых значениях переменной. Объяснить
какие значения являются для заданной дроби допустимыми, а какие не допустимыми.

Учитель предлагает распределить по группам: 1) алгебраическая
дробь, 2) целое выражение. Следующие выражения:

; ; ; ; ; ; ; .

                  
VII.     
Закрепление нового материала.

Решение у доски по образцу:

При каких значениях переменной не имеет смысла алгебраическая дробь
ОДЗ: и , т. к

Решаются у доски задания в № 3(а, б), 4(а, б), 8 (а, б), 9 (а, б), дополнительные вопросы из
№ 17, 18:

1) № 3(а), 17(а) 5) № 8(а), 17(б)

2) № 3(б), 18(г) 6) № 8(б), 18(b)

3) № 4(а), 17(г) 7) № 9(а), 17(b)

4) № 4(б), 18(а) 8) №9 (б), 18(б).

Подведение итогов.

Домашнее задание: №
5, 6, 10, 11.

Полный текст материала смотрите в скачиваемом файле.
На странице приведен только фрагмент материала.

tak-to-ent.net