Контрольная работа №8 по теме » Неравенства» 8 класс
Тема: Контрольная работа № 8 по теме «Неравенства»
Цель: проверка знаний учащихся с использованием разноуровневых вариантов.
Ход урока
I. Сообщение темы и цели урока
II. Характеристика контрольной работы
Контрольная работа составлена в 6 вариантах различной сложности (варианты 1, 2 — самые простые, варианты 3, 4 — сложнее и варианты 5, 6 — самые сложные). При этом сложность вариантов нарастает не очень резко. Каждый вариант содержит 6 задач примерно одинаковой сложности (может быть, несколько сложнее две последние задачи).
При проверке вариантов 1, 2 оценка «5» ставится за правильное решение пяти задач, оценка «4» — четырех задач и оценка «3» — трех задач. Одна задача является резервной (или запасной) и дает некоторую возможность выбора учащимся. При таких же критериях оценки в случае вариантов 3, 4 дается дополнительно 0,5 балла и в случае вариантов 5, 6 — дополнительно 1,0 балла (учитывая более высокую сложность этих вариантов). Поэтому в случае вариантов 5, 6 оценку «5» можно получить за правильное решение четырех задач.
Выбор вариантов может быть сделан учителем или учащимся (при этом число экземпляров вариантов должно быть достаточным). Разумеется, учащиеся должны знать о различной сложности вариантов и критериях оценки контрольной работы.
III. Варианты работы
КР-8
Вариант 1
Решите неравенство:
3. Решите систему неравенств
4. При каких значениях x функция y = 2 — 4х принимает отрицательные значения?
5. Найдите область определения функции
КР-7
Вариант 2
Решите неравенство:
3. Решите систему неравенств
4. При каких значениях х функция y = 3 — 5х принимает положительные значения?
5. Найдите область определения функции
IV.Итог урока
КР-7
Вариант 3
1. Докажите неравенство х2 + 4х +16 ≥ 12х.
Решите неравенство:
4. Найдите область определения функции
5. Известно, что 1,4 < х < 1,5 и 2,7 < y < 2,8. Оцените величину 7x – 3y.
6. При всех значениях параметра я решите неравенство ах + 1 ≥ а2 — х.
КР-7
Вариант 4
1. Докажите неравенство х2 + 5х + 25 ≥ 15х.
Решите неравенство:
4. Найдите область определения функции
5. Известно, что 2,2 < х < 2,3 и 3,5 < у < 3,6. Оцените величину 5х — 2у.
6. При всех значениях параметра а решите неравенство ах + 1 ≥ а2 + х.
КР-7
Вариант 5
Решите неравенство:
3. Найдите область определения функции
4. При каких значениях а решения уравнения 4х = ах — 3 положительны?
5. На координатной плоскости изобразите множество точек (х; у), координаты которых удовлетворяют неравенству |у + 2х| ≤ 1.
6. При всех значениях а решите неравенство (а + 2)х ≥ а2 – а — 6.
КР-7
Вариант 6
Решите неравенство:
3. Найдите область определения функции
4. При каких значениях а решения уравнения 3х = ах — 7 отрицательны?
5 На координатной плоскости изобразите множество точек (х; у), координаты которых удовлетворяют неравенству |y — 3х| ≤ 2.
6. При всех значениях а решите неравенство (а + 3)х ≤ а2 + а — 6.
infourok.ru
Контрольная работа на тему «Числовые неравенства» (8 класс)
Контрольная работа на тему «Числовые неравенства и их свойства» Вариант 1
1.Известно, что а > b. Сравните: а) 21а и 21b;
б) -3,2а и -3,2b; в) а + 8 и b + 8.
2.Докажите неравенство: а) (х + 7)2 > х(х + 14);
б) b2 + 5  10(b — 2).
10(b — 2).
3.Известно, что 3,1 < < 3,2. Оцените: а) 3
< 3,2. Оцените: а) 3 ; б) —
; б) — .
.
4.Зная, что 7,2 < а < 8,4 и 2 < b < 2,5, оцените:
а) ab; б) -2a + b; в)  .
.
5.Оцените периметр и площадь прямоугольника со сторонами
а см и b см, если известно, что 1,5<а<1,6 и 3,2<b<3,3.
Контрольная работа на тему «Числовые неравенства и их свойства» Вариант 2
1.Известно, что а < b. Сравните: а) 18а и 18b;
б) -6,7а и -6,7b; в) а + 5 и b + 5.
2.Докажите неравенство: а) (х – 2)2 > х(х – 4);
б) а2 + 1  2(3а – 4).
2(3а – 4).
3.Известно, что 2,6 < < 2,7. Оцените: а) 2
< 2,7. Оцените: а) 2 ; б) —
; б) — .
.
4.Зная, что 1,5 < а < 1,8 и 1,2 < с < 1,5, оцените:
а) aс; б) –с + 4a; в)  .
.
5.Оцените периметр и площадь прямоугольника со сторонами
а см и b см, если известно, что 2,6<а<2,7 и 1,2<b<1,3.
Контрольная работа на тему «Числовые неравенства и их свойства» Вариант 1
1.Известно, что а > b. Сравните: а) 21а и 21b;
б) -3,2а и -3,2b; в) а + 8 и b + 8.
2.Докажите неравенство: а) (х + 7)2 > х(х + 14);
б) b2 + 5  10(b — 2).
10(b — 2).
3.Известно, что 3,1 < < 3,2. Оцените: а) 3
< 3,2. Оцените: а) 3 ; б) —
; б) — .
.
4.Зная, что 7,2 < а < 8,4 и 2 < b < 2,5, оцените:
а) ab; б) -2a + b; в)  .
.
5.Оцените периметр и площадь прямоугольника со сторонами
а см и b см, если известно, что 1,5<а<1,6 и 3,2<b<3,3.
Контрольная работа на тему «Числовые неравенства и их свойства» Вариант 2
1.Известно, что а < b. Сравните: а) 18а и 18b;
б) -6,7а и -6,7b; в) а + 5 и b + 5.
2.Докажите неравенство: а) (х – 2)2 > х(х – 4);
б) а2 + 1  2(3а – 4).
2(3а – 4).
3.Известно, что 2,6 <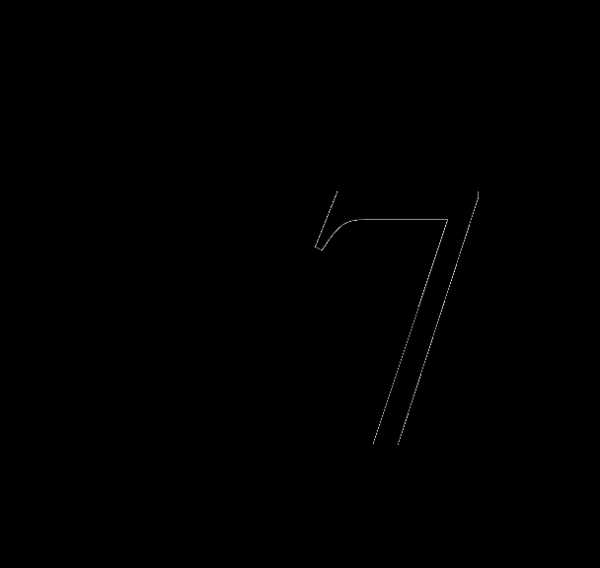 < 2,7. Оцените: а) 2
< 2,7. Оцените: а) 2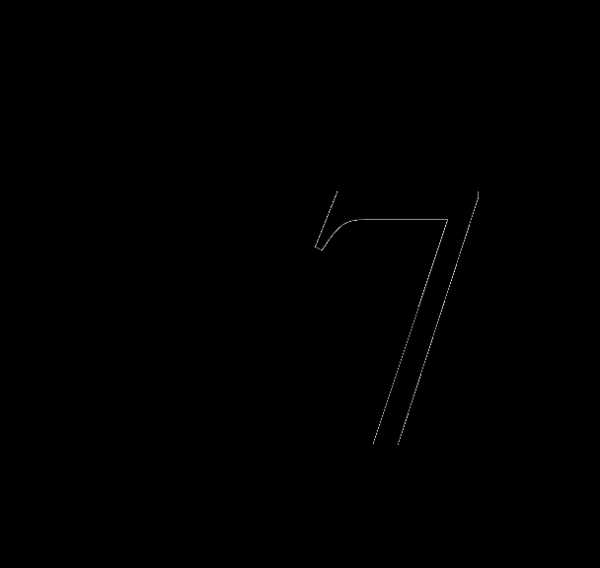 ; б) —
; б) —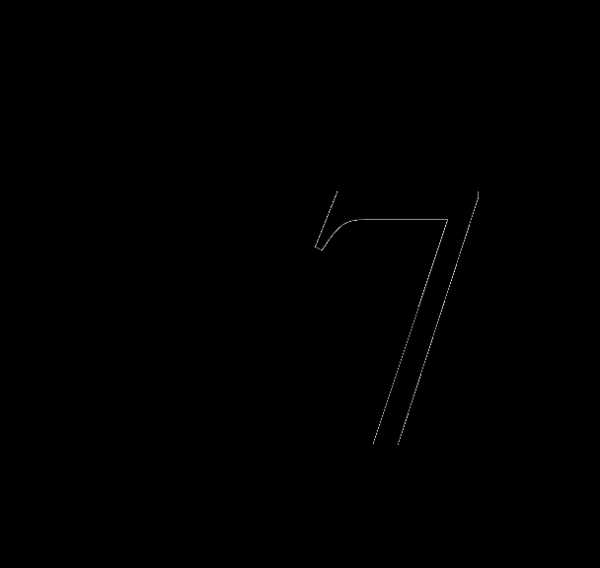 .
.
4.Зная, что 1,5 < а < 1,8 и 1,2 < с < 1,5, оцените:
а) aс; б) –с + 4a; в)  .
.
5.Оцените периметр и площадь прямоугольника со сторонами
а см и b см, если известно, что 2,6<а<2,7 и 1,2<b<1,3.
Контрольная работа на тему «Числовые неравенства и их свойства» Вариант 1
1.Известно, что а > b. Сравните: а) 21а и 21b;
б) -3,2а и -3,2b; в) а + 8 и b + 8.
2.Докажите неравенство: а) (х + 7)2 > х(х + 14);
б) b2 + 5  10(b — 2).
10(b — 2).
3.Известно, что 3,1 < < 3,2. Оцените: а) 3
< 3,2. Оцените: а) 3 ; б) —
; б) — .
.
4.Зная, что 7,2 < а < 8,4 и 2 < b < 2,5, оцените:
а) ab; б) -2a + b; в)  .
.
5.Оцените периметр и площадь прямоугольника со сторонами
а см и b см, если известно, что 1,5<а<1,6 и 3,2<b<3,3.
Контрольная работа на тему «Числовые неравенства и их свойства» Вариант 2
1.Известно, что а < b. Сравните: а) 18а и 18b;
б) -6,7а и -6,7b; в) а + 5 и b + 5.
2.Докажите неравенство: а) (х – 2)2 > х(х – 4);
б) а2 + 1  2(3а – 4).
2(3а – 4).
3.Известно, что 2,6 <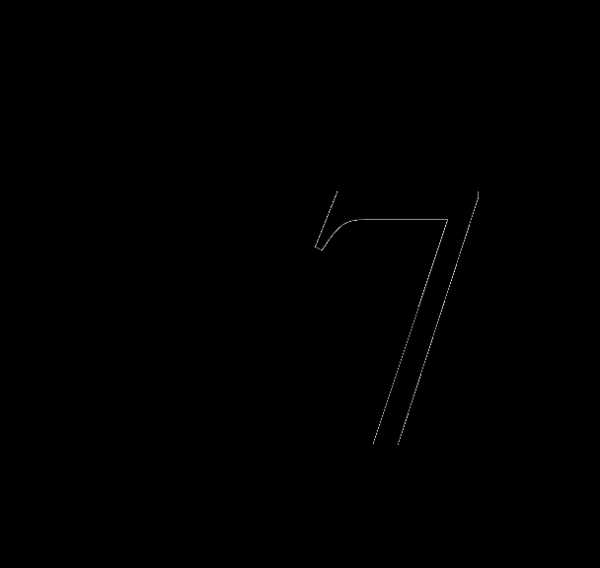 < 2,7. Оцените: а) 2
< 2,7. Оцените: а) 2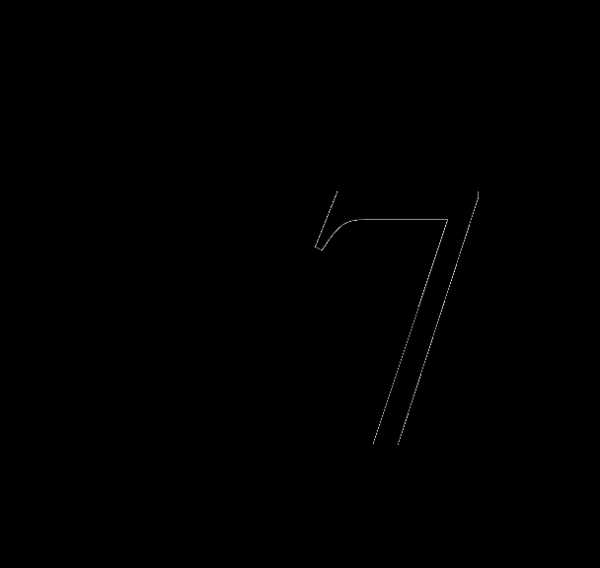 ; б) —
; б) —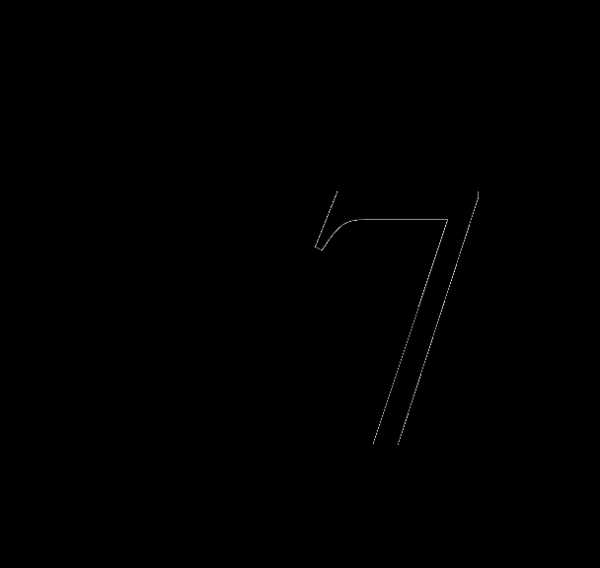 .
.
4.Зная, что 1,5 < а < 1,8 и 1,2 < с < 1,5, оцените:
а) aс; б) –с + 4a; в)  .
.
5.Оцените периметр и площадь прямоугольника со сторонами а см и b см, если известно, что 2,6<а<2,7 и 1,2<b<1,3.
Контрольная работа на тему «Числовые неравенства и их свойства» Вариант 1
1.Известно, что а > b. Сравните: а) 21а и 21b;
б) -3,2а и -3,2b; в) а + 8 и b + 8.
2.Докажите неравенство: а) (х + 7)2 > х(х + 14);
б) b2 + 5  10(b — 2).
10(b — 2).
3.Известно, что 3,1 < < 3,2. Оцените: а) 3
< 3,2. Оцените: а) 3 ; б) —
; б) —
4.Зная, что 7,2 < а < 8,4 и 2 < b < 2,5, оцените:
а) ab; б) -2a + b; в)  .
.
5.Оцените периметр и площадь прямоугольника со сторонами
а см и b см, если известно, что 1,5<а<1,6 и 3,2<b<3,3.
Контрольная работа на тему «Числовые неравенства и их свойства» Вариант 2
1.Известно, что а < b. Сравните: а) 18а и 18b;
б) -6,7а и -6,7b; в) а + 5 и b + 5.
2.Докажите неравенство: а) (х – 2)2 > х(х – 4);
б) а2 + 1  2(3а – 4).
2(3а – 4).
3.Известно, что 2,6 <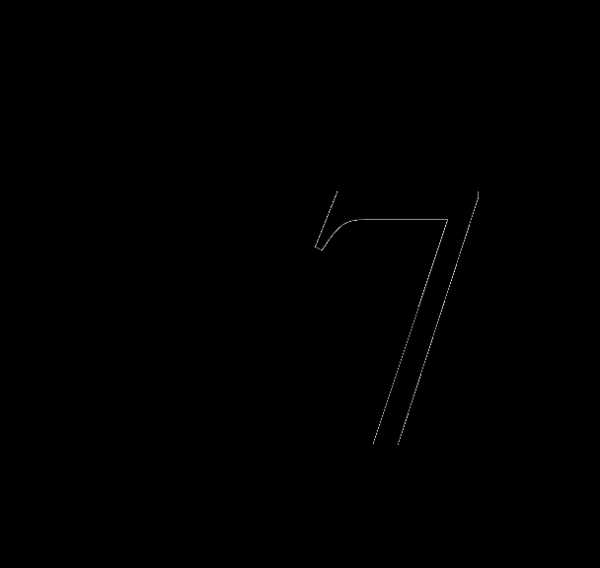 < 2,7. Оцените: а) 2
< 2,7. Оцените: а) 2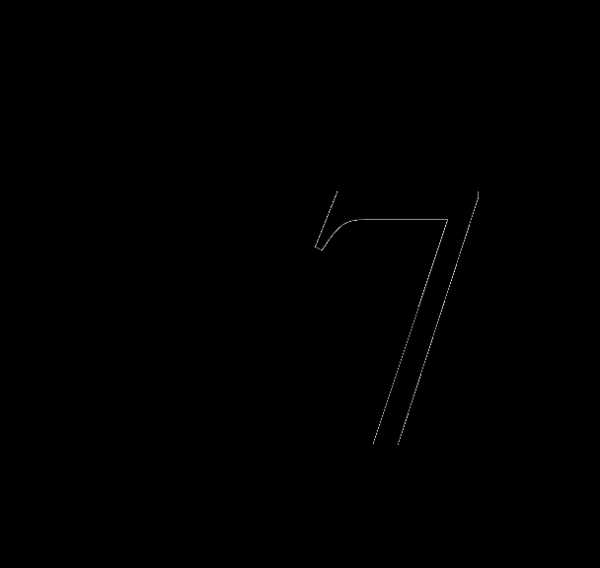 ; б) —
; б) — .
.
4.Зная, что 1,5 < а < 1,8 и 1,2 < с < 1,5, оцените:
а) aс; б) –с + 4a; в)  .
.
5.Оцените периметр и площадь прямоугольника со сторонами
а см и b см, если известно, что 2,6<а<2,7 и 1,2<b<1,3.
Контрольная работа на тему «Числовые неравенства и их свойства» Вариант 1
1.Известно, что а > b. Сравните: а) 21а и 21b;
б) -3,2а и -3,2b; в) а + 8 и b + 8.
2.Докажите неравенство: а) (х + 7)2 > х(х + 14);
б) b2 + 5  10(b — 2).
10(b — 2).
3.Известно, что 3,1 < < 3,2. Оцените: а) 3
< 3,2. Оцените: а) 3 ; б)
; б)  .
.
4.Зная, что 7,2 < а < 8,4 и 2 < b < 2,5, оцените:
а) ab; б) -2a + b; в)  .
.
5.Оцените периметр и площадь прямоугольника со сторонами
а см и b см, если известно, что 1,5<а<1,6 и 3,2<b<3,3.
Контрольная работа на тему «Числовые неравенства и их свойства» Вариант 2
1.Известно, что а < b. Сравните: а) 18а и 18b;
б) -6,7а и -6,7b; в) а + 5 и b + 5.
2.Докажите неравенство: а) (х – 2)2 > х(х – 4);
б) а2 + 1  2(3а – 4).
2(3а – 4).
3.Известно, что 2,6 < < 2,7. Оцените: а) 2
< 2,7. Оцените: а) 2 ; б) —
; б) — .
.
4.Зная, что 1,5 < а < 1,8 и 1,2 < с < 1,5, оцените:
а) aс; б) –с + 4a; в)  .
.
5.Оцените периметр и площадь прямоугольника со сторонами
а см и b см, если известно, что 2,6<а<2,7 и 1,2<b<1,3.
infourok.ru
Контрольная работа по теме: «Неравенства» 8 класс
Просмотр содержимого документа
«Контрольная работа по теме: «Неравенства» 8 класс»
Контрольная работа по теме: «Неравенства»
Вариант №1
1. Решите неравенства:
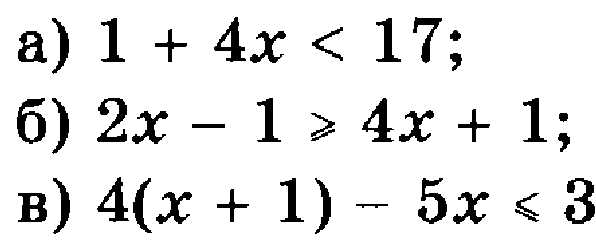
2. Решите систему неравенств:

3. Решите неравенство
и укажите, на каком рисунке изображено множество его решений
4.Решите неравенство и запишите ответ тремя способами
5*. При каких значениях выражение принимает отрицательные значения?
Контрольная работа по теме: «Неравенства»
Вариант №2
1. Решите неравенства:
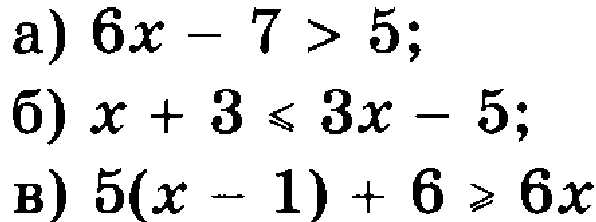
2. Решите систему неравенств:
3. Решите неравенство
и укажите, на каком рисунке изображено множество его решений
4. Решите неравенство и запишите ответ тремя способами
5*. При каких значениях выражение принимает отрицательные значения?
Контрольная работа по теме: «Неравенства»
Вариант №3
1. Решите неравенства:
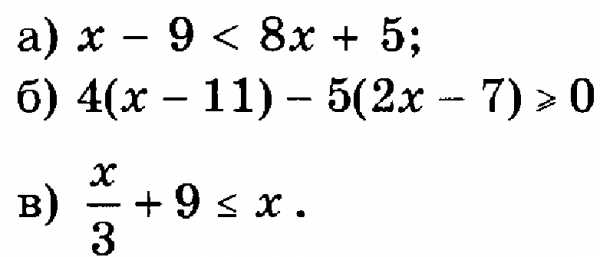
2. Решите систему неравенств:
3. Решите неравенство и запишите ответ тремя способами
4. На каком рисунке изображено решение системы:
5*. При каких значениях корень уравнения является положительным числом?
Контрольная работа по теме: «Неравенства»
Вариант №4
1. Решите неравенства:

2. Решите систему неравенств:
3. Решите неравенство и запишите ответ тремя способами
4. На каком рисунке изображено решение системы:
5*. При каких значениях корень уравнения является отрицательным числом?
multiurok.ru
Алгебра 8 Контрольные Макарычев (КИМ Глазков)
Контрольные работы по алгебре 8 класс (УМК Макарычев и др.)
Алгебра 8 Контрольные Макарычев (КИМ Глазков) — это контрольные работы (цитаты) из учебного пособия Контрольно-измерительные материалы (КИМ) по алгебре 8 класс: к учебнику Ю.Н. Макарычева и др. «Алгебра 8 класс» / Ю.А. Глазков, М.Я. Гаиашвили, В.И. Ахременкова — М.: Издательство «Экзамен», 2014, которое используется в комплекте с учебником «Алгебра 8 класс» авторов: Ю.Н. Макарычев и др.
Цитаты из пособия указаны в учебных целях, а также во избежание редакционных ошибок (в разных изданиях книги встречаются разные вопросы). При постоянном использовании контрольных работ в 8 классе рекомендуем купить книгу: Глазков, Гаиашвили, Ахременкова: КИМ. Алгебра. 8 класс. Итоговая аттестация, в которой кроме 10 контрольных работ (в 4-х вариантах) есть 15 тестов и ответы на них.
Для увеличения изображения — нажмите на картинку !
Чтобы скачать работу — нажмите на правую кнопку мыши и выберите «Сохранить изображение как …»
Контрольная работа № 1.
Рациональные дроби и их свойства. Сумма и разность дробей

Алгебра 8 Контрольные Макарычев. Ответы на Контрольную работу 1 «Рациональные дроби и их свойства. Сумма и разность дробей»:

Контрольная работа № 2.
Произведение и частное дробей. Преобразование рациональных выражений

Алгебра 8 Макарычев. Ответы на Контрольную работу 2 «Произведение и частное дробей. Преобразование рациональных выражений».

Контрольная работа № 3.
Действительные числа. Арифметический квадратный корень

Алгебра 8 Макарычев. Ответы на Контрольную работу 3 «Действительные числа. Арифметический квадратный корень».

Контрольная работа № 4.
Свойства арифметического квадратного корня.
Применение свойств арифметического квадратного корня.

Алгебра 8 Макарычев. Ответы на Контрольную работу 4 «Свойства арифметического квадратного корня. Применение свойств арифметического квадратного корня».
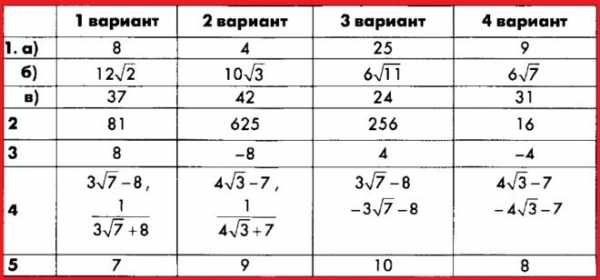
Контрольная работа № 5.
Квадратное уравнение и его корни. Формула корней квадратного уравнения
Алгебра 8 Макарычев. Ответы на Контрольную работу 5 «Квадратное уравнение и его корни. Формула корней квадратного уравнения».
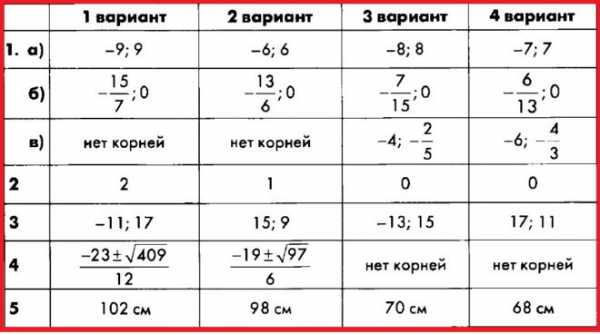
Контрольная работа № 6.
Дробные рациональные уравнения
Алгебра 8 Контрольные Макарычев. Ответы на Контрольную работу 6 «Дробные рациональные уравнения».
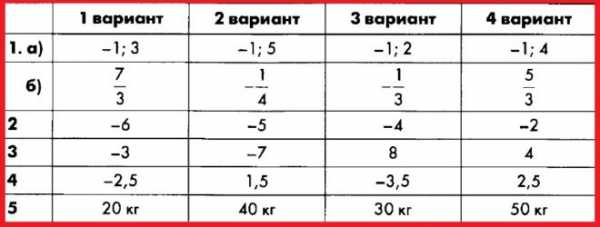
Контрольная работа № 7.
Числовые неравенства и их свойства
Алгебра 8 Макарычев. Ответы на Контрольную работу 7 «Числовые неравенства и их свойства».
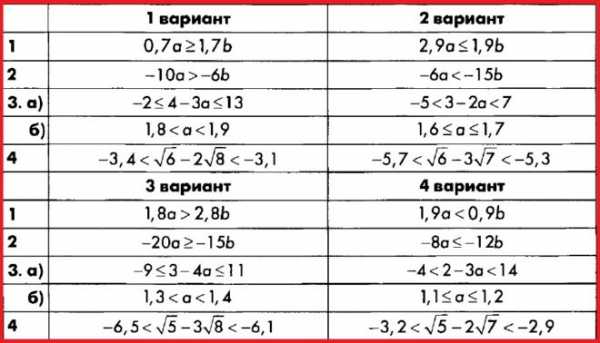
Контрольная работа № 8.
Решение неравенств с одной переменной и их систем

Алгебра 8 Контрольные Макарычев. Ответы на Контрольную работу 8 «Решение неравенств с одной переменной и их систем»
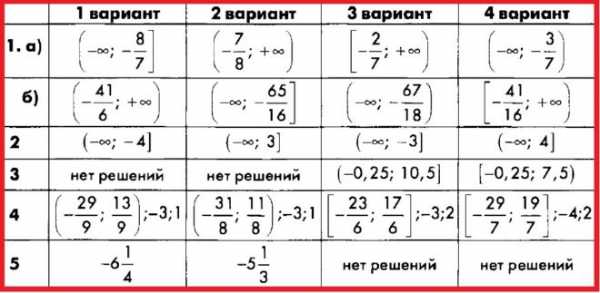
Контрольная работа № 9.
Степень с целым показателем и её свойства

Алгебра 8 Макарычев. Ответы на Контрольную работу 9 «Степень с целым показателем и её свойства».
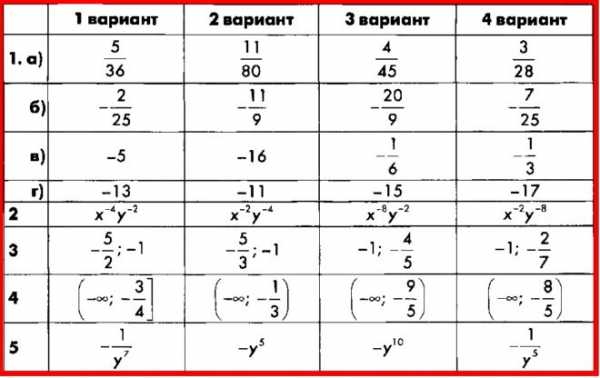
Контрольная работа № 10.
Итоговая работа за 8 класс

Алгебра 8 Макарычев. Ответы на Контрольную работу 10
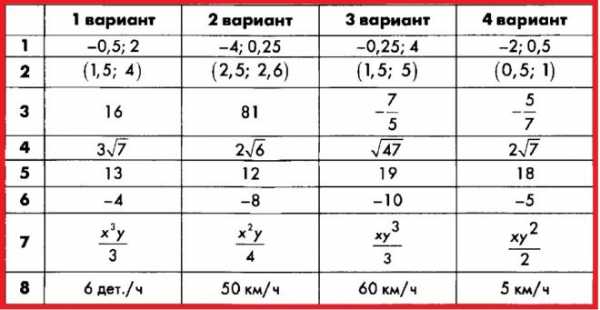
Вы смотрели страницу «Алгебра 8 Контрольные Макарычев» — контрольные работы (цитаты) из учебного пособия Контрольно-измерительные материалы (КИМ) по алгебре 8 класс: к учебнику Ю.Н. Макарычева и др. «Алгебра 8 класс» / Ю.А. Глазков, М.Я. Гаиашвили, В.И. Ахременкова — М.: Издательство «Экзамен», 2014, которое используется в комплекте с учебником «Алгебра 8 класс» авторов: Ю.Н. Макарычев и др.
Просмотры: 5 834
xn--b1agatflbfbtgq5jm.xn--p1ai
Проверочный тест по алгебре по теме «Решение неравенств с одной переменной», (8 класс)
Проверочный тест по теме
«Решение неравенств с одной переменной» (8 класс)
Цели:
Образовательная:
— проверка теоретических знаний учащихся по теме: «Неравенства с одной переменной»;
— контроль и коррекция знаний, умений и навыков при работе с неравенствами.
Развивающая:
— повышение алгоритмической культуры учащихся;
— развитие логического мышления.
Воспитательная:
— формирование у учащихся положительной мотивации учения, умения преодолевать посильные трудности;
— формирование навыков самостоятельной работы и самоконтроля.
Инструкция по выполнению работы
На выполнение данного теста отводится 25 минут.
Тест составлен в двух вариантах. Каждый вариант состоит из обязательной части А и дополнительной части В. Всего 7 заданий . Часть А содержит 5 заданий с выбором ответа. Часть В состоит из 2 заданий, которые подразумевают под собой запись подробного решения.
Ответы записываются в бланке самого теста. Если вы хотите изменить ответ, зачеркните его и рядом запишите новый.
При выполнении теста нельзя пользоваться учебниками, рабочими тетрадями, справочными материалами и калькулятором. При необходимости можно пользоваться черновиком. Записи в черновике не проверяются и не оцениваются.
Задание, которое не удается выполнить сразу, пропускайте и переходите к следующему. Постарайтесь выполнить как можно больше заданий.
Желаю успеха!
I вариант:
Обязательная часть.
А1. Какое из чисел НЕ является решением неравенства 4,5 + 3у >0?
Варианты ответов:
1) 0
2) 4,5
3) 3
4) -1,5
Ответ: ___
А2. Решите неравенство 6 -7х > 3х – 7:
Варианты ответов:
1) (-∞; 1,3)
2) (0,1; +∞)
3) (-∞; 0,1)
4) (1,3; +∞)
Ответ: ___
А3. Сколько целых решений неравенства 2с < -1,3 принадлежит промежутку (-6; 3]?
Варианты ответов:
1) 3
2) 4
3) 5
4) 6
Ответ: ___
А4. Какое из приведенных ниже неравенств является верным при любых значениях
х и у, удовлетворяющих условию х > у?
Варианты ответов:
1) у – х > 0
2) у – х < -1
3) х – у > 3
4) х – у > -2
Ответ: ___
А5. При каких значениях х значение выражения 6х – 7 больше значения выражения
7х + 8?
Варианты ответов:
1) х < -1
2) х > -1
3) х > -15
4) х < -15
Ответ: ___
Дополнительная часть.
В1. Решите неравенство 6х + 3(-5 – 8х) > 2х + 4.
Решение:
______________________________________________________________________________________________________________________________________________________
_______________________________________________________________________
Ответ: ________
В2. Решите неравенство методом интервалов: (2,5- х)(2х +3)(х +4) > 0.
Решение:
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Ответ:_________
II вариант:
Обязательная часть.
А1. Какое из чисел НЕ является решением неравенства 2,6 + 2у < 0?
Варианты ответов:
1) — 2
2) 4,5
3) — 3
4) -1,3
Ответ: ___
А2. Решите неравенство 2х — 4 ≥ 7х – 1:
Варианты ответов:
1) (-∞; -0,6]
2) (0,1; +∞)
3) [-0,6; +∞]
4) [1; +∞)
Ответ: ____
А3. Сколько натуральных решений неравенства 3с > -2,7 принадлежит промежутку
[0; 4)?
Варианты ответов:
1) 4
2) 3
3) 5
4) 2
Ответ: ___
А4. Какое из приведенных ниже неравенств является верным при любых значениях
х и у, удовлетворяющих условию х > — у?
Варианты ответов:
1) у – х > -1
2) у + х < 1
3) х + у > -1
4) х – у > 1
Ответ: ___
А5. При каких значениях х значение выражения 5х + 2 меньше значения выражения
4х + 8?
Варианты ответов:
1) х < 10
2) х > 10
3) х > 6
4) х < 6
Ответ: ___
Дополнительная часть.
В1. Решите неравенство 3х + 4(-7 + 6х) ≤ -7х + 6.
Решение:
______________________________________________________________________________________________________________________________________________________
_______________________________________________________________________
Ответ: ________
В2. Решите неравенство методом интервалов: (х -3)(2х + 4)(1,5 –х) < 0.
Решение:
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Ответ:_________
Рекомендации для учителя при оценивании работы
Оценивание заданий части А
Каждый верный ответ оценивается в 1 балл.
За неверный ответ или отсутствие ответа выставляется 0 баллов.
Оценивание заданий части В
Каждый верный ответ оценивается в 1 балл.
За неверный ответ или отсутствие ответа выставляется 0 баллов.
Шкала перевода тестового балла в отметку
|
Количество баллов |
1-2 |
3-4 |
5-6 |
7 |
|
Отметка |
«2» |
«3» |
«4» |
«5» |
Ответы к тесту:
|
Номер задания |
А1 |
А2 |
А3 |
А4 |
А5 |
В1 |
В2 |
|
Вариант 1 |
4 |
1 |
3 |
4 |
5 |
х <-1 |
(-∞; -4) U (-1,5; 2,5) |
|
Вариант 2 |
4 |
1 |
2 |
3 |
4 |
х <1 |
(-2; 1,5)U (3; +∞) |
xn--j1ahfl.xn--p1ai
Тест по алгебре (8 класс) на тему: Тест 26, неравенства, алгебра 8 класс
Тест 26. Решение неравенств с одной переменной. Вариант 1
А1. Решите неравенство – х
- (– ∞; 10) 2) [10; +∞) 3) [–10; 10] 4) (–10; + ∞)
А2. Найдите наибольшее целое число, удовлетворяющее неравенству х
- 1 2) 2 3) 18 4) 17
A3. Найдите количество целых решений неравенства – 3х > 1,1, принадлежащих промежутку [–5; 5].
1) 5 2) 4 3) 3 4) 2
А4. При каких значениях х функция принимает значения больше 0?
- х > – 4 2) х х > 4 4) х
А5. При каких значениях х значение выражения 3(2 + х) больше соответствующего значения выражения 4 – х ?
- х х х > – 2 4) х > – 0,5
В1. Найдите множество решений неравенства
В2. При каких значениях а уравнение 4 + З х = а – 5 имеет отрицательный корень?
С1. При каких значениях а неравенство ах 8 имеет такое же множество решений, что и неравенство х > ?
Тест 26. Решение неравенств с одной переменной. Вариант 2
А1. Решите неравенство – х
- (– ∞; 24) 2) (24; +∞) 3) (–24; +∞) 4) (– ∞; – 24)
А2. Найдите наименьшее целое число, удовлетворяющее неравенству х > 2.
1) 5 2) 5 3) 1 4) 7
A3. Найдите количество целых решений неравенства – 9х > 1,3, принадлежащих промежутку [–5; 5].
1) –5 2) 5 3) 6 4) 4
А4. При каких значениях х функция принимает значения больше 0?
- х > 3,5 2) х х – 3,5 4) х > – 3,5
А5. При каких значениях х значение выражения 3(2 + х) больше соответствующего значения выражения 4 – х ?
- х > – 2 2) х х > – 0,5 4) х
В1. Найдите множество решений неравенства
В2. При каких значениях b уравнение 5 – 2х = b – 1 имеет положительный корень?
С1. При каких значениях b неравенство bх > 6 имеет такое же множество решений, что и неравенство х > ?
Ответы. Вар. 1
|
А1 |
А2 |
А3 |
А4 |
А5 |
В1 |
В2 |
С1 |
|
4 |
4 |
1 |
2 |
4 |
[-7/6; +∞) |
a |
a |
Ответы. Вар. 2
|
А1 |
А2 |
А3 |
А4 |
А5 |
В1 |
В2 |
С1 |
|
3 |
4 |
2 |
2 |
1 |
(−∞; -5/3) |
b |
b > 0 |
nsportal.ru
Проверочный тест по алгебре по теме «Числовые неравенства», (8 класс)
Проверочный тест по теме
«Числовые неравенства» (8 класс)
I вариант:
Обязательная часть.
А1. Какие из неравенств верны?
Варианты ответов:
1)
2) 2 ≥ -2
3) 6, 129 > 6,131
4) 4 ∙ 103 > 4 ∙ 102
Ответ: ___
А2. Каким из данных чисел может выражаться разность х – у, если у > х?
Варианты ответов:
1) 0
2) 2,5
3) -3
4) -2,5
Ответ: ___
А3. Известно, что х > у. Расположите в порядке убывания числа: х +1; у -7; х + 10;
у – 15.
Варианты ответов:
1) у – 15; у -7; х +1; х + 10.
2) х + 10; х +1; у -7; у – 15.
3) у -7; х +1; х + 10; у – 15.
4) у -7; у – 15; х +1; х + 10.
Ответ: ___
А4. Выберите верное утверждение относительно чисел a и b, расположенных на числовой прямой.
Варианты ответов:
1)
2)
3)
4)
Ответ: ___
А5. Укажите решение неравенства -3 -3х > 7х – 9.
Варианты ответов:
1) (0,6; +∞)
2) (-∞; 1,2)
3) (1,2; +∞)
4) (-∞; 0,6)
Ответ: ___
Дополнительная часть.
В1. Решите неравенство 2(4х – 7) < -3 – 2х.
Решение:
______________________________________________________________________________________________________________________________________________________
_______________________________________________________________________
Ответ: ________
В2. В Докажите, что при любом значении х верно неравенство 4х2 + 1 ≥ 4х.
Решение:
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Ответ:_________
II вариант:
Обязательная часть.
А1. Какие из неравенств НЕверны?
Варианты ответов:
1)
2) 2 ≤ -2
3) 6, 129 > 6,131
4) 4 ∙ 103 > 4 ∙ 102
Ответ: ___
А2. Какое из неравенств является верным при любых значениях х и у, если х >-у?
Варианты ответов:
1) у – х > -1
2) у + х <1
3)
4) х – у > 1
Ответ: ___
А3. Известно, что х > у. Расположите в порядке возрастания числа: х +1; у -7; х + 10;
у – 15.
Варианты ответов:
1) у – 15; у -7; х +1; х + 10.
2) х + 10; х +1; у -7; у – 15.
3) у -7; х +1; х + 10; у – 15.
4) у -7; у – 15; х +1; х + 10.
Ответ: ___
А4. На координатной прямой отмечено число .
Какое из утверждений относительно этого числа является верным?
Варианты ответов:
1) 2)
3) 4)
Ответ: ___
А5. Укажите решение неравенства 9х + 8 < 8х – 8.
Варианты ответов:
1) (-16; +∞)
2) (-∞; 0)
3) (0; +∞)
4) (-∞; -16)
Ответ: ___
Дополнительная часть.
В1. Решите неравенство -2(х – 1) < -7 + 4х.
Решение:
______________________________________________________________________________________________________________________________________________________
_______________________________________________________________________
Ответ: ________
В2. В Докажите, что при любом значении х верно неравенство 9х2 — 15 > (3х -4)(3х +4).
Решение:
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Ответ:_________
xn--j1ahfl.xn--p1ai