Разноуровневый дидактический материал по алгебре 8 класс (карточки)
Школа-лицей №3
Разноуровневый дидактический материал по
алгебре 8 класс.
(карточки)
Учитель: Чеснокова С. А.
Г. Кызылорда
Аннотация
на разноуровневые дидактический материал (карточки)
по алгебре 8 класса.
Предлагаемые дидактические материалы дают возможность закрепить полученные знания и самостоятельно их усвоить.
Задания карточек даны в нескольких вариантах, разбиты по темам.
Карточки носят разноуровневый характер. Задание, помеченное треугольником на оценку «3», если ученик выполняет задания с треугольником и квадратом, то получает оценку «4», а если он выполнит ещё задание и со звёздочкой, то получит оценку «5».
Данные карточки проверяют уровень усвоения полученных знаний по темам. Уровень сложности заданий в соответствующих карточках примерно одинаков.
Цели дидактических карточек:
-
Индивидуальная деятельность учащихся.
-
Развитие у учащихся самооценки.
-
Развитие умения выбора своего уровня заданий.
-
Развитие стремления улучшить свои результаты.
-
Развитие мыслительной деятельности учащихся.
-
Воспитание самостоятельности при выполнении заданий карточек.
-
Накопляемость оценок.
Используемая литература:
-
Приложение к журналу « 1 сентября – математика»
-
Учебник « Алгебра – 8» — автор С.А. Теляковский.
-
Учебник « Алгебра – 8» — автор Ю.Н. Макарычев, Н.г. Миндюк, В.М. Монахов
-
Дидактические материалы по алгебре В.И. Жохов, Ю.Н.Макарычев.
-
Учебник « Алгебра – 8» автор Н.Я.Виленкин
Каталог
дидактических карточек
по алгебре
8 класс.
1. Повторение
-
Повторение материала за курс алгебры 7 класс.
2. Квадратные корни.
-
Арифметический квадратный корень.
-
Свойства арифметического квадратного корня.
-
Применение свойств арифметического квадратного корня.
-
Функция
 и её график.
и её график.
-
-
Квадратное уравнение.
-
-
Определение квадратного уравнения. Решение неполных квадратных уравнений.
-
Формула корней квадратного уравнения.
-
Дробно-рациональные уравнения.
-
Свойство корней квадратного уравнения. Теорема Виета
-
Квадратный трёхчлен, разложение квадратного трёх члена на множители.
-
Некоторые виды уравнений, приводимые к квадратным.
-
Квадратное неравенство.
-
Системы линейных неравенств с одной переменной.
-
Уравнения и неравенства, содержащие выражения под знака модуля.
-
Квадратные неравенства.
-
Решение неравенств методом интервалов.
-
Функция , её график.
-
Система уравнений.
-
Уравнение с двумя переменными и его график.
-
Алгебраический метод решения систем уравнений с двумя переменными.
-
Решение задач на составление уравнений.
-
Системы неравенств с двумя переменными.
Тема № 1: «Повторение материала за курс алгебры
7 кл.».
1. Сократите дробь :
2. Сократите дробь: 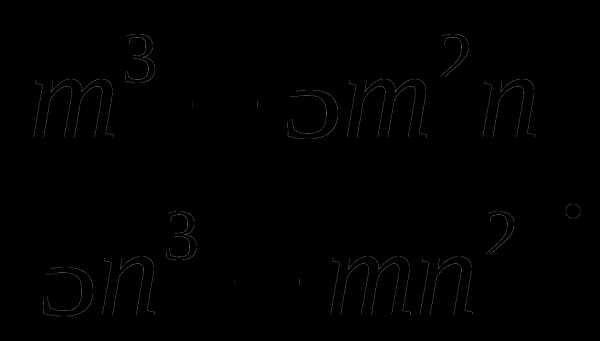
3.Найдите значение дроби:
Тема № 1: «Повторение материала за курс алгебры
7 кл.».
Тема № 1: «Повторение материала за курс алгебры
7 кл.».
-
3. Вычислите:
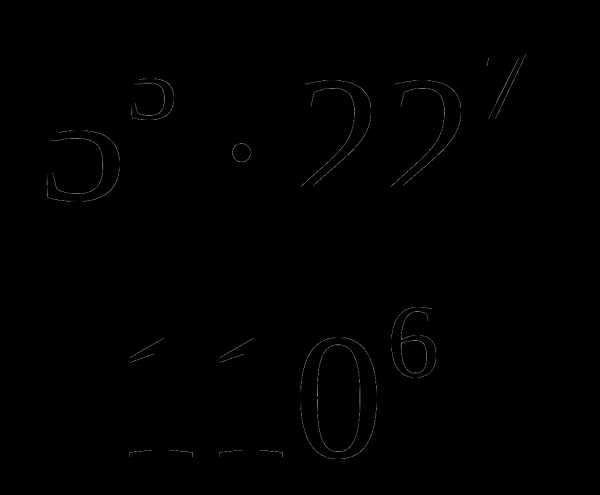
Тема № 1: «Повторение материала за курс алгебры
7 кл.».
-
3. Вычислите :
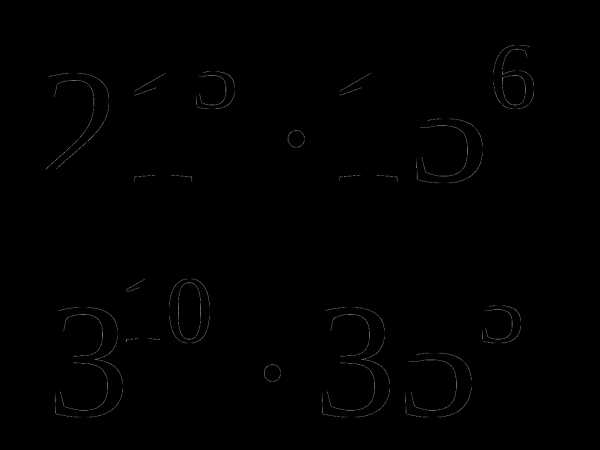
Тема № 1: «Повторение материала за курс алгебры
7 кл.».
2. . Представьте в виде дроби :
Тема № 1: «Повторение материала за курс алгебры
7 кл.».
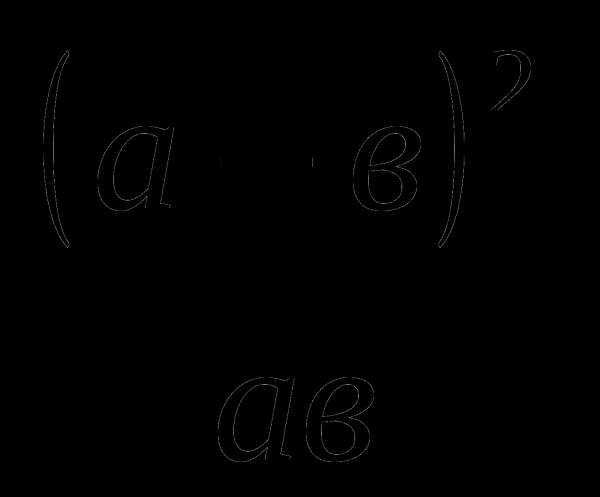
Тема № 1: «Повторение материала за курс алгебры
7 кл.».
Тема № 1: «Повторение материала за курс алгебры
7 кл.».
Тема № 1: «Повторение материала за курс алгебры
7 кл.».
Тема № 1: «Повторение материала за курс алгебры
7 кл.».
Тема № 2: «Арифметический квадратный корень».
-
1. Вычислите :
Тема № 2: «Арифметический квадратный корень».
-
1. Вычислите :
Тема № 2: «Арифметический квадратный корень».
-
1. Вычислите :
Тема № 2: «Арифметический квадратный корень».
Тема № 2: «Арифметический квадратный корень».
Тема № 2: «Арифметический квадратный корень».
-
1. Вычислите :
Тема № 3: «Свойства арифметического квадратного корня».
-
2. Вычислите :
Тема № 3: «Свойства арифметического квадратного корня».
-
2. Вычислите :
Тема № 3: «Свойства арифметического квадратного корня».
-
2. Вычислите:
Тема № 3: «Свойства арифметического квадратного корня».
-
2. Вычислите:

Тема № 3: «Свойства арифметического квадратного корня».
-
2. Вычислите:
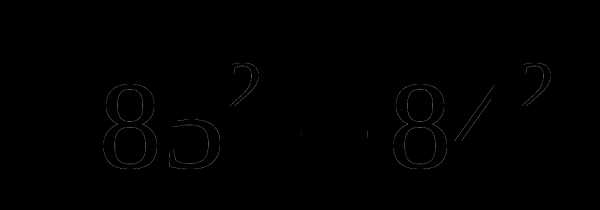
Тема № 3: «Свойства арифметического квадратного корня».
-
2. Вычислите:
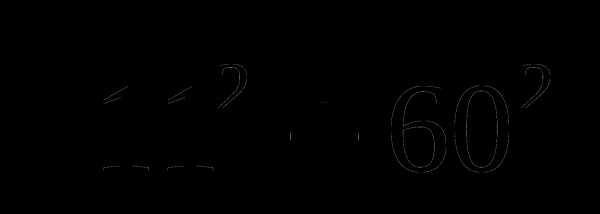
Тема № 3: «Свойства арифметического квадратного корня».
-
2. Вычислите:
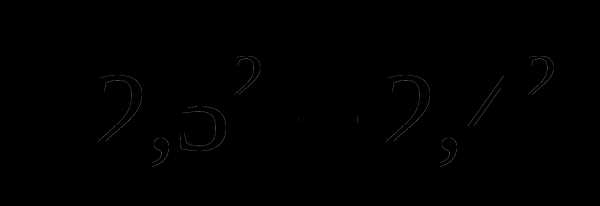

Тема № 3: «Свойства арифметического квадратного корня».
Тема № 4: «Применение свойств арифметического квадратного корня».
Тема № 4: «Применение свойств арифметического квадратного корня».
Тема № 4: «Применение свойств арифметического квадратного корня».
Тема № 4: «Применение свойств арифметического квадратного корня».
Тема № 4: «Применение свойств арифметического квадратного корня».
Тема № 4: «Применение свойств арифметического квадратного корня».
Тема № 4: «Применение свойств арифметического квадратного корня».
Тема № 4: «Применение свойств арифметического квадратного корня».
Тема № 5: «Функция  ».
».
Тема № 5: «Функция  ».
».
Тема № 5: «Функция  ».
».
Тема № 5: «Функция  ».
».
Тема № 6: «Определение квадратного уравнения. Решение неполных квадратных уравнений».
Тема № 6: «Определение квадратного уравнения. Решение неполных квадратных уравнений».
Тема № 6: «Определение квадратного уравнения. Решение неполных квадратных уравнений».
Тема № 6: «Определение квадратного уравнения. Решение неполных квадратных уравнений».
Тема № 6: «Определение квадратного уравнения. Решение неполных квадратных уравнений».
Тема № 6: «Определение квадратного уравнения. Решение неполных квадратных уравнений».
Тема № 7: «Формула корней квадратного уравнения».
Тема № 7: «Формула корней квадратного уравнения».
Тема № 7: «Формула корней квадратного уравнения».
Тема № 7: «Формула корней квадратного уравнения».
Тема № 7: «Формула корней квадратного уравнения».
Тема № 7: «Формула корней квадратного уравнения».
2. При каком m один из корней уравнения равен -2?
Тема № 7: «Формула корней квадратного уравнения».
Тема № 7: «Формула корней квадратного уравнения».
Тема № 8: «Дробно – рациональные уравнения».
Тема № 8: «Дробно – рациональные уравнения».
Тема № 8: «Дробно – рациональные уравнения».
Тема № 8: «Дробно – рациональные уравнения».
Тема № 8: «Дробно – рациональные уравнения».
Тема № 8: «Дробно – рациональные уравнения».
Тема № 9: «Теорема Виета».
1. Найдите сумму и произведение корней уравнения: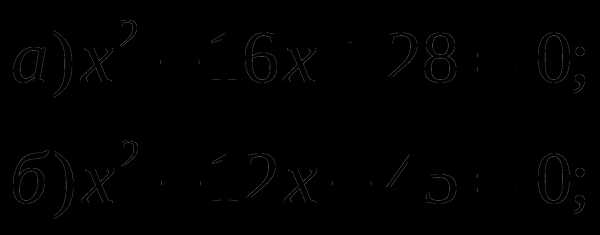
:
Тема № 9: «Теорема Виета».
:
Тема № 9: «Теорема Виета».
:
Тема № 9: «Теорема Виета».
Тема № 10: «Квадратный трехчлен. Разложение квадратного трехчлена на множители».
Тема № 10: «Квадратный трехчлен. Разложение квадратного трехчлена на множители».
Тема № 10: «Квадратный трехчлен. Разложение квадратного трехчлена на множители».
Тема № 10: «Квадратный трехчлен. Разложение квадратного трехчлена на множители».
Тема № 10: «Квадратный трехчлен. Разложение квадратного трехчлена на множители».
Тема № 10: «Квадратный трехчлен. Разложение квадратного трехчлена на множители».
Тема № 11: «Некоторые виды уравнений приводимые к квадратным».

Тема № 11: «Некоторые виды уравнений приводимые к квадратным».
Тема № 11: «Некоторые виды уравнений приводимые к квадратным».
Тема № 11: «Некоторые виды уравнений приводимые к квадратным».
Тема № 11: «Некоторые виды уравнений приводимые к квадратным».
Тема № 11: «Некоторые виды уравнений приводимые к квадратным».
Тема № 12: «Системы линейных неравенств с одной переменной».
Тема № 12: «Системы линейных неравенств с одной переменной».
Тема № 12: «Системы линейных неравенств с одной переменной».
Тема № 12: «Системы линейных неравенств с одной переменной».
Тема № 12: «Системы линейных неравенств с одной переменной».
Тема № 12: «Системы линейных неравенств с одной переменной».
Тема № 13: «Уравнения и неравенства, содержащие выражения под знаком модуля».
Тема № 13: «Уравнения и неравенства, содержащие выражения под знаком модуля».
Тема № 13: «Уравнения и неравенства, содержащие выражения под знаком модуля».
Тема № 13: «Уравнения и неравенства, содержащие выражения под знаком модуля».
Тема № 13: «Уравнения и неравенства, содержащие выражения под знаком модуля».
Тема № 13: «Уравнения и неравенства, содержащие выражения под знаком модуля».
Тема № 14: «Квадратные неравенства».
Тема № 14: «Квадратные неравенства».
Тема № 14: «Квадратные неравенства».
Тема № 14: «Квадратные неравенства».
Тема № 14: «Квадратные неравенства».
Тема № 14: «Квадратные неравенства».
Тема № 15: «Решение неравенств методом интервалов».
Тема № 15: «Решение неравенств методом интервалов».
Тема № 15: «Решение неравенств методом интервалов».
Тема № 15: «Решение неравенств методом интервалов».
Тема № 15: «Решение неравенств методом интервалов».
Тема № 15: «Решение неравенств методом интервалов».
Тема № 15: «Решение неравенств методом интервалов».
Тема № 15: «Решение неравенств методом интервалов».
Тема № 15: «Решение неравенств методом интервалов».
Тема № 16: «Функция и ее график».
-
3. Найдите коэффициенты у функции , зная, что график проходит через точки А(2; -5), В(-1; 16)
Тема № 16: «Функция и ее график».
Тема № 16: «Функция и ее график».
Тема № 16: «Функция и ее график».
Тема № 17: «Уравнение с двумя переменными и его график».
Тема № 17: «Уравнение с двумя переменными и его график».
Тема № 17: «Уравнение с двумя переменными и его график».
Тема № 17: «Уравнение с двумя переменными и его график».
Тема № 18: «Алгебраический метод решения систем уравнений с двумя переменными».
infourok.ru
Карточки по алгебре для 8 класса
Вариант1
-
Упростите выражение:
2.Выполните сложение

3. Решите уравнение
9х + 8х2 = -1.
4. Выполните вычитание
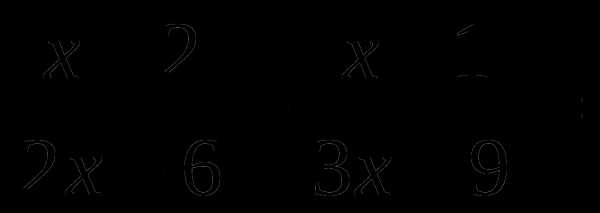
Вариант1
1.Упростите выражение:
2.Выполните сложение

3. Решите уравнение
9х + 8х2 = -1.
4. Выполните вычитание
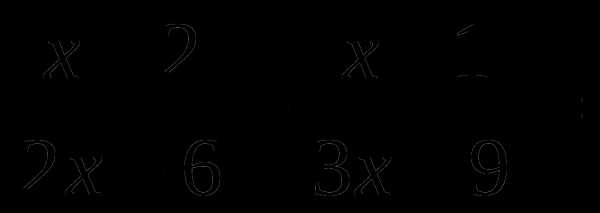
Вариант2
1.Упростите выражение: 2.Выполните вычитание а — 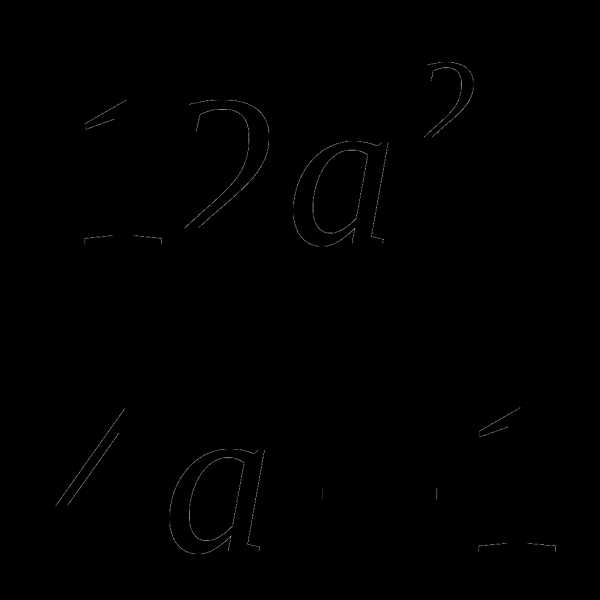
3.Решите уравнение
-
+ 3х2 = 4х.
4.Выполните вычитание
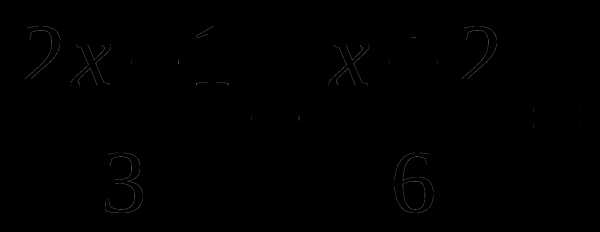
Вариант2
1.Упростите выражение: 2.Выполните вычитание а — 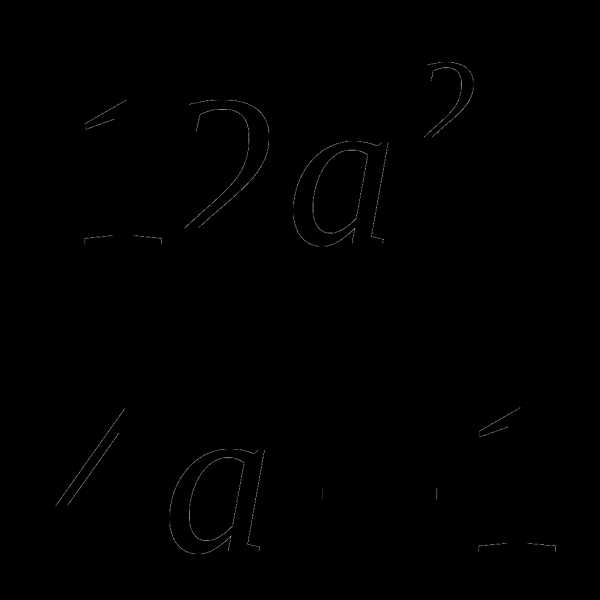
3.Решите уравнение
-
+ 3х2 = 4х.
4.Выполните вычитание
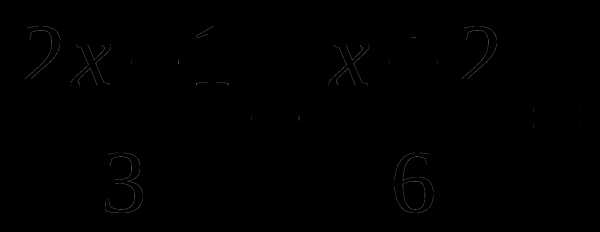
Вариант3
-
Упростите выражение:
-
Выполните сложение
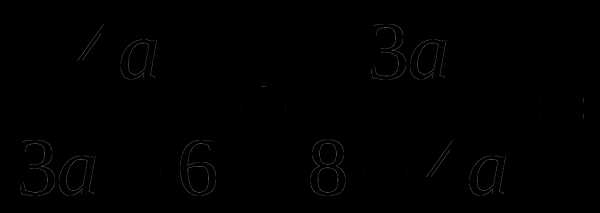
3.Решите уравнение
25 -10х + х2 = 0.
4.Выполните вычитание
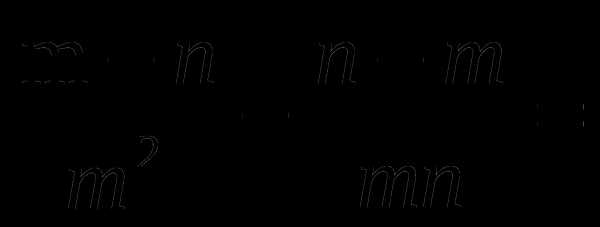
Вариант3
1.Упростите выражение:
2.Выполните сложение
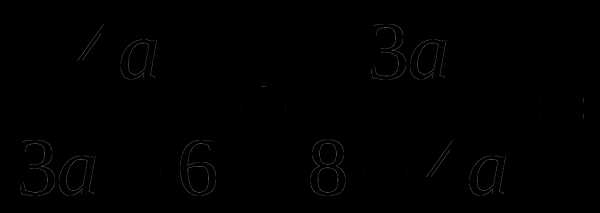
3.Решите уравнение
25 -10х + х2 = 0.
4.Выполните вычитание
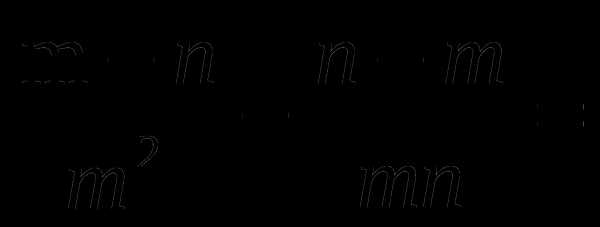
Вариант4
-
Упростите выражение:
-
Выполните вычитание:
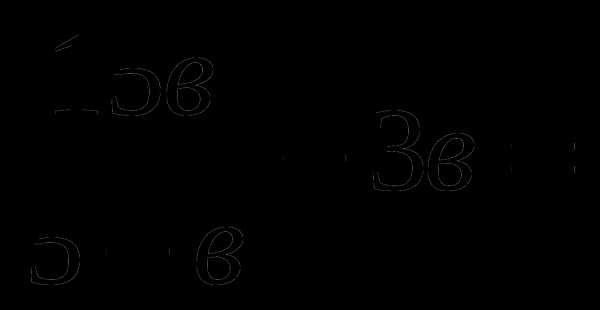
-
Решите уравнение
4х — 4х2 = 1.
4.Выполните вычитание
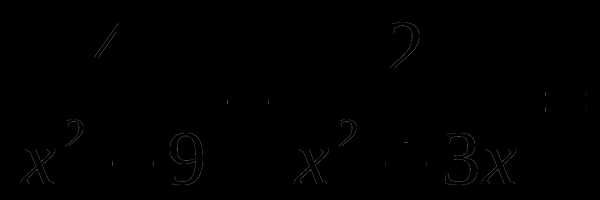
Вариант4
-
Упростите выражение:
-
Выполните вычитание:
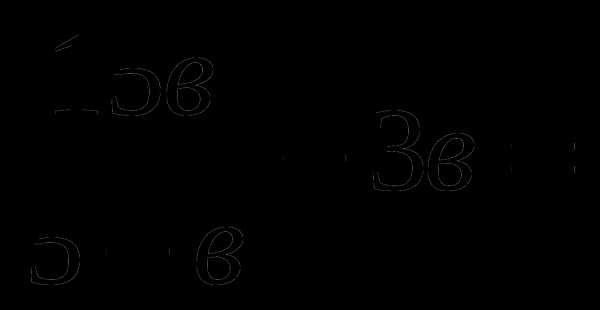
-
Решите уравнение
4х — 4х2 = 1.
4.Выполните вычитание
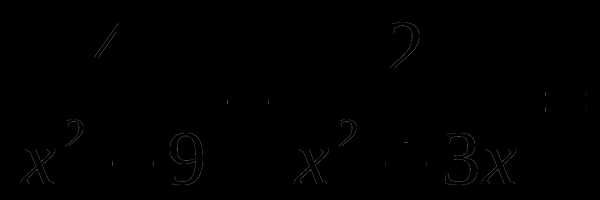
Вариант5
1.Упростите выражение:
2
2.Выполните сложение
3.Решите уравнение
= 2.
4Решите способом подстановки систему уравнений
Вариант 6
1.Решите способом сложения систему уравнений
2.Упростите выражение .
3. Решите уравнение
2х + = 2.
4. Выполните умножение: .
Вариант 7
1.Выполните деление: : .
2. Вычислите:
3. Теплоход, собственная скорость которого 18 км/ч, прошел 50 км по течению реки и 8 км против течения, затратив на весь путь 3 часа. Какова скорость течения реки, если известно, что она не превосходит 10 км/ч?
4. Решите неравенство .
Вариант8
1.Упростите выражение:
2
2.Решите систему неравенств
3.Упростите выражение .
4. Решите уравнение = 2.
Вариант 9
1. Преобразуйте в дробь выражение
2. Решите уравнение = 2.
3. Упростите выражение
.
4. Числитель обыкновенной дроби на 4 меньше ее знаменателя. Если к числителю прибавить 19, а к знаменателю 28, то она увеличится на . Найдите эту дробь.
Вариант10
1. Упростите выражение .
2. Теплоход, собственная скорость которого 18 км/ч, прошел 50 км по течению реки и 8 км против течения, затратив на весь путь 3 часа. Какова скорость течения реки, если известно, что она не превосходит 10 км/ч?
3. Решите систему неравенств
4.Решите неравенство .
infourok.ru
Материал по алгебре (8 класс) на тему: Коррекционные карточки по алгебре 7-8 класс
Коррекционная карточка 7 класс:
Вычисление значений выражений (п.2)
|
Правило |
Примеры |
|
(3m+4x)y, при m=3, x=,y= |
|
|
1. Подставить вместо всех переменных их значения |
|
|
2. Выполнить действия |
Коррекционная карточка 7 класс:
Приведение подобных слагаемых (п.6)
|
Правило |
Примеры |
|
|
3х–7х+9х–15х |
9х–4y+9+5x–3+3y–2x |
|
|
1. Подчеркнуть одинаковыми черточками слагаемые с одинаковой буквенной частью. |
3х–7х+9х–15х= |
9х–4y+9+5x–3+3y–2x= |
|
2. Сложить коэффициенты (вместе со знаками) одинаково подчеркнутых слагаемых. |
=(3+(–7)+9+(–15))х= =(3–7+9–15)х= |
=(9+5+(–2))x+((–4)+3)y+(9+(–3))= =(9+5–2)x+(–4+3)y+(9–3)= |
|
3. Полученный в п.2 коэффициент умножить на общую буквенную часть. |
= –10х |
=12x+(–1)y+6=12x–y+6 |
Коррекционная карточка 7 класс:
Раскрытие скобок, если перед ними стоит знак + или – (п.6)
|
Правило |
Примеры |
|
1а)Если перед скобкой стоит + или не стоит никакой знак, то можно убрать скобки, сохраняя знаки всех слагаемых, стоящих внутри скобок. |
(a–b+c)= a–b+c +(x+y–z)= x+y–z +(–a+c–1)= –a+c–1 |
|
1б)Если перед скобкой стоит –, то можно убрать скобки, меняя знаки всех слагаемых, стоящих внутри скобок, на противоположные (то есть + на –, а – на +) |
–(a–x+c)= –a+x–c –(1–x+a)= –1+x–a |
|
2. Если нужно привести подобные слагаемые. |
Коррекционная карточка 7 класс:
Переместительный, сочетательный и распределительные свойства (п.4,6)
|
Правило |
Примеры |
|
ab=ba (ab)c=a(bc) |
–3,2a.5,6b=(–3,2.5,6)ab= –17,92ab |
|
a(b+c)=ab+ac |
1,3(4–3b)=1,3.4–1,3.3b=5,2–3,9b –4(3a–7b)= –4.3a–(–4).7b= –12a+28b |
Коррекционная карточка 7 класс:
Преобразование выражений (п.6)
|
Правило |
Примеры |
||
|
b–(4–2b)+(3b–1) |
3(6–5x)+17x–10 |
12n+9–6(3n+1) |
|
|
1. Раскрыть скобки |
=b–4+2b+3b–1= |
=3.6–3.5x+17x–10= =18–15x+17x–10= |
=12n+9–6.3n+(–1).n= =12n+9–18n–6= |
|
2. Привести подобные слагаемые. |
=(1+2+3)b+(–4–1)= =6b–5 |
(18–10)+(–15+17)x= =8+2x |
=(12–18)n+(9–6)= = –4n+4 |
Коррекционная карточка 7 класс:
Решение линейных уравнений (п.8)
|
Правило |
Примеры |
||
|
–5х–150=0 |
15(х+2)–19=12х |
6(1+5х)=5(1+6х) |
|
|
1. Если нужно, раскрыть скобки. |
–––––––––––– |
15(х+2)–19=12х 15х+15.2–19=12х 15х+30–19=12х |
6(1+5х)=5(1+6х) 6.1+6.5х=5.1+5.6х 6+30х=5+30х |
|
2. Перенести слагаемые с переменной в левую, а без переменной в правую часть уравнения, меняя их знаки на противоположные (+ на – , а – на +) |
–5х–150=0 –5х=150 |
15х+30–19=12х 15х–12х= –30+19 |
6+30х=5+30х 30х–30х=5–6 |
|
3. Привести в обеих частях уравнения подобные слагаемые. Получится уравнение вида ax=b |
–––––––––––– |
(15–12)х=–30+19 3х= –21 |
(30–30)х=5–6 0х= –1 |
|
4. Если а≠0, то (x=b:a) Если a=0, b≠0, то уравнение не имеет корней Если a=0, b=0, то уравнение имеет бесконечное множество корней, т.е. х может принимать любые значения |
а= –5≠0⇒ x=150:(–5) x= –30 Ответ: х= –30 |
а=3≠0⇒ x= –21:3 x= –7 Ответ: х= –7 |
а=0⇒ решений нет Ответ: решений нет |
Коррекционная карточка 7 класс:
Нахождение x и y по формуле (п.11)
|
Правило |
Примеры |
|||||
|
y=3x–5 |
||||||
|
x |
4 |
|||||
|
y |
–2 |
|||||
а) Подставить вместо х его значение |
x=4 y=3.4–5= |
|||||
|
б) Выполнить действия |
=12–5=7 |
|||||
а) Подставить вместо y его значение |
y= –2 –2=3x–5 |
|||||
|
б) Решить получившееся уравнение |
–2=3x–5 –3x= –5+2 –3x= –3 x= –3:(–3) x=1 |
x |
4 |
1 |
||
|
y |
7 |
–2 |
||||
Коррекционная карточка 7 класс:
Нахождение координат точки пересечения графиков функций (п.15)
|
Правило |
Примеры |
|
Функции заданы формулами. 1. Приравнять правые части данных формул |
y=3x–5 y=4x+3 3x–5=4x+3 |
Получим х–координату точки пересечения |
3x–4x=3+5 –x=8 x= –8 |
|
3. Подставить в одну из формул вместо х найденное в п.2 решение |
y=3.(–8)–5= |
|
4. Вычислить y |
= –24–5= –29 |
|
5. Записать ответ в виде (х;y) |
(–8;–29) |
Коррекционная карточка 7 класс:
Сложение и вычитание многочленов (п.25)
|
Правило |
Примеры |
|
Коррекционная карточка 7 класс:
Умножение одночлена на многочлен (п.26)
|
Правило |
Примеры |
|
Коррекционная карточка 7 класс:
Преобразование выражений (п.25,26)
|
Правило |
Примеры |
|
Коррекционная карточка 7 класс:
Решение уравнений вида (п.26)
|
Правило |
Примеры |
||
|
1. Найти наименьший общий знаменатель (НОЗ) всех дробей, входящих в уравнение |
НОЗ знаменателей 5 и 3: 15 |
НОЗ знаменателей 7 и 1: 7 |
НОЗ знаменателей 4, 12 и 1: 12 |
|
2. Умножить каждую дробь уравнения на НОЗ |
|||
|
3. Если нужно, сократить дроби |
4–3х= –14 |
||
|
4. Решить получившееся уравнение |
9х+15= 5х+5 9х–5х= –15+5 4х= –10 х= –2,5 |
4–3х= –14 –3х= –4–14 –3х= –18 х= –18:(–3) х=6 |
18y+21–7+5y=60 18y+5y= –21+7+60 23y=46 y= 46:23 y=2 |
|
5. Записать ответ |
Ответ: х= –2,5 |
Ответ: х=6 |
Ответ: y=2 |
Коррекционная карточка 7 класс:
Вынесение общего множителя за скобку (п.27)
|
Правило |
Примеры |
||
|
4×2–12x+8a2x3 |
3(b–2c)+x(b–2c) |
5(x–y)+a(y–x) |
|
|
1. Представить каждое слагаемое в виде произведения |
4×2–12x+8a2x3 = = 4xx–4.3x+4.2aaxxx= |
3(b–2c)+x(b–2c)= |
5(x–y)+a(y–x)= =5(x–y)–a(x–y)= |
|
2. Подчеркнуть в каждом слагаемом одинаковые множители |
= 4xx–4.3x+4.2aaxxx= |
=3(b–2c)+x(b–2c)= |
=5(x–y)–a(x–y)= |
|
3.Записать подчеркнутый одинаковый множитель за скобками 4. В скобках записать слагаемые без подчеркнутого множителя |
= 4x(x–3+2aaxx)= = 4x(x–3+2a2x2) |
=(b–2c)(3+x) |
=(x–y)(5–a) |
Коррекционная карточка 7 класс:
Умножение многочлена на многочлен (п.28)
|
Правило |
Примеры |
|
(2x–y)(4x+3y)= =2x.4x+2x.3y+(–y).4x+(–y).3y= =8×2+6xy –4xy–3y2=8×2+(6–4)xy–3y2= =8×2+2xy–3y2 (2a–3)(5–a)= =2a.5–2a.a+(–3).5–(–3).a= =10a–2a2–15+3a=(10+3)a–2a2–15= = –2a2+13a–15 |
Коррекционная карточка 7 класс:
Квадрат суммы, квадрат разности (п.31, 32)
|
Правило |
Примеры |
||||
|
(I ± II)2 = I2 ±2. I . II + II2 |
(I ± II)2 |
I |
II |
I2 ±2. I . II + II2 |
|
|
(3x+4)2 |
3x |
4 |
(3x)2+2.3x.4+42 |
||
|
(3x–4)2 |
3x |
4 |
(3x)2–2.3x.4+42 |
||
|
Краткая запись |
(3x+4)2=(3x)2+2.3x.4+42=9×2+24x+16 (3x–4)2=(3x)2–2.3x.4+42=9×2–24x+16 |
||||
|
I2 ±2. I . II + II2 = (I ± II)2 |
|||||
|
25×2+10xy+y2 = ?
II2 =y2 ⇒ II = y
10xy=10xy – верно ⇒ можно воспользоваться формулой 25×2+10xy+y2 = (5x+y)2 9×2+12x+16 = ?
II2 =16 ⇒ II = 4
24x=12x – неверно ⇒ воспользоваться формулой нельзя |
25×2–10xy+y2 = ?
II2 =y2 ⇒ II = y
10xy=10xy – верно ⇒ можно воспользоваться формулой 25×2–10xy+y2 = (5x–y)2 9×2–12x+16 = ?
II2 =16 ⇒ II = 4
24x=12x – неверно ⇒ воспользоваться формулой нельзя |
||||
nsportal.ru
Тренажёр по алгебре (8 класс) на тему: Карточки по теме «Квадратные уравнения» алгебра 8 класс
Карточка «Выделение полного квадрата» Алгебра 8.
Выделить полный квадрат из квадратного трехчлена .
|
|
Преобразование (логические шаги): |
Формулы : |
|
1. |
Вынесем за скобки коэффициент при |
|
|
2. |
Выражение представим в виде (удвоенное произведение числа на число х): |
|
|
3. |
Выражение дополним до полного квадрата. Для этого к выражению, стоящему в скобках, прибавим и вычтем число , являющееся квадратом числа (выражение от этого не изменится): |
|
|
4. |
Заметим, что , поэтому : |
|
|
5. |
Итак, |
. |
Пример : Выделить полный квадрат из выражения: .
Решение:
= ,
.
Логические шаги:
1. Вынесем за скобки коэффициент при .
2. Выражение 2 х запишем в виде 2 · х · 1(удвоенное произведение числа х на число 1).
3. Выражение дополним до полного квадрата — прибавим и вычтем по 1
(выражение от этого не изменится).
4. Произведем замену выражения + 1 выражением .
Ответ: = 2- 5.
Выделить полный квадрат из выражения (выполнить самостоятельно) :
а) б) .
Квадратное уравнение общего вида Алгебра 8.
Так называется уравнение = 0, где а ≠ 0 и а ≠ 1.
1. Разделим обе части уравнения на а: .
2. Выделим полный квадрат и получим: или
, обозначим D = , тогда , если D > 0,
то .
3. D = — называется дискриминантом уравнения = 0 ( 1) :
А) Если D > 0, то уравнение ( 1) имеет два различных действительных корня:
, .
Б) Если D = 0, то уравнение ( 1) имеет один действительный корень или
два равных корня: .
В) Если D , то уравнение ( 1) не имеет действительных корней.
Карточка «Решение квадратных уравнений» Алгебра 8
1. Решить уравнения: а) ; б) .
2. Использую понятие дискриминанта квадратного уравнения, определить, не решая
уравнения, имеет ли оно корни и если да, то какие (два различных действительных
корня, два равных действительных корня ):
а) ; б) ;
в) ; г) .
Приведенное квадратное уравнение. Алгебра 8
Уравнение — называется приведенным, если а = 1.
Уравнение вида , где p и q – числа, называется приведенным.
1. Назвать уравнения, которые являются приведенными квадратными уравнениями:
а) ; в) ;
б) ; г) .
2. Вывести формулу корней приведенного квадратного уравнения .
Решение:
.
Имеем: ; .
Корни приведенного квадратного уравнения .
Имеем приведенное квадратное уравнение
Найти сумму и произведение его корней.
Решение: 1. В заданном уравнении p = — 5 , q = 6.
Применим формулу .
Имеем: , х = 2, х = 3.
2. Найдем сумму и произведение корней:
.
Вывод: Для данного уравнения мы получили, что сумма корней его равна второму коэффициенту, взятому с противоположным знаком, а произведение – свободному члену.
Что это – простое совпадение или закономерность?
Теорема Виета.
Пусть дано приведенное квадратное уравнение вида
Тогда , .
Найдем сумму корней. Легко заметить, что .
Найдем произведение корней :
() · () = .
Откуда q.
Значит, для приведенного квадратного уравнения где — корни данного уравнения, верно :.
Карточка №1. «Приведенное квадратное уравнение» Алгебра 8
Не решая данных уравнений, определить их корни:
а) ; б) ; в) .
Ответы записать в таком виде:
1) 1 и 4; 2) 1 и – 4; 3) — 1 и 4; 4) — 1 и – 4; 5) нет действительных корней.
Карточка №2. «Приведенное квадратное уравнение» Алгебра 8
Не решая данных уравнений, определить их корни:
а) ; б) ; в) .
Ответы записать в таком виде:
1) 1 и 4; 2) 1 и – 4; 3) — 1 и 4; 4) — 1 и – 4; 5) нет действительных корней.
Теорема, обратная теореме Виета. Алгебра 8
● Если даны два действительных числа , такие, что , то
эти числа являются корнями квадратного уравнения .
Задача. Составить квадратное уравнение, корнями которого были бы числа 3 и – 5 .
Решение:
1. Приведенное квадратное уравнение имеет вид :
2. Применим теорему, обратную теореме Виета:
3 + (- 5) = — p, 3 · ( — 5) = q. Отсюда p = 2; q = — 15.
3. Составим уравнение:
Ответ: .
Карточка №3. «Приведенное квадратное уравнение» Алгебра 8
Составить квадратное уравнение, корнями которого были бы числа: А) 2 и 3; Б) 6 и – 2.
Решение:
1. Запишем приведенное квадратное уравнение :
2. Применим теорему, обратную теореме Виета: ; …
3. Составим уравнение: ….
Карточка №4. «Приведенное квадратное уравнение» Алгебра 8
Составить квадратное уравнение, корнями которого были бы числа: А) — 5 и — 3; Б) 1 и – 2.
Решение:
1. Запишем приведенное квадратное уравнение :
2. Применим теорему, обратную теореме Виета: ; …
3. Составим уравнение: ….
Ответ: 1а) ; 1б) . 2а) ; 2б) .
Разложение квадратного трехчлена на линейные множители. Алгебра 8
Квадратный трехчлен тогда и только тогда представим в виде произведения линейных множителей с действительными коэффициентами:
=
когда дискриминант D = этого квадратного трехчлена неотрицателен
( здесь и — корни трехчлена ).
Пример.
Разложить на линейные множители выражение: .
Решение: 1. D = , D = , D > 0.
2. Выносим коэффициент при за скобку:
.
3. Находим корни уравнения: :
.
4. Запишем: = .
Ответ: = или .
nsportal.ru
|
РАЗРАБОТКИ |
8 классВ категории разработок: 38 Фильтр по целевой аудитории — Целевая аудитория -для 1 классадля 2 классадля 3 классадля 4 классадля 5 классадля 6 классадля 7 классадля 8 классадля 9 классадля 10 классадля 11 классадля учителядля классного руководителядля дошкольниковдля директорадля завучейдля логопедадля психологадля соц.педагогадля воспитателя В разработке предоставлены таблички, с помощью которых дети могут быстро усвоить и запомнить, а учитель проверить навыки работы со свойствами площади, с формулами площадей прямоугольника, параллелограмма, трапеции и треугольника, и с теоремой Пифагора. Целевая аудитория: для 8 класса Восемь задач, при решении каждой необходимо знание теоремы Пифагора, формулы площади треугольника, свойств точки пересечения медиан треугольника. Отдельно в таблице предоставлены ответы к задачам. Целевая аудитория: для 8 класса Зачетная работа по теме «Четырехугольники» содержит 4 варианта, состоящие из 10 вопросов. Последний вопрос требует доказательства одного свойства или признака параллелограмма. Работа рассчитана на 15 минут урока. Составлены тестовые вопросы к УМК Л.С.Атанасян и другие. Целевая аудитория: для 8 класса Тесты по теме «Параллелограмм» входят в серию тематических тестов для проведения зачетов в 8 классе. В тесты включены задачи, которые встречаются в открытом банке задач ГИА и ЕГЭ. Создана демоверсия и 12 вариантов тестов с ответами, которые могут быть использованы для зачета по теме «Параллелограмм» в 8 классе, а также для подготовки к ГИА и ЕГЭ. В приложении опорный конспект по теме «Параллелограмм», который ребята заполняют сами по мере прохождения материала по принципу «заполни пропущенные места», а на зачете удобно пользоваться этой заготовкой для проверки теоретических знаний учащихся. Целевая аудитория: для 8 класса Тесты по теме «Трапеция» входят в серию тематических тестов для проведения зачетов в 8 классе. В тесты включены задачи, которые встречаются в открытом банке задач ГИА и ЕГЭ. Создана демоверсия и 18 вариантов тестов с ответами, которые могут быть использованы для зачета по теме «Трапеция» в 8 классе, а также для подготовки к ГИА и ЕГЭ. В приложении опорный конспект по теме «Трапеция», который ребята заполняют сами по мере прохождения материала по принципу «заполни пропущенные места», а на зачете удобно пользоваться этой заготовкой для проверки теоретических знаний учащихся. Целевая аудитория: для 8 класса Итоговый тест по математике за курс 8 класса. Составлен по принципу ГИА. Можно использовать как вводный тест в начале 9 класса. При проведении теста использую бланк для внесения ответов. Целевая аудитория: для 8 класса
Здесь представлены карточки для проведения самостоятельной работы по алгебре в 8 классе по теме «Определение квадратного уравнения». Два варианта. Предполагается двусторонняя печать. Целевая аудитория: для 8 класса Тестовые задания по математике в 4 вариантах с ответами (8 класс, 1 полугодие) содержат 7 заданий по алгебре и 3 задания по геометрии в каждом варианте. Эти задания составлены автором на основе стабильных учебников математики «Алгебра 8» под. ред. С.А. Теляковского и «Геометрия 7-9» А.В. Погорелова. Предназначены для проверки уровня обученности учащихся 8 классов и обеспечивают простоту проверки ответов, позволяя выявить пробелы в знаниях учеников. Тесты можно использовать при повторении материала в рамках подготовки к ГИА. Целевая аудитория: для 8 класса Тест по теме: Квадратный корень. Тест содержит 10 задач с выбором ответа, составлен в двух вариантах. Ключи. Целевая аудитория: для 8 класса Задачи представлены в 2-х вариантах по 10 задач в каждом. Могут быть использованы и в текущей работе, и при подготовке к ГИА. Есть ответы. Целевая аудитория: для 8 класса |
Конкурсы Диплом и справка о публикации каждому участнику! |
www.uchportal.ru