Помогите, пожалуйста:) Ответы на вопросы по геометрии 8 класс к главе 7
Помогите, пожалуйста:)
Ответы на вопросы по геометрии 8 класс к главе 7
Ответы:
1)Отношением двух отрезков называется величина,характеризующая какую часть один отрезок составляет от другого отрезка.
2) Пропорциональные отрезки — отрезки, для длин которых выполняется пропорция.
Отношением отрезков AB и CD называется отношение их длин.
3) Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого.
4) Отношение площадей 2 подобных треугольников равно квадрату коэффициента подобия.
Пусть треугольники ABC и А1В1С1 подобны, причем коэффициент подобия равен k O, обозначим буквами S и S1 площади этих треугольников. Так как A=A1, то
S/S1 = AB*AC/A1B1*A1C1
(по тереме об отношении площадей треугольника) . По формулам имеем: АВ/А1В1 = k, AC/A1C1 = k
поэтому
S/S1 = k2
Теорема доказана.
5) Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Доказательство. Пусть у треугольников ABC и A1B1C1 ∠ A = ∠ A1, AB = A1B1, AC = A1C1.
Пусть есть треугольник A1B2C2 – треугольник равный треугольнику ABC, с вершиной B2, лежащей на луче A1B1, и вершиной С2 в той же полуплоскости относительно прямой A1B1, где лежит вершина С1.
Так как A1B1=A1B2, то вершины B1 и B2 совпадают.
Так как ∠ B1A1C1 = ∠ B2A1C2, то луч A1C1 совпадает с лучом A1C2.
Так как A1C1 = A1C2, то точка С1 совпадает с точкой С2. Следовательно, треугольник A1B1C1 совпадает с треугольником A1B2C2, а значит, равен треугольнику ABC. Теорема доказана.
6) Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Доказательство:
Рассмотрим треугольники АВС и А1В1С1, у которых АВ=А1В1, угол А= углу А1, угол В=углу В1. Докажем, что треугольник АВС=треугольнику А1В1С1.
Наложим треугольник АВС на треугольник А1В1С1, так, чтобы вершина А совместилась с вершиноу А1, сторона АВ совместилась с равной ей стороной А1В1, а вершины С и С1 оказались по одну сторону от прямой А1В1.
Так как угол А= углу А1 и угол В=углу В1, то сторона АС наложится на луч А1С1, а сторона ВС- на луч В1С1. Поэтому вершина С — общая точка сторон АС и ВС — окажется лежащей как на луче А1С1, так и на луче В1С1 и, следовательно, совместятся с общей точкой этих лучей — вершиной С. Значит совместятся стороны АС и А1С1, АС и В1С1.
Итак, треугольник АВС и А1В1С1 полностью совместятся, поэтому они равны. Теорема доказана.
7)Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.
Доказательство.
Пусть треугольники ABC и A1B1C1 такие, что AB=A1B1, AC=A1C1, BC=B1C1. Требуется доказать, что треугольники равны.
Допустим, что треугольники не равны. Тогда ∠ A ≠ ∠ A1, ∠ B ≠ ∠ B1, ∠ C ≠ ∠ C1 одновременно. Иначе треугольники были бы равны по первому признаку.
Пусть треугольник A1B1C2 – треугольник, равный треугольнику ABC, у которого вершина С2 лежит в одной полуплоскости с вершиной С1 относительно прямой A1B1.
Пусть D – середина отрезка С1С2. треугольники A1C1C2 и B1C1C2 равнобедренные с общим основанием С1С2. Поэтому их медианы A1D и B1D являются высотами. Значит, прямые A1D и B1D перпендикулярны прямой С1С2. Прямые A1D и B1D не совпадают, так как точки A1, B1, D не лежат на одной прямой. Но через точку D прямой С1С2 можно провести только одну перпендикулярную ей прямую. Мы пришли к противоречию. Теорема доказана.
8) Средняя линия треугольника— отрезок, соединяющий середины двух сторон этой фигуры,она параллельна третьей стороне и равна её половине. Дано:
DABC, ED — средняя линияДоказать:
EDчч AB,
ED=1/2 ABДоказательство:
Пусть DE-средняя линия DABC.
Через (Ч) D проведем прямую b, bччAB.
По теореме Фалеса b З AC=E — в его середине, т. е. DEМb. Следовательно DE чч AB.
Проведем теперь среднюю линию DF ЮDFчч АС.
DFчч АС, DE чч ABЮ четырехугольник AEDF — параллелограмм.
По свойству параллелограмма ED=AF, а так как AF=FB (по построению DF — средняя линия) , то ED=1/2 AB.
Теорема доказана.
9)оказательство9Обозначим буквой О точку пересечения двух медиан АА1 и ВВ1 треугольника АВС и проведём среднюю линию А1В1 этого треугольника (рис. 1). Отрезок А1В1 параллелен стороне АВ (по теореме о средней линии треугольника) , поэтому 1= 2 и 3= 4. Следовательно, треугольники АОВ и А1ОВ подобны по двум углам, и, значит их стороны пропорциональны, т. е. равны отношения сторон АО и А1О, ВО и В1О, АВ и А1В. Но АВ=2А1В1, поэтому АО=2А1О и ВО=2В1О. Таким образом, точка О пересечения медиан ВВ1 и СС1 делит каждую из них в отношении 2:1, считая от вершины. Теорема доказана.
10) Треугольник АВС , угол С — 90Перпендикуляр СД на АВ (гипотенуза)Треугольник АВС подобен треугольнику АСД по общему углу А (если в прямоугольном теругольнике острый угол одного равен осторому углу другого то треугольники подобны )Треугольник АВС подобен треугольнику СДВ по общему углу ВЕсли два треугольника подобны между содой то третий им подобен.
Дальше устала писать, сорь)
cwetochki.ru
ГДЗ и Решебник для 8 класса по Геометрии на Мегарешеба ком
-
- Решебники, ГДЗ
-
11 класс
- Русский язык
- Английский язык
- Немецкий язык
- Математика
- Алгебра
- Геометрия
- Химия
- Физика
- История
- Биология
- Информатика
- Белорусский язык
- Литература
- География
- Обществознание
- Астрономия
-
10 класс
- Русский язык
- Английский язык
- Немецкий язык
- Математика
- Алгебра
- Геометрия
- Химия
- Физика
- История
- Биология
- Информатика
- Белорусский язык
- Литература
- ОБЖ
- География
- Обществознание
- Испанский язык
- Кубановедение
-
9 класс
- Русский язык
- Английский язык
- Немецкий язык
- Математика
- Алгебра
- Геометрия
- Химия
- Физика
- История
- Биология
- Черчение
- Информатика
- Белорусский язык
- Литература
- Французский язык
- ОБЖ
- География
- Обществознание
- Испанский язык
- Искусство
- Кубановедение
-
8 класс
- Русский язык
- Английский язык
- Немецкий язык
- Математика
- Алгебра
- Геометрия
- Химия
- Физика
- История
- Биология
- Черчение
- Информатика
- Белорусский язык
- Литература
- Французский язык
- ОБЖ
- География
- Обществознание
- Экология
megaresheba.com
❺ ГДЗ (решебник) — геометрия 8 класс по учебнику Атанасян, Бутузов, Кадомцев, 2009
Авторы учебника: Атанасян, Бутузов, Кадомцев
Год учебника: 2009
Пособие содержит много оригинальных приёмов изложения, что делает его доступным для понимания учащимися. Здесь представлены различные типы задач. Одни задачи рассматривают тему каждого параграфа. Вторые задачи являются дополнительными к теме. Третьи задачи, с более высоким уровнем сложности, рассчитаны на детей, которые проявляют высокий интерес к предмету.
Наличие иллюстраций к заданиям в какой-то мере облегчает понимание задачи. Наглядное изображение всегда способствует быстрому решению.
Пользуясь изданием необходимо понимать, что это для самопроверки, а не для бездумного списывания.
Ответы по геометрии 8 класс Атанасян:
Глава V. Четырехугольники:
Развернуть все
Глава VI. Площадь:
Глава VII. Подобные треугольники:
Глава VIII. Окружность:
Глава IX. Векторы:
Задачи повышенной трудности:
← Предыдущая
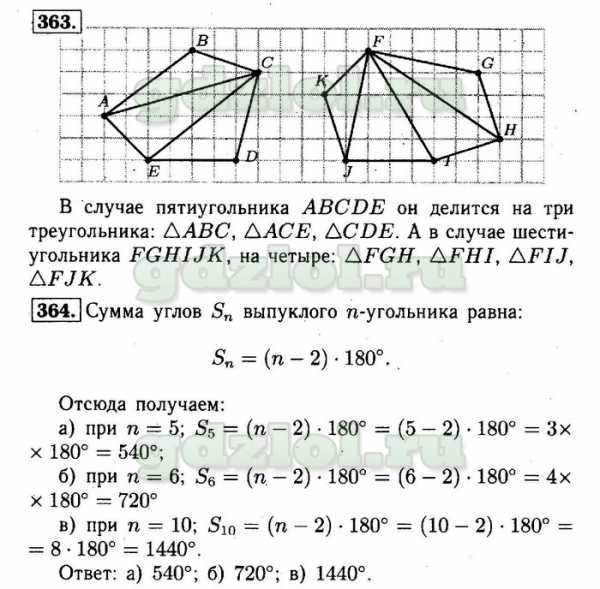
363-364
Следующая →
Посмотреть полный решебник
Понравился материал? Загрузка…
otlgdz.online
ГДЗ по геометрии для 8 класса Бутузов В. Ф. МГУ
ГДЗ от Путина
Найти
-
-
1 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Природоведение
- Основы здоровья
- Музыка
- Литература
- Окружающий мир
- Человек и мир
-
2 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Белорусский язык
- Украинский язык
- Информатика
- Природоведение
- Основы здоровья
- Музыка
- Литература
- Окружающий мир
- Человек и мир
- Технология
-
3 класс
- Математика
- Английский язык
- Русский язык
-
1 класс
gdzputina.ru
ГДЗ по Геометрии за 8 класс А.Д. Александров, А.Л. Вернер, В.И. Рыжик
Решебники, ГДЗ
-
1 Класс
-
Математика
-
Русский язык
-
Английский язык
-
Информатика
-
Немецкий язык
-
Литература
-
Человек и мир
-
Природоведение
-
Основы здоровья
-
Музыка
-
Окружающий мир
-
-
2 Класс
-
Математика
-
Русский язык
-
Белорусский язык
-
Английский язык
-
Информатика
-
Украинский язык
-
Немецкий язык
-
Литература
-
Человек и мир
-
Природоведение
-
Основы здоровья
-
Музыка
-
Окружающий мир
-
Технология
-
-
3 Класс
-
Математика
-
Русский язык
-
Белорусский язык
-
Английский язык
-
Информатика
-
Украинский язык
-
Немецкий язык
-
Литература
-
Человек и мир
-
Музыка
-
Окружающий мир
-
Испанский язык
-
-
4 Класс
-
Математика
-
Русский язык
-
Белорусский язык
-
Английский язык
-
Информатика
-
Украинский язык
-
Немецкий язык
-
Литература
-
Человек и мир
-
Основы здоровья
-
megaresheba.ru
ГДЗ по геометрии для 8 класса А.Г. Мерзляк Алгоритм успеха
ГДЗ от Путина
Найти
-
-
1 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Природоведение
- Основы здоровья
- Музыка
- Литература
- Окружающий мир
- Человек и мир
-
2 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Белорусский язык
- Украинский язык
- Информатика
- Природоведение
- Основы здоровья
- Музыка
- Литература
- Окружающий мир
- Человек и мир
- Технология
-
3 класс
- Математика
- Английский язык
- Русский язык
-
1 класс
gdzputina.ru
ГДЗ по геометрии 8 класс
Геометрия 8 класс. Л.С.Атанасян
Автор: Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Домашняя работа по геометрии за 8 класс.
Учебник: К учебнику «Геометрия, 7-9 класс». Учебник для общеобразовательных учреждений.
Издательство: М.: Просвещение, 2003-2012 год.
Ответы на вопросы к учебнику Л.С.Атанасян
Выберите из задачника номер упражнения, чтобы просмотреть решение.
Глава V. Четырехугольники
§ 1. Многоугольники
§ 2. Параллелограм и трапеция
§ 3. Прямоугольник, ромб, квадрат
Глава VI. Площадь
§ 1. Площадь многоугольника
§ 2. Площади параллелограма, прямоугльника и трапеции
§ 3. Теорема Пифагора
Глава VII. Подобные треугольники
§ 1. Определение подобных треугольников
§ 2. Признаки подобия треугольников
§ 3. Применения подобия к доказательству теорем и решению задач
§ 4. Соотношения между сторонами и углами прямоугольного треугольника
Глава VIII. Окружность
§ 1. Касательные окружности
§ 2. Центральные и вписанные углы
§ 3. Четыре замечательные точки треугольника
§ 4. Вписанная и описанная окружности
Глава IX. Векторы
§ 1. Понятие вектора
§ 2. Сложение и вычитание векторов
§ 3. Умножение вектора на число. Применение векторов к решению задач
Учебник по геометрии Л.С. Атанасяна, крупнейшего отечественного математика, внесшего огромный вклад с советскую и российскую науку, давно стал настоящей классикой. В нем доступно и информативно излагается материал, предлагаются к решению задачи различной степени сложности. Занимаясь по нему системно, восьмиклассники с успехом осваивают премудрости подобия треугольников или же применения вектора для решения задач. Однако определенному проценту школьников изучение геометрии в 8 классе дается с трудом. Этому есть объективные причины. Возможно, был плохо усвоен материал предыдущего года или проявлено недобросовестное отношение к самостоятельным занятиям. Возможно и банальное – школьник является очевидным гуманитарием, которому любые точные науки в тягость.
Однако учиться надо и делать это нужно качественно, ведь учебный год закончится прохождением ГИА, куда геометрия входит в обязательном порядке. Предлагаем вниманию восьмиклассников онлайн решебник по геометрии 8 класса к учебнику Л.С. Атанасяна. Воспользовавшись им, можно еще раз изучить пройденный в классе материал, подробно рассмотреть разобранные на уроке задания, попробовать самостоятельно решить аналогичные.
Решебник – отличное сочетание теоретического и практического материала. На примере разбора задач можно проследить основной алгоритм из решения, опробовать его при работе над домашними упражнениями. На примере предлагаемых чертежей и схем можно понять логику построения изображений геометрических фигур и соотношений предметов, увидеть, что нужно и важно учитывать при решении тех или иных стереометрических задач.
Решебник станет «палочкой-выручалочкой» и для родителей. Давно позабыв премудрости геометрии, родным восьмиклассника фактически приходится изучать материал заново. Помочь в этом смогут ГДЗ. Контроль со стороны взрослых зачастую необходим, чтобы дети не просто списывали готовые решения, а попытались продумать, как был получен тот или иной ответ, какие были использованы методы и закономерности.
Незаменимыми ГДЗ по геометрии за 8 класс станут и при подготовке к ЕГЭ. Можно будет вернуться к пройденному материалу, еще раз уточнить забытые или непонятые детали, что поможет увеличить шансы на успешную сдачу единого государственного экзамена.
www.ggdz.ru