Домашняя зачетная работа по алгебре 8 класс – Домашние зачетные работы по алгебре для 8 класса скачать

Тест по алгебре (8 класс) на тему: Домашние зачетные работы по алгебре для 8 класса

По теме: методические разработки, презентации и конспекты

Контрольные работы по алгебре для 8 класса

Контрольгые работы №1, №2,№5…

Задания для подготовки к первой части годовой контрольной работы по алгебре для 8 классов.

В данном материале предлагается задания для подготовки учащихся 8 классов к написанию годовой контрольной работы по алгебре. Ученики изучали алгебру по учебнику А.Г. Мордковича  «Алгебра. 8 класс…

Задания для подготовки ко второй части годовой контрольной работы по алгебре для 8 классов.

В материале предлагаются  подготовительные задания по алгебре 8 класса.Ученики изучали алгебру по учебнику  А.Г. Мордковича «Алгебра.8 класс».Задания ориенированы на учащихся, имеющий повыше…

Самостоятельные работы по алгебре для 8 класса по теме «Рациональные дроби».

Многовариативные обучающие самостоятельные работы. Их основу составляет одно задание. Индивидуальная ориентация задания на различные группы учащихся осуществляется с помощью специальных указаний….

Разноуровневая домашняя контрольная работа по геометрии для 8 класса

Публикация содержит задания домашней контрольной работы по теме «Четырехугольники. Площади. Теорема Пифагора». Задания рассчитаны на 3 уровня усвоения материала…

Зачетная работа по алгебре в 8 классе по теме: преобразование выражений, содержащих квадратный корень.

Зачетная работа по алгебре в 8 классе по теме: преобразование выражений, содержащих квадратный корень….

Проверочная работа по алгебре для 8 класса по теме «Квадратные уравнения»

Проверочная работа направлена на проверку  знаний по теме «Квадратные уравнения».Работу можно проводить в качестве зачета в конце изучения темы, а можно как дополнительное задание для учеников.Ма…

nsportal.ru

Домашние зачетные работы по алгебре. 8 класс

Домашние зачетные работы по алгебре

для 8 класса по темам:

Преобразования алгебраических дробей

Арифметический квадратный корень

Функции и графики

Преобразование графиков функций

Решение квадратных уравнений

Решение линейных неравенств

Решение квадратных неравенств

Решение систем неравенств

Решение систем квадратных неравенств

Решение систем уравнений

Разработано учителем математики МОУ «СОШ» п. Аджером Корткеросского района Республики Коми

Мишариной Альбиной Геннадьевной

Домашняя зачетная работа №1.

Преобразования алгебраических дробей.

1). Упростить выражения:

а) б) — в) — г) — д) +

е) — ж) · з) · и) ·

к) 27а³ : л) : м) : н) ( +) ·

2). Выполнить действия:

а) (— ) : (+ ) б) (+ ) :

в) (— ) : г) · —

д) (1 —) : (- )+ 1

3). Упростить выражения:

а) : + б) (- ) : (+ )

в) : (- — ) г) ( у —+ х ) : ( у-х)

д) (+ )²– (—)² е) ж)

4). Решить уравнение:

а) = б) = в) += 2 г) = х

д) = е) = ж) +=3з) — =

и) += 0к)+—= 0л) ——=0

Домашняя зачетная работа №2.

Арифметический квадратный корень

1). Вынести множитель из-под знака корня:

а) б) в) г) д) е)

ж) з) и) к) л)

2). Внести множитель под знак корня:

а) а²в б) 3ху³ в) авс г) 2х²у д) 20с³ахе) хус³

3). Упростить выражение:

а) 2- + б) 2- + в) +- г) — 3+

д) 2· 5· е) 3· · 4 ж) · · з) ·· и)

к) л) ( )⁴м) ··- 8 н) ·· — 7 о) ( )⁶ п) ( )⁴

п) (3 — )²р) (4 — )²с) (3 — 2 )²т) (4 — 3 )²у) (3 — )²ф) (+ )²

х) ч) ц) щ) ы) ю)

4). Используя определение квадратного корня, решите уравнение: а) = 3 б) = 2 в) =0 г) =5

д) =13 е) = 24 ж) = 2 з) = 8

и) =8 к) =12 л) =0 м) = 7

Домашняя зачетная работа №3.

Функции и графики

1). Построить графики функций:

а) у = б) у = — в) у = г) у = — д) у = + 1 е) у = -+ 2

ж) у = — 4 з) у = х² – 4 и) у = – х² + 4 к) у = — 2х²л) у = 4х²м) у = х² – 2х – 3

н) у = х² + 2х — 3 о) у = -х² + 4х + 5 п) у = х² + 4х – 5 р) у = х² – 6х + 5 с) у = -х² + 6х – 5

т) у = х² + 4х – 3 у) у = — х² + 4х — 3 ф) у = х² – 4х х) у = 2х — х²ч) у = 4х — х²

2). Решить графически уравнение:

а) — 8 + 1,5х = 0 б) х² + = 0 в) х² — — 2 = 0 г) — х² = 0

д) + х² = 0 е) = 2х – х²ж) = (х -1)²з) 5х² = 5х — 6 и) |х| — 3 = —

к) — — 1 = л) |х| + 2 = (х — 2)²м) — + 4 = 3х²н) — 5 = — х

3). Решить графически систему уравнений:

а) ху + 3 = 0 б) у + 2х² = 3 в) ху – 8 = 0 г) ху + 4 = 0 д) ху = — 4

у = х² + 2 у = |х| у = у = (х — 1)² у – х² = 1

4). Построить график функции:

а) у = 3 + 2х, если х < 0 б) у = |х|, если х < 2 в) у = 2 – 2х², если -1 ≤ х ≤ 1

www.prodlenka.org

Зачётная работа по алгебре 8 класс

ЗАЧЁТНАЯ РАБОТА

Тема: «Арифметический квадратный корень»

8 класс

(теория и практика)

подготовил: ПрокопьеваС.Р.

МБОУ «Сятра- Лапсарская ООШ»

2017г.

Зачётная работа по теме «Арифметический квадратный корень »

8 класс

Вариант 1

ТЕОРИЯ:

1. Что называется квадратным корнем?

2. Что называется арифметическим квадратным корнем?

3.Какие свойства квадратного корня вы знаете?

4. Как называется знак корня?

5.Какая функция связана √ ?

6. Что является графиком этой функции?

ПРАКТИКА:

1. Найдите значение арифметического квадратного корня:

а) ;в) ;д) .

2.Вычислите:

а) – б) — ; в) ∙

3.Решить уравнение:

а) х² = 25; б)2х² + 32 =0.;

в) х² – 0,4 = 0,09; г) 3х² = 27.

Вариант 3

ТЕОРИЯ:

1. Что называется квадратным корнем?

2. Что называется арифметическим квадратным корнем?

3.Какие свойства квадратного корня вы знаете?

4. Как называется знак корня?

5.Какая функция связана √ ?

6. Что является графиком этой функции?

ПРАКТИКА:

1. Найдите значение арифметического квадратного корня:

а) ;в) ;д) .

2.Вычислите:

а) – б) +;

в)( )²+ ; г) — 5( )² .

3.Решить уравнение:

а)0,3 х² = 0,075; б) -2х² + 32 =0.;

в)( х-3)² – 0,4 = 0,09; г) 3х³ – 3х = 27.

Вариант 2

ТЕОРИЯ:

1. Что называется квадратным корнем?

2. Что называется арифметическим квадратным корнем?

3.Какие свойства квадратного корня вы знаете?

4. Как называется знак корня?

5.Какая функция связана √ ?

6. Что является графиком этой функции?

ПРАКТИКА:

1. Найдите значение арифметического квадратного корня:

а) ;в) ;д) .

2.Вычислите:

а) – б) -; в) ∙

3.Решить уравнение:

а) х² = 9; б) 2х² = 50;

в) х² – 0,2 = 0,05; г) 3х² + 27 =0.

Вариант 4

ТЕОРИЯ:

1. Что называется квадратным корнем?

2. Что называется арифметическим квадратным корнем?

3.Какие свойства квадратного корня вы знаете?

4. Как называется знак корня?

5.Какая функция связана √ ?

6. Что является графиком этой функции?

ПРАКТИКА:

1. Найдите значение арифметического квадратного корня:

а) ;в) ;д) .

2.Вычислите:

а) – б) +;

в)( )²+ ; г) — 5( )² .

3.Решить уравнение:

а) 0,5х² = 0,08; б) -3х² + 48 =0.;

в)( х+2 )² – 0,4 = 0,09; г) х³ — 5х = 0.

infourok.ru

Тематические зачетные работы по алгебре в 8 классе

Тематический зачёт №3 по алгебре в 8 классе.

Тема: «Квадратные уравнения».

Вариант 1.

Обязательная часть

1. Определите, сколько корней имеет уравнение .

2. Определите, сколько корней имеет уравнение .

3. Решите уравнение .

4. Решите уравнение .

5. Решите уравнение .

6. Решите уравнение .

7. Решите уравнение .

8. Решите задачу с помощью уравнения.

Площадь прямоугольника 96см². Найдите сторону

прямоугольника, если одна из них в 1,5 раза больше другой.

Дополнительная часть

9.(3 балла). Решите уравнение .

10.(3 балла). Найдите коэффициенты и в уравнении

, если известно, что его корни равны и

.

11.(5 баллов). Выделив квадрат двучлена, покажите, что

выражение принимает только положительные

значения..

12.(5 баллов). Найдите три последовательных натуральных числа,

сумма квадратов которых равна 50.

Тематический зачёт №3 по алгебре в 8 классе.

Тема: «Квадратные уравнения».

Вариант 2.

Обязательная часть

1. Определите, сколько корней имеет уравнение .

2. Определите, сколько корней имеет уравнение .

3. Решите уравнение .

4. Решите уравнение .

5. Решите уравнение .

6. Решите уравнение .

7. Решите уравнение .

8. Решите задачу с помощью уравнения.

В зале расставили одинаковыми рядами 48 стульев. Рядов

оказалось на 8 больше, чем стульев в каждом ряду. Сколько

стульев в каждом ряду?

Дополнительная часть

9.(3 балла). Решите уравнение .

10.(3 балла). Существуют ли такие значения , при которых

значения двучленов и равны?

11.(5 баллов). Выделив квадрат двучлена, покажите, что

выражение принимает только отрицательные

значения..

12.(5 баллов). Сумма квадратов двух последовательных

натуральных чисел на 91 больше их произведения. Найдите эти

числа.

Тематический зачёт №4 по алгебре в 8 классе

Тема: «Дробные рациональные выражения»

Вариант 1.

Обязательная часть

1. Решите уравнение .

2. Решите уравнение .

3. Решите уравнение .

4. Решите уравнение .

Дополнительная часть

5.(3 балла). Решите уравнение:

.

6.(3 балла). С помощью графиков выясните, сколько корней имеет

уравнение . 7.(5 баллов). Из города А в город В, расстояние между которыми

равно 30км, выехал грузовик. Через 10 минут вслед за ним

отправился легковой автомобиль и прибыл в город В на 5 минут

раньше грузовика. Найдите скорость каждой машины, если

известно, что скорость грузовика на 20км/ч меньше скорости

легкового автомобиля.

8.(5 баллов). Найдите координаты точек пересечения графиков

функций и .

Тематический зачёт №4 по алгебре в 8 классе

Тема: «Дробные рациональные выражения»

Вариант 2.

Обязательная часть

1. Решите уравнение .

2. Решите уравнение .

3. Решите уравнение .

4. Решите уравнение .

Дополнительная часть

5.(3 балла). Решите уравнение:

.

6.(3 балла). С помощью графиков выясните, сколько корней имеет

уравнение . 7.(5 баллов). Велосипедист должен был проехать от посёлка до

железнодорожной станции 24км. Проехав 10км, он сделал

остановку на 10 минут. Увеличив после этого скорость на 2км/ч,

он прибыл на железнодорожную станцию вовремя. Найдите

первоначальную скорость велосипедиста.

8.(5 баллов). Найдите координаты точек пересечения графика функции с осью и с осью .

Тематический зачёт №5 по алгебре в 8 классе.

Тема: «Неравенства».

Вариант 1.

Обязательная часть

1. Решите неравенство: .

2. Решите неравенство: .

3. Решите неравенство: .

4. Решите систему неравенств:

5. Решите систему неравенств:

6. Решите двойное не равенство .

7. Оцените площадь прямоугольника, если известны границы его

сторон и (в мм): ,

Дополнительная часть

8.(3 балла). Решите неравенство: .

9.(3 балла). Докажите, что при всех значениях верно

неравенство: .

10.(5 баллов). Определите, при каких значениях значения

функции принадлежат промежутку .

11.(5 баллов). При каких значениях уравнение

имеет два корня?

Тематический зачёт №5 по алгебре в 8 классе.

Тема: «Неравенства».

Вариант 2.

Обязательная часть

1. Решите неравенство: .

2. Решите неравенство: .

3. Решите неравенство: .

4. Решите систему неравенств:

5. Решите систему неравенств:

6. Решите двойное не равенство .

7. Измеряя длину и ширину прямоугольного участка земли (в

метрах), нашли, что , оцените длину

границы участка.

Дополнительная часть

8.(3 балла). Решите систему неравенств:

9.(3 балла). Найдите наибольшее целое число, являющиеся

решением неравенства

10.(5 баллов). При каких значениях значения

функции принадлежат промежутку .

11.(5 баллов). При каких значениях выражение

имеет смысл?

Тематический зачёт №6 по алгебре в 8 классе

Тема: «Степень с целым показателем»

Вариант 1.

Обязательная часть

1. Вычислите .

2. Вычислите .

3. Вычислите .

4. Представьте дробь в виде произведения.

5. Выполните действия .

6. Выполните действия .

7. Выполните действия .

8. Упростите выражение .

9. Упростите выражение .

10. Запишите в стандартном виде число 52000.

11. Запишите в стандартном виде число 0,062.

12. Выполните действия и запишите в стандартном виде:

.

Дополнительная часть

13.(3 балла). Вычислите .

14.(3 балла). Упростите выражение .

15.(5 баллов). Сократите дробь .

16.(5 баллов). Сравните числа:

а) и ; б) и .

Тематический зачёт №6 по алгебре в 8 классе

Тема: «Степень с целым показателем»

Вариант 2.

Обязательная часть

1. Вычислите .

2. Вычислите .

3. Вычислите .

4. Представьте дробь в виде произведения.

5. Выполните действия .

6. Выполните действия .

7. Выполните действия .

8. Упростите выражение .

9. Упростите выражение .

10. Запишите в стандартном виде число 34000.

11. Запишите в стандартном виде число 0,023.

12. Выполните действия и запишите в стандартном виде:

.

Дополнительная часть

13.(3 балла). Вычислите .

14.(3 балла). Упростите выражение .

15.(5 баллов). Представьте в виде степени с основанием 3

выражения: а) ; б) .

16.(5 баллов). Сравните числа:

а) и ; б) и .

infourok.ru

Домашние зачетные работы по алгебре для 8 класса по темам

Домашние зачетные работы по алгебре

для 8 класса по темам:

• Преобразования алгебраических дробей
• Арифметический квадратный корень
• Функции и графики
• Преобразование графиков функций
• Решение квадратных уравнений
• Решение линейных неравенств
• Решение квадратных неравенств
• Решение систем неравенств
• Решение систем квадратных неравенств
• Решение систем уравнений

Разработано учителем математики МОУ «СОШ» п. Аджером Корткеросского района Республики Коми

Мишариной Альбиной Геннадьевной

^

Преобразования алгебраических дробей.

1). Упростить выражения:

а) б) — в) — г) — д) +

е) — ж) · з) · и) ·

к) 27а³ : л) : м) : н) (+ ) ·

2). Выполнить действия:

а) ( — ) : ( + ) б) ( + ) :

в) ( — ) : г) · —

д) (1 — ) : ( — ) + 1

3). Упростить выражения:

а) : + б) ( — ) : ( + )

в) : ( — — ) г) ( у — + х ) : ( у-х )

д) ( + )²– (— )² е) ж)

^

а) = б) = в) + = 2 г) = х

д) = е) = ж) + = 3 з) — =

и) + = 0 к) + — = 0 л) — — = 0

Домашняя зачетная работа.

Арифметический квадратный корень

1). Вынести множитель из-под знака корня:

а) б) в) г) д) е)

ж) з) и) к) л)

2). Внести множитель под знак корня:

а) а²в б) 3ху³ в) авс г) 2х²у д) 20с³ах е) хус³

^

а) 2 — +б) 2 — +в) + — г) — 3 +

д) 2 · 5 · е) 3 · · 4ж) · · з) · · и)

к) л) ()⁴м) · · — 8 н) · · — 7 о) ()⁶ п) ()⁴

п) (3 — )²р) (4 — )²с) (3 — 2)²т) (4 — 3)²у) (3 — )²ф) ( + )²

х) ч) ц) щ) ы) ю)

4). Используя определение квадратного корня, решите уравнение: а) = 3 б) = 2 в) =0 г) =5

д) =13 е) = 24 ж) = 2 з) = 8

и) =8 к) =12 л) =0 м) = 7

Домашняя зачетная работа.

Функции и графики

1). Построить графики функций:

а) у = б) у = — в) у = г) у = — д) у = + 1 е) у = — + 2

ж) у = — 4 з) у = х² – 4 и) у = – х² + 4 ^{к) у = — 2х2л) у = 4х2м) у = х2 – 2х – 3}

н) у = х² + 2х — 3 о) у = -х² + 4х + 5 п) у = х² + 4х – 5 р) у = х² – 6х + 5 с) у = -х² + 6х – 5

т) у = х² + 4х – 3 у) у = — х² + 4х — 3 ф) у = х² – 4х х) у = 2х — х²ч) у = 4х — х²

2). Решить графически уравнение:

а) — 8 + 1,5х = 0 б) х² + = 0 в) х² — — 2 = 0 г) — х² = 0

д) + х² = 0 е) = 2х – х²ж) = (х -1)²з) 5х² = 5х — 6 и) |х| — 3 = —

к) — — 1 = л) |х| + 2 = (х — 2)²м) — + 4 = 3х²н) — 5 = — х

3). Решить графически систему уравнений:

а) ху + 3 = 0 б) у + 2х² = 3 в) ху – 8 = 0 г) ху + 4 = 0 д) ху = — 4

у = х² + 2 у = |х| у = у = (х — 1)² у – х² = 1

4). Построить график функции:

а) у = 3 + 2х, если х б) у = |х|, если х в) у = 2 – 2х², если -1 ≤ х ≤ 1

3 – 2х, если х ≥ 0 2, если х ≥ 2 х² – 1, если х 1

г) у = 2 – 2х² , если -1≤ х ≤ 1 д) у = — х² + 2, если -2 ≤ х ≤ 1

х – 1, если х >1 х , если 1

— х – 1, если х

Домашняя зачетная работа.

Преобразование графиков функций

Построить графики функций:

а) у = — 3 б) у = в) у = + 5 г) у = + 2

д) у = — 4 е) у = (х + 4)² ж) у = (х — 2)² + 3 з) у = (х + 3)² — 4 и) у = |х — 4| к) у = |х + 2| — 5 л) у = |х²| м) у = |- х² + 6х + 9|

н) у = + 4 о) у = — 4 п) у = + 5 р) у = |х² — 4| с) у = — |х — 1| + 4 т) у = — 2(х+2)² + 2

Домашняя зачетная работа.

Решение квадратных уравнений

1). Решить уравнения:

а) 2х² + 3х – 2 = 0 б) 5 х² – 7х + 2 = 0 в) 3 х² + 8х – 3 = 0

г) — х² + 2х + 8 = 0 д) 3 х² + 5х – 2 = 0 е) 2 х² – 7х + 3 = 0

ж) — х² + 7х – 10 = 0 з) 3 х² + 2х – 5 = 0 и) 9 х² – 6х + 1 = 0

к) 5 х² — 3х – 2 = 0 л) 4 х² + 4х + 1 = 0 м) 6 х² + х — 1 = 0

н) — х² + 7х + 8 = 0 о) 2 х² – 5х + 3 = 0 п) — х² – 2х +15 = 0

р) х² – 5х – 1 = 0 с) 5 х²5- 8х – 4 = 0 т) х² + 3х + 1 = 0

у) 6х² – 7х + 1 = 0 ф) 3 х² + 7х – 6 = 0 ч) 5 х² – 8х + 3 = 0

ц) 2 х² – 9х + 4 = 0 ш) 7х² + 9х + 2 = 0 щ) 2 х² + 3х – 5 = 0

2). Решить уравнения, приводящиеся к квадратным:

а) 3 х² + 9 = 12х — х²б) 18 — х²= 14 в) х² + 3 = 3 – х

г) х(х+2)=2 д) х²— 6х = 4х – 25 е) х(2х+1) = 3х + 4

ж) (10х — 4)(3х + 2)=0 з) (х-1)(5х+)= 0 и) 9(х-8)(6х-4) = 0

к) = л) 3 + = х м) + = 5

н) х — = 4 о) + = 3 п) = 0

р) (2х-1)(2х+1) + х(х-1) = 2х(х+1) с) (3х +1)² – х(7х+5) = 4

т) (2х+1)² + 2 = 2 – 6х²у) (3х-1)(1+3х) – 2х(1+4х)= -2

ф) = ч) — = ц) =

ш) — = 1 щ) = ы) + = 2

ю) х(х+3) – 4(х-5) = 7(х+4) – 8 я) 6х⁴ + х² – 1 = 0

^

Решение линейных неравенств.

1) 6х – 5(2х+8) > 14 + 2х

2) 3(3х — 1) > 2(5х — 7)

3) 3х – 4(х+1)

4) 3(1 — х) – (2 — х) ≤ 2

5) 4(х + 8) – 7(х — 1)

6) 5х – 2(х — 4) ≥ 9х + 23

7) 5 – 2х ≤ 1 –(х — 2)

8) 3 – х ≤ 1 – 7(х + 1)

9) 11х – (3х + 4) > 9х – 7

10) 6 – 6(х — 3) ≥ 2(х+1) -10

11) 2х – 3(х+4)

12) 3х + 5 ≥ 9х – (5 – 2х)

13) 6 – 3х

14) 2х – 3(х+1) > 2 + х

15) 10х – 3(4 — 2х) > 16 + 20х

16) 19 – 7х

17) 2(х-1) > 5х – 4(2х + 1)

18) 2(1 — х) ≥ 5х – (3х + 2)

19) 5 + х > 3х – 3(4х + 5)

20) 5(х+4)

21) х+2

22) 4(х — 1) – (9х — 5) ≥ 3

23) 3(х — 2) – 5(х + 3) > 27

24) 6х – 3(х — 1) ≤ 2 + 5х

25) 14 – (4 + 2х) > 1 + х

26) 2 – 5(х — 1) ≤ 1 + 3х

27) 3 + 10х

28) 5(х — 1) + 8 ≤ 1 – 3(х + 2)

29) х – 5(х — 4) > 6х + 20

30) 1 – х ≤ 6х – (3х — 1)

31) + ≤ 3 —

32) — ≥ — 1

33) — > 0

34) +

35) ≤ +

36) ≤ +

37) х — + >

38) х + — >

39) 1 —

40) 2 — > 1 —

41) 2 — > 0

Домашняя зачетная работа.

Решение квадратных неравенств

1. х² – 1 ≤ 0
2. х² + х – 6 ≤ 0
3. х² + 3х + 2
4. х² – 9 ≥ 0
5. х² + 4х – 5 ≤ 0
6. х² + 7х + 12
7. х² – 144 > 0
8. 2х² – 9х + 4
9. х²
10. х² – 25 ≤ 0
11. х² ≤ 0
12. 4 — х²
13. — х² – х + 12 > 0
14. х² – х – 6 > 0
15. х² – 10х + 16
16. 3х² – 2х – 1
17. х² – 121
18. 3х² – 4х + 1
19. х² – 36 ≥ 0
20. х² ≥ 64
21. 16 — х² > 0
22. — х² + 3х + 4 > 0
23. х² + 3х – 4 > 0
24. х² – 3х + 2
25. 2х² – 3х – 5 > 0
26. 4х(х + 2)
27. х² – 2х ≤ 2
28. х² + 2х ≤ 1
29. 3 – 2х — х² ≥ 0
30. 10 + 3х — х² ≥ 0
31. 10 х² – 3х – 1 > 0
32. х² > 4
33. х²
34. х² > 0
35. х² > -4

36) > +

37) +

37) — ≤

38) — ≥

39) 2х(3х -1) > 4х² + 5х +9

40) 3х² + 40х + 10

41) у⁴ + 12у² – 64 ≥ 0

42) х⁴ + 6х² – 7 > 0

43) а⁴ + 3а² – 28 ≤ 0

^

Решение систем неравенств.

1. 2х — 1> 0

15 – 3х > 0

2) х – 1 ≤ 3х – 6

5х + 1 ≥ 0

3. 3х > 12 + 11х

5х – 1

3. 3 – х

3х – 1 > 1 – 2х

3. х – 1 ≤ 2х + 2

3х + 5 ≤ х + 1

3. 2х + 7

18 + х > 2 – х

7) х – 1 ≤ 7х + 2

11х + 13 > х + 3

8. 5у + 5

2 – 3у

9) 10у – 1 ≥ 2

4 – у ≥ 2у + 1

10) 3х – 2 ≥ х + 1

13) 2 — > 1 —

3 —

14) ≥ 0

1 – 3х ≤ 2х -1

3 – х

15) 2 – х > 0

2 – х ≥ 2х + 1

≤ 0

16) 3х – 4

5х ≤ 0

х : 2 > — 1

17) 0

18) — 2

19) — 1

20) — 4 ≤ 2х – 1 ≤ 2

21) -6 ≤ 5х – 1 ≤ 5

22) 0,1 ≤ 0,1х – 0,8 ≤ 0,5

23) — 15

24) 0 ≤ 4х + 3

25) -2

4 – 2х ≤ х – 2

11. 5х + 12 ≤ 5х + 20

х

2х + 7 ≥ 0

11. 2х + 1 ≥ 0

х > 3х – 1

5х – 6

Домашняя зачетная работа.

Решение систем квадратных неравенств.

1). х² — 6х + 8 > 0

5 – 2х ≤ 0

2). 2х² – 7х + 5 ≤ 0

2 – х > 0

3). х² — 10х + 9 ≥ 0

10 – 3х

4). 6х² – 5х + 1 > 0

4х – 1 ≥ 0

5). 2х² + 3х – 14 ≥ 0

3х + 11 > 0

6). х² – 5х + 4 ≤ 0

12). х² – 9 ≥ 0

х + 2 >0

х² + 3х + 2

13). 3 – 5х – 2х² ≥ 0

3х² – х – 14 ≥

14). – х² + 3х – 2

2х² – 3х – 5 > 0

15). – 36 + х² ≥ 0

4х² – 1

9 – 4х

7). 4х² – 1 ≤ 0

х² > 0

8). (х — 1)² > 0

169 – х² ≥ 0

9). 2х² – 3х – 5 > 0

х² – 3х + 2

10). х² – х – 6 > 0

3х² – 2х – 1

11). 3х² – 4х + 1

х² – 1 ≥ 0

х + 5 > 0

^

Решение систему уравнений

1). 3х – у = 3

3х – 2у = 0

2). 2х – 3у = 1

3х = у = 7

3). 3х – 2у = 16

4х + у = 3

4). х – у = 3

3х + 4у = 2

5). 5х – 4у = 12

х – 5у = — 6

6). 2х + у = 2

х² – у = — 2

7). х – у = 7

ху = — 12

8). х² – 3у = — 9

х + у = 3

9). х + у = 10

х² – у² = 40

10). ху = 8

х + у = 6

11). х – у = 2

3х – у² = 6

12). 2х² — 3ху = — 4

3х + у = 5

13). х + 2у = 7

2у² + ху = 14

14). х + у = 5

(х — 3)(у + 5) = 6

15). х – у = 7

х² + у² = 9 – 2ху

16). (х + 6)(у — 4) = 4

х + у = 3

17). у – х = 2

у² – 2 ху – х² = — 28

18). х + у = 8

х² + у² = 16 + 2ху

19). х + у = 3

х² + 3ху + у² – х – у = 2

20). х + у = 12

+ =

21). — = —

х – у = 12

lib3.podelise.ru

Зачетная работа по алгебре для учащихся 8 класса по теме «Квадратные уравнения».

8 класс

Зачет № 2 по алгебре по теме «Квадратные уравнения».

I вариант

Теоретическая часть

1. Общий вид квадратного уравнения.

2. Общий вид приведенного квадратного уравнения.

3. Формулы для решения квадратного уравнения (полного).

4. Теорема Виета.

5. Формула разложения квадратного трехчлена на множители.

6. Общий вид биквадратного уравнения.

7. Как определить количество корней полного квадратного уравнения?

Практическая часть

1. Решить уравнения:

а)

б)

в)

г)

д)

2. Разложить на множители: .

3. Решить задачу:

Найти два числа, сумма которых равна 3, а сумма их квадратов равна 5.

4. Решить систему уравнений:

Оценка «3» — теоретическая часть + задачи № 1-2 практической части

Оценка «4» — теоретическая часть + задачи № 1-3 практической части

Оценка «5» — за все верно выполненные задания

8 класс

Зачет № 2 по алгебре по теме «Квадратные уравнения».

II вариант

Теоретическая часть

1. Общий вид квадратного уравнения.

2. Общий вид приведенного квадратного уравнения.

3. Формулы для решения квадратного уравнения (полного).

4. Теорема Виета.

5. Формула разложения квадратного трехчлена на множители.

6. Общий вид биквадратного уравнения.

7. Как определить количество корней полного квадратного уравнения?

Практическая часть

1. Решить уравнения:

а)

б)

в)

г)

д)

2. Разложить на множители: .

3. Решить задачу:

Одна сторона прямоугольника на 5 м больше другой, а его площадь равна 84м². Найти стороны прямоугольника.

4. Решить систему уравнений:

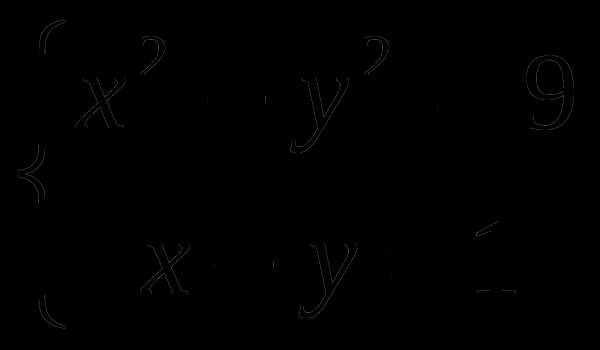
Оценка «3» — теоретическая часть + задачи № 1-2 практической части

Оценка «4» — теоретическая часть + задачи № 1-3 практической части

Оценка «5» — за все верно выполненные задания

infourok.ru

Зачеты по математике в 8 классе

Зачет №2 по алгебре по теме

«Дробно-рациональные уравнения. Неравенства. Степень с целыми показателем. Элементы статистики» 8 класс.

Ф.И.О.________________________________________________________дата________

1. Решите уравнение .

2.Моторная лодка курсирует между двумя пристанями, расстояние между которыми по реке равно 4км. На путь по течению у нее уходит на 3 мин. меньше, чем на путь против течения. Чему равна скорость течения реки, если известно, что скорость лодки в стоячей воде равна 18км/ч?

Пусть х км/ч – скорость течения реки. Какое из уравнений соответствует условию задачи?

3. Решите графически уравнение .

Ответ:______________

4.Какое из приведенных ниже неравенств верно при любых значениях а и , удовлетворяющих условию

5. Какие из неравенств

А) Б) В)

верны при любых значениях х и у, удовлетворяющих условию , ?

6. Укажите на рисунке множество решений системы неравенств

7. Найдите значение выражения при .

8. Вычислите .

Ответ:______________________

9. При каком верно равенство ?

10.

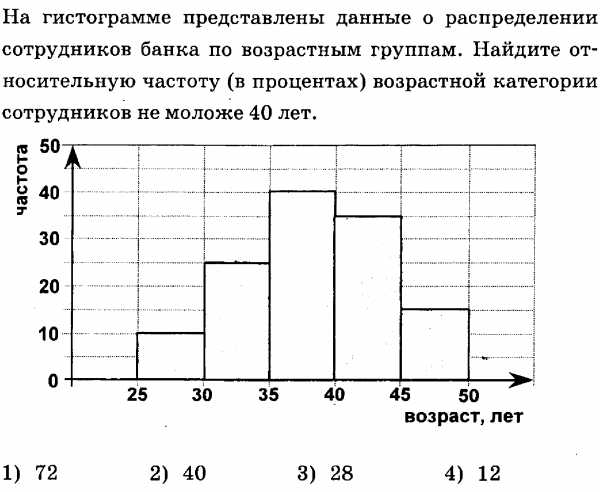
Ответы

videouroki.net