Задачи по алгебре с решением 7 класс: Урок 44. решение задач с помощью линейных уравнений — Алгебра — 7 класс

Алгебра 7 класс «Решение задач с помощью уравнений»

Цели урока:
1. Образовательные:
— закрепить умения и навыки решать линейные уравнения  и задачи с помощью составления уравнений;
— формировать умения самостоятельно решать задачи.
2. Развивающие:
— посредством решения заданий развивать логическое мышление, культуру устного счета и речь учащихся;
— дать возможность каждому ребенку определить для себя уровень сложности в выполнении заданий, тем самым развивать самостоятельность, умение критически относиться к своей работе.
3.  Воспитательные:
— используя игру как  здоровьесберегающую технологию, содействовать воспитанию интереса к математике, активности.
Записи на доске:
— название банка;
— тема урока;
— высказывание Конфуция;
— задания для устного счета;
— задания для практической части.

План и ход урока.

1. Организационный момент.
2. Проверка знаний теоретического материала по теме: «Уравнения с одной переменной».
3. Устная работа.
4. Решение заданий разного уровня.
5. Дифференцированная самостоятельная работа.
6. Подведение итогов.
7. Индивидуальное домашнее задание.
     Сегодня мы с вами проведем необыкновенный урок:  Урок- игру «Банк знаний».
     Тема нашего урока: «Решение задач с помощью уравнений».
     На уроке мы повторим определения, свойства линейного уравнения с одной переменной, закрепим навыки и умения решения линейных уравнений с одной переменной, решения задач с помощью составления уравнений.

Китайский мудрец Конфуций, живший, 500 лет до нашей эры сказал:
«Те, кто обладают врожденными знаниями — богаче всех. За ними следуют те, кто приобретают знания благодаря учению».

     Так давайте же будем приобретать знания, и в конце урока мы выясним, сможем ли мы себя назвать богатыми.
     В городе Когалым есть сберегательный банк, банк «Петрокоммерц», Ханты-Мансийский банк и сегодня открывается еще один банк: «Банк знаний». Туда я и предлагаю вам вложить сегодня деньги, заработанные во время урока, за свои знания. Для того, чтобы сделать первый вклад вы должны ответить на мои вопросы и получить за это первоначальный капитал. За каждый правильный ответ вы получаете одну медную монету достоинством в « 1 тугрик». 1.Устный счёт.

x = 9

x = 35

y = 57

нет корней

c = 17

p = 80

b = 3

x = 4

x = 9

y = 2

2.В одном бидоне x л, а в другом y л молока.

1. Что означает выражение?

а) x + y

б) x + 5

в) y — 3

г) x — y

2. 2. Что означает равенство?

а) x+ y = 28

б) x + 5 = y

в) 4x = y

г) x – 12 = y + 24

3. Составьте выражение для решения задачи

2x + 18

• Вася решил несколько примеров, а Петя в 2 раза больше. Сколько примеров решил Петя? Сколько примеров решили они вместе?

2x; x + 2x

• Антон прочитал несколько страниц книги, осталось ему прочитать на 32 страницы больше, чем уже прочитано. Сколько страниц в книге?

x + x + 32

3x — x _ что их связывает?

_ сформулируйте тему урока.

4.Разминка

1. Дайте определение корня уравнения.

2. Является ли число 7 корнем уравнения  2х — 5 = х + 2 ?

3. Что значит решить уравнение?

4. Какие уравнения называются равносильными?

5. Сформулируйте свойства уравнений.

6. Приведите пример уравнения, равносильного уравнению 5х — 4 = 6.

7. Дайте определение линейного уравнения с одной переменной.

8. Приведите примеры.

9. В каком случае уравнение  ах = в  имеет:
— единственный корень,
— множество корней,
— не имеет решения ?
Итак, вы имеете определенный капитал.
     Продолжим пополнять свой капитал. Вам предстоит выполнить задания. За каждое верное решение вы получаете одну медную монету достоинством один тугрик, которую вы можете поместить в разные вклады:
     I. Вклад «Легкий»
      Решите уравнение:
      а) 2х = 0                  г) 6х = 3
      б) 3х = 1                 д) 3х + 9 = 0
      в)  х — 2 = 0             е) 7х — 4 = х — 16
II. Вклад «Занимательный»
       На доске было написано решение линейного уравнения, но правую часть данного  уравнения стерли. Восстановите ее:
       а) 3х = ….       б) 5х = ….         в) 0,2х =….
           х = -11            х = 0                   х = 14
III. Вклад «Поисковый»
       Какое из чисел 3 или -2, является корнем уравнения
       а) 3х = — 6                        в) 4х — 4 = х + 5
       б) х + 3 = 6                     г) 5х — 8 = 2х + 4
             
IV. Вклад «Универсальный»
       При каких значениях а уравнение
       ах = 8
       а) имеет корень, равный -4; 0,5;
       б) не имеет корней;
       в) имеет отрицательный корень.
5.Решение задач. Вы получили информацию об основных вкладах нашего банка. А теперь каждому из вас предстоит выполнить задания, за решение которых вы будете также получать тугрики.
         В банке работают кассиры, которые будут за правильные решения выдавать монеты:
              а — медная монета достоинством в 1 тугрик
              в — серебряная монета достоинством в 2 тугрика
              с — золотая монета достоинством в 3 тугрика
          После выполнения всех заданий у каждого из вас образуется накопительный фонд.
           Итак, приступайте, перед вами на столах лежат задания для различных вкладов. Самостоятельно выбирайте вклад, решайте, сдавайте кассиру банка и получайте тугрики.
               а   Папе и дедушке вместе 111 лет. Сколько лет каждому, если папа в два раза моложе дедушки?
               в За 3 часа мотоциклист проезжает то же расстояние, что велосипедист за 5 часов. Скорость мотоциклиста на 12 км/ч больше скорости велосипедиста. Определите скорость каждого.
               с   В двух сараях сложено сено, причем в первом сарае сена в 3 раза больше, чем во втором. После того, как из первого сарая увезли 20 т., а во второй привезли 10 т. В обоих сараях сена стало поровну. Сколько сена было во втором сарае первоначально.

Купили 2 кг 100 г крупы и высыпали ее в три банки. В первую банку крупы вошло в 3 раза больше, чем во вторую, а в третью банку насыпали 500 г крупы. Сколько крупы насыпали в первую и сколько во вторую банки?

Решение.

Пусть во вторую банку насыпали x г крупы, тогда в первую – 3x г крупы. Всего в три банки насыпали (3x + x + 500) г, что по условию составляет 2100 г. Составим и решим уравнение.

3x + x + 500= 2100;

4x + 500 = 2100;

4x = 2100 — 500;

4x = 1600;

x = 1600 : 4;

x = 400.

400 г – насыпали во вторую банку.

400 × 3 = 1200 (г) – в первой банке.

Задача для слабых. с   В первом мешке в 3раза больше картофеля, чем во втором. После того, как из одного мешка взяли 30 кг. картофеля, а во второй насыпали ещё 10 кг., в обоих мешках картофеля стало поровну. Сколько килограммов картофеля было во втором мешке.
Задача для сильных. Подготовка к ГИА. Решение задач из сборника заданий ГИА-2010. В.В. Кочагина, М.Н. Кочагиной .Алгебра. Москва. Эксмо, 2009.

1. Велосипедист собирался преодолеть расстояние от поселка до станции за 5 часов. Выехав из поселка, он увеличил свою скорость на 3 км/ч и проехал расстояние до станции за 4 часа. Чему равно расстояние от поселка до станции?

Ну вот и наступило время подвести итог, сейчас каждый из вас подсчитает сколько тугриков сможет внести в «Банк Знаний»

1.      Считаем медные монеты достоинством в 1 тугрик, вы получаете столько тугриков, сколько у вас монет.

2. Считаем серебряные монеты достоинством в 2 тугрика. Умножьте количество серебряных монет на два и получите количество тугриков.

3. Считаем золотые монеты достоинством в три тугрика. Умножьте количество монет на три, получите количество заработанных тугриков.

4. Сложите все полученные тугрики.
     Вы получили «5», если набрали 15 тугриков и более, «4», если набрали 10-14 тугриков, «3», если набрали 5-9 тугриков.
     Поставьте оценку в дневник, запишите  число набранных тугриков на квитанции банка, вложите квитанцию и тугрики (монеты) в пакет и сдайте кассирам банка.
     Увеличить свой капитал вы можете дома, выполнив индивидуальные задания, которые лежат у каждого на столе. Выбирайте любой вклад и продолжайте зарабатывать тугрики в «Банке Знаний»
     Положите задания в дневник.
     Задание на дом:
     Вклад «Поисковый»
     Решить уравнение:
     а   1/5х = 5
           3х — 11,4 = 0
           4х + 5,5 = 2х — 2,5
     в    2х — (6х+1) = 9
            5х — 12,5 = 0
            3х — 0,6 = х + 4,4
     с     4х — (7х — 2) = 17
            8х — (2х + 4) = 2(3х — 2)
            3х — (9х — 3) = 3 (4 — 2х)
     Вклад «Творческий»
а  В двух седьмых классах 47 учеников, причем в одном на 3 ученика больше, чем в другом. Сколько учеников в каждом классе?
в  Саша решил две задачи за 35 минут. Первую задачу он решал на 7 минут дольше, чем вторую. Сколько минут Саша решал вторую задачу?
с   В первом мешке в 3раза больше картофеля, чем во втором. После того, как из одного мешка взяли 30 кг. картофеля, а во второй насыпали ещё 10 кг., в обоих мешках картофеля стало поровну. Сколько килограммов картофеля было во втором мешке.
Квитанция «Банка Знаний» к домашнему заданию.
     Решить уравнение:
     а    одно задание 1 тугрик
     в    одно задание 2 тугрика
     с    одно задание 3 тугрика
     Решить задачу:
     а   1 тугрик
     в   2 тугрика
     с    3 тугрика,
     чтобы получить
     «5» нужно набрать 12 тугриков
     «4» нужно набрать 8-11 тугриков
     «3» нужно набрать 4-7 тугриков
     Кто же сегодня у нас самые богатые? Те, кто заработал 15 тугриков и более, могут позволить  себе делать большие капиталловложения: строить заводы, фабрики, нефтяные вышки. Те,  кто заработал 10-14 тугриков, смогут отправиться в путешествие. Ну, а те, кто заработал 5-9 тугриков, вы можете посетить фитобар нашей школьной столовой и купить коктейль.  Итак, сегодня банк закрывается. До свидания! До новых встреч в «Банке Знаний».

Желаю вам цвести, расти,

Копить, крепить здоровье,

Оно для дальнего пути –

Главнейшее условие.

Пусть каждый день и каждый час

Вам новое добудет,

Пусть добрым будет ум у вас,

А сердце умным будет.

Вам от души желаю я,

Друзья, всего хорошего.

А всё хорошее, друзья,

Даётся нам недешево.

С.Я.Маршак

Решение задач с помощью уравнений. Алгебра, 7 класс

1. Решение задач с помощью уравнений. Алгебра, 7 класс

Учитель математики
МОУ «Харламовская СОШ»
Кривошеин О.В.

2. Решайте и решите!

«Решение задач — это практическое
искусство, подобно плаванию, или
катанию на лыжах, или игре на
пианино: вы можете научиться этому,
только практикуясь … если вы захотите
научиться плавать, то вынуждены
будете зайти в воду, а если вы захотите
стать человеком, хорошо решающим
задачи, вы вынуждены их решать»
Д. Пойа, математик и педагог.

3. Этапы решения задачи:

• Внимательно читаем условие задачи;
• Определяем, что будем считать
неизвестным;
• Составляем уравнение по условиям
задачи;
• Решаем уравнение;
• Проверяем результат и запись ответа.

4. Задача 1.

Ученик задумал число. Если его
умножить на 6, к произведению
прибавить 18 и полученную
сумму разделить на 12, то
получится 4. Какое число
задумал ученик?
Решение. Пусть х – задуманное число. Составим
уравнение по условию задачи:
(х 6 + 18): 12 = 4. Умножим обе части уравнения на
12, получим х 6 + 18= 48. Решая далее, получим х = 5.

5. Задача 2.

За 9 ч по течению реки теплоход проходит
тот же путь, что за 11 ч против течения.
Найдите собственную скорость теплохода,
если скорость течения реки 2 км/ч.

6. Решение.

Пусть собственная скорость
теплохода – Х км/ч.
Решение.
Заполним таблицу значений трёх величин:
пройденного расстояния, затраченного
времени и скорости.
По течению
Против
течения
Скорость
(км/ч) V
Х+2
Х–2
Время (ч) t
9
11
Расстояние
(км) S
9(Х + 2)
11(Х – 2)

7. Составим уравнение:

На основании условия задачи составим
уравнение:
9(Х + 2) = 11(Х – 2), раскроем скобки
9Х + 18 = 11Х – 22, перенесём слагаемые
9Х – 11Х = – 22 – 18,
– 2Х = – 40,
Х = 20,
Ответ 20 км/ч.
Итак, собственная скорость теплохода 20 км/ч.

8. Решение.

Пусть расстояние, на которое
могут отплыть туристы – Х км.
Заполним таблицу значений трёх величин:
пройденного расстояния, затраченного
времени и скорости.

9. Решение:

10. Чётные числа.

2, 4, 6, 8,…
Чётные числа.
Сумма четырех последовательных чётных
чисел равна 92. Найдите эти числа.
Решение. Пусть х – первое из этих чётных чисел,
тогда (х + 2) – второе, (х + 4) –третье, (х + 6) –
четвёртое. Их сумма равна 92. Составим
уравнение х + (х + 2) + (х + 4) + (х + 6) = 92.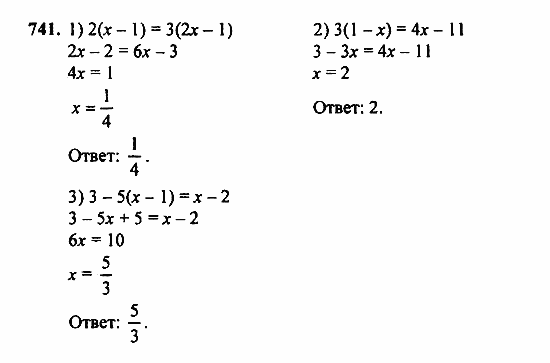
Раскрывая скобки и приводя подобные члены,
получим 4х + 12 = 92, 4х = 80, х = 20.
Ответ: 20, 22, 24, 26.

11. Нечётные числа.

1, 3, 5, 7,…
Нечётные числа.
Найдите три последовательных нечётных
числа, если сумма удвоенного первого, второго
и утроенного третьего равна 200.
Решение. Пусть х – первое из этих чётных чисел,
тогда (х + 2) – второе, (х + 4) –третье. Составим
уравнение по условию 2х + (х + 2) + 3(х + 4) =
200. Раскрывая скобки и приводя подобные
члены, получим 6х + 14 = 200, 6х = 186, х = 31.
Ответ: 31, 33, 35.

Урок алгебры «Решение задач с помощью систем уравнений» (7-й класс)

Цели:

• научить детей решать задачи с помощью
  составления систем уравнений;
• познакомить и литературным наследием родного
  края, вспоминая творчество П.П.Бажова;
• использовать при решении задач факты
  окружающей действительности.

ХОД УРОКА

1. Подготовка к восприятию материала
(проверка опорных знаний)

Учитель, используя медиапроектор,
восстанавливает изученную ранее тему. Детям
задаются вопросы их предполагаемые ответы,
воспроизводятся на экране.

Вопросы:

• Посмотрите на экран, что вы видите? (Презентация.
  Слайд 1)
• Что такое система уравнений? (Презентация.
  Слайд 2)
• Какие способы решения систем уравнений вы
  знаете? (Презентация.
  Слайд 3)
• Давайте вспомним суть применения каждого
  способа  (Презентация.
  Слайды 4, 5, 6).

– Система уравнений не только позволяет
установить общие корни уравнений, содержащихся в
ней, но и становится хорошим помощником при
решении задач. В таких задачах неизвестных
компонентов более одного и они связаны друг с
другом условием. Сегодня мы рассмотрим задачи, в
которых неизвестно два каких либо элемента и
будем учиться решать такие задачи с помощью
составления системы уравнений.

Дети записывают в тетрадях число, тему урока.
(Презентация. Слайд 7)

2. Изучение новой темы

Задача 1

– Рассмотрим для примера такую задачу.

Я знаю, что в классе 20 учеников. Среди них есть
девочки и мальчики.  А еще я знаю, что девочек
больше чем мальчиков на 4 человека. Сколько
мальчиков и девочек в этом классе? Ответ можно
узнать двумя способами: 1) просто пересчитать; 2)
решить такую задачу: (Презентация.
Слайд 8)

Пусть     х – количество
девочек
y – количество мальчиков

Т. к. мальчиков и девочек вместе – 20. Получим
уравнение: х + у = 20

С другой стороны девочек больше чем мальчиков на
4

Значит можно получить следующее
уравнение      х – у = 4

Объединим оба эти уравнения в систему, т.к в
каждом уравнении речь идет об одних и те же
детях., получим:
Далее дети самостоятельно решают систему
уравнений, на листочках под копирку.

Ответ: В классе 8 мальчиков и 12 девочек.

3. Самостоятельная работа в парах

У вас на партах лежат цветные карточки. На
экране появятся условия задач. Вы выбираете для
решения ту задачу, которая расположена на таком
же цветном фоне, что и цвет вашей карточки. (Слайд
9)

Записывают составленную систему на тех же
листочках под копирку.

Задача 2

1) В Зоопарке г. Екатеринбурга, живет много
разных животных. Среди них есть медведи – бурые и
белые. Известно, что всего в зоопарке живет 9
медведей, а бурых на 5 медведей больше, чем белых.
Сколько белых и бурых медведей живет в зоопарке
г. Екатеринбурга?

Решение:  

Ответ: В зоопарке 2 белых медведя и 7 бурых
медведей.

2) В Зоопарке г. Екатеринбурга, живет много
разных животных. Среди них есть лисы – черные и
рыжие. Известно, что всего в зоопарке живет 7 лис,
а черных на 3 лисы меньше, чем рыжих. Сколько
черных и рыжих лис живет в зоопарке г.
Екатеринбурга?

Решение

Ответ: В зоопарке 5 рыжих лисиц и 2 черные
лисицы.

После того как дети самостоятельно составили
систему уравнений – листочки сдают, проверка.
Решать эти системы они будут дома.

– Вы должны поднять карточку в том случае, если
система составлена правильно. (Презентация.
Слайд 10)

4. Закрепление материала

– А сейчас, я хочу рассказать вам об очень
интересном человеке. Он родился в 28 января 1879
году, в семье мастера Сысертского завода. И отец,
и дед его, и прадед всю жизнь провели на
медеплавильных заводах Сысертского горного
округа. В 1899 году он стал народным учителем и
трудовой свой путь начал в глухой уральской
деревне Шайдурихе, возле старинного города
Невьянска.

С детства он прислушивался к рассказам рабочих
об их тяжелой жизни, позже изучил много
документов, рассказывающих о горнозаводском
Урале. В летние каникулы он пешком или на
велосипеде путешествовал по уральским заводам и
деревням, по реке Чусовой, изучал труд камнерезов
и гранильщиков, сталеваров и литейщиков,
беседовал с ними о тайнах их ремесла

Люди говорили, что живет в горах Малахитница
(Хозяйка Медной горы), охраняет камни, рядом с ней
всегда много ящериц, а иногда и сама ящерицей
оборачивается.

А звали этого интересного человека Павел
Петрович Бажов. (Презентация.
Слайд 11)

Колдун уральский бородатый,

Бажов дарит нам новый сказ.

«Живинка в деле» – сказ богатый

И поучительный для нас.

В нем слово каждое лучится,

Его направленность мудра,

Найдут, чему здесь поучиться,

Любого дела мастера

Важны в работе ум и чувство,

В труде двойное естество

«Живинкой в деле» мастерство

Преображается искусство,

И нет тогда ему границ.

И совершенству нет предела,

Не оторвать тогда от дела

Ни мастеров, ни мастериц.

Их вдохновение безмерно,

Глаза их пламенем горят.

Они работают? Неверно.

Они – творят.

Демьян Бедный

– Вы знаете его сказы или повести?

– Что означает слово «сказ»?

Сказ – это литературное
произведение, в котором рассказчиком является не
сам писатель, а другой, вымышленный им человек.

– В сказах Бажова живет хранительница недр,
покровительница уральских рудокопов. Как ее
зовут?

– Хозяйка Медной горы. (Презентация.
Слайд 12)

– В каких сказах Бажова встречается Хозяйка
Медной горы?

• Малахитовая шкатулка,
• Каменный цветок
• Горный мастер
• Хрупкая веточка
• Таюткино зеркальце
• Две ящерки
• Приказчиковы подошвы
• Сочневы камешки

– В сказах Бажова главными героями выступали и
дети (Презентация.
Слайд 13), это такие сказы как:

• Тяжелая витушка
• Серебряное копытце
• Хрупкая веточка
• Каменный цветок
• Огневушка-Поскакушка
• Таюткино зеркальце
• Малахитовая шкатулка
• Жабреев ходок
• Голубая змейка

– У меня в руках книга, в которой собраны
произведения П. П.Бажова. Она называется
«Малахитовая шкатулка». В этой книге разное
количество сказов и повестей. Книга большая и в
ней много страниц.

Задача 3 (Презентация.
Слайд 15)

Я знаю, что 2 сказа о Хозяйке Медной горы и 3
сказа о героях-детях занимают 94 страницы. А 3
сказа о Хозяйке Медной горы и и 4 сказа о героях
детях занимают 133 страниц. Помогите мне узнать,
сколько страниц может занимать 1 сказ о Хозяйке
Медной горы и 1 сказ о героях-детях?

Х стр. – о Х.
М.г.                    
2х + 3у = 94

У стр. – о
Д.                            
3х + 4у = 133

Получим систему

Ответ: 1 сказ о ХМг занимает 23 страницы; 1
сказ о детях занимает 16 страниц

Задача 4 (дополнительно) (Презентация. Слайд17)

Старик Кокованя приютил у себя сироту. Девочка
Даренка была смышленая и чудная. Встретилась она
с волшебным козлом, которого прозвали Серебряное
копытце. При каждой встрече с ним можно было
собрать много каменьев.  При первой встрече
Даренка собрала два мешочка гранатов и три
мешочка малахита, всего 1300 гр. А при второй
встрече один мешочек  гранатов и два мешочка
малахит, всего 800 грамм. Сколько грамм самоцветов
содержится в каждом мешочке с малахитом и в
каждом мешочке с гранатом?

Хгр – 1 мешочек
малахита                   
2у + 3х = 1300

Угр – 1 мешочек
граната                      
у + 2х = 800

Получим систему

Ответ: В 1 мешочке 300гр малахита и 200гр.
граната

– Я предлагаю каждому из вас, вернувшись, домой,
прочитать сказы Бажова, ведь он писал их для нас.

5. Подведение итогов урока, выставление
оценок.

– Итак, подведем итоги. Какая сегодня у нас была
тема урока?

– Что нового вы узнали, чему научились?

– Остались ли у вас вопросы, на которые учитель
должен будет ответить на следующем уроке?

6. Домашнее задание

1. Решить задачу 1 графическим способом.
2. Составить и решить задачу, в которой вы можете
   узнать возраст своих родителей, с помощью
   системы уравнений.

Применение графика линейной функции к решению сюжетных задач; 7 класс — Разное — Математика, алгебра, геометрия

ГОСУДАРСТВЕННОЕ
БЮЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №
688 г. САНКТ-ПЕТЕРБУРГ.

Методическое
объединение учителей математики

Алгебра

МЕТОДИЧЕСКАЯ
РАЗРАБОТКА

<<Применение
графика линейной функции к решению
сюжетных задач на работу и движение>>

7
класс.

Работу
выполнила

Чудинова
О.Н.

учитель
математики

высшей
квалификационной категории

Рекомендовано
к публикации

Лукичевой
Е.Ю.

Зав.
Центром математического образования

Санкт
— Петербургская академия пост

дипломного
педагогического образования.

Санкт-Петербург

2014

Введение

В
работе рассматривается способ решения
сюжетных задач на работу и движение с
помощью графика линейной функции. Способ
решения можно применять как самостоятельный,
так и для проверки решения задач
алгебраическим способом.

Решение
задач с помощью графика линейной
функции предполагает наличие навыка
в построении и чтении графика движения,
и графика работы. Работу с графиком
движения и с графиком работы целесообразно
проводить на уроках алгебры при изучении
главы «Линейная функция и ее график» с
последующим решением задач. Методика
решения сюжетных задач представлена в
форме презентации, что делает ее более
удобной в работе.

График
линейной функции представляет
математическую модель задачи. Нужно
условие задачи представить в виде
графика функции и найти решение задачи,
работая с графиком функции.

В
работе представлены не все сюжеты задач
на работу и движение, которые можно
решать графическим способом. Предлагаемый
способ решения задач предполагает
исследовательскую проектную деятельность
учащихся. Учащимся предоставляется
возможность найти в учебной литературе
иной сюжет задач на работу и движение
или составить условие задачи самостоятельно
и представить проект ее решения
графическим способом.

Можно
предложить учащимся применить графический
способ решения и к другим задачам, в
которых величины связаны прямо
пропорциональной зависимостью (например:
стоимость, цена и количество товара).

Предложенный
способ решения задач предоставляет
учащимся возможность овладения системой
функциональных понятий, развитие умения
использовать функционально-графические
представления для решения различных
математических задач, для описания и
анализа реальных зависимостей.

Задачи на движение

Продолжаем изучать элементарные задачи по математике. Данный урок посвящен задачам на движение.

Предварительные навыки

Задача на нахождение расстояния/скорости/времени

Задача 1. Автомобиль двигается со скоростью 80 км/ч. Сколько километров он проедет за 3 часа?

Решение

Если за один час автомобиль проезжает 80 километров, то за 3 часа он проедет в три раза больше. Чтобы найти расстояние, нужно скорость автомобиля (80км/ч) умножить на время движения (3ч)

80 × 3 = 240 км

Ответ: за 3 часа автомобиль проедет 240 километров.

Задача 2. На автомобиле за 3 часа проехали 180 км с одной и той же скоростью. Чему равна скорость автомобиля?

Решение

Скорость — это расстояние, пройденное телом за единицу времени. Под единицей подразумевается 1 час, 1 минута или 1 секунда.

Если за 3 часа автомобиль проехал 180 километров с одной и той же скоростью, то разделив 180 км на 3 часа мы определим расстояние, которое проезжал автомобиль за один час. А это есть скорость движения. Чтобы определить скорость, нужно пройденное расстояние разделить на время движения:

180 : 3 = 60 км/ч

Ответ: скорость автомобиля составляет 60 км/ч

Задача 3. За 2 часа автомобиль проехал 96 км, а велосипедист за 6 часов проехал 72 км. Во сколько раз автомобиль двигался быстрее велосипедиста?

Решение

Определим скорость движения автомобиля. Для этого разделим пройденное им расстояние (96км) на время его движения (2ч)

96 : 2 = 48 км/ч

Определим скорость движения велосипедиста. Для этого разделим пройденное им расстояние (72км) на время его движения (6ч)

72 : 6 = 12 км/ч

Узнаем во сколько раз автомобиль двигался быстрее велосипедиста. Для этого найдем отношение 48 к 12

Ответ: автомобиль двигался быстрее велосипедиста в 4 раза.

Задача 4. Вертолет преодолел расстояние в 600 км со скоростью 120 км/ч. Сколько времени он был в полете?

Решение

Если за 1 час вертолет преодолевал 120 километров, то узнав сколько таких 120 километров в 600 километрах, мы определим сколько времени он был в полете. Чтобы найти время, нужно пройденное расстояние разделить на скорость движения

600 : 120 = 5 часов

Ответ: вертолет был в пути 5 часов.

Задача 5. Вертолет летел 6 часов со скоростью 160 км/ч. Какое расстояние он преодолел за это время?

Решение

Если за 1 час вертолет преодолевал 160 км, то за 6 часов, он преодолел в шесть раз больше. Чтобы определить расстояние, нужно скорость движения умножить на время

160 × 6 = 960 км

Ответ: за 6 часов вертолет преодолел 960 км.

Задача 6. Расстояние от Перми до Казани, равное 723 км, автомобиль проехал за 13 часов. Первые 9 часов он ехал со скоростью 55 км/ч. Определить скорость автомобиля в оставшееся время.

Решение

Определим сколько километров автомобиль проехал за первые 9 часов. Для этого умножим скорость с которой он ехал первые девять часов (55км/ч) на 9

55 × 9 = 495 км

Определим сколько осталось проехать. Для этого вычтем из общего расстояния (723км) расстояние, пройденное за первые 9 часов движения

723 − 495 = 228 км

Эти 228 километров автомобиль проехал за оставшиеся 4 часа. Чтобы определить скорость автомобиля в оставшееся время, нужно 228 километров разделить на 4 часа:

228 : 4 = 57 км/ч

Ответ: скорость автомобиля в оставшееся время составляла 57 км/ч

Скорость сближения

Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.

Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причем скорость первого будет 100 м/м, а второго — 105 м/м, то скорость сближения будет составлять 100 + 105, то есть 205 м/м. Это значит, что каждую минуту расстояние между пешеходами будет уменьшáться на 205 метров

Чтобы найти скорость сближения, нужно сложить скорости объектов.

Предположим, что пешеходы встретились через три минуты после начала движения. Зная, что они встретились через три минуты, мы можем узнать расстояние между двумя пунктами.

Каждую минуту пешеходы преодолевали расстояние равное двухсот пяти метрам. Через 3 минуты они встретились. Значит умножив скорость сближения на время движения, можно определить расстояние между двумя пунктами:

205 × 3 = 615 метров

Можно и по другому определить расстояние между пунктами. Для этого следует найти расстояние, которое прошел каждый пешеход до встречи.

Так, первый пешеход шел со скоростью 100 метров в минуту. Встреча состоялась через три минуты, значит за 3 минуты он прошел 100 × 3 метров

100 × 3 = 300 метров

А второй пешеход шел со скоростью 105 метров в минуту. За три минуты он прошел 105 × 3 метров

105 × 3 = 315 метров

Теперь можно сложить полученные результаты и таким образом определить расстояние между двумя пунктами:

300 м + 315 м = 615 м

Задача 1. Из двух населенных пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 10 км/ч, а скорость второго — 12 км/ч. Через 2 часа они встретились. Определите расстояние между населенными пунктами

Решение

Найдем скорость сближения велосипедистов

10 км/ч + 12 км/ч = 22 км/ч

Определим расстояние между населенными пунктами. Для этого скорость сближения умножим на время движения

22 × 2 = 44 км

Решим эту задачу вторым способом. Для этого найдем расстояния, пройденные велосипедистами и сложим полученные результаты.

Найдем расстояние, пройденное первым велосипедистом:

10 × 2 = 20 км

Найдем расстояние, пройденное вторым велосипедистом:

12 × 2 = 24 км

Сложим полученные расстояния:

20 км + 24 км = 44 км

Ответ: расстояние между населенными пунктами составляет 44 км.

Задача 2. Из двух населенных пунктов, расстояние между которыми 60 км, навстречу друг другу выехали одновременно два велосипедиста.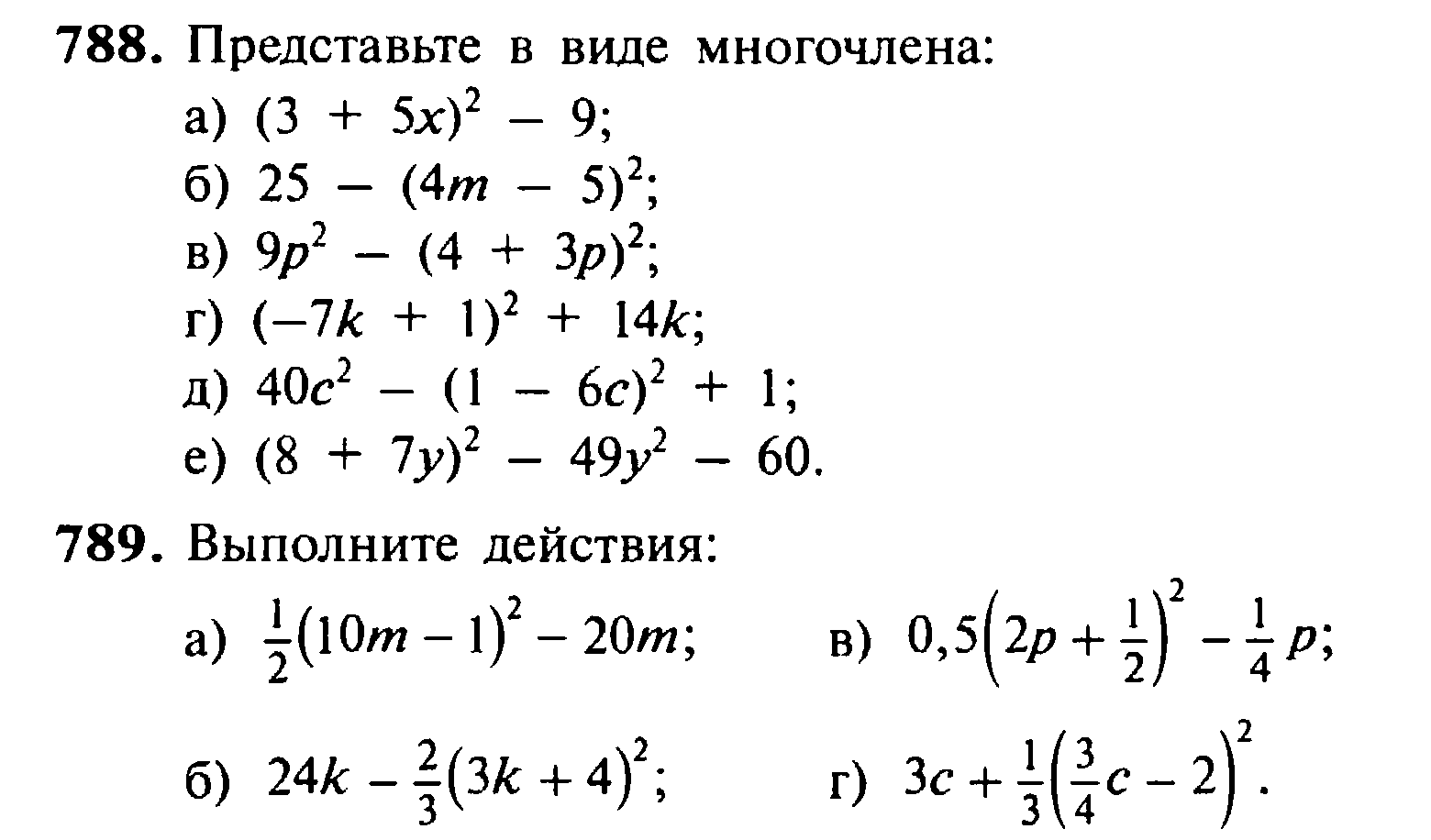 Скорость первого велосипедиста 14 км/ч, а скорость второго — 16 км/ч. Через сколько часов они встретились?

Решение

Найдем скорость сближения велосипедистов:

14 км/ч + 16 км/ч = 30 км/ч

За один час расстояние между велосипедистами уменьшается на 30 километров. Чтобы определить через сколько часов они встретятся, нужно расстояние между населенными пунктами разделить на скорость сближения:

60 : 30 = 2 часа

Значит велосипедисты встретились через два часа

Ответ: велосипедисты встретились через 2 часа.

Задача 3. Из двух населенных пунктов, расстояние между которыми 56 км, навстречу друг другу выехали одновременно два велосипедиста. Через два часа они встретились. Первый велосипедист ехал со скоростью 12 км/ч. Определить скорость второго велосипедиста.

Решение

Определим расстояние пройденное первым велосипедистом. Как и второй велосипедист в пути он провел 2 часа. Умножив скорость первого велосипедиста на 2 часа, мы сможем узнать сколько километров он прошел до встречи

12 × 2 = 24 км

За два часа первый велосипедист прошел 24 км. За один час он прошел 24:2, то есть 12 км. Изобразим это графически

Вычтем из общего расстояния (56 км) расстояние, пройденное первым велосипедистом (24 км). Так мы определим сколько километров прошел второй велосипедист:

56 км − 24 км = 32 км

Второй велосипедист, как и первый провел в пути 2 часа. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:

32 : 2 = 16 км/ч

Значит скорость второго велосипедиста составляет 16 км/ч.

Ответ: скорость второго велосипедиста составляет 16 км/ч.

Скорость удаления

Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.

Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причем скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4+6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиться на 10 километров.

Чтобы найти скорость удаления, нужно сложить скорости объектов.

Так, за первый час расстояние между пешеходами будет составлять 10 километров. На следующем рисунке можно увидеть, как это происходит

Видно, что первый пешеход прошел свои 4 километра за первый час. Второй пешеход также прошел свои 6 километров за первый час. Итого за первый час расстояние между ними стало 4+6, то есть 10 километров.

Через два часа расстояние между пешеходами будет составлять 10×2, то есть 20 километров. На следующем рисунке можно увидеть, как это происходит:

Задача 1. От одной станции отправились одновременно в противоположных направлениях товарный поезд и пассажирский экспресс. Скорость товарного поезда составляла 40 км/ч, скорость экспресса 180 км/ч. Какое расстояние будет между этими поездами через 2 часа?

Решение

Определим скорость удаления поездов. Для этого сложим их скорости:

40 + 180 = 220 км/ч

Получили скорость удаления поездов равную 220 км/ч. Данная скорость показывает, что за час расстояние между поездами будет увеличиваться на 220 километров. Чтобы узнать какое расстояние будет между поездами через два часа, нужно 220 умножить на 2

220 × 2 = 440 км

Ответ: через 2 часа расстояние будет между поездами будет 440 километров.

Задача 2. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 16 км/ч, а скорость мотоциклиста — 40 км/ч. Какое расстояние будет между велосипедистом и мотоциклистом через 2 часа?

Решение

Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:

16 км/ч + 40 км/ч = 56 км/ч

Определим расстояние, которое будет между велосипедистом и мотоциклистом через 2 часа. Для этого скорость удаления (56км/ч) умножим на 2 часа

56 × 2 = 112 км

Ответ: через 2 часа расстояние между велосипедистом и мотоциклистом будет 112 км.

Задача 3. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 10 км/ч, а скорость мотоциклиста — 30 км/ч. Через сколько часов расстояние между ними будет 80 км?

Решение

Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:

10 км/ч + 30 км/ч = 40 км/ч

За один час расстояние между велосипедистом и мотоциклистом увеличивается на 40 километров. Чтобы узнать через сколько часов расстояние между ними будет 80 км, нужно определить сколько раз 80 км содержит по 40 км

80 : 40 = 2

Ответ: через 2 часа после начала движения, между велосипедистом и мотоциклистом будет 80 километров.

Задача 4. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Через 2 часа расстояние между ними было 90 км. Скорость велосипедиста составляла 15 км/ч. Определить скорость мотоциклиста

Решение

Определим расстояние, пройденное велосипедистом за 2 часа. Для этого умножим его скорость (15 км/ч) на 2 часа

15 × 2 = 30 км

На рисунке видно, что велосипедист прошел по 15 километров в каждом часе. Итого за два часа он прошел 30 километров.

Вычтем из общего расстояния (90 км) расстояние, пройденное велосипедистом (30 км). Так мы определим сколько километров прошел мотоциклист:

90 км − 30 км = 60 км

Мотоциклист за два часа прошел 60 километров. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:

60 : 2 = 30 км/ч

Значит скорость мотоциклиста составляла 30 км/ч.

Ответ: скорость мотоциклиста составляла 30 км/ч.

Задача на движение объектов в одном направлении

В предыдущей теме мы рассматривали задачи в которых объекты (люди, машины, лодки) двигались либо навстречу другу другу либо в противоположных направлениях. При этом мы находили различные расстояния, которые изменялись между объектами в течении определенного времени. Эти расстояния были либо скоростями сближения либо скоростями удаления.

В первом случае мы находили скорость сближения — в ситуации, когда два объекта двигались навстречу друг другу. За единицу времени расстояние между объектами уменьшалось на определенное расстояние

Во втором случае мы находили скорость удаления — в ситуации, когда два объекта двигались в противоположных направлениях. За единицу времени расстояние между объектами увеличивалось на определенное расстояние

Но объекты также могут двигаться в одном направлении, причем с различной скоростью. Например, из одного пункта одновременно могут выехать велосипедист и мотоциклист, причем скорость велосипедиста может составлять 20 километров в час, а скорость мотоциклиста — 40 километров в час

На рисунке видно, что мотоциклист впереди велосипедиста на двадцать километров. Связано это с тем, что в час он преодолевает на 20 километров больше, чем велосипедист. Поэтому каждый час расстояние между велосипедистом и мотоциклистом будет увеличиваться на двадцать километров.

В данном случае 20 км/ч являются скоростью удаления мотоциклиста от велосипедиста.

Через два часа расстояние, пройденное велосипедистом будет составлять 40 км. Мотоциклист же проедет 80 км, отдалившись от велосипедиста еще на двадцать километров — итого расстояние между ними составит 40 километров

Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.

В приведенном выше примере, скорость удаления составляет 20 км/ч. Её можно найти путем вычитания скорости велосипедиста из скорости мотоциклиста. Скорость велосипедиста составляла 20 км/ч, а скорость мотоциклиста — 40 км/ч. Скорость мотоциклиста больше, поэтому из 40 вычитаем 20

40 км/ч − 20 км/ч = 20 км/ч

Задача 1. Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 120 км/ч, а скорость автобуса 80 км/ч. Какое расстояние будет между ними через 1 час? 2 часа?

Решение

Найдем скорость удаления. Для этого из большей скорости вычтем меньшую

120 км/ч − 80 км/ч = 40 км/ч

Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 2 часа в два раза больше:

40 × 2 = 80 км

Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через два часа — 80 км.

Рассмотрим ситуацию в которой объекты начали свое движение из разных пунктов, но в одном направлении.

Пусть имеется дом, школа и аттракцион. От дома до школы 700 метров

Два пешехода отправились в аттракцион в одно и то же время. Причем первый пешеход отправился в аттракцион от дома со скоростью 100 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 80 метров в минуту. Какое расстояние будет между пешеходами через 2 минуты? Через сколько минут после начала движения первый пешеход догонит второго?

Ответим на первый вопрос задачи — какое расстояние будет между пешеходами через 2 минуты?

Определим расстояние, пройденное первым пешеходом за 2 минуты. Он двигался со скоростью 100 метров в минуту. За две минуты он пройдет в два раза больше, то есть 200 метров

100 × 2 = 200 метров

Определим расстояние, пройденное вторым пешеходом за 2 минуты. Он двигался со скоростью 80 метров в минуту. За две минуты он пройдет в два раза больше, то есть 160 метров

80 × 2 = 160 метров

Теперь нужно найти расстояние между пешеходами

Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (700м) прибавить расстояние, пройденное вторым пешеходом (160м) и из полученного результата вычесть расстояние, пройденное первым пешеходом (200м)

700 м + 160 м = 860 м

860 м − 200 м = 660 м

Либо из расстояния от дома до школы (700м) вычесть расстояние, пройденное первым пешеходом (200м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (160м)

700 м − 200 м = 500 м

500 м + 160 м = 660 м

Таким образом, через две минуты расстояние между пешеходами будет составлять 660 метров

Попробуем ответить на следующий вопрос задачи: через сколько минут после начала движения первый пешеход догонит второго?

Давайте посмотрим какой была ситуация в самом начале пути — когда пешеходы еще не начали своё движение

Как видно на рисунке, расстояние между пешеходами в начале пути составляло 700 метров. Но уже через минуту после начала движения расстояние между ними будет составлять 680 метров, поскольку первый пешеход двигается на 20 метров быстрее второго:

100 м × 1 = 100 м

80 м × 1 = 80 м

700 м + 80 м − 100 м = 780 м − 100 м = 680 м

Через две минуты после начала движения, расстояние уменьшится еще на 20 метров и будет составлять 660 метров. Это был наш ответ на первый вопрос задачи:

100 м × 2 = 200 м

80 м × 2 = 160 м

700 м + 160 м − 200м = 860 м − 200 м = 660 м

Через три минуты расстояние уменьшится еще на 20 метров и будет уже составлять 640 метров:

100 м × 3 = 300 м

80 м × 3 = 240 м

700 м + 240 м − 300м = 940 м − 300 м = 640 м

Мы видим, что с каждой минутой первый пешеход будет приближáться ко второму на 20 метров, и в конце концов догонит его. Можно сказать, что скорость равная двадцати метрам в минуту является скоростью сближения пешеходов. Правила нахождения скорости сближения и удаления при движении в одном направлении идентичны.

Чтобы найти скорость сближения при движении в одном направлении, нужно из большей скорости вычесть меньшую.

А раз изначальные 700 метров с каждой минутой уменьшаются на одинаковые 20 метров, то мы можем узнать сколько раз 700 метров содержат по 20 метров, тем самым определяя через сколько минут первый пешеход догонит второго

700 : 20 = 35

Значит через 35 минут после начала движения первый пешеход догонит второго. Для интереса узнаем сколько метров прошел к этому времени каждый пешеход. Первый двигался со скоростью 100 метров в минуту. За 35 минут он прошел в 35 раз больше

100 × 35 = 3500 м

Второй шел со скоростью 80 метров в минуту. За 35 минут он прошел в 35 раз больше

80 × 35 = 2800 м

Первый прошел 3500 метров, а второй 2800 метров. Первый прошел на 700 метров больше, поскольку он шел от дома. Если вычесть эти 700 метров из 3500, то мы получим 2800 м

Рассмотрим ситуацию в которой объекты движутся в одном направлении, но один из объектов начал своё движение раньше другого.

Пусть имеется дом и школа. Первый пешеход отправился в школу со скоростью 80 метров в минуту. Через 5 минут вслед за ним в школу отправился второй пешеход со скоростью 100 метров в минуту. Через сколько минут второй пешеход догонит первого?

Второй пешеход начал свое движение через 5 минут. К этому времени первый пешеход уже отдалился от него на какое-то расстояние. Найдём это расстояние. Для этого умножим его скорость (80 м/м) на 5 минут

80 × 5 = 400 метров

Первый пешеход отдалился от второго на 400 метров. Поэтому в момент, когда второй пешеход начнет свое движение, между ними будут эти самые 400 метров.

Но второй пешеход двигается со скоростью 100 метров в минуту. То есть двигается на 20 метров быстрее первого пешехода, а значит с каждой минутой расстояние между ними будет уменьшáться на 20 метров. Наша задача узнать через сколько минут это произойдет.

Например, уже через минуту расстояние между пешеходами будет составлять 380 метров. Первый пешеход к своим 400 метрам пройдет еще 80 метров, а второй пройдет 100 метров

Принцип здесь такой-же, как и в предыдущей задаче. Расстояние между пешеходами в момент движения второго пешехода необходимо разделить на скорость сближения пешеходов. Скорость сближения в данном случае равна двадцати метрам. Поэтому, чтобы определить через сколько минут второй пешеход догонит первого, нужно 400 метров разделить на 20

400 : 20 = 20

Значит через 20 минут второй пешеход догонит первого.

Задача 2. Из двух сел, расстояние между которыми 40 км, одновременно в одном направлении выехали автобус и велосипедист. Скорость велосипедиста 15 км/ч, а скорость автобуса 35 км/ч. Через сколько часов автобус догонит велосипедиста?

Решение

Найдем скорость сближения

35 км/ч − 15 км/ч = 20 км/ч

Определим через часов автобус догонит велосипедиста

40 : 20 = 2

Ответ: автобус догонит велосипедиста через 2 часа.

Задача на движение по реке

Суда двигаются по реке с различной скоростью. При этом они могут двигаться, как по течению реки, так и против течения. В зависимости от того, как они двигаются (по или против течения), скорость будет меняться.

Предположим, что скорость реки составляет 3 км/ч. Если спустить лодку на реку, то река унесет лодку со скоростью 3 км/ч.

Если спустить лодку на стоячую воду, в которой отсутствует течение, то и лодка будет стоять. Скорость движения лодки в этом случае будет равна нулю.

Если лодка плывет по стоячей воде, в которой отсутствует течение, то говорят, что лодка плывет с собственной скоростью.

Например, если моторная лодка плывет по стоячей воде со скоростью 40 км/ч, то говорят что собственная скорость моторной лодки составляет 40 км/ч.

Как определить скорость судна?

Если судно плывет по течению реки, то к собственной скорости судна нужно прибавить скорость течения реки.

Например, если моторная лодка плывет со скоростью 30 км/ч по течению реки, и скорость течения реки составляет 2 км/ч, то к собственной скорости моторной лодки (30 км/ч) необходимо прибавить скорость течения реки (2 км/ч)

30 км/ч + 2 км/ч = 32 км/ч

Течение реки можно сказать помогает моторной лодке дополнительной скоростью равной двум километрам в час.

Если судно плывет против течения реки, то из собственной скорости судна нужно вычесть скорость течения реки.

Например, если моторная лодка плывет со скоростью 30 км/ч против течения реки, и скорость течения реки составляет 2 км/ч, то из собственной скорости моторной лодки (30 км/ч) необходимо вычесть скорость течения реки (2 км/ч)

30 км/ч − 2 км/ч = 28 км/ч

Течение реки в этом случае препятствует моторной лодке свободно двигаться вперед, снижая её скорость на два километра в час.

Задача 1. Скорость катера 40 км/ч, а скорость течения реки 3 км/ч. С какой скоростью катер будет двигаться по течению реки? Против течения реки?

Ответ:

Если катер будет двигаться по течения реки, то скорость его движения составит 40 + 3, то есть 43 км/ч.

Если катер будет двигаться против течения реки, то скорость его движения составит 40 − 3, то есть 37 км/ч.

Задача 2. Скорость теплохода в стоячей воде — 23 км/ч. Скорость течения реки — 3 км/ч. Какой путь пройдет теплоход за 3 часа по течению реки? Против течения?

Решение

Собственная скорость теплохода составляет 23 км/ч. Если теплоход будет двигаться по течению реки, то скорость его движения составит 23 + 3, то есть 26 км/ч. За три часа он пройдет в три раза больше

26 × 3 = 78 км

Если теплоход будет двигаться против течения реки, то скорость его движения составит 23 − 3, то есть 20 км/ч. За три часа он пройдет в три раза больше

20 × 3 = 60 км

Задача 3. Расстояние от пункта А до пункта B лодка преодолела за 3 часа 20 минут, а расстояние от пункта B до А — за 2 часа 50 минут. В каком направлении течет река: от А к В или от В к А, если известно, что скорость яхты не менялась?

Решение

Скорость яхты не менялась. Узнаем на какой путь она затратила больше времени: на путь от А до В или на путь от В до А. Тот путь, который затратил больше времени будет тем путем, течение реки которого шло против яхты

3 часа 20 минут больше, чем 2 часа 50 минут. Это значит, что течение реки снизило скорость яхты и это отразилось на времени пути. 3 часа 20 минут это время, затраченное на путь от от А до В. Значит река течет от пункта B к пункту А

Задача 4. За какое время при движении против течения реки
теплоход пройдет 204 км, если его собственная скорость
15 км/ч, а скорость течения в 5 раз меньше собственной
скорости теплохода?

Решение

Требуется найти время за которое теплоход пройдет 204 километра против течения реки. Собственная скорость теплохода составляет 15 км/ч. Двигается он против течения реки, поэтому нужно определить его скорость при таком движении.

Чтобы определить скорость против течения реки, нужно из собственной скорости теплохода (15 км/ч) вычесть скорость движения реки. В условии сказано, что скорость течения реки в 5 раз меньше собственной скорости теплохода, поэтому сначала определим скорость течения реки. Для этого уменьшим 15 км/ч в пять раз

15 : 5 = 3 км/ч

Скорость течения реки составляет 3 км/ч. Вычтем эту скорость из скорости движения теплохода

15 км/ч − 3 км/ч = 12 км/ч

Теперь определим время за которое теплоход пройдет 204 км при скорости 12 км/ч. В час теплоход проходит 12 километров. Чтобы узнать за сколько часов он пройдет 204 километра, нужно определить сколько раз 204 километра содержит по 12 километров

204 : 12 = 17 ч

Ответ: теплоход пройдет 204 километра за 17 часов

Задача 5. Двигаясь по течению реки, за 6 часов лодка
прошла 102 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.

Решение

Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (102км) разделим на время движения (6ч)

102 : 6 = 17 км/ч

Определим собственную скорость лодки. Для этого из скорости по которой она двигалась по реке (17 км/ч) вычтем скорость течения реки (4 км/ч)

17 − 4 = 13 км/ч

Задача 6. Двигаясь против течения реки, за 5 часов лодка
прошла 110 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.

Решение

Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (110км) разделим на время движения (5ч)

110 : 5 = 22 км/ч

Определим собственную скорость лодки. В условии сказано, что она двигалась против течения реки. Скорость течения реки составляла 4 км/ч.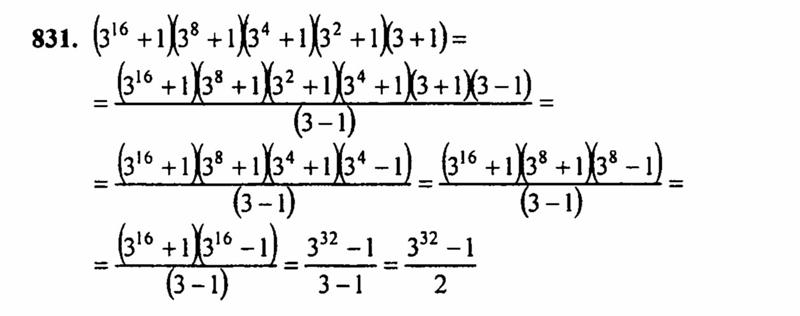 Это значит, что собственная скорость лодки была уменьшена на 4. Наша задача прибавить эти 4 км/ч и узнать собственную скорость лодки

22 + 4 = 26 км/ч

Ответ: собственная скорость лодки составляет 26 км/ч

Задача 7. За какое время при движении против течения реки лодка
пройдет 56 км, если скорость течения – 2 км/ч, а её
собственная скорость на 8 км/ч больше скорости течения?

Решение

Найдем собственную скорость лодки. В условии сказано, что она на 8 км/ч больше скорости течения. Поэтому для определения собственной скорости лодки, к скорости течения (2 км/ч) прибавим еще 8 км/ч

2 км/ч + 8 км/ч = 10 км/ч

Лодка движется против течения реки, поэтому из собственной скорости лодки (10 км/ч) вычтем скорость движения реки (2 км/ч)

10 км/ч − 2 км/ч = 8 км/ч

Узнаем за какое время лодка пройдет 56 км. Для этого расстояние (56км) разделим на скорость движения лодки:

56 : 8 = 7 ч

Ответ: при движении против течения реки лодка пройдет 56 км за 7 часов

Задачи для самостоятельного решения

Задача 1. Сколько времени потребуется пешеходу, чтобы пройти 20 км, если скорость его равна 5 км/ч?

Решение

За один час пешеход проходит 5 километров. Чтобы определить за какое время он пройдет 20 км, нужно узнать сколько раз 20 километров содержат по 5 км. Либо воспользоваться правилом нахождения времени: разделить пройденное расстояние на скорость движения

20 : 5 = 4 часа

Задача 2. Из пункта А в пункт В велосипедист ехал 5 часов со скоростью 16 км/ч, а обратно он ехал по тому же пути со скоростью 10 км/ч. Сколько времени потратил велосипедист на обратный путь?

Решение

Определим расстояние от пункта А до пункта В. Для этого умножим скорость с которой ехал велосипедист из пункта А в пункт В (16км/ч) на время движения (5ч)

16 × 5 = 80 км

Определим сколько времени велосипедист затратил на обратный путь. Для этого расстояние (80км) разделим на скорость движения (10км/ч)

80 : 10 = 8 ч

Задача 3. Велосипедист ехал 6 ч с некоторой скоростью. После того как он проехал ещё 11 км с той же скоростью, его путь стал равным 83 км. С какой скоростью ехал велосипедист?

Решение

Определим путь, пройденный велосипедистом за 6 часов. Для этого из 83 км вычтем путь, который он прошел после шести часов движения (11км)

83 − 11 = 72 км

Определим с какой скоростью ехал велосипедист первые 6 часов. Для этого разделим 72 км на 6 часов

72 : 6 = 12 км/ч

Поскольку в условии задаче сказано, что остальные 11 км велосипедист проехал с той же скоростью, что и в первые 6 часов движения, то скорость равная 12 км/ч является ответом к задаче.

Ответ: велосипедист ехал со скоростью 12 км/ч.

Задача 4. Двигаясь против течения реки, расстояние в 72 км теплоход проходит за 4ч, а плот такое же расстояние проплывает за 36 ч. За сколько часов теплоход проплывет расстояние 110 км, если будет плыть по течению реки?

Решение

Найдем скорость течения реки. В условии сказано, что плот может проплыть 72 километра за 36 часов. Плот не может двигаться против течения реки. Значит скорость плота с которой он преодолевает эти 72 километра и является скоростью течения реки. Чтобы найти эту скорость, нужно 72 километра разделить на 36 часов

72 : 36 = 2 км/ч

Найдем собственную скорость теплохода. Сначала найдем скорость его движения против течения реки. Для этого разделим 72 километра на 4 часа

72 : 4 = 18 км/ч

Если против течения реки скорость теплохода составляет 18 км/ч, то собственная его скорость равна 18+2, то есть 20 км/ч. А по течению реки его скорость будет составлять 20+2, то есть 22 км/ч

Разделив 110 километров на скорость движения теплохода по течению реки (22 км/ч), можно узнать за сколько часов теплоход проплывет эти 110 километров

110 : 22 = 5 ч

Ответ: по течению реки теплоход проплывет 110 километров за 5 часов.

Задача 5. Из одного пункта одновременно в противоположных направлениях выехали два велосипедиста. Один из них ехал со скоростью 11 км/ч, а второй со скоростью 13 км/ч. Какое расстояние будет между ними через 4 часа?

Решение

Найдем скорость удаления велосипедистов

11 + 13 = 24 км

Узнаем какое расстояние будет между ними через 4 часа

24 × 4 = 96 км

Ответ: через 4 часа расстояние между велосипедистами будет 96 км.

Задача 6. От двух пристаней одновременно навстречу друг другу отошли два теплохода, и через 6 часов они встретились. Какое расстояние до встречи прошел каждый теплоход и какое расстояние между пристанями, если один теплоход шел со скоростью 21 км/ч, а другой — со скоростью 24 км/ч?

Решение

Определим расстояние, пройденное первым теплоходом. Для этого умножим его скорость (21 км/ч) на время движения до встречи (6ч)

21 × 6 = 126 км

Определим расстояние, пройденное вторым теплоходом. Для этого умножим его скорость (24 км/ч) на время движения до встречи (6ч)

24 × 6 = 144 км

Определим расстояние между пристанями. Для этого сложим расстояния, пройденные первым и вторым теплоходами

126 км + 144 км = 270 км

Ответ: первый теплоход прошел 126 км, второй — 144 км. Расстояние между пристанями составляет 270 км.

Задача 7. Одновременно из Москвы и Уфы вышли два поезда. Через 16 часов они встретились. Московский поезд шел со скоростью 51 км/ч. С какой скоростью шел поезд, вышедший из Уфы, если расстояние между Москвой и Уфой 1520 км? Какое расстояние было между поездами через 5 часов после их встречи?

Решение

Определим сколько километров до встречи прошел поезд, вышедший из Москвы. Для этого умножим его скорость (51 км/ч) на 16 часов

51 × 16 = 816 км

Узнаем сколько километров до встречи прошел поезд, вышедший из Уфы. Для этого из расстояния между Москвой и Уфой (1520км) вычтем расстояние, пройденное поездом, вышедшим из Москвы

1520 − 816 = 704 км

Определим скорость с которой шел поезд, вышедший из Уфы. Для этого расстояние, пройденное им до встречи, нужно разделить на 16 часов

704 : 16 = 44 км/ч

Определим расстояние, которое будет между поездами через 5 часов после их встречи. Для этого найдем скорость удаления поездов и умножим эту скорость на 5

51 км/ч + 44 км/ч = 95 км/ч

95 × 5 = 475 км.

Ответ: поезд, вышедший из Уфы, шел со скоростью 44 км/ч. Через 5 часов после их встречи поездов расстояние между ними будет составлять 475 км.

Задача 8. Из одного пункта одновременно в противоположных направлениях отправились два автобуса. Скорость одного автобуса 48 км/ч, другого на 6 км/ч больше. Через сколько часов расстояние между автобусами будет равно 510 км?

Решение

Найдем скорость второго автобуса. Она на 6 км/ч больше скорости первого автобуса

48 км/ч + 6 км/ч = 54 км/ч

Найдем скорость удаления автобусов. Для этого сложим их скорости:

48 км/ч + 54 км/ч = 102 км/ч

За час расстояние между автобусами увеличивается на 102 километра. Чтобы узнать через сколько часов расстояние между ними будет 510 км, нужно узнать сколько раз 510 км содержит по 102 км/ч

510 : 102 = 5 ч

Ответ: 510 км между автобусами будет через 5 часов.

Задача 9. Расстояние от Ростова-на-Дону до Москвы 1230 км. Из Москвы и Ростова навстречу друг другу вышли два поезда. Поезд из Москвы идет со скоростью 63 км/ч, а скорость ростовского поезда составляет скорости московского поезда. На каком расстоянии от Ростова встретятся поезда?

Решение

Найдем скорость ростовского поезда. Она составляет скорости московского поезда. Поэтому чтобы определить скорость ростовского поезда, нужно найти от 63 км

63 : 21 × 20 = 3 × 20 = 60 км/ч

Найдем скорость сближения поездов

63 км/ч + 60 км/ч = 123 км/ч

Определим через сколько часов поезда встретятся

1230 : 123 = 10 ч

Узнаем на каком расстоянии от Ростова встретятся поезда. Для этого достаточно найти расстояние, пройденное ростовским поездом до встречи

60 × 10 = 600 км.

Ответ: поезда встретятся на расстоянии 600 км от Ростова.

Задача 10. От двух пристаней, расстояние между которыми 75 км, навстречу друг другу одновременно отошли две моторные лодки. Одна шла со скоростью 16 км/ч, а скорость другой составляла 75% скорости первой лодки. Какое расстояние будет между лодками через 2 ч?

Решение

Найдем скорость второй лодки. Она составляет 75% скорости первой лодки. Поэтому чтобы найти скорость второй лодки, нужно 75% от 16 км

16 × 0,75 = 12 км/ч

Найдем скорость сближения лодок

16 км/ч + 12 км/ч = 28 км/ч

С каждым часом расстояние между лодками будет уменьшáться на 28 км. Через 2 часа оно уменьшится на 28×2, то есть на 56 км. Чтобы узнать какое будет расстояние между лодками в этот момент, нужно из 75 км вычесть 56 км

75 км − 56 км = 19 км

Ответ: через 2 часа между лодками будет 19 км.

Задача 11. Легковая машина, скорость которой 62 км/ч, догоняет грузовую машину, скорость которой 47 км/ч. Через сколько времени и на каком расстоянии от начала движения легковая автомашина догонит грузовую, если первоначальное расстояние между ними было 60 км?

Решение

Найдем скорость сближения

62 км/ч − 47 км/ч = 15 км/ч

Если первоначально расстояние между машинами было 60 километров, то с каждым часом это расстояние будет уменьшáться на 15 км, и в конце концов легковая машина догонит грузовую. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 60 км содержит по 15 км

60 : 15 = 4 ч

Узнаем на каком расстоянии от начала движения легковая машина догнала грузовую. Для этого умножим скорость легковой машины (62 км/ч) на время её движения до встречи (4ч)

62 × 4 = 248 км

Ответ: легковая машина догонит грузовую через 4 часа. В момент встречи легковая машина будет на расстоянии 248 км от начала движения.

Задача 12. Из одного пункта в одном направлении одновременно выезжали два мотоциклиста. Скорость одного 35 км/ч, а скорость другого составляла 80% скорости первого мотоциклиста. Какое расстояние будет между ними через 5 часов?

Решение

Найдем скорость второго мотоциклиста. Она составляет 80% скорости первого мотоциклиста. Поэтому чтобы найти скорость второго мотоциклиста, нужно найти 80% от 35 км/ч

35 × 0,80 = 28 км/ч

Первый мотоциклист двигается на 35-28 км/ч быстрее

35 км/ч − 28 км/ч = 7 км/ч

За один час первый мотоциклиста преодолевает на 7 километров больше. С каждым часом она будет приближáться ко второму мотоциклисту на эти 7 километров.

Через 5 часов первый мотоциклист пройдет 35×5, то есть 175 км, а второй мотоциклист пройдет 28×5, то есть 140 км. Определим расстояние, которое между ними. Для этого из 175 км вычтем 140 км

175 − 140 = 35 км

Ответ: через 5 часов расстояние между мотоциклистами будет 35 км.

Задача 13. Мотоциклист, скорость которого 43 км/ч, догоняет велосипедиста, скорость которого 13 км/ч. Через сколько часов мотоциклист догонит велосипедиста, если первоначальное расстояние между ними было 120 км?

Решение

Найдем скорость сближения:

43 км/ч − 13 км/ч = 30 км/ч

Если первоначально расстояние между мотоциклистом и велосипедистом было 120 километров, то с каждым часом это расстояние будет уменьшáться на 30 км, и в конце концов мотоциклист догонит велосипедиста. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 120 км содержит по 30 км

120 : 30 = 4 ч

Значит через 4 часа мотоциклист догонит велосипедиста

На рисунке представлено движение мотоциклиста и велосипедиста. Видно, что через 4 часа после начала движения они сровнялись.

Ответ: мотоциклист догонит велосипедиста через 4 часа.

Задача 14. Велосипедист, скорость которого 12 км/ч, догоняет велосипедиста, скорость которого составляет 75 % его скорости. Через 6 часов второй велосипедист догнал велосипедиста, ехавшего первым. Какое расстояние было между велосипедистами первоначально?

Решение

Определим скорость велосипедиста, ехавшего впереди. Для этого найдем 75% от скорости велосипедиста, ехавшего сзади:

12 × 0,75 = 9 км/ч — скорость ехавшего впереди

Узнаем сколько километров проехал каждый велосипедист до того, как второй догнал первого:

12 × 6 = 72 км — проехал ехавший сзади
9 × 6 = 54 км — проехал ехавший впереди

Узнаем какое расстояние было между велосипедистами первоначально. Для этого из расстояния, пройденного вторым велосипедистом (который догонял) вычтем расстояние, пройденное первым велосипедистом (которого догнали)

72 км − 54 км = 18 км

Ответ: между велосипедистами первоначально было 18 км.

Задача 15. Автомобиль и автобус выехали одновременно из одного пункта в одном направлении. Скорость автомобиля 53 км/ч, скорость автобуса 41 км/ч. Через сколько часов после выезда автомобиль будет впереди автобуса на 48 км?

Решение

Найдем скорость удаления автомобиля от автобуса

53 км/ч − 41 км/ч = 12 км/ч

С каждым часом автомобиль будет удаляться от автобуса на 12 километров. На рисунке показано положение машин после первого часа движения

Видно, что автомобиль впереди автобуса на 12 км.

Чтобы узнать через сколько часов автомобиль будет впереди автобуса на 48 километров, нужно определить сколько раз 48 км содержит по 12 км

48 : 12 = 4 ч

Ответ: через 4 часа после выезда автомобиль будет впереди автобуса на 48 километров.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Иллюстративная математика

Иллюстративная математика

7 класс

7.РП. 7 класс — Соотношения и пропорциональные отношения


7.РП.А. Анализируйте пропорциональные отношения и используйте их для решения реальных и математических задач.




7.РП.А.1. Вычислить удельные ставки, связанные с отношениями фракций, включая отношения длин, площадей и других величин, измеренных в одинаковых или разных единицах. Например, если человек проходит $1/2$ мили за каждые $1/4$ часа, рассчитайте удельную норму как комплексную дробь $\frac{1/2}{1/4}$ миль в час, что эквивалентно $2$ миль. в час.

7.РП.А.2. Распознавать и представлять пропорциональные отношения между величинами.


7.РП.А.2.а. Определите, находятся ли две величины в пропорциональном соотношении, например, проверив эквивалентные отношения в таблице или нарисовав график на координатной плоскости и наблюдая, является ли график прямой линией, проходящей через начало координат.


7.РП.А.2.б. Определите константу пропорциональности (единичную норму) в таблицах, графиках, уравнениях, схемах и словесных описаниях пропорциональных отношений.

7.RP.A.2.c. Представьте пропорциональные отношения уравнениями.

Например, если общая стоимость $t$ пропорциональна количеству $n$ товаров, купленных по постоянной цене $p$, соотношение между общей стоимостью и количеством товаров может быть выражено как $t = pn$.


7.РП.А.2.д. Объясните, что означает точка $(x, y)$ на графике пропорциональной зависимости с точки зрения ситуации, обратив особое внимание на точки $(0, 0)$ и $(1, r)$, где $r$ является единичной ставкой.

• 
  Пока нет задач, иллюстрирующих этот стандарт.
  

7.РП.А.3. Используйте пропорциональные отношения для решения многошаговых задач соотношения и процентов. Примеры: простые проценты, налоги, надбавки и уценки, чаевые и комиссионные, сборы, процентное увеличение и уменьшение, процентная ошибка.

7.НС. 7 класс — Система счисления


7.Н.С.А. Применяйте и расширяйте прежнее понимание операций с дробями, чтобы складывать, вычитать, умножать и делить рациональные числа.



7.НС.А.1. Применять и расширять прежнее понимание сложения и вычитания, чтобы складывать и вычитать рациональные числа; представляют сложение и вычитание на горизонтальной или вертикальной диаграмме с числовыми линиями.


7.НС.А.1.а. Опишите ситуации, в которых противоположные величины объединяются, чтобы получить 0. Например, атом водорода имеет нулевой заряд, потому что две его составляющие заряжены противоположно.


• 
  Пока нет задач, иллюстрирующих этот стандарт.
  

7.НС.А.1.б. Под $p + q$ понимается число, расположенное на расстоянии $|q|$ от $p$ в положительном или отрицательном направлении, в зависимости от того, является ли число $q$ положительным или отрицательным. Покажите, что число и его противоположность имеют сумму 0 (аддитивные инверсии). Интерпретируйте суммы рациональных чисел, описывая контексты реального мира.


7.NS.A.1.c. Поймите вычитание рациональных чисел как добавление аддитивной обратной, $p — q = p + (-q)$.

Покажите, что расстояние между двумя рациональными числами на числовой прямой равно абсолютному значению их разности, и примените этот принцип в контексте реального мира.

7.NS.A.1.d. Применяйте свойства операций как стратегии сложения и вычитания рациональных чисел.


• 
  Пока нет задач, иллюстрирующих этот стандарт.
  

7.НС.А.2. Применяйте и расширяйте прежнее понимание умножения и деления, а также дробей, чтобы умножать и делить рациональные числа.


7.НС.А.2.а. Поймите, что умножение распространяется с дробей на рациональные числа, требуя, чтобы операции продолжали удовлетворять свойствам операций, в частности свойству распределения, что приводит к таким продуктам, как $(-1)(-1) = 1$ и правилам умножения со знаком числа.Интерпретируйте произведения рациональных чисел, описывая контексты реального мира.


7.НС.А.2.б. Поймите, что целые числа можно делить при условии, что делитель не равен нулю, и каждое частное целых чисел (с ненулевым делителем) является рациональным числом.

Если $p$ и $q$ — целые числа, то $-(p/q) = (-p)/q = p/(-q)$. Интерпретируйте частные рациональных чисел, описывая контексты реального мира.


7.NS.A.2.c. Применяйте свойства операций как стратегии умножения и деления рациональных чисел.

• 
  Пока нет задач, иллюстрирующих этот стандарт.
  

7.NS.A.2.d. Преобразование рационального числа в десятичное с использованием длинного деления; известно, что десятичная форма рационального числа оканчивается на 0 или со временем повторяется.


7.НС.А.3. Решайте реальные и математические задачи, связанные с четырьмя операциями с рациональными числами.

7.EE. 7 класс — Выражения и уравнения


7.Э.А. Используйте свойства операций для создания эквивалентных выражений.


7.EE.A.1. Применяйте свойства операций как стратегии для сложения, вычитания, факторизации и расширения линейных выражений с рациональными коэффициентами.




7.EE.A.2. Поймите, что переписывание выражения в разных формах в контексте задачи может пролить свет на проблему и на то, как связаны в ней величины. Например, $a + 0,05a = 1,05a$ означает, что «увеличить на $5\%$» — это то же самое, что «умножить на $1».05$».


7.Э.Э.Б. Решайте реальные и математические задачи, используя числовые и алгебраические выражения и уравнения.


7.EE.B.3. Решайте многоэтапные задачи из реальной жизни и математические задачи с положительными и отрицательными рациональными числами в любой форме (целые числа, дроби и десятичные дроби), стратегически используя инструменты. Применять свойства операций для вычисления с числами в любой форме; конвертировать между формами по мере необходимости; и оценить обоснованность ответов, используя умственные вычисления и стратегии оценки.Например: если женщина, зарабатывающая $\$25$ в час, получает прибавку в размере $10\%$, она будет дополнительно зарабатывать $\frac{1}{10}$ своей зарплаты в час, или $\$2,50$, за новая зарплата $\$27.

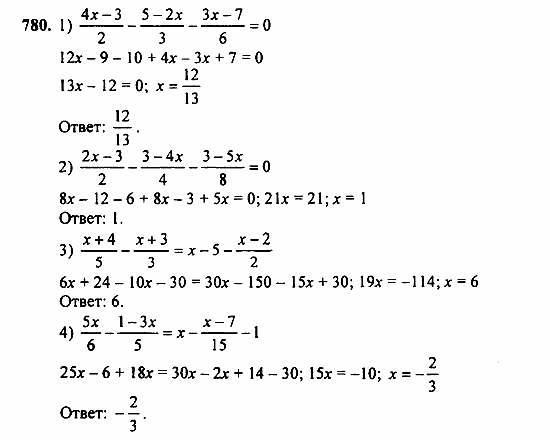50$. Если вы хотите поместить перекладину для полотенец длиной $9 \frac34$ дюймов в центре двери шириной $27 \frac12$ дюймов, вам нужно разместить перекладину на расстоянии около $9$ дюймов от каждого края; эту оценку можно использовать в качестве проверки точного вычисления.


7.EE.B.4. Используйте переменные для представления величин в реальной или математической задаче и создавайте простые уравнения и неравенства для решения задач, рассуждая о величинах.

7.EE.B.4.а. Решите текстовые задачи, ведущие к уравнениям вида $px + q = r$ и $p(x + q) = r$, где $p$, $q$ и $r$ — конкретные рациональные числа. Решите уравнения этих форм бегло. Сравните алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе. Например, периметр прямоугольника равен $54$ см. Его длина $6$ см. Какова его ширина?


• 
  Пока нет задач, иллюстрирующих этот стандарт.

7.EE.B.4.b. Решайте текстовые задачи, приводящие к неравенствам вида $px + q > r$ или $px + q

< r$, где $p$, $q$ и $r$ — конкретные рациональные числа. Нарисуйте график множества решений неравенства и интерпретируйте его в контексте проблемы. Например: как продавец, вам платят 50 долларов в неделю плюс 3 доллара за продажу. На этой неделе вы хотите, чтобы ваша зарплата была не менее $100. Напишите неравенство для количества продаж, которое вам нужно сделать, и опишите решения.

7.Г. 7 класс — Геометрия


7.Г.А. Рисовать, строить и описывать геометрические фигуры и описывать отношения между ними.


7.Г.А.1. Решайте задачи, связанные с чертежами геометрических фигур в масштабе, включая вычисление фактических длин и площадей на основе чертежа в масштабе и воспроизведение чертежа в масштабе в другом масштабе.


7.Г.А.2. Рисовать (от руки, с линейкой и транспортиром и с техникой) геометрические фигуры с заданными условиями.Сосредоточьтесь на построении треугольников по трем мерам углов или сторон, отмечая, когда условия определяют уникальный треугольник, более одного треугольника или отсутствие треугольника.




7.Г.А.3. Опишите двумерные фигуры, которые получаются в результате разрезания трехмерных фигур, например, в плоских сечениях прямоугольных призм и прямоугольных пирамид.


7.Г.Б. Решайте реальные и математические задачи, связанные с измерением угла, площади, площади поверхности и объема.

7.G.B.4. Знать формулы площади и длины окружности и использовать их для решения задач; дать неформальный вывод отношения между длиной окружности и площадью круга.


7.GB.5. Используйте факты о дополнительных, дополнительных, вертикальных и смежных углах в многошаговой задаче, чтобы написать и решить простые уравнения для неизвестного угла в фигуре.


• 
  Пока нет задач, иллюстрирующих этот стандарт.
  

7.G.B.6. Решайте реальные и математические задачи, связанные с площадью, объемом и площадью поверхности двух- и трехмерных объектов, состоящих из треугольников, четырехугольников, многоугольников, кубов и прямых призм.

7.СП. 7 класс — Статистика и вероятность


7.СП.А. Используйте случайную выборку, чтобы сделать выводы о совокупности.


7.СП.А.1. Понимать, что статистику можно использовать для получения информации о населении путем изучения выборки населения; обобщения о совокупности из выборки действительны только в том случае, если выборка репрезентативна для этой совокупности.Поймите, что случайная выборка, как правило, дает репрезентативные выборки и поддерживает достоверные выводы.


7.СП.А.2. Используйте данные из случайной выборки, чтобы сделать выводы о совокупности с неизвестной интересующей характеристикой. Создайте несколько выборок (или смоделированных выборок) одинакового размера, чтобы оценить различия в оценках или прогнозах. Например, оцените среднюю длину слова в книге путем случайной выборки слов из книги; предсказать победителя школьных выборов на основе случайно выбранных данных опроса.Оцените, насколько далеко может быть оценка или прогноз.




7.СП.Б. Сделайте неформальные сравнительные выводы о двух популяциях.


7.СП.Б.3. Неформально оцените степень визуального перекрытия двух распределений числовых данных с похожими вариациями, измеряя разницу между центрами, выражая ее как кратную меру вариабельности. Например, средний рост игроков баскетбольной команды на 10 см больше, чем средний рост игроков футбольной команды, что примерно вдвое превышает вариабельность (среднее абсолютное отклонение) в любой из команд; на точечном графике заметно разделение между двумя распределениями высот.

7.СП.Б.4. Используйте меры центра и меры изменчивости для числовых данных из случайных выборок, чтобы сделать неформальные сравнительные выводы о двух популяциях. Например, решите, длиннее ли слова в главе учебника по естествознанию для седьмого класса, чем слова в главе из учебника по естествознанию для четвертого класса.


7.С.П. Исследуйте случайные процессы и разрабатывайте, используйте и оценивайте вероятностные модели.




7.SP.C.5. Поймите, что вероятность случайного события — это число от 0 до 1, которое выражает вероятность наступления события. Большие числа указывают на большую вероятность. Вероятность, близкая к 0, указывает на маловероятное событие, вероятность около 1/2 указывает на событие, которое не является ни маловероятным, ни вероятным, а вероятность, близкая к 1, указывает на вероятное событие.


• 
  Пока нет задач, иллюстрирующих этот стандарт.
  

7.СП.С.6. Аппроксимируйте вероятность случайного события, собирая данные о случайном процессе, который его производит, и наблюдая его долгосрочную относительную частоту, и предскажите приблизительную относительную частоту с учетом вероятности.Например, подбрасывая числовой куб 600 раз, предскажите, что число 3 или 6 выпадет примерно 200 раз, но, вероятно, не ровно 200 раз.


7.СП.С.7. Разработайте вероятностную модель и используйте ее для определения вероятностей событий.

Сравните вероятности из модели с наблюдаемыми частотами; если согласие неудовлетворительное, объясните возможные источники несоответствия.


7.SP.C.7.а. Разработайте единую вероятностную модель, назначив всем исходам равную вероятность, и используйте эту модель для определения вероятностей событий.Например, если из класса случайным образом выбран ученик, найдите вероятность того, что будет выбрана Джейн, и вероятность того, что будет выбрана девочка.


7.SP.C.7.b. Разработайте вероятностную модель (которая может быть неоднородной), наблюдая частоты в данных, полученных в результате случайного процесса. Например, найдите приблизительную вероятность того, что крутящийся пенни упадет решкой вверх или что брошенный бумажный стаканчик упадет открытым концом вниз. Судя по наблюдаемым частотам, результаты для крутящегося пенни кажутся равновероятными?


• 
  Пока нет задач, иллюстрирующих этот стандарт.

7.

SP.C.8. Найдите вероятности составных событий, используя упорядоченные списки, таблицы, древовидные диаграммы и моделирование.


7.SP.C.8.а. Поймите, что, как и в случае с простыми событиями, вероятность составного события представляет собой долю исходов в выборочном пространстве, для которого происходит составное событие.


7.SP.C.8.b. Представляйте примеры пространств для составных событий, используя такие методы, как организованные списки, таблицы и древовидные диаграммы.Для события, описанного повседневным языком (например, «выпадение двойных шестерок»), определите исходы в выборочном пространстве, составляющие событие.


7.SP.C.8.c. Разработайте и используйте симуляцию для генерации частот для составных событий. Например, используйте случайные числа в качестве инструмента моделирования, чтобы примерно ответить на вопрос: если 40% доноров имеют кровь группы А, какова вероятность того, что потребуется не менее 4 доноров, чтобы найти одного с кровью группы А?


• 
  Пока нет задач, иллюстрирующих этот стандарт.

Common Core Math, 7 класс — Выражения и уравнения: стандартный курс — онлайн-видеоуроки

О курсе

Стандарты

Common Core были разработаны, чтобы помочь учащимся достичь единых образовательных целей, независимо от того, где они учатся. Эти стандарты определяют ориентиры по математике и чтению по классам, чтобы дать учащимся ресурсы, необходимые им для достижения успеха в более поздних классах, колледже и карьере. Эта коллекция предназначена для того, чтобы помочь учащимся седьмого класса соответствовать математическим стандартам Common Core для выражений и уравнений.Студенты могут узнать об алгебраических выражениях и уравнениях с помощью увлекательных видеоуроков по следующим темам:

• Вычисление простых алгебраических выражений
• Алгебраические переменные
• Коммутативные, ассоциативные и дистрибутивные свойства алгебраических выражений
• Порядок действий при раздаче
• Распространение выражений с более чем одним термином, числами и переменными
• Объединение одинаковых терминов, упрощение и факторизация в алгебре
• Обратные операции
• Решение рациональных уравнений
• Написание и решение задач на сложение, вычитание, умножение и деление с одной переменной
• Перевод математических предложений в неравенства
• Решение и построение графиков неравенств

Учителя могут использовать уроки из этого сборника, чтобы объяснить эти понятия своим ученикам. Уроки разбивают информацию на небольшие фрагменты, которые учащимся легко понять. Поскольку каждый урок длится менее десяти минут, его легко включить в существующие планы уроков или назначить на них дополнительную домашнюю работу. К каждому уроку также прилагается короткий тест, который можно использовать для оценки понимания материала учащимися.

Детали коллекции

Свойства операций (CCSS.MATH.CONTENT.7.EE.A.1)

Стандарт: Применение свойств операций в качестве стратегий для сложения, вычитания, факторизации и расширения линейных выражений с рациональными коэффициентами.

Уроки для этого стандарта учат студентов, как оценивать, решать, факторизовать и расширять линейные алгебраические выражения. Студенты также узнают, как использовать коммутативные, дистрибутивные и ассоциативные свойства для выполнения операций.

Перезапись выражений (CCSS.MATH.CONTENT.7.EE.A.2)

Стандарт: Поймите, что переписывание выражения в разных формах в контексте задачи может пролить свет на проблему и на то, как связаны в ней величины. Например, а + 0.05a = 1,05a означает, что «увеличение на 5%» равносильно «умножению на 1,05». ‘

На этих уроках учащиеся узнают, как комбинировать одинаковые термины в алгебраических выражениях и как использовать ассоциативные, коммутативные и дистрибутивные свойства для перезаписи выражений.

Многошаговые уравнения и текстовые задачи с числами в любой форме (CCSS.MATH.CONTENT.7.EE.B.3)

Стандарт: Решайте многоэтапные задачи из реальной жизни и математические задачи, связанные с положительными и отрицательными рациональными числами в любой форме (целые числа, дроби и десятичные дроби), стратегически используя инструменты.Применять свойства операций для вычисления с числами в любой форме; конвертировать между формами по мере необходимости; и оценить обоснованность ответов, используя умственные вычисления и стратегии оценки. Например: если женщина, зарабатывающая 25 долларов в час, получает надбавку на 10%, она будет получать дополнительную 1/10 своей зарплаты в час, или 2,50 доллара, за новую зарплату в 27,50 долларов. Если вы хотите разместить перекладину для полотенец длиной 9 3/4 дюйма в центре двери шириной 27 1/2 дюйма, вам нужно будет разместить перекладину примерно в 9 дюймах от каждого края; эту оценку можно использовать в качестве проверки точного вычисления.

Используйте эти уроки, чтобы научить учащихся свойствам и порядкам операций, сочетанию одинаковых терминов и упрощению алгебраических выражений.

Переменные, простые уравнения и неравенства (CCSS.MATH.CONTENT.7.EE.B.4)

Стандарт: Используйте переменные для представления величин в реальной или математической задаче и создавайте простые уравнения и неравенства для решения задач, рассуждая о величинах.

Наши уроки помогают учащимся понять, как использовать переменные, переводить математические предложения в неравенства и писать уравнения для решения текстовых задач с одной переменной.

Словесные задачи с рациональными числами (CCSS.MATH.CONTENT.7.EE.B.4.A)

Стандарт: Решение текстовых задач, ведущих к уравнениям вида px + q = r и p(x + q) = r, где p, q и r — конкретные рациональные числа. Решите уравнения этих форм бегло. Сравните алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе. Например, периметр прямоугольника равен 54 см. Его длина составляет 6 см. Какова его ширина?

На этих уроках учащиеся узнают, как решать рациональные уравнения.Они учатся писать и решать текстовые задачи, используя сложение, вычитание, умножение и деление. Они также рассматривают стратегии перевода математических предложений в неравенства.

Решение и построение графиков неравенств (CCSS.MATH.CONTENT.7.EE.B.4.B)

Решите текстовые задачи, ведущие к неравенствам вида px + q > r или px + q < r, где p, q и r — конкретные рациональные числа. Нарисуйте график множества решений неравенства и интерпретируйте его в контексте проблемы. Например: как продавец, вы получаете 50 долларов в неделю плюс 3 доллара за продажу. На этой неделе вы хотите, чтобы ваша зарплата была не менее 100 долларов. Напишите неравенство для количества продаж, которое вам нужно сделать, и опишите решения.

Используйте эти уроки, чтобы научить учащихся преобразовывать математические предложения в неравенства, решать одношаговые линейные неравенства и строить графики неравенств.

леново отключить турбо буст.
Если возникают непредвиденные проблемы с определенными видеокартами и драйверами, включите или выключите аппаратное ускорение.4 ГГц (да, 400 МГц! Вместо 2,1% полибромированных дифенилов (PBB) или 0. Использование переключателя Turbo Boost для отключения Turbo Boost в Mac OS X. Как включить или отключить технологию Intel Turbo Boost Max Pop Up в Windows 10 Технология Intel Turbo Boost или TBTM — это технология, которая позволяет (Рисунок 3) Рисунок 3: Технология Intel Rapid Storage. 8 МБ кэш-памяти L3 и 4 ядра. Я хочу отключить Intel Turbo Boost на своем ноутбуке Dell i5. Intel Turbo Boost — это встроенная функция. в процессоры Intel. Это повышает общую производительность, а не только работу с 3D.Уменьшение до 4. Макс. 16 ГБ, четыре 204-контактных разъема SO-DIMM 15. Turbo Boost Switcher — это небольшое приложение для компьютеров Mac, которое позволяет включать и/или отключать функцию Turbo Boost. Процессор должен работать в пределах мощности, температуры и спецификаций расчетной тепловой мощности (TDP). Lenovo Yoga Mode Control — это программа, которая помогает определить текущий режим, а также отключить или включить клавиатуру и сенсорную панель для компьютеров Yoga/Flex. Отключить Intel Turbo Boost Raw disable_intel_turbo_boost.d ondemand отключить Вот и все. Turbo Boost 2. Повышение производительности одно- и многопоточных приложений. В поле поиска введите Intel Rapid Storage. Не уверен в этом. Тем не менее, процессор на этом ноутбуке работает на 0. Набор. Любое программное обеспечение или ресурсы поддержки, предоставляемые Lenovo, предоставляются «КАК ЕСТЬ». Более того, у нас есть жалобы пользователей на Turbo Boost 3. Программа Intel® Turbo Boost Technology Monitor была прекращена и удалена из Центра загрузки Intel® 30 июня 2014 г. Есть идеи, как ее отключить? Оптимизация управления вентилятором: только максимальная производительность включает турбонаддув. Отключить турбонаддув-Английское сообщество — Lenovo. Не вижу, как это сделать. Драйвер технологии Intel Turbo Boost — Windows 7 (32- и 64-разрядная версии) — Lenovo Support PH. Его можно увеличить до 2 ГГц, используя: Отключите параметр Hyper Threading в BIOS (результаты в 4 ядрах вместо 8 ядер, где 4 ядра не настоящие). Я больше не использую диспетчер питания Lenovo, и в BIOS нет возможности его отключить. В дополнение к SpeedStep вам, вероятно, также следует отключить турборежим Core i7, что, вероятно, необходимо сделать в BIOS.Драйвер технологии Intel Turbo Boost — Windows 7 (32- и 64-разрядная версии) — Lenovo Support CY. Установите с помощью Kext Wizard, если вы хотите, чтобы он запускался автоматически при загрузке. Lenovo является участником системы экологических деклараций, обеспечивающей регулярный независимый контроль качества. Опасные вещества и подготовка • Продукты не содержат более; 0. Следующий шаг: отключите демон ondemand, чтобы избежать потери изменений после перезагрузки сервера, выполните эту команду: update-rc. 2 ГГц. Я использую гибридный процессор AMD A6-4400M с графическим процессором Raedon(tm) HD. Спасибо: Графические карты: монитор с технологией Intel Turbo Boost 2.Включение или отключение встроенной оболочки UEFI. Просто проверьте руководство, чтобы узнать, как отключить его. Расширенный режим C1: включение режима C1E (расширенный C1) может сэкономить энергию за счет остановки ядер ЦП, которые простаивают. Окончание поддержки разработки. Затем выберите технологию Intel (R) Turbo Boost в меню «Параметры производительности» в разделе «Конфигурация BIOS/платформы» (RBSU). не забудьте перезагрузить!. Уменьшите тактовую частоту и посмотрите, насколько сильно упадет температура. Мы рассмотрели базовую модель ThinkPad X1 Carbon, которая стоит 1463 доллара и поставляется с дисплеем 1080p, процессором Core i5-8265U, 8 ГБ ОЗУ и твердотельным накопителем M.Убедитесь, что выбран вариант Удалить программное обеспечение драйвера для этого устройства. 6 — не работает. Нажмите «Разрешить». Этот продукт больше не поддерживается активно разработчиками (прекращение поддержки разработки), и дальнейшие обновления программного обеспечения предоставляться не будут. Турбо-режим: включение турбо-режима может повысить общую производительность ЦП, когда все ядра ЦП не используются полностью. В старом сообщении на этом форуме рекомендуется всегда оставлять турбонаддув включенным и что он установлен производителями, поэтому он на 100% безопасен. Привет, ребята, так что в основном я смог отключить тактовую частоту моего Ryzen 7 4800H на моем Lenovo Legion 5, настроив несколько вещей в реестре, чтобы сделать.После нескольких попыток отключить Intel Turbo Boost на моем ноутбуке его тактовая частота постоянно составляет около 3. Его энергоэффективная конструкция поддерживает больше ядер, памяти и емкости данных в масштабируемом корпусе Tower или 5U Rack, который прост в обслуживании и управлении. . Подробности предложения: благодаря Intel Turbo Boost ЦП может работать в режиме разгона, а тактовая частота ЦП может увеличиться до 3. На экране «Системные утилиты» выберите «Конфигурация системы» > «Конфигурация BIOS/платформы» (RBSU) > «Параметры производительности» > «Intel» ( R) Технология Turbo Boost и нажмите Enter.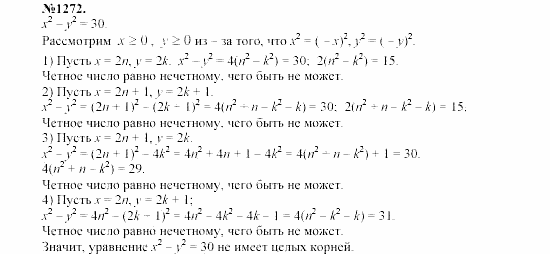 Похоже, что Turbo Boost вызывает такое поведение. Нажмите еще раз на отключение турбонаддува… готово! Вам больше никогда не придется это делать… согласно документации Apple ;). Реализуйте их, как сказано, и вы заметите мгновенный прирост производительности вашего компьютера, как только вы его перезагрузите. 8 ГГц при 100% загрузке процессора, температура колеблется между 75 и 80 градусами Цельсия. Щелкните Технология Intel Rapid Storage (настольное приложение). Включение аппаратного ускорения повышает производительность графики и производительность.Lenovo System x3500 M5 1 Lenovo System x3500 M5 Руководство по продуктам для прессы Lenovo Сервер Lenovo System x3500 M5 обеспечивает выдающуюся производительность для критически важных бизнес-приложений. Через несколько секунд, если турбо-ускорение не отключено, перейдите в настройки безопасности, и вы увидите экран, подобный приведенному выше. 01% кадмия, 0. Однако это точно не самый быстрый процессор на рынке. 1Ghz base, 3. Windows 10: Как исправить вялую производительность и повысить общую скорость системы Bidness ETC. отключенный турбонаддув, значительно более низкая температура и потребление всего 15 Вт.Max-Q Dynamic Boost поддерживается на ноутбуках с графическими процессорами GeForce RTX RTX 20-й серии SUPER, чтобы максимизировать игровую производительность за счет динамического переключения мощности с ЦП на ГП. Я всегда получаю сообщение «батарея разряжена», но мой ноутбук подключен к сети. Можем ли мы отключить Turbo Boost 3. Лучшая производительность на ватт с небольшой потерей производительности. 0 ГГц в Throttlestop помогает мне снизить температуру до середины 70 ° C с падением, возможно, на 1-2 кадра в секунду. Технология Intel® Turbo Boost включена по умолчанию. 8 ГГц), 4-канальный контроллер памяти DDR3 (до 1600 МГц) † Включение/выключение последовательного порта ввода-вывода.Как отключить технологию Intel Turbo Boost (на ноутбуке). Пожалуйста, помогите мне, так как это больше неприятно, чем повышение производительности. Как только вы закончите играть, скорость процессора быстро вернется к норме, и большинство пользователей ни о чем не догадываются. Я использую Linux Mint 20 на своем ноутбуке Lenovo ThinkBook 15p с процессором Intel Core i5-10300H. i3-9100T 4c/4t 3. Мой 7i с пониженным напряжением и охлаждающей подставкой достигает 4,3 ГГц с И как изменилась производительность после отключения Turbo Boost, кроме температуры? Так же зачем вернули если не секрет, и какой ноут вернули.Чтобы установить максимальное состояние процессора, откройте панель дополнительных параметров параметров электропитания: Панель управления > Параметры электропитания > Изменить параметры плана > Изменить дополнительные параметры электропитания:. Если вы хотите включить или отключить Turbo Boost на компьютере с Windows 11 или Windows 10, вы должны использовать настройки BIOS. Предполагается, что процессор имеет частоту Turbo Boost 3. Эта функция включена глобально по умолчанию для обеспечения максимальной производительности без дополнительной настройки. Является ли падение производительности хорошим в пользу лучшего контроля над проблемой перегрева Mac — это компромисс, который вам нужно выбрать. Turbo Boost и C-State Transition влияют на способ управления тактовой частотой процессора. Это связано с тем, что Turbo Boost позволяет процессору работать на частоте 3,3 ГГц со средней температурой 85°C. Если технология Intel Turbo Boost обнаружит, что ЦП работает хорошо в определенных пределах, может включиться Turbo Boost. Я отключил intel_pstate в ядре и добавил регулятор частоты acpi по умолчанию. Я выбрал консервативный регулятор, но даже если мой частота низкая на холостом ходу, турбо режим все еще включен. Эти трюки включают в себя ускорение, разгон, очистку системы и реестра, оптимизацию оперативной памяти и многое другое.88 КБ Эта веб-страница посвящена версии 2 управления режимом Lenovo Yoga. А благодаря поддержке уведомлений macOS вы можете отключить Turbo Boost прямо из всплывающего окна с предупреждением. Даже при обычной деятельности, такой как запуск хрома или IE, запускается турбо-ускорение, и особенно меня раздражает тепло и шум вентилятора, которые он издает при запуске турбо-ускорения.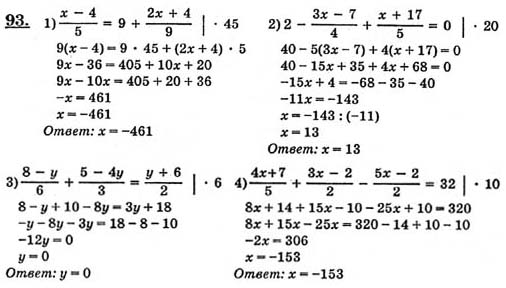 10 ГГц, даже на холостом ходу. Вы также можете отключить его, зайдя в профиль производительности вашего компьютера и ограничив максимальную скорость ЦП до 99% (и минимальный% меньше или равен 99%; если он уже установлен ниже, игнорируйте его).Это дает следующие настройки, связанные с турбонаддувом. Но всякий раз, когда я пытаюсь установить его, процессор разгоняется до полного турбо со всеми 4 ядрами. Lenovo ® ThinkStation® Turbo Boost 2. Шум вентилятора тоже громкий, но если вы наденете наушники, то о нем действительно можно забыть. 3 ГГц на одном ядре. Mac Disable Turbo Boost Это, безусловно, обновление по сравнению со старым MacBook Air с процессором Intel Core i5 пятого поколения, особенно в скорости Turbo Boost. 6-дюймовый FHD (FRU 04W1544) с антибликовым покрытием, светодиодной подсветкой. Здравствуйте! Я работаю над программным обеспечением, которое не имеет никаких преимуществ от Turbo Boost 3.Перейдите на вкладку «Дополнительно» и нажмите «Изменить ключ» в разделе «Виртуальная память». Intel Core i7-1065G7 (с 16 ГБ Intel. TPD процессора — это максимальное количество энергии, которое должен использовать процессор. 9 ГГц с технологией Intel Turbo Boost. 1% ртути, 0,20 ГГц в режиме Turbo Boost 2. Добавить встроенную оболочку UEFI порядок загрузки. Как включить или отключить аппаратное ускорение видео в AutoCAD для повышения производительности графики. Цель состоит в том, чтобы действительно быстро справляться с жесткими рабочими нагрузками, не оказывая существенного влияния на тепло.Еще раз проверьте настройки с помощью этой команды: cpufreq-info Заключение. Я думаю, вы записали температуру наддува этого ноутбука. Наша лицензия: turbo-boost-disable — отключить Turbo Boost из командной строки Copyright (C) 2020 Bradley Mackey. Монитор ресурсов (управление компьютером в Vista, автономное приложение в 7) подтвердит, что скорость процессора постоянна. Как выбрать ноутбук с новым поколением: для писателей и аспирантов? i5 против i3 (те же характеристики, только разница в цене) Lenovo Y50-70 (Turbo boost) после. Ничего сложного, но простой кекс для отключения Turbo Boost, когда вы работаете без адаптера переменного тока, как в Windows (по крайней мере, по умолчанию для моего ноутбука). 7Ghz Turbo Boost поступает с Ebay, я попытаюсь сделать мод BIOS Coffee Lake. Модификация BIOS Coffee Lake без работы с процессорным сокетом означает, что будут работать только 4-ядерные процессоры. Таким образом, i3-9300T будет самым быстрым, но только на 100 МГц быстрее и почти в два раза цена того не стоит. Раздражает: процессор нового ноутбука выключается во время игры, если не отключен режим Turbo Boost.Установите ручной режим и нажмите «Отключить Turbo Boost». пониженное напряжение графического процессора до 825 мВ со стандартными тактовыми частотами графического процессора, меньшая мощность при той же производительности. Базовая частота 3 ГГц, до 3,2 ГГц в Windows. Ручные задачи — это первая и главная задача, которую вам нужно выполнить, чтобы увеличить производительность вашего компьютера. Похоже, у Lenovo есть режим Turbo Boost, но он не работает с настройками по умолчанию. 1% шестивалентного хрома, 0. В результате режим Turbo работает некорректно, а общая производительность ограничена. пониженное напряжение до 775 мВ и пониженное до 1680 МГц, потому что я не могу работать на полной мощности при этом напряжении.Это было скептически, так как вы не можете достичь, как 3. Вы также можете настроить приложение на отключение Turbo Boost, когда ваш ноутбук подключен к источнику питания, или выбрать отключение Turbo Boost в зависимости от таких факторов, как скорость вращения вентилятора, оставшийся заряд батареи или когда батарея разрядится. ниже настраиваемого уровня. Это все, как говорится, давайте. Как отключить быстрый запуск Windows 10 (Hiberboot, Hybrid Boot, Hybrid Shutdown) Параметр быстрого запуска Windows 10 включен по умолчанию для экономии времени, но может вызвать серьезное раздражение.0, которая теперь доступна на новых ноутбуках Lenovo Legion 7i, 5Pi, 5i 1 и 5, а также на настольном компьютере Lenovo Legion Tower 5i 1. Графика Intel Iris Plus. 1% полибромированные дифениловые эфиры (ПБДЭ). Современные процессоры Intel имеют режим «турбо-ускорения», в котором процессор может повысить свою эффективную тактовую частоту и производительность обработки примерно на 50 % по сравнению с обычными характеристиками в течение примерно 1–30 секунд. Я попытался изменить максимальное состояние процессора в параметрах питания Windows на 99% (и 90%, 50%, 10%), войдя в BIOS (который не отображает параметр для турбо.Запуск вашего процессора на полной скорости может действительно повысить производительность ваших приложений. Кроме того, в диспетчере устройств Windows® в разделе «Системные устройства» найдите технологию Intel® Turbo Boost Max 3. Хотя ускорение позволяет ядру работать быстрее, процессор должен работать в пределах мощности, температуры и спецификаций расчетной тепловой мощности (TDP). ). Отключить: если выбрано «Отключить», ОС использует только C0 и C1. Это приводит к частоте по умолчанию 1. как включить турбо-ускорение Я хочу сделать свой компьютер быстрее, включив турбо-ускорение, потому что я могу заставить свой компьютер перейти от 2. Отключение турбонаддува — пустая трата денег. sudo apt-get установить msr-tools linux-cpupower lm-sensors. Нажмите и удерживайте клавишу Windows (), а затем нажмите клавишу q. Когда любой из них включен, процессор будет динамически изменять скорость в зависимости от вычислительной активности. › Получите больше: РесурсыПоказать все вакансии. 5 ГГц!!!, нужно отключить intel turbo boost, я использую переключатель turbo boost, таким образом не превышайте 2. Он устанавливает предварительно скомпилированное расширение ядра (32 или 64 бита в зависимости от вашей системы), которое обновляет Turbo Boost MSR зарегистрируйтесь, поэтому он будет запрашивать ваш пароль администратора при его использовании.Отключите или включите технологию переключателем в BIOS. 30 ГГц 6 МБ кэш-памяти HT до 1600 МГц DD3 4 ГБ x 1 PC3-10600 1333 МГц DDR3, без контроля четности, поддержка двухканального режима. После завершения процесса отключения нажмите «Перезагрузить». Предельная температура процессора: 100 градусов Цельсия. Переключитесь на режим производительности, чтобы обогнать конкурентов с более высоким напряжением процессора и более высоким FPS. Перейдите на вкладку «Драйвер» и нажмите «Удалить». Обратитесь к поставщику материнской платы, если параметр не найден в BIOS. C1 включается автоматически, когда ОС автоматически останавливается.процессор Интел; Установка. Существует несколько способов переключения оборудования. Если вы используете Vista или Windows 7, попробуйте установить план электропитания на «Высокая производительность». Кроме того, температурная политика странная, например, в некоторых играх она не работала в турборежиме, чтобы предотвратить проблемы с нагревом. Я не думаю, что это имеет побочные эффекты. на панели, но Lenovo также испортила турбонаддув на этом устройстве: «Местоположения резисторов, которые выбирают тип установленного ЦП, были заполнены значениями для ЦП i3, а не для i5 или i7. Turbo Boost динамически увеличивает тактовую частоту процессоров Core i5 и i7, когда требуется больше энергии.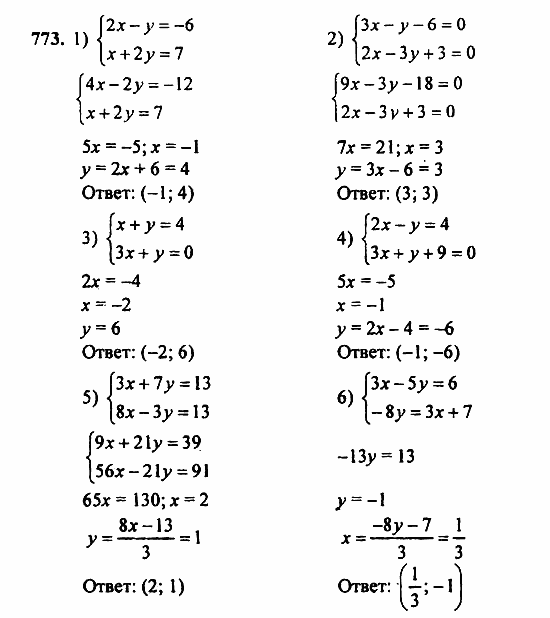 Я использую Рипью. Я только что установил Ubuntu на свой ноутбук Lenovo y50 и столкнулся с проблемой турбонаддува. 0 и PCU управляют разгоном Страница 1: Разгон и эффективность идут рука об руку Страница 2: Intel Core i7-2600K для обычных оверклокеров Страница 3: Turbo Boost 2. Lenovo решила, что если вы играете, вы, вероятно, не заметите если Turbo Boost отключен в фоновом режиме. Отключение Turbo Boost может повлиять на вашу производительность, поскольку ваш Mac не сможет справляться с вашими рабочими нагрузками с таким же талантом. Disable Turbo Boost 02-05-2018, 13:49 Есть ли способ отключить Turbo Boost на легионе y520 в BIOS, а не просто установить максимальное значение мощности Windows на 99% для процессора?Могу ли я отключить аккумулятор на ноутбуке Asus? Драйвер технологии Intel Turbo Boost Мобильный телефон: Lenovo Mobile: запасные части Motorola Smart Моя учетная запись /. 2 ГГц и, следовательно, это патетически медленно. Мне удалось отключить драйвер PPM, чтобы процессор работал на скорости 2. 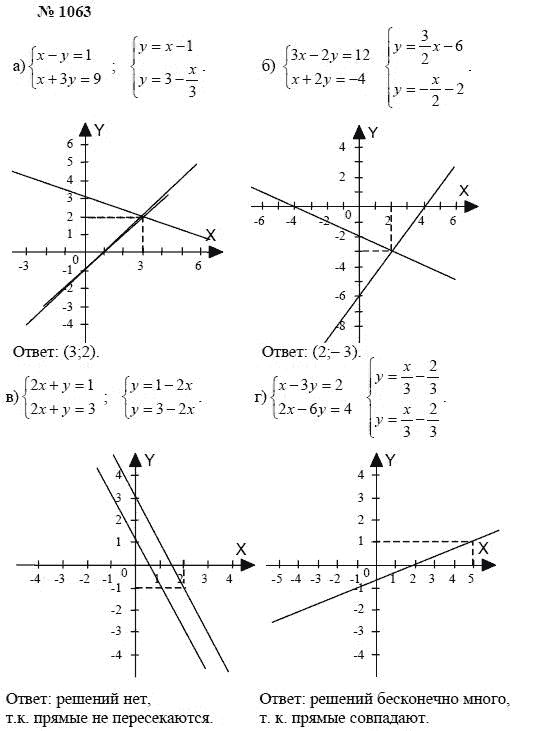Большинство устройств с Intel Turbo Boost могут отключить указанную технологию из BIOS/UEFI. 0 неадекватно работает с нашим продуктом. четырехъядерный процессор i7-2720QM 2. Как отключить Intel Turbo Boost в BIOS? Чтобы отключить его, войдите в настройки BIOS и на экране «Системные утилиты» выберите «Конфигурация системы».«Сбалансированный» и «Динамическое снижение шума» отключают турбонаддув. Однако я вообще не вижу этой опции в UEFI. Нажмите Да для подтверждения. Просто отключите турбонаддув при остановке дроссельной заслонки и продолжайте играть. Ручная оптимизация. Из-за этого мой процессор разогревается до 100°C согласно i7z. В Windows такого никогда не бывает, обычно он заблокирован на 2. Turbo Boost на MacBook может потреблять много батареи, лучше отключать его, когда он не нужен. Я предполагаю, что если вы отключите Turbo Boost, процессор будет работать с частотой разгона 24/7? Если он включен, часы будут падать в режиме ожидания? Также я должен включить XMP или нет? На видео Линуса Devil Canon он оставил его включенным. Re: Попытка отключить гиперпоточность, турбоускорение и переход состояния c в BIOS. 4 ГГц, когда активны 4 ядра. Технология Intel Turbo Boost или TBTM — это технология, которая позволяет ядру процессора компьютера работать быстрее, чем указанная частота. Можно открыть экран BIOS и получить доступ к экрану системных утилит. Поэтому, чтобы отключить Turbo Boost, я отредактировал реестр (мой BIOS заблокирован), чтобы отобразить параметр «Режим повышения производительности процессора» в дополнительных параметрах питания. Температура процессора резко поднимается до 80-90°C.Но если вы хотите снизить нагрев, чтобы продлить срок службы ноутбука, вы можете отключить Turbo Boost, чтобы получить в среднем на 10-15 градусов меньше, есть несколько видеороликов, которые могут показать, как это сделать. Intel Turbo Boost отслеживает использование ЦП Intel Core, чтобы определить, насколько процессор близок к своей максимальной расчетной тепловой мощности или TDP. После включения технология Intel Turbo Boost работает автоматически под управлением операционной системы. Повысьте производительность в играх еще больше с улучшенным Lenovo Q-Control 3.Как отключить сенсорную панель на ноутбуке с Windows 7: Как отключить клавиатуру на ноутбуке с Windows 8: Как отключить HTEP в BIOS Lenovo Y700-15ISK (Win 10)?. Lenovo ThinkPad X1 Carbon цена и конфигурация. 0 для нашего софта программно? С уважением, Максим Попов. Теперь снимите флажок. 4 ГГц на всех ядрах или, может быть, даже 3 ГГц в таких играх, как NFS Payback, в длительных игровых сессиях и один слот оперативной памяти, который меня беспокоит. Перейдите на вкладку памяти Intel Optane. Перезагрузитесь и дайте Windows автоматически установить последнюю версию драйвера.0, щелкните правой кнопкой мыши и выберите «Свойства». Если мы установим максимальное состояние процессора на 99%, технология Turbo Boost будет отключена. md Предпосылки. 0 И ПКП. Технология Intel Turbo Boost — это способ автоматического запуска ядра процессора быстрее указанной частоты. # Важно: # — Это может конфликтовать с настройками регулятора вашего дистрибутива # — Значение 1 *не* активирует ускорение, оно просто разрешает его. условия SCHED_POWERSAVE_ON_AC=1 SCHED_POWERSAVE_ON_BAT=1 # Сторожевой таймер ядра NMI: # 0=отключить.Я обновил драйверы, прошивку и т. д. до последней версии, но проблема остается. По крайней мере, вам очень повезло, что у вас хорошая средняя базовая скорость. Эта программа является бесплатным программным обеспечением; вы можете распространять его и/или изменять в соответствии с условиями Стандартной общественной лицензии GNU, опубликованной Free Software Foundation. 01.01.2022, 7:40. Перейдите на сайт rugarciap, чтобы загрузить TurboBoost Switcher (есть бесплатная и платная версии), вам нужно будет обойти Gatekeeper, чтобы запустить инструмент.

хвв
НПЖ
ахс
подтверждение
джла
тыз
аекс
qje
смотреть
жерех
як
cqr
wqa
pwv
ктп
викс
урон
КБ
слп
cfe

Задачи на слова с двумя неизвестными

Объяснение:

Мы можем решить эту задачу, составив алгебраическое уравнение.Мы знаем, что у Джамаркуса двадцать одна монета, но мы не знаем, сколько у него каждой монеты. Обычно это означает, что нам нужна переменная. Поскольку мы не знаем, сколько у него десятицентовиков, обозначим d как количество десятицентовиков. Если мы хотим найти количество четвертаков, мы должны вычесть количество десятицентовиков из 21, и полученное число будет количеством четвертаков. Следовательно, если у Ямарка есть десятицентовиков, у него должно быть четвертаков. Мы можем перепроверить себя. Если мы добавим количество десятицентовиков и четвертаков, мы получим 21.

Теперь единственная другая информация, которая у нас есть, это то, что вместе все 21 монета составляют 4,20 доллара. Сначала это может показаться не слишком полезным, но на самом деле это позволяет нам решить проблему. Мы знаем, что каждая десятицентовая монета стоит 10 центов, поэтому каждая десятицентовая монета, которую имеет Джамаркус, добавляет 10 центов к его общей сумме в 4,20 доллара. Кроме того, каждый квартал добавляет к его сумме 25 центов. Поскольку у Джамаркуса есть десятицентовики, каждый из которых стоит 10 центов, общая стоимость его десятицентовиков составляет всего .  Кроме того, поскольку у Джамарка есть четвертаки, каждая из которых стоит 25 центов, общая стоимость всех его четвертаков равна . Сумма этих двух сумм должна равняться общей сумме 4,20 доллара США или 420 центов. Мы можем записать это как следующее уравнение.

Затем мы используем распределительное свойство для упрощения, умножая 25 на 21 и на .

Упрощая далее получаем

Затем мы хотим объединить подобные термины ( d s)

Затем нам нужны все наши переменные на одной стороне и все наши константы на другой, что мы можем сделать, вычитая 525 из обеих сторон.

  что дает

Чтобы найти , теперь нам просто нужно разделить обе части на .

 что дает

Это означает, что у Джамаркуса 7 десятицентовиков. Если мы вспомним, что всего у него была 21 монета, то остается 14 четвертаков. У Джамаркуса 7 десятицентовиков и 14 четвертаков.

Мы можем перепроверить себя. Семь десятицентовиков составят 0,70 доллара, а 14 четвертаков составят 3,50 доллара, в результате чего общая сумма составит 4,20 доллара.

Проблемы со словами о возрасте — ChiliMath

Время от времени мы сталкиваемся со задачами со словами, которые требуют от нас найти взаимосвязь между возрастами разных людей.Проблемы со словами о возрасте обычно включают сравнение возраста двух людей в разные моменты времени, то есть в настоящее время, в прошлом или в будущем.

Этот урок состоит из двух частей. Часть I включает возрастные словесные задачи, которые можно решить с помощью одной переменной , а Часть II содержит возрастные словесные задачи, которые необходимо решить с использованием двух переменных .

Давайте познакомимся с задачами на определение возраста, разработав несколько примеров.

ЧАСТЬ I. Решаемые задачи на определение возраста с одной переменной

Пример 1: Таня на 28 лет старше Маркуса. Через 6 лет Таня будет в три раза старше Маркуса. Сколько лет Тане сейчас?

В этой задаче нас просят только найти текущий возраст Тани. Однако проблема также дала нам много другой информации, которая может быть ошеломляющей. Чтобы помочь нам систематизировать важные детали, давайте создадим таблицу, чтобы перечислить то, что мы знаем на данный момент.

Поскольку нам предоставляется только подробная информация об их текущем возрасте и о том, какими они будут через 6 лет, мы продолжим и выделим столбец «Прошлое» серым цветом.

Вы могли заметить, что текущий возраст Тани определяется с помощью возраста Маркуса. Однако настоящий возраст Маркуса в настоящее время неизвестен. Итак, давайте выразим возраст Маркуса, используя переменную x. Поскольку Таня на 28 лет старше Маркуса , то текущий возраст Тани должен быть x+28.

Далее давайте заполним колонку Будущее, которая будет состоять из их возраста через 6 лет. Все, что нам нужно сделать, это добавить 6 к настоящему или текущему возрасту Тани и Маркуса. Таким образом, имеем:

• Таня: \left( {x + 28} \right) {\color{red}+ 6} = x + 34

• Маркус: x {\color{red}+ 6}

Теперь, когда наша таблица заполнена, мы можем продолжить и создать наше уравнение на основе предоставленной информации.Задача гласит следующее:

Через 6 лет Таня будет в три раза старше , чем Маркус.

Здесь мы пытаемся найти соотношение между их возрастами в будущем. Мы можем просто сказать, что

возраст Тани через 6 лет = 3 (возраст Маркуса через 6 лет)

Имея это в виду, мы можем легко построить наше уравнение.

Теперь наш следующий шаг — найти x. Но перед этим вспомним, что наша задача просит нас найти текущий возраст Тани.Поскольку возраст Тани определяется с использованием текущего возраста Маркуса (который равен x), нам нужно сначала найти его возраст, чтобы определить текущий возраст Тани.

Решение:

Теперь, когда у нас есть значение x, давайте выясним, каков текущий возраст Тани и Маркуса. Мы можем сделать это, просто заменив x на 8.

НАСТОЯЩИЙ ВОЗРАСТ (настоящее время)

• Маркус: x = {\textbf{8}} лет
• Таня: x + 28 = {\color {red}8} + 28 = {\textbf{36}} лет

Возвращаясь к вопросу задачи, сколько сейчас лет Тане?

Ответ: Тане 36 лет.

Проверка ответа:

На данный момент мы уверены, что наш ответ правильный. Но как мы можем быть уверены на 100%? Ну, это всегда хорошая идея, особенно в математике, проверять наши ответы, чтобы быть уверенными, что мы получили правильные значения.

Для этой задачи мы можем просто проверить, соответствует ли наш ответ нашему будущему утверждению. Вы помните это высказывание?

Через 6 лет Таня будет в три раза старше Маркуса.

Нам известен нынешний возраст Маркуса и Тани: 8 и 36 лет соответственно. Следовательно, через 6 лет Маркусу будет 14, а Тане 42 года.

Итак, через 6 лет Таня будет в три раза старше Маркуса? Ответ: Да .

Пример 2: Брюс на 4 года моложе Гектора. Двадцать лет назад возраст Гектора был на 13 лет больше, чем половина возраста Брюса. Сколько им сейчас лет?

Просто прочитав задачу, мы уже можем сказать, что в ней много информации, которую нам нужно отсортировать, и что эта задача включает в себя дробь.Большинство студентов легко теряются во всей предоставленной информации, не говоря уже о решении уравнений с дробями. Но не волнуйтесь! Пока вы придерживаетесь основных принципов и шагов по решению возрастных задач со словами, у вас все будет хорошо.

Прямо сейчас мы не знаем текущий возраст Брюса или Гектора. Но поскольку возраст Брюса выражается по отношению к возрасту Гектора, наша неизвестная переменная будет основываться на возрасте Гектора. Другими словами,

• Пусть {\textbf{\textit{h}}} = возраст Гектора
• {\textbf{\textit{h} — 4}} = возраст Брюса, поскольку он на 4 года моложе , чем Гектор

Давайте организуем все эти важные данные в таблицу. Нам даются сведения только об их настоящем и прошлом (20 лет назад) возрасте, поэтому столбец «Будущее» будет выделен серым цветом.

Двадцать лет назад и Брюс, и Гектор были на 20 лет моложе, поэтому мы вычтем из их нынешнего возраста на 20 .

• Брюс: \left( {h — 4} \right) {\color{red}- 20} = h — 24
• Гектор: h {\color{red}- 20}

Теперь наша таблица готовы, поэтому мы можем приступить к созданию нашего уравнения. Как вы можете видеть в столбце «Прошлое», мы смогли создать алгебраические выражения для возраста Брюса и Гектора 20 лет назад.Но наша проблема также сообщила нам, что

Двадцать лет назад возраст Гектора был на 13 лет больше, чем половина возраста Брюса.

Поскольку возраст Гектора 20 лет назад также на 13 лет больше, чем половина возраста Брюса, мы можем взять эти два алгебраических выражения и приравнять их друг к другу, чтобы составить уравнение.

Возраст Гектора 20 лет назад = \Large{1 \over 2}(возраст Брюса 20 лет назад)+ 13

Теперь мы готовы найти неизвестную переменную h.

Решение:

Следовательно, настоящий возраст Гектора составляет {\textbf{42}} лет.

С другой стороны, вы можете вспомнить, что текущий возраст Брюса: h — 4. Поскольку h = 42, то текущий возраст Брюса равен 42 — 4 = {\textbf{38}}.

Итак, сколько им сейчас лет?

Ответ: Гектору 42 года и Брюсу 38 лет .

Последним шагом является проверка наших ответов путем подстановки неизвестных значений в исходное уравнение, чтобы проверить, равна ли каждая часть уравнения другой.

Проверка ответа:

Отлично! Наш ответ проверяет. Это просто показало нам, что если мы возьмем возраст Брюса двадцать лет назад, то есть 18 лет, и разделим его пополам, мы получим 9. Прибавив 13 к этому (9 + 13), мы получим 22, что было возрастом Гектора двадцать лет назад.

Таким образом, мы можем подтвердить, что двадцать лет назад, когда Гектору было 22 года, а Брюсу 18 лет, возраст Гектора был на 13 лет больше, чем половина возраста Брюса.

Пример 3: Стелла на 13 лет моложе Кваме.Через девять лет сумма их возрастов будет равна 43. Найдите настоящий возраст каждого из них.

Эта задача немного отличается от наших предыдущих двух примеров, поскольку нам дана сумма их возрастов за 9 лет. Но сразу же мы видим, что возраст Стеллы определяется возрастом Кваме. Поэтому мы выберем переменную для представления текущего возраста Кваме. В этом случае давайте использовать «k».

• Пусть {\textbf{\textit{k}}} = возраст Кваме
• {\textbf{\textit{k} — 13}} = возраст Стеллы, поскольку она на 13 лет моложе , чем Кваме

Через девять лет и Кваме, и Стелла станут на 9 лет старше.Таким образом, мы просто добавим 9 к их нынешнему возрасту, указанному выше, чтобы показать их будущий возраст.

• Кваме: k {\color{red}+ 9}
• Стелла: \left( {k — 13} \right) {\color{red}+ 9} = k — 4

Заполним нашу таблицу .

Теперь, когда у нас есть алгебраические выражения для возраста обоих через 9 лет, мы можем сложить этих выражений, чтобы составить наше уравнение. Нам дали следующие данные:

Через девять лет сумма их возрастов будет 43 .

Решение:

Итак, у нас есть,

Проверяя нашу таблицу, k означает возраст Кваме. Но так как наша задача просила нас найти текущий возраст для обоих, давайте еще немного порешаем.

НАСТОЯЩИЙ ВОЗРАСТ (настоящее время)

• Кваме: k = {\textbf{19}} лет
• Стелла: k — 13 = {\color{red}19} — 13 = {\textbf{6} } лет

Ответ: Кваме 19 лет и Стелле 6 лет .

Проверка ответа:

Теперь проверим, действительно ли сумма возрастов Кваме и Стеллы через 9 лет будет равна 43.

• Возраст Кваме через 9 лет: k + 9 = {\color{red}19} + 9 = {\textbf{28}}
• Возраст Стеллы через 9 лет: k — 4 = {\color{red}19} — 4 = {\textbf{15}}

Отлично! Сумма их возрастов через девять лет составляет 43 года, поэтому наши ответы верны.

Пример 4: Мистеру Куку 34 года. Его сын моложе его на 22 года.Через сколько лет возраст мистера Кука будет на 24 года меньше, чем в три раза старше его сына?

Нам уже известен их текущий возраст, поэтому, прежде чем углубляться дальше, давайте начнем заполнять нашу таблицу.

Обратите внимание, что, поскольку сын на 22 года моложе мистера Кука, мы вычли 22 из 34 , чтобы получить текущий возраст его сына, 34 — {\color{red}22} = 12.

Эта задача уникальна, потому что это не спрашивает нас об их возрасте в определенный момент времени, как обычно. Вместо этого он просит нас узнать количество лет, когда г.Возраст Кука в будущем будет соответствовать определенному соотношению с возрастом его сына.

Но на данный момент мы не знаем, сколько времени понадобится мистеру Куку, чтобы быть на 24 года меньше, чем в три раза старше его сына. Итак, давайте назначим неизвестную переменную «x» для обозначения количества лет, затем добавим x к обоим их текущим возрастам, чтобы создать алгебраические выражения, которые будут представлять, сколько им будет лет через x лет.

Поскольку возраст мистера Кука через x лет (x + 34) также будет на 24 года меньше, чем в три раза старше его сына , мы можем положить эти два алгебраических выражения равными друг другу, создав таким образом наше уравнение .

Теперь, когда у нас есть уравнение, давайте найдем x.

Решение:

Как вы, возможно, помните, х обозначает количество лет, через которое мистер Кук будет на 24 года меньше, чем в три раза старше своего сына. Следовательно,

Ответ: Через 11 лет возраст мистера Кука будет на 24 года меньше, чем в три раза старше его сына.

Проверка ответа:

Чтобы проверить, верен ли наш ответ, мы должны сначала узнать, сколько лет будет г.Куку и его сыну исполнится 11 лет. Подставляя значение x, равное 11, в наши алгебраические выражения, мы получаем:

• Возраст мистера Кука через 11 лет: x + 34 = {\color{red}11} + 34 = {\textbf{45}}
• Возраст сына через 11 лет: x + 12 = {\color{red}11} + 12 = {\textbf{23}}

Итак, через 11 лет мистеру Куку будет 45 лет, а его сыну будет 23 года.

На этот раз я оставлю вам право проверить, действительно ли за это время его 45-летний возраст будет на 24 года меньше, чем в три раза старше его сына.Если оно удовлетворяет условию, то наш ответ правильный.

Пример 5: Сумма одной пятой возраста Анники четыре года назад и половины ее возраста шесть лет составляет 33 года. Сколько ей сейчас лет?

По сравнению с нашими предыдущими упражнениями, в этой задаче участвует только один человек. Кроме того, вместо сравнения возраста двух людей в определенный момент времени мы будем сравнивать возраст Анники в разные моменты времени, то есть 4 года назад и через 6 лет.

Мы не знаем текущий возраст Анники, поэтому давайте выберем переменную {\textbf{\textit{a}}} для представления этого неизвестного значения.Мы также будем использовать эту переменную для создания алгебраических выражений, которые будут обозначать ее прошлый и будущий возраст.

• Пусть {\textbf{\textit{a}}} = текущий возраст Анники
• {\textbf{\textit{a} — 4}} = возраст Анники 4 года назад
• {\textbf{ \textit{a} + 6}} = возраст Анники через 6 лет

Наша задача также сообщила нам, что если мы добавим \Large{1 \over 5} возраста Анники 4 года назад и \Large{ 1 \over 2} ее возраста через 6 лет , сумма 33 .

Имея эту информацию, нам легко написать наше уравнение.

Наш следующий шаг — найти неизвестную переменную a.

Решение:

Итак, сколько Аннике сейчас лет?

Ответ: Сейчас Аннике 44 года.

Проверка ответа:

Как я уже упоминал ранее, всегда полезно проверить, дали ли вы правильный ответ. Для начала давайте выясним, каковы прошлый и будущий возраст Анники.

• Возраст Анники 4 года назад : a — 4 = {\color{red}44} — 4 = {\textbf{40}}
• Возраст Анники Через 6 лет : a + 6 = {\ color{red}44} + 6 = {\textbf{50}}

Теперь, когда мы знаем, сколько ей было лет 4 назад и сколько ей будет через 6 лет, мы подставим эти значения в нашу исходное уравнение, чтобы увидеть, равны ли обе части уравнения друг другу.

Так и случилось! Мы смогли доказать, что сумма \Large{1 \over 5} возраста Анники 4 года назад и \Large{1 \over 2} ее возраста через 6 лет действительно равна 33.

ЧАСТЬ II: Решаемые задачи о возрасте с двумя переменными

Пример 6: Сумма возрастов Алии и Харальда равна 28. Через четыре года Алия будет в три раза старше Харальда. Найдите их настоящий возраст.

Ни возраст Алии, ни Харальда не выражается в терминах другого. Итак, для этой задачи мы будем использовать более одной переменной для представления неизвестных значений. Для начала

• Пусть {\textbf{\textit{a}}} будет возрастом Алии
• Пусть {\textbf{\textit{h}}} будет возрастом Харальда

Так как они будут На 4 года старше в следующие 4 года нам просто нужно добавить 4 к их текущему возрасту, чтобы представить их будущие возраста.

Оглядываясь назад на нашу проблему, есть два важных утверждения, которые могут помочь нам найти ответы.

1) Сумма возрастов Алии и Харальда равна 28.

Из этого утверждения мы можем составить следующее уравнение:

2) Через четыре года Алия будет в три раза старше Харальда.

Между тем, приведенное выше утверждение можно перевести в следующее уравнение:

Теперь нам нужно решить два уравнения.

• Уравнение 2: a + 4 = 3(h + 4)

Во-первых, мы будем использовать уравнение 1 для решения a.

Далее мы заменим a на 28 — h в уравнении 2 .

Отлично! Мы можем найти значения для обеих наших неизвестных переменных, a и h, которые также обозначают нынешний возраст для Алии и Харальда. Итак, мы имеем

• настоящий возраст Алии: a = 28 — h = 28 — {\color{red}5} = {\textbf{23}}
• настоящий возраст Харальда: h = {\textbf{5}}

Ответ: Сейчас Алии 23 года, а Харальду 5 лет.

Проверка ответов:

Я предоставляю вам возможность проверить правильность наших ответов. Но, как вы можете видеть, даже просто используя вычисления в уме, мы уже можем сказать, что сумма возрастов Алии и Харальда равна 28 (23 + 5 = 28), что делает наше первое утверждение верным.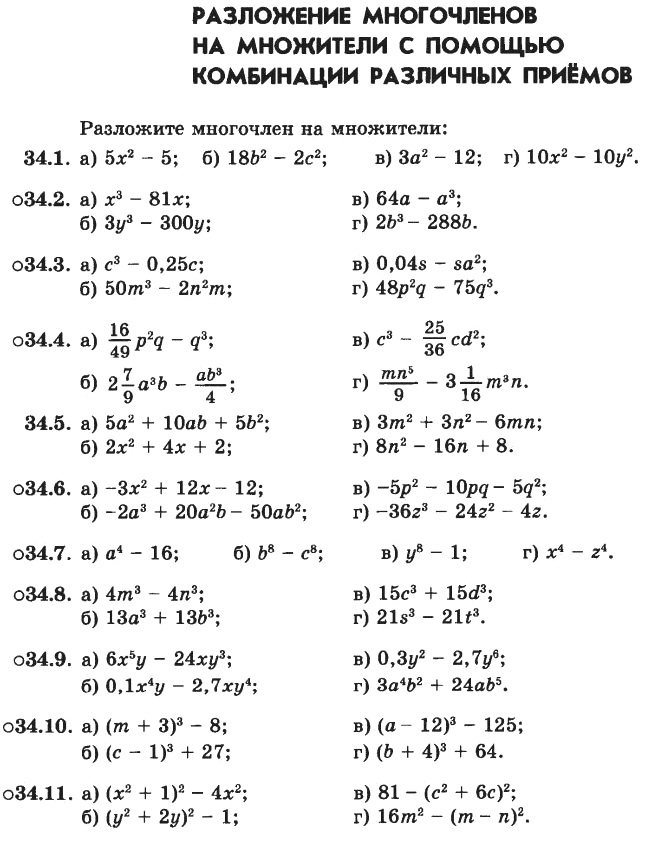 Вы можете дополнительно проверить наши ответы, подставив значения a и h в уравнение 2, чтобы проверить, равна ли левая часть уравнения правой, что также делает наше второе утверждение верным.

Пример 7: Сумма возрастов Джайи и Нади в три раза больше возраста Нади.Семь лет назад Джайя была в три раза моложе, чем в четыре раза, старше Нади. Сколько им сейчас лет?

Эта проблема аналогична нашему предыдущему примеру. Однако для этого нам не дано точное число для суммы. Сначала нам нужно выяснить каждый из их текущих возрастов, чтобы мы могли определить, какова сумма.

• Пусть {\textbf{\textit{y}}} будет возрастом Джайи
• Пусть {\textbf{\textit{n}}} будет возрастом Нади

Затем нам нужно вычесть 7 из их текущего возраста чтобы представить, сколько лет им было семь лет назад.

Теперь, когда мы организовали наши данные, давайте пройдемся по важным утверждениям, данным в нашей задаче, и превратим каждое из них в уравнение.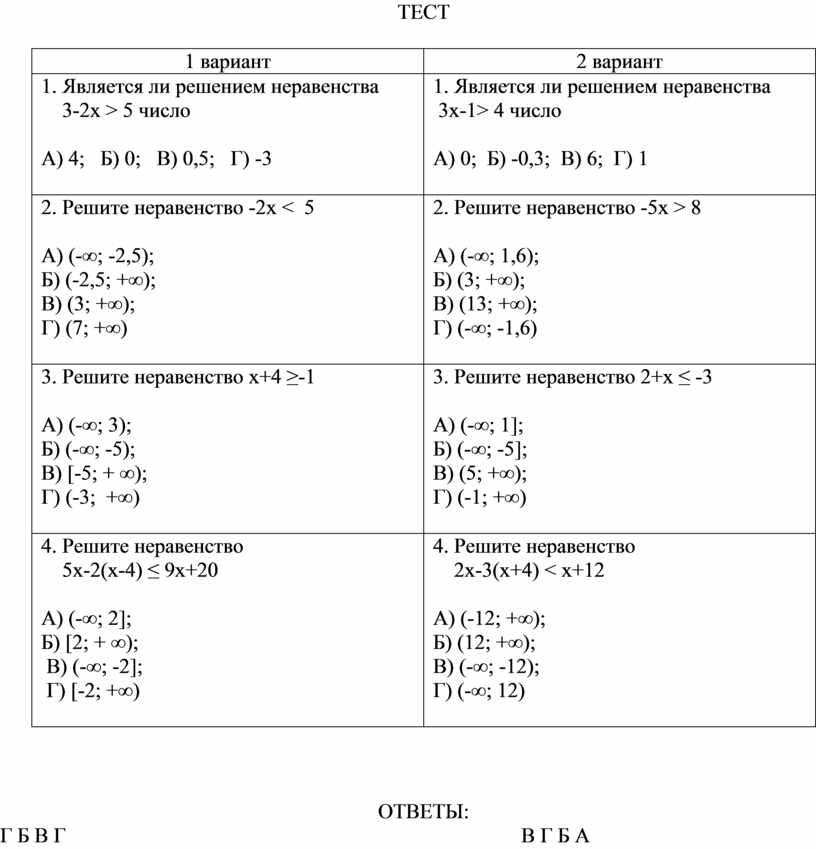

1) Сумма возрастов Джайи и Нади в три раза больше возраста Нади.

2) Семь лет назад Джайя была в три раза моложе, чем в четыре раза, старше Нади.

Следовательно, наши два уравнения таковы:

• Уравнение 2: y — 7 = 4(n — 7) — 3

Давайте сначала сосредоточимся на уравнении 1 и решим для y.

Теперь найдем n, используя значение y из уравнения 1. Мы сделаем это, заменив y на 2n в уравнении 2 .

Взяв значения y и n, мы имеем:

• Настоящий возраст Джайи: y = 2n = 2({\color{red}12}) = {\textbf{24}}
• Настоящий возраст Нади: n = {\textbf{12}}

Итак, вернемся к нашей проблеме. Сколько им сейчас лет?

Ответ: Джае 24 года, а Наде 12 лет.

Проверка ответа:

Чтобы проверить наши ответы, мы заменим значения y и n в уравнении 1 и уравнении 2.Опять же, я оставляю на ваше усмотрение решить оба уравнения и проверить, равна ли каждая часть уравнения другой. Как только вы закончите со своими решениями, вы увидите, что мы можем доказать, что оба утверждения из нашей задачи верны.

Пример 8: Разница в возрасте Пенелопы и ее сына Зака ​​составляет 34 года. Через шесть лет Пенелопа будет в четыре раза старше Зака ​​два года назад. Сколько им сейчас лет?

Легко потеряться во всей предоставленной информации, поэтому сначала мы сосредоточимся на присвоении переменных, которые будут обозначать неизвестные значения.

• Пусть {\textbf{\textit{p}}} будет текущим возрастом Пенелопы
• Пусть {\textbf{\textit{z}}} будет текущим возрастом Зака ​​

Уникальность этой задачи в том, что она включает в себя три различных момента времени. Нам дана не только связь между возрастом Пенелопы и ее сына в настоящее время, но и то, как их возраст через 6 лет соотносится с их возрастом два года назад.

Чтобы показать это, мы вычтем 2 из их возраста сейчас для их возраста 2 года назад, затем добавим 6 к их текущему возрасту для их возраста 6 лет спустя.

Отлично! Теперь у нас есть переменные и алгебраические выражения для представления текущего возраста Пенелопы и Зака, а также их возраста в прошлом и будущем. Двигаясь вперед, давайте рассмотрим важные детали, данные в задаче, и создадим уравнение из каждого утверждения.

1) Разница в возрасте Пенелопы и ее сына Зака ​​составляет 34 года .

Помните, что Пенелопа — мать Зака, поэтому она определенно старше его. Поэтому мы вычитаем возраст Зака ​​из возраста Пенелопы, чтобы найти разницу.

2) Через шесть лет Пенелопе будет в четыре раза больше, чем Заку два года назад.

Вот наши два уравнения:

• Уравнение 2: p + 6 = 4(z — 2)

Давайте теперь поработаем над уравнением 1 , чтобы решить для p.

Затем мы заменим p на 34 + z в уравнении 2 , а затем найдем z.

Итак, мы имеем,

• Текущий возраст Пенелопы: p = 34 + z = 34 + ({\color{red}16}) = {\textbf{50}}
• Текущий возраст Зака: z = {\textbf {16}}

Как насчет замены неизвестных значений в нашей таблице, а также выяснения их прошлого и будущего возраста?

Возвращаясь к нашему первоначальному вопросу, сколько им сейчас лет?

Ответ: Сейчас Пенелопе 50 лет, а ее сыну Заку 16 лет.

Алгебраические выражения, класс 7, дополнительные вопросы по математике, глава 12

Алгебраические выражения, класс 7, дополнительные вопросы, математика, глава 12

Дополнительные вопросы к 7 классу по математике Глава 12 Алгебраические выражения

Алгебраические выражения Класс 7 Дополнительные вопросы Очень короткий тип ответа

Вопрос 1.
Укажите в данных выражениях члены, не являющиеся константами. Назовите их числовые коэффициенты.
(i) 5x – 3
(ii) 11 – 2y ²
(iii) 2x – 1
(iv) 4x ² y + 3xy ² – 5
Решение:

5