Задачи 7 класс геометрия – Задачи по геометрии на повторение 7 класс

Задачи по геометрии на повторение 7 класс

Задачи по теме « Равнобедренный треугольник»

1. В треугольнике АВС углы ВАС и ВСА равны, их биссектрисы АА1 и СС1 пересекаются в точке О. Докажите, что треугольник АОС равнобедренный.

2. Найдите периметр треугольника АВС если два его угла равны, а две стороны имеют длины 40 см и 20см.

3. В треугольнике АВС угол В=120⁰ , а угол А= 30⁰ . Точка D принадлежит стороне АС, причем угол ВDС тупой. Докажите, что АВ ВD.

4.Разность длин двух сторон равнобедренного тупоугольного треугольника равна 4 см, а его периметр равен 19 см.Найдите длины сторон треугольника.

5. В равнобедренном треугольнике АВС угол В — тупой. Высота ВD равна 4 см. Найдите периметр треугольника АВС, если периметр треугольника АВD равен 12 см.

6.В треугольнике АВС внешние углы при вершинах А и С равны. Найдите длину биссектрисы ВD , если периметр треугольника АВС равен 72 см, а периметр треугольника АВD равен 48 см.

Задачи по теме « Признаки равенства треугольников»

1. На высоте АН равнобедренного треугольника с углом А=900 взята точка О. Докажите, что треугольники ВОН и НОС равны.

2. В треугольнике КМР КМ=МР. Точки А и В середины сторон KM и MP соответственно. АС и ВD перпендикулярны прямой КР. Докажите, что треугольники КАС и DВР равны.

3. Даны равносторонние треугольники АВС и А1В1С1 точки О и О1 – точки пересечения высот этих треугольников, причем ОА= О1А1 . Докажите, что треугольники АВС и А1В1С1 равны.

4. Треугольник АВС равносторонний. AC – основание. Точки К , L , М- середины сторон АВ , ВС и АС соответственно . Докажите, что треугольники АКМ и МLC равны.

5. Даны треугольники АВС , с высотой СН , и KMN с высотой NL . Причем , угол В=600, угол М=600, СН=LN и АВ=KM. Докажите , что треугольники АВС и KMN равны.

6. В равнобедренном треугольнике АВС ВК – медиана, проведенная к основанию. Точки М и N принадлежат боковым сторонам. Луч КВ – биссектриса угла МКN . Докажите, что АМ=NC.

Задачи по теме « Окружность»

1. В окружности с центром О проведены радиусы ОК , ОМ , ОN , таким образом ,что углы КОМ и МОN равны. Докажите , что треугольники КОМ и МОN равны.

2. В окружности с центром О диаметру АС перпендикулярен радиус ОВ. Докажите, что АВ=ВС.

3. В окружности с центром О проведены две непараллельные хорды КМ и РN , причем КМ= РN. Точка А – середина КМ, точка В – середина Р N . Докажите, что треугольник АОВ равнобедренный.

Задачи по теме «Смежные и вертикальные углы»

1. Один из углов, образовавшихся при пересечении двух прямых равен 480 .Найти остальные углы.

2. Дан треугольник АВС. На продолжении сторон АВ и ВС за вершину В отмечены точки К и М соответственно. Угол КВМ=300 Угол А в 3 раза больше угла С. Найти угол, смежный с углом С.

3. На окружности с центром О последовательно отмечены точки А, В, С, D, К так, что точки А и К являются концами диаметра, углы АОС и СОК равны. Угол АОВ= 300 , угол DОК=600 . Докажите, что ВD=АС.

Задачи по теме «Параллельные прямые»

1. Отрезки KM и PL –диаметры некоторой окружности. Докажите, что прямые KP и ML параллельны.

2. Точки А и С лежат по разные стороны от прямой BD . Известно, что АВ параллельна DC и AD параллельна ВС. Докажите, что угол BAD равен углу DCB, АВ=DC и AD= BC.

3. На биссектрисе CD равнобедренного треугольника АВС взята точка М. Через эту точку проведены прямые, параллельные сторонам АС и ВС и пересекающие основание АВ в точках Н и К. Докажите, что АН=КВ.

4. На сторонах MP и PN треугольника MPN взяты точки А и В соответственно. Угол PMN равен углу РАВ и равен 600, угол MNP равен 500. Найдите, чему равен угол АВN.

5. В треугольнике АВС угол А равен 300, угол С равен 1200. Докажите, что биссектриса внешнего угла при вершине С лежит на прямой, параллельной прямой АВ.

6. На одной стороне неразвернутого угла взяты точки E и F, на другой – G и H , так, чтобы EG параллельно FH , точка М принадлежит отрезку EG , угол MFE равен углу MFH, угол MHF равен MHG. Докажите, что EG= EF+GH.

multiurok.ru

Окружность. Задачи на построение — урок. Геометрия, 7 класс.

Окружность — геометрическая фигура, состоящая из всех точек плоскости, которые находятся на заданном расстоянии от данной точки.

Эту точку называют центром окружности, а заданное расстояние — радиусом окружности.

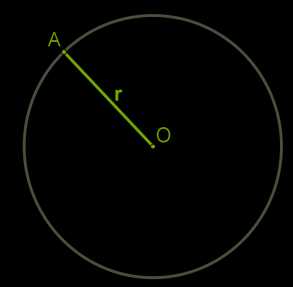
Радиус — это отрезок, соединяющий центр окружности с любой точкой окружности. Из определения следует, что можно провести бесконечное количество радиусов, и они все имеют одинаковую длину.

Отрезок, который соединяет две точки на окружности, называют хордой.

Если хорда проходит через центр окружности, то её называют диаметром окружности.

Диаметр — самая длинная хорда.

В окружности также можно провести бесконечное количество диаметров.

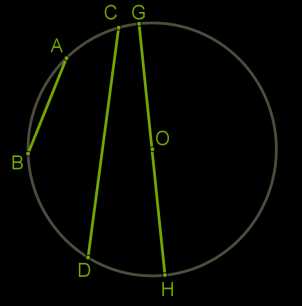
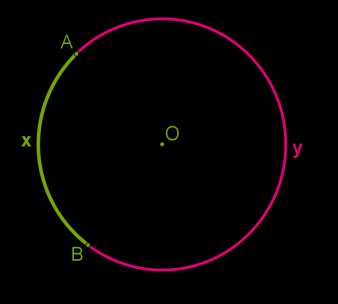
Если соединить две точки окружности не отрезком, а кривой, проходящей по самой окружности, то часть окружности между двумя точками называют дугой.

Если на окружности отметить две точки, то получаются две дуги. Поэтому для названия дуги используют три латинские буквы, которые могут быть как маленькие, так и большие.

На рисунке выше можем назвать: дуга \(BDH\), дуга \(ACG\) и другие.

На рисунке ниже нарисованы: дуга \(AxB\) и дуга \(AyB\).

Часть плоскости, ограниченная окружностью, называется кругом.

Задачи на построение

В задачах, где необходимо выполнить конструкции, используются циркуль и линейка.

Очень важно запомнить, что в этих задачах линейка используется не как инструмент для измерения, а исключительно только для того, чтобы провести прямую, луч или отрезок через две данные точки, то есть, чтобы провести прямую линию. Циркуль используется для построения окружности или дуги окружности.

Рассмотрим пять основных построений, в которых используем упомянутые действия — построение прямой линии и окружности:

1. на данном луче от его начала отложить отрезок, равный данному.
2. Построение угла, равного данному.
3. Построение биссектрисы угла.

4. Построение перпендикулярных прямых.
5. Построение середины отрезка.

1. На данном луче от его начала отложить отрезок, равный данному.
См. видео.

Ясно, что таким образом мы получили отрезок, равный данному. Соответственно определению окружности, она состоит из точек, расположенных на заданном расстоянии (радиусе) от некоей точки (центра окружности).

Если центром служит начальная точка луча \(C\), радиусом — данный отрезок \(AB\), то точка пересечения окружности и луча \(D\) и есть искомая конечная точка отрезка \(CD\), равного данному отрезку \(AB\).

2. Построение угла, равного данному.

См. видео.

Докажем, что построенный угол \(ECD\) и есть тот искомый угол, равный данному углу \(AOB\).

Если мы построили окружность с центром \(C\) — начальной точкой луча и таким же радиусом, как у окружности с центром \(O\), то \(CD\) \(=\) \(OB\).

Если далее мы построили окружность с центром \(D\) и радиусом, равным отрезку \(BA\), и получили точку пересечения обеих окружностей \(E\), то \(BA\) \(=\) \(DE\).

Провели луч \(CE\). Очевидно, \(OA\) \(=\) \(CE\).

Значит, треугольники \(AOB\) и \(ECD\) равны по третьему признаку равенства треугольников, у них равны и углы, в том числе угол \(ECD\) равен углу \(AOB\).

3. Построение биссектрисы угла.

См. видео.

Чтобы доказать, что \(OC\) действительно делит угол \(AOB\) пополам, достаточно рассмотреть треугольники \(AOC\) и \(BOC\). 

\(OA = OB\) как радиусы одной окружности, а \(AC = BC\), так как мы при построении выбрали одинаковые радиусы для обеих окружностей.

Сторона \(OC\) — общая.

Эти треугольники равны по третьему признаку.

Следовательно, их соответствующие углы равны.

Значит, \(AOC\) и \(BOC\) — две равные части одного угла, это означает, что луч \(OC\) делит угол пополам.

4. Построение перпендикулярных прямых.

См. видео.

Почему \(DE\) является перпендикулярной к \(BC\)?

\(AB = AC\) — так эти точки были отложены при построении.

\(BD = CD\), так как мы обе окружности построили с одинаковыми радиусами.

Значит, \(DA\) или \(EA\) — медианы, проведённые к основанию равнобедренных треугольников \(BDC\) или \(BEC\).

Медиана в равнобедренном треугольнике является также высотой, то есть перпендикулярна к основанию.

5. Построение середины отрезка.

См. видео.

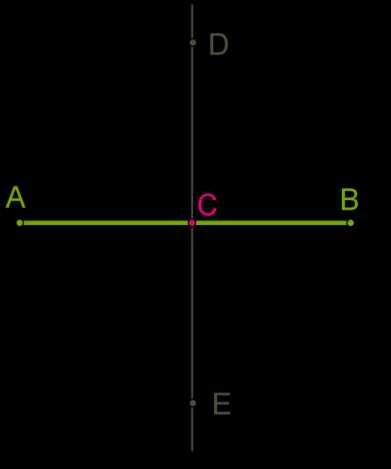
Эта конструкция такая же, как в случае построения перпендикулярных прямых, и уже доказано, что \(DC\) или \(EC\) делит \(AB\) пополам, то есть \(C\) — серединная точка отрезка \(AB\).

www.yaklass.ru

Задачи на построение. Геометрия 7 класс.

Задачи на построение

Основными чертежными инструментами, с помощью которых производятся геометрические построения, являются линейка и циркуль.

Основными чертежными инструментами, с помощью которых производятся геометрические построения, являются линейка и циркуль.

С помощью циркуля проводят окружности с данным центром и данного радиуса. В частности, с помощью циркуля на луче от его начала можно отложить отрезок, равный данному.

Задача 1 По данному рисунку объясните, как построить серединный перпендикуляр к заданному отрезку AB.

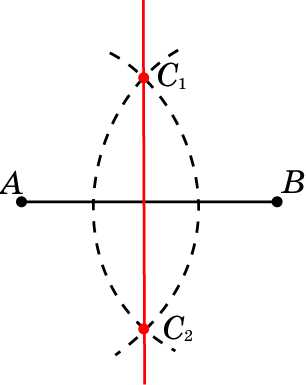
Решение.

Опишем окружности с центрами в точках А и В и радиусом, большим половины АВ. Обозначим точки их пересечения, лежащие по разные стороны от прямой АВ, через С₁ и C₂. Точки С₁ и C₂ одинаково удалены от концов отрезка АВ. Следовательно, они принадлежат серединному перпендикуляру к этому отрезку. Значит, прямая C₁С₂ будет искомым серединным перпендикуляром.

Задача 2 По данному рисунку объясните, как построить середину заданного отрезка AB.

Решение:

Строим серединный перпендикуляр к данному отрезку и находим его точку пересечения с этим отрезком. Она и будет искомой серединой.

По данному рисунку объясните, как через данную точку O, принадлежащую данной прямой a, провести прямую b, перпендикулярную прямой a.

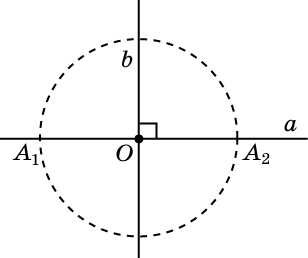
Решение.

С центром в точке O проведем окружность и обозначим A₁, A₂ ее точки пересечения с прямой a. Проведем серединный перпендикуляр b к отрезку A₁A₂. Прямая b является искомой.

Задача 4. По данному рисунку объясните, как из данной точки O, не принадлежащей данной прямой a, опустить перпендикуляр на эту прямую.

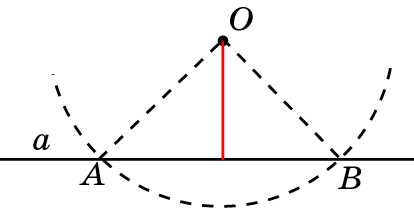
Решение.

На прямой a отметим какую-нибудь точку A. Если отрезок OA перпендикулярен a, то он является искомым.

В противном случае проведем окружность с центром в точке O и радиусом OA. Она пересечет прямую a в точке A и некоторой точке B. Так как OA = OB, то точка O принадлежит серединному перпендикуляру к отрезку AB. Искомый перпендикуляр будет лежать на серединном перпендикуляре к отрезку AB. После этого можно воспользоваться построением серединного перпендикуляра.

Задача 5. По данному рисунку объясните, как построить биссектрису данного угла.

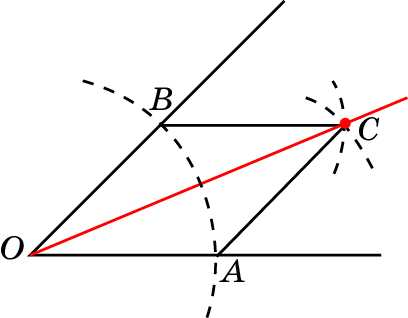
Решение.

Опишем окружность с центром в вершине О данного угла, пересекающую стороны угла в точках А и В. Затем этим же раствором циркуля с центрами в точках А и В опишем еще две окружности. Их точку пересечения, отличную от О, обозначим С. Проведем луч ОС. Треугольники ОАС и ОВС равны по третьему признаку равенства треугольников. Следовательно, AOC = BOC, т.е. луч ОС является искомой биссектрисой.

Задача 6. По данному рисунку объясните, как построить угол, равный данному, одна из сторон которого совпадает с данным лучом.

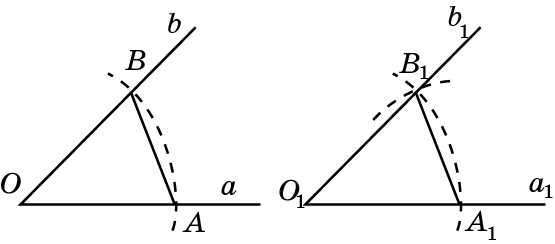
Задача 7.

Постройте треугольник ABC по двум данным сторонам AB = c, AC = b и углу между ними.

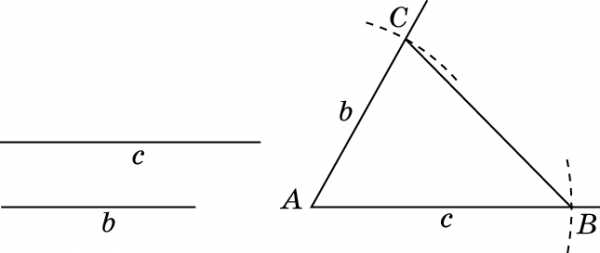
Решение:

На сторонах данного угла отложим отрезки AB = c и AC = b. Проведем отрезок BC. Получим искомый треугольник ABC.

Задача 8.

Постройте прямоугольный треугольник ABC по двум данным катетам BC = a, AC = b.

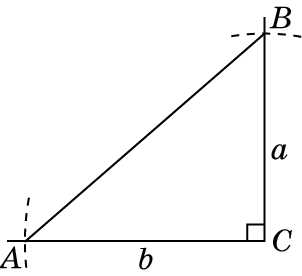
Решение:

Построим прямой угол с вершиной C. На его сторонах отложим отрезки BC = a и AC = b. Проведем отрезок AB. Получим искомый треугольник ABC.

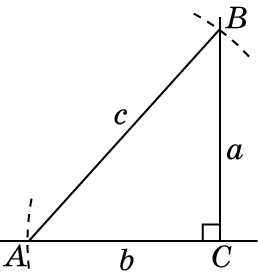
Задача 9.

Постройте прямоугольный треугольник ABC по катету AC = b и гипотенузе AB = c.

Решение:

Построим прямой угол с вершиной C. На одной его стороне отложим отложим отрезок AC = b. C центром в точке A проведем дугу окружности радиуса c. Обозначим B ее точку пересечения со второй стороной данного угла. Проведем отрезок AB. Получим искомый треугольник ABC. Заметим, что решение существует в случае, если c > b.

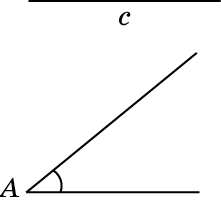
Задача 10.

Постройте прямоугольный треугольник ABC по гипотенузе AB = c и острому углу A.

Решение:

На одной стороне данного угла отложим отрезок AB = c Из точки B опустим перпендикуляр BC на другую сторону угла. Получим искомый треугольник ABC.

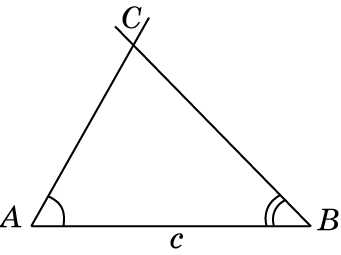
Задача 11.

Постройте треугольник ABC по данной стороне AB = c и двум данным углам A и B.

Решение:

На прямой отложим отрезок AB = c. С вершинами в концах этого отрезка в одну сторону от прямой отложим данные углы A и B. Обозначим C их точку пересечения. Полученный треугольник ABC будет искомым. Заметим, что решение существует в случае, если если стороны углов пересекаются.

Задача 12. Постройте треугольник ABC по трем данным сторонам AB = c, AC = b, AC = b.

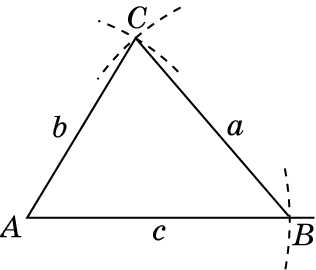
Решение:

На прямой отложим отрезок AB = c. С центром в точке A проведем дугу окружности радиуса b. С центром в точке B проведем дугу окружности радиуса a. Обозначим C их точку пересечения. Соединим ее отрезками с точками A и B. Полученный треугольник будет искомым. Заметим, что решение существует в случае, если a – b < c < a + b.

infourok.ru

Решение задач. Видеоурок. Геометрия 7 Класс

На этом уроке мы будем решать задачи по пройденной теме. Вначале повторим изученный материал. Вспомним аксиому о параллельных прямых и следствие из нее. Повторим определение луча и угла и единицы измерения отрезков и углов. Вспомним определение равных геометрических фигур и то, как сравнивают и измеряют отрезки и углы. Вспомним, что такое середина отрезка и биссектриса угла, какие углы называются острыми, прямыми и тупыми. Повторим теоремы о сумме смежных углов и о равенстве вертикальных углов. Вспомним, что такое перпендикулярные прямые и теорему о том, что две перпендикулярные к третьей прямые не пересекаются. И будем решать типовые задачи на повторенный материал.

Вспомним сведения, изученные в текущей теме:

— Аксиома. Через две точки можно провести прямую, и только одну.

— Прямые на плоскости могут пересекаться, могут не иметь общих точек.

— Угол измеряется в градусах. 1 градус – это сто восьмидесятая часть от развернутого угла.

— Сумма смежных углов равна 180^о.

— Вертикальные углы равны между собой.

— Прямые, пересекающиеся под углом 90^о, называются перпендикулярными.

— Прямые, перпендикулярные одной прямой, не пересекаются.

Пример 1: Найти угол между биссектрисами смежных углов.

Решение:

Рис. 1. Чертеж к примеру 1

Биссектриса BL₁ угла ∠DBC = β делит его на два угла, градусная мера которых равна . Биссектриса BL₂ угла ∠АBC = α делит его на два угла, градусная мера которых равна . Необходимо найти угол ∠ L₁ ВL₂. Выполним сложение углов: ∠ L₁ ВL₂ = ∠ L₁ ВС + ∠СВL₂ = . Сумма углов α + β равна 180^о, поскольку данные углы – смежные.

Ответ: 90^о.

Отметим, что в данной задаче нам не было известно, какие градусные меры углов ∠DBC и ∠АBC, однако мы знаем, что их сумма равна 180^о.

Пример 2: Отрезок длиной 36 см поделили на 4 неравных части. Расстояние между серединами крайних частей равно 30 см. Найдите расстояние между серединами средних частей отрезка.

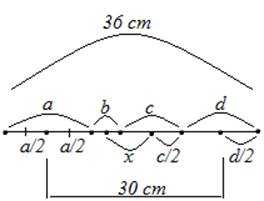
Рис. 2. Чертеж к примеру 2

Решение:

Найдем величину суммы отрезков  Соответственно,

Вычислим сумму длин оставшихся отрезков:

Найдем расстояние между серединами средних частей отрезка.

Ответ: 12 см.

Пример 3: Отрезок длиной m разделен на три части. Найти расстояние между серединами крайних частей.

Решение:

Выполним рисунок.

Рис. 3. Чертеж к примеру 3

Поскольку длина трети отрезка равна , то длина половины этой части равна . Тогда чтобы найти расстояние между серединами крайних частей, необходимо выполнить действие: .

Ответ: .

Список рекомендованной литературы

1. Александров  А.Д., Вернер А.Л., Рыжик В.И. и др. Геометрия 7. – М.: Просвещение.
2. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7. 5-е изд. – М.: Просвещение.
3. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А.  – М.: Просвещение, 2010.

Рекомендованные ссылки на интернет-ресурсы

1. Геометрические задачи (Источник).
2. Обобщающий урок по геометрии в 7-м классе (Источник).
3. Прямая линия, отрезок (Источник).

Рекомендованное домашнее задание

1. № 14, 16. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А. – М.: Просвещение, 2010.
2. Определите длину отрезка АВ, если АС : ВС = 3 : 2, а ВС = 3 см.
3. При пересечении прямых образовалось 4 неразвернутых угла. Определите градусные меры этих углов, если сумма трех углов 320^о.
4. Может ли быть такое, что один из смежных углов больше другого в 100 раз?

interneturok.ru

Задачи на построение. Геометрия, 7 класс: уроки, тесты, задания.

www.yaklass.ru

Задачи по геометрии для 7 класса. Равные треугольники, равнобедренный треугольник, свойство биссектрис, высот и серединных перпендикуляров. Уровень С

На этой странице публикуются наиболее интересные задачи по геометрии для 7 класса уровня С, которые или составлены мной лично или проходили через меня в тот или иной период репетиторской работы. Преподавание геометрии способному ребенку — истинное удовольствие для любого репетитора по математике, особенно если под рукой хороший комплект уникальных и содержательных задач. Для маленьких учеников репетитору всегда не хватает хороших задач, их мало, так как дети еще многого не знают. Возможности составителей придумать что-то новое и интересное в рамках программы, сильно ограничены. Одно из направлений работы сайта «профессиональный репетитор по математике» — поиск, сортировка и составление таких задач. Именно тех, над которыми можно и нужно размышлять, задачи, которые не решаются одним взглядом по образцу и подобию, которые можно показать не только одаренным детям. Не путайте их с олимпиадными и конкурсными.

Уважаемые репетиторы по математике: присылайте ссылки и тексты таких задач. Я с удовольствием размещу их на сайте.

1) В четырехугольнике точки и  — соответственно середины равных сторон и . Серединные перпендикуляр к стороне пересекает серединный перпендикуляр к стороне в точке . Докажите, что серединный перпендикуляр, проведенный к отрезку проходит через точку .

2) В четырехугольнике серединные перпендикуляры к сторонам и пересекаются на стороне . Известно, что . Докажите, что в четырехугольнике диагонали равны.

3) В квадрате даны точки и соответственно на сторонах и ,причем . Докажите равенство

Комментарий репетитора по математике: для решения этой задачи достаточно элементарных представлений о квадрате. Обычно они у 7 классника есть. И тем более они есть у того, кто пробует решать такие задачи.

4) В треугольнике проведены биссектрисы и , пересекающиеся в точке M, а в треугольнике проведены биссектрисы и , пересекающиеся в точке . Докажите, что и лежат на одной прямой.

5) В равнобедренном треугольнике c основанием на боковых сторонах отложены равные отрезки и . Отрезки и пересекаются в точке. Докажите, что  — биссектриса угла .

6) В равнобедренном треугольнике на боковых сторонах и даны точки и так, что . На основании отмечены еще две точки и такие, что . Известно, что и . Докажите, что .

7) В треугольнике проведены две биссектрисы и , пересекающиеся в точке . Известно, что , . Доказать, что  — равнобедренный.

8) Дан треугольник ABC, у которого . Докажите, что треугольник, с вершинами в основаниях его биссектрис — прямоугольный.

P.S. Конечно, для решения первых задач семиклассник должен иметь элементарные представления о четырехугольниках. Однако, учитывая низкую смысловую нагрузку на новые понятия и уровень проявляющего интерес к математике школьника, репетитору не придется тратить время на разжевывание и закрепление элементарного. Хватит и пяти минут. При использовании понятия «диагональ» репетитор по математике примитивнейшим образом показывает ее на рисунке. В других ситуациях (когда ученик слабый) придется готовить специальные задания на отработку нового термина.

Обычно дети, проявляющие способности и интерес к математике, легко обучаемы ее основам, поэтому репетитор вполне может немного «забежать вперед» по программе. Если он не собирается опережать школу — следует изменить условия первых задач. Вместо четырехугольника репетитору по математике следует указать самые обычные 4 точки с равными отрезками.

Удачного изучения и использования материалов на индивидуальных занятиях.
Колпаков А.Н. Репетитор по математике Москва, Строгино.

Метки:
Геометрия,
Задачник по геометрии,
Ученикам,
Элементарная математика

ankolpakov.ru

Задачи для уроков обобщающего повторения курса геометрии 7 класса (УМК «Геометрия 7-9» Л. Г. Атанасян)

МАОУ «Лицей №19» г. Королев

Исаева Надежда Васильевна, учитель математики

7 класс

Задачи по геометрии ( обобщающее повторение)

1.Докажите, что основание равнобедренного треугольника параллельно биссектрисе одного из внешних углов.

2. Докажите, что в равнобедренном треугольнике биссектрисы углов при основании равны.

3. Докажите, что в равнобедренном треугольнике медианы, проведенные к боковым сторонам, равны.

4. Докажите, что в равнобедренном треугольнике две высоты равны.

5. Докажите, что если в треугольнике две высоты равны, то этот треугольник равнобедренный.

6. Высоты равнобедренного треугольника, проведенные из вершин при основании, образуют угол 140⁰. Определите углы данного треугольника.

7. Биссектриса угла при основании равнобедренного треугольника равна стороне треугольника. Определите углы данного треугольника.

8. В треугольнике АВС АВ=1, длина стороны АС выражается целым числом. Биссектриса угла А перпендикулярна медиане, выходящей из вершины В. Найдите периметр треугольника АВС.

9. Доказать, что сумма расстояний от какой-нибудь точки внутри треугольника до его вершин более половины периметра.

10.В треугольнике одна сторона равна 1,9м, а другая 0,7м. Определите третью сторону, зная, что она выражается в целых метрах.

11.Доказать теорему: если две стороны и медиана одного треугольника соответственно равны двум сторонам и медиане другого треугольника, то такие треугольники равны. Рассмотрите два случая: 1) медиана проведена к одной из данных сторон; 2) медиана проведена между данными сторонами.

12.Докажите, что биссектрисы внутренних односторонних углов, образованных при пересечении параллельных прямых третьей, перпендикулярны.

13.АВС и АРК два равных треугольника. Известно, что АВ=3, АС=АР=4, АК=5. Чему равны стороны ВС и РК?

14.В треугольнике АВС известны углы:ВАС=52⁰, ВСА=44⁰. Из вершины В провели медиану и высоту и продолжили их за сторону АС на расстояния, равные им. Получили точки Р и K. Чему равен РСК?

15.Отрезок АА₁ – медиана треугольника АВС. Докажите, что 2АА₁

16.Отрезок АА₁ – биссектриса треугольника АВС. Докажите, что АС 1С.

17.Пусть К – точка, лежащая во внутренней области прямоугольного треугольного треугольника АВС с прямым углом АСВ. Докажите, что АКВ – тупой.

18.Докажите, что прямая, перпендикулярная биссектрисе угла, образует равные углы со сторонами данного угла.

19.В равнобедренном треугольнике АВС на боковых сторонах АВ и ВС соответственно отложены равные отрезки АР и СК. Докажите, что АК = СР.

20.Равны ли треугольники АВС и А₁В₁С₁, если АВ=А₁В₁, ВС=В₁С₁ и высоты ВК и В₁К₁ равны? Ответ обоснуйте.

21.В треугольнике АВС медианы пересекаются в точке М. Известно, что МАВ=МВА, МСВ=МВС. Найдите АВС.

22.Докажите равенство прямоугольных треугольников по острому углу и высоте, опущенной на гипотенузу.

23.Докажите равенство остроугольных треугольников по двум углам и высоте, проведенной из вершины третьего угла.

24. В прямоугольном треугольнике НРЕ (Н=90⁰) ЕL – биссектриса угла Е. Отрезок LE в два раза больше отрезка LH и на 8см меньше отрезка НР. Найти катет РН.

25. Один из внешних углов равнобедренного треугольника равен 40⁰. Чему равен угол, образованный высотами треугольника, проведенными к его боковым сторонам?.

26. Биссектриса угла треугольника пересекает сторону под углом 85⁰ и биссектрису одного из углов под углом в 54⁰. Найти величины углов треугольника.

27.В треугольнике АВС С=90⁰, CD ^— высота треугольника, ВС = 2 BD. Докажите, что AD=3DB

28.Две биссектрисы треугольника пересекаются в точке О. Докажите, что третья биссектриса проходит через точку О.

29.Гипотенуза прямоугольного треугольника в 4 раза больше проведенной к ней высоты. Найдите острые углы треугольника.

30.В треугольнике длины двух сторон равны 6,38 и 1, 54. Найдите длину третьей стороны, если известно, что она является целым числом.

31.На отрезке MN=8дм лежат точки А и В по разные стороны от середины С отрезка MN. CA=7см, CB=0,24м. Найти длины отрезков АN и BN в дм.

32.Какой угол образует часовая и минутная стрелки часов в 17 часов 05 минут?

33. В треугольнике АВС угол В равен 90⁰. Из точки D отрезка ВС проведен отрезок DE, перпендикулярный отрезку ВС и пересекает АС в точке О, угол DOC равен 70⁰, DEC=45⁰, BAD=50⁰ . Найти угол AED.

34.В треугольнике XYZ X=30⁰, Z=15⁰. Перпендикуляр YQ к ZY делит сторону XZ на части XQ и QZ. Найдите XY, если QZ=1,5м.

videouroki.net