ГДЗ домашние контрольные работы / КР-3. вариант 2 алгебра 7 класс задачник Мордкович
Решение есть!
-
1 класс
- Математика
- Английский язык
- Русский язык
- Музыка
- Литература
- Окружающий мир
- Человек и мир
-
2 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Человек и мир
-
3 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
-
4 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
-
5 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Украинский язык
- Биология
- История
- Информатика
- ОБЖ
- География
- Музыка
- Литература
- Обществознание
- Технология
- Естествознание
-
6 класс
- Математика
Алгебра 7 Контрольные Макарычев | КОНТРОЛЬНЫЕ РАБОТЫ
Контрольные работы по алгебре в 7 классе, УМК Макарычев и др.
Алгебра 7 Контрольные Макарычев (ДМ Звавич) — это контрольные работы (цитаты) в 4-х вариантах из пособия для учащихся «Алгебра. Дидактические материалы. 7 класс / Л.И. Звавич, Л.В. Кузнецова, С.Б. Суворова — М.: Просвещение, 2012».
Цитаты из указанного учебного пособия использованы на сайте в незначительных объемах, исключительно в учебных и информационных целях (пп. 1 п. 1 ст. 1274 ГК РФ): цитаты переработаны в удобный формат , что дает экономию денежных средств учителю и образовательному учреждению в использовании бумаги и ксерокопирующего оборудования.
При постоянном использовании данных контрольных работ по математике в 7 классе рекомендуем купить книгу: Алгебра. Дидактические материалы. 7 класс / Л.И. Звавич, Л.В. Кузнецова, С.Б. Суворова — М.: Просвещение, в которой кроме контрольных работ есть еще много самостоятельных работ по каждой теме. Контрольно-измерительные материалы используются в комплекте с учебным пособием «Алгебра. Учебник для 7 класса / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; Под редакцией С.А. Теляковского — М.: Просвещение».
Алгебра 7 Контрольные Макарычев
(задания + решения + ответы):
Контрольная № 1. Проверяемые темы: § 1. Выражения. § 2. Преобразование выражений.
К-1. Вариант 1 К-1. Вариант 2 К-1. Вариант 3 К-1. Вариант 4
Контрольная № 2. Проверяемые темы: § 3. Уравнения с одной переменной.
К-2. Вариант 1 К-2. Вариант 2 К-2. Вариант 3 К-2. Вариант 4
Контрольная № 3. Проверяемые темы: § 5. Функции и их графики. § 6. Линейная функция.
К-3. Вариант 1 К-3. Вариант 2 К-3. Вариант 3 К-3. Вариант 4
Контрольная № 4. Проверяемые темы: § 7. Степень и её свойства. § 8. Одночлены.
К-4. Вариант 1 К-4. Вариант 2 К-4. Вариант 3 К-4. Вариант 4
Контрольная № 5. Темы: § 9. Сумма и разность многочленов. § 10. Произведение одночлена и многочлена.
К-5. Вариант 1 К-5. Вариант 2 К-5. Вариант 3 К-5. Вариант 4
Контрольная № 6. Проверяемые темы: § 11. Произведение многочленов.
К-6. Вариант 1 К-6. Вариант 2 К-6. Вариант 3 К-6. Вариант 4
Контрольная № 7. Темы: § 12. Квадрат суммы и квадрат разности. § 13. Разность квадратов. Сумма и разность кубов.
К-7. Вариант 1 К-7. Вариант 2 К-7. Вариант 3 К-7. Вариант 4
Контрольная № 8. Проверяемые темы: § 14. Преобразование целых выражений.
К-8. Вариант 1 К-8. Вариант 2 К-8. Вариант 3 К-8. Вариант 4
Контрольная № 9. Темы: § 15. Линейные уравнения с двумя переменными и их системы. § 16. Решение систем линейных уравнений.
К-9. Вариант 1 К-9. Вариант 2 К-9. Вариант 3 К-9. Вариант 4
ИК-1. Итоговая контрольная работа № 1
ИК-1. Вариант 1 ИК-1. Вариант 2 ИК-1. Вариант 3 ИК-1. Вариант 4
ИК-2. Итоговая контрольная работа № 2
ИК-2. Вариант 1 ИК-2. Вариант 2 ИК-2. Вариант 3 ИК-2. Вариант 4
Смотрите также Решебник к новому учебнику «Алгебра 7 класс Макарычев 2018» (решения и ответы):
ГДЗ Алгебра 7 Макарычев
Алгебра 7 Контрольные Макарычев (ДМ — Звавич) — контрольные работы (цитаты) в 4-х вариантах из пособия для учащихся «Алгебра. Дидактические материалы. 7 класс / Л.И. Звавич, Л.В. Кузнецова, С.Б. Суворова — М.: Просвещение, 2012». Контрольно-измерительные материалы используются в комплекте с учебным пособием «Алгебра. Учебник для 7 класса / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; Под редакцией С.А. Теляковского — М.: Просвещение».
КР-3 Алгебра 7 Макарычев ОТВЕТЫ на В-1
Контрольная работа № 3 по алгебре с ответами (К-3 В-1)
КР-3 Алгебра 7 Макарычев ОТВЕТЫ на Вариант № 1. Задания, решения и ответы на контрольную работу № 3 «Функции и их графики. Линейная функция» (в 4-х вариантах) из пособия для учащихся «Алгебра. Дидактические материалы. 7 класс / Л.И. Звавич, Л.В. Кузнецова, С.Б. Суворова — М.: Просвещение, 2012», которое используется в комплекте с учебником по алгебре в 7 классе авторов: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; Под редакцией С.А. Теляковского.
Алгебра 7 класс (УМК Макарычев и др.)
Контрольная работа № 3. Вариант 1
Проверяемые темы учебника: § 5. Функции и их графики. § 6. Линейная функция.
• 1. Функция задана формулой у = 6x + 19. Определите:
а) значение у, если x = 0,5; б) значение х, при котором у = 1; в) проходит ли график функции через точку А(–2; 7).
• 2. а) Постройте график функции у = 2х–4.
б) Укажите с помощью графика, чему равно значение у при х= 1,5.
• 3. В одной и той же системе координат постройте графики функций: а) у = –2х; б) у = 3.
4. Найдите координаты точки пересечения графиков функций у = 47x – 37 и у = –13x + 23.
5. Задайте формулой линейную функцию, график которой параллелен прямой у = 3х – 7 и проходит через начало координат.
Контрольная работа № 3 по алгебре с ответами (К-3 В-1)
Решения и ответы на контрольную К-3 В-1
Вариант 1. ОТВЕТЫ:
№1. а) 22; б) х = –3; в) 6 • (–2) +19 = 7; 7 = 7 – верно, график проходит через А(–2; 7).
№2. y = 2 • 1,5 – 4 = –1.
№3. а) у = –2х; б) у = 3.
№4. 47х – 37 = –13х + 23; х = 1; у = 10; А(1; 10).
№5. y = 3x – 7; 0 = 3 • 0 + b график проходит через координаты (0; 0) ==> b = 0. Ответ: у = 3х.
Смотреть РЕШЕНИЕ заданий Варианта 1
КР-3 Алгебра 7 Макарычев ОТВЕТЫ на В-1. Задания, решения и ответы на контрольную работу из пособия для учащихся «Алгебра. Дидактические материалы. 7 класс / Звавич и др., 2012» (УМК Макарычев и др.).
Другие варианты: К-3. Вариант 2 К-3. Вариант 3 К-3. Вариант 4
Вернуться к Списку контрольных работ по алгебре 7 класс (ДМ — Звавич).
Алгебра 7 Контрольные Макарычев | КОНТРОЛЬНЫЕ РАБОТЫ
Алгебра 7 Контрольные Макарычев
(Контрольные работы по алгебре в 7 классе, УМК Макарычев и др.)
Алгебра 7 Контрольные Макарычев (ДМ Звавич) — это контрольные работы (цитаты) в 4-х вариантах из пособия для учащихся «Алгебра. Дидактические материалы. 7 класс / Л.И. Звавич, Л.В. Кузнецова, С.Б. Суворова — М.: Просвещение, 2012». Цитаты из указанного учебного пособия использованы на сайте в незначительных объемах, исключительно в учебных и информационных целях (пп. 1 п. 1 ст. 1274 ГК РФ): цитаты переработаны в удобный формат , что дает экономию денежных средств учителю и образовательному учреждению в использовании бумаги и ксерокопирующего оборудования.
При постоянном использовании данных контрольных работ по математике в 7 классе рекомендуем купить книгу: Алгебра. Дидактические материалы. 7 класс / Л.И. Звавич, Л.В. Кузнецова, С.Б. Суворова — М.: Просвещение, в которой кроме контрольных работ есть еще много самостоятельных работ по каждой теме. Контрольно-измерительные материалы используются в комплекте с учебным пособием «Алгебра. Учебник для 7 класса / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; Под редакцией С.А. Теляковского — М.: Просвещение».
КР-01. Темы учебника: § 1. Выражения. § 2. Преобразование выражений.
Контрольная работа № 1 + Ответы
КР-02. Темы учебника: § 3. Уравнения с одной переменной.
Контрольная работа № 2 + Ответы
КР-03. Темы учебника: § 5. Функции и их графики. § 6. Линейная функция.
Контрольная работа № 3 + Ответы
КР-04. Темы учебника: § 7. Степень и её свойства. § 8. Одночлены.
Контрольная работа № 4 + Ответы
КР-05. Темы учебника: § 9. Сумма и разность многочленов. § 10. Произведение одночлена и многочлена.
Контрольная работа № 5 + Ответы
КР-06. Темы учебника: § 11. Произведение многочленов.
Контрольная работа № 6 + Ответы
КР-07. Темы учебника: § 12. Квадрат суммы и квадрат разности. § 13. Разность квадратов. Сумма и разность кубов.
Контрольная работа № 7 + Ответы
КР-08. Темы учебника: § 14. Преобразование целых выражений.
Контрольная работа № 8 + Ответы
КР-09. Темы учебника: § 15. Линейные уравнения с двумя переменными и их системы. § 16. Решение систем линейных уравнений.
Контрольная работа № 9 + Ответы
ИК-1. Итоговая контрольная 1
ИТОГОВАЯ работа № 1 + Ответы
ИК-2. Итоговая контрольная 2
ИТОГОВАЯ работа № 2 + Ответы
Смотрите также Решебник к новому учебнику «Алгебра 7 класс Макарычев 2018» (решения и ответы):
ГДЗ Алгебра 7 Макарычев
Алгебра 7 Контрольные Макарычев (ДМ Звавич) — это контрольные работы (цитаты) в 4-х вариантах из пособия для учащихся «Алгебра. Дидактические материалы. 7 класс / Л.И. Звавич, Л.В. Кузнецова, С.Б. Суворова — М.: Просвещение, 2012». Контрольно-измерительные материалы используются в комплекте с учебным пособием «Алгебра. Учебник для 7 класса / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; Под редакцией С.А. Теляковского — М.: Просвещение».
|
Контрольная работа №1 М7кл l Вариант 1. Найдите значение выражения: 6х – 8у, при 2. Сравните значения выражений: – 0,8х – 1 и 0,8х – 1, при х = 6. 3. Упростите выражение: а) 2х – 3у – 11х + 8у; б) 5(2а + 1) – 3; в) 14х – (х – 1) + (2х + 6). 4. Упростите выражение и найдите его значение: – 4(2,5а – 1,5) + 5,5а – 8, при 5. Из двух городов, расстояние между которыми Sкм, одновременно навстречу друг другу выехали легковой автомобиль и грузовик, и встретились через tч. Скорость легкового автомобиля Ѵкм/ч. Найдите скорость грузовика. Ответьте на вопрос задачи, если S = 200, t = 2, Ѵ = 60. 6. Раскройте скобки: 3х – (5х – (3х – 1)). |
Контрольная работа №1 М7кл ll Вариант 1. Найдите значение выражения: 16а + 2у, при 2. Сравните значения выражений: 2 + 0,3а и 2 – 0,3а, при а = – 9. 3. Упростите выражение: а) 5а + 7в – 2а – 8в; б) 3(4х + 2) – 5; в) 20b – (b – 3) + (3b – 10). 4. Упростите выражение и найдите его значение: – 6(0,5х – 1,5) – 4,5х – 8, при 5. Из двух городов одновременно навстречу друг другу выехали автомобиль и мотоцикл, и встретились через tч. Найдите расстояние между городами, если скорость автомобиля Ѵ1 км/ч, а скорость мотоцикла Ѵ2 км/ч. Ответьте на вопрос задачи, если t = 3, Ѵ1 = 80, Ѵ2 = 60. 6. Раскройте скобки: 2р – (3р – (2р – с)). |
Контрольная работа №1 М7кл l Вариант 1. Найдите значение выражения: 6х – 8у, при 2. Сравните значения выражений: – 0,8х – 1 и 0,8х – 1, при х = 6. 3. Упростите выражение: а) 2х – 3у – 11х + 8у; б) 5(2а + 1) – 3; в) 14х – (х – 1) + (2х + 6). 4. Упростите выражение и найдите его значение: – 4(2,5а – 1,5) + 5,5а – 8, при 5. Из двух городов, расстояние между которыми Sкм, одновременно навстречу друг другу выехали легковой автомобиль и грузовик, и встретились через tч. Скорость легкового автомобиля Ѵкм/ч. Найдите скорость грузовика. Ответьте на вопрос задачи, если S = 200, t = 2, Ѵ = 60. 6. Раскройте скобки: 3х – (5х – (3х – 1)). |
Контрольная работа №1 М7кл ll Вариант 1. Найдите значение выражения: 16а + 2у, при 2. Сравните значения выражений: 2 + 0,3а и 2 – 0,3а, при а = – 9. 3. Упростите выражение: а) 5а + 7в – 2а – 8в; б) 3(4х + 2) – 5; в) 20b – (b – 3) + (3b – 10). 4. Упростите выражение и найдите его значение: – 6(0,5х – 1,5) – 4,5х – 8, при 5. Из двух городов одновременно навстречу друг другу выехали автомобиль и мотоцикл, и встретились через tч. Найдите расстояние между городами, если скорость автомобиля Ѵ1 км/ч, а скорость мотоцикла Ѵ2 км/ч. Ответьте на вопрос задачи, если t = 3, Ѵ1 = 80, Ѵ2 = 60. 6. Раскройте скобки: 2р – (3р – (2р – с)). |
Контрольная работа №1 М7кл lll Вариант 1. Найдите значение выражения: 4х + 3у, при 2. Сравните значения выражений: – 0,4а + 2 и – 0,4а – 2, при а = 10. 3. Упростите выражение: а) 5х + 3у – 2х – 9у; б) 2(3а – 4) + 5; в) 15а – (а – 3) + (2а – 1). 4. Упростите выражение и найдите его значение: – 2(3,5у – 2,5) + 4,5у – 1, при 5. Из двух пунктов, расстояние между которыми Sкм, одновременно навстречу друг другу отправились пешеход и велосипедист, и встретились через tч. Скорость велосипедиста Ѵ км/ч. Найдите скорость пешехода. Ответьте на вопрос задачи, если S =9, t = 0,5, Ѵ = 12. 6. Раскройте скобки: 5а – (3а – (2а – 4)). |
Контрольная работа №1 М7кл lV Вариант 1. Найдите значение выражения: 12а – 3b, при 2. Сравните значения выражений: 1 – 0,6х и 1 + 0,6х , при х = 5. 3. Упростите выражение: а) 12а – 10b – 10а + 6b; б) 4(3х – 2) + 7; в) 8х – (2х + 5) + (х – 1). 4. Упростите выражение и найдите его значение: – 5(0,6с – 1,2) – 1,5с – 3, при 5. Из двух пунктов одновременно навстречу друг другу вышли два пешехо – да и встретились через tч. Найдите расстояние между пунктами, если скорость одного пешехода Ѵ1 км/ч, а другого Ѵ2 км/ч. Ответьте на вопрос задачи, если Ѵ1 = 5, Ѵ2 = 4, t = 3. 6. Раскройте скобки: 7х – (5х – (3х + у)). |
Контрольная работа №1 М7кл lll Вариант 1. Найдите значение выражения: 4х + 3у, при 2. Сравните значения выражений: – 0,4а + 2 и – 0,4а – 2, при а = 10. 3. Упростите выражение: а) 5х + 3у – 2х – 9у; б) 2(3а – 4) + 5; в) 15а – (а – 3) + (2а – 1). 4. Упростите выражение и найдите его значение: – 2(3,5у – 2,5) + 4,5у – 1, при 5. Из двух пунктов, расстояние между которыми Sкм, одновременно навстречу друг другу отправились пешеход и велосипедист, и встретились через tч. Скорость велосипедиста Ѵ км/ч. Найдите скорость пешехода. Ответьте на вопрос задачи, если S =9, t = 0,5, Ѵ = 12. 6. Раскройте скобки: 5а – (3а – (2а – 4)). |
Контрольная работа №1 М7кл lV Вариант 1. Найдите значение выражения: 12а – 3b, при 2. Сравните значения выражений: 1 – 0,6х и 1 + 0,6х , при х = 5. 3. Упростите выражение: а) 12а – 10b – 10а + 6b; б) 4(3х – 2) + 7; в) 8х – (2х + 5) + (х – 1). 4. Упростите выражение и найдите его значение: – 5(0,6с – 1,2) – 1,5с – 3, при 5. Из двух пунктов одновременно навстречу друг другу вышли два пешехо – да и встретились через tч. Найдите расстояние между пунктами, если скорость одного пешехода Ѵ1 км/ч, а другого Ѵ2 км/ч. Ответьте на вопрос задачи, если Ѵ1 = 5, Ѵ2 = 4, t = 3. 6. Раскройте скобки: 7х – (5х – (3х + у)). |
ГДЗ Алгебра 7 класс Кузнецова
Тетрадь для контрольных работ по алгебре – это пособие, предназначенное для проверки знаний и навыков учеников. Оно является логическим дополнением к учебнику одноименного автора. Тетрадь позволяет подготовиться к предстоящим ОГЭ и ЕГЭ по дисциплине, так как структура заданий соответствует экзаменационным требованиям. Это отличное дополнение к теоретическому материалу, изложенному в учебнике. Автор удачно подобрал задания и разделил их на 4 уровня: начальный, средний, достаточный и высокий.
Преимущества сборника
Тетрадь для контрольных работ по алгебре – это хорошая подборка заданий. Ее отличает:
- Обучающий характер;
- Разные уровни сложности;
- Наличие олимпиадных заданий.
Особого внимания заслуживает последний пункт. Педагоги часто используют пособие для подготовки учебников к школьным и городским олимпиадам. Здесь содержатся нестандартные номера, которые решаются другими способами и требуют наличия логического мышления и смекалки.
Что такое ГДЗ
ГДЗ – это готовые домашние задания, книга с решением и ответами ко всем номерам. Пособие позволяет научиться правильно записывать условие и оформлять решение. Вы сможете проверить правильность выполнения номеров и оформить работу в соответствии с требованиями ФГОС. Это очень важно для успешной сдачи экзамена в конце 9 класса и для участия в олимпиадах. Так как ответы, записанные неправильно, не засчитываются. Решебник восполнит пробелы в знаниях, если вы пропустили несколько уроков алгебры в школы. Вы сможете провести самоанализ, выполнив, а затем проверив ответы.
Наше предложение
Наш сайт предлагает воспользоваться онлайн-версией ГДЗ с помощью мобильного телефона или компьютера. В любое удобное для вас время выберите необходимый раздел, вариант и номер упражнения. Перед вами откроется изображение с записанным условием, решением и ответом. Все задания решены лучшими математиками, можете не сомневаться в их правильности.
Учитесь с нами! Повышайте баллы по алгебре!
ГДЗ Алгебра 7 класс Попов, Мордкович
Решебник к учебнику «Алгебра 7 класс Тетрадь для самостоятельных и контрольных работ Попов, Мордкович, Экзамен» — это пособие, в котором можно найти решение и ответы ко всем номерам книги. Оно поможет в выполнении домашнего задания ученикам и в проверке работ преподавателям. Родители часто используют его как подсказку, когда нет времени на то, чтобы вникать в материал, изучаемый по алгебре.
Преимущества решебника
ГДЗ (готовые домашние задания) четко структурированы. Вы с легкостью найдете нужный материал. Как и учебник по алгебре, решебник состоит из 8 разделов:
- Математический язык и модель;
- Линейная функция;
- Системы двух линейных уравнений;
- Степень и свойства натурального показателя;
- Одночлены;
- Многочлены;
- Разложение на множители;
- Функция.
Структура ГДЗ
К каждой теме дается несколько самостоятельных и одна контрольная работа. Самостоятельные работы идут в 2 вариантах, контрольные – в 4. Первые задания соответствуют базовым знаниям и даются в виде тестирования. Ученикам предлагается выбрать только положительный или отрицательный ответ без объяснений действия. Поэтому в ГДЗ ответы к таким номерам даны только в виде «да» и «нет». Остальные упражнения предполагают более развернутого решения. В ГДЗ четко прописаны все действия и дан развернутый ответ.
Как пользоваться
На нашем сайте размещена онлайн-версия пособия. Вам необходимо выбрать раздел, вариант и номер задания. Все упражнения решены математиками, поэтому ответы корректны. ГДЗ используют для подготовки домашнего задания, отработки навыков дома и проверки выполненных номеров. Старайтесь только сверяться с ответами и исправлять их в случае необходимости. Так вы сможете выявить, с каким материалом у вас возникли трудности и проработать его еще раз. Обычное списывание не приведет к желаемому результату.
CogAT Test (Тест когнитивных способностей) | 2 класс
(-12: 00) Международная линия перемены дат Запад (-11: 00) Остров Мидуэй, Самоа (-10: 00) Гавайи (-09: 00) Аляска (-08: 00) Тихоокеанское время (США И Канада) (- 07:00) Горное время (США и Канада) (- 07:00) Аризона (-06: 00) Центральное время (США и Канада), Гвадалахара, Мехико (-06: 00) Центральная Америка, Саскачеван (-05: 00) Восточное время (США и Канада) (-05:00) Индиана, Богота, Лима, Кито, Рио-Бранко (-04: 00) Атлантическое время (Канада), Манаус, Сантьяго (-04: 00 ) Каракас, Ла-Пас (-03: 30) Ньюфаундленд (-03: 00) Гренландия, Бразилиа, Монтевидео (-03: 00) Буэнос-Айрес, Джорджтаун (-02: 00) Среднеатлантический (-01: 00) Азорские острова ( -01: 00) Острова Кабо-Верде.(00:00) Касабланка, Монровия, Рейкьявик (00:00) GMT: Дублин, Эдинбург, Лиссабон, Лондон (+01: 00) Амстердам, Берлин, Рим, Вена, Прага, Брюссель (+01: 00) Западная Центральная Африка (+02: 00) Амман, Афины, Стамбул, Бейрут, Каир, Иерусалим (+02: 00) Хараре, Претория (+03: 00) Багдад, Москва, Санкт-Петербург, Волгоград (+03: 00) Кувейт, Эр-Рияд , Найроби, Тбилиси (+03: 30) Тегеран (+04: 00) Абу-Дади, Маскат (+04: 00) Баку, Ереван (+04: 30) Кабул (+05: 00) Екатеринбург (+05: 00) Исламабад, Карачи, Ташкент (+05: 30) Ченнаи, Калькутта, Мумбаи, Нью-Дели, Шри-Джаяварденепура (+05: 45) Катманду (+06: 00) Астана, Дакка (+06: 00) Алматы, Ноносибирск (+06 : 30) Янгон (Рангун) (+ 07:00) Красноярск (+07: 00) Бангкок, Ханой, Джакарта (+08: 00) Пекин, Гонконг, Сингапур, Тайбэй (+08: 00) Иркутск, Улан-Батаар, Перт (+09: 00) Якутск (+09: 00) Сеул, Осака, Саппоро, Токио (+09: 30) Дарвин (+09: 30) Аделаида (+10: 00) Брисбен, Гуам, Порт-Морсби (+10 : 00) Канберра, Мельбурн, Сидней, Хобарт, Владивосток (+11: 00) Магадан, Соломоновы острова., Новая Каледония (+12: 00) Окленд, Веллингтон (+12: 00) Фиджи, Камчатка, о-в Маршалла (+ 13:00) Нукуалофа
.
Комплексные числа
Комплексный номер
Комплексное число — это комбинация действительного числа
и мнимого числа
Действительные числа — это числа вроде:
| 1 | 12,38 | -0,8625 | 3/4 | √2 | 1998 |
Практически любое число, которое вы можете придумать, является действительным числом!
Мнимые числа при возведении в квадрат дает отрицательный результат .
Обычно этого не происходит, потому что:
Но только представьте, что такие числа существуют, потому что мы хотим их.
Давайте поговорим еще о мнимых числах …
«Единичное» мнимое число (например, 1 для действительных чисел) — это i, который является квадратным корнем из −1
.
Потому что, возводя i в квадрат, мы получаем −1
я 2 = -1
Примеры мнимых чисел:
| 3i | 1.04i | −2,8i | 3i / 4 | (√2) я | 1998i |
И мы оставляем там маленькое «i», чтобы напомнить нам, что нам нужно умножить на √ − 1
Комплексные числа
Когда мы объединяем действительное число и мнимое число, мы получаем комплексное число :
Примеры:
| 1 + я | 39 + 3i | 0,8 — 2,2i | −2 + πi | √2 + я / 2 |
Может ли число быть комбинацией двух чисел?
Можем ли мы составить одно из двух других чисел? Мы можем точно!
Мы постоянно делаем это с дробями.Дробь 3 / 8 — это число, состоящее из 3 и 8. Мы знаем, что это означает «3 из 8 равных частей».
Ну, комплексное число — это всего лишь , два числа, сложенные вместе (действительное и мнимое число).
Любая часть может быть нулевой
Итак, комплексное число имеет действительную и мнимую части.
Но любая часть может быть 0 , поэтому все действительные и мнимые числа также являются комплексными числами.
| Комплексное число | Реальная часть | Воображаемая часть | |
|---|---|---|---|
| 3 + 2i | 3 | 2 | |
| 5 | 5 | 0 | Чисто Настоящее |
| −6i | 0 | −6 | Чисто воображаемое |
Сложно?
Сложный не означает сложный.
Это означает, что два типа чисел, действительные и мнимые, вместе образуют комплекс , точно так же, как комплекс зданий (здания, соединенные вместе).
A Визуальное объяснение
Вы знаете, как проходит числовая линия слева направо ?
Что ж, пусть воображаемые числа идут вверх-вниз :
И получаем сложный самолет
Комплексное число теперь может отображаться как точка:
Комплексный номер 3 + 4 и
Добавление
Чтобы сложить два комплексных числа, складываем каждую часть отдельно:
(a + b i ) + (c + d i ) = (a + c) + (b + d) i
Пример: сложите комплексные числа 3 + 2 i и 1 + 7 i
- сложите действительные числа и
- сложите мнимые числа:
(3 + 2i) + (1 + 7i)
= 3 + 1 + (2 + 7) i
= 4 + 9i
Попробуем еще:
Пример: сложите комплексные числа 3 + 5 i и 4 — 3 i
(3 + 5 i ) + (4 — 3 i )
= 3 + 4 + (5 — 3) i
= 7 + 2 i
В комплексной плоскости это:
Умножение
Для умножения комплексных чисел:
Каждая часть первого комплексного числа умножается на
каждая часть второго комплексного числа
Просто используйте «FOIL», что означает « F irsts, O uters, I nners, L assts» (см. Биномиальное умножение для более подробной информации):
|
|
|
(a + b i ) (c + d i ) = ac + ad i + bc i + bd i 2 |
|
Как это:
Пример: (3 + 2i) (1 + 7i)
(3 + 2i) (1 + 7i) = 3 × 1 + 3 × 7i + 2i × 1 + 2i × 7i
= 3 + 21i + 2i + 14i 2
= 3 + 21i + 2i — 14 (потому что i 2 = −1)
= −11 + 23i
А это:
Пример: (1 + i) 2
(1 + я) (1 + я) = 1 × 1 + 1 × я + 1 × я + я 2
= 1 + 2i — 1 (поскольку i 2 = −1)
= 0 + 2i
Но есть способ быстрее!
Используйте это правило:
(a + b i ) (c + d i ) = (ac − bd) + (ad + bc) i
Пример: (3 + 2i) (1 + 7i) = (3 × 1-2 × 7) + (3 × 7 + 2 × 1) i = −11 + 23i
Почему это правило работает?
Это просто метод «ФОЛЬГА» после небольшой работы:
(a + b i ) (c + d i ) = ac + ad i + bc i + bd i 2 FOIL method
= ac + ad i + bc i — bd (потому что i 2 = −1)
= (ac — bd) + (ad + bc) i (собирает похожие термины)
И вот у нас есть шаблон (ac — bd) + (ad + bc) i .
Это правило, безусловно, быстрее, но если вы его забудете, просто запомните метод FOIL.
Давайте попробуем i 2
Ради интереса воспользуемся методом расчета i 2
Пример: i 2
Мы можем записать i с действительной и мнимой частью как 0 + i
i 2 = (0 + i) 2 = (0 + i) (0 + i)
= (0 × 0 — 1 × 1) + (0 × 1 + 1 × 0) и
= -1 + 0 и
= −1
И это хорошо согласуется с определением, что i 2 = −1
Так что все прекрасно работает!
Узнайте больше об умножении комплексных чисел.
Конъюгаты
Нам нужно будет узнать о конъюгатах через минуту!
Сопряжение — это где мы меняем знак в середине вот так:
Сопряжение часто пишется с чертой над ним:
Пример:
5 — 3 i = 5 + 3 i
Деление
Конъюгат используется для облегчения сложного деления.
Уловка состоит в том, чтобы умножить верхний и нижний на , сопряженный с нижним .
Пример: Сделайте это Подразделение:
2 + 3 i 4-5 i
Умножить верхнюю и нижнюю на конъюгат 4-5 i :
2 + 3 i 4-5 i × 4 + 5 i 4 + 5 i = 8 + 10 i + 12 i + 15 i 2 16 + 20 i — 20 i — 25 i 2
Теперь запомните, что i 2 = −1, поэтому:
= 8 + 10 i + 12 i -15 16 + 20 i -20 i + 25
Добавить условия «Нравится» (и обратите внимание, как внизу 20 i — 20 i отменяются!):
= −7 + 22 i 41
Наконец, мы должны вернуть ответ в форму a + b i :
= −7 41 + 22 41 i
СДЕЛАНО!
Да, нужно сделать небольшой расчет.Но это можно сделать и .
Умножение на конъюгат
Но есть способ быстрее.
В предыдущем примере было интересно то, что произошло внизу:
(4-5 i ) (4 + 5 i ) = 16 + 20 i -20 i -25 i 2
Средние условия (20 i — 20 i ) аннулируются! Также i 2 = −1, поэтому получаем:
(4-5 i ) (4 + 5 i ) = 4 2 + 5 2
Это действительно довольно простой результат.Общее правило:
(a + b i ) (a — b i ) = a 2 + b 2
Мы можем использовать это, чтобы сэкономить время при делении, например:
Пример: попробуем еще раз
2 + 3 i 4-5 i
Умножить верхнюю и нижнюю на конъюгат 4-5 i :
2 + 3 i 4-5 i × 4 + 5 i 4 + 5 i = 8 + 10 i + 12 i + 15 я 2 16 + 25
= −7 + 22 i 41
И затем обратно в форму a + b i :
= −7 41 + 22 41 i
СДЕЛАНО!
Обозначение
Мы часто используем z для комплексного числа.И Re () для действительной части и Im () для мнимой части, например:
Что выглядит так на комплексной плоскости:
Набор Мандельброта
|
Прекрасный набор Мандельброта (на фото) основан на комплексных числах. Это график того, что происходит, когда мы берем простое уравнение z 2 + c (оба комплексных числа) и снова и снова возвращаем результат в z . Цвет показывает, насколько быстро z 2 |
.
Среднее, Медиана, Режим и Диапазон
Purplemath
Среднее, медиана и мода — это три вида «средних». В статистике есть много «средних» значений, но я думаю, что это три наиболее распространенных, и, безусловно, те три, с которыми вы, скорее всего, столкнетесь на курсах, предшествующих статистике, если эта тема вообще возникнет.
«Среднее» — это «среднее», к которому вы привыкли, когда вы складываете все числа, а затем делите их на количество чисел.«Медиана» — это «среднее» значение в списке чисел. Чтобы найти медиану, ваши числа должны быть перечислены в числовом порядке от наименьшего к наибольшему, поэтому вам, возможно, придется переписать свой список, прежде чем вы сможете найти медиану. «Режим» — это значение, которое встречается чаще всего. Если ни один номер в списке не повторяется, то для списка нет режима.
MathHelp.com
«Диапазон» списка чисел — это просто разница между наибольшим и наименьшим значениями.
-
Найдите среднее значение, медианное значение, режим и диапазон для следующего списка значений:
13, 18, 13, 14, 13, 16, 14, 21, 13
Среднее значение является обычным средним, поэтому я сложу и разделю:
(13 + 18 + 13 + 14 + 13 + 16 + 14 + 21 + 13) ÷ 9 = 15
Обратите внимание, что в этом случае среднее значение не является значением из исходного списка.Это обычный результат. Вы не должны предполагать, что ваше среднее значение будет одним из ваших исходных чисел.
Медиана — это среднее значение, поэтому сначала мне придется переписать список в числовом порядке:
13, 13, 13, 13, 14, 14, 16, 18, 21
В списке девять чисел, поэтому средним будет (9 + 1) ÷ 2 = 10 ÷ 2 = 5-е число:
13, 13, 13, 13, 14, 14, 16, 18, 21
13, 13, 13, 13, 14, 14, 16, 18, 21
Итак, медиана равна 14.
Режим — это число, которое повторяется чаще, чем любое другое, поэтому 13 — это режим.
Наибольшее значение в списке — 21, а наименьшее — 13, поэтому диапазон составляет 21–13 = 8.
означает: 15
медиана: 14
режим: 13
диапазон: 8
Примечание. Формула для определения места нахождения медианы: «([количество точек данных] + 1) ÷ 2», но вам необязательно использовать эту формулу.Вы можете просто рассчитывать с обоих концов списка, пока не встретитесь в середине, если хотите, особенно если ваш список короткий. В любом случае будет работать.
Партнер

-
Найдите среднее значение, медианное значение, режим и диапазон для следующего списка значений:
1, 2, 4, 7
Среднее значение является обычным средним:
(1 + 2 + 4 + 7) ÷ 4 = 14 ÷ 4 = 3.5
Медиана — это среднее число. В этом примере числа уже перечислены в числовом порядке, поэтому мне не нужно переписывать список. Но «среднего» числа нет, потому что есть четное количество чисел. Из-за этого медиана списка будет средним (то есть обычным средним) двух средних значений в списке. Средние два числа — 2 и 4, поэтому:
.
(2 + 4) ÷ 2 = 6 ÷ 2 = 3
Таким образом, медиана этого списка равна 3, значение, которого нет в списке вообще.
Режим — это номер, который повторяется наиболее часто, но все числа в этом списке появляются только один раз, поэтому режима нет.
Наибольшее значение в списке — 7, наименьшее — 1, а их разница — 6, поэтому диапазон равен 6.
означает: 3,5
медиана: 3
режим: нет
диапазон: 6
Все значения в списке выше были целыми числами, но среднее значение в списке было десятичным.Получение десятичного значения для среднего (или для медианы, если у вас четное количество точек данных) совершенно нормально; не округляйте свои ответы, чтобы попытаться сопоставить формат других чисел.
-
Найдите среднее значение, медианное значение, режим и диапазон для следующего списка значений:
8, 9, 10, 10, 10, 11, 11, 11, 12, 13
Среднее значение является обычным средним, поэтому я сложу и разделю:
(8 + 9 + 10 + 10 + 10 + 11 + 11 + 11 + 12 + 13) ÷ 10 = 105 ÷ 10 = 10.5
Медиана — это среднее значение. В списке из десяти значений это будет (10 + 1) ÷ 2 = 5,5-е значение; формула напоминает мне с этой пятой точкой, что мне нужно усреднить пятое и шестое числа, чтобы найти медиану. Пятое и шестое числа — это последние 10 и первые 11, поэтому:
(10 + 11) ÷ 2 = 21 ÷ 2 = 10,5
Режим — это номер, который повторяется чаще всего. В этом списке два значения, которые повторяются трижды; а именно 10 и 11, каждое повторяется трижды.
Наибольшее значение — 13, наименьшее — 8, поэтому диапазон составляет 13-8 = 5.
означает: 10,5
медиана: 10,5
режимы: 10 и 11
диапазон: 5
Как видите, два средних значения (в данном случае среднее и медианное) могут иметь одно и то же значение. Но это , а не , как обычно, и вы должны , а не этого ожидать.
Примечание. В зависимости от вашего текста или преподавателя, приведенный выше набор данных может рассматриваться как не имеющий режима, а не как имеющий два режима, потому что ни один отдельный номер не повторялся чаще, чем любой другой. Я видел книги, в которых говорится об этом; похоже, что нет единого мнения относительно «правильного» определения «режима» в приведенном выше случае. Поэтому, если вы не знаете, как ответить на «режим» в приведенном выше примере, спросите своего инструктора перед следующего теста.
Единственная сложная часть нахождения среднего, медианы и моды — это точно определить, какое «среднее» есть какое. Просто запомните следующее:
означает: обычное значение «среднего»
медиана: среднее значение
режим: чаще всего
(Выше я использовал термин «среднее» довольно случайно. Техническое определение того, что мы обычно называем «средним», технически называется «средним арифметическим»: сложение значений и последующее деление на количество значений.Поскольку вам, вероятно, больше знакомо понятие «среднее», чем «мера центральной тенденции», я использовал более удобный термин.)
-
Учащийся получил следующие оценки на тестах: 87, 95, 76 и 88. Он хочет в целом 85 или выше. Какую минимальную оценку он должен получить за последний тест, чтобы достичь этого среднего?
Минимальная оценка — это то, что мне нужно найти.Чтобы найти среднее значение всех его оценок (известных и неизвестных), я должен сложить все оценки, а затем разделить их на количество оценок. Поскольку у меня еще нет оценок за последний тест, я буду использовать переменную для обозначения этого неизвестного значения: « x ». Затем вычисление для нахождения желаемого среднего:
(87 + 95 + 76 + 88 + x ) ÷ 5 = 85
Умножая на 5 и упрощая, получаем:
87 + 95 + 76 + 88 + 901 12 x = 425
346 + х = 425
х = 79
Ему нужно набрать не менее 79 баллов за последний тест.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в нахождении медианы. Попробуйте выполнить указанное упражнение или введите свое собственное. Или попробуйте ввести любой список чисел, а затем выбрать вариант — среднее, медианное, режим и т. Д. — из того, что предлагает вам виджет. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway.
(Щелкните здесь, чтобы перейти непосредственно на сайт Mathway, если вы хотите проверить их программное обеспечение или получить дополнительную информацию.)
URL: https://www.purplemath.com/modules/meanmode.htm
,
Числовые основы: введение и двоичные числа
Purplemath
Преобразование между различными системами счисления на самом деле довольно просто, но идея, лежащая в основе этого, поначалу может показаться немного запутанной. И хотя тема различных основ может показаться вам несколько бессмысленной, рост компьютеров и компьютерной графики увеличил потребность в знаниях о том, как работать с различными (недесятичными) базовыми системами, особенно с двоичными системами (с единицами и нулями) и шестнадцатеричная система (числа от нуля до девяти, за которыми следуют буквы от A до F).
MathHelp.com

В нашей обычной десятичной системе у нас есть цифры для чисел от нуля до девяти.У нас нет однозначного числа для «десяти». (Римляне использовали иероглиф «X».) Да, мы пишем «10», но это означает «1 десять и 0 единиц». Это две цифры; у нас нет единственной цифры, обозначающей «десять».
Вместо этого, когда нам нужно считать на единицу больше девяти, мы обнуляем столбец единиц и добавляем единицу к столбцу десятков. Когда мы становимся слишком большими в столбце десятков — когда нам нужно на один больше, чем девять десятков и девяти единиц («99»), мы обнуляем столбцы десятков и единиц и добавляем единицу к десятикратным десяти или сотням. , столбец.Следующий столбец — это столбец десять раз десять, или тысячи. И так далее, причем каждый столбец большего размера в десять раз больше предыдущего. Мы помещаем цифры в каждый столбец, сообщая нам, сколько копий этой степени десяти нам нужно.
Единственная причина, по которой математика с основанием десять кажется «естественной», а другие — нет, заключается в том, что вы использовали десятичный алгоритм с детства. И (почти) каждая цивилизация использовала математику по основанию десять, вероятно, по той простой причине, что у нас десять пальцев.Если бы вместо этого мы жили в мире мультфильмов, где у нас было бы только четыре пальца на каждой руке (сосчитайте их в следующий раз, когда будете смотреть телевизор или читать комиксы), тогда «естественной» базовой системой, вероятно, была бы система с основанием восемь, или «восьмеричный».
двоичный
Давайте посмотрим на числа с основанием два или двоичные числа. Как бы вы записали, например, 12 10 («двенадцать, основание десять») в виде двоичного числа? Вам нужно будет преобразовать в столбцы с основанием два, аналог столбцов с основанием десять.В десятичной системе координат у вас есть столбцы или «места» для 10 0 = 1, 10 1 = 10, 10 2 = 100, 10 3 = 1000 и так далее. Точно так же в основании два у вас есть столбцы или «места» для 2 0 = 1, 2 1 = 2, 2 2 = 4, 2 3 = 8, 2 4 = 16 и т. вперед.
Первый столбец в математике с основанием два — это столбец единиц. Но в колонке единиц может быть только «0» или «1». Когда вы дойдете до «два», вы обнаружите, что нет единственной цифры, которая обозначает «два» в математике с основанием два.Вместо этого вы помещаете «1» в столбец двоек и «0» в столбец единиц, указывая «1 два и 0 единиц». Десятичное число «два» (2 10 ) записывается в двоичной системе как 10 2 .
«Тройка» в основании два на самом деле означает «1, два и 1, один», поэтому записывается как 11 2 . «Четыре» на самом деле означает дважды два, поэтому мы обнуляем столбец двоек и столбец единиц и помещаем «1» в столбец четверок; 4 10 записывается в двоичной форме как 100 2 . Вот список первых чисел:
Преобразование между двоичными и десятичными числами довольно просто, если вы помните, что каждая цифра в двоичном числе представляет собой степень двойки.
-
Преобразует 101100101 2 в соответствующее десятичное число.
Я перечислю цифры по порядку, так как они появляются в номере, который они мне дали. Затем в другом ряду я отсчитываю эти цифры от ПРАВА, начиная с нуля:
Первая строка выше (помеченная как «цифры») содержит цифры из двоичного числа; вторая строка (обозначенная как «нумерация») содержит степень двойки (основание), соответствующую каждой цифре.Я воспользуюсь этим списком, чтобы преобразовать каждую цифру в степень двойки, которую он представляет:
1 × 2 8 + 0 × 2 7 + 1 × 2 6 + 1 × 2 5 + 0 × 2 4 + 0 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0
= 1 × 256 + 0 × 128 + 1 × 64 + 1 × 32 + 0 × 16 + 0 × 8 + 1 × 4 + 0 × 2 + 1 × 1
= 256 + 64 + 32 + 4 + 1
= 357
Затем 101100101 2 преобразуется в 357 10 .
Преобразование десятичных чисел в двоичные почти так же просто: просто разделите на 2.
-
Преобразует 357 10 в соответствующее двоичное число.
Чтобы выполнить это преобразование, мне нужно несколько раз делить на 2, отслеживая остатки по ходу дела.Смотрите ниже:
Приведенный выше рисунок анимирован на «живой» веб-странице.
Как видите, после многократного деления на 2 я получил следующие остатки:
Эти остатки говорят мне, что такое двоичное число. Я читаю числа с внешней стороны деления, начиная сверху с конечного значения и его остатка, и заканчиваю свой путь вокруг и вниз по правой части последовательного деления.Тогда:
357 10 преобразуется в 101100101 2 .
Партнер

Этот метод преобразования работает для преобразования в любое недесятичное основание.Только не забудьте поставить эту первую цифру вверху перед списком остатков. Если вам интересно, объяснение того, почему этот метод работает, доступно здесь.
Вы можете преобразовать десятичную систему счисления в любую другую. Когда вы изучаете эту тему в классе, вы, вероятно, должны будете преобразовывать числа в различные другие основы, поэтому давайте рассмотрим еще несколько примеров …
URL: https: // www.purplemath.com/modules/numbbase.htm
,
 .
.  .
.  .
. 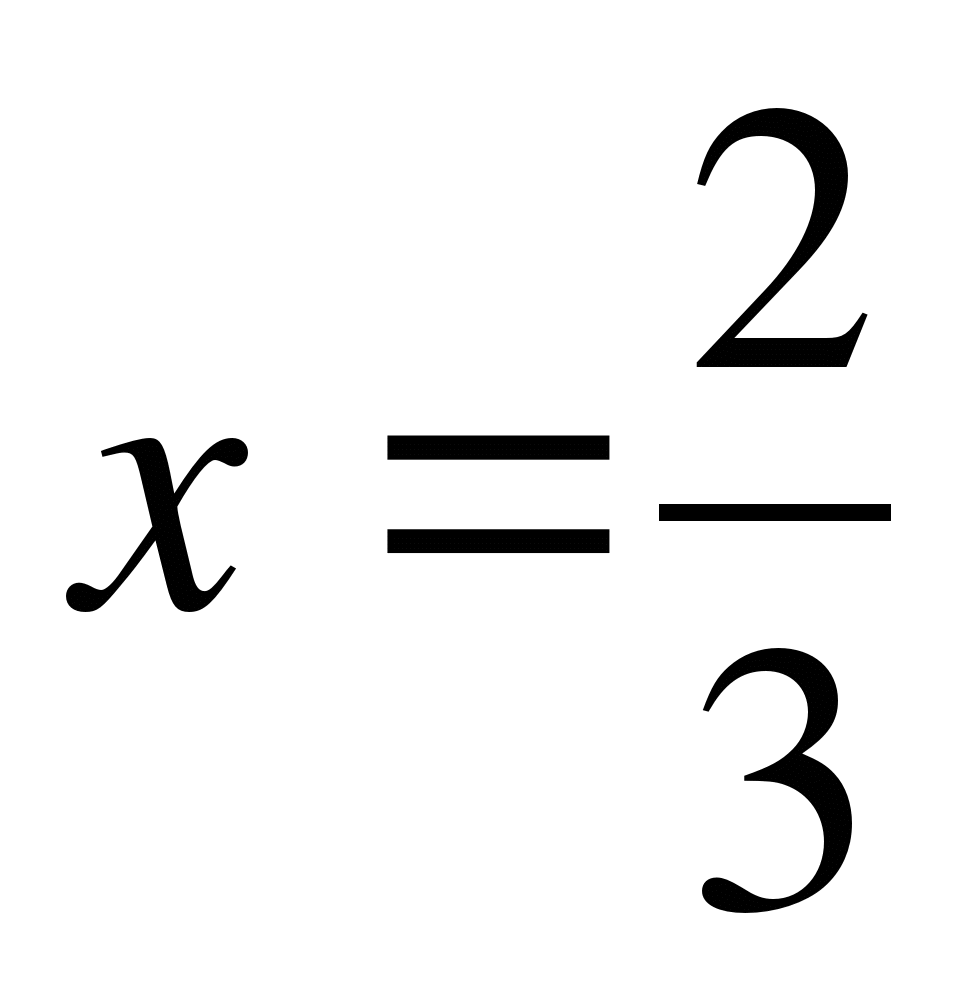 .
. 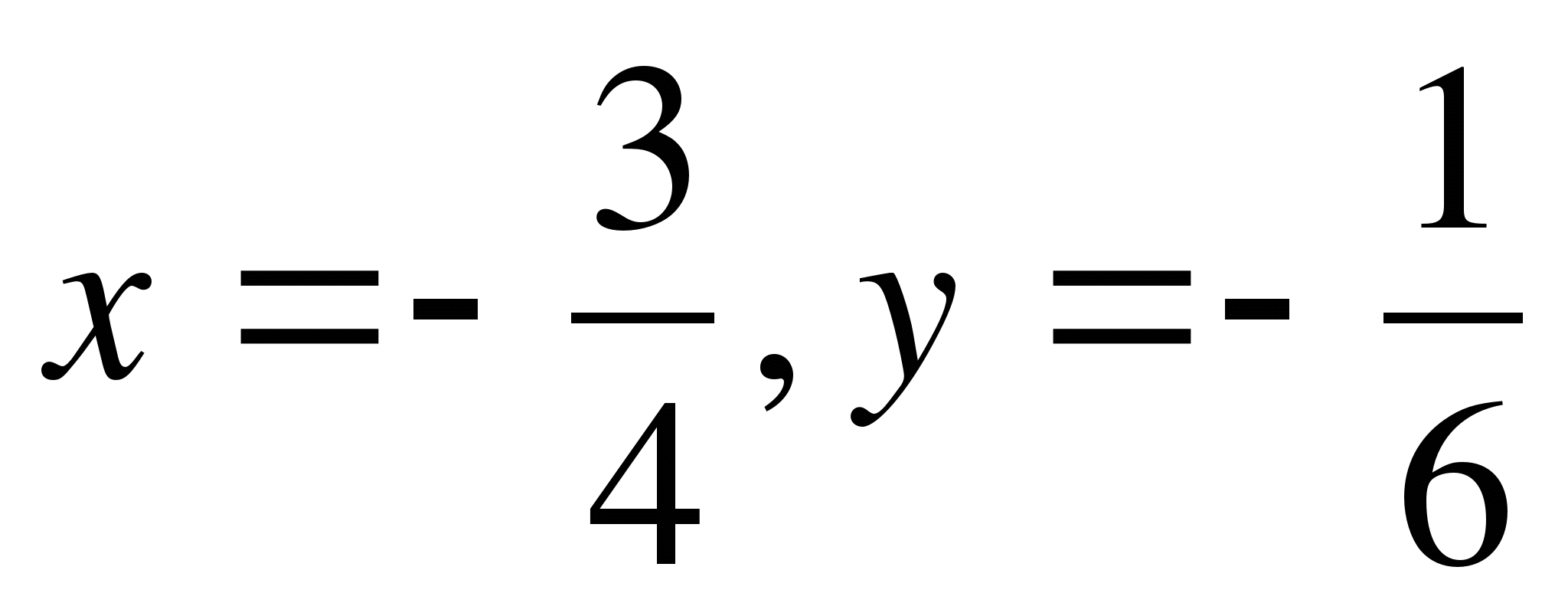 .
. 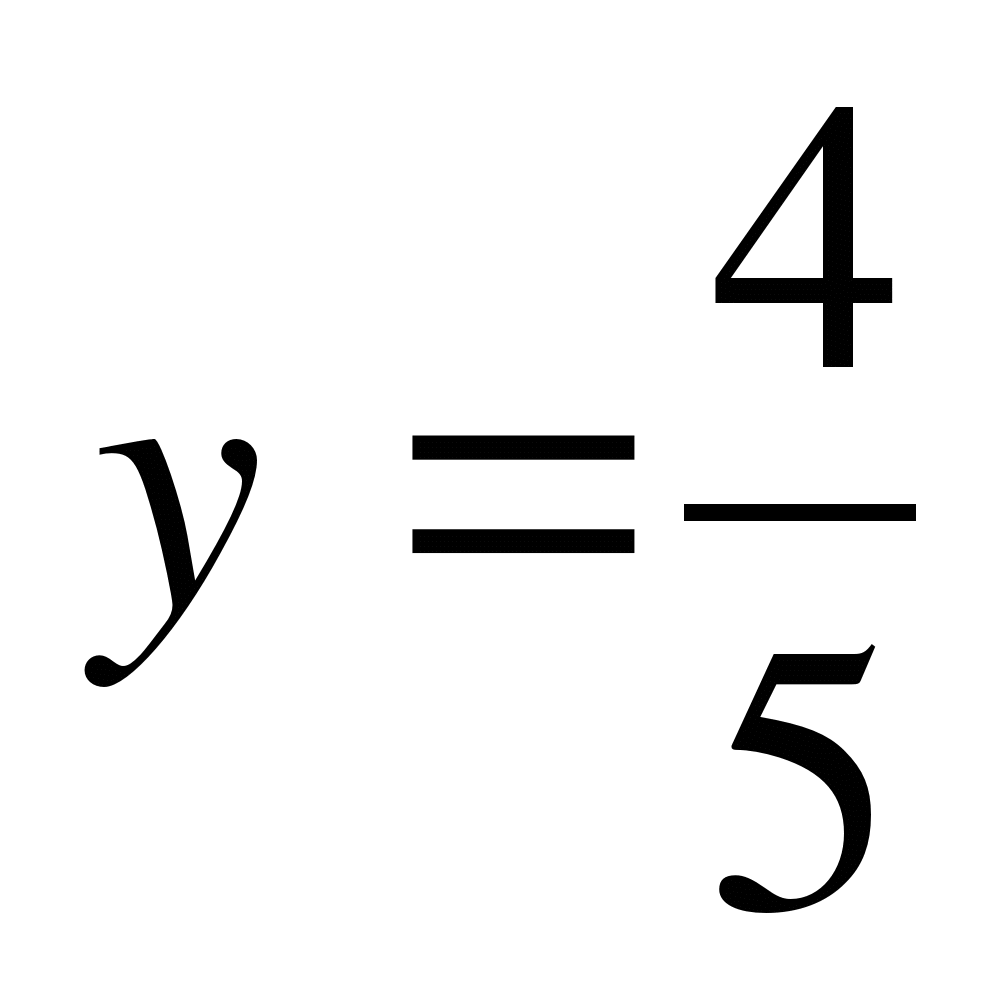 .
. 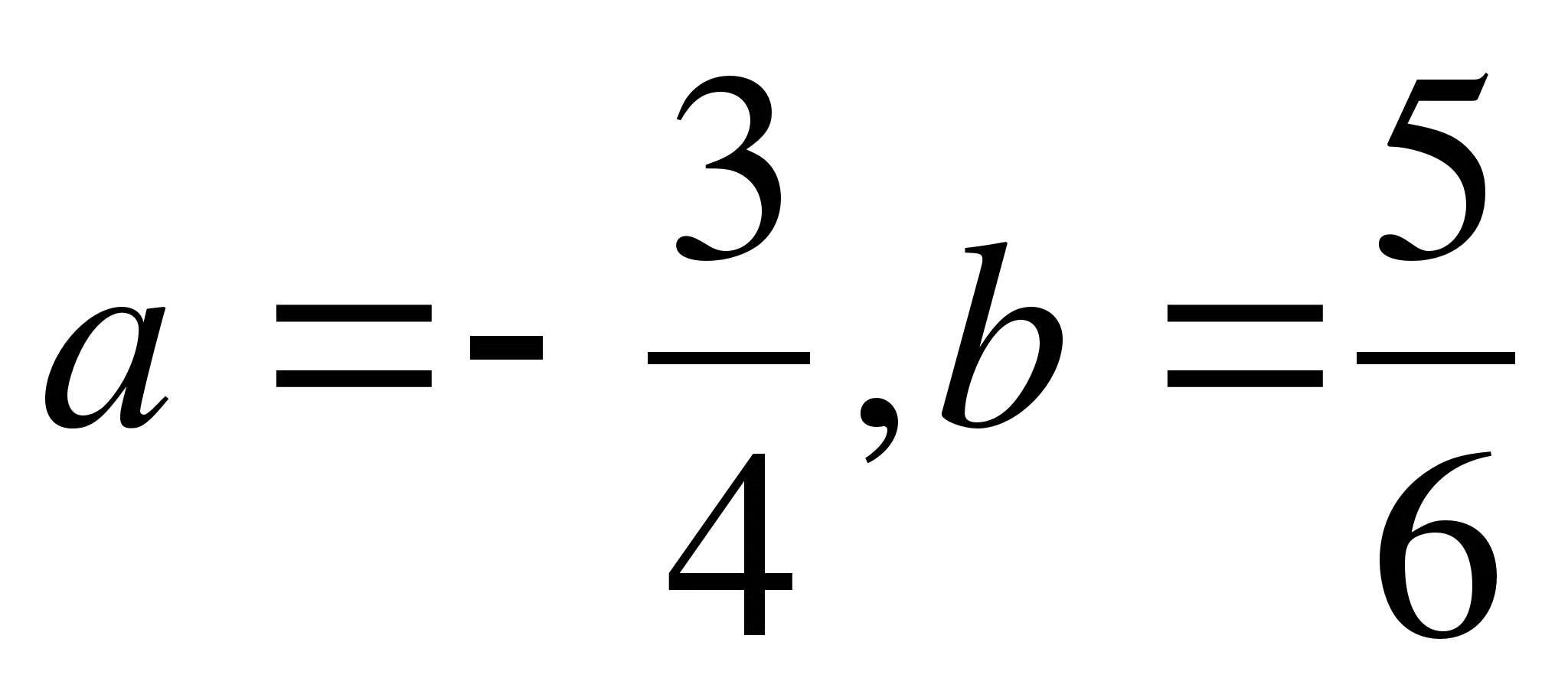 .
.  .
.