Правила по алгебре 7 класс
— это выражение, состоящее из чисел.
— это выражение, состоящее из чисел и переменных (букв)
Уравнение вида где переменная, некоторые числа, называют линейным уравнением с одной переменной.
Математическая модель – составленное по данному условию уравнение.
Алгоритм – последовательность действий.
Выражения, соответственные значения которых равны при любых значениях, входящих в них переменных, называют тождественно равными.
Равенство, верное при любых значениях входящих в него переменных, называют тождеством.
Степень числа а с показателем 1 называют само это число.
При возведении отрицательного числа в степень с чётным показателем получаем положительное число. При возведении отрицательного числа в степень с нечётным показателем получаем отрицательного числа.
Свойства степени:
Одночлен – произведение чисел, переменных и их степеней.
Коэффициент одночлена – числовой множитель одночлена, записанного в стандартном виде.
Подобные одночлены – одночлены, имеющие одинаковую буквенную часть.
Многочлены – выражения, состоящие из суммы нескольких одночленов.
Многочлен стандартного вида – многочлен, состоящий из одночленов стандартного вида.
Степень многочлена стандартного вида – наибольшая степень из степени одночлена, из которых составлен многочлен.
Нуль – многочлен – число нуль, также многочлены, тождественно равные нулю.
Тождественно равные выражения – выражения, соответственные значения которых равны при любых значениях входящих в них переменных.
Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить.
Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить.
Разложение многочлена на множители: представление многочлена в виде произведения нескольких многочленов.
Формулы сокращенного умножения
Полный квадрат – трехчлен, который можно представить в виде квадрата двучлена.
P=4a, где а – независимая переменная(может принимать любые значения), Р – зависимая(изменятся в зависимости от а)
Функция – правило, с помощью которого по каждому значению независимой переменной можно найти единственное значение зависимой переменной.
Функциональная зависимость – зависимость одной переменной от другой.
Аргумент — независимая переменная.
Область определения – все значения, которые принимает аргумент.
Значение функции – значение зависимой переменной.
Заданная функция – функция, где указаны её область определения и правило, с помощью которого можно по каждому значению независимой переменной найти значение зависимой переменной.
Область значений функций – все значения, которые принимает зависимая переменная.
Способы задание функции: 1. Описательный, 2. С помощью формул, 3. Табличный.
Все точки координатной плоскости, которые можно отметить, действуя таким способом, образуют график функции.
График функции f – геометрическая фигура, состоящая из всех тех, и только тех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции f.
Линейная функция – функция, которую можно задать формулой Её график – прямая.
Линейная функция, которая задается формулой называют прямой пропорциональностью.
Случай, когда значение функции будет оставаться неизменным при любых значениях аргумента.
Равенство, содержащее две переменные называется уравнением с двумя переменными.
Пару значений, обращающую уравнение в верное равенство называют решением уравнения с двумя переменными.
Решить уравнение с двумя переменными – значит найти все его решения или показать, что оно не имеет решений.
График уравнения с двумя переменными – геометрическая фигура, состоящая из всех тех, и только тех точек координатной плоскости, координаты которых (пары чисел) являются решением данного уравнения.
Линейное уравнение с двумя переменными называют уравнение вида
Случай, когда графиком уравнения является прямая.
Решить систему уравнений – значит найти все её решения или показать, что оно не имеет решений.
Суть графического метода: 1) построить на одной координатной плоскости графики уравнений, входящих в систему, 2) найти координаты всех точек пересечения графиков, 3) полученные пары чисел будут искомыми рениями.
Суть метода подстановки: 1) выразить из любого уравнения системы одну переменную через другую, 2) подставить в другое уравнение системы, вместо этой переменной, 3) решить уравнение с одной переменной, 4) подставить найденное значение переменной в выражение, получено на первом шаге, 5) вычислить значение другой переменной.
Суть метода сложения: 1) подобрав «выгодные» множители, преобразовать одно или оба уравнения системы так, чтобы коэффициентом при одной из переменных стали противоположными числами, 2) сложить почленно левые и правые части уравнений, 3) решить уравнение с одной переменной, 4)подставить найденное на третьем шаге значение переменной в любое из уравнений исходной системы, 5) вычислить значение другой переменной.
Числовым выражением называют всякую запись из чисел, знаков арифметических действий и скобок, составленную со смыслом.
Например:
3+5⋅7−4 — числовое выражение;
3+:−5 — не числовое выражение, а бессмысленный набор символов.
Очень часто вместо конкретных чисел употребляются буквы, тогда получается алгебраическое выражение.
Алгебраическим выражением называется запись из букв, знаков арифметических действий, чисел и скобок, составленная со смыслом.
Например:
a2−3b — алгебраическое выражение.
Поскольку буквам, входящим в состав алгебраического выражения, можно придавать различные числовые значения (т. е. можно менять значения букв), эти буквы называют переменными.
Алгебраические выражения могут быть очень громоздкими, и алгебра учит их упрощать, используя правила, законы, свойства, формулы.
При упрощении вычислений часто используются законы сложения и умножения.
Законы сложения
1) От перемены мест слагаемых сумма не изменяется, т. е.
a+b=b+a — переместительный закон сложения.
2) Чтобы к сумме двух слагаемых прибавить третье слагаемое, можно к первому слагаемому прибавить сумму второго и третьего слагаемых, т. е.
a+b+c=a+b+c — сочетательный закон сложения.
Законы умножения
1) От перемены мест множителей произведение не меняется, т. е.
a⋅b=b⋅a — переместительный закон умножения.
2) Произведение не зависит от группировки его сомножителей, т. е.
a⋅b⋅c=a⋅b⋅c — сочетательный закон умножения.
3) Произведение суммы нескольких чисел на какое-нибудь число равно сумме произведений каждого слагаемого на это число, т. е.
a+b⋅c=ac+bc — распределительный закон умножения относительно сложения.
В результате упрощений числового выражения получается число, которое называют значением числового выражения.
Выполнив указанные действия в первом примере, получим
3+5⋅7−4=18.
Число \(18\) в ответе есть значение данного числового выражения.
О значении алгебраического выражения можно говорить только при конкретных значениях входящих в него букв.
Например, алгебраическое выражение a2−3b при \(a=-16\) и \(b=-14\) имеет значение \(298\), т. к.
a2−3b=−162−3⋅−14=256+42=298,
а вот алгебраическое выражение a2−3a+2 при \(a=-4\) имеет значение \(-6,5\),
т. к. −42−3−4+2=16−3−2=13−2=−6,5.
И это же алгебраическое выражение a2−3a+2 при \(a=-2\) не имеет смысла, т. к. a+2=−2+2=0, т. е. будет деление на ноль.
Обрати внимание!
А на ноль делить нельзя!
Вывод:
если при конкретных значениях букв алгебраическое выражение имеет числовое значение, то указанные значения переменных называют допустимыми;
если же при конкретных значениях букв алгебраическое выражение не имеет смысла, то указанные значения переменных называют недопустимыми.
Так, в примере a2−3a+2 значение \(a=-4\) — допустимое, а
значение \(a=-2\) — недопустимое, т. к. при нём будет деление на ноль, а делить на ноль нельзя!
Основные понятия — урок. Алгебра, 7 класс.
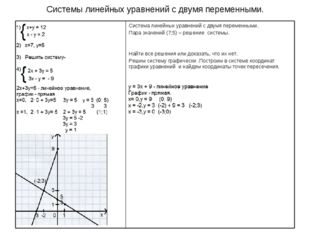
1. решить систему уравнений:
x+2y−5=0,2x+4y+3=0.
Графиком уравнения x+2y−5=0 является прямая.
Найдём две пары значений переменных \(x\) и \(y\), удовлетворяющих этому уравнению.
| \(x\) | \(5\) | \(0\) |
| \(y\) | \(0\) | \(2,5\) |
Построим на координатной плоскости \(xОy\) прямую l1, проходящую через эти две точки.
Графиком уравнения 2x+4y+3=0 также является прямая.
Найдём две пары значений переменных \(x\) и \(y\), удовлетворяющих этому уравнению.
| \(x\) | \(-1,5\) | \(2,5\) |
| \(y\) | \(0\) | \(-2\) |
Построим на координатной плоскости \(xОy\) прямую l2, проходящую через эти две точки.

Прямые l1 и l2 параллельны, значит, система не имеет решений, так как нет точек, удовлетворяющих одновременно и одному, и другому уравнению, т. е. принадлежащих одновременно и одной, и другой из построенных прямых.
Ответ: система не имеет решений.
2. Решить систему уравнений:
2x−y−5=0,2x+y−7=0.
Построим графики уравнений системы, преобразуя каждое уравнение к виду линейной функции. Получим из первого уравнения \(y=2x-5\) и из второго уравнения \(y=-2x+7\).
Графиком уравнения \(y=2x-5\) является прямая.
Найдём две пары значений переменных \(x\) и \(y\), удовлетворяющих этому уравнению.
| \(x\) | \(0\) | \(3\) |
| \(y\) | \(-5\) | \(1\) |
Построим на координатной плоскости \(xОy\) прямую l1, проходящую через эти две точки.
Графиком уравнения \(y=-2x+7\) также является прямая.
Найдём две пары значений переменных \(x\) и \(y\), удовлетворяющих этому уравнению.
| \(x\) | \(0\) | \(1\) |
| \(y\) | \(7\) | \(5\) |
Построим на координатной плоскости \(xОy\) прямую l2, проходящую через эти две точки.

Прямые l1 и l2 пересекаются в точке \(A\), координаты которой — единственное решение заданной системы.
Ответ: \((3;1)\).
Алгебра 7 класс. Все формулы и определения.
Краткий курс алгебры за 7 класс.
«Алгебра 7 класс. Все формулы и определения» — это краткий курс алгебры за 7 класс. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского) — М.: Просвещение, 2013.
Выражения и их преобразования
☑ 1. Степенью числа а с натуральным показателем n, большим 1, называют произведение n множителей, каждый из которых равен а: Степенью числа а с показателем 1 называют само число а: а1 = а.
Степенью числа а с показателем 1 называют само число а: а1 = а.
Степень числа а ≠ 0 с показателем 0 равна 1: а0 = 1.
☑ 2. Свойства степеней с натуральными показателями:
аm • аn = аm+n
При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.
аm : аn = аm-n, где а ≠ 0, m ≥ n
(аm)n = аmn
При возведении степени в степень основание оставляют прежним, а показатели перемножают.
(ab)n = аnbn
При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают.
☑ 3. Одночленами называют произведения чисел, переменных и их степеней, а также сами числа, переменные и их степени. Например, 5а2х, –3а2b3, 4, х, у5 — одночлены.
Степенью одночлена называют сумму показателей степеней всех переменных, входящих в одночлен. Например, степень одночлена –8а2b4 равна 6.
☑ 4. Многочленом называют сумму одночленов. Например, 3х5 – 4х2 + 1, 7a3b – ab2 + ab + 6—многочлены. Одночлены считают многочленами, состоящими из одного члена.
Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. Например, степень многочлена 5х3у + 3х2у5 + ху равна степени одночлена 3х2у5, т. е. равна 7.
Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида.
☑ 5. При сложении многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки. Например,
(3аb + 5с2) + (ab – с2) = 3ab + 5с2 + ab – с2 = 4аb + 4с2
При вычитании многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки. Например,
(6x2 – у) – (2x2 – 8у) = 6х2 – у – 2х2 + 8у = 4х2 + 7у
Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить. Например,
а2 (3аb – b3 + 1) = 3а3b – а2b3 + а2
Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить. Например,
(5х – 1)(3х + 2) = 15x2 – Зx + 10x – 2 = 15x2 + 7x – 2
☑ 6. Формулы сокращённого умножения:
(а + b)2 = а2 + 2аb + b2
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.
(а – b)2 = а2 – 2аb + b2
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.
(а + b)3 = а3 + 3а2b + 3ab2 + b3
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(а – b)3 = а3 – 3а2b + Заb2 – b3
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(а – b)(а + b) = а2 – b2
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
а3 + b3 = (а + b)(a2 – аb + b2)
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
а3 – b3 = (а – b)(a2 + ab + b2)
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
☑ 7. Разложением многочлена на множители называют представление многочлена в виде произведения многочленов.
Для разложения многочленов на множители применяют вынесение общего множителя за скобки, группировку, формулы сокращённого умножения. Например, многочлен 5х3 – х2у можно разложить на множители, вынеся за скобки х2 : 5х3 – х2у = х2 (5х – у). Многочлен 3х – 3у – ах + ау можно разложить на множители, используя способ группировки:
3х – 3у – ах + ау = (3x – 3у) – (ах – ау) = 3(х – у) – а (х – у) = (х – у)(3 – а).
Многочлен а4 – 25x2 можно разложить на множители, используя формулу разности квадратов двух выражений:
а4 – 25x2 = (а2)2 – (5x)2 = (а2 – 5x)(а2 + 5x).
Иногда многочлен удаётся разложить на множители, применив последовательно несколько способов.
Уравнения
☑ 8. Корнем уравнения с одной переменной называют значение переменной, при котором уравнение обращается в верное равенство. Например, число 8 — корень уравнения 3x +1 = 5х – 15, так как верно равенство 3•8 + 1= 5•8 – 15.
Решить уравнение с одной переменной — значит найти все его корни или доказать, что корней нет.
☑ 9. Уравнения с одной переменной, имеющие одни и те же корни, называют равносильными. Например, уравнения x2 = 25 и (х + 5)(х – 5) = 0 равносильны. Каждое из них имеет два корня: –5 и 5. Уравнения, не имеющие корней, также считают равносильными.
При решении уравнений с одной переменной используются следующие свойства:
- если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;
- если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
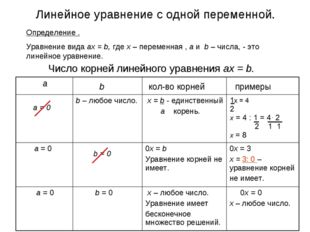
☑ 10. Линейным уравнением с одной переменной называют уравнение вида ах = b, где х — переменная, а и b — числа.
Если а ≠ 0, то уравнение ах = b имеет единственный корень b/a.
Например, уравнение 7х = 2 имеет корень 2/7.
Если а = 0 и b ≠ 0, то уравнение ах = b не имеет корней. Например, уравнение 0 • х = 7 не имеет корней.
Если а = 0 и b = 0, то корнем уравнения ах = b является любое число.
☑ 11. Решением уравнения с двумя переменными называют пару значений переменных, обращающую это уравнение в верное равенство. Например, пара чисел х = -1, у = 4 — решение уравнения 5х + 3у = 7.
Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными. Уравнения с двумя переменными, не имеющие решений, также считают равносильными.
В уравнении с двумя переменными можно переносить слагаемые из одной части в другую, изменяя их знаки, и обе части уравнения можно умножать или делить на одно и то же число, не равное нулю. При этом получаются уравнения, равносильные исходному.
☑ 12. Линейным уравнением с двумя переменными называют уравнение вида ах + by = с, где х и у — переменные, а, b и с — числа.
☑ 13. Графиком уравнения с двумя переменными называют множество точек координатной плоскости, координаты которых являются решениями этого уравнения.
Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.
☑ 14. Решением системы уравнений с двумя переменными называют пару значений переменных, обращающую каждое уравнение системы в верное равенство. Например, пара чисел х = 7, у = –1 — решение системы так как является верным каждое из равенств 7 + (–1) = 6 и 2 • 7 – (–1) = 15.
так как является верным каждое из равенств 7 + (–1) = 6 и 2 • 7 – (–1) = 15.
Решить систему уравнений — значит найти все её решения или доказать, что решений нет.
Системы уравнений с двумя переменными, имеющие одни и те же решения, называют равносильными. Системы, не имеющие решений, также считают равносильными.
☑ 15. Для решения систем линейных уравнений с двумя переменными используются графический способ, способ подстановки, способ сложения.
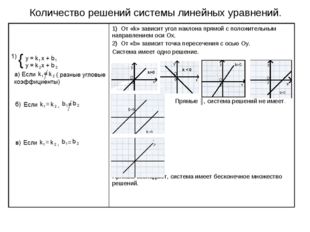
При графическом способе строят графики линейных уравнений (прямые) и анализируют их расположение:
- если прямые совпадают, то система имеет бесконечно много решений, причём координаты любой точки прямой являются решением системы;
- если прямые параллельны, то система не имеет решений; если прямые пересекаются, то система имеет единственное решение, причём координаты точки пересечения прямых являются решением системы.
При решении системы двух линейных уравнений с двумя переменными способом подстановки поступают следующим образом:
- выражают из какого–либо уравнения системы одну переменную через другую;
- подставляют в другое уравнение системы вместо этой переменной полученное выражение;
- решают получившееся уравнение с одной переменной; подставляют значение найденной переменной в одно из уравнений и находят соответствующее значение другой переменной.
При решении системы двух линейных уравнений с двумя переменными способом сложения поступают следующим образом:
- умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали в уравнениях противоположными числами;
- складывают почленно левые и правые части уравнений системы; решают получившееся уравнение с одной переменной; подставляют значение найденной переменной в одно из уравнений и находят соответствующее значение другой переменной.
Функции
☑ 16. Функциональная зависимость, или функция, — это такая зависимость между двумя переменными, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной.
Независимую переменную иначе называют аргументом, а о зависимой переменной говорят, что она является функцией этого аргумента. Все значения, которые принимает независимая переменная, образуют область определения функции.
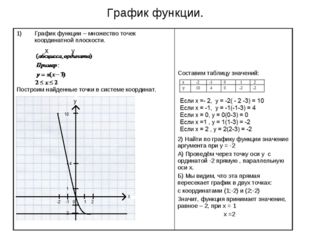
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
☑ 17. Линейной функцией называют функцию, которую можно задать формулой вида у = kx + b, где х — независимая переменная, k и b — числа.
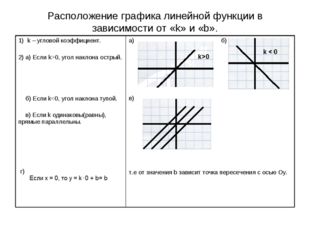
Графиком линейной функции у = kx + b является прямая. Число k называют угловым коэффициентом прямой, являющейся графиком функции у = kx + b.
Если k ≠ 0, то график функции у = kx + b пересекает ось х; если k = 0 и b ≠ 0, то прямая — график функции у = kx + b, параллельна оси х; если k = 0 и b = 0, то график функции совпадает с осью х.
Графики двух линейных функций пересекаются, если их угловые коэффициенты различны, и параллельны, если их угловые коэффициенты одинаковы.
Линейную функцию, задаваемую формулой у = kx при k ≠ 0, называют прямой пропорциональностью.
График прямой пропорциональности есть прямая, проходящая через начало координат. При k > 0 график расположен в первой и третьей координатных четвертях, а при k < 0 — во второй и четвёртой координатных четвертях.
☑ 18. График функции у = х2 — парабола. Этот график проходит через начало координат и расположен в первой и второй координатных четвертях. Он симметричен относительно оси у.
График функции у = х3 проходит через начало координат и расположен в первой и третьей координатных четвертях. Он симметричен относительно начала координат.
Статистические характеристики
☑ Средним арифметическим ряда чисел называют частное от деления суммы этих чисел на число слагаемых.
Модой ряда чисел называют число, которое встречается в данном ряду чаще других. Ряд чисел может иметь более одной моды или не иметь моды совсем.
Медианой упорядоченного ряда чисел с нечётным числом членов называют число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называют среднее арифметическое двух чисел, записанных посередине.
Например, медиана ряда чисел 17, 21, 27, 29, 32, 37, 41 равна 29, а медиана ряда чисел 28, 43, 54, 56, 58, 62 равна 55.
Медианой произвольного ряда чисел называют медиану соответствующего упорядоченного ряда.
Размахом ряда чисел называют разность между наибольшим и наименьшим из этих чисел.
Вы смотрели Конспект «Алгебра 7 класс. Все формулы и определения» — краткий курс алгебры за 7 класс. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского). Выберите дальнейшие действия:
Инфоурок
›
Алгебра
›Презентации›Опорные таблицы по учебнику «Алгебра 7 класс» автор Макарычев Ю.Н.
Описание презентации по отдельным слайдам:
1 слайд

Описание слайда:
Числовые выражения.
2 слайд

Описание слайда:
Выражения с переменными.
3 слайд

Описание слайда:
Сравнение значений выражений.
4 слайд

Описание слайда:
Свойства действий над числами.
5 слайд

Описание слайда:
Тождества. Тождественные преобразования выражений.
6 слайд

Описание слайда:
Уравнение и его корни.
7 слайд
Описание слайда:
Линейное уравнение с одной переменной. Определение . Уравнение вида ax = b, где x – переменная , а и b – числа, — это линейное уравнение. Число корней линейного уравнения ax = b.
8 слайд

Описание слайда:
Решение задач с помощью уравнений. 1) Пусть x яблок было в корзине. По условию задачи в ящике стало яблок в 5 раз больше. Составляем уравнение : 2х + 10 = (х -10)5 2х + 10 = 5х – 50 2х – 5х = -50 -10 -3х = -60 х= 60 :3 х= 20 20 яблок было в корзине. 20 2 = 40 40 яблок было в ящике. Ответ:20 яблок, 40 яблок. 2) Пусть х саженцев в 1 бригаде. По условию задачи всего 78 саженцев. Составляем уравнение: х + 2х + х+ 12 = 78 4х = 78 – 12 4х = 66 х = 66 : 4 х = 16, 5 16,5 саженцев 16,5 – ненатуральное число. Ответ: Таким способом распределить саженцы невозможно. 1 бригада х шт. 2 бригада 2х шт. 3 бригада (х+12) шт Всего х + 2х + (х+12) шт
9 слайд

Описание слайда:
Среднее арифметическое, размах и мода.
10 слайд

Описание слайда:
Медиана как статистическая характеристика.
11 слайд

Описание слайда:
Что такое функция?
12 слайд

Описание слайда:
Вычисление значений функции по формуле.
13 слайд
Описание слайда:
График функции.
14 слайд

Описание слайда:
Прямая пропорциональность и её график.
15 слайд

Описание слайда:
Линейная функция и её график.
16 слайд

Описание слайда:
Определение степени с натуральным показателем.
17 слайд

Описание слайда:
Умножение и деление степеней
18 слайд

Описание слайда:
Возведение в степень произведения и степени
19 слайд

Описание слайда:
Одночлен и его стандартный вид.
20 слайд

Описание слайда:
Умножение одночленов. Возведение одночлена в степень.
21 слайд

Описание слайда:
График функции y =
22 слайд

Описание слайда:
23 слайд

Описание слайда:
Многочлен и его стандартный вид.
24 слайд

Описание слайда:
Сложение и вычитание многочленов.
25 слайд

Описание слайда:
Умножение одночлена на многочлен.
26 слайд

Описание слайда:
Вынесение общего множителя за скобки.
27 слайд

Описание слайда:
Умножение многочлена на многочлен.
28 слайд

Описание слайда:
Разложение многочлена на множители способом группировки
29 слайд

Описание слайда:
Возведение в квадрат суммы и разности двух выражений.
30 слайд

Описание слайда:
Разложение на множители с помощью формул квадрата суммы и квадрата разности.
31 слайд

Описание слайда:
Умножение разности двух выражений на их сумму.
32 слайд

Описание слайда:
Разность квадратов двух выражений.
33 слайд

Описание слайда:
Сумма и разность кубов.
34 слайд

Описание слайда:
Преобразование целого выражения в многочлен.
35 слайд

Описание слайда:
Способы разложения на множители. Вынесение за скобки общего множителя. Формулы сокращенного умножения. Способ группировки.
36 слайд

Описание слайда:
Различные способы разложения на множители.
37 слайд

Описание слайда:
Линейное уравнение с двумя переменными.
38 слайд

Описание слайда:
График линейного уравнения с двумя переменными.(1)
39 слайд

Описание слайда:
График линейного уравнения с двумя переменным.(2)
40 слайд
Описание слайда:
Системы линейных уравнений с двумя переменными.
41 слайд

Описание слайда:
Способ подстановки.
42 слайд

Описание слайда:
Способ сложения.
43 слайд

Описание слайда:
Решить уравнение.
44 слайд
Описание слайда:
Расположение графика линейной функции в зависимости от «k» и «b».
45 слайд
Описание слайда:
Количество решений системы линейных уравнений.

Курс повышения квалификации
Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию:
Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс:
Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник:
Все учебники
Выберите тему:
Все темы
также Вы можете выбрать тип материала:

Краткое описание документа:
Ученики, составляя опорные таблицы под руководством учителя, отрабатывают умение работы с научной литературой для этого нужно:
- Прочитать пункт учебника
- Научиться выбирать главное, обосновывать, пояснять.
- Научиться применять полученные умения на других уроках
- В течение учебного года составляются опорные таблицы по пунктам учебника;
- Выполняют электронную версию этих таблиц;
- Применяют данные таблицы на этапе повторения и подготовки к сдаче экзамена.
Общая информация
Номер материала:
ДБ-384369
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Конспекты по предмету «Алгебра»
Изучение Алгебры шаг за шагом. Онлайн-учебник.
Кодификатор ОГЭ
ТЕСТЫ по АЛГЕБРЕ
Справочник для ОГЭ
Глава 1. Математика до алгебры
Математика 5 и 6 классов
Дорофеев 5 кл. Контрольные с ответами
Глава 2. Алгебра 7 класс
(остальные материалы готовятся к публикации)
Макарычев 7 кл. Контрольные с ответами
Глава 3. Алгебра 8 класс
(остальные материалы готовятся к публикации)
Макарычев 8 кл. Поурочные планы
Глава 4. Алгебра 9 класс
(остальные материалы готовятся к публикации)
Макарычев 9 кл. Контрольные с ответами
Глава 5. Материалы для подготовки к ОГЭ
- Задание 1 ОГЭ по математике
- Задание 2 ОГЭ по математике
Глава 6. Алгоритмы решения задач по алгебре
Материалы для УМК Мерзляк
Электронные формы учебников для 6-9 классов (ссылки):
Алгебра (от араб. الْجَبْر, «аль-джабр» — восполнение) — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики. Слово «алгебpа» также употребляется в общей алгебре в названиях различных алгебраических систем. В более широком смысле под алгеброй понимают раздел математики, посвящённый изучению операций над элементами множества произвольной природы, обобщающий обычные операции сложения и умножения чисел.
Алгeбра как раздел математики традиционно включает следующие категории: Элементарная, Общая, Универсальная, Линейная (включая матрицы) и Алгебраическая комбинаторика.
Элементарная алгебpа, которая изучает свойства операций с вещественными числами. В ней постоянные и переменные обозначаются буквенными символами. Элементарная алгeбpа содержит правила преобразования математических выражений и уравнений с использованием этих символов. Обычно преподаётся в школе под названием aлгебра.
Кодификатор ОГЭ
ТЕСТЫ по АЛГЕБРЕ
Подобрать репетитора
Учебные пособия для подготовки к ОГЭ




Источники идей и цитат для конспектов по Алгебре:
- Макарычев Ю.Н. Учебники по Алгебре для 7, 8, 9 классов. — М.: Мнемозина.
- Лахова Н.В. Алгебрa за 7 занятий. 7 класс: учебное пособие — М.: Просвещение, 2016.
- Томилина М.Е. Справочник по математике. 5-9 классы — СПб.: Издательский дом «Литера».
- ОГЭ. Математика : универсальный справочник / И.В. Третьяк. — М.: Эксмо, 2016
- Мерзляк А.Г. Учебники по Алгебре для 7, 8, 9 классов. — М.: Вентана-Граф.
- ОГЭ. Математика. Справочник с комментариями ведущих экспертов / Л.В. Кузнецова — М.: Просвещение.
(с) Цитаты из вышеуказанных учебных пособий использованы на сайте в незначительных объемах, исключительно в учебных и информационных целях (пп. 1 п. 1 ст. 1274 ГК РФ).
|
1. |
Вопросы по теме «Многочлены»
|
1 |
|
2. |
Противоположные многочлены
|
1 |
|
3. |
Определение вида многочлена
|
1 |
|
4. |
Выбор вида многочлена
|
1 |
|
5. |
Коэффициент и степень членов многочлена
|
2 |
|
6. |
Степень многочлена
|
1 |
|
7. |
Составление многочлена
|
1 |
|
8. |
Упрощение многочлена (преобразование одночленов)
|
3 |
|
9. |
Приведение подобных слагаемых
|
2 |
|
10. |
Многочлен
|
2 |
|
11. |
Подобные слагаемые многочлена
|
2 |
|
12. |
Стандартный вид, подобные члены многочлена
|
3 |
|
13. |
Приведение подобных членов многочлена
|
3 |
|
14. |
Подобные члены многочлена
|
3 |
|
15. |
Числовое значение многочлена (целые числа)
|
3 |
|
16. |
Приведение подобных членов (обыкновенные дроби)
|
3 |
|
17. |
Значение многочлена
|
4 |
|
18. |
Числовое значение многочлена (десятичные дроби)
|
5 |
|
19. |
Числовое значение многочлена (обыкновенные дроби)
|
5 |
|
20. |
Стандартный вид многочлена (противоположный)
|
5 |
|
21. |
Стандартный вид многочлена
|
4 |
Представление и сравнение чисел (N)
Часть A (Уроки 1–7)
Темы включают представление и сравнение положительных рациональных чисел (целых, дробных и десятичных), поиск кратных и множителей положительных целых чисел, а также определение наименьшего общего кратного (LCM) и наибольшего общего множителя ( GCF) пары натуральных чисел.
Часть B (Уроки 8–12)
Темы включают представление отрицательных дробей и отрицательных десятичных дробей, сравнение значений любых двух рациональных чисел, экспоненциальную запись и использование деревьев факторов и простых факторизаций для нахождения LCM или GCF пары целые положительные числа.
В этом уроке рассматриваются три разные системы счисления: целые числа, целые и рациональные числа. Связи между различными системами счисления выделены, чтобы установить основу для сравнений и операций.
Математики часто используют числовую линию для решения задач.В этом уроке мы рассмотрим числовую линию, сосредоточившись на построении дробей.
В математике символы важны для общения. В этом уроке мы рассмотрим символы «больше» и «меньше». Кроме того, мы представляем две методики, используемые для сравнения дробей.
Рациональные числа могут быть записаны в виде дроби или десятичной дроби. В этом уроке мы обсудим связи между дробными представлениями и десятичными представлениями, в частности, когда речь идет о построении чисел на числовой линии.
В этом уроке мы рассмотрим, как создать список, кратный целому числу.Используя наши списки, мы идентифицируем общие кратные двух целых чисел, обращая особое внимание на наименьшее общее кратное (LCM).
Факторы, как и кратные, имеют отношение к умножению. В этом уроке мы решаем проблемы, определяя факторы натуральных чисел.
Расширяя урок факторов, мы сравниваем факторы двух натуральных чисел, чтобы найти общие факторы; в частности, мы часто заинтересованы в определении наибольших общих факторов (GCF). Мы заключаем, решая проблемы со словами, которые требуют от нас применения факторов к различным контекстам.
Дробные количества могут быть положительными или отрицательными. Как и отрицательные целые числа, отрицательные дроби лежат слева от нуля в числовой строке. В этом уроке мы наносим на числовую строку отрицательные дроби, чтобы помочь нам понять и сравнить значения этих чисел.
,
7-й класс математика
ТРЕУГОЛЬНИКИ И ЕГО СВОЙСТВА
РАБОЧИЕ ЛИСТЫ 7-ГО СОРТА
Помимо материалов, приведенных в этом разделе, если вам нужны какие-либо другие материалы по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Вы также можете посетить следующие веб-страницы по различным предметам в математике.
ЗАДАЧИ СЛОВА
Задачи со словами в HCF и LCM
Задачи со словами в простых уравнениях
Задачи со словами в линейных уравнениях
Задачи в словах по квадратным уравнениям
Задачи в алгебре
Проблемы со словами в поездах
Проблемы со словами в области и по периметру
Проблемы со словами при прямом и обратном изменении
Проблемы со словами в цене за единицу
Проблемы со словами в цене за единицу
Слово задачи по сравнению ставок
Преобразование словарных задач в обычных единицах измерения
Преобразование словарных задач в метрических единицах
Задачи со словами по простым интересам
Задачи со словами по сложным процентам
Задачи со словами по типам ngles
Задачи с дополнительными и дополнительными углами слов
Задачи с двойными фактами
Задачи с тригонометрическими словами
Процентные проблемы с словами
Проблемы с прибылью и убытками
Уценка наценки и разметки задачи
Проблемы с десятичными словами
Задачи на слова на дробях
Задачи на слова на смешанных дробях
Задачи на слово с одним уравнением шага
Задачи на слово с линейными неравенствами
Соотношение и пропорции слова задачи
Задачи со временем и работой
Задачи со словами на множествах и диаграммах Венна
Задачи со словами в возрасте
Задачи со словами в теореме Пифагора
Процент числа слова про oblems
Задачи на слово с постоянной скоростью
Задачи на слово на средней скорости
Задачи на слово на сумму углов треугольника составляет 180 градусов
ДРУГИЕ ТЕМЫ
Сочетания прибылей и убытков
Процентные ярлыки
Ярлыки временного стола
Сокращения времени, скорости и расстояния
Сокращения соотношений и пропорций
Область и диапазон рациональных функций
Область и диапазон функции с отверстиями
Графические рациональные функции
Графические рациональные функции с отверстиями
Преобразование повторяющихся десятичных дробей в дроби
Десятичное представление рациональных чисел
Поиск квадратного корня с помощью long di зрение
л.Метод CM для решения задач времени и работы
Перевод словесных задач в алгебраические выражения
Остаток при делении 2-й степени 256 на 17
Остаток при делении 17-й степени 23 на 16
Сумма всех трехзначных чисел, кратных 6
Сумма всех трехзначных чисел, кратных 7
Сумма всех трехзначных чисел, кратных 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
,