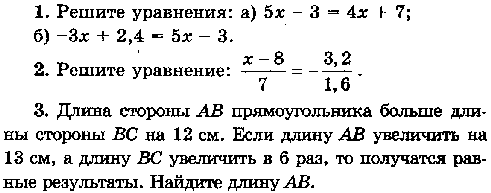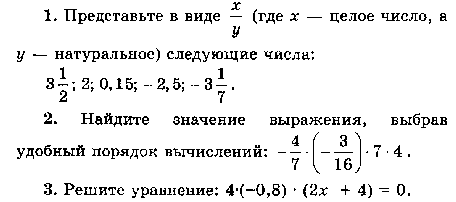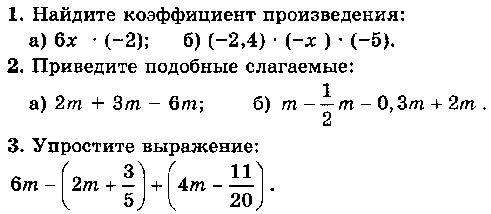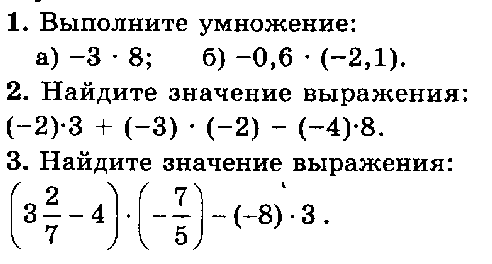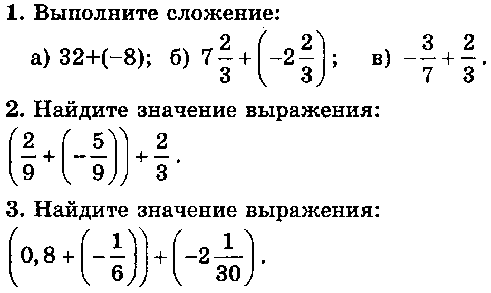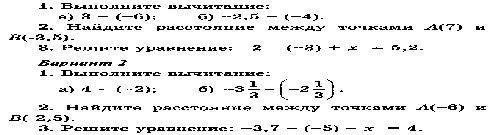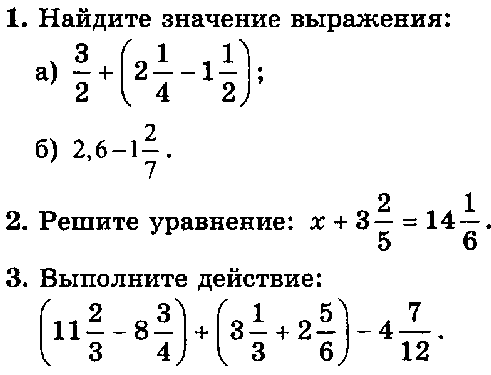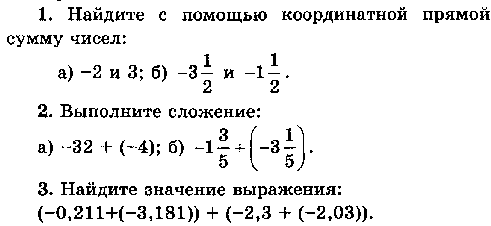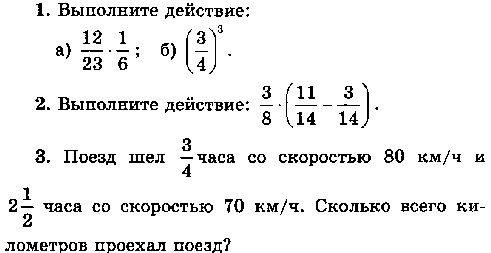Задание не найдено
Самостоятельные работы
К §1. Делимость чисел
СР №1. Делители и кратные
СР №2. Признаки делимости на 10; 5; 2 и 9; 3
СР №3. Простые и составные числа. Разложение на простые множители
СР №4. Наибольший общий делитель. Взаимно простые числаСР №5 Наименьшее общее кратное
СР №5. Наименьшее общее кратное
К §2. Сложение и вычитание дробей с разными знаменателями
СР №6. Основное свойство дроби. Сокращение дробей
СР №7. Приведение дробей к общему знаменателю
СР №8. Сравнение, сложение и вычитание дробей с разными знаменателями
СР №9. Сравнение, сложение и вычитание дробей с разными знаменателями
СР №10. Сложение и вычитание смешанных чисел
СР №11. Сложение и вычитание смешанных чисел
К §3. Умножение и деление обыкновенных дробей
СР №12. Умножение дробей
СР №13. Умножение дробей
СР №14. Нахождение дроби от числа
СР №15. Применение распределительного свойства умножения. Взаимно обратные числа
СР №16. Деление
СР №17. Нахождение числа по его дроби
СР №18. Дробные выражения
К §4. Отношения и пропорции
СР №19. Отношения
СР №20. Пропорции, прямая и обратная пропорциональные зависимости
СР №21. Масштаб
СР №22. Длина окружности и площадь круга. Шар
К §5. Положительные и отрицательные числа
СР №23. Координаты на прямой. Противоположные числа
СР №24. Модуль числа
СР №25. Сравнение чисел. Изменение величин
К §6. Сложение и вычитание положительных и отрицательных чисел
СР №26. Сложение чисел с помощью координатной прямой. Сложение отрицательных чисел
СР №27. Сложение чисел с разными знаками
СР №28. Вычитание
К §7. Умножение и деление положительных и отрицательных чисел
СР №29. Умножение
СР №30. Деление
СР №31. Рациональные числа. Свойства действий с рациональными числами
К §8. Решение уравнений
СР №32. Раскрытие скобок
СР №33. Коэффициент. Подобные слагаемые
СР №34. Решение уравнений
Контрольные работы
К §1 КР №1 Делители и кратные. Наибольший общий делитель. Взаимно простые числа
К §2 КР №2 Основное свойство дроби. Сложение и вычитание дробей с разными знаменателями
К § 3
КР №3 Умножение дробей. Нахождение дроби от числа. Взаимообратные числа
КР №4 Деление, Нахождение числа по его дроби. Дробные выражения
К §4 КР №5 Отношения, пропорции. Масштаб. Длина окружности и площадь круга
К §5 КР №6 Координаты на прямой. Противоположные числа. Модуль числа. Сравнение чисел. Изменения величин
К §6 КР №7 Сложение чисел с помощью координатной прямой. Сложение чисел с разными знаками
К §7 КР №8 Умножение. Деление. Свойства действий с рациональными числами
К §8 КР №9 Раскрытие скобок. Коэффициент. Подобные слагаемые. Решение уравнений
Самостоятельная работа №1. Делители и кратные:
Самостоятельная работа №2. Признаки делимости на 10, на 5 и на 2:
Самостоятельная работа №3. Признаки делимости на 9 и на 3:
Самостоятельная работа №4. Простые и составные числа:
Самостоятельная работа №5. Разложение на простые множители:
Самостоятельная работа №6. Наибольший общий делитель Взаимно простые числа:
Самостоятельная работа №7. Наименьшее общее кратное:
Самостоятельная работа №8. Основное свойство дроби:
Самостоятельная работа №9. Сокращение дробей:
Самостоятельная работа №10. Приведение дробей к общему знаменателю:
Самостоятельная работа №11. Сравнение, сложение и вычитание дробей с разными знаменателями:
Самостоятельная работа №12. Сложение и вычитание смешанных чисел:
Самостоятельная работа №13. Умножение дробей:
Самостоятельная работа №14. Нахождение дроби от числа:
Самостоятельная работа №15. Применение распределительного свойства:
Самостоятельная работа №16. Взаимно обратные числа:
Самостоятельная работа №17. Деление:
Самостоятельная работа №18. Нахождение числа по его дроби:
Самостоятельная работа №19. Дробные выражения:
Самостоятельная работа №20. Отношения:
Самостоятельная работа №21. Пропорции. Прямая и обратная пропорциональные зависимости:
Самостоятельная работа №22. Масштаб:
Самостоятельная работа №23. Длина окружности и площадь круга. Шар:
Самостоятельная работа №24. Координаты на прямой:
Самостоятельная работа №25. Противоположные числа:
Самостоятельная работа №26. Модуль числа:
Самостоятельная работа №27. Сравнение чисел. Изменение величин:
Самостоятельная работа №28. Сложение чисел с помощью координатной прямой. Сложение отрицательных чисел:
Самостоятельная работа №29. Сложение чисел с разными знаками:
Самостоятельная работа №30. Вычитание:
Самостоятельная работа №31. Умножение:
Самостоятельная работа №32. Деление:
Самостоятельная работа №33. Рациональные числа:
Самостоятельная работа №34. Раскрытие скобок:
Самостоятельная работа №35. Коэффициент. Подобные слагаемые:
Самостоятельная работа №36. Решение уравнений:
Самостоятельная работа №37. Перпендикулярные прямые. Параллельные прямые. Координатная плоскость:
Самостоятельная работа №38. Столбчатые диаграммы. Графики:
|
СР – 1 Делители и кратные |
СР – 34 Решение уравнений |
|
|
|
|
СР – 2 Признаки делимости |
СР – 35 Перпендикулярные прямые |
|
|
|
|
СР – 3 Простые и составные числа |
СР – 36 Столбчатые диаграммы |
|
|
|
|
СР – 31 Рациональные числа |
СР – 4 НОД |
|
|
|
|
СР – 32 Раскрытие скобок |
СР – 5 НОК |
|
|
|
|
СР – 33 Коэффициенты |
СР – 6 Сокращение дробей |
|
|
|
|
СР – 7 Приведение дробей к ОЗ |
СР – 29 Умножение |
|
|
|
|
СР – 8 Сложение дробей с разными знаменателями |
СР – 30 Деление |
|
|
|
|
СР – 27 Сложение чисел с разными знаками |
СР – 9 Вычитание дробей с разными знаменателями |
|
|
|
|
СР – 28 Вычитание |
СР – 10 Сложение смешанных чисел |
|
|
|
|
СР – 11 Вычитание смешанных чисел |
СР – 25 Сравнение чисел |
|
|
|
|
СР – 12 Умножение дробей |
СР – 26 Сложение отрицательных чисел |
|
|
|
|
СР – 23 Координаты на прямой |
СР – 13 Умножение дробей |
|
|
|
|
СР – 24 Модуль числа |
СР – 14 Нахождение дроби от числа |
|
|
|
|
СР – 15 Взаимно обратные числа |
СР – 21 Масштаб |
|
|
|
|
СР – 16 Деление |
СР – 22 Длина окружности |
|
|
|
|
СР – 19 Отношения |
СР – 17 Нахождение числа по его дроби |
|
|
|
|
СР – 20 Пропорции |
СР – 18 Дробные выражения |
|
|
|
Математика 6 Контрольные Виленкин (ДМ Попов)
Математика 6 Контрольные Виленкин (ДМ Попов) — это цитаты контрольных работ и ответы на задачи контрольных работ из учебного пособия: «Дидактические материалы по математике 6 класс к учебнику Н.Я. Виленкина и др. «Математика 6 класс» ФГОС (к новому учебнику) / М.А. Попов — М.: Издательство «Экзамен», 2017 (серия «учебно-методический комплект»)». Представленные ниже контрольные работы ориентированы на школьный учебник Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд «Математика 6 класс», рекомендованный Министерством образования и науки РФ и включенный в Федеральный перечень учебников. Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания.
Нажмите на необходимую вам тему контрольной работы. В начале указана цитата (материал контрольной работы, вариант 1) из вышеуказанного учебного пособия. Каждая цитата представлена в форме удобной для проверки знаний (на одной странице). Затем представлены ответы на все 4 варианта контрольной. При постоянном использовании контрольных работ рекомендуем КУПИТЬ книгу: Математика. 6 класс. Дидактические материалы к учебнику Н. Я. Виленкина и др. ФГОС (переход по ссылке в интернет-магазин «Лабиринт.Ру»). Кроме 10 контрольных (в 4-х вариантах) в книге представлены 38 самостоятельных работ (в 2-х вариантах), а также задания на смекалку. Вопросы и ответы представлены в настоящей статье в учебных целях, а также для ознакомления и покупки учебного пособия.
Математика 6 класс. Контрольные работы
по УМК Виленкин (ДМ Попов)
Выберите нужную вам контрольную работу:
Контрольная № 1 + Ответы
КР-01: Делители и кратные. Признаки делимости на 10, на 5 и на 2. Признаки делимости на 9 и на 3. Простые и составные числа. Разложение на простые множители. Наибольший общий делитель. Взаимно простые числа. Наименьшее общее кратное.
Контрольная № 2 + Ответы
КР-02: Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю. Сравнение, сложение и вычитание дробей с разными знаменателями. Сложение и вычитание смешанных чисел.
Контрольная № 3 + Ответы
КР-03: Умножение дробей. Нахождение дроби от числа. Применение распределительного свойства умножения. Взаимно обратные числа.
Контрольная № 4 + Ответы
КР-04: Деление. Нахождение числа по его дроби. Дробные выражения
Контрольная № 5 + Ответы
КР-05: Отношения. Пропорции. Прямая и обратная пропорциональные зависимости. Масштаб. Длина окружности и площадь круга.
Контрольная № 6 + Ответы
КР-06: Координаты на прямой. Противоположные числа. Модуль числа. Сравнение чисел. Изменение величин.
Контрольная № 7 + Ответы
КР-07: Сложение чисел с помощью координатной прямой. Сложение отрицательных чисел. Сложение чисел с разными знаками. Вычитание.
Контрольная № 8 + Ответы
КР-08: Умножение. Деление. Рациональные числа. Свойства действий с рациональными числами.
Контрольная № 9 + Ответы
КР-09: Раскрытие скобок. Коэффициент. Подобные слагаемые. Решение уравнений
Итоговая контрольная, Ответы
КР-10: Обобщение и систематизация знаний по математике за курс 6 класса.
Вы смотрели страницу Математика 6 Контрольные Виленкин (ДМ Попов). Цитаты контрольных работ и ответы на задачи контрольных работ из учебного пособия: «Дидактические материалы по математике 6 класс к учебнику Н.Я. Виленкина и др. «Математика 6 класс» ФГОС (к новому учебнику) / М.А. Попов — М.: Издательство «Экзамен», 2017 (серия «учебно-методический комплект»)». Представленные ниже контрольные работы ориентированы на школьный учебник Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд «Математика 6 класс». Вернуться на страницу «Все Тесты и Контрольные по Математике 6 класс»
Если Вы считаете, что какой-то пример решен неправильно обязательно напишите нам в поле для Комментариев (ниже) с указанием № контрольной работы, № варианта и № задачи.
Другие контрольные работы по математике в 6 классе:
Контрольные работы по математике 6 класс Мерзляк (12 контрольных)
Контрольные работы по математике 6 класс Попова КИМ (15 контрольных)
Выберите документ из архива для просмотра:
Выбранный для просмотра документ Ср 10.1 Координатная плоскость.doc
Выбранный для просмотра документ Ср 11.1 Графики.doc
Выбранный для просмотра документ Ср 11.2 Решение комбинаторных задач.doc
Выбранный для просмотра документ Ср 12.1 Арифметические действия с рациональными числами.doc
Выбранный для просмотра документ Ср 12.2 Выражения и их преобразования.doc
Выбранный для просмотра документ Ср 12.3 Уравнения.doc
Выбранный для просмотра документ Ср 12.4 Решение задач.doc
Выбранный для просмотра документ Ср 2.1 Признаки делимости чисел.doc
Выбранный для просмотра документ Ср 2.2 Наибольший общий делитель.doc
Выбранный для просмотра документ Ср 2.3 Наименьшее общее кратное.doc
Выбранный для просмотра документ Ср 3.1 Основное свойство дроби. Сокращение дробей.doc
Выбранный для просмотра документ Ср 3.2 Сравнение, сложение и вычитание дробей с разными знаменателями.doc
Выбранный для просмотра документ Ср 3.3 Сложение и вычитание смешанных чисел.doc
Выбранный для просмотра документ Ср 4.1 Умножение дробей.doc
Выбранный для просмотра документ Ср 4.2 Нахождение дроби от числа.doc
Выбранный для просмотра документ Ср 4.3 Распределительное свойство умножения.doc
Выбранный для просмотра документ Ср 4.4 Деление дробей.doc
Выбранный для просмотра документ Ср 4.5 Нахождение числа по его дроби.doc
Выбранный для просмотра документ Ср 4.6 Дробные выражения.doc
Выбранный для просмотра документ Ср 5.1 Отношения. Пропорции.doc
Выбранный для просмотра документ Ср 5.2 Прямая и обратная пропорциональная зависимости.doc
Выбранный для просмотра документ Ср 6.1 Положительные и отрицательные числа.doc
Выбранный для просмотра документ Ср 6.2 Сравнение чисел. Изменение величин.doc
Выбранный для просмотра документ Ср 7.1 Сложение положительных и отрицательных чисел.doc
Выбранный для просмотра документ Ср 7.2 Вычитание положительных и отрицательных чисел.doc
Выбранный для просмотра документ Ср 8.1 Умножение и деление.doc
Выбранный для просмотра документ Ср 9.1 Преобразование выражений при решении уравнений.doc
Выбранный для просмотра документ Ср 9.2 Решение уравнений.doc

Курс повышения квалификации
Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию:
Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс:
Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник:
Все учебники
Выберите тему:
Все темы
также Вы можете выбрать тип материала:

Краткое описание документа:
ПРЕДЛАГАЕМЫЕ САМОСТОЯТЕЛЬНЫЕ РАБОТЫ ПО МАТЕМАТИКЕ ДЛЯ 6 КЛАССА ПО УЧЕБНИКУ Н.Я.ВИЛЕНКИНА, В.И.ЖОХОВА, А.С.ЧЕСНОКОВА, С.И.ШВАРЦБУРДА (ПРИЛОЖЕНИЕ К РАБОЧЕЙ ПРОГРАММЕ) включают в себя:
- признаки делимости чисел
- НОД
- НОК
- основное свойство дроби
- сравнение, сложение и вычитание дробей с разными знаменателями
- сложение и вычитание смешанных чисел
- умножение дробей
- нахождение дроби от числа
- распределительное свойство умножения
- деление дробей
- нахождение числа по его дроби
- дробные выражения
- отношения. пропорции
- сравнение чисел
- сложение, вычитание, умножение, деление положительных и отрицательных чисел
- решение уравнений
- координатная плоскость
- графики
- уравненя
- комбинаторные задачи
Общая информация
Номер материала:
175917
Похожие материалы
Оставьте свой комментарий
Контрольная работа № 10 (6 класс)
Вариант I.
1. Выполните действия:
а) –3,8 – 5,7; в) 3,9 – 8,4; д)
б) –8,4 + 3,7; г) –2,9 + 7,3; е) .
2. Найдите значение выражения:
.
3. Решите уравнение:
а) х + 3,12 = –5,43; б) .
4. Найдите расстояние между точками
А (–2,8) и В (3,7) на координатной прямой.
5. Напишите все целые значения п, если 4 < |п| < 7.
Вариант II.
1. Выполните действия:
а) –3,5 + 8,1; в) –7,5 + 2,8; д)
б) –2,9 – 3,6; г) 4,5 – 8,3; е) .
2. Найдите значение выражения:
3. Решите уравнение:
а) 5,23 + х = –7,24; б) .
4. Найдите расстояние между точками
С (–4,7) и Д (–0,8) на координатной прямой.
5. Напишите все целые значения у, если
2 < |у| < 7.
Контрольные работы по математике в 6 классе
Математика 6 Контрольные Виленкин — это цитаты контрольных работ из пособия для учащихся «Дидактические материалы по математике 6 класс к учебнику Н.Я. Виленкина и др. «Математика 6 класс» ФГОС (к новому учебнику) / М.А. Попов — М.: Издательство «Экзамен». Представленные ниже контрольные работы ориентированы на школьный учебник Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд «Математика 6 класс»
Цитаты из пособия указаны в учебных целях, а также во избежание редакционных ошибок (в разных изданиях книги встречаются разные вопросы). При постоянном использовании контрольных работ в классе рекомендуем купить книгу: Математика. 6 класс. Дидактические материалы к учебнику Н. Я. Виленкина и др. ФГОС (переход по ссылке в интернет-магазин «Лабиринт.Ру»). Кроме 10 контрольных (в 4-х вариантах) в книге представлены 38 самостоятельных работ (в 2-х вариантах), а также задания на смекалку.
Для увеличения изображения — нажмите на картинку !
Чтобы скачать работу — нажмите на правую кнопку мыши и выберите «Сохранить изображение как …»
Контрольная работа № 1 + ОТВЕТЫ (4 варианта)
Делители и кратные. Признаки делимости на 10, на 5 и на 2. Признаки делимости на 9 и на 3. Простые и составные числа. Разложение на простые множители. Наибольший общий делитель. Взаимно простые числа. Наименьшее общее кратное
Контрольная работа КР-01
Контрольная работа № 2 + ОТВЕТЫ (4 варианта)
Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю. Сравнение, сложение и вычитание дробей с разными знаменателями. Сложение и вычитание смешанных чисел
Контрольная работа КР-02
Контрольная работа № 3 + ОТВЕТЫ (4 варианта)
Умножение дробей. Нахождение дроби от числа.
Применение распределительного свойства умножения. Взаимно обратные числа
Контрольная работа КР-03
Контрольная работа № 4 + ОТВЕТЫ (4 варианта)
Деление. Нахождение числа по его дроби. Дробные выражения
Контрольная работа КР-04
Контрольная работа № 5 + ОТВЕТЫ (4 варианта)
Отношения. Пропорции. Прямая и обратная пропорциональные зависимости.
Масштаб. Длина окружности и площадь круга
Контрольная работа КР-05
Контрольная работа № 6 + ОТВЕТЫ (4 варианта)
Координаты на прямой. Противоположные числа.
Модуль числа. Сравнение чисел. Изменение величин
Контрольная работа КР-06
Контрольная работа № 7 + ОТВЕТЫ (4 варианта)
Сложение чисел с помощью координатной прямой. Сложение отрицательных чисел.
Сложение чисел с разными знаками. Вычитание
Контрольная работа КР-07
Контрольная работа № 8 + ОТВЕТЫ (4 варианта).
Умножение. Деление. Рациональные числа.
Свойства действий с рациональными числами
Контрольная работа КР-08
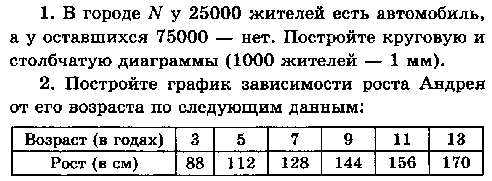
Контрольная работа № 9 + ОТВЕТЫ (4 варианта)
Раскрытие скобок. Коэффициент. Подобные слагаемые. Решение уравнений
Контрольная работа КР-09
Контрольная работа № 10 + ОТВЕТЫ (4 варианта)
Итоговая контрольная работа
Контрольная работа КР-10
Вы смотрели страницу «Математика 6 Контрольные Виленкин» — Контрольные работы из из пособия для учащихся «Дидактические материалы по математике 6 класс к учебнику Н.Я. Виленкина и др. «Математика 6 класс» ФГОС (к новому учебнику) / М.А. Попов — М.: Издательство «Экзамен».
Smart-Kids Практика теста по математике 6 класс с ответами | Smartkids
Вы здесь
- Деятельность
- »Тесты
- » Практический тест Smart-Kids по математике 6 класс с ответами
Smart-Kids практический тест по математике 6 класс с ответами

Предмет:
Оценка:


,
Топ 20 Математика Интервью Вопросы и ответы
1) Какие существуют классы математики и какую математику вы предпочитаете?
Различные типы полей для математики: исчисление, алгебра и дроби. Я использую все виды математики, но исчисление является основным.
2) W это Алгебра?
Алгебра — это одна из областей математики, которая использует символы и буквы для представления чисел, точек и объектов, а также отношений между ними.Он используется, чтобы знать неизвестные переменные.
Например, вы потеряли 5 ручек, и у вас осталось 10 ручек, чтобы узнать общее количество ручек, которые у вас были. Вы будете использовать алгебраическое уравнение.
X -5 = 10
X = 10 + 5 = 15 — это общее количество перьев, которые вы имели.
3) Сколько места потребуется полке на 30 чашек, если шкаф с 12 раковинами требует 18 футов пространства на стене?
Раковина 30 чашек требует 45 футов стены
4) В комнате для персонала четыре стойки с 10 ящиками для мела.В данный день используется 10 коробок меловой палочки. Какая фракция остается в стойке?
Если каждая стойка состоит из 10 ящиков меловой палочки, то общее количество ящиков на 4 стойках будет
4X 10 = 40
Теперь вторая часть состоит из 10 используемых ящиков, что означает, что общее количество оставленных ящиков составляет = 40 — 10 = 30.
Теперь фракция будет
Осталось / всего = 30/40 = 3/4 — доля остается в стойке
5) W hat — это формула для расчета процентной ставки?
Существует два типа процентов, которые можно рассчитать по другой формуле.
Простой интерес
Сложные проценты
Для расчета простого процента используется формула (PX RX T) / 100
Где P — основная сумма, R — для процентной ставки, а t — для времени
.
Формула для расчета сложных процентов: PX (1 + r / 100) ^ т

6) W Что такое Коммутативные, Ассоциативные и Распределительные законы в математике?
- Коммутативные законы говорят, что мы можем поменять числа, и вы все равно получите одно и то же число при добавлении, например, a + b = b + a и то же самое для умножения.
- Ассоциативные законы говорят, что не имеет значения, как мы сгруппируем число, окончательное значение останется прежним, например, (a + b) + c = (a + b) + c, и то же самое для умножения
- Законы о распределении говорят, что мы можем иметь один и тот же ответ, умножая число на группу чисел, сложенных вместе, или умножая их по отдельности, а затем добавляя их, например, a x (b + c) = axb + axc
7) В небольшой компании средняя зарплата трех сотрудников составляет 1000 долларов в неделю.Если один сотрудник зарабатывает 1100 долларов, а другой — 500 долларов, сколько заработает третий сотрудник?
Формула для расчета этого,
(e1 + e2 + e3) / 3 = 1000 долларов
1100 + 500 + e3 = 1000 x 3
1600 + e3 = 3000
e3 = 3000-1600
= 1400
Третий сотрудник заработает $ 1400
8) Объясните в сложном расчете, например 8 + (9 x 5 2 +8), откуда вы начнете вычислять?
Чтобы избежать путаницы, откуда начинать вычисления, вы должны следовать BODMAS
- B = скобка первая
- O = Заказы (полномочия и квадратные корни)
- DM = деление и умножение
- AS = сложение и вычитание
После того, как вы сделали с B или O, продолжайте слева направо, выполняя любые «D» или «M», как указано в задаче, а затем продолжайте слева направо, выполняя любые «A» или «S» как дано в проблеме.
9) W Что такое геометрия?
Геометрию можно разделить на два класса
- Плоская геометрия: речь идет о плоских формах, таких как треугольники, линии и круги, которые можно нарисовать на листе бумаги.
- Solid Geometry: речь идет о трехмерных объектах, таких как цилиндры, кубы, призмы и сферы.
10) W Что такое разница между линией, точкой, плоскостью и телом?
- Точка не имеет размеров
- Линия одномерная
- Самолет двухмерный
- Твердое трехмерное
11) W Что такое внешний угол в многоугольниках?
В многоугольниках угол между любой стороной фигуры и линией, простирающейся от следующей стороны, называется внешними углами.Все внешние углы многоугольника составляют в целом 360 °. Каждый внешний угол должен быть 360 °
12) H ау можно ли перевести дробь в проценты?
Чтобы преобразовать дробь в процент, мы рассмотрим пример для 4/9
- Первое деление 4/9 = 0,44
- Затем умножьте на 100 = 0,44 х 100 = 44,44
- Добавьте знак «%» к ответу = 44,44%
Процент от 4/9 = 44,4%
13) H ау можно ли перевести процент в дробь?
Чтобы перевести процент в дробь, скажем, 70% в дробь
- Преобразовать 70% в десятичную = 70/100 = 0.7
- Запишите десятичное число «сверх» числа 1 = 0,7 / 1
- Затем умножьте верх и низ на 10 = 0,7x 10 = 7/10
Для каждого числа после десятичной точки 1 x 10
(10 на 1, 100 на 2)
- который даст = 7/10
- 7/10 это фракция
14) W это кубический метр?
кубический метр — это стандартная единица измерения объема объекта по длине.Единица написана в м 3.
1 м 3 (кубический метр) = 1000 литров
15) H Сколько стоит гектар и сколько квадратный миллиметр?
- 1 гектар = 100 метров с каждой стороны, таким образом, гектар имеет 100 х 100 м = 10000 м 2
- Квадратный миллиметр — миллиметров х миллилитров ; миллиметр — это тысячная часть метра, поэтому квадратный миллиметр — это одна миллионная часть квадратного метра
1 X 1 = 1 квадратного метра
1000 1000 1,000, 000
16) Если проводник автобуса выдает 50 билетов за 30 минут, сколько билетов он сможет выдать за 8 часов.?
Если проводник автобуса выдает 50 билетов за 30 минут, значит, количество билетов выдается за 8 часов. будет
(480 x50) / 30 = 800 билетов
Таким образом, дирижер может выдать 800 билетов за 8 часов.
17) W Что такое перестановка?
Упорядоченное расположение группы объекта известно как Перестановка, например, перестановка расположения 9 шариков, различающихся по цветам в 3 разных рядах, может быть выполнена 9 P 3 = 504 способами.
18) W hat это линейное уравнение? Для чего его используют?
Для расчета или решения проблем, связанных с расстоянием, скоростью и временем, мы используем линейное уравнение. Он также используется для поиска решений, связанных с весом, массой и плотностью. Линейное уравнение может быть выражено как Ax + By + Cz +… = D.
19) Приведите пример, где вы можете использовать линейное уравнение в своей повседневной жизни?
Например, если ваш офис находится в 20 милях от вашего офиса, и вы достигли 8 часов утра, и вы знаете, что трафик движется со скоростью 40 миль в час.
Чтобы узнать, в какое время вы должны выходить из дома, используйте это уравнение
Время = расстояние / скорость передвижения
т = 20/40 = ½ или полчаса. Чтобы добраться до офиса в 8 часов утра, вы должны выйти из дома в 7:30 утра
20) W это касательная?
Линия, которая касается кривой в одной точке, не проходя и не пересекая ее, называется касательной.
21) W hat — это стандартное отклонение?
Стандартное отклонение — это мера разброса данных о среднем значении.Он называется сигма и представлен как символ σ.
,
Что я могу сделать со степенью математики?
Изучение математики помогает вам развить навыки логического мышления, решения проблем и принятия решений, которые ценятся работодателями во многих сферах работы
Варианты работы
Работы, непосредственно связанные с вашей степенью, включают:
Работа, где ваша степень будет быть полезным:
Помните, что многие работодатели принимают заявления от выпускников с любой степенью, поэтому не ограничивайте свое мышление работой, перечисленной здесь.
Потратьте несколько минут, чтобы ответить на викторину Job Match и выясните, какие профессии вам подойдут
Попробуйте Job Match
Опыт работы
Если вы хотите использовать свои математические навыки в выбранной карьере, соответствующем промышленному году В конце концов, будет полезен проект за последний год или диссертация. Возможны зачисления на некоторые курсы по математике в таких областях, как:
- , банковское дело
- , гражданская служба,
- , вычислительная
- , консалтинг,
- , финансовые услуги,
- розничная торговля.
Иногда также есть возможность работать с преподавателями над исследовательским проектом в рамках летней стажировки. Независимо от роли, на которую вы претендуете, опыт работы поможет вам выделиться. Оплаченный или добровольный опыт работы в соответствующей области покажет ваш интерес и приверженность выбранной вами карьере, а также даст вам возможность создать сеть полезных контактов и развить ключевые навыки.
Если вы хотите обучаться в качестве преподавателя после получения степени, вам понадобится опыт работы с детьми в классе и / или в смежных условиях, таких как игровые схемы или спортивные клубы.Опыт работы в классе, будь то наблюдатель, помощник в классе или волонтер, имеет важное значение.
Ищите места размещения и узнавайте больше об опыте работы и стажировках.
Типичные работодатели
Существует спрос на математиков и статистиков в различных секторах. Математики работают в нефтяной и атомной промышленности, медицине и здравоохранении, информационных технологиях, бизнес-консалтинге и оперативных исследованиях, космической науке и астрономии, а также во многих инженерных и различных государственных учреждениях.
Типичные работодатели включают в себя:
- местное и центральное правительство NHS
- образовательных учреждений
- фармацевтическую промышленность
- ИТ-компании
- инжиниринговых компаний
- страховых компаний
- маркетинговых компаний и маркетинговых компаний
- финансы, банковское дело и бухгалтерские фирмы.
Существуют также возможности трудоустройства в государственных научно-исследовательских институтах или государственных учреждениях.
Найдите информацию о работодателях в области бухгалтерии, банковского дела и финансов, бизнеса, консалтинга и менеджмента и в других сферах труда.
Работодатели теперь нанимают выпускников по математике
Инженер-платформенный инженер
- Egress
- Шеффилд
- Конкурентоспособная зарплата
Аналитик продукта
- Хансон Уэйд
- Лондон
- £ 22,001- £ 50000
Стажер
Просмотреть больше рабочих мест в сфере бухгалтерского учета и ИТ
Навыки для вашего резюме
Степень по математике помогает вам развить навыки:
- разработка и проведение наблюдательных и экспериментальных исследований
- исследовать, анализировать и интерпретировать данные, находить закономерности и делать выводы
- информационные технологии
- подходить к задачам аналитическим и строгим образом, формулировать теории и применять их для решения задач
- , связанных с абстрактными понятиями
- , представляющих математические аргументы Выводы и выводы с точностью и ясностью
- продвинули в цифрах и проанализировали большое количество данных
- логического мышления.
Вы также развиваете основные общие навыки, которые ожидают все работодатели, в том числе:
- коммуникационные навыки
- тайм-менеджмент
- организационные навыки и умение работать методично и точно
- навыки принятия решений
- самоуправление
- работа в команде и умение работать самостоятельно.
Дальнейшее обучение
Дальнейшее обучение является популярным вариантом для выпускников математики. Например, аспирантура на уровне магистратуры может быть полезна для некоторых профессий, связанных с математикой, таких как операционные исследования, медицинская статистика в фармацевтических компаниях, метеорология и проектирование.Аспирант может быть полезен для поиска работы в этих областях и имеет важное значение для академической карьеры.
Большинство профессий и актуарной работы, связанной с финансами, требуют дополнительного обучения во время работы для завершения профессиональных экзаменов. Обычно вы должны учиться в свое время.
Вы можете изучать определенный курс статистики, такой как прикладная, медицинская и официальная статистика.
Для получения дополнительной информации о дальнейшем обучении и поиске курса, который вас интересует, см. Степень магистра и поиск курсов для аспирантов.
Что делают выпускники математики?
Через шесть месяцев после выпуска почти две трети выпускников математики заняты или совмещают работу и дальнейшее обучение. Четверть выпускников математики находятся в дальнейшем изучении.
Главные должности выпускников математики — это бизнес-профессионал, финансовый и инвестиционный аналитик и консультант, а также дипломированный или сертифицированный бухгалтер. Другие роли в первой пятерке включают программиста и разработчика программного обеспечения.
| Направление | Процент |
|---|---|
| Занято | 57.2 |
| Дальнейшее исследование | 25 |
| Разработка и исследование | 5,2 |
| Безработные | 7,5 |
| Другие направления | 5,1 |
Магистратура по математике
| Тип работа | Процент |
|---|---|
| Бизнес, кадры и финансы | 41,9 |
| Информационные технологии | 12 |
| Профессионалы образования | 9.3 |
| Розничная торговля, общественное питание и работа в барах | 8.5 |
| Прочее | 28.3 |
Типы работ, введенных в Великобритании
Подробную информацию о том, чем занимаются выпускники математики через шесть месяцев после окончания учебного заведения, см. Чем занимаются выпускники?
Данные о направлениях выпускников из Агентства статистики высшего образования.

Написано редакторами AGCAS
февраль 2019 г.
© Copyright AGCAS & Graduate Prospects Ltd · Отказ от ответственности
— £ 22 000
Просмотр работы.
математика | Академический календарь
Профессор и заведующий кафедрой
J. Quastel, магистр наук, доктор философии, FRSC
Профессор и доцент кафедры (исследования)
S. Alexakis, BA, Ph D
Профессор и доцент кафедры (выпускник)
К. Рафи, B Sc, Ph D
Профессор и доцент (Бакалавриат)
J. Repka, B Sc, Ph D (U)
профессора университета
J.G.Артур, MA, PhD, FRSC, FRS
J. Friedlander, MA, PhD, FRSC (UTSC)
И.М. Сигал, BA, PhD, FRSC
профессора
D. Бар-Натан, B Sc, Ph D
E. Bierstone, MA, Ph D, FRSC
I. Binder, B Sc, M Sc, Ph D (UTM)
J. Bland, M Sc , Ph D
A. Braverman, B Sc, Ph D
A. Burchard, B Sc, Ph D
G. Elliott, B Sc, Ph D, FRSC
M. Goldstein, B Sc, Ph D (UTSC)
M Gualtieri, B Sc, Ph D
V. Иврий, MA, Ph D, доктор Math, FRSC
L.Джеффри, AB, PhD, FRSC (UTSC)
R. Джеррард, M Sc, PhD (U), FRSC
J. Kamnitzer, B Sc, Ph D
В. Капович, B Sc, Ph D
Y. Karshon , B Sc, Ph D (UTM)
К. Ханин, M Sc, Ph D (UTM)
Б. Хесин, M Sc, Ph D
А. Хованский, M Sc, Ph D
H. Ким, B Sc, Ph D
S. Kudla, BA, MA, Ph D, FRSC
M. Marcolli, M Sc, Ph D
R. McCann, BSc, Ph D, FRSC
E. Meinrenken, B Sc, Ph D, FRSC
P Milman, Dipl Maths, PhD, FRSC
F. Murnaghan, M Sc, Ph D
K.Murty, B Sc, Ph D, FRSC
A. Nabutovsky, M Sc, Ph D
A. Nachman, B Sc, Ph D
D. Panchenko, B Sc, M Sc, Ph D
M. Pugh, BSc, Ph D
R. Rotman BA, Ph D
L. Seco, BA, Ph D (UTM)
C. Сулем, M Sc, Dr D’Etat, FRSC
S. Todorcevic, B Sc, Ph D, FRSC
B. Virag, BA, Ph D (UTSC)
WAR Weiss, M Sc, Ph D (UTM)
М. Ямпольский, B Sc, Ph D (UTM)
доценты
Ф. Херциг, BA, Ph D
J. Scherk, D Phil (UTSC)
J.Цимерман, Ph D
доцентов, учебный поток
Д. Бурбулла, B Sc, B Ed, MA
доценты
S. Aretakis, MA, Ph D (UTSC)
C. Blois, B Sc, M Sc, Ph D
J. de Simoi, M Sc, Ph D (UTM)
V. Dimitrov, AB , M Sc, Ph D (Coxeter, CLTA)
M. Groechenig, B Sc, D Phil (UTM)
R. Haslhofer, B Sc, M Sc, Ph D (UTSC)
J. Lefebvre, B Sc, Ph D
Y. Лиокумович, B Sc, M Sc, Ph D (UTM)
F. Pusateri, BS, MS, Ph D
B.Россман, BA, MA, Ph D
K. Serkh, Ph D
A. Shankar, B Sc, Ph D (UTM)
A. Stinchombe, BMath, Ph D
G. Tiozzo, MA, Ph D (UTSC)
I. Varma, Ph D
W. Yu, Ph D (UTSC)
H. Yuen, BA, Ph D
A. Zaman, B Sc, M Sc, Ph D
K. Zhang, B Sc, Ph D (UTM) )
доценты, учебный поток
Б. Гальвао-Соуза, Ph D
A. Gracia-Saz, Ph D
Н. Hoell BA, MA, M Phil, Ph D — CLTA
S. Mayes-Tang, Bc, MS, Ph D
F. Parsch, B Sc, M Sc, Ph D
B.Россман, BA, MA, Ph D
J. Siefken, HBS, MS, Ph D
Лекторы
S. Homayouni, B Sc, Ph D
N. Jung, BA, MSc, Ph D
E.A.P. LeBlanc, MA, Ph D
J. Tate, B Sc, B Ed
S. Uppal, M Sc
профессора Emeriti
M.A. Akcoglu, M Sc, PhD, FRSC
E.J. Barbeau, MA Ph D (U)
T. Bloom, MA, Ph D, FRSC
M. D. Choi, MA, Ph D, FRSC
H.C. Davis, MA, Ph D (N)
E.W. Ellers, Dr Rer Nat
I.R. Грэм, B Sc, Ph D (UTM)
S.Гальперин, M Sc, PhD, FRSC
V. Jurdjevic, MS, PhD
J.W. Lorimer, M Sc, Ph D (U)
E. Mendelsohn, M Sc, Ph D (UTSC)
K. Murasugi, MA, D Sc, FRSC
P. Rosenthal, MA, Ph D, LLB
P. Selick, B Sc, MA, Ph D (UTSC)
DK Sen, M Sc, Dr s Sc
F. D. Tall, AB, Ph D (UTM)
доценты Emeriti
Н.А. Дерзко, B Sc, Ph D
S.M. Tanny, B Sc, Ph D (UTM)
доцента Emeriti, Обучающий поток
A.Igelfeld, M Sc
A. Lam, M Sc
Старшие преподаватели Emeriti
П. Кергин, Ph D
F. Recio, MSc, Ph D
,