Задачи на движение 4-5 класс: скорость, время и расстояние
Скорость – это физическая величина, показывающая какое расстояние пройдет объект за единицу времени.
Сегодня мы будем решать задачи на:
- движение
- скорость \(v=s/t\)
- время \(t=s/v\)
- расстояние \(s=v*t\)
Расстояние — путь, который нужно преодолеть во время движения.
Время — промежуток действия движения.
Скорость — характеристика движения.
Для решения задач необходимо ввести неизвестную, верно составить и решить уравнение.
Задача 1. Легковая машина прошла расстояние в \(160\) км за два часа. С какой скоростью двигалась машина?
Решение.
\(160/2=80\) км/час
Ответ: \(80.\)
Задача 2. Из города Минск в Смоленск, расстояние между которыми \(346\) км, отправились одновременно велосипедист и автомобилист. Скорость автомобиля \(20\) м/с, а велосипедиста \(20\) км/ч. Какое расстояние будет между ними через \(2\) часа?
Какое расстояние будет между ними через \(2\) часа?
Решение.
Мы не можем складывать разные единицы измерения, поэтому надо перевести м/с в км/ч. Как нам перевести км/ч в м/с? В км – 1000 м, в \(1\) ч \(-3600\), в \(1\) км/час\(-1000/3600\) м/c, то есть в \(1\) км/c \(-3600/1000\) м/c. \(20*\frac{3600}{1000}=72\). Итого скорость автомобиля \(72\) км/ч.
Так как автомобилист и велосипедист выехали из одного места и двигаются в одном направлении, расстояние между ними будет нарастать со скоростью:
- 72-20=52(км/ч)
- 52∗2=104 (км) – расстояние между ними через два часа.
Ответ: \(104\) км.
В таких задачах важно понимать:
- если мы умножаем скорость на время, то получаем расстояние;
- если расстояние делим на время, то получаем скорость;
- если расстояние делим на скорость, то получаем время ;
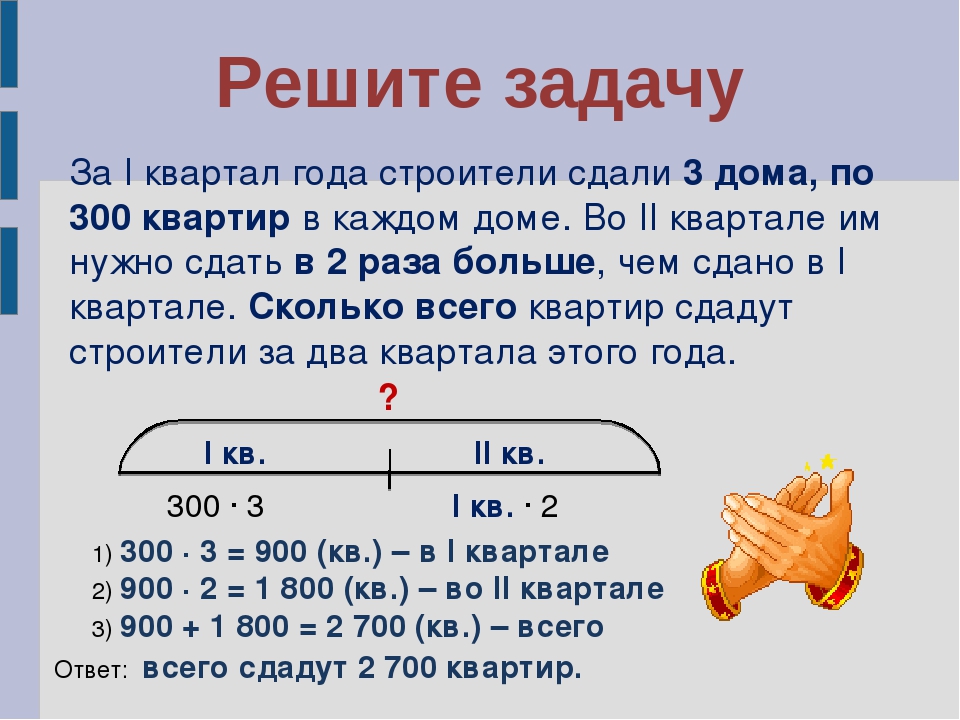
Задача 3. Из А в В тронулись в одно время турист пешком, а второй турист – на велосипеде. В то же время из В в А выдвинулся мотоцикл, который встретился с велосипедистом через 3 часа, а с пешеходом через 4 часов после своего выезда из В. Найти расстояние от А до В, зная, что скорость пешехода 3 км/ч, а велосипедиста 10 км/ч.
В то же время из В в А выдвинулся мотоцикл, который встретился с велосипедистом через 3 часа, а с пешеходом через 4 часов после своего выезда из В. Найти расстояние от А до В, зная, что скорость пешехода 3 км/ч, а велосипедиста 10 км/ч.
10 * 3 = 30 (км) – мотоциклист от А через 3 часа.
3* 4 = 12 (км) – мотоциклист от А через 4 часов.
30 – 12 = 18 (км/ч) – скорость автомобиля.
10 + 18 = 28 (км/ч) – скорость сближения мотоциклиста и велосипедиста.
28 * 3 = 84 (км) – расстояние от А до В.
Ответ: 84 км.
Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Оставить заявку
Репетитор по математике
Могилёвский государственный университет имени А. А.Кулешова
А.Кулешова
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике для 4-9 классов.
Мой подход в преподавании — не только устранить пробелы в теории, но и привить любовь к предмету, научить самостоятельно, “интуитивно” в нём ориентироваться. Мои ученики успешно сдают выпускные экзамены и пишут республиканские контрольные!
«В математике есть своя красота, как в живописи и поэзии».
Оставить заявку
Репетитор по математике
Новосибирский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-7 классов. Применяю различные методы работы, учитываю индивидуальные особенности учащихся, делаю упор на повышение уровня качества знаний. Работаю на результат — чтобы ученики поняли и усвоили. С удовольствием провожу занятия , в каждом ученике вижу личность, помогаю понять и полюбить математику.
Применяю различные методы работы, учитываю индивидуальные особенности учащихся, делаю упор на повышение уровня качества знаний. Работаю на результат — чтобы ученики поняли и усвоили. С удовольствием провожу занятия , в каждом ученике вижу личность, помогаю понять и полюбить математику.
Оставить заявку
Репетитор по математике
Одесский национальный университет им. И. И. Мечникова
И. И. Мечникова
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-9 классов. Закончила университет с красным дипломом, аспирантуру. Почему я люблю математику? Во-первых, в математике все просто: если получил правильный ответ, то правильным он будет всегда. Если вы мыслите верно, то какими бы вы способами не решали, они все ведут к одному — правильному решению. И всегда можно доказать и проверить правильность ответа. Во- вторых, математика сближает людей, это международный язык. Математические формулы, символы, знаки будут понятны человеку, не владеющим языком, на котором говорите вы. В-третьих, люблю ее за постоянство во времени и независимость от расстояния. Математические законы, теоремы, понятия как были справедливы много тысяч лет назад и в любой стране мира, так и будут всегда соблюдаться. В-четвертых, математика — это не сухие формулы, законы и понятия, а она основана, как и физика, на наблюдениях окружающего мира, она отражает реальность. Математика — это язык, на котором написана книга природы. И, в-пятых, математика тренирует ум, развивает пространственное воображение и способность мыслить логически.
Закончила университет с красным дипломом, аспирантуру. Почему я люблю математику? Во-первых, в математике все просто: если получил правильный ответ, то правильным он будет всегда. Если вы мыслите верно, то какими бы вы способами не решали, они все ведут к одному — правильному решению. И всегда можно доказать и проверить правильность ответа. Во- вторых, математика сближает людей, это международный язык. Математические формулы, символы, знаки будут понятны человеку, не владеющим языком, на котором говорите вы. В-третьих, люблю ее за постоянство во времени и независимость от расстояния. Математические законы, теоремы, понятия как были справедливы много тысяч лет назад и в любой стране мира, так и будут всегда соблюдаться. В-четвертых, математика — это не сухие формулы, законы и понятия, а она основана, как и физика, на наблюдениях окружающего мира, она отражает реальность. Математика — это язык, на котором написана книга природы. И, в-пятых, математика тренирует ум, развивает пространственное воображение и способность мыслить логически. Возможно, многое из того что мы изучаем никогда и не пригодится. Но… Математика — это гимнастика для ума. С ее помощью очень хорошо тренировать свои умственные способности. А это уж точно понадобится в жизни!
Возможно, многое из того что мы изучаем никогда и не пригодится. Но… Математика — это гимнастика для ума. С ее помощью очень хорошо тренировать свои умственные способности. А это уж точно понадобится в жизни!
Функция
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Математика по Skype
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Математика 11 класс
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Похожие статьи
Страница 40 №104-112 ГДЗ к учебнику «Математика» 5 класс Бунимович, Дорофеев, Суворова
Упражнения
Задачи, похожие на задачу о цифровых кодах
Задание 104. Какие двузначные коды можно составить, используя только цифры 3 и 7?
Какие двузначные коды можно составить, используя только цифры 3 и 7?
Ответ
Можно составить 4 кода: 33, 37, 73, 77.
Задание 105. Составьте все двузначные числа, в записи которых используются только цифры 3, 5, 7, 9. Сколько двузначных чисел можно записать, если использовать при записи числа каждую из указанных цифр только один раз?
Решение
Если при записи числа каждую из указанных цифр можно использовать 2 раза.
Для выбора первого числа есть 4 варианта.
Для выбора второго числа есть 4 варианта.
4 * 4 = 16 (вариантов) − чисел можно записать:
33, 35, 37, 39, 55, 53, 57, 59, 77, 73, 75, 79, 99, 93, 95, 97.Если при записи числа каждую из указанных цифр можно использовать 1 раз.
Для выбора первого числа есть 4 варианта.
Для выбора второго числа есть 3 варианта.
4 * 3 = 12 (вариантов) − чисел можно записать:
35, 37, 39, 53, 57, 59, 73, 75, 79, 93, 95, 97.
Задание 106. Запишите все двузначные числа, которые можно составить из цифр 0, 1, 2. Сколько получится чисел, если каждую цифру использовать только один раз?
Решение
Если при записи числа каждую из указанных цифр можно использовать 2 раза.
Для выбора первого числа есть 2 варианта.
Для выбора второго числа есть 3 варианта.
2 * 3 = 6 (вариантов) − чисел можно записать:
11, 10, 12, 22, 21, 20.Если при записи числа каждую из указанных цифр можно использовать 1 раз.
Для выбора первого числа есть 2 варианта.
Для выбора второго числа есть 2 варианта.
2 * 2 = 4 (варианта) − чисел можно записать:
10, 12, 21, 20.
Задание 107. Девять школьников, сдавая экзамены по математике, русскому и английскому языкам, получили отметки «4» и «5». Можно ли утверждать, что по крайней мере двое из них получили по каждому предмету одинаковые отметки?
Решение
Для математики можно выбрать 2 варианта оценок.

Для русского можно выбрать 2 варианта оценок.
Для английского можно выбрать 2 варианта оценок.
2 * 2 * 2 = 8 (вариантов) − оценок есть всего.
9 > 8 − значит можно утверждать, что по крайней мере двое из учеников получили по каждому предмету одинаковые отметки.
Задачи, похожие на задачу о расписании
Задание 108. Шифр для сейфа составляется из трех разных цифр. Запишите все шифры, которые можно составить, используя цифры 1, 2 и 3.
Решение
Для первой цифры есть 3 варианта выбора.
Для второй цифры есть 2 варианта выбора.
Для третьей цифры есть 1 вариант выбора.
3 * 2 * 1 = 6 (вариантов) − есть всего:
123, 132, 213, 231, 312, 321.
Задание 109. Сколько новых чисел можно получить из числа 546, переставляя цифры?
Решение
Для первой цифры есть 3 варианта выбора.
Для второй цифры есть 2 варианта выбора.
Для третьей цифры есть 1 вариант выбора.
3 * 2 * 1 = 6 (вариантов) − есть всего:
546 уже есть, значит можно получить 5 новых чисел.
456, 465, 564, 654, 645.
Задание 110. В магазине продаются полотенца трех видов: в полоску, в клетку и в горошек. Мама хочет подарить каждой из трех дочерей по полотенцу, причем так, чтобы одинаковых у них не было. Сколькими способами она может раздать три разных полотенца девочкам?
Указание.
Введите обозначения:
П − полоска,
К − клетка,
Г − горошек.
Решение и ответ
6 способами мама может раздать три разных полотенца:
ПКГ, ПГК, КПГ, КГП, ГПК, ГКП.
Задание 111. Хоккейная комбинация.
На поле пять игроков (рис.2.6). Начал комбинацию игрок №1, продолжили игроки с другими номерами, а забил гол игрок №5. Каждый хоккеист ударил по шайбе один раз. На рисунке с помощью стрелок изображен один из возможных вариантов комбинации. Сколько всего вариантов этой комбинации существует?
Сколько всего вариантов этой комбинации существует?
Решение и ответ от 7 гуру
Всего возможны 6 вариантов:
234, 243, 324, 342, 423, 432.
Задание 112. Дано число 3241. Запишите все числа, большие данного, которые можно получить с помощью перестановки цифр этого числа.
Ответ
Всего 8 чисел:
3412, 3421, 4123, 4132, 4213, 4231, 4312, 4321.
Топ-5 приложений для решения задач по математике
Мы отобрали для вас лучшие приложения для Android, которые созданы для решения практически любых задач по математике в два счета.
Математику по праву можно назвать царицей наук, которую в равной степени можно как любить, так и ненавидеть. Если задуматься всерьез, то мы используем знания по математике каждый день. Повсюду сталкиваемся с числами – на циферблате часов, на денежных банкнотах, в расписании уроков. Нам все время приходится выполнять простые и сложные математические операции – посчитать, через сколько минут начнется любимый фильм, сколько сдачи должны дать в магазине, когда приедет автобус.
Но для многих математика — это непонятные действия, числа, правила и задачи. Говорят, все познается в сравнении. Математика позволяет нам узнать, насколько что-то больше, длиннее, шире, дороже другого. Без знания математики невозможно построить дом, автомобиль. Если бы не математика, у нас бы никогда не было ни компьютеров, ни планшетов и смартфонов. Математическими расчетами пользуются все другие науки в мире.
Простая арифметика, превращающаяся в дальнейшем в сложную алгебру и геометрию, заставляла многих ненавидеть эти дисциплины. Кому-то математика в школе давалась легко, а для кого-то она так и осталась чем-то далеким и непостижимым. Как ни крути, иногда умение считать деньги не спасает от необходимости решения сложных математических уравнений и неравенств. «Смартфон» дословно переводится как «умный телефон», и благодаря стороннему софту ему можно доверить даже самые сложные задачи. В век информационных технологий дела с этим обстоят совсем иначе. На помощь школьникам и студентам пришли смартфоны и планшеты с «умными» приложениями-калькуляторами, речь о которых пойдет в этой статье. Оговоримся сразу, что приложения не могут быть панацеей. Вам всё равно придется учить математику, а они лишь помогут вам, подскажут ход решения. Пока что данные приложения не могут справляться со сложными заданиями, но кое-что умеют.
Оговоримся сразу, что приложения не могут быть панацеей. Вам всё равно придется учить математику, а они лишь помогут вам, подскажут ход решения. Пока что данные приложения не могут справляться со сложными заданиями, но кое-что умеют.
Photomath
Одно из самых известных приложений для решения математических задач с первого же дня назвали ужасом для учителей математики. А разработчики просто называют его «камерой-калькулятором». Photomath интересно тем, что способно решить практически любую математическую задачу. Вам тяжело разобраться в решении логарифмических, квадратных, тригонометрических уравнений и неравенств? Трудно решать задачи с корнями, модулями, степенями, дробями, интегралами и факториалами? Теперь с помощью приложения Photomath решать такие задания не составит большого труда. Но самое интересно — приложение не просто решает математические задачи, а подробно расписывает ход расчетов. Это понравится не только учащимся и студентам, а также родителям, которые захотят проверить домашнее задание своего чада.
Пользователю понравится, что приложение Photomath способно работать в автоматическом режиме. Достаточно просто открыть его и сразу же активируется встроенный интерфейс камеры с заданной областью распознавания. Для того, что начать работу, необходимо расположить камеру так, чтобы математическая задача вместилась в эту область. Буквально через мгновение умные алгоритмы программы начнут анализировать данные на экране и практически моментально выдадут ответ. Если захотите увидеть весь ход решения вашей задачи, то просто нажмите на результат в красном прямоугольнике. В истории приложения сохраняются 10 последних записей, поэтому в любой момент сможете просмотреть решение предыдущей задачи.
Иногда случается, что программа некорректно распознала те или иные математические символы в задании, решив неправильно при этом задачу. Но не отчаивайтесь. В Photomath у вас есть возможность отредактировать их в режиме калькулятора. Стоит отметить, разработчики очень хорошо продумали эту функцию. Здесь доступен калькулятор со всевозможными операторами, есть цифровая, текстовая и символьная раскладки.
Здесь доступен калькулятор со всевозможными операторами, есть цифровая, текстовая и символьная раскладки.
Долгое время приложение умело распознавать только напечатанное задание. Причем из книги было намного легче отсканировать его, чем с экрана ноутбука. Теперь же, наконец-то, появилась долгожданная функция распознавания рукописного текста. Все работает почти безупречно, но для лучшего результата желательно, чтобы запись была аккуратным почерком.
Мне очень понравилось пользоваться приложением. Оно практически справляется с любым заданием со всей школьной программы по математике и алгебре, включая старшую и высшую школы. Да, приложение стоящее, абсолютно бесплатное, не содержит рекламы, как обычно бывает с такими приложениями, есть русский язык интерфейса, способно работать без подключения к Интернету, но и ошибок предостаточно.
MalMath: Step by step solver
С помощью данного приложения вы сумеете решить математические задачи не только получив пошаговое описание процесса вычисления, но и построение необходимых графиков. Само приложение MalMath для Android полностью бесплатное, к тому же совершенно не содержит рекламы. Также у вас есть возможность использовать его без подключения к Интернету. Это является большим плюсом для него. Программа в первую очередь приглянется ученикам старших классов, студентам колледжей, а также университетов и академий. Дело в том, что MalMath умеет решать интегралы, производные, пределы, логарифмы, тригонометрические уравнения и неравенства, примеры с корнями и модулями. По крайней мере большую часть. Однако, вам придется в ручную вводить условие задания, так как функция распознавания с помощью камеры здесь не предусмотрена. Что касается его способностей, то они ограничиваются лишь задачами средней сложности с более скромным, чем у остальных приложений, описанием решений.
Само приложение MalMath для Android полностью бесплатное, к тому же совершенно не содержит рекламы. Также у вас есть возможность использовать его без подключения к Интернету. Это является большим плюсом для него. Программа в первую очередь приглянется ученикам старших классов, студентам колледжей, а также университетов и академий. Дело в том, что MalMath умеет решать интегралы, производные, пределы, логарифмы, тригонометрические уравнения и неравенства, примеры с корнями и модулями. По крайней мере большую часть. Однако, вам придется в ручную вводить условие задания, так как функция распознавания с помощью камеры здесь не предусмотрена. Что касается его способностей, то они ограничиваются лишь задачами средней сложности с более скромным, чем у остальных приложений, описанием решений.
Интерфейс MalMath представлен на русском языке, выполнен в классическом стиле и оптимизирован под экраны смартфонов. У вас есть возможность в настройках изменить размер шрифта и скорость анимации. Открыв боковое меню, увидите, что оно включает пять пунктов: главный экран, рабочий лист, график, генератор задач, избранное. Но больше всего вам будет интересна функция «генератор задач». С ее помощью можно создавать случайные математические задачи с несколькими категориями и уровнями сложности, заданными в настройках. Все выражения и графики можно сохранять в избранном.
Открыв боковое меню, увидите, что оно включает пять пунктов: главный экран, рабочий лист, график, генератор задач, избранное. Но больше всего вам будет интересна функция «генератор задач». С ее помощью можно создавать случайные математические задачи с несколькими категориями и уровнями сложности, заданными в настройках. Все выражения и графики можно сохранять в избранном.
Сам процесс добавления задачи очень похож на вставку формул в Microsoft Word. Из собственного опыта отмечу, что, вроде бы все понятно и просто, но иногда довольно неудобно, особенно, что касается ввода сложных комбинаций с дробями и корнями. Придется потратить немного времени, чтобы привыкнуть к определенному принципу набора, но все же оно того стоит.
Mathway
Еще одно весьма заслуживающее внимания приложение, которое поможет справиться с математическими заданиями. Приложение является своеобразным инструмент для решения задач, который, помимо школьного курса математики, охватывает математический анализ, статистику, тригонометрию, линейную алгебру и даже химию.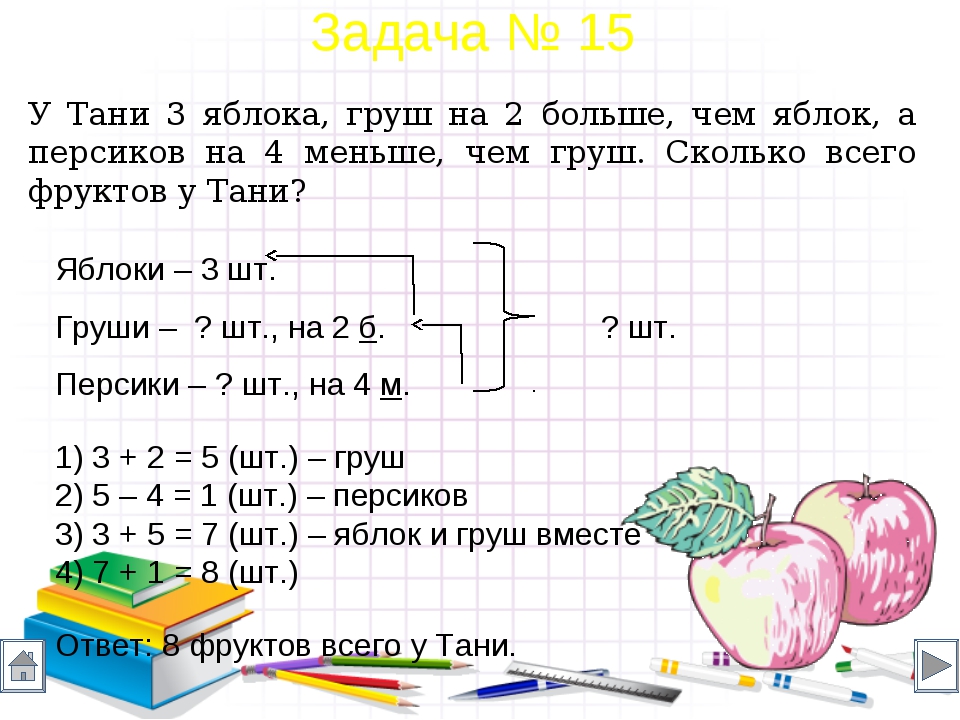 Если вы когда-то использовали веб-версию сервиса Mathway, то сразу же узнаете внешний вид и функциональные возможности данного приложения. Практически тот же интерфейс в виде мессенджера, в котором все действия происходят как бы в диалоге с виртуальным помощником.
Если вы когда-то использовали веб-версию сервиса Mathway, то сразу же узнаете внешний вид и функциональные возможности данного приложения. Практически тот же интерфейс в виде мессенджера, в котором все действия происходят как бы в диалоге с виртуальным помощником.
Стоит заметить, что именно данное приложение из рассматриваемых в этой статье является одним из самых интересных в плане качества решения. Вам понравится, что получите, пожалуй, наиболее развернутые пошаговые решения задач, к тому же на понятном русском языке. Немного странным выглядит тот факт, что в описании указано, что для просмотра пошагового решения, нужна платная подписка, хотя все функциональные возможности приложения совершенно бесплатны. Mathway поможет вам не только с решением уравнений, неравенств и прочих сложных выражений, но также сумеет построить графики, может найти число молекул в определенной массе тела.
Mathway для Android тоже решает задачи с помощью камеры устройства, правда, реализована эта функция не самым лучшим образом. Для такого вывода у нас есть несколько веских причин. Во-первых, интерфейс камеры в программе крайне минималистичный, в нем почему-то нет даже области распознавания. Вам придется приловчится, чтобы выражение находилось по центру экрана, а рядом не должно быть других надписей, иначе приложение будет выдавать неправильное решение. Часто на практике камера захватывала только часть приложения, отсюда и ошибки. К тому же камера автоматически настроена на макро-режим, поэтому алгоритмы распознавания часто плохо срабатывают и выдают неправильный ответ. Лично мне иногда было гораздо проще и быстрее ввести задачу вручную. К тому же для этого в приложении есть просто шикарные возможности. Дело в том, что выдвигающееся боковое меню позволит вам получить доступ аж к 10 разделам, у каждого из которых есть свой собственный калькулятор с определенными символами, операторами, константами и прочими функциями. Очень удобно и практично.
Для такого вывода у нас есть несколько веских причин. Во-первых, интерфейс камеры в программе крайне минималистичный, в нем почему-то нет даже области распознавания. Вам придется приловчится, чтобы выражение находилось по центру экрана, а рядом не должно быть других надписей, иначе приложение будет выдавать неправильное решение. Часто на практике камера захватывала только часть приложения, отсюда и ошибки. К тому же камера автоматически настроена на макро-режим, поэтому алгоритмы распознавания часто плохо срабатывают и выдают неправильный ответ. Лично мне иногда было гораздо проще и быстрее ввести задачу вручную. К тому же для этого в приложении есть просто шикарные возможности. Дело в том, что выдвигающееся боковое меню позволит вам получить доступ аж к 10 разделам, у каждого из которых есть свой собственный калькулятор с определенными символами, операторами, константами и прочими функциями. Очень удобно и практично.
Мне очень понравилось, что Mathway предлагает пользователю самому выбрать способ решения задачи, в зависимости от этого результаты могут меняться. Если не подходит один из способов, достаточно снова тапнуть на математическое выражение и выбрать другой вариант решения. Скажем сразу, если вы хотите быстро и оперативно получить нужный ответ к задаче, то Mathway вряд ли подойдет вам. Но, если хотите точности и развернутости ответа, а также у вас есть терпение самостоятельно вводить математические символы и знаки, то данное приложение весьма вам понравится.
Если не подходит один из способов, достаточно снова тапнуть на математическое выражение и выбрать другой вариант решения. Скажем сразу, если вы хотите быстро и оперативно получить нужный ответ к задаче, то Mathway вряд ли подойдет вам. Но, если хотите точности и развернутости ответа, а также у вас есть терпение самостоятельно вводить математические символы и знаки, то данное приложение весьма вам понравится.
Mathpix
Mathpix — первое приложение, которое позволяет вам решать и визуализировать решения, распознавая рукописный текста, включая сложные формулы. Mathpix стремится заменить дорогие и устаревшие графические калькуляторы, чтобы обеспечить бесплатное и интересное учебное пособие для студентов-математиков по всему миру.
Я и вовсе хотел написать его первым среди всех приложений, так как это один из старожилов подобных приложений для решения математических задач. Оно намного раньше, в отличие от Photomath, получило способность распознавать рукописные математические задачи.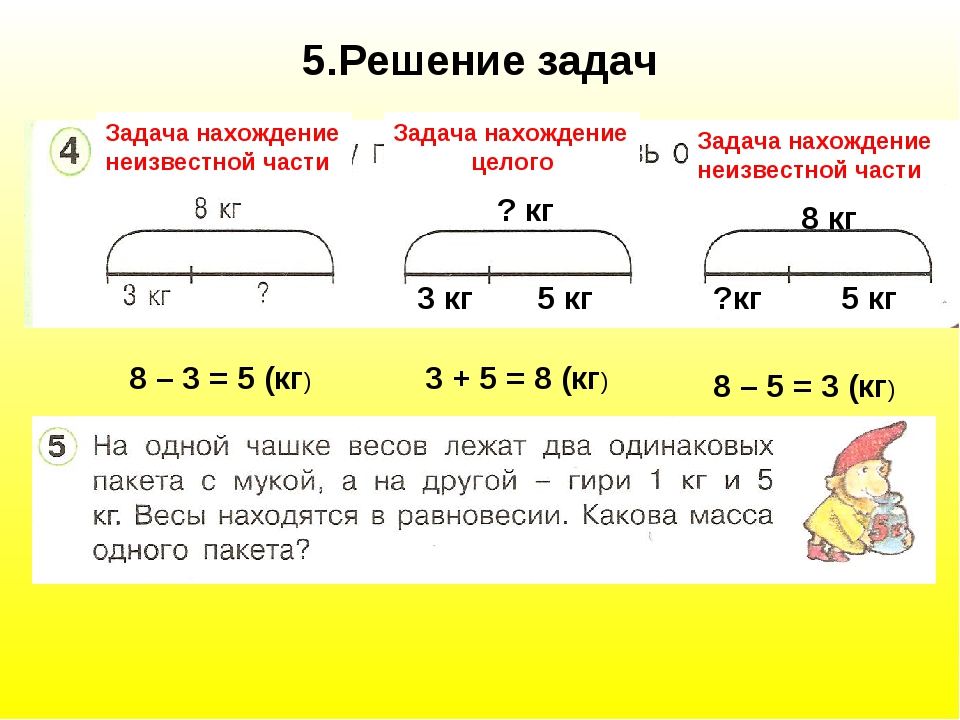 Стоит заметить, что суть и принцип работы обоих приложений очень похожи, но в целом сервис Mathpix рассчитан на более взрослую аудиторию. Оно умеет решать простые и не очень квадратные уравнения, легко справляется с задачами, в которых есть дробные выражения, а также корнями, логарифмами, интегралами, производными и т. д. То есть практически все, что есть в старших классах школы и первых курсов университета. Но особенно я бы отметил возможность построения графиков функций, благодаря интеграции с передовым графическим калькулятором Desmos. Этого нет ни у одного из представленных приложений, а это очень важно для решения задач алгебры и начала анализа.
Стоит заметить, что суть и принцип работы обоих приложений очень похожи, но в целом сервис Mathpix рассчитан на более взрослую аудиторию. Оно умеет решать простые и не очень квадратные уравнения, легко справляется с задачами, в которых есть дробные выражения, а также корнями, логарифмами, интегралами, производными и т. д. То есть практически все, что есть в старших классах школы и первых курсов университета. Но особенно я бы отметил возможность построения графиков функций, благодаря интеграции с передовым графическим калькулятором Desmos. Этого нет ни у одного из представленных приложений, а это очень важно для решения задач алгебры и начала анализа.
Вам очень понравится работа алгоритмов распознавания текстов и условий у Mathpix. Программа практически в считанные секунды сканирует и считывает условие задачи. Тут же отправляет на сервер данные условия и почти мгновенно выдает ответ. Но ошибки тоже случаются, хотя довольно редко. При этом пользователю доступны инструменты для работы с задачами в режиме графика: редактирование вводных данных, добавление таблиц, заметок и дополнительных функций для нескольких графиков.
Я тут так пафосно расписал возможности приложения, но отмечу, что оно хорошо справляется только с несложными задачами. Если еще с построением элементарных графиков приложение справится, то с более сложными заданиями, которые включают тригонометрические и логарифмические уравнения, неравенства, а также уравнения с модулем, возникали большие проблемы. Приложение просто игнорировало их решение. Так что разработчикам еще необходимо потрудиться над возможностями своей программы.
Большинству пользователей не понравится, что отсутствует интерфейс на русском языке, а также подробное описания решения задач. Да и само приложение довольно-таки сложновато в использовании, элементы управления неудобны на смартфоне с небольшим экраном. Создалось впечатление,что это веб-версия приложения. Но решение всё же остается за вами.
MyScript Calculator
Ну и, наконец, самое интересное приложение MyScript Calculator, которое впервые появилось в начале 2013 года. К тому же, сразу получило признание на международной выставке CES и было отмечено за инновации. Мы привыкли, что в онлайн-калькуляторах либо роль считывателя играет камера устройства, либо вручную вводим данные. В приложении MyScript Calculator принцип подхода к математическим вычислениям кардинально отличается. Особенность MyScript Calculator заключается в том, что приложение работает только с рукописным вводом данных. Здесь даже отсутствуют кнопки, как таковые, а все, что имеется — это чистое полотно на весь экран, имитирующее бумагу-миллиметровку. Примеры для вычисления пользователь пишет пальцем или с помощью стилуса. В данном случае предпочтительнее будет использование планшета или фаблета с цифровым пером.
Мы привыкли, что в онлайн-калькуляторах либо роль считывателя играет камера устройства, либо вручную вводим данные. В приложении MyScript Calculator принцип подхода к математическим вычислениям кардинально отличается. Особенность MyScript Calculator заключается в том, что приложение работает только с рукописным вводом данных. Здесь даже отсутствуют кнопки, как таковые, а все, что имеется — это чистое полотно на весь экран, имитирующее бумагу-миллиметровку. Примеры для вычисления пользователь пишет пальцем или с помощью стилуса. В данном случае предпочтительнее будет использование планшета или фаблета с цифровым пером.
Вам понравится, что приложение автоматически сумеет распознать написанное вручную, переведет записи в нормальный цифровой вид и буквально в то же мгновение выдаст результат. Стоит отметить, что алгоритмы распознавания MyScript Calculator просто великолепные. На практике программа умудряется определить даже самые откровенные каракули. Также вы сможете отменить или повторить последние действия и полностью очистить экран от написанного. К тому же вас определенно порадует довольно большой список поддерживаемых символов и операторов, который поможет решить даже сложные задания. Несмотря на все это, приложение вряд ли пригодится студентам университетов. Даже несмотря на возможность работать с дробями, квадратными корнями, константами, решать уравнения, находить переменные, MyScript Calculator решит школьную программу, не более.
К тому же вас определенно порадует довольно большой список поддерживаемых символов и операторов, который поможет решить даже сложные задания. Несмотря на все это, приложение вряд ли пригодится студентам университетов. Даже несмотря на возможность работать с дробями, квадратными корнями, константами, решать уравнения, находить переменные, MyScript Calculator решит школьную программу, не более.
Основным недостатком MyScript Calculator для Android можно считать отсутствие подробного описания решений, программа выдает только итоговый результат. Хотя, учитывая концепцию приложения, возможно оно было бы лишним. А вот то, что здесь не хватает различных удобных мелочей, так это скорее пожелание разработчикам на будущее. К примеру, хотелось бы увидеть историю вычислений, возможность масштабировать экран и сохранять введенные задачи. Но, если все это отбросить в сторону, приложение действительно полезное, простое и оригинальное.
Вместо тысячи слов…
Ну и в заключение все же хочется сказать, что хоть приведенные приложения и помогут вам справиться с математическими заданиями, но не забывайте, что это всего лишь программа. Она призвана помочь вам, а не добавлять вам знаний. Но еще раз повторюсь, данные приложения не являются панацеей для решения задач. Так, с некоторыми заданиями оно и вовсе не справится. К тому же иногда ошибаются в самых простейших случаях. Поэтому не стоит доверять им всецело, а все-таки учить математику.
Она призвана помочь вам, а не добавлять вам знаний. Но еще раз повторюсь, данные приложения не являются панацеей для решения задач. Так, с некоторыми заданиями оно и вовсе не справится. К тому же иногда ошибаются в самых простейших случаях. Поэтому не стоит доверять им всецело, а все-таки учить математику.
Будем признательны, если в комментариях поделитесь своим опытом использования подобных приложений, которые облегчают изучение математики.
стратегий решения математических задач, которые заставят учащихся сказать: «Я понял!»
Даже учащиеся, которые быстро разбираются в математических фактах, могут застрять, когда дело доходит до решения задач.
Как только понятие переводится в словесную задачу или простое математическое предложение содержит неизвестное, они заблуждаются.
Это потому, что решение проблем требует от нас сознательного выбора стратегий, наиболее подходящих для решения проблемы под рукой . И не все студенты обладают этой метакогнитивной способностью.
И не все студенты обладают этой метакогнитивной способностью.
Но вы можете обучить этим стратегиям решения проблем. Вам просто нужно знать, что это такое.
Мы собрали их здесь, разделив на четыре категории:
- Стратегии понимания проблемы
- Стратегии решения проблемы
- Стратегии отработки
- Стратегии проверки решения
Ознакомьтесь с этими стратегиями, а затем объясните их своим ученикам.В следующий раз, когда они погрузится в сложную задачу, они будут заполнять свою рабочую бумагу быстрее, чем когда-либо!
Стратегии понимания проблемы
Прежде чем учащиеся смогут решить задачу, они должны знать, о чем она их просит. Часто это первое препятствие для текстовых задач, в которых не указана конкретная математическая операция.
Поощряйте своих учеников:
Прочитать и перечитать вопрос
Говорят, что читали, но действительно ли ? Иногда учащиеся перескакивают вперед, как только замечают одну знакомую информацию, или отказываются от попыток понять ее, если проблема не имеет смысла на первый взгляд.
Научите учащихся интерпретировать вопрос, используя стратегии самоконтроля, такие как:
- Медленнее перечитывать вопрос, если он не имеет смысла с первого раза
- Просьба о помощи
- Выделение или подчеркивание важной информации.
Определение важной и лишней информации
Джон собирает деньги на день рождения своего друга Ари. Он начинает со своих 5 долларов, затем Маркус дает ему еще 5 долларов.Сколько у него сейчас?
Будучи взрослыми, глядя на вышеприведенную задачу, мы можем мгновенно отвлечься от имен и сценария дня рождения, чтобы увидеть простую задачу на сложение. Студенты, однако, могут изо всех сил пытаться определить, что важно в информации, которую им предоставили.
Научите учащихся сортировать и просеивать информацию в задаче, чтобы найти то, что важно. Хороший способ сделать это — попросить их поменять местами информацию, чтобы посмотреть, изменится ли решение. Если изменение имен, элементов или сценариев не повлияет на конечный результат, они поймут, что им не нужно уделять особое внимание при решении проблемы.
Если изменение имен, элементов или сценариев не повлияет на конечный результат, они поймут, что им не нужно уделять особое внимание при решении проблемы.
Схема подхода
Это стратегия математического вмешательства, которая может упростить решение задач для всех учащихся, независимо от их способностей.
Сравните разные текстовые задачи одного типа и составьте формулу или математическую основу предложения, которая применима ко всем ним. Например, простые задачи на вычитание можно выразить так:
.
[Количество/количество A] с удаленным [Количество/количество B] становится [конечным результатом].
Это базовая процедура или схема , которую учащимся предлагается использовать .Когда у них есть список схем для различных математических операций (сложение, умножение и т. д.), они могут по очереди применять их к незнакомой текстовой задаче и смотреть, какая из них подходит.
Бесплатные рабочие листы для решения задач
Стратегии решения проблемы
Отстающие ученики часто считают, что математика — это то, что вы либо делаете автоматически, либо не делаете вообще. Но это не так. Помогите учащимся понять, что у них есть выбор стратегий решения проблем, и если одна из них не сработает, они могут попробовать другую.
Но это не так. Помогите учащимся понять, что у них есть выбор стратегий решения проблем, и если одна из них не сработает, они могут попробовать другую.
Вот четыре общие стратегии, которые учащиеся могут использовать для решения задач.
Визуализация
Визуализация абстрактной проблемы часто облегчает ее решение. Студенты могли нарисовать картинку или просто поставить отметки на листе рабочей бумаги.
Поощряйте визуализацию, моделируя ее на доске и предоставляя графические органайзеры, в которых есть место для рисования учащимися перед тем, как они запишут окончательное число.
Угадай и проверь
Покажите учащимся, как сделать обоснованное предположение, а затем вставить этот ответ обратно в исходную задачу.Если это не сработает, они могут изменить свое первоначальное предположение соответственно выше или ниже.
Найти шаблон
Чтобы найти закономерности, покажите учащимся, как извлекать и перечислять все релевантные факты в задаче, чтобы их можно было легко сравнивать. Если они найдут закономерность, то смогут найти недостающую часть информации.
Если они найдут закономерность, то смогут найти недостающую часть информации.
Работа в обратном направлении
Работа в обратном порядке полезна, если учащимся нужно найти неизвестное число в задаче или математическом предложении. Например, если задача 8 + x = 12, учащиеся могут найти x по:
.
- Начиная с 12
- Выбрать 8 из 12
- Осталось 4
- Проверка работы 4 при использовании вместо x
Стратегии тренировки
Теперь, когда студенты поняли проблему и сформулировали стратегию, пришло время применить ее на практике.Но если они просто начнут и сделают это, они могут усложнить себе задачу. Покажите им, как эффективно решать проблему:
Документирование разработки
Смоделируйте процесс записи каждого шага, который вы предпринимаете для решения математической задачи, и предоставьте рабочий лист, когда учащиеся решают задачу. Это позволит учащимся отслеживать свои мысли и выявлять ошибки до того, как они придут к окончательному решению.
Это позволит учащимся отслеживать свои мысли и выявлять ошибки до того, как они придут к окончательному решению.
Проверка по пути
Проверка работы на ходу — еще одна важная стратегия самоконтроля для изучающих математику.Смоделируйте это для них с вопросами для размышления вслух, такими как:
- Последний шаг выглядит правильно?
- Является ли это следствием предыдущего шага?
- Вычислил ли я какие-нибудь «меньшие» суммы в рамках более крупной задачи, которую нужно проверить?
Стратегии проверки решения
Студенты часто ошибаются, думая, что скорость — это все в математике, поэтому они спешат записать ответ и двигаться дальше, не проверяя.
Но проверка тоже важна.Это позволяет им выявлять проблемные области по мере их возникновения и решать более сложные проблемы, требующие многократных проверок , прежде чем дойти до окончательного ответа.
Вот несколько стратегий проверки, которые вы можете продвигать:
Уточнить у партнера
Сравнение ответов с лидами сверстников — более рефлексивный процесс, чем просто получение галочки от учителя. Если у учащихся есть два разных ответа, предложите им рассказать о том, как они к ним пришли, и сравнить методы разработки.Они выяснят, где именно они ошиблись, а что сделали правильно.
Перечитайте проблему с вашим решением
В большинстве случаев учащиеся смогут определить, верен ли их ответ, вернувшись к исходной задаче. Если это не работает или просто «выглядит неправильно», пришло время вернуться и исправить это.
Исправление ошибок
Покажите учащимся, как вернуться назад, чтобы найти то место, где они допустили ошибку.Подчеркните, что они не могут этого сделать, если они не записали все в первую очередь — так что один ответ без проработки не так впечатляет, как они могут подумать!
Нужна дополнительная помощь в развитии навыков решения проблем?
Узнайте о том, как настроить задание на решение задач и рассуждение или изучите Mathseeds и Mathletics, наши отмеченные наградами онлайн-программы по математике. У них есть более 900 заданий по решению проблем, проверенных учителями!
У них есть более 900 заданий по решению проблем, проверенных учителями!
Категории
Математика, Стратегии обучения
Решение текстовых задач по математике — Математический блог для дифференциации
Что такое словесная задача? (И как их решить!)
Узнайте, что такое текстовые задачи и как их решить за 7 простых шагов.В реальной жизни математические задачи обычно не представляются как 3 + 5. Вместо этого все немного сложнее. Чтобы показать это, иногда создатели учебных программ по математике используют текстовые задачи, чтобы помочь учащимся увидеть, что происходит в реальном мире.
Словесные задачи часто показывают, что математика происходит более естественным образом в реальном мире. Вы, вероятно, решили несколько словесных задач за день! Вот несколько примеров.
Примеры задач Word
Проблемы Word могут варьироваться от простых до сложных. Вот несколько, чтобы дать вам представление:
– У Сары было 3 яблока. Ее мать купила еще 8 яблок и дала ей. Итак, сколько всего яблок у Сары?
Ее мать купила еще 8 яблок и дала ей. Итак, сколько всего яблок у Сары?
— Было 15 ручек и 12 карандашей. На сколько ручек больше, чем карандашей?
— У Джорджа одна дюжина яиц. Его семья съела 3 на завтрак. Итак, сколько яиц осталось?
— 12 печенек. Сара, Джордж, Сью и Дилан хотят их съесть. Сколько печенья должен получить каждый из друзей?
Как видите, текстовые задачи могут включать практически любую операцию. От сложения до вычитания и деления текстовые задачи также могут включать в себя несколько операций.Если вы учитель, вы можете задаться вопросом, как научить детей решать текстовые задачи. Это может помочь научить студентов основным шагам, которые нужно использовать при решении проблемы. Таким образом, их процесс управляется. Итак, какие шаги нужно сделать учащимся для решения текстовой задачи по математике?
Шаги по решению задачи Word
Чтобы решить любую текстовую задачу, учащиеся должны выполнить следующие шаги.
1. Прочитайте задачу : Во-первых, учащиеся должны прочитать задачу один раз.
2. Выделите факты : Затем учащийся должен еще раз прочитать задачу и выделить или подчеркнуть важные факты, такие как числа или слова, обозначающие операцию.
3. Нарисуй картинку : Рисование картинки иногда может помочь учащимся более четко представить проблему. Это также может помочь учащимся уточнить операции, которые им необходимо выполнить. (следующий шаг!)
4. Определите операцию(-и) : Затем учащийся должен определить операцию или операции, которые ему необходимо выполнить.Это сложение, вычитание, умножение, деление? Что должно произойти? Рисунок должен сильно помочь в этом. Однако они могут искать подсказки в таких словах, как:
– Сложение : добавить, принести, всего, в целом и, плюс, объединить, больше, всего
– Вычитание : меньше, чем, отнять, вычесть, влево
– Умножение : раз, дважды, утроить, всего, всего
– Деление : каждый, равные части, разделить, на, из, в среднем
Дженнифер Финдли предлагает еще один способ определения операции — поиск определенных ситуаций. У нее есть отличный ресурс, в котором перечислены различные ситуации, которые вы можете найти в наиболее распространенных текстовых задачах, и какие операции применимы к каждой ситуации.
У нее есть отличный ресурс, в котором перечислены различные ситуации, которые вы можете найти в наиболее распространенных текстовых задачах, и какие операции применимы к каждой ситуации.
5. Составьте математическое предложение : Затем учащиеся должны попытаться перевести слово «задача» и «рисунки» в математическое или числовое предложение. Это означает, что учащиеся могут написать такое предложение, как 3 + 8 =
6. Решить задачу : Затем учащиеся могут решить числовое предложение и найти решение. Например, 3 + 8 = 11.
7.Проверьте свой ответ : Наконец, учащиеся должны проверить свою работу, чтобы убедиться, что ответ правильный.
С этими 7 шагами решение текстовых задач по математике становится проще простого! Конечно, студенты также нуждаются в большом количестве практики. Поэтому позаботьтесь о том, чтобы у ваших учеников было достаточно возможностей попрактиковаться в решении словесных задач!
В Happy Numbers мы включаем текстовые задачи в учебную программу. Проверьте это!
Проверьте это!
Глава 9 — Раздел 6: Проблемы со смесями
%PDF-1.3
%
327 0 объект
>/Metadata 324 0 R/OCProperties>/OCGs[368 0 R]>>/OpenAction[329 0 R/XYZ null null null]/Outlines 7 0 R/PageLabels 322 0 R/PageMode/UseNone/Pages 325 0 R/ PieceInfo>>>/StructTreeRoot 328 0 R/Тип/Каталог>>
эндообъект
367 0 объект
>/Шрифт>>>/Поля 372 0 R>>
эндообъект
324 0 объект
>поток
Acrobat Distiller 5.0 (Windows)2001-10-24T16:09:57Z2013-04-18T09:55:40-05:002013-04-18T09:55:40-05:00Acrobat PDFMaker 5.0 для приложения Word/pdf
UUID: cdc01df2-50f1-47bc-aa8e-1ce31dcdb525uuid: c2683698-9749-4ebc-82f8-e60939d4d206
конечный поток
эндообъект
7 0 объект
>
эндообъект
322 0 объект
>
эндообъект
325 0 объект
>
эндообъект
328 0 объект
>
эндообъект
15 0 объект
>
эндообъект
154 0 объект
>
эндообъект
309 0 объект
>
эндообъект
17 0 объект
>
эндообъект
310 0 объект
[13 0 R 18 0 R 21 0 R 24 0 R 26 0 R 25 0 R 27 0 R 27 0 R 28 0 R 29 0 R 30 0 R 31 0 R 32 0 R 34 0 R 36 0 R 38 0 R 39 0 R 39 0 R 39 0 R 39 0 R 41 0 R 42 0 R 43 0 R 44 0 R 45 0 R 46 0 R 47 0 R 48 0 R 50 0 R 52 0 R 53 0 R 54 0 R 55 0 R 56 0 Р 57 0 Р 58 0 Р 59 0 Р 60 0 Р 62 0 Р 63 0 Р 64 0 Р 65 0 Р 66 0 Р 67 0 Р 69 0 Р 70 0 Р 71 0 Р 72 0 Р 73 0 Р 74 0 Р 76 0 Р 77 0 Р 78 0 Р 79 0 Р 80 0 Р 81 0 Р 81 0 Р 83 0 Р 85 0 Р 86 0 Р 87 0 Р 88 0 Р 89 0 Р 90 0 Р 91 0 Р 92 0 Р]
эндообъект
316 0 объект
[94 0 R 96 0 R 95 0 R 97 0 R 97 0 R 98 0 R 99 0 R 100 0 R 101 0 R 102 0 R 103 0 R 104 0 R 105 0 R 106 0 R 107 0 R 108 0 R 109 0 R 110 0 R 110 0 R 110 0 R 111 0 R 112 0 R 113 0 R 114 0 R 115 0 R 116 0 R 117 0 R 118 0 R 119 0 R 120 0 R 121 0 R 122 0 R 123 0 R 124 0 R 126 0 R 127 0 R 129 0 R 130 0 R 131 0 R 132 0 R 134 0 R 135 0 R 137 0 R 138 0 R 139 0 R 140 0 R 142 0 R 143 0 R 145 0 R 146 0 Р 147 0 Р 148 0 Р 149 0 Р 149 0 Р 149 0 Р 150 0 Р 151 0 Р 152 0 Р 153 0 Р]
эндообъект
94 0 объект
>
эндообъект
96 0 объект
>
эндообъект
95 0 объект
>
эндообъект
97 0 объект
>
эндообъект
98 0 объект
>
эндообъект
99 0 объект
>
эндообъект
100 0 объект
>
эндообъект
101 0 объект
>
эндообъект
102 0 объект
>
эндообъект
103 0 объект
>
эндообъект
104 0 объект
>
эндообъект
105 0 объект
>
эндообъект
106 0 объект
>
эндообъект
107 0 объект
>
эндообъект
108 0 объект
>
эндообъект
109 0 объект
>
эндообъект
110 0 объект
>
эндообъект
111 0 объект
>
эндообъект
112 0 объект
>
эндообъект
113 0 объект
>
эндообъект
114 0 объект
>
эндообъект
115 0 объект
>
эндообъект
116 0 объект
>
эндообъект
117 0 объект
>
эндообъект
118 0 объект
>
эндообъект
119 0 объект
>
эндообъект
120 0 объект
>
эндообъект
121 0 объект
>
эндообъект
122 0 объект
>
эндообъект
123 0 объект
>
эндообъект
124 0 объект
>
эндообъект
126 0 объект
>
эндообъект
127 0 объект
>
эндообъект
129 0 объект
>
эндообъект
130 0 объект
>
эндообъект
131 0 объект
>
эндообъект
132 0 объект
>
эндообъект
134 0 объект
>
эндообъект
135 0 объект
>
эндообъект
137 0 объект
>
эндообъект
138 0 объект
>
эндообъект
139 0 объект
>
эндообъект
140 0 объект
>
эндообъект
142 0 объект
>
эндообъект
143 0 объект
>
эндообъект
145 0 объект
>
эндообъект
146 0 объект
>
эндообъект
147 0 объект
>
эндообъект
148 0 объект
>
эндообъект
149 0 объект
>
эндообъект
150 0 объект
>
эндообъект
151 0 объект
>
эндообъект
152 0 объект
>
эндообъект
153 0 объект
>
эндообъект
1 0 объект
>/ExtGState>/Font>/ProcSet[/PDF/Text]/XObject>>>/Rotate 0/StructParents 1/Type/Page>>
эндообъект
373 0 объект
>поток
HW[o6~70/vLEQL]}JAG#e$I(ɔ3Q~,Wi~_A?Z/V@C6_ Gjlhs̜WĒ»@?i5N0! ٢U («w?q
Решение словесных вопросов
МНОГО примеров!
В алгебре у нас часто возникают словесные вопросы, например:
Пример: Сэм и Алекс играют в теннис.

В выходные Сэм сыграл на 4 игры больше, чем Алекс, а вместе они сыграли 12 игр.
Сколько игр сыграл Алекс?
Как их решить?
Хитрость заключается в том, чтобы разбить решение на две части:
Превратите английский в алгебру.
Затем используйте алгебру для решения.
Превращение английского языка в алгебру
Превратить английский язык в алгебру поможет:
- Сначала прочитайте все
- Сделайте эскиз если возможно
- Назначить букв для значений
- Найти или вычислить формулы
Вы также должны записать то, что на самом деле запрашивается , чтобы вы знали, куда вы идете и когда вы прибыли!
Также ищите ключевые слова:
| Когда вы видите | Подумай | |
|---|---|---|
|
добавить, итого, сумма, увеличить, больше, вместе, вместе, плюс, более |
+ | |
|
минус, меньше, разность, меньше, меньше, меньше |
— | |
|
умножить, раз, произведение, коэффициент |
× | |
|
разделить, частное, на, вне, отношение, отношение, процент, показатель |
÷ | |
| увеличить или уменьшить | геометрия формулы |
|
| Скорость, скорость | расстояние формулы |
|
| Как долго, дни, часы, минуты, секунды | время |
Мыслить ясно
Некоторые формулировки могут быть сложными, из-за чего трудно думать «правильно», например:
$
Пример: У Сэма на 2 доллара меньше, чем у Алекса.
 Как мы запишем это в виде уравнения?
Как мы запишем это в виде уравнения?
- Пусть S = доллары У Сэма есть
- Пусть A = долларов У Алекса есть
Теперь… это: S − 2 = A
или должно быть: S = A — 2
или должно быть: S = 2 — A
Правильный ответ S = A − 2
( S − 2 = A — распространенная ошибка, так как вопрос пишется «Сэм… на 2 меньше… Алекс»)
Пример: на нашей улице собак вдвое больше, чем кошек.Как мы запишем это в виде уравнения?
- Пусть D = количество собак
- Пусть C = количество кошек
Теперь… это что: 2D = C
или должно быть: D = 2C
Подумайте хорошенько!
Правильный ответ: D = 2C
( 2D = C — распространенная ошибка, так как вопрос пишется «дважды… собаки… кошки»)
Примеры
Давайте начнем с очень простого примера , чтобы мы увидели, как это делается:
Пример: прямоугольный сад размером 12 м на 5 м, какова его площадь?
Превратите английский в алгебру:
Эскиз:
Буквы:
- Используйте ш для ширины прямоугольника: ш = 12 м
- Используйте h для высоты прямоугольника: h = 5 м
Формула для площади прямоугольника: A = w × h
Нас спрашивают о Районе.
Решить:
A = ш × в = 12 × 5 = 60 м 2
Площадь 60 квадратных метров .
Теперь давайте попробуем пример из верхней части страницы:
Пример: Сэм и Алекс играют в теннис. В выходные Сэм сыграл на 4 игры больше, чем Алекс, а вместе они сыграли 12 игр. Сколько игр сыграл Алексей?
Превратите английский в алгебру:
Буквы:
- Используйте S для того, сколько игр сыграл Сэм
- Используйте A для того, сколько игр сыграл Алекс
Мы знаем, что Сэм сыграл на 4 игры больше, чем Алекс, поэтому: S = A + 4
А мы знаем, что вместе они сыграли 12 игр: S + A = 12
Нас спрашивают, сколько игр сыграл Алекс: A
Решить:
Начните с: S + A = 12
S = A + 4 , поэтому мы можем
заменить «A + 4» на S: (A + 4) + A = 12
Упростить: 2А + 4 = 12
Вычесть 4 с обеих сторон: 2A = 12 − 4
Упростить: 2A = 8
Разделите обе части на 2:А = 4
Это означает, что Алекс сыграл 4 игры в теннис.
Проверка: Сэм сыграл на 4 игры больше, чем Алекс, поэтому Сэм сыграл 8 игр.
Вместе они сыграли 8 + 4 = 12 игр. Да!
Чуть более сложный пример:
Пример: Алекс и Сэм тоже строят столы.
Вместе они делают 10 столов за 12 дней.
Алекс, работая в одиночку, может сделать 10 штук за 30 дней.
Сколько времени потребуется Сэму, работающему одному, чтобы сделать 10 столов?
Превратите английский в алгебру:
Буквы:
- Используйте и для скорости работы Алекса
- Используйте s для скорости работы Сэма
12 дней Алекса и Сэма это 10 столов, значит: 12а + 12с = 10
30 дней одного Алекса тоже 10 столов: 30а = 10
Нас спрашивают, сколько времени потребуется Сэму, чтобы сделать 10 столов.
Решить:
30a = 10 , поэтому ставка Алекса (столов в день): a = 10/30 = 1/3
Начните с: 12a + 12s = 10
Поставьте «1/3» вместо: 12(1/3) + 12s = 10
Упростить: 4 + 12 с = 10
Вычесть 4 с обеих сторон: 12s = 6
Разделите обе части на 12: с = 6/12
Упростить: с = 1/2
Это означает, что ставка Сэма составляет полтаблицы в день (быстрее, чем у Алекса!)
Итак, на 10 столов Сэму потребуется всего 20 дней.
Интересно, Сэму должны платить больше?
И еще пример «подстановки»:
Пример: Дженна усердно тренируется, чтобы пройти отбор на Национальные игры.
У нее регулярный еженедельный распорядок: в некоторые дни она тренируется по пять часов в день, а в другие дни — по 3 часа.
Всего она тренируется 27 часов в неделю. Сколько дней она тренируется по пять часов?
Буквы:
- Количество «5-часовых» дней: d
- Количество «3-х часовых» дней: e
Мы знаем, что в неделе семь дней, поэтому: d + e = 7
И она тренируется 27 часов в неделю, с d 5-часовыми днями и e 3-часовыми днями: 5d + 3e = 27
Нас спрашивают сколько дней она тренируется по 5 часов :d
Решить:
d + e = 7
Итак: e = 7 − d
Поместите это в 5d + 3e = 27 5d + 3 (7−d) = 27
Упростить: 5d + 21 − 3d = 27
Вычесть 21 с обеих сторон: 5d − 3d = 6
Упростить: 2d = 6
Разделить обе стороны на 2: d = 3
Количество «5-часовых» дней равно 3
Чек : Она тренируется по 5 часов 3 дня в неделю, поэтому она должна тренироваться по 3 часа в день в остальные 4 дня недели.
3 × 5 часов = 15 часов плюс 4 × 3 часа = 12 часов дает в сумме 27 часов
Несколько примеров из геометрии:
Пример: площадь круга 12 мм
2 , каков его радиус?
Буквы:
- Используйте A для площади: A = 12 мм 2
- Используйте r для радиуса
И формула площади: A = π r 2
Нас спрашивают о радиусе.
Решить:
Нам нужно изменить формулу, чтобы найти площадь
Начните с: A = π r 2
Поменять местами: π r 2 = A
Разделите обе части на π : r 2 = A / π
Извлечь квадратный корень из обеих сторон: r = √(A / π)
Теперь мы можем использовать формулу: r = √(12/ π)
И получаем: r = 1.954 (до 3 мест)
Пример: куб имеет объем 125 мм
3 , какова площадь его поверхности?
Сделать быстрый набросок:
Буквы:
- Используйте V для тома
- Используйте A для Зоны
- Используйте s для длины стороны куба
Формулы:
- Объем куба: V = s 3
- Площадь поверхности куба: A = 6s 2
Нас спрашивают о площади поверхности.
Решить:
Сначала вычислите s , используя формулу объема:
Начните с: В = с 3
Поменять стороны местами: с 3 = V
Извлечь кубический корень из обеих сторон: s = ∛(V )
И получаем: с = ∛(125 ) = 5
Теперь мы можем рассчитать площадь поверхности:
Начните с: A = 6 с 2
И получаем: А = 6(5) 2
A = 6 × 25 = 150 мм 2
Пример про Деньги:
Пример: Джоэл работает в местной пиццерии.Когда он работает сверхурочно, он зарабатывает в 1¼ раза больше обычной ставки.
Одну неделю Джоэл работал 40 часов по обычной ставке, а также работал сверхурочно 12 часов. Если Джоэл в общей сложности заработал 660 долларов за эту неделю, какова его нормальная ставка?
Буквы:
- Обычная ставка Джоэла: $N в час
Формулы:
- Джоэл работает 40 часов по N долларов в час = 40N долларов
- Когда Джоэл работает сверхурочно, он зарабатывает в 1¼ раза больше обычной ставки = 1 доллар.
 25 Н в час
25 Н в час - Джоэл работает 12 часов за 1,25 н. долл. США в час = (12 × 1¼ Н) = 15 н. долл. США
- И вместе он заработал 660 долларов, так что:
40$ + $(12 × 1¼N) = 660$
Нас спрашивают об обычной ставке Джоэла $N.
Решить:
Начните с 40N $ + $(12 × 1¼N) = 660 $
Упрощение: 40 тысяч долларов + 15 тысяч долларов = 660 долларов
Упростите больше: 55 тысяч долларов = 660 долларов
Разделите обе части на 55: $N = $12
Итак, нормальная ставка Джоэла составляет 12 долларов в час.
Чек
Обычная ставка Джоэла составляет 12 долларов в час, поэтому его ставка сверхурочной работы составляет 1¼ × 12 долларов в час = 15 долларов в час.Таким образом, его обычная заработная плата 40 × 12 = 480 долларов плюс оплата сверхурочных 12 × 15 = 180 долларов дает нам в сумме 660
долларов.
Подробнее о деньгах, с этими двумя примерами, связанными со сложными процентами
Пример: Алекс кладет в банк 2000 долларов под сложные проценты в размере 11% годовых.
 Сколько он будет стоить через 3 года?
Сколько он будет стоить через 3 года?
Это формула сложных процентов:
Итак, мы будем использовать эти буквы:
- Приведенная стоимость PV = 2000 долларов США
- Процентная ставка (в виде десятичной дроби): r = 0.11
- Количество периодов: n = 3
- Будущая стоимость (значение, которое мы хотим): FV
Нас спрашивают о будущей стоимости: FV
Решить:
Начните с: FV = PV × (1+r) n
Введите то, что мы знаем: FV = $2000 × (1+0,11) 3
Рассчитать: FV = $2000 × 1,367631
Рассчитайте: FV = 2735 долларов США.26 (с точностью до цента)
Пример: Роджер положил 1000 долларов на сберегательный счет. Начисленные проценты начислялись ежегодно по той же ставке. Через девять лет депозит Роджера вырос до $1551,33
Какова была годовая процентная ставка по сберегательному счету?
Формула сложных процентов:
С:
- Приведенная стоимость PV = 1000 долларов США
- Процентная ставка (значение, которое мы хотим): r
- Количество периодов: n = 9
- Будущая стоимость: FV = 1551 доллар.
 33
33
У нас запрашивают процентную ставку: r
Решить:
Начните с: FV = PV × (1+r) n
Введите то, что мы знаем: 1551,33 доллара = 1000 долларов × (1+r) 9
Поменять местами: 1000 долл. США × (1+r) 9 = 1551,33 долл. США
Разделите обе части на 1000: (1+r) 9 = 1551,33 долл. США / 1000 долл. США
Упрощение: (1+r) 9 = 1.55133
9-й корень: 1+r = 1,55133 (1/9)
Рассчитать: 1+r = 1,05
Рассчитать: r = 0,05 = 5%
Таким образом, годовая процентная ставка составляет 5%
Чек : 1000 долл. США × (1,05) 9 = 1000 долл. США × 1,55133 = 1551,33 долл. США
И пример вопроса о соотношении:
Пример: В начале года соотношение мальчиков и девочек в классе было 2 : 1
Но сейчас, спустя полгода, из класса ушли четыре мальчика и две новые девочки. Соотношение мальчиков и девочек теперь 4 : 3
Соотношение мальчиков и девочек теперь 4 : 3
Сколько сейчас всего учеников?
Буквы:
- Количество мальчиков сейчас: b
- Количество девушек сейчас: г
Коэффициент текущей ликвидности 4 : 3
б г = 4 3
Который можно переставить в 3b = 4g
В начале года было (b + 4) мальчиков и (g − 2) девочек, и соотношение было 2 : 1
б + 4 г — 2 = 2 1
Которое можно преобразовать в b + 4 = 2(g − 2)
Нас спрашивают, сколько сейчас всего учеников: b + g
Решить:
Начните с: б + 4 = 2(г — 2)
Упростить: б + 4 = 2г — 4
Вычесть 4 с обеих сторон: b = 2g − 8
Умножаем обе части на 3 (получаем 3b): 3b = 6g − 24
Помните 3b = 4g : 4g = 6g − 24
Вычесть 6g с обеих сторон : −2g = − 24
Разделите обе части на −2: г = 12
Есть 12 девушек !
И 3b = 4g , поэтому b = 4g/3 = 4 × 12/3 = 16 , поэтому 16 мальчиков
Итак, теперь в классе 12 девочек и 16 мальчиков, всего 28 учеников .
Чек
Сейчас 16 мальчиков и 12 девочек, поэтому соотношение мальчиков и девочек 16 : 12 = 4 : 3
В начале года было 20 мальчиков и 10 девочек, поэтому соотношение было 20 : 10 = 2 : 1
А теперь немного квадратных уравнений:
Пример: Произведение двух последовательных четных целых чисел равно 168. Что это за целые числа?
Последовательный означает один за другим. И они даже , так что они могут быть 2 и 4, или 4 и 6, и т. д.
Мы будем называть меньшее целое число n , поэтому большее целое должно быть n+2
И нам говорят, что произведение (то, что мы получим после умножения) равно 168, поэтому мы знаем:
n(n + 2) = 168
Нас просят ввести целые числа
Решить:
Начните с: n(n + 2) = 168
Расширить: n 2 + 2n = 168
Вычесть 168 с обеих сторон: n 2 + 2n − 168 = 0
Это квадратное уравнение, и есть много способов его решить. Используя Решатель квадратных уравнений, мы получаем -14 и 12.
Используя Решатель квадратных уравнений, мы получаем -14 и 12.
Проверка −14: −14(−14 + 2) = (−14)×(−12) = 168 ДА
Проверка 12: 12(12 + 2) = 12×14 = 168 ДА
Итак, есть два решения: −14 и −12 — одно, 12 и 14 — другое.
Примечание: мы могли бы также попробовать «угадать и проверить»:
- Можно попробовать, скажем, n=10: 10(12) = 120 НЕТ (слишком мало)
- Далее мы можем попробовать n=12: 12(14) = 168 ДА
Но если мы не будем помнить, что умножение двух отрицательных чисел дает положительное, мы можем упустить из виду другое решение (−14)×(−12).
А:
Пример: Вы архитектор. Ваш клиент хочет, чтобы комната была в два раза длиннее, чем ее ширина. Они также хотят веранду шириной 3 метра вдоль длинной стороны.
У вашего клиента есть 56 квадратных метров красивой мраморной плитки, чтобы покрыть всю площадь.
Какой длины должна быть комната?
Давайте сначала сделаем набросок, чтобы все получилось правильно!:
Буквы:
- длина номера: L
- ширина комнаты: Ш
- Общая площадь включая веранду: А
Мы знаем:
- ширина комнаты равна половине ее длины: Ш = ½Д
- общая площадь равна (ширине комнаты + 3), умноженной на длину: A = (W+3) × L = 56
Нас спрашивают о длине комнаты: L
Решить:
Начните с: (Ш + 3) × Д = 56
Заменитель Ш = ½ л : (½ л + 3) × Д = 56
Упрощение: ½ л 2 + 3 л = 56
Умножить все члены на 2: L 2 + 6L = 112
Вычесть 112 с обеих сторон : L 2 + 6L − 112 = 0
Это квадратное уравнение , есть много способов его решить, на этот раз воспользуемся факторингом:
Начните с: л 2 + 6 л — 112 = 0
Два числа, при умножении которых получается ac=−112,
и
сложите, чтобы получить b = 6, 14 и -8: L 2 + 14L — 8L — 112 = 0
Группа: L(L + 14) — 8(L + 14) = 0
Группа: (L — 8) (L + 14) = 0
Итак, L = 8 или −14
У квадратного уравнения есть два решения, но возможно только одно из них, так как длина комнаты не может быть отрицательной!
Итак, длина комнаты 8 м
Чек
L = 8, поэтому W = ½L = 4
Итак, площадь прямоугольника = (W+3) × L = 7 × 8 = 56
Вот и мы.