5 класс

Мерзляк математика 5 класс контрольная работа: Учебно-методический материал по математике (5 класс) на тему: Контрольные работы по математике 5 класс УМК Мерзляк А.Г., Полонский В.Б., Якир М.С.

Контрольная работа по математике за I полугодие 5 класс Мерзляк

5класс

Контрольная работа по математике за I полугодие

Вариант 1

  1. Сравните числа: 1) 6 894 и 6 983; 2) 12 471 и 12 324;

3) 3 км и 2 974 м; 4) 912 кг и 8 ц.

  1. Вычислите: 1) 26 832 + 573 468; 2) 54 073 507 – 6 829 412.

3) 9 м 41 см + 4 м 72 см; 4) 18 ч 18 мин – 5 ч 24 мин.

  1. Начертите отрезок MN, длина которого равна 6 см 4 мм, отметьте на нём точку A. Запишите все отрезки, образовавшиеся на рисунке, и измерьте их длины.

  2. Решите уравнение: 1) 𝑥 + 53 = 97; 2) (58 + 𝑥) – 23 = 96

  3. Из вершины прямого угла DMK (см рис.) проведены два луча MB и MC так, что ∠DMB = 51, ∠KMC = 65. Вычислите градусную меру угла BMC.hello_html_6796b78c.png

5класс

Контрольная работа по математике за I полугодие

Вариант 2

  1. Сравните числа: 1) 5 678 и 5 489; 2) 14 092 и 14 605;

3) 3 986 г и 4 кг; 4) 586 см и 6 м.

  1. Вычислите: 1) 19 829 + 123 471; 2) 61 030 504 – 8 695 371.

3)7 м 23 см + 4 м 81 см; 4) 6 ч 38 мин – 4 ч 43 мин.

  1. Начертите отрезок АВ, длина которого равна 7 см 8 мм, отметьте на нём точку D. Запишите все отрезки, образовавшиеся на рисунке, и измерьте их длины.

  2. Решите уравнение: 1) 𝑥 + 42 = 94; 2) (41 + 𝑥) – 12 = 83hello_html_5070624a.png

  3. Из вершины развёрнутого угла FAN (см рис.) проведены два луча AK и AP так, что ∠NAP = 110, ∠FAK = 132. Вычислите градусную меру угла PAK.

5класс

Контрольная работа по математике за I полугодие

Вариант 1

  1. Сравните числа: 1) 6 894 и 6 983; 2) 12 471 и 12 324;

3) 3 км и 2 974 м; 4) 912 кг и 8 ц.

  1. Вычислите: 1) 26 832 + 573 468; 2) 54 073 507 – 6 829 412.

3) 9 м 41 см + 4 м 72 см; 4) 18 ч 18 мин – 5 ч 24 мин.

  1. Начертите отрезок MN, длина которого равна 6 см 4 мм, отметьте на нём точку A. Запишите все отрезки, образовавшиеся на рисунке, и измерьте их длины.

  2. Решите уравнение: 1) 𝑥 + 53 = 97; 2) (58 + 𝑥) – 23 = 96

  3. Из вершины прямого угла DMK (см рис.) проведены два луча MB и MC так, что ∠DMB = 51, ∠KMC = 65. Вычислите градусную меру угла BMC.hello_html_6796b78c.png

5класс

Контрольная работа по математике за I полугодие

Вариант 2

  1. Сравните числа: 1) 5 678 и 5 489; 2) 14 092 и 14 605;

3) 3 986 г и 4 кг; 4) 586 см и 6 м.

  1. Вычислите: 1) 19 829 + 123 471; 2) 61 030 504 – 8 695 371.

3)7 м 23 см + 4 м 81 см; 4) 6 ч 38 мин – 4 ч 43 мин.

  1. Начертите отрезок АВ, длина которого равна 7 см 8 мм, отметьте на нём точку D. Запишите все отрезки, образовавшиеся на рисунке, и измерьте их длины.

  2. Решите уравнение: 1) 𝑥 + 42 = 94; 2) (41 + 𝑥) – 12 = 83hello_html_5070624a.png

  3. Из вершины развёрнутого угла FAN (см рис.) проведены два луча AK и AP так, что ∠NAP = 110, ∠FAK = 132. Вычислите градусную меру угла PAK.

КР-07 В-1 Математика 5 Мерзляк

КР-07 В-1 Математика 5 Мерзляк — контрольная работа по математике в 5 классе № 7 «Понятие о десятичной дроби. Сравнение, округление, сложение и вычитание десятичных дробей» в 2-х вариантах из пособия для учащихся «Математика. Дидактические материалы. 5 класс ФГОС» (авт. А.Г. Мерзляк, В.Б. Полонский, Е.М. Рабинович, М.С. Якир, изд-во «Вентана-Граф»), а также решения и ОТВЕТЫ на нее (нет в пособии).

Цитаты из вышеуказанного учебного пособия использованы на сайте в незначительных объемах, исключительно в учебных и информационных целях (пп. 1 п. 1 ст. 1274 ГК РФ).

 

Математика 5 класс (УМК Мерзляк)
Контрольная работа № 7. Вариант № 1

 

КР-07 В-1 «Понятие о десятичной дроби. Сравнение, округление, сложение и вычитание десятичных дробей» (транскрипт заданий)

  1. Сравните: 1) 19,4 и 19,398; 2) 0,5384 и 0,539.
  2. Округлите: 1) до десятых: 6,786; 0,53924; 2) до сотых: 13,421; 0,3659.
  3. Выполните действия: 1) 6,67 + 24,793; 3) 12 — 6,256; 2) 88,17 — 8,345; 4) 10,4 — (0,87 + 3,268).
  4. Скорость теплохода против течения реки равна 24,8 км/ч, а скорость течения — 2,6 км/ч. Найдите скорость теплохода по течению реки.
  5. Вычислите, записав данные величины в метрах: 1) 23,4 м — 82 см; 2) 3,4 м + 630 см.
  6. Ломаная состоит из трёх звеньев. Длина первого звена равна 7,4 см, что на 2,7 см меньше длины второго звена и на 3,8 см больше длины третьего. Чему равна длина ломаной?
  7. Напишите три числа, каждое из которых больше 6,44 и меньше 6,46.
  8. Какие цифры можно поставить вместо звёздочек, чтобы образовалось верное неравенство (в правой и левой частях неравенства звёздочкой обозначена одна и та же цифра): 1) 0,*3 > 0,5*; 2) 0,*4 < 0,4*?

 

Ответы на контрольную работу:

Смотреть РЕШЕНИЯ заданий Варианта № 1

 

КР-07 В-2 Математика 5 класс — Контрольная работа «Понятие о десятичной дроби. Сравнение, округление, сложение и вычитание десятичных дробей» (по УМК Мерзляк и др.): задания, решения и ответы на нее.

Перейти к другому варианту этой контрольной: КР-07 Вариант 2

Вернуться к Списку контрольных работ по математике в 5 классе (Мерзляк).

Итоговая контрольная работа по математике 5 класс по УМК А.Г. Мерзляк

Итоговая работа по математике 5 класс

2016 — 2017 учебный год

УМК:

  1. «Математика 5 «- учебник для общеобразовательных учреждений /А.Г.Мерзляк; Москва, «Вентана-Граф» 2013г./

  2. «Математика 5»- дидактические материалы для общеобразовательных учреждений /А.Г. Мерзляк и др., Москва, «Вентана-Граф» 2016 г./

3. «Рабочая тетрадь по математике 5»- рабочие тетради в двух частях для общеобразовательных учреждений /А.Г. Мерзляк и др., Москва, «Вентана-Граф» 2016 г./

Абдрахманова Людмила Анатольевна,

учитель математики МБОУ «СОШ с. Терновка» Энгельсского района

Контрольная работа составлена на два варианта. Структура работы напоминает структуру ОГЭ по математике. Содержит три модуля: алгебра, геометрия и реальная математика. Всего заданий 14. На выполнение работы отводится 90 минут.

Критерии оценивания:

I часть (12 заданий) по одному баллу;

II часть: 13-14 заданий — 2 балла.

«5» — 14 -16 баллов;

«4» — 10-13 баллов;

«3» — 7-9 баллов;

«2» — 0-6 баллов.

Итоговая контрольная работа по математике 5 класс

I вариант

Часть 1

  1. Преобразуйте обыкновенную дробь в десятичную дробь.

Ответ:____________________________________________________________

  1. Преобразуйте неправильную дробь в смешанное число.

Ответ:____________________________________________________________

  1. Решите уравнение 6x+3,7=38,5.

Ответ:____________________________________________________________

  1. Расположите числа 5,01; 5,3; 5,27; 5,298 в порядке убывания.

Ответ:____________________________________________________________

  1. Выразите в см 0,23 м.

Ответ:____________________________________________________________

  1. На спортивных соревнованиях пятеро судей оценили выступление фигуриста оценками: 4,9; 4,7; 5,6; 5,3; 4,7. Найдите среднюю арифметическую оценку фигуриста.

Ответ:____________________________________________________________

  1. Вычислите: .

Ответ:____________________________________________________________

  1. Начертите угол AОC равный 135 ̊. Лучом ОВ разделите этот угол так, чтобы получившийся угол AОВ был равен 85 ̊. Вычислите градусную меру угла BОC.

Ответ:____________________________________________________________

  1. Определите вид угла, если его градусная мера равна 91°.

   а) острый;                  в) прямой;

   б) тупой;                    г) развёрнутый.

Ответ:____________________________________________________________

  1. В школьном саду 40 фруктовых деревьев. 30% этих деревьев – яблони. Сколько яблонь в школьном саду?

Ответ:____________________________________________________________

  1. В книге 520 страниц. Вася прочитал книги. Сколько ему осталось прочитать?

Ответ:____________________________________________________________

  1. Переведи смешанное число в неправильную дробь.

Ответ:____________________________________________________________

Часть 2

  1. Лодка шла по течению реки 0,9 ч и против течения 0,5 ч. Собственная скорость лодки 4,7 км/ч, а скорость течения 1,2 км/ч. Какой путь прошла лодка за это время?

Ответ:____________________________________________________________

  1. Найдите высоту прямоугольного параллелепипеда, если его объём равен 20,9 см3, а площадь дна составляет 3,8 см².

Ответ:____________________________________________________________

Итоговая контрольная работа по математике 5 класс

II вариант

Часть 1

  1. Преобразуйте обыкновенную дробь в десятичную дробь.

Ответ:____________________________________________________________

  1. Преобразуйте неправильную дробь в смешанное число.

Ответ:____________________________________________________________

  1. Решите уравнение .

Ответ:____________________________________________________________

  1. Расположите в порядке убывания числа: 4,07; 4,18; 4,5; 4,493.

Ответ:____________________________________________________________

  1. Выразите в килограммах 0,12 ц.

Ответ:____________________________________________________________

  1. Купили четырех телят массой 77,3кг; 68,5кг; 65,8кг и 59,8кг. Найдите среднюю массу купленных телят..

Ответ:____________________________________________________________

  1. Вычислите: .

Ответ:____________________________________________________________

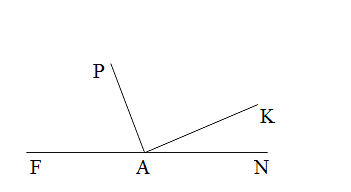
  1. Начертите угол МNK, равный 140°. Лучом NP разделите этот угол так, чтобы получившийся угол PNK был равен 55°. Вычислите градусную меру угла MNP.

Ответ:_____________________________________________________

  1. Определите вид угла, если его градусная мера равна 76.

   а) острый;                  в) прямой;

   б) тупой;                    г) развёрнутый.

.Ответ:____________________________________________________________

  1. В книге 120 страниц. Рисунки занимают 35% книги. Сколько страниц занимают рисунки?

Ответ:____________________________________________________________

  1. На склад привезли 210 ящиков яблок и слив, причем из них занято сливами. Сколько ящиков яблок привезли на склад?

Ответ:____________________________________________________________

  1. Переведи смешанное число в неправильную дробь.

Ответ:____________________________________________________________

Часть 2

  1. Собственная скорость лодки 3,8 км/ч, а скорость течения реки 1,3 км/ч. Сначала лодка шла 0,3 ч против течения реки, а затем 0,8 ч по течению. Какой путь прошла за все это время лодка?

Ответ:____________________________________________________________

  1. Объём прямоугольного параллелепипеда 9,1 см3. Найдите его высоту, если площадь дна составляет 2,6 см2.

Ответ:____________________________________________________________

Контрольные работы по математике 5 класс УМК Мерзляк А.Г., Полонский В.Б., Якир М.С.

Контрольные работы по математике 5 класс
УМК Мерзляк А.Г., Полонский В.Б., Якир М.С.
Контрольная работа № 1
Натуральные числа
Вариант  1
1. Запишите цифрами число:
1) шестьдесят пять миллиардов сто двадцать три миллиона девятьсот сорок одна тысяча 
восемьсот тридцать семь;
2) восемьсот два миллиона пятьдесят четыре тысячи одиннадцать:
3) тридцать три миллиарда девять миллионов один.
2. Сравните числа:      1) 5 678 и 5 489;               2)   14 092 и 14 605.
3. Начертите координатный луч и отметьте на нём точки, соответствующие числам 2, 5, 7, 9.
4. Начертите отрезок FK, длина которого равна 5 см 6 мм, отметьте на нём точку C. Запишите все 
отрезки, образовавшиеся на рисунке, и измерьте их длины.
5. Точка К принадлежит отрезку МЕ, МК = 19 см, отрезок КЕ на 17 см больше отрезка МК. Найдите
длину отрезка МЕ. 
6. Запишите цифру, которую можно поставить вместо звёздочки, чтобы образовалось верное 
неравенство (рассмотрите все возможные случаи):
1) 3 78*  ¿  3 784;                          2) 5 8*5  ¿  5 872.
7. На отрезке CD длиной 40 см отметили точки P и Q так, что CP = 28 см, QD =26 см. Чему равна 
длина отрезка PQ?
8. Сравните:  1) 3 км  и 2 974 м;        2) 912 кг и 8 ц.
Вариант  2
1. Запишите цифрами число:
1) семьдесят шесть миллиардов двести сорок два  миллиона семьсот восемьдесят три тысячи сто 
девяносто пять;
2) четыреста три миллиона тридцать восемь тысяч сорок девять;
3) сорок восемь миллиардов семь миллионов два.
2. Сравните числа:      1) 6 894 и 6 983;               2)   12 471 и 12 324.
3. Начертите координатный луч и отметьте на нём точки, соответствующие числам 3, 4, 6, 8.
4. Начертите отрезок АВ, длина которого равна 4 см 8 мм, отметьте на нём точку D. Запишите все 
отрезки, образовавшиеся на рисунке, и измерьте их длины.
5. Точка T принадлежит отрезку МN, МT = 19 см, отрезок TN на 18 см меньше отрезка МT. Найдите
длину отрезка МN. 
6. Запишите цифру, которую можно поставить вместо звёздочки, чтобы образовалось верное 
неравенство (рассмотрите все возможные случаи):
2) 2 *14  ¿  2 316;                          2) 4 78*  ¿  4 785.
7. На отрезке SK длиной 30 см отметили точки A и B так, что SA = 14 см, BK =19 см. Чему равна 
длина отрезка AB?
8. Сравните:  1) 3 986 г и 4 кг;        2) 586 см и 6 м. 1. Запишите цифрами число:
1) сорок семь миллиардов двести девяносто три  миллиона восемьсот пятьдесят шесть тысяч сто 
Вариант  3
двадцать четыре;
2) триста семь миллионов семьдесят восемь тысяч двадцать три;
3) восемьдесят пять миллиардов шесть миллионов пять.
2. Сравните числа:      1) 7 356 и 7 421;               2)   17 534 и 17 435.
3. Начертите координатный луч и отметьте на нём точки, соответствующие числам 2, 4, 6, 9.
4. Начертите отрезок MN, длина которого равна 6 см 4 мм, отметьте на нём точку A. Запишите все 
отрезки, образовавшиеся на рисунке, и измерьте их длины.
5. Точка E принадлежит отрезку CK, CE = 15 см, отрезок EK на 24 см больше отрезка CE. Найдите 
длину отрезка CK. 
6. Запишите цифру, которую можно поставить вместо звёздочки, чтобы образовалось верное 
неравенство (рассмотрите все возможные случаи):
1) 3 344  ¿  3 34*;                          2) 2 724  ¿  * 619.
7. На отрезке AC длиной 60 см отметили точки E и F так, что AE = 32 см, FC =34 см. Чему равна 
длина отрезка EF?
8. Сравните:  1) 6 т и 5 934кг;        2) 4 м и 512 см.
Вариант  4
1. Запишите цифрами число:
1) восемьдесят шесть миллиардов пятьсот сорок один миллион триста семьдесят две тысячи 
триста сорок два;
2) шестьсот пять миллионов восемьдесят три тысячи  десять;
3) сорок четыре миллиарда девять миллионов три.
2. Сравните числа:      1) 9 561 и 9 516;               2)   18 249 и 18 394.
3. Начертите координатный луч и отметьте на нём точки, соответствующие числам 2, 5, 8, 10.
4. Начертите отрезок АВ, длина которого равна 7 см 8 мм, отметьте на нём точку D. Запишите все 
отрезки, образовавшиеся на рисунке, и измерьте их длины.
5. Точка A принадлежит отрезку BM, BA = 25 см, отрезок AM на 9 см меньше отрезка BA. Найдите 
длину отрезка BM. 
6. Запишите цифру, которую можно поставить вместо звёздочки, чтобы образовалось верное 
неравенство (рассмотрите все возможные случаи):
1) 5 64*   ¿  5 646;                          2) 1 4*2  ¿  1 431.
7. На отрезке OP длиной 50 см отметили точки M и N так, что OM = 24 см, NP =38 см. Чему равна 
длина отрезка M N?
8. Сравните:  1) 8 км и 7 962 м;        2) 60 см и 602 мм.
Сложение и вычитание натуральных чисел. Числовые и буквенные
Контрольная работа № 2
выражения. Формулы.
Вариант  1 1. Вычислите:   1) 15 327+ 496 383;       2) 38 020 405 – 9 497 653.
2. На одной стоянке было 143 автомобиля, что на 17 автомобилей больше, чем на второй. 
Сколько автомобилей было на обеих стоянках?
3. Выполните сложение, выбирая удобный порядок вычислений:
(325 + 791) + 675;                           2) 428 + 856 + 572 + 244.
1)
4. Проверьте, верно ли неравенство:
1 674 – (736 + 328)  ¿  2 000 – (1 835 – 459).
5. Найдите значение  по формуле = 4 – 16 при = 8.
6. Упростите выражение 126 + + 474 и найдите его значение при = 278.
7. Вычислите:
1) 4 м 73 см + 3 м 47 см; 2) 12 ч 16 мин – 7 ч 32 мин.

8. Найдите значение выражения, выбирая удобный порядок вычислений:
1)
(713 + 529) – 413;                           2) 624 – (137 + 224).
Вариант  2
1. Вычислите:   1) 17 824+ 128 356;       2) 42 060 503 – 7 456 182.
2. На одной улице 152 дома, что на 18 домов меньше, чем на другой. Сколько всего домов на 
обеих улицах?
3. Выполните сложение, выбирая удобный порядок вычислений:
(624 + 571) + 376;                           2) 212 + 497 + 788 + 803.
1)
4. Проверьте, верно ли неравенство:
1 826 – (923 + 249)  ¿  3 000 – (2 542 – 207).
5. Найдите значение  по формуле = 40 – 7 при = 4.
6. Упростите выражение 235 + y + 465 и найдите его значение при y = 153.
7. Вычислите:
1) 6 м 23 см + 5 м 87 см; 2) 14 ч 17 мин – 5 ч 23 мин.
8. Найдите значение выражения, выбирая удобный порядок вычислений:
1)
(837 + 641) – 537;                           2) 923 – (215 + 623).     
Вариант  3
1. Вычислите:   1) 26 832 + 573 468;       2) 54 073 507 – 6 829 412.
2. В одном классе 37 учащихся, что на 9 человек больше, чем во втором. Сколько всего 
учащихся в обоих классах?
3. Выполните сложение, выбирая удобный порядок вычислений:
(736 + 821) + 264;                           2) 573 + 381 + 919 + 627.
1)
4. Проверьте, верно ли неравенство:
2 491 – (543 + 1 689)  ¿  1 000 – (931 – 186).
3
5. Найдите значение  по формуле = + 18 при = 5.
6. Упростите выражение 433 + + 267 и найдите его значение при = 249.
7. Вычислите:
1) 7 м 23 см + 4 м 81 см; 2) 6 ч 38 мин – 4 ч 43 мин. 8. Найдите значение выражения, выбирая удобный порядок вычислений:
1) (674 + 245) – 374;                           2) 586 – (217 + 186).
Вариант  4
1. Вычислите:   1) 19 829 + 123 471;       2) 61 030 504 – 8 695 371.
2. На одной книжной полке стоят 23 книги, что на 5 книг меньше, чем на другой. Сколько всего 
книг стоит на обеих полках?
3. Выполните сложение, выбирая удобный порядок вычислений:
(349 + 856) + 651;                           2) 166 + 452 + 834 + 748.
1)
4. Проверьте, верно ли неравенство:
1 583 – (742 + 554)  ¿ 1 000 – (883 – 72).
5. Найдите значение  по формуле = 16 + 8
6. Упростите выражение 561 + + 139 и найдите его значение при = 165.
7. Вычислите:
при = 7.

1) 9 м 41 см + 4 м 72 см; 2) 18 ч 18 мин – 5 ч 24 мин.
1) (563 + 721) – 363;                           2) 982 – (316 + 582).
8. Найдите значение выражения, выбирая удобный порядок вычислений:

Контрольная работа № 3
Уравнение. Угол. Многоугольники.
Вариант  1
1. Постройте угол МКА, величина которого равна 74 ° . Проведите произвольно луч КС между 

сторонами угла МКА. Запишите образовавшиеся углы и измерьте их величины.
2. Решите уравнение:      1)  +37 = 81 2) 150 – = 98.
3. Одна из сторон треугольника равна 24 см, вторая – в 4 раза короче первой, а
третья – на 16 см длиннее второй. Вычислите периметр треугольника.
4. Решите уравнение: 1) (34 + ) – 83 = 42 2) 45 – – 16) = 28.
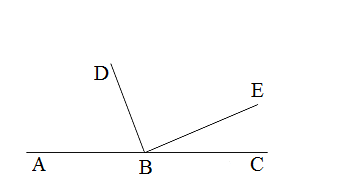
5. Из вершины развёрнутого угла АВС (см рис.) проведены два луча ВD и ВЕ так,
(

что ∠АВЕ = 154 ° , ∠DВС = 128 ° . Вычислите градусную меру угла DВЕ.
6. Какое число надо подставить вместо , чтобы корнем уравнения
52 – – ) = 24 было число 40?
( 1. Постройте угол ABC, величина которого равна 168 ° . Проведите произвольно луч BM между 
Вариант  2
сторонами угла ABC. Запишите образовавшиеся углы и измерьте их величины.
2. Решите уравнение:      1) 21 +  = 58 2) – 135 = 76.
3. Одна из сторон треугольника равна 32 см, вторая – в 2 раза короче первой, а
третья – на 6 см короче первой. Вычислите периметр треугольника.
= 64 2) 31 – ( + 11) = 18.
4. Решите уравнение: 1) (96 – ) – 15
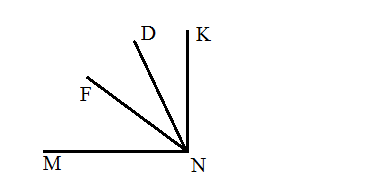
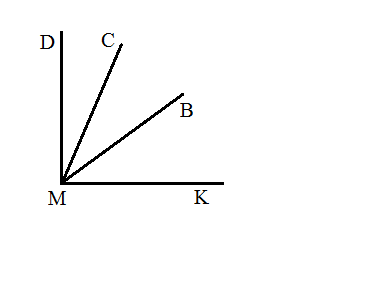
5. Из вершины прямого угла MNK (см рис.) проведены два луча ND и NE так, что

∠MND = 73 ° , ∠KNF = 48 ° . Вычислите градусную меру угла DNF.
6. Какое число надо подставить вместо , чтобы корнем уравнения
64 – – ) = 17 было число 16?
(

1. Постройте угол FDK, величина которого равна 56 ° . Проведите произвольно луч DT между 
Вариант  3
сторонами угла FDK. Запишите образовавшиеся углы и измерьте их величины.
2. Решите уравнение:      1)  + 42 = 94 2) 284 – = 121
3. Одна из сторон треугольника равна 12 см, вторая – в 3 раза длиннее первой,
а третья – на 8 см короче второй. Вычислите периметр треугольника.
4. Решите уравнение: 1) (41 + ) – 12 = 83 2) 62 – – 17) = 31.
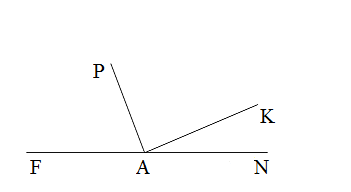
5. Из вершины развёрнутого угла FAN (см рис.) проведены два луча AK и AP так,
(

.
что ∠NAP = 110 ° , ∠FAK = 132 ° . Вычислите градусную меру угла PAK.
6. Какое число надо подставить вместо , чтобы корнем уравнения
(69 – ) – = 23

было число 12? 1. Постройте угол NMC, величина которого равна 58 ° . Проведите произвольно луч MB между 
Вариант  4
сторонами угла NMC. Запишите образовавшиеся углы и измерьте их величины.
2. Решите уравнение:      1)  + 53 = 97 2) 142 – = 76
3. Одна из сторон треугольника равна 30 см, вторая – в 5 раза короче первой, а
третья – на 22 см длиннее второй. Вычислите периметр треугольника.
4. Решите уравнение: 1) (58 + ) – 23 = 96 2) 54 – – 19) = 35.
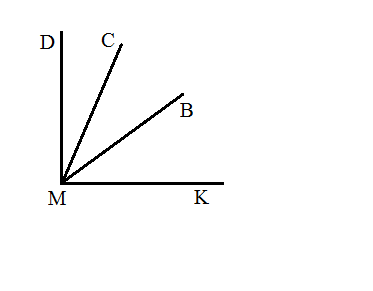
5. Из вершины прямого угла DMK (см рис.) проведены два луча MB и MC так,
(

.
что ∠DMB = 51 ° , ∠KMC = 65 ° . Вычислите градусную меру угла BMC.
6. Какое число надо подставить вместо , чтобы корнем уравнения
( – ) – 14 = 56

было число 5?
Умножение и деление натуральных чисел. Свойства умножения.
Контрольная работа № 4
Вариант 1
1. Вычислите:
1) 36 ∙ 2 418;                               3) 1 456 : 28;
2) 175 ∙ 204;                                4) 177 000 : 120.
2. Найдите значение выражения:   (326 ∙ 48 – 9 587) : 29.
3. Решите уравнение:
1)  ∙ 14 = 364;        2) 324 :  = 9;           3) 19 ­ 12 = 126.
4. Найдите значение выражения наиболее удобным способом:
1) 25 ∙ 79 ∙ 4;                                2) 43 ∙ 89 + 89 ∙ 57.
5. Купили 7 кг конфет и 9 кг печенья, заплатив за всю покупку 1 200 р. Сколько стоит 1 кг 
печенья, если 1 кг конфет стоит 120 р? 6. С одной станции одновременно в одном направлении отправились два поезда. Один из поездов 
двигался со скоростью 56 км/ч, а второй – 64 км/ч. Какое расстояние будет между поездами 
через 6 ч после начала движения?
7. Сколькими нулями оканчивается произведение всех натуральных чисел от 19 до 35 
включительно?
Вариант 2
1. Вычислите:
1) 24 ∙ 1 246;                               3) 1 856 : 32;
2) 235 ∙ 108;                                4) 175 700 : 140.
2. Найдите значение выражения:   (625 ∙ 25 – 8 114) : 37.
3. Решите уравнение:
1)  ∙ 28 = 336;        2) 312 :  = 8;           3) 16  ­ 11 = 225.
4. Найдите значение выражения наиболее удобным способом:
1) 2 ∙ 83 ∙ 50;                                2) 54 ∙ 73 + 73 ∙ 46.
5. Для проведения ремонта электрической проводки купили 16 одинаковых мотков 
алюминиевого и 11 одинаковых мотков медного провода. Общая длина купленного провода 
составляла 650 м. Сколько метров алюминиевого провода было в мотке, если медного провода
в одном мотке было 30 м?
6. Из одного города одновременно в одном направлении выехали два автомобиля. Один из них 
двигался со скоростью 74 км/ч, а второй – 68 км/ч. Какое расстояние будет между 
автомобилями через 4 ч после начала движения?
7. Сколькими нулями оканчивается произведение всех натуральных чисел от 23 до 42 
включительно?
Вариант 3
1. Вычислите:
1) 32 ∙ 1 368;                               3) 1 664 : 26;
2) 145 ∙ 306;                                4) 216 800 : 160.
2. Найдите значение выражения:   (546 ∙ 31 – 8 154) : 43.
3. Решите уравнение:
1)  ∙ 22 = 396;        2) 318 :  = 6;           3) 19  ­ 7 = 144.
4. Найдите значение выражения наиболее удобным способом:
2) 5 ∙ 97 ∙ 20;                                2) 68 ∙ 78  ­  78 ∙ 58.
5. В автомобиль погрузили 5 одинаковых мешков сахара и 3 одинаковых мешка муки. Оказалось,
что общая масса груза равна 370 кг. Какова масса одного мешка муки, если масса одного 
мешка сахара равна 50 кг?
6. Из одного села одновременно в одном направлении отправились пешеход и велосипедист. 
Пешеход двигался со скоростью 3 км/ч, а велосипедист – 12 км/ч. Какое расстояние будет 
между ними через 3 ч после начала движения?
7. Сколькими нулями оканчивается произведение всех натуральных чисел от 34 до 53 
включительно? Вариант 4
1. Вычислите:
1) 28 ∙ 2 346;                               3) 1 768 : 34;
2) 185 ∙ 302;                                4) 220 500 : 180.
2. Найдите значение выражения:   (224 ∙ 46 – 3 232) : 34.
3. Решите уравнение:
1)  ∙ 16 = 384;        2) 371 :  = 7;           3) 22  ­ 14 = 112.
4. Найдите значение выражения наиболее удобным способом:
1) 2 ∙ 87 ∙ 50;                                2) 167 ∙ 92  ­  92 ∙ 67.
5. В школьную столовую завезли 8 одинаковых ящиков яблок и 6 одинаковых ящиков 
апельсинов. Сколько килограммов апельсинов было в одном ящике, если всего было 114 кг 
яблок и апельсинов, а яблок в каждом ящике было 9 кг?
6. От одной пристани одновременно в одном направлении отплыли лодка и катер. Лодка плыла 
со скоростью 14 км/ч, а катер – 21 км/ч. Какое расстояние будет между ними через 5 ч после 
начала движения?
7. Сколькими нулями оканчивается произведение всех натуральных чисел от 41 до 64 
включительно?
Деление с остатком. Площадь прямоугольника. Прямоугольный
Контрольная работа № 5
параллелепипед и его объем. Комбинаторные задачи.
Вариант 1
1. Выполните деление с остатком:    478 : 15.
2. Найдите площадь прямоугольника, одна сторона  которого равна 14 см, а вторая сторона в 
3 раза больше первой. 
3. Вычислите объем и площадь поверхности куба с ребром 3 см.
4. Длина прямоугольного параллелепипеда равна 18 см, ширина – в 2 раза меньше длины, а 
высота – на 11 см больше ширины. Вычислите объем параллелепипеда.
5. Чему равно делимое, если делитель равен 11, неполное частное – 7, а остаток – 6? 
6. Поле прямоугольной формы имеет площадь 6 га. Ширина поля 150 м. Вычислите периметр
поля.
7. Запишите все трёхзначные числа, для записи которых используются только цифры 5, 6 и 0 
(цифры не могут повторяться).
8. Сумма длин всех рёбер прямоугольного параллелепипеда равна 116 см, а два его  
измерения – 12 см и 11 см. Найдите третье измерение параллелепипеда.
1. Выполните деление с остатком:    376 : 18.
Вариант 2 2. Найдите площадь прямоугольника, одна сторона  которого равна 21 см, а вторая сторона в 
3 раза меньше первой. 
3. Вычислите объем и площадь поверхности куба с ребром 4 дм.
4. Ширина прямоугольного параллелепипеда равна 6 см, длина – в 5 раз больше ширины, а 
высота – на 5 см меньше длины. Вычислите объем параллелепипеда.
5. Чему равно делимое, если делитель равен 17, неполное частное – 5, а остаток – 12? 
6. Поле прямоугольной формы имеет площадь 3 га, его длина – 200 м. Вычислите периметр 
поля.
7. Запишите все трёхзначные числа, для записи которых используются только цифры 0, 9 и 4 
(цифры не могут повторяться).
8. Сумма длин всех рёбер прямоугольного параллелепипеда равна 80 см, а два его  измерения
– 10 см и 4 см. Найдите третье измерение параллелепипеда.
Вариант 3
1. Выполните деление с остатком:    516 : 19.
2. Найдите площадь прямоугольника, одна сторона  которого равна 17 см, а вторая сторона в 
2 раза больше первой. 
3. Вычислите объем и площадь поверхности куба с ребром 5 дм.
4. Высота прямоугольного параллелепипеда равна 20 см, длина – на 4 см больше высоты, а 
ширина – в 2 раза меньше длины. Вычислите объем параллелепипеда.
5. Чему равно делимое, если делитель равен 14, неполное частное – 8, а остаток – 9? 
6. Поле прямоугольной формы имеет площадь 7 га, его длина – 350 м. Вычислите периметр 
поля.
7. Запишите все трёхзначные числа, для записи которых используются только цифры 1, 2 и 0 
(цифры не могут повторяться).
8. Сумма длин всех рёбер прямоугольного параллелепипеда равна 100 дм, а два его  
измерения – 8 дм и 13 дм. Найдите третье измерение параллелепипеда.
Вариант 4
1. Выполните деление с остатком:    610 : 17.
2. Найдите площадь прямоугольника, одна сторона  которого равна 45 см, а вторая сторона в 
5 раз меньше первой. 
3. Вычислите объем и площадь поверхности куба с ребром 2 см.
4. Длина прямоугольного параллелепипеда равна 20 см, высота – в 4 раза меньше длины, а 
ширина – на 7 см больше высоты. Вычислите объем параллелепипеда.
5. Чему равно делимое, если делитель равен 15, неполное частное – 6, а остаток – 14? 
6. Поле прямоугольной формы имеет площадь 4 га, его ширина – 50 м. Вычислите периметр 
поля.
7. Запишите все трёхзначные числа, для записи которых используются только цифры 7, 0 и 8 
(цифры не могут повторяться).
8. Сумма длин всех рёбер прямоугольного параллелепипеда равна 72 см, а два его  измерения
– 6 см и 8 см. Найдите третье измерение параллелепипеда. Контрольная работа № 6
Обыкновенные дроби
Вариант 1
1. Сравните числа:
13
24 ;                 2) 
17
24  и 
1)
16
19     и 1;                     3) 
47
35    и  1.
2. Выполните действия:
15
28 −¿  
1)
3
28  + 
3 7
23−1 4
2)
23  + 5 
28 ;                                     3)  1−17
11
20 ;
9
23 ;                             4)  5 3
8−3 5
8  .
3. В саду растёт 72 дерева, из них 
3
8  составляют яблони. Сколько яблонь растёт в саду?
4. Кирилл прочёл 56 страниц, что составило 
7
12  книги. Сколько страниц было в книге?
5. Преобразуйте в смешанное число дробь:
7
3 ;              2) 
30
7  .
1)
6. Найдите все натуральные значения , при которых верно неравенство  2 3
7 <¿  
x
7 <3 1
7
.
7. Каково наибольшее натуральное значение  n, при котором верно неравенство n  ¿
100
19  ?
8. Найдите все натуральные значения , при которых одновременно выполняются условия: 
1
a  правильная, а дробь  
7
a   неправильная.
дробь
1. Сравните числа:
Вариант 2
1¿ 9
17  и 
14
17 ;                 2) 
31
32     и 1;                     3) 
23
21    и  1.
2. Выполните действия:
1¿ 5
26  + 
11
26 −¿  
7
26 ;                                     3)  1−15
17 ; 2¿5 8
21−2 3
21  + 1 
5
21 ;                             4)  6 4
11−3 7
11  .
3. В гараже стоят 63 машины, из них 
5
7 составляют легковые. Сколько легковых машин 
стоит в гараже?
4. В классе 12 учеников изучают французский язык, что составляет 
2
5  всех учеников 
класса. Сколько учеников в классе?
5. Преобразуйте в смешанное число дробь:
1¿ 12
5 ;              2) 
25
9  .
6. Найдите все натуральные значения , при которых верно неравенство  1 2
5 <¿  
5 <2 1
x
5
.
7. Каково наименьшее натуральное значение  n, при котором верно неравенство n  ¿
100
17  ?
8. Найдите все натуральные значения , при которых одновременно выполняются условия: 
a
11  правильная, а дробь  
a
6   неправильная.
дробь
1. Сравните числа:
Вариант 3
1¿ 16
31  и 
11
31 ;                 2) 
21
23     и 1;                     3) 
37
33    и  1.
2. Выполните действия:
1¿ 7
27  + 
16
27 −¿  
27 ;                                     3)  1−18
19
27 ;
2¿4 5
19−2 2
19  + 7 
19 ;                             4)  6 2
9
9−4 5
9  .
3. В классе 36 учеников, из них 
11
12  занимаются спортом. Сколько учеников занимаются 
спортом?
4. Ваня собрал 16 вёдер картофеля, что составляет 
картофеля составляет урожай?
5. Преобразуйте в смешанное число дробь:
8
19  всего урожая. Сколько вёдер 1¿ 11
4 ;              2) 
43
8  .
6. Найдите все натуральные значения , при которых верно неравенство  2 4
9 <¿  
x
9 <3 1
9
.
7. Каково наибольшее натуральное значение  n, при котором верно неравенство n  ¿
100
23  ?
8. Найдите все натуральные значения , при которых обе дроби  
a
5   и   
9
a   
одновременно будут неправильными.
Вариант 4
1. Сравните числа:
1¿ 12
19  и 
14
19 ;                 2) 
28
35     и 1;                     3) 
43
39    и  1.
2. Выполните действия:
1¿ 8
29  + 
14
29 −¿  
17
29 ;                                     3)  1− 14
19 ;
2¿7 5
31−4 2
31  + 2 
11
31 ;                             4)  7 3
7−2 6
7  .
3. В пятых  классах 64 ученика, из них 
3
16 составляют отличники. Сколько отличников в 
пятых классах?
4. Мама приготовила вареники с творогом, а Коля съел 9 штук, что составляет 
3
17  всех 
вареников. Сколько вареников приготовила мама?
5. Преобразуйте в смешанное число дробь:
1¿ 15
6 ;              2) 
39
12  .
6. Найдите все натуральные значения , при которых верно неравенство 2
5
8 <¿  
8 <3 3
x
8
 .
7. Каково наименьшее натуральное значение  n, при котором верно неравенство n  ¿
100
29  ? 8. Найдите все натуральные значения , при которых одновременно выполняются условия: 
a
4   будет неправильная, а дробь  
a
9   правильная.
дробь
Контрольная работа № 7
Понятие о десятичной дроби. Сравнение, округление, сложение и вычитание
десятичных дробей.
Вариант 1
1. Сравните:     1) 14,396   и 14,4;                      2) 0,657  и  0, 6565.
2. Округлите:   1)  16,76 до десятых;               2) 0,4864 до тысячных.
3. Выполните действия:    1)    3,87 + 32,496;       2) 23,7 – 16,48;          3) 20 – 12,345.
4. Скорость катера по течению реки равна 24,2 км/ч, а собственная скорость  катера – 22,8 км/ч. 
Найдите скорость катера против течения реки.
5. Вычислите, записав данные величины в килограммах:
1) 3,4 кг + 839 г;                       2) 2 кг 30 г – 1956 г.
6. Одна сторона треугольника равна 5,6 см, что на 1,4 см больше второй стороны и на 0,7 см меньше 
третьей. Найдите периметр треугольника.
7. Напишите три числа, каждое из которых больше 5,74 и меньше 5,76.
8. Найдите значение выражения, выбирая удобный порядок вычислений:
1)
(8,63 + 3,298) – 5,63;                         2) 0,927 – (0,327 + 0,429).
Вариант 2
1. Сравните:     1) 17,497   и 17,5;                      2) 0,346  и  0, 3458.
2. Округлите:   1)  12,88 до десятых;               2) 0,3823 до сотых.
3. Выполните действия:    1)    5,62 + 43,299;       2) 25,6 – 14,52;          3) 30 – 14,265.
4. Скорость катера против течения реки равна 18,6 км/ч, а собственная скорость 
 катера – 19,8 км/ч. Найдите скорость катера по течению реки.
5. Вычислите, записав данные величины в метрах:
1) 8,3 м + 784 см;                       2) 5 м 4 см – 385 см.
6. Одна сторона треугольника равна 4,5 см, что на 3,3 см меньше второй стороны и на 0,6 см больше 
третьей. Найдите периметр треугольника.
7. Напишите три числа, каждое из которых больше 3,82 и меньше 3,84.
8. Найдите значение выражения, выбирая удобный порядок вычислений:
1)
(5,94 + 2,383) – 3,94;                         2) 0,852 – (0,452 + 0,214). 
Вариант 3
1. Сравните:     1) 12,598   и 12,6;                      2) 0,257  и  0, 2569.
2. Округлите:   1)  17,56 до десятых;               2) 0,5864 до тысячных.
3. Выполните действия:    1)    4,36 + 27,647;       2) 32,4 – 17,23;          3) 50 – 22,475. 4. Скорость катера по течению реки равна 19,6 км/ч, а собственная скорость  катера – 18,3 км/ч. 
Найдите скорость катера против течения реки.
5. Вычислите, записав данные величины в центнерах:
1) 6,7 ц + 584 кг;                       2) 6 ц 2 кг – 487 кг.
6. Одна сторона треугольника равна 3,7 см, что на 0,9 см больше второй стороны и на 1,2 см меньше 
третьей. Найдите периметр треугольника.
7. Напишите три числа, каждое из которых больше 7,87 и меньше 7,89.
8. Найдите значение выражения, выбирая удобный порядок вычислений:
1)
(6,73 + 4,594) – 2,73;                         2) 0,791 – (0,291 + 0,196). 
Вариант 4
1. Сравните:     1) 16,692   и 16,7;                      2) 0,745  и  0, 7438.
2. Округлите:   1)  24,87 до десятых;               2) 0,8653 до тысячных.
3. Выполните действия:    1)    6,72 + 54,436;       2) 27,6 – 15,72;          3) 40 – 11,825.
4. Скорость катера против течения реки равна 17,8 км/ч, а собственная скорость 
 катера – 19,4 км/ч. Найдите скорость катера по течению реки.
5. Вычислите, записав данные величины в метрах:
2) 2,8 м + 524 см;                       2) 4 м 6 см – 257 см.
6. Одна сторона треугольника равна 5,1 см, что на 2,1 см меньше второй стороны и на 0,7 см больше 
третьей. Найдите периметр треугольника.
7. Напишите три числа, каждое из которых больше 1,34 и меньше 1,36.
8. Найдите значение выражения, выбирая удобный порядок вычислений:
2)
(7,86 + 4,183) – 2,86;                         2) 0,614 – (0,314 + 0,207). 
Контрольная работа № 8
Умножение и деление десятичных дробей
Вариант 1
1. Вычислите:
1) 0,024 ∙ 4,5;                           3)  2,86 :  100;                             5)  0,48 : 0,8;
2) 29,41 ∙ 1 000;                       4)   4 : 16;                                    6)   9,1 : 0,07.
2. Найдите значение выражения:     (4 – 2,6) ∙ 4,3 + 1,08 : 1,2.
3. Решите уравнение:    2,4 ( + 0,98) = 4,08.
4. Моторная лодка плыла 1,4 ч по течению реки и 2,2 ч против течения. Какой путь преодолела 
лодка за всё время движения, если скорость течения равна 1,7 км/ч, а собственная скорость лодки
– 19,8 км/ч?
5. Если в некоторой десятичной дроби перенести запятую вправо через одну цифру, то она 
увеличится на 14,31. Найдите эту дробь.
Вариант 2
1. Вычислите:
1) 0,036 ∙ 3,5;                           3)  3,68 :  100;                             5)  0,56 : 0,7;
2) 37,53 ∙ 1 000;                       4)   5 : 25;                                    6)   5,2 : 0,04.
2. Найдите значение выражения:     (5 – 2,8) ∙ 2,4 + 1,12 : 1,6.
3. Решите уравнение:    0,084 :  (6,2 – )  = 1,2. 4. Катер плыл 1,6 ч против течения реки и 2,4 ч по течению. На сколько больше проплыл катер, 
двигаясь по течению реки, чем против течения, если скорость течения реки равна 2,1 км/ч, а 
собственная скорость катера – 28,2 км/ч?
5. Если в некоторой десятичной дроби перенести запятую влево через одну цифру, то она 
уменьшится на 23,76. Найдите эту дробь.
Вариант 3
1. Вычислите:
1) 0,064 ∙ 6,5;                           3)  4,37 :  100;                             5)  0,63 : 0,9;
2) 46,52 ∙ 1 000;                       4)   6 : 15;                                    6)   7,2 : 0,03.
2. Найдите значение выражения:     (6 – 3,4) ∙ 1,7 + 1,44 : 1,6.
3. Решите уравнение:    1,6 ( + 0,78) = 4,64.
4. Теплоход  плыл 1,8 ч против течения реки и 2,6 ч по течению. Какой путь преодолел теплоход за 
всё время движения, если скорость течения равна 2,5 км/ч, а собственная скорость теплохода – 
35,5 км/ч?
5. Если в некоторой десятичной дроби перенести запятую вправо через одну цифру, то она 
увеличится на 15,93. Найдите эту дробь.
Вариант 4
1. Вычислите:
1) 0,096 ∙ 5,5;                           3)  7,89 :  100;                             5)  0,76 : 0,4;
2) 78,53 ∙ 100;                          4)   6 : 24;                                    6)   8,4 : 0,06.
2. Найдите значение выражения:     (7 – 3,6) ∙ 2,8 + 1,32 : 2,2.
3. Решите уравнение:    0,144 :  (3,4 – )  = 2,4.
4. Моторная лодка плыла 3,6 ч против течения реки и 1,8 ч по течению. На сколько километров 
больше проплыла лодка, двигаясь против течения , чем по течению, если скорость течения реки 
равна 1,2 км/ч, а собственная скорость лодки – 22,4 км/ч?
5. Если в некоторой десятичной дроби перенести запятую влево через одну цифру, то она 
уменьшится на 29,52. Найдите эту дробь.
Контрольная работа № 9
Среднее арифметическое. Проценты.
Вариант 1
1. Найдите среднее арифметическое чисел:  32,6; 38,5; 34; 35,3.
2. Площадь поля равна 300 га. Рожью засеяли 18 % поля. Сколько гектаров поля засеяли рожью?
3. Петя купил книгу за 90 р., что составляет 30 % всех денег, которые у него были. Сколько 
денег было у Пети?
4. Лодка плыла 2 ч со скоростью 12,3 км/ч и 4 ч со скоростью 13,2 км/ч. Найдите среднюю 
скорость лодки на всём пути.
5. Турист прошёл за три дня 48 км. В первый день он прошёл 35 % всего маршрута. Путь 
пройденный в первый день, составляет 80 % расстояния , пройденного во второй день. 
Сколько километров прошёл турист в третий день?
6. В первый день Петя прочитал 40 % всей книги, во второй – 60 % остального, а в третий  ­ 
оставшиеся 144 страницы. Сколько всего страниц в книге? 1. Найдите среднее арифметическое чисел:  26,3; 20,2; 24,7; 18.
2. В школе 800 учащихся. Сколько пятиклассников в этой школе, если известно, что их 
Вариант 2
количество составляет 12 % количества всех учащихся?
3. Насос перекачал в бассейн 42  м3
 воды, что составляет 60 % объёма бассейна. Найдите 
объём бассейна.
4. Автомобиль ехал 3 ч со скоростью 62,6 км/ч и 2 ч со скоростью 65 км/ч. Найдите среднюю 
скорость автомобиля на всём пути.
5. Токарь за три дня изготовил 80 деталей. В первый день он выполнил 30 % всей работы. 
Известно, что количество деталей, изготовленных в первый день, составляет 60 % количества 
деталей , изготовленных во второй день. Сколько деталей изготовил токарь в третий день?
6. В первый день тракторная бригада вспахала  30 % площади всего поля, во второй –  75% 
остального, а в третий  ­ оставшиеся 14 га. Найдите площадь поля. 
Вариант 3
1. Найдите среднее арифметическое чисел:  26,4; 42,6; 31,8; 15.
2. В магазин завезли 600 кг овощей. Картофель составляет 24% всех завезённых овощей. Сколько
килограммов картофеля завезли в магазин?
3. За первый день турист прошёл расстояние 18 км, что составляет 40 % всего пути, который он 
должен преодолеть. Найдите длину пути, который должен пройти турист.
4. Катер плыл 1,5 ч со скоростью 34 км/ч и 2,5 ч со скоростью 30 км/ч. Найдите среднюю 
скорость катера на всём пути.
5. За три дня оператор набрал на компьютере 60 страниц. В первый день было выполнено    35 % 
всей работы. Объём работы, выполненной в первый день, составляет 70 % работы, 
выполненной во второй день. Сколько страниц было набрано в третий день?
6. За первый час было продано 84 % всего мороженого, за второй – 78 % остального, а за третий 
– оставшиеся 44 порции. Сколько порций мороженого было продано за три часа?
 
Вариант 4
1. Найдите среднее арифметическое чисел:  43,6; 21,8; 32,4; 11.
2. Площадь парка равна 40 га. Площадь озера составляет 15 % площади парка. Найдите площадь 
озера.
3. За первый час движения автомобиль преодолел расстояние 72 км, что составляет 24 % длины 
всего пути, который ему надо проехать. Найдите общий путь, который преодолел автомобиль.
4. Черепаха ползла 2 ч со скоростью 15,3 м/ч и 3 ч со скоростью 12, 4 м/ч. Найдите среднюю 
скорость черепахи на всём пути.
5. Три насоса наполнили водой бассейн объёмом 320  м3
. Первый насос заполнил бассейн на 
30 %, что составляет 80 % объёма воды, которую перекачал второй насос. Найдите объём 
воды, которую перекачал третий насос.
6. В первый день турист прошёл 20% всего пути, во второй – 60 % остального, а в третий – 
оставшиеся 24 км. Найдите длину пути, который прошёл турист за три дня.
Контрольная работа № 10 Обобщение и систематизация знаний учащихся 
за курс математики 5 класса
Вариант 1
1. Найдите значение выражения:  (4,1 – 0,66 : 1,2) ∙ 0,6.
2. Миша шёл из одного села в другое 0,7 ч по полю и 0,9 ч через лес, пройдя всего 5,31 км. С 
какой скоростью шёл Миша через лес, если по полю он двигался со скоростью 4,5 км/ч?
3. Решите уравнение: 9,2 – 6,8 + 0,64 = 1
4. Ширина прямоугольного параллелепипеда равна 4 см, что составляет 
8
15   его длины, а 
высота составляет 40 % длины. Вычислите объем параллелепипеда.
5. Выполните действия:   20 : ( 6 3
14  +  1 11
14 ) – ( 4 1
4  –  2 3
4 ) : 5.
6. Среднее арифметическое четырёх чисел равно 1,4, а среднее арифметическое трёх других 
чисел – 1,75. Найдите среднее арифметическое этих семи чисел.
  
Вариант 2
1. Найдите значение выражения:  (0,49 : 1,4 – 0,325) ∙ 0,8.
2. Катер плыл 0,4 ч по течению реки и 0,6 ч против течения, преодолев всего 16,8 км. С какой 
скоростью плыл катер по течению, если против течения он плыл со скоростью 16 км/ч?
3. Решите уравнение: 7,2 – 5,4 + 0,55 = 1
4. Ширина прямоугольного параллелепипеда равна 3,6 см, что составляет 
высота составляет 42 % длины. Вычислите объем параллелепипеда.
5. Выполните действия:   30 : ( 17 16
19−5 16
19 ) + ( 7 3
5  –  4 4
5 ) : 7.
9
25   его длины, а 
6. Среднее арифметическое трёх чисел равно 2,5, а среднее арифметическое двух других чисел –
1,7. Найдите среднее арифметическое этих пяти чисел.
1. Найдите значение выражения:  (5,25 – 0,63 : 1,4) ∙ 0,4.
2. Пётр шёл из  села к озеру 0,7 ч по одной дороге, а возвратился по другой дороге за  0,8 ч, 
Вариант 3
пройдя всего 6,44 км. С какой скоростью шёл Пётр к озеру, если возвращался он  со 
скоростью 3,5 км/ч?
3. Решите уравнение: 7,8 – 4,6 + 0,8 = 12.
6
25   его длины, а 
4. Ширина прямоугольного параллелепипеда равна 4,8 см, что составляет 
высота составляет 45 % длины. Вычислите объем параллелепипеда.
5. Выполните действия:   10 : ( 2 12
17  +  1 5
17 ) – ( 3 4
5  + 1
3
5 ) : 6.
6. Среднее арифметическое пяти чисел равно 2,3, а среднее арифметическое трёх других чисел –
1,9. Найдите среднее арифметическое этих восьми чисел. Вариант 4
1. Найдите значение выражения:  (4,4 – 0,63 :1,8) ∙ 0,8.
2. Автомобиль ехал 0,9 ч по асфальтированной дороге и 0,6 ч по грунтовой, проехав всего 93,6 
км. С какой скоростью двигался автомобиль по асфальтированной дороге, если по грунтовой 
он ехал со скоростью 48 км/ч?
3. Решите уравнение: 3,23 + 0,97 + 0,74 = 2.
8
25   его длины, а 
4. Ширина прямоугольного параллелепипеда равна 3,2 см, что составляет 
высота составляет 54 % длины. Вычислите объем параллелепипеда.
5. Выполните действия:   50 : ( 14 8
23 +5 15
23 ) – ( 6 1
5  –  2 3
5 ) : 9.
6. Среднее арифметическое шести чисел равно 2,8, а среднее арифметическое четырёх других 
чисел – 1,3. Найдите среднее арифметическое этих десяти чисел.

Контрольные работы по математике УМК Мерзляк А.Г., Полонский В.Б., Якир М.С. 5 класс

Контрольные работы по математике 5 класс

УМК Мерзляк А.Г., Полонский В.Б., Якир М.С.

Контрольная работа № 1

Натуральные числа

Вариант 1

  1. Запишите цифрами число:

  1. шестьдесят пять миллиардов сто двадцать три миллиона девятьсот сорок одна тысяча восемьсот тридцать семь;

  2. восемьсот два миллиона пятьдесят четыре тысячи одиннадцать:

  3. тридцать три миллиарда девять миллионов один.

  1. Сравните числа: 1) 5 678 и 5 489; 2) 14 092 и 14 605.

  2. Начертите координатный луч и отметьте на нём точки, соответствующие числам 2, 5, 7, 9.

  3. Начертите отрезок FK, длина которого равна 5 см 6 мм, отметьте на нём точку C. Запишите все отрезки, образовавшиеся на рисунке, и измерьте их длины.

  4. Точка К принадлежит отрезку МЕ, МК = 19 см, отрезок КЕ на 17 см больше отрезка МК. Найдите длину отрезка МЕ.

  5. Запишите цифру, которую можно поставить вместо звёздочки, чтобы образовалось верное неравенство (рассмотрите все возможные случаи):

  1. 3 78* 3 784; 2) 5 8*5 5 872.

  1. На отрезке CD длиной 40 см отметили точки P и Q так, что CP = 28 см, QD =26 см. Чему равна длина отрезка PQ?

  2. Сравните: 1) 3 км и 2 974 м; 2) 912 кг и 8 ц.

Вариант 2

  1. Запишите цифрами число:

  1. семьдесят шесть миллиардов двести сорок два миллиона семьсот восемьдесят три тысячи сто девяносто пять;

  2. четыреста три миллиона тридцать восемь тысяч сорок девять;

  3. сорок восемь миллиардов семь миллионов два.

  1. Сравните числа: 1) 6 894 и 6 983; 2) 12 471 и 12 324.

  2. Начертите координатный луч и отметьте на нём точки, соответствующие числам 3, 4, 6, 8.

  3. Начертите отрезок АВ, длина которого равна 4 см 8 мм, отметьте на нём точку D. Запишите все отрезки, образовавшиеся на рисунке, и измерьте их длины.

  4. Точка T принадлежит отрезку МN, МT = 19 см, отрезок TN на 18 см меньше отрезка МT. Найдите длину отрезка МN.

  5. Запишите цифру, которую можно поставить вместо звёздочки, чтобы образовалось верное неравенство (рассмотрите все возможные случаи):

  1. 2 *14 2 316; 2) 4 78* 4 785.

  1. На отрезке SK длиной 30 см отметили точки A и B так, что SA = 14 см, BK =19 см. Чему равна длина отрезка AB?

  2. Сравните: 1) 3 986 г и 4 кг; 2) 586 см и 6 м.

Вариант 3

  1. Запишите цифрами число:

  1. сорок семь миллиардов двести девяносто три миллиона восемьсот пятьдесят шесть тысяч сто двадцать четыре;

  2. триста семь миллионов семьдесят восемь тысяч двадцать три;

  3. восемьдесят пять миллиардов шесть миллионов пять.

  1. Сравните числа: 1) 7 356 и 7 421; 2) 17 534 и 17 435.

  2. Начертите координатный луч и отметьте на нём точки, соответствующие числам 2, 4, 6, 9.

  3. Начертите отрезок MN, длина которого равна 6 см 4 мм, отметьте на нём точку A. Запишите все отрезки, образовавшиеся на рисунке, и измерьте их длины.

  4. Точка E принадлежит отрезку CK, CE = 15 см, отрезок EK на 24 см больше отрезка CE. Найдите длину отрезка CK.

  5. Запишите цифру, которую можно поставить вместо звёздочки, чтобы образовалось верное неравенство (рассмотрите все возможные случаи):

  1. 3 344 3 34*; 2) 2 724 * 619.

  1. На отрезке AC длиной 60 см отметили точки E и F так, что AE = 32 см, FC =34 см. Чему равна длина отрезка EF?

  2. Сравните: 1) 6 т и 5 934кг; 2) 4 м и 512 см.

Вариант 4

  1. Запишите цифрами число:

  1. восемьдесят шесть миллиардов пятьсот сорок один миллион триста семьдесят две тысячи триста сорок два;

  2. шестьсот пять миллионов восемьдесят три тысячи десять;

  3. сорок четыре миллиарда девять миллионов три.

  1. Сравните числа: 1) 9 561 и 9 516; 2) 18 249 и 18 394.

  2. Начертите координатный луч и отметьте на нём точки, соответствующие числам 2, 5, 8, 10.

  3. Начертите отрезок АВ, длина которого равна 7 см 8 мм, отметьте на нём точку D. Запишите все отрезки, образовавшиеся на рисунке, и измерьте их длины.

  4. Точка A принадлежит отрезку BM, BA = 25 см, отрезок AM на 9 см меньше отрезка BA. Найдите длину отрезка BM.

  5. Запишите цифру, которую можно поставить вместо звёздочки, чтобы образовалось верное неравенство (рассмотрите все возможные случаи):

  1. 5 64* 5 646; 2) 1 4*2 1 431.

  1. На отрезке OP длиной 50 см отметили точки M и N так, что OM = 24 см, NP =38 см. Чему равна длина отрезка M N?

  2. Сравните: 1) 8 км и 7 962 м; 2) 60 см и 602 мм.

Контрольная работа № 2

Сложение и вычитание натуральных чисел. Числовые и буквенные выражения. Формулы.

Вариант 1

  1. Вычислите: 1) 15 327+ 496 383; 2) 38 020 405 – 9 497 653.

  2. На одной стоянке было 143 автомобиля, что на 17 автомобилей больше, чем на второй. Сколько автомобилей было на обеих стоянках?

  3. Выполните сложение, выбирая удобный порядок вычислений:

  1. (325 + 791) + 675; 2) 428 + 856 + 572 + 244.

  1. Проверьте, верно ли неравенство:

1 674 – (736 + 328) 2 000 – (1 835 – 459).

  1. Найдите значение 𝑎 по формуле 𝑎 = 4𝑏 – 16 при 𝑏 = 8.

  2. Упростите выражение 126 + 𝒙 + 474 и найдите его значение при 𝒙 = 278.

  3. Вычислите:

  1. 4 м 73 см + 3 м 47 см; 2) 12 ч 16 мин – 7 ч 32 мин.

  1. Найдите значение выражения, выбирая удобный порядок вычислений:

  1. (713 + 529) – 413; 2) 624 – (137 + 224).

Вариант 2

  1. Вычислите: 1) 17 824+ 128 356; 2) 42 060 503 – 7 456 182.

  2. На одной улице 152 дома, что на 18 домов меньше, чем на другой. Сколько всего домов на обеих улицах?

  3. Выполните сложение, выбирая удобный порядок вычислений:

  1. (624 + 571) + 376; 2) 212 + 497 + 788 + 803.

  1. Проверьте, верно ли неравенство:

1 826 – (923 + 249) 3 000 – (2 542 – 207).

  1. Найдите значение 𝑝 по формуле 𝑝= 40 – 7𝑞 при 𝑞 = 4.

  2. Упростите выражение 235 + y + 465 и найдите его значение при y = 153.

  3. Вычислите:

  1. 6 м 23 см + 5 м 87 см; 2) 14 ч 17 мин – 5 ч 23 мин.

  1. Найдите значение выражения, выбирая удобный порядок вычислений:

  1. (837 + 641) – 537; 2) 923 – (215 + 623).

Вариант 3

  1. Вычислите: 1) 26 832 + 573 468; 2) 54 073 507 – 6 829 412.

  2. В одном классе 37 учащихся, что на 9 человек больше, чем во втором. Сколько всего учащихся в обоих классах?

  3. Выполните сложение, выбирая удобный порядок вычислений:

  1. (736 + 821) + 264; 2) 573 + 381 + 919 + 627.

  1. Проверьте, верно ли неравенство:

2 491 – (543 + 1 689) 1 000 – (931 – 186).

  1. Найдите значение 𝑦 по формуле 𝑦 = 3𝑥 + 18 при 𝑥 = 5.

  2. Упростите выражение 433 + 𝑎 + 267 и найдите его значение при 𝑎 = 249.

  3. Вычислите:

  1. 7 м 23 см + 4 м 81 см; 2) 6 ч 38 мин – 4 ч 43 мин.

  1. Найдите значение выражения, выбирая удобный порядок вычислений:

  1. (674 + 245) – 374; 2) 586 – (217 + 186).

Вариант 4

  1. Вычислите: 1) 19 829 + 123 471; 2) 61 030 504 – 8 695 371.

  2. На одной книжной полке стоят 23 книги, что на 5 книг меньше, чем на другой. Сколько всего книг стоит на обеих полках?

  3. Выполните сложение, выбирая удобный порядок вычислений:

  1. (349 + 856) + 651; 2) 166 + 452 + 834 + 748.

  1. Проверьте, верно ли неравенство:

1 583 – (742 + 554) 1 000 – (883 – 72).

  1. Найдите значение 𝑥 по формуле 𝑥 = 16 + 8𝑧 при 𝑧 = 7.

  2. Упростите выражение 561 + 𝑏 + 139 и найдите его значение при 𝑏 = 165.

  3. Вычислите:

  1. 9 м 41 см + 4 м 72 см; 2) 18 ч 18 мин – 5 ч 24 мин.

  1. Найдите значение выражения, выбирая удобный порядок вычислений:

  1. (563 + 721) – 363; 2) 982 – (316 + 582).

Контрольная работа № 3

Уравнение. Угол. Многоугольники.

Вариант 1

  1. Постройте угол МКА, величина которого равна 74. Проведите произвольно луч КС между сторонами угла МКА. Запишите образовавшиеся углы и измерьте их величины.

  2. Решите уравнение: 1) 𝑥 +37 = 81 2) 150 – 𝑥 = 98.

  3. Одна из сторон треугольника равна 24 см, вторая – в 4 раза короче первой, а третья – на 16 см длиннее второй. Вычислите периметр треугольника.

  4. Решите уравнение: 1) (34 + 𝑥) – 83 = 42 2) 45 – (𝑥 – 16) = 28.

  5. Из вершины развёрнутого угла АВС (см рис.) проведены два луча ВD и ВЕ так, что ∠АВЕ = 154, ∠DВС = 128. Вычислите градусную меру угла DВЕ.

  6. Какое число надо подставить вместо 𝑎, чтобы корнем уравнения

52 – (𝑎 – 𝑥) = 24 было число 40?

hello_html_m42e43427.png

Вариант 2

  1. Постройте угол ABC, величина которого равна 168. Проведите произвольно луч BM между сторонами угла ABC. Запишите образовавшиеся углы и измерьте их величины.

  2. Решите уравнение: 1) 21 + 𝑥 = 58 2) 𝑥 – 135 = 76.

  3. Одна из сторон треугольника равна 32 см, вторая – в 2 раза короче первой, а третья – на 6 см короче первой. Вычислите периметр треугольника.

  4. Решите уравнение: 1) (96 – 𝑥) – 15 = 64 2) 31 – (𝑥 + 11) = 18.

  5. Из вершины прямого угла MNK (см рис.) проведены два луча ND и NE так, что ∠MND = 73, ∠KNF = 48. Вычислите градусную меру угла DNF.

  6. Какое число надо подставить вместо 𝑎, чтобы корнем уравнения

64 – (𝑎 – 𝑥) = 17 было число 16?

hello_html_54cf3cf5.png

Вариант 3

  1. Постройте угол FDK, величина которого равна 56. Проведите произвольно луч DT между сторонами угла FDK. Запишите образовавшиеся углы и измерьте их величины.

  2. Решите уравнение: 1) 𝑥 + 42 = 94 2) 284 – 𝑥 = 121.

  3. Одна из сторон треугольника равна 12 см, вторая – в 3 раза длиннее первой, а третья – на 8 см короче второй. Вычислите периметр треугольника.

  4. Решите уравнение: 1) (41 + 𝑥) – 12 = 83 2) 62 – (𝑥 – 17) = 31.

  5. Из вершины развёрнутого угла FAN (см рис.) проведены два луча AK и AP так, что ∠NAP = 110, ∠FAK = 132. Вычислите градусную меру угла PAK.

  6. Какое число надо подставить вместо 𝑎, чтобы корнем уравнения

(69 – 𝑎) – 𝑥 = 23 было число 12?

hello_html_5070624a.png

Вариант 4

  1. Постройте угол NMC, величина которого равна 58. Проведите произвольно луч MB между сторонами угла NMC. Запишите образовавшиеся углы и измерьте их величины.

  2. Решите уравнение: 1) 𝑥 + 53 = 97 2) 142 – 𝑥 = 76.

  3. Одна из сторон треугольника равна 30 см, вторая – в 5 раза короче первой, а третья – на 22 см длиннее второй. Вычислите периметр треугольника.

  4. Решите уравнение: 1) (58 + 𝑥) – 23 = 96 2) 54 – (𝑥 – 19) = 35.

  5. Из вершины прямого угла DMK (см рис.) проведены два луча MB и MC так, что ∠DMB = 51, ∠KMC = 65. Вычислите градусную меру угла BMC.

  6. Какое число надо подставить вместо 𝑎, чтобы корнем уравнения

(𝑎 – 𝑥) – 14 = 56 было число 5?

hello_html_6796b78c.png

Контрольная работа № 4

Умножение и деление натуральных чисел. Свойства умножения.

Вариант 1

  1. Вычислите:

  1. 36 ∙ 2 418; 3) 1 456 : 28;

  2. 175 ∙ 204; 4) 177 000 : 120.

  1. Найдите значение выражения: (326 ∙ 48 – 9 587) : 29.

  2. Решите уравнение:

  1. 𝑥 ∙ 14 = 364; 2) 324 : 𝑥 = 9; 3) 19𝑥 — 12𝑥 = 126.

  1. Найдите значение выражения наиболее удобным способом:

  1. 25 ∙ 79 ∙ 4; 2) 43 ∙ 89 + 89 ∙ 57.

  1. Купили 7 кг конфет и 9 кг печенья, заплатив за всю покупку 1 200 р. Сколько стоит 1 кг печенья, если 1 кг конфет стоит 120 р?

  2. С одной станции одновременно в одном направлении отправились два поезда. Один из поездов двигался со скоростью 56 км/ч, а второй – 64 км/ч. Какое расстояние будет между поездами через 6 ч после начала движения?

  3. Сколькими нулями оканчивается произведение всех натуральных чисел от 19 до 35 включительно?

Вариант 2

  1. Вычислите:

  1. 24 ∙ 1 246; 3) 1 856 : 32;

  2. 235 ∙ 108; 4) 175 700 : 140.

  1. Найдите значение выражения: (625 ∙ 25 – 8 114) : 37.

  2. Решите уравнение:

  1. 𝑥 ∙ 28 = 336; 2) 312 : 𝑥 = 8; 3) 16𝑥 — 11𝑥 = 225.

  1. Найдите значение выражения наиболее удобным способом:

  1. 2 ∙ 83 ∙ 50; 2) 54 ∙ 73 + 73 ∙ 46.

  1. Для проведения ремонта электрической проводки купили 16 одинаковых мотков алюминиевого и 11 одинаковых мотков медного провода. Общая длина купленного провода составляла 650 м. Сколько метров алюминиевого провода было в мотке, если медного провода в одном мотке было 30 м?

  2. Из одного города одновременно в одном направлении выехали два автомобиля. Один из них двигался со скоростью 74 км/ч, а второй – 68 км/ч. Какое расстояние будет между автомобилями через 4 ч после начала движения?

  3. Сколькими нулями оканчивается произведение всех натуральных чисел от 23 до 42 включительно?

Вариант 3

  1. Вычислите:

  1. 32 ∙ 1 368; 3) 1 664 : 26;

  2. 145 ∙ 306; 4) 216 800 : 160.

  1. Найдите значение выражения: (546 ∙ 31 – 8 154) : 43.

  2. Решите уравнение:

  1. 𝑥 ∙ 22 = 396; 2) 318 : 𝑥 = 6; 3) 19𝑥 — 7𝑥 = 144.

  1. Найдите значение выражения наиболее удобным способом:

  1. 5 ∙ 97 ∙ 20; 2) 68 ∙ 78 — 78 ∙ 58.

  1. В автомобиль погрузили 5 одинаковых мешков сахара и 3 одинаковых мешка муки. Оказалось, что общая масса груза равна 370 кг. Какова масса одного мешка муки, если масса одного мешка сахара равна 50 кг?

  2. Из одного села одновременно в одном направлении отправились пешеход и велосипедист. Пешеход двигался со скоростью 3 км/ч, а велосипедист – 12 км/ч. Какое расстояние будет между ними через 3 ч после начала движения?

  3. Сколькими нулями оканчивается произведение всех натуральных чисел от 34 до 53 включительно?

Вариант 4

  1. Вычислите:

  1. 28 ∙ 2 346; 3) 1 768 : 34;

  2. 185 ∙ 302; 4) 220 500 : 180.

  1. Найдите значение выражения: (224 ∙ 46 – 3 232) : 34.

  2. Решите уравнение:

  1. 𝑥 ∙ 16 = 384; 2) 371 : 𝑥 = 7; 3) 22𝑥 — 14𝑥 = 112.

  1. Найдите значение выражения наиболее удобным способом:

  1. 2 ∙ 87 ∙ 50; 2) 167 ∙ 92 — 92 ∙ 67.

  1. В школьную столовую завезли 8 одинаковых ящиков яблок и 6 одинаковых ящиков апельсинов. Сколько килограммов апельсинов было в одном ящике, если всего было 114 кг яблок и апельсинов, а яблок в каждом ящике было 9 кг?

  2. От одной пристани одновременно в одном направлении отплыли лодка и катер. Лодка плыла со скоростью 14 км/ч, а катер – 21 км/ч. Какое расстояние будет между ними через 5 ч после начала движения?

  3. Сколькими нулями оканчивается произведение всех натуральных чисел от 41 до 64 включительно?

Контрольная работа № 5

Деление с остатком. Площадь прямоугольника. Прямоугольный параллелепипед и его объем. Комбинаторные задачи.

Вариант 1

  1. Выполните деление с остатком: 478 : 15.

  2. Найдите площадь прямоугольника, одна сторона которого равна 14 см, а вторая сторона в 3 раза больше первой.

  3. Вычислите объем и площадь поверхности куба с ребром 3 см.

  4. Длина прямоугольного параллелепипеда равна 18 см, ширина – в 2 раза меньше длины, а высота – на 11 см больше ширины. Вычислите объем параллелепипеда.

  5. Чему равно делимое, если делитель равен 11, неполное частное – 7, а остаток – 6?

  6. Поле прямоугольной формы имеет площадь 6 га. Ширина поля 150 м. Вычислите периметр поля.

  7. Запишите все трёхзначные числа, для записи которых используются только цифры 5, 6 и 0 (цифры не могут повторяться).

  8. Сумма длин всех рёбер прямоугольного параллелепипеда равна 116 см, а два его измерения – 12 см и 11 см. Найдите третье измерение параллелепипеда.

Вариант 2

  1. Выполните деление с остатком: 376 : 18.

  2. Найдите площадь прямоугольника, одна сторона которого равна 21 см, а вторая сторона в 3 раза меньше первой.

  3. Вычислите объем и площадь поверхности куба с ребром 4 дм.

  4. Ширина прямоугольного параллелепипеда равна 6 см, длина – в 5 раз больше ширины, а высота – на 5 см меньше длины. Вычислите объем параллелепипеда.

  5. Чему равно делимое, если делитель равен 17, неполное частное – 5, а остаток – 12?

  6. Поле прямоугольной формы имеет площадь 3 га, его длина – 200 м. Вычислите периметр поля.

  7. Запишите все трёхзначные числа, для записи которых используются только цифры 0, 9 и 4 (цифры не могут повторяться).

  8. Сумма длин всех рёбер прямоугольного параллелепипеда равна 80 см, а два его измерения – 10 см и 4 см. Найдите третье измерение параллелепипеда.

Вариант 3

  1. Выполните деление с остатком: 516 : 19.

  2. Найдите площадь прямоугольника, одна сторона которого равна 17 см, а вторая сторона в 2 раза больше первой.

  3. Вычислите объем и площадь поверхности куба с ребром 5 дм.

  4. Высота прямоугольного параллелепипеда равна 20 см, длина – на 4 см больше высоты, а ширина – в 2 раза меньше длины. Вычислите объем параллелепипеда.

  5. Чему равно делимое, если делитель равен 14, неполное частное – 8, а остаток – 9?

  6. Поле прямоугольной формы имеет площадь 7 га, его длина – 350 м. Вычислите периметр поля.

  7. Запишите все трёхзначные числа, для записи которых используются только цифры 1, 2 и 0 (цифры не могут повторяться).

  8. Сумма длин всех рёбер прямоугольного параллелепипеда равна 100 дм, а два его измерения – 8 дм и 13 дм. Найдите третье измерение параллелепипеда.

Вариант 4

  1. Выполните деление с остатком: 610 : 17.

  2. Найдите площадь прямоугольника, одна сторона которого равна 45 см, а вторая сторона в 5 раз меньше первой.

  3. Вычислите объем и площадь поверхности куба с ребром 2 см.

  4. Длина прямоугольного параллелепипеда равна 20 см, высота – в 4 раза меньше длины, а ширина – на 7 см больше высоты. Вычислите объем параллелепипеда.

  5. Чему равно делимое, если делитель равен 15, неполное частное – 6, а остаток – 14?

  6. Поле прямоугольной формы имеет площадь 4 га, его ширина – 50 м. Вычислите периметр поля.

  7. Запишите все трёхзначные числа, для записи которых используются только цифры 7, 0 и 8 (цифры не могут повторяться).

  8. Сумма длин всех рёбер прямоугольного параллелепипеда равна 72 см, а два его измерения – 6 см и 8 см. Найдите третье измерение параллелепипеда.

Контрольная работа № 6

Обыкновенные дроби

Вариант 1

  1. Сравните числа:

  1. и ; 2) и 1; 3) и 1.

  1. Выполните действия:

  1. + ; 3) ;

  2. + 5 ; 4) .

  1. В саду растёт 72 дерева, из них составляют яблони. Сколько яблонь растёт в саду?

  2. Кирилл прочёл 56 страниц, что составило книги. Сколько страниц было в книге?

  3. Преобразуйте в смешанное число дробь:

  1. ; 2) .

  1. Найдите все натуральные значения 𝑥, при которых верно неравенство .

  2. Каково наибольшее натуральное значение n, при котором верно неравенство n ?

  3. Найдите все натуральные значения 𝑎, при которых одновременно выполняются условия: дробь правильная, а дробь неправильная.

Вариант 2

  1. Сравните числа:

и ; 2) и 1; 3) и 1.

  1. Выполните действия:

+ ; 3) ;

+ 1 ; 4) .

  1. В гараже стоят 63 машины, из них составляют легковые. Сколько легковых машин стоит в гараже?

  2. В классе 12 учеников изучают французский язык, что составляет всех учеников класса. Сколько учеников в классе?

  3. Преобразуйте в смешанное число дробь:

; 2) .

  1. Найдите все натуральные значения 𝑥, при которых верно неравенство .

  2. Каково наименьшее натуральное значение n, при котором верно неравенство n ?

  3. Найдите все натуральные значения 𝑎, при которых одновременно выполняются условия: дробь правильная, а дробь неправильная.

Вариант 3

  1. Сравните числа:

и ; 2) и 1; 3) и 1.

  1. Выполните действия:

+ ; 3) ;

+ 7 ; 4) .

  1. В классе 36 учеников, из них занимаются спортом. Сколько учеников занимаются спортом?

  2. Ваня собрал 16 вёдер картофеля, что составляет всего урожая. Сколько вёдер картофеля составляет урожай?

  3. Преобразуйте в смешанное число дробь:

; 2) .

  1. Найдите все натуральные значения 𝑥, при которых верно неравенство .

  2. Найдите все натуральные значения 𝑎, при которых обе дроби и одновременно будут неправильными.

Вариант 4

  1. Сравните числа:

и ; 2) и 1; 3) и 1.

  1. Выполните действия:

+ ; 3) ;

+ 2 ; 4) .

  1. В пятых классах 64 ученика, из них составляют отличники. Сколько отличников в пятых классах?

  2. Мама приготовила вареники с творогом, а Коля съел 9 штук, что составляет всех вареников. Сколько вареников приготовила мама?

  3. Преобразуйте в смешанное число дробь:

; 2) .

  1. Найдите все натуральные значения 𝑥, при которых верно неравенство 2 .

  2. Найдите все натуральные значения 𝑎, при которых одновременно выполняются условия: дробь будет неправильная, а дробь правильная.

Контрольная работа № 7

Понятие о десятичной дроби. Сравнение, округление, сложение и вычитание десятичных дробей.

Вариант 1

  1. Сравните: 1) 14,396 и 14,4; 2) 0,657 и 0, 6565.

  2. Округлите: 1) 16,76 до десятых; 2) 0,4864 до тысячных.

  3. Выполните действия: 1) 3,87 + 32,496; 2) 23,7 – 16,48; 3) 20 – 12,345.

  4. Скорость катера по течению реки равна 24,2 км/ч, а собственная скорость катера – 22,8 км/ч. Найдите скорость катера против течения реки.

  5. Вычислите, записав данные величины в килограммах:

  1. 3,4 кг + 839 г; 2) 2 кг 30 г – 1956 г.

  1. Одна сторона треугольника равна 5,6 см, что на 1,4 см больше второй стороны и на 0,7 см меньше третьей. Найдите периметр треугольника.

  2. Напишите три числа, каждое из которых больше 5,74 и меньше 5,76.

  3. Найдите значение выражения, выбирая удобный порядок вычислений:

  1. (8,63 + 3,298) – 5,63; 2) 0,927 – (0,327 + 0,429).

Вариант 2

  1. Сравните: 1) 17,497 и 17,5; 2) 0,346 и 0, 3458.

  2. Округлите: 1) 12,88 до десятых; 2) 0,3823 до сотых.

  3. Выполните действия: 1) 5,62 + 43,299; 2) 25,6 – 14,52; 3) 30 – 14,265.

  4. Скорость катера против течения реки равна 18,6 км/ч, а собственная скорость

катера – 19,8 км/ч. Найдите скорость катера по течению реки.

  1. Вычислите, записав данные величины в метрах:

  1. 8,3 м + 784 см; 2) 5 м 4 см – 385 см.

  1. Одна сторона треугольника равна 4,5 см, что на 3,3 см меньше второй стороны и на 0,6 см больше третьей. Найдите периметр треугольника.

  2. Напишите три числа, каждое из которых больше 3,82 и меньше 3,84.

  3. Найдите значение выражения, выбирая удобный порядок вычислений:

  1. (5,94 + 2,383) – 3,94; 2) 0,852 – (0,452 + 0,214).

Вариант 3

  1. Сравните: 1) 12,598 и 12,6; 2) 0,257 и 0, 2569.

  2. Округлите: 1) 17,56 до десятых; 2) 0,5864 до тысячных.

  3. Выполните действия: 1) 4,36 + 27,647; 2) 32,4 – 17,23; 3) 50 – 22,475.

  4. Скорость катера по течению реки равна 19,6 км/ч, а собственная скорость катера – 18,3 км/ч. Найдите скорость катера против течения реки.

  5. Вычислите, записав данные величины в центнерах:

  1. 6,7 ц + 584 кг; 2) 6 ц 2 кг – 487 кг.

  1. Одна сторона треугольника равна 3,7 см, что на 0,9 см больше второй стороны и на 1,2 см меньше третьей. Найдите периметр треугольника.

  2. Напишите три числа, каждое из которых больше 7,87 и меньше 7,89.

  3. Найдите значение выражения, выбирая удобный порядок вычислений:

  1. (6,73 + 4,594) – 2,73; 2) 0,791 – (0,291 + 0,196).

Вариант 4

  1. Сравните: 1) 16,692 и 16,7; 2) 0,745 и 0, 7438.

  2. Округлите: 1) 24,87 до десятых; 2) 0,8653 до тысячных.

  3. Выполните действия: 1) 6,72 + 54,436; 2) 27,6 – 15,72; 3) 40 – 11,825.

  4. Скорость катера против течения реки равна 17,8 км/ч, а собственная скорость

катера – 19,4 км/ч. Найдите скорость катера по течению реки.

  1. Вычислите, записав данные величины в метрах:

  1. 2,8 м + 524 см; 2) 4 м 6 см – 257 см.

  1. Одна сторона треугольника равна 5,1 см, что на 2,1 см меньше второй стороны и на 0,7 см больше третьей. Найдите периметр треугольника.

  2. Напишите три числа, каждое из которых больше 1,34 и меньше 1,36.

  3. Найдите значение выражения, выбирая удобный порядок вычислений:

  1. (7,86 + 4,183) – 2,86; 2) 0,614 – (0,314 + 0,207).

Контрольная работа № 8

Умножение и деление десятичных дробей

Вариант 1

  1. Вычислите:

  1. 0,024 ∙ 4,5; 3) 2,86 : 100; 5) 0,48 : 0,8;

  2. 29,41 ∙ 1 000; 4) 4 : 16; 6) 9,1 : 0,07.

  1. Найдите значение выражения: (4 – 2,6) ∙ 4,3 + 1,08 : 1,2.

  2. Решите уравнение: 2,4 (𝑥 + 0,98) = 4,08.

  3. Моторная лодка плыла 1,4 ч по течению реки и 2,2 ч против течения. Какой путь преодолела лодка за всё время движения, если скорость течения равна 1,7 км/ч, а собственная скорость лодки – 19,8 км/ч?

  4. Если в некоторой десятичной дроби перенести запятую вправо через одну цифру, то она увеличится на 14,31. Найдите эту дробь.

Вариант 2

  1. Вычислите:

  1. 0,036 ∙ 3,5; 3) 3,68 : 100; 5) 0,56 : 0,7;

  2. 37,53 ∙ 1 000; 4) 5 : 25; 6) 5,2 : 0,04.

  1. Найдите значение выражения: (5 – 2,8) ∙ 2,4 + 1,12 : 1,6.

  2. Решите уравнение: 0,084 : (6,2 – 𝑥) = 1,2.

  3. Катер плыл 1,6 ч против течения реки и 2,4 ч по течению. На сколько больше проплыл катер, двигаясь по течению реки, чем против течения, если скорость течения реки равна 2,1 км/ч, а собственная скорость катера – 28,2 км/ч?

  4. Если в некоторой десятичной дроби перенести запятую влево через одну цифру, то она уменьшится на 23,76. Найдите эту дробь.

Вариант 3

  1. Вычислите:

  1. 0,064 ∙ 6,5; 3) 4,37 : 100; 5) 0,63 : 0,9;

  2. 46,52 ∙ 1 000; 4) 6 : 15; 6) 7,2 : 0,03.

  1. Найдите значение выражения: (6 – 3,4) ∙ 1,7 + 1,44 : 1,6.

  2. Решите уравнение: 1,6 (𝑥 + 0,78) = 4,64.

  3. Теплоход плыл 1,8 ч против течения реки и 2,6 ч по течению. Какой путь преодолел теплоход за всё время движения, если скорость течения равна 2,5 км/ч, а собственная скорость теплохода – 35,5 км/ч?

  4. Если в некоторой десятичной дроби перенести запятую вправо через одну цифру, то она увеличится на 15,93. Найдите эту дробь.

Вариант 4

  1. Вычислите:

  1. 0,096 ∙ 5,5; 3) 7,89 : 100; 5) 0,76 : 0,4;

  2. 78,53 ∙ 100; 4) 6 : 24; 6) 8,4 : 0,06.

  1. Найдите значение выражения: (7 – 3,6) ∙ 2,8 + 1,32 : 2,2.

  2. Решите уравнение: 0,144 : (3,4 – 𝑥) = 2,4.

  3. Моторная лодка плыла 3,6 ч против течения реки и 1,8 ч по течению. На сколько километров больше проплыла лодка, двигаясь против течения , чем по течению, если скорость течения реки равна 1,2 км/ч, а собственная скорость лодки – 22,4 км/ч?

  4. Если в некоторой десятичной дроби перенести запятую влево через одну цифру, то она уменьшится на 29,52. Найдите эту дробь.

Контрольная работа № 9

Среднее арифметическое. Проценты.

Вариант 1

  1. Найдите среднее арифметическое чисел: 32,6; 38,5; 34; 35,3.

  2. Площадь поля равна 300 га. Рожью засеяли 18 % поля. Сколько гектаров поля засеяли рожью?

  3. Петя купил книгу за 90 р., что составляет 30 % всех денег, которые у него были. Сколько денег было у Пети?

  4. Лодка плыла 2 ч со скоростью 12,3 км/ч и 4 ч со скоростью 13,2 км/ч. Найдите среднюю скорость лодки на всём пути.

  5. Турист прошёл за три дня 48 км. В первый день он прошёл 35 % всего маршрута. Путь пройденный в первый день, составляет 80 % расстояния , пройденного во второй день. Сколько километров прошёл турист в третий день?

  6. В первый день Петя прочитал 40 % всей книги, во второй – 60 % остального, а в третий — оставшиеся 144 страницы. Сколько всего страниц в книге?

Вариант 2

  1. Найдите среднее арифметическое чисел: 26,3; 20,2; 24,7; 18.

  2. В школе 800 учащихся. Сколько пятиклассников в этой школе, если известно, что их количество составляет 12 % количества всех учащихся?

  3. Насос перекачал в бассейн 42 воды, что составляет 60 % объёма бассейна. Найдите объём бассейна.

  4. Автомобиль ехал 3 ч со скоростью 62,6 км/ч и 2 ч со скоростью 65 км/ч. Найдите среднюю скорость автомобиля на всём пути.

  5. Токарь за три дня изготовил 80 деталей. В первый день он выполнил 30 % всей работы. Известно, что количество деталей, изготовленных в первый день, составляет 60 % количества деталей , изготовленных во второй день. Сколько деталей изготовил токарь в третий день?

  6. В первый день тракторная бригада вспахала 30 % площади всего поля, во второй – 75% остального, а в третий — оставшиеся 14 га. Найдите площадь поля.

Вариант 3

  1. Найдите среднее арифметическое чисел: 26,4; 42,6; 31,8; 15.

  2. В магазин завезли 600 кг овощей. Картофель составляет 24% всех завезённых овощей. Сколько килограммов картофеля завезли в магазин?

  3. За первый день турист прошёл расстояние 18 км, что составляет 40 % всего пути, который он должен преодолеть. Найдите длину пути, который должен пройти турист.

  4. Катер плыл 1,5 ч со скоростью 34 км/ч и 2,5 ч со скоростью 30 км/ч. Найдите среднюю скорость катера на всём пути.

  5. За три дня оператор набрал на компьютере 60 страниц. В первый день было выполнено 35 % всей работы. Объём работы, выполненной в первый день, составляет 70 % работы, выполненной во второй день. Сколько страниц было набрано в третий день?

  6. За первый час было продано 84 % всего мороженого, за второй – 78 % остального, а за третий – оставшиеся 44 порции. Сколько порций мороженого было продано за три часа?

Вариант 4

  1. Найдите среднее арифметическое чисел: 43,6; 21,8; 32,4; 11.

  2. Площадь парка равна 40 га. Площадь озера составляет 15 % площади парка. Найдите площадь озера.

  3. За первый час движения автомобиль преодолел расстояние 72 км, что составляет 24 % длины всего пути, который ему надо проехать. Найдите общий путь, который преодолел автомобиль.

  4. Черепаха ползла 2 ч со скоростью 15,3 м/ч и 3 ч со скоростью 12, 4 м/ч. Найдите среднюю скорость черепахи на всём пути.

  5. Три насоса наполнили водой бассейн объёмом 320 . Первый насос заполнил бассейн на 30 %, что составляет 80 % объёма воды, которую перекачал второй насос. Найдите объём воды, которую перекачал третий насос.

  6. В первый день турист прошёл 20% всего пути, во второй – 60 % остального, а в третий – оставшиеся 24 км. Найдите длину пути, который прошёл турист за три дня.

Контрольная работа № 10

Обобщение и систематизация знаний учащихся

за курс математики 5 класса

Вариант 1

  1. Найдите значение выражения: (4,1 – 0,66 : 1,2) ∙ 0,6.

  2. Миша шёл из одного села в другое 0,7 ч по полю и 0,9 ч через лес, пройдя всего 5,31 км. С какой скоростью шёл Миша через лес, если по полю он двигался со скоростью 4,5 км/ч?

  3. Решите уравнение: 9,2𝑥 – 6,8𝑥 + 0,64 = 1

  4. Ширина прямоугольного параллелепипеда равна 4 см, что составляет его длины, а высота составляет 40 % длины. Вычислите объем параллелепипеда.

  5. Выполните действия: 20 : ( + ) – ( – ) : 5.

  6. Среднее арифметическое четырёх чисел равно 1,4, а среднее арифметическое трёх других чисел – 1,75. Найдите среднее арифметическое этих семи чисел.

Вариант 2

  1. Найдите значение выражения: (0,49 : 1,4 – 0,325) ∙ 0,8.

  2. Катер плыл 0,4 ч по течению реки и 0,6 ч против течения, преодолев всего 16,8 км. С какой скоростью плыл катер по течению, если против течения он плыл со скоростью 16 км/ч?

  3. Решите уравнение: 7,2𝑥 – 5,4𝑥 + 0,55 = 1

  4. Ширина прямоугольного параллелепипеда равна 3,6 см, что составляет его длины, а высота составляет 42 % длины. Вычислите объем параллелепипеда.

  5. Выполните действия: 30 : () + ( – ) : 7.

  6. Среднее арифметическое трёх чисел равно 2,5, а среднее арифметическое двух других чисел – 1,7. Найдите среднее арифметическое этих пяти чисел.

Вариант 3

  1. Найдите значение выражения: (5,25 – 0,63 : 1,4) ∙ 0,4.

  2. Пётр шёл из села к озеру 0,7 ч по одной дороге, а возвратился по другой дороге за 0,8 ч, пройдя всего 6,44 км. С какой скоростью шёл Пётр к озеру, если возвращался он со скоростью 3,5 км/ч?

  3. Решите уравнение: 7,8𝑥 – 4,6𝑥 + 0,8 = 12.

  4. Ширина прямоугольного параллелепипеда равна 4,8 см, что составляет его длины, а высота составляет 45 % длины. Вычислите объем параллелепипеда.

  5. Выполните действия: 10 : ( + ) – ( + 1) : 6.

  6. Среднее арифметическое пяти чисел равно 2,3, а среднее арифметическое трёх других чисел – 1,9. Найдите среднее арифметическое этих восьми чисел.

Вариант 4

  1. Найдите значение выражения: (4,4 – 0,63 :1,8) ∙ 0,8.

  2. Автомобиль ехал 0,9 ч по асфальтированной дороге и 0,6 ч по грунтовой, проехав всего 93,6 км. С какой скоростью двигался автомобиль по асфальтированной дороге, если по грунтовой он ехал со скоростью 48 км/ч?

  3. Решите уравнение: 3,23𝑥 + 0,97𝑥 + 0,74 = 2.

  4. Ширина прямоугольного параллелепипеда равна 3,2 см, что составляет его длины, а высота составляет 54 % длины. Вычислите объем параллелепипеда.

  5. Выполните действия: 50 : () – ( – ) : 9.

  6. Среднее арифметическое шести чисел равно 2,8, а среднее арифметическое четырёх других чисел – 1,3. Найдите среднее арифметическое этих десяти чисел.

УМК Мерзляк Математика 5-9 классы

В линии «УМК Мерзляк Математика» объяснения отличаются простотой, ясностью и логичностью, а большое разнообразие задач различного уровня сложности позволяет реализовать дифференциацию обучения и индивидуальный подход — таким образом у школьников формируется активный познавательный интерес к математике. Учебники сочетают традиционные и современные методики, обеспечивая качественную математическую подготовку школьников. Ниже представлены материалы в помощь обучающимся по линии УМК Мерзляк и другие.

Контрольные работы

1. К учебникам математики УМК Мерзляк, Полонский, Якир

Из пособия «Мерзляк. Дидактические материалы по математике 5 класс»
Из пособия «Ерина. Тесты по математике 5 класс к новому учебнику»

Из пособия «Мерзляк. Дидактические материалы по математике 6 класс»

2. К учебникам алгебры УМК Мерзляк, Полонский, Якир

Из пособия «Мерзляк. Дидактические материалы по алгебре 7 класс»
Из пособия «Мерзляк. Дидактические материалы по алгебре 8 класс»
Из пособия «Мерзляк. Дидактические материалы по алгебре 9 класс».

3. К учебникам алгебры УМК Мерзляк, Поляков (углубленное изучение)

Из пособия «Мерзляк. Контрольные и самостоятельные работы. 7 класс»
Из пособия «Мерзляк. Контрольные и самостоятельные работы. 8 класс»
Из пособия «Мерзляк. Контрольные и самостоятельные работы. 9 класс»

4. К учебникам геометрии УМК Мерзляк, Полонский, Якир

Из пособия «Мерзляк и др. Дидактические материалы по геометрии 7 класс»
Из пособия «Мерзляк и др. Дидактические материалы по геометрии 8 класс»
Из пособия «Мерзляк и др. Дидактические материалы по геометрии 9 класс»

 

Электронные формы конспектов

Конспекты по математике 5-6 классы и алгебре 7-9 классы

Онлайн-учебник: Математика 6 кл. / Мерзляк, Полонский, Якир (2014)

Онлайн-учебник: Алгебра 7 (углубленное изучение). Мерзляк, Поляков (2019)

Онлайн-учебник: Алгебра 8 (углубленное изучение). Мерзляк, Поляков (2019)

Онлайн-учебник: Геометрия 7 Мерзляк   Глава 1,   Глава 2,   Глава 3,   Глава 4.

Онлайн-учебник: Геометрия 8 Мерзляк   Глава 1,   Глава 2,    Глава 3,   Глава 4.

 

 

Тексты контрольных работ по математике по учебнику А.Г.Мерзляк (5 класс)

Контрольная работа № 1 по теме «Натуральные числа»

Вариант 1

  1. Запишите цифрами число:

  1. шестьдесят пять миллиардов сто двадцать три миллиона девятьсот сорок одна тысяча восемьсот тридцать семь;

  2. восемьсот два миллиона пятьдесят четыре тысячи одиннадцать:

  3. тридцать три миллиарда девять миллионов один.

  1. Сравните числа: 1) 5 678 и 5 489; 2) 14 092 и 14 605.

  2. Начертите координатный луч и отметьте на нём точки, соответствующие числам 2, 5, 7, 9.

  3. Начертите отрезок FK, длина которого равна 5 см 6 мм, отметьте на нём точку C. Запишите все отрезки, образовавшиеся на рисунке, и измерьте их длины.

  4. Точка К принадлежит отрезку МЕ, МК = 19 см, отрезок КЕ на 17 см больше отрезка МК. Найдите длину отрезка МЕ.

  5. Запишите цифру, которую можно поставить вместо звёздочки, чтобы образовалось верное неравенство (рассмотрите все возможные случаи):

  1. 3 78* 3 784; 2) 5 8*5 5 872.

  1. На отрезке CD длиной 40 см отметили точки P и Q так, что CP = 28 см, QD =26 см. Чему равна длина отрезка PQ?

  2. Сравните: 1) 3 км и 2 974 м; 2) 912 кг и 8 ц.

Вариант 2

  1. Запишите цифрами число:

  1. семьдесят шесть миллиардов двести сорок два миллиона семьсот восемьдесят три тысячи сто девяносто пять;

  2. четыреста три миллиона тридцать восемь тысяч сорок девять;

  3. сорок восемь миллиардов семь миллионов два.

  1. Сравните числа: 1) 6 894 и 6 983; 2) 12 471 и 12 324.

  2. Начертите координатный луч и отметьте на нём точки, соответствующие числам 3, 4, 6, 8.

  3. Начертите отрезок АВ, длина которого равна 4 см 8 мм, отметьте на нём точку D. Запишите все отрезки, образовавшиеся на рисунке, и измерьте их длины.

  4. Точка T принадлежит отрезку МN, МT = 19 см, отрезок TN на 18 см меньше отрезка МT. Найдите длину отрезка МN.

  5. Запишите цифру, которую можно поставить вместо звёздочки, чтобы образовалось верное неравенство (рассмотрите все возможные случаи):

  1. 2 *14 2 316; 2) 4 78* 4 785.

  1. На отрезке SK длиной 30 см отметили точки A и B так, что SA = 14 см, BK =19 см. Чему равна длина отрезка AB?

  2. Сравните: 1) 3 986 г и 4 кг; 2) 586 см и 6 м.

Контрольная работа № 2 по теме «Сложение и вычитание натуральных чисел. Числовые и буквенные выражения. Формулы.»

Вариант 1

  1. Вычислите: 1) 15 327+ 496 383; 2) 38 020 405 – 9 497 653.

  2. На одной стоянке было 143 автомобиля, что на 17 автомобилей больше, чем на второй. Сколько автомобилей было на обеих стоянках?

  3. Выполните сложение, выбирая удобный порядок вычислений:

  1. (325 + 791) + 675; 2) 428 + 856 + 572 + 244.

  1. Проверьте, верно ли неравенство:

1 674 – (736 + 328) 2 000 – (1 835 – 459).

  1. Найдите значение 𝑎 по формуле 𝑎 = 4𝑏 – 16 при 𝑏 = 8.

  2. Упростите выражение 126 + 𝒙 + 474 и найдите его значение при 𝒙 = 278.

  3. Вычислите:

  1. 4 м 73 см + 3 м 47 см; 2) 12 ч 16 мин – 7 ч 32 мин.

  1. Найдите значение выражения, выбирая удобный порядок вычислений:

  1. (713 + 529) – 413; 2) 624 – (137 + 224).

Вариант 2

  1. Вычислите: 1) 17 824+ 128 356; 2) 42 060 503 – 7 456 182.

  2. На одной улице 152 дома, что на 18 домов меньше, чем на другой. Сколько всего домов на обеих улицах?

  3. Выполните сложение, выбирая удобный порядок вычислений:

  1. (624 + 571) + 376; 2) 212 + 497 + 788 + 803.

  1. Проверьте, верно ли неравенство:

1 826 – (923 + 249) 3 000 – (2 542 – 207).

  1. Найдите значение 𝑝 по формуле 𝑝= 40 – 7𝑞 при 𝑞 = 4.

  2. Упростите выражение 235 + y + 465 и найдите его значение при y = 153.

  3. Вычислите:

  1. 6 м 23 см + 5 м 87 см; 2) 14 ч 17 мин – 5 ч 23 мин.

  1. Найдите значение выражения, выбирая удобный порядок вычислений:

  1. (837 + 641) – 537; 2) 923 – (215 + 623).

Контрольная работа № 3 «Уравнение. Угол. Многоугольники.»

Вариант 1

  1. Постройте угол МКА, величина которого равна 74. Проведите произвольно луч КС между сторонами угла МКА. Запишите образовавшиеся углы и измерьте их величины.

  2. Решите уравнение: 1) 𝑥 +37 = 81 2) 150 – 𝑥 = 98.

  3. Одна из сторон треугольника равна 24 см, вторая – в 4 раза короче первой, а третья – на 16 см длиннее второй. Вычислите периметр треугольника.

  4. Решите уравнение: 1) (34 + 𝑥) – 83 = 42 2) 45 – (𝑥 – 16) = 28.

  5. Из вершины развёрнутого угла АВС (см рис.) проведены два луча ВD и ВЕ так, что ∠АВЕ = 154, ∠DВС = 128. Вычислите градусную меру угла DВЕ.

  6. Какое число надо подставить вместо 𝑎, чтобы корнем уравнения

52 – (𝑎 – 𝑥) = 24 было число 40?

hello_html_m42e43427.png

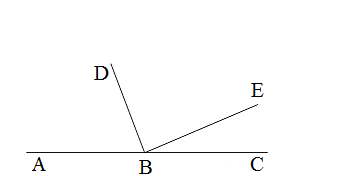
Вариант 2

  1. Постройте угол ABC, величина которого равна 168. Проведите произвольно луч BM между сторонами угла ABC. Запишите образовавшиеся углы и измерьте их величины.

  2. Решите уравнение: 1) 21 + 𝑥 = 58 2) 𝑥 – 135 = 76.

  3. Одна из сторон треугольника равна 32 см, вторая – в 2 раза короче первой, а третья – на 6 см короче первой. Вычислите периметр треугольника.

  4. Решите уравнение: 1) (96 – 𝑥) – 15 = 64 2) 31 – (𝑥 + 11) = 18.

  5. Из вершины прямого угла MNK (см рис.) проведены два луча ND и NE так, что ∠MND = 73, ∠KNF = 48. Вычислите градусную меру угла DNF.

  6. Какое число надо подставить вместо 𝑎, чтобы корнем уравнения

64 – (𝑎 – 𝑥) = 17 было число 16?

hello_html_54cf3cf5.png

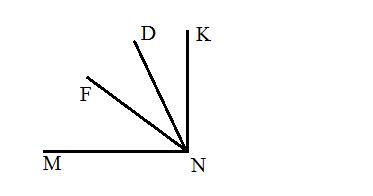
Контрольная работа № 4 по теме «Умножение и деление натуральных чисел. Свойства умножения.»

Вариант 1

  1. Вычислите:

  1. 36 ∙ 2 418; 3) 1 456 : 28;

  2. 175 ∙ 204; 4) 177 000 : 120.

  1. Найдите значение выражения: (326 ∙ 48 – 9 587) : 29.

  2. Решите уравнение:

  1. 𝑥 ∙ 14 = 364; 2) 324 : 𝑥 = 9; 3) 19𝑥 — 12𝑥 = 126.

  1. Найдите значение выражения наиболее удобным способом:

  1. 25 ∙ 79 ∙ 4; 2) 43 ∙ 89 + 89 ∙ 57.

  1. Купили 7 кг конфет и 9 кг печенья, заплатив за всю покупку 1 200 р. Сколько стоит 1 кг печенья, если 1 кг конфет стоит 120 р?

  2. С одной станции одновременно в одном направлении отправились два поезда. Один из поездов двигался со скоростью 56 км/ч, а второй – 64 км/ч. Какое расстояние будет между поездами через 6 ч после начала движения?

  3. Сколькими нулями оканчивается произведение всех натуральных чисел от 19 до 35 включительно?

Вариант 2

  1. Вычислите:

  1. 24 ∙ 1 246; 3) 1 856 : 32;

  2. 235 ∙ 108; 4) 175 700 : 140.

  1. Найдите значение выражения: (625 ∙ 25 – 8 114) : 37.

  2. Решите уравнение:

  1. 𝑥 ∙ 28 = 336; 2) 312 : 𝑥 = 8; 3) 16𝑥 — 11𝑥 = 225.

  1. Найдите значение выражения наиболее удобным способом:

  1. 2 ∙ 83 ∙ 50; 2) 54 ∙ 73 + 73 ∙ 46.

  1. Для проведения ремонта электрической проводки купили 16 одинаковых мотков алюминиевого и 11 одинаковых мотков медного провода. Общая длина купленного провода составляла 650 м. Сколько метров алюминиевого провода было в мотке, если медного провода в одном мотке было 30 м?

  2. Из одного города одновременно в одном направлении выехали два автомобиля. Один из них двигался со скоростью 74 км/ч, а второй – 68 км/ч. Какое расстояние будет между автомобилями через 4 ч после начала движения?

  3. Сколькими нулями оканчивается произведение всех натуральных чисел от 23 до 42 включительно?

Контрольная работа № 5 по теме «Деление с остатком. Площадь прямоугольника. Прямоугольный параллелепипед и его объем. Комбинаторные задачи.»

Вариант 1

  1. Выполните деление с остатком: 478 : 15.

  2. Найдите площадь прямоугольника, одна сторона которого равна 14 см, а вторая сторона в 3 раза больше первой.

  3. Вычислите объем и площадь поверхности куба с ребром 3 см.

  4. Длина прямоугольного параллелепипеда равна 18 см, ширина – в 2 раза меньше длины, а высота – на 11 см больше ширины. Вычислите объем параллелепипеда.

  5. Чему равно делимое, если делитель равен 11, неполное частное – 7, а остаток – 6?

  6. Поле прямоугольной формы имеет площадь 6 га. Ширина поля 150 м. Вычислите периметр поля.

  7. Запишите все трёхзначные числа, для записи которых используются только цифры 5, 6 и 0 (цифры не могут повторяться).

  8. Сумма длин всех рёбер прямоугольного параллелепипеда равна 116 см, а два его измерения – 12 см и 11 см. Найдите третье измерение параллелепипеда.

Вариант 2

  1. Выполните деление с остатком: 376 : 18.

  2. Найдите площадь прямоугольника, одна сторона которого равна 21 см, а вторая сторона в 3 раза меньше первой.

  3. Вычислите объем и площадь поверхности куба с ребром 4 дм.

  4. Ширина прямоугольного параллелепипеда равна 6 см, длина – в 5 раз больше ширины, а высота – на 5 см меньше длины. Вычислите объем параллелепипеда.

  5. Чему равно делимое, если делитель равен 17, неполное частное – 5, а остаток – 12?

  6. Поле прямоугольной формы имеет площадь 3 га, его длина – 200 м. Вычислите периметр поля.

  7. Запишите все трёхзначные числа, для записи которых используются только цифры 0, 9 и 4 (цифры не могут повторяться).

  8. Сумма длин всех рёбер прямоугольного параллелепипеда равна 80 см, а два его измерения – 10 см и 4 см. Найдите третье измерение параллелепипеда.

Контрольная работа № 6 по теме «Обыкновенные дроби»

Вариант 1

  1. Сравните числа:

  1. и ; 2) и 1; 3) и 1.

  1. Выполните действия:

  1. + ; 3) ;

  2. + 5 ; 4) .

  1. В саду растёт 72 дерева, из них составляют яблони. Сколько яблонь растёт в саду?

  2. Кирилл прочёл 56 страниц, что составило книги. Сколько страниц было в книге?

  3. Преобразуйте в смешанное число дробь:

  1. ; 2) .

  1. Найдите все натуральные значения 𝑥, при которых верно неравенство .

  2. Каково наибольшее натуральное значение n, при котором верно неравенство n ?

  3. Найдите все натуральные значения 𝑎, при которых одновременно выполняются условия: дробь правильная, а дробь неправильная.

Вариант 2

  1. Сравните числа:

и ; 2) и 1; 3) и 1.

  1. Выполните действия:

+ ; 3) ;

+ 1 ; 4) .

  1. В гараже стоят 63 машины, из них составляют легковые. Сколько легковых машин стоит в гараже?

  2. В классе 12 учеников изучают французский язык, что составляет всех учеников класса. Сколько учеников в классе?

  3. Преобразуйте в смешанное число дробь:

; 2) .

  1. Найдите все натуральные значения 𝑥, при которых верно неравенство .

  2. Каково наименьшее натуральное значение n, при котором верно неравенство n ?

  3. Найдите все натуральные значения 𝑎, при которых одновременно выполняются условия: дробь правильная, а дробь неправильная.

Контрольная работа № 7 по теме «Понятие о десятичной дроби. Сравнение, округление, сложение и вычитание десятичных дробей.»

Вариант 1

  1. Сравните: 1) 14,396 и 14,4; 2) 0,657 и 0, 6565.

  2. Округлите: 1) 16,76 до десятых; 2) 0,4864 до тысячных.

  3. Выполните действия: 1) 3,87 + 32,496; 2) 23,7 – 16,48; 3) 20 – 12,345.

  4. Скорость катера по течению реки равна 24,2 км/ч, а собственная скорость катера – 22,8 км/ч. Найдите скорость катера против течения реки.

  5. Вычислите, записав данные величины в килограммах:

  1. 3,4 кг + 839 г; 2) 2 кг 30 г – 1956 г.

  1. Одна сторона треугольника равна 5,6 см, что на 1,4 см больше второй стороны и на 0,7 см меньше третьей. Найдите периметр треугольника.

  2. Напишите три числа, каждое из которых больше 5,74 и меньше 5,76.

  3. Найдите значение выражения, выбирая удобный порядок вычислений:

  1. (8,63 + 3,298) – 5,63; 2) 0,927 – (0,327 + 0,429).

Вариант 2

  1. Сравните: 1) 17,497 и 17,5; 2) 0,346 и 0, 3458.

  2. Округлите: 1) 12,88 до десятых; 2) 0,3823 до сотых.

  3. Выполните действия: 1) 5,62 + 43,299; 2) 25,6 – 14,52; 3) 30 – 14,265.

  4. Скорость катера против течения реки равна 18,6 км/ч, а собственная скорость

катера – 19,8 км/ч. Найдите скорость катера по течению реки.

  1. Вычислите, записав данные величины в метрах:

  1. 8,3 м + 784 см; 2) 5 м 4 см – 385 см.

  1. Одна сторона треугольника равна 4,5 см, что на 3,3 см меньше второй стороны и на 0,6 см больше третьей. Найдите периметр треугольника.

  2. Напишите три числа, каждое из которых больше 3,82 и меньше 3,84.

  3. Найдите значение выражения, выбирая удобный порядок вычислений:

  1. (5,94 + 2,383) – 3,94; 2) 0,852 – (0,452 + 0,214).

Контрольная работа № 8 по теме «Умножение и деление десятичных дробей»

Вариант 1

  1. Вычислите:

  1. 0,024 ∙ 4,5; 3) 2,86 : 100; 5) 0,48 : 0,8;

  2. 29,41 ∙ 1 000; 4) 4 : 16; 6) 9,1 : 0,07.

  1. Найдите значение выражения: (4 – 2,6) ∙ 4,3 + 1,08 : 1,2.

  2. Решите уравнение: 2,4 (𝑥 + 0,98) = 4,08.

  3. Моторная лодка плыла 1,4 ч по течению реки и 2,2 ч против течения. Какой путь преодолела лодка за всё время движения, если скорость течения равна 1,7 км/ч, а собственная скорость лодки – 19,8 км/ч?

  4. Если в некоторой десятичной дроби перенести запятую вправо через одну цифру, то она увеличится на 14,31. Найдите эту дробь.

Вариант 2

  1. Вычислите:

  1. 0,036 ∙ 3,5; 3) 3,68 : 100; 5) 0,56 : 0,7;

  2. 37,53 ∙ 1 000; 4) 5 : 25; 6) 5,2 : 0,04.

  1. Найдите значение выражения: (5 – 2,8) ∙ 2,4 + 1,12 : 1,6.

  2. Решите уравнение: 0,084 : (6,2 – 𝑥) = 1,2.

  3. Катер плыл 1,6 ч против течения реки и 2,4 ч по течению. На сколько больше проплыл катер, двигаясь по течению реки, чем против течения, если скорость течения реки равна 2,1 км/ч, а собственная скорость катера – 28,2 км/ч?

  4. Если в некоторой десятичной дроби перенести запятую влево через одну цифру, то она уменьшится на 23,76. Найдите эту дробь.

Контрольная работа № 9 по теме «Среднее арифметическое. Проценты.»

Вариант 1

  1. Найдите среднее арифметическое чисел: 32,6; 38,5; 34; 35,3.

  2. Площадь поля равна 300 га. Рожью засеяли 18 % поля. Сколько гектаров поля засеяли рожью?

  3. Петя купил книгу за 90 р., что составляет 30 % всех денег, которые у него были. Сколько денег было у Пети?

  4. Лодка плыла 2 ч со скоростью 12,3 км/ч и 4 ч со скоростью 13,2 км/ч. Найдите среднюю скорость лодки на всём пути.

  5. Турист прошёл за три дня 48 км. В первый день он прошёл 35 % всего маршрута. Путь пройденный в первый день, составляет 80 % расстояния , пройденного во второй день. Сколько километров прошёл турист в третий день?

  6. В первый день Петя прочитал 40 % всей книги, во второй – 60 % остального, а в третий — оставшиеся 144 страницы. Сколько всего страниц в книге?

Вариант 2

  1. Найдите среднее арифметическое чисел: 26,3; 20,2; 24,7; 18.

  2. В школе 800 учащихся. Сколько пятиклассников в этой школе, если известно, что их количество составляет 12 % количества всех учащихся?

  3. Насос перекачал в бассейн 42 воды, что составляет 60 % объёма бассейна. Найдите объём бассейна.

  4. Автомобиль ехал 3 ч со скоростью 62,6 км/ч и 2 ч со скоростью 65 км/ч. Найдите среднюю скорость автомобиля на всём пути.

  5. Токарь за три дня изготовил 80 деталей. В первый день он выполнил 30 % всей работы. Известно, что количество деталей, изготовленных в первый день, составляет 60 % количества деталей , изготовленных во второй день. Сколько деталей изготовил токарь в третий день?

  6. В первый день тракторная бригада вспахала 30 % площади всего поля, во второй – 75% остального, а в третий — оставшиеся 14 га. Найдите площадь поля.

Контрольная работа № 10

Обобщение и систематизация знаний учащихся

за курс математики 5 класса

Вариант 1

  1. Найдите значение выражения: (4,1 – 0,66 : 1,2) ∙ 0,6.

  2. Миша шёл из одного села в другое 0,7 ч по полю и 0,9 ч через лес, пройдя всего 5,31 км. С какой скоростью шёл Миша через лес, если по полю он двигался со скоростью 4,5 км/ч?

  3. Решите уравнение: 9,2𝑥 – 6,8𝑥 + 0,64 = 1

  4. Ширина прямоугольного параллелепипеда равна 4 см, что составляет его длины, а высота составляет 40 % длины. Вычислите объем параллелепипеда.

  5. Выполните действия: 20 : ( + ) – ( – ) : 5.

  6. Среднее арифметическое четырёх чисел равно 1,4, а среднее арифметическое трёх других чисел – 1,75. Найдите среднее арифметическое этих семи чисел.

Вариант 2

  1. Найдите значение выражения: (0,49 : 1,4 – 0,325) ∙ 0,8.

  2. Катер плыл 0,4 ч по течению реки и 0,6 ч против течения, преодолев всего 16,8 км. С какой скоростью плыл катер по течению, если против течения он плыл со скоростью 16 км/ч?

  3. Решите уравнение: 7,2𝑥 – 5,4𝑥 + 0,55 = 1

  4. Ширина прямоугольного параллелепипеда равна 3,6 см, что составляет его длины, а высота составляет 42 % длины. Вычислите объем параллелепипеда.

  5. Выполните действия: 30 : () + ( – ) : 7.

  6. Среднее арифметическое трёх чисел равно 2,5, а среднее арифметическое двух других чисел – 1,7. Найдите среднее арифметическое этих пяти чисел.

5 класс по математике — тест 2 ТАКС практика

Вопрос 1: Каков периметр прямоугольника на рисунке ниже?

6,2 м

6,6 м

8 м

8,2 м

Вопрос 2: Какова площадь треугольника ABC, если AD = BC = 6 дюймов?

12 квадратных дюймов

16 квадратных дюймов

18 квадратных дюймов

22 квадратных дюйма

Вопрос 3: Что из перечисленного не является составным числом?
13

14

15

16

Вопрос 4: Группа учеников средней школы заработала 46 долларов.5 продавая лимонад. Они взяли 1,5 доллара за чашку лимонада. Сколько чашек лимонада они продали?

33

25

31

21

Вопрос 5: Питер ходил в 3 класса ежедневно в течение 5 дней подряд. Количество занятий, которые посетил Питер, можно рассчитать следующим образом:
вычитая 3 из 5

умножая 3 на 5

прибавляя 5 к 3

делив 5 на 3

Вопрос 6: Студент потратил 34 доллара на тетради. Цена ноутбуков указана в таблице ниже:

Большие ноутбуки Маленькие ноутбуки
4 2

Сколько ноутбуков он купил?
6 больших ноутбуков и 6 маленьких ноутбуков

5 больших ноутбуков и 6 маленьких ноутбуков

6 больших ноутбуков и 5 маленьких ноутбуков

5 больших ноутбуков и 5 маленьких ноутбуков

Вопрос 7: Какая из следующих дробей больше 1/5, но меньше 1/2?
3/5

2/3

1/3

1/6

Вопрос 8: Какая дробь эквивалентна 2/5?
10/30

5/2

5/20

12/30

Вопрос 9: Медали, выигранные Соединенными Штатами, Соединенным Королевством и Россией во время соревнований по гимнастике, показаны в таблице ниже:

США Великобритания Россия
5 1 4

Из медалей, выигранных этими тремя странами, какой процент медалей выиграли Соединенные Штаты?
50%

40%

10%

90%

Вопрос 10: Какая цифра соответствует разряду тысяч в числе 23 090 562?
6

9

0

5

Нажмите кнопку «Отправить», чтобы увидеть результаты.

,

Практика по математике для 5-х классов — Общая математика

Согласно CCSS, ученики пятого класса должны сосредоточиться на трех важнейших областях:
a) развитие навыков сложения и вычитания дробей и развитие понимания умножения дробей и деления дробей в ограниченных случаях,
б) расширение деления до 2-значных делителей, интеграция десятичных дробей в систему значений разряда и развитие понимания операций с десятичными дробями до сотых, а также развитие беглости работы с целыми числами и десятичными операциями,
в) развитие понимания объема.

Следующие ниже практические наборы вопросов по математике предназначены для проверки знаний учащихся пятого класса. Мы не связаны с Центром передового опыта Национальной ассоциации губернаторов (Центр NGA) или Советом директоров школ штата (CCSSO), которые координируют инициативу CCSS.

Общие основные операции и алгебраическое мышление 5-го класса
5.OA: Студенты должны писать и интерпретировать числовые выражения, а также анализировать закономерности и взаимосвязи.

Общие основные числа 5-го класса и операции в десятичной системе счисления
5.NTB: понимание системы значений разрядов, выполнение операций с многозначными целыми числами и десятичными дробями с точностью до сотых.

Общие керны 5-го класса
5.NF: ​​Студенты должны использовать эквивалентные дроби в качестве стратегии для сложения и вычитания дробей, а также применять и расширять предыдущее понимание умножения и деления для умножения и деления дробей.

Измерение и данные общего ядра 5-го класса
5.МД: Стандарты 5.MD CCS требуют, чтобы учащиеся пятого класса преобразовывали одинаковые единицы измерения в рамках данной системы измерения, представляли и интерпретировали данные, понимали концепции объема и связывали объем с умножением и сложением.

Геометрия общего сердечника 5-го класса
5.G: Предполагается, что учащиеся пятого класса смогут наносить точки на координатную плоскость для решения реальных и математических задач, а также классифицировать двумерные фигуры по категориям на основе их свойств.

,

alexxlab

Related Articles

5 класс

Решебник естествознание 5 класс гуревич рабочая тетрадь – ГДЗ по биологии 5 класс рабочая тетрадь Гуревич, Краснов, Нотов

Содержание ГДЗ по биологии 5 класс рабочая тетрадь Гуревич, Краснов, НотовГДЗ по естествознанию 5 класс рабочая тетрадь Гуревич ИсаеваГДЗ Физика рабочая тетрадь 5 класс А.Е. Гуревич, М.В. КрасновГДЗ за 5 класс по Физике А.Е. Гуревич, М.В. Краснов рабочая тетрадьНавигация по гдзГДЗ А.Е. Гуревич 5 класс по Физике рабочая тетрадь на Мегарешеба комГДЗ ЛОЛ за 5 […]

5 класс

Решебник по белорусскому 5 класс: ГДЗ по Белорусскому языку 5 класс Валочка часть 1, 2

Содержание ГДЗ по Белорусскому языку 5 класс Валочка часть 1, 2Персональный репетитор – решебникЧто представляет собой онлайн-справочникЧему учит онлайн-решебник по белорусскому языку для 5 класса ВалочкаРешебник (ГДЗ) по белорусскому языку за 5 классГДЗ по Белорусскому языку за 5 класс Валочка Г.М., Зелянко В.У. Решебник по белорусскому языку 5 класс Валочка – персональный репетитор Что включено […]

5 класс

Ответы на вопросы география 5 класс домогацких – ГДЗ решебник по географии 5 класс Домогацких, Введенский, Плешаков учебник

Содержание ГДЗ за 5 класс по Географии Е.М. Домогацких, Э.Л. ВведенскийНавигация по гдзГдз по Географии за 5 класс , авторы Е.М. Домогацких, Э.Л. Введенский, А.А. Плешаков5 класс География Домогацких и Введенский. Введение в географию 2013Мелкое описание учебника (пособия):Домогацких Е.М. География 5 класс, чтение в онлайн ГДЗ за 5 класс по Географии Е.М. Домогацких, Э.Л. Введенский […]

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *