Страница 27. Урок 14 — ГДЗ Математика 2 класс. Петерсон. Учебник часть 1
- Главная
- ГДЗ
-
2 класс -
Математика - Петерсон. Учебник часть 1
- Страница 27. Урок 14
Вернуться к содержанию учебника
Вопрос
Задание № 1. Вычисли устно. Что ты замечаешь?
| 40 — 30 | 10 — 5 | 40 — 35 |
Как можно вычесть двузначные числа по частям с переходом через разряд?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Задание № 2. Реши с объяснением, вычитая по частям. Что интересного в этих примерах?
Что интересного в этих примерах?
| 72 — 8 | 96 — 7 | 31 — 25 | 54 — 19 |
| 72 — 38 | 96 — 47 | 81 — 25 | 64 — 19 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Задание № 3. Реши примеры, вычитая по частям:
| 23 — 7 | 71 — 56 | 64 — 28 | 42 — 19 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Задание № 4.
а) Составь все возможные равенства из чисел 23, 18, 41. Какими способами можно проверить правильность решения примеров на сложение, примеров на вычитание.
б) Выполни вычитание и сделай проверку сложением.
| 91 — 19 | 82 — 28 | 73 — 37 | 64 — 46 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Задание № 5. Можно ли сравнивать эти длины, не видя закрытых цифр?
| 2 дм * см 3 дм * см | 7 дм * см * дм 9 см |
| 6 дм * см 6 дм 9 см | 2 * см 5 дм 1 см |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Задание № 6.
а) В классе было 6 девочек и 7 мальчиков. Потом 5 детей на автобусе уехали домой. Сколько детей осталось?
Сколько детей осталось?
б) В ведре было 11 л воды. Отлили 2 л воды в банку и 5 л воды в кастрюлю. Сколько литров воды осталось в ведре?
Ответ
Поделись с друзьями в социальных сетях:
Вернуться к содержанию учебника
конспект урока математики 2 класс Л.Г.Петерсон «Метр» | Презентация к уроку по математике (2 класс) на тему:
Автор: Смирнова Ирина Евгеньевна, учитель начальных классов МБОУ г. Мурманска гимназия № 2
Предмет: математика
Класс: 2 класс
Тип урока: урок открытия новых знаний
Вид урока: урок — сказка
Время проведения: сентябрь
Технологическая карта изучения темы
«Метр»
|
Тема |
«Метр» |
|
Цели |
— сформировать представление о новой единице измерения – метре; — развивать умение измерения длины с помощью метра; — развивать мышление детей при сопоставлении различных мерок; — способствовать развитию устной математической речи; — воспитывать культуру поведения при фронтальной и групповой работе; — проявлять способность к самооценке на основе критерия успешности учебной деятельности; — определять и формулировать тему и цель урока с помощью учителя; — использовать различные способы обработки, анализа и представления информации; -совместно договариваться о правилах поведения общения в группе и следовать им |
|
Основные понятия |
единицы измерения, мерки, метр, дециметр, сантиметр |
|
Межпредметные связи |
окружающий мир, изобразительное искусство, музыка |
|
Ресурсы: — основные — дополнительные |
Петерсон Л. — презентация; — план работы группы; — правила работы в группе (Приложение №1) — задание группам (Приложение №2) |
|
Условные обозначения |
|
|
Формы работы |
фронтальная, групповая, парная |
|
Этапы урока |
Ход урока |
|
I.Организационный момент |
1. Психологический настрой. — Посмотрите на экран (СЛАЙД). — Сегодня на уроке математики мы отправимся в гости к Удаву, обезьяне и их друзьям. |
|
II.Актуализация знаний |
— Однажды друзья собрались, как обычно, на поляне и решили развлечься. А надо вам сказать, они любили все пересчитывать. Выполните вместе с героями мультфильма задания и вы узнаете, какой вопрос мучил удава больше всего в это утро. 1.Сосчитайте (СЛАЙД) 59 — 9 83+5 90 – 7 60 + 40 2.Соедините числа в порядке увеличения. Какая фигура получится? (прямоугольник)(СЛАЙД) 3.Перед вами прямоугольник (у учителя в руках). Определите на глаз, чему равны стороны прямоугольника? Какие единицы измерения использовали? Сантиметр (слово – опора вывешивается на доску). Что можно найти у прямоугольника со сторонами 4 см и 7 см? (периметр) Найдите. 4.Логическая задача. Какое слово появилось? Дециметр (слово – опора вывешивается на доску).(СЛАЙД) |
|
III.Создание проблемной ситуации |
— Посмотрите отрывок из мультфильма. — Какой вопрос мучил удава? (измерить длину) Поможем. Посмотрите, какие мерки для измерения длины мы уже знаем? Какой из них можно воспользоваться? |
|
IV. Формулирование проблемы |
— Какой у вас возникает вопрос? Что нам сегодня предстоит выяснить? (Какой меркой можно воспользоваться, измеряя длинные предметы?) |
|
VI. Открытие нового знания |
1.– Попробуйте помочь удаву, работая в группах. Инструктаж о последовательности работы. — Вспомним порядок работы в группе. Расставь карточки-опоры по порядку. (СЛАЙД) Вспомним правила работы в группе? (Опоры — символы на доске). 1. Правило аплодисментов. (Приложение 1) 2. Правило поднятых рук. (Приложение 1) 3. Будь доброжелательным друг к другу. (Приложение 1) 4. Внимательно выслушивай каждого. (Приложение 1) Распределение ролей. — Чтобы работа протекала дружно, распределим роли в группе. (СЛАЙД) Особенности работы. Работа состоит из трех этапов. Выполнив задание одного этапа правильно, вы можете приступить к следующему. (Приложение 2) Работа в группе.
— Будьте внимательны. Представители группы отвечают, а вы слушаете и…(слышите), смотрите и…(видите), думаете и…(оцениваете). (Карточки-опоры с изображением правил обсуждения ответов размещены на доске).
|
|
V. Формулирование темы и целей урока |
Сформулируйте тему урока. ( Метр) Сформулируйте цель урока, используя опорные слова и знаки: (СЛАЙД) 1. Использовать… ( метр для измерения длины). 2. Решать …(задачи, примеры с новой единицей измерения). 3.Учиться работать … , (в паре, в группе). |
|
IX. Применение нового знания |
1.Проверьте в учебнике на с. 36 правильные ли выводы мы сделали? 2.Удаву интересно, какие предметы можно измерить метром? (СЛАЙД) 3.Песня «То березка, то рябина…».(СЛАЙД) О каких деревьях идет речь? Кто их видел? Какой высоты были деревья? Решение задачи №2(б) с. 36 (СЛАЙД) Проанализируйте задачу, решите самостоятельно, запишите решение в тетрадь.(2 человека работают у доски) Проверьте решение ребят у доски, можно ли читать его эталоном?
— Удавы, живущие в Южной Америке имеют длину около2 -12 м.(СЛАЙД) 5.Удаву понравилась самая большая мерка(метр), обезьяне чуть поменьше(дециметр), попугаю самая маленькая (сантиметр). Используя эти знания, заполните таблицу на с.36 №3. Работаем в паре. Как можно организовать работу, чтобы каждый принял в ней посильное участие? ( по очереди или по столбикам). Проверим выполнение задания по эталону на экране. У кого были ошибки, почему вы их допустили? Физминутка. 5. Необычное озеро в лесу. Все предметы, попав в него, меняют свое измерение. Маленькие единицы укрупняются, а большие становятся маленькими. Игра «Сказочное озеро». (СЛАЙД) Одно задание выполним вместе.Мерка 3м попала в озеро. Какими единицами более мелкими мы сможем ее заменить? 30 дм, 300см. Возьми единицу измерения из конверта, замени ее в озере (на доске картина озеро на нем различные единицы длины). |
|
Проверка знаний |
Проверь свои знания, выполни тест. (СЛАЙД) |
|
X. |
— Какие единицы измерения помогли быстро узнать длину удава? Что знаете о метре? Задайте вопросы по теме ребятам других групп. |
|
XI. Рефлексия |
-Посмотрите следующий отрывок мультфильма. Вспомните, какой вклад вы внесли в работу группы: если старались помочь — хлопайте в ладоши. Молодцы! Дружба нам помогла в работе. |
Элементарные методы и содержание | АМТЭ
Видеоресурсы для инструкторов
- Видеотека K-4 от Annenberg Media, демонстрирующая, как стандарты NCTM отражаются в начальных классах. http://www.learner.org/resources/series32.html
- Карпентер, Т., Франке, М.Л., и Леви, Л. (2003). Мыслить математически: интегрировать арифметику и алгебра в начальной школе. Портсмут, Нью-Хэмпшир: Heinemann.
- Карпентер и его коллеги работают над вторым изданием CGI, которое, как говорят, включает обновленные видеоклипы
- Видеоресурсы Кэтрин Фосно и ее коллег, посвященные программе «Молодые математики за работой» (комплекты для фасилитаторов включают обзорное руководство, руководство для фасилитаторов и интерактивный компакт-диск). http://www.heinemann.com/authors/productsByAuthor.aspx?id=293
- Пэрриш, С. (2010). Number Talks: помощь детям в построении умственной арифметики и вычислительных стратегий (мультимедийные профессиональные учебные ресурсы) . Саусалито, Калифорния: Математические решения.
- Филипп, Р. и Шаппель, Б. (2012). Интеграция математики и педагогики (IMAP): доступная для поиска коллекция видеоклипов о математическом мышлении детей. Бостон, Массачусетс: Пирсон.
- Сторейгард, Дж. (2009). Мои дети могут: сделать математику доступной для всех учащихся, K-5. Портсмут, Нью-Хэмпшир: Heinemann.
Исследование детского математического мышления
- Карпентер, Т.
 (1985). Учимся складывать и вычитать: упражнение в решении задач. В Э. Сильвер (ред.), Преподавание и обучение решению математических задач: множественные исследования точки зрения (стр. 17–40). Хиллсдейл, Нью-Джерси: Эрлбаум.
(1985). Учимся складывать и вычитать: упражнение в решении задач. В Э. Сильвер (ред.), Преподавание и обучение решению математических задач: множественные исследования точки зрения (стр. 17–40). Хиллсдейл, Нью-Джерси: Эрлбаум. - Карпентер Т., Феннема Э., Петерсон П. и Кэри Д. (1988). Педагогическое содержание знаний учителей о решении задач учащихся по элементарной арифметике. Journal for Research в области математического образования , 19 , 385-401.
- Карпентер Т., Феннема Э., Петерсон П., Чанг К. и Лоеф М. (1989). Использование знаний о детском математическом мышлении в обучении в классе: экспериментальное исследование. American Educational Research Journal , 26 (4), 499-531.
- Карпентер, Т., Франке, М.Л., и Леви, Л. (2003). Математическое мышление: объединение арифметики и алгебры в начальной школе. Портсмут, Нью-Хэмпшир: Heinemann.
- Чемберлен, М.
 (2005). Учителя обсуждают мышление студентов: решение проблемы внимания к мышлению студентов. Журнал образования для учителей математики, 8 , 141-170.
(2005). Учителя обсуждают мышление студентов: решение проблемы внимания к мышлению студентов. Журнал образования для учителей математики, 8 , 141-170. - Эмпсон, С. Б., Джанк, Д., Домингес, Х., и Тернер, Э. (2006) Дроби как координация мультипликативно связанных величин: перекрестное исследование детского мышления. Образовательные исследования в области математики, 63, 1, 1-28.
- Эмпсон, С. Б., и Леви, Л. (2011). Расширение детских математических дробей и десятичных знаков: Инновации в когнитивном обучении. Портсмут, Нью-Хэмпшир: Heinemann.
- Феннема, Э., Франке, М.Л., Карпентер, Т.П., и Кэри, Д.А. (осень, 1993 г.). Использование знаний детей в обучении. Американский журнал исследований в области образования, 30 (3), 555-583.
- Фьюсон, К. (1992). Исследование сложения и вычитания целых чисел. В D. Grouws (Ed.), Справочник по исследованиям в области преподавания и обучения математике (стр.
 243–275). Нью-Йорк: Макмиллан.
243–275). Нью-Йорк: Макмиллан. - Джейкобс, В., Амвросий, Р., Клемент, Л. и Браун, Д. (2006). Использование подготовленных учителем видеозаписей студенческих интервью в качестве катализаторов обсуждения. Обучение детей математике , 276–281.
- Каземи, Э., и Франке, М. (2004). Обучение учителей математике: использование работы учащихся для поощрения коллективных исследований . Журнал образования для учителей математики , 7 (3), 203–235.
- Вилласенор, А., и Кепнер, Х., «Арифметика с точки зрения решения задач: городская реализация», Journal for Research in Mathematics Education, 24 (1), 1993, стр. 62–69.
Исследования в области разнообразия, справедливости и детских фондов знаний, связанных с математикой
- Бреннер, М. (1998). Развитие математической коммуникации в группах по решению задач студентами языковых меньшинств. Двуязычный исследовательский журнал , 22, 2, 3 и 4, 149–175.
- Канманн, М.
 и Ремиллард, Дж. (2002). Что считается и как: преподавание математики в культурно, лингвистически и социально-экономически разнообразных городских условиях. The Urban Review, 34 (3), 179-204.
и Ремиллард, Дж. (2002). Что считается и как: преподавание математики в культурно, лингвистически и социально-экономически разнообразных городских условиях. The Urban Review, 34 (3), 179-204. - Гражданский, М. (2006). Опираясь на знания сообщества: путь к справедливости в математическом образовании. В Н. Насир и П. Кобб (ред.), Улучшение доступа к математике: разнообразие и равенство в классе (стр. 105–117) . Нью-Йорк: Издательство Педагогического колледжа.
- Гражданский, М. (2002). Культура и математика: общественный подход. Журнал межкультурных исследований Исследования , 23 (2), 133-148.
- де Абреу, Г. (1995). Понимание того, как дети переживают взаимосвязь между домашней и школьной математикой. Разум, культура и деятельность , 2(2), 119–142.
- Прапорщик, Дж. (2005). Помощь учителям в использовании домашней культуры учеников на уроках математики: этапы развития, чтобы стать эффективными учителями разных учеников.
 В A. Rodriguez & R. Kitchen (Eds.), Подготовка учителей математики и естественных наук для различных классов : Перспективные стратегии трансформационной педагогики (стр. 225-242). Махва, Нью-Джерси: Лоуренс Эрлбаум.
В A. Rodriguez & R. Kitchen (Eds.), Подготовка учителей математики и естественных наук для различных классов : Перспективные стратегии трансформационной педагогики (стр. 225-242). Махва, Нью-Джерси: Лоуренс Эрлбаум. - Гири, Д. (2004). Математика и проблемы с обучением. Journal of Learning Disability, 37 (10), 4–15.
- Гонсалес, Н., Молл, Л. и Аманти, К. (2005). Фонды знаний: Теоретические практики в домашних хозяйствах, сообществах и классах. Махва, Нью-Джерси: Лоуренс Эрлбаум.
- Гонсалес, Н., Андраде, Р., Сивил, М., Молл, Л. (2001). Объединение фондов распределенных знаний: создание зон практики по математике. Журнал образования для студентов, размещенный по адресу Risk , 6 (1 и 2), 115–132.
- Гутьеррес, Р. (2002). Помимо эссенциализма: сложность языка в преподавании математики латиноамериканским студентам. Американский журнал исследований в области образования, 39 (4), 1047-1088.

- Гуцетин Э., Липман П., Эрнандес П. и Рейес Р. (1997). Культурно значимое преподавание математики в мексиканско-американском контексте. Journal for Mathematics Research Education , 28 (6), 709-737.
- Карп, К. (2004). Формирование ответственности за обучение у учащихся с особыми потребностями. Обучение детей математике, 11 (3), 118–126.
- Хисты, Л. (1995). Создание неравенства: вопросы языка и смысла в обучении математике латиноамериканских студентов. В W. Secada, E. Fennema, & L. Adajain (Eds.), Новые направления для справедливости в математическом образовании (стр. 279-297). Нью-Йорк: Кембридж.
- Ладсон-Биллингс, Г. (1995). К теории культурно значимой педагогики. American Журнал исследований образования , 32 (3), 465-491.
- Липка, Дж. (2005). Математика в культурном контексте: два тематических исследования успешного математического проекта, основанного на культуре.
 Ежеквартальный журнал «Антропология и образование» , 36 (4), 367–385.
Ежеквартальный журнал «Антропология и образование» , 36 (4), 367–385. - Лубенски, С. Т. (2007). Исследования, реформы и равенство в математическом образовании. В N. S. Nasir & P. Cobb [Eds.] Улучшение доступа к математике: разнообразие и равенство в классе (стр. 10-23). Нью-Йорк: Издательство педагогического колледжа.
- Лубенски, С. Т. (2000). Решение задач как средство достижения «математики для всех»: исследовательский взгляд через призму класса. Журнал исследований в области математического образования , 31 (4), 454-482.
- Мальдонадо, Л., Тернер, Э., Домингес, Х. и Эмпсон, С. (2008 г., в печати). Учащиеся, изучающие английский язык, учатся и участвуют в математических дискуссиях . Для публикации в Математика для ВСЕХ: Учебные стратегии для разных классов: классы 3- 5 . Рестон, Вирджиния: NCTM.
- Мэтьюз, Л. (2003). Дети за бортом! Сложности включения культурно значимого обучения в обучение математике.
 Образовательные исследования по математике, 53, 61–82.
Образовательные исследования по математике, 53, 61–82. - Молл, Л. К., Аманти, К., Нефф, Д., и Гонсалес, Н. (1992). Фонды знаний для обучения: использование качественного подхода для соединения дома и классной комнаты. Теория на практике , 31 (2), 132–141.
- Мошкович, Дж. (2002). Ситуативный и социокультурный взгляд на двуязычных учащихся математики. Математическое мышление и обучение, 4 (2 и 3), 289–212.
- Насир, Н., Хэнд, В. и Тейлор, Э. (2008). Культура и математика в школе: границы между «культурными» и «предметными» знаниями на уроках математики и за их пределами. Обзор исследований в области образования , 32(1): 187–240.
- Тейт, В. (1994, февраль). Раса, сокращение и реформа школьной математики. Фи Дельта Каппан , 477-484.
- Вейджер, А. А., и Уайт, К. (2013). Математика для детей младшего возраста: чьи домашние занятия являются привилегированными? Journal of Urban Mathematics Education, 6 (1), 81–95.

- Вейджер, А.А. (2012). Включение внешкольной математики: от культурного контекста к встроенной практике. Журнал педагогического образования по математике, 15 (1), 9 – 23.
Исследования по интеграции детского математического мышления с детскими фондами знаний
- Агирре, Дж., Тернер, Э. Э., Бартелл, Т., Крейг, К. ). Установление связей на практике: как будущие учителя начальных классов подключаются к математическому мышлению детей и общественным фондам знаний в обучении математике. Журнал педагогического образования 64 (2), 178-192.
- Фут, М. (2006). Присоединение к изучению культуры и математического мышления путем изучения отдельного ребенка. In Alatorre, S., Cortina, J.L., Sáiz, M., and Méndez, A. (Eds) Proceedings of the 28 Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, 2, 693 . Мерида, Мексика: Национальный педагогический университет.

- Фут, М. К. (2009). Выход из класса: формирование знаний учителя для развития практики в классе. Педагогическое образование Ежеквартальный , 36 (3), 39-53.
- Родригес, А. (2005). Использование социотрансформационного конструктивизма для ответа на сопротивление учителей идеологическим и педагогическим изменениям. В A. Rodriguez & R. Kitchen (Eds.), Подготовка учителей математики и естественных наук для различных классов: перспективные стратегии трансформационной педагогики (стр. 17-32). Махва, Нью-Джерси: Лоуренс Эрлбаум.
- Тернер, Э., Селедон-Паттичис, С., и Маршалл, Массачусетс (2008). Возможности для изучения проблем Решение и математический дискурс среди латиноамериканцев/учащихся детского сада. In R. Kitchen & E. Silver (Eds.) Содействие активному участию и успеху в математике латиноамериканских учащихся: изучение возможностей и изучение многообещающих практик [Исследовательская монография TODOS: Математика для ВСЕХ] Вашингтон, округ Колумбия: National Education Association Press.

Литература, связанная с общественными математическими исследованиями
- Бак, П. и Скилтон-Сильвестр, П. (2005). Учителя до начала работы входят в городские сообщества: объединение фонда исследований знаний и критической педагогики в педагогическом образовании. В Гонсалес, Н., Молл, Л. и Аманти, К. (ред.), Фонды знаний: Теоретические практики в домашних хозяйствах, сообществах и классах. (стр. 213–232). Махва, Нью-Джерси: Лоуренс Эрлбаум.
- Гражданский, М. (2006). Опираясь на знания сообщества: путь к справедливости в математическом образовании. В Н. Насир и П. Кобб (ред.), Улучшение доступа к математике: разнообразие и равенство в классе (стр. 105–117) . Нью-Йорк: Издательство педагогического колледжа.
- Гражданский, М. (2002). Культура и математика: общественный подход. Журнал межкультурных исследований Исследования , 23 (2), 133-148.
- де Абреу, Г.
 (1995). Понимание того, как дети переживают взаимосвязь между домашней и школьной математикой. Разум, культура и деятельность , 2(2), 119–142.
(1995). Понимание того, как дети переживают взаимосвязь между домашней и школьной математикой. Разум, культура и деятельность , 2(2), 119–142. - Дрейк, К. и Нортон-Мейер, Л. (2007). Создание третьих пространств: интеграция семейных и общественных ресурсов в элементарные математические методы. Документ, представленный на ежегодном собрании PME-NA, 25 октября 2007 г.
- Прапорщик, Дж. (2005). Помощь учителям в использовании домашней культуры учеников на уроках математики: этапы развития, чтобы стать эффективными учителями разных учеников. В A. Rodriguez & R. Kitchen (Eds.), Подготовка учителей математики и естественных наук для различных классов : перспективные стратегии для преобразующей педагогики (стр. 225–242). Махва, Нью-Джерси: Лоуренс Эрлбаум.
- Гонсалес, Н., Молл, Л. и Аманти, К. (2005). Фонды знаний: теоретические практики в домохозяйств, сообществ и классных комнат. Махва, Нью-Джерси: Лоуренс Эрлбаум.

- Лэдсон-Биллингс, Г.Дж. (1999). Подготовка учителей к разнообразным студенческим контингентам: критическая перспектива расовой теории. Обзор исследований в области образования , 24, 211-247.
- Ладсон-Биллингс, Г. (1995). К теории культурно значимой педагогики. American Журнал исследований образования , 32 (3), 465-491.
- Липка, Дж. (2005). Математика в культурном контексте: два тематических исследования успешного математического проекта, основанного на культуре. Ежеквартальный журнал «Антропология и образование» , 36 (4), 367–385.
- Милнер, Х. Р. и Смитни, М. (2003). Как педагоги-педагоги создали учебную программу курса, чтобы бросить вызов и улучшить мышление и опыт учителей, работающих в начальной школе, с разнообразием. Педагогическое образование, 14 (3), 293-305.
- Civil, M. & Kahn, LH (2001). Обучение математике разработано на основе садовой темы. Обучение детей математике, 7 (7), 400-405.

- Флорес, А. (1997). Sí se puede. Это можно сделать: Качественная математика на нескольких языках. В Дж. Тентракоста (ред.), Многокультурное и гендерное равенство в классе математики (стр. 81-91). Рестон, Вирджиния: Национальный совет учителей математики.
- Гонсалес, Н., Андраде, Р., и Карсон, К. (2001). Создание связей между домашними и школьными занятиями по математике. Э. Макинтайр, А. Роузбери и Н. Гонсалес (ред.), Классная комната Разнообразие: связь учебной программы с жизнью учащихся (стр. 100–114). Портсмут, Нью-Хэмпшир: Хайнеманн.
- Гутштейн Э. и Петерсон Б. (2005). Переосмысление математики: преподавание социальной справедливости с помощью чисел (стр. 117–120). Милуоки: переосмысление школьных публикаций.
- Кан, Л. и Сивил, М. (2001). Раскопки математики классного сада. В Э. Макинтайр, А. Роузбери и Н. Гонсалес (ред.), Разнообразие в классе: подключение школы к жизни учащихся, (стр.
 37–50). Портсмут, Нью-Хэмпшир: Хайнеманн.
37–50). Портсмут, Нью-Хэмпшир: Хайнеманн. - Кайл, Д., Макинтайр, Э., и Мур, Г. (2001). Связь обучения математике с семьями детей раннего возраста. Обучение детей математике , 80-86.
- Ло Цицерон, А., Фьюсон, К., и Аллекссахт-Снайдер, М. (2001), Математика детских рассказов, помощь детям в решении словесных задач и поддержка участия родителей . В В. Секаде (ред.) Изменение лица математики: взгляды на латиноамериканцев (стр. 59-70). Рестон, Вирджиния: NCTM.
- Торрес-Веласкес, Д. (2004). Обучение математике с учетом культурных особенностей и изучающих английский язык. Обучение детей математике , 249-255.
- Тернер, Э. и Фонт Строун, Б. (2007 г., май). Постановка важных проблем: исследование переполненности школ. Обучение детей математике . (стр. 457-463).
- Тернер, Э. и Фонт Строхун, Б. (2005). С математикой у вас как будто больше защиты. В Gutstein E. & Peterson, B. (Eds.), Переосмысление математики: преподавание социальной справедливости по числам (стр.
 81–87). Милуоки: переосмысление школьных публикаций.
81–87). Милуоки: переосмысление школьных публикаций.
Математические задачи
- Брейфогл, М.Л. и Уильямс, Л.Е. (2008/2009). Разработка и реализация полезных задач. Обучение детей математике, 276–280.
- Кофилд, Р., Харкнесс, С.С. и Райли, Р. (2003). Сюрприз! Превращение рутинных проблем в стоящую задачу. Преподавание математики в средней школе, 198 – 201.
- Чирилло, М., Хербель-Айзенманн, Б. и Дрейк, К. (2009). Использование учебной программы, чтобы сосредоточиться на понимании. Преподавание математики в средней школе, 15 (1), 51–56.
- Фелтон, доктор медицины (2010). Является ли математика политически нейтральной? Обучение детей математике, 60–63.
- Кабири, М.С. и Смит, Н.Л. (2003). Превращение традиционных задач учебника в открытые задачи. Преподавание математики в средней школе, 186–192.
- Лэнд, Т., Дрейк, К., Бартелл, Т.Г., Агирре, Дж., Фут, М.К., Рот Макдаффи, А.
 , и Тернер, Э.Э. (в печати). Три стратегии открытия учебных пространств. Обучение детей Математика.
, и Тернер, Э.Э. (в печати). Три стратегии открытия учебных пространств. Обучение детей Математика. - Перессини, Д. и Кнут, Э. (2000). Роль задач в развитии сообществ математических исследований. Обучение детей математике, 391–397.
- Смит, М.С., Билл, В. и Хьюз, Э.К. (2008). Продумывание урока: успешное выполнение задач высокого уровня. Преподавание математики в средней школе, 14 (3), 132–138.
- Сталлингс, Л.Л. (2007). Смотрите другую математику. Преподавание математики в средней школе, 13 (4), 212–217.
Дискуссия в классе/нормы для обсуждения
- Чапин, С. Х., О’Коннор, К., и Андерсон, Н. К. (2009). Обсуждения в классе: использование математических разговоров для помощи учащимся в изучении (издание 2 и ). Саусалито, Калифорния: Scholastic, Inc.
- Чапин, С. Х., и О’Коннор, К. (2007). Академически продуктивный разговор: поддержка обучения учащихся математике.
 В WG Martin & ME Strutchens (Eds.), Изучение математики (стр. 113–128). Рестон, Вирджиния: Национальный совет учителей математики.
В WG Martin & ME Strutchens (Eds.), Изучение математики (стр. 113–128). Рестон, Вирджиния: Национальный совет учителей математики. - Эсмонд, И. (2009). Идеи и идентичность: поддержка справедливости в совместном обучении математике. Review of Educational Research, 79 (2), 1008-1043.
- Хербель-Эйзенманн, Б., и Чирилло, М. (ред.). (2009 г.). Содействие целенаправленному дискурсу . Рестон, Вирджиния: NCTM.
- Джейкобс, В. Р. и Амвросий, Р. К. (2008/2009). Максимальное использование сюжетных задач. Преподавание Математика для детей , 260 – 266.
- Мальдано, Л. А., Тернер, Э. Э., Домингес, Х., и Эмпсон, С. Б. (2009). Учащиеся, изучающие английский язык, изучают математические дискуссии и участвуют в них. In D. White & J. Spitzer (Eds.) Математика для каждого учащегося: ответ на разнообразие, классы PreK-5 (стр. 7–22). Рестон, Вирджиния: Национальный совет учителей математики.
- Парков, А.
 Н. (2009). Могут ли учителя быть слишком открытыми? Обучение детей математике, 424–428.
Н. (2009). Могут ли учителя быть слишком открытыми? Обучение детей математике, 424–428. - Рот Макдаффи, А., и Янг, Т.А. (2003). Продвижение математического дискурса через детскую литературу. Обучение детей математике, 385–389.
- Смит, М.С. и Штейн, М.К. (2011). 5 практик для продуктивной математики дискуссий. Рестон, Вирджиния: Национальный совет учителей математики.
- Staples, M., & Colonis, MM (2007). Максимальное использование математических дискуссий. Учитель математики, 101 (4), 257-261.
- Тернер, Э., Селедон-Паттичис, С., и Маршалл, Массачусетс (2008). Возможности научиться решать задачи и говорить о математике среди латиноамериканцев и учащихся детского сада. В R. Kitchen & E. Silver (Eds.), Содействие активному участию и успеху в математике латиноамериканских учащихся : изучение возможностей и изучение перспективных практик [Научная монография TODOS: Математика для ВСЕХ] Вашингтон, округ Колумбия: Издательство Национальной образовательной ассоциации.

Пейдж Петерсон, автор Клубов мальчиков и девочек округа Кинг
В прошлом месяце наша программа Magnolia Pre-K усердно работала над их математическими навыками, изучением новых музыкальных инструментов и чтением!
Продолжить чтение >
В «Молодежном квартале» члены наших клубов награждаются и чествуются за их достижения и вклад в области академической успеваемости, здорового образа жизни, хорошего характера и гражданственности.
Продолжить чтение >
В программе Киркланда STEAM дети получают опыт связи между академическими уроками и реальными приложениями с программированием, адаптированным к их интересам.
Продолжить чтение >
North Beach Учащиеся с 3 по 5 классы тренируют навыки лидерства, планируя, организуя и проводя 6-недельные мини-клубы для младших членов клуба.
Продолжить чтение >
Учащиеся средних классов в Robert Eagle Staff подают нашему сообществу пример того, как поддерживать и уважать наших соседей.
Продолжить чтение >
Сотрудничество между клубом и школой Хотя Международный клуб мальчиков и девочек средней школы Гамильтона начал свою работу только в прошлом году, за это время между школой и клубом сложились невероятно тесные партнерские отношения. Эти две группы сотрудничают, чтобы предоставить детям постоянные ресурсы и внимание, чтобы они не сбились с пути в учебе и обществе. Клубы мальчиков и девочек начали работать за пределами школы с шестинедельным летним лагерем в 2018 году, в котором участвовали учителя государственной школы Сиэтла и были ориентированы на 9 человек.0411
Продолжить чтение >
Юные члены Sacajawea Torch Club (от детского сада до 5-го класса) стремятся улучшить свои сообщества и помочь другим. Недавно дети собрали 600 долларов на новые коврики в спортзале Sacajawea Elementary, продавая выпечку, которую они сделали сами в клубе. С тех пор дети проявляют интерес и узнают все о животных. В среду, 15 мая, Бренна из «Тихой гавани» в Пасадо приехала, чтобы поговорить с членами клуба Sacajawea Torch Club о том, как они могут помочь нуждающимся животным. Пасадо
Пасадо
Продолжить чтение >
Выходи и отпразднуй последний танец года в средней школе на острове Мерсер! Классы: 6–8. Дата: пятница, 31 мая 2019 г.. Время: 19:00. до 22:00 Цена: 5 долларов США для участников / 10 долларов США для лиц, не являющихся членами. Для входа требуется карта ASB.
Часы работы Дневная программа: конец учебного дня до 18:30. Ежедневное дневное расписание 2:25 – Прибывают дети, вожатые забирают детей из детского сада 1-го класса. Бесплатная игра на улице до 3:00. 3:00-3:30 – Закуски подаются в семейном стиле в каждом номере. 3:30-4:00 – В зависимости от возрастной группы дети либо начнут Час силы, либо другое занятие. 4:00–5:00 – Дети начинают свое второе занятие, которое может включать в себя: занятия в тренажерном зале, занятия в компьютерной лаборатории, художественные занятия, кулинарные занятия и т. д. 5:00–5:40
Продолжить чтение >
Keystone — замечательная часть клубов для мальчиков и девочек по всей стране. Эта группа общественных работ, возглавляемая учащимися, помогает старшеклассникам помогать своим сообществам там, где они считают это необходимым.
 Г.Математика.2 класс.Часть 1.- М.:Издательство «Ювента»,2012. – 80с.:ил.
Г.Математика.2 класс.Часть 1.- М.:Издательство «Ювента»,2012. – 80с.:ил.
 (СЛАЙД)
(СЛАЙД)
 Вспомним, какова зависимость между ними. Что она вам напоминает( соотношение сотен, десятков, единиц)(СЛАЙД)
Вспомним, какова зависимость между ними. Что она вам напоминает( соотношение сотен, десятков, единиц)(СЛАЙД)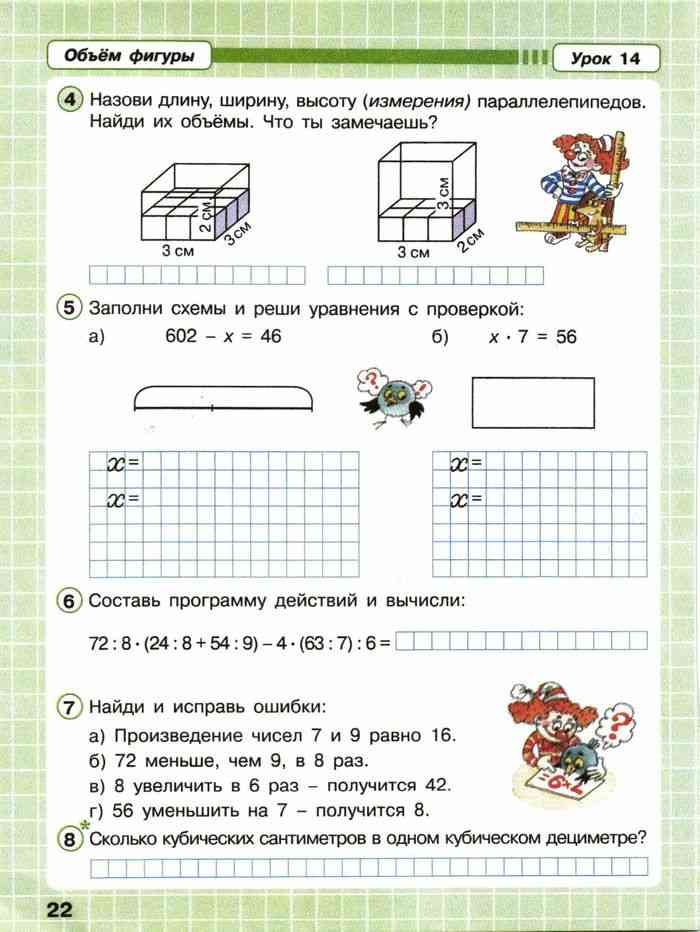 Итог урока
Итог урока