Контрольная работа по алгебре 10 класс ответы и решения – 404

Тест по алгебре (10 класс) по теме: Контрольные работы по Алгебре 10 класс

КОНТРОЛЬНАЯ РАБОТА № 1

Вариант 1

1. Задает ли указанное правило функцию

В случае положительного ответа:

а) найдите область определения функции;

б) вычислите значения функции в точках 0, 1, 3, –1;

в) постройте график функции;

г) найдите промежутки монотонности функции.

2. Исследуйте функцию  на четность.

3. На числовой окружности взяты точки  Найдите все числа t, которым на данной окружности соответствуют точки, принадлежащие дуге MN. Сделайте чертёж.

4. Задайте аналитически и постройте график функции  у которой

5. Найдите функцию, обратную функции  Постройте на одном чертеже графики этих взаимно обратных функций.

6. Известно, что функция  убывает на R. Решите неравенство

Вариант 2

1. Задает ли указанное правило функцию

В случае положительного ответа:

а) найдите область определения функции;

б) вычислите значения функции в точках –4, –2, 0, 4;

в) постройте график функции;

г) найдите промежутки монотонности функции.

2. Исследуйте функцию  на четность.

3. На числовой окружности взяты точки  Найдите все числа t, которым на данной окружности соответствуют точки, принадлежащие дуге MN. Сделайте чертёж.

4. Задайте аналитически и постройте график функции  у которой

5. Найдите функцию, обратную функции  Постройте на одном чертеже графики этих взаимно обратных функций.

6. Известно, что функция  возрастает на R. Решите неравенство

ройте график функции  у которой

5. Найдите функцию, обратную функции  Постройте на одном чертеже графики этих взаимно обратных функций.

6. Известно, что функция  возрастает на R. Решите неравенство

Рекомендации по оцениванию контрольной работы

Каждый вариант контрольной работы выстроен по одной и той же схеме: задания обязательного минимума – до первой черты, задания среднего уровня – между первой и второй чертой, задания уровня выше среднего – после второй черты. Шкала оценок за выполнение контрольной работы может выглядеть так: за успешное выполнение только заданий обязательного минимума – оценка «3»; за успешное выполнение заданий обязательного минимума и одного дополнительного (после первой или второй черты) – оценка «4»; за успешное выполнение заданий всех трех уровней – оценка «5». При этом оценку не рекомендуется снижать за одно неверное решение в первой части работы (допустимый люфт).

Решение контрольной работы

Вариант 1

1. Правило задает функцию, если, во-первых, можно выполнить действия, а во-вторых, соблюдается однозначность функции.

В случае

условия не соблюдаются: f(0) = 0 и f(0) = –1.

б)  – не определено;

г) на [0; 2) и на [2; +∞) функция возрастает, в точке х = 2 функция имеет разрыв.

2.  – симметрична относительно начала координат.

 значит, функция f(х) – нечетная.

5. у = 2 – х2 Квадратичная функция определена и убывает при х ≥ 0, значит, существует обратная функция: у = 2 – х2;

Функция

6. у = f(х) убывает на R.

 значит, неравенство верно при  Возведем обе части в квадрат:

Ответ:

nsportal.ru

Учебно-методический материал по алгебре (10 класс) на тему: контрольные работы по алгебре 10 класс

Вариант1.

1. Вычислить:

а)

б)

2. Упростить выражение:

3. Известно, что 8 х = 5. Найдите 8 –х + 2.

4. Решите уравнение: 8 3х + 1 = 8 5 .

5. Записать в виде обыкновенной дроби число 0,3(6).

6. Сократить дробь:

.

7. Упростить выражение:

Вариант 2.

1. Вычислите:

      а)

       б)  

      2. Упростить выражение:

      3. Известно, что 12 х = 3. Найдите 12 2 х — 1.

      4. Решите уравнение: .

      5. Записать в виде обыкновенной дроби   число 0,(43).

      6. Сократить дробь:

      .

     7. Упростить выражение:

        .

Вариант 3.

1. Вычислите:

       а)

       б)

      2. Упростить выражение:

       3. Известно, что 1,2 х = 3. Найдите 1,2 3х + 1 .

    4. Решите уравнение: 6 2х = .

    5. Записать в виде обыкновенной дроби число 0,2(7).

    6. Сократите дробь:

    .

7. Упростить выражение:

Вариант 4.

1. Вычислите:

а)

б) (

         2. Упростить выражение:

   3. Известно, что 0,7 х = 5. Найдите 0,7 2х +1 .

    4. Решите уравнение: .

    5. Записать в виде обыкновенной дроби число 0,3(1).

    6. Сократить дробь:

       .

   7. Упростить выражение:

nsportal.ru

Контрольные работы «Алгебра 10 класс»

А-10 Контрольная работа №1. Действительные числа

Вариант 1

1. Вычислите: ;

2. Упростите выражение

3. Решите уравнение

4. Запишите бесконечную периодическую дробь 0,(43) в виде обыкновенной дроби.

5. Сократите дробь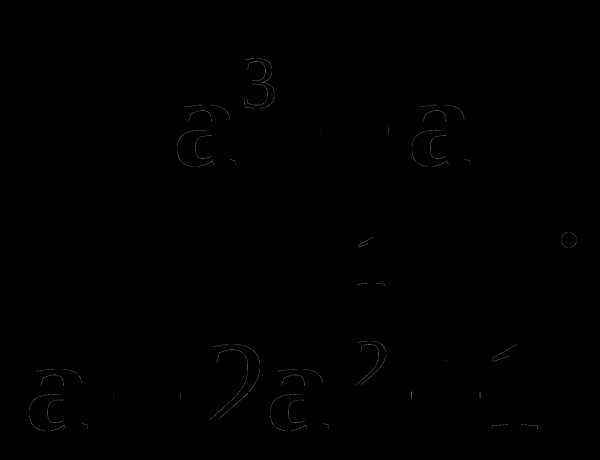

6. Сравните числа: и 1;

7*. Упростите выражение

1. Контрольная работа №1. Действительные числа

Вариант 2

1. Вычислите:

2. Упростите выражение

3. Решите уравнение

4. Запишите бесконечную периодическую дробь 0,3(6) в виде обыкновенной дроби.

5. Сократите дробь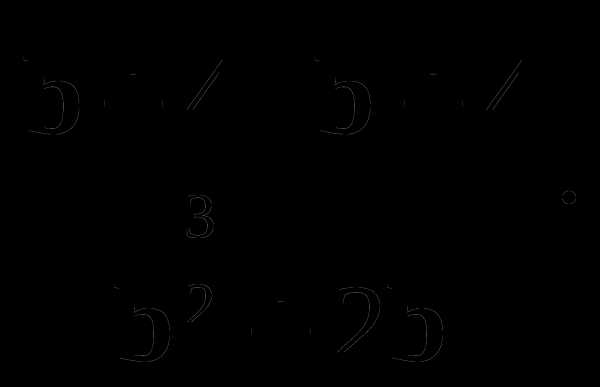

6. Сравните числа: 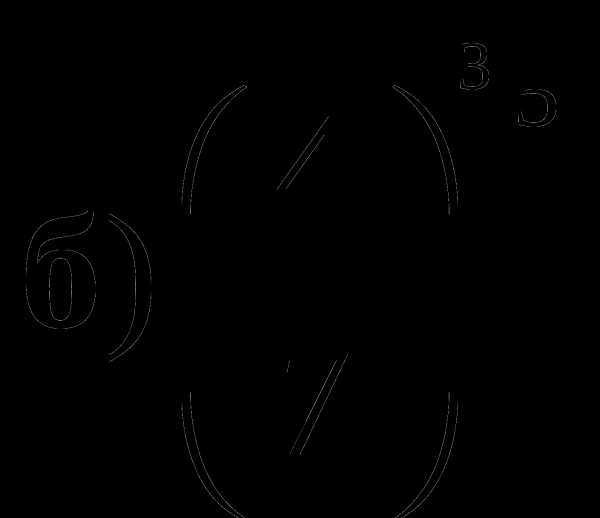и 1;

7*. Упростите выражение

А – 10 Контрольная работа № 2

Степенная функция

Вариант 1

1. Найдите область определения функции .

2. Схематически изобразите график функции и перечислите её основные свойства. Пользуясь свойствами этой функции, сравните:

.

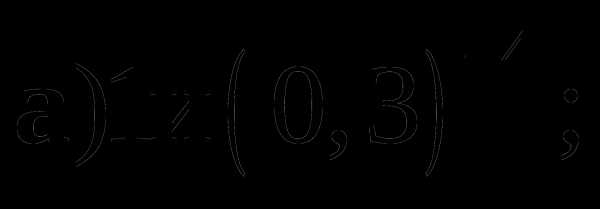3. Решите уравнение

4. Решите уравнение

5. Установите, равносильны ли неравенства и

6. Найдите функцию, обратную функции 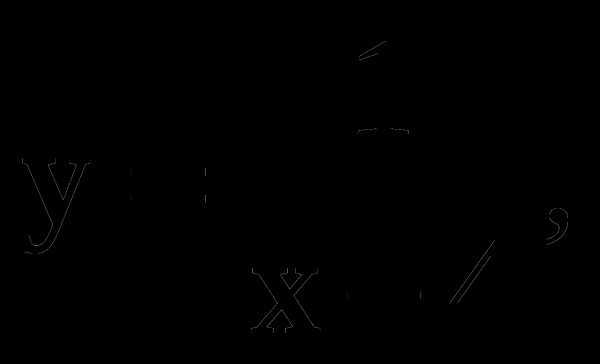и укажите её область определения и множество значений.

7*. Решите неравенство

Контрольная работа № 2

Степенная функция

Вариант 2

1. Найдите область определения функции

2. Схематически изобразите график функции 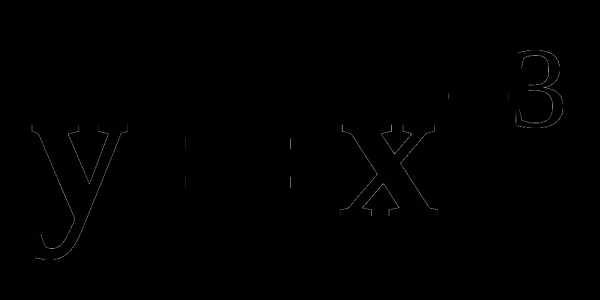и перечислите её основные свойства. Пользуясь свойствами этой функции, сравните:

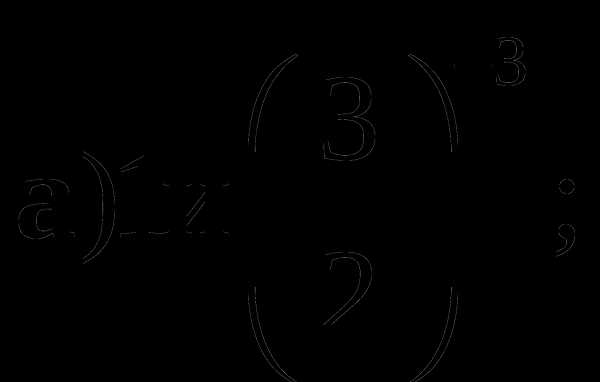
3. Решите уравнение

4. Решите уравнение

5. Установите, равносильны ли неравенства и

6. Найдите функцию, обратную функции и укажите её область определения и множество значений.

7*. Решите неравенство

А – 10 Контрольная работа № 3

Показательная функция

Вариант 1

1. Сравните числа: б)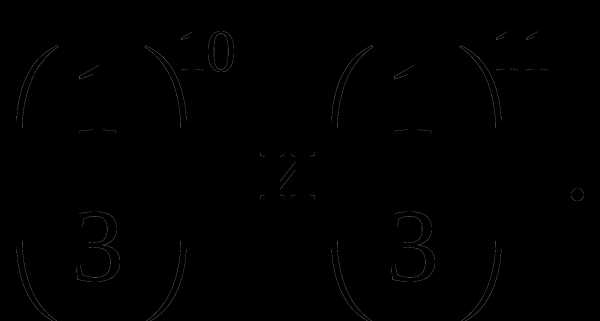

2. Решите уравнение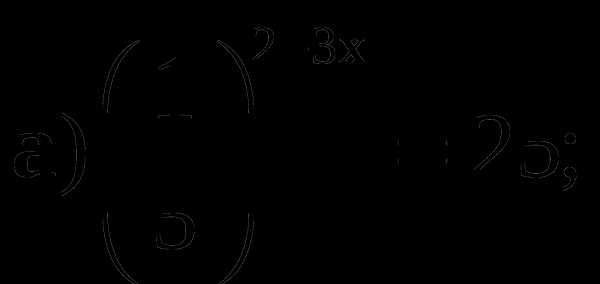

3. Решите неравенство .

4. Решите неравенство: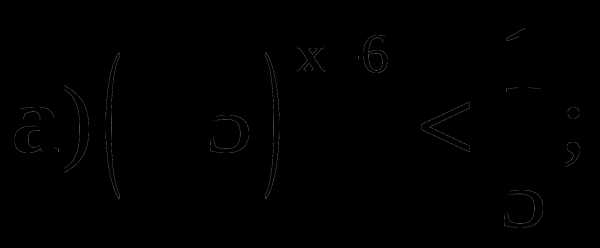

5. Решите систему уравнений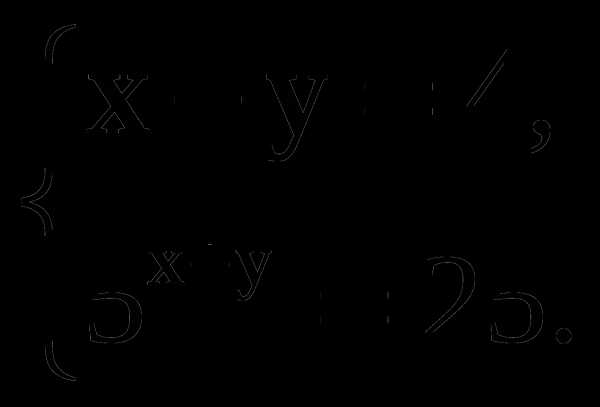

6. Решите уравнение:

Контрольная работа № 3

Показательная функция

Вариант 2

1. Сравните числа: б)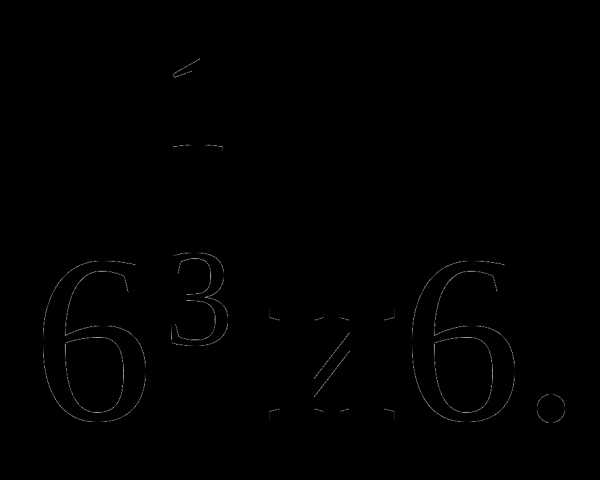

2. Решите уравнение

3. Решите неравенство .

4. Решите неравенство:

5. Решите систему уравнений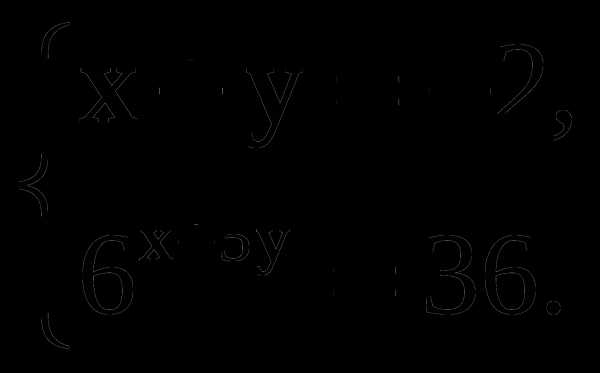

6. Решите уравнение:

А – 10 Контрольная работа № 4

Логарифмическая функция

Вариант 1

1. Вычислите:

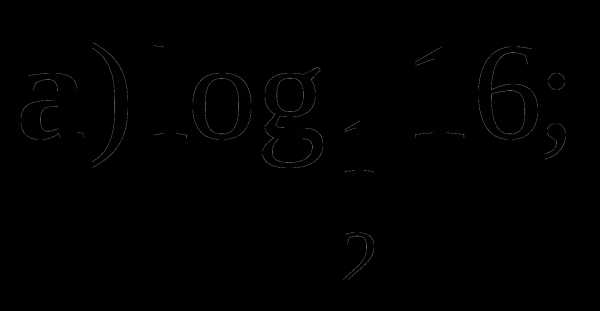
2. Сравните числа и

3. Решите уравнение

4. Решите неравенство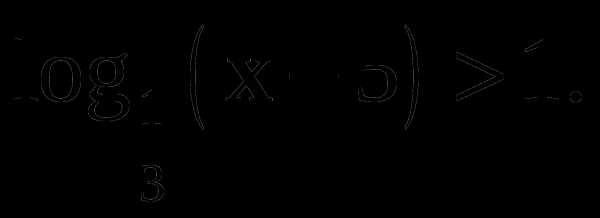

5. Решите уравнение

6. Решите неравенство:

Контрольная работа № 4

Логарифмическая функция

Вариант 2

1. Вычислите:

2. Сравните числа 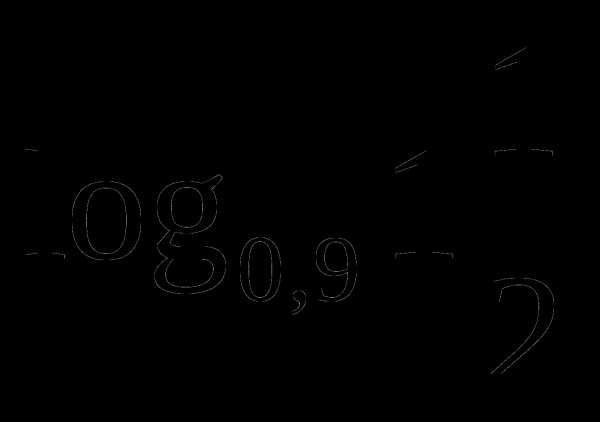и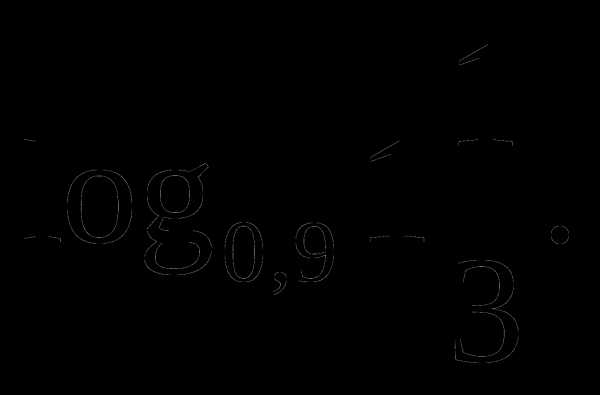

3. Решите уравнение

4. Решите неравенство

5. Решите уравнение

6. Решите неравенство:

А – 10 Контрольная работа №5

Тригонометрические формулы

Вариант 1

1. Вычислите:

2. Вычислите sinα, если и

3. Упростите выражение:

4. Решите уравнение

5. Докажите тождество

Контрольная работа №5

Тригонометрические формулы

Вариант 2

1. Вычислите:

2. Вычислите cosα, если и

3. Упростите выражение:

4. Решите уравнение

5. Докажите тождество

А – 10 Контрольная работа № 6

Тригонометрические уравнения

Вариант 1

1. Решите уравнение:

2. Найдите решение уравнения 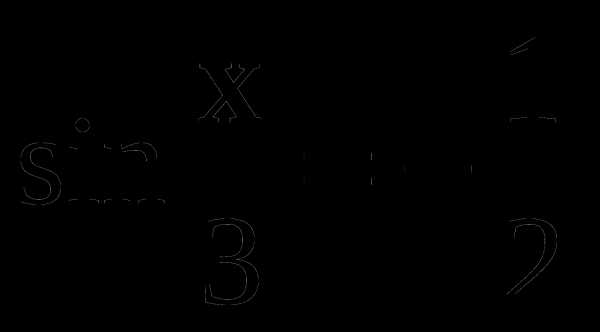на отрезке .

3. Решите уравнение:

.

4. Решите уравнение:

Контрольная работа № 6

Тригонометрические уравнения

Вариант 2

1. Решите уравнение:

2. Найдите решение уравнения на отрезке .

3. Решите уравнение:

4. Решите уравнение:

Контрольная работа № 7

Элементы комбинаторики

1. Вычислите:

2. Сколько существует способов для обозначения вершин четырехугольника с помощью букв A, B, C, D, E, F?

3. Запишите разложение бинома

Контрольная работа №7

1.Из урны, содержащей 15 белых, 10 красных и 5 синих шаров, наугад выбирают один шар. Какова вероятность того, что шар окажется: а) красного цвета; б) зеленого цвета?

2.Бросаются монета и игральная кость. Какова вероятность того, что появится решка и 5 очков?

3. Вероятность попадания по мишени равна 0.7. Какова вероятность того, что, не попав по мишени при первом выстреле, стрелок попадет при втором?

infourok.ru

ГДЗ по алгебре за 10 класс контрольные работы Глизбург В.И. Базовый уровень

GDZ.RU

• 1 класс
  

  • Математика
  • Английский язык
  • Русский язык
  • Информатика
  • Музыка
  • Литература
  • Окружающий мир
  • Человек и мир

• 2 класс
  

  • Математика
  • Английский язык
  • Русский язык
  • Немецкий язык
  • Белорусский язык
  • Информатика
  • Музыка
  • Литература
  • Окружающий мир
  • Человек и мир

• 3 класс
  

  • Математика
  • Английский язык
  • Русский язык
  • Немецкий язык
  • Белорусский язык
  • Информатика
  • Музыка
  • Литература
  • Окружающий мир
  • Человек и мир
  • Испанский язык

• 4 класс
  

  • Математика
  • Английский язык
  • Русский язык
  • Немецкий язык
  • Информатика
  • Музыка
  • Литература
  • Окружающий мир
  • Человек и мир
  • Испанский язык

• 5 класс
  

  • Математика
  • Английский язык
  • Русский язык
  • Немецкий язык

gdz.ru

ГДЗ по алгебре для 10 класса контрольные работы Глизбург В.И.

ГДЗ от Путина

Найти

• • 1 класс
    • Математика
    • Английский язык
    • Русский язык
    • Немецкий язык
    • Информатика
    • Природоведение
    • Основы здоровья
    • Музыка
    • Литература
    • Окружающий мир
    • Человек и мир
  • 2 класс
    • Математика
    • Английский язык
    • Русский язык
    • Немецкий язык
    • Белорусский язык
    • Украинский язык
    • Информатика
    • Природоведение
    • Основы здоровья
    • Музыка
    • Литература
    • Окружающий мир
    • Человек и мир
    • Технология
  • 3 класс
    • Математика
    • Английский язык
    • Русский язык

gdzputina.ru

Сборник контрольных работ по алгебре, (10 класс)

Контрольная работа № 1

по теме «Функции и их свойства»

Цель: проверить уровень усвоение ГОСО

— умение находить значение функции в точке;

— умение находить область определения функции;

— умения строить эскиз графика функции и находить по эскизу промежутки

возрастания и убывания , экстремумы функции, точки пересечения с осями

координат;

— знания свойств четных и нечетных функций.

1. Вычислите:

y = f(x) является нечетной y = f(x) является четной

2 f(-4) + f(3) f(-3) + 2 f(1)

eсли f(4)=1, f(-3)=2 eсли f(3)=4, f(-1)=2

2. Найдите значение функции в точке X0.

X0 = -2 и X0 = 4 X0 = -3 и X0 = 1

3. Постройте эскиз функции и найдите координаты точек его пересечения с осями координат.

4. Найдите область определения функции

5. Найдите промежутки возрастания и убывания и экстремумы функции.

Критерии оценки.

0-10 баллов – «2»

11-14баллов – «3»

15-19 баллов – «4»

20-21 баллов – «5»

Распределение заданий по содержанию и видам деятельности.

Критерии оценивания

Контрольная работа № 2

по теме «Тригонометрические функции»

Цель: проверить уровень усвоение ГОСО

— умение находить период тригонометрических функций;

— уменияупрощать тригонометрические выражения с помощью основных формул

тригонометрии;

— знание значений тригонометрических функций;

— умения строить графики тригонометрических функций;

— умения по графику определять свойства тригонометрических функций;

1. Найдите наименьший положительный период функции

2. Вычислите значение выражения

3. Постройте график функции

4. Не выполняя построений, найдите область определения и область значений функции.

5. Вычислите:

cos(2 arcsin1\3) cos(2 arcsin1\5)

Критерии оценки.

0-10 баллов – «2»

11-14 баллов – «3»

15-19 баллов – «4»

20-21 баллов – «5»

Распределение заданий по содержанию и видам деятельности.

Критерии оценивания

Контрольная работа № 3

по теме «Тригонометрические уравнения и неравенства»

Цель: проверить уровень усвоение ГОСО

— умение находить значение обратных тригонометрических функций;

— умение решать простейшие тригонометрические уравнения;

— умения решать однородные тригонометрические уравнения;

— умения преобразовывать уравнения с помощью основных формул тригонометрии.

— умения решать системы тригонометрических уравненийи неравенств;

1. Решите уравнение

а) а)

б) б)

2. Решите уравнение

а) а)

б) б)

3. Решите неравенство

4. Решите систему уравнений

5. Решите систему неравенств

Критерии оценки.

0-12 баллов – «2»

13-16 баллов – «3»

17-21 баллов – «4»

22-23 баллов – «5»

Распределение заданий по содержанию и видам деятельности.

Критерии оценивания

Контрольная работа № 4

по теме «Определение производной функции. Геометрический и физический смысл производной»

Цель: проверить уровень усвоения ГОСО

— знание формул и правил нахождения производных, уравнения касательной;

— умения применять таблицу и правила нахождения производных;

— умение составлять уравнение касательной к графику функции;

— умения находить производную в точке;

— умения составлять уравнения и неравенства с производной и решать их*

— умения применять производную при решении физических задач.

1. Найти производную функции:

а) а) б) — 8х3 б) )+ 3х5

2. Составьте уравнение касательной к графику функции f(x) в точке x0.

, x0=-1 , x0 = 1

3. Решите уравнение:

если если

4. Составьте и решите неравенство

5.Материальная точка движется по закону

x(t)= 5t + 6t2 – t3 x(t) = – t2 + 2t – 4

( х – метров, t – в секундах)

Определите

скорость точки в момент, когда ускорение точки в момент, когда

ее ускорение равно нулю. ее скорость равна 1м/с

Критерии оценки.

0-12 баллов – «2»

13-16 баллов – «3»

17-21 баллов – «4»

22-23 баллов – «5»

Распределение заданий по содержанию и видам деятельности.

Критерии оценивания

Контрольная работа № 5

по теме «Производные сложных и тригонометрических функции»

Цель: проверить уровень усвоение ГОСО

— знание формул и правил нахождения производных тригономкерических функций,;

— умения находить производную сложной функции;

— умения составлять уравнения и неравенства с производной и решать их.

1. Найти производную функции:

б) ,

xn--j1ahfl.xn--p1ai

Контрольные работы по математике 10 класс.

Контрольная работа № 1

1 вариант

1). Основание АD трапеции АВСD лежит в плоскости α. Через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках Е и F соответственно.

а). Каково взаимное расположение прямых

ЕF и АВ?

б). Чему равен угол между прямыми ЕF и АВ,

если АВС = 150⁰?

Ответ обоснуйте.

2). Дан пространственный четырехугольник АВСD, в котором диагонали АС и ВD равны. Середины сторон этого четырехугольника соединены последовательно отрезками.

а). Выполните рисунок к задаче;

б). Докажите, что полученный четырех –

угольник – ромб.

2 вариант

1). Треугольники АВС и АDС лежат в разных плоскостях и имеют общую сторону АС. Точка Р – середина стороны АD, точка К – середина DС.

а). Каково взаимное расположение прямых

РК и АВ?

б). Чему равен угол между прямыми РК и

АВ, если АВС = 40⁰ и ВСА = 80?

Ответ обоснуйте.

2). Дан пространственный четырехугольник АВСD, М и N – середины сторон АВ и ВС соответственно, Е СD, К D, DА : ЕС = 1 : 2, DК : КА = 1 : 2.

а). Выполните рисунок к задаче;

б). докажите, что четырехугольник МNЕК –

трапеция.

Контрольная работа № 2

1 вариант

1). Прямые a и b лежат в параллельных плоскостях α и β. Могут ли эти прямые быть:

а). Параллельными;

б). Скрещивающимися?

Сделайте рисунок для каждого возможного случая.

2). Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А₁ и А₂ соответственно, прямая m – в точках В₁ и В₂. Найдите длину отрезка А₂В₂, если А₁В₁ = 12 см, В₁О : ОВ₂ = 3 : 4.

3). Изобразите параллелепипед ABCDA₁B₁C₁D₁ и постройте его сечение плоскостью, проходящей через точки M, N и K, являющиеся серединами ребер АВ, ВС и DD₁.

2 вариант

1). Прямые a и b лежат в пересекающихся плоскостях α и β. Могут ли эти прямые быть:

а). Параллельными;

б). Скрещивающимися?

Сделайте рисунок для каждого возможного случая.

2). Через точку О, не лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А₁ и А₂ соответственно, прямая m – в точках В₁ и В₂. Найдите длину отрезка А₁В₁, если А₂В₂ = 15 см, ОВ₁ : ОВ₂ = 3 : 5.

3). Изобразите тетраэдр DABC и постройте его сечение плоскостью, проходящей через точки M и N, являющиеся серединами ребер DC и BC, и точку K, такую, что K DA, АK : KD = 1 : 3.

Контрольная работа № 3

1 вариант

1). Диагональ куба равна 6 см. Найдите:

а). Ребро куба;

б). Косинус угла между диагональю куба и

плоскостью одной из его граней.

2). Сторона АВ ромба ABCD равна a, один из углов равен 60°. Через сторону АВ проведена плоскость α на расстоянии от точки D.

а). Найдите расстояние от точки С до плоскости α;

б). Покажите на рисунке линейный угол двугранного угла DABM, М α.

в) Найдите синус угла между плоскостью ромба и плоскостью α.

2 вариант

1). Основанием прямоугольного параллелепипеда служит квадрат, диагональ параллелепипеда равна см, а его измерения относятся как 1:1:2. Найдите:

а). Измерения параллелепипеда;

б). Синус угла между диагональю параллеле –

пипеда и плоскостью его основания.

2). Сторона квадрата ABCD равна а. Через сторону AD проведена плоскость α на расстоянии от точки В.

а). Найдите расстояние от точки С до плоскости α.

б). Покажите на рисунке линейный угол

двугранного угла BADM, М α.

в). Найдите синус угла между плоскостью

квадрата и плоскостью α.

Контрольная работа № 4

1 вариант

1). Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площадь боковой поверхности пирамиды.

2). Основанием прямого параллелепипеда ABCDA₁B₁C₁D₁ является ромб ABCD, сторона которого равна а и угол равен 60°. Плоскость AD₁C₁ составляет с плоскостью основания угол в 60°. Найдите:

а) высоту ромба;

б) высоту параллелепипеда;

в) площадь боковой поверхности параллелепипеда;

г) площадь поверхности параллелепипеда.

2 вариант

1). Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM = a. Найдите площадь поверхности пирамиды.

2). Основанием прямого параллелепипеда ABCDA₁B₁C₁D₁ является параллелограмм ABCD, стороны которого равны 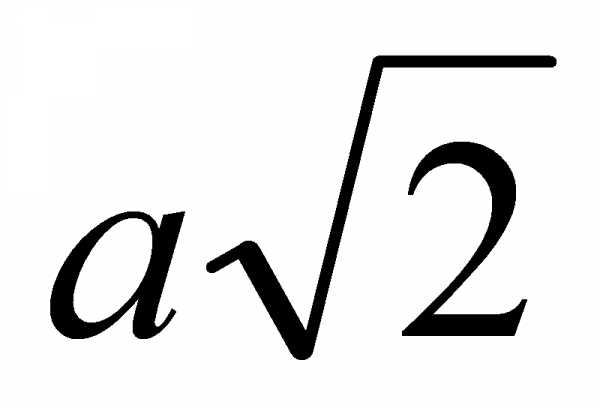и 2а, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:

а). меньшую высоту параллелограмма;

б). угол между плоскостью АВС₁ и плоскостью основания;

в). площадь боковой поверхности параллелепипеда;

г). площадь поверхности параллелепипеда.

infourok.ru