Материал по алгебре (10 класс) на тему: Контрольные работы А-10 класс
А – 10 Контрольная работа № 1.2
Степенная функция
Вариант 1
1. Найдите область определения функции .
2. Схематически изобразите график функции и перечислите её основные свойства. Пользуясь свойствами этой функции, сравните:
.
3. Решите уравнение
4. Решите уравнение
5. Установите, равносильны ли неравенства и
6. Найдите функцию, обратную функции и укажите её область определения и множество значений.
7*. Решите неравенство
Контрольная работа № 1.2
Степенная функция
Вариант 2
1. Найдите область определения функции
2. Схематически изобразите график функции и перечислите её основные свойства. Пользуясь свойствами этой функции, сравните:
3. Решите уравнение
4. Решите уравнение
5. Установите, равносильны ли неравенства и
6. Найдите функцию, обратную функции и укажите её область определения и множество значений.
7*. Решите неравенство
nsportal.ru
Контрольные работы по математике 10 класс.
Контрольная работа № 1
1 вариант
1). Основание АD трапеции АВСD лежит в плоскости α. Через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках Е и F соответственно.
а). Каково взаимное расположение прямых
ЕF и АВ?
б). Чему равен угол между прямыми ЕF и АВ,
если АВС = 1500?
Ответ обоснуйте.
2). Дан пространственный четырехугольник АВСD, в котором диагонали АС и ВD равны. Середины сторон этого четырехугольника соединены последовательно отрезками.
а). Выполните рисунок к задаче;
б). Докажите, что полученный четырех –
угольник – ромб.
2 вариант
1). Треугольники АВС и АDС лежат в разных плоскостях и имеют общую сторону АС. Точка Р – середина стороны АD, точка К – середина DС.
а). Каково взаимное расположение прямых
РК и АВ?
б). Чему равен угол между прямыми РК и
АВ, если АВС = 400 и ВСА = 80?
Ответ обоснуйте.
2). Дан пространственный четырехугольник АВСD, М и N – середины сторон АВ и ВС соответственно, Е СD, К D, DА : ЕС = 1 : 2, DК : КА = 1 : 2.
а). Выполните рисунок к задаче;
б). докажите, что четырехугольник МNЕК –
трапеция.
Контрольная работа № 2
1 вариант
1). Прямые a и b лежат в параллельных плоскостях α и β. Могут ли эти прямые быть:
а). Параллельными;
б). Скрещивающимися?
Сделайте рисунок для каждого возможного случая.
2). Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А2В2, если А1В1 = 12 см, В1О : ОВ2 = 3 : 4.
3). Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через точки M, N и K, являющиеся серединами ребер АВ, ВС и DD1.
2 вариант
1). Прямые a и b лежат в пересекающихся плоскостях α и β. Могут ли эти прямые быть:
а). Параллельными;
б). Скрещивающимися?
Сделайте рисунок для каждого возможного случая.
2). Через точку О, не лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А1В1, если А2В2 = 15 см, ОВ1 : ОВ2 = 3 : 5.
3). Изобразите тетраэдр DABC и постройте его сечение плоскостью, проходящей через точки M и N, являющиеся серединами ребер DC и BC, и точку K, такую, что K DA, АK : KD = 1 : 3.
Контрольная работа № 3
1 вариант
1). Диагональ куба равна 6 см. Найдите:
а). Ребро куба;
б). Косинус угла между диагональю куба и
плоскостью одной из его граней.
2). Сторона АВ ромба ABCD равна a, один из углов равен 60°. Через сторону АВ проведена плоскость α на расстоянии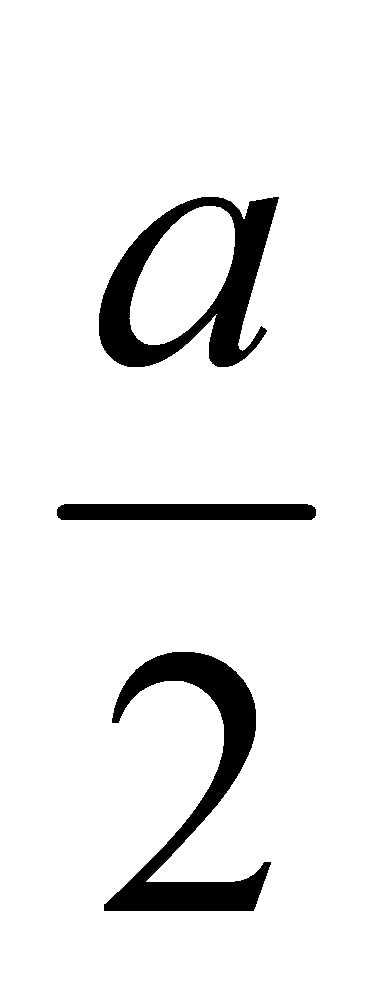 
от точки D.
а). Найдите расстояние от точки С до плоскости α;
б). Покажите на рисунке линейный угол двугранного угла DABM, М α.
в) Найдите синус угла между плоскостью ромба и плоскостью α.
2 вариант
1). Основанием прямоугольного параллелепипеда служит квадрат, диагональ параллелепипеда равна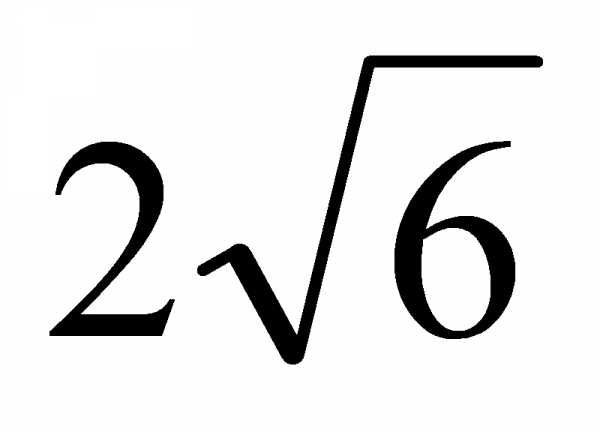 
см, а его измерения относятся как 1:1:2. Найдите:
а). Измерения параллелепипеда;
б). Синус угла между диагональю параллеле –
пипеда и плоскостью его основания.
2). Сторона квадрата ABCD равна а. Через сторону AD проведена плоскость α на расстоянии 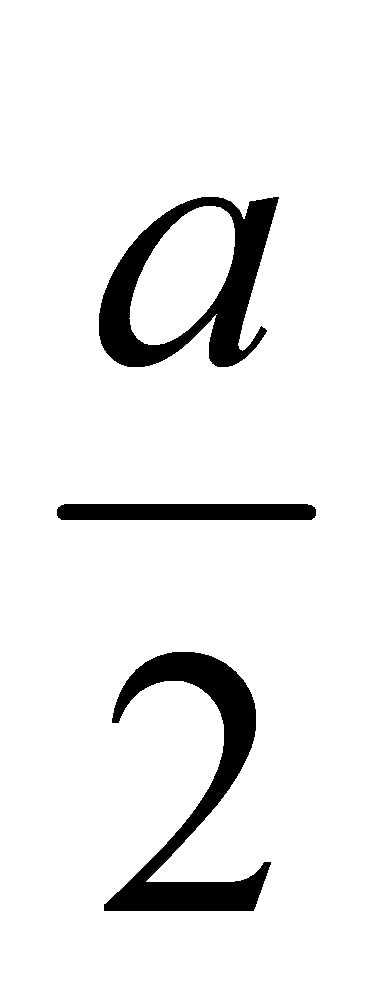от точки В.
а). Найдите расстояние от точки С до плоскости α.
б). Покажите на рисунке линейный угол
двугранного угла BADM, М α.
в). Найдите синус угла между плоскостью
квадрата и плоскостью α.
Контрольная работа № 4
1 вариант
1). Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площадь боковой поверхности пирамиды.
2). Основанием прямого параллелепипеда ABCDA1B1C1D1 является ромб ABCD, сторона которого равна а и угол равен 60°. Плоскость AD1C1 составляет с плоскостью основания угол в 60°. Найдите:
а) высоту ромба;
б) высоту параллелепипеда;
в) площадь боковой поверхности параллелепипеда;
г) площадь поверхности параллелепипеда.
2 вариант
1). Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM = a. Найдите площадь поверхности пирамиды.
2). Основанием прямого параллелепипеда ABCDA1B1C1D1 является параллелограмм ABCD, стороны которого равны 
и 2а, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:
а). меньшую высоту параллелограмма;
б). угол между плоскостью АВС1 и плоскостью основания;
в). площадь боковой поверхности параллелепипеда;
г). площадь поверхности параллелепипеда.
infourok.ru
Контрольные работы 10 класс
Контрольная работа по алгебре и началам анализа 10 класс
Вариант1.
1.Найти наименьший положительный период функции у = 5 cos ( 0,3 х — ).
2.Найти область определения и область значений функции у = -4 sin 2х + 5.
3. Определить функцию на четность или не четность : у = 2 cos 5х ; у = 3sinх cosх.
4.Построить и прочитать график функции у = -5 sin 4х + 4.
5. Упростить выражение : а) tg ( ) tg (п — 8α) + ; б) .
Вариант2.
1.Найти наименьший положительный период функции у = -13 sin ( 0,4 х — ).
2.Найти область определения и область значений функции у = -9 cos 0,6х — 3.
3. Определить функцию на четность или не четность : у = х2 cos 5х ; у = х3 – ctg 7х.
4.Построить и прочитать график функции у = 2 cos — 3.
5. Упростить выражение : а) ctg ( ) ctg (п — 11α) + ; б) .
Контрольная работа по алгебре и началам анализа 10 класс
Вариант1.
1.Найти наименьший положительный период функции у = 5 cos ( 0,3 х — ).
2.Найти область определения и область значений функции у = -4 sin 2х + 5.
3. Определить функцию на четность или не четность : у = 2 cos 5х ; у = 3sinх cosх.
4.Построить и прочитать график функции у = -5 sin 4х + 4.
5. Упростить выражение : а) tg ( ) tg (п — 8α) + ; б) .
Вариант2.
1.Найти наименьший положительный период функции у = -13 sin ( 0,4 х — ).
2.Найти область определения и область значений функции у = -9 cos 0,6х — 3.
3. Определить функцию на четность или не четность : у = х2 cos 5х ; у = х3 – ctg 7х.
4.Построить и прочитать график функции у = 2 cos — 3.
5. Упростить выражение : а) ctg ( ) ctg (п — 11α) + ; б) .
Контрольная работа по алгебре и началам анализа 10 класс
Вариант1.
1.Найти наименьший положительный период функции у = 5 cos ( 0,3 х — ).
2.Найти область определения и область значений функции у = -4 sin 2х + 5.
3. Определить функцию на четность или не четность : у = 2 cos 5х ; у = 3sinх cosх.
4.Построить и прочитать график функции у = -5 sin 4х + 4.
5. Упростить выражение : а) tg ( ) tg (п — 8α) + ; б) .
Вариант2.
1.Найти наименьший положительный период функции у = -13 sin ( 0,4 х — ).
2.Найти область определения и область значений функции у = -9 cos 0,6х — 3.
3. Определить функцию на четность или не четность : у = х2 cos 5х ; у = х3 – ctg 7х.
4.Построить и прочитать график функции у = 2 cos — 3.
5. Упростить выражение : а) ctg ( ) ctg (п — 11α) + ; б) .
infourok.ru
+Контрольная работа № 1 | |
1 вариант 1). Для функции f (х) = х3 + 2х2 – 1. Найти f (0), f (1), f (-3), f (5). 2). Найти D(у), если: 3). Построить график функции: а). у = – х + 5 б). у = х2 – 2 По графику определить : а). Монотонность функции; б). Ограниченность функции; в). Минимальное ( максимальное ) значение функции 4). Для заданной функции найти обратную: | 2 вариант 1). Для функции f (х) = 3х2 – х3 + 2. Найти f (0), f (1), f (-3), f (5). 2). Найти D(у), если: 3). Построить график функции: а). у = х – 7 б). у = – х2 + 2 По графику определить : а). Монотонность функции; б). Ограниченность функции; в). Минимальное ( максимальное ) значение функции 4). Для заданной функции найти обратную: |
Контрольная работа № 2 | |
1 вариант 1). Вычислите: 2). Упростите: 3). Известно, что: . Вычислить . 4). Решите уравнение: . 5). Докажите тождество: . | 2 вариант 1). Вычислите: 2). Упростите: 3). Известно, что: . Вычислить . 4). Решите уравнение: . 5). Докажите тождество: . |
Контрольная работа № 3 | |
1 вариант 1). Найти наименьшее и наибольшее значения функций: на отрезке ; на отрезке . 2). Упростить выражение: 3). Исследуйте функцию на четность: 4). Постройте график функции: 5). Известно, что . Докажите, что . | 2 вариант 1). Найти наименьшее и наибольшее значения функций: на отрезке ; на отрезке . 2). Упростить выражение: 3). Исследуйте функцию на четность: 4). Постройте график функции: 5). Известно, что . Докажите, что . |
Контрольная работа № 4 | |
1 вариант 1). Решить уравнение: 2). Найти корни уравнения на отрезке . 3). Решить уравнение: 4). Найти корни уравнения , принадлежащие отрезку . | 2 вариант 1). Решить уравнение: 2). Найти корни уравнения на отрезке . 3). Решить уравнение: 4). Найти корни уравнения , принадлежащие отрезку . |
Контрольная работа № 5 | |
1 вариант 1). Вычислить: 2). Упростить выражение: 3). Доказать тождество: 4). Решить уравнение а). 5). Зная, что и , найти . | 2 вариант 1). Вычислите: 2). Упростить выражение: 3). Доказать тождество: 4). Решить уравнение а). 5). Зная, что и , найти . |
Контрольная работа № 6 | |
1 вариант 1). Найдите производную функции: а). ; б). ; в). ; г). ; д). . 2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции в точке х0 = 1. 3). Прямолинейное движение точки описывается законом . Найдите ее скорость в момент времени с. 4). Дана функция . Найдите: а). Промежутки возрастания и убывания функции; б). Точки экстремума; в). Наибольшее и наименьшее значения функции на отрезке . | 2 вариант 1). Найдите производную функции: а). ; б). ; в). ; г). ; д). . 2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции в точке х0 = 1. 3). Прямолинейное движение точки описывается законом . Найдите ее скорость в момент времени t = 2с. 4). Дана функция . Найдите: а). Промежутки возрастания и убывания функции; б). Точки экстремума; в). Наибольшее и наименьшее значения функции на отрезке . |
Контрольная работа № 7 ( итоговая ) | |
1 вариант 1). Дана функция. Составить уравнение касательной к графику в точке с абсциссой . Установить, в каких точках промежутка касательная к графику данной функции составляет с осью Ох угол 600. 2). Решите уравнение: 3). Упростите выражение: а). ; б). . 4). Постройте график функции с полным исследованием функции . | 2 вариант 1). Дана функция. Составить уравнение касательной к графику в точке с абсциссой . Установить точки минимума и максимума, а также наибольшее и наименьшее значение на промежутке . 2). Решите уравнение: 3). Упростите выражение: а). ; б). . 4). Постройте график функции с полным исследованием функции . |
infourok.ru
Контрольная работа по химии №1, 10 класс
КОНТРОЛЬНАЯ РАБОТА № 1 по теме: «АЛКАНЫ» (10 класс)
Вариант 1
ЧАСТЬ А
При выполнении заданий этой части для каждого задания (А1 – А10) запишите цифру, которая соответствует номеру выбранного вами ответа.
Задание A1
Общая формула циклоалканов
1) СnH2n–6
2) CnH2n–2
3) CnH2n
4) CnH2n+2
Задание A2
Название углеводорода, формула которого C5H12
1) этан
2) пентан
3) бутан
4) пропан
Задание A3
Изомером октана является:
1) 2,3-диметилгептан;
2) 2,3-диметилбутан;
3) 2,3-диметилпентан;
4) 2,3-диметилгексан.
Задание A4
Молекулярная формула бутана
1) СH4
2) C3H6
3) C4H10
4) C4H8
Задание A5
Гомологом 2,4-диметилоктана является:
1) 2,5-диметилгептан;
2) 3,3-диметилбутан;
3) 2,3-диметилпентан;
4) 2,4-диметилгексан.
Задание A6
Процесс разложения углеводородов нефти на более летучие вещества называется
1) крекинг
2) дегидрирование
3) гидрирование
4) дегидратация
Задание A7
Пропан реагируют
1) с водой
2) с раствором KMnO4
3) с водородом
4) с хлором
Задание A8
Сумма коэффициентов в уравнении реакции полного сгорания этана равна
1) 10
2) 9
3) 19
4) 16
Задание A9
Известно термохимическое уравнение горения метана CH4 + 2O2 → CO2 +2H2O + 896 кДж. Какое количество метана расходуется при выделении 89,6 кДж теплоты?
1) 0,1 моль
2) 0,2 моль
3) 0,25 моль
4) 0,5 моль
Задание A10
Реакция горения алкана
1) 2C3H6 + 9О2 6 CО2 +6 H2О
2) 2С2H2 +5О2 4CО2 + 2H2О
3) C3H8+ 5О2 3CО2 +4 H2О
4) С2H4 +3О2 2CО2 + 2H2О
ЧАСТЬ В
Ответом к заданиям этой части (В1 – В2) является набор чисел и букв, которые следует записать как соответствия, например: 1-А, 2-Д, 3-Г, 4-В.
Задание B1
Установите соответствие между формулой органического вещества и названием , принадлежащим ему.
ФОРМУЛА
1) СН3 — СН — СН2 — СН2 — СН3
|
СН3
2) СН3 — СН2 — СН2 — СН2 — CH2 — CH3
3) СН3 — СH — CH3 — СН3
|
СН3
4) СН3 — СН — СН — СН2 — CH2 — CH3
| |
НАЗВАНИЕ ВЕЩЕСТВА НАЗВАНИЕ ВЕЩЕСТВА
А) 2 — метилбутан
Б) 2 — метилпентан
В) 2 — метил — 3 — этилгексан
Г) гексан
СН3 С2Н5
Задание B2
Установите соответствие между названием вещества и формулой его гомолога.
НАЗВАНИЕ ВЕЩЕСТВА ФОРМУЛА ГОМОЛОГА
1) циклопентан A) СН3
|
Н3С − С −СН2 − СН3
|
СН3
2) 2,4-диметилгептан Б) CH3 – CH – CH2 – CH – CH3
||
CH3CH3
3) Изобутан (2-метилпропан) В) CH2 – CH2
||
CH2 – CH2
4) 2,2-диметилгексан Г) CH3 – CH2 – CH – CH3
|
CH3
ЧАСТЬ С
При ответе на задания этой части запишите полный ответ
Задание C1
Составьте структурную формулу органического вещества
2,2,4 – триметилгексана.
Задание C2
При полном сгорании циклического углеводорода образовался оксид углерода (IV) массой 3,52 г и вода массой 1,44 г. Относительная плотность этого углеводорода по воздуху равна 1,448. Найдите молекулярную формулу углеводорода.
Примерное распределение времени, отводимое на выполнение отдельных заданий составляет:
для каждого задания части 1–1-2 минуты;
для каждого задания части 2 – 5-7 минут;
для каждого задания части 3 – до 10-12 минут.
Оценки за тестовый вариант контрольной работы:
10 — 13 баллов – оценка «3».
14-17 баллов – оценка «4»
18-21 балл – оценка «5».
ОТВЕТЫ (Вариант 1):
№
Вариант ответа
Оценка
A1
3
1
A2
2
1
A3
4
1
A4
3
1
A5
4
1
A6
1
1
A7
4
1
A8
3
1
A9
1
1
A10
3
1
B1
БГАВ
2
B2
ВБГА
2
С1
СН3
|
Н3С − С −СН2 − СН−СН2 − СН3
| |
СН3 СН3
2
С2
1.Составим схему горения неизвестного углеводорода, представив его формулу в виде CxHy.
CxHy + O2 → CO2 + H2O
2. 44 г/моль CO2 содержит 12 г/моль C
3,52 г CO2 содержит y г C
m(C) = 0,96 г
3. 18 г/моль H2O содержит 2 г/моль H
1,44 г H2O содержит х г H
m(H) = 0,16 г
4. ν(C) = m(C)/M(C)
ν(C) = 0,96 г/12 г/моль
ν(C) = 0,08 моль
5. ν(H) = m(H)/M(H)
ν(H) = 0,16 г/1 г/моль
ν(H) = 0,16 моль
6. ν(C): ν(H) =0,08 моль : 0,16 моль (: 0,08 моль)
C: H=1:2
CH2 –простейшая формула углеводорода
M(CH2)= 12+2=14 г/моль
7. M(CxHy) = D(возд.) ×M(возд.)
M(CxHy) = 1,448 × 29 г/моль = 42 г/моль
8. . n= M(CxHy) / M(CH2)= 42 г/моль: 14 г/моль=3
9. C3H6 формула циклического углеводорода- циклопропана.
Ответ: C3H6 — циклопропан.
5
infourok.ru
1 вариант 1). Найдите производную функции: а). ; б). ; в). ; г). ; д). . 2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции в точке х0 = 1. 3). Найти значение производной функции в точке х0=π/3, если f(х) = 2sinx + 3x2 — 2πx. 4). Прямолинейное движение точки описывается законом . Найдите ее скорость в момент времени с. 5)Решить неравенство f′(х)0, если f(х) =12х –х3. 6) Решить уравнение f′(х)=0, если f(х) = cos2xх. Найти корни уравнения, принадлежащие интервалу [ 0; 4π]. | 2 вариант 1). Найдите производную функции: а). ; б). ; в). ; г). ; д). . 2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции в точке х0 = 1. 3). Найти значение производной функции в точке х0=π/6, если f(х)=1,5 x2 -x•π/2 — 4cosx . 4). Прямолинейное движение точки описывается законом . Найдите ее скорость в момент времени t = 2с. 5) Решить неравенство f′(х)0, если f(х) =6х2 — х3. 6) Решить уравнение f′(х)=0, если f(х) = sin2x — х. Найти корни уравнения, принадлежащие интервалу [ 0; 4π]. | 1 вариант 1). Найдите производную функции: а). ; б). ; в). ; г). ; д). . 2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции в точке х0 = 1. 3). Найти значение производной функции в точке х0=π/3, если f(х) = 2sinx + 3x2 — 2πx. 4). Прямолинейное движение точки описывается законом . Найдите ее скорость в момент времени с. 5)Решить неравенство f′(х)0, если f(х) =12х –х3. 6) Решить уравнение f′(х)=0, если f(х) = cos2xх. Найти корни уравнения, принадлежащие интервалу [ 0; 4π]. | 2 вариант 1). Найдите производную функции: а). ; б). ; в). ; г). ; д). . 2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции в точке х0 = 1. 3). Найти значение производной функции в точке х0=π/6, если f(х)=1,5 x2 -x•π/2 — 4cosx . 4). Прямолинейное движение точки описывается законом . Найдите ее скорость в момент времени t = 2с. 5) Решить неравенство f′(х)0, если f(х) =6х2 — х3. 6) Решить уравнение f′(х)=0, если f(х) = sin2x — х. Найти корни уравнения, принадлежащие интервалу [ 0; 4π]. |
multiurok.ru
ГДЗ по алгебре для 10 класса Дидактические материалы Ивлев Б.М.
ГДЗ от Путина
Найти
- 1 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Природоведение
- Основы здоровья
- Музыка
- Литература
- Окружающий мир
- Человек и мир
- 2 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Белорусский язык
- Украинский язык
- Информатика
- Природоведение
- Основы здоровья
- Музыка
- Литература
- Окружающий мир
- Человек и мир
- Технология
- 1 класс
gdzputina.ru
