Контрольные работы по алгебре и началам анализа в 11 классе
ТЕМАТИЧЕСКАЯ КОНТРОЛЬНАЯ РАБОТА
по теме « Показательная функция.
Решение показательных уравнений и неравенств»
ВАРИАНТ-1
№ 1. Сравнить m и n, если:
а) (; (1 б.) б) . (1 б.)
№ 2. Решить показательные уравнения:
а)  =9; (1 б.)
=9; (1 б.)
б) 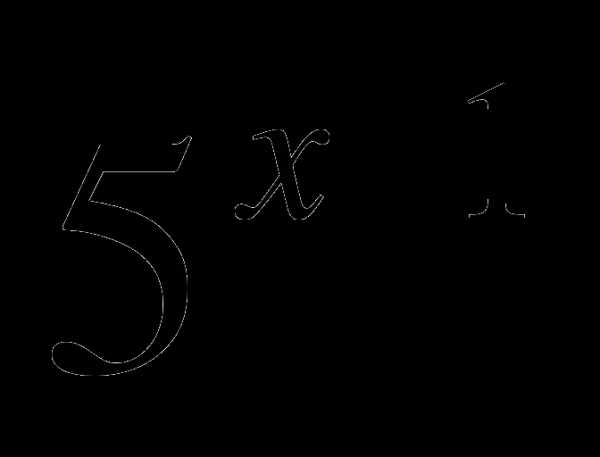 -3
-3  =122; (2 б.)
=122; (2 б.)
в) . (2 б.)
№ 3. Решить показательные неравенства:
а) 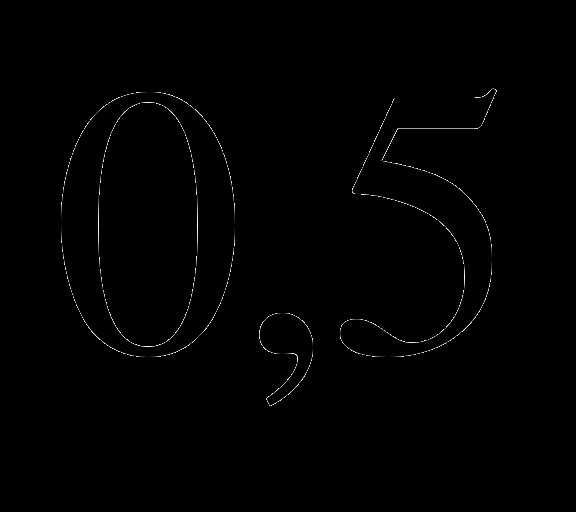
 ; (1 б.) б) . (2 б.)
; (1 б.) б) . (2 б.)
№ 4. Решить систему уравнений:
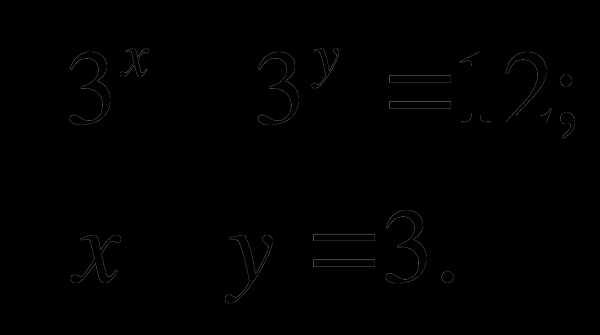
( 2 б.)
ВАРИАНТ-2
№ 1. Сравнить a и в, если:
а) ; (1 б.) б) . (1 б.)
№ 2. Решить показательные уравнения:
а)  =25; (1 б.)
=25; (1 б.)
б) =69; (2 б.)
в) . (2 б.)
№ 3. Решить показательные неравенства:
а) 0,3
 ; (1 б.) б) . (2 б.)
; (1 б.) б) . (2 б.)
№ 4. Решить систему уравнений:
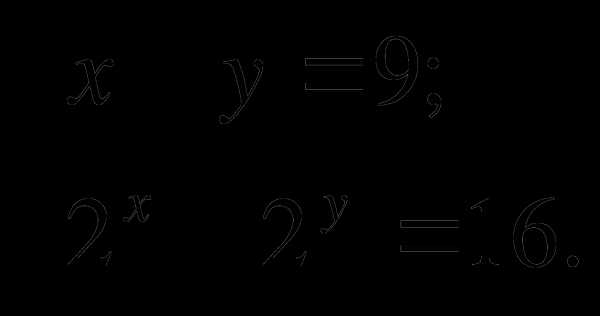 ( 2 б.)
( 2 б.)
ТЕМАТИЧЕСКАЯ КОНТРОЛЬНАЯ РАБОТА
по теме «Логарифмическая функция.
Решение логарифмических уравнений и неравенств».
Вариант-1
№1. Найти область определения функции: y=lg (4x+5)
№2. Сравнить числа: log 7 и log
7 и log 23.
23.
№3. Решить уравнения:
а) log (3х-5)= -2; б) log
(3х-5)= -2; б) log (х
(х +11х-3)=log
+11х-3)=log 9;
9;
в) log (х+1)+ log
(х+1)+ log (2х+1)=1; г) log
(2х+1)=1; г) log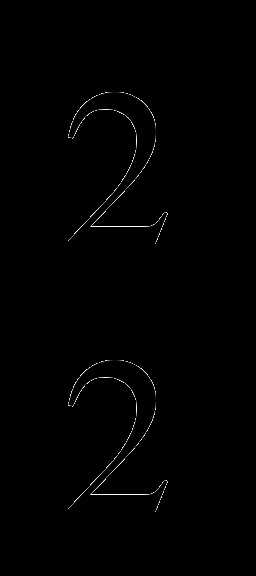 х+ log
х+ log х
х =4.
=4.
№4. Решить неравенства:
а) log (х+4)
(х+4)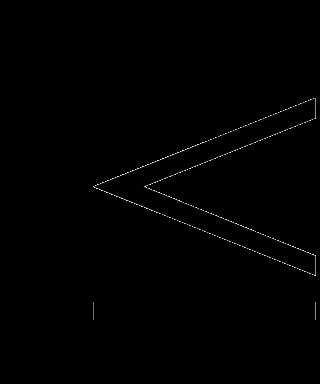 log
log 8; б) log
8; б) log (х
(х +4х)
+4х) -1.
-1.
№5. Решить систему уравнений:
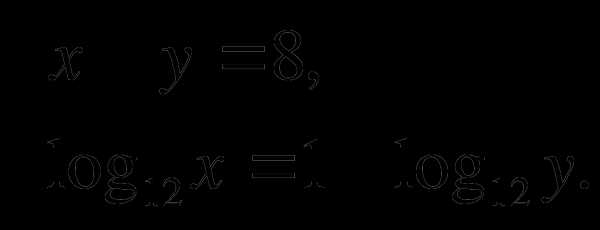
Вариант-2
№1. Найти область определения функции: y=log (3x-2)
(3x-2)
№2. Сравнить числа: log 0,8 и log
0,8 и log 1.
1.
№3. Решить уравнения:
а) log (2х-3)= -1; б) log
(2х-3)= -1; б) log (х
(х -8х+25)=log
-8х+25)=log 10;
10;
в) lg (2х-1)+ lg (х-9)=2; г) log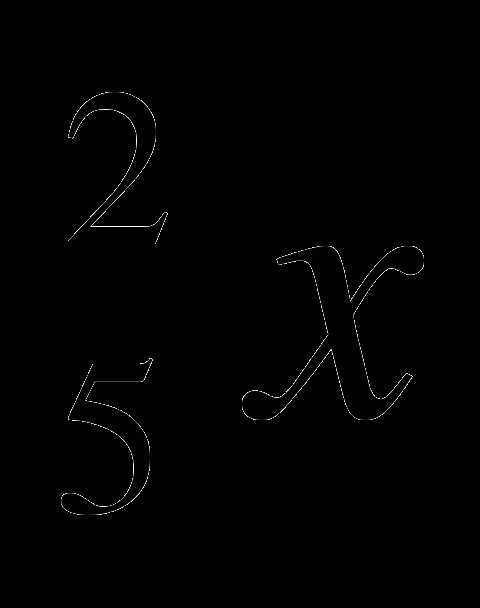 -8 log
-8 log =4.
=4.
№4. Решить неравенства:
а) log (х+2)
(х+2) log
log 4; б) log
4; б) log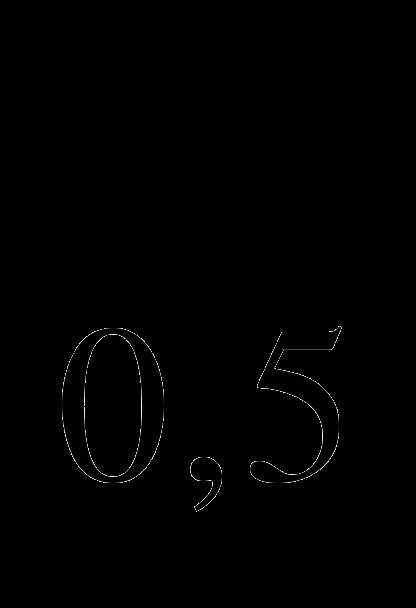 (х
(х +х)
+х) -1.
-1.
№5. Решить систему уравнений:

Вариант-3
№1. Найти область определения функции: y=lg (5x-3)
№2. Сравнить числа: log 42 и log
42 и log 23.
23.
№3. Решить уравнения:
а) log (7х-5)= -2; б) log
(7х-5)= -2; б) log (х
(х +3х-8)=log
+3х-8)=log 2;
2;
в) log (х+3)+ log
(х+3)+ log (х+15)=3; г) 2log
(х+15)=3; г) 2log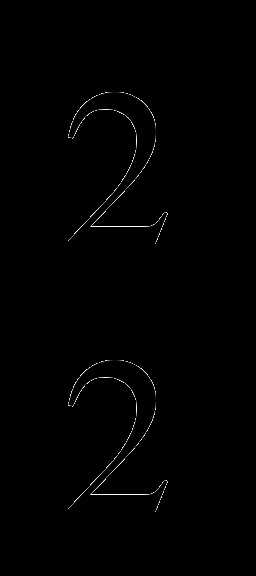 х+3 log
х+3 log х
х =5.
=5.
№4. Решить неравенства:
а) log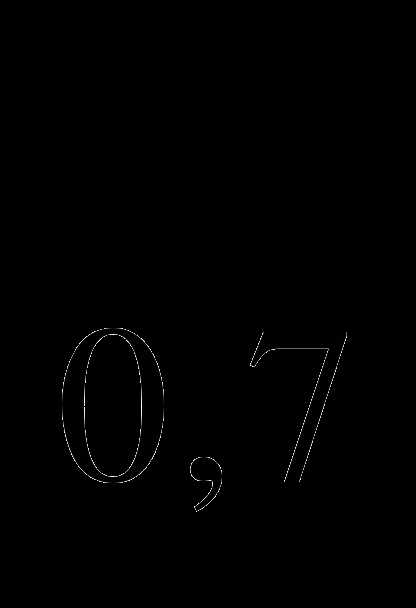 (х — 4)
(х — 4) log
log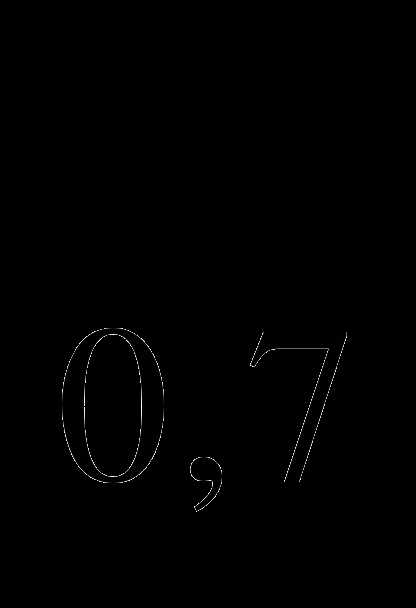 14; б) log
14; б) log (х
(х +3х)
+3х) 2.
2.
№5. Решить систему уравнений:
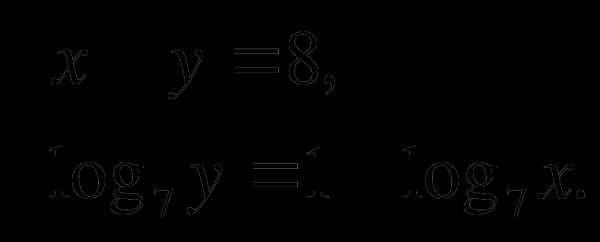
Вариант-4
№1. Найти область определения функции: y=log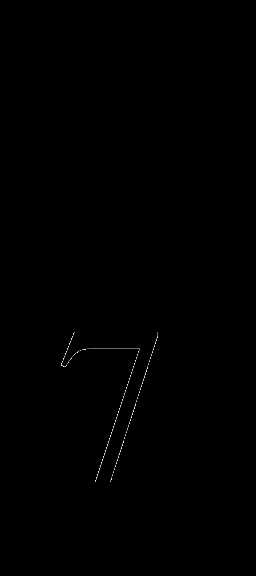 (2x-9)
(2x-9)
№2. Сравнить числа: log 12 и log
12 и log 10.
10.
№3. Решить уравнения:
а) log (4х-3)= -2; б) log
(4х-3)= -2; б) log (х
(х +х-9)=log
+х-9)=log 3;
3;
в) log (х-2)+ log
(х-2)+ log (х-11)=2; г) log
(х-11)=2; г) log +2 log
+2 log =2.
=2.
№4. Решить неравенства:
а) log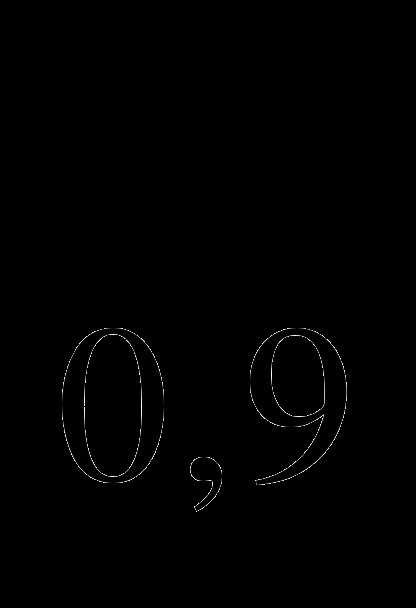 (х — 5)
(х — 5) log
log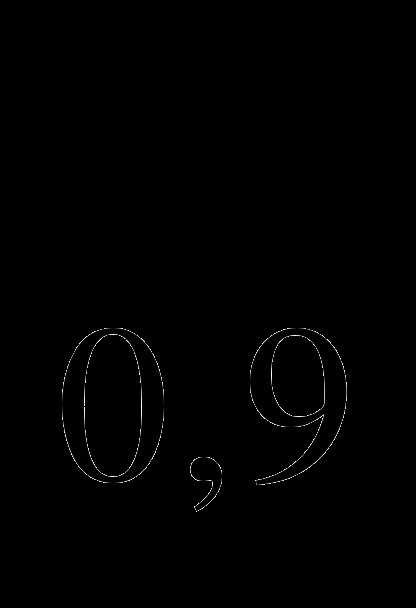 11; б) log
11; б) log (х
(х +4х)
+4х) 1.
1.
№5. Решить систему уравнений:

СЕМЕСТРОВАЯ КОНТРОЛЬНАЯ РАБОТА
ВАРИАНТ-1
-
Решить неравенство:
-
Решить уравнение: log
 x-3 log
x-3 log x+2=0
x+2=0
-
Найти экстремум функции:
-
Найти наибольшее и наименьшее значение функции на отрезке

ВАРИАНТ-2
-
Решить неравенство: log
 (3x+1)
(3x+1)  log
log (2x+3)
(2x+3) -
Решить уравнение:

-
Найти экстремум функции:

-
Найти наибольшее и наименьшее значение функции на отрезке

Контрольная работа
по теме «Первообразная. Интеграл»
Вариант-1
-
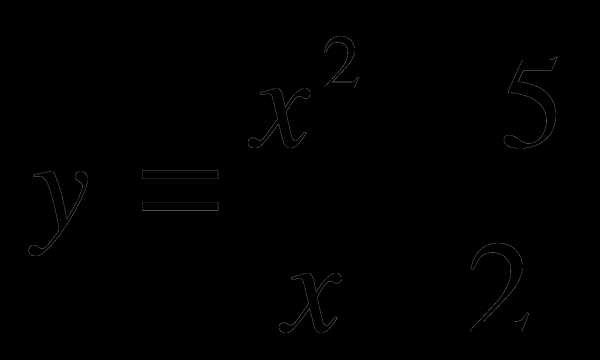
Найти первообразную функции f(x)=, график которой
проходит через точку М(1;4).
-
Для функции f(x)=cos x найти первообразную, график которой проходит
через точку А( ;0).
;0).
-
Найти: а)
 ; б)
; б) 
4. Вычислить интегралы:
1) ) dx; 2)
) dx; 2) 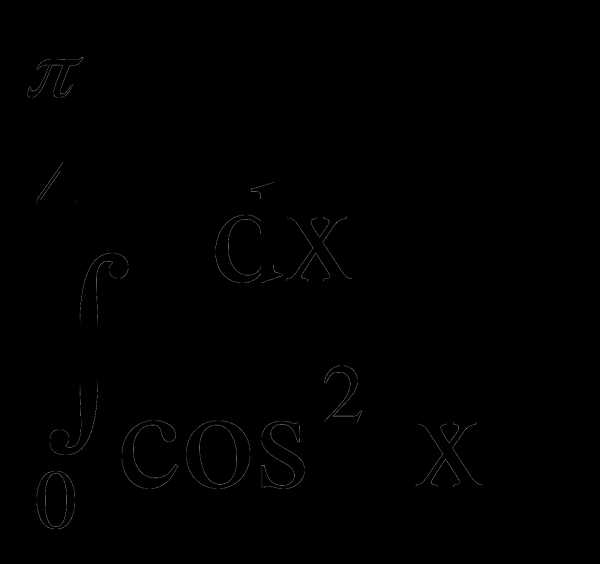 ; 3)
; 3)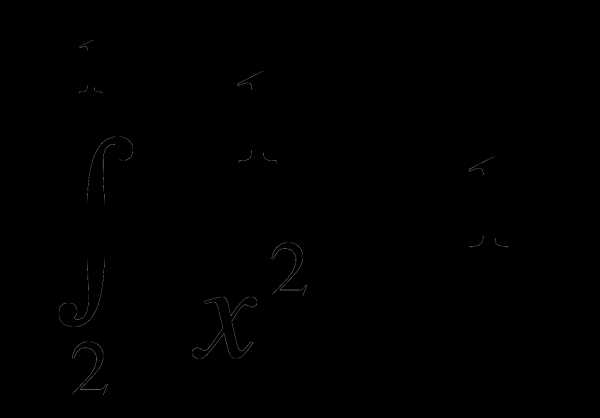 dx;
dx;
4) dx; 5)
dx; 5)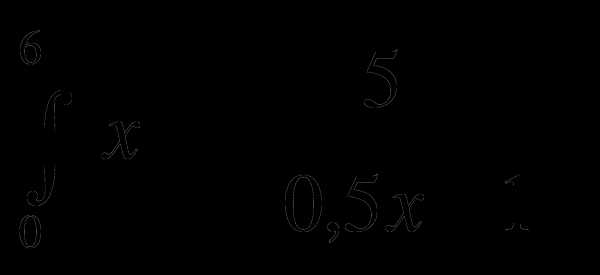 dx.
dx.
Вариант-2
-
Найти первообразную функции f(x)=, график которой
проходит через точку А(1;3).
-
Для функции f(x)=е
 найти первообразную, график которой проходит
найти первообразную, график которой проходит
через точку А(0;0).
-
Найти: а)
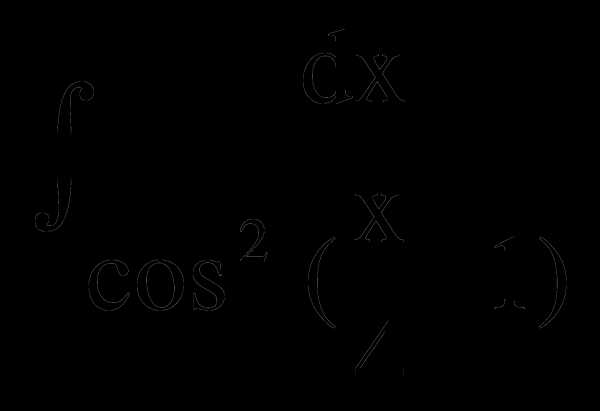 ; б)
; б) 
4. Вычислить интегралы:
1)
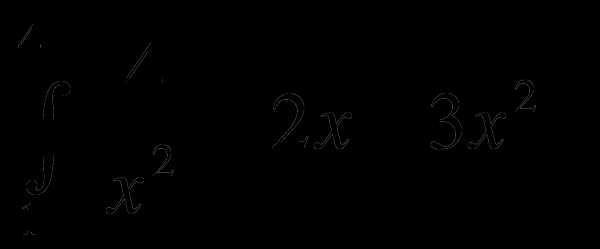 dx; 2)
dx; 2) 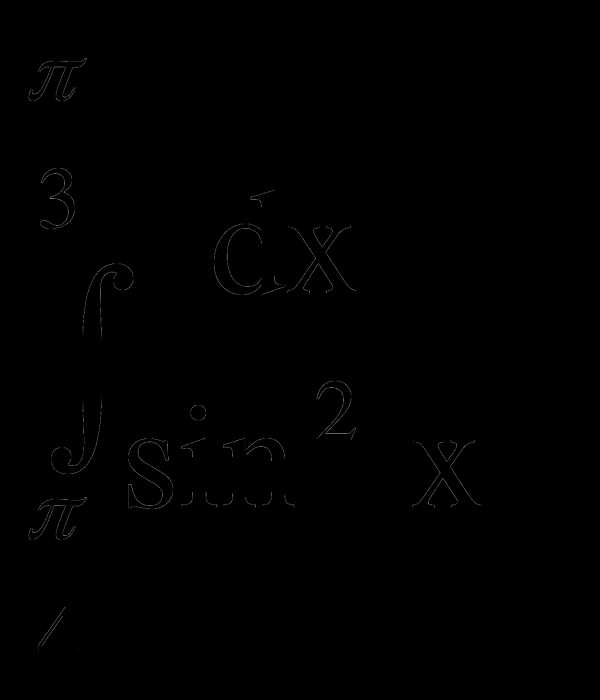 ; 3)
; 3)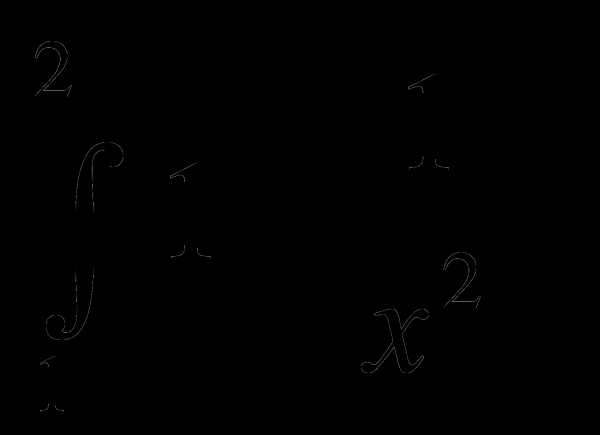 dx;
dx;
4) dx; 5)
dx; 5)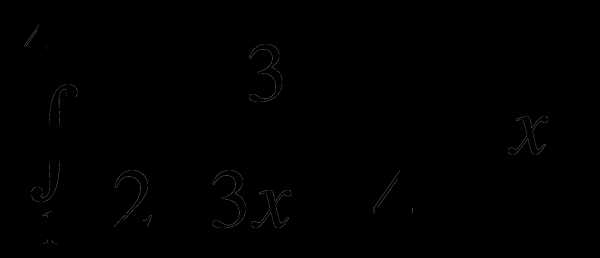 dx.
dx.
Контрольная работа по теме «Применение интеграла»
Вариант-1
-
Вычислить площадь фигуры, ограниченной параболой
 и прямыми у = 0; х = 3.
и прямыми у = 0; х = 3. -
Найти площадь фигуры, ограниченной графиками функций
 и
и 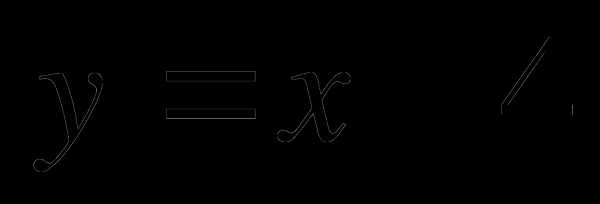 .
. -
Вычислить площадь фигуры, ограниченной линиями
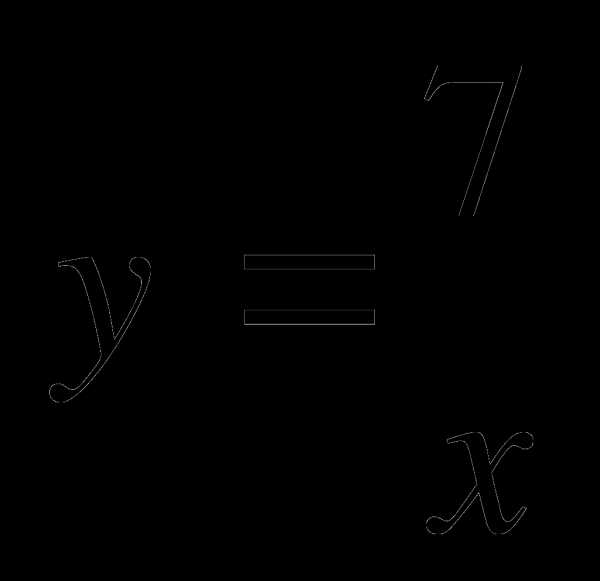 , х+ у = 8.
, х+ у = 8.
Вариант-2
-
Вычислить площадь фигуры, ограниченной параболой
 и прямыми у =0; х =1.
и прямыми у =0; х =1. -
Найти площадь фигуры, ограниченной графиками функций
 и .
и .
3. Вычислить площадь фигуры, ограниченной линиями
 , у =
, у = , х = 1.
, х = 1.
Вариант-3
-
Вычислить площадь фигуры, ограниченной параболой
 и прямыми у = 0; х = 2.
и прямыми у = 0; х = 2. -
Найти площадь фигуры, ограниченной графиками функций
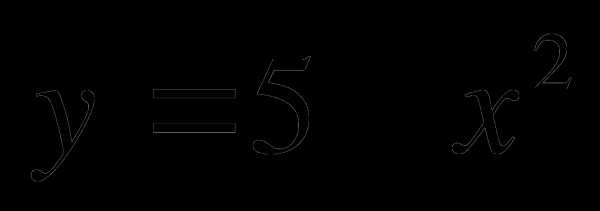 и
и  .
. -
Вычислить площадь фигуры, ограниченной линиями
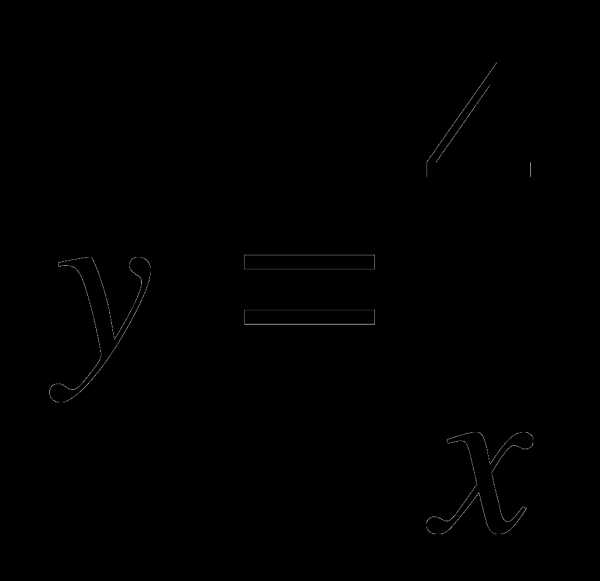 , х + у = 5.
, х + у = 5.
Вариант-4
-
Вычислить площадь фигуры, ограниченной параболой
 и прямыми у = 0; х = 4.
и прямыми у = 0; х = 4. -
Найти площадь фигуры, ограниченной графиками функций
 и
и  .
. -
Вычислить площадь фигуры, ограниченной линиями
 , х + у = 6.
, х + у = 6.
Контрольная работа по теме «Уравнения»
Вариант – 1
-
Решить уравнение:
-
Решить уравнение:
-
Решить уравнение:
4. Решить уравнение:
Контрольная работа по теме «Уравнения»
Вариант – 2
-
Решить уравнение:
-
Решить уравнение:
-
Решить уравнение:
4. Решить уравнение:
Контрольная работа по теме «Неравенства»
Вариант – 1
-
Решить неравенство:
-
Решить неравенство:
-
Решить неравенство:
-
Решить неравенство:
Контрольная работа по теме «Неравенства»
Вариант – 2
-
Решить неравенство:
-
Решить неравенство:
-
Решить неравенство:
4. Решить неравенство:
infourok.ru
Контрольная работа по алгебре 11 класс по теме «Уравнения» (по материалам ЕГЭ)
Вариант № 4
1. Задание 6 . Решите уравнение .
2. Задание 6 . Найдите корень уравнения .
3. Задание 6 . Решите уравнение
4. Задание 6 . Решите уравнение .
5. Задание 6 . Решите уравнение .
6. Задание 6 .
Решите уравнение .
В ответе напишите наибольший отрицательный корень.
7. Задание 15 .
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
8. Задание 15 .
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
9. Задание 17 . Решите неравенство:
Вариант № 1
1. Задание 6 . Решите уравнение .
2. Задание 6 .
Решите уравнение .
Если уравнение имеет более одного корня, в ответе запишите больший из корней.
3. Задание 6 . Решите уравнение .
4. Задание 6 . Найдите корень уравнения .
5. Задание 6 . Найдите корень уравнения .
6. Задание 6 .
Решите уравнение .
В ответе напишите наименьший положительный корень.
7. Задание 15 .
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
8. Задание 15 . Решите уравнение
9. Задание 17 . Решите неравенство:
Вариант № 6
1. Задание 6 . Найдите корень уравнения: .
2. Задание 6 . Решите уравнение .
Если уравнение имеет более одного корня, в ответе запишите больший из корней.
3. Задание 6 . Найдите корень уравнения
4. Задание 6 . Найдите корень уравнения:
5. Задание 6 . Решите уравнение .
Если уравнение имеет более одного корня, в ответе укажите меньший из них.
6. Задание 6 .
Найдите корень уравнения:
В ответе запишите наибольший отрицательный корень.
7. Задание 15 . Решите уравнение:
8. Задание 15 .
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
9. Задание 17 .
Решите неравенство:
Вариант №5
1. Задание 6 . Решите уравнение .
2. Задание 6 . Найдите корень уравнения: . Если уравнение имеет более одного корня, в ответе укажите больший из них.
3. Задание 6 . Решите уравнение .
4. Задание 6 . Найдите решение уравнения:
5. Задание 6 . Найдите корень уравнения .
6. Задание 6 .
Решите уравнение .
В ответе напишите наибольший отрицательный корень.
7. Задание 15 . Дано уравнение
а) Решите уравнение;
б) Укажите корни уравнения, принадлежащие промежутку
8. Задание 15 .
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
9. Задание 17 .
Решите неравенство:
Вариант № 3
1. Задание 6 . Найдите корень уравнения .
2. Задание 6 . Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
3. Задание 6 . Решите уравнение:
4. Задание 6 . Найдите корень уравнения .
5. Задание 6 . Решите уравнение .
6. Задание 6 . Найдите корень уравнения:
В ответе запишите наибольший отрицательный корень.
7. Задание 15 .
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
8. Задание 15 . Решите уравнение:
9. Задание 17 .
Решите неравенство
Вариант № 2
-
Задание 6 . Решите уравнение .
Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
2. Задание 6 . Найдите корень уравнения:
3. Задание 6 . Решите уравнение .
Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
4. Задание 6 . Найдите корень уравнения .
5. Задание 6 . Найдите корень уравнения .
6. Задание 6 .
Решите уравнение .
В ответе напишите наименьший положительный корень.
7. Задание 15 .
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
8. Задание 15 .
Решите уравнение:
9. Задание 17 .
Решите неравенство:
infourok.ru
Итоговая контрольная работа по алгебре 11 класс
Итоговая контрольная работа по алгебре 11 класс. Вариант 1 1.Найдите значение выражения: а)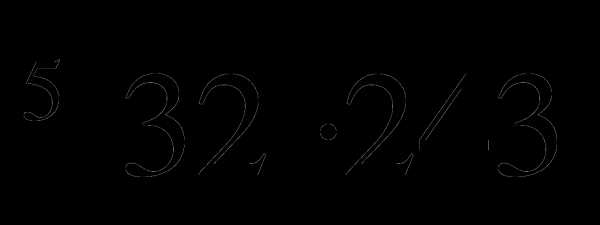 ;
;
б) 2.Найдите общий вид первообразной для функции
f(x) = 2(3x + 1)5 3.Дана функция f(x) = 8x2 – x4 . Найдите: А) промежутки возрастания и убывания функции; Б) точки максимума и минимума функции; В) наибольшее и наименьшее значения функции на
отрезке [-1; 3] . 4.Решите иррациональное уравнение и неравенство: а); б) 5. Решите показательное уравнение:
Итоговая контрольная работа по алгебре 11 класс. Вариант 2 1.Найдите значение выражения: а)  ; б) 2.Найдите общий вид первообразной для функции f(x) = 3(4x + 5)6 3.Дана функция f(x) = x3 — 3x2 + 4. Найдите: А) промежутки возрастания и убывания функции; Б) точки максимума и минимума функции; В) наибольшее и наименьшее значения функции на отрезке [0; 4] . 4.Решите иррациональное уравнение и неравенство: а); б) 5. Решите показательное уравнение:
; б) 2.Найдите общий вид первообразной для функции f(x) = 3(4x + 5)6 3.Дана функция f(x) = x3 — 3x2 + 4. Найдите: А) промежутки возрастания и убывания функции; Б) точки максимума и минимума функции; В) наибольшее и наименьшее значения функции на отрезке [0; 4] . 4.Решите иррациональное уравнение и неравенство: а); б) 5. Решите показательное уравнение:
Итоговая контрольная работа по алгебре 11 класс. Вариант 1 1.Найдите значение выражения: а)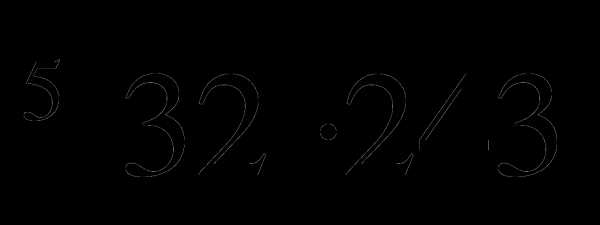 ;
;
б) 2.Найдите общий вид первообразной для функции
f(x) = 2(3x + 1)5 3.Дана функция f(x) = 8x2 – x4 . Найдите: А) промежутки возрастания и убывания функции; Б) точки максимума и минимума функции; В) наибольшее и наименьшее значения функции на
отрезке [-1; 3] . 4.Решите иррациональное уравнение и неравенство: а); б) 5. Решите показательное уравнение:
Итоговая контрольная работа по алгебре 11 класс. Вариант 2 1.Найдите значение выражения: а)  ; б) 2.Найдите общий вид первообразной для функции f(x) = 3(4x + 5)6 3.Дана функция f(x) = x3 — 3x2 + 4. Найдите: А) промежутки возрастания и убывания функции; Б) точки максимума и минимума функции; В) наибольшее и наименьшее значения функции на отрезке [0; 4] . 4.Решите иррациональное уравнение и неравенство: а); б) 5. Решите показательное уравнение:
; б) 2.Найдите общий вид первообразной для функции f(x) = 3(4x + 5)6 3.Дана функция f(x) = x3 — 3x2 + 4. Найдите: А) промежутки возрастания и убывания функции; Б) точки максимума и минимума функции; В) наибольшее и наименьшее значения функции на отрезке [0; 4] . 4.Решите иррациональное уравнение и неравенство: а); б) 5. Решите показательное уравнение:
Итоговая контрольная работа по алгебре 11 класс. Вариант 1 1.Найдите значение выражения: а)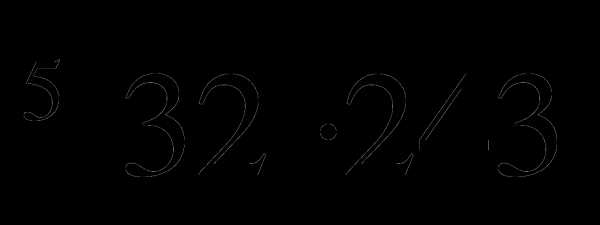 ;
;
б) 2.Найдите общий вид первообразной для функции
f(x) = 2(3x + 1)5 3.Дана функция f(x) = 8x2 – x4 . Найдите: А) промежутки возрастания и убывания функции; Б) точки максимума и минимума функции; В) наибольшее и наименьшее значения функции на
отрезке [-1; 3] . 4.Решите иррациональное уравнение и неравенство: а); б) 5. Решите показательное уравнение:
Итоговая контрольная работа по алгебре 11 класс. Вариант 2 1.Найдите значение выражения: а)  ; б) 2.Найдите общий вид первообразной для функции f(x) = 3(4x + 5)6 3.Дана функция f(x) = x3 — 3x2 + 4. Найдите: А) промежутки возрастания и убывания функции; Б) точки максимума и минимума функции; В) наибольшее и наименьшее значения функции на отрезке [0; 4] . 4.Решите иррациональное уравнение и неравенство: а); б) 5. Решите показательное уравнение:
; б) 2.Найдите общий вид первообразной для функции f(x) = 3(4x + 5)6 3.Дана функция f(x) = x3 — 3x2 + 4. Найдите: А) промежутки возрастания и убывания функции; Б) точки максимума и минимума функции; В) наибольшее и наименьшее значения функции на отрезке [0; 4] . 4.Решите иррациональное уравнение и неравенство: а); б) 5. Решите показательное уравнение:
Итоговая контрольная работа по алгебре 11 класс. Вариант 1 1.Найдите значение выражения: а)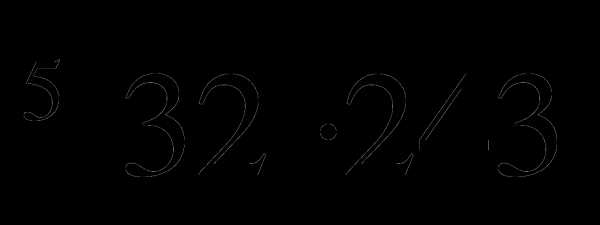 ;
;
б) 2.Найдите общий вид первообразной для функции
f(x) = 2(3x + 1)5 3.Дана функция f(x) = 8x2 – x4 . Найдите: А) промежутки возрастания и убывания функции; Б) точки максимума и минимума функции; В) наибольшее и наименьшее значения функции на
отрезке [-1; 3] . 4.Решите иррациональное уравнение и неравенство: а); б) 5. Решите показательное уравнение:
Итоговая контрольная работа по алгебре 11 класс. Вариант 2 1.Найдите значение выражения: а)  ; б) 2.Найдите общий вид первообразной для функции f(x) = 3(4x + 5)6 3.Дана функция f(x) = x3 — 3x2 + 4. Найдите: А) промежутки возрастания и убывания функции; Б) точки максимума и минимума функции; В) наибольшее и наименьшее значения функции на отрезке [0; 4] . 4.Решите иррациональное уравнение и неравенство: а); б) 5. Решите показательное уравнение:
; б) 2.Найдите общий вид первообразной для функции f(x) = 3(4x + 5)6 3.Дана функция f(x) = x3 — 3x2 + 4. Найдите: А) промежутки возрастания и убывания функции; Б) точки максимума и минимума функции; В) наибольшее и наименьшее значения функции на отрезке [0; 4] . 4.Решите иррациональное уравнение и неравенство: а); б) 5. Решите показательное уравнение:
infourok.ru
Тест по алгебре (11 класс) по теме: Контрольная работа по алгебре за 1 полугодие 11 класс
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа №1»
УТВЕРЖДАЮ:
Директор МБОУ «СОШ №1» ______________А.В.Петряев
«____» ____________ 2012 г.
Согласовано:
Зам. директора МБОУ «СОШ №1»
___________________________
«____» _____________ 2012 г.
Протокол заседания методического
совета школы №____ от _________
КОНТРОЛЬНО – ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ
по предмету «Алгебра и начала анализа»
( наименование предмета)
для 11-х классов
Составитель:
Хайржанова Ольга Николаевна
учитель математики
высшей квалификационной категории
Содержание
|
Пояснительная записка |
3 |
|
Спецификация работы |
4 |
|
Текст работы |
5 |
|
Ключ работы |
9 |
|
Бланк анализа работы |
10 |
- Пояснительная записка
1). Цель проведения работы – проверить практические навыки и умения обучающихся по темам «Показательная функция», «Степени и корни».
2). Документы, на которые опирались при составлении работы – Федеральные государственные образовательные стандарты.
3). Класс, на который рассчитана данная работа — 11
4). Рекомендуемое время для проведения работы (количество часов на выполнение работы) — 1 урок (40 минут)
5). Описание структуры контрольно-измерительного материала: работа состоит из трёх частей.
Часть А содержит семь заданий базового уровня с выбором ответов, которые проверяют овладение конкретным материалом по данным темам. Ученик решает задание и выбирает букву, под которой, по его мнению, записан верный ответ и заносит данную букву в бланк ответов. Предлагаемые варианты ответов, кроме правильного, подобраны так, что содержат наиболее характерные для данных тем ошибки.
Часть В содержит два задания повышенного уровня, которые обеспечивают овладение учащимися общими и специфическими приемами учебной и умственной деятельности. Ученик решает задание и записывает полученный ответ в бланк ответов.
Часть С содержит два задания высокого уровня, которые предусматривают свободное овладение практическим материалом, приемами учебной работы умственных действий и поднимают учащихся на уровень осознанного творческого применения знаний. Ученик решает задание и полностью записывает решение на бланке ответов.
Согласно методике составления теста, разработанной в лаборатории образования ИОСО РАО, основная часть должна состоять из заданий первого и второго уровней. Именно задания этих уровней соответствуют обязательным требованиям к знаниям и умениям учащихся.
6). Суть ключа.
Работа состоит из трёх частей.
Каждое задание части А (А1-А7) оценивается в 1 балл.
Каждое задание части В (В1,В2) оценивается в 1 балл.
Задания части С (С1, С2) оцениваются от 0 до 2 баллов.
|
Баллы |
Критерии оценки выполнения задания С1. |
|
2 |
Верно применены свойства степеней и выполнен переход от показательных уравнений к линейным. Верно решена система линейных уравнений и записан верно ответ. |
|
1 |
Верно применены свойства степеней и выполнен переход от показательных уравнений к линейным. Верно решена система линейных уравнений, но при записи ответа допущена ошибка. |
|
0 |
Все случаи решения, которые не соответствуют вышеуказанным критериям. |
|
Баллы |
Критерии оценки выполнения задания С2. |
|
2 |
Верно выполнен переход от показательного неравенства к квадратному. Верно решено квадратное неравенство и в ответе указаны целочисленные решения неравенства. |
|
1 |
Верно выполнен переход от показательного неравенства к квадратному. Верно решено квадратное неравенство, но не указаны целочисленные решения неравенства. |
|
0 |
Все случаи решения, которые не соответствуют вышеуказанным критериям. |
Соотношение тестового балла и аттестационной отметки:
|
Тестовый балл |
Аттестационная отметка |
|
11-13 |
5 |
|
8-9 |
4 |
|
5-7 |
3 |
|
0-4 |
2 |
- Спецификация работы
|
Проверяемое содержание |
Номер задания в работе |
|
Умение находить значение выражения, содержащего радикалы. |
А1 |
|
Умение упрощать выражение, содержащее радикалы и степени. |
А2 |
|
Умение решать иррациональное уравнение. |
А3 |
|
Умение распознавать показательную функцию по графику. |
А4 |
|
Умение решать простейшее показательное уравнение. |
А5 |
|
Умение соотнести корень показательного уравнения числовому промежутку. |
А6 |
|
Умение решать показательное неравенство. |
А7 |
|
Умение находить значение выражения, содержащего степени. |
В1 |
|
Умение решать показательное уравнение, сводящееся к квадратному уравнению. |
В2 |
|
Умение решать систему показательных уравнений. |
С1 |
|
Умение решать показательное неравенство, сводящееся к квадратному неравенству и записывать целочисленные решения, принадлежащие найденному промежутку. |
С2 |
- Текст работы.
Административная контрольная работа
по алгебре и началам анализа
11 класс
Вариант № 1.
Инструкция по выполнению работы.
На выполнение работы отводится 40 минут.
Работа состоит из трёх частей. Часть А содержит семь заданий (А1-А7) обязательного уровня, часть В содержит два задания (В1,В2) повышенного уровня и часть С содержит два задания (С1, С2) высокого уровня по материалу курса «Алгебры и началам анализа» 11 класса. К каждому заданию части А даны 4 варианта ответов, из которых только один верный. В бланк ответов на задания части А вписывается буква, соответствующая верному, на Ваш взгляд, ответу. При решении заданий части В в бланк ответов вписывается ответ, получившийся в результате решения задания. Если Вы записали неверный ответ, аккуратно зачеркните его и рядом запишите другой ответ.
Задания части С с развёрнутым ответом требует записи полного решения с необходимым обоснованием выполненных действий.
За каждое верно выполненное задание части А и В Вы получаете 1 балл, за задание части С – от 0 до 2 баллов.
Советуем для экономии времени пропускать задание, которое не удаётся выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у Вас останется время.
Желаем успехов!
Часть А.
А1. Найдите значение выражения: 5 +2- —
а) — 15 б) 15 в) 35 г) -5
А2. Упростите выражение: у*
А) у б) 1 в) у2 г) у3
А3. Решите уравнение = 5
а) — 37 б) 9 в) 3 г) 37
А4. Укажите, на каком рисунке изображен график функции у= 6х.
а) у б) у
х х
в) г)
у у
х х
А5. Решите уравнение 52х = 625
а) — 3 б) 0 в) 1 г) 2
А6. Какому промежутку принадлежит корень уравнения 25х – 4 = 16х+3
а) (-∞; -16) б) (-16;0) в) (0;17) г) (18;+∞)
А7. Решите неравенство 46х – 3 ≤ 1
а) [0,5;+∞) б) (-∞; 0,5] в) [2;+∞) г) (-∞; 2]
Часть В.
В1. Найдите значение выражения:
В2. Решите уравнение 32х – 2*3х – 3 = 0
Часть С.
С1. Решите систему уравнений:
= 27
32х × 2у =16
С2. Найдите целочисленные решения неравенства ≥
Административная контрольная работа
по алгебре и началам анализа
11 класс
Вариант № 2.
Инструкция по выполнению работы.
На выполнение работы отводится 40 минут.
Работа состоит из трёх частей. Часть А содержит семь заданий (А1-А7) обязательного уровня, часть В содержит два задания (В1,В2) повышенного уровня и часть С содержит два задания (С1, С2) высокого уровня по материалу курса «Алгебры и началам анализа» 11 класса. К каждому заданию части А даны 4 варианта ответов, из которых только один верный. В бланк ответов на задания части А вписывается буква, соответствующая верному, на Ваш взгляд, ответу. При решении заданий части В в бланк ответов вписывается ответ, получившийся в результате решения задания. Если Вы записали неверный ответ, аккуратно зачеркните его и рядом запишите другой ответ.
Задания части С с развёрнутым ответом требует записи полного решения с необходимым обоснованием выполненных действий.
За каждое верно выполненное задание части А и В Вы получаете 1 балл, за задание части С – от 0 до 2 баллов.
Советуем для экономии времени пропускать задание, которое не удаётся выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у Вас останется время.
Желаем успехов!
Часть А.
А1. Найдите значение выражения: 3- +- 7
а) — 1 б) 1 в) 5 г) -5
А2. Упростите выражение: * с
а) с б) 1 в) с2 г) с3
А3. Решите уравнение = 4
а) — 4 б) 16 в) 4 г) 7
А4. Укажите, на каком рисунке изображен график функции у= ()х.
а) у б) у
х х
в) г)
у у
х х
А5. Решите уравнение 44х = 256
а) — 3 б) 0 в) 1 г) 2
А6. Какому промежутку принадлежит корень уравнения 35х +2 = 81х-1
а) (-∞; -7] б) (6;+∞) в) [6;+∞) г) (– 10; 10)
А7. Решите неравенство 72х+5 ≥ 49
а) [-1,5;+∞) б) (-∞; -1,5] в) [1,5;+∞) г) (-∞; 5]
Часть В.
В1. Найдите значение выражения:
91,5 —
В2. Решите уравнение 22х – 3*2х – 4 = 0
Часть С.
С1. Решите систему уравнений:
9х × 27у =27
= 32
С2. Найдите целочисленные решения неравенства ≥
- Ключ к работе
1 вариант.
|
Номер задания |
Правильный ответ |
|
А1 |
б |
|
А2 |
г |
|
А3 |
в |
|
А4 |
а |
|
А5 |
г |
|
А6 |
в |
|
А7 |
б |
|
В1 |
6 |
|
В2 |
1 |
|
С1 |
(1; -1) |
|
С2 |
0; 1; 2 |
2 вариант.
|
Номер задания |
Правильный ответ |
|
А1 |
б |
|
А2 |
а |
|
А3 |
в |
|
А4 |
б |
|
А5 |
в |
|
А6 |
г |
|
А7 |
а |
|
В1 |
12 |
|
В2 |
2 |
|
С1 |
(3; -1) |
|
С2 |
-1; 0; 1; 2 |
- Бланк анализа работы
Анализ контрольных работ (тестов) по алгебре и началам анализа
Дата проведения ________________________________
Класс __________________
Учитель ________________________________________
Таблица 1
|
Класс |
Дата проведения |
Результаты |
||||||||
|
По списку |
Писали |
Оценки |
% успевае мости |
% качества |
СОК |
|||||
|
«5» |
«4» |
«3» |
«2» |
|||||||
Таблица 2
|
Ф.И. обучающегося |
Содержание работы |
||||||||||
|
Часть А |
Часть В |
Часть С |
|||||||||
|
А1. Умение находить значение выражения, содержащего радикалы. |
А2. Умение упрощать выражение, содержащее радикалы и степени. |
А3. Умение решать иррациональное уравнение. |
А4. Умение распознавать показательную функцию по графику. |
А5. Умение решать простейшее показательное уравнение. |
А6. Умение соотнести корень показательного уравнения числовому промежутку. |
А7. Умение решать показательное неравенство. |
В1. Умение находить значение выражения, содержащего степени. |
В2. Умение решать показательное уравнение, сводящееся к квадратному. |
С1. Умение решать систему показательных уравнений. |
С2. Умение решать показательное неравенство, сводящееся к квадратному и записывать целочисленные решения, принадлежащие найденному промежутку. |
|
Таблица 3
|
Класс/тип работы/дата проведения |
Содержание работы |
||||||||||
|
Часть А |
Часть В |
Часть С |
|||||||||
|
А1. Умение находить значение выражения, содержащего радикалы. |
А2. Умение упрощать выражение, содержащее радикалы и степени. |
А3. Умение решать иррациональное уравнение. |
А4. Умение распознавать показательную функцию по графику. |
А5. Умение решать простейшее показательное уравнение. |
А6. Умение соотнести корень показательного уравнения числовому промежутку. |
А7. Умение решать показательное неравенство. |
В1. Умение находить значение выражения, содержащего степени. |
В2. Умение решать показательное уравнение, сводящееся к квадратному. |
С1. Умение решать систему показательных уравнений. |
С2. Умение решать показательное неравенство, сводящееся к квадратному и записывать целочисленные решения, принадлежащие найденному промежутку. |
|
Таблица 4
|
Типичные ошибки |
Класс |
Ф.И. обучающегося |
nsportal.ru
Контрольная работа 11 класс
СОШ им.Ы.Алтынсарина
Контрольные работы по алгебре и началам анализа.
11 класс
Учитель математики:
Ташенова Гульнара Узакбаевна
2014
Контрольная работа №1
( по теме « Первообразная.Интеграл.» )
І вариант
1 Найдите первообразные данных функций:
а) б)
2 Вычислите интеграл:
а) б) в)
3 Решите неравенство:
4 Найдите площадь фигуры, ограниченной линиями:
; у=0;х=1;х=2.
5 Найдите площадь фигуры, ограниченной данной параболой и осью абсцисс:
ІІ вариант
1 Найдите первообразные данных функций:
а) б)
2 Вычислите интеграл:
а) б) в)
3 Решите неравенство:
4 Найдите площадь фигуры, ограниченной линиями:
; у=0;х=1;х=2.
5 Найдите площадь фигуры, ограниченной данной параболой и осью абсцисс:
Контрольная работа №2
( по теме «Степенная функция.» )
І вариант
1 Вычислите:
а) б) в)
2 Упростите:
3 Решите неравенство:
4 Решите уравнения:
а) б)
5 Решите систему уравнений:
ІІ вариант
1 Вычислите:
а) б) в)
2 Упростите:
3 Решите неравенство:
4 Решите уравнения:
а) б)
5 Решите систему уравнений:
Контрольная работа №3
( І- полугодие)
І вариант
1 Найдите первообразные данных функций:
а) б)
2 Вычислите интеграл:
а) б)
3 Вычислите:
4 Решите уравнение:
5 Найдите значение выражения:
ІІ вариант
1 Найдите первообразные данных функций:
а) б)
2 Вычислите интеграл:
а) б)
3 Вычислите:
4 Решите уравнение:
5 Найдите значение выражения:
Контрольная работа №4
( по теме « Показательная и логарифмическая функции»)
І вариант
1 Решите уравнения:
а) б)
2 Вычислите:
а) б)
3 Найдите область определения функции:
у = log0.4(5х-х2-6)
4 Решите неравенства:
а) б)
5 Решите систему уравнений:
ІІ вариант
1 Решите уравнения:
а) б)
2 Вычислите:
а) б)
3 Найдите область определения функции:
у = log2(х+6)+ log2(6-х)
4 Решите неравенства:
а) б)
5 Решите систему уравнений:
Контрольная работа №5
( по теме « Уравнения и неравенства.»)
І вариант
1 Решите уравнения:
а) б)
2 Решите неравенство:
3 Найдите значение х: |х-| =
4 Решите систему уравнений:
5 Решите систему неравенств:
ІІ вариант
1 Решите уравнения:
а) б)
2 Решите неравенство:
3 Найдите значение х: |2х-3| = х+1
4 Решите систему уравнений:
5 Решите систему неравенств:
Контрольная работа №6(Итоговая)
І вариант
1 Вычислите интеграл:
а) б)
2 Решите неравенство:
3 Решите уравнения:
а) б)
4 Решите систему уравнений:
5 Решите систему неравенств:
ІІ вариант
1 Вычислите интеграл:
а) б)
2 Решите неравенство:
3 Решите уравнения:
а) б)
4 Решите систему уравнений:
5 Решите систему неравенств :
www.metod-kopilka.ru
Итоговая контрольная работа по математике за первое полугодие для 11 класса
|
11 класс Итоговая контрольная работа за 1 полугодие Вариант 1 А1. А2. А3. А4. А5. Найдите координаты вектора и середины отрезка АВ, если А(2; — 4; 1) и В( — 2; 0; 3). В1.
В2. Найдите угол между прямыми АВ и СD, если А(1;1;2), В(0;1;1), С(2; — 2; 2), D(2; — 3; 1). С1. Решите неравенство . |
11 класс Итоговая контрольная работа за 1 полугодие Вариант 2 А1. А2. А3. А4. А5. Найдите координаты вектора и середины отрезка АВ, если А(- 3; 1; 2) и В( 1; — 1; — 2). В1. В2. Найдите угол между прямыми АВ и СD, если А(3; — 1;3), В(3; — 2;2), С(2; 2; 3), D(1; 2; 2). С1.Решить неравенство |
11 класс Итоговая контрольная работа за 1 полугодие
Вариант 3
А1.
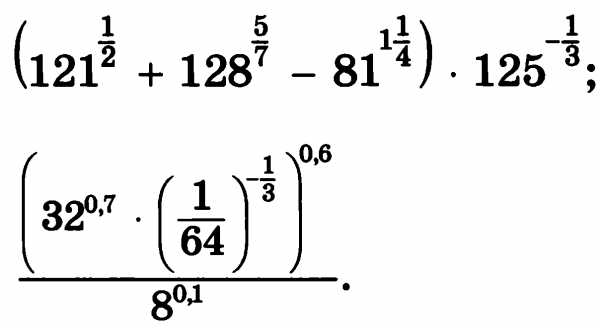
А2. Найдите корень уравнения
А3.
А4.
А5. Найдите координаты вектора и середины отрезка АВ, если
А(- 3; 2; 4) и В( 5; 0; — 2).
В1.
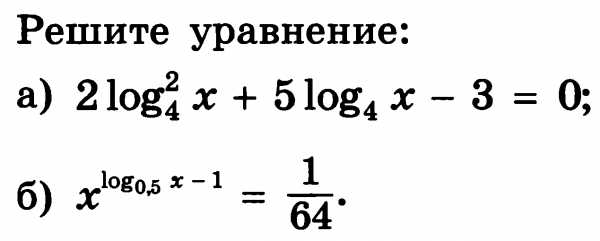
В2. Найдите угол между прямыми АВ и СD, если А(1;1;0), В(3;- 1;0),
С(4; — 1; 2), D(0; 1; 0).
С1.Решите неравенство
16 х — 1 – 67 ∙ 4 х – 2 + 12 ≤ 0.
11 класс Итоговая контрольная работа за 1 полугодие
Вариант 4
А1.
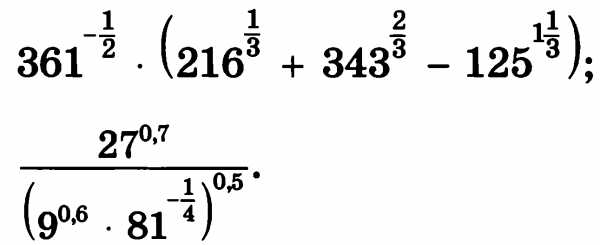
А2. Найдите корень уравнения
А3. Найдите значение выражения
А4.
А5. Найдите координаты вектора и середины отрезка АВ, если
А(1; 2; — 5) и В( — 3; 4; 1).
В1.

В2. Найдите угол между прямыми АВ и СD, если А(3; — 2;4), В(4; — 1;2), С(6; — 3; 2), D(7; — 3; 1).
С1. Решите неравенство
9 х – 1 – 35 ∙ 3 х – 2 + 24 ≤ 0.
infourok.ru
Методическая разработка по алгебре (11 класс) по теме: вводная контрольная работа в 11 классе по алгебре
Вводная контрольная работа 11 класс
|
Вариант 1 |
Вариант 2 |
|
1). Найдите , если и 2). Найдите значение выражения: 3). Найдите корень уравнения: . В ответе запишите наибольший отрицательный корень. 4). На рисунке изображен график функции , определенной на интервале (–9;8). Определите количество целых точек, в которых производная функции положительна. 5). На рисунке изображён график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке . 6). Прямая параллельна касательной к графику функции . Найдите абсциссу точки касания. 7). Найдите наименьшее значение функции на отрезке . Часть II 8). Решите уравнение =0 |
1). Найдите , если и 2). Найдите значение выражения: 3). Найдите корень уравнения: В ответе запишите наибольший отрицательный корень 4). На рисунке изображен график функции , определенной на интервале (–5;5). Определите количество целых точек, в которых производная функции отрицательна. 5). На рисунке изображён график функции и касательная нему в точке с абсциссой . Найдите значение производной функции в точке . 6). Прямая параллельна касательной к графику функции . Найдите абсциссу точки касания. 7). Найдите наибольшее значение функции на отрезке . Часть II 8). Решите уравнение =0 |
Видутова Татьяна Владимировна. МБОУ СОШ № 203 ХЭЦ г. Новосибирск.
Пояснительная записка.
Спецификация контрольной работы
по алгебре и началам анализа за курс 10 класса
- Назначение работы: определить степень сформированности знаний, основных умений и навыков, оценить качество подготовки учащихся по темам: «Тригонометрические функции числового аргумента», «Основные свойства функции», «Решение тригонометрических уравнений», «Применение производной для исследования функций на монотонность и экстремумы», «Уравнение касательной к графику функции», «Применение производной для отыскания наибольших и наименьших значений велечин»
- Апробация работ: Все задания 1 части взяты банка открытых заданий по математике http://mathege.ru/or/ege/Main, задание 2 части взято из текстов ЕГЭ.
- Условия применения: Работа рассчитана на учащихся 10 класса, изучающих курс алгебры и начала анализа, отвечает обязательному минимуму содержания основного и среднего (полного) общего образования по алгебре и началам анализа.
- Инструкция для учащихся.
На выполнение тестовой работы отводится 1 урок (45минут). Работа состоит из 8 заданий, которые разделены на две части.
Часть I состоит из 7 заданий с кратким ответом.
Часть II состоит из 1 более сложного задания. Это задание необходимо решить и записать ответ. Результаты выполнения этой части работы позволяют дифференцировать учащихся, имеющих повышенную математическую подготовку.
Советуем выполнять задания в том порядке, в котором они даны. Однако, если какое-то задание вам не удается выполнить сразу, то для экономии времени пропустите его и постарайтесь выполнить те, в которых вы уверены. Если останется время, то можно вернуться к пропущенным заданиям.
- Система оценивания.
Задание 1- 7 первой части оценивается в 1 балл, задание 8 второй части оценивается в 2 балла.
Критерии оценивания задания 8.
|
Содержания критерия |
Балл |
|
Обоснованно получен правильный ответ |
2 |
|
Тригонометрическое уравнение решено верно, но отбор корней не произведен или произведен неверно |
1 |
|
Решение не соответствует ни одному из критериев, перечисленных выше |
0 |
0 – 3 балла «2»
4 – 5 балла «3»
6 – 7 балла «4»
8 – 9 балла «5»
Составила Видутова Татьяна Владимировна.
учитель математике МБОУ СОШ № 203 ХЭЦ г. Новосибирск 2010-2011 уч. год
nsportal.ru



