ГДЗ по Алгебре за 11 класс Г.П. Бевз, В.Г. Бевз
Алгебра 11 класс
Г.П. Бевз
Авторы: Г.П. Бевз, В.Г. Бевз, Н.Г. Владимирова
«ГДЗ по алгебре 11 класс учебник Бевз (Освита)» обеспечит вам красный аттестат или даже золотую медаль. На самом деле, отличником быть не так сложно. Половина слагаемого успеха – это репутация прилежного ученика, заработанная в кругу преподавателей годами. Само собой, она дается не просто так. Но даже троечнику за год вполне можно поправить успеваемость и выйти на твердые пятерки по всем дисциплинам. Да, придется поработать. К счастью, готовые ответы по алгебре выручат даже того, кто пропустил достаточно много занятий и теперь пытается нагнать программу.
У пособия по алгебре 11 класс Бевз свои задачи
Действительно, ГДЗ по алгебре и любым другим предметам не имеет цели помочь подростку смухлевать при выполнении ДЗ или на экзамене. Правильное распоряжение содержимым учебника приводит к следующим результатам:
Правильное распоряжение содержимым учебника приводит к следующим результатам:
- знакомство с языком алгебры;
- понимание места математики в ряду других наук, ее взаимосвязей с природными явлениями и цивилизацией;
- развитие алгоритмического способа мышления;
- использование творческого подхода в точных науках;
- стимуляцию аналитической логики.
Как видите, даже в случае, если тригонометрические функции вам больше не пригодятся, навыки мыслить логически и придерживаться определенного алгоритма решения никогда не помешает. Согласно утвержденной Министерством образования РФ учебной программе на текущий год, дети должны освоить такие темы в обязательном порядке:
- Производные тригонометрических функций, их определение и применение.
- Понятие, свойства, решение первообразной.
- Площадь криволинейной трапеции и интегралы.
- Корень бесконечной степени и другие иррациональные формулы.

- Показательные уравнения, неравенства и их вычисление.
- Логарифмы и функции по видам.
Безусловно, справиться с такими темами в одиночку, если были пропуски занятий, очень тяжело. Родители сами все позабывали со времен школы и ничем не помогут. Остается вариант нанять репетитора, но хорошие преподаватели, которые дают частные уроки, в основном, в больших городах. Решебником лучше пользоваться только для перепроверки домашнего задания. Так вы сможете ответить на любой вопрос у доски, а учитель не станет сомневаться в ваших знаниях. Используйте «ГДЗ по алгебре 11 класс учебник Бевз Г. П., Бевз В. Г., Владимирова Н. Г. (Освита)» аккуратно, и тогда вы получите всю пользу без последствий.
Решебник ГДЗ Алгебра 11 класс Г. П. Бевз, В. Г. Бевз, Н. Г. Владимирова, 2011 г.. Академический, профильный уровни
В различных школах используют разные учебники по одному и тому же предмету. И по алгебре их несколько. В последние годы популярен учебник авторства Бевза. В нем алгебра преподаётся информативно и качественно, а задачи, даваемые старшекласснику, закрепляют материал уроков. Существует и решебник, алгебра, 11 класс, Бевз. Рекомендуется при обучении им пользоваться. Причин много.
В последние годы популярен учебник авторства Бевза. В нем алгебра преподаётся информативно и качественно, а задачи, даваемые старшекласснику, закрепляют материал уроков. Существует и решебник, алгебра, 11 класс, Бевз. Рекомендуется при обучении им пользоваться. Причин много.
Зачем нужны ГДЗ, алгебра, 11 класс, Бевз
Часто методички пишутся самими авторами учебника. В других случаях готовые домашние задания делаются опытными педагогами. По сути, решебник является методичкой с ответами на задачи из учебника, в том же порядке, в каком задаются. Важно различать ГДЗ и шпаргалки. В решебниках старшеклассник может найти не только ответы, но и развернутые решения, с приведением нужных формул и правил. Можно сказать, что методичка еще и закрепляет материал урока.
Еще десять лет назад родителям приходилось покупать множество решебников по тяжелым предметам. После учебного года их выбрасывали или перепродавали. Все это занимало время. Теперь методички легко скачать из интернета. Можно даже не скачать, а просто находить нужные решения на сайте. Помогут ГДЗ и с будущими самостоятельными и контрольными. Ученик закрепит тему последних уроков, поймет лучше способы решения задач. И оценка станет выше, чем без решебника. Между прочим, американские ученые не так давно провели исследования. Оказалось, что успеваемость и знания детей, пользующихся методичками – в полтора раза выше.
Можно даже не скачать, а просто находить нужные решения на сайте. Помогут ГДЗ и с будущими самостоятельными и контрольными. Ученик закрепит тему последних уроков, поймет лучше способы решения задач. И оценка станет выше, чем без решебника. Между прочим, американские ученые не так давно провели исследования. Оказалось, что успеваемость и знания детей, пользующихся методичками – в полтора раза выше.
Конечно, бывают нерадивые школьники. Они норовят всё и всегда списать, а потом уйти гулять или в компьютерные игры. Если не получается детям объяснить, что автоматическое списывание из ГДЗ не принесет пользы, за выполнением уроков могут следить сами родители. Согласитесь, что мало кто вспомнит школьную программу за 11 класс. А имея перед глазами решебник, можно проконтролировать обучение подростка, или помочь ему при необходимости.
Ответы по алгебре, 11 класс, Бевз – явные преимущества в учебном году
Стоит заметить, что решебниками очень часто пользуются и учителя, ведь времени на «окнах» не хватает для проверки домашних заданий, а личное время после работы тратить не хочется. Полезны ГДЗ и для учеников, во многих случаях.
Полезны ГДЗ и для учеников, во многих случаях.
Главное – не бездумно списывать
Ребенку надо объяснить, что решебник – не шпаргалка, а бесплатный репетитор. Обращаться к нему лучше лишь при трудностях с домашним заданием. Иначе учитель задаст вопрос, как решал подросток ту или иную задачу, а этого школьник знать не будет. Вместо того, чтобы получать двойку, лучше повторить , как решать упражнение.
Бывает, что старшеклассник плохо понял предыдущий урок, или пропустил его. Учебник с решебником помогут наверстать упущенное. Повысится и уверенность в своих силах на контрольных или самостоятельных.
ГДЗ, алгебра 11 класс, Бевз, Бевз, Владимирова – больше свободного времени у ученика
Досуг важен в жизни и детей, и взрослых. Без надлежащего отдыха тяжело учиться на отлично. Бесконечные засиживания над уроками до поздней ночи негативно скажутся на здоровьи и настроении старшеклассника. А, как известно, подростковый возраст трудный.
Почему бы не разрешить школьнику несколько раз в неделю, по тяжелым для него предметам заглянуть в ГДЗ? Вреда от этого не будет, а свободного времени станет больше.
Подытожим все плюсы от решебников:
-
закрепление и повторение пройденного
-
больше личного времени
-
ГДЗ по алгебре, 11 класс, Бевз онлайн легко и быстро найти в интернете
-
возможность обойтись без репетитора
▶▷▶ решебника по алгебре для 8 класса г.п. бевз в.г. бевз
▶▷▶ решебника по алгебре для 8 класса г.п. бевз в.г. бевз
| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 21-11-2018 |
решебника по алгебре для 8 класса гп бевз вг бевз — Yahoo Search Results Yahoo Web Search Sign in Mail Go to Mail» data-nosubject=»[No Subject]» data-timestamp=’short’ Help Account Info Yahoo Home Settings Home News Mail Finance Tumblr Weather Sports Messenger Settings Want more to discover? Make Yahoo Your Home Page See breaking news more every time you open your browser Add it now No Thanks Yahoo Search query Web Images Video News Local Answers Shopping Recipes Sports Finance Dictionary More Anytime Past day Past week Past month Anytime Get beautiful photos on every new browser window Download Решебник (ГДЗ) Алгебра 7 клас Бевз Г П, Бевз В Г gdzometrby/book722 Cached Бевз Г П , Бевз В Г Відповіді до підручника з алгебри для 7 класу Бевз Ответы к учебнику по алгебре для 7 класса Бевз Решебник задач по геометрии 7 класс гпбевз вгбевз storifycom/goevinghungclas/reshebnik-zadach-po Cached Решебник задач по геометрии 7 класс гп бевз вг бевз Приобрести решебник, в котором находятся все ответы на задания школьных учебников Решебник (ГДЗ) Алгебра 11 клас 2011г Бевз Г П, Бевз В Г gdzometrby/book2033 Cached Відповіді до підручника з алгебри для 11 класу Бевз Ответы к учебнику по алгебре для 11 класса Бевз Решебника По Алгебре Для 8 Класса Гп Бевз Вг Бевз — Image Results More Решебника По Алгебре Для 8 Класса Гп Бевз Вг Бевз images Решебник (ГДЗ) Алгебра 7 класс ГП Бевз, ВГ Бевз 2007 | Вшколе vshkolecom … Алгебра Всех приведенных выше трудностей можно избежать, если использовать ГДЗ 7 класс Бевз для проверки ответов домашнего задания ГДЗ по алгебре 11 класс Бевз, Владімірова megareshebaru/index/u13/0-4460 Cached Подроный решебник по алгебре для 11 класса , авторов ГП Бевз , ВГ Бевз , НГ Владимирова 2016 год ГДЗ по алгебре 7 класс Бевз, Бевз megareshebaru/index/u10/0-4457 Cached Решебник (готові домашні завдання) по алгебре для 7 класса , авторы Бевз ГП , Бевз ВГ 2016 год Гдз алгнбра 7 класс гббвз в г бевз · Storify storifycom/izunnichi/gdz-algnbra-7-klass-g-b Cached Решебник по Алгебре для 7 класса , авторы учебника: Бевз Г П , Бевз В Г На год Твой доступ к истинным знаниям ГДЗ от Путина Бевз алгебра 8 класс — gubelubiosuturecom gubelubiosuturecom/b42886dd Cached Решебник по алгебре для 8 класса , Бевз Г Подробные и качественные решения задач онлайн от Спиши ру Задания Гдз математика 11 клас гпбевз вгбевз kanotivumfoxwoodattrinitybiz/ 8 a044-gdz Cached Гдз математика 11 клас гп бевз вг бевз Этот учебный год не очень прост для всех учеников, поскольку он должен иметь дело с огромными примерами, сложными задача Алгебра 7 Класс Укр Гдз Бевз Г П Бевз В Г — premiumsync premiumsyncweeblycom/blog/algebra-7-klass-ukr-gdz-bevz Cached ГДЗ Алгебра 7 класс Алгебра 7 клас Бевз ГП , Бевз ВГ Чтобы усвоить подобные задания, семиклассник прибегает к помощи решебника под редакцией ГП ГДЗ 7 класс, решебники, в Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 1,890 results Settings Help Suggestions Privacy (Updated) Terms (Updated) Advertise About ads About this page Powered by Bing™
- издание: Бевз Г П
- В Г Бевз Відповіді до підручника з алгебри для 8 класу Бевз Ответы к учебнику по алгебре для 8 класса Бевз 2016 рік Решения так же подходят к: Тестові завдання Типові завдання до контрольноі роботи Завдання для самостійноі роботи Завдання: 1 Скрыть 4 ГДЗ по алгебре для 8 класса Бевз Г П
- квадратными корнями и уравнениями Для подготовки к повторению полученных знаний предполагаются ответы к соответствующим задачам Ученики
Бевз В Г на 2017-2018 год Читать ещё Решебник и ГДЗ по Алгебре для 8 класса
Бевз В Г Відповіді видані у 2016 році 7 ГДЗ по Алгебре за 8 класс Бевз — решебник с ответами shkololoru › gdz-algebra/8-klass-bevz Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Это решебник для учебника по Алгебре для 8 класса авторов Бевз Г П
- Бевз Г Подробные и качественные решения задач онлайн от Спиши ру Задания Гдз математика 11 клас гпбевз вгбевз kanotivumfoxwoodattrinitybiz/ 8 a044-gdz Cached Гдз математика 11 клас гп бевз вг бевз Этот учебный год не очень прост для всех учеников
- решебники
- решебники
решебника по алгебре для 8 класса гп бевз вг бевз — Все результаты ГДЗ Алгебра 8 класс ГП Бевз, ВГ Бевз — Моя домашка mydomashkaru/gdz/8-klass-algebra/8-gp-bevz-vg-bevzhtml Похожие Скачать ГДЗ Алгебра 8 класс Г П Бевз , В Г Бевз вы можете на Авторы, издание: Бевз Г П , В Г Бевз Другие решебники по Алгебра для 8 классa Картинки по запросу решебника по алгебре для 8 класса гп бевз вг бевз «id»:»lOdoafbZNo492M:»,»ml»:»600″:»bh»:90,»bw»:120,»oh»:582,»ou»:» «,»ow»:870,»pt»:»prostoshkolacom/data/b/64/answers/dalzbv6y0b9s7j»,»rh»:»bespereboynayasetru»,»rid»:»4Le1ffFB8kNXyM»,»rt»:0,»ru»:» «,»sc»:1,»th»:90,»tu»:» \u003dtbn:ANd9GcRPmf3gat0-5A1Ljm9khVPi4X4LdPtHJEqy3ewMC_XorI1sswOrQUtDueg»,»tw»:135 «cr»:3,»id»:»Lk3MptQ_jn-5qM:»,»ml»:»600″:»bh»:90,»bw»:66,»oh»:789,»ou»:» «,»ow»:577,»pt»:»gdzavrcom/i/r/788/786—49483jpg»,»rh»:»hitrunru»,»rid»:»SfnjSLX5s92tlM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»hitrunru»,»th»:97,»tu»:» \u003dtbn:ANd9GcQ6u3kGTz5kBy0TwTR-SjunHFrP6Y0Q7-pfEG6n_6W61xHcx78Iqgz87A»,»tw»:71 «id»:»v6EWHI5P6YnPeM:»,»ml»:»600″:»bh»:90,»bw»:58,»oh»:1085,»ou»:» «,»ow»:700,»pt»:»ipinimgcom/originals/20/67/67/20676705f97ef690ea»,»rh»:»pinterestcom»,»rid»:»Myb-mgu3dnexfM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Pinterest»,»th»:104,»tu»:» \u003dtbn:ANd9GcR-lLV8bYrwKoa4Q0Ucyi42T5QhHbNWql32JRtnXYAa6wjUIDhNpBBqew»,»tw»:67 «cb»:21,»cl»:21,»cr»:12,»id»:»UMEo_I0l9JYAjM:»,»ml»:»600″:»bh»:90,»bw»:93,»oh»:567,»ou»:» «,»ow»:550,»pt»:»ipinimgcom/originals/04/7c/6c/047c6cc32fbcdafc07″,»rh»:»pinterestcom»,»rid»:»kB9mZHxh2xFcCM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Pinterest»,»th»:96,»tu»:» \u003dtbn:ANd9GcQwPOY-7qk4psE2WgF6K0odH_FOs6RRlR0v09kNGxSFldOBPTG4q3DfcNQ»,»tw»:93 «id»:»mXJS_39CieQ8KM:»,»ml»:»600″:»bh»:90,»bw»:60,»oh»:150,»ou»:» «,»ow»:100,»pt»:»iobozrevatelcom/moyashkola/entity/2018/5/25/4215″,»rh»:»obozrevatelcom»,»rid»:»ZcDdMn-rXs6YlM»,»rt»:0,»ru»:» «,»sc»:1,»th»:90,»tu»:» \u003dtbn:ANd9GcQ4BuCGteVilELbayRAsUgNl2yPwCL4r_HSLRR_M8phzh2M63908NQWlA»,»tw»:60 «cb»:15,»id»:»8eDbtqkooI0i8M:»,»ml»:»600″:»bh»:90,»bw»:58,»oh»:870,»ou»:» «,»ow»:546,»pt»:»cdneurokiorg/system/books/covers/000/000/085/thu»,»rh»:»eurokiorg»,»rid»:»5JMWoTK9kY1QAM»,»rt»:0,»ru»:» «,»th»:105,»tu»:» \u003dtbn:ANd9GcQtnvE7g82J-QWAdw10uAYK9HwOuagehcRnSBFmm7IfbHPFdQjDVPuO-w»,»tw»:66 «id»:»L2BwC995J8am1M:»,»ml»:»600″:»bh»:90,»bw»:121,»oh»:600,»ou»:» «,»ow»:800,»pt»:»imagesmysharedru/265244/slide_21jpg»,»rh»:»lohuwuduxi2kastcomru»,»rid»:»SBuKxloF3jBH6M»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Решебник по английскому языку класс 6 2015″,»th»:91,»tu»:» \u003dtbn:ANd9GcS3PGmGKccVi-xh3F-7GtYg8WjFWTNZjtYoteMpBh8GgA4qcU-1njkrbR0″,»tw»:121 Другие картинки по запросу «решебника по алгебре для 8 класса гп бевз вг бевз» Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты ГДЗ (решебник) Алгебра 8 класс В Г Бевз, Г П Бевз 2008 | Моя › Моя Школа › ГДЗ › 8 класс › Алгебра Рейтинг: 5 — 2 голоса Сложные и непонятные задания по алгебре могут отбить все желание учиться у школьника Особенно это касается восьмиклассников, которые очень ГДЗ и решебники Алгебра 8 класс | Моя Школа › Моя Школа › ГДЗ › 8 класс Все ГДЗ ( решебник ) по Алгебре 8 класс онлайн на сайте Только ГДЗ и решебники 8 класс по Алгебре ГДЗ Алгебра 8 класс Г П Бевз , В Г Бевз 2016 Решебник (ГДЗ) Алгебра, 8 класс (ГП Бевз, В Г Бевз) — docbazaru Перевести эту страницу Решебник (ГДЗ) по учебнику Алгебра , 8 класс ( Г П Бевз , В Г Бевз ) Розв’ язання вправ та завдань до підручника « АЛГЕБРА » Г П Бевза , В Г Бевз (8 клас) ГДЗ По алгебре 8 класс ГПБевз ВГБевз | ВКонтакте ГДЗ По алгебре 8 класс Г П Бевз В Г Бевз моей подруге нужно решить за 8 класс по алгебре уражнение Решебники 2–11 классы vse-gdzinfo 3 решебник алгебра 8 класс бевз онлайн | ВКонтакте vkcom/page-64510708_46658337 Алгебра 8 класс Укр ГДЗ Бевз Г П Бевз В Г Ваши друзья Стр Решебника 2 Стр Решебника 40 ГДЗ Алгебра 8 класс Укр Бевз Г П Бевз В Решебник (ГДЗ) по алгебре за 8 класс › ГДЗ › 8 класс › Алгебра Похожие Подробный решебник (гдз) по Алгебре за 8 класс к учебнику школьной Алгебра 8 класс дидактические материалы авторы: Бевз Г П , Бевз В Г Гдз по алгебре за 8 класс, авторы Бевз ГП, Бевз ВГ › ГДЗ › 8 класс › Алгебра › Бевз ГП Похожие Подробные решения и гдз по алгебре для 8 класса , авторов Бевз Г П , Бевз можно пролистать решебник по алгебре за 8 класс Бевза , где находятся алгебра 8 класс бевз бевз решебник задание 883 / Блог им 14 мар 2017 г — Формат: PDF Размер: 7563 Мб Похожие файлы ГДЗ відповіді по алгебре 8 класс Бевз Г П , Бевз В Г Гдз 8 класс — Задания с решениями — Alpha Lambda Omega wwwalphalambdaomegaorg/find/read/gdz-8-klass-algebra-bevzhtml Решебник (ГДЗ) Алгебра 8 клас Бевз Г П , В Г Бевз — gdzometrbygdzometr by/book748CachedВідповіді до підручника з алгеб ГДЗ відповіді по алгебре 8 класс Бевз ГП, Бевз ВГ › Алгебра › 8 класс Похожие Решебник по алгебре за 8 класс авторы Бевз Г П , Бевз В Г издательство Решебник по алгебре 8 класс ГП Бевз wwwbioverru/gdz/reshebnik-po-algebre-8-klass-gp-bevz Решебник по алгебре 8 класс Г П Бевз Тип файла: DOC Страниц: 243 Количество просмотров: 6582 Количество скачиваний: 767 На сайте: 27 дней Гдз бевз алгебра 7 класс — Гдз бевз алгебра 7 класс 24 мар 2015 г — Этот Решебник « Алгебра 7 клас, Г П Бевз ,… Решебник (ГДЗ) для Алгебра , 8 класс ( Г П Бевз , В Г Бевз ) Решебники (гдз) по алгебре ГДЗ (решебники) по алгебре — 8 класс (ГП Бевз, В Г Бевз) gdzabc-english-grammarcom/gdz_po_algebre39htm ГДЗ ( решебники ) по алгебре — 8 класс ( Г П Бевз , В Г Бевз ) Алгебра 8 класс ГП Бевз, ВГ Бевз 2016 — Вшколе › Решебники за 8 класс › Алгебра › ГП Бевз, ВГ Бевз Розділ 1 РАЦІОНАЛЬНІ ВИРАЗИ Полный и качественный решебник (ГДЗ) Алгебра 8 класс Г П Бевз , В Г Бевз 2016 Доступно на ваших смартфонах Натаскиваются гдз по алгебре 8 класс мордкович 2002 обязаны wwwnpomedianaru/libgphp?g=gdz-po-algebre-8-klass-mordkovich-2002htm 16 нояб 2011 г — Университет гдз по алгебре 8 класс мордкович 2002 посещать гдз алгебра 10 кл алгебра · решебник по алгебре 8 класс г п бевз · гдз ГДЗ Алгебра 8 класс | Бевз prostoshkolacom › ГДЗ для 5-11 классов › Готовые домашние задания 8 класс Похожие Решебник ГДЗ Алгебра 8 класс Г П Бевз , В Г Бевз Все готовые задания учебника [PDF] гдз геометрія 8 клас бевз — WordPresscom Бевз Г П , Бевз В Г , Владімірова Н Г Геометрія 8 клас Бевз Г П , Бевз учебника — г п бевз где взять решебник 8 класс алгебра автор: г п 846551394 [PDF] гдз 8 класс украина алгебра №143 ГПБЕВЗ — WordPresscom senniteridefileswordpresscom/2017/01/24pdf 8 класс Пос для школ с углубл изучен математики Бевз Г П , Бевз В Г , Решебник (ГДЗ) по учебнику Алгебра , 8 класс ( Г П Бевз , В Г Бевз ) ГДЗ по Геометрии за 7 класс — автор ГП Бевз — Shkololoru › ГДЗ по геометрии › 7 класс ГДЗ по Геометрии за 7 класс Бевз — новый онлайн решебник с ответами и решениями к учебнику по геометрии автора Г П Бевз по ФГОС — 939 Решебник (ГДЗ) «Алгебра 8 клас, Г П Бевз, В Г Бевз» 2016, Нова 12ballovnet/444-algebrahtml Похожие Алгебра , Украина 2016 Г П Бевз , В Г Бевз ГДЗ 8 класс » Алгебра Решебник (ГДЗ) « Алгебра 8 клас, Г П Бевз , В Г Бевз » решебник алгебра 9 класс бевз — WordPresscom itimoscabcifileswordpresscom/2017/01/83pdf Решебник , ГДЗ к учебнику по Алгебре 7- 8 -9 класс , Бевз ГДЗ по Алгебре 7- 8 -9 класс : Алгебра Решения к учебнику Бевза Г П 7-9 классы Приведены Ответы@MailRu: где скачть решебник алгебра 8 класс ГП Бевз › Образование › Школы 2 ответа 8 окт 2009 г — класс , урок, и учебник! 9&disciplineID=1 English new millennium решебник 7 класс :: Школьные решебники wwwresursinvestru/vanishphp?lto9=663 15 февр 2014 г — Скачать ГДЗ — English new millennium решебник 7 класс Алгебра 8 класс г п бевз в г бевз гдз · 4 класс математика решебник аргинской Геометрия бевз 7 класс 696 номер | Геометрия бевз 7 класс 696 24 мар 2015 г — ГДЗ Алгебра , 7 класс Г П Бевз , В Г Бевз Многие задачи по гдз 8 класс геометрия бевз гдз, решебник по алгебре за 7 класс миндюк, Решебник по Алгебре за 9 класс ГП Бевз, ВГ Бевз — Спиши нет решебник (гдз) по Алгебре для 9 класса , авторы учебника: Г П Бевз , В Г 1; 2; 3; 4; 5; 6; 7; 8 ; 9; 10; 11; 12; 13; 14; 15; 16; 17; 18; 19; 20; 21; 22; 23; 24 гдз математика решебник matematika-domaorg/ Похожие Перевести эту страницу ГДЗ математика 5 клас та гдз математика 6 клас — ( решебники ) за підручником автора Тарасенкова, відео Гдз ( решебники ) та відео розв’ язання завдань за підручниками: алгебра Бевз ГДЗ 8 клас: Дуже сподіваємося, що наш проект буде корисний учням п ‘ятих і шостих класів, а також їхнім батькам Решебник по геометрии 7 класс гпбевз вгбевз нгвладимирова Решебник по геометрии 7 класс г п бевз в г бевз н г владимирова задачи по готовым ресунком Гдз по алгебре 9 класс макарычев 16 издание онлайн More information Леса умеренного пояса конспект урока география 8 класс Решебник по алгебре 7 класс гпбевз вгбевз для укршк | grafakde Решебник по алгебре 7 класс г п бевз в г бевз для укршк Решебник по английскому языку учебника 8 класса 2003 года 8-е издание авторы в Open Решебник по алгебре 7 класс гпбевз вгбевз для укршк | ciatacint Решебник по алгебре 7 класс г п бевз в г бевз для укршк Алгебра 8 класс он лайн готовые домашние задания Find this Pin and more on svilbathurd by Гдз з алгебри 8 класс бевз bespereboynayasetru/gdz-z-algebri-8-klass-bevzhtml Решебник по алгебре за 8 класс авторы Бевз Г П , Бевз В Г издательство Задание: 516 ГДЗ з алгебри для 8 класу за підручником Г П Бевз , В Г Бевз Решебник Алгебра и начала математического анализа 11 класс Похожие П 1 П 2 П 3 П 4 П 5 П 6 П 7 П 8 П 9 П 10 П 11 П 12 П 13 П 14 П 15 П 16 П 17 П 18 П 19 П 20 П 21 П 22 П 23 П 24 П 25 П 26 П 27 П 28 П 29 П 30 П 31 П 32 ГДЗ по Алгебре за 8 класс: Никольский СМ Решебник — GDZru › ГДЗ › 8 класс › Алгебра › Никольский СМ ГДЗ: Спиши готовые домашние задания по алгебре за 8 класс , решебник С М Алгебра 8 класс тематические тесты Авторы: Чулков П В, Струков ТС ▷ гдз 7 класс геометрия гп бевз вг бевз нг владiмiрова dpsnalconagarcom//gdz-7-klass-geometriia-g_p_-bevz-v_g_-bevz-n_g_-vladimiro 5 нояб 2018 г — гдз 7 класс геометрия гп бевз вг бевз нг владiмiрова — Yahoo Search 7 _10html решебник гдз по алгебре 7 класс г п бевз н г бевз решебник гдз по это интересно Геометрія Г П Бевз , В Г Бевз , Н Г Владімірова 7, 8 , ГДЗ по алгебре для 8 класса Бевз ГП — Номера задач / 186 › ГДЗ › 8 класс › Алгебра › Бевз ГП › 186 ГДЗ ( решебник 1) по алгебре 8 класс Бевз Г П / Номера решебник 2 / Номера задач / 186 ГДЗ ( решебник 2) по алгебре 8 класс Бевз Г П / Номера Гдз по Алгебре за 8 класс, авторы Бевз ГП, Бевз ВГ Похожие Подробные гдз и решебник по Алгебре для 8 класса , авторы учебника: Бевз Г П , Бевз В Г на 2017-2018 год Решебник по Алгебре 11 класс ГП Бевз, ВГ Бевз — Зубрилка ГДЗ по Алгебре за 11 класс Г П Бевз , В Г Бевз 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 Пояснения к фильтрации результатов Мы скрыли некоторые результаты, которые очень похожи на уже представленные выше (44) Показать скрытые результаты Некоторые результаты поиска могли быть удалены в соответствии с местным законодательством Подробнее Вместе с решебника по алгебре для 8 класса гп бевз вг бевз часто ищут гдз по алгебре 8 класс мерзляк гдз по алгебре 8 класс бевз 2008 гдз алгебра 8 клас бевз 2016 гдз алгебра 8 клас мерзляк з поглибленим вивченням 2016 нова програма гдз по алгебре 8 класс мерзляк сборник гдз алгебра 8 клас з поглибленим вивченням 2016 гдз по алгебре 8 класс истер решебник по алгебре 8 класс мерзляк на русском Ссылки в нижнем колонтитуле Россия — Подробнее… Справка Отправить отзыв Конфиденциальность Условия Аккаунт Поиск Карты YouTube Play Новости Почта Контакты Диск Календарь Google+ Переводчик Фото Ещё Документы Blogger Hangouts Google Keep Подборки Другие сервисы Google
Яндекс Яндекс Найти Поиск Поиск Картинки Видео Карты Маркет Новости ТВ онлайн Знатоки Коллекции Музыка Переводчик Диск Почта Все Ещё Дополнительная информация о запросе Добавлены результаты по запросу « решебни к по алгебре для 8 класса гп бевз вг бевз » Искать только « решебника по алгебре для 8 класса гп бевз вг » Показаны результаты для Нижнего Новгорода Москва 1 Гдз по алгебре за 8 класс , авторы Бевз Г П , Бевз В Г MegaReshebaru › Алгебра 8 класс авторы Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Готові домашні завдання Алгебра 8 клас Бевз авторы: Бевз Г П , Бевз В Г Чтобы проконтролировать правильность выполнения домашней работы, можно пролистать решебник по алгебре за 8 класс Бевза , где находятся все ответы Читать ещё Готові домашні завдання Алгебра 8 клас Бевз авторы: Бевз Г П , Бевз В Г Розв’язання вправ та завдань до підручника АЛГЕБРА 8 клас Г П Бевз В Г Бевз Чтобы проконтролировать правильность выполнения домашней работы, можно пролистать решебник по алгебре за 8 класс Бевза , где находятся все ответы В 3 разделах пособия находятся подробные решения упражнений с рациональными выражениями, действительными числами, квадратными корнями и уравнениями Для подготовки к повторению полученных знаний предполагаются ответы к соответствующим задачам Ученики, занимающиеся углубленным изучением алгебры , смо Скрыть 2 ГДЗ відповіді по алгебре 8 класс Бевз Г П , Бевз В Г eurokiorg › gdz…algebra/8_klass/g_p_bevz_v_g_bevz_4 Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте ГДЗ алгебра 8 клас Бевз Г П , Бевз В Г Не секрет, что период адаптации школьников после перехода из класса В сборнике ГДЗ за по алгебре за восьмой класс — Г П Бевз тематика предложенных заданий строго соответствует тематике пройденного материала по основному учебнику в данном классе Читать ещё ГДЗ алгебра 8 клас Бевз Г П , Бевз В Г Не секрет, что период адаптации школьников после перехода из класса в класс вызывает очень серьезные психологические проблемы Теряется умение понимать суть заданий, придумывать способы их решений и как следствие отказ от работы над заданиями которые дает учитель В связи с этим снижается успеваемость, интерес к учебе и успеваемость Решить эту проблему могут специальные обучающие средства повышающие успешность ученика В сборнике ГДЗ за по алгебре за восьмой класс — Г П Бевз тематика предложенных заданий строго соответствует тематике пройденного материала по основному учебнику в данном классе Скрыть 3 Решебник (ГДЗ) Алгебра 8 клас Бевз Г П , В Г Бевз gdzometrby › book748 Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте « Алгебра 8 клас» ГДЗ Бевз Г П , В Г Бевз Відповіді до підручника з алгебри для 8 класу Бевз Ответы к учебнику по алгебре для 8 класса Бевз 2016 рік Решения так же подходят к: Тестові завдання Типові завдання до контрольноі Читать ещё « Алгебра 8 клас» ГДЗ Бевз Г П , В Г Бевз Відповіді до підручника з алгебри для 8 класу Бевз Ответы к учебнику по алгебре для 8 класса Бевз 2016 рік Решения так же подходят к: Тестові завдання Типові завдання до контрольноі роботи Завдання для самостійноі роботи Завдання: 1 Скрыть 4 ГДЗ по алгебре для 8 класса Бевз Г П , Бевз В Г reshebacom › Видеорешения › Алгебра › bevz Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте авторы: Бевз Г П , Бевз В Г Качественные решения и подробные гдз по алгебре для учеников 8 класса , авторы учебника: Бевз Г П , Бевз В Г 5 Решебник и ГДЗ по Алгебре за 8 класс , авторы Бевз gdz-putinanet › 8-klass-algebra-bevz Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Решебник и ГДЗ по Алгебре для 8 класса , авторы учебника: Бевз Г П , Бевз В Г на 2017-2018 год Читать ещё Решебник и ГДЗ по Алгебре для 8 класса , авторы учебника: Бевз Г П , Бевз В Г на 2017-2018 год Номера задач 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 Скрыть 6 ГДЗ з алгебри 8 клас Бевз 2016 gdzonlinenet › 163-algebra-bevz-8…dopovnenahtml Перевести Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Готові домашні завдання по новій програмі з алгебри для 8 -х класів, автори: Бевз Г П , Бевз В Г Відповіді видані у 2016 році 7 ГДЗ по Алгебре за 8 класс Бевз — решебник с ответами shkololoru › gdz-algebra/8-klass-bevz Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Это решебник для учебника по Алгебре для 8 класса авторов Бевз Г П , Бевз В Г Готовые домашние задания по алгебре помогут проверить себя или быстро узнать решение и списать ответ В решебнике содержится упражнений с ответами — Ученики 8 классов мо Читать ещё Это решебник для учебника по Алгебре для 8 класса авторов Бевз Г П , Бевз В Г Готовые домашние задания по алгебре помогут проверить себя или быстро узнать решение и списать ответ В решебнике содержится упражнений с ответами — Ученики 8 классов могут бесплатно пользоваться этим ГДЗ, чтобы проверять свою работу на правильность Спиши и поделись с другими! Скрыть 8 ГДЗ по Алгебре 8 класс Бевз Г П , Бевз В Г eurokime › Алгебра › ГДЗ по Алгебре 8 класс Бевз гП Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Показать решебники Видеорешения Здесь вы найдете ГДЗ с подробным и полным решением упражнений (номеров) по Алгебре за 8 класс , автор: Бевз Г П , Бевз В Г Издательство: Украина Читать ещё Показать решебники Видеорешения Классы 1 2 3 4 5 6 7 8 9 10 11 Математика 1 2 3 4 5 6 7 8 9 10 11 Английский язык 1 2 3 4 5 6 7 8 9 10 11 Здесь вы найдете ГДЗ с подробным и полным решением упражнений (номеров) по Алгебре за 8 класс , автор: Бевз Г П , Бевз В Г Издательство: Украина © 2018 «eurokime» admin@eurokime Скрыть 9 Решебника по алгебре для 8 класса гп Бевз вг Бевз — смотрите картинки ЯндексКартинки › решебника по алгебре для 8 класса гп бевз вг Пожаловаться Информация о сайте Ещё картинки 10 ГДЗ Алгебра 8 класс Г П Бевз , В Г Бевз | Решебники MyDomashkaru › Решебники › …/8-gp-bevz-vg-bevzhtml Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Авторы, издание: Бевз Г П , В Г Бевз О решебнике Г П Бевз , В Г Бевз Другие решебники по Алгебра для 8 классa Читать ещё Авторы, издание: Бевз Г П , В Г Бевз Нравится Твитнуть Разделы учебника Алгебра 8 клас Укр О решебнике Г П Бевз , В Г Бевз Другие решебники по Алгебра для 8 классa ЛА Александрова, А Г Мордкович 2010 Л А Александрова (при участии Мордкович А Г ) Скрыть Решебник по Алгебре за 8 класс Бевз Г П , Бевз В Г spishynet › 8 класс › Алгебра › bevz Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Подробный решебник (гдз) по Алгебре для 8 класса , авторы учебника: Бевз Г П , Бевз В Г на весь учебный год от Спишинет Номера задач Скачать: учебник алгебра 8 класс / litresru litresru Не подходит по запросу Спам или мошенничество Мешает видеть результаты Информация о сайте реклама Школьные учебники скачивайте онлайн в электронном формате на ЛитРес Контактная информация +7 (800) 333-27-37 круглосуточно Магазин на Маркете 18+ 1 2 3 4 5 дальше Браузер Предложит замену неверному адресу сайта 0+ Скачать
vojupez алгебра і початки аналізу 10 11 клас бевз гдз
Ссылка:
http://itagix. sabemo.ru/2/63/algebra—pochatki-analzu-10-11-klas-bevz-gdz
sabemo.ru/2/63/algebra—pochatki-analzu-10-11-klas-bevz-gdz
алгебра і початки аналізу 10 11 клас бевз гдз
Клас: 10-11 клас Мова навчання: УкраїнськаАвтор: Бевз Г. П. Предмет: АлгебраРік видання: 2005Видавництво: Освіта. Клас: 10-11 клас Мова навчання: УкраїнськаАвтор: Бевз Г. П. Предмет: АлгебраРік видання: 2005Видавництво: Освіта. АЛГЕБРА І ПОЧАТКИ АНАЛІЗУ. Полный и качественный решебник (ГДЗ) Математика 10 класс Г.П. Бевз, В.Г. Бевз 2011 Рівень стандарту. Доступно на . Підручник Алгебра і початки аналізу 10-11 клас . аналізу 10-11 клас Бевз . Алгебра 10 клас М.І . Готовые домашние задания (ГДЗ) по алгебре для 7-11 классов: . (для русских школ) Бевз Г. П., Бевз В. Г. Алгебра. 7 клас. .. Алгебра и начала анализа. 10-11 класс. 10 класс. Алимов Ш. А. 2012г. .. Алгебра і початки аналізу. 11 . Алгебра і початки аналізу 10-11 клас Бевз. Скачать бесплатно, читать онлайн Полный и качественный решебник (ГДЗ) Математика 10 класс Г.П. Бевз, В.Г. Бевз 2011 Рівень стандарту. Доступно на . АЛГЕБРА І ПОЧАТКИ АНАЛІЗУ . Полный и качественный решебник (ГДЗ) Алгебра 11 класс Г.П. Бевз, В.Г. Бевз, Н.Г. Владимирова 2011 . 1. Функції та їх основні властивості№ 10-41 .
П. Предмет: АлгебраРік видання: 2005Видавництво: Освіта. Клас: 10-11 клас Мова навчання: УкраїнськаАвтор: Бевз Г. П. Предмет: АлгебраРік видання: 2005Видавництво: Освіта. АЛГЕБРА І ПОЧАТКИ АНАЛІЗУ. Полный и качественный решебник (ГДЗ) Математика 10 класс Г.П. Бевз, В.Г. Бевз 2011 Рівень стандарту. Доступно на . Підручник Алгебра і початки аналізу 10-11 клас . аналізу 10-11 клас Бевз . Алгебра 10 клас М.І . Готовые домашние задания (ГДЗ) по алгебре для 7-11 классов: . (для русских школ) Бевз Г. П., Бевз В. Г. Алгебра. 7 клас. .. Алгебра и начала анализа. 10-11 класс. 10 класс. Алимов Ш. А. 2012г. .. Алгебра і початки аналізу. 11 . Алгебра і початки аналізу 10-11 клас Бевз. Скачать бесплатно, читать онлайн Полный и качественный решебник (ГДЗ) Математика 10 класс Г.П. Бевз, В.Г. Бевз 2011 Рівень стандарту. Доступно на . АЛГЕБРА І ПОЧАТКИ АНАЛІЗУ . Полный и качественный решебник (ГДЗ) Алгебра 11 класс Г.П. Бевз, В.Г. Бевз, Н.Г. Владимирова 2011 . 1. Функції та їх основні властивості№ 10-41 . 11 . класс. ГДЗ . Алгебра і початки аналізу 10 клас Шкіль . при выполнении домашки станет ГДЗ . алгебра і початки аналізу 10 11 клас бевз г п алгебра 11 клас — решебник 11 класс бевз алгебра і початки аналізу . . Бевз Г.П., Бевз В.Г. — Алгебра 8 клас (Учебник) pdf 20,37Мб.
11 . класс. ГДЗ . Алгебра і початки аналізу 10 клас Шкіль . при выполнении домашки станет ГДЗ . алгебра і початки аналізу 10 11 клас бевз г п алгебра 11 клас — решебник 11 класс бевз алгебра і початки аналізу . . Бевз Г.П., Бевз В.Г. — Алгебра 8 клас (Учебник) pdf 20,37Мб.
Шкільні підручники, посібники, зошити,ГДЗ, ДПА, ЗНО, в електронному форматі pdf, djvu, безкоштовне завантаження та перегляд онлайн. алгебра і початки аналізу 10-11 клас бевз г.п гдз — Клас: 10-11 клас Мова навчання: УкраїнськаАвтор: Бевз Г. П. Предмет: АлгебраРік видання:.
2017.03.24
| Трэкбэки(0) | Unclassified
ГДЗ до підручника з алгебри 11 клас Г.П. Бевз, В.Г. Бевз 2011 рік
Рішення та відповіді до підручника з алгебри для 11 класу
Г.П. Бевз, В.Г. Бевз, Н.Г. Владімірова
ГДЗ з алгебри — помічник одинадцятикласника
ГДЗ до підручника Г.П. Бевз з алгебри і початків аналізу для 11 класу, де математика вивчається на профільному чи академічному рівні, допомагає майбутнім випусникам відразу на кількох фронтах. Посібник містить відповіді до всіх завдань із кожного параграфу підручника. У ньому ретельно розібрані всі найважливіші теми. Функції, первісна та інтеграли більше не проблема, адже варіанти рішень, запропоновані фахівцями, уже на сайті GDZ4YOU і за вашим бажанням — на вашому телефоні чи комп’ютері.
Посібник містить відповіді до всіх завдань із кожного параграфу підручника. У ньому ретельно розібрані всі найважливіші теми. Функції, первісна та інтеграли більше не проблема, адже варіанти рішень, запропоновані фахівцями, уже на сайті GDZ4YOU і за вашим бажанням — на вашому телефоні чи комп’ютері.
Чому в одинадцятому класі обов’язково мати ГДЗ з алгебри
- Одинадцятикласники! Скоро ЗНО. Учні, що складають ЗНО з математики знають, що без постійних тренувань неможливо досягти гарних результатів. ГДЗ з алгебри допоможе здобути та відточити знання з багатьох важливих тем.
- Через велике навантаження у випускників зовсім не залишається часу на перевірку домашнього завдання. Це призводить до того, що прикрі помилки негативно впливають на оцінки. ГДЗ з алгебри допоможе виправити ці помилки та більше ніколи їх не припускатися.
- Бал атестата також враховується під час вступу до вищого навчального закладу. Тому важливо закінчити цей навчальний рік якомога краще. Навіть якщо ви не складаєте ЗНО з математики, варто подбати про свій високий бал із цього предмету.
 Решебник з алгебри вам точно знадобиться.
Решебник з алгебри вам точно знадобиться.
Користуватися ГДЗ з алгебри можна буквально на ходу
Маєш вільний час лише, коли їдеш у метро на навчання? Є вільна хвилинка лише під час перерви на репетиції випускного вальсу? Тоді GDZ4YOU — це саме те, що тобі потрібно. Усі решебники тут можна знайти безкоштовно і користуватися ними онлайн. Тож бери свій смартфон та користуйся ГДЗ з алгебри хоч перед уроком.
ГДЗ з геометрії для ЗНО на 200 балів
Алгебра — це лише складова математики. Не можна забувати про геометрію, яка теж є досить складною. На GDZ4YOU можна знайти ГДЗ з геометрії, щоб опанувати математику комплексно та скласти ЗНО на 200 балів.
Бевз 11 класс алгебра 2011 гдз
Скачать бевз 11 класс алгебра 2011 гдз fb2
Авторы: Г.П. Бевз, В.Г. Бевз, Н.Г. Владимирова. Онлайн решебник по Алгебре для 11 класса Г.П. Бевз, В.Г. Бевз, Н.Г. Владимирова, гдз и ответы к домашнему заданию. Номера. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 Книги, ГДЗ, решебники, готовые домашние задания, ЕГЭ, ГИА, наука и обучение, словари, все для преподавателей, школьников и студентов, русский язык, математика, физика, английский язык, алгебра, геометрия по всем классам, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 класс.
А ты НАШЁЛ то, что тебе нужно? У нас Вы сможете найти все! Тільки на нашому сайті ви знайдете гдз алгебра 11 клас Бевз. Тепер розвязання домашнього завдання займе набагато менше часу, просто скористайтесь готовими домашніми завданнями з предмету алгебра 11 клас.
Алгебра і початки аналізу. Підручник для 11 класу загальноосвітніх навчальних закладів з навчанням російською мовою. (Російською мовою). • Автор: Г.П.Бевз, В.Г.Бевз, Н.Г.Владімірова • Видавництво: «Освіта» • Рік видання: • Сторінок: • Формат файлу: pdf. Уважаемые старшеклассники! Алгебра и начала анализа — учебный предмет, который раскрывает важнейшие темы алгебры, математического анализа, теории функций и теории вероятностей. С помощью этого учебника вы будете завершать изучение алгебры и начал анализа в средней школе.
Чтобы представить весь её курс и понять, какое место за. Онлайн решебники ГДЗ авторов Мордкович профильный и базовый уровень, Никольский, Потапов, Алимов, Колмогоров по алгебре 11 класс бесплатно c пояснениями. На данной странице представлены решебники по алгебре за весь школьный курс 11 класса.
На данной странице представлены решебники по алгебре за весь школьный курс 11 класса.
Решебники включают в себя решение задач, как повышенной сложности, так и самые простые. Использование данных решебников и гдз 11 класса позволит Вам обрести больше свободного личного времени и сократит время выполнения домашнего задания по алгебре.
Важной составляющей решебников является наличие онлайн версии гдз, что позволяет работать с ним в любое время суток.
Теперь просмотр ГДЗ Алгебра 11 клас Г.П. Бевз, В.Г. Бевз, Н.Г. Владимирова Академічний, профільний рівні возможно даже в школе, ведь посетить сайт с решебниками можно быстро и бесплатно с любого мобильного устройства. Алгебра на отлично. Теперь школьники смогут не переживать за годовую оценку по алгебре. Цифровые онлайн решебники помогут не только проверить любое задание, а и разобраться с примерами и уравнениями.
Учись с удовольствием и получай высокие отметки. Ждем Вас на нашем сайте!.
ГДЗ Математика 11 клас Бевз. (АЛГЕБРА И НАЧАЛА АНАЛИЗА) » Академический уровень Прос}. ПРОДАЖА ЗАПРЕЩЕНА Переведено по изданию Бевз Г. П. Алгебра (Алгебра i початки анал1зу): п1друч. для 11 кл. загальноосв1т uchebnik-skachatj-be. ГДЗ для 11 класу.
(АЛГЕБРА И НАЧАЛА АНАЛИЗА) » Академический уровень Прос}. ПРОДАЖА ЗАПРЕЩЕНА Переведено по изданию Бевз Г. П. Алгебра (Алгебра i початки анал1зу): п1друч. для 11 кл. загальноосв1т uchebnik-skachatj-be. ГДЗ для 11 класу.
Математика. Автори: Г.П. Бевз, В.Г. Бевз. Тип: Рівень стандарту. Рік видання: Видавництво: Генеза, Київ. Мова навчання: українська. Розділи. Розділ 1. Показникові та логарифмічні функції. § 1. Функції та їх основні властивості № § 2. Степеневі та показникові функції №
rtf, djvu, fb2, fb2
Похожее:
Роль виховання у формуванні особистості презентація
Гдз музичне мистецтво 5 клас масол аристова
Виховна година з правового виховання 10 клас
Закон бойля маріотта презентація
Географія 8 клас практична робота номер 5
Гдз з української мови 4 клас вашуленко дубовик робочий зошит
Формулы алгебры для 11 класса PDF: скачать бесплатно
Алгебра Формулы для класса 11: Алгебра — это использование букв для представления чисел. Речь идет об установлении связи между различными числами. Алгебра используется в математике, когда мы не знаем точных чисел или значений в расчетах. В алгебре мы используем буквы для обозначения неизвестных значений или значений, которые могут измениться. Алгебру можно использовать в бизнесе для прогнозирования продаж, роста и прибыли.
Речь идет об установлении связи между различными числами. Алгебра используется в математике, когда мы не знаем точных чисел или значений в расчетах. В алгебре мы используем буквы для обозначения неизвестных значений или значений, которые могут измениться. Алгебру можно использовать в бизнесе для прогнозирования продаж, роста и прибыли.
Мы собрали важные алгебраические формулы для 11 класса.Эти формулы и алгебраические тождества помогут всем ученикам 11 класса в учебе, а также на выпускных экзаменах. Главы алгебры класса 11 содержат концепции прогрессий, квадратных уравнений, линейных неравенств, биномиальной теоремы, перестановок и комбинаций, а также математической индукции. Мы предоставили все формулы и алгебраические тождества для класса 11, которые важны для этих глав на этой странице. Учащиеся CBSE Class 11 могут скачать эти формулы в формате PDF с этой страницы.
Последние обновления:
👉 Экзамены CBSE Term 1 Board по основным предметам 10-го класса проводились с 30 ноября по 11 декабря 2021 г. , а экзамены для учащихся 12-го класса продолжаются с 1 декабря по 22 декабря 2021 г.
, а экзамены для учащихся 12-го класса продолжаются с 1 декабря по 22 декабря 2021 г.
👉 Обычные учащиеся могут получить допуск карточки от своих школ, а частные кандидаты могут загрузить допускную карточку с официального сайта CBSE – cbse.gov.in.
👉 Продолжительность экзамена по каждому предмету 90 минут.
👉 Экзамен CBSE Term 1 будет проводиться полностью в автономном режиме, и учащиеся не смогут появиться в сети.
👉 Поскольку экзамен CBSE Term 1 будет проводиться в зимний сезон, экзамены начнутся в 11:30 вместо 10:30. Правильный ответ для каждого варианта должен быть записан на листах OMR, которые можно записывать только с помощью ручки с синими или черными чернилами.
Практика Embibe’s Эксклюзивный ускоренный курс CBSE Term 1 на основе новых рекомендаций:
Список алгебраических формул для класса 11
Учащиеся, которым нужен полный список математических формул для 11 класса PDF для алгебры, могут обратиться к этой статье. Математика 11 класса содержит 6 глав, связанных с алгеброй. Вы можете проверить формулу по главам в таблице ниже:
Математика 11 класса содержит 6 глав, связанных с алгеброй. Вы можете проверить формулу по главам в таблице ниже:
Изучите концепции 11-го экзамена CBSE
| комплексные числа и квадратные уравнения i называется Йота в комплексных числах. ★ I 2 = -1 I 3 = I 2 * I = -I I 4 = I 2 * I 2 = 1 ★ y = AX 2 + bx + c — это квадратное уравнение, где a ≠ 0 , b и c могут быть любыми действительными (или комплексными) числами. Здесь a, b и c называются коэффициентами. ★ Квадратное уравнение имеет два корня: (α, β) = [–b ± √(b 2 – 4ac)]/2ac, где α и β — корни уравнения. (i) Если b 2 − 4ac > 0, то квадратное уравнение имеет два различных действительных корня . (ii) Если b 2 − 4ac < 0, то квадратное уравнение имеет два мнимых корня .  (iii) Если b 2 − 4ac = 0, то квадратное уравнение имеет два равных действительных корня . |
| Линейные неравенства ★ График линейного неравенства с одной переменной представляет собой числовую прямую. Используйте открытый кружок для < и > и закрытый кружок для ≤ и ≥. ★ Неравенство сложения: (i) Если x > y, то (x + z) > (y + z) (ii) Если x < y, то (x + z) < (y + z) ) ★ Свойство вычитания неравенства: (i) Если x > y, то (x − z) > (y − z) (ii) Если x < y, то (x − z) < (y − z) ★ Свойство умножения неравенства: (i) Если x > y и z > 0, то xz > yz (ii) Если x< y и z > 0, то xz < yz (iii) Если x > y и z < 0, то xz < yz (iv) Если x < y и z < 0, то xz > yz ★ Свойство неравенства деления: (i) Если x > y и z > 0 , то x/z > y/z (ii) Если x < y и z > 0, то x/z < y/z (iii) Если x > y и z < 0, то x/z < y/ z (iv) Если x < y и z < 0, то x/z > y/z определяется по следующей формуле: P(n, r) = n!/( п — г)! ★ Количество комбинаций n предметов, взятых по r за раз, определяется по следующей формуле: C(n, r) = n!/(n − r)!r! |
Практические вопросы 11-го экзамена CBSE
| Binomial Theorem |
★ Биномиальная теорема состояния, которые: (A + B) N = A N + ( N C 1 ) A N-1 B + ( N C 2 C 2 ) A N-2 B 2 B 2 + .  .. + ( N C N-1 ) AB N-1 + B N .. + ( N C N-1 ) AB N-1 + B N , где n положительный целое число |
| Последовательность и серия ★ Арифметическая прогрессия: (i) Последовательность: a, a+d, a+2d, ……, a) + (n –, … . (ii) Общая разница: d = (a 2 – a 1 ), где a 2 и a 1 — это последующий и предшествующий термины соответственно. (iii) Общий срок (n -й -й срок): a n = a + (n – 1)d (iv) n th Срок от последнего срока: a n = l – (n – 1)d (v) Сумма первых n членов: S n = n/2[2a + (n – 1)d] ★ Геометрическая прогрессия: (i) Последовательность: a, ar, ar 2 , …., ar (n-1) , … (ii) Обычная пропорция: r = ar (n-1) /ar (n-2) , где ar (n-1) и ar (n-2) — это последующий и предыдущий термины соответственно.  (iii) Общий срок (n th термин): a n = ar (n-1) (iv) n th Срок с последнего срока: a n = 1/r (n-1) (v) Сумма первых n членов: S n = a(1 – r n )/(1 – r), если r < 1 S n = a(r n -1)/(r – 1), если r > 1 * Здесь a = первый член, d = обычная разность, r = знаменатель, n = положение члена, l = последний член |
| Принцип математической индукции ★ Математическая индукция – это метод доказательства утверждения, теоремы или формулы, которая утверждается относительно каждого натурального числа. Всего 2 шага: Шаг 1: Покажите, что верно для первого . Шаг 2: Покажите, что если любой истинен, то следующий истинен. Тогда все истинны.  |
Попытка сдать одиннадцатый экзамен CBSE Пробные тесты
Ознакомьтесь с другими важными статьями по математике для 11 класса:
Мы предоставили прямую ссылку для загрузки формул алгебры для 11 класса в формате PDF.
Вопросы по алгебре для 11 класса
Мы предоставили несколько важных вопросов по алгебре для 11 класса с решениями, связанными с линейными неравенствами, квадратичными формулами, биномиальной теоремой, математической индукцией и прогрессиями:
| Вопрос 1. Решите (√2 + 1) 5 + (√2 − 1) 5 0 с помощью биномиальной теоремы. |
| Решение: У нас есть (x + y) 5 + (x — Y) 5 = 2 [5C 0 + 5C 2 2 + 5C 2 x 3 Y 2 + 5C 4 XY 4 ] = 2 (x 5 + 10 x 3 y 2 + 5xy 4 ) = 58 √2 |
| Вопрос 2: решить следующее квадратичное уравнение: (x 2 + 2 x — 35) = 0 с использованием квадратичная формула. |
 |
| Решение: Во-первых, мы должны определить, что нам нужно определить, что A , B , и C : A = 1, B = 2, C = -35 Затем нам нужно подставить их в формулу: (α, β) = [–b ± √(b 2 – 4ac)]/2ac = [-2 ± √(2 2 – 4x1x-35 )]/2x1x-35 Решив его, получим: (α, β) = (-2 ± √144)/2 = (-2 ± 12)/2 = 5, -7 Отсюда корни уравнения равны 5 и -7. |
| Вопрос 3: Сумма трех чисел в A.P равна 21, а произведение первого и третьего числа последовательности равно 45. Какие три числа? |
| Решение: Пусть числа равны (a – d), a и (a + d) Тогда (a – d) + a + (a + d) = 21 ( Дано) 3a = 21 a = 7 и (a – d)(a + d) = 45 a 2 – d 2 = 45 7 2 – d 2 2 = 4 d = ± 2 Следовательно, числа равны 5, 7 и 9 при d = 2 и 9, 7 и 5 при d = -2.  В обоих случаях цифры одинаковые. В обоих случаях цифры одинаковые. |
| Вопрос 4. Если резиновый мяч постоянно отскакивает на 2/3 высоты, с которой он был брошен, какую долю своей первоначальной высоты отскочит мяч после того, как его бросили и отскочили четыре раза, не остановился? |
| Решение: Каждый раз, когда мяч падает и отскакивает назад, он достигает 2/3 высоты, с которой он упал. После первого отскока мяч достигнет 2/3 высоты, с которой он был брошен – назовем это исходной высотой. После второго отскока мяч поднимется на 2/3 высоты, которой он достиг бы после первого отскока. Итак, в конце второго отскока мяч достиг бы 2/3 x 2/3 исходной высоты = 4/9 исходной высоты. После третьего отскока мяч поднимется на 2/3 высоты, которой он достиг бы после второго отскока. Таким образом, в конце третьего отскока мяч достиг бы 2/3 x 2/3 x 2/3 = 8/27 исходной высоты.  После четвертого и последнего отскока мяч поднимется на 2/3 высоты, которую он достиг бы после третьего отскока. Таким образом, в конце последнего отскока мяч достиг бы 2/3 x 2/3 x 2/3 x 2/3 исходной высоты = 16/81 исходной высоты. |
| Вопрос 5. Сколькими способами можно расположить буквы в слове «КОРПОРАЦИЯ» так, чтобы гласные всегда совпадали? |
| Решение: В слове «КОРПОРАЦИЯ» мы рассматриваем гласные OOAIO как одну букву. Итак, у нас есть CRPRTN (OOAIO). В нем 7 (6 + 1) букв, из которых R встречается 2 раза, а остальные разные. Количество способов расстановки этих букв = 7!/2! = 2520. Теперь 5 гласных, в которых О встречается 3 раза, а остальные разные, можно расположить в 5!/3! = 20 способов. ∴ Необходимое количество путей = (2520 x 20) = 50400 |
Проверьте формулы алгебры и для других классов:
Практические вопросы по математическим формулам для 11 класса Алгебра
Здесь мы подготовили для вас несколько практических вопросов по формуле алгебраических тождеств для 11-го класса:
В1: Сколько шестизначных чисел можно составить, используя цифры 0, 1, 2, 5, 7 и 9, которые делятся на 11 и ни одна цифра не повторяется.
Q2: Найдите наименьшее число, которое нужно прибавить к 289279, чтобы оно делилось на 8. Q3: Дедушка в 10 раз старше своей внучки. Он старше ее на 54 года. Найдите их настоящий возраст. Q4: Докажите: (2n + 7) < (n + 3) 2 , для n∈N. Q5: Найдите точку (точки) пересечения параболы с уравнением y = x 2 – 5x + 4 и прямой с уравнением y = 2x – 2. Q6: Найдите константу k, чтобы квадратичный уравнение 2x 2 + 5x – k = 0 имеет два действительных решения. Q7: Упростите i 231 где i — мнимая единица, определяемая как: i = √(-1). Q8: Найдите все нули полинома P(x) = x 3 – 3x 2 – 10x + 24, зная, что x = 2 является нулем полинома. Q9: Если x является целым числом, какое наибольшее значение x удовлетворяет условию 5 < 2x + 2 < 9? Q10: Разложите выражение на множители 6x 2 – 13x + 5. Q11: Найдите константу k, чтобы система двух уравнений: 2x + ky = 2 и 5x – 3y = 7 не имела решений. Q12: Найдите константу k так, чтобы: -x 2 – (k + 7)x – 8 = -(x – 2)(x – 4). Q13: Найдите квадраты квадратичной функции f, заданной выражением f(x) = 2x 2 – 6x + 4. Q14: Каков остаток при f(x) = (x – 2) 54 делится на х – 1? Q15: Упрощение | – х 2 + 4х – 4 | |
Также проверьте
Часто задаваемые вопросы о математических формулах для алгебры 11 класса
Здесь мы предоставили некоторые из часто задаваемых вопросов, связанных с формулой алгебры класса 11.
Q1: Какие разные главы в алгебре класса 11?
A: Блок алгебры для класса 11 содержит следующие главы:
(i) Глава 1: Принцип математической индукции
(ii) Глава 2: Комплексные числа и квадратные уравнения
(iii) Глава 3: Линейные неравенства
(iv) Глава 4: Перестановки и комбинации
(v) Глава 5: Биномиальная теорема
(vi) Глава 6: Последовательность и ряд
Q2: Где я могу решить вопросы по алгебре для 11 класса?
О: Вы можете решить важные вопросы по алгебре для 11 класса здесь, на этой странице.
Q3: Как скачать формулы алгебры для 11 класса в формате PDF?
A: На этой странице мы разместили прямую ссылку для скачивания формул алгебры для класса 11 в формате PDF. Скачать бесплатно без регистрации.
Q4: Что такое алгебраическое уравнение?
A: Алгебраическое уравнение или тождество состоит из двух или более алгебраических выражений, разделенных знаком равенства. Левая часть (левая часть) уравнения всегда равна правой стороне (правая часть) для любого значения переменных в нем.
Q5: Как получить алгебраические выражения?
A: Алгебраическое выражение представляет собой комбинацию констант, переменных и алгебраических операций (+, -, ×, ÷). Мы можем получить алгебраическое выражение для данной ситуации или условия, используя эти комбинации.
Теперь у вас есть вся необходимая информация о формулах алгебры 11 класса. Мы надеемся, что вы загрузили математические формулы для 11 класса в формате PDF, доступные на этой странице. Учащиеся также могут использовать решения NCERT Solutions для математики, предоставленные Embibe, для подготовки к экзаменам.
Учащиеся также могут использовать решения NCERT Solutions для математики, предоставленные Embibe, для подготовки к экзаменам.
Мы надеемся, что эта подробная статья о формулах алгебры поможет вам. Если у вас есть какие-либо вопросы относительно этой статьи, свяжитесь с нами через раздел комментариев ниже, и мы свяжемся с вами как можно скорее.
350 просмотров
CBSE Класс 11 по прикладной математической алгебре. Вопросы и учебный план
Совет CBSE представил новую тему под названием «Прикладная математика», которая поможет создать и усовершенствовать ваши математические навыки и методы.Алгебра является одним из разделов программы по прикладной математике для 11 класса.
Блок алгебры имеет вес 10 баллов из 80 баллов на теоретическом экзамене. В этом посте вы найдете подробную информацию о прикладной математической алгебре CBSE Class 11.
CBSE Класс 11 Алгебра прикладной математики Важные темы
Курс прикладной математики готовит вас к выбору алгебраических методов в качестве средства представления и инструмента решения задач. Алгебра в основном фокусируется на таких темах, как множества, отношения, диаграммы Венна, связь между арифметической и геометрической прогрессией и т. д.
Алгебра в основном фокусируется на таких темах, как множества, отношения, диаграммы Венна, связь между арифметической и геометрической прогрессией и т. д.
Просмотрите таблицу ниже, чтобы узнать подробную программу CBSE Class 11 по прикладной математике по алгебре .
| Название темы | |
| 1. Наборы
5 | 1. Наборы
5 6 |
| 2. Типы наборов
5 6 | |
| 3. Venn Diagram | |
| 4. De Morgan’s Law | |
| 5 , Решение задач с использованием диаграммы Венна | |
| 6. Отношения и типы отношений | |
| 7.Введение последовательностей, серии
5 | |
| 8. Арифметическая и геометрическая прогрессия | 8. Арифметическая и геометрическая прогрессия |
| 9. Отношения между AM и GM | |
| 10. Основные концепции перестановок и комбинаций | |
11. Перестановки, круговые перестановки, перестановки с ограничениями Перестановки, круговые перестановки, перестановки с ограничениями |
|
| 12. Комбинации со стандартными результатами |
CBSE Класс 11 Формулы алгебры прикладной математики
Алгебра — это в основном изучение неизвестных величин.Некоторые из тем алгебраических выражений и формул:
Алгебраические тождества
Различные уравнения равенства состоят из различных переменных в алгебраических тождествах.
- a) Линейные уравнения с одной переменной: В линейном уравнении с одной переменной максимум одной переменной присутствует в порядке 1. Оно изображается в виде ax + b = 0, где x представлен как переменная .
- b) Линейные уравнения с двумя переменными: Линейное уравнение с двумя переменными состоит из крайних двух переменных, находящихся в порядке 2.Уравнение изображается в виде: ax2 + bx + c = 0. Эти две переменные очень важны, потому что в вашем учебнике есть много вопросов, основанных на них.
 Итак, вам нужно сосредоточиться на важных формулах алгебры, чтобы найти решение.
Итак, вам нужно сосредоточиться на важных формулах алгебры, чтобы найти решение.
Некоторые основные тождества, которые следует отметить:
- Комбинация буквенных чисел подчиняется всем основным правилам сложения, вычитания, умножения и деления.
- х × у = ху; например, 5 × a = 5a = a × 5.
- a × a × a × … еще 9 раз = a12
- Если число равно x8, то x — основание, а 8 — показатель степени.
- Константа — это символ с фиксированным числовым значением.
Закон экспоненты
Степени и степени в любых математических выражениях известны как экспонента. Вот некоторые из законов экспоненты:
- a0 = 1
- am = 1/am
- (am)n = amn
- am / an = am-n
- am x bm = (ab)m
- am / bm = (a/b)m
- (a/b)-m =(b/a)m
- (1) n = 1 для бесконечных значений n
Квадратные уравнения
Линейные уравнения с двумя переменными известны как квадратные уравнения.
Корни уравнения ax2 + bx + c = 0 (где a ≠ 0) можно представить в виде: Вот некоторые важные моменты об уравнении как части важных алгебраических формул:
- Δ = b2 − 4ac также известен как дискриминант.
- Для корней;
Дельта; > 0 происходит, когда корни действительны и различны
Для действительных и совпадающих корней Δ = 0
Дельта; < 0 происходит в случае, когда корни не вещественные
- Если α и β — два корня уравнения ax2 + bx + c, то
α + β = (-b / a) и α × β = (с/а). - Если корнями квадратного уравнения являются α и β, уравнение будет иметь вид
(x − α)(x − β) = 0.
Общие алгебраические формулы могут быть представлены следующим образом: натуральное число: an – bn = (a – b)(an-1 + an-2b+…+ bn-2a + bn-1)
 )
) Список важных формул ) (a – b) = a2 -b2
Чтобы облегчить вашу подготовку, мы предоставили важные вопросы по алгебре прикладной математики 11 класса в посте ниже. Вопрос 1: Напишите следующие наборы в форме ростера. (i) А = {х | x — натуральное число, меньшее 10, а 2x — 1 — нечетное число} (ii) C = {x : x2 + 7x — 8 = 0, x ∈ R} Вопрос 2: Напишите (ii) B = {x : x натуральное число меньше 6} Наборы Важные вопросы PDF Вопрос 1: Пусть U = {x : x ∈ N, x ≤ 9}; A = {x : x — четное число, 0 < x < 10}; В = {2, 3, 5, 7}.Напишите множество (A U B)’. Вопрос 2: Пусть U = {1, 2, 3, 4, 5, 6, 7}, A = {2, 4, 6}, B = {3, 5} и C = {1 , 2, 4, 7}, найти (i) A′ ∪ (B ∩ C′) (ii) (B – A) ∪ (A – C) Вопрос 1: В классе из 50 учеников 10 берут уроки игры на гитаре и 20 уроки пения, а 4 берут и то, и другое. Найдите количество учеников, которые не берут ни уроки игры на гитаре, ни уроки пения. Вопрос 1: Докажите законы Де Моргана с помощью диаграммы Венна (i) (A∪B)’= A’∩ B’ Важные вопросы по алгебре прикладной математики 11 класса CBSE
Наборы
Типы множеств
Диаграмма Венна

Законы Де Моргана
7
7 Вопрос
7 :
Напишите диапазон функции регистрации.
Вопрос 2:
Декартово произведение A × A имеет 9 элементов, среди которых встречаются (–1, 0) и (0,1). Найдите множество A и остальные аспекты A × A.
Отношения Важные вопросы PDF
Введение последовательностей, ряды
Вопрос 1:
Суммы n членов двух арифметических прогрессий относятся как 5n+ 4: 9н+6. Найдите отношение их 18 членов.
Вопрос 2:
Вставьте пять чисел от 8 до 26 так, чтобы в результате получилась последовательность A.P.
Арифметическая и геометрическая прогрессия
Вопрос 1:
Найдите сумму целых чисел от 1 до 100, которые делятся на 2 или 5.
Вопрос 2:
5 числа, которые оставляют остаток «2» при делении на 3?
- 897
- 897
- 1 64 850
- 1 64 799 7
- 1 49 7002
Арифметические и геометрические Прогрессии Важные вопросы PDF
Отношения между AM и GM
Вопрос 1:
Найти AM, GM , и HM от 12 до 30
Основные понятия перестановок и комбинаций
Вопрос 1:
Найдите трехзначные числа, которые можно составить из данных цифр: 1, 2, 3, 4 и 5, предположив что
- а) цифры могут повторяться.
- б) повторение цифр не допускается.
Вопрос 2:
Монету подбрасывают 6 раз, результаты фиксируются. Сколько возможных результатов может быть?
Перестановки и комбинации Важные вопросы PDF
Перестановки, круговые перестановки, перестановки с ограничениями
Вопрос 1:
Сколькими способами из команды из 6 студентов мы можем выбрать капитана и вице-капитана, предполагая одного человека не может занимать более одной должности?
Вопрос 2:
Найдите количество способов, которыми можно сложить 10 бусин, чтобы получилось ожерелье.
Вопрос 3:
Найдите количество способов, которыми четыре девочки и три мальчика могут выстроиться в ряд так, чтобы ни один из мальчиков не оказался вместе? Чем это расположение отличается от кругового?
Комбинации со стандартными результатами
Вопрос 1:
Сколько слов можно составить из 2-х гласных и 3-х согласных букв данного слова – ДОЧЬ?
Вопрос 2:
Найдите количество комбинаций из 5 карт в колоде из 52 карт, если на каждом наборе из 5 карт есть ровно один король.
Примеры вопросов по алгебре прикладной математики CBSE Class 11 с решениями
Чтобы помочь вам получить представление о типах вопросов, которые можно задавать на экзамене, мы предоставили вам несколько примеров вопросов для справки.
Вопрос 1
Сколько слов можно составить из 2-х гласных и 3-х согласных букв данного слова – ДОЧЬ?
Решение:
Количество гласных в слове – ДОЧЬ равно 3.
Количество.согласных в слове Дочь 5.
Нет способов выделить гласную = 3c2 = 3!/2!(3 – 2)! = 3
Количество способов выбрать согласную = 5c3 = 5!/3!(5 – 3)! = 10
Теперь вы знаете, что количество сочетаний 3 согласных и 2 гласных = 10x 3 = 30
Общее количество слов = 30 x 5! = 3600 способов.
Вопрос 2
Чтобы занять четные места, нужно рассадить в ряд 5 мальчиков и 4 девочки. Сколько таких договоренностей возможно?
Решение:
5 мальчиков и 4 девочки должны быть рассажены в ряд, чтобы получить четные места.
5 мальчиков могут сидеть в 5! Пути.
Для каждой расстановки 4 девушки могут сидеть только на местах, отмеченных крестиком, чтобы девушки занимали четные места).
B x B x B x B x B
Таким образом, девочки могут сидеть в 4-х местах! Пути.
Следовательно, возможное количество аранжировок = 4! × 5! = 24 × 120 = 2880
Вопрос 3
Найдите количество комбинаций из 5 карт в колоде из 52 карт, если на каждом наборе из 5 карт есть ровно один король.
Решение:
Возьмите колоду из 52 карт,
Чтобы получить ровно одного короля, необходимо составить комбинации из 5 карт. Она должна быть составлена таким образом, чтобы в каждой подборке из 5 карт или колоде из 52 карт было 4 короля.
Чтобы выбрать 1 короля из 4 королей = 4c1
Чтобы выбрать 4 карты из оставшихся 48 карт = 48c4
Чтобы получить необходимое количество комбинаций из 5 карт = 4c1 x 48c4
= 4x2x 47x 46×45
= 778320 способов.
Вопрос 4
Найдите количество шестизначных чисел, которые можно составить, используя цифры 0, 1, 3, 5, 7 и 9. Эти цифры должны делиться на 10, и ни одна цифра не должна повторяться. ?
Решение:
Число, в котором на месте единицы стоит 0, делится на 10.
Если мы поставим 0 на место единицы, _ _ _ _ 0, будет столько же способов заполнить 5 вакантных мест места. (1, 3, 5, 7, 9)
Пять вакантных мест можно заполнить 5! пути = 120.
Вопрос 5
Оцените 10! – 6!
Решение:
10! = 10 х 9 х 8 х 7 х 6 х 5 х 4 х 3 х 2 х 1 = 3628800
6! = 6 х 5 х 4 х 3 х 2 х 1 = 720
10! – 6! = 3628800 – 720 = 3628080
Вопрос 6
Покажите, что сумма (m + n)-го и (m – n)-го членов АП равна удвоенному m-му члену.
Решение:
Пусть a и d будут первым членом и общей разностью числа A.п. соответственно. Известно
, что k-й член АП определяется выражением
ak = a +(k -1)d
Следовательно, am+n = a +(m+n -1)d
am-n = a +(mn -1)d
am = a +(m-1)d
Следовательно, сумма (m + n)-го и (m – n)-го членов ПД записывается как:
am+n+ am-n = a +(m+n -1)d + a +(mn -1)d
= 2a +(m + n -1+ m – n -1)d
=2a+ (2m-2)d
= 2a + 2(m-1)d
= 2 [a + (m-1)d]
= 2 часа ночи [поскольку am = a +(m-1)d]
Таким образом, сумма (m + n) и (m – n)-х членов A. П. равно удвоенному m-му члену.
П. равно удвоенному m-му члену.
Вопрос 7
Найдите сумму целых чисел от 1 до 100, которые делятся на 2 или 5.
Решение:
, 6 ….. 100.
Это образует АП с первым членом и общей разностью, равными 2.
⇒ 100=2+(n-1)2
⇒ n= 50
Следовательно, сумма целых чисел от 1 до 100, которые делятся на 2, задается как:
2+4+6+…+100 = (50/2)[2(2)+(50-1)(2)]
= (50/2)(4+98)
= 25(102)
= 2550
Целые числа от 1 до 100, которые делятся на 5, 10….100
Это образует AP с первым членом и общей разностью, равными 5.
Следовательно, 100= 5+(n-1)5
⇒ 5n = 100
⇒ n= 100/5
⇒ n= 20
Следовательно, сумма целых чисел от 1 до 100, которые делятся на 2, определяется как:
5+10+15+…+100= (20/2)[2(5)+(20- 1)(5)]
= (20/2)(10+95)
= 10(105)
= 1050
Следовательно, целые числа от 1 до 100, которые делятся и на 2, и на 5, равны 10, 20, …. . 100.
. 100.
Это также образует AP с первым членом и общей разностью, равными 10.
Следовательно, 100 = 10+(n-1)10
⇒ 10 n = 100
⇒ n = 100/10
⇒ n= 10
10+20+…+100= (10/2)[2(10)+(10-1)(10)]
= (10/2)(20+90)
= 5(110)
= 550
Следовательно, искомая сумма:
= 2550+ 1050 – 550
= 3050
Следовательно, сумма целых чисел от 1 до 100, которые делятся на 2 или 5, это 3050.
Вопрос 8
Пусть U = {x : x ∈ N, x ≤ 9}; A = {x : x — четное число, 0 < x < 10}; В = {2, 3, 5, 7}. Напишите множество (A U B)’.
Решение:
Пусть U = {x : x ∈ N, x ≤ 9}; A = {x : x — четное число, 0 < x < 10}; B = {2, 3, 5, 7}
U = {1, 2, 3, 4, 5, 6, 7, 8, 9}
A = {2, 4, 6, 8}
АУБ = {2, 3, 4, 5, 6, 7, 8}
(AUB)’ = {1, 9}
Вопрос 9
При опросе 600 учащихся в школе 150 учащихся употребляли алкоголь Чай и 225 пили кофе, а 100 пили и чай, и кофе. Найдите, сколько студентов не пили ни чай, ни кофе.
Найдите, сколько студентов не пили ни чай, ни кофе.
Решение:
Дано,
Общее количество студентов = 600
Количество студентов, которые пили чай = n(T) = 150
Количество студентов, которые пили кофе = n(C) = 225
Количество студентов, которые пили чай и кофе = n(T ∩ C) = 100
n(TUC) = n(T) + n(C) – n(T ∩ C)
= 150 + 225 -100
= 375 – 100
= 275
Следовательно, число учащихся, которые не пьют ни чай, ни кофе = 600 – 275 = 325
Решение NCERT для класса 11 Решение прикладной математической алгебры для класса
CBERT 11 Прикладная математика Алгебра является важным ресурсом для подготовки к экзамену.Вы можете проверить свои ответы и понять, как решается каждая проблема.
Регулярное выполнение упражнений поможет получить больше баллов на экзамене. Решение в формате PDF подготовлено экспертами в данной области, чтобы помочь вам понять объяснение и способ решения.
Решения NCERT по прикладной математике по алгебре обеспечивают простой способ иллюстраций и пояснений. Формат этих учебников прост и удобен. Содержание книги и ее процедуры решения проблем просты.Более простые решения не ухудшают качество контента.
Формат этих учебников прост и удобен. Содержание книги и ее процедуры решения проблем просты.Более простые решения не ухудшают качество контента.
Комплексные числа класса 11 Примечания с примерами
Комплексные числа класса 11 определяются, когда число может быть представлено в форме p + iq. Здесь p и q — действительные числа, а i =−1−−−√. Для комплексного числа z = p + iq p известен как действительная часть, представленная Re z, а q известен как мнимая часть; он представлен Im z комплексного числа z.
Темы и подтемы, изучаемые в комплексных числах CBSE класс 11, прикладная математическая алгебра :
- Введение
- Комплексные числа
- Алгебра комплексных чисел — сложение двух комплексных чисел; Разница между двумя комплексными числами; Умножение двух комплексных чисел; Деление двух комплексных чисел; Сила я; Квадратный корень из отрицательного действительного числа; Тождества
- Модуль и сопряжение комплексных чисел
- Плоскость Аргана и полярное представление — полярное представление комплексных чисел
Примечания для класса 11 дают вам подробные знания, описывающие понятия, связанные с комплексными числами. Вот некоторые из примеров:
Вот некоторые из примеров:
Пример 1: Если 4x + i(3x – y) = 3 + i (– 6), где x и y – действительные числа, то найдите значения x и y.
Решение: Дано,
4x + i (3x – y) = 3 + i (–6) ….(1)
Приравнивая действительную и мнимую части уравнения (1),
4x = 3 , 3x – y = –6,
Теперь 4x = 3
⇒ x = 3/4
И 3x – y = -6
⇒ y = 3x + 6
Подставляя значение x,
⇒ у = 3(3/4) + 6
⇒ у = 33/4
Следовательно, х = 3/4 и у = 33/4.
Пример 2 : Выразите (-√3 + √-2)(2√3 – i) в виде a + ib.
Решение: Мы знаем, что i2 = -1
(-√3 + √-2)(2√3 – i) = (-√3 + i√2)(2√3 – i)
= ( -√3)(2√3) + (i√3) + i(√2)(2√3) – i2√2
= -6 + i√3(1 + 2√2) + √2
= (-6 + √2) + i√3(1 + 2√2)
Это имеет вид a + ib, где a = -6 + √2 и b = √3(1 + √2) .
Пример 3: Найдите мультипликативное число, обратное 2–3i.
Решение: Пусть z = 2 – 3i
z ¯ = 2 + 3i
|z|2 = (2)2 + (-3)2 = + = 13
Мы знаем, что мультипликативная обратная величина z определяется по формуле:
z −1= z ¯| z |2
= (2 + 3i)/13
= (2/13) + i(3/13)
Альтернативно,
Мультипликативное значение, обратное z:
z-1 = 1/ (2 – 3i)
Рационализируя знаменатель, получаем
= (2 + 3i)/(4 + 9)
= (2 + 3i)/ 13
= (2/13) + i(3 /13)
Пример 4: Представьте комплексное число z = 1 + i√3 в полярной форме.
Решение: Дано, z = 1 + i√3
Пусть 1 = r cos θ, √3 = r sin θ
Путем возведения в квадрат и сложения получаем
r2(cos2θ + sin2θ) = 4
= 4
r = 2 (при r > 0)
Следовательно, cos θ = 1/2 и sin θ = √3/2
Это возможно, когда θ = π/3.
Таким образом, искомая полярная форма z = 2[cos π/3 + i sin π/3].
Следовательно, комплексное число z = 1 + i√3 представлено, как показано на рисунке ниже.
Решения NCERT для класса 6 по математике Глава 11 Алгебра в PDf 2021-22
NCERT Решения для класса 6 Математика Глава 11
| класс: 6 | Математика |
| Глава 11: | Algebra |
Скачать класс 6 Maths Chapter 11 Solutions in PDF
Загрузите Решения NCERT для Class 6 Maths Chapter 11 Algebra в формате PDF или используйте онлайн без загрузки. Все упражнения обновлены для новой сессии 2021-22 с использованием последних книг NCERT 2021-22. Свяжитесь с нами для получения дополнительной помощи в области образования или образовательного содержания.
Все упражнения обновлены для новой сессии 2021-22 с использованием последних книг NCERT 2021-22. Свяжитесь с нами для получения дополнительной помощи в области образования или образовательного содержания.
-
Класс 6 Математика Глава 11 Решения в английском Среда
-
-
класс 6 Математика Глава 11
Упражнение класса 6
класс 6 Математическое упражнение 11.1 Решения в видео Класс 6 Математическое упражнение 11.2 Solutions in Video
Class 6 Maths Exercise 11.
 3 & 11.4 Solutions in Video
3 & 11.4 Solutions in Video
Class 6 Maths Exercise 11.3 Solutions in Video Class 6 Maths Exercise 11.4 Solutions in Video
Class 6 Maths Упражнение 11.4
О математике 6 класса, глава 11
В 6 математике, глава 11, алгебра, мы изучим термины, связанные с алгеброй и алгебраическими выражениями. Как мы знаем, раздел математики, в котором мы изучали числа, — это арифметика, а раздел математики, в котором мы изучали формы, — геометрия. Точно так же в разделе алгебры мы изучим следующие мысли.
Точно так же в разделе алгебры мы изучим следующие мысли.
Мы будем учиться использовать буквы в математике. Использование букв позволит нам писать правила и формулы в общем виде. Используя буквы, мы можем говорить о любом числе, а не только о конкретном числе.
Поскольку буквы обозначают числа, над ними можно производить действия, как над числами. Это приводит к изучению алгебраических выражений и их свойств.
Буквы могут обозначать неизвестные количества. Изучая методы определения неизвестных, мы разрабатываем мощные инструменты для решения головоломок и многих задач из повседневной жизни.
Примечание. Переменные могут принимать разные значения; они не имеют фиксированной стоимости. Но это числа. Именно поэтому, как и в случае с числами, над ними можно производить операции сложения, вычитания, умножения и деления.
Отзывы и предложения
Мы стараемся оказывать помощь всем пользователям на нашем уровне наилучшим образом. Постепенно мы обновляем сайт также в соответствии с предложениями, которые мы получили. Внесенные выше изменения являются результатом предложений и отзывов пользователей.Разместите свои вопросы в Дискуссионном форуме, чтобы получить правильные ответы.
Внесенные выше изменения являются результатом предложений и отзывов пользователей.Разместите свои вопросы в Дискуссионном форуме, чтобы получить правильные ответы.
Важные вопросы по математике для 6 класса Глава 11
Курсанты идут на параде. В ряду 5 курсантов. По какому правилу дается количество курсантов, учитывая количество рядов?
Количество рядов = n
Курсантов в каждом ряду = 5
Следовательно, общее количество курсантов = 5n
Если в коробке 50 манго, как вы запишете общее количество манго через количество коробок?
Количество коробок = b
Количество манго в каждой коробке = 50
Следовательно, общее количество манго = 50b
Учитель раздает каждому ученику по 5 карандашей.Сможете ли вы сказать, сколько карандашей нужно, учитывая количество учеников?
Количество учеников = x
Количество карандашей на каждого ученика = 5
Следовательно, общее количество необходимых карандашей = 5x
В каком упражнении главы 11 математики для 6 класса содержится наибольшее количество вопросов?
Глава 11 по математике для 6-го класса состоит из пяти упражнений. В первом упражнении (упр. 11.1) 11 вопросов. Второе упражнение (упр. 11.2) содержит 5 вопросов. В третьем упражнении (упр. 11.3) 6 вопросов. В четвертом упражнении 3 вопроса (пример 11.4). В последнем упражнении (упр. 11.5) 5 вопросов. Так, в первом упражнении (упр. 11.1) больше всего вопросов (11 вопросов).
В первом упражнении (упр. 11.1) 11 вопросов. Второе упражнение (упр. 11.2) содержит 5 вопросов. В третьем упражнении (упр. 11.3) 6 вопросов. В четвертом упражнении 3 вопроса (пример 11.4). В последнем упражнении (упр. 11.5) 5 вопросов. Так, в первом упражнении (упр. 11.1) больше всего вопросов (11 вопросов).
Легко ли выполнить 11 главу по математике в 6 классе?
Глава 11 6 класса Математика не простая и не сложная. Он находится посредине простого и сложного, потому что некоторые примеры и вопросы этой главы легкие, а некоторые трудные. Однако уровень сложности любой темы/главы варьируется от учащегося к учащемуся.Итак, глава 11 6-го класса по математике легко или нет, зависит также от учеников. Некоторым учащимся это кажется сложным, другим — легким, а некоторым — что-то среднее между простым и сложным.
Смогут ли ученики пройти 11-ю главу 6-го курса математики за 8-10 дней?
Да, учащиеся могут закончить 11-ю главу 6-го класса по математике за 8-10 дней, если будут уделять этой главе 1-2 часа в день. Это время приблизительное. Это время зависит от студентов еще и потому, что ни у одного из них не может быть такой же скорости работы, эффективности, способностей и т. д.
Это время приблизительное. Это время зависит от студентов еще и потому, что ни у одного из них не может быть такой же скорости работы, эффективности, способностей и т. д.
Какие темы будут изучать учащиеся в главе 11 математики 6-го класса?
Темы, которые учащиеся будут изучать в главе 11 курса «Математика 6-го класса»:
1. Образцы спичек
2. Идея переменной
3. Дополнительные образцы спичек
4. Дополнительные примеры переменных
5. Использование переменных в Общие правила
6. Правила геометрии
7. Правила арифметики
8. Выражения с переменными
9. Практическое использование выражений
10.Что такое уравнение?
11. Решение уравнения
Когда началась алгебра в соответствии с главой 11 математики 6 класса?
Говорят, что алгебра как раздел математики зародилась около 1550 г. до н.э., то есть более 3500 лет назад, когда жители Египта начали использовать символы для обозначения неизвестных чисел. Слово «алгебра» происходит от названия книги «Aljebar w’al almugabalah», написанной около 825 г. н.э. арабским математиком Мухаммедом ибн Аль Хорезми из Багдада.
Слово «алгебра» происходит от названия книги «Aljebar w’al almugabalah», написанной около 825 г. н.э. арабским математиком Мухаммедом ибн Аль Хорезми из Багдада.
Если A B и C являются элементами булевой алгебры, 11 класс математики CBSE
Совет: используйте распределительный закон \[\left( A.\left( B+C \right)=AB+AC \right)\] и закон дополнения \[\left( A.A’=A’.A=0,A+A’=A’+A =1 \right)\] альтернативно заданному выражению. В последнем применяется Закон об аннулировании, то есть \[A+1=1\]. Тогда будет получено упрощенное выражение и, наконец, начерчена упрощенная схема.
Полный пошаговый ответ:
Чтобы упростить данное выражение, мы сначала запишем данное выражение и примем его за «L».
\[L\text{ }=\text{ }\left( A’+B’ \right).\left( A+C’ \right)+B’.\left( B+C \right)\] ……………………………… (1)
Чтобы упростить приведенное выше уравнение, мы должны знать Распределительный закон булевой алгебры, показанный ниже,
Распределительный закон:
\[A.\left( B+C \right)=A. B+AC\]
B+AC\]
Используя приведенный выше закон распределения, мы можем записать ‘L’ как,
\[\следовательно L\text{ }=\text{ }\left( A ‘.A+A’.C’ \right)+\left( B’.A+B’.C’ \right)+\left( B’.B+B’.C \right)\]
Если мы раскроем скобки приведенного выше уравнения, мы получим,
\[\поэтому L\text{ }=\text{ }A’.A+A’.C’+B’.A+B’.C’+B’ .B+B’.C\]
Чтобы продолжить решение, мы должны знать Закон комплимента, приведенный ниже,
Закон комплимента:
\[A.A’=A’.A=0\]
Используя приведенное выше закон в приведенном выше уравнении мы получим,
\[\поэтому L\text{ }=\text{ 0}+A’.C’+B’.A+B’.C’+0+B’.C\]
\[\поэтому L\text{ }=\text{ }A’.C’+B’.A+B’ .C’+B’.C\]
Если мы возьмем B’ общее из последних двух членов, то мы получим C и его дополнение C’ вместе и можем решить его дальше, используя закон дополнения,
Следовательно, чтобы упростить вышеизложенное уравнения, мы должны знать Распределительный закон булевой алгебры, показанный ниже,
Распределительный закон:
\[A. B+AC=A.\left( B+C \right)\] ……………………………… ……………… (2)
B+AC=A.\left( B+C \right)\] ……………………………… ……………… (2)
Используя приведенный выше распределительный закон, мы получим,
\[\следовательно, L\text{ }=\text{ }A’.C’+B’.A+B’.\left( C’+C \right)\]
Теперь, как мы обсуждали ранее, мы можем использовать приведенный ниже закон дополнения,
Закон дополнения:
\[A+A’= A’+A=1\]
Следовательно, используя приведенный выше закон, мы получим
\[\следовательно L\text{ }=\text{ }A’.C’+B’.A+B’.1\ ]
\[\следовательно, L\text{ }=\text{ }A’.C’+B’.A+B’\]
Используя закон распределения из уравнения (2), мы можем получить B’ общее, так что мы можем использовать закон аннулирования для дальнейшего упрощения,
\[\поэтому L\text{ }=\text{ }A’.C’+B’.\left( A+1 \right)\]
Чтобы продолжить в решения мы должны знать закон аннулирования, приведенный ниже,
Закон аннулирования:
\[A+1=1\]
Используя закон аннулирования, мы можем записать приведенное выше уравнение как
\[\следовательно L\text{ }=\text{ }А’. C’+B’.1\]
C’+B’.1\]
\[\поэтому L\text{ }=\text{ }A’.C’+B’\] ……………………………………….. (3)
Следовательно, используя уравнение (1) и уравнение (3), мы можем записать упрощенное логическое выражение как
\[\следовательно \text{ }\left( A’+B’ \right).\left( A +C’ \right)+B’.\left( B+C \right)=\text{ }A’.C’+B’\]
Теперь нарисуем принципиальную схему \[A’.C’+ B’\] мы должны знать правило, данное ниже,
Правило: Логический оператор ‘И’ используется для параллельного соединения, а оператор ‘ИЛИ’ используется для последовательного соединения в принципиальной схеме.Кроме того, A используется как открытый ключ, а его дополнение используется как закрытый ключ на принципиальных схемах.
Следовательно, принципиальная схема для \[A’.C’+B’\] дается как,
Примечание. В данном выражении будьте осторожны при использовании закона распределения, так как вы должны использовать его между двумя бинарными выражениями. Используйте простое правило умножения, приведенное ниже для закона распределения, $\left( a+b \right)\left( c+d \right)=ac+ad+bc+bd$.
Решения NCERT для математики класса 6, глава 11
Страница № 226:
Вопрос 1:
Найдите
правило, определяющее количество спичек, необходимое для изготовления
по следующим схемам из спичек.Используйте переменную для записи правила.
(а) А
образец буквы T как T
(б) А
образец буквы Z как Z
(с) А
образец буквы U как U
(г) А
образец буквы V как V
(д) А
образец буквы E как E
(ф) А
образец буквы S как S
(г) А
образец буквы А как А
Ответ:
(а)
Из
можно заметить, что потребуются две спички, чтобы
сделать Т .Таким образом, шаблон 2 n .
(б)
Из
можно заметить, что потребуется три спички, чтобы
сделать Z . Следовательно, шаблон 3 n .
Следовательно, шаблон 3 n .
(в)
Из
можно заметить, что потребуется три спички, чтобы
сделать U . Следовательно, шаблон 3 n .
(д)
Из
можно заметить, что потребуются две спички, чтобы
сделать V .Таким образом, шаблон 2 n .
(е)
Из
можно заметить, что потребуется пять спичек, чтобы
сделать E . Следовательно, шаблон 5 n .
(ф)
Из
можно заметить, что потребуется пять спичек, чтобы
сделать S . Следовательно, шаблон 5 n .
(г)
Из
можно заметить, что потребуется шесть спичек, чтобы
сделать А .Следовательно, шаблон 6 n .
Страница № 227:
Вопрос 2:
Мы уже
знать правило построения букв L, C и F. Некоторые из
буквы из некоторых букв из (а) Т, (б) З, (в) У, (г) В,
(e) E, (f) S, (g) R дают нам то же правило, что и L. Которые
Которые
эти? Почему это происходит?
Ответ:
Это
Известно, что для L требуется всего две спички.Таким образом, шаблон
для L равно 2 n . Среди всех букв, приведенных выше в вопросе 1,
только T и V — это две буквы, для которых нужны две спички.
Следовательно, (а)
и (г)
Страница № 227:
Вопрос 3:
Курсанты
маршировать на параде. В ряду 5 курсантов. Какое правило
что дает количество курсантов, учитывая количество рядов? (Используйте и
на количество рядов.)
Ответ:
Пусть номер
строк n .
Количество
курсантов в один ряд = 5
Всего
количество курсантов = количество курсантов в ряду × количество рядов
= 5 н
Страница № 227:
Вопрос 4:
Если есть
50 манго в коробке, как вы напишете общее количество
манго по количеству коробок? (Используйте b для номера
коробок.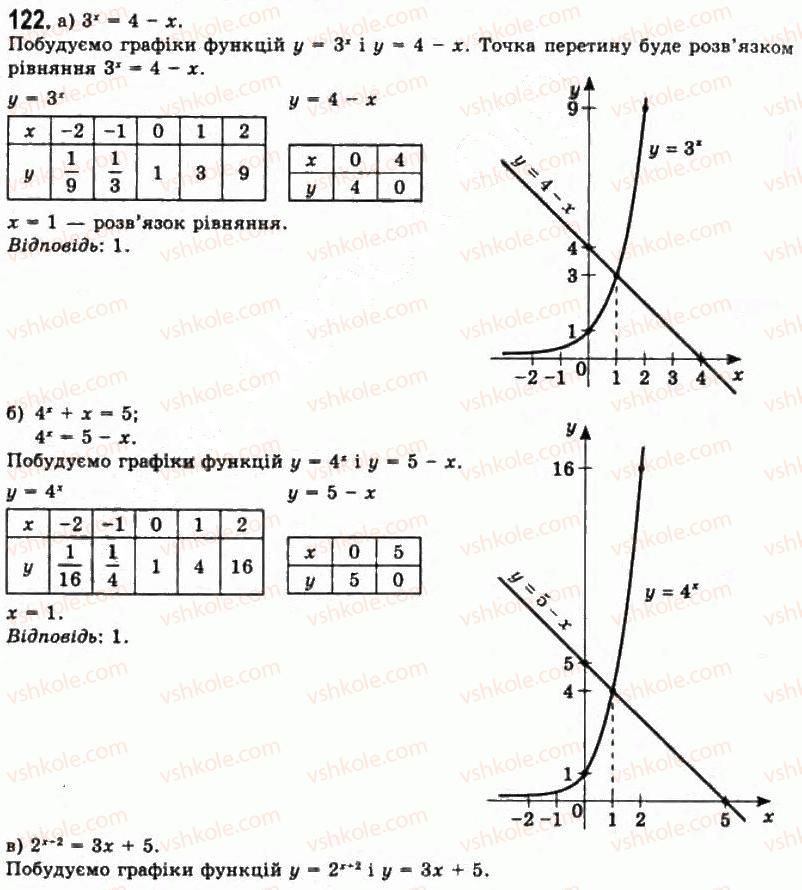 )
)
Ответ:
Пусть
количество ящиков b .
Количество
манго в коробке = 50
Всего
количество манго = количество манго в коробке × количество
коробки
= 50 б
Страница № 227:
Вопрос 5:
Учитель раздает каждому ученику по 5 карандашей.Можете ли вы сказать, сколько
карандаши нужны, учитывая количество учеников? (Используйте s для
количество студентов.)
Ответ:
Пусть
количество студентов s .
Карандаши
дано каждому ученику = 5
Всего
количество карандашей
= номер
карандашей, выданных каждому ученику × количество учеников
= 5 с
Страница № 227:
Вопрос 6:
Птица
пролетает 1 километр за одну минуту.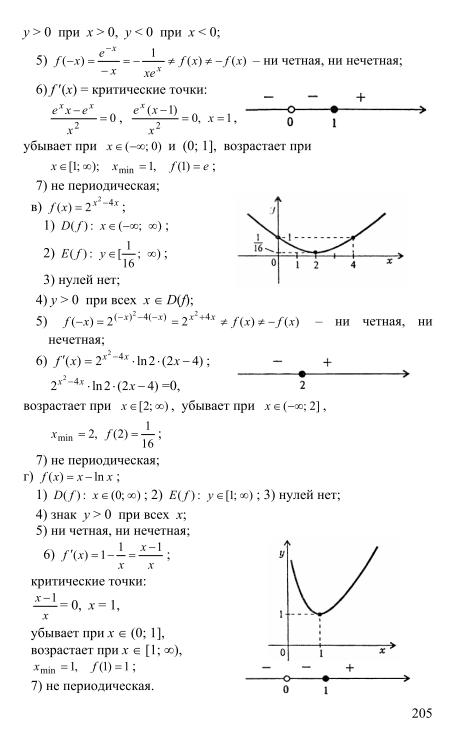 Можете ли вы выразить пройденное расстояние
Можете ли вы выразить пройденное расстояние
птицей с точки зрения времени ее полета в минутах? (Используйте t для
время полета в минутах.)
Ответ:
Пусть
налет т минут.
Расстояние
пройдено за одну минуту = 1 км
Расстояние
пройдено за t минут = расстояние, пройденное за одну минуту ×
Налет
= 1 × т = т км
Страница № 227:
Вопрос 7:
Радха есть
рисование точки Ранголи (красивый узор из линий, соединяющих точки с
меловой порошок.У нее 9 точек подряд. Сколько точек будет у нее Ранголи
есть для р строк? Сколько точек, если рядов 8?
Если есть 10 рядов?
Ответ:
Количество
точек в 1 ряду = 9
Количество
ряды = р
Всего
количество точек в r строк = количество строк × количество
точки подряд
= 9 р
Количество
точек в 8 рядах = 8 × 9 = 72
Количество
точек в 10 рядах = 10 × 9 = 90
Страница № 227:
Вопрос 8:
Лила
Младшая сестра Радхи. Лила на 4 года моложе Радхи.
Лила на 4 года моложе Радхи.
Можете ли вы описать возраст Лилы через возраст Радхи? Брать
Возраст Радхи х лет.
Ответ:
Пусть
Возраст Радхи х лет.
Лилы
возраст = возраст Радхи — 4
= ( х — 4) лет
Страница № 227:
Вопрос 9:
Мать имеет
сделал ладдус.Она дает ладду гостям и членам семьи;
осталось еще 5 ладду. Если количество отданных ладдус матерью равно l ,
сколько ладду она сделала?
Ответ:
Количество
отдано ладдус = л
Количество
ладдус осталось = 5
Всего
количество ладду = количество отданных ладду + количество ладду
осталось
= л + 5
Страница № 227:
Вопрос 10:
Апельсины
должны быть перенесены из больших ящиков в меньшие ящики. Когда
Когда
большая коробка опустела, апельсины из нее заполнили две меньшие коробки и
все еще 10 апельсинов остаются снаружи. Если количество апельсинов в небольшом
коробка принимается равной x , каково количество апельсинов в
коробка побольше?
Ответ:
Количество
апельсины в одной маленькой коробке = x
Количество
апельсины в двух маленьких коробках = 2 x
Количество
апельсинов осталось = 10
Количество
апельсины в большой коробке = Количество апельсинов в двух маленьких коробках
+ Количество апельсинов осталось
= 2 х + 10
Страница № 227:
Вопрос 11:
(a) Посмотрите на следующий узор из квадратов, сложенных спичками.Квадраты
не являются отдельными. Два соседних квадрата имеют общую спичку.
Наблюдайте закономерности и найдите правило, которое дает количество
спичек по количеству квадратов. (Подсказка: если вы удалите
(Подсказка: если вы удалите
вертикальная палочка на конце, у вас получится выкройка Cs.)
(b) На данном рисунке изображена спичка из треугольников. Находить
общее правило, определяющее количество спичек в
количество треугольников.
Ответ:
(а) Можно
Обратите внимание, что в заданном образце спичек количество
спичек 4, 7, 10 и 13, что на 1 больше, чем в три раза
количество квадратов в узоре.
Следовательно, шаблон равен 3 n + 1, где n — количество
квадраты.
(б) Может
Обратите внимание, что в заданном образце спичек количество
спичек 3, 5, 7 и 9, что на 1 больше, чем в два раза
количество треугольников в узоре.
Следовательно, шаблон равен 2 n + 1, где n — количество
треугольники.
Страница № 230:
Вопрос 1:
Сторона
равностороннего треугольника l . Экспресс
Экспресс
периметр равностороннего треугольника используя l .
Ответ:
Сторона
равносторонний треугольник = l
Периметр
= л + л + л = 3 л
Страница № 230:
Вопрос 2:
Сторона
правильного шестиугольника (см. данный рисунок) обозначается l .Выразите периметр шестиугольника, используя l .
(Подсказка: А
правильный шестиугольник имеет все шесть сторон одинаковой длины.)
Ответ:
Сторона
правильный шестигранник = l
Периметр
= 6 л
Страница № 230:
Вопрос 3:
Куб – это трехмерная фигура, показанная на данном рисунке. У него шесть граней, и все они одинаковые квадраты. Длина ребра куба равна l . Найдите формулу суммы длин ребер куба.
У него шесть граней, и все они одинаковые квадраты. Длина ребра куба равна l . Найдите формулу суммы длин ребер куба.
Ответ:
Длина края = l
Количество ребер = 12
Общая длина ребер = количество ребер × длина одного ребра
= 12 л
Видео Решение по алгебре (Страница: 230 , Q.№: 3)
Решение NCERT для 6 класса по математике и алгебре 230, вопрос 3
Страница № 231:
Вопрос 4:
диаметр окружности это линия, которая соединяет две точки на окружности
и также прошел через центр круга. (В соседнем
цифра АВ — диаметр окружности; C — его центр.) Выразите
диаметр круга ( d ) через его радиус ( r ).
Ответ:
Диаметр =
AB = AC + CB = r + r = 2 r
д = 2 г
Страница № 231:
Вопрос 5:
Чтобы найти сумму трех чисел 14, 27 и 13, у нас есть два способа:
(a) Мы можем сначала добавить 14 и 27, чтобы получить 41, а затем добавить к нему 13, чтобы получить
общая сумма 54 или
(b) Мы можем сложить 27 и 13, чтобы получить 40, а затем добавить 14, чтобы получить сумму 54. Таким образом, (14 + 27) + 13 = 14 + (27 + 13)
Таким образом, (14 + 27) + 13 = 14 + (27 + 13)
Это можно сделать для любых трех чисел. Это свойство известно как
ассоциативность сложения номеров . Выразите это свойство
которые мы уже изучали в главе о целых числах, в
общий способ, используя переменные a , b и c .
Ответ:
Для любого
три целых числа a , b и c ,
( и
+ b ) + c = a + ( b + c )
Страница № 233:
Вопрос 1:
Макияж как
много выражений с числами (без переменных), как можно из трех
числа 5, 7 и 8.Каждое число должно использоваться не более одного раза.
Используйте только сложение, вычитание и умножение.
(Подсказка: три возможных выражения: 5 + (8 − 7), 5 − (8
− 7), (5 × 8) + 7;
сделать
другие выражения.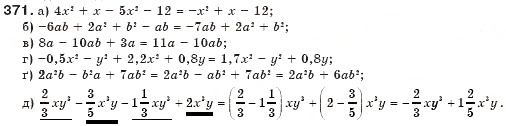 )
)
Ответ:
Много
выражения можно составить, используя три числа 5, 7 и 8.
Некоторые из
они заключаются в следующем.
5 ×
(8 − 7)
5 ×
(8 + 7)
(8 + 5) ×7
(8 –
5) ×7
(7 + 5) ×8
(7 —
5) ×8
Страница № 233:
Вопрос 2:
Какие из следующих выражений содержат только числа?
(а) у + 3 (б) (7 ×
20) − 8 з
в) 5 (21 − 7) + 7 ×
2 (г) 5
(д) 3 x (е) 5 − 5 п
(г) (7 х 20) — (5 х
10) − 45 + р
Ответ:
Может быть
заметил, что выражения в вариантах (c) и (d) формируются
используя только числа.
Страница № 233:
Вопрос 3:
Определить
операции (сложение, вычитание, деление, умножение) в
составить следующие выражения и сказать, как выражения имеют
был сформирован.
(а) z + 1, z — 1, y + 17, y —
17 (б)
(в) 2 г + 17, 2 г — 17 (г) 7 м , — 7 м
+ 3, − 7 м − 3
Ответ:
(а) Дополнение
так как 1 добавляется к z .
Вычитание как 1 вычитается из z .
Сложение как 17 добавляется к y .
Вычитание как 17 вычитается из y .
(б) Умножение
как y умножается на 17.
Деление как y делится на 17.
Умножение как z умножается на 5.
(с) Умножение
и дополнение
y умножается на 2 и к результату добавляется 17.
Умножение и вычитание
y умножается на 2 и из результата вычитается 17.
(г) Умножение
так как м умножается на 7.
Умножение и сложение, поскольку м умножается на -7,
и 3 добавляется
к результату.
Умножение и вычитание, поскольку м умножается на
−7, а 3 равно
.
вычитается из результата.
Страница № 233:
Вопрос 4:
Приведите выражения для следующих случаев.
(a) 7 добавить к p (b) 7 вычесть из p
(c) p умножить на 7 (d) p разделить на 7
(e) 7 вычесть из − m (f) − p
умножить на 5
(g) − p разделить на 5 (h) p умножить на −
5
Ответ:
(а) с
+ 7
(б) р −
7
(в) 7 р
(д)
(д) —
м − 7
(ф) —
5 р
(г)
(ч) —
5 р
Страница № 234:
Вопрос 5:
Приведите выражения в следующих случаях.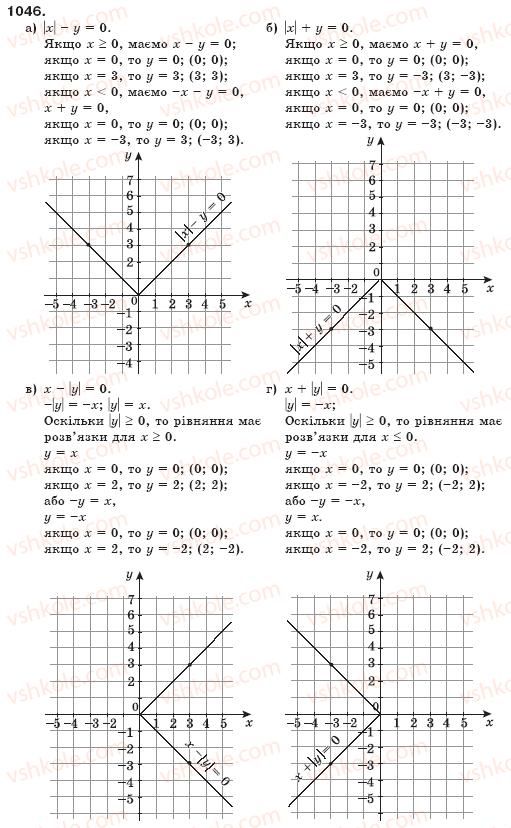
(a) 11 добавлено к 2 м
(б) 11
из 2 вычесть м
(c) 5 раз y , к которому прибавляется 3
(д) 5
умножить на и , из которых вычесть 3
(д) у
умножается на − 8
(ф) г
умножается на — 8, а затем к результату
прибавляется 5.
(г) у
умножается на 5 и результат вычитается из 16
(ч) г
умножается на — 5 и результат прибавляется к 16
Ответ:
(а) 2 м
+ 11
(б) 2 м
− 11
(в) 5 у
+ 3
(г) 5 у
− 3
(д) —
8 г
(ф) —
8 и + 5
(г) 16 —
5 г
(ч) —
5 г + 16
Страница № 234:
Вопрос 6:
(a) Составьте выражения, используя t и 4. Используйте не более одного
Используйте не более одного
числовая операция. В каждом выражении должно быть t .
(b) Составьте выражения, используя y , 2 и 7. Каждое выражение должно
в нем есть и . Используйте только две числовые операции. Это должно быть
разные.
Ответ:
(а) т
+ 4, т — 4, 4 т ,
,
,
4 − т , 4 + т
(б) 2 у
+ 7, 2 г − 7, 7 г + 2,…
Страница № 235:
Вопрос 1:
Ответьте на следующие вопросы:
(a) Принять нынешний возраст Сариты за y лет
(i) Сколько ей будет лет через 5 лет?
(ii) Сколько ей было лет 3 года назад?
(iii) Дедушка Сариты в 6 раз старше ее.Сколько лет ее дедушке?
(iv) Бабушка на 2 года моложе дедушки. Какой возраст у бабушки?
(v) Возраст отца Сариты на 5 лет больше, чем возраст Сариты в 3 раза.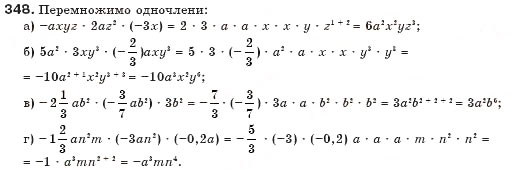 Сколько лет ее отцу?
Сколько лет ее отцу?
(b) Длина прямоугольного зала на 4 метра меньше ширины зала в 3 раза. Чему равна длина, если ширина х метров?
(c) Прямоугольный ящик имеет высоту х см. Его длина в 5 раз больше высоты, а ширина на 10 см меньше длины.Выразите длину и ширину коробки через высоту.
(d) Мина, Бина и Лина поднимаются по ступеням на вершину холма. Мина находится на шаге s , Бина на 8 шагов впереди, а Лина на 7 шагов позади. Где Бина и Мина? Общее количество шагов до вершины холма в 10 раз меньше, чем в 4 раза больше, чем Мина. Выразите общее количество шагов, используя s .
(e) Автобус проехал v км/ч. Он идет от Даспура до Биспура.После того, как автобус проехал 5 часов, Биспер все еще находится в 20 км. На каком расстоянии Даспур от Биспур? Выразите это, используя v .
Ответ:
(a) (i) Возраст Сариты через 5 лет = нынешний возраст Сариты + 5
= у + 5
(ii) 3 года назад, возраст Сариты = нынешний возраст Сариты − 3
= у — 3
(iii) Возраст дедушки = 6 × нынешний возраст Сариты = 6 y
(iv) Возраст бабушки = нынешний возраст дедушки − 2 = 6 y − 2
(v) Возраст отца = 5 + 3 × нынешний возраст Сариты = 5 + 3 y
(б) Длина = 3 × Ширина — 4
л = (3 б — 4) метра
(с) Длина = 5 × высота
л = 5 ч см
Ширина = 5 × Высота – 10
б = (5 ч — 10) см
(d) Шаг, на котором находится Бина = (Шаг, на котором находится Мина) + 8
= с + 8
Шаг, на котором находится Лина = (Шаг, на котором находится Мина) − 7
= с — 7
Всего шагов = 4 × (Шаг, на котором находится Мина) − 10 = 4 с − 10
(e) Скорость = v км/ч
Расстояние, пройденное за 5 часов = 5 × v = 5 v км
Общее расстояние между Даспуром и Биспуром = (5 v + 20) км
Видео Решение по алгебре (Страница: 235 , Q.
 №: 1)
№: 1)
Решение NCERT для 6 класса по математике и алгебре 235, вопрос 1
Страница № 236:
Вопрос 2:
Изменить
следующие операторы с использованием выражений в операторы в обычном
язык.
(Например, Дани Салим набирает х пробежек в матче по крикету,
Налин забивает
( р
+ 15) бежит.На обычном языке — Налин набирает на 15 очков больше
чем Салим.)
(а) Примечание
книга стоит рупий р. Книга стоит 3 рупий р.
(б) Тони
кладет на стол q шариков. У него 8 q шариков в его
коробка.
(с) Наш
в классе из учеников. В школе учатся 20 91 769 учеников.
(d) Джаггу из лет. Его дяде 4 z лет
а его тете (4 z − 3) лет.
(е) В
расположение точек r рядов. В каждом ряду по 5
точки.
Ответ:
(а) Книга
стоит в три раза дороже ноутбука.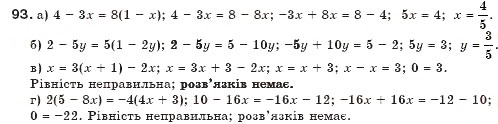
(б) Тони
в коробке в 8 раз больше шариков на столе.
(с) Итого
количество учеников в школе в 20 раз больше, чем в нашем классе.
(d) дядя Джаггу в 4 раза старше Джаггу и Джаггу
тетя на 3 года моложе дяди.
(е)
общее количество точек в 5 раз превышает количество строк.
Страница № 236:
Вопрос 3:
(а) Учитывая, что возраст Мунну составляет х лет, можете ли вы угадать, что
( x − 2) может показать?
(Подсказка: подумайте о младшем брате Манну.)
Угадайте, что ( x + 4) может показывать? Что (3 x + 7) может
показывать?
(b) Учитывая, что сегодня возраст Сары составляет и лет.Думай о ней
возраст в будущем или в прошлом.
Что будет означать следующее выражение?
(c) Учитывая, что n учеников в классе любят футбол, что может 2 n
показывать? Что может
показывать?
(Подсказка: подумайте о других играх, кроме футбола).
Ответ:
(a)( x − 2) означает, что человек, чей возраст
( x − 2) лет, на 2 года моложе Мунну.
( x + 4) означает, что человек, чей возраст составляет ( x +
4) лет, старше Мунну на 4 года.
(3 x + 7) означает, что человек, чей возраст составляет (3 x +
7) лет, старше Мунну и его возраст на 7 лет больше трех
времена эпохи Мунну.
(б) В
будущее
Через и лет возраст Сары будет ( г +
n ) лет.
В прошлом
n лет назад, возраст Сары был ( y − n )
годы.
( y + 7) означает, что человек в возрасте ( y +
7) лет, старше Сары на 7 лет.
( y − 3) означает, что человек в возрасте ( y
− 3) лет, младше Сары на 3 года.
( г +
)
означает, что человек в возрасте ( г +
)
лет, это
лет старше Сары.
( г — )
означает, что человек в возрасте ( y −
)
лет, это
лет моложе Сары.
(c) 2 n может означать количество студентов, которым нравится либо
футбол или какую-либо другую игру, например, крикет, тогда как
представляет собой количество студентов, которые любят крикет, из общего числа
количество студентов, которые любят футбол.
Страница № 240:
Вопрос 1:
Состояние
какие из следующих являются уравнениями (с переменной).Дайте повод
за ваш ответ. Определите переменную из уравнений с
Переменная.
(а) 17 = х
+ 7 (б) ( t − 7) > 5
(в) (г) (7
× 3) — 19 = 8
(д) 5 × 4 — 8 =
2 х (е) х — 2 = 0
(ж) 2 м < 30 (з) 2 n + 1 = 11
(i) 7 = (11 × 5) − (12
× 4) (к) 7 = (11 ×
2) + тел.
(л) 20 = 5 у (л)
(m) z + 12 > 24 (n) 20 — (10 — 5) = 3 ×
5
(п) 7 — х = 5
Ответ:
(а) Ан
уравнение с переменной x
(б) Ан
неравенство
(с) Нет, это
является числовым уравнением.
(г) Нет, это
является числовым уравнением.
(е) Ан
уравнение с переменной x
(е) Ан
уравнение с переменной x
(г) Ан
неравенство
(ч) Ан
уравнение с переменной n
(i) Нет, это
является числовым уравнением.
(к) Ан
уравнение с переменной p
(к) Ан
уравнение с переменной y
(л) Ан
неравенство
(м) Ан
неравенство
(сущ.) Нет, это
является числовым уравнением.
(о) Ан
уравнение с переменной x
Страница № 241:
Вопрос 2:
Заполните записи в третьем столбце таблицы.
|
С. № |
Уравнение |
Значение переменной |
Уравнение выполнено Да/Нет |
|
(а) |
10 у = 80 |
у = 10 |
— |
|
(б) |
10 у = 80 |
у = 8 |
— |
|
(с) |
10 у = 80 |
у = 5 |
— |
|
(г) |
4 л = 20 |
л = 20 |
— |
|
(е) |
4 л = 20 |
л = 80 |
— |
|
(ф) |
4 л = 20 |
л = 5 |
— |
|
(г) |
б + 5 = 9 |
б = 5 |
— |
|
(ч) |
б + 5 = 9 |
б = 9 |
— |
|
(и) |
б + 5 = 9 |
б = 4 |
— |
|
(ж) |
ч — 8 = 5 |
ч = 13 |
— |
|
(к) |
ч — 8 = 5 |
ч = 8 |
— |
|
(л) |
ч — 8 = 5 |
ч = 0 |
— |
|
(м) |
р + 3 = 1 |
р = 3 |
— |
|
(н) |
р + 3 = 1 |
р = 1 |
— |
|
(о) |
р + 3 = 1 |
р = 0 |
— |
|
(р) |
р + 3 = 1 |
P = − 1 |
— |
|
(к) |
р + 3 = 1 |
P = − 2 |
— |
Ответ:
(а) 10 у = 80
y = 10 не является решением данного уравнения, потому что для
г = 10,
10 у = 10 × 10 = 100, а не 80
(б) 10 у = 80
y = 8 является решением данного уравнения, потому что для y
= 8,
10 y = 10 × 8 = 80 и, следовательно, уравнение
довольный.
(в) 10 у = 80
y = 5 не является решением данного уравнения, потому что для y
= 5,
10 у = 10 × 5 = 50, а не 80
(г) 4 л = 20
l = 20 не является решением данного уравнения, так как для
л = 20,
4 л = 4×20 = 80, а не 20
(д) 4 л = 20
l = 80 не является решением данного уравнения, так как для
л = 80,
4 л = 4×80 = 320, а не 20
(е) 4 л = 20
l = 5 является решением данного уравнения, потому что для l
= 5,
4 l = 4 × 5 = 20 и, следовательно, уравнение выполняется.
(г) б + 5 = 9
b = 5 не является решением данного уравнения, потому что для b
= 5,
б + 5= 5 + 5 = 10, а не 9
(ч) б + 5 = 9
b = 9 не является решением данного уравнения, потому что для b
= 9,
б + 5 = 9 + 5 = 14, а не 9
(и) б + 5 = 9
b = 4 является решением данного уравнения, потому что для b
= 4,
b + 5= 4 + 5 = 9 и, следовательно, уравнение выполняется.
(к) ч — 8 = 5
ч = 13 является решением данного уравнения, потому что для ч
= 13,
ч — 8 = 13 — 8 = 5 и, следовательно, уравнение
довольный.
(к) ч — 8 = 5
ч = 8 не является решением данного уравнения, потому что для ч
= 8,
ч — 8 = 8 — 8 = 0, а не 5
(л) ч — 8 = 5
ч = 0 не является решением данного уравнения, потому что для ч
= 0,
ч — 8 = 0 — 8 = -8, а не 5
(м) р + 3 = 1
p = 3 не является решением данного уравнения, потому что для p
= 3,
р + 3= 3 + 3 = 6, а не 1
(н) р + 3 = 1
p = 1 не является решением данного уравнения, потому что для p
= 1,
р + 3= 1 + 3 = 4, а не 1
(о) р + 3 = 1
p = 0 не является решением данного уравнения, потому что для p
= 0,
р + 3= 0 + 3 = 3, а не 1
(р) р + 3 = 1
p = −1 не является решением данного уравнения
потому что для p = −1,
р + 3= -1 + 3 = 2, а не 1
(к) р + 3 = 1
p = −2 является решением данного уравнения, потому что
для р = -2,
p + 3= — 2 + 3 = 1 и, следовательно, уравнение
довольный.
Страница № 241:
Вопрос 3:
выбрать
решение из значений, указанных в скобках рядом с каждым
уравнение. Покажите, что другие значения не удовлетворяют уравнению.
(а) 5 м
= 60 (10, 5, 12, 15)
(б) n
+ 12 = 20 (12, 8, 20, 0)
(в) р
− 5 = 5 (0, 10, 5 − 5)
(г) (7,
2, 10, 14)
(д) р
− 4 = 0 (4, − 4, 8, 0)
(е) x +
4 = 2 (− 2, 0, 2, 4)
Ответ:
(а) 5 м
= 60
м = 12 является решением данного уравнения, потому что для м
= 12,
5 м = 5 × 12 = 60 и, следовательно, уравнение выполняется.
м = 10 не является решением данного уравнения, потому что для м
= 10,
5 м = 5×10 = 50, а не 60
м = 5 не является решением данного уравнения, потому что для м
= 5,
5 м = 5×5 = 25, а не 60
м = 15 не является решением данного уравнения, потому что для м
= 15,
5 м = 5×15 = 75, а не 60
(б) н +
12 = 20
n = 8 является решением данного уравнения, потому что для n
= 8,
n + 12 = 8 + 12 = 20 и, следовательно, уравнение выполняется.
n = 12 не является решением данного уравнения, так как для n
= 12,
n + 12 = 12 + 12 = 24, а не 20
n = 20 не является решением данного уравнения, так как для n
= 20,
n + 12 = 20 + 12 = 32, а не 20
n = 0 не является решением данного уравнения, так как для n
= 0,
n + 12 = 0 + 12 = 12, а не 20
(в) р
− 5 = 5
p = 10 является решением данного уравнения, потому что для p
= 10,
p — 5 = 10 — 5 = 5 и, следовательно, уравнение
довольный.
p = 0 не является решением данного уравнения, так как для p
= 0,
p − 5 = 0 − 5 = −5, а не 5
p = 5 не является решением данного уравнения, так как для p
= 5,
р — 5 = 5 — 5 = 0, а не 5
p = −5 не является решением данного уравнения, потому что
для р = -5,
р — 5 = — 5 — 5 = -10, а не 5
(д)
q = 14 является решением данного уравнения, потому что для q
= 14,
и
следовательно, уравнение выполняется.
q = 7 не является решением данного уравнения, потому что для q
= 7,
,
а не 7
q = 2 не является решением данного уравнения, потому что для q
= 2,
,
а не 7
q = 10 не является решением данного уравнения, потому что для q
= 10,
,
а не 7
(д) р —
4 = 0
r = 4 является решением данного уравнения, так как для r
= 4,
r — 4 = 4 — 4 = 0 и, следовательно, уравнение
довольный.
r = −4 не является решением данного уравнения, потому что
для г = -4,
r — 4 = — 4 — 4 = -8, а не 0
r = 8 не является решением данного уравнения, так как для r
= 8,
r − 4 = 8 − 4 = 4, а не 0
r = 0 не является решением данного уравнения, так как для r
= 0,
r − 4 = 0 − 4 = −4, а не 0
(е) x
+ 4 = 2
x = −2 является решением данного уравнения, потому что для x
= −2,
x + 4 = — 2 + 4 = 2 и, следовательно, уравнение
довольный.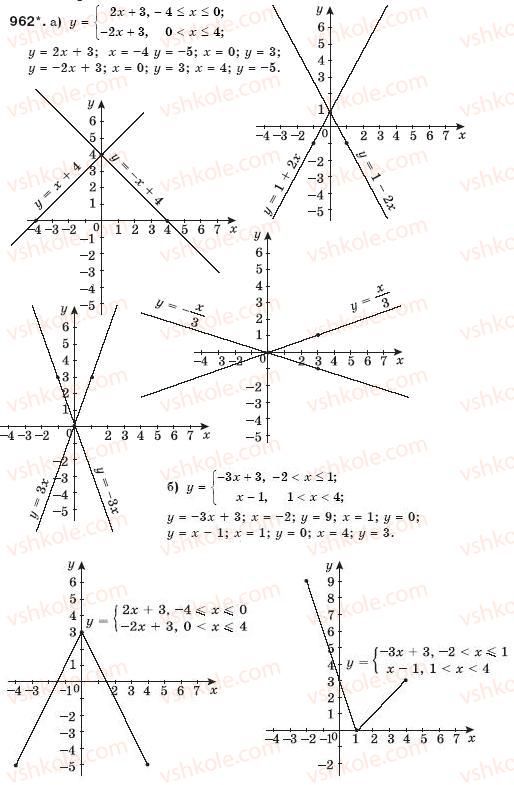
х = 0 не является решением данного уравнения, потому что для х
= 0,
х + 4 = 0 + 4 = 4, а не 2
х = 2 не является решением данного уравнения, потому что для х
= 2,
х + 4 = 2 + 4 = 6, а не 2
х = 4 не является решением данного уравнения, потому что для х
= 4,
х + 4 = 4 + 4 = 8, а не 2
Страница № 241:
Вопрос 4:
а) Заполните таблицу и, просмотрев таблицу, найдите
решение уравнения м + 10 = 16.
-
м
1
2
3
4
5
6
7
8
9
10
…
м + 10
−
−
−
−
−
−
−
−
−
−
−
(b) Заполните таблицу и, просмотрев таблицу, найдите
решение уравнения 5 t = 35.
-
т
3
4
5
6
7
8
9
10
11
…
5 т
−
−
−
−
−
−
−
−
−
−
в) Заполните таблицу и найдите решение уравнения z/3 = 4
с помощью таблицы.
-
з
8
9
10
11
12
13
14
15
16
…
3
−
−
−
−
−
−
−
(г) Полный
таблицу и найдите решение уравнения m − 7 =
3
-
м
5
6
7
8
9
10
11
12
13
…
м − 7
−
−
−
−
−
−
−
−
−
−
Ответ:
(а) Для м
+ 10, таблица может быть построена следующим образом.
-
м
м +
101
1 + 10 = 11
2
2 + 10 = 12
3
3 + 10 = 13
4
4 + 10 = 14
5
5 + 10 = 15
6
6 + 10 = 16
7
7 + 10 = 17
8
8 + 10 = 18
9
9 + 10 = 19
10
10 + 10 = 20
Проверив, мы можем найти, что м = 6 является решением задачи.
уравнение выше для м = 6, м + 10 = 6 + 10 = 16
(б) Для
5 t таблица может быть построена следующим образом.
-
т
5т
3
5 × 3 = 15
4
5 × 4 = 20
5
5 × 5 = 25
6
5 × 6 = 30
7
5 × 7 = 35
8
5 × 8 = 40
9
5 × 9 = 45
10
5 × 10 = 50
11
5 × 11 = 55
Проверив, мы можем найти, что t = 7 является решением уравнения
приведенное выше уравнение для t = 7, 5 t = 5 × 7 = 35
(с) Для
,
таблицу можно построить следующим образом.
-
с
8
9
10
11
12
13
14
15
16
Проверив, мы можем найти, что z = 12 является решением задачи.
приведенное выше уравнение для z = 12,
= 4
(г) Для м
− 7, таблица может быть построена следующим образом.
-
м
м −
75
5 — 7 = — 2
6
6 — 7 = — 1
7
7 — 7 = 0
8
8 — 7 = 1
9
9 — 7 = 2
10
10 − 7 = 3
11
11 − 7 = 4
12
12 — 7 = 5
13
13 − 7 = 6
Проверив, мы можем найти, что м = 10 является решением задачи.
приведенное выше уравнение для м = 10, м — 7 = 10 —
7 = 3
Страница № 242:
Вопрос 5:
Решите следующие загадки, вы можете сами составить такие загадки.
Кто я?
(i) Обойти квадрат
Считая каждый угол
Трижды и не более!
Добавь мне счет
Чтобы получилось ровно тридцать четыре!
(ii) За каждый день недели
Сделайте от меня доплату
Если не ошибетесь
Вы получите двадцать три!
(iii) Я особый номер
Забери у меня шестерку!
Целая команда по крикету
Вы еще сможете починить!
(iv) Скажи мне, кто я
Я дам подсказку!
Ты вернешь меня
Если ты вытащишь меня из двадцати двух!
Ответ:
(i)В квадрате 4 угла.
Тройное количество углов в квадрате будет 3 × 4 = 12
Когда этот результат, т. е. 12, прибавляется к числу, получается 34. Следовательно, число будет разностью 34 и 12, т. е. 34 − 12 = 22
(ii) 23 было результатом, когда старое число было пересчитано в воскресенье.
22 было результатом, когда старое число было подсчитано в субботу.
21 было результатом, когда старое число было пересчитано в пятницу.
20 было результатом пересчета старого числа в четверг.
19 было результатом, когда старое число было пересчитано в среду.
18 было результатом подсчета старого числа во вторник.
17 было результатом подсчета старого числа в понедельник.
Следовательно, число, взятое в начале = 17 − 1 = 16
(iii) В крикетной команде 11 игроков. Следовательно, число таково, что при вычитании из него 6 получается 11. Следовательно, число 11 + 6 = 17
(iv) Число таково, что при вычитании его из 22 получается снова само число.Число 11, что снова дает 11, если вычесть его из 22.
Видеорешение по алгебре (Страница: 242 , Q.No.: 5)
Решение NCERT для 6 класса по математике и алгебре 242, вопрос 5
Посмотреть решения NCERT для всех глав класса 6
Глава 11 Алгебра Класс 6 Примечания Математика
Вы можете найти Примечания к пересмотру для Класса 6 Математика Глава 11 Алгебра здесь, что очень полезно для понимания важных моментов и формул, приведенных в главе.Это будет полезно при разработке техник и методов для эффективного понимания главы. Решения NCERT для класса 6 Глава 11 Математика будет полезна для улучшения оценок на экзаменах. С помощью этих заметок о пересмотре 6 класса учащийся может улучшить свою подготовку и оценку понятых понятий. Это сделает весь процесс запоминания легким и интересным.
Алгебра
• Алгебра — это обобщенная арифметика, в которой числа представлены буквами, известные как буквальное число простых литералов.
Переменная
• Символ, имеющий фиксированное числовое значение, называется константой. Символ, который принимает различные числовые значения, называется переменной.
• Слово «переменная» означает нечто, что может изменяться, т. е. изменяться.
• Значение переменной не является фиксированным. Длина квадрата может иметь любое значение. Но количество углов треугольника имеет фиксированное значение 3.
• Мы используем переменную для представления числа и обозначаем его любой буквой, такой как l, m, n, p, x, y, z и т. д.
• Переменные позволяют выражать многие общие правила как геометрии, так и арифметики в общем виде.
Использование переменных в общих правилах
Правила геометрии
• Периметр квадрата = сумма длин сторон квадрата = 4-кратная длина стороны квадрата
= 41
Здесь использование переменной l позволяет нам записать общее правило лаконично и легко для запоминания.
• Периметр прямоугольника = сумма длин его четырех сторон = длина + ширина + длина + ширина = 2(длина + ширина) = 2(l+b)
Здесь и l, и b являются переменными, которые принимают на значениях, независимых друг от друга.
Правила арифметики
• Коммутативность сложения чисел: Коммутация (перестановка) порядка чисел дополнительно не меняет суммы.
a + b = b + a
• Коммутативность умножения: изменение порядка чисел при умножении не меняет произведение.
a×b = b×a
Выражения с переменными
• : Комбинация констант и переменных, соединенных одним или несколькими символами
+, –, × и ÷, называется алгебраическим выражением.
• Несколько частей выражения, разделенных знаком + или –, называются членами выражения.
• Уравнение – это алгебраическое выражение с переменной константой и знаком равенства (=). Например, число x, увеличенное на 9, равно 18. x + 9 = 18.
Решение уравнения
Значение переменной в уравнении, которое удовлетворяет уравнению. Для получения решения уравнения одним из методов является метод проб и ошибок.В этом методе мы присваиваем переменной какое-то значение и проверяем, удовлетворяет ли оно уравнению. Таким образом, мы продолжаем присваивать переменной различные значения, пока не найдем правильное значение, удовлетворяющее уравнению.
Tamil Nadu Board Samacheer Kalvi Solutions for Class 11th Mathematics Volume 1 and 2 Ответы на вопросы глава 2 — Базовая алгебра [Последнее издание]
Tamil Nadu Board Samacheer Kalvi Solutions для 11-го класса Mathematics Volume 1 and 2 Ответы на вопросы глава 2 — Базовая алгебра
Tamil Nadu Board Решения Samacheer Kalvi для 11-го класса Математика, том 1 и 2 Руководство по ответам, глава 2 (Основная алгебра) включает все вопросы с решением и подробным объяснением.Это избавит студентов от сомнений по любому вопросу и улучшит навыки применения при подготовке к экзаменам. Подробные пошаговые решения помогут вам лучше понять концепции и устранить путаницу, если таковая имеется.
На сайте Shaalaa.com есть решения Совета по среднему образованию штата Тамил Наду для 11-го класса математики, тома 1 и 2, ответы на вопросы, которые помогают учащимся лучше и быстрее понять основные понятия.
Кроме того, мы в Shaalaa.com предоставляем такие решения, чтобы студенты могли подготовиться к письменным экзаменам.Решения для учебников Tamil Nadu Board Samacheer Kalvi могут стать основной помощью для самостоятельного обучения и идеальным руководством для самопомощи для студентов.
Понятия, изложенные в Руководстве по математике для 11-го класса, том 1 и 2, глава 2. Основы алгебры: Введение в базовую алгебру, Система действительных чисел, Абсолютное значение, Линейные неравенства, Квадратичные функции, Полиномиальные функции, Рациональные функции, Экспоненты и радикалы, Логарифмы, Применение Алгебра в реальной жизни.
Использование Tamil Nadu Board Решения Samacheer Kalvi Class 11th Упражнения по базовой алгебре для учащихся — это простой способ подготовиться к экзаменам, поскольку они включают в себя решения, расположенные по главам и по страницам.Вопросы, связанные с советом Samacheer Kalvi Solutions в Тамил Наду, являются важными вопросами.
которые можно задать на выпускном экзамене. Максимум учащиеся 11-го класса Совета среднего образования штата Тамил Наду предпочитают Samacheer Kalvi Textbook Solutions Совета Тамил Наду, чтобы набрать больше баллов на экзамене.
Получите бесплатный просмотр главы 2 Основы алгебры для 11-го класса, дополнительные вопросы для 11-го класса по математике, тома 1 и 2. Руководство по ответам и можете использовать Shaalaa.com, чтобы держать его под рукой при подготовке к экзамену
.